GIS-8 第九章 DTM与地形分析
第9章-数字地形模型与地形分析-第一讲

▪ DEM数据的高程分层设色显示 ▪ DEM数据与影像数据联结三维场景显示 ▪ 三维静态场景的输出功能 ▪ 三维动态飞行场景的录制与播放功能 ▪ 简单DEM模型分析功能
GIS 电子沙盘 ——高程分层设色
GIS DEM应用举例 ——城市景观
城市景观系统通过运用数字技术构造出某一区域的 虚拟场景来辅助人们进行观测, 是一个可视现实和虚拟 现实集成的系统。
垂直线 典型线
山脊线 谷底线 海岸线 坡度变换线
GIS 3.DEM的表示法
数学方法 整体拟合方法, 即根据区域所有的高程点
数据, 用傅立叶级数和高次多项式拟合统 一的地面高程曲面 局部拟合方法, 将地表复杂表面分成正方 形规则区域或面积大致相等的不规则区 域进行分块搜索, 根据有限个点进行拟合 形成高程曲面
➢DEM的表示方法
➢一个地区的地表 高程的变化可以
采用多种方法表
达
DEM 表示方法
➢用数学定义的表 面或点、线、影 像都可用来表示 DEM
数学方法 图形法
整体 局部 点数据
线数据
傅立叶级数 高次多项式
规则数学分块
不规则数学分块
密度一致
规则
密度不一致
不规则 典型特征 水平线
三角网 邻近网 山峰、洼坑
隘口、边界
点信息
ID
边1 边2 边3
1
E1
E3
E9
2
E2
E3
E4 面
3
E4
E5
E6
信 息
4
E6
E7
E8
5
E7
E9
E10
ID
起点
终点
左多 边形
右多 边形
GIS地形分析方法步骤

G I S地形分析方法步骤-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN一.做地形分析:等高线必须是有高程的才行。
但是很多情况下地形图中的地形线都没有高程,那就需要在香源中进行转换,步骤如下:1. 地形工具---字转高程---然后框选地形图中的所有高程数据,回车;2. 地形工具---地表分析---三角剖分—回车后会生成三角网格线(红色的线条);3. 地形工具---地表分析---等高线图—根据地形和高差大小选择等高线高程间距;4. 将生成好的等高线用原基点复制粘贴命令重新保存个只有一个等高线图层的CAD文件。
备注:如果向前面提到的:等高线有高程的话,也需要1.2.3.的操作生成等高线后,用香源的默认等高线图层将原地向等高线刷下(因为香源生的等高线不圆滑,后面的效果就不好看了;如果原来等高线有高程那么直接刷下图层就好,这样的等高线圆滑些。
)GIS文件不能移动,否则就打不开了。
所以之前就把文件都固定在一个地方。
二. 打开MapInfo Professional 9.0,页面如下:1.点:Tools 工具栏——Universal Translator——Universal Translator,出现如下对话框:2. 下面要进行2次格式转换:一是DWG文件转成TAB文件如图:二是TAB文件转成Shape(也就是GIS的文件了)文件如图:转换完成。
三. 打开GIS (其中还要装个附带软件:ArcView_3D_Analyst_1.0)1. 工具栏:file——extensions——选择3D Analyst ——OK!2. 工具栏:View——Add Theme 出现对话框选择文件;3. 工具栏:Surface——Create TIN from Features出现对话框,直接OK,——出现Output TIN Name 保存文件的对话框;选择文件保存(保存的文件不可移动,否则打不开)。
MAPGIS平台解决方案之DTM分析篇
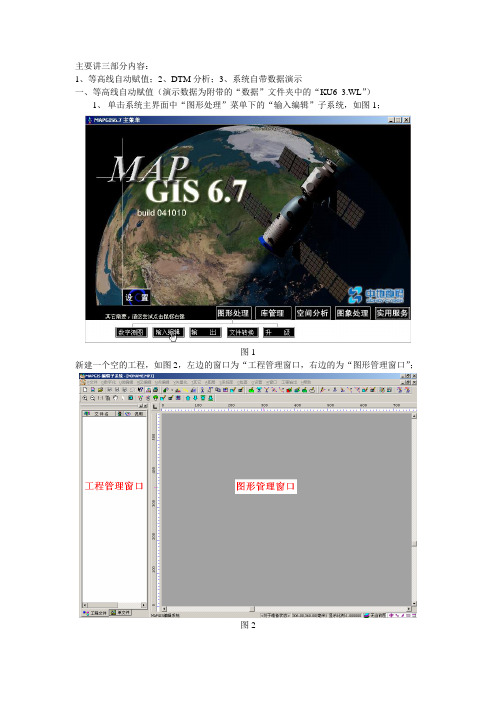
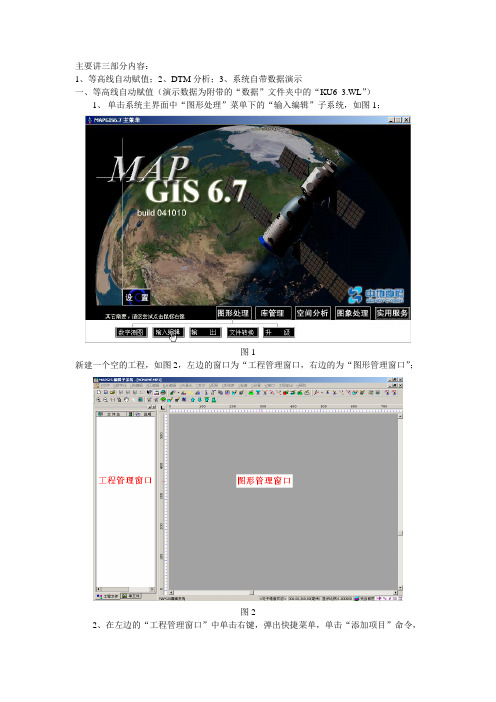
主要讲三部分内容:1、等高线自动赋值;2、DTM分析;3、系统自带数据演示一、等高线自动赋值(演示数据为附带的“数据”文件夹中的“KU6_3.WL”)1、单击系统主界面中“图形处理”菜单下的“输入编辑”子系统,如图1;图1新建一个空的工程,如图2,左边的窗口为“工程管理窗口,右边的为“图形管理窗口”;图22、在左边的“工程管理窗口”中单击右键,弹出快捷菜单,单击“添加项目”命令,如图3;图3则系统弹出对话框,选择演示数据“KU6_3.WL”,如图4;图4然后单击“打开”按钮,将“KU6_3.WL”线文件装入当前的工程中,如图5;3、单击“线编辑”菜单下“参数编辑”命令中的“编辑线属性结构”命令,如图6;图6则系统弹出“编辑属性结构”对话框,给“KU6_3.WL”线文件添加一“高程”属性字段,如图7;图74、单击“矢量化”菜单下的“高程自动赋值”命令,如图8;图8然后将鼠标放在等高线的中央,按住左键拖动,如图9所示;图9然后再次单击左键,则系统会弹出“高程增量设置”对话框,假设当前的高程值为1000,高程距为-10(可以知道这个生成的地形应该为一山峰),如图10;然后单击“确定”按钮,即可实现等高线自动赋值,结果如图11;图11剩余部分的等高线(即上图中黑色的等高线)赋值的方法如下:先通过查询属性,查询如图中红色所示的线的高程值,知道为680,如图12;图12则其左侧的线就可以推断出其当前的高程值为670,所以通过“矢量化”菜单下的“高程自动赋值”命令,即可实现左侧部分的等高线赋值情况,如图13;赋值后的结果如图14;图14剩下的部分依照类似的方法,实现等高线自动赋值;这时每个等高线就都具备了高程值,可以通过查阅线的属性来查看,如果个别线没有高程值,则可以手工输入正确的值即可;最后要记得保存赋值后的等高线文件;二、DTM分析1、单击系统主界面中“空间分析”菜单下的“DTM分析”子系统,如图15;图15系统弹出DTM分析子系统,如图16;图162、单击“文件”菜单下的“打开数据文件/线数据文件”命令,如图17;图17则系统弹出打开文件对话框,找到等高线赋值后的文件“KU6_3.WL”,如图18;图18然后单击“打开”按钮,将“KU6_3.WL”打开,结果如图19;3、单击“处理点线”菜单下的“线数据高程点提取”命令,如图21;则系统弹出“设置线抽稀点参数”对话框,如图22;图22其中,“抽稀提点”参数越小,则在等高线上提取的高程点就会越多,则后面生成的GRD 数据的精度就会越高,则生成三维地形后,对实际的地形拟合也就越精确;需注意的是“线属性高程数据域”要选择高程值所在的字段;设置好各项参数后,单击“确定”按钮,提点后的结果如图23;图234、单击“GRD模型”菜单下的“离散数据网格化”命令,如图24;图24系统弹出“离散数据网格化”对话框,如图25图25然后单击对话框中的“文件换名”按钮,系统会弹出一保存文件的对话框,如图26;单击“保存”按钮,则生成的文件的路径就会在对话框的底部显示出来,如图27;然后单击“确定”按钮,即可生成GRD数据;5、单击“文件”菜单下的“打开三角剖分文件”命令,如图28;图28系统弹出打开文件对话框,如图29;图29选中上一步生成的“TmpGrid.GRD”,单击“打开”按钮,结果如图30;图306、接下来,有四条独立的途径可以走,分别如下:①、格网立体图绘制:单击“Grd模型”菜单下的“格网立体图绘制”命令,如图31;图31系统弹出如下对话框,如图32:图32单击“确定”按钮即可,生成的结果图,如图33;图33这里结果是点、线、面文件,可以保存修改并打印输出,保存后关闭结果;②、平面等值线图的绘制:单击“Grd模型”菜单下的“平面等值线图的绘制”命令,如图34;则系统会弹出“设置等值线参数”对话框,如图35;图35下面一次来说明上图35中标注的7个地方的作用:在图35中,将标注为“1”处的“等值线套区”打“√”,将标注为“4”处的“等值线光滑处理”打“√”,并将光滑度选择为“高程度”;在图35中,单击标注为“2”处的“等值层值”按钮,系统会弹出一对话框,如图36;图36这里我们可以修改高程值之间的间隔,比如将上图中的“步长增”改为20,这是要单击“更新当前分段”按钮,否则修改无效,然后单击“确定”按钮;在图35中,单击标注为“3”处的“线参数”按钮,系统将弹出修改线参数对话框,以供我们修改结果文件的线型,如图37;图37在图35中,双击标注“6”处的颜色,系统弹出颜色表,如图38,以供我们修改相应等高线的颜色,不过一般情况下默认就可以了;图38在图35中,双击标注“7”处的“Y es”或“No”,来决定是否将对应该等高线的高程值标注出来;在图35中,将标注“5”处的“制图幅面”改为“原始数据范围”;最后单击图35中的“确定”按钮,即可生成等值线图,结果如图39,保存后关闭结果;图39③、彩色等值立体图绘制:单击“Grd模型”下的“彩色等值立体图绘制”,如图40;系统弹出参数设置对话框,如图41;单击“等值图参数设置”按钮,则系统有弹出一对话框,如图42;图42在“等值线套区”前打“√”,单击“确定”按钮,返回图41所示的对话框,并单击该对话框中的“确认”按钮,则生成结果文件,如图43,保存后关闭结果;图43④、单击“窗口”菜单下的“新建三维窗口”,如图44;图44则系统会直接生成三维的立体模型,如图45;图45然后在当前窗口里,单击右键,在弹出的快捷菜单中选择“图形旋转”,如图46,可以实现绕X、Y、Z轴选择立体模型;而且还可以实现三维模型的漫游飞行;图46三、系统自带演示数据(安装MAPGIS时,将所有的选项都选中,则在MAPGIS的安装文件夹下“D:\mapgis67\sample\image\flydata”会有该演示数据)1、打开DTM分析子系统,如图16;2、单击“文件”菜单下的“打开三角剖分文件”,打开“数据”文件夹下的“Fly.grd”数据,如图47;图473、单击“窗口”下的“新建三维窗口”命令,则在该数据的基础上,系统会自动生成三维立体模型,如图48;图48同理,在当前窗口里,单击右键,在弹出的快捷菜单中选择“图形旋转”,可以实现绕X、Y、Z轴选择立体模型;而且还可以实现三维模型的漫游飞行;4、单击“数据”菜单下的“装入纹理文件”,如图49;图49则系统弹出打开文件对话框,如图50,找到“数据”文件夹下的“rgbfly.msi”文件(该文件为此三维模型区域对应的遥感影像),并单击打开;图50则系统弹出“纹理参数设置”对话框,如图51,纹理象素格式任选一种即可,单击“确定”按钮,则最终三维结果如图52所示,实现了三维地形模型和相应地区遥感影像的叠加显示;图51三维模型绕X轴旋转效果:三维模型绕Y轴旋转效果:三维模型绕Z轴旋转效果:单击右键快捷菜单中的“自动飞行”(也可以在电子沙盘中来实现上述效果):。
GIS中的数据分析

二、GIS中的数据分析第1节空间数据分析地理信息系统(GIS)与普通的计算机辅助制图(CAM / CAD)系统的主要区别在于GIS具有空间数据的分析、变换能力。
除一些基本的变换功能如数据更新、比例尺变换,投影变换外.主要的空间分析和变换功能为地理数据的拓扑和空间状况运算,属性综合运算,几何要素与属性的联合运算等。
为了完成这些运算,GIS 普通都以用户和系统交互的形式提供以上分析处理能力。
应指出,栅格数据结构与矢量数据结构的空间分析方法有所不同。
普通来说,栅格结构组织数据的空间分析方法要简单一些。
下图以分级结构形式概括的各种空间分析类型和方法:r -數据变换——柵格矢最豆换-图形分折一喪转,锹影变换、比例尺变换G1S 唯何分析-- I -- '.丄维显示一一逻辑/数学长算 一-或者分类「単变量分级分析 L 多变量统计分析I 一地形分析一]一空冋内插分析 卜坡度、坡向金析 卜地形剖面分析 卜三维地形显示 L 流域,打水雄分析图:GIS 空间分析方法一、综合属性数据分析GIS 中属性数据普通采用关系型数据库管理,因此,关系数据库 中各种分析功能都可以对属性性数据进行分析。
(一)数学计算属性数据中的数字型数据可以进行“加” “减” “乘” “除” “乘方”等数学运算,以产生新的属性值,如人口数/图斑面积(km ) =人口密度。
(二)逻辑运算逻辑运算的基本原理是布尔代数,这种逻辑分析几乎可以在所有 的空间分析中得到应用。
它按属性数据的组合条件来检索其他属性项 目或者图形数据,以及进行空间聚类.-辱性分析一彫像分析一「增受分析类分析(数字图橡处理内容)|-多元信息叠合分析L 滤波分析 L-拓扑与届性联合分斬 代化藉径分析 一时间和距寓计算 一网流量的摹拟分析 一致推检索 一曜冲区分折一疊密分析L 网绻分析 」开窗分析者分析 多边形廉置 得裕裁据叠置(三)单变量分级分析属性的单变量分级分析是把单个属性作为变量,依据布尔逻辑方法分成若干个类别。
MAPGIS平台解决方案之DTM分析篇
在“等值线套区”前打“√”,单击“确定”按钮,返回图35所示的对话框,并单击该对话框中的“确认”按钮,则生成结果文件,如图37,保存后关闭结果;
图37
3、单击“窗口”菜单下的“新建三维窗口”,如图38;
图38
则系统会直接生成三维的立体模型,如图39;
图39
然后在当前窗口里,单击右键,在弹出的快捷菜单中选择“图形旋转”,如图40,可以实现绕X、Y、Z轴选择立体模型;
主要讲三部分内容:
1、等高线自动赋值;2、DTM分析;3、系统自带数据演示
一、等高线自动赋值(演示数据为附带的“数据”文件夹中的“KU6_3.WL”)
1、单击系统主界面中“图形处理”菜单下的“输入编辑”子系统,如图1;
图1
新建一个空的工程,如图2,左边的窗口为“工程管理窗口,右边的为“图形管理窗口”;
图32
单击“确定”按钮即可,生成的结果图,如图33;
图33
这里结果是点、线、面文件,可以保存修改并打印输出,保存后关闭结果;
2、彩色等值立体图绘制:单击“Grd模型”下的“彩色等值立体图绘制”,如图34;
图34
系统弹出参数设置对话框,如图35;
图35
单击“等值图参数设置”按钮,则系统有弹出一对话框,如图36;
图6
则系统弹出“编辑属性结构”对话框,给“KU6_3.WL”线文件添加一“高程”属性字段,如图7;
图7
4、单击“矢量化”菜单下的“高程自动赋值”命令,如图8;
图8
然后将鼠标放在等高线的中央,按住左键拖动,如图9所示;
图9
然后再次单击左键,则系统会弹出“高程增量设置”对话框,假设当前的高程值为1000,高程距为-10(可以知道这个生成的地形应该为一山峰),如图10;
GIS原理——数字地形模型(DTM)与地形分析

是反映地表的起伏变化和侵蚀程度的指标,一般定义为地表单元 的曲面面积与其水平面上的投影面积之比。
Grid DEM上制作坡度、坡向图
(二)等高线的绘制
在格网DEM上自动绘制等高线主要包括两个步骤: 1、等高线追踪,利用DEM矩形格网点的高程内插出格网边上的等 高线点,并将这些等高线点排序; 2、等高线光滑,进一步加密等高线点并绘制光滑曲线。
此外,从DEM还能派生以下主要产品:平面等高线图、立体等高线图、 等坡度图、晕渲图、通视图、纵横断面图、三维立体透视图、三维立体彩色 图等。
二、DEM建立
1、数据获取与处理 1)数据采集
选点采集 沿断面采集
2) 数据处理
2、DEM 生成
1)人工网格法
在地形图上蒙上格网,逐 格读取中心点或交点的高程 值。
2)三角网法
对有限个离散点,每三个邻近点 联结成三角形,每个三角形代表一个 局部平面,再根据每个平面方程,可 计算各格网点高程,生成DEM。
2、D3E)M曲生面成拟合法
根据有限个离散点的高程,采用多项式或样条函数求 得拟合公式,再逐个计算各点的高程,得到拟合的DEM。 可反映总的地势,但局部误差较大。
DTM:当z为其他二维表面上连续变化的地理特征,如地 面温度、降雨、地球磁力、重力、土地利用、土壤类型等 其他地面诸特征,此时的DEM成为DTM(Digital Terrain Models)。
一、DEM 概述
2、表示法
1) 等高线法
等高线通常被存储成一个有序的坐标点 序列,可以认为是一条带有高程值属性的简 单多边形或多边形弧段。由于等高线模型只 是表达了区域的部分高程值,往往需要一种 插值方法来计算落在等高线以外的其他点的 高程。
浅谈GIS地形分析

浅谈GIS地形分析GIS地形分析是指利用地理信息系统(GIS)技术对地球上的地理现象进行分析和处理,进而获得地形特征、地形变化及其相关信息的过程。
GIS地形分析在地质学、地理学、环境科学以及城市规划等领域具有重要的应用价值。
本文将从GIS地形分析的概念、方法和实际应用等方面进行探讨。
GIS地形分析的概念主要包括地形特征、地形变化和地形相关信息三个方面。
地形特征是指地球表面的高程、坡度、曲率等特征,地形变化是指地形特征随时间和空间的演变,地形相关信息是指地形特征对其他地理现象的影响和与之相关的属性信息。
通过对这些地形信息的分析,可以获取到地表特征的空间分布、变化趋势以及其与其他地理现象之间的关联。
在GIS地形分析中,最基础的方法是数字地形模型(DTM)的构建。
DTM是利用高程数据来描述地面的数字模型,一般包括数字高程模型(DEM)和数字地面模型(DSM)两种。
DEM用来表示地表的高程信息,DSM则包括地表物体(如建筑物、树木等)的高程信息。
基于DTM数据,可以计算获取到地形特征,如坡度、坡向、高程曲率等。
地形分析的核心方法之一是剖面分析。
剖面分析可以通过提取地表特征的沿线剖面数据,来获取该区域的地形横截面信息。
通过剖面分析,可以了解地表的地势变化情况,包括山脉、河流等地貌特征。
另外,剖面分析也可以用来解决地质勘探中的问题,如确定地下岩层的结构和分布等。
此外,GIS地形分析还包括可视化、地形分类、地表流、视域分析等方法。
其中,可视化是将地表特征以图形形式展现出来,使人们更直观地了解地形特征。
地表流分析是通过模拟雨水流动,来研究地表的水文过程,包括河流的形成、径流的方向等。
视域分析则是通过模拟地表的可见性,来分析地表的视野范围,对于建筑物的选址和遮挡物的分析具有重要意义。
GIS地形分析在很多领域都有广泛的应用。
在城市规划中,可以利用GIS地形分析技术进行地形脆弱性评估,为城市规划和设计提供依据。
在环境科学中,通过对地形特征的分析,可以研究土壤侵蚀、洪水灾害等地表过程,为环境保护和自然灾害风险管理提供支持。
数字地形模型(DTM)与地形分析.PPT文档共54页

61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
数字地形模型(DTM)与地形分析.
1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律,就难以成功。
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸 美纽斯
5、教导儿童服从真理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
谢谢!
第八章 DEM分析

4、DEM应用
1)作为国家地理信息的基础数据; 2)土木工程、景观建筑与矿山工程规划与设计; 3)为军事目的而进行的三维显示; 4)景观设计与城市规划; 5)流水线分析、可视性分析; 6)交通路线的规划与大坝选址; 7)不同地表的统计分析与比较; 8)生成坡度图、坡向图、剖面图、辅助地貌分析、估计侵蚀和径流等; 9)作为背景叠加各种专题信息如土壤、土地利用及植被覆盖数据等,以 进行显示与分析; 10)与GIS联合进行空间分析; 11)虚拟现实(Virtual Reality);
在计算出各地表单元的坡度后,可对不同的坡度设定不同的灰度 级,可得到坡度图。
2、坡向
坡向是地表单元的法向量在水平面上的投影与X轴之间的夹角,
在计算出每个地表单元的坡向后,可制作坡向图,通常把坡向分为东、 南、西、北、东北、西北、东南、西南8类,再加上平地,共9类,用 不同的色彩显示,即可得到坡向图。
2)三角网法
对有限个离散点,每三个邻近点 联结成三角形,每个三角形代表一个 局部平面,再根据每个平面方程,可 计算各格网点高程,生成DEM。
2、DEM 生成 3)曲面拟合法
根据有限个离散点的高程,采用多项式或样条函数求 得拟合公式,再逐个计算各点的高程,得到拟合的DEM。 可反映总的地势,但局部误差较大。
(三)基于DEM的可视化分析
1、剖面分析
1)意义:
常常可以以线代面,研究区域的地貌形态、轮廓形状、 地势变化、地质构造、斜坡特征、地表切割强度等。
如果在地形剖面上叠加其它地理变量,例如坡度、土 壤、植被、土地利用现状等,可以提供土地利用规划、工 程选线和选址等的决策依据。
GIS课件第9章 DEM与数字地形分析

第9章 DEM 与数字地形分析数字地面模型于1958年提出,特别是基于DEM 的GIS 空间分析方法的出现,使传统的地形分析方法产生了革命性的变化,数字地形分析方法逐步形成和完善。
目前,基于DEM 的数字地形分析已经成为GIS 空间分析中最具特色的部分,在测绘、遥感及资源调查、环境保护、城市规划、灾害防治及地学研究各方面发挥越来越重要的作用。
本章首先介绍了数字高程模型的基本概念和建立步骤,然后从基本坡面因子、特征地形因子、水文因子和可视域等方面简述数字地形分析的主要内容和研究方法。
9.1 基本概念9.1.1 数字高程模型数字高程模型(Digital Elevation Model ,简称DEM )是通过有限的地形高程数据实现对地形曲面的数字化模拟(即地形表面形态的数字化表示),它是对二维地理空间上具有连续变化特征地理现象的模型化表达和过程模拟。
由于高程数据常常采用绝对高程(即从大地水准面起算的高度),DEM 也常常称为DTM (Digital Terrain Model )。
“Terrain”一词的含义比较广泛,不同专业背景对“Terrain”的理解也不一样,因此DTM 趋向于表达比DEM 更为广泛的内容。
从研究对象与应用范畴角度出发,DEM 可以归纳为狭义和广义两种定义。
从狭义角度定义,DEM 是区域表面海拔高程的数字化表达。
这种定义将描述的范畴集中地限制在“地表”、“海拔高程”及“数字化表达”内,观念较为明确。
从广义角度定义,DEM 是地理空间中地理对象表面海拔高度的数字化表达。
这是随着DEM 的应用不断向海底、地下岩层以及某些不可见的地理现象(如空中的等气压面等)延伸,而提出的更广义的概念。
该定义将描述对象不再限定在“地表面”,因而具有更大的包容性,有海底DEM 、下伏岩层DEM 、大气等压面DEM 等。
数学意义上的数字高程模型是定义在二维空间上的连续函数),(y x f H =。
由于连续函数的无限性,DEM 通常是将有限的采样点用某种规则连接成一系列的曲面或平面片来逼近原始曲面,因此DEM 的数学定义为区域D 的采样点或内插点Pj 按某种规则ζ连接成的面片M 的集合:},,1,,1,),,()({m i n j D H y x P P M DEM j j j j j i ==∈==ζ (9.1)DEM 按照其结构,可分为规则格网DEM 、TIN 、基于点的DEM 和基于等高线的DEM 等。
地理信息系统_第八章_DEM与数字地形分析

1 3 1 2 4 5 10 2 4 7 6 6 9 10 8 7
5
3
11
8
9
DEM建立
DEM数据采集方法
地面测量 现有地图数字化 空间传感器 数字摄影测量获取DEM
DEM建立
数据采集遵循的原则
确定合理的采集精度 确定合理的取样密度 保证最低的采点密度
DEM建立
第八章 DEM与数字地形分析
学习目标:
1. 基本概念
2. DEM建立
3. 数字地形分析
重点:数字地形分析
基本概念
数字高程模型 (DEM,Digital Elevation Model)
是通过有限的地形高程数 据实现对地形曲面的数字化 模拟(即地形表面形态的数 字化表示),它是对二维地 理空间上具有连续变化特征 地理现象的模型化表达和过 程模拟。
网格单元(可以是正方 形或三角形),每个单
X
91 78 63 50 53 63 44 94 81 64 51 57 62 50 99 84 66 55 64 66 54 95 84 66 56 72 71 58 96 82 66 63 80 78 60
元对应一个数值。
Y
91 79 66 63 80 80 62
300 200 100
DEM模型在GIS中的应用
3、土石方计算 在DEM基础上进行土石方计算非常方便。 如果是规则网格模型,那么把三维空间实体转变为 长方体 集合就能方便进行计算。 如果是TIN模型,可通过插值达到规则网格模型的密 集度。当然会有一定的误差。
4 等高线绘制
5 渲染图的制作
Байду номын сангаас
规则格网模型
测绘技术中常见的地形分析方法

测绘技术中常见的地形分析方法地形分析是测绘技术中一个重要的方向,通过对地势起伏、坡度、高程等地形特征进行研究和分析,可以为城市规划、环境保护、资源开发等提供科学依据。
本文将介绍一些测绘技术中常见的地形分析方法。
1. 高程插值高程插值是地形分析中最基本的方法之一。
它通过利用已知高程数据点的空间关系,推算出其它位置的高程值。
常用的高程插值方法有反距离权重插值、克里金插值和三角网插值。
反距离权重插值方法是根据距离远近来确定权重,距离越远权重越小;克里金插值方法则根据已知数据点的空间关系来计算权重;而三角网插值方法则根据已知数据点之间的三角形网格来拟合曲面。
2. 地形参数提取地形参数是描述地形形状、特征以及地貌类型的数值指标。
常用的地形参数有坡度、坡向、地形湿度指数等。
坡度指的是地面倾斜的程度,可以通过测量高程变化来计算;坡向指的是地面倾斜的方向,可以根据高程数据计算得出;地形湿度指数则是根据地形起伏等指标来评估地表湿度程度,有助于土地利用规划和水源管理。
3. 剖面分析剖面分析是通过在二维地图上选择两点,并沿这两点间的直线绘制地形剖面图,来研究地表的高程变化。
剖面分析可以揭示出地形的起伏、坡度以及地表水流情况等。
通过剖面分析,我们可以直观地观察到地表的地势起伏情况,并据此来评估地形对工程建设的影响。
4. 遥感影像分析遥感影像分析是利用航空遥感或卫星遥感技术获取的影像数据来进行地形分析的方法。
遥感影像可以提供全面、连续的地表高程信息。
通过遥感影像分析,可以确定地表特征、地形类型、植被分布等,从而为环境保护、资源开发等提供科学依据。
5. 地形模型构建地形模型是一种对地表形状和特征进行数学建模的方法。
常见的地形模型有数字高程模型(DEM)和数字地形模型(DTM)。
DEM是一种以栅格形式表达地表高程的模型,它可以通过遥感影像或测量数据生成。
DTM则是在DEM基础上添加了其它地理信息(如地物分类、坡度等)的三维模型。
数字地形模型分析讲解

2、等高线光滑: – 进一步加密等高线点并绘制光滑曲线。
3.基于DEM的等高线的绘制
3.基于DEM的等高线的绘制
4.基于DEM的可视化分析
基于DEM的可视化分析 – 剖面分析 – 通视分析 – 地形三维图绘制 – 地貌晕渲图绘制 – 地形三维可视化
地形分析:坡度、坡向与曲率
坡度、坡向与曲率的连续函数数学表达
设地形曲面为:z f (x, y)
坡度:Slope arctg
f
2 x
f
2 y
坡向:Aspect 180 arctg f y 90 f x
fx
fx
剖面曲率:Prof
ileCurturv e
f xx
f
2 x
(
f
2 x
北:y
e1 e2 e3
e4 c0 e5
x
e6 e7 e8
Horn算法
坡向:Aspect
坡向值有如下规定:正北方向为0°,顺时针方向计算, 取值范围为0°~360°。
坡向可在DEM数据中直接提取。求出坡向有与y轴正向 和y轴负向夹角之分,此时就要根据fx和fy的符号来进一 步确定坡向值。
通视分析
通视分析:是指以某一点为观察点,研究某一区域通视 情况的地形分析。
剖面分析
意义: – 以线代面,研究区域的地貌形态、轮廓形状、地势 变化、地质构造、斜坡特征、地表切割强度等。 – 如果在地形剖面上叠加其它地理变量,可以提供土 地利用规划、工程选线和选址等的决策依据。
剖面分析
绘制数据 剖面图高程的插值
– 对于格网DEM,可通过其周围的4个格网点内插出, – 对于三角网DEM,可通过该点所在的三角形的三个顶
DEM分析——ArcGIS实践ppt课件

计算公式
.
37
得到地面粗糙度
.
38
DEM分析操作二
地形特征信息的提取
.
39
运行环境:ArcGIS 9
数据来源:某区域分辨率为5米的DEM数据。
要求:利用所提供DEM数据,提取该区域山脊线、
山谷线栅格数据层。
.
40
地形特征要素,主要是指对地形在地表的空间 分布特征具有控制作用的点、 线或面状要素。
地形起伏度,是指在特定的区域内,最高
点海拔高度与最低点海拔高度的差值。
地形起伏度是描述一个区域地形特征的宏观 性指标。
.
24
添加并选中DEM数据,使用栅格领域计算工具
.
25
添加并选中DEM数据,使用栅格领域计算工具
.
26
添加并选中DEM数据,使用栅格领域计算工具
设置为最大值 根据自身需要选择
.
32
得到地形起伏度数据
.
33
4. 地面粗糙度的提取
地面粗糙度,是特定的区域内地球表面积
与其投影面积之比。
地面粗糙度是描述一个区域地形特征的宏观 性指标。
.
34
点击DEM数据层,选择表面分析中的坡度(Slope) 工具,提取坡度
.
35
得到坡度Slope数据层
.
36
使用栅格计算器,计算获取地面粗糙度数据层
DEM 分析
.
1
DTM模型与DEM模型的区别
DTM(数字地面模型):是定义于二维区域上
的一个有限项的向量序列,它以离散分布的平面 点来模拟连续分布的地形。每一个点上的地面属 性数据,包括土地权属、土壤类型、土地利用等。
DEM(数字高程模型):当DTM中的属性为
第八章 数字地形模(DTM)与地形分析

1.概述 2.DEM的主要表示模型 3.DEM模型之间的相互转换 4.DEM的建立
5.DEM的分析和应用
第一节 概述
DEM和DTM主要用于描述地面起伏状况,可
以用于提取各种地形参数,如坡度、坡向、粗
糙度等,并进行通视分析、流域结构生成等应
三、DEM数据质量控制
第五节
DEM的分析与应用
一、 格网DEM的应用
(一 DEM最基本的应用是求DEM范围内任意点的高程, 在此基础上进行地形属性分析。方法:利用有限个格 网点的高程,拟合一个地形曲面,推求区域内任意点 的高程。 算法:对已知规格格网数据进行空间插值。 插值方法:距离到数加权平均法、克里金插值方 法、样条函数插值方法
第一节 概述
三、DEM的表示法
1、数学方法 用数学方法来表达,可以采用整体拟合方法,, 也可用局部拟合方法。 2、图形方法 (1)线模式 等高线是表示地形最常见的形式。其它的地形特 征线也是表达地面高程的重要信息源,如山脊线、谷 底线、海岸线及坡度变换线等。 (2)点模式 用离散采样数据点建立DEM是DEM建立常用的方法 之一。数据采样可以按规则格网采样,可以是密度一 致的或不一致的;可以是不规则采样,如不规则三角 网、邻近网模型等;也可以有选择性地采样,采集山 峰、洼坑、隘口、边界等重要特征点。
(二)立体透视图 局部放大、改变高程值z的放大倍数以夸大立体形 态、改变视点位置从不同角度进行观察、转动立体图
第五节
DEM的分析与应用
一、 格网DEM的应用
(三)通视分析 点对区域的通视:视线不能被地形挡住。 应用:观测哨所的设定、森林中火灾监测点的设定、 无线发射塔的设定。 同视问题分五种情况: 1、已知一个或一组观察点,找出某一地形的可视区域; 2、欲观测到某一区域的全部地形表面,计算最少观测点 数量; 3、在观测点数量一定的前提下,计算能获得最大观测区 域; 4、以最小代价建造观察塔,要求全部区域可视; 5、在给定代价的前提下,求最大可见区。
GIS-8 第九章 DTM与地形分析

2.1 规则格网模型
• 规则格网法把DEM表示成高程矩阵时,其DEM来源于直接规 则矩形格网采样点或由不规则离散数据点内插产生。
• 不规则离散采样点可以按照两种方法产生高程矩阵:一是将规 则格网覆盖在这些数据的分布图上,然后用内插技术产生高程 矩阵,并且内插技术也可用来从一个粗略的高程矩阵产生更精 细的高程矩阵;二是把离散点作为店模式中不规则三角网系统 的基础。
第九章 DTM与地形分析
• 课
题: DTM与地形分析
• 目的要求: 理解DTM和DEM概念;掌握DEM的主要表示方 法,并能分析其优缺点;了解DEM的数据采集方法;了解 DEM的插值方法;掌握DEM建立的一般作业过程;了解 DEM在地学分析中的主要用途;了解地形可视化的方法。 • 教学重点:DTM,DEM的概念及相互转换方法,DEM的作 业过程。 • 教学难点:DEM分析和应用 • 教学课时:4课时 • 教学方法: 讲授 • 本次课涉及的学术前沿:
2 5 X 1 3 6 X 4 2 3 X 8 1 X 6 2 5 7 6 8 X 4 7 X
8
点文件
三角网的一种存储方式
若对于每个三角形、边和节点都对应一个记录,三角形记 录三条边的指针、边记录两个顶点以及相邻多边形指针, 怎么表达?(用关系模型表示)
TIN模型的存储方式
No 1 2 3 : 10 X 90.0 50.7 67.2 : 10.0 Y 10.0 10.0 23.9 : 90.0 Z 43.5 67.3 62.6 : 81.0
2.3 不规则三角网(TIN)模型
• TIN的数据存储方式比GRID复杂,它不仅 要存储每个点的高程,还要存储其平面坐 标、节点连接的拓扑关系,三角形及邻接 三角形等关系。TIN模型在概念上类似于多 边形网络的矢量拓扑结构,只是TIN模型不 需要定义“岛”和“洞”的拓扑关系。
ArcGIS实验九DTM实习

实验九DTM实习一、实验目的:掌握MapGis生成数字高程模型的方法二、试验内容:DTM的生成、TIN模型和GRID模型的应用三、试验步骤1.首先生成等高线文件。
1.1打开光栅文件矢量化等高线。
(1)启动MAPGIS的输入编辑功能模块。
(2)新建工程。
(3)“新建线”建立线文件“实习七”。
(4)打开光栅文件。
由于大家打开的光栅文件不是黑白二值图,所以不能光栅文件求反。
(5)交互式矢量化。
只要求对光栅文件的中心四个矩形区域内的等高线进行矢量化。
放大窗口到适当大小。
开始交互矢量化(注意:加点(第一点)F8;退点F9;移动屏幕F6。
)(6)给每条等高线符高程值。
首先建立属性结构。
修改通过回车和光标在窗口中找到一个高程点,本次矢量化的是1:25的地形图,等高线之间的差为10米。
接下来启动自动赋高程值的工具。
然后从已知高程点处向外引一条延长线。
点击后出现一个对话框。
同样的方法将所有的线属性录入。
2.利用生成的等高线进行DTM分析。
2.1生成TIN模型。
(1)启动DTM分析功能模块。
(2)装入等高线文件。
(3)由线数据提取高程点。
(4)快速生成三角剖分网。
(5)另存三角剖分网文件。
(6)观看三维效果(7)参数设置。
(8)TIN模型应用。
首先可以生成坡度图。
最后生成的文件为一个区文件,坡度值在其属性中。
(9)GRID模型的应用。
首先关闭TIN模型窗口,重新打开等高线文件。
然后将等高线栅格化。
改变格网DX和DY的值为0.1(如果计算机处理速度太慢可设为1)。
接下来打开我们生成的GRID文件。
新建三维窗口观察其立体效果。
关闭三维窗口,GRID模型比TIN模型更强大,它除了可以进行坡度坡向分析之外还可进行其它一系列分析,下面进行一下介绍。
A、蓄积量分析。
用鼠标选取任意区域的含义是用鼠标在窗口中选定要计算土方量的区域然后进行计算。
接下来我们点击确认按键,鼠标变成一个小铲形,我们任意划定一个多边形进行土方量的计算。
点击鼠标右键结束多边形的输入,这时系统有相关提示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 5 X 1 3 6 X 4 2 3 X 8 1 X 6 2 5 7 6 8 X 4 7 X
8
点文件
三角网的一种存储方式
若对于每个三角形、边和节点都对应一个记录,三角形记 录三条边的指针、边记录两个顶点以及相邻多边形指针, 怎么表达?(用关系模型表示)
TIN模型的存储方式
No 1 2 3 : 10 X 90.0 50.7 67.2 : 10.0 Y 10.0 10.0 23.9 : 90.0 Z 43.5 67.3 62.6 : 81.0
1.概述
三、DEM的表示法
– 数学方法 • 整体拟合 • 局部拟合 图形方法 • 等高线 • 规则格网 • 不规则格网
–
DEM的表示方法
●使用三维函数模 拟复杂曲面; ●将一个完整曲面 分解成方格网或面 积上大体相等的不 规则格网,每个格 网中有一个点的观 测值,即为格网值; ●适用于曲面插值 来表示地下水或土 壤的特性;
3.DEM模型之间的相互转换
(一)不规则点集生成TIN (二)格网DEM转成TIN (三)等高线转成格网DEM (四)利用格网DEM提取等高线 (五)TIN转成格网DEM
以下是使用arcgis进行转换的例子。
不规则点集生成TIN
格网DEM转成TIN
TIN转成格网DEM
利用格网DEM提取等高线
3.DEM模型之间的相互转换
(一)不规则点集生成TIN
• 将该点集转成TIN,最常用的方法是Delaunay三 角剖分方法,生成过程分两步完成: • 1)利用P中点集的平面坐标产生Delaunay三角 网; 2)给Delaunay三角形中的节点赋予高程值。
• 不规则三角网模型的缺点:
1)算法实现复杂,由于形成三角网方法不同有不同算法 2)对特殊的地形线要调整
2.3 不规则三角网(TIN)模型
• 不规则三角网数字高程由连续的三角面组 成,三角面的形状和大小取决于不规则分 布的测点,或节点的位置和密度。不规则 三角网与高程矩阵方法不同之处是随地形 起伏变化的复杂性而改变采样点的密度和 决定采样点的位置,因而它能够避免地形 平坦时的数据冗余,又能按地形特征点如 山脊、山谷线等表示数字高程特征。
2.1 规则格网模型
• 规则格网法把DEM表示成高程矩阵时,其DEM来源于直接规 则矩形格网采样点或由不规则离散数据点内插产生。
• 不规则离散采样点可以按照两种方法产生高程矩阵:一是将规 则格网覆盖在这些数据的分布图上,然后用内插技术产生高程 矩阵,并且内插技术也可用来从一个粗略的高程矩阵产生更精 细的高程矩阵;二是把离散点作为店模式中不规则三角网系统 的基础。
1.概述
一、相关概念 • 数字地形模型(DTM, Digital Terrain Model):
是地形表面形态属性信息的数字表达,是带有空间位置特 征和地形属性特征的数字描述。通常被描述为地形表面形 态空间位置和地形属性分布的有序数值阵列。它是地表单 元上地形参数的集合,通常DTM可由DEM生成。
2.4 层次模型
• 层次模型
– 一种表达多种不同精度水平的数字高程模型, – 大多数层次模型是基于不规则三角网模型的, 通常不规则三角网的数据点越多精度越高,数 据点越少精度越低,但数据点多则要求更多的 计算资源。所以如果在精度满足要求的情况下, 最好使用尽可能少的数据点。
– 层次地形模型允许根据不同的任务要求选 择不同精度的地形模型。
3.DEM模型之间的相互转换
(一)不规则点集生成TIN
Delaunay三角形产生的基本准则:
1. Delaunay三角形产生准则的最简明的形式是:任何 一个Delaunay三角形的外接圆的内部不能包含其它 任何点[Delaunay 1934]。 2. Lawson[1972]提出了最大化最小角原则:每两个相 邻的三角形构成的凸四边形的对角线,在相互交换后, 六个内角的最小角不再增大。 3. Lawson [1977]又提出了一个局部优化过程LOP (Local Optimization Procedure)方法。
2.DEM的主要表示模型
• • • • 2.1 规则格网模型(DEM的点表示) 2.2 等高线模型(DEM的线表示) 2.3 不规则三角网模型(DEM的点表示) 2.4 层次模型(DEM的点表示)
2.1 规则格网模型
• 规则格网:将区域空间
切分成为规则的格网单元, 每个格网单元对应一个数 值。数学上有一个矩阵表 示,计算机里面表示为一 个二维数组。
3.DEM模型之间的相互转换
• TIN的三角剖分
3.DEM模型之间的相互转换
(一)不规则点集生成TIN Delaney三角网的特性 • 对于给定的初始点集,有多种三角网剖分 方式,而Delaney三角网具有以下特性:
1)其Delaunay三角网是唯一的; 2)三角网的外边界构成了点集P的凸多边形“外壳”; 3)没有任何点在三角形的外接圆内部,反之,如果一 个三角网满足此条件,那么它就是Delaunay三角网; 4)如果将三角网中的每个三角形的最小角进行升序排 列,则Delaunay三角网的排列得到的数值最大,从这 个意义上讲,Delaunay三角网是"最接近于规则化"的三 角网。
• 它被用于各种线路选线(铁路、公路、输电线) 的设计以及各种工程的面积、体积、坡度计算, 任意两点间的通视判断及任意断面图绘制。
1.概述
• 高程模型:高程Z关于平面坐标X,Y两个自变量的连续函 数,数字高程模型(DEM)只是它的一个有限的离散表示。
• 数字高程模型DEM(Digital Elevation Model):当数字 地形模型中地形属性为高程时即为DEM;它是地表单元上 高程的集合,通常用矩阵表示; • 广义的DEM可包括等高线,三角网等。这里我们特指由地 表矩阵单元构成的高程矩阵。DEM是DTM的一个子集,是 DTM的一个特例。
等高线和相应的自由树
C
2.3 不规则三角网(TIN)模型
不规则三角网是专为产生DEM数据而设计的一种采样表示 系统。 TIN模型根据区域所有采样点取得的离散数据,按照优化组 合的原则,把这些离散点(各三角形的顶点)连接成相 互连续的三角面,在连接时尽可能地使每个三角形为锐 角三角形或为三边的长度近似相等, 如下图
1.概述
二、DEM的应用简介
1)作为国家地理信息的基础数据; 2)土木工程、景观建筑与矿山工程规划与设计; 3)为军事目的而进行的三维显示; 4)景观设计与城市规划; 5)流水线分析、可视性分析; 6)交通路线的规划与大坝选址; 7)不同地表的统计分析与比较; 8)生成坡度图、坡向图、剖面图、辅助地貌分析、估计侵蚀和径流等; 9)作为背景叠加各种专题信息如土壤、土地利用及植被覆盖数据等,以 进行显示与分析; 10)与GIS联合进行空间分析; 11)虚拟现实(Virtual Reality); 此外,从DEM还能派生以下主要产品:平面等高线图、立体等高线图、等 坡度图、晕渲图、通视图、纵横断面图、三维立体透视图、三维立体彩色图 等。
3.DEM模型之间的相互转换
• (一)不规则点集生成TIN
– 不规则三角网(Triangulated Irregular Network, TIN)是另外一种表示数字高程模型的方法,它既减 少规则格网方法带来的数据冗余,同时在计算(如坡 度)效率方面又优于纯粹基于等高线的方法。 – TIN模型根据区域有限个点集将区域划分为相连的三 角面网络,区域中任意点落在三角面的顶点、边上或 三角形内。如果点不在顶点上,该点的高程值通常通 过线性插值的方法得到(在边上用边的两个顶点的高 程,在三角形内则用三个顶点的高程)。所以TIN是 一个三维空间的分段线性模型,在整个区域内连续但 不可微
B
等高线模型中,高程值的集 等高线 合是已知的。每条等高线对 应一个已知的高程值,一系 列等高线集合和它们的高程 值一起构成了一种地面高程 模型。
等高线模型只表达了区域的部分 F E 高程值,因此等高线以外的其他 A D 点的高程,要通过插值进行计算, G 通常只使用外包的两型
• TIN的数据存储方式比GRID复杂,它不仅 要存储每个点的高程,还要存储其平面坐 标、节点连接的拓扑关系,三角形及邻接 三角形等关系。TIN模型在概念上类似于多 边形网络的矢量拓扑结构,只是TIN模型不 需要定义“岛”和“洞”的拓扑关系。
2.3 不规则三角网(TIN)模型
1 2 3 4 5 6 7 8 X Y Z X Y Z X Y Z X Y Z X Y Z X Y Z X Y Z X Y Z
6 5 6 7 7 1 1 3 2 5 4 8 4 3 2 顶点 邻接三角形
1 2 3 4 5 6 7 8
1 5 6 1 4 5 1 2 4 2 3 4 5 6 8 4 5 8 4 7 8 3 4 7 三角形文件
第九章 DTM与地形分析
• 课
题: DTM与地形分析
• 目的要求: 理解DTM和DEM概念;掌握DEM的主要表示方 法,并能分析其优缺点;了解DEM的数据采集方法;了解 DEM的插值方法;掌握DEM建立的一般作业过程;了解 DEM在地学分析中的主要用途;了解地形可视化的方法。 • 教学重点:DTM,DEM的概念及相互转换方法,DEM的作 业过程。 • 教学难点:DEM分析和应用 • 教学课时:4课时 • 教学方法: 讲授 • 本次课涉及的学术前沿:
3.DEM模型之间的相互转换
(一)不规则点集生成TIN
• 局部优化过程(LOP)(Lawson,1997)
如图9-7所示。先求出包含新插入点p的外接圆的三角形,这种三角形称为影响三 角形(Influence Triangulation)。删除影响三角形的公共边,将p与全部影响三 角形的顶点连接,完成p点在原Delaunay三角形中的插入。
•规则格网模型结构简单,计算机对矩阵的处理比较方 便,高程矩阵已成为DEM最通用的形式。
