江苏省邳州市第二中学高三数学第66课时多面体与球复习学案苏教版
江苏省邳州市第二中学高三数学滚动练习6苏教版

14.如图,直线 l1 : y kx 1 k (k 0, k
1
11
)与l 2 : y
x
相交于点 P ,直线 l1与
2
22
x 轴交于点 P1 ,过点 P1 作 x 轴的垂线交直线 l2 于点 Q1,过点 Q1 作 y 轴的垂线交直线 l1
于点 P2 ,过点 P2作 x 轴的垂线交直线 l2 于点 Q2 ,…,这样一直作下去,可得到一系
f 2 5, f 5 2, f 2 8, 那么 g 2 , g 5 , g 8 , g 2 中,一定能求
出具体数值的是 _______________________ .
10.已知数列 an ,满足 a1 1 ,an a1 2a2 3a3
通项公式为 an
1, ( n 1) ( n 2)
( n 1)an 1, (n 2) 则 an 的
) 的值为 4
2
A.
10
72
B.
10
72
C.
10
2
D.
10
4.首项为 1,公差不为零的等差数列 等比数列的第 4 项为
an 中 , a3, a4, a6 是一个等比数列的前三项, 则这
A. 8
5.数列 an 中, a1 A. 2 5
B. - 8
1 , an an 1
5 B. 2 7
6 5n 1 , n
] 时, f ( x)
sin x ,则
f
5 (
) 的值为
2
3
A. 1 2
1
B.
2
C.
3
2
3
D.
2
8.农民收入由工资性收入和其它收入两部分构成. 2003 年某地区农民人均收入为
江苏省邳州市第二中学高三数学 第60课时 平面与平面垂

江苏省邳州市第二中学高三数学复习:第60课时 平面与平面垂直学案 苏教版一.复习目标:1.掌握平面与平面垂直的概念和判定定理性质定理,并能运用它们进行推理论证和解决有关问题。
2.在研究垂直问题时,要善于应用“转化”和“降维”的思想,通过线线、线面、面面平行与垂直关系的转化,从而使得问题获得解决 二.主要知识:三.课前预习:PA ⊥ABCD A ,,,,PB PC PD AC BD ()A ()B ()C ()DαβαI βl P α∈Q l ∈PQ l ⊥PQ β⊥()A 充分但不必要条件 ()B 必要但不充分条件 ()C 充要条件 ()D 既不充分也不必要条件γβα,,α⊥γβ⊥γαβ()A ()B ()C ()Dαβl ⊄αl ⊄βl α⊥//l βαβ⊥()A ()B ()C ()D 四.例题分析ABCD 3,2AB AC AD ===60DAC BAC BAD ∠=∠=∠=o BCD ADCABC ∆EC ⊥ABC //BD CE 2CE CA BD ==M EA DE DA =BDM ⊥ECA DEA ⊥ECAP ABCD -ABCD PA ⊥ABCD ,E F ,AB PD P CD B --45o //AF PEC PEC ⊥PCD 2,22AD CD ==A PECA DP EFαα()A ()B ()C ()Dα⊥βn ⊂αm ⊂βm n ⊥()A n ⊥β ()B n ⊥β且m ⊥α ()C m ⊥α ()D n ⊥β与m ⊥α中至少有一个成立,m n ,αβα⊥β()A m n ⊥//,//m n αβ()B ,,m n m n αβα⊥=⊂I ()C //,,m n n m βα⊥⊄()D ,,m n m n αβ⊥⊥⊥,,l m n ,,αβγ,l m αα⊥⊥//l m ,m n β⊂l βm l ⊥m n ⊥,//m m n α⊂//n α,αγβγ⊥⊥//αβ()A ()B ()C ()DP ABCD -PA ⊥ABCD M PC M MBD ⊥PCDP ABC -,PB PC AB AC ==D BC AH PD ⊥H BH ABH ⊥PBC1111ABCD A B C D -,,,E F M N 111111,,,A B BC C D B C MNF ⊥ENFOAPB CM DCAD BPHP ABCD -a PA ⊥ABCD E AB PA AB =PCE ⊥PCD D PCEACPEBD。
江苏省邳州市第二中学高三数学 第55课时 圆锥曲线应用(1)复习学案 苏教版

江苏省邳州市第二中学高三数学复习:第55课时 圆锥曲线应用(1)学案 苏教版一.复习目标:会按条件建立目标函数研究变量的最值问题及变量的取值范围问题,注意运用“数形结合”、“几何法”求某些量的最值.二.知识要点:1.与圆锥曲线有关的参数问题的讨论常用的方法有两种:(1)不等式(组)求解法:利用题意结合图形列出所讨论的参数适合的不等式(组),通过解不等式(组)得出参数的变化范围;(2)函数值域求解法:把所讨论的参数作为一个函数,通过讨论函数的值域来求参数的变化范围.2.圆锥曲线中最值的两种求法:(1)几何法:若题目中的条件和结论能明显体现几何特征和意义,则考虑利用图形性质来解决,这就是几何法;(2)代数法:若题目中的条件和结论能体现明确的函数关系,则可首先建立起目标函数,再求这个函数的最值.三.课前预习:1.点P 是双曲线221412x y -=上的一点,1F 、2F 分别是双曲线的左、右两焦点,1290F PF ∠=,则12||||PF PF ⋅等于 ( D )()A 48 ()B 32 ()C 16 ()D 242.双曲线221x y -=的左焦点为F ,P 为双曲线在第三象限内的任一点,则直线PF 的斜率的取值范围是 ( B )()A 0k ≤或1k > ()B 0k <或1k > ()C 1k ≤-或1k ≥ ()D 1k <-或1k >3.椭圆2214x y +=的短轴为12B B ,点M 是椭圆上除12,B B 外的任意一点,直线12,MB MB 在x 轴上的截距分别为12,x x ,则12x x ⋅= 4 .4.已知椭圆长轴、短轴及焦距之和为8,则长半轴长的最小值是1).5.已知,,a b c 分别是双曲线的实半轴、虚半轴和半焦距,若方程20ax bx c ++=无实数根,则此双曲线的离心率e 的取值范围是(1,2.四.例题分析:例1.过抛物线24y x =(0)a >的焦点F ,作相互垂直的两条焦点弦AB 和CD ,求||||AB CD +的最小值.解:抛物线的焦点F 坐标为(,0)a ,设直线AB 方程为()y k x a =-,则CD 方程为1()y x a k=--,分别代入24y x =得: 22222(24)0k x ak a x k a -++=及2222211(24)0a x a a x k k k-++=, ∵22||22A B a AB x x p a a k=++=++,2||242C D CD x x p a ak a =++=++,∴224||||8416a AB CD a ak a k+=++≥,当且仅当21k =时取等号, 所以,||||AB CD +的最小值为16a .例2.已知椭圆的焦点1(3,0)F -、2(3,0)F ,且与直线90x y -+=有公共点,求其中长轴最短的椭圆方程.解:(法一)设椭圆方程为222219x y a a +=-(29a >), 由22221990x y a a x y ⎧+=⎪-⎨⎪-+=⎩得22224(29)18900a x a x a a -++-=,由题意,a 有解,∴22224(18)4(29)(90)0a a a a ∆=---≥,∴42544050a a -+≥,∴245a ≥或29a ≤(舍), ∴2min 45a =,此时椭圆方程是2214536x y +=. (法二)先求点1(3,0)F -关于直线90x y -+=的对称点(9,6)F -,直圆的交点为M ,则12222||||||||||a MF MF MF MF FF =+=+≥=∴min a =2214536x y +=. 小结:本题可以从代数、几何等途径寻求解决,通过不同角度的分析和处理,拓宽思路.例3.直线1y kx =+与双曲线221x y -=的左支交于,A B 两点,直线l 经过点(2,0)-及AB 中点,求直线l 在y 轴上截距b 的取值范围.解:由2211y kx x y =+⎧⎨-=⎩得22(1)220k x kx ---=,设11(,)A x y 、22(,)B x y ,则221212248(1)00200110201k k k x x k k x x k⎧⎪+->∆>⎧⎪⎪⎪+<⇒<⇒<<⎨⎨-⎪⎪⋅>⎩-⎪>⎪-⎩,AB 中点为221(,)11k k k --, ∴l 方程为2222x y k k +=-++,令0x =, 得2222117222()48b k k k ==-++--+,∵1k <<211722()148k <--+<, 所以,b的范围是(,2(2,)-∞-+∞.小结:用k 表示b 的过程即是建立目标函数的过程,本题要注意k 的取值范围.五.课后作业: 班级 学号 姓名1.AB 为过椭圆22221x y a b+=(0)a b >>中心的弦,(,0)F c 是椭圆的右焦点,则ABF ∆面积的最大值是( ) ()A bc()B ac ()C ab ()D 2b 2.若抛物线2y x m =+与椭圆2212x y +=有四个不同的交点,则m 的取值范围是( ) ()A 2m >- ()B 178m >- ()C 21m -<<- ()D 1718m -<<- 3.椭圆中,a c 是关于x 的方程2230x ax ac -+=中的参数,已知该方程无解,则其离心率的取值范围为 . 4.已知(,)P x y 是椭圆22221x y a b+=(0)a b >>上的动点,12,F F 是焦点,则12||||PF PF ⋅的取值范围是 .5.抛物线24y x =上的点P 到直线l :20x y ++=的距离最小,则点P 坐标是 .6.由椭圆22221x y a b+=(0)a b >>的顶点(0,)B b -引弦BP ,求BP 长的最大值.7.过点(2,4)A --且斜率为1的直线l 交抛物线22y px =(0)p >于,B C 两点,若||AB 、 ||BC 、||CA 成等比数列,求抛物线方程.8.已知椭圆的两个焦点分别是12(0,F F -,离心率e = (1)求椭圆的方程;(2)一条不与坐标轴平行的直线l 与椭圆交于不同的两点,M N ,且线段MN 中点的横坐标为12-,求直线l 的倾斜角的范围.。
江苏省邳州市第二中学高三数学 不等式小结复习学案 苏教版

江苏省邳州市第二中学高三数学复习:不等式小结学案 苏教版一.复习目标:1.进一步巩固不等式的解法、证明不等式的一般方法、利用不等式求最值的方法; 2.能熟练运用不等式的思想方法解决有关应用问题. 二.课前预习:1.已知c d <,0a b >>,下列不等式中必成立的一个是()()A a c b d +>+()B a c b d ->-()C ad bc <()D a b c d> 2.设,x y 满足220x y +=的正数,则lg lg x y +的最大值是()()A 50()B 2 ()C 1lg5+ ()D 1 3.设,x y R ∈,221x y +=,(1)(1)m xy xy =-+,则m 的取值范围是 ( )()A 1[,1]2 ()B (0,1] ()C 3[,1]4 ()D 3[,1)44.设12x >,则函数821y x x =+-的最小值是 ,此时x = .5.关于x 的不等式260x ax a --<的解集不是空集,且区间长度不超过5,则实数a 的取值范围是 .6.使2log ()1x x -<+成立的x 的取值范围是 .7.锐角三角形ABC 中,已知边1,2a b ==,则边c 的取值范围是 . 三.例题分析:例1.(1)已知0x y >>,且1xy =,求22x y x y+-的最小值及相应的,x y 的值;(2)已知0x y >>,且3412x y +=,求lg lg x y +的最大值及相应的,x y 的值.例2.设绝对值小于1的全体实数的集合为S ,在S 中定义一种运算*,使得*1a ba b ab+=+, 求证:如果a 与b 属于S ,那么*a b 也属于S .例3.证明:1112(11)1223n n n+-<++++<*()n N ∈.例4.某种商品原来定价每件p 元,每月将卖出n 件.若定价上涨x 成(注:x 成即10x,010x <≤),每月卖出数量将减少y 成,而售货金额变成原来的z 倍. (1)若y ax =,其中a 是满足113a ≤<的常数,用a 来表示当售货金额最大时的x 值; (2)若23y x =,求使售货金额比原来有所增加的x 的取值范围.四.课后作业: 班级 学号 姓名 1.已知0,0a b >>,则不等式1b a x-<<等价于 ( )()A 1x a <-或1x b > ()B 1x b <-或1x a >()C 10x a -<<或10x b << ()D 10x b -<<或10x a<<2.一批货物随17列火车从A 市以 /v km h 的速度匀速直达B 市,已知两地铁路线长为400km ,为了安全,两列货车的距离不得小于2() 20v km (货车的长度忽略不计),那么这批货物全部运到B 市,最快需要( )()A 6h()B 8h()C 10h()D 12h3.若,a b 是实数,且a b >,则在下面三个不等式:①11a ab b ->-;②22()(1)a b b +>+;③22(1)(1)a b ->-,其中不成立的有 个.4.设,a b 都是大于0的常数,则当0x >时,函数()()()x a x b f x x++=的最小值是 .5.已知()21f x ax a =++,当[1,1]x ∈-时,()f x 的值有正有负,则a 的取值范围为 .6.已知,x y R ∈,且22222x xy y -+=,则||x y +的最大值是 .7.设2()13f x x x =-+,实数a 满足||1x a -<,求证:|()()|2(||1)f x f a a -<+.8.已知,,a b c 都是正数,求证:111111222a b c b c c a a b++≥+++++.9.某商场预计全年分批购入每台价值为2000元的电视机共3600台,每批都购入x 台*()x N ∈,且每批均需付运费400元,贮存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比,若每批购入400台,则全年需用运输和保管费用总计43600元,现在全年只有24000元资金可以用于支付这笔费用,请问:能否恰当安排每批进货的数量,使资金够用?求出结论,并说明理由.。
江苏省邳州市第二中学高三数学 第10课时 函数的奇偶性复习学案 苏教版

江苏省邳州市第二中学高三数学复习:第10课时 函数的奇偶性学案 苏教版一.课题:二.教学目标:掌握函数的奇偶性的定义及图象特征,并能判断和证明函数的奇偶性,能利用函数的奇偶性解决问题.三.教学重点:函数的奇偶性的定义及应用. 四.教学过程: (一)主要知识:1.函数的奇偶性的定义; 2.奇偶函数的性质:(1)定义域关于原点对称;(2)偶函数的图象关于y 轴对称,奇函数的图象关于原点对称; 3.()f x 为偶函数()(||)f x f x ⇔=.4.若奇函数()f x 的定义域包含0,则(0)0f =. (二)主要方法:1.判断函数的奇偶性,首先要研究函数的定义域,有时还要对函数式化简整理,但必须注意使定义域不受影响;2.牢记奇偶函数的图象特征,有助于判断函数的奇偶性;3.判断函数的奇偶性有时可以用定义的等价形式:()()0f x f x ±-=,()1()f x f x =±-. 4.设()f x ,()g x 的定义域分别是12,D D ,那么在它们的公共定义域上:奇+奇=奇,奇⨯奇=偶 偶+偶=偶,偶⨯偶=偶,奇⨯偶=奇. 5.注意数形结合思想的应用. (三)例题分析:例1.判断下列各函数的奇偶性:(1)()(f x x =-(2)22lg(1)()|2|2x f x x -=--;(3)22(0)()(0)x xx f x x xx ⎧+<⎪=⎨-+>⎪⎩.解:(1)由101xx +≥-,得定义域为[1,1)-,关于原点不对称,∴()f x 为非奇非偶函数. (2)由2210|2|20x x ⎧->⎪⎨--≠⎪⎩得定义域为(1,0)(0,1)-,∴22lg(1)()(2)2x f x x -=---22lg(1)x x -=-, ∵2222lg[1()]lg(1)()()x x f x x x----=-=--()f x = ∴()f x 为偶函数 (3)当0x <时,0x ->,则22()()()()f x x x x x f x -=---=-+=-,当0x >时,0x -<,则22()()()()f x x x x x f x -=--=--+=-,综上所述,对任意的(,)x ∈-∞+∞,都有()()f x f x -=-,∴()f x 为奇函数.例2.已知函数()f x 对一切,x y R ∈,都有()()()f x y f x f y +=+, (1)求证:()f x 是奇函数;(2)若(3)f a -=,用a 表示(12)f .解:(1)显然()f x 的定义域是R ,它关于原点对称.在()()()f x y f x f y +=+中, 令y x =-,得(0)()()f f x f x =+-,令0x y ==,得(0)(0)(0)f f f =+,∴(0)0f =, ∴()()0f x f x +-=,即()()f x f x -=-, ∴()f x 是奇函数.(2)由(3)f a -=,()()()f x y f x f y +=+及()f x 是奇函数, 得(12)2(6)4(3)4(3)4f f f f a ===--=-.例3.(1)已知()f x 是R 上的奇函数,且当(0,)x ∈+∞时,()(1f x x =,则()f x的解析式为(10()(10x x f x x x ⎧+≥⎪=⎨<⎪⎩.(2) (《高考A 计划》考点3“智能训练第4题”)已知()f x 是偶函数,x R ∈,当0x >时,()f x 为增函数,若120,0x x <>,且12||||x x <,则 ( B )A .12()()f x f x ->-B .12()()f x f x -<-C .12()()f x f x ->-D . 12()()f x f x -<-例4.设a 为实数,函数2()||1f x x x a =+-+,x R ∈. (1)讨论()f x 的奇偶性; (2)求 ()f x 的最小值.解:(1)当0a =时,2()()||1()f x x x f x -=-+-+=,此时()f x 为偶函数;当0a ≠时,2()1f a a =+,2()2||1f a a a -=++,∴()(),()(),f a f a f a f a -≠-≠- 此时函数()f x 既不是奇函数也不是偶函数.(2)①当x a ≤时,函数2213()1()24f x x x a x a =-++=-++, 若12a ≤,则函数()f x 在(,]a -∞上单调递减,∴函数()f x 在(,]a -∞上的最小值为2()1f a a =+; 若12a >,函数()f x 在(,]a -∞上的最小值为13()24f a =+,且1()()2f f a ≤.②当x a ≥时,函数2213()1()24f x x x a x a =+-+=+-+,若12a ≤-,则函数()f x 在[,)a +∞上的最小值为13()24f a -=-,且1()()2f f a -≤;若12a >-,则函数()f x 在[,)a +∞上单调递增,∴函数()f x 在[,)a +∞上的最小值2()1f a a =+.综上,当12a ≤-时,函数()f x 的最小值是34a -,当1122a -<≤时,函数()f x 的最小值是21a +,当12a >,函数()f x 的最小值是34a +.例5.(《高考A 计划》考点3“智能训练第15题”)已知()f x 是定义在实数集R 上的函数,满足(2)()f x f x +=-,且[0,2]x ∈时,2()2f x x x =-,(1)求[2,0]x ∈-时,()f x 的表达式;(2)证明()f x 是R 上的奇函数. (参见《高考A 计划》教师用书57P )(四)巩固练习:《高考A 计划》考点10智能训练6.五.课后作业:《高考A 计划》考点10,智能训练2,3, 8,9,10,11,13.。
江苏省邳州市第二中学高三数学 第7课时 函数的概念复习学案 苏教版

1江苏省邳州市第二中学高三数学复习:第7课时 函数的概念学案 苏教版一.课题:二.教学目标:了解映射的概念,在此基础上加深对函数概念的理解;能根据函数的三要素判断两个函数是否为同一函数;理解分段函数的意义.三.教学重点:函数是一种特殊的映射,而映射是一种特殊的对应;函数的三要素中对应法则是核心,定义域是灵魂.四.教学过程: (一)主要知识:1.对应、映射、像和原像、一一映射的定义; 2.函数的传统定义和近代定义; 3.函数的三要素及表示法. (二)主要方法:1.对映射有两个关键点:一是有象,二是象惟一,缺一不可;2.对函数三要素及其之间的关系给以深刻理解,这是处理函数问题的关键; 3.理解函数和映射的关系,函数式和方程式的关系.(三)例题分析: 例1.(1)A R =,{|0}B y y =>,:||f x y x →=; (2)*{|2,}A x x x N =≥∈,{}|0,B y y y N =≥∈,2:22f x y x x →=-+;(3){|0}A x x =>,{|}B y y R =∈,:f x y x →=±. 上述三个对应(2)是A 到B 的映射.例2.已知集合{}(,)|1M x y x y =+=,映射:f M N →,在f 作用下点(,)x y 的象是(2,2)x y ,则集合N = ( D )()A {}(,)|2,0,0x y x y x y +=>> ()B {}(,)|1,0,0x y xy x y =>> ()C {}(,)|2,0,0x y xy x y =<< ()D {}(,)|2,0,0x y xy x y =>>解法要点:因为2x y +=,所以2222xyx y+⋅==.例3.设集合{1,0,1}M =-,{2,1,0,1,2}N =--,如果从M 到N 的映射f 满足条件:对M 中的每个元素x 与它在N 中的象()f x 的和都为奇数,则映射f 的个数是 ( D )()A 8个 ()B 12个 ()C 16个 ()D 18个 解法要点:∵()x f x +为奇数,∴当x 为奇数1-、1时,它们在N 中的象只能为偶数2-、0或2,由分步计数原理和对应方法有239=种;而当0x =时,它在N 中的象为奇数1-或1,共有2种对应方法.故映射f 的个数是9218⨯=.例4.矩形ABCD 的长8AB =,宽5AD =,动点E 、F 分别在BC 、CD 上,且CE CF x ==,(1)将AEF ∆的面积S 表示为x 的函数()f x ,求函数()S f x =的解析式; (2)求S 的最大值. 解:(1)2111()408(5)5(8)222ABCD CEF ABE ADF S f x SS S S x x x ∆∆∆==---=--⨯⨯--⨯⨯-222113113169()22228x x x =-+=--+.∵CE CB CD ≤≤,∴05x <≤,∴函数()S f x =的解析式:2113169()()(05)228S f x x x ==--+<≤; (2)∵()f x 在(]0,5x ∈上单调递增,∴max (5)20S f ==,即S 的最大值为20.例5.函数()f x 对一切实数x ,y 均有()()(21)f x y f y x y x +-=++成立,且(1)0f =, (1)求(0)f 的值;(2)对任意的11(0,)2x ∈,21(0,)2x ∈,都有12()2log a f x x +<成立时,求a 的取值范围. 解:(1)由已知等式()()(21)f x y f y x y x +-=++,令1x =,0y =得(1)(0)2f f -=, 又∵(1)0f =,∴(0)2f =-.(2)由()()(21)f x y f y x y x +-=++,令0y =得()(0)(1)f x f x x -=+,由(1)知(0)2f =-,∴2()2f x x x +=+.∵11(0,)2x ∈,∴22111111()2()24f x x x x +=+=+-在11(0,)2x ∈上单调递增,∴13()2(0,)4f x +∈.要使任意11(0,)2x ∈,21(0,)2x ∈都有12()2log a f x x +<成立,当1a >时,21log log 2a ax <,显然不成立. 当01a <<时,21log log 2a a x >,∴0113log 24a a <<⎧⎪⎨≥⎪⎩,解得3414a ≤< ∴a 的取值范围是34[,1)4.(四)巩固练习:1.给定映射:(,)(2,)f x y x y xy →+,点11(,)66-的原象是11(,)32-或12(,)43-.2.下列函数中,与函数y x =相同的函数是( C )()A 2x y x= ()B 2()y x = ()C lg10x y =()D 2log 2xy =3.设函数3,(10)()((5)),(10)x x f x f f x x -≥⎧=⎨+<⎩,则(5)f =8.五.课后作业:《高考A 计划》考点7,智能训练5,7,9,10,13,14.。
江苏省邳州市第二中学高三数学 第50课时 椭圆复习学案 苏教版

江苏省邳州市第二中学高三数学复习:第50课时 椭圆学案 苏教版一.复习目标:熟练掌握椭圆的定义、标准方程、简单的几何性质及参数方程.二.知识要点:1.椭圆的定义(1)第一定义: .(2)第二定义: .2.标准方程: .3.几何性质: .4.参数方程 .三.课前预习:1.设一动点P 到直线3x =的距离与它到点(1,0)A 的距离之比为3,则动点P 的轨迹方程是 ( )()A 22132x y += ()B 22132x y -= ()C 22(1)132x y ++= ()D 22123x y += 2.曲线192522=+y x 与曲线)9(192522<=-+-k ky k x 之间具有的等量关系 ( ) ()A 有相等的长、短轴 ()B 有相等的焦距()C 有相等的离心率 ()D 3.已知椭圆的长轴长是短轴长的3方程是 .4.底面直径为12cm 的圆柱被与底面成30该椭圆的长轴长 ,短轴长 ,离心率为5.已知椭圆22221(0)x y a b a b +=>>的离心率为35针方向旋转2π后,所得新椭圆的一条准线方程3是 ;新椭圆方程是 .四.例题分析:例1.设,A B 是两个定点,且||2AB =,动点M 到A 点的距离是4,线段MB 的垂直平分线l 交MA 于点P ,求动点P 的轨迹方程.例2.已知椭圆22221(0)x y a b a b+=>>,P 为椭圆上除长轴端点外的任一点,12,F F 为椭圆的两个焦点,(1)若α=∠21F PF ,β=∠21F PF ,求证:离心率2cos 2cosβαβα-+=e ; (2)若θ221=∠PF F ,求证:21PF F ∆的面积为2tan b θ⋅.例3.设椭圆2211x y m +=+的两个焦点是12(,0),(,0)(0)F c F c c ->,且椭圆上存在点P ,使得直线1PF 与直线2PF 垂直.(1)求实数m 的取值范围;(2)设l 是相应于焦点2F 的准线,直线2PF 与l 相交于点Q,若22||2||QF PF =,求直线2PF 的方程. 五.课后作业: 班级 学号 姓名1.P 是椭圆14522=+y x 上的一点,1F 和2F 是焦点,若1230F PF ∠=,则12F PF ∆的面积等于 ( )()A 3316 ()B )32(4- ()C )32(16+ ()D 16 2.已知椭圆22221(0)x y a b a b+=>>的左焦点为 F ,(,0),(0,)A a B b -为椭圆的两个顶点,若F 到AB,则椭圆的离心率为 ( )()A 77- ()B 77()C 12 ()D 453. 椭圆C 与椭圆14)2(9)3(22=-+-y x ,关于直线0x y +=对称,则椭圆C 的方程是___________________.4.到两定点12(3,0),(9,0)F F 的距离和等于10的点的轨迹方程是 .5.已知椭圆19822=++y a x 的离心率21=e ,则a 的值等于 .6.如图,PMN ∆中,1tan 2PMN ∠=,tan 2PNM ∠=-,PMN ∆面积为1,建立适当的坐标系,求以M 、N 为焦点,经过点P 的椭圆方程.7.AB 是椭圆22221(0)x y a b a b+=>>中不平行于对称轴的一条弦,M 是AB 的中点, O 是椭圆的中心,求证:OM AB k k ⋅为定值.8.已知椭圆13422=+y x ,能否在此椭圆位于y 轴左侧的部分上找到一点M ,使它到左准线的距离为它到两焦点12,F F 距离的等比中项,若能找到,求出该点的坐标,若不能找到,请说明理由. M NP。
江苏省邳州市第二中学高三数学 巩固练习(3) 苏教版
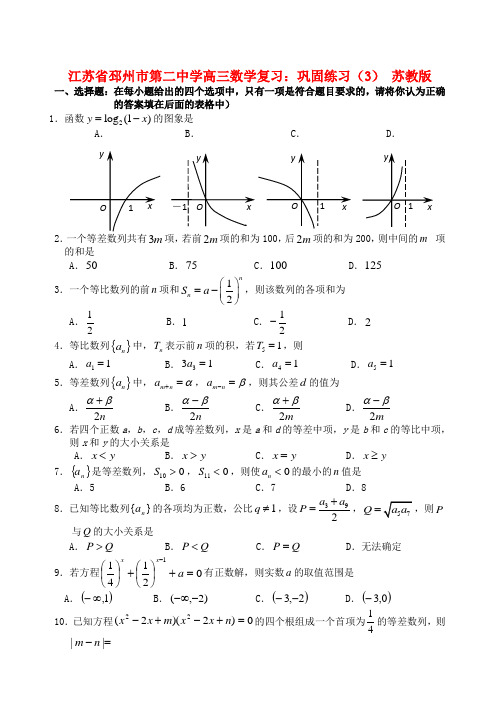
江苏省邳州市第二中学高三数学复习:巩固练习(3) 苏教版一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请将你认为正确的答案填在后面的表格中)1.函数2log (1)y x =-的图象是 A . B . C . D .2.一个等差数列共有项,若前2m 项的和为100,后2m 项的和为200,则中间的m项的和是 A .50 B .75 C .100 D .1253.一个等比数列的前n 项和12nn S a ⎛⎫=- ⎪⎝⎭,则该数列的各项和为A .12 B .1 C .12- D .24.等比数列{}n a 中,n T 表示前n 项的积,若51T =,则A .11a =B .331a =C .41a =D .51a =5.等差数列{}n a 中,m n a α+=,m n a β-=,则其公差d 的值为A .2n αβ+ B .2n αβ- C .2m αβ+ D .2mαβ- 6.若四个正数a ,b ,c ,d 成等差数列,x 是a 和d 的等差中项,y 是b 和c 的等比中项,则x 和y 的大小关系是 A .x y < B .x y > C .x y = D .x y ≥ 7.{}n a 是等差数列,100S >,110S <,则使0n a <的最小的n 值是A .5B .6C .7D .88.已知等比数列}{n a 的各项均为正数,公比1q ≠,设392a a P +=,Q =P 与Q 的大小关系是A .P Q >B .P Q <C .P Q =D .无法确定9.若方程021411=+⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-a x x有正数解,则实数a 的取值范围是A .()1,∞-B .)2,(--∞C .()2,3--D .()0,3-10.已知方程0)2)(2(22=+-+-n x x m x x 的四个根组成一个首项为41的等差数列,则=-||n mA .1B .3 C .1 D .3 11.在等比数列{}n a 中,7116a a ⋅=,4145a a +=,则2010a a 的值是________; 12.已知()f x =1,01,0x x ≥⎧⎨-<⎩,则不等式(2)(2)5x x f x ++⋅+≤的解集是______ ____;13.某航空公司规定,乘机所携带行李的重量(kg )与其运费(元)由如图的一次函数图像确定, 那么乘客免费可携带行李的最大重量为 ____________;14.若干个能唯一确定一个数列的量称为该数列的“基本量”。
高三数学第一轮复习教案第66课时——多面体与球(学案)

高三数学第一轮复习讲义(66)球与多面体一.复习目标:1. 了解多面体、正多面体的概念,了解多面体的欧拉公式,并利用欧拉公式解决有关问题;2.了解球、球面的概念, 掌握球的性质及球的表面积、体积公式, 理解球面上两点间距离的概念, 了解与球的有的内接、外切几何问题的解法.二.主要知识:1.欧拉公式 ;2.球的表面积 ;球的体积公式 ;3.球的截面的性质: .三.课前预习:1.一个凸多面体的顶点数为20,棱数为30,则它的各面多边形的内角和为 ( )()A 2160 ()B 5400 ()C 6480 ()D 72002.一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积是 ( )()A 3π ()B 4π ()C ()D 6π3.正四面体的中心到底面的距离与这四面体的高的比是 ( )()A 21 ()B 31 ()C 41 ()D 61 4.地球表面上从A 地(北纬45,东经120)到B 地(北纬45,东经30)的最短距离为(球的半径为R ) ( )()A 4R π ()B R π ()C 3R π ()D 2R π5.设,,,P A B C 是球O 面上的四点,且,,PA PB PC 两两互相垂直,若PA PB PC a ===则球心O 到截面ABC 的距离是 .四.例题分析:例1.已知三棱锥P ABC -内接于球, 三条侧棱两两垂直且长都为1, 求球的表面积与体积.例2.在北纬60圈上有甲、乙两地,它们的纬度圆上的弧长等于2R π (R 为地球半径),求甲,乙两地间的球面距离。
例3.如图,球心到截面的距离为半径的一半,BC 是截面圆的直径,D 是圆周上一点,CA 是球O 的直径,(1) 求证:平面ABD ⊥平面ADC ;(2) 如果球半径是13,D 分BC 为两部分, 且:1:2BD DC =,求AC 与BD 所成的角;(3) 如果:2BC DC =,求二面角B AC D --的大小。
江苏省邳州市第二中学高三数学 第68课时 二项式定理(1)复习学案 苏教版

江苏省邳州市第二中学高三数学复习:第68课时 二项式定理(1)学案 苏教版一.复习目标:1.掌握二项式定理和二项展开式的性质,并能用它们讨论整除、近似计算等相关问题.2.能利用二项展开式的通项公式求二项式的指数、求满足条件的项或系数.二.知识要点:1.二项式定理: .2.二项展开式的性质:(1)在二项展开式中,与首末两端“等距离”的两项的二项式系数 .(2)若n 是偶数,则 的二项式系数最大;若n 是奇数,则 的二项式系数最大.(3)所有二项式系数的和等于 .(4)奇数项的二项式系数的和与偶数项的二项式系数的和 .三.课前预习:1.设二项式n xx )13(3+的展开式的各项系数的和为P ,所有二项式系数的和为S ,若272=+S P ,则=n ( A )()A 4 ()B 5 ()C 6 ()D 82.当+∈N n 且2≥n 时,q p n +=++++-52221142 (其中N q p ∈,,且50<≤q ),则q 的值为 ( A )()A 0 ()B 1 ()C 2 ()D 与n 有关3.在62)12(xx -的展开式中常数项是605=T ;中间项是34160x T -=. 4.在1033)3(x x -的展开式中,有理项的项数为第3,6,9项.5.求62)321(x x -+展开式里5x 的系数为-168.6.在7)1(+ax 的展开式中,3x 的系数是2x 的系数与4x 的系数的等差中项,若实数1>a ,那么=a 5101+. 四.例题分析:例1.求9)23(x -展开式中系数绝对值最大的项.解:9)23(x -展开式的通项为r r r r r r r r x C x C T ⋅⋅⋅-=-⋅⋅=--+999913)2()2(3,设第1+r 项系数绝对值最大,即⎪⎩⎪⎨⎧⋅⋅≥⋅⋅⋅⋅≥⋅⋅-----++-r r r r r r r r r r r r C C C C 101919981919932323232, 所以⎩⎨⎧≥--≥+rr r r 322021833,∴43≤≤r 且N r ∈,∴3=r 或4=r ,故系数绝对值最大项为3448988x T -=或45489888x T =.例2.已知n x x )12(2lg lg ++展开式中最后三项的系数的和是方程0)7272lg(2=--y y 的正数解,它的中间项是2lg 2410+,求x 的值.解:由0)7272lg(2=--y y 得073722=--y y ,∴1-=y (舍去)或73=y , 由题意知,732412=+⋅+⋅--n n n n n n C C C ,∴6=n已知条件知,其展开式的中间项为第4项,即20001016022lg 24)2lg (lg 3)2lg (lg 3336==⋅=⋅⋅+++x x x x C ,∴012lg lg 2lg lg 2=-+⋅+x x ,∴1lg -=x 或5lg 2lg 1lg =-=x ,∴101=x 或5=x .经检验知,它们都符合题意。
江苏省邳州市第二中学高三数学第9课时函数的值域复习学案苏教版

( 4) y x 4 1 x ; ( 5) y x 1 x2 ;
( 6) y | x 1| | x 4 | ;
(7) y
2x2 x 2 ; x2 x 1
( 8) y
解:( 1)(一)公式法(略)
2x2 x 1 (x
2x 1
1 ) ; ( 9) y 2
1 sin x . 2 cos x
(二)(配方法)
已知 2003 年,生产化妆品的固定投入为 3 万元,每生产 1 万件化妆品需再投入 32 万元.当将每件
化妆品的售价定为“年平均每件成本的
150%”与“年平均每件所占促销费的一半”之和,则当年
产销量相等.
( 1)将 2003 年的年利润 y 万元表示为年促销费 t 万元的函数;
( 2)该企业 2003 年的促销费投入多少万元时,企业的年利润最
( 2)求复合函数的值域:设
x2 6 x 5 (
0 ),则原函数可化为 y
.
又∵
x2 6x 5 (x 3)2 4 4 ,∴ 0
4 ,故
[0,2] ,
∴y
x2 6x 5 的值域为 [0, 2] .
( 3)(法一)反 函数法: y 3x 1 的反函数为 y 2x 1 ,其定义域为 { x
x2
x3
∴原函数 y 3x 1 的值域为 { y R | y 3} . x2
∴当促销费定为 7 万元时, 2003 年该化妆品的值域为 (0,1) . 2x 1
2.若函数 f ( x) log a x 在 [2, 4] 上的最大值与最小值之差为
2,则 a
2或 2. 2
五.课后作业: 《高考 A 计划》考点 1,智能训练 3, 4, 9,12, 13,14.
江苏省邳州市第二中学高三数学 第1课时 集合的概念复习学案 苏教版

1江苏省邳州市第二中学高三数学复习:第1课时 集合的概念学案 苏教版一.课题:二.教学目标:理解集合、子集的概念,能利用集合中元素的性质解决问题,掌握集合问题的常规处理方法. 三.教学重点:集合中元素的3个性质,集合的3种表示方法,集合语言、集合思想的运用.四.教学过程:(一)主要知识:1.集合、子集、空集的概念;2.集合中元素的3个性质,集合的3种表示方法;3.若有限集A 有n 个元素,则A 的子集有2n 个,真子集有21n -,非空子集有21n -个,非空真子集有22n -个.(二)主要方法:1.解决集合问题,首先要弄清楚集合中的元素是什么;2.弄清集合中元素的本质属性,能化简的要化简;3.抓住集合中元素的3个性质,对互异性要注意检验;4.正确进行“集合语言”和普通“数学语言”的相互转化.(三)例题分析:例1.已知集合2{1}P y x ==+,2{|1}Q y y x ==+,2{|1}E x y x ==+,2{(,)|1}F x y y x ==+,{|1}G x x =≥,则( D ) ()A P F = ()B Q E = ()C E F =()D Q G =解法要点:弄清集合中的元素是什么,能化简的集合要化简.例2.设集合{},,P x y x y xy =-+,{}2222,,0Q x y x y =+-,若P Q =,求,x y 的值及集合P 、Q . 解:∵P Q =且0Q ∈,∴0P ∈.(1)若0x y +=或0x y -=,则220x y -=,从而{}22,0,0Q x y =+,与集合中元素的互异性矛盾,∴0x y +≠且0x y -≠;(2)若0xy =,则0x =或0y =.当0y =时,{},,0P x x =,与集合中元素的互异性矛盾,∴0y ≠;当0x =时,{,,0}P y y =-,22{,,0}Q y y =-,由P Q =得220y y y y y -=⎧⎪=-⎨≠⎪⎩ ① 或220y y y y y -=-⎧⎪=⎨≠⎪⎩ ② 由①得1y =-,由②得1y =,∴{01x y ==-或{01x y ==,此时{1,1,0}P Q ==-.例3.设集合1{|,}24k M x x k Z ==+∈, 1{|,}42k N x x k Z ==+∈,则 ( B ) ()A M N = ()B M N ⊂≠ ()C M N ⊇ ()D M N φ= 解法一:通分;2 解法二:从14开始,在数轴上表示. 例4.若集合{}2|10,A x x ax x R =++=∈,集合{}1,2B =,且A B ⊆,求实数a 的取值范围. 解:(1)若A φ=,则240a ∆=-<,解得22a -<<;(2)若1A ∈,则2110a ++=,解得2a =-,此时{1}A =,适合题意;(3)若2A ∈,则22210a ++=,解得52a =-,此时5{2,}2A =,不合题意; 综上所述,实数m 的取值范围为[2,2)-.例5.设2()f x x px q =++,{|()}A x x f x ==,{|[()]}B x f f x x ==,(1)求证:A B ⊆;(2)如果{1,3}A =-,求B .解答见《高考A 计划(教师用书)》第5页.(四)巩固练习:1.已知2{|2530}M x x x =--=,{|1}N x mx ==,若N M ⊆,则适合条件的实数m 的集合P 为1{0,2,}3-;P 的子集有 8 个;P 的非空真子集有 6 个.2.已知:2()f x x ax b =++,{}{}|()22A x f x x ===,则实数a 、b 的值分别为2,4-.3.调查100名携带药品出国的旅游者,其中75人带有感冒药,80人带有胃药,那么既带感冒药又带胃药的人数的最大值为 75 ,最小值为 55 .4.设数集3{|}4M x m x m =≤≤+,1{|}3N x n x n =-≤≤,且M 、N 都是集合{|01}x x ≤≤的子集,如果把b a -叫做集合{}|x a x b ≤≤的“长度”,那么集合M N 的长度的最小值是112.五.课后作业:《高考A 计划》考点1,智能训练4,5,6,7,8,9,11,12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
以这些线段为棱的八面体的体积为
(D) a3 12
()
4.有一棱长为 a 的正方体框架,其内放置一气球,是其充气且尽可能地膨胀
的形状 ) ,则气球表面积的最大值为
( A) a2
(B) 2 a2
(C) 3 a2
(D) 4 a2
( 仍保持为球 ()
5.以正方体的顶点为顶点作正四面体,则正方体的表面积与正四面体的表面积之比为(
(A) 3
(B) 4
(C) 3 3
( D) 6
3.正四面体的中心到底面的距离与这四面体的高的比是
()
( A) 1 2
(B) 1 3
(C ) 1 4
(D) 1 6
4.地球表面上从 A 地 ( 北纬 45 ,东经 120 ) 到 B 地 ( 北纬 45 ,东经 30 ) 的最短距离为 (球
的半径为 R )
()
R ( A)
4
(B) R
(C ) R 3
(D) R 2
5.设 P, A, B , C 是球 O 面上的四点 , 且 PA, PB, PC 两两互相垂直 , 若 PA PB PC a
则球心 O 到截面 ABC 的距离是
.
四.例题分析:
例 1.已知三棱锥 P ABC 内接于球 , 三条侧棱两两垂直且长都为 1, 求球的表面积与体积 .
二.主要知识:
1.欧拉公式
;
2.球的表面积
;球的体积公式
;
3.球的截面的性质:
.
三.课前预习:
1.一个凸多面体的顶点数为 20 ,棱数为 30,则它的各面多边形的内角和为
()
( A) 2160
( B) 5400
(C ) 6480
( D ) 7200
2.一个四面体的所有棱长都为
2 ,四个顶点在同一球面上, 则此球的表面积是 ( )
1
例 2.在北纬 60 圈上有甲、 乙两地, 它们的纬度圆上的弧长等于
求甲,乙两地间的球面距离。
R ( R 为地球半径 ) , 2
例 3.如图 , 球心到截面的距离为半径的一半,
是球 O 的直径, (1) 求证:平面 ABD 平面 ADC ;
BC 是截面圆的直径 , D 是圆周上一点, CA
(2) 如果球半径是 13 ,D 分 BC 为两部分 , 且 BD : DC 1: 2 ,求 AC 与 BD 所成的角;
球心,则直线 OA 与截面 ABC 所成的角是
()
( A) arcsin 3 6
( B) arccos 3 6
3 (C ) arcsin
3
( D ) arccos 3 3
10.一个多面体共有 10 个顶点 , 每个顶点处都有四条棱 , 面的形状只有三 角形和四边形 ,
求该多面体中三角形和四边形的个数分别是
江苏省邳州市第二中学高三数学复习:第 66 课时 多面体与球学案
苏教版
一.复习目标:
1. 了解多面体、正多面体的概念 , 了解多面体的欧拉公式 , 并利用欧拉公式解决有关问题;
2.了解球、球面的概念 , 掌握球的性质及球的表面积、体积公式 , 理解球面上两点间距
离的概念 , 了解与球的有的内接、外切几何问题的解法.
( A) 2
( B) 3
33 (C )
2
( D ) 12
()
8.已知球 O的半径为 1, A、B、C 三点都在球面上,且每两点间的球面距离均为
心 O到平面 ABC的距离为
( A) 1
3
( B) 3
3
(C ) 2
3
(
(D) 6
3
,则球
2
)
3
9.如图, A, B, C 是表面积为 48 的球面上三点, AB 2, BC 4, ABC 60 , O 为
.
11.有 30 个顶点的凸多面体,它的各面多边形内角总和是
_____
___
.
12.球面上三点 A, B, C 组成这个球的一个截面的内接三角形,
且球心到该截面的距离为球的半径的一半,
(1) 求球的体积;
(2)
求 A, C 两点的球面距离。
AB 18,BC 24,AC 30,
4
(3) 如果 BC : DC 3 : 2 ,求二面角 B AC D 的大小。
2
五.课后作业:
班级 学号
姓名
1.给出下列命题:①正四棱柱是正多面体;②正四棱柱是简单多面体;③简单多面体是
凸多面体;④以正四面体各面的中心为顶点的四面体仍然是正四面体;其中正确的命题个
数为
()
( A) 1 个
(B)2 个
)
( A) 3:1
(B) 3 :1
(C) 3 : 2
(D) 2: 3
6.地球半径为 R, A、B 两地均在北纬 45°圈上,两地的球面距离为
经度之差的绝对值为
( A) 3
( B) 2
(C) 2 3
(D ) 4
R ,则 A, B 两地的 3
()
7.棱长为 1 的正方体的八个顶点ቤተ መጻሕፍቲ ባይዱ在同一个球的表面上,则这个球的表面积为
(C)3 个
(D) 4 个
2.已知一个简单多面体的各个顶点都有三条棱, 则顶点数 V 与面数 F 满足的关系是 ( ) ( A) 2F V 4 (B) 2F V 4 (C) 2F V 2 (D) 2F V 2
3.棱长为 a 的正方体中, 连接相邻两个面的中心,
a3 ( A)
3
( B ) a3 4
(C ) a3 6
