化学反应工程知识点复习
(版)化学反应工程基础知识(笔记)

化学反响工程根底知识总结〔笔记〕1、化学反响工程是一门研究涉及化学反响的工程问题的学科。
如何将其在工业规模上实现是化学反响工程的主要任务。
2、理想置换反响器的特点:①由于流体沿同一方向,以相同速度向前推进,在反响器内没有物料的返混,所有物料通过反响器的时间都是相同的②在垂直于流动方向上的同一截面,不同径向位置的流体特性是一致的③在定常态下操作,反响器内状态只随轴向位置改变,不随时间改变。
3、全混流反响器的特性①物料在反响器内充分返混②反响器内各物料参数均一③反响器的出口组成与器内物料组成相同④反响过程中连续进料与出料,是一定常态过程。
4、返混的定义:物料在反响器内不仅有空间上的混合而是有时间上的混合,这种混合过程称返混。
5、非均相催化反响过程步骤①反响组分从流体主体向固体催化剂外外表传递②反响组分从外外表向催化剂内外表传递③反响组分在催化剂外表的活性中心上吸附④在催化剂外表上进行化学反响⑤反响产物在催化剂外表上解吸⑥反响产物从催化剂内外表向外外表传递⑦反响产物从催化剂的外外表向流体主体传递6、兰格缪尓〔Langmuir〕吸附模型条件①催化剂外表上活性中心分布是均匀的②吸附活化能和脱附活化能与外表吸附的程度无关③每个活性中心仅能吸附一个气相分子④被吸附分子间互不影响,也不影响空位对气相分子的吸附。
7、焦姆金〔Temkhh〕吸附模型:一般吸附活化能随覆盖率的增加而增大,脱附活化能那么随覆盖率的增加而减小,因此吸附热必然随覆盖率的增加而减小。
8、催化剂颗粒内气体扩散:多孔催化剂颗粒内的扩散现象是很复杂的。
除扩散路径极不规那么外,孔的大小不同时,气体分子扩散机理亦有所不同。
当孔径较大时,分子的扩散阻力要是由于分子间碰撞所致,这种扩散通常所称的分子扩散或容积扩散。
当微孔的孔径小于分子的平均自由程时,分子与孔壁的碰撞时机超过了分子间的相互碰撞,从而使分子与孔壁的碰撞成为扩散阻力的主要因素,称为克努森〔Knudson〕扩散。
反应工程复习要点

燃烧,就是燃料和氧化剂之间产生剧烈的氧化反映,并且燃烧化学反应受到流动、扩散和传热过程的影响,特别是在工业窑炉内进行的燃烧过程更加复杂。
烧成,就是把原料或坯件置于窑炉内经受高温处理通过十分复杂的物理化学反应最后变成人们所需的硅酸盐产品。
化学反应速率:单位时间内单位反应区域内物料量的变化。
r=反应量/(单位时间×单位反应区)转化率(反应率):表示反应过程中的小时的反应物摩尔量与初始反应混合物中该细分的摩尔量之比。
均相反应是指在均一的气相或液相中进行的化学反应,如气体燃料和空气充分混合后的燃烧就是典型的均气反应过程。
分为简单反应和复杂反应。
基元反应:任何化学反应的发生都必须以反应物分子之间的相互碰撞或直接作用为前提,如果在碰撞时一步就能直接转变为生成物分子,则称该反应为基元反应简单反应又称单一反应,是指一组特定的反应物只形成一组特定的生成物的化学反应。
它可以是基元反应,也可以是非基元反应。
大多数的无机反应属于简单反应,例如碳酸钠与氢氧化钙的反应。
简单反应的特点是只需要用一个化学反应方程式和一个动力学方程式便能加以描述。
具有幂函数型的化学反应动力学模型。
复杂反应又称多个反应,是指反应混合物中同时进行几组不同的反应,因此要用几个动力学方程式才能加以描述。
复杂反应都是非基元反应,即由两个或两个以上的基元反应组合而成的。
复杂反应具有双曲函数型的动力学模型。
反应级数是指动力学方程式中浓度项的幂指数。
一般情况下,级数在一定温度范围内保持不变,它的绝对值不超过三,可以是零或分数,也可以是负数。
反应级数的实验室测定:根据处理实验数据的方法不同,可以分为积分法,微分法,半衰期法。
反应速率常数K是反应物浓度等于1时的反应速率,故称为反应的比速率。
K=K0·e(-E/RT)K0:频率因子(常数);E:活化能,J/mol;R=8.314J/(mol.k);K:kmol反应活化能E表示为使反应物分子“激发”到活化能状态所需给予的能量。
(完整word版)化学反应工程学知识点总结

第一章1、过程工业:以物质转化为核心2、装置与产品制造工业:以物件的加工和组装为核心3、化工过程:原料获取(预处理)、化学反应过程、产品分离和提纯4、本科目研究的对象:以工业规模进行化学反应过程,目的:实现工业反应过程的优化5、实现工业反应过程的优化分两类:设计优化、操作优化6、反应过程优化的技术指标:反应速率、反应选择率、反应收率、能量消耗7、决策变量:结构变量、操作方式、工艺条件(结构变量:反应器类型,单相:均相管式反应器和均相釜式反应器,两相,:固定床反应器,液化床,气液相反应器,三相:)(操作方式:间歇、连续、半连续,加料方式:一次性、分批加料、分段加料)8、化学反应工程研究的内容:1化学反应过程(容积、表面反应过程)1、物理传递过程(反混合不均匀性、传质过程、传热过程)9、研究方法(数学模型法):数学表达式即动力学方程式(一反)、物料、热量、动量衡算式(三传)、参数计算式10、数学模型法基本特征:过程分解、过程简化第二章1、化学反应动力学是研究化学反应速率和机理的科学2、本征动力学(微观):排除物理过程,表观动力学(宏观):包含物理过程3、反应速率定义:反应量/(反应时间)(反应区)4、均相前提:分子尺度上混合均匀、特征:无物理过程5、复杂反应(可逆反应、自催化反应、平行反应、串联反应)6、固体催化剂的组成及活化:特点:活性、选择性、稳定性,组成:活性成分、载体、助催化剂,活化:还原。
7、化学反应过程分为:容积反应过程、表面反应过程8、气固相催化反应过程包括:(内、外)扩散过程、表面反应过程9、吸附模型:理想吸附模型、真实吸附模型10、反应级数的工程意义是:表示反应速率对于反应物浓度变化的敏感程度11、气液非均相反应过程的反应区取法分为:选用液相体积、选用反应器体积12、在包含物理过程影响下测得的反应速率称为表观反应速率。
13、物理传质过程与化学反应过程串联时,通常是慢一步速率的决定表现反应速率(过程速率的控制步骤)14、均相反应动力学是研究反应在同一项中进行的规律性.15、工程上实际的均相反应应满足两个条件:反应系统可以成为均相、预混合过程的时间远小于反应时间吸附分为物理、化学吸附16、化学吸附可分为:活化化学吸附、非活化化学吸附17、化学反应速率特征可以概括地表示为反应速率的浓度效应、温度效应18、基本的物理过程有:返混、传质、传热19、气固相催化反应是指气体在固体催化剂上进行的催化反应第三章1、反应器设计的基本内容:选择合适的反应器类型、确定最佳工艺条件、计算反应器体积2、反应器设计的基本方程包括反应动力学方程式、物料衡算方程式、热量衡算方程式、动量衡算方程式3、物料衡算和反应速率式式描述反应器性能的两个最基本的方程式4、辅助时间是指装料、升温、降温、卸料、清洗时间的总和5、反应后期转化问题的严重程度顺序是:二级>一级>零级6、反应物同时进行两个或两个以上的反应成为平行反应7、平行反应选择率的温度效应是:高温度有利于活化能高的反应8、串联反应:反应物能进一步反应生成其他副产物的反应9、间歇反应器的反应体积是指反应物在反应器中所占的体积第四章1、反应前后物料浓度变化不明显:衡容反应系统2、表征反应前后分子数变化程度的方法的有:膨胀率发、膨胀因子法3、膨胀率¢的定义是指反应组分全部转化后系统体积变化的分率第五章1、全混流:釜式反应器中,一边连续加料、另一边连续出料2、返混:停留时间不同物料的混合3、造成返混的原因:设备中存在不同尺度的环流、不均匀的速度分布4、限制返混的主要措施:分割(横向、纵向)5、连续釜反应器特点:反应物料浓度降低至出料水平,降低了反应速度6、返混是连续化反应时伴生的现象,原因是空间的反向运动和不均匀速度分布第六章1、混合现象:宏观、微观混合2示踪物的输入方法有阶跃注入法、脉冲注入法、周期注入法3、连续反应过程的考察方法:以反应器、反应物料为对象的的考察方法4、非理想流动模型分为:数学模型方法、扩散模型(适合于返混程度较小的非理想流动模型)、多级全混流模型。
化学反应工程知识点梳理
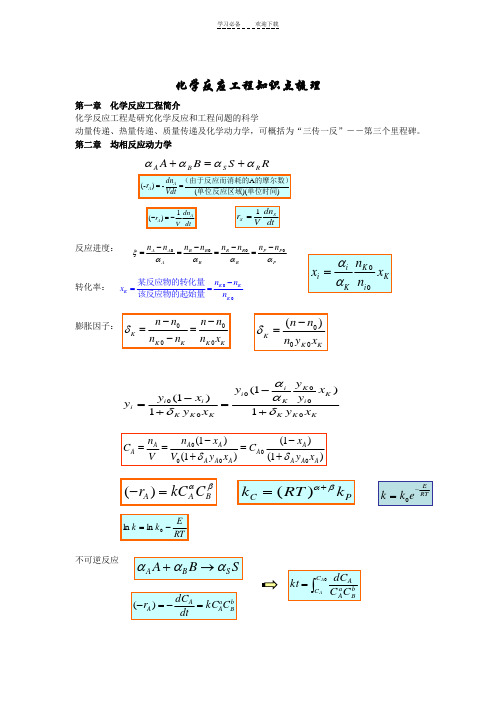
化学反应工程知识点梳理第一章化学反应工程简介化学反应工程是研究化学反应和工程问题的科学动量传递、热量传递、质量传递及化学动力学,可概括为“三传一反”--第三个里程碑。
第二章均相反应动力学反应进度:转化率:膨胀因子:不可逆反应A(-)-()()AAdnrVdt==(由于反应而消耗的的摩尔数)单位反应区域单位时间RSBARSBAαααα+=+1()AAdnrV dt-=-dtdnVr SS1=PPPRRRBBBAAAnnnnnnnnααααξ0-=-=-=-=K KKKn nxn-==某反应物的转化量该反应物的起始量KiKKiixnnxαα=0000KK K K Kn n n nn n n xδ--==-00()KK Kn nn y xδ-=KKKKiKKiiKKKiii xyxyyyxyxyy1)1(1)1(δααδ+-=+-=000(1)(1)(1)(1)A AA AA AA A A A A An xn xC CV V y x y xδδ--===++()A A Br kC Cαβ-=()C Pk RT kαβ+=ERTk k e-=RTEkk-=lnlnSBASBAααα→+bBaAAACkCdtdCr=-=-)(⎰=0AACC bBaAACCdCkt均相催化反应 CC 为催化剂浓度自催化反应A + C → 2C + R …串联反应总收率瞬时收率得率yield总选择性 目的产物P 所生成的摩尔数与副产物S 生成的摩尔数之比,用S0表示:平行反应串联反应()()AA C A dC r kC C dt-=-=CA A A C kCdt dCr =-=-)(A + B P R+S 00PP P A A n n n n -Φ=-/()/p P P A A A r dC dt dC P A r dC dt dC φ====---单位时间内生成的摩尔数单位时间内消耗的摩尔数00/)(A P P P n n n X -=000PP S S n n S n n -=-αA2A αS S (副)αA1A αP P (主),11A A r k C -=(),22A A r k C -=(),1,212()()AA A A A dC r r r k k C dt-=-+-=+=()()A A P A A p P P C k r dt dC r 11,1,1,)(αααα-=--==AA S S S C k dt dC r 22,αα-==tk k A A eC C )(021+-=A P S (均为一级反应)k 1k 2P A P P C k C k dt dC r 21-==PSS C k dt dC r 2==第三章 理想均相反应器 间歇反应器(BSTR)反应时间实际操作时间(operating time)= 反应时间(t) + 辅助时间auxiliary time (t') 反应体积V 是指反应物料在反应器中所占的体积 V = v0 (t + t')为装料系数(the volume charge coefficient),通常在0.4~0.85平推流反应器PFR 空时全混流反应器(CSTR)绝热操作恒容间歇反应器的设计式为:变温平推流反应器⎰⎰--=-=A A A C C A Ax A A A r dC r dx C t 0)()(00等容过程,液相反应 VV ϕ=实际实际的反应器体积为:0V v τ==反应器的容积进料的体积流量0R V dV t v ==⎰反应器中物料反应期的容积的体积流量000()()A A A AA A C C C x V v r r τ-===--0()A A A x V F r =-005000024R R R F v C M ==⨯00000000()(1)A A A A A A x x x A AA A A A E nx x x n n A ART A A dx dx dx t C C C r kC k e C x -===--⎰⎰⎰1001()A A x A A n xA t I x dx k C -=⎰20()()4A A A P A F dx r dV r D dl π=-=-20()4A A A dx D r dl F π-=00000()A x A A A A A dx V V F r v C C τ===-⎰化学反应工程研究的目的是实现工业化学反应过程的优化 全混流平推流多级CSTR 串联的优化对于一级不可逆反应应有PFR: 同间歇釜CSTR:全混流反应器的热衡算方程第四章 非理想流动 停留时间分布()⎰-==A x AAA B A B r dx C t F V 000BR : ()⎰-==Ax A AA P A P r dxCF V 000τPF R: ()000m m A A A A V x F C r τ-==-CST R: 112100010200...(1)(1)(1)Am Am A A A R A A A A A A Am x x x x x V v C kC x kC x kC x -⎛⎫---=+++ ⎪---⎝⎭0121110(1,2,.....1)(1)1Ai RAi Ai Ai v x V i m x k x x -+⎡⎤-∂=-==-⎢⎥∂--⎣⎦11111Ai Ai Ai Ai Ai Ai x xx x x x -++--=--221max 1max 02()k k k P P A C k X C k -==max max 1202211[(/)1]P P A C X C k k ==+1212ln(/)opt k k k k τ=-121opt k k τ=)()1())((0000Pm P P r A c v UAT T c v UA T c v H r V ρρρ+-+=∆--)()1(000P m P r c v UAT T c v UAT Q ρρ+-+= (){}E t P t residence time t t ∆=<<+停留时间分布函数 (){}=<F t P residence time t方差PFRCSTR最大层流流动 轴向扩散模型 0()()d t F t E t t=⎰22222()()()()()()t t t E t dtt t E t dt t E t dt tE t dtσ∞∞∞∞-==-=-⎰⎰⎰⎰0 t t () t t 0 t t E t <⎧⎪=∞=⎨⎪>⎩2220()()()0t t t E t dt t t σ∞=-=-=⎰0 t t () 1 t tF t <⎧=⎨≥⎩()11()t tt tF t e E t et---=-=222 1.0ttθσσ==22()()[2()]r r F t R R =-222/222()2()(1)212()(1)Z t uL E z z Pe tE Ee uL uL e Pe Peθσσ--==--=--。
化学反应工程知识点回顾

化学反应⼯程知识点回顾第⼀章知识点1.化学反应⼯程学的范畴和任务2.化学反应⼯程学的基本⽅法3.化学反应⼯程学的学科系统和编排第⼆章均相反应动⼒学基础知识点 1、概念:①化学计量⽅程:反应物 - ,产物 + ②化学反应速率等温定容反应dtdc r AA -=-反应速率之⽐等于各计量系数的⽐值。
③反应转化率反应程度膨胀因⼦δA 关键组分A 的膨胀因⼦物理意义:每反应掉⼀个摩尔A 所引起反应体系总摩尔数的变化量。
④反应速率⽅程:反应级数 a 、b 由实验确定 k 遵循Arrhenius ⽅程i α1A A dn r V dt-=-00-=K KK K n n x n 0kk k n nξα-=1sii A A αδα==∑a bA AB r kC C -=2、单⼀反应的速率⽅程重点:求取动⼒学参数 1)不可逆反应微分⽅程: 积分⽅程: 2)可逆反应微分⽅程: 反应平衡时: 3)均相催化反应微分⽅程积分⽅程4)⾃催化反应当C A = C M0/2 时,反应速率最⼤ 3、复合反应:平⾏反应串联反应总收率选择性exp[]a E k k RT=-a bA A A BdC r kC C dt-==-0A A C Aa b C ABdC kt C C =?'A A A SdC r kC k C dt-=-=-0A Ae Se r kC k C '-=-=()AA C A dC r kC C dt-=-=A A A C dC r kC C dt-=-=0max 0001ln[]A M M A C t C kC C =-0121()ln ln1A C A A C k k C t C x +==-A B P R +→+A B S +→A B P R S+→→+0000()/()///--Φ==P P P P P A A n n p C C pn a C a 0000()/()/;;()/()/--==--p p p p p p A A A A n n P C C PS S n n a C C a第三章理想反应器1返混的基本定义2⼏个时间的定义反应持续时间t r--在间歇反应器中反应达到⼀定转化率所需时间(不包括辅助时间)。
化学反应工程知识点

化学反应工程知识点1.反应机理和动力学反应机理是指反应的分子层面的步骤和中间产物,它对理解和控制反应过程非常重要。
动力学研究反应速率与反应物浓度的关系,了解反应速率规律,通过动力学模型可以预测反应速率和产物选择性。
2.反应条件的选择反应条件的选择包括温度、压力、反应物浓度、反应物配比和催化剂等。
化学反应的速率和选择性往往受到反应条件的影响,优化反应条件可以提高反应速率和产物质量。
3.反应器的设计和优化反应器是进行化学反应的设备,其设计和优化对反应过程的效率和产品质量具有重要影响。
常见的反应器类型有批式反应器、连续式反应器和循环式反应器等。
反应器的选择和设计要考虑反应物性质、反应过程的控制方式、热传导和质量传递等因素。
4.反应工艺的控制反应工艺的控制包括对反应过程的监测和调节,以维持所需的反应条件和优化产品质量。
常用的控制策略有温度、压力和反应物供给的控制等。
控制系统的设计和优化需要考虑反应机理、反应动力学和工艺实际操作的特点。
5.安全与环保化学反应过程中会产生化学品和能量的变化,单个反应步骤可能会产生副产物和废物。
因此,反应工程也需要关注安全性和环保性。
安全性考虑的因素包括反应物和产物的毒性、易燃性和爆炸性等,以及反应条件的选择和操作的威胁。
环保方面,需要考虑减少废物的生成,回收利用资源,优化反应条件以减少能耗和污染物排放。
6.规模放大与工业化化学反应工程要实现从实验室到工业生产的规模放大和工艺转化。
这涉及到规模放大的技术、成本评估和安全规范,以及将实验室的合成路线或方法转化为适合大规模生产的工艺。
同时,也需要考虑工艺的稳定性和连续运营的可行性。
以上是化学反应工程的一些基本知识点,化学反应工程涵盖了多个学科领域,是化学工程和化学的交叉学科。
化学反应工程的研究和应用有助于解决实际生产中的技术问题,提高反应过程的效率和产品质量,同时也倡导可持续发展和环保意识。
【精品】化学反应工程考点总结

【精品】化学反应工程考点总结化学反应工程是化学反应与化学工程相结合的领域,它涉及到反应热力学、动力学、工艺设计等诸多方面。
在考试中,涉及到化学反应工程的知识点不少,以下就是一些较为重要的考点总结。
1. 化学反应平衡常数在化学反应工程中,平衡常数是一个很重要的概念,它可以用于描述反应的平衡态。
平衡常数被定义为反应物和生成物之间的比例关系。
在考试中,会出现很多计算和应用化学反应平衡常数的问题。
2. 反应热力学反应热力学是另一个非常重要的考点。
它可以用于描述反应中的热量变化,包括反应热、焓变、熵变等。
在实际工业生产中,反应热力学常常被用来设计反应器和预测反应的产物。
3. 反应动力学反应动力学可以用来研究反应速率随反应物浓度、温度、催化剂等因素的变化规律。
在考试中,会经常出现与反应动力学有关的计算题和实际应用题。
4. 反应器设计与控制反应器是进行化学反应的设备,反应器设计与控制是反应器工程的核心内容。
在考试中,会出现和反应器设计、控制有关的题目。
例如,如何选择反应器类型、如何设计反应器容积等。
5. 反应器模型与模拟反应器模型与模拟是指通过建立数学模型来描述反应器中反应的过程。
在考试中,会涉及到一些如何建立反应器模型、如何进行反应器模拟的问题。
6. 催化剂催化剂是化学反应中扮演着重要角色的物质。
在化学反应工程中,催化剂被广泛应用,例如催化剂可以提高反应速率,使反应条件更加温和。
在考试中,催化剂也是很重要的一个考点。
总结以上就是化学反应工程的一些重要考点总结。
在考试中,如果掌握上述考点,相信大家一定会取得不错的成绩。
《化学反应工程》综合复习资料

《化学反应工程》综合复习资料一、填空题1、全混流反应器的E 函数表达式为 ,其无因次方差= ,而平推流反应器的无因次方差= 。
2、工业催化剂性能优劣的三种最主要的性质是 、 、和 。
3、在间歇反应器中进行一恒压气相反应,原料为A 和B 的混合物,其中A 含量为20%(mol),若物料初始体积为2升,则A 转化50%时,物料的总体积为 。
4、基元反应的分子数 (可能/不可能)是小数。
5、某液相反应于50℃下在间歇反应器中进行,反应物A 转化80%需要10min ,如果于相同条件下在平推流反应器中进行,则达到同样的转化率需要的空时为 ;如果同样条件下在全混流反应器中进行,达到同样的转化率需要的空时 。
6、测定非理想流动的停留时间分布函数时,两种最常见的示踪物输入方法为 和 。
7、完全混合反应器(全混流反应器)内物料的温度和浓度 ,并且 (大于/小于/等于)反应器出口物料的温度和浓度。
8、多级混合模型的唯一模型参数为 ,轴向扩散模型的唯一模型参数为: 。
9、对于单一反应,在相同的处理量和最终转化率条件下,选择反应器时主要考虑 ;而对于复合反应,选择反应器时主要考虑的则是 。
2θσ2θσ32A B R +→A R →10、对于反应23A B R +→,各物质反应速率之间的关系为:(-r A ):(-r B ):r R = 。
11、某重油催化裂化装置处理量为100吨重油/h ,未转化重油为6吨/h ,汽油产量为42吨/h ,则重油的转化率为_ _,工业上汽油的收率及选择性为_ _和_ _。
12、某反应的计量方程为A R S →+,则其反应速率表达式 。
13、反应级数 (可能/不可能)大于3, (可能/不可能)是0,基元反应的分子数 (可能/不可能)是0。
14、在一个完整的气—固相催化反应的七大步骤中,属于本征动力学范畴的三步为 、 和 。
15、在均相反应动力学中,利用实验数据求取化学反应速率方程式的两种最主要的方法为 和 。
化学反应工程知识点复习共162页文档

11、不为五斗米折腰。 12、芳菊开林耀,青松冠岩列。怀此 贞秀姿 ,卓为 霜下杰 。
13、归去来兮,田蜀将芜胡不归。 14、酒能祛百虑,菊为制颓龄。 15、春蚕收长丝,秋熟靡王税。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特ቤተ መጻሕፍቲ ባይዱ58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
化学反应工程总复习

化学反应工程综合复习资料一、填空题1.多级混合模型的唯一模型参数为 ,轴向扩散模型的唯一模型参数为 ;2.在均相反应动力学中,利用实验数据求取化学反应速率方程式的两种最主要的方法为和 ;3.反应级数 可能/不可能是0,基元反应的分子数 可能/不可能是0;4.测定非理想流动的停留时间分布函数时,两种最常见的示踪物输入方法为 和 ;5.某一级液相反应在间歇式反应器中进行,5min 转化率为50%,则转化率达到80%需时间__ ____min;6.某反应的速率方程式为n A A r kC -= mol/,则反应级数n 为2时,k 的单位为 _;7.某反应的计量方程为A R S →+,则其反应速率表达式 ;8.所谓“三传一反”是化学反应工程学的基础,其中“三传”是指 、 和 ,“一反”是指 ;9.完全混合反应器全混流反应器内物料的温度和浓度 ,并且 大于/小于/等于反应器出口物料的温度和浓度;10.在一个完整的气—固相催化反应的七大步骤中,属于本征动力学范畴的三步为 、和 ;二、选择题1.对于瞬时收率和总收率,下列正确的说法有 多项选择; A. 对于平推流反应器,反应的瞬时收率与总收率相等; B. 对于全混流反应器,反应的瞬时收率与总收率相等;C. 对于平推流反应器,反应的瞬时收率与总收率之间是积分关系;D. 对于全混流反应器,反应的瞬时收率与总收率之间是积分关系; 2.某反应速率常数的单位为m 3/,该反应为 级反应;A. 零级B. 一级C. 二级D. 不能确定. 3..对于平行反应SA RA 222111n ,E ,k n E ,k −−−→−−−−→−,,活化能E 1>E 2,反应级数n 1<n 2,如果目的产物是R 的话,我们应该在 条件下操作;A. 高温、反应物A 高浓度;B. 高温、反应物A 低浓度;C. 低温、反应物A 高浓度;D. 低温、反应物A 低浓度 4.关于E 函数和F 函数,下面正确的是 ;多项选择A. ⎰∞=0dt )t (E )t (FB. ⎰=t0dt )t (E )t (F ; C. dt /)t (dF )t (E = D. 1dt )t (E )(F 0==∞⎰∞5.t /t e t1)t (E -=是A. 平推流的E 函数B. 全混流的E 函数;C. 平推流串联全混流的E 函数D. 全混流串联平推流的E 函数 6.关于E 函数和F 函数,下面不正确的是 ;A. ⎰∞=0dt )t (E )t (F ;B. ⎰=t0dt )t (E )t (F ; C. dt /)t (dF )t (E =; D. 1dt )t (E )(F 0==∞⎰∞7.对于一级恒容和一级变容不可逆反应,下面叙述正确的是A. 在同一平推流反应器内、在同样条件下进行反应,反应的转化率是一样的;B. 在同一全混流反应器内、在同样条件下进行反应,反应的转化率是一样的;C. 在同一间歇式反应器内、在同样条件下进行反应,反应的转化率是一样的;D. 在同一平推流反应器或间歇式反应器内、在同样条件下进行反应,反应的转化率是一样的8.对于瞬时收率和总收率,下列正确的判断有多项选择;A. 对于平推流反应器,反应的瞬时收率与总收率相等;B. 对于全混流反应器,反应的瞬时收率与总收率相等;C. 对于平推流反应器,反应的瞬时收率与总收率之间是积分关系;D. 对于全混流反应器,反应的瞬时收率与总收率之间是积分关系;9.关于基元反应的认识,正确的是 ;A. 分子数可以是任意的整数;B. 基元反应的计量系数与对应物种的反应级数之间存在一一对应关系;C. 基元反应R2→意义是一样的;A2A→和RD. 基元反应的总反应级数可能是小数;10.对于瞬时收率和总收率,下列正确的判断是A. 对于全混流反应器,反应的瞬时收率与总收率相等;B. 对于平推流反应器,反应的瞬时收率与总收率相等;C. 对于平推流反应器,反应的瞬时收率与总收率之间是积分关系;D. 对于全混流反应器,反应的瞬时收率与总收率之间是积分关系;11.轴向分散系数与扩散系数,下面论述正确的是A. 两者实质上是相同的,都符合Fick定律;B. 两者实质上是不同的,轴向分散系数的定义实际上是借用了Fick定律的形式;C. 轴向分散系数是与流动有关系的;D. 扩散系数是物质本身的一种属性12.对于一个气固相催化反应,减小外扩散和内扩散影响的措施正确的是A. 提高反应器内气体的流速,减小催化剂颗粒的直径;B. 降低反应器内气体的流速,减小催化剂颗粒的直径;C. 降低反应器内气体的流速,增大催化剂颗粒的直径;D. 增加催化剂颗粒的直径,提高反应器内气体的流速13.对于化学反应的认识,下面正确的是A. 化学反应的转化率、目的产物的收率仅与化学反应本身和使用的催化剂有关系;B. 化学反应的转化率、目的产物的收率不仅与化学反应本身和使用的催化剂有关,而且还与反应器内流体的流动方式有关;C. 反应器仅仅是化学反应进行的场所,与反应目的产物的选择性无关;D. 反应器的类型可能直接影响到一个化学反应的产物分布14.关于非理想流动与停留时间分布,论述正确的是A. 一种流动必然对应着一种停留时间分布;B. 一种停留时间分布必然对应着一种流动;C. 一种停留时间分布可能对应着多种流动;D. 流动与停留时间分布存在一一对应关系15.对于一个串联反应,目的产物是中间产物,适宜的反应器是A. 全混流反应器B. 平推流反应器;C. 循环反应器D. 平推流与全混流串联在一起的反应器吸附等温的四个假定:均匀表面、单层吸附、吸附机理相同和无相互作用这几点应该说是非常苛刻的,实际情况很难满足上述要求;然而,对于多数的化学反应,应用这几点假定进行有关的推导,结果一般是可以接受的,其主要原因在于A. 实际反应过程中催化剂表面吸附物种的覆盖度很低;B. 实际的催化剂表面一般很平整;C. 实际的催化剂表面上活性位间的距离较远;D. 实际的催化剂表面上活性位的数量有限三、计算题1、在一反应器入口输入理想脉冲示踪物后,不同时间检测出口示踪物的浓度C,结果如下所示:现有某液相反应物A 在该反应器中进行分解反应,速率方程为:A A r kC -= , k = min -1,若用多级混合流模型预测时,该反应器的出口转化率为多少2、液体反应物AC A0=1mol/L 通过两个串联的全混流反应器发生某不可逆反应,第一个反应器出口的浓度为 mol/L,两个反应器的体积比V 2/V 1=2,反应级数为2:A A r kC -=2mol/求第二个反应器出口的浓度;3、某一级液相反应A R →在一只全混流反应器中进行,转化率为90%,如果再串连一只同样的全混流反应器,使转化率仍维持在90%,试问处理量增加多少4、某速率常数为的一级不可逆反应在一非理想反应器内进行反应,示踪结果表明,t 和2θσ分别为17min 和;求用多级混合流模型预测的转化率;5、纯组分A 发生下述平行反应,A 的起始浓度为2mol/L, 反应在恒温的条件下进行,试确定在全混流反应器中目的产物S 所能达到的最大浓度;6、反应物A 反应首先生成R k 1=5 hr -1,R 进一步反应生成S k 2=3 hr -1和T k 3=1 hr -1;如果浓度为 mol/L 的纯A 在一个全混流反应器内进行反应,求R 浓度达到最大值的空时及R 的最大浓度;7、某速率常数为 min -1的一级不可逆反应在一非理想反应器内进行反应,示踪结果表明,t 和2θσ分别为15min 和;求用多级混合流模型预测的转化率;8、纯组分A 发生下述平行反应,A 的起始浓度为2mol/L,反应在恒温的条件下进行,试确定在平推流反应器中目的产物S 所能达到的最大浓度;四、推导题1.假设含反应物A 的新鲜原料进入体积为V 的全混流反应器进行反应,其组成为C A0,空时为τ,出口转化率为X A ,出口处的反应速率为-r A ,请推导全混流反应器的设计方程AA AX C r τ=-; 答案一、填空题1. 串联的全混区的个数N 、 Pe =zuLE 2. 积分法 、 微分法 ;3. 可能、不可能4. 脉冲法 、 阶跃法 ;5.6. m 3/ 7. 不能确定8. 质量传递 、 动量传递 和 热量传递 、反应动力学 9. 均一 、 等于10. 反应物吸附 、 表面反应、 反应产物的脱附二、选择题1. BC2. C3.. B4. BCD5. B6. A7. C8. BC9. B 10. AC 11. BCD 12. A 13. BD 14. AC 15. B 16. A三、计算题1、在一反应器入口输入理想脉冲示踪物后,不同时间检测出口示踪物的浓度C,结果如下所示:现有某液相反应物A 在该反应器中进行分解反应,速率方程为:A A r kC -= , k = min -1,若用多级混合流模型预测时,该反应器的出口转化率为多少 解:根据脉冲示踪数据可得:()()(()()i i i i i i i it C t t t C t t C t t C t ∆==∆∑∑∑∑等时间间隔)=15min=222t tθσσ==故:2114.900.204N θσ=== 则:01110.959(1)AA NA C x C kt N=-=-=+ 2、液体反应物AC A0=1mol/L 通过两个串联的全混流反应器发生某不可逆反应,第一个反应器出口的浓度为 mol/L,两个反应器的体积比V 2/V 1=2,反应级数为2:A A r kC -=2mol/求第二个反应器出口的浓度; 解:全混流反应器的设计方程:0A AAC C r τ-=- 得:010111221110.50.5A A A A A A C C C C V v r kC k τ---====- 所以:12k τ=同理:2121222022A A A A A A V C C C C v r kC τ--===- 由:22112V V ττ== 得:2124k k ττ==故:12224A A A C C C -= 解得: C A2=L3、某一级液相反应A R →在一只全混流反应器中进行,转化率为90%,如果再串连一只同样的全混流反应器,使转化率仍维持在90%,试问处理量增加多少 解: 当反应在一个全混流反应器内进行时,根据全混流反应器的设计方程,有1111τ+=-k x A ……………….1 当两个等体积全混流反应器串联时,转化率不变,则有2)21(11τ+=-k x A (2)根据式1,得1τk =9;根据式2,得=τk 处理量之比等于空时的反比,即0100101, 2.08v v v v ττ==;也就是说,处理量为原来的倍,增加了倍;4、某速率常数为的一级不可逆反应在一非理想反应器内进行反应,示踪结果表明,t 和2θσ分别为17min 和;求用多级混合流模型预测的转化率;解:根据多级混合流模型无因次方差与N 之间的关系,有2/1N θσ==4根据一级不可逆反应多级混合流模型转化率的表达式,有5、纯组分A 发生下述平行反应,A 的起始浓度为2mol/L, 反应在恒温的条件下进行,试确定在全混流反应器中目的产物S 所能达到的最大浓度; 解:S 的瞬时收率: 对于全混流反应器: 0SS S A AC C C ϕΦ==-故:200()()()1A SA A S A A AC C C C C C C ϕ=-=-+ 令 0SA dC dC =,得:20320A A A C C C +-=解得:C A =1mol/L故:22,max 01()()(21)()0.25111A S A A A C C C C C =-=-=++mol/L 6.反应物A 反应首先生成R k 1=5 hr -1,R 进一步反应生成S k 2=3 hr -1和T k 3=1 hr -1;如果浓度为 mol/L 的纯A 在一个全混流反应器内进行反应,求R 浓度达到最大值的空时及R 的最大浓度;解:根据一级不可逆串联反应在全混流反应器中进行反应时中间物种最大浓度及达到最大浓度空时的公式,有=+=τ)(1321k k k opt hr说明:上述两公式也可通过对反应物A 和产物R 两次应用全混流反应器设计方程,求得产物R 的浓度表达式,然后R 的浓度对空时求导,并令导数为零,推导求出; 7.某速率常数为 min -1的一级不可逆反应在一非理想反应器内进行反应,示踪结果表明,t 和2θσ分别为15min 和;求用多级混合流模型预测的转化率;解:根据多级多级混合流模型知: 则:8.纯组分A 发生下述平行反应,A 的起始浓度为2mol/L,反应在恒温的条件下进行,试确定在平推流反应器中目的产物S 所能达到的最大浓度;解:22(1)S A S A A dC C dC C ϕ==-+对于平推流反应器:当S ϕ~C A 曲线下的面积最大,即A 完全转化C A =0时C S 最大,即:=四、推导题1.假设含反应物A 的新鲜原料进入体积为V 的全混流反应器进行反应,其组成为C A0,空时为τ,出口转化率为X A ,出口处的反应速率为-r A ,请推导全混流反应器的设计方程0A A AX C r τ=-; 解:针对反应器列出物料平衡方程:入方=出方+反应消失的量+累积量全混流反应器为连续稳定流动式反应器,累积量为0,反应器中的浓度及反应速率均与出口处相同,其中:入方为:F A0出方为:F A =F A01-X A ,反应消失的量为:-r A V则得:00(1)()A A A A F F X r V =-+-即:0A A A F X r V =- 或者:00A A A A X V C F r τ==-。
化学反应工程知识点复习

三传一反
动量传递 热量传递 质量传递 反应工程
2·1 概 述
• 均相反应--在均一液相或气相中进行的反应 • 均相反应动力学是解决均相反应器的选型、操
作与设计计算所需的重要理论基础 • 公式:P15
1、化学反应速率及其表示
对于均相反应aA+bB=rR+sS反应速率定义为:
rA
1 V
dpA dt
k1 pA
k2 pP
k1 pA
2.5k2 pA0
pA
积分,得
(k1 2.5k2 )t
ln
pAe pA0 pA pAe
以(-ln(pA-pAe))对t作图
y 0.1633t 2.5035
k1 2.5k2 0.1633
K
k1 k2
2.5( pA0 pAe
pAe )
2.5(1 0.2) 0.2
10
k1 0.131 k2 0.0131
rA 0.131pA 0.0327 pA0 pA
2.2.2 复合反应
复合反应是指同时存在两个以上独立进行反应的反应过 程。
从相同的反应物按各自的计量关系同时地发生的过程称为 平行反应。
如果这些反应是依次发生的,这样的复合反应称为串联反 应。
反应的反应级数或总反应级数:指浓度函数中各组分 浓度的幂数之和。
对可逆反应,有正反应的反应级数和逆反应的反应级数 。
分子数:
对于基元反应:aA+bB=rR+sS
(rA ) k AcA cB
• 分子数:基元反应中反应物分子或离子的个数。 对于基元反应来讲α,β必须是正整数,α+β是基
元反应的分子数,不能大于3(根据碰撞理论, α+β的取值不能大于3,必须是一个小于等于3 的正整数)。
《化学反应工程》总复习总结

管式与釜式反应器反应体积的比较
1.正常动力学
A
1 (−RA )
F
0
B
D
E
H
K
X A1 X A
X A2
VrM
= Q0cA0 X A2 [−RA ( X A )]
VrM
= Q0cA0 X A1 + Q0cA0 ( X A2 − X A1)
[−RA ( X A1)]
[−RA ( X A2 )]
∫ Vrp
移热速率变化率 大于放热速率
M、N、 P为定态 点,N点 最佳
连续釜式反应器的操作温度
AHUT
第四章 管式反应器
返混:在流体流动方向上停留时间不同的流体粒 子之间的混合称为返混,也称为逆向混合。
管径较小,流速较大的管式反应器——可按活塞 流处理 剧烈搅拌的连续釜式反应器——可按全混流处理
管式反应器的反应体积计算及与CSBR与CSTR的比 较(正常、反常动力学及反应速率有极大值的情 况)
固定床反应器的分类
固定床催化反应器按催化剂床是否与外界进行热量交换分为绝热 反应器和换热反应器。绝热反应器分为单段绝热反应器和多段绝 热反应器。多段绝热反应器,按段间换热方式的不同,可分为三 类, 间接换热式、原料气冷激式和非原料气冷激式。
(1)浓度的影响与主、副反应级数有关,α=β , 与浓度无关;α>β,浓度增高,瞬时选择性增加; α< β,浓度增高,瞬时选择性降低
AHUT
第二章 反应动力学基础
(2)温度的影响与主副反应活化能有关:E主=E 副 ,与温度无关E主>E副,温度增高,瞬时选择性增 加;E主< E副,温度增高,瞬时选择性降低 提高连串反应中间产物收率的措施 (1)采用合适的催化剂; (2)采用合适的反应器和操作条件; (3)采用新的工艺(如反应精馏,膜反应器等) 催化剂主要组成 主催化剂、助催化剂、载体 物理吸附与化学吸附的特点
化学反应工程考点总结

1.BR的特点:1)由于充分搅拌、混合,以至于反应器有效容积内各个位置物料的特性(T+C)都相同。
2)由于是一次投料和一次放料,在反应过程中既无物料的加入,也无物料的放出,则在反应器内所有物料的空间停留时间相同,无空间停留时间不同的无聊之间的混合,即不存在反混。
3)反应器出料口的物料组成与反应器内最终得到的物料组成相同。
4)间歇操作过程存在辅助生产时间。
2.PFR的特点:1)由于物料都是沿着同一方向、且同一速度在反应器内向前推进,则所有物料流出反应器的时间都相同。
2)在垂直流动方向的任意一截面上,不同径向位置的物料的特性一致,即不存在反混。
3)在定常态下操作,反应器内状态只随轴向位置改变,不随t改变。
3.CSTR特点:1)物料在反应器内充分反混。
2)反应器内各处物料参数均一。
3)反应器的出口组成与器内物料组成相同。
4)反应过程中连续进料出料,是一定常态操作。
4.化学反应工程学研究的主要内容:1)化学的------化学反应动力学特性的研究。
2)物理的------流动、传递过程对反应的影响的研究。
3)工程的------反应器的设计计算、过程的分析及最优化。
5.利用数学模型解决化学工程问题的基本步骤:1)小试研究化学反应规律2大型冷模实验研究传递过程规律。
3通过计算机或其它手段综合化学反应规律与传递过程规律,预测大型反应器的特性,寻找优化条件。
4热模检验数学模型的等效性。
6.气固相催化反应的七个步骤、三个过程:1)反应组分从气流主体扩散到催化剂外表面。
2)反应组分从催化剂外表面扩散到催化剂的内表面。
3)反应组分在催化剂活性表面中心上吸附。
4)吸附在表面活性中心上的反应物进行化学反应。
5)产物在催化剂表面活性中心上脱附。
6)产物从催化剂的内表面扩散到催化剂的外表面。
7)产物从催化剂的外表面扩散到气流主体。
其中1)、7)过程是外扩散过程,2)、6)是内扩散过程,3)、4)、5)是化学反应动力学过程。
7.动力学方程的实验测定时,有采用循环反应器的,为什么?由于循环反应器的行为与CSTR的相同,可以得到反应速率的点数据,而且反应器进口浓度差比较大,对分析精度要求不很高。
化学反应工程复习提纲

淮海工学院化学反应工程复习参考1 绪论1.化学反应工程研究的内容P12 通常所说的三传一反指什么P13 什么是转化率关键组分的转化率与100%的关系P34 单程转化率与全程转化率的大小关系P45 收率与转化率是针对什么物质而言的,数值能否大于100%P56 收率与转化率,选择性的关系P52 反应动力学基础1.反应速率定义P152 流动系统的反应速率三种表示形式及换算方法P163 基元反应速率方程的写法与级数的分析, 基元反应与非基元反应的关系P17-184温度对三种反应速率的影响,对反应速率常数的影响,不可逆.可逆吸热与放热反应P235 复合反应的类型P26-296 δA的计算方法P317 多相催化反应的步骤P368 物理吸附与化学吸附及理想吸附的特点分析P373 釜式反应器1.等温间歇釜式反应器的计算有单一反应,平行反应及连串反应最大收率的计算P57-652 空时,空速与生产能力的关系P66-673 连续釜式反应器体积的计算P67-684 什么是正常动力学与反常动力学,连续釜式反应器串并联特点P695 釜式反应器的总收率与总选择性的变化特点P75-766 平行反应分析P767 连串反应分析P79-80 4 管式反应器1.理想反应器模型的特点,与实际反应器对应的是什么反应器P982 等温管式反应器的计算P1003 管式与釜式反应器反应体积比较结果P107-1095 停留时间分布与反应器的流动模型1.停留时间的年龄分布与寿命分布定义P1282 停留时间分布的定量描述E(t)与F(t)的定义P128-1293 停留时间分布的实验测定有几种方法及分别测定什么P130-1324 停留时间统计值有两个参数分别表示什么P1345 理想反应器停留时间分布的计算F(θ) E(θ)的计算6 多相系统中的化学反应与传递现象1.颗粒的三个密度大小比较P1592 气固催化反应过程进行的步骤P1603 外扩散对催化反应的影响分析单一反应,复合反应分析P165-1664 孔扩散的三种方式P1675 内扩散有效因子Φ的分析P1706 内外扩散有效因子分析P1767 内扩散对复合反应选择性的影响分析P1778 消除内外扩散影响的方法P178-1797 多相催化反应器的设计与分析1.固定床内空隙率大小分析P1862 多段固定床绝热反应器的类型P1943 流化床反应器中压降与流速的变化关系P211 8 多相反应器1.气液反应机理P2222 η值大小分析P224-2253 气液固反应器机理P2324 滴流床反应器的四个区域P2339 生化反应工程基础1.酶的组成与类型P2442 生化反应过程的特点P2453 酶催化反应特点P2464 酶催化反应的四种抑制机理P248-2505 影响酶催化反应速率的因素p2516 酶与细胞固定化技术P257-2587 影响固定化酶催化反应动力学的因素p2581一、单项选择题1.下列反应器可视为活塞流的反应器是()反应器A:管式B:釜式C:塔式2.对于基元反应2A+B→2C,则反应速率方程为()反应器A:r=kc A2C B B:r A=kC A C B C:r A=Kc A C B2D: r A=kC A C B C c3.在全混流反应器中,反应器的有效容积V R与进料流体的流速Q0之比为()A:空时τB:反应时间t C:停留时间t D:平均停留时间t4.化学反应速率式为-r A=K C CαA C Bβ,如果用浓度表示的速率常数为K C,用压力表示的速率常数为K P,则K C=()K P A:(RT)-(α+β)B:(RT)(α+β) C:(RT)(α-β)5.对于基元反应:2A+B→2P的反应,对A的反应总级数为()级A:1 B:3 C:2 D:06.在平行反应中,A→P,2A→Q,r P=k1C A,r Q=k2C A2,P为目的产物,k1,k2为常数,浓度对瞬时选择性S的影响是()7.完成同样的任务所需反应器体积在()时,平推流反应器与全混釜一样A:反应级数大于零B:零级反应C、反应级数小于零8.阶跃示踪法测定停留时间分布对应的曲线为()A:E(t)曲线 B:F(t)曲线 C:I(t)曲线 D:y(t)曲线9.对正常动力学,完成同样的任务,所需反应器体积最小的操作是()A:单釜 B:二釜串联 C:三釜串联 D:四釜串联O,已知k=0.01L/s.mol,则反应级数为()10.反应NaOH+HCl→NaCl+H2A:1 B:2 C:3 D:011.对于基元反应A+B→2C,则反应速率方程为()反应器A:r=kc A2C B B:r A=kC A C B C:r A=Kc A C B2D: r A=kC A C B C c12.在连续操作的全混流反应器中,反应物的平均停留时间为()A:大于空时τB:小于空时τC:等于空时τ13.完成同样的任务所需反应器体积在()时,平推流反应器与全混釜一样A:反应级数大于零B:零级反应C、反应级数小于零14. 对正常动力学,瞬时选择性S随转化率增大而降低的情况下,反应器内的目的产物最终收率最大的操作是()A:间歇釜反应器 B:连续单釜 C:二釜串联=()15.气相反应2A+B→3P+S,进料时为惰性气体,A与B的摩尔比为2:1进料,则膨胀因子δAA:-1 B:-0.5 C:0.5 D:116.反应产物的质量收率,其最大值为()A:100% B:大于100% C:小于100%117.催化剂颗粒上的反应速率大小与三个有效因子有关,分别是外扩散ηx 、内扩散η、内外扩散总有效因子η,忽略内扩散影响时,它们之间的关系是( )A:ηX >η B:ηX=η C:ηX=ηD:η=η18. 对于()的反应器,在恒容反应过程的平均停留时间、反应时间、空时是一致的。
化学反应工程期末总结重点知识点

1、化学反应分类:(按相类分类)均相反应,非均相反应,(按操作分类)间歇操作,连续操作,半连续操作。
2、反应器分类:⑴ 管式反应器,一般长径比大于30⑵ 槽式反应器,一般高径比为1—3 ⑶ 塔式反应器,一般高径比在3—30之间;按传热条件分类:等温反应器,绝热反应器,非等温、非绝热反应器3、化学反应速率:4、化学反应动力学方程: 阿累尼乌斯关系:5、反应级数:m ,n :A ,B 组分的反应级数,m +n 为此反应的总级数。
如果反应级数与反应组份的化学计量系数相同,即m =a 并且n =b ,此反应可能是基元反应。
基元反应的总级数一般为1或2,极个别有3,没有大于3级的基元反应。
6、有如下基元反应过程,请写出各组分生成速率与浓度之间的关系。
7、动力学方程的方法:积分法、微分法8、化学反应器的设计基础:按混淆分类:间歇反应器,平推流反13s m mol d d 1--⋅=t V r ξ13B A c A s m mol --⋅=-n m c c k r RT Ek k -=ec0c 222A B C A C DB D E +↔+↔+↔222123422125622212342345656222222A A BC A CD B A B C B DE C A B C A C DD A C D B D EE B D Er k c c k c k c c k c r k c c k c k c c k c r k c c k c k c c k c r k c c k c k c c k c r k c c k c =-+-+=-+-+=--+=--+=-应器(理想置换反应器、活塞流反应器),全混流反应器9、间歇反应器的特点:①由于剧烈搅拌、混合,反应器内有效空间中各位置的物料温度、浓度都相同;②由于一次加料,一次出料,反应过程中没有加料、出料,所有物料在反应器中停留时间相同,不存在不同停留时间物料的混合,即无返混现象;③出料组成与反应器内物料的最终组成相同;④为间歇操作,有辅助生产时间。
化学反应工程复习公式指导

化学反应工程复习公式指导化学反应工程是化学工程的重要分支之一,主要涉及到反应速率、反应平衡、反应热力学等方面的问题。
在进行化学反应工程的设计和优化时,需要运用一系列的公式,以指导实际操作和解决问题。
以下是一些常见的化学反应工程公式,供复习和参考。
1.反应速率公式在化学反应中,反应速率是指单位时间内反应物消失或产物生成的量。
一般来说,化学反应速率与反应物浓度之间存在一定的关系。
根据实验数据,可以通过拟合得到反应速率公式。
常见的反应速率公式有:-零级反应速率:r=k-一级反应速率:r=k[A]-二级反应速率:r=k[A]²-伴随一级反应速率:r=k[A]·[B]其中,r为反应速率,k为反应速率常数,[A]和[B]为反应物浓度。
2.反应平衡公式在反应平衡条件下,反应物和生成物的浓度保持不变。
根据反应平衡常数,可以得到反应平衡公式。
常见的反应平衡公式有:-简单反应物与生成物的摩尔比例:aA+bB⇌cC+dD其中,a、b、c、d分别为反应物和生成物的系数,A、B、C、D分别为反应物和生成物的摩尔浓度。
反应物和生成物的关系可以表示为:Kc=[C]ᶜ[D]ᵈ/[A]ᵃ[B]ᵇ-简单反应物与生成物的分压比例:aA+bB⇌cC+dD其中,a、b、c、d分别为反应物和生成物的系数,A、B、C、D分别为反应物和生成物的分压。
反应物和生成物的关系可以表示为:Kp=(Pc/RT)ᶜ(Pd/RT)ᵈ/(Pa/RT)ᵃ(Pb/RT)ᵇ其中,R为理想气体常量,T为温度,Pa、Pb、Pc、Pd分别为反应物和生成物的分压。
3.反应热力学公式反应热力学研究反应热效应与反应过程的关系。
常见的反应热力学公式有:-反应焓变公式:ΔH=Σ(nᵢHᵢ)其中,ΔH为反应焓变,nᵢ为反应物或生成物的摩尔数,Hᵢ为反应物或生成物的摩尔焓。
-熵变公式:ΔS=Σ(nᵢSᵢ)其中,ΔS为反应熵变,nᵢ为反应物或生成物的摩尔数,Sᵢ为反应物或生成物的摩尔熵。
反应工程重点笔记

反应工程重点笔记1. 反应工程基本概念反应工程是研究化学反应在工业生产中的应用过程的一门学科,它主要涉及到化学反应动力学、反应器设计和操作等方面的知识。
通过对反应工程的研究,可以提高反应的效率,减少资源的浪费,实现工业化生产的稳定性和可持续性发展。
2. 反应动力学反应动力学是研究反应速率与反应物浓度、温度、压力和催化剂等因素之间关系的学科。
反应速率可以用速率方程来描述,一般为: [rate = k[A]a[B]b[C]^c…]其中,[k]为反应速率常数,([A])、([B])、([C])等为反应物的浓度,(a)、(b)、(c)等为反应物的反应级数。
反应动力学的研究可以提供反应速率与反应条件之间的关系,进而可以帮助我们优化反应条件,提高反应效率。
3. 反应器设计反应器是进行化学反应的设备,常见的反应器有批式反应器、连续流动反应器和催化剂床等。
反应器的设计需要考虑反应动力学、传热传质、材料强度等因素。
反应器的设计目标包括:提高产率、提高选择性、降低副产物生成、减少能量消耗、提高安全性等。
为了实现这些目标,可以通过控制反应温度、压力和催化剂用量等方式进行优化。
4. 反应器操作反应器的操作包括起始阶段、稳态运行和关闭阶段。
在起始阶段,需要进行原料的投与、加热和搅拌等操作,以实现反应体系的建立。
稳态运行阶段是为了维持反应物的浓度和温度在合适的范围内,保证反应能够持续进行。
在反应器操作过程中,需要掌握反应器的温度、压力和流量等参数,并及时采取措施以调整反应条件,保证反应在可控的范围内进行。
5. 催化剂的应用催化剂在反应工程中起到了至关重要的作用。
催化剂可以降低活化能,提高反应速率,同时还可以提高反应的选择性和效果。
催化剂的应用可以大大提高反应工程的效率和经济性。
常见的催化反应有氧化反应、氢化反应、加氢反应、脱氢反应等。
选择合适的催化剂对于不同的反应系统来说至关重要。
6. 质量传递和传热问题在反应工程中,质量传递和传热问题是非常重要的。
化学反应工程复习资料

化学反应⼯程复习资料化学反应⼯程复习资料⼀.填空1.理想反应器是指 _______、______ _。
2.全混流反应器的返混_______。
平推流反应器的返混为_______。
3.反应器物料的停留时间的分布曲线是通过物理⽰踪法来测定的,根据⽰踪剂的输⼊⽅式不同分为_______、_______、_______。
4.平推流管式反应器t t =时,E (t )=____。
;平推流管式反应器t t ≠时,E (t )=_____。
;平推流管式反应器t t ≥时,F (t )=___ 。
;平推流管式反应器t <t 时,F (t )=____。
5.平推流管式反应器其E (θ)曲线的⽅差=2θσ_______。
;平推流管式反应器其E (t )曲线的⽅差=2t σ_______。
6.全混流反应器t=0时E (t )=_______。
;全混流反应器其E (θ)曲线的⽅差=2θσ_______。
;全混流反应器其E (t )曲线的⽅差=2t σ_______。
7.催化剂“三性”是指、和。
8.凡是流体通过不动的固体物料所形成的床层⽽进⾏反应的装置都称作___ ____。
9. 化学反应过程按操作⽅法分为____ ___、___ ____、_____ __操作。
10. 化学反应⼯程中的“三传⼀反”中的三传是指____ ___、___ ____、_______。
11. 化学反应的总级数为n ,如⽤浓度表⽰的速率常数为C K ,⽤逸度表⽰的速率常数f K ,则C K =_______f K 。
12.在构成反应机理的诸个基元反应中,如果有⼀个基元反应的速率较之其他基元反应慢得多,他的反应速率即代表整个反应的速率,其他基元反应可视为处于____ ___。
13. ⼀级连串反应A S P在全混流釜式反应器中,则⽬的产物P 的最⼤浓度0 0.2 0.40.6 0.8 1.0 0.2 0.40.60.81.0A RS K 1K 2P 在平推流反应器中,则⽬的产物P 的最⼤浓度=max ,P C _______、=opt t ______。
化学反应工程复习+公式指导

化学反应工程复习总结一、知识点1.化学反应工程的研究对象与目的,研究内容。
化学反应工程的优化的技术指标。
2.化学反应动力学转化率、收率与选择性的概念。
反应速率的温度效应和活化能的意义。
反应速率的浓度效应和级数的意义。
3.理想反应器与典型反应特征理想反应器的含义。
等温间歇反应器的基本方程。
简单不可逆反应和自催化反应的特征和计算方法。
可逆反应、平行反应和串联反应的动力学特征和计算方法。
4.理想管式反应器管式平推流反应器的基本方程典型反应的计算。
停留时间、空时和空速的概念。
膨胀因子和膨胀率的概念。
5.连续流动釜式反应器全混流模型的意义。
全混流反应器的基本方程全混流反应器的计算。
循环反应器的特征与计算方法。
返混的概念、起因、返混造成的后果。
返混对各种典型反应的利弊及限制返混的措施。
6.停留时间分布与非理想流动停留时间分布的意义,停留时间分布的测定方法。
活塞流和全混流停留时间分布表达式,固相反应的计算方法。
多釜串联模型的基本思想,模型参数微观混合对反应结果的影响。
7.反应器选型与操作方式简单反应、自催化和可逆反应的浓度效应特征与优化。
平行反应、串联反应的浓度效应特征与优化。
反应器的操作方式、加料方式。
8.气固催化反应中的传递现象催化剂外部传递过程分析,极限反应速率与极限传递速率。
Da和外部效率因子的定义及相互关系。
流速对外部传递过程的影响。
催化剂内部传递过程分析,Φ和内部效率因子的定义及相互关系。
扩散对表观反应级数及表观活化能的影响。
一级反应内外效率因子的计算。
内外传递阻力的消除方法。
9.热量传递与反应器热稳定性定态、热稳定性、临界着火温度、临界熄火温度的概念。
催化剂颗粒热稳定性条件和多态特性。
全混流反应器、管式固定床反应器热稳定条件。
最大允许温差。
绝热式反应器中可逆放热反应的最优温度分布。
二、具体内容解析 一、 绪论 1.研究对象是工业反应过程或工业反应器研究目的是实现工业反应过程的优化 2. 决策变量:反应器结构、操作方式、工艺条件 3.优化指标——技术指标:反应速率、选择性、能耗 掌握转化率、收率与选择性的概念 4.工程思维方法二、化学反应动力学1. 反应类型:简单反应、自催化、可逆、平行、串联反应基本特征、分析判断2. 化学反应速率的工程表示))((反应区反应时间反应量反应速率=3. 工业反应动力学规律可表示为:)()(T f C f r T i C i ⋅=a) 浓度效应——n 工程意义是:反应速率对浓度变化的敏感程度。
反应工程重点笔记

反应工程重点笔记反应工程是化学工程的一个重要分支,主要研究化学反应的过程和机理,以及如何设计和优化化学反应过程。
在实际工程中,反应工程的目标是实现高效、可持续和经济的化学反应。
以下是反应工程的重点笔记:1. 反应动力学:反应动力学研究反应速率如何随着反应物浓度变化以及温度变化而变化。
了解反应动力学可以帮助工程师选择合适的反应条件,并预测反应过程中可能出现的问题。
2. 反应器设计:反应器是进行化学反应的关键设备。
反应器设计需要考虑反应物质的传质、传热和混合问题,以及反应过程中可能的副反应和催化剂失活问题。
工程师需要选择合适的反应器类型,并进行流体力学和传质传热计算,以确保反应器能够实现预期的反应效果。
3. 反应条件优化:选择合适的反应条件对于提高反应效率和产率非常重要。
反应条件包括温度、压力、反应物浓度、催化剂选择等。
工程师需要通过试验和模拟计算来确定最佳的反应条件,以及优化反应过程中可能出现的问题。
4. 安全与环境:在设计和操作化学反应过程时,安全与环境是非常重要的考虑因素。
工程师需要评估反应过程中可能的危险和污染问题,并采取相应的安全措施和环保措施,保护工人和环境免受潜在的风险。
5. 规模放大:从实验室规模到工业规模的反应放大是反应工程的关键任务之一。
工程师需要考虑如何将实验室条件下的反应条件和反应器设计放大到工业生产规模,并解决可能出现的问题,例如传质、传热和混合等。
6. 动态模拟与控制:建立反应过程的动态模型可以帮助工程师预测反应过程中的动态响应,并设计合适的反馈控制策略。
动态模拟和控制有助于提高反应过程的稳定性、响应性和鲁棒性。
总之,反应工程涉及多个方面的知识和技术,需要工程师综合运用化学、传质传热、流体力学、动力学等学科和工程原理,从而实现高效、可持续和经济的化学反应过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从而得到对应此最高浓度的反应时间为:
ln( k 2 k1 ) topt k 2 k1
CP ,max
k1 C A0 k 2
k2 k2 k1
2.3 等温变容过程
α+β=n,n为非基元反应的总反应级数,取值可以是小于或 等于3的任何数,α和β的值与计量系数a和b的值无关。
取值是通过实验测定的。
注意:区分反应级数和反应的分子数。
相同点:非基元反应中的反应级数与基元反应中的分子数
,取值n≤3;α、β仍称做反应物A或B的反应级数。 不同点:非基元反应n的取值还可以是负数、0、小数; 分子数是专对基元反应而言的,非基元过程因为不反映直 接碰撞的情况,故不能称作单分子或双分子反应。
反应级数的大小反映了该物料浓度对反应速率影响的程 度。级数愈高,则该物料浓度的变化对反应速率的影响
愈显著。
2、速率常数k
• 化学反应速率方程体现了浓度和温度两方面 的影响,浓度的影响体现在浓度项上,反应 级数表明了反应速率对浓度变化的敏感程度。
• 温度的影响则是由速率常数k体现的。
2.1反应速率常数
化学反应工程
三传一反
动量传递 热量传递 质量传递 反应工程
2· 1
概
述
• 均相反应--在均一液相或气相中进行的反应 • 均相反应动力学是解决均相反应器的选型、操
作与设计计算所需的重要理论基础
• 公式:P15
1、化学反应速率及其表示
对于均相反应aA+bB=rR+sS反应速率定义为:
1 dnA 由于反应而消耗的 A物质的量 rA V dt (单位体积)(单位时 间)
dC P k1 k 2 t k1C A 0 e dt
rP dC P k1 P rA dC A k 1 k 2
rS k2 S rA k1 k 2
C P C P0 k1 ( )( C A 0 C A ) k1 k 2
分离变量积分得:
(3) 基元反应 基元反应指反应物分子一步直接转化为产物分子的反 应。 凡是基元反应,其反应速率遵循质量作用定律,即根 据化学计量关系,就可以写出反应速率方程。 (4)反应级数 反应级数:指浓度函数中各组分浓度的幂数。 反应的反应级数或总反应级数:指浓度函数中各组 分浓度的幂数之和。 对可逆反应,有正反应的反应级数和逆反应的反应级 数。
( r A
)
k
A
c
A
c B
式中k称作反应速率常数;α 、β 是反应级数。
对于(恒容)气相反应,由于分压与浓度成正比,也可 用分压来表示。
1 dnA ( rA ) k p PA PB V dt
问题:
r K C C A CB 化学反应速率式为, A
如用浓度表示的速率常数为Kc, 用压力表 示的速率常数Kp,则Kc= Kp
rP dC P s P= = rS dC S
积分得:
CP CP 0
k1 CS CS 0 k2
根据实验数据,以(CP-CP0)对(CS-CS0)作图,得到斜率为k1/k2的直线 。结合上述(k1+k2),从而可确定k1和k2。
② 产物分布
则有:
CA CA0e
k1 k2 t
• 答:(A)
•答:(A)
•答:1/3
1/2
冪数型动力学方程和双曲型动力学方程
1)幂数型动力学方程 aA+bB=rR+sS 实验研究得知,均相反应速率取决于物料的浓度 和温度,反应速率符合下述方程,称之为幂数型 动力学方程,是经验方程。
rA kc c
,( mol ) m3 s
A B
1
对二级不可逆反应:
A + B → 产物
其反应速率方程为:
dCA dxA rA C A0 kCAC B dt dt kCA0 1 x A C B 0 C A0 x A
2 kCA 1 x A x A 0
CB0 / CA0
当CA0=CB0时,积分结果为:
α和β,
α和β分别称作组分A和组分B的反应级数α+β=n,n是 基元反应的总反应级数。
,( mol ) m3 s
( rA ) k A c c A B
A 后者
R与2A –rA=kACA2
2R意义不同,前者
–rA=kACA
非基元反应: aA+bB=rR+Ss
( rA ) k A c A c B
在一般情况下,反应速率常数 kc与绝对温度T之间的关系可以 用Arrhenius 经验方程表示,即:
k k0 e
E / RT
k0 指前因子,其单位与反应速率常数相同 Ec 化学反应的活化能,J/mol Rg 气体常数,8.314J/(mol.K)
对于恒温反应因为影响不大 k0指前因子或频率因子,看做与温度无关的常数
图2-1
时更加敏感 。
速率常数k及活化能E的求取
选择几组不同的反应温度,在等温、 恒容下得到均相反应的实验数据,并据此 求出相应的k值,进而就可以求得活化能E 的值。
k1 k 0 e E / RT1 k 2 k 0e
E / RT2
E 1 1 ln k 2 ln k1 R T2 T1
以(-ln(pA-pAe))对t作图
y 0.1633t 2.5035 k1 2.5k2 0.1633 k1 2.5( pA0 pAe ) 2.5(1 0.2) K 10 k2 pAe 0 .2 k1 0.131 k2 0.0131 rA 0.131 pA 0.0327 pA0 pA
①动力学方程的建立
A P
k1 k2 A S
dCP rP k1C A dt dCS rS k 2C A dt
dCA rA (k1 k 2 )CA dt
分离变量积分得到:
C A0 k1 k 2 t ln CA
组织实验,得到Ci与t的数据,并以ln(CA0/CA)对t作图,应得到一条通过原 点的直线。该直线的斜率为(k1+k2)。 瞬时选择性为:
⑶ 连串反应
对反应:
k1 k2 A P S
dCA rA k1C A dt dCP rP k1C A k 2C P dt dCS rS k 2C P dt
对-rA分离变量积分得:
CA CA0 exp k1t
对A作物料衡算,则有:
CA0 C ACP CS
1 1 1 C A C A0 C A0
xA 1 x A
kt
例题1:
• 在0℃时纯气相组分A在一恒容间歇反应器依以下 计量方程反应:A→2.5P,实验测得如下数据:
• 解: • 当t→∞时,pAe=0.02,故为可逆反应,设 此反应为一级可逆反应,则
dp A k1 p A k 2 p P k1 p A 2.5k 2 p A0 p A dt p Ae p A0 积分,得 (k1 2.5k 2 )t ln p A p Ae
rA 23c 400R
2 A
2
同理: 500K下:
2 500R rA 23cA 2
rA 400 16 E 1 1 exp rA 500 25 8 . 314 400 500
E 7421 J mol
a a a (rA ) (rB ) (rr ) (rS ) b r s
或可说,我们用不同的着眼组分来描述化学反应速 率,那么反应速率与计量系数之比是相等的。
rA rB rr rs a b r s
若以浓度表示则为:
1 dc A 1 dcB 1 dcR 1 dcS a dt b dt r dt s dt
k0 ∝ T
0 ~1
k之所以称之为常数,是指当反应温度不变时,k是个 常数,当反应温度变化较大时它就不再是常数。 活化能E,根据过度状态理论,反应物生成产物,要 超过一个能垒,因此E的取值永远是正值。
lnk与1/T是直线关系 -E/R为斜率 lnk0为截距
Hale Waihona Puke 通过实验测出不同温度下的速率常数k,作图根据截距 就可以求出指前因子k0,再 根据直线的斜率求出活化能 E 对给定的反应,反应速率与 温度的关系在低温时比高温
•
一气相分解反应在常压间歇反应器中 进行,在400K和500K温度下,其反应 速率均可表达为−rA=23pA2 mol· m-3s-1, 式中pA 的单位为kPa。求该反应的活 化能。
将分压换算成浓度: pA cA RT 400K下: rA 23 p kmol m s
2 A 3 1
2.2.2 复合反应
复合反应是指同时存在两个以上独立进行反应的反应 过程。 从相同的反应物按各自的计量关系同时地发生的过程 称为平行反应。 如果这些反应是依次发生的,这样的复合反应称为串 联反应。 在这些反应产物中,有的产物是需要的对象,称为目 的产物或主产物,而其余产物都称为副产物。得到目的产 物的反应称为主反应,其余反应称为副反应。 研究复合反应的目标是如何提高主反应的反应速率、 减少副反应的发生的途径,改善产物分布,以提高原料利 用率。
⑴ 收率、得率和选择性
收率:
n P n P0 目的产物的生成量 P = 关键反应物的转化量 n A0 n A
得率:
P P xA
nP nP 0 目的产物的生成量 P = 关键反应物的起始量 n A0
