清北学堂物理竞赛模拟题参考答案
清北学堂物理竞赛考前练习题第一套(附答案详解)

北京清北学堂竞赛模拟一1、我国于2007年10月24日发射的“嫦娥一号”探月卫星简化后的路线示意图如图所示。
卫星由地面发射后,经过发射轨道进入停泊轨道,然后在停泊轨道经过调速后进入地月转移轨道,再次调速后进入工作轨道,卫星开始对月球进行探测。
已知地球与月球的质量之比为a,卫星的停泊轨道与工作轨道的半径之比为b,卫星在停泊轨道与工作轨道上均可视为做匀速圆周运动,则()A.卫星在停泊轨道运行的速度大于地球的第一宇宙速度aB.卫星在停泊轨道和工作轨道运行的速度之比为bC.卫星在停泊轨道和工作轨道运行的周期之比为3baD.卫星在停泊轨道和工作轨道运行的向心加速度之比为2b2、如图所示,一条足够长的水平张紧的弹性绳上,有两列小振幅的简谐横波a(实线)和b (虚线),分别沿相反方向传播,a波向右,b波向左,两列波的波长λa=1.5λb,振幅均为A。
图为在t0时刻两列波相遇的情况,在此时刻,绳上P点的合位移恰好为零。
为了在以后的t1时刻P点的合位移为2A,且位于平衡位置上方,这两列波在t0至t1时间内沿水平方向各自传播的距离可以是()A.1λa和1.5λb B.2λa和3λbC.2λa和4.5λb D.4λa和6λb3.已知如图,带电小球A、B的电荷分别为Q A、Q B,OA=OB,都用长L的丝线悬挂在O点,其中球A与左边绝缘墙紧靠但不粘连。
静止时A、B相距为d。
为使平衡时AB间距离减为d/2,可采用以下哪些方法A.将小球A、B的质量都增加到原来的2倍B.将小球B的质量增加到原来的8倍C.将小球A、B的电荷量都增加到原来的3倍D.将小球A、B的电荷量都减小到原来的一半4.在空中某处同时以大小相同的速度υ=20m/s抛出两个小球,其中一个小球水平抛出,另一个小球与水平面成60 斜向下抛出,两个小球的运动在同一竖直平面内,经过3s后两小球之间的距离为234A. 30mB. 45mC. 60mD. 10 m5. 一个灯泡的电阻R0=2Ω,正常工作电压U0=4.5V,由电动势U=6V、内阻可忽略的电池供电。
清北学堂第37届全国中学生物理竞赛理论考试模拟试题

三、(40 分) 两块相对介电常数分别为ϵ1 的半无限大电介质拼接在一起。有一个带电量为 q0
的电荷被放置在电介质 1 中,距离界面 a。 (1)利用电介质电相法说明在介质 1、2 中的电场等效于哪一个或多个点电荷产生的电场。 (2)利用电介质电相法算出两介质表面某一位置的总电荷面密度。 (3)不利用电介质电相法算出两介质表面某一位置的总电荷面密度。 (4)算出两介质表面的总电荷
二、(40 分) 当太阳系不再适合人类生存时,人类的其中一个选择便是给地球安装“行星发动
机”,带着地球离开太阳系,我们下面计算这个模型。 (1)行星发动机是通过常见元素的核聚变获得能量的。已知两个碳-12 通过核反应形
成镁元素。假设两个反应的碳-12 反应时几乎静止,发动机通过发射该反应产生的能量的 光子获得推力。已知碳-12 质量 12.00000u,镁-24 质量 23.98513u,试求一秒钟反应一千 克碳-12 产生的推力。(uc2=931.49MeV)
八、(40 分)
玻色子(boson)是遵循玻色-爱因斯坦统计,自旋量子数子可以同时处于同一个状态。它在低温时可以发生一种
清北学堂高中物理竞赛试题1

清北学堂全国中学生物理竞赛复赛模拟题1一、(40’)电磁送分题:如图所示,圆柱形筒壁内有垂直于纸面向里的匀强磁场B,某中性粒子质量为m,初始位置在圆心(粒子与筒壁的碰撞均为弹性碰撞),圆筒半径R=P0/qB,其中P0为粒子初动量(1)t=0时刻,粒子裂变为等质量的两个带电量分别为+q、-q的粒子,试定性画出运动轨迹并求出周期。
(2)若正负粒子的质量之比为1:2,重新解答第一问。
二、(40’)华丽粒子曲线:如图在无限大光滑水平面上有三个质点,从左到右质量分别为3m、2m、m,他们之间有原长不计,劲度系数为k的轻弹簧相连接,初速度分别为v、3v、3v(从左到右),其中质量为3m的质点初速度方向沿y轴向下,其余两个质点初速度均沿y轴向上,初始位置见图中,不计万有引力试定性画出运动轨迹并求周期。
三、(40’)运动光学成像:如图,折射率为n,半径为r的玻璃球B以速度v²=2gr冲出平台,与此同时(离开平台边缘的瞬间)点亮了边缘的点光源s,求s Array通过B傍轴成像的像点的轨迹方程。
四、(40’)同心球电容器:给定一个半径为R的金属球,外部套有半径为αR的同心金属球壳,在球与球壳之间存在着某种颗粒(可视为半径为a的匀质小球,其中a<<R),内球带电量为Q,温度为T,假设颗粒带电q0,(不考虑极化),试求其在球与球壳之间分子数密度n的分布函数n(r).列出微分方程即可不要求解出。
五、(40’)热学气体分布:考虑三维气体分子的热运动速率分布在速度空间有球对称性。
分布函数维f(v),分子数密度为n (1)求任意方向如x方向的v x的分布函数F(v x).v x∈R(2)求速率为v的分子单位时间单位面积上碰撞分子个数N(我们认为仅有v x>0的分子可发生碰撞)(3)求证全部气体单位时间单位面积上碰撞的分子个数为n⎺v/4 其中⎺v=∫0∞vf(v)dv六、(40’)旋转双电容球:两个半径为R,质量为M的金属球通过一线度可略的轴承焊接在一起.求这一系统作为孤立导体对无穷远处的电容.七、(40’)四端电阻网络:某物竞球金学霸曾说:“一个四端纯电阻网络第一次在左边接理想电压源U1,右边接理想安培表得到示数I1;第二次右边接U2,左边得到示数为I2,应有U1I2=U2I1”试证明这个结论成立.(友情提示:注意符号法则)八、(40’)薄透镜再成像:薄透镜旁边有三角形物体ABC ,其像A ’B ’C ’,设AB 与A ’B ’所在直线交于点D ,BC 与BC 所在直线交于点E ,CA 与CA 所在直线交于点F ,求证:D 、E 、F 三点共线.(注:在一些脑洞比较大的特例中,D 、E 、F 中的一个或几个在无穷远处,与上述结论并不矛盾)※提供一个引理:设A ’、B ’、C ’分别为△ABC 三边BC 、CA 、AB 所在直线上的点,则A ’、B ’、C ’三点共线的充分必要条件为:C A BA ''·A B CB ''·''BC AC =1。
清北学堂物理竞赛模拟试题一
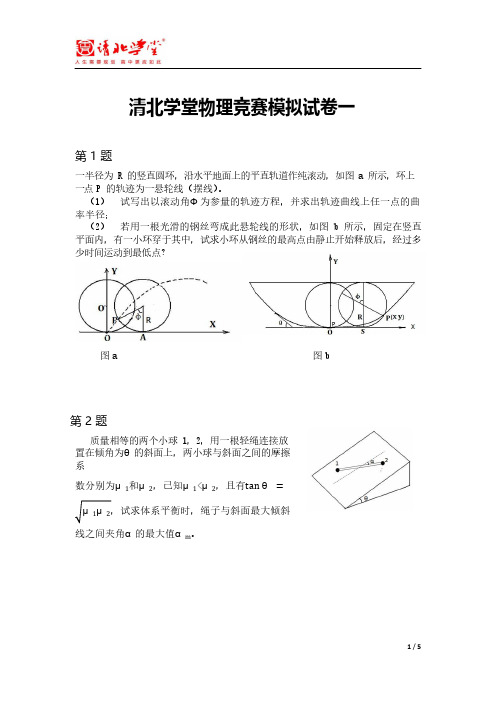
清北学堂物理竞赛模拟试卷一第 1 题一半径为 R 的竖直圆环,沿水平地面上的平直轨道作纯滚动,如图 a 所示,环上一点P 的轨迹为一悬轮线(摆线)。
(1)试写出以滚动角Ф为参量的轨迹方程,并求出轨迹曲线上任一点的曲率半径;(2)若用一根光滑的钢丝弯成此悬轮线的形状,如图 b 所示,固定在竖直平面内,有一小环穿于其中,试求小环从钢丝的最高点由静止开始释放后,经过多少时间运动到最低点?图a 图b第 2 题质量相等的两个小球 1,2,用一根轻绳连接放置在倾角为θ的斜面上,两小球与斜面之间的摩擦系数分别为μ1和μ2,已知μ1<μ2,且有tan θ=μ1μ2,试求体系平衡时,绳子与斜面最大倾斜线之间夹角α的最大值αm。
第 3 题一摩尔单原子分子理想气体经历图示的过程。
(1)确定 T−V 的关系;(2)试确定此过程的热容量 C 与V 的关系`。
第 4 题有人用两个共轴的凸透镜 L1、L2 制成开普勒望远镜,L1(物镜)和 L2(目镜)的焦距和直径分别为 f1=1m、d1=12.5cm; f2=10cm、d2=1cm,(1)当用它观察 50m 远处的直立旗杆,并使之最终成像于 10m 远处,则镜筒应多长?(2)旗杆上有多长一段被看到?(3)如果要使被观察到的旗杆长度增加一倍,并且尽可能增加亮度,在不改变镜筒长度的情况下,可在物镜和目镜之间再放置一个适当的凸透镜,则此透镜应放在什么位置?直径和焦距又各为多大?第 5 题在一块很大的水平接地导体平板上方存在竖直方向的匀强电场,场强为E0,现将一个质量密度为ρ、半径为 R 的导体半球平放在导体平板上(使球面向上),如图所示,试求E0至少多大,才能将这导体半球从平板上拉起?第 6 题一圆柱形的长电子束,电子均匀分布,电子数密度为 n ,平均速率为 v ,试求:(1) 电子束内离轴 r 处的电场强度 E 和磁感应强度 B 。
(2) 某电子通过该点时所受到的向外合力。
清北学堂高中物理竞赛模拟题2

一类是磁化电流,它是由磁介质的分子决定的电流(安培曾提出过分子环流假说),没有热效应。
为便于理解,如下图所示, 0为线圈中的传导电流, 为磁介质中的磁化电流。现定义,在线性磁
介质中,
0 , 称为磁介质的磁导率, 定义为磁场强度。在本题中我们认为
,
然而对于空气(或真空),
恒成立。可以证明
0
0
其中 0 为通过环路 L 的传导电流。 如图一,设环形细铁芯的磁导率为 ,由于 很大,磁场线几乎全部集中在铁芯环中,漏磁可以 忽略。在铁芯的一部分处缠绕线圈,匝数为 N,线圈电流为 I,铁芯的横截面积为 S,周长为 l, 试求出磁通量大小 。磁通量仍然定义为:
(3.2)在上一问的条件下,试讨论 e 0 R μ的取值,求发生第 n 次碰撞后的瞬间球体的速度 、转动 角速度 以及此时的时刻 。
第8页共8页
头方向的夹角 0 的可能取值(逆时针为正)。
第3页共8页
第4页共8页
五、(40 分) 磁场的作用,从宏观到微观,从电流到粒子: 众所周知,磁场和电流满足安培环路定理
0
其中
为通过环路 L 的所有电流。,我们现将该定律扩展一下:
“所有电流”包含两个部分:一类是传导电流,这是由导线中的自由电子决定的电流,有热效应;
二、温室效应对地表温度的影响。(35 分) 假设把太阳和地球当做理想黑体,太阳的辐射场均匀,且不考虑太阳和地球相对运动带来的影响。已 知太阳的温度为 ,半径为 R;日地距离为 d,地球的半径为 r,地球表面由于冰川的存在对太阳辐射的 平均反射率为 Q。试利用此简化模型进行估算( 6000K,R 7 × 0 , ͳ × 0 , 6㌳00 ,Q 0ͳ3) (1)假设地球上没有大气,试计算地球达到辐射平衡时的温度 。 (2)考虑大气的影响,把大气理想化为灰体,已知太阳的辐射主要为短波辐射,大气层对这部分热 辐射不吸收也不反射,而地球的热辐射主要为长波辐射,大气对其吸收率和热辐射的放射率均为P, 试 求辐射平衡时地球和大气的温度分别为多少?(P 0ͳ7 ) (3)如果温室气体增多,且与大气分布在不同的高度,在大气层之内,相当于又增加了一层温室气体 层,大气和温室气体的辐射也为长波辐射,温室气体对长波辐射吸收率和热辐射的放射率均为 W,试 求稳定时地球的温度和由于温室气体增多带来的升温为多少(与第 2 问相比)?(W 0ͳ7 )
清北学堂第37 届全国中学生物理竞赛理论考试模拟试题

五、(40 分)
(1) t ±
㤶 逆时针取正
㤶
±∓
∴v
tt
㤶 逆时针取+,顺时针取-
(2)
×
t
∴
㈠㤶
×
× × ㈠㤶
×
×
×
t
××
ht
㤶
tt
, 正方向向内,β
××
㤶
t 㤶 (其中方向 2’)
另解
tβ
㈠㤶
t
t
㈠㤶
t
t
㤶
∴ ± t 㤶 (其中方向 2’)
(3)
ht
t
tt
ht
∴
t ㈠㤶
其中
t
≪
径向微分方程:
h
t m/s 㤶 t m/s
三、(40 分) (1)(16 分)设在计算介质 1 中的电场时,我 们将一个像电荷放置在介质 2 距离界面为 a 处, 电荷量 q2’;同样的,设在计算介质 2 中的电场 时,我们将一个像电荷放置在介质 1 距离界面为 a 处,电荷量 q1’。 注意 q0 的四周也会极化出一部分电荷,这部分极
,作辅助图: 㤶
t 。不难由几何关系
得到
临界
h t 㤶t
㤶
㈠䁂 t耀 㤶
临界 t耀 h
h 㤶t t 耀t
㤶 t耀 t
t m/s 㤶
至此,我们得到了(尚未考虑洛希极限的情况下)地球
末速度的方向范围,下面考虑洛希极限的影响:
t
木星系中地球能量和轨道半长轴:
;
t耀 㤶
木星与地球的最短间距:
h
t ht
h t䁂 耀 耀㈠
长。设在体积 V 一定的空间内有一定个数 N 的玻色子,试利用波的观点定性说明当温度不
【试题及答案】清北学堂2014年暑假物理竞赛模拟试题四
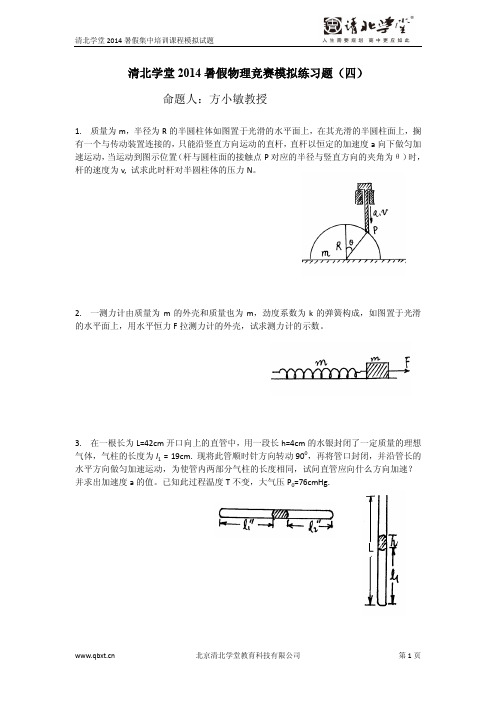
清北学堂2014暑假物理竞赛模拟练习题(四)命题人:方小敏教授1. 质量为m,半径为R的半圆柱体如图置于光滑的水平面上,在其光滑的半圆柱面上,搁有一个与传动装置连接的,只能沿竖直方向运动的直杆,直杆以恒定的加速度a向下做匀加速运动,当运动到图示位置(杆与圆柱面的接触点P对应的半径与竖直方向的夹角为θ)时,杆的速度为v, 试求此时杆对半圆柱体的压力N。
2. 一测力计由质量为m的外壳和质量也为m,劲度系数为k的弹簧构成,如图置于光滑的水平面上,用水平恒力F拉测力计的外壳,试求测力计的示数。
3. 在一根长为L=42cm开口向上的直管中,用一段长h=4cm的水银封闭了一定质量的理想气体,气柱的长度为l1 = 19cm. 现将此管顺时针方向转动900,再将管口封闭,并沿管长的水平方向做匀加速运动,为使管内两部分气柱的长度相同,试问直管应向什么方向加速?并求出加速度a的值。
已知此过程温度T不变,大气压P0=76cmHg.4. 两块厚度均为d的无限大平面带电层紧靠在一起,两带电层各带有体密度为-ρ和+ρ的电荷,一质量为m、电量为-e的粒子,以初速度v0、沿与平面成α角的方向向正电荷层运动。
试问:(1)为使粒子进不了负电荷层,则v0应小于何值?(2)若v0满足(1)中的条件,则粒子从进入正电荷层到出正电荷层共需多少时间?并求出进、出点之间的距离l .5. 一条直导线MN和半径为a的导体圆环叠放在光滑的水平面上,直导线固定而圆环可以自由移动,开始圆环的圆心O与直线的距离为a/2,两者之间电接触良好,整个空间存在一竖直方向的匀强磁场,磁感应强度为B0。
磁场的磁感应强度在极短的时间内迅速变为零,试求磁场刚变为零时圆环的速度v。
已知直导线和圆环是用同一电阻丝制成,其单位长度的质量为m0,电阻为r0.6. 一圆柱形的薄壁玻璃容器浮于水面上,容器底的水深为h,横截面的直径为d,容器内底的正中有一物点A,如图所示。
人眼位于容器壁外水面的上方,斜向下去看物点A,发现人眼在某些位置将看不到物点A,试求此“盲区”的范围(用人眼和B点的连线与竖直方向的夹角θ表示),已知水的折射率n=4/3.7. 两个质量均为m的物块A、B用劲度系数为k的轻弹簧连接,而A用一根绳悬于天花板的O点,如图所示,在B上施加一向下的恒力F=nmg, 达平衡后撤去此力,在以后的向上运动过程中,当A与天花板相碰时,弹簧第一次达到最大伸长,且伸长量为5mg/k, 试求:(1)n的值;(2)A碰天花板时的速度v A;(3) 绳的长度l ..参考答案1解:设此时半圆柱体的速度和加速度分别为V R , a R,取半圆柱体为参照系,p点的相对速度和相对加速度分别为V P‘,a P’, 由相对运动,得V P = V P’ + V R V P = V V P’ = V/sinθ(1)a P = a p’ + a R=a Pn’ + a Pt’ + a R (2)a P’= V P’2/R =(3)将(2)式的各矢量沿半径OP方向投影a P cosθ= a R sinθ+ a Pn’∴a R = actgθ-由半圆柱体受力得Nsinθ= ma R N = ( acosθ)2解:整体运动加速度 a = F/2m将弹簧分成n个等分(n→∞)每份的劲度系数k’ = nk , 质量为Δm= m/n当弹簧的总伸长为Δx时, 从左至右各小段的伸长各为Δx1,,Δx2,Δx3•…,K’Δx1=Δma Δx1 = Δma/k’K’Δx1-k’Δx2 =Δma Δx2 = 2Δma/k’…Δx n = nΔm/k’∴Δx = Δx1+Δx2+…+Δx n = (1+2+…+n)Δma/k’ = =测力计的示数即是弹簧与外壳连接处的弹力F’F’ = k Δx = ma/2 = F/43解:下部气体 P1 = P0 + d = 80cmHgV1 = L1S转过900后P1‘= P0 = 76cmHgV1’ = L1’S由玻意尔定律,得P1V1=P1’V1’L1’ = 20cm原上部气体此时的长度L2’= 18cm管封闭后应向右加速,才能使其长度变成L2’’‘= 19cmP0V2=P2’’V2’’’P2‘‘= 72cmHgP0V1‘=P1’‘V1’‘P1’‘=80cmHg对水银柱(P1-P2'')S=ρdSaa==2g=19.6m/s24解:(1)如图取坐标轴x,由高斯定律可求得x处的电场强度为E(x)=4πkρx粒子在正电荷层中运动方程为-4πkρex=m+x=0ω=初条件:x0=00=v0sinα振动的振幅为A==要求到不了负电荷层,应A≦d∴v0≦(2)t=T/2=l=vcosαt=5解:设磁场变化的时间为Δt,变化率k=B0/Δt图中θ=π/3ε1=2πa2k/3 ε2=πa2k/3 ε3=a2kR1=4πar0/3 R2=2πar0/3 R3=ar0等效电路如图所示:由基尔霍夫定律,得I1=I2+I3(1)I1R1+I2R2=ε1+ε2(2)I1R1+I3R3=ε1+ε3(3)由以上三式可解得:I1=I2=在adc上任取一小段,长Δl=aΔθ,受安培力Δf1=I1l,方向如图,有对称性可知adc段所受的合力F1必沿x方向F1===I1=I1同理,a’bc’段所受合力F2沿-x方向F2= I2而aa’,cc’两段所受的合力为零,因此,整个圆环所受的合力F=F1+F2=(I1-I2) a由动量定理,得FΔt = mv v=FΔt/m =6解:光从角B上方能直接射出,而射向角B下方的光有tgα1=2h/d sinα1=由折射定律: sinα1=nsinβ1 sinβ1=要光能从水面射出,则应满足:sinα2=conβ1=≦1- ≦可得:h≧ d(1) 若h≧d,则射到角B处的光能从水面射出,射出时的折射角为β2nsinα2=sinβ2 sinβ2=“盲区”的范围为:π/2 –α1≦θ≦β2(2) 若 h<d, 则射到角B处的光不能从水面射出,发生全反射,“盲区”的范围为:π/2 –α1≦θ<π/27解:(1)未加F力时,弹簧伸长量 x0=mg/k加上F力后,弹簧又伸长了 x=F/k撤去力后,当A开始上升时,弹簧压缩了 x1=mg/k由机械能守恒,得-mgg(x0+x)+k(x0+x)2/2 =mgx+kx12/2+mv02/2V0= g当A开始向上运动时,质心的速度为 v C0=v0/2, 在质心系中, A相对质心的速度v Ao’=-v Co,与A连接的半根弹簧的形变量x A’=-mg/2k,直到A碰天花板时,形变量为x A=5mg/2k, 由机械能守恒,得:2k+ m=2k n =(2) 质心系中,A做简谐振动,ω=振幅 A=5mg/2k, 初始条件: x A0’=-mg/2kCosϕ==ϕ=0.436π= =1.436π此时质心的速度v C=v C0-gt=0.39g, ∴v A=v C=0.39g(3) 质心的位移Δx C=v C0t - -gt2 = 11.92, A相对质心的位移Δx A’=6mg/2k ,A相对地面的位移Δx A=Δx C +Δx A’=8.96∴绳长L=Δx A=8.。
清北学堂物理竞赛考前练习题第九套

F K1x K2 x (K1 K2 )x
(2)根据牛顿第二定律得
(K1
K2
)x
m
d2x dt 2
即 m d 2 x K1 K2 x 0
dt 2
m
这表明系统作为简谐振动,其角频率和周期为 K1 K 2 ,T 2
m
m
K1 K2
通常称 K K1 K2 为并联弹簧的有效倔强系数。
S vt l vt l
A 如图(a)所示 小孩在此刻的加速度(即法向加速度)大小为
a an
v2
v2 l
2、分析:将篮球视为质点,出手后篮球在空中的运动轨迹是抛物线 。要使球能够投入篮筐, 则篮筐的坐标( x,y )应处于抛物线的下降段。根据运动的叠加原理,写出篮球的轨迹即
抛物线方程,已知 x、y 和 v0 即可求得 tan 。
五、(1)如图 4-35(1)所示,一频率为 2040Hz 的波源以速速 vs 向一个反射面(如墙壁等)
接近,一观察者在 A 点听到拍频率为 3.0Hz ,若波速为 u 340ms 1 ,求波源的移动
速度 vs ; (2)若 波 源不 动, 反射 面以 v 20ms 1 向 A 点 ( 观 察者 )运 动 ,这 时听 到的 拍频 为
在考察各小孩追逐目标时,容易发现,在依次追逐过 程中,追逐速度在指向正方形中心的 分速度保持不变,为
v cos45 2 v 2
因此,自那一时刻起(即正方形边长为 l 时刻),直至追到 目标,需时间 t 为
t
Ao v cos45
2l 2 l 2v 2 v
2)因此,每个小孩跑的路程为 S vt l
v V
)
1 v fV
1 v
f V v V v
清北学堂物理竞赛考前练习题第三套

A
B
图 2-4-15
4、有一空气平行板电容器,极板面积为 S,与电池连接,极板上充有电荷 Q0 和 Q0 ,
断开电源后,保持两板间距离不变,在极板中部占极板间的一半
体积的空间填满(相对)介电常数为 的电介质,如图 1-3-4 所
2、质量为 m 的小球随着质量也为 m 的甲车一起以速度 v0 做匀速运动。而后与质量同为 m 的乙车发生完全非弹性碰撞。不计车内轨道及水平地面的摩擦,试求:(1)求小球能上升 的最大高度;(2)小球再回到轨道最低点时对轨道的压力(已知轨道为圆弧,且半径为 r)。
3、如图 2-4-15 所示,框架是用同种金属丝制成的,单位长度的电阻为 ,一连串内接
总质量为
m
4 3
R 3
4 3
R 3 0
水
4 3
水 (3R2h
3Rh2
h3 )
①
由于 R h ,故①式可略去其中 h 的高次项面是近似写为
m 4 水 R 2 h
②
根据均匀球体表面处重力加速度的公式,可得此星球表层海洋的底面和表面处的重力加
速度分别为
g表
GM R2
g底
G(M R02
m)
依题述有 g 表 g 底 ,即
Q0
示。求:
(1)图中极板间 a 点的电场强度 Ea ? (2)图中极板间 b 点的电场强度 Eb ?
b a
Q0
图 1-3-4
(3)图中与电介质接触的那部分正极板上的电荷 Q1 ? (4)图中与空气接触的那部分正极板上的电荷 Q2 ? (5)图中与正极板相接触的那部分介质界面上的极化电荷 Q1 ?
清北学堂物理竞赛模拟试题赠六

清北学堂物理竞赛模拟试题(赠六)命题人:黄洪才老师一、完成下列两小题:(1)一个半径为r 的球状金属薄膜,厚度为a ,电阻率为ρ,如图。
证明任一直径AB 两端间的等效电阻R AB 与半径r 无关。
(2)任意一个二端电阻网络,在网络中用导线连接其中的任意两个节点,网络的等效电阻如何变化?二、物理学界一个著名的问题是“最速降线问题”,就是在重力场中有两点,如何找到一条连接此两点的轨迹,使小球从最高点由静止出发到最低点所用的时间最少。
1697年,伯努利根据光学类比的方法解决了此问题。
试说明其理由。
三、如图所示,质量为M 的滑块静止在地面上,左端固定一根劲度系数为k (足够大)的轻弹簧,右端用抗断力为T 的细绳与墙壁连接。
不计所有摩擦。
今有一质量为m 的小物块以一定的初速度滑上滑块向左运动。
(1)小物块的初速度多大时,细绳能被拉断?(2)若小物块的初速度v 0已知,细绳被拉断后,滑块的最大加速度多大?最大速度多大?四、如图所示,内部横截面积S =1.70×10-2m 2的圆柱形绝热容器内,有两个用劲度系数k =1.50×104N/m 的轻弹簧相连的绝热活塞,中部有带孔的固定隔板,容器壁上有开口与大气相通,左、右两气室中装有同种理想气体,左室中有加热器。
起初时,活塞位置如图,其中l 0=10.0cm ,两气室内气体的温度均为T 0=300K ,压强均与大气压强相同,即p 0=1.00×105Pa 。
现对左室气体缓慢加热,使左室气体吸收Q =1.00×103J 的热量,该过程中弹簧长度的最大改变量l m =7.40cm 。
求两气室中气体的最终压强和温度。
活塞所受的摩擦不计,且不漏气。
第四题图 第三题图 第一题图五、四个半径均为R 的光滑圆球静置于一个水平放置的半球形碗内,四个球的球心恰在同一水平面上。
现再将一个相同的圆球放在四球之上,系统仍能平衡。
求碗的半径。
六、如图所示,单色光(偏振光)从介质Ⅰ射到介质Ⅱ的表面上,两种介质的折射率分别为n 1、n 2。
【答案】清北学堂2014年暑假物理竞赛模拟试题二

U II = U III =
(2)当 n 趋于无穷时, CI 上的电量也就是通过电源的总电量,由(10)式可知所有电 源提供的能量为
2 W = Q = C 3
各电容器储存的能量分别为
2
1 2 Q 2 2 WI = = C C 9
2
北京清北学堂教育科技有限公司
R2 − r 2
第1页
清北学堂 2014 暑假集中培训课程模拟试题
∴ r ≤ R 2 − (8m h) 2 = 6cm
在求解过程中,我们是假设小物块与盘面碰撞的极短时间 ∆t 内两者间始终存在相对滑动, 这就要求 vx ≤ ω r 由于 vx = 2 mm v0 = 2 2 gh = 2 × 0.1× 2 = 0.2 2m / s 而 ωr = 2π × 0.06 = 0.12π m / s 可见 vx < ω r ,则以上计算有效。
QI = Q1 + Q2 + + Qn
(2)
在第 n 次接通 oa 之前,即第 n- 1 次接通 ob 之后, CI 上的总电荷量为 Q1 + Q2 + Qn−1 ,根 据电荷守恒,此时 CII 、 CIII 上的总电荷量应为 Q1 + Q2 + Qn−1 ,因为 CII 、 CIII 并联,两
根据动量定理可得反弹后小物块 x 方向的速度 vx
2 µ v0 = I f 2= m mv0 mvx ∴ vx =
= t 小物体跳起后又落下,所经时间为 t , ∆
2v0 2h = 2 g g
v0 2 = 8µ h g
在此期小物块沿 x 方向的位移 ∆x = vx ∆t = 2 µ
x 8µ h ≤= l 由图可知,只要满足下式关系,小物块就不会落到圆盘外 ∆=
清北学堂物理竞赛考前练习题第七套

环相对于柱是一个加速度a 为常值得匀变速运动。如果环对柱停滑前未滑脱,就可以
在柱参考系中(尽管它是一个加速参考系,但运动学关系仍成立)计算环滑行的距离 S1
S1
v2
2a
2
2 2gh
22kg
1 k
2h g
滑行所需时间 t1 为
v 2 2gh 1 2h
t1 a
2kg
k
g
这个时间可以与碰地后柱达最高点所需时间 t2 相比
七、
有 mol 的理想气体经过1 2 3 1如图习 7-2 所示的循环过程,过程1 2 和 2 3
在图中是直线段而过程 3 1可表达为 T 0.5T1(3 BV )BV ,式中 B 是未知的常数,图
中的 T 是绝对温标的温标,求气体在一个循环中所做的功。
答案解析 1、 分析与解
若喷头球面上小孔喷水的速度 v0 保持不变(由控制水压办到),则每一个孔喷出的水注将按
接入电源 E 后,设电容器 A1B1 和 B2 A2 上的电压分别为U 1 和U 2 ,则
U1 150 50 100 (V)
U2 50 (150) 200 (V)
B1 , B2 板上的电量分别为 q1 C1U1 300C0
q2 C2U 2 600C0 因金属板 B 原不带电,所以接入电源 E 后电源 E 输给金属板 B 的电量为 Q q1 q2 300C0 9 108 (C)
取一后金属板 B ,其面积与 A1 及 A2 相同,厚度为电容器极
板间距离的三分之一,插入电容器两极板 A1 , A2 的正中央,
如图 1-练 20 所示。 (1)取一电动势 50V 为的电源 E ,正极连金属板 B ,负极 接地。问此时由电源 E 输送到金属板 B 的总电量是多少? (2)在上述情况下,左右平移金属板 B ,改变它在电容器两 级板间的位置,使 B 板上的电量向电源 E 回输,直到电源 E 原来输给金属板 B 的电量全部送回电源时,固定 B 的位置, 然后切断三个电源,并将 B 板从电容器中抽出。求此时电容
清北学堂物理竞赛模拟题

清北学堂全国中学生物理竞赛模拟试题180分钟320分第一题(40分)一长直气缸竖直放置于重力场中。
气缸内装有单原子分子理想气体,总分子数为N,每个分子的质量为m。
平衡态时系统温度均匀分布。
考虑玻尔茲曼分布,玻尔曼常数为k,重力加速度为g。
活塞可无摩擦地上下滑动,活塞质量引起的附加压强远大于外界大气压。
求系统的定压热容量与温度的关系。
第二题(40分)种可能的质子蜕变方式为:P→π0+e+中性介子π0立即蜕变为两个光子:π0→γ+γ已知质子、π0介子、正电子的静质量分别为m1、m2、m3,求能够获得的光子能量最值.第三题(40分)重力场中固定一根长直椭圆柱,一根轻细绳垂直于椭圆柱轴向搭在椭圆柱侧面上,用外力拉住绳子的一端在椭圆柱横截面椭圆的上顶点,另一端经过椭圆右顶点下垂并系一质量为m的重物。
绳子与椭圆柱侧面间的摩擦系数为μ,椭圆柱横截面椭圆的离心率ε远小于1。
已知重力加速度g,求外力的大小(略去二阶及以上小量)。
第四题(40分)回旋加速器中匀强磁场的磁感应强度B=1T,高频电源的频率f=7.5MHz,D形电极的半径R=1m,带电粒子束输出时的平均电流强度I=1mA.如果粒子束进入缓慢流动的冷却水并停止相对运动,试问可使水温升高多少度?设流动水的流量μ=1kg⋅s−1,水的比热c=4200J⋅kg−1⋅K−1.(保留两位有效数字)无线电真空管抽气抽到最后阶段时,还应将真空管内的金属加热再继续抽空,原因是金属表面上吸附有单原子层的气体分子。
当金属受热时,被吸附分子获得足够动能后能挣脱固体表面分子束缚而被释放出来。
设真空管的灯丝是用半径r=0.2mm、长度L=6×102mm的铂丝绕制的,而每个气体分子所占面积S0=9×10−20m2,真空管的容积V=2.5×10−5m3当灯丝加热至1000∘C时,所有被吸附的分子都从铂丝上跑出来散布到整个泡内。
如果此气体不抽出,试问由它所引起的压强是多大(帕斯卡)?第六题(40分)两个半径为R,质量为M的金属球通过一线度可略的轴承焊接在一起.求这一系统作为孤立导体对无穷远处的电容.绕长轴旋转而成的椭球导体电容.(1)平面上有一段长为2 的均匀带电直线段F1F2,取其长度方向为x轴方向,取其中O点为零点,设置Oxy坐标面(1.1)试证明Oxy面上任意一点P的电场强度方向均为∠F1PF2的角平分线方向(1.2)导出Oxy坐标面上的电场线方程(1.3)导出Oxy坐标面上的等势线方程(2)试求半长轴为 ,半短轴为 ,绕长轴旋转而成的椭球导体电容提示:依据椭圆常用性质(几何)答题第八题(40分)盖上盖的容器里装满水,水中有两个小气泡,如果这两个气泡合并,那么水中压强变化多少Δp(取绝对数值)?水中初压强为p0,水的表面张力系数为σ,每个小气泡半径为r0,合并过程是等温的.。
清北学堂第37届全国中学生物理竞赛决赛模拟试题及答案【完整版】

清北学堂第37届全国中学生物理竞赛决赛模拟试题一、如1图所示,一斜面与水平面夹角为α,其上放置以横截面为正六边形的铅笔,边长为a ,质量为M ,其长度a l >>。
铅笔棱边与水平面方向夹角为ϕ,铅笔与桌面摩擦系数足够大。
一根细绳穿过斜面与桌面上的狭缝系在铅笔的一角,如图2,另一端悬挂一质量为m 的小球。
为使铅笔既不向前滚,也不向后滚,试分析m 取值范围。
图一 图二二、一根光滑的细杆被弯成如图所示的形状,并被固定在竖直平面内,形状曲线方程为221x a y =(a 为正常数)。
杆上套有一质量为m 的小环。
(1)若小环从杆上a x 2=处静止释放,求运动到a x =处时对杆的作用力大小; (2)若杆绕y 轴以固定角速度0w 转动,问0w 为多大事,小环可在杆任意处平衡;(3)若杆绕 轴转动角速度去(2)问中的22,即022w w =,则小环从杆上的a x 2=处 由相对静止释放,求小环运动到a x =处时对杆的作用力大小。
三、如图,光滑水平面上放有一质量为M 的直角细构件ABD ,L BD BE AE 2121===,初始静止。
质量为m 的质点P 以平行于BD 方向的速度与构件的E 点相碰,碰撞时恢复系数为4.0=e ,之后质点P 又能与构件的D 点相碰,求mM 。
四、几何图形化的R 、L 网络如图所示,其中每一根直线段都代表一条相同的R 、L 串联电路,对于所取的交流角频率w ,有R wL 3= 。
(1)计算A 、B 之间的等效电抗(答案仅用R 表示);(2)以A 为输入段,B 为输出端,为使A 、D 之间网络总功率的功率因数成为22cos =ϕ,可在每一支路上串联一个相同的电容1C 。
求最小的1C 值(答案仅用w 和R 表示);(3)每一支路都不串联电容,但在D 点之外串联一个电容2C ,使网络AD 与2C 构成的串联组总功率的功率因数成为22cos =ϕ,求最小的2C 值(答案仅用w 和R 表示)。
2022年清北学堂第39届全国中学生物理竞赛复赛模拟试题

2022年清北学堂第39届全国中学生物理竞赛复赛模拟试题 学校:___________姓名:___________班级:___________考号:___________一、解答题1.本题忽略重力,当0=t 时,桌面上有一质量为M ,初始高度为H ,半径恒定为R ,电荷量密度ρ,质量和密度均匀分布,杨氏模量为A 的绝缘弹性体,圆柱体底面时刻与地面相连,可绕中心无摩擦转动;全空间电磁场只考虑在z 方向上的()01cos ωE t E t =-(), 0 )sin ωz B z t B e t γ-=(,,(1z γ<<), 以及该磁场附加的涡旋电场;随着时间变化,圆柱体在z 方向电场力作用下,上下周期性运动,质量、电荷密度变得不均匀,并且由于电场较大可认为各处在z 方向上时时受力平衡,即拉力与电场力平衡,同时在涡旋电场力矩下开始转动,本题探究仅在该两项电场力作用足够长时间后:(1)圆柱体高度H H t =();(2)圆柱体绕z 轴转角可近似为()2t Ct φφ==的形式,求C 。
2.想必大家都转过硬币吧,如果没有转过也可以拿手边一元硬币试试。
我们在硬币旋转过程中可以观察到如下现象:(a )你会发现从上面看来硬币旋转速度在变慢(b )硬币发出响声的频率在加快这两者似乎是矛盾的,因为前面告诉我们硬币越转越慢,后者告诉我们它越转越快。
本题尝试建立模型解释这种奇妙的现象。
首先我们假定我们给硬币一个初始角动量,使硬币转起来获得较大的z 轴角动量,然后硬币掉落在摩擦系数极小的光滑桌面上,因此能量损失会较为缓慢,能作为准静态考虑。
硬币边缘对于桌面是纯滚的,旋转过程可以看作是旋转对称的。
设硬币(抽象成一个均质圆柱体)厚度为h ,半径为R ,质量为m ,请回答下列问题:(1)图中x y z ,,轴为硬币的主轴(原点在质心),求转动惯量xx yy zz I I I 、、;(2)我们考虑硬币对于桌面倾斜角为θ时的旋转。
清北学堂物理竞赛考前练习题第二套
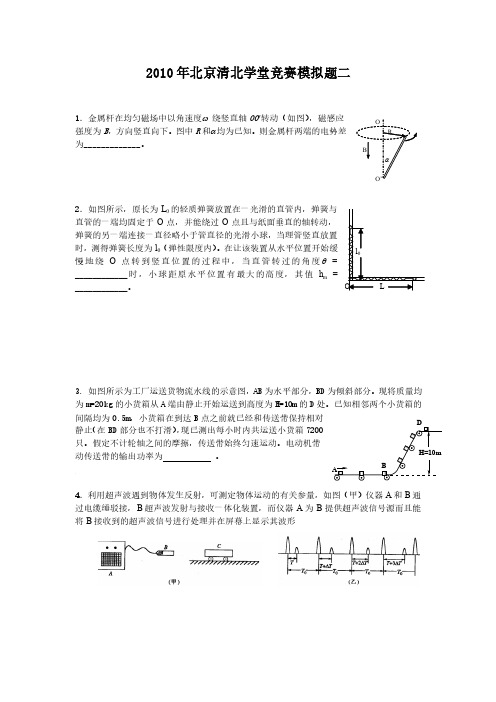
的夹角为 ,则 a qE ①
m
t1
2 y0 a
②
v0
x0 t1
③
其中 x0 2
3l,
y0
l 。又有 tan
at1 v0
④
联立②③④式,得 30
因为 M、O、Q 点在圆周上, MOQ=90 ,所以 MQ 为直径。从图中的几何关系可
知。
R 2 3l ⑥
MO 6l ⑦
(8 分)(2)设粒子在磁场中运动的速度为v ,从 Q 到 M 点运动的时间为t2 ,
(4)若金属框运动时受到恒定的阻力 f = 0.1 N 作用时,金属框的最大速度;
(5)在(4)的情况下,当金属框达到最大速度时,为维持它的运动,磁场必须提供的功率。
M
N
v
××
××
××
B1 ×B2× B1 B×2 × B1 ×B×2
××
A ××
××
P
B1 Q
参考答案: 1.12 BR2
3.2040W
为 m=20kg 的小货箱从 A 端由静止开始运送到高度为 H=10m 的 D 处。已知相邻两个小货箱的
间隔均为 0.5m,小货箱在到达 B 点之前就已经和传送带保持相对
D
静止(在 BD 部分也不打滑),现已测出每小时内共运送小货箱 7200
只。假定不计轮轴之间的摩擦,传送带始终匀速运动。电动机带
动传送带的输出功率为
(3)金属框最大运动速度为 vm= 4m/s
(2 分)
当磁场向左运动时,金属框和磁场发生相对运动,切割磁感线,产生感应电流,感应
电流受到的安培力水平向左,金属框在安培力作用下开始向左做加速运动。这样,感应电流、安培力跟着减小。当两者速度相等时,
清北学堂全国中学生物理竞赛模拟卷参考答案

⑥
故至多可布置7 长。
8
化学反应速率的统计估算 设想存在两种单原子分子气体A与B,两种分子的质量分别为m1与m2,直径分别为 d1与d2。现将其混合在一个温度为T0的恒温容器中,在均匀混合的瞬间, 、 数密度分 别为n1与n2,此时,它们开始反应生成气体 。 ( + → ) 现假设化学反应无明显的热效应,为估算化学反应的速率,取如下简化模型:假设 两分子完成有效碰撞至少需要消耗ε0的能量(仅是活化能),且有效碰撞中发生反应的概 率为p(p<1)。试估算此瞬间气体C的化学反应速率。
解答:
线框棱边电阻 = 0,底边电阻 = 2 0 ( )。采用
回路电流法解本题。 对第n条棱,其上的复电动势为
ℰ = ℰ0
ℰ0 =
= 2= 0 ①
设上下底面的复回路电流为 ,对侧面n,设其复回路电流为 = 0
2 + − −1 − +1 = ℰ − ℰ +1
②
从而,消去时间因子 ,得
,则该侧面回路内有
若①收到③的反射信号后,便立即再次向②发信号,试求③第n次 收到信号时,在①看来自发第一次信号过去了多久(∆ ),在③看来自离 开①过去了多久(∆ ')?
3)在太空中有六个人,分别记为①~⑥。设某时刻②~⑥以图 2 所 示方式于同一平面内同时离开①,若每个人看另外五个人都看到一样的 景象。试问,若已知β3,则β1,β2,θ1,θ2 为何?
13 =
1+ 1− 12
⑧
21 = 1 +
13
=
(
1+ 1−
3
)2∙
11
⑨
递推之,可得
1
=
(
1+ 1−
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1.2)由抛物线的光学性质可知,以F F 为两焦点的双曲线,取其 中任一点 P,过 P 作双曲线的法线 MPN,则由F 到 P 的入射光线必 经过F 点,作过 P 点的切线 SPT,则∠F PF 的角平分线.若F F 均匀 带电,则 P 点场强 方向必沿 SPT 方向,即为该双曲线.据上述讨论 可知,Oxy 坐标面上的电场线即为以F F 为两焦点的双曲线(簇), 其方程为
(1.3)由椭圆光学性质可知,同(1.2)理,椭圆即为等势线,其方程为
(2)由(1.3)可得到下述结论 以 A 为长半轴,B 为短半轴,绕长轴旋转而成的椭圆球面内,若
令两焦点连线段上均匀带电,则此椭球面必为该线电荷电场的一个等 势面.
设要讨论的椭球导体,由题解图 4 所示 Oxy 平面上长半轴为 A, 短半轴为 B 焦点为F F 的椭圆绕 x 轴旋转成.为计算电容 ,设椭球 导体带电量为 未知,但静电平衡后椭球面电视 为已知量.采用 静电镜像法,设镜像电荷总量为 均匀分布在点F F 连线上.根据前 面给出的“推论”可知,旋转椭球面确定为此镜像电荷电场的等势面.
Δt =5.6(K)
题五、题目较长,但有效信息并不多,算出溢出气体物质的量,再由 气体分压原理和理想气体状态方程即可求解,较为简单,设被释放气 体总分子数为ΔN,由此而引起真空管中气体分子数密度的变化为Δn, 所引起气体压强的变化为Δp.由于Δp=ΔnkTΔp=ΔnkT,Δn=ΔNV, ΔN=2πrLS0,故Δp=0.59Pa
Δp<0 可见水中压强减小,减小量为
Δp= (1- )
T=2πm/qB =1/f R=mv/qB
联立解得粒子输出时的速率 v= 2πfR
设粒子输出时,单位时间飞出回旋加速器的粒子数为 N,则电流强度 I=Nq
则粒子束的输出功率为 P =πIBR2f
因水流速度很小,这部分功率被单位时间流过的水所吸收,得热平衡 方程
P=πIBR2f=cμΔt 由此解得水温升高
1 x
=0
∴C=0
⑥,故 G(x)=ln(1+x)+C ⑦,而 G(0) ⑧
∴G(x)=ln(1+x) ⑨
即
(-1)k+1/k=ln2
k 1
⑩,故 Q=4πε0Ruln2 ⑪
∴C= Q =8πε0Rln2
⑫
U
题七、(1.1)用于小量分析方法可以证明(此处从略),F F 处电荷对 P 点的场强与一段半径等于 P 到F F 的距离以 P 为圆心,张角相同电荷 线密度与F F 中电荷线密度相同的带电圆弧 P 点处的场强.后者由对 称性可知,场强方向必沿角平分线方向,故本小题获证,图中设F F 带正电画出 方向
,
故 产生的 为 故
ln
ln ln ,
题八、 由于盖上盖的容器里装满水,水的体积不变,故,则大 气泡的半径
r= R 初态时小气泡内气体的压强
p1=2σ/R−p0 由于合并过程是等温的,有
故有
2⋅p1V0=p2⋅2V0
p1=p2 因此两个小气泡合并,水中压强变化
清北学堂物理竞赛模拟题参考答案
题一、由玻尔兹曼分布得: P(H)=n(H)kT=Mg/A 由此得: H= u ln(1+ ) 写出内能表达式: U= NkT- u ln(1+ ) 微分分析并由热力学第一定律可得: dQ=dU+dW= NkdT 由定义得: Cp=dQ/dT= Nk
题二、由狭义相对论能动量关系可得: Eπ=(m12+m22-m32)c2/2m1 在π0 介子静止的参考系中,两光子能动量大小为: E= m2c2 p= m2c 在实验室参考系中,当两光子和π0 介子的速度方向共线时,速度与π0 介子同向的光子能量最大,速度与π0 介子反向的光子能量最小,由洛 伦兹变换得光子能量最值: Emax= γm2c2(1+β) Emin= γm2c2(1-β)
题三、对绳子上一小段微元作受力分析,得
dT=μdN dN=Tdα
设椭圆上一点对两焦点的张角为 2β,将曲率半径取一阶近似得ρ≈p
将几何关系取一阶近似得:dl≈
dθ
联立微分方程并取一阶近似得: u≈μ(1-εcosθ)dθ
u
积分得:F≈mgeμπ/2
题四、带电粒子的质量为 m,带电量为 q.则粒子在输出前瞬时的周 期 T 和圆轨道半径 R 分别为
题六、第 k 级像电荷距离轴承的距离为:xk=R/k ①
像电荷大小为:qk=(-1)k+1q0/n ,k=2、3、4、、、 ②
设电势为 u,则:q0=4πε0Ru ③
∴总电量
Q=2q0
(-1)k+1xk/k,x∈(0,1】
④
k 1
为了求级数和,引入:G(x)=
(-1)k+1xk/k,
⑤
k 1
求导得:G(x)= 1
