根据正弦型函数的图象求解析式
高中数学人教A版必修4第一章正弦型函数y=Asin(ωx+φ)的图像平移及解析式的求法

正弦型函数y =Asin(ωx +φ)的图像平移及解析式的求法【知识点梳理及分析】一、有关正弦型函数y =Asin(ωx +φ)基础知识1.用五点法画y =A sin(ωx +φ)一个周期内的简图时,要找五个特征点如A 叫做振幅,T =2πω叫做周期,f =1T叫做频率,ωx +φ叫做相位,φ叫做初相.3.函数y =A sin(ωx +φ) (A >0,ω>0)的性质如下: 4.图象的对称性函数y =A sin(ωx +φ)(A >0,ω>0)的图象是轴对称也是中心对称图形,具体如下:(1)函数y =A sin(ωx +φ)的图象关于直线x =x k (其中 ωx k +φ=k π+π2,k∈Z)成轴对称图形.(2)函数y =A sin(ωx +φ)的图象关于点(x k,0)(其中ωx k +φ=k π,k ∈Z)成中心对称图形. 二、图像的平移转换图像的平移转换遵循左加右减,上加下减原则 1.函数y =A sin(ωx +φ)图像变换(1)左右平移:由y =sinx 的图象向左或向右平行移动|φ|个单位,得到y =sin (x +φ)的图象.(2)胖瘦变换:由y =sinx 的图象上的点的纵坐标保持不变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到原来的1||ω倍,得到y =sin ω x 的图象.(3)高矮变换:由y =sinx 的图象上的点的横坐标保持不变,纵坐标伸长(当|A|>1)或缩短(当0<|A|<1)到原来的|A|倍,得到y =Asinx 的图象.2.两种变换方法注意:左侧为先平移后伸缩,右侧为先伸缩后平移 三、正弦型函数y =Asin(ωx +φ)解析式的求法1.表达式的化简(主要利用辅助角公式)(1)辅助角公式sin cos a b αα+22)a b αϕ++(其中,辅助角ϕ所在象限由点(,)a b 所在的象限决定,2222sin tan ba ab a b ϕϕϕ===++ ,该法也叫合一变形).(2)所涉及到公式① 两角和与差的正弦、余弦公式: (1)βαβαβαsin cos cos sin )sin(+=+ (2)βαβαβαsin cos cos sin )sin(-=- (3)βαβαβαsin sin cos cos )cos(-=+ (4)βαβαβαsin sin cos cos )cos(+=-②二倍角公式(1)a a a cos sin 22sin =(2)1cos 2sin 21sin cos 2cos 2222-=-=-=a a a a a③降幂公式:(1)22cos 1cos 2a a += (2) 22cos 1sin 2aa -=注:表达式的化简攻略可化简的表达式多种多样,很难靠举例一一道明,化简往往能够观察并抓住式子的特点来进行操作,主要有以下几个特征:(1)观察式子:主要有三点①系统:整个表达式是以正余弦为主,如果有正切需要切化弦进行统一 ②确定研究对象:是以x 作为角来变换,还是以x 的表达式看做一个角来进行变换③式子是否齐次:式子要做到齐次统一,利用所涉及到三角函数恒等式的公式进行转换,把同一角转换为齐二次式或是齐一次式在使用辅助角公式,使结果成为y =A sin(ωx +φ)(2)向“同角齐次正余全”靠拢,能拆就拆,能降幂就降幂(注意平方降幂).2. 求解A 、ω、φ以及确定解析式 (1)A 的求解A 的求解:根据图象的最高点和最低点,即A =最高点-最低点2(2)ω的求解结合图象,先求出周期,然后由T =2πω(ω>0)来确定ω①如果y =Asin(ωx +φ)相邻的两条对称轴为x=a ,x=b (a<b ),则T=2(b-a).②如果y =Asin(ωx +φ)相邻的两个对称中心为(a ,0)、(b ,0)(a<b ),则T=2(b-a).③如果y =Asin(ωx +φ)相邻的对称轴与对称中心分别为x=a ,(b ,0)则T=4a -b .注意:在y =Asin(ωx +φ)中,对称轴与最值点等价,对称中心与零点等价.(3)φ的求解①代入法:把图上已知点代入即可. ②五点法确定φ值时,往往以寻找“五点法”中的特殊点作为突破口.具体如下:“第一点”(即图像上升时与x 轴交点)为ωx +φ=0;“第二点”(即图像的“峰点”)为ωx +φ=π2;“第三点”(即图像下降时与x 轴交点)为ωx +φ=π;“第四点”(即图像的“谷点”)为ωx +φ=3π2;“第五点”为ωx +φ=2π.(4)y =Asin(ωx +φ)+B 中“B ”的确定 B 的确定:根据图象的最高点和最低点,即B =最高点+最低点2补充:函数的最值(几种常见的函数及其最值的求法):①b x a y +=sin (或)cos b x a +型:利用三角函数的值域,须注意对字母的讨论②x b x a y cos sin +=型:引进辅助角化成)sin(22ϕ++=x b a y 再利用有界性③c x b x a y ++=sin sin 2型:配方后求二次函数的最值,应注意1sin ≤x 的约束④dx c bx a y ++=sin sin 型:反解出x sin ,化归为1sin ≤x 解决⑥c x x b x x a y +⋅++=cos sin )cos (sin 型:常用到换元法:x x t cos sin +=,但须注意t 的取值范围:2≤t 。
由三角函数图像求解析式(适合讲课使用)

图像的变换与对称性
01
平移变换
三角函数图像可以在x轴或y轴方向上平移,而不改变其形状和性质。
例如,正弦函数向右平移a个单位后变为$y=sin(x-a)$。
02
伸缩变换
三角函数图像可以在x轴或y轴方向上伸缩,从而改变其周期和振幅。
例如,正弦函数在x轴方向上伸缩a倍后变为$y=sin(frac{1}{a}x)$。
余弦函数
定义域
全体实数,即$R$。
值域
$[-1,1]$。
周期性
余弦函数具有周期性,最小正 周期为$2pi$。
单调性
在每个周期内,余弦函数在$[0, pi]$上单调递减,在$[pi, 2pi]$
上单调递增。
正切函数
定义域
01
不连续,无周期性。
值域
02
全体实数,即$R$。
单调性
03
正切函数在每一个开区间$(kpi-frac{pi}{2}, kpi+frac{pi}{2})$内
01
1. 绘制直角坐标系
根据解析式的定义域,绘制直角 坐标系。
02
03
2. 确定关键点
3. 绘制图像
根据解析式的值,确定直角坐标 系中的关键点。
根据关键点,绘制三角函数的图 像。
例题三:综合应用题
1. 分析题目
仔细阅读题目,理解题目的要求和条件。
2. 确定解题步骤
根据题目要求,确定解题步骤,包括已知条件的分析、未知条件的推导等。
由三角函数图像求解析式
contents
目录
• 引言 • 三角函数的基本性质 • 三角函数图像的绘制 • 由三角函数图像求解析式的方法 • 实例分析 • 总结与思考
4.4正弦型函数的图像与性质
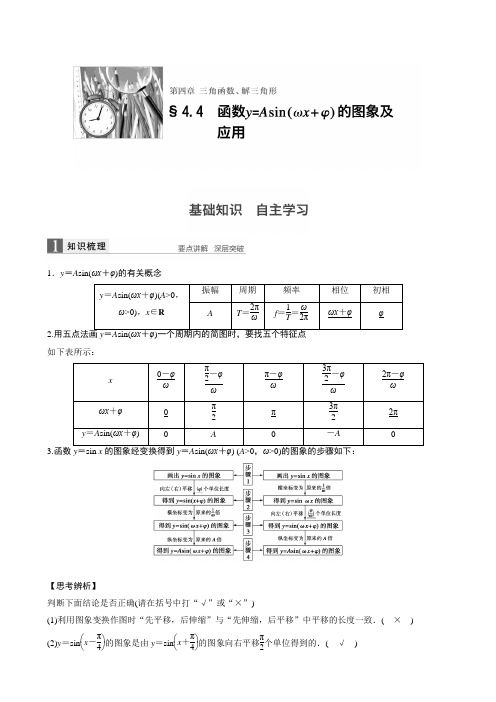
1.y =A sin(ωx +φ)的有关概念y =A sin(ωx +φ)(A >0,ω>0),x ∈R振幅 周期 频率 相位 初相 AT =2πωf =1T =ω2πωx +φφ2.用五点法画y =A sin(ωx +φ)一个周期内的简图时,要找五个特征点 如下表所示:x0-φω π2-φω π-φω 3π2-φω 2π-φω ωx +φ 0 π2 π 3π2 2π y =A sin(ωx +φ)A-A3.函数y =sin x 的图象经变换得到y =A sin(ωx +φ) (A >0,ω>0)的图象的步骤如下:【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)利用图象变换作图时“先平移,后伸缩”与“先伸缩,后平移”中平移的长度一致.( × ) (2)y =sin ⎝⎛⎭⎫x -π4的图象是由y =sin ⎝⎛⎭⎫x +π4的图象向右平移π2个单位得到的.( √ )(3)由图象求解析式时,振幅A 的大小是由一个周期内的图象中的最高点的值与最低点的值确定的.( √ ) (4)函数f (x )=A sin(ωx +φ)的图象的两个相邻对称轴间的距离为一个周期.( × )(5)函数y =A cos(ωx +φ)的最小正周期为T ,那么函数图象的两个相邻对称中心之间的距离为T2.( √ )1.y =2sin ⎝⎛⎭⎫2x -π4的振幅、频率和初相分别为( ) A .2,1π,-π4.2,12π,-π4C .2,1π,-π8.2,12π,-π8答案 A2.为了得到函数y =sin(2x +1)的图象,只需把函数y =sin 2x 的图象上所有的点( ) A .向左平行移动12个单位长度B .向右平行移动12个单位长度C .向左平行移动1个单位长度D .向右平行移动1个单位长度 答案 A解析 y =sin 2x 的图象向左平移12个单位长度得到函数y =sin 2(x +12)的图象,即函数y =sin(2x +1)的图象.3.(2015·湖南)将函数f (x )=sin 2x 的图象向右平移φ⎝⎛⎭⎫0<φ<π2个单位后得到函数g (x )的图象,若对满足|f (x 1)-g (x 2)|=2的x 1,x 2,有|x 1-x 2|min =π3,则φ等于( )A.5π12B.π3 C.π4 D.π6答案 D解析 因为g (x )=sin 2(x -φ)=sin(2x -2φ), 所以|f (x 1)-g (x 2)|=|sin 2x 1-sin(2x 2-2φ)|=2. 因为-1≤sin 2x 1≤1,-1≤sin(2x 2-2φ)≤1,所以sin 2x 1和sin(2x 2-2φ)的值中,一个为1,另一个为-1,不妨取sin 2x 1=1,sin(2x 2-2φ)=-1,则2x 1=2k 1π+π2,k 1∈Z,2x 2-2φ=2k 2π-π2,k 2∈Z,2x 1-2x 2+2φ=2(k 1-k 2)π+π,(k 1-k 2)∈Z ,得|x 1-x 2|=⎪⎪⎪⎪(k 1-k 2)π+π2-φ. 因为0<φ<π2,所以0<π2-φ<π2,故当k 1-k 2=0时,|x 1-x 2|min =π2-φ=π3,则φ=π6,故选D.4.(教材改编)如图,某地一天从6~14时的温度变化曲线近似满足函数y =A sin(ωx +φ)+b ,则这段曲线的函数解析式为________________________________.答案 y =10sin ⎝⎛⎭⎫π8x +3π4+20,x ∈[6,14] 解析 从图中可以看出,从6~14时的是函数 y =A sin(ωx +φ)+b 的半个周期, 所以A =12×(30-10)=10,b =12×(30+10)=20, 又12×2πω=14-6, 所以ω=π8.又π8×10+φ=2π, 解得φ=3π4,所以y =10sin ⎝⎛⎭⎫π8x +3π4+20,x ∈[6,14].5.(2014·安徽)若将函数f (x )=sin(2x +π4)的图象向右平移φ个单位,所得图象关于y 轴对称,则φ的最小正值是________. 答案3π8解析 ∵函数f (x )=sin(2x +π4)的图象向右平移φ个单位得到g (x )=sin[2(x -φ)+π4]=sin(2x +π4-2φ),又∵g (x )是偶函数,∴π4-2φ=k π+π2(k ∈Z ).∴φ=-k π2-π8(k ∈Z ).当k =-1时,φ取得最小正值3π8.题型一 函数y =A sin(ωx +φ)的图象及变换 例1 已知函数y =2sin ⎝⎛⎭⎫2x +π3. (1)求它的振幅、周期、初相;(2)用“五点法”作出它在一个周期内的图象;(3)说明y =2sin ⎝⎛⎭⎫2x +π3的图象可由y =sin x 的图象经过怎样的变换而得到. 解 (1)y =2sin ⎝⎛⎭⎫2x +π3的振幅A =2, 周期T =2π2=π,初相φ=π3.(2)令X =2x +π3,则y =2sin ⎝⎛⎭⎫2x +π3=2sin X . 列表如下:x -π6 π12 π3 7π12 5π6 X 0 π2 π 3π2 2π y =sin X 0 1 0 -1 0 y =2sin ⎝⎛⎭⎫2x +π3 02-2描点画出图象,如图所示:(3)方法一 把y =sin x 的图象上所有的点向左平移π3个单位长度,得到y =sin ⎝⎛⎭⎫x +π3的图象; 再把y =sin ⎝⎛⎭⎫x +π3的图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到y =sin ⎝⎛⎭⎫2x +π3的图象; 最后把y =sin ⎝⎛⎭⎫2x +π3上所有点的纵坐标伸长到原来的2倍(横坐标不变),即可得到y =2sin ⎝⎛⎭⎫2x +π3的图象. 方法二 将y =sin x 的图象上所有点的横坐标缩短为原来的12倍(纵坐标不变),得到y =sin 2x 的图象;再将y =sin 2x 的图象向左平移π6个单位长度,得到y =sin ⎣⎡⎦⎤2⎝⎛⎭⎫x +π6=sin ⎝⎛⎭⎫2x +π3的图象; 再将y =sin ⎝⎛⎭⎫2x +π3的图象上所有点的纵坐标伸长为原来的2倍(横坐标不变),即得到y =2sin ⎝⎛⎭⎫2x +π3的图象.思维升华 (1)五点法作简图:用“五点法”作y =A sin(ωx +φ)的简图,主要是通过变量代换,设z =ωx +φ,由z 取0,π2,π,32π,2π来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象.(2)图象变换:由函数y =sin x 的图象通过变换得到y =A sin(ωx +φ)的图象,有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.(1)把函数y =sin(x +π6)图象上各点的横坐标缩短到原来的12(纵坐标不变),再将图象向右平移π3个单位长度,那么所得图象的一条对称轴方程为( ) A .x =-π2B .x =-π4C .x =π8D .x =π4(2)设函数f (x )=cos ωx (ω>0),将y =f (x )的图象向右平移π3个单位长度后,所得的图象与原图象重合,则ω的最小值等于( ) A.13B .3C .6D .9 答案 (1)A (2)C解析 (1)将y =sin(x +π6)图象上各点的横坐标缩短到原来的12(纵坐标不变),得到函数y =sin(2x +π6);再将图象向右平移π3个单位长度,得到函数y =sin[2(x -π3)+π6]=sin(2x -π2),故x =-π2是其图象的一条对称轴方程.(2)由题意可知,nT =π3 (n ∈N +),∴n ·2πω=π3(n ∈N +),∴ω=6n (n ∈N +),∴当n =1时,ω取得最小值6. 题型二 由图象确定y =A sin(ωx +φ)的解析式例2 (1)将函数f (x )=sin(2x +θ)⎝⎛⎭⎫-π2<θ<π2的图象向右平移φ(φ>0)个单位长度后得到函数g (x )的图象,若f (x ),g (x )的图象都经过点P ⎝⎛⎭⎫0,32,则φ的值可以是( ) A.5π3 B.5π6 C.π2D.π6(2)函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π)的部分图象如图所示,则函数f (x )的解析式为__________.答案 (1)B (2)f (x )=2sin(2x +π3)解析 (1)∵P ⎝⎛⎭⎫0,32在f (x )的图象上, ∴f (0)=sin θ=32. ∵θ∈⎝⎛⎭⎫-π2,π2, ∴θ=π3,∴f (x )=sin ⎝⎛⎭⎫2x +π3. ∴g (x )=sin ⎣⎡⎦⎤2(x -φ)+π3. ∵g (0)=32, ∴sin ⎝⎛⎭⎫π3-2φ=32. 验证φ=56π时,sin ⎝⎛⎭⎫π3-2φ=sin ⎝⎛⎭⎫π3-53π=sin ⎝⎛⎭⎫-43π=32成立. (2)由题图可知A =2, T 4=7π12-π3=π4, 所以T =π,故ω=2, 因此f (x )=2sin(2x +φ), 又⎝⎛⎭⎫712π,-2为最小值点, ∴2×712π+φ=2k π+3π2,k ∈Z ,∴φ=2k π+π3,k ∈Z ,又|φ|<π, ∴φ=π3.故f (x )=2sin(2x +π3).思维升华 确定y =A sin(ωx +φ)+b (A >0,ω>0)的步骤和方法: (1)求A ,b ,确定函数的最大值M 和最小值m , 则A =M -m 2,b =M +m 2.(2)求ω,确定函数的最小正周期T ,则可得ω=2πT .(3)求φ,常用的方法有:①代入法:把图象上的一个已知点代入(此时A ,ω,b 已知)或代入图象与直线y =b 的交点求解(此时要注意交点在上升区间上还是在下降区间上).②特殊点法:确定φ值时,往往以寻找“最值点”为突破口.具体如下:“最大值点”(即图象的“峰点”)时ωx +φ=π2;“最小值点”(即图象的“谷点”)时ωx +φ=3π2.函数f (x )=2sin(ωx +φ)⎝⎛⎭⎫ω>0,-π2<φ<π2的部分图象如图所示,则φ=________.答案 -π3解析 ∵T 2=1112π-512π,∴T =π.又T =2πω(ω>0),∴2πω=π, ∴ω=2.由五点作图法可知当x =512π时,ωx +φ=π2,即2×512π+φ=π2,∴φ=-π3.题型三 三角函数图象性质的应用 命题点1 三角函数模型的应用例3 如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置P (x ,y ).若初始位置为P 0⎝⎛⎭⎫32,12,当秒针从P 0(注:此时t =0)正常开始走时,那么点P 的纵坐标y 与时间t 的函数关系式为( )A .y =sin ⎝⎛⎭⎫π30t +π6B .y =sin ⎝⎛⎭⎫-π60t -π6 C .y =sin ⎝⎛⎭⎫-π30t +π6 D .y =sin ⎝⎛⎭⎫-π30t -π3 答案 C解析 由题意可得,函数的初相位是π6,排除B 、D.又函数周期是60(秒)且秒针按顺时针旋转,即T =⎪⎪⎪⎪2πω=60,所以|ω|=π30,即ω=-π30. 命题点2 方程根(函数零点问题)例4 已知关于x 的方程2sin 2x -3sin 2x +m -1=0在⎝⎛⎭⎫π2,π上有两个不同的实数根,则m 的取值范围是________. 答案 (-2,-1)解析 方程2sin 2x -3sin 2x +m -1=0可转化为 m =1-2sin 2x +3sin 2x =cos 2x +3sin 2x =2sin ⎝⎛⎭⎫2x +π6,x ∈⎝⎛⎭⎫π2,π. 设2x +π6=t ,则t ∈⎝⎛⎭⎫76π,136π, ∴题目条件可转化为m2=sin t ,t ∈⎝⎛⎭⎫76π,136π,有两个不同的实数根. ∴y =m2和y =sin t ,t ∈⎝⎛⎭⎫76π,136π的图象有两个不同交点,如图:由图象观察知,m 2的范围为(-1,-12),故m 的取值范围是(-2,-1). 引申探究例4中,“有两个不同的实数根”改成“有实根”,则m 的取值范围是__________. 答案 [-2,1)解析 由例4知,m2的范围是⎣⎡⎭⎫-1,12,∴-2≤m <1, ∴m 的取值范围是[-2,1).命题点3 图象性质综合应用例5 已知函数f (x )=3sin(ωx +φ)-cos(ωx +φ)(0<φ<π,ω>0)为偶函数,且函数y =f (x )图象的两相邻对称轴间的距离为π2.(1)求f ⎝⎛⎭⎫π8的值;(2)求函数y =f (x )+f ⎝⎛⎭⎫x +π4的最大值及对应的x 的值. 解 (1)f (x )=3sin(ωx +φ)-cos(ωx +φ) =2⎣⎡⎦⎤32sin (ωx +φ)-12cos (ωx +φ) =2sin ⎝⎛⎭⎫ωx +φ-π6. 因为f (x )是偶函数, 则φ-π6=π2+k π(k ∈Z ),所以φ=2π3+k π(k ∈Z ),又因为0<φ<π,所以φ=2π3,所以f (x )=2sin ⎝⎛⎭⎫ωx +π2=2cos ωx . 由题意得2πω=2·π2,所以ω=2. 故f (x )=2cos 2x . 因此f ⎝⎛⎭⎫π8=2cos π4= 2. (2)y =2cos 2x +2cos 2⎝⎛⎭⎫x +π4 =2cos 2x +2cos ⎝⎛⎭⎫2x +π2 =2cos 2x -2sin 2x =22sin ⎝⎛⎭⎫π4-2x=-22sin ⎝⎛⎭⎫2x -π4 令2x -π4=2k π-π2(k ∈Z )时,y 有最大值22,所以当x =k π-π8(k ∈Z )时,y 有最大值2 2.思维升华 (1)三角函数模型的应用体现在两方面:一是已知函数模型求解数学问题;二是把实际问题抽象转化成数学问题,建立数学模型再利用三角函数的有关知识解决问题. (2)方程根的个数可转化为两个函数图象的交点个数.(3)研究y =A sin(ωx +φ)的性质时可将ωx +φ视为一个整体,利用换元法和数形结合思想进行解题.设函数f (x )=3sin(ωx +φ)(ω>0,-π2<φ<π2)的图象关于直线x =2π3对称,它的周期是π,则下列说法正确的是________.(填序号) ①f (x )的图象过点(0,32);②f (x )在[π12,2π3]上是减函数;③f (x )的一个对称中心是(5π12,0);④将f (x )的图象向右平移|φ|个单位长度得到函数y =3sin ωx 的图象. 答案 ①③解析 ∵周期为π,∴2πω=π⇒ω=2,∴f (x )=3sin(2x +φ),f (2π3)=3sin(4π3+φ),则sin(4π3+φ)=1或-1.又φ∈(-π2,π2),4π3+φ∈(5π6,116π),∴4π3+φ=3π2⇒φ=π6, ∴f (x )=3sin(2x +π6).①:令x =0⇒f (x )=32,正确.②:令2k π+π2<2x +π6<2k π+3π2,k ∈Z⇒k π+π6<x <k π+2π3,k ∈Z .令k =0⇒π6<x <2π3,即f (x )在(π6,2π3)上单调递减,而在(π12,π6)上单调递增,错误.③:令x =5π12⇒f (x )=3sin π=0,正确. ④:应平移π12个单位长度,错误. 4.三角函数图象与性质的综合问题典例 (12分)已知函数f (x )=23sin(x 2+π4)·cos(x 2+π4)-sin(x +π). (1)求f (x )的最小正周期;(2)若将f (x )的图象向右平移π6个单位长度,得到函数g (x )的图象,求函数g (x )在区间[0,π]上的最大值和最小值.思维点拨 (1)先将f (x )化成y =A sin(ωx +φ)的形式再求周期;(2)将f (x )解析式中的x 换成x -π6,得g (x ),然后利用整体思想求最值. 规范解答解 (1)f (x )=23sin(x 2+π4)·cos(x 2+π4)-sin(x +π)=3cos x +sin x [3分] =2sin(x +π3),[5分] 于是T =2π1=2π.[6分] (2)由已知得g (x )=f (x -π6)=2sin(x +π6),[8分] ∵x ∈[0,π],∴x +π6∈[π6,7π6], ∴sin(x +π6)∈[-12,1],[10分] ∴g (x )=2sin(x +π6)∈[-1,2].[11分] 故函数g (x )在区间[0,π]上的最大值为2,最小值为-1.[12分]解决三角函数图象与性质的综合问题的一般步骤:第一步:(化简)将f (x )化为a sin x +b cos x 的形式;第二步:(用辅助角公式)构造f (x )=a 2+b 2·(sin x ·a a 2+b 2+cos x ·b a 2+b 2); 第三步:(求性质)利用f (x )=a 2+b 2sin(x +φ)研究三角函数的性质;第四步:(反思)反思回顾,查看关键点、易错点和答题规范.温馨提醒 (1)在第(1)问的解法中,使用辅助角公式a sin α+b cos α=a 2+b 2sin(α+φ)(其中tan φ=b a ),或a sin α+b cos α=a 2+b 2cos(α-φ)(其中tan φ=a b),在历年高考中使用频率是相当高的,几乎年年使用到、考查到,应特别加以关注.(2)求g (x )的最值一定要重视定义域,可以结合三角函数图象进行求解.[方法与技巧]1.五点法作图及图象变换问题(1)五点法作简图要取好五个关键点,注意曲线凸凹方向;(2)图象变换时的伸缩、平移总是针对自变量x 而言,而不是看角ωx +φ的变化.2.由图象确定函数解析式由图象确定y =A sin(ωx +φ)时,φ的确定是关键,尽量选择图象的最值点代入;若选零点代入,应根据图象升降找“五点法”作图中第一个零点.3.对称问题函数y =A sin(ωx +φ)的图象与x 轴的每一个交点均为其对称中心,经过该图象上坐标为(x ,±A )的点与x 轴垂直的每一条直线均为其图象的对称轴,这样的最近两点间横坐标的差的绝对值是半个周期(或两个相邻对称中心的距离).[失误与防范]1.由函数y =sin x 的图象经过变换得到y =A sin(ωx +φ)的图象,如先伸缩,再平移时,要把x 前面的系数提取出来.2.复合形式的三角函数的单调区间的求法.函数y =A sin(ωx +φ)(A >0,ω>0)的单调区间的确定,基本思想是把ωx +φ看做一个整体.若ω<0,要先根据诱导公式进行转化.3.函数y =A sin(ωx +φ)在x ∈[m ,n ]上的最值可先求t =ωx +φ的范围,再结合图象得出y =A sin t 的值域.A 组 专项基础训练(时间:35分钟)1.函数y =cos ⎝⎛⎭⎫2x -π3的部分图象可能是( )答案 D解析 ∵y =cos ⎝⎛⎭⎫2x -π3,∴当2x -π3=0, 即x =π6时,函数取得最大值1,结合图象看,可使函数在x =π6时取得最大值的只有D. 2.将函数y =sin(2x +φ)的图象沿x 轴向左平移π8个单位后,得到一个偶函数的图象,则φ的一个可能取值为( )A.3π4B.π4 C .0 D .-π4答案 B解析 把函数y =sin(2x +φ)沿x 轴向左平移π8个单位后得到函数y =sin 2⎝⎛⎭⎫x +φ2+π8=sin ⎝⎛⎭⎫2x +φ+π4为偶函数,则φ的一个可能取值是π4. 3.已知函数f (x )=2sin(ωx +φ)(ω>0,且|φ|<π2)的部分图象如图所示,则函数f (x )的一个单调递增区间是( )A .[-7π12,5π12] B .[-7π12,-π12] C .[-π12,7π12] D .[-π12,5π12] 答案 D解析 由函数的图象可得14T =23π-512π, ∴T =π,则ω=2.又图象过点(512π,2),∴2sin(2×512π+φ)=2, ∴φ=-π3+2k π,k ∈Z , ∵|φ|<π2,∴取k =0,则φ=-π3,即得f (x )=2sin(2x -π3), 其单调递增区间为[k π-π12,k π+5π12],k ∈Z ,取k =0,即得选项D. 4.已知曲线f (x )=sin ωx +3cos ωx (ω>0)相邻的两条对称轴之间的距离为π2,且曲线关于点(x 0,0)中心对称,若x 0∈⎣⎡⎦⎤0,π2,则x 0等于( ) A.π12B.π6C.π3D.5π12答案 C解析 f (x )=sin ωx +3cos ωx=2⎝⎛⎭⎫12sin ωx +32cos ωx =2sin ⎝⎛⎭⎫ωx +π3. ∵曲线f (x )=2sin ⎝⎛⎭⎫ωx +π3相邻的两条对称轴之间的距离为π2, ∴最小正周期T =π=2πω, ∴ω=2,∴f (x )=2sin ⎝⎛⎭⎫2x +π3. ∵曲线关于点(x 0,0)中心对称;∴2x 0+π3=k π(k ∈Z ), ∴x 0=k π2-π6(k ∈Z ), 又x 0∈⎣⎡⎦⎤0,π2,∴x 0=π3. 5.函数f (x )=sin(2x +φ)⎝⎛⎭⎫|φ|<π2的图象向左平移π6个单位后所得函数图象的解析式是奇函数,则函数f (x )在⎣⎡⎦⎤0,π2上的最小值为( ) A .-32 B .-12 C.12D.32答案 A解析 由函数f (x )的图象向左平移π6个单位得g (x )=sin ⎝⎛⎭⎫2x +φ+π3的图象,因为是奇函数,所以φ+π3=k π,k ∈Z , 又因为|φ|<π2,所以φ=-π3, 所以f (x )=sin ⎝⎛⎭⎫2x -π3. 又x ∈⎣⎡⎦⎤0,π2,所以2x -π3∈⎣⎡⎦⎤-π3,2π3, 所以当x =0时,f (x )取得最小值为-32. 6.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图象如右图所示,则当t =1100秒时,电流强度是________安.答案 -5解析 由图象知A =10,T 2=4300-1300=1100, ∴ω=2πT=100π.∴I =10sin(100πt +φ). ∵图象过点⎝⎛⎭⎫1300,10, ∴10sin(100π×1300+φ)=10, ∴sin(π3+φ)=1,π3+φ=2k π+π2,k ∈Z , ∴φ=2k π+π6,k ∈Z , 又∵0<φ<π2,∴φ=π6. ∴I =10sin ⎝⎛⎭⎫100πt +π6, 当t =1100秒时,I =-5安. 7.若函数f (x )=sin(ωx +φ) (ω>0且|φ|<π2)在区间⎣⎡⎦⎤π6,2π3上是单调递减函数,且函数从1减小到-1,则f ⎝⎛⎭⎫π4=________.答案 32解析 由题意可得,函数的周期为2×⎝⎛⎭⎫2π3-π6=π,即2πω=π,∴ω=2,∴f (x )=sin(2x +φ). 由sin ⎝⎛⎭⎫2×π6+φ=1,|φ|<π2可得φ=π6, ∴f (x )=sin ⎝⎛⎭⎫2x +π6, ∴f ⎝⎛⎭⎫π4=sin ⎝⎛⎭⎫π2+π6=cos π6=32. 8.已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)在一个周期内的图象如图所示.若方程f (x )=m 在区间[0,π]上有两个不同的实数x 1,x 2,则x 1+x 2的值为________.答案 π3或43π 解析 由图象可知y =m 和y =f (x )图象的两个交点关于直线x =π6或x =23π对称, ∴x 1+x 2=π3或43π. 9.(2015·天津)已知函数f (x )=sin 2x -sin 2⎝⎛⎭⎫x -π6,x ∈R . (1)求f (x )的最小正周期;(2)求f (x )在区间⎣⎡⎦⎤-π3,π4上的最大值和最小值. 解 (1)由已知,有f (x )=1-cos 2x 2-1-cos ⎝⎛⎭⎫2x -π32 =12⎝⎛⎭⎫12cos 2x +32sin 2x -12cos 2x =34sin 2x -14cos 2x =12sin ⎝⎛⎭⎫2x -π6. 所以f (x )的最小正周期T =2π2=π. (2)因为f (x )在区间⎣⎡⎦⎤-π3,-π6上是减函数,在区间⎣⎡⎦⎤-π6,π4上是增函数,且f ⎝⎛⎭⎫-π3=-14, f ⎝⎛⎭⎫-π6=-12,f ⎝⎛⎭⎫π4=34, 所以f (x )在区间⎣⎡⎦⎤-π3,π4上的最大值为34, 最小值为-12.10.设函数f (x )=32-3sin 2ωx -sin ωx cos ωx (ω>0),且y =f (x )图象的一个对称中心到最近的对称轴的距离为π4.(1)求ω的值;(2)求f (x )在区间⎣⎡⎦⎤π,3π2上的最大值和最小值.解 (1)f (x )=32-3sin 2ωx -sin ωx cos ωx =32-3×1-cos 2ωx 2-12sin 2ωx =32cos 2ωx -12sin 2ωx=-sin ⎝⎛⎭⎫2ωx -π3.依题意知2π2ω=4×π4,ω>0,所以ω=1.(2)由(1)知f (x )=-sin ⎝⎛⎭⎫2x -π3.当π≤x ≤3π2时,5π3≤2x -π3≤8π3. 所以-32≤sin ⎝⎛⎭⎫2x -π3≤1.所以-1≤f (x )≤32.故f (x )在区间⎣⎡⎦⎤π,3π2上的最大值和最小值分别为32,-1.B 组 专项能力提升(时间:25分钟)11.已知函数f (x )=2sin ωx 在区间[-π3,π4]上的最小值为-2,则ω的取值范围是() A .(-∞,-92]∪[6,+∞)B .(-∞,-92]∪[32,+∞)C .(-∞,-2]∪[6,+∞)D .(-∞,-2]∪[32,+∞)答案 D解析 当ω>0时,-π3ω≤ωx ≤π4ω, 由题意知-π3ω≤-π2,即ω≥32;当ω<0时,π4ω≤ωx ≤-π3ω, 由题意知π4ω≤-π2,∴ω≤-2. 综上可知,ω的取值范围是(-∞,-2]∪[32,+∞). 12.(2014·天津)已知函数f (x )=3sin ωx +cos ωx (ω>0),x ∈R .在曲线y =f (x )与直线y =1的交点中,若相邻交点距离的最小值为π3,则f (x )的最小正周期为( ) A.π2B.2π3 C .πD .2π答案 C解析 f (x )=3sin ωx +cos ωx =2sin(ωx +π6)(ω>0). 由2sin(ωx +π6)=1得sin(ωx +π6)=12, ∴ωx +π6=2k π+π6或ωx +π6=2k π+56π(k ∈Z ). 令k =0,得ωx 1+π6=π6,ωx 2+π6=56π, ∴x 1=0,x 2=2π3ω. 由|x 1-x 2|=π3,得2π3ω=π3,∴ω=2. 故f (x )的最小正周期T =2π2=π. 13.已知函数f (x )=cos ⎝⎛⎭⎫3x +π3,其中x ∈⎣⎡⎦⎤π6,m ,若f (x )的值域是⎣⎡⎦⎤-1,-32,则m 的取值范围是______. 答案 ⎣⎡⎦⎤2π9,5π18解析 画出函数的图象.由x ∈⎣⎡⎦⎤π6,m ,可知5π6≤3x +π3≤3m +π3, 因为f ⎝⎛⎭⎫π6=cos 5π6=-32, 且f ⎝⎛⎭⎫2π9=cos π=-1,要使f (x )的值域是⎣⎡⎦⎤-1,-32, 所以π≤3m +π3≤76π,则2π9≤m ≤5π18, 即m ∈⎣⎡⎦⎤2π9,5π18.14.已知f (x )=sin ⎝⎛⎭⎫ωx +π3 (ω>0),f ⎝⎛⎭⎫π6=f ⎝⎛⎭⎫π3,且f (x )在区间⎝⎛⎭⎫π6,π3上有最小值,无最大值,则ω=________________________________________________________________________.答案 143解析 依题意,x =π6+π32=π4时,y 有最小值, ∴sin ⎝⎛⎭⎫π4ω+π3=-1, ∴π4ω+π3=2k π+3π2(k ∈Z ), ∴ω=8k +143(k ∈Z ), ∵f (x )在区间⎝⎛⎭⎫π6,π3上有最小值,无最大值,∴π3-π4<πω,即ω<12,令k =0,得ω=143. 15.已知函数f (x )=3sin ωx cos ωx +cos 2ωx -12(ω>0),其最小正周期为π2. (1)求f (x )的表达式; (2)将函数f (x )的图象向右平移π8个单位长度,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数y =g (x )的图象,若关于x 的方程g (x )+k =0在区间[0,π2]上有且只有一个实数解,求实数k 的取值范围. 解 (1)f (x )=3sin ωx cos ωx +cos 2ωx -12=32sin 2ωx +cos 2ωx +12-12=sin(2ωx +π6), 由题意知f (x )的最小正周期T =π2,T =2π2ω=πω=π2, 所以ω=2,所以f (x )=sin(4x +π6). (2)将f (x )的图象向右平移π8个单位长度后,得到y =sin(4x -π3)的图象;再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y =sin(2x -π3)的图象,所以g (x )=sin(2x -π3),因为0≤x ≤π2,所以-π3≤2x -π3≤2π3, 所以g (x )∈[-32,1]. 又g (x )+k =0在区间[0,π2]上有且只有一个实数解,即函数y =g (x )与y =-k 在区间[0,π2]上有且只有一个交点,由正弦函数的图象可知-32≤-k <32或-k =1, 解得-32<k ≤32或k =-1, 所以实数k 的取值范围是(-32,32]∪{-1}.。
第一章 1.3.1正弦函数的图象与性质(五)

(k∈Z) 得到
研一研·问题探究、课堂更高效
1.3.1(五)
探究点一
本 课 时 栏 目 开 关
“五点法”作函数 y=Asin(ωx+φ)(A>0,ω>0)的图象
利用“五点法”作出函数 y=Asin(ωx+φ)(A>0,ω>0)在一个周 期上的图象, 要经过“取值、 列表、 描点、 连线”这四个步骤. 请 完成下面的填空. ωx+φ x y 0 π 2 π 3 π 2 2π
研一研·问题探究、课堂更高效
描点、连线,如图所示.
1.3.1(五)
本 课 时 栏 目 开 关
小结 “五点法”作图时,五点的确定,应先令 ωx+φ 分别为 π 3π 0、2、π、 2 、2π,解出 x,从而确定这五点.
研一研·问题探究、课堂更高效
π 跟踪训练 1 作出 y=2.5sin2x+4 的图象. π π 1 解 令X=2x+ ,则x= X-4.列表: 4 2
φ - ω
0
φ π φ 3π φ 2π φ π -ω+2ω - + - + ω 2ω -ω+ ω ω ω
A 0 -A 0
研一研·问题探究、课堂更高效
1.3.1(五)
φ - ,0 ω
本 课 时 栏 目 开 关
所以,描点时的五个关键点的坐标依次是 , φ φ φ π π 3π - + - + ,0 - + ,A ,-A ω 2ω , ω ω , ω 2ω , φ 2π - + ,0 ω ω . φ T φ 2π - + - 若设 T= ω , 则这五个关键点的横坐标依次为 ω , ω 4 , φ 3 φ φ T - + T -ω+T -ω+2 , ω 4 , .
T 7π π π 解析 由图象知4=12-3=4,∴T=π,ω=2. 7π π 且 2×12+φ=kπ+π(k∈Z),φ=kπ-6(k∈Z). π π 又|φ|< ,∴φ=- . 2 6
正弦型三角函数的图像-简单难度-讲义

正弦型三角函数的图像知识讲解一、正弦型三角函数的性质1.函数()sin y A x ωϕ=+的图像与函数sin y x =图像的关系振幅变换:()sin 0,1y A x A A =>≠的图像,可以看成是sin y x =图像上所有点的纵坐标都伸长()1A >或缩短()01A <<到原来的A 倍(横坐标不变)而得到的.周期变换:)1,0(sin ≠>=w w wx y 的图像,可以看成是sin y x =的图像上各点的横坐标都缩短()1ω>或伸长()01ω<<到原点的1ω倍(纵坐标不变)而得到的,由于sin y x =的图像得到()sin y A x ωϕ=+的图像主要有下列两种方法:()()()sin sin sin sin y x y x y x A x ϕωϕωϕ=−−−−→=+−−−−→=+−−−−→+相位变换周期变换振幅变换()()sin sin sin sin y x y x y x y A x ωωϕωϕ=−−−−→=−−−−→=+−−−−→=+周期变换相位变换振幅变换2.三角函数的性质函数 sin y x =cos y x =tan y x = cot y x =定义 域 R R{|,,}2x x R x k k ππ∈≠+∈Z 且{|,,}x x R x k k π∈≠∈Z 且值域 [1,1]-[1,1]-RR奇偶性奇函数 偶函数奇函数奇函数3.sin y x=与sin y x=的性质典型例题一.选择题(共10小题)1.(2018•全国)要得到y=cosx,则要将y=sinx()A.向左平移π个单位B.向右平移π个单位C.向左平移个单位D.向右平移个单位【解答】解:要将y=sinx的图象向左平移个单位,可得y=sin(x+)=cosx的图象,故选:C.2.(2018•榆林一模)已知曲线,则下列说法正确的是()A.把C1上各点横坐标伸长到原来的2倍,再把得到的曲线向右平移,得到曲线C2B.把C1上各点横坐标伸长到原来的2倍,再把得到的曲线向右平移,得到曲线C2C.把C1向右平移,再把得到的曲线上各点横坐标缩短到原来的,得到曲线C2D.把C1向右平移,再把得到的曲线上各点横坐标缩短到原来的,得到曲线C2【解答】解:根据曲线=sin(x﹣),把C1上各点横坐标伸长到原来的2倍,可得y=sin(x)的图象;再把得到的曲线向右平移,得到曲线C2:y=sin(x﹣)的图象,故选:B.3.(2018•岳阳二模)若将函数y=sin2x的图象向左平移个单位长度,则平移后图象的对称轴方程为()A.B.C.D.【解答】解:将函数y=sin2x的图象向左平移个单位长度,则平移后图象对应的函数解析式为y=sin(2x+),令2x+=kπ+,求得x=+,k∈Z,故所得图象的对称轴方程为x=+,k∈Z,故选:D.4.(2018•四川模拟)若将函数的图象向左平移个单位长度,则平移后图象的对称轴方程为()A.B.C.D.【解答】解:将函数=2sin(2x+)的图象向左平移个单位长度,可得y=2sin(2x++)=2sin(2x+)的图象,令2x+=kπ+,可得x=﹣,k∈Z,则平移后图象的对称轴方程为x=﹣,k∈Z,故选:A.5.(2018•一模拟)已知函数(ω>0)的相邻两个零点差的绝对值为,则函数f(x)的图象()A.可由函数g(x)=cos4x的图象向左平移个单位而得B.可由函数g(x)=cos4x的图象向右平移个单位而得C.可由函数g(x)=cos4x的图象向右平移个单位而得D.可由函数g(x)=cos4x的图象向右平移个单位而得【解答】解:函数=sin(2ωx)﹣•+=sin(2ωx﹣)(ω>0)的相邻两个零点差的绝对值为,∴•=,∴ω=2,f(x)=sin(4x﹣)=cos[(4x﹣)﹣]=cos (4x﹣).故把函数g(x)=cos4x的图象向右平移个单位,可得f(x)的图象,故选:B.6.(2018•通渭县模拟)函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<)的图象如图所示,为了得到y=cos2x的图象,则只要将f(x)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度 D.向右平移个单位长度【解答】解:由函数f(x)=Asin(ωx+φ)的图象可得A=1,=﹣,∴ω=2.再根据五点法作图可得2×+φ=π,求得φ=,故f(x)=2sin(2x+).故把f(x)=2sin(2x+)的图象向左平移个单位长度,可得y=2sin[2(x+)+]=2sin(2x+)=2cos2x的图象,故选:C.7.(2018•一模拟)已知函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤)的部分图象如图所示,将函数f(x)的图象向左平移个单位长度后,所得图象与函数y=g(x)的图象重合,则()A.g(x)=2sin(2x+)B.g(x)=2sin(2x+)C.g(x)=2sin2x D.g(x)=2sin(2x﹣)【解答】解:根据函数f(x)=2sin(ωx+φ)(ω>0,|φ|≤)的部分图象,可得==+,∴ω=2,根据+φ=2•(﹣)+φ=0,∴φ=,故f(x)=2sin(2x+).将函数f(x)的图象向左平移个单位长度后,所得图象与函数y=g(x)的图象重合,故g(x)=2sin(2x++)=2sin(2x+).故选:A.8.(2018•红桥区二模)设函数f(x)=sinωx+cosωx(ω>0)的最小正周期为π,将y=f(x)的图象向左平移个单位得函数y=g(x)的图象,则()A.g(x)在(0,)上单调递增B.g(x)在(,)上单调递减C.g(x)在(0,)上单调递减D.g(x)在(,π)上单调递增【解答】解:∵f(x)=sinωx+cosωx=sin(ωx+),∵T==π,∴ω=2,∴f(x)=sin(2x+),∴将y=f(x)的图象向左平移个单位得函数y=g(x)的图象,则y=g(x)=sin[2(x+)+]=sin(2x+)=cos2x,∴令2kπ≤2x≤2kπ+π,k∈Z可解得:k,k∈Z,当k=0时,x∈[0,],即g(x)在(0,)上单调递减.故选:C.9.(2018•佛山一模)把曲线上所有点向右平移个单位长度,再把得到的曲线上所有点的横坐标缩短为原来的,得到曲线C2,则C2()A.关于直线对称 B.关于直线对称C.关于点对称D.关于点(π,0)对称【解答】解:把曲线上所有点向右平移个单位长度,可得y=2sin(x﹣﹣)=2sin(x﹣)的图象;再把得到的曲线上所有点的横坐标缩短为原来的,得到曲线C2:y=2sin(2x ﹣)的图象,对于曲线C2:y=2sin(2x﹣):令x=,y=1,不是最值,故它的图象不关于直线对称,故A错误;令x=,y=2,为最值,故它的图象关于直线对称,故B正确;令x=,y=﹣1,故它的图象不关于点对称,故C错误;令x=π,y=﹣,故它的图象不关于点(π,0)对称,故D错误,故选:B.10.(2018•渭南二模)函数y=Asin(x+φ)(A>0,>0,0<φ<π)在一个周期内的图象如图,此函数的解析式为()A.y=2sin(2x+) B.y=2sin(2x+) C.y=2sin(﹣)D.y=2sin(2x﹣)【解答】解:根据函数y=Asin(x+φ)(A>0,>0,0<φ<π)在一个周期内的图象,可得A=2,•=﹣(﹣),∴=2.再根据当x=﹣时,y=2sin(﹣+φ)=2,可得sin(﹣+φ)=1,故有﹣+φ=2kπ+,求得φ=2kπ+,结合0<φ<π,求得φ=,故函数y=Asin(2x+),故选:A.二.填空题(共3小题)11.(2016•淮安一模)函数f(x)=2sin(ωx+ϕ)(ω>0)的部分图象如图所示,若AB=5,则ω的值为.【解答】解:∵函数f(x)=2sin(ωx+φ),图象中AB两点距离为5,设A(x1,2),B(x2,﹣2),∴(x2﹣x1)2+42=52,解得:x2﹣x1=3,∴函数的周期T=2×3=,解得:ω=.故答案为:.12.(2016•海淀区模拟)把函数y=sin(﹣2x)向右平移个单位,然后把横坐标变为原来的2倍,则所得到的函数的解析式为y=cosx.【解答】解:函数向右平移个单位,得,把横坐标变为原来的2倍,得函数的解析式为y=cosx.故答案为:y=cosx.13.(2016春•南通期末)函数y=sin2x图象的振幅为.【解答】解:函数y=sin2x图象的振幅为,故答案为:.三.解答题(共2小题)14.(2018春•双台子区校级期末)已知函数f(x)=cosx•sin(x+)﹣cos2x+,x∈R.(1)求f(x)的最小正周期及图象的对称中心;(2)求f(x)在闭区间[﹣,]上的最大值和最小值.【解答】解:(1)∵函数f(x)=cosx•sin(x+)﹣cos2x+=cosx﹣cos2x+=sin2x﹣cos2x+=sin2x﹣•+=sin2x﹣cos2x=•sin(2x﹣),故它的最小正周期为=π,令2x﹣=kπ,求得x=+,可得函数的图象的对称中心为(+,0).(2)在闭区间[﹣,]上,2x﹣∈[﹣,],故当2x﹣=﹣时,函数f(x)取得最小值为﹣,当2x﹣=时,函数f(x)取得最大值为.15.(2010•广州模拟)已知函数,x∈R.(1)求它的振幅、周期、初相;(2)用五点法作出它的简图;(3)该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?【解答】解:(1)函数的振幅为,周期为π,初相为.(2)列表:x0π2π00画简图:(3)函数y=sinx的图象向左平移个单位,得到函数的图象,再保持纵坐标不变,把横坐标缩短为原来的一半得到函数的图象,再保持横坐标不变,把纵坐标缩短为原来的一半得到函数的图象.。
关于正弦型函数y=Asin(ωx+φ)中φ角确定的探究

关于正弦型函数y=Asin(ωx+φ)中φ角确定的探究摘要:根据正弦型函数f(x)=asin(ωx+φ)的图象求其解析式是教学中的一个难点问题,难点在于如何根据图象准确地确定φ角的值,下面将介绍如何来确定φ角的值。
关键词:正弦型函数;φ角;确定问题:(苏教版高中数学必修4第48页)函数f(x)=asin(ωx+φ)(a>0,ω>0,φ∈[0,2π))的图象如图所示,试求该函数的解析式。
■误解:由图象知:a=3,t=2[3-(-1)]=8,ω=■=■=■,所以函数f(x)=asin(ωx+φ)的解析式可设为f(x)=3sin(■x+φ),又点(3,0)在函数f(x)=asin(ωx+φ)的图象上,故有3sin(■×3+φ)=0即sin(■×3+φ)=0,所以■×3+φ=kπ,(k∈z),则φ=kπ-■×3,(k∈z);又φ∈[0,2π),因此φ=■或■,所以函数f(x)=asin(ωx+φ)的解析式为f(x)=3sin (■x+■)或f(x)=3sin(■x+■)。
分析:本题的解题过程看上去似乎并无错误,但我们发现f(x)=3sin(■x+■)的图象并不是本题中的图象(其图象见图中虚线部分),这是为什么呢?根据正弦型函数的图象求其解析式是教学中的一个难点问题,难点在于如何根据图象准确地确定φ角的值,本文从另一个角度来研究这个问题。
首先对于任意一个形如y=asin(ωx+φ)的函数均可以转化为y=a′sin(ω′x+φ′),其中a′>0,ω′>0,-π0,则y=asin (ωx+φ)=-asin(ωx+φ)=asin(ωx+φ+π).如果ω0,则y=asin(ωx+φ)=asin(ωx+φ)=asin[-(ωx-φ)]=-asin(ωx-φ)=asin(ωx-φ+π).如果a0,ω′>0.由于正弦型函数y=asin(ωx+φ)中φ角是任意角,故转化后的函数y=a’sin(ω’x+β)(其中a’>0,ω’>0)中的β角的取值可能是正角也可能是负角还可能为0,不妨设φ’角的取值范围为(-π,π〕,β角在φ′角的取值范围(-π,π)内总能找到与其终边相同的角,即总有β=φ′+2kπ,(k∈z),又因为终边相同的角的三角函数值相等,所以上面y=a′sin(ω′x+β)=a′sin (ω′x+φ′+2kπ)=a′sin(ω′x+φ′),所以正弦型函数y=asin(ωx+φ)可转化为函数y=a’sin(ω’x+φ’),(其中a′>0,ω′>0,φ′∈([-π,π]),并且函数y=a′sin(ω′x+φ′),(其中a′>0,ω′>0,φ′∈(-π,π〕)为其最简形式。
最新中专校-正弦型函数练习题

15.3正弦型函数 练习题(2)1. y =2sin ⎝⎛⎭⎫2x -π4 的振幅、频率和初相分别为( ). A .2,1π,-π4 B .2,12π,-π4C .2,1π,-π8D .2,12π,-π82.根据所给正弦型函数的图象,求出其表达式(1)函数的最大值是____,最小值是______,因此A=________(2)函数的一个周期T =___________,因此w =___________(3)函数图象五个点中的第一个点的坐标为____________,因此函数的图象向_____平移了__________个单位,综上得出此函数图象的表达式为____________________3.根据正弦型函数的图象求其表达式。
(1)函数的最大值是____,最小值是______,因此A=________(2)函数的一个周期T=___________,因此w =___________(3)函数的图象向_____平移了_________个单位,综上得出此函数图象的表达式为_____________4.根据正弦型函数的图象求其表达式。
(1)函数的最大值是____,最小值是______,因此A=________(2)函数的一个周期T =___________,因此w =___________(3)函数图象五个点中的第一个点的坐标为____________,因此函数的图象向_____平移了__________个单位,综上得出此函数图象的表达式为____________________5.根据正弦型函数的图象求其表达式。
(1)函数的最大值是____,最小值是______,因此A=________(2)函数的一个周期T =___________,因此w =___________(3)函数图象五个点中的第一个点的坐标为____________,因此函数的图象向_____平移了__________个单位,综上得出此函数图象的表达式为____________________6.已知函数f (x )=A sin(ωx +φ)⎝⎛⎭⎫|φ|<π2的部分图象如图所示,则该函数的最小正周期T 和初相φ分别为( ).A .T =6π,φ=π6B .T =6π,φ=π3C .T =6,φ=π6D .T =6,φ=π3(6) (7)7.已知函数f (x )=sin(ωx +φ)(ω>0)的图象如图所示,则ω=________是.函数x x y cos sin 8= ( )A .周期为2π的偶函数B .周期为2π的奇函数C .周期为π的偶函数D .周期为π的奇函数9.函数f (x )=A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)的部分图象如图所示,则T 的值是________.10. 函数)4sin()(π-=x x f 的图像的一条对称轴是( ) A .4π=x B .2π=x C .4π-=x D .2π-=x的最小正周期是函数x x x f 2cos 2sin )(.11-= ( )A.2π B.π C .π2 D.π412.已知函数f (x )=A sin(ωx +φ),x ∈R (其中A >0,ω>0,0<φ<π2)的图象与x 轴的交点中,相邻两个交点之间的距离为π2,且图象上的一个最低点为M ⎝⎛⎭⎫2π3,-2. (1)求f (x )的解析式;(2)当x ∈⎣⎡⎦⎤π12,π2时,求f (x )的值域.13.已知=(x sin 3,-x cos ),=(x cos ,x cos ),且函数)(x f =∙. 求函数)(x f 的最小正周期及最大值。
正弦型函数的解析式求法

课堂小结
本节课我们共同学习了 正弦型函数解析式求法 , 关键是确定A,, 及K的值,其中可用平移法, 也可用五点法,特殊点 可用代入法,根据 的范围 确定其取值
x
12
3
7 12
5 6
13 12
-2
变式1
下面是y A sin(x )( A 0,W 0,
2
)
的图像,确定其函数解 析式 (5) y=2sin(2x- ) 6 y 2
o
x
12 3 7 12 5 6 13 12
-2
变式2
下面是y A sin(x )( A 0,W 0, 的部分图像,确定其函 数解析式
1.已知简谐运动
π f(x)=Asin(ωx+φ)|φ|<2的部分图象如图所
示,则该简谐运动的最小正周期 T 和初相 φ 分别为(
C
).
π A.T=6π,φ=6 π C.T=6,φ=6
π B.T=6π,φ=3 π D.T=6,φ=3
A 0 0 | | 2.已知函数 y A sin( x ) B, 2 的最大值为 2 2 ,最小值为 2 ,周期为 3 2 ,求这个函数的解析式。 (0, ) 且图象过点 4
最大 - 最小 离 • (1)确定 A A 离开平衡位置的最大距 2 最大 最小 K 最大最小值的中间 2 2 • (2)确定 T
• (3)确定
方法一:平移法
方法二:五点法:
上升零点: x 0 2k,k z 下降零点: x 2k,k z 最大值点: x 2k,k z 2 最小值点: x 3 2k,k z 2
正弦型函数y=Asin(ωx+φ)的图像和性质

正弦型函数y=Asin(ωx+φ)的图像和性质导入新课思路1(情境引入)在物理和工程技术的许多问题中,都要遇到形如y=Asin(ωx+φ)的函数(其中A 、ω、φ是常数)。
例如,物体做简谐振动时位移y 与时间x 的关系,交流电中电流强度y 与时间x 的关系等,都可用这类函数来表示。
这些问题的实际意义往往可从其函数图象上直观地看出,因此,我们有必要画好这些函数的图象。
揭示课题:函数y=Asin(ωx+φ)的图象。
思路2(直接导入)从解析式来看,函数y=sinx 与函数y=Asin(ωx+φ)存在着怎样的关系?从图象上看,函数y=sinx 与函数y=Asin(ωx+φ)存在着怎样的关系?接下来,我们就分别探索φ、ω、A 对y=Asin(ωx+φ)的图象的影响。
一、新知探究 提出问题(1)你能用学过的三角函数知识描述大观览车周而复始的运动吗?(2)你能算出某一时刻你的“座位”离开地面的高度吗?活动:教师可先制作一个大观览车模型,让学生动手画出大观览车的示意图,或先演示课件然后和学生一起探究上述问题。
如图1是大观览车的示意图。
设观览车转轮半径长为R ,转动的角度为ωrad/s.点P 0表示座椅的初始位置.此时∠xoP 0=φ,当转轮转动t 秒后,点P 0P 位置,射线OP 的转角为ωt+φ,由正弦函数的定义,得点P 的纵坐标y 与时间t 的函数关系为y=Rsin(ωt+φ).这样,如果已知车轮半径R ,转动的角速度ω和初始的角度φ你就可计算出某一时刻你的“座位”离开地面的高度了。
在函数y= Rsin(ωt+φ)中,点P 旋转一周所需要的时间 T=ϖπ2,叫做点P 的转动周期。
在一秒内,点P 旋转的周数f=,2π=T 叫做转动的频率。
OP 0与x 轴正向的夹角φ叫做初相。
例如一动点以角速度4πrad/s 做匀速圆周运动,则T=.21,2142Hz Tf s ===ππ形如y=Asin(ωx+φ)(其中A ,ω,φ都是常数)的函数,在物理、工程等科学的研究中经常遇到,这种类型的函数通常叫做正弦函数。
正弦型函数的图象及应用经典教案【强烈推荐】

第4讲 正弦型函数y =A sin(ωx +ϕ)+B 的图象及应用【考试会这样考】1.考查正弦型函数y =A sin(ωx +ϕ)的图象变换.2.结合三角恒等变换考查y =A sin(ωx +ϕ)的性质及简单应用. 3.考查y =sin x 到y =A sin(ωx +ϕ)的图象的两种变换途径.【复习指导】本讲复习时,重点掌握正弦型函数y =A sin(ωx +ϕ)的图象的“五点”作图法,图象的三种变换方法,以及利用三角函数的性质解决有关问题.基础梳理1.用五点法画y =A sin(ωx +ϕ)一个周期内的简图时,要找五个特征点 如下表所示x ωϕ-0ωϕπ-2ωϕπ- ωϕπ-23ωϕπ-2ωx +ϕ 0 π2π 3π2 2π y =A sin(ωx +ϕ)A-A2.函数y =sin x 的图象变换得到y =A sin(ωx +ϕ)的图象的步骤3.当函数y =A sin(ωx +ϕ)(A >0,ω>0,x ∈[0,+∞))表示一个振动时,A 叫做振幅,T =2πω叫做周期,f =1T叫做频率,ωx +ϕ叫做相位,ϕ叫做初相.4.图象的对称性函数y =A sin(ωx +ϕ)(A >0,ω>0)的图象是轴对称也是中心对称图形,具体如下:(1)函数y =A sin(ωx +ϕ)的图象关于直线x =x k (其中 ωx k +ϕ=k π+π2,k ∈Z )成轴对称图形.(2)函数y =A sin(ωx +ϕ)的图象关于点(x k,0)(其中ωx k +ϕ=k π,k ∈Z )成中心对称图形.一种方法在由图象求三角函数解析式y =A sin(ωx +ϕ) + B 时,若最大值为M ,最小值为m ,则A =M -m 2,B =M +m 2,ω由周期T 确定,即由2πω=T 求出,ϕ由特殊点确定.一个区别 由y =sin x 的图象变换到y =A sin (ωx +ϕ)的图象,两种变换的区别:先相位变换再周期变换(伸缩变换),平移的量是|φ|个单位;而先周期变换(伸缩变换)再相位变换,平移的量是|φ|ω(ω>0)个单位.原因在于相位变换和周期变换都是针对x 而言,即x 本身加减多少值,而不是依赖于ωx 加减多少值.双基自测1.y =2sin ⎝⎛⎭⎪⎫2x -π4 的振幅、频率和初相分别为( ). A .2,1π,-π4 B .2,12π,-π4 C .2,1π,-π8 D .2,12π,-π8答案 A2.已知简谐运动f (x )=A sin(ωx +φ)⎝⎛⎭⎪⎫|φ|<π2的部分图象如图所示,则该简谐运动的最小正周期T 和初相φ分别为( ).A .T =6π,φ=π6B .T =6π,φ=π3C .T =6,φ=π6D .T =6,φ=π3答案 C 解析 由题图象知T =2(4-1)=6⇒ω=π3,由图象过点(1,2)且A =2,可得sin ⎝ ⎛⎭⎪⎫π3×1+φ=1,又|φ|<π2,得φ=π6.3.函数y =cos x (x ∈R )的图象向左平移π2个单位后,得到函数y =g (x )的图象,则g (x )的解析式应为( ).A .-sin xB .sin xC .-cos xD .cos x答案 A 解析 由图象的平移得g (x )=cos ⎝⎛⎭⎪⎫x +π2=-sin x .4.已知函数f (x )=sin(ωx +φ)(ω>0)的图象如图所示,则ω=________.解析 由题意设函数周期为T ,则T 4=23π-π3=π3,故T =43π.∴ω=2πT =32.5.把函数y =cos 2x +1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是 ( )答案 A解析 y =cos 2x +1――→横坐标伸长2倍纵坐标不变y =cos x +1――→向左平移1个单位长度y =cos(x +1)+1――→向下平移1个单位长度y =cos(x +1). 结合选项可知应选A.考向一 作函数y =A sin(ωx +φ)的图象【例1】►设函数f (x )=cos(ωx +ϕ)⎝ ⎛⎭⎪⎫ω>0,-π2<φ<0的最小正周期为π,且f ⎝ ⎛⎭⎪⎫π4=32. (1)求ω和ϕ的值;(2)在给定坐标系中作出函数f (x )在[0,π]上的图象.解 (1)周期T =2πω=π,∴ω=2,∵f ⎝⎛⎭⎫π4=cos ⎝⎛⎭⎫2×π4+φ=cos ⎝⎛⎭⎫π2+φ=-sin φ=32, ∵-π2<φ<0,∴φ=-π3.(2)由(1)知f (x )=cos ⎝⎛⎭⎫2x -π3,列表如下:2x -π3 -π3 0 π2 π 32π 53πx 0 π6 512π 23π 1112π πf (x ) 12 1 0 -1 0 12图象如图:【训练1】 已知函数f (x )=3sin ⎝ ⎛⎭⎪⎫12x -π4,x ∈R .(1)画出函数f (x )在长度为一个周期的闭区间上的简图;(2)将函数y =sin x 的图象作怎样的变换可得到f (x )的图象?解 (1)列表取值:xπ232π 52π 72π 92π 12x -π4 0 π2π 32π 2π f (x ) 0 3 0-3(2)先把y =sin x 的图象向右平移π4个单位,然后把所有的点的横坐标扩大为原来的2倍,再把所有点的纵坐标扩大为原来的3倍,得到f (x )的图象. 考向二 求函数y =A sin(ωx +ϕ)+B 的解析式【例2】►已知函数f (x )=A sin(ωx +ϕ)+B (A >0,ω>0)的图象如图所示,则f (x )的解析式为_______.答案:.()2sin 363f x x ππ⎛⎫=++ ⎪⎝⎭【训练2】 (1)若函数f (x )=A sin(ωx +ϕ)(A >0,|ϕ|<π2,ω>0)的图象的一部分如图所示.则f (x )的解析式为_______.(2)已知f (x )=2sin (ωx+φ)的部分图象如图所示,则f (x )的表达式为 A . B .C .D .解 (1) f (x )=2sin ⎝⎛⎭⎫2x +π6. (2)答案:.B考向三 函数y =A sin(ωx +ϕ)的图象与性质的综合应用【例3】►已知函数的 部分图象如图所示:(1)求f (x )的解析式;(2)求f (x )的单调区间和对称中心坐标; (3)将f (x )的图象向左平移个单位,在将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数g (x )的图象,求函数y=g (x )在上的最大值和最小值.【解答】解:(1)由图象可知,又由于, 所以,由图象及五点法作图可知:, 所以,所以.(2)由(1)知,, 令,得,所以f (x )的单调递增区间为,令,得,所以f (x )的对称中心的坐标为. (3)由已知的图象变换过程可得:, 因为, 所以,所以当,得时,g (x )取得最小值,当时,即x=0g (x )取得最小值.【训练3】 已知函数y =A sin(ωx +ϕ)(A >0,ω>0)的图象过点P ⎝ ⎛⎭⎪⎫π12,0,图象上与点P 最近的一个最高点是Q ⎝ ⎛⎭⎪⎫π3,5.(1)求函数的解析式;(2)求函数f (x )的递增区间.解 (1)依题意得:A =5,周期T =4⎝⎛⎭⎫π3-π12=π,∴ω=2ππ=2.故y =5sin(2x +φ),又图象过点P ⎝⎛⎭⎫π12,0, ∴5sin ⎝⎛⎭⎫π6+φ=0, 由已知可得π6+φ=0,∴φ=-π6 ∴y =5sin ⎝⎛⎭⎫2x -π6.(2)由-π2+2k π≤2x -π6≤π2+2k π,k ∈Z , 得:-π6+k π≤x ≤π3+k π,k ∈Z ,故函数f (x )的递增区间为:⎣⎡⎦⎤k π-π6,k π+π3(k ∈Z ).A 组 专项基础训练一、选择题1.将函数()πsin 23f x x ⎛⎫=+⎪⎝⎭的图象向左平移π6个单位,所得的图象对应的函数解析式是 A. sin2y x = B. cos2y x = C. 2πsin 23y x ⎛⎫=+ ⎪⎝⎭ D. πsin 26y x ⎛⎫=- ⎪⎝⎭ 【答案】C2、将函数cos 3y x π⎛⎫=-⎪⎝⎭的图象向左平移6π个单位,再各点横坐标伸长到原来的2倍(纵坐标不变),所得函数解析式是( )A. )621cos(π-=x y B. )1221cos(π-=x y C. )62cos(π-=x y D. )32cos(π-=x y 【答案】A3、若函数()sin 23f x x π⎛⎫=+⎪⎝⎭图象的横坐标伸长到原来的2倍, 纵坐标不变,再向左平移6π得到函数()g x 的图象,则有( )A. ()cos g x x =B. ()sin g x x =C. ()cos 3g x x π⎛⎫=+⎪⎝⎭D. ()sin 3g x x π⎛⎫=+⎪⎝⎭【答案】A 【解析】26sin 2sin sin cos 332y x y x y x x ππππ⎛⎫⎛⎫⎛⎫=+→=+→=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭左移横坐标变为倍.4、为了得到函数1y 3sin 25x π⎛⎫=-⎪⎝⎭的图象,只要把13sin 2y x =上所有点( )A. 向右平移5π个单位长度 B. 向左平移5π个单位长度 C. 向右平移25π个单位长度 D. 向左平移25π个单位长度【答案】C5、若函数f (x )=2sin(ωx +φ),x ∈R (其中ω>0,|φ|<π2)的最小正周期是π,且f (0)=3,则( )A .ω=12,φ=π6B .ω=12,φ=π3C .ω=2,φ=π6D .ω=2,φ=π3答案 D 解析 ∵T =π,∴ω=2.又2sin φ=3,|φ|<π2,∴φ=π3.6、函数()sin()02f x A wx A ϕϕ=+π其中>,<)的图像如图所示,为得到x x g 3sin )(=的图像,则只要将)(x f 的图象( )A .向右平移4π个单位B .向右平移12π个单位C .向左平移4π个单位D .向左平移12π个单位 答案 B7、将函数y =sin(x +φ)的图像F 向左平移π6个单位长度后得到图像F ′,若F ′的一个对称中心为⎝⎛⎭⎫π4,0,则φ的一个可能取值是 ( ) A.π12 B.π6 C.5π6 D.7π12答案 D 解析 图像F ′对应的函数y ′=sin ⎝⎛⎭⎫x +π6+φ, 则π4+π6+φ=k π,k ∈Z ,即φ=k π-5π12,k ∈Z ,令k =1时,φ=7π12,故选D. 8、将函数y =sin x 的图像向左平移φ (0≤φ<2π)个单位后,得到函数y =sin ⎝⎛⎭⎫x -π6的图像,则φ等于( ) A.π6B.5π6C.7π6D.11π6答案 D 解析 将函数y =sin x 向左平移φ(0≤φ<2π)个单位得到函数y =sin(x +φ).只有φ=116π时有y =sin ⎝⎛⎭⎫x +116π=sin ⎝⎛⎭⎫x -π6. 二、填空题(每小题5分) 1、将函数()3sin 46f x x π⎛⎫=+⎪⎝⎭图象上所有点的横坐标伸长到原来的2倍,再向右平移6π个单位长度,得到函数g(x)的图象,则g(x)的解析式为 。
三角函数的图象与性质6大题型(解析版)--2024高考数学常考题型精华版

三角函数的图象与性质6大题型【题型目录】题型一:三角函数的周期性题型二:三角函数对称性题型三:三角函数的奇偶性题型四:三角函数的单调性题型五:三角函数的值域题型六:三角函数的图像【典例例题】题型一:三角函数的周期性【例1】(2022·全国·兴国中学高三阶段练习(文))下列函数中,最小正周期为π的奇函数是().A .tan y x =B .sin 2y x =C .sin cos y x x =D .sin y x=【例2】(2022江西景德镇一中高一期中(文))下列函数中①sin y x =;②sin y x =;③tan y x =;④12cos y x =+,其中是偶函数,且最小正周期为π的函数的个数为()A .1B .2C .3D .4【答案】B【解析】①的图象如下,根据图象可知,图象关于y 轴对称,sin y x =是偶函数,但不是周期函数,∴排除①;②的图象如下,根据图象可知,图象关于y 轴对称,sin y x =是偶函数,最小正周期是π,∴②正确;③的图象如下,根据图象可知,图象关于y 轴对称,tan y x =是偶函数,最小正周期为π,∴③正确;④的图象如下,根据图象可知,图象关于y 轴对称,12cos y x =+是偶函数,最小正周期为2π,∴排除④.故选:B.【例3】(2022·全国·高三专题练习)函数ππ()sin 2cos 233f x x x ⎛⎫⎛⎫=-+ ⎪ ⎪⎝⎭⎝⎭的最小正周期是()A .π4B .π2C .πD .2π【例4】设函数()c x b x x f ++=sin 2cos ,则()x f 的最小正周期()A .与b 有关,且与c 有关B .与b 有关,但与c 无关C .与b 无关,且与c 无关D .与b 无关,但与c 有关【答案】B【解析】因x y 2cos =的最小正周期为ππ==22T ,x y sin =的最小正周期为ππ212==T 所以当0≠b 时,()x f 的最小正周期为π2;当0=b 时,()x f 的最小正周期为π;【例5】(2022·全国·高一课时练习)函数22cos 14y x π⎛⎫=+- ⎪⎝⎭的最小正周期为()A .4πB .2πC .πD .2π【例6】(2022·广西桂林·模拟预测(文))函数()2sin6cos6f x x x =+的最小正周期是()A .2πB .3πC .32πD .6π【例7】(2022·全国·高一专题练习)()|sin ||cos |f x x x =+的最小正周期是()A .2πB .πC .2πD .3π【题型专练】1.(2023全国高三题型专练)在函数①cos |2|y x =,②|cos |y x =,③πcos 26y x ⎛⎫=+ ⎪⎝⎭,④πtan 24y x ⎛⎫=- ⎪⎝⎭中,最小正周期为π的所有函数为()A .②④B .①③④C .①②③D .②③④【答案】C【解析】∵cos |2|y x ==cos2x ,∴T =22π=π;|cos |y x =图象是将y =cos x 在x 轴下方的图象对称翻折到x 轴上方得到,所以周期为π,由周期公式知,cos(2)6y x π=+为π,tan(2)4y x π=-为2π,故选:C .2.(2022·河北深州市中学高三阶段练习)下列函数中,最小正周期为π的奇函数是()A .sin 4y x π⎛⎫=+ ⎪⎝⎭B .()()sin cos y x x ππ=+-C .22cos cos 2y x x π⎛⎫=-+ ⎪D .sin 2y x=3.(2022·北京昌平·高一期末)下列函数中,最小正周期为π的奇函数是()A .sin 4y x π⎛⎫=+ ⎪⎝⎭B .sin 2y x =C .sin cos y x x =D .22cos sin y x x=-4.(2022·陕西渭南·高二期末(理))函数()2sin cos f x x x x =+的最小正周期是________.5.(2022·全国·高一专题练习)已知函数()cos f x x x ωω=-(0)ω>的最小正周期为π,则ω=___.6.(2022·浙江·杭十四中高一期末)函数2cos cos cos 2y x x x π⎛⎫=+- ⎪的最小正周期为__________.题型二:三角函数对称性【例1】(江西省“红色十校”2023届高三上学期第一联考数学(文)试题)已知函数π()sin()0,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的两个相邻的零点为12,33-,则()f x 的一条对称轴是()A .16x =-B .56x =-C .13x =D .23x =,【例2】(2022全国高一课时练习)函数cos 23y x ⎛⎫=+ ⎪⎝⎭的图象()A .关于点,03π⎛⎫⎪⎝⎭对称B .关于点,06π⎛⎫⎪⎝⎭对称C .关于直线6x π=对称D .关于直线3x π=对称【答案】D【解析】由题设,由余弦函数的对称中心为,2)0(k ππ+,令232x k πππ+=+,得212k x ππ=+,k Z ∈,易知A 、B 错误;由余弦函数的对称轴为x k π=,令23x k ππ+=,得26k x ππ=-,k Z ∈,当1k =时,3x π=,易知C 错误,D 正确;故选:D 【例3】(2022·江西省万载中学高一阶段练习)把函数4πsin 23y x ⎛⎫=+ ⎪⎝⎭的图像向右平移()0ϕϕ>个单位长度,所得图像关于y 轴对称,则ϕ的最小值是()A .5π6B .2π3C .5π12D .π6【例4】(2023福建省福州屏东中学高三开学考试多选题)已知函数()()3sin 222f x x ππϕϕ⎛⎫=+-<< ⎪⎝⎭的图像关于直线3x π=对称,则()A .函数12f x π⎛⎫+ ⎪⎝⎭为奇函数B .函数()f x 在,32ππ⎡⎤⎢⎥⎣⎦上单调递增C .函数()f x 的图像向右平移()0a a >个单位长度得到的函数图像关于6x π=对称,则a 的最小值是3πD .若方程()f x a =在2,63ππ⎡⎤⎢⎥上有2个不同实根12,x x ,则12x x -的最大值为2π故结合正弦函数的性质可知,若方程()f x a =在2,63ππ⎡⎤⎢⎥⎣⎦上有2个不同实根12,x x ,不妨设12x x <,则12x x -取得最大值时满足1266x ππ-=且25266x ππ-=,所以,12x x -的最大值为3π,故错误.故选:AC【例5】(2023江西省高三月考)若函数y cos 6x πω⎛⎫=+ ⎪⎝⎭(ω∈N +)图象的一个对称中心是,06π⎛⎫⎪⎝⎭,则ω的最小值为()A .1B .2C .4D .8【答案】B 【解析】当6x π=时,0y =,即cos 066πωπ⎛⎫+=⎪⎝⎭,()662k k Z πωπππ∴+=+∈,解得62k ω=+,N ω*∈ ,故当0k =时,ω取最小值2.【例6】【2016高考新课标2理数】若将函数2sin 2y x =的图像向左平移12π个单位长度,则平移后图象的对称轴为()(A )()26k x k Z ππ=-∈(B )()26k x k Z ππ=+∈(C )()212k x k Z ππ=-∈(D )()212k x k Z ππ=+∈【答案】B【解析】由题意,将函数2sin 2y x =的图像向左平移12π个单位得2sin 2()2sin(2)126y x x ππ=+=+,则平移后函数的对称轴为2,62x k k Z πππ+=+∈,即,62k x k Z ππ=+∈,故选B.【题型专练】1.(2020·四川省泸县第四中学高三开学考试)已知函数()sin 22f x x π⎛⎫=+ ⎪⎝⎭,则函数()f x 的图象的对称轴方程为()A .,4x k k Z ππ=-∈B .+,4x k k Z ππ=∈C .1,2x k k Z π=∈D .1+,24x k k Zππ=∈【答案】C【解析】由已知,()cos 2f x x =,令2,π=∈x k k Z ,得1,2x k k Z π=∈.故选:C.2.【2017·天津卷】设函数()2sin()f x x ωϕ=+,x ∈R ,其中0ω>,||ϕ<π.若5(28f π=,(08f 11π=,且()f x 的最小正周期大于2π,则A .23ω=,12ϕπ=B .23ω=,12ϕ11π=-C .13ω=,24ϕ11π=-D .13ω=,24ϕ7π=【答案】A【解析】由题意得125282118k k ωϕωϕππ⎧+=π+⎪⎪⎨π⎪+=π⎪⎩,其中12,k k ∈Z ,所以2142(2)33k k ω=--,又22T ωπ=>π,所以01ω<<,所以23ω=,11212k ϕ=π+π,由ϕ<π得12ϕπ=,故选A .3.(2023·全国·高三专题练习)将函数sin 22y x x =的图象沿x 轴向右平移a 个单位(a >0)所得图象关于y 轴对称,则a 的最小值是()A .712πB .4πC .12πD .6π4.【2018·江苏卷】已知函数()ππsin 2()22y x =+-<<ϕϕ的图象关于直线π3x =对称,则ϕ的值是________.【答案】π6-【解析】由题意可得2sin π13⎛⎫+=± ⎪⎝⎭ϕ,所以2πππππ()326k k k +=+=-+∈Z ,ϕϕ,因为ππ22-<<ϕ,所以π0,.6k ==-ϕ5.(2022·广西南宁·高二开学考试多选题)把函数()sin f x x =的图像向左平移π3个单位长度,再把横坐标变为原来的12倍(纵坐标不变)得到函数()g x 的图像,下列关于函数()g x 的说法正确的是()A .最小正周期为πB .单调递增区间5πππ,π()1212k k k ⎡⎤-+∈⎢⎥⎣⎦Z C .图像的一个对移中心为π,03⎛⎫- ⎪⎝⎭D .图像的一条对称轴为直线π12x =题型三:三角函数的奇偶性【例1】(2022·全国·清华附中朝阳学校模拟预测)已知函数()sin 2sin 23f x x x π⎛⎫=++ ⎪⎝⎭向左平移θ个单位后为偶函数,其中0,2π⎡⎤θ∈⎢⎥⎣⎦.则θ的值为()A .2πB .3πC .4πD .6π【例2】(2022·广东·执信中学高一期中)对于四个函数sin y x =,cos y x =,sin y x =,tan y x =,下列说法错误的是()A .sin y x =不是奇函数,最小正周期是π,没有对称中心B .cos y x =是偶函数,最小正周期是π,有无数多条对称轴C .sin y x =不是奇函数,没有周期,只有一条对称轴D .tan y x =是偶函数,最小正周期是π,没有对称中心由图可知,函数sin y x =不是奇函数,最小正周期是π,没有对称中心,A 对;对于B 选项,如下图所示:由图可知,cos y x =是偶函数,最小正周期是π,有无数多条对称轴,B 对;对于C 选项,如下图所示:由图可知,sin y x =不是奇函数,没有周期,只有一条对称轴,C 对;对于D 选项,如下图所示:由图可知,函数tan y x =是偶函数,不是周期函数,没有对称中心,D 错.故选:D.【例3】(2022·陕西师大附中高一期中)已知函数2π()sin ()24f x x =++,若(lg5)a f =,1(lg 5b f =,则()A .0a b +=B .0a b -=C .5a b +=D .5a b -=【例4】(2022·江西省铜鼓中学高二开学考试)将函数()sin 22f x x x =+的图象向左平移()0ϕϕ>个单位长度得到一个偶函数,则ϕ的最小值为()A .12πB .6πC .3πD .56π【例5】(2022·四川成都·模拟预测(理))函数2()ln(2)sin(1)211f x x x x x x -=+--+++在[0,2]上的最大值与最小值的和为()A .-2B .2C .4D .6【例6】(2022·贵州贵阳·高三开学考试(理))已知函数()2cos(2)02f x x πϕϕ⎛⎫=+<< ⎪⎝⎭的图象向右平移3π个单位长度后,得到函数()g x 的图象,若()g x 的图象关于原点对称,则ϕ=()A .3πB .4πC .6πD .12π【例7】(2022·陕西·定边县第四中学高三阶段练习(理))已知函数()sin cos f x a x b x =-在4x π=处取到最大值,则4f x π⎛⎫+ ⎪⎝⎭()A .奇函数B .偶函数C .关于点(),0π中心对称D .关于2x π=轴对称【例8】(2023·全国·高三专题练习)写出一个最小正周期为3的偶函数()f x =___________.【题型专练】1.(2022·全国·高一课时练习)下列函数中,既为偶函数又在,02π⎛⎫- ⎪⎝⎭上单调递增的是()A .cos y x =B .cos y x=C .sin 2y x π⎛⎫=- ⎪D .tan cos y x x=-2.(2022·陕西·武功县普集高级中学高三阶段练习(文))已知函数()e e sin x xf x x a -=-++,若()1ln 1,ln 3f m f m ⎛⎫== ⎪⎝⎭,则=a ()A .1B .2C .1-D .2-3.(2022·湖南·周南中学高二期末)函数为()sin 23f x x πϕ⎛⎫=++ ⎪⎝⎭偶函数的一个充分条件是()A .6π=ϕB .3πϕ=C .2ϕπ=D .()3k k πϕπ=+∈Z故选:A4.(2022·贵州黔东南·高二期末(理))已知函数()πcos 2(0)3f x x ωω⎛⎫=-> ⎪⎝⎭的最小正周期为π,将其图象向右平移(0)ϕϕ>个单位长度,得到函数()g x 的图象,若函数()g x 为偶函数,则ϕ的最小值为()A .6πB .π4C .π3D .π25.(2023·全国·高三专题练习)已知函数2()(2)sin(1)1f x x x x x =--+-在[1,1)-(1,3]⋃上的最大值为M ,最小值为N ,则M N +=()A .1B .2C .3D .4可得()h t 的最大值与最小值之和为0,那么()g t 的最大值与最小值之和为2.故选:B .6.(2022辽宁丹东·高一期末)写出一个最小正周期为1的偶函数()f x =______.【答案】cos2πx【解析】因为函数cos y x ω=的周期为2π||ω,所以函数cos 2πy x =的周期为1.故答案为:cos2πx .(答案不唯一)7.(2022·全国·高三专题练习)已知()2sin()cos f x x x α=++是奇函数,则sin α的值为______.8.(2022·河南·高二开学考试)将函数()()cos 06f x x πωω⎛⎫=+> ⎪⎝⎭的图像向左平移4π个单位长度后得到偶函数()g x 的图像,则ω的最小值是______.【答案】1039.(2022·全国·高一单元测试)写出一个同时具有性质①()02f =;②()()πf x f x +=的函数()f x =______(注:()f x 不是常数函数).题型四:三角函数的单调性【例1】(湖南省永州市2023届高三上学期第一次高考适应性考试数学试题)将函数2()cos cos 1f x x x x =+-的图象向右平移6π个单位长度,然后将所得函数图象上所有点的横坐标变为原来的12(纵坐标不变),得到函数()y g x =的图象,则()g x 的单调递增区间是()A .ππππ,(Z)12262k k k ⎡⎤-++∈⎢⎥⎣⎦B .ππ5ππ,(Z)242242k k k ⎡⎤-++∈⎢⎥⎣⎦C .π2π2π,2π(Z)33k k k ⎡⎤-++∈⎢⎥D .π5π2π,2π(Z)66k k k ⎡⎤-++∈⎢⎥故选:A【例2】(2022·陕西师大附中高一期中)sin1,sin 2,sin 3按从小到大排列的顺序为()A .sin3sin2sin1<<B .sin3sin1sin2<<C .sin1sin2sin3<<D .sin2sin1sin3<<【例3】(2022·全国·高一单元测试)下列四个函数中,以π为周期且在π0,2⎛⎫ ⎪⎝⎭上单调递增的偶函数有()A .cos 2y x =B .sin 2y x =C .tan y x =D .lg sin y x=也是以【例4】(2023·全国·高三专题练习)已知函数()()cos 02f x x πωϕωϕ⎛⎫=+≤ ⎪⎝⎭>,,4x π=-为f (x )的零点,4x π=为y =f (x )图象的对称轴,且f (x )在186ππ⎛⎫⎪⎝⎭,上单调,则ω的最大值为()A .3B .4C .5D .6当ππ,π2u k k ⎡⎤=+⎢⎥⎣⎦,k Z ∈时,函数sin y u =递增.即πππ,π42x k k ⎡⎤+∈+⎢⎥⎣⎦,解得:πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦,k Z ∈,所以函数sin()4πy x =+的单调递增区间是πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦,k Z ∈.故答案为:πππ,π44x k k ⎡⎤∈-+⎢⎥⎣⎦,k Z ∈.【例6】(2023·全国·高三专题练习)函数πsin(2)3y x =-+的单调递减区间是()A .π5π[π,π],Z 1212k k k -+∈B .π5π[2π,2π],Z 1212k k k -+∈C .π5π[π,πZ66k k k -+∈D .π5π[2π,2πZ66k k k -+∈【题型专练】1.(2022·辽宁·新民市第一高级中学高一阶段练习)已知函数2sin()y x ωθ=+为偶函数(0)θπ<<,其图像与直线2y =的两个交点的横坐标分别为12x x 、,若21||x x -的最小值为π,则该函数的一个单调递增区间为()A .ππ,24⎛⎫-- ⎪B .ππ,44⎛⎫- ⎪C .π0,2⎛⎫ ⎪⎝⎭D .π3π,44⎛⎫⎪⎝⎭2.(2022·四川省成都市新都一中高二开学考试(理))已知函数()sin(),022f x x ππωϕϕω⎛⎫=+-<<> ⎪⎝⎭,若()00166f x f x ππ⎛⎫⎛⎫==≠ ⎪ ⎪⎝⎭⎝⎭,0min6x ππ-=,则函数()f x 的单调递减区间为()A .2,()63k k k ππππ⎛⎫++∈ ⎪⎝⎭Z B .22,2()63Z k k k ππππ⎛⎫++∈ ⎪⎝⎭C .,()36Z k k k ππππ⎛⎫-++∈ ⎪D .2,2()36Z k k k ππππ⎛⎫-++∈ ⎪3.(2022六盘山高级中学)函数tan 23y x π⎛⎫=- ⎪⎝⎭的单调增区间为()A .5,()212212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B .5,()212212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭C .5,()1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦D .5,()1212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭【答案】B【解析】因为函数tan y x =的单调递增区间为,()22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭,所以2()223,k k k x Z πππππ-<-<+∈,解得5,()212212k k x k Z ππππ-<<+∈,所以函数tan 23y x π⎛⎫=- ⎪⎝⎭的单调增区间为5,()212212k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭.故选:B 4.(2023·全国·高三专题练习)已知函数()()sin 2f x x ϕ=+,其中()0,2πϕ∈,若()6f x f π⎛⎫≤ ⎪⎝⎭对于一切R x ∈恒成立,则()f x 的单调递增区间是()A .,2k k πππ⎡⎤+⎢⎥⎣⎦()k ∈Z B .,36k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z C .2,63k k ππππ⎡⎤++⎢⎥()k ∈Z D .,2k k πππ⎡⎤-⎢⎥()k ∈Z 5.(2022·全国·高二单元测试)已知函数()cos f x x x =,()()g x f x '=,则().A .()g x 的图像关于点π,06⎛⎫⎪⎝⎭对称B .()g x 图像的一条对称轴是π6x =C .()g x 在5π5π,66⎛⎫- ⎪上递减D .()g x 在ππ,33⎛⎫- ⎪的值域为(0,1)6.(2022天津市静海区大邱庄中学高三月考)设函数()cos 26f x x π⎛⎫=- ⎪⎝⎭,给出下列结论:①()f x 的一个周期为π②()y f x =的图象关于直线12x π=对称③()y f x =的图象关于点,06π⎛⎫-⎪⎝⎭对称④()f x 在2,63ππ⎡⎤⎢⎥⎣⎦单调递减其中所有正确结论的编号是()A .①④B .②③C .①②③D .②③④【答案】C【解析】对于①,2T ππω==,故①正确;对于②,12x π=时,(112f π=,函数取得最大值,故②正确;对于③,6x π=-时,()06f π-=,故③正确;对于④,2,63x ππ⎡⎤∈⎢⎥⎣⎦ ,当712x π=时,7112f π⎛⎫=- ⎪⎝⎭,函数取得最小值,()f x ∴在2,63ππ⎡⎤⎢⎥⎣⎦有增有减,故④不正确.故选:C .7.(2022·全国·高一课时练习)关于函数1()sin sin f x x x=+,下列说法正确的是()A .()f x 的一个周期是πB .()f x 的最小值为2C .()f x 在π(0,2上单调递增D .()f x 的图象关于直线π2x =对称上单调递减,而8.(2022·内蒙古包头·高三开学考试(文))若()sin cos f x x x =+在[]0,a 是增函数,则a 的最大值是()A .4πB .2πC .34πD .π9.(2022·全国·高一专题练习)若函数()sin 23f x x ⎛⎫=- ⎪⎝⎭与()cos 4g x x ⎛⎫=+ ⎪⎝⎭都在区间()(),0πa b a b <<<上单调递减,则b a -的最大值为()A .π3B .π2C .6πD .π10.(2022·全国·高三专题练习)将函数()2sin()(0)3f x x ωω=->的图象向左平移3ωπ个单位得到函数()y g x =的图象,若()y g x =在[,64ππ-上为增函数,则ω最大值为()A .32B .2C .3D .11.(2022·全国·高一课时练习多选题)已知直线8x =是函数()sin(2)(0π)f x x ϕϕ=+<<图象的一条对称轴,则()A .π8f x ⎛⎫+ ⎪⎝⎭是偶函数B .3π8x =是()f x 图象的一条对称轴C .()f x 在ππ,82⎡⎤⎢⎥⎣⎦上单调递减D .当π2x =时,函数()f x 取得最小值题型五:三角函数的值域【例1】(2022·陕西·安康市教学研究室高三阶段练习(文))下列函数中,最大值是1的函数是()A .|sin ||cos |=+y x xB .2cos 4sin 4y x x =+-C .cos tan y x x =⋅D .y =【例2】(2022·全国·高三专题练习)函数1ππ()sin()cos()363f x x x =++-的最大值是()A .43B .23C .1D .13【答案】8【解析】【分析】由题意可得()22sin sin 1f x x x =-++,令[]sin 0,1x t ∈=,可得[]221,0,1y t t t =-++∈,利用二次函数的性质可求f (x )的最大值.【详解】解:()22cos 2sin 2sin sin 12sin sin 1f x x x x x x x =+=-++=-++,令[]sin 0,1x t ∈=,可得[]2219212,0,148y t t t t ⎛⎫=-++=--+∈ ⎪⎝⎭,当14t =时,y 取得最大值为98,故答案为:98.【例4】(2022·江西·高三开学考试(文))已知函数()()2πsin sin 022f x x x x ωωωω⎛⎫+--> ⎪⎝⎭的最小正周期为π,则()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的值域为()A .11,22⎡⎤-⎢⎥⎣⎦B .22⎡-⎢⎥⎣⎦C .⎡⎤⎢⎥⎣⎦D .⎡-⎢⎣⎦【例5】(2022·湖北·襄阳五中模拟预测)已知函数()sin()0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭在区间,33ππ⎛⎫⎪⎝⎭上单调,且对任意实数x 均有4()33f f x f ππ⎛⎫⎛⎫≤≤⎪ ⎪⎝⎭⎝⎭成立,则ϕ=()A .12πB .6πC .4πD .3π【例6】(2023·全国·高三专题练习)已知函数()22sin s ()3in f x x x π+=+,则()f x 的最小值为()A .12B .14C .D .2【例7】(2022·全国·高三专题练习)函数2()cos 2f x x x =+-0,2x π⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭的最大值是__________.【答案】14-##-0.25【解析】【详解】22()1sin 2sin 1f x x x x x =--=--=21sin24x ⎛⎫-- ⎪ ⎪⎝⎭,所以当sin x =时,有最大值14-.故答案为14-.【例8】(2022·全国·高三专题练习)已知函数()sin cos 2sin cos 2f x x x x x =+++,则()A .()f x 的最大值为3,最小值为1B .()f x 的最大值为3,最小值为-1C .()f x的最大值为3,最小值为34D .()f x的最大值为33【例9】(2022·全国·高一课时练习)已知关于x 的方程2cos sin 20x x a -+=在02π⎛⎤⎥⎝⎦,内有解,那么实数a 的取值范围()A .58a -≤B .102a -≤≤C .1122a -<≤D .12a -<≤0【题型专练】1.(2022·江西九江·高一期末)函数()193sin cos 2R 24y x x x =+-∈的最小值是()A .14B .12C .234-D .414-2.(2022·河南焦作·高一期末)函数2cos22cos y x x =+的最小值为()A .3-B .2-C .1-D .0【答案】C【分析】利用二倍角的降幂公式化简函数解析式,利用余弦型函数的有界性可求得结果.【详解】2cos 22cos cos 2cos 212cos 21y x x x x x =+=++=+ ,min 211y ∴=-+=-.故选:C.3.【2018·北京卷】设函数f (x )=πcos(0)6x ωω->,若π()()4f x f ≤对任意的实数x 都成立,则ω的最小值为__________.【答案】23【解析】因为()π4f x f ⎛⎫≤ ⎪⎝⎭对任意的实数x 都成立,所以π4f ⎛⎫⎪⎝⎭取最大值,所以()()ππ22π 8463k k k k -=∈∴=+∈Z Z ,ωω,因为0>ω,所以当0k =时,ω取最小值为23.4.(2022·广西南宁·高二开学考试)已知函数ππ()sin ,0,36f x x x ⎛⎫⎡⎤=+∈ ⎪⎢,则函数()f x 的最大值为__________.5.(2022·全国·高一课时练习)函数()1sin cos =++f x x x的值域为_____________.6.(2022·全国·高一专题练习)若奇函数()f x 在其定义域R 上是单调减函数,且对任意的R x ∈,不等式2(cos 3sin )(sin )0f x x f x a -+-≤恒成立,则a 取值范围是_________.【答案】(,2]-∞-【分析】根据给定条件,脱去法则“f ”,再利用含sin x 的二次函数求解作答.【详解】因奇函数()f x 在R 上单调递减,则R x ∀∈,2(cos 3sin )(sin )0f x x f x a -+-≤2(cos 3sin )(sin )f x x f a x ⇔-≤-22cos 3sin sin cos 2sin x x a x a x x ⇔-≥-⇔≤-,令222cos 2sin sin 2sin 1(sin 1)2y x x x x x =-=--+=-++,而1sin 1x -≤≤,因此当sin 1x =时,min 2y =-,即有2a ≤-,所以a 取值范围是(,2]-∞-.故答案为:(,2]-∞-【点睛】思路点睛:涉及求含正(余)的二次式的最值问题,可以换元或整体思想转化为二次函数在区间[-1,1]或其子区间上的最值求解.7.【2018·全国Ⅲ】函数()πcos 36f x x ⎛⎫=+ ⎪⎝⎭在[]0π,的零点个数为________.【答案】3【解析】0πx ≤≤ ,ππ19π3666x ∴≤+≤,由题可知πππ3π336262x x +=+=,或π5π362x +=,解得π4π,99x =,或7π9,故有3个零点.8.(2022·上海市第十中学高一期末)已知函数()2cos 2cos 1f x x x x =+-(R x ∈).求函数()f x 的最小正周期及在区间0,2π⎡⎤⎢⎥上的最大值和最小值.9.(2022·湖南·雅礼中学高一期末)已知函数()2cos sin 4f x x a x a =-++-,[]0,x π∈.(1)求()f x 的最小值()g a ;(2)若()f x 在[]0,π上有零点,求a 的取值范围,并求所有零点之和.题型六:三角函数的图像【例1】(2022·陕西师大附中高三开学考试(理))函数()sin()(0,0,0)f x A x A ωϕωπϕ=+>>-<<的部分图象如图所示,为了得到()sin g x A x ω=的图象,只需将函数()y f x =的图象()A .向左平移6π个单位长度B .向左平移12π个单位长度C .向右平移6π个单位长度D .向右平移12π个单位长度【例2】(2022·陕西·延安市第一中学高一期中)函数()()sin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,则()2f π的值为()A .B .C .D .1-的部分图象知,【例3】(2022·湖南·宁乡市教育研究中心模拟预测)如图表示电流强度I 与时间t 的关系()()()sin 0,0I A x A ωϕω=+>>在一个周期内的图像,则下列说法正确得是()A .50πω=B .π6ϕ=C .0=t 时,I =D .1300100t I ==时,【例4】(2022·江苏·沭阳如东中学高三阶段练习多选题)已知函数()()sin f x A x ωϕ=+(其中0A >,0>ω,2πϕ<)的部分图象如图所示,则()A .2ω=B .()f x 的图象关于直线23x π=对称C .()2cos 26f x x π⎛⎫=- ⎪⎝⎭D .()f x 在5[,63ππ--上的值域为[2,1]-【例5】(2022·河北·沧县风化店中学高二开学考试多选题)函数()()cos 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,且满足223f π⎛⎫=- ⎪⎝⎭,现将()f x 图象沿x 轴向左平移4π个单位,得到函数()y g x =的图象.下列说法正确的是()A .()g x 在,126ππ⎡⎤-⎢⎥⎣⎦上是增函数B .()g x 的图象关于56x π=对称C .()g x 是奇函数D .()g x 的最小正周期为23π【例6】(2022·福建·高三阶段练习多选题)函数()sin()(0,0,02π)f x A x A ωϕωϕ=+>><<的部分图像如图所示,则()A .3π2ωϕ+=B .(2)2f -=-C .()f x 在区间()0,2022上存在506个零点D .将()f x 的图像向右平移3个单位长度后,得到函数π()cos 4g x x ⎛⎫=- ⎪的图像【例7】(2022·江苏南通·高三开学考试多选题)已知函数()()sin 20,02f x x ωϕωϕ⎛⎫=+><< ⎪⎝⎭的部分图象如图所示,则下列结论正确的是()A .()f x 的图象关于点π,03⎛⎫- ⎪⎝⎭对称B .()f x 的图象向右平移π12个单位后得到sin2y x =的图象C .()f x 在区间π,2π⎡⎤--⎢⎥⎣⎦上单调递増D .π6f x ⎛⎫+ ⎪为偶函数【例8】(2022·全国·高一单元测试多选题)已知函数()()sin f x A x =+ωϕ(0A >,0>ω,2πϕ<)的部分图象如图所示,下列说法错误的是()A .()f x 的图象关于直线23x π=-对称B .()f x 的图象关于点5,012π⎛⎫-⎪⎝⎭对称C .将函数2sin 26y x π⎛⎫=- ⎪⎝⎭的图象向左平移2π个单位长度得到函数()f x 的图象D .若方程()f x m =在,02π⎡⎤-⎢⎥上有两个不相等的实数根,则m 的取值范围是(2,-【题型专练】1.(2022·广东·仲元中学高三阶段练习多选题)已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示.将函数()f x 的图象向右平移316π个单位长度,再将图象上所有点的横坐标变为原来的2倍(纵坐标不变),得到函数()y g x =的图象,则()A .()2sin 24x f x π⎛⎫=+ ⎪⎝⎭B .()g x 的图象关于直线8x π=-对称C .()g x 的图象关于点,08π⎛⎫⎪⎝⎭对称D .函数()()f x g x +的最小值为4-2.(2022·湖北·襄阳市襄州区第一高级中学高二阶段练习多选题)函数()()()2sin 0,f x x ωϕωϕπ=+><的部分图像如图所示,则下列结论正确的是()A .()12sin 33f x x π⎛⎫=- ⎪⎝⎭B .若把()f x 图像上的所有点的横坐标变为原来的23倍,纵坐标不变,得到函数()g x 的图像,则函数()g x 在[],ππ-上是增函数C .若把函数()f x 的图像向左平移2π个单位长度,得到函数()h x 的图像,则函数()h x 是奇函数D .,33x ππ⎡⎤∀∈-⎢⎥,若()332f x a f π⎛⎫+≥ ⎪恒成立,则a 的取值范围为)2,+∞3.(2022·安徽·高三开学考试)已知函数π()2sin()0,||2f x x ωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图象如图所示,其中ππ,2,,0123A B ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,则下列说法错误的是()A .()f x 的最小正周期为πB .将()f x 的图象向右平移6π个单位长度后关于原点对称C .()f x 在2ππ,3⎡⎤--⎢⎣⎦上单调递减D .直线7π12x =为()f x 图象的一条对称轴4.(2022·天津·南开中学高三阶段练习)已知函数π()sin()(R,0,0,)2f x A x x A ωϕωϕ=+∈>><的部分图象如图所示,则下列说法正确的是()A .直线πx =是()f x 图象的一条对称轴B .()f x 图象的对称中心为π(π,0)12k -+,Z k ∈C .()f x 在区间ππ,36⎡⎤-⎢⎥⎣⎦上单调递增D .将()f x 的图象向左平移π12个单位长度后,可得到一个奇函数的图象5.(2022·江苏省如皋中学高三开学考试多选题)函数()()sin 0,0,0πy A x A ωϕωϕ=+>><<在一个周期内的图象如图所示,则().A .该函数的解析式为2π2sin 33y x ⎛⎫=+ ⎪⎝⎭B .该函数图象的对称中心为ππ,03k ⎛⎫- ⎪⎝⎭,Zk ∈C .该函数的单调递增区间是5ππ3π,3π44k k ⎛⎫-+ ⎪⎝⎭,Zk ∈D .把函数π2sin 3y x ⎛⎫=+ ⎪的图象上所有点的横坐标伸长为原来的32倍,纵坐标不变,可得到该函数图象6.(2021·福建·福州十八中高三开学考试多选题)已知函数()sin()(010f x x ωϕω=+<<,0π)ϕ<<的部分图象。
利用图像求解三角函数解析式-解析版

利用图像求解三角函数解析式第I 卷(选择题)一、单选题1.已知函数()sin()f x x ωϕ=+0,||2πωϕ⎛⎫><⎪⎝⎭的图象如图所示,则( )A .函数()f x 的最小正周期是2πB .函数()f x 在区间,2ππ⎛⎫⎪⎝⎭上单调递减 C .函数()f x 在区间34,43ππ⎡⎤⎢⎥⎣⎦上的最小值是1- D .曲线12y f x π⎛⎫=+ ⎪⎝⎭关于直线2x π=-对称 【答案】C 【分析】根据函数图象求出函数解析式,再结合选项一一判断即可; 【详解】解:由函数图象可知541264T πππ=-=,所以T π=,因为2T ππω==,所以最小正周期为π,所以2ω=,故A 错误; 又函数过点5,112π⎛⎫⎪⎝⎭,所以55sin 211212f ππϕ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,所以52,62k k Z ππϕπ+=+∈,解得2,3k k Z πϕπ=-+∈,因为||2ϕπ<,所以3πϕ=-,所以()sin 23πf x x ⎛⎫=-⎪⎝⎭,当,2x ππ⎛⎫∈ ⎪⎝⎭,所以252,333πππx ⎛⎫-∈ ⎪⎝⎭,因为sin y x =在25,33x ππ⎛⎫∈⎪⎝⎭上不单调,故B 错误; 当34,43πx π∈⎡⎤⎢⎥⎣⎦,所以,267733x πππ⎡⎤⎢⎥⎣∈⎦-,所以sin 23x π⎡⎛⎫-∈-⎢ ⎪⎝⎭⎣⎦,故C 正确;s s 2i in 2112n 236y f x x x ππππ⎛⎫⎡⎤⎛⎫=+=+=⎪⎛⎫- ⎪ ⎝- ⎪⎢⎭⎝⎭⎝⎣⎦⎭⎥,当2x π=-时,116in2s y π=≠±=,故2x π=-不是函数12y f x π⎛⎫=+ ⎪⎝⎭的对称轴,故D 错误故选:C2.函数()sin()f x A x ωϕ=+(其中0A >,0>ω,||)2πϕ<的图象如图所示,为了得到()f x 的图象,只需将()sin g x A x ω=图象( )A .向左平移4π个单位长度 B .向右平移4π个单位长度 C .向左平移12π个单位长度 D .向右平移12π个单位长度【答案】C 【分析】根据图象最值可得1A =,求出周期,即可得出ω,将,04π⎛⎫⎪⎝⎭代入可求得ϕ,即可得出结论. 【详解】根据函数()sin()f x A x ωϕ=+(其中0A >,0>ω,||)2πϕ<的图象,可得1A =,15141246T ππ=-=,即23T =,2323πω∴==.将,04π⎛⎫⎪⎝⎭代入,可得()sin(3)044f ππϕ=⨯+=,则3,4k k Z πϕπ⨯+=∈,3,4k k Z πϕπ∴=-∈, 又||2ϕπ<,4πϕ∴=,故()sin(3)4f x x π=+. 故把()sin3g x x =图象向左平移12π个单位长度,即可得到()sin(3)4f x x π=+的图象.故选:C . 【点睛】方法点睛:根据三角函数()()sin f x A x =+ωϕ部分图象求解析式的方法: (1)根据图象的最值可求出A ; (2)求出函数的周期,利用2T πω=求出ω;(3)取点代入函数可求得ϕ. 3.设函数()()cos 06f x x πωω⎛⎫=+> ⎪⎝⎭,在[],ππ-上的图象大致如图,将该图象向右平移()0m m >个单位后所得图象关于直线6x π=对称,则m 的最小值为( )A .4π B .29π C .518π D .3π 【答案】C 【分析】根据五点作图法可构造方程求得ω,得到()f x ;由三角函数平移变换可求得平移后解析式,利用代入检验的方法,根据图象关于6x π=可构造方程求得m ,由此确定最小值.【详解】根据五点法作图知:4962πππω-+=-,解得:32ω=,()3cos 26f x x π⎛⎫∴=+ ⎪⎝⎭;将()f x 向右平移m 个单位得:()33cos 262f x m x m π⎛⎫-=+-⎪⎝⎭,()f x m -图象关于6x π=对称,()332662m k k Z πππ∴⨯+-=∈, 解得:()52183m k k Z ππ=-∈, 由0m >,可令0k =得m 的最小值518π. 故选:C. 【点睛】方法点睛:根据余弦型函数()cos y A x ωϕ=+的对称轴、对称中心和单调区间求解参数值时,通常采用代入检验的方式,即将x 的取值代入x ωϕ+,整体对应cos y x =的对称轴、对称中心和单调区间,由此求得结果. 4.函数f (x )=A sin(ωx +φ)(0,0,||)2A πωϕ>><的部分图象如图所示,为了得到g (x )=sin 3x 的图象,则只要将f (x )的图象( )A .向右平移4π个单位长度B .向右平移12π个单位长度C .向左平移4π个单位长度D .向左平移12π个单位长度【答案】B 【分析】根据函数的图象可以得到函数图象所经过的特殊点,进而可以确定函数的解析式,最后利用正弦型函数的图象变换方法进行求解即可. 【详解】由函数的图象可知:函数的图象过5(,0),(,1)412ππ-这两点, 设函数()f x 的最小正周期为T , 所以有:15241243T T πππ=-⇒=,而23,0,3T πωωωω=⇒=>∴=, 所以()()sin 3f x x ϕ=+,因为函数图象过(,0)4π点,所以32()2()44k k Z k k Z ππϕππϕπ⋅+=+∈⇒=+∈,因为π2ϕ<,所以0k =,即4πϕ=,因此()sin 34f x x π⎛⎫=+⎪⎝⎭,而()sin 3sin 3412f x x x ππ⎡⎤⎛⎫⎛⎫=+=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 因此为了得到()sin3g x x =的图象,只需将()f x 的图像向右平移π12个单位长度即可;故选:B5.如图,图象对应的函数解析式可能是( )A .cos sin y x x x =+B .sin cos y x x x =+C .sin y x x =D .cos y x x =【答案】A 【分析】分析各选项中函数的奇偶性、及各函数在2x π=处的函数值,结合排除法可得出合适的选项. 【详解】对于A 选项,设()1cos sin f x x x x =+,该函数的定义域为R ,()()()()()11cos sin cos sin cos sin f x x x x x x x x x x f x -=--+-=--=-+=-,该函数为奇函数,且1cos sin 102222f ππππ⎛⎫=+=> ⎪⎝⎭,满足条件; 对于B 选项,设()2sin cos f x x x x =+,该函数的定义域为R ,()()()()22sin cos sin cos f x x x x x x x f x -=--+-=+=,该函数为偶函数,不满足条件;对于C 选项,设()3sin f x x x =,该函数的定义域为R ,()()()33sin sin f x x x x x f x -=--==,该函数为偶函数,不满足条件;对于D 选项,设()4cos f x x x =,该函数的定义域为R ,()()()44cos cos f x x x x x f x -=--=-=-,该函数为奇函数,4cos 0222f πππ⎛⎫== ⎪⎝⎭,不满足条件.故选:A. 【点睛】思路点睛:函数图象的辨识可从以下方面入手: (1)从函数的定义域,判断图象的左右位置; (2)从函数的值域,判断图象的上下位置. (3)从函数的单调性,判断图象的变化趋势; (4)从函数的奇偶性,判断图象的对称性; (5)函数的特征点,排除不合要求的图象. 6.将函数1()sin(2)123f x x π=++的图象向右平移( )个单位后,再进行周期变换可以得到如图所示的图象.A .12πB .6πC .3π D .4π 【答案】B 【分析】设图象对应的函数为()sin y A x B ωϕ=++,根据图象最值可求得,A B ,根据周期可求得ω,将()0,1代入可求得ϕ,进而得出解析式,判断出结论. 【详解】设图象对应的函数为()sin y A x B ωϕ=++,根据函数的图象可得 1.510.5A =-=,240T πω==-,则2πω=,1.50.512B +==,即1sin 122y x πϕ⎛⎫=++ ⎪⎝⎭,将()0,1代入可得1sin 112ϕ+=,可解得0ϕ=, 故所给的图为1sin 122y x π⎛⎫=+ ⎪⎝⎭的图象, 故将函数1()sin(2)123f x x π=++的图象向右平移6π个单位后,再进行周期变换可以得到如图所示的图象. 故选:B . 【点睛】方法点睛:根据三角函数()()sin f x A x =+ωϕ部分图象求解析式的方法: (1)根据图象的最值可求出A ; (2)求出函数的周期,利用2T πω=求出ω;(3)取点代入函数可求得ϕ.7.已知函数()sin()(0,)2f x A x A πωϕϕ=+><的图像如图所示,且()f x 的图像关于点()0,0x 对称,则0x 的最小值为( )A .23πB .6π C .3π D .56π 【答案】B 【分析】先由函数图像求出函数()2sin 6f x x π⎛⎫=+⎪⎝⎭,再根据函数关于()0,0x 对称求出06x k ππ=-,从而当0k =时,0x 取得最小值为6π. 【详解】由题可知4112,2363A T πππ⎛⎫==⨯-= ⎪⎝⎭21Tπω∴== 则()()2sin ,2sin 233f x x f ππϕϕ⎛⎫⎛⎫=+=+=⎪ ⎪⎝⎭⎝⎭232k ππϕπ∴+=+又2πϕ<6πϕ∴=()2sin 6f x x π⎛⎫∴=+ ⎪⎝⎭由()f x 的图像关于点()0,0x 对称,可得0066x k x k ππππ+=∴=-,∴当0k =时,0x 取得最小值为6π故选:B 【点睛】已知f (x )=Asin (ωx +φ)(A >0,ω>0)的部分图象求其解析式时,A 比较容易看图得出,困难的是求待定系数ω和φ,常用如下两种方法: (1)由ω=2Tπ即可求出ω;确定φ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x 0,则令ωx 0+φ=0(或ωx 0+φ=π),即可求出φ.(2)代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出ω和φ,若对A ,ω的符号或对φ的范围有要求,则可用诱导公式变换使其符合要求.8.已知函数f (x )=Atan (ωx+φ)(ω>1,|φ|<),y=f (x )的部分图象如图,则f()=A .B .C .D .【答案】B 【详解】试题分析:根据函数的图象,求出函数的周期,然后求出ω,根据函数过(0.1),过(),确定φ的值,A 的值,求出函数的解析式,然后求出即可.解:由题意可知T=,所以ω=2,函数的解析式为:f (x )=Atan (2x+φ), 因为函数过(0,1),所以,1=Atanφ…①, 函数过(),0=Atan (+φ)…①,解得:φ=,A=1.①f (x )=tan (2x+).则f ()=tan ()=故选B .考点:由y=Asin (ωx+φ)的部分图象确定其解析式.9.如图,函数sin f x A x ωϕ=+()()(其中00||2A ωϕπ≤>,>,)与坐标轴的三个交点P Q R 、、满足204P PQR M π∠=(,),,为QR 的中点,PM =A 的值为( )A.BC .8D .16【答案】A 【分析】由题意设出(20)0Q a a ,>,用a 表示出R 点坐标以及M 点坐标,根据PM =,利用距离公式求出Q 坐标,通过五点法求出函数的解析式,即可求出A . 【详解】解:设(2,0),0Q a a >,函数()sin(x+)f x A ϖϕ=(其中0,0,||2A πωφ>>≤)与坐标轴的三个交点P Q R 、、满足4PQR π∠=,∴(0,2a)R -,M 为QR 的中点,∴(,)M a a -,PM =,=解得4a =,80Q ∴(,),又20P (,),18262T ∴=-=, 2T 12πω∴==,解得6π=ω.函数经过(20)(08)P R -,,,,∴sin 206 sin 086A A πϕπϕ⎧⎛⎫⨯+= ⎪⎪⎪⎝⎭⎨⎛⎫⎪⨯+=- ⎪⎪⎝⎭⎩,||2πϕ≤,,3πϕ∴=-,解得A =, 故选A . 【点睛】本题考查由sin x y A ωϕ=+()的部分图象确定其解析式,求得Q 点与P 点的坐标是关键,考查识图、运算与求解能力,属于中档题.二、多选题10.函数()()()2sin 0,0f x x ωϕωϕπ=+><<的图象如图,把函数()f x 的图象上所有的点向右平移6π个单位长度,可得到函数()y g x =的图象,下列结论正确的是( )A .3πϕ=B .函数()g x 的最小正周期为πC .函数()g x 在区间,312ππ⎡⎤-⎢⎥⎣⎦上单调递增 D .函数()g x 关于点,03π⎛-⎫⎪⎝⎭中心对称 【答案】BC 【分析】根据图象先分析出ω的取值范围,然后根据()0f =ϕ的可取值,然后分类讨论ϕ的可取值是否成立,由此确定出,ωϕ的取值,则A 可判断;根据图象平移确定出()g x 的解析式,利用最小正周期的计算公式,则B 可判断;先求解出()g x 的单调递增区间,然后根据k 的取值确定出,312ππ⎡⎤-⎢⎥⎣⎦是否为单调递增区间,则C 可判断;根据3g π⎛⎫- ⎪⎝⎭的值是否为0判断D 是否正确. 【详解】由图可知:1112113124T T ππ⎧<⎪⎪⎨⎪>⎪⎩,所以11211129πππω<<,所以18241111ω<<,又因为()02sin f ϕ==0ϕπ<<,所以3πϕ=或23ϕπ=, 又因为11112sin 21212f ππωϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,所以112,122k k Z ππωϕπ+=+∈,又因为113,2122ππωπ⎛⎫∈ ⎪⎝⎭,所以113,3122ππωϕπ⎛⎫⎛⎫+∈ ⎪ ⎪⎝⎭⎝⎭,所以1k =, 当3πϕ=时,1113126πωπ=,解得2611ω=,这与18241111ω<<矛盾,不符合;当23ϕπ=时,1111126πωπ=,解得2ω=,满足条件,所以()22sin 23f x x π⎛⎫=+ ⎪⎝⎭,所以()22sin 22sin 2633g x x x πππ⎛⎫⎛⎫⎛⎫=-+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, A .由上可知A 错误;B .因为()2sin 23g x x π⎛⎫=+ ⎪⎝⎭,所以()g x 的最小正周期为2=2ππ,故B 正确; C .令222,232k x k k Z πππππ-≤+≤+∈,所以5,1212k x k k Z ππππ-≤≤+∈, 令0k =,此时单调递增区间为5,1212ππ⎡⎤-⎢⎥⎣⎦,且5,,3121212ππππ⎡⎤⎡⎤-⊆-⎢⎥⎢⎥⎣⎦⎣⎦,故C 正确; D.因为2sin 20333g πππ⎛⎫⎛⎫⎛⎫-=⨯-+=≠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以,03π⎛-⎫ ⎪⎝⎭不是对称中心,故D 错误; 故选:BC. 【点睛】方法点睛:已知函数()()sin g x A x ωϕ=+()0ω>, 若求函数()g x 的单调递增区间,则令ππ2π2π22k x k ωϕ-<+<+,Z k ∈; 若求函数()g x 的单调递减区间,则令π3π2π2π22k x k ωϕ+<+<+,Z k ∈; 若求函数()g x 图象的对称轴,则令ππ2x k ωϕ+=+,Z k ∈;若求函数()g x 图象的对称中心或零点,则令πx k ωϕ+=,Z k ∈. 11.已知函数()()sin f x A x =+ωϕπ0,0,2A ωϕ⎛⎫>>< ⎪⎝⎭的部分图像如图所示,则下列说法正确的是()A .()f x 的最小正周期的最大值为2πB .当ω最小时,()f x 在π3π,24⎛⎫⎪⎝⎭上单调递减 C .π3ϕ=-D .当ω最小时,直线2π3x =是()f x 图像的一条对称轴 【答案】BC 【分析】由给出的函数图像,求出函数解析式,结合函数性质一一分析即可. 【详解】 由题图得1A =. 因为()30sin 2f ϕ==-,又π2ϕ<,所以π3ϕ=-.由πππsin 0333f ω⎡⎤⎛⎫⎛⎫-=⨯--= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,即ππsin 033ω⎡⎤+=⎢⎥⎣⎦, 得πππ2π33k ω+=+,Z k ∈,即26k ω=+,Z k ∈, 又>0ω,所以min 2ω=,所以()f x 的最小正周期的最大值为π,故A 错误,C 正确;取2ω=,则()πsin 23f x x ⎛⎫=- ⎪⎝⎭,当π3π,24x ⎛⎫∈ ⎪⎝⎭时,令π23t x =-,则2π7π,36t ⎛⎫∈ ⎪⎝⎭,因为sin y t =在2π7π,36⎛⎫⎪⎝⎭上单调递减,所以()f x 在π3π,24⎛⎫⎪⎝⎭上单调递减,故B 正确;2π2ππsin 2sin π0333f ⎛⎫⎛⎫=⨯-== ⎪ ⎪⎝⎭⎝⎭,所以直线2π3x =不是()f x 图像的一条对称轴,故D 错误. 故选:BC. 【点睛】方法点睛:整体法求一般三角函数单调区间及对称性等相关问题.12.若函数1()sin()(0,0,0)22f x A x A ωϕωϕπ=+>><<在一个周期内的图象如图所示,则( )A .()2sin 23()3f x x π=+B .()f x 的图象的一个对称中心为7(,0)2π- C .()f x 的单调递增区间是5[3,3]44k k πππ-π-,k Z ∈ D .把π()2sin()3g x x =+的图象上所有点的横坐标变为原来的23,纵坐标不变,可得()f x 的图象 【答案】AB 【分析】根据图像求出()f x 的解析式,借助于正弦函数的性质一一验证: 对于A ,根据图像求出()f x 的解析式进行判断; 对于B ,利用代入法进行判断; 对于C ,求出单增区间进行判断; 对于D ,利用图像变换判断. 【详解】由题图可知2A =,函数()f x 的最小正周期4()34T π=⨯π-=π,故24312T ωωππ===π,解得43ω=,所以2()2sin()3f x x ϕ=+,又函数()f x 的图象经过点(,2)4π,所以()2sin(2)2434f ϕππ=⨯+=,即sin()16πϕ+=,因为02πϕ<<,所以2663ϕπππ<+<,所以62ππϕ+=,解得3πϕ=,所以()2sin 23()3f x x π=+,故A 正确;因为2377()2sin[()]2sin(2)0223f πππ-=⨯-+=-π=,所以()f x 的图象的一个对称中心为7(,0)2π-,故B 正确; 令2222332πππk πx k π-≤+≤+,k Z ∈,解得5ππ3π3π44k x k -≤≤+,k Z ∈,所以()f x 的单调递增区间是5[3,3]44k k πππ-π+,k Z ∈,故C 错误; 把π()2sin()3g x x =+的图象上所有点的横坐标变为原来的23,纵坐标不变,可得到32sin()23y x π=+的图象,故D 错误.故选:AB . 【点睛】(1)利用图像求三角函数解析式的方法:①求A 通常用最大值或最小值;①求ω通常用周期;①求φ通常利用函数上的点带入即可求解.(2)三角函数问题通常需要先求出系数A 、ω、φ或把它化为“一角一名一次”的结构,借助于sin y x =或cos y x =的性质解题.13.已知函数1π()sin()(0,0,0)22f x A x A ωϕωϕ=+>><<在一个周期内的图象如图所示,则( )A .该函数图象的一个对称中心为(π,0)B .π()2sin()323f x x =+C .该函数的单调递增区间是5ππ[3π,3π],44k k k Z --∈ D .把函数π()2sin()3g x x =+图象上所有点的横坐标变为原来的23,纵坐标不变,可得函数f (x )的图象 【答案】AB 【分析】根据图像求出()f x 的解析式,借助于正弦函数的性质一一验证: 对于A ,由图象可以直接判断;对于B ,根据图像求出()f x 的解析式进行判断; 对于C ,求出单增区间进行判断; 对于D ,利用图像变换判断. 【详解】对于A ,由图象可以看出,该函数图象的一个对称中心为(π,0),故A 正确; 对于B ,由题图可知2A =,函数f (x )的最小正周期为π4(π)3π4⨯-=,故2π4π43π,132T ωωω====,即()2sin(23f x x =)ϕ+,代入最高点π(,2)4,即πππ22sin()sin()134632ϕϕϕ,=⨯+⇒+==,故π()2sin()323f x x =+,故B 正确;对于C ,单调递增区间需满足π2ππ2π2π2332k x k -≤+≤+,解得5ππ[3π,3π],44x k k k Z ∈-+∈,故C 错误; 对于D ,把函数π()2sin()3g x x =+的图象上所有点的横坐标变为原来的23,纵坐标不变,可得到函数3π2sin()23y x =+的图象.故D 错误.故选:AB . 【点睛】(1)利用图像求三角函数解析式的方法:①求A 通常用最大值或最小值;①求ω通常用周期;①求φ通常利用函数上的点带入即可求解.(2)三角函数问题通常需要先求出系数A 、ω、φ或把它化为“一角一名一次”的结构,借助于sin y x =或cos y x =的性质解题.14.已知函数()()cos 2f x A x b ϕ=++(0A >,0ϕπ<<)的部分图像如图所示,则( )A .2A =B .点7,112π⎛⎫⎪⎝⎭是()f x 图像的一个对称中心 C .6π=ϕ D .直线3x π=是()f x 图像的一条对称轴【答案】ABD 【分析】由图知函数最大值为3,最小值为1-,且函数图像与y 轴的交点为()0,2,进而待定系数得()2cos 213f x x π⎛⎫=++ ⎪⎝⎭,再整体换元讨论B,D 选项即可. 【详解】因为0A >,所以31A b A b +=⎧⎨-+=-⎩,解得21A b =⎧⎨=⎩,故A 正确;()02cos 12f ϕ=+=,则1cos 2ϕ=.又0ϕπ<<,所以3πϕ=,故C 错误;()2cos 213f x x π⎛⎫=++ ⎪⎝⎭,令23x k ππ+=,k ∈Z ,解得62πk πx =-+,k ∈Z , 所以()f x 图像的对称轴方程为62πk πx =-+, 令1k =,则3x π=,D 正确;令232x k πππ+=+,k ∈Z ,解得122k x ππ=+,k ∈Z ,令1k =,则712x π=且7112f π⎛⎫= ⎪⎝⎭,故B 正确. 故选:ABD 【点睛】本题考查三角函数图像求解析式,三角函数的对称轴,对称中心等,考查运算求解能力,是中档题.解题的过程中,需要注意形如()()sin 0y A x B A ωϕ=++>,()()cos 0y A x B A ωϕ=++>,max min ,y A B y A B =+=-+,ϕ的求解通常采用待定系数法求解.第II 卷(非选择题)三、填空题15.已知()()4sin sin 0,22f x x x ππωϕωϕωϕ⎛⎫⎛⎫=+++><⎪⎪⎝⎭⎝⎭,如图是()y f x =的部分图象,则ϕ=___________;()f x 在区间[]0,2020π内有___________条对称轴.【答案】6π8080 【分析】先化简,得到函数解析式,根据图像求得函数中的参数值,由此判断在给定区间内的对称轴. 【详解】()()()4sin sin 2sin 222f x x x x πωϕωϕωϕ⎛⎫=+++=+ ⎪⎝⎭,由图可知()0f =()sin 22ϕ=,由于(在单调递增的区间内,故223k πϕπ=+,k ∈Z ,解得6k πϕπ=+,k ∈Z ,根据题意知6π=ϕ; 由图象过点5,012π⎛⎫⎪⎝⎭,则有5263ππωπ+=;解得2ω=.故()2sin 43πf x x ⎛⎫=+⎪⎝⎭,则令432x k πππ+=+,k ∈Z , 解得244k x ππ=+,k ∈Z . 令02020244k πππ≤+≤,即11808066k -≤≤-. ()f x 在[]0,2020π内有8080条对称轴.故答案为:6π;8080. 【点睛】方法点睛:根据函数图像求得参数,从而求得相关性质. 16.已知函数()()sin f x A x =+ωϕ0,0,2A πωϕ⎛⎫>>< ⎪⎝⎭的部分图象如图所示,则函数()f x 的解析式为____________.【答案】()2sin 26f x x π⎛⎫=+ ⎪⎝⎭【分析】由函数的最值求出A ,由周期求出ω,由图像经过23π⎛⎫⎪⎝⎭,-2及2πϕ<求出ϕ,即可得到()f x 的解析式. 【详解】由最小值为-2知:A=2;由32343124T πππ⎛⎫=--= ⎪⎝⎭得,T π=,所以222T ππωπ===; 由223f π⎛⎫=-⎪⎝⎭得:232=232k ππϕπ⨯++,又2πϕ<, 解得:6π=ϕ. 即()2sin 26f x x π⎛⎫=+⎪⎝⎭. 故答案为:()2sin 26f x x π⎛⎫=+ ⎪⎝⎭【点睛】求三角函数解析式的方法:(1)求A 通常用最大值或最小值; (2)求ω通常用周期;(3)求φ通常利用函数上的点带入即可求解.四、解答题17.已知函数()sin()0,0,22f x M x M ππωϕωϕ⎛⎫=+>>-<<⎪⎝⎭的部分图象如图所示.(1)求()f x 的解析式;(2)在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若2b ac =,求()f B 的取值范围.【答案】(1)()2sin 23f x x π⎛⎫=- ⎪⎝⎭;(2)(. 【分析】(1)由图得出最大值和周期,由此求出,M T ,代入最高点坐标求出ϕ,由此求出解析式(2)由基本不等式求出cos B 的取值范围,从而求出B 角取值范围,再结合三角函数性质求解()f B 范围即可. 【详解】(1)由图知2M =,115212122T πππ=-=, ①T π=,22Tπω==.522()122k k Z ππϕπ⨯+=+∈, 又22ππϕ-<<,①3πϕ=-,①()2sin 23f x x π⎛⎫=-⎪⎝⎭. (2)①22221cos 222a cb ac ac B ac ac +--=≥=,当且仅当a c =取“=”,①(0,)B π∈, ①0,3B π⎛⎤∈ ⎥⎝⎦,①2,333B πππ⎛⎤-∈- ⎥⎝⎦,①(()2sin 23f B B π⎛⎫=-∈ ⎪⎝⎭. 【点睛】求三角函数的解析式时,由2Tπω=即可求出ω;确定ϕ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标0x ,则令00x ωϕ+=或0x ωϕπ+=),即可求出ϕ,否则需要代入点的坐标,利用一些已知点的坐标代入解析式,再结合函数的性质解出ω和ϕ,若对,A ω的符号或对ϕ的范围有要求,则可用诱导公式变换使其符合要求. 18.已知函数()()sin (0,0,02)f x A x A ωϕωϕπ=+>><<的部分图象如图所示.(1)求函数()f x 的解析式;(2)若()()()()0,g x f x t t π=+∈为偶函数,求t 的值. (3)若()(),0,64h x f x f x x ππ⎛⎫⎡⎤=⋅-∈ ⎪⎢⎥⎝⎭⎣⎦,求()h x 的取值范围.【答案】(1)()23f x x π⎛⎫=+ ⎪⎝⎭;(2)12π或712π;(3)90,4⎡⎤⎢⎥⎣⎦【分析】(1)由图可先得出A 和T ,即可求出ω,再利用712f π⎛⎫= ⎪⎝⎭ϕ即可得出解析式;(2)可得()223t x x g π⎛⎫++ ⎪⎝⎭=,令2,32t k k Z πππ+=+∈即可求出;(3)利用三角恒等变换可化简得出()33sin 4264h x x π⎛⎫=-+ ⎪⎝⎭,再根据x 的取值范围即可求出. 【详解】(1)由图可得A =37341264T πππ⎛⎫=--= ⎪⎝⎭,T π∴=, 22πωπ∴==,则()()2f x x ϕ=+,又7721212f ππϕ⎛⎫⎛⎫=⨯+=⎪⎪⎝⎭⎝⎭2,3k k Z πϕπ=+∈,02,3πϕ∴=,()23f x x π⎛⎫∴=+ ⎪⎝⎭;(2)()()223x g t x f x t π⎛⎫++== ⎝+⎪⎭为偶函数,2,32t k k Z πππ∴+=+∈,解得,122k t k Z ππ=+∈, ()0,t π∈,t ∴=12π或712π; (3)()()6h x f x f x π⎛⎫=⋅-⎪⎝⎭22363x x πππ⎡⎤⎛⎫⎛⎫=+-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦3sin 2sin 23x x π⎛⎫=+ ⎪⎝⎭3sin 2cos cos 2sin sin 233x x x ππ⎛⎫=+ ⎪⎝⎭23sin 22cos 222x x x =+334cos 4444x x =-+ 33sin 4264x π⎛⎫=-+ ⎪⎝⎭, 0,4x π⎡⎤∈⎢⎥⎣⎦,54,666x πππ⎡⎤∴-∈-⎢⎥⎣⎦,则当466x ππ-=-时,()h x 取得最小值为0,当462x ππ-=时,()h x 取得最大值为94, ∴()h x 的取值范围为90,4⎡⎤⎢⎥⎣⎦【点睛】方法点睛:根据三角函数()()sin f x A x =+ωϕ部分图象求解析式的方法: (1)根据图象的最值可求出A ; (2)求出函数的周期,利用2T πω=求出ω;(3)取点代入函数可求得ϕ.19.函数()()cos 0,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的部分图象如图所示.(1)求()f x 的最小正周期和单调递增区间; (2)若,312ππα⎡⎤∈--⎢⎥⎣⎦,()35f α=,求6f πα⎛⎫- ⎪⎝⎭的值.【答案】(1)T π=,()5,1212k k k z ππππ⎡⎤-+∈⎢⎥⎣⎦;(2 【分析】(1)由给定的函数()f x 的图象,得到周期T π=,求得2ω=,再结合()112f π=,求得6πϕ=-,得到()cos(2)6f x x π=-,结合三角函数的性质,即可求解.(2)由()35f α=,利用三角函数的基本关系式,求得4sin 265πα⎛⎫-=- ⎪⎝⎭,结合两角和的正弦公式,即可求解. 【详解】(1)根据给定的函数()f x 的图象,可得35346124T πππ=-=,可得最小正周期为T π=由2T πω=,可得2ω=,所以()()cos 2f x x φ=+,又由()cos()1126f ππϕ=+=,可得22,12k k Z πϕπ⨯+=∈, 又因为2πϕ<,所以6πϕ=-,所以()cos(2)6f x x π=-,令222,6k x k k Z ππππ-≤-≤∈,解得5,1212k x k k Z ππππ-<<+∈,所以函数()f x 的单调递增区间为()5,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. (2)由()3cos 235f παα⎛⎫=+= ⎪⎝⎭, 因为,312ππα⎡⎤∈--⎢⎥⎣⎦,可得52,663πππα⎡⎤-∈--⎢⎥⎣⎦,所以4sin 265πα⎛⎫-=- ⎪⎝⎭, 则()cos 2sin 2sin 26266f ππππαααα⎛⎫⎛⎫⎛⎫-=-==-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭3sin 2cos cos 2sin 666610ππππαα-⎛⎫⎛⎫=-+-= ⎪ ⎪⎝⎭⎝⎭. 【点睛】由三角函数的图象确定三角函数的解析式的策略: (1)A 主要是根据图象的最高点或最低点的纵坐标确定;(2)w 的值主要由周期T 的值确定,而T 的值的确定主要是根据图象的零点与最值点的横坐标确定;(3)ϕ值的确定主要是由图象的特殊点的坐标确定.。
人教版高中数学必修第一册第五单元《三角函数》测试(答案解析)(2)

一、选择题1.将函数sin 4y x π⎛⎫=- ⎪⎝⎭的图像上所有点的横坐标变为原来的2倍(纵坐标不变),再将所得的图像向左平移π6个单位,则所得图像对应的解析式为( ) A .sin 212y x π⎛⎫=+ ⎪⎝⎭B .sin 212y x π⎛⎫=- ⎪⎝⎭C .sin 26x y π⎛⎫=-⎪⎝⎭ D .sin 212x y π⎛⎫=-⎪⎝⎭ 2.若函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭的图象的相邻两条对称轴之间的距离为2π,且该函数图象关于点()0,0x 成中心对称,00,2x π⎡⎤∈⎢⎥⎣⎦,则0x 等于( ) A .512π B .4π C .3π D .6π3.已知()0,πα∈,2sin cos 1αα+=,则cos 21sin 2αα=-( ) A .2425-B .725-C .7-D .17-4.已知3sin 5α=-,则cos2=α( ) A .15-B .15C .725-D .7255.已知函数()()2sin ,0,2f x x x x π=∈⎛⎫⎡⎤ ⎪⎢⎥⎣⎦⎝⎭,则()f x 的单调递增区间是( ) A .06,π⎡⎤⎢⎥⎣⎦B .0,4⎡⎤⎢⎥⎣⎦πC .0,3π⎡⎤⎢⎥⎣⎦D .0,2π⎡⎤⎢⎥⎣⎦6.已知函数()()sin 20,2f x A x A πϕϕ⎛⎫=+>< ⎪⎝⎭满足03f π⎛⎫=⎪⎝⎭,则()f x 图象的一条对称轴是( ) A .6x π=B .56x π=C .512x π=D .712x π=7.已知函数()cos 2cos sin(2)sin f x x x ϕπϕ=⋅-+⋅在3x π=处取得最小值,则函数()f x 的一个单调递减区间为( )A .4,33ππ⎛⎫⎪⎝⎭B .2,33ππ⎛⎫-⎪⎝⎭ C .5,36ππ⎛⎫⎪⎝⎭D .,63ππ⎛⎫-⎪⎝⎭ 8.sin15cos15+=( ) A .12B .22C .32D .629.已知函数()()ππ36sin 0f x A x A ⎛⎫=> ⎪⎝⎭+在它的一个最小正周期内的图像上,最高点与最低点的距离是5,则A 等于( ). A .1B .2C .2.5D .410.()()sin f x A x =+ωϕ0,0,2A πωϕ⎛⎫>>< ⎪⎝⎭的部分图象如图所示,若将函数()f x 的图象向右平移2π个单位长度,得到函数()g x 的图象,则( )A .()12sin 212g x x π⎛⎫=- ⎪⎝⎭ B .()12sin 212g x x π⎛⎫=+⎪⎝⎭ C .()2sin 212g x x π⎛⎫=- ⎪⎝⎭ D .()2sin 212g x x π⎛⎫=+⎪⎝⎭11.已知函数()y f x =的图象如图所示,则此函数可能是( )A .sin 6()22x x x f x -=- B .sin 6()22x x x f x -=- C .cos6()22x xx f x -=- D .cos6()22x x xf x -=-12.已知某扇形的弧长为32π,圆心角为2π,则该扇形的面积为( ) A .4π B .6π C .2π D .94π 二、填空题13.已知()0,απ∈且tan 3α=,则cos α=______. 14.已知()tan 3πα+=,则2tan 2sin αα-的值为_______.15.已知α、β均为锐角,且sin 10α=,()cos 5αβ+=,则cos 2β=_______________16.下列函数中,以π2为周期且在区间ππ,42⎛⎫⎪⎝⎭单调递增的是______.①()cos2f x x =;②()sin 2f x x =;③()cos f x x =;④()sin f x x = 17.若函数()|2cos |f x a x =+的最小正周期为π,则实数a 的值为____.18.方程21sin cos 2x x x =在[0,]4π上的解为___________19.已知函数()cos 2f x x =,若12,x x 满足12|()()|2f x f x -=,则12||x x -的一个取值为________. 20.若0,2x π⎛⎫∀∈ ⎪⎝⎭,sin cos m x x ≥+恒成立,则m 的取值范围为_______________. 三、解答题21.已知函数()()0,22f x x ππωϕωϕ⎛⎫=+>-≤<⎪⎝⎭的图象关于直线3x π=对称,且图象上相邻两个最高点的距离为π. (1)求ω和ϕ的值;(2)当0,2x π⎡⎤∈⎢⎥⎣⎦时,求函数()y f x =的最大值和最小值. 22.已知向量2(cos ,sin )m x a x =,(3,cos )n x =-,函数3()f x m n =⋅-. (1)若1a =,当[0,]2x π∈时,求()f x 的值域; (2)若()f x 为偶函数,求方程3()4f x =-在区间[,]-ππ上的解.23.已知 3sin 5α=,12cos 13,,2παπ⎛⎫∈ ⎪⎝⎭,3,2πβπ⎛⎫∈ ⎪⎝⎭求sin()αβ+,cos()αβ-,tan2α的值. 24.已知函数25()23sin cos()2cos (0)32f x wx wx wx w π=+-+>的图像上相邻的两个最低点的距离为π. (1)求w 的值;(2)求函数()f x 的单调递增区间.25.在①函数()()sin 20,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的图象向右平移6π个单位长度得到()g x 的图像,()g x 图像关于,012π⎛⎫⎪⎝⎭对称;②函数()()12cos sin 062f x x x πωωω⎛⎫=+-> ⎪⎝⎭这两个条件中任选一个,补充在下而问题中,并解答.已知______,函数()f x 的图象相邻两条对称轴之间的距离为2π. (1)若()f x 在[]0,α上的值域为1,12⎡⎤⎢⎥⎣⎦,求a 的取值范围; (2)求函数()f x 在[]0,2π上的单调递增区间.26.如图,扇形ABC 是一块半径为2千米,圆心角为60的风景区,P 点在弧BC 上,现欲在风景区中规划三条商业街道,要求街道PQ 与AB 垂直,街道PR 与AC 垂直,线段RQ 表示第三条街道.(1)如果P 位于弧BC 的中点,求三条街道的总长度;(2)由于环境的原因,三条街道PQ 、PR 、RQ 每年能产生的经济效益分别为每千米300万元、200万元及400万元,问:这三条街道每年能产生的经济总效益最高为多少?【参考答案】***试卷处理标记,请不要删除一、选择题1.C 解析:C 【分析】根据正弦型函数的图像的变换规律进行求解即可. 【详解】 将函数sin 4y x π⎛⎫=-⎪⎝⎭的图像上所有点的横坐标变为原来的2倍(纵坐标不变),所得到的函数的解析式为:sin 24x y π⎛⎫=-⎪⎝⎭,将sin 24x y π⎛⎫=- ⎪⎝⎭的图像向左平移π6个单位,得到的函数的解析式为:1sin[]264y x ππ⎛⎫=+- ⎪⎝⎭,化简得:sin 26x y π⎛⎫=- ⎪⎝⎭. 故选:C2.A解析:A 【分析】由已知条件求得函数()f x 的最小正周期T ,可求得ω的值,再由已知可得()026x k k Z ππ+=∈,结合00,2x π⎡⎤∈⎢⎥⎣⎦可求得0x 的值. 【详解】由题意可知,函数()f x 的最小正周期T 满足22T π=,T π∴=,22T πω∴==,()sin 26f x x π⎛⎫∴=+ ⎪⎝⎭,由于函数()f x 的图象关于点()0,0x 成中心对称,则()026x k k Z ππ+=∈,解得()0212k x k Z ππ=-∈, 由于00,2x π⎡⎤∈⎢⎥⎣⎦,解得0512x π=. 故选:A. 【点睛】结论点睛:利用正弦型函数的对称性求参数,可利用以下原则来进行: (1)函数()()sin f x A x =+ωϕ关于直线0x x =对称()02x k k Z πωϕπ⇔+=+∈;(2)函数()()sin f x A x =+ωϕ关于点()0,0x 对称()0x k k Z ωϕπ⇔+=∈.3.D解析:D 【分析】利用22sin cos 1αα+=以及2sin cos 1αα+=解出sin α,cos α的值,再利用二倍角公式化简即可求解. 【详解】因为2sin cos 1αα+=,所以cos 12sin αα=-, 代入22sin cos 1αα+=得()22sin 12sin 1αα+-=, 因为()0,πα∈,所以4sin 5α,所以43cos 12sin 1255αα=-=-⨯=-,所以4324sin 22sin cos 25525ααα⎛⎫==⨯⨯-=- ⎪⎝⎭, 2247cos 212sin 12525αα⎛⎫=-=-⨯=- ⎪⎝⎭cos 211sin 2717252425αα-==--⎛⎫- ⎪⎭-⎝, 故选:D 【点睛】关键点点睛:本题的关键点是熟记同角三角函数基本关系,以及三角函数值在每个象限内的符号,熟记正余弦的二倍角公式,计算仔细.4.D解析:D 【分析】由题中条件,根据二倍角的余弦公式,可直接得出结果. 【详解】 因为3sin 5α=-, 所以297cos 212sin 122525αα=-=-⨯=. 故选:D.5.A解析:A 【分析】根据三角恒等变换公式化简()f x ,结合x 的范围,可得选项. 【详解】因为()()2sin ,0,2f x x x x π=+∈⎛⎫⎡⎤ ⎪⎢⎥⎣⎦⎝⎭,所以 ()()222sin sin cos +3cos f x x xx x x x +==222cos +12cos 2+22sin 2+26x x x x x π⎛⎫=+=+=+ ⎪⎝⎭,因为0,2x π⎡⎤∈⎢⎥⎣⎦,所以72+,666x πππ∈⎡⎤⎢⎥⎣⎦,所以由2+662x πππ≤≤,解得06x π≤≤, 所以()f x 的单调递增区间是06,π⎡⎤⎢⎥⎣⎦,故选:A.6.D解析:D 【分析】利用三角函数的性质,2()sin()033f A ππϕ=+=,求ϕ,然后,令()f x A =,即可求解 【详解】根据题意得,2()sin()033f A ππϕ=+=,得23k πϕπ+=,k z ∈又因为2πϕ<,进而求得,3πϕ=,所以,()sin(2)3f x A x π=+,令()f x A =,所以,sin(2)13x π+=,所以,2,32x k k z πππ+=+∈,解得,k x k z 122ππ=+∈,当1k =时,712x π=,所以,()f x 图象的一条对称轴是712x π= 故选D 【点睛】关键点睛:求出ϕ后,令()f x A =,所以,sin(2)13x π+=,进而求解,属于中档题7.D解析:D 【分析】先化简()f x 并根据已知条件确定出ϕ的一个可取值,然后根据余弦函数的单调递减区间求解出()f x 的一个单调递减区间. 【详解】 因为()()()cos2cos sin 2sin cos2cos sin 2sin cos 2f x x x x x x ϕπϕϕϕϕ=⋅-+⋅=⋅+⋅=-,且()f x 在3x π=处有最小值,所以2cos 133f ππϕ⎛⎫⎛⎫=-=-⎪ ⎪⎝⎭⎝⎭,所以22,3k k Z πϕππ-=+∈, 所以2,3k k Z πϕπ=--∈,取ϕ的一个值为3π-, 所以()cos 23f x x π⎛⎫=+ ⎪⎝⎭,令222,3k x k k Z ππππ≤+≤+∈,所以,63k x k k Z ππππ-≤≤+∈,令0k =,所以此时单调递减区间为,63ππ⎡⎤-⎢⎥⎣⎦, 故选:D. 【点睛】思路点睛:求解形如()()cos f x A x ωϕ=+的函数的单调递减区间的步骤如下: (1)先令[]2,2+,k k k x Z ωϕπππ+∈∈;(2)解上述不等式求解出x 的取值范围即为()f x 的单调递减区间.8.D解析:D 【分析】由辅助角公式可直接计算得到结果. 【详解】()6sin15cos152sin 15452sin 60+=+==. 故选:D.9.B解析:B【分析】根据正弦型函数图象性质确定函数()f x 的最小正周期T ,再根据最高点与最低点的距离是55=,从而解得A 的值. 【详解】解:函数()()ππ36sin 0f x A x A ⎛⎫=> ⎪⎝⎭+的最小正周期2263T πππω=== 函数()()ππ36sin 0f x A x A ⎛⎫=>⎪⎝⎭+在它的一个最小正周期内的图像上,最高点与最低点的距离是5,5=,解得2A =.故选:B. 【点睛】对于三角函数,求最小正周期和最值时可先把所给三角函数式化为()sin y A ωx φ=+或()cos y A x ωϕ=+的形式,则最小正周期为2T ωπ=,最大值为A ,最小值为A -;奇偶性的判断关键是解析式是否为sin y A x ω=或cos y A x ω=的形式.10.A解析:A 【分析】根据图象易得2A =,最小正周期T 2433ππ⎛⎫=-- ⎪⎝⎭,进而求得ω,再由图象过点2,23π⎛⎫⎪⎝⎭求得函数()f x ,然后再根据平移变换得到()g x 即可. 【详解】由图象可知2A =,最小正周期2T 4433πππ⎡⎤⎛⎫=--= ⎪⎢⎥⎝⎭⎣⎦, ∴212T πω==,1()2sin 2f x x ϕ⎛⎫=+ ⎪⎝⎭, 又22sin 233f ππϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭,∴232k ππϕπ+=+,26k πϕπ=+,∵||2ϕπ<,∴6π=ϕ,1()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,将其图象向右平移2π个单位长度得 11()2sin 2sin 226212g x x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故选:A 11.D解析:D 【分析】由函数图象可得()y f x =是奇函数,且当x 从右趋近于0时,()0f x >,依次判断每个函数即可得出.【详解】由函数图象可得()y f x =是奇函数,且当x 从右趋近于0时,()0f x >,对于A ,当x 从右趋近于0时,sin60x >,22x x -<,故()0f x <,不符合题意,故A 错误; 对于B ,()()sin 6sin 6()2222x x x xx xf x f x ----===--,()f x ∴是偶函数,不符合题意,故B 错误; 对于C ,()()cos 6cos 6()2222x x x xx xf x f x ----===--,()f x ∴是偶函数,不符合题意,故C 错误; 对于D ,()()cos 6cos 6()2222x x x xx xf x f x ----===---,()f x ∴是奇函数,当x 从右趋近于0时,cos60x >,22x x ->,()0f x ∴>,符合题意,故D 正确. 故选:D. 【点睛】思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.12.D解析:D 【分析】由弧长公式求出3r =,再由扇形的面积公式求出答案. 【详解】扇形的圆心角322l r r ππθ===,所以3r =,则扇形的面积113932224S lr ππ==⨯⨯=. 故选:D. 二、填空题13.【分析】本题考查同角三角函数及其关系借助公式求解即可求解时需要判定符号的正负【详解】解:法一:由可得代入解得因为所以所以法二:由且可取终边上的一点坐标为根据三角函数终边定义公式故答案为:【点睛】方法解析:10【分析】本题考查同角三角函数及其关系,借助公式sin tan cos ααα=,22sin +cos =1αα求解即可,求解时需要判定符号的正负. 【详解】解:法一:由sin tan =3cos ααα=可得sin =3cos αα,代入22sin +cos =1αα解得cos α= 因为()0,tan 30απα∈=>,,所以0,2πα⎛⎫∈ ⎪⎝⎭,所以cos α=. 法二:由()0,απ∈且tan 3α=可取α终边上的一点坐标为(1,3),根据三角函数终边定义公式cos 10α===.【点睛】方法点睛:同角三角函数基本关系的3个应用技巧: (1)弦切互化利用公式sin tan ()cos 2k απααπα=≠+实现角α的弦切互化; (2)和(差)积转换利用2(sin cos )=1sin 2ααα±±进行变形、转化;(3)巧用“1”的变换22222211sin+cos =cos (tan 1)sin (1)tan αααααα=+=+. 14.【分析】利用诱导公式求出再利用二倍角公式求出以及同角三角函数的基本关系求出即可得解;【详解】解:由题意所以所以所以故答案为: 解析:3320-【分析】利用诱导公式求出tan α,再利用二倍角公式求出tan2α,以及同角三角函数的基本关系求出2sin α,即可得解; 【详解】解:由题意()tan 3πα+=,所以tan 3α=,所以22tan 3tan 21tan 4ααα==--,222222sin tan 9sin sin cos tan 110αααααα===++,所以23933tan 2sin 41020αα-=--=-.故答案为:3320-15.【分析】先由题意得到求出根据由两角差的余弦公式求出再由二倍角公式即可求出结果【详解】因为均为锐角所以又所以所以则故答案为:解析:45【分析】先由题意得到,0,2πα⎛⎫∈ ⎪⎝⎭,0,2πβ⎛⎫∈ ⎪⎝⎭,()0,αβπ+∈,求出sin 10α=,()cos 5αβ+=,根据()cos cos βαβα=+-,由两角差的余弦公式,求出cos β,再由二倍角公式,即可求出结果. 【详解】因为α、β均为锐角,所以0,2πα⎛⎫∈ ⎪⎝⎭,0,2πβ⎛⎫∈ ⎪⎝⎭,()0,αβπ+∈,又sin 10α=,()cos 5αβ+=,所以cos 10α==,()sin 5αβ+==, 所以()()()cos cos cos cos sin sin βαβααβααβα=+-=+++==, 则294cos 22cos 1155ββ=-=-=. 故答案为:45. 16.①【分析】利用与的关系确定①②的周期在给定区间上去掉绝对值符号后确定单调性化简和后可得其性质从而判断③④【详解】周期是时是增函数①满足题意;周期是时是减函数②不满足题意;周期是③不满足题意;不是周期解析:① 【分析】利用()f x 与()f x 的关系确定①②的周期,在给定区间上去掉绝对值符号后确定单调性,化简cos x 和sin x 后可得其性质,从而判断③④【详解】()cos2f x x =周期是2π,,42x ππ⎛⎫∈ ⎪⎝⎭时,()cos2cos2f x x x ==-是增函数,①满足题意;()sin 2f x x =周期是2π,,42x ππ⎛⎫∈ ⎪⎝⎭时,()sin 2sin 2f x x x ==是减函数,②不满足题意;()cos cos f x x x ==,周期是2π,③不满足题意; sin ,0()sin sin ,0x x f x x x x ≥⎧==⎨-<⎩不是周期函数,④不满足题意.故答案为:①. 【点睛】结论点睛:本题考查三角函数的周期性与单调性,解题时可利用如下结论:①()sin()f x A x ωϕ=+(或cos()A x ωϕ+,函数()y f x =的周期是函数()y f x =周期的一半;②sin y x ω=不是周期函数.17.【分析】利用来求解【详解】因为函数的最小正周期为所以都有成立故则故答案为: 解析:0【分析】利用()()f x f x π=+来求解. 【详解】因为函数()f x 的最小正周期为π,所以x R ∀∈,都有()()f x f x π=+成立, 故()2cos 2cos 2cos a x a x a x π+=++=-,则0a =. 故答案为:0.18.【分析】由二倍角公式和两角差的正弦公式化简变形后由正弦函数性质得出结论【详解】由得得∴又∴故答案为:【点睛】方法点睛:本题考查求解三角方程解题方法:(1)利用三角函数的恒等变换公式化方程为的形式然后解析:12π 【分析】 由二倍角公式和两角差的正弦公式化简变形后由正弦函数性质得出结论. 【详解】由21sin cos 2x x x =得1cos 21222x x -+=,得sin 206x π⎛⎫-= ⎪⎝⎭,∴26x k ππ-=,,212k x k Z ππ=+∈,又0,4x π⎡⎤∈⎢⎥⎣⎦,∴12x π=. 故答案为:12π.【点睛】方法点睛:本题考查求解三角方程,解题方法:(1)利用三角函数的恒等变换公式化方程为sin()x k ωϕ+=的形式,然后由正弦函数的定义得出结论.(2)用换元法,如设sin x t =,先求得方程()0f t =的解0t ,然后再解方程0sin x t =.19.(答案不唯一)【分析】根据的值域为可知若满足则必有的值分别为再根据三角函数的性质分析即可【详解】因为的值域为故若满足则必有的值分别为故的最小值当且仅当为相邻的两个最值点取得此时为的半个周期即故答案为解析:π2(答案不唯一) 【分析】根据()cos2f x x =的值域为[]1,1-可知若12,x x 满足()()122f x f x -=则必有()()12,f x f x 的值分别为±1,再根据三角函数的性质分析即可.【详解】因为()cos2f x x =的值域为[]1,1-,故若12,x x 满足()()122f x f x -=则必有()()12,f x f x 的值分别为±1,故12x x -的最小值当且仅当12,x x 为()cos2f x x =相邻的两个最值点取得.此时12x x -为()cos2f x x =的半个周期,即12222ππ⨯=. 故答案为:2π【点睛】关键点点睛:相邻的两个最值点的横坐标的距离为半个周期是解题的突破点.20.【分析】根据三角函数的性质求得的最大值进而可求出结果【详解】因为由可得所以则因为恒成立所以只需故答案为:解析:)+∞【分析】根据三角函数的性质,求得sin cos x x +的最大值,进而可求出结果. 【详解】因为sin cos 4x x x π⎛⎫+=+ ⎪⎝⎭,由0,2x π⎛⎫∈ ⎪⎝⎭可得3,444x πππ⎛⎫+∈ ⎪⎝⎭,所以sin 42x π⎛⎤⎛⎫+∈ ⎥ ⎪ ⎝⎭⎝⎦,则(sin cos 4x x x π⎛⎫+=+∈ ⎪⎝⎭,因为0,2x π⎛⎫∀∈ ⎪⎝⎭,sin cos m x x ≥+恒成立,所以只需m ≥故答案为:)+∞.三、解答题21.(1)2ω=,6πϕ=-;(2)max ()f x =min ()2f x =-. 【分析】(1)由图象上相邻两个最高点的距离为π得()f x 的最小正周期T π=,故2ω=,由函数图象关于直线3x π=对称得232k ππϕπ⨯+=+,k Z ∈,再结合范围得6πϕ=-;(2)由(1)得()26f x x π⎛⎫=- ⎪⎝⎭,进而得52666x πππ-≤-≤,再结合正弦函数的性质即可得答案. 【详解】(1)因为()f x 的图象上相邻两个最高点的距离为π, 所以()f x 的最小正周期T π=,从而22Tπω==. 又因为()f x 的图象关于直线3x π=对称,所以232k ππϕπ⨯+=+,k Z ∈,又22ππϕ-≤<,所以2236ππϕπ=-=-. 综上,2ω=,6πϕ=-.(2)由(1)知()26f x x π⎛⎫=- ⎪⎝⎭.当0,2x π⎡⎤∈⎢⎥⎣⎦时,可知52666x πππ-≤-≤.故当226x ππ-=,即3x π=时,max ()f x =当266x ππ-=-,即0x =时,min ()f x =. 【点睛】本题解题的关键在于先根据0,2x π⎡⎤∈⎢⎥⎣⎦得52666x πππ-≤-≤,进而结合正弦函数的性质,采用整体思想求解,考查运算求解能力,是中档题.22.(1)[-;(2)75,1212x ππ=±±. 【分析】(1)将()f x 化为()cos(2)6f x x π=+,然后可得答案; (2)由()f x 为偶函数可求出0a =,然后可得答案. 【详解】(1)2()sin cos 2sin 2222a f x x a x x x x =--=-当1a =,1()cos 2sin 2cos(2)226f x x x x π=-=+由7[0,],2[,],cos(2)[1,266662x x x πππππ∈∴+∈∴+∈-所以()f x 的值域为[-(2)若()f x 为偶函数,则()()f x f x -=恒成立2sin 22sin 222a a x x x x +=-成立,整理得sin 20,0a x a =∴=所以由3()24f x x ==-得cos 22x =-又752[2,2],,1212x x ππππ∈-∴=±± 23.1665-;3365;247- 【分析】由已知条件,利用同角三角函数基本关系结合角所在的象限求出cos α,sin β,以及tan α的值,再利用两角和的正弦公式,两角差的余弦公式,正切的二倍角公式即可求解.【详解】 因为,2παπ⎛⎫∈⎪⎝⎭,3sin 5α=,所以4cos 5α===-,因为3,2πβπ⎛⎫∈ ⎪⎝⎭,12cos 13,所以5sin13β===-,所以3124516 sin()sin cos cos sin51351365αβαβαβ⎛⎫⎛⎫⎛⎫+=+=⨯-+-⨯-=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,4123533cos()cos cos sin sin51351365αβαβαβ⎛⎫⎛⎫⎛⎫-=+=-⨯-+⨯-=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因为sin3tancos4ααα==-,所以22322tan244tan21tan7314ααα⎛⎫⨯-⎪⎝⎭===--⎛⎫-- ⎪⎝⎭,综上所述:16sin()65αβ+=-,33cos()65αβ-=,24tan27α=-.24.(1)1;(2)()36k k k Zππππ⎡⎤-++∈⎢⎥⎣⎦,.【分析】本题考查三角函数的图像和性质、三角恒等变换,根据三角恒等变换公式()f x化简函数解析式,根据图像和性质求单调递增区间.【详解】(1)5()(cos cos sin sin)(1cos2)332f x wx wx wx wxππ=--++23sin23sin cos222wx wx wx=--+1cos2323cos222wxwx wx-=-⨯-+12cos22wx wx=+sin(2)6wxπ=+又因为()f x图象上相邻的两个最低点间的距离为π,0w>,所以22w,解得1w=.(2)据(1)求解知,()sin(2)6f x xπ=+令222()262k x k k Zπππππ-+≤+≤+∈,所以()36k x k k Zππππ-+≤≤+∈,所以所求的单调递增区间是()36k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦,.【点睛】思路点睛:三角恒等变换综合应用的解题思路:(1)利用降幂、升幂公式将()f x 化为sin cos a x b x 的形式;(2)构造())f x x x +;(3)和差公式逆用,得())f x x ϕ=+ (其中ϕ为辅助角,tan b aϕ=);(4)利用())f x x ϕ=+研究三角函数的性质; (5)反思回顾,查看关键点、易错点和答题规范. 25.(1),63ππ⎡⎤⎢⎥⎣⎦;(2)06,π⎡⎤⎢⎥⎣⎦,27,36ππ⎡⎤⎢⎥⎣⎦,5,23ππ⎡⎤⎢⎥⎣⎦.【分析】先选条件①或条件②,结合函数的性质及图像变换,求得函数()sin 26f x x π⎛⎫+ ⎝=⎪⎭,(1)由[]0,x α∈,得到2,2666x πππα⎡⎤+∈+⎢⎥⎣⎦,根据由正弦函数图像,即可求解; (2)根据函数正弦函数的形式,求得36k x k ππππ-+≤≤+,k Z ∈,进而得出函数的单调递增区间. 【详解】 方案一:选条件①由函数()f x 的图象相邻两条对称轴之间的距离为2π,可得22T ππω==,解得1ω=, 所以()()sin 2f x x ϕ=+,又由函数()f x 的图象向右平移6π个单位长度得到πsin 2φ3g x x, 又函数()g x 图象关于,012π⎛⎫⎪⎝⎭对称,可得6k πϕπ=+,k Z ∈,因为2πϕ<,所以6π=ϕ,所以()sin 26f x x π⎛⎫+ ⎝=⎪⎭.(1)由[]0,x α∈,可得2,2666x πππα⎡⎤+∈+⎢⎥⎣⎦, 因为函数()f x 在[]0,α上的值域为1,12⎡⎤⎢⎥⎣⎦,根据由正弦函数图像,可得52266ππαπ≤+≤,解得63ππα≤≤,所以α的取值范围为,63ππ⎡⎤⎢⎥⎣⎦.(2)由222262k x k πππππ-+≤+≤+,k Z ∈,可得36k x k ππππ-+≤≤+,k Z ∈,当0k =时,可得66x ππ-≤≤;当1k =时,可得2736x ππ≤≤; 当2k =时,可得51336x ππ≤≤, 所以函数()f x 在[]0,2π上的单调递增区间为06,π⎡⎤⎢⎥⎣⎦,27,36ππ⎡⎤⎢⎥⎣⎦,5,23ππ⎡⎤⎢⎥⎣⎦. 方案二:选条件②: 由()12cos sin 62f x x x πωω⎛⎫=+- ⎪⎝⎭12cos sin cos cos sin 662x x x ππωωω⎛⎫=+- ⎪⎝⎭211cos cos 2cos 2222x x x x x ωωωωω=+-=+sin 26x πω⎛⎫=+ ⎪⎝⎭,因为函数()f x 的图象相邻两条对称轴之间的距离为2π,可得22T ππω==,所以1ω=, 可得()()sin 2f x x ϕ=+, 又由函数()f x 的图象向右平移6π个单位长度得到πsin 2φ3g x x, 又函数()g x 图象关于,012π⎛⎫⎪⎝⎭对称,可得6k πϕπ=+,k Z ∈,因为2πϕ<,所以6π=ϕ,所以()sin 26f x x π⎛⎫+ ⎝=⎪⎭.(1)由[]0,x α∈,可得2,2666x πππα⎡⎤+∈+⎢⎥⎣⎦, 因为函数()f x 在[]0,α上的值域为1,12⎡⎤⎢⎥⎣⎦, 根据由正弦函数图像,可得52266ππαπ≤+≤,解得63ππα≤≤,所以α的取值范围为,63ππ⎡⎤⎢⎥⎣⎦.(2)由222262k x k πππππ-+≤+≤+,k Z ∈,可得36k x k ππππ-+≤≤+,k Z ∈,当0k =时,可得66x ππ-≤≤;当1k =时,可得2736x ππ≤≤; 当2k =时,可得51336x ππ≤≤, 所以函数()f x 在[]0,2π上的单调递增区间为06,π⎡⎤⎢⎥⎣⎦,27,36ππ⎡⎤⎢⎥⎣⎦,5,23ππ⎡⎤⎢⎥⎣⎦. 【点睛】解答三角函数图象与性质的综合问题的关键是首先将已知条件化为()sin()f x A wx ϕ=+或()cos()f x A wx ϕ=+的形式,然后再根据三角函数的基本性质,结合数形结合法的思想研究函数的性质(如:单调性、奇偶性、对称性、周期性与最值等),进而加深理解函数的极值点、最值点、零点及有界性等概念与性质.26.(1)2+(千米);(2). 【分析】(1)根据P 位于弧BC 的中点,则P 位于BAC ∠的角平分线上,然后分别在,,Rt APQ Rt APR 正AQR 中求解.(2)设PAB θ∠=,060θ<<︒,然后分别在,Rt APQ Rt APR 表示 PQ ,PR ,在AQR 中由余弦定理表RQ ,再由300200400W PQ PR RQ =⨯+⨯+⨯求解.【详解】(1)由P 位于弧BC 的中点,在P 位于BAC ∠的角平分线上, 则1||||||sin 2sin30212PQ PR PA PAB ==∠=⨯︒=⨯=,||cos 22AQ PA PAB =∠=⨯= 由60BAC ∠=︒,且AQ AR =,∴QAR 为等边三角形,则||RQ AQ ==三条街道的总长||||||112l PQ PR RQ =++=++ ; (2)设PAB θ∠=,060θ︒<<︒, 则sin 2sin PQ AP θθ==,PR AP =()()sin 602sin 603cos sin θθθθ-=-=-, cos 2cos AQ AP θθ==,||||cos(60)2cos(60)cos AR AP θθθθ=-=-=+,由余弦定理可知:2222cos60RQ AQ AR AQ AR =+-,22(2cos )(cos )22cos (cos )cos 603θθθθθθ=+-⨯+=,则|RQ =设三条街道每年能产生的经济总效益W , 300200400W PQ PR RQ =⨯+⨯+⨯,3002sin sin )200θθθ=⨯+-⨯+,400sin θθ=++200(2sin )θθ=++)θϕ=++tan 2ϕ=,当()sin 1θϕ+=时,W 取最大值,最大值为【点睛】方法点睛:解三角形应用题的两种情形:(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解;(2)实际问题经抽象概括后,已知量与未知量涉及到两个或两个以上的三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.。
1.5 正弦型函数的图像-人教A版高中数学必修四讲义(解析版)
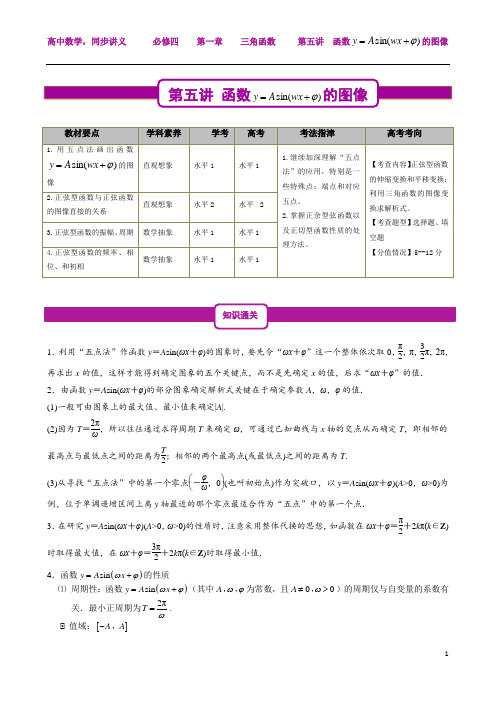
1.利用“五点法”作函数y =A sin(ωx +φ)的图象时,要先令“ωx +φ”这一个整体依次取0,π2,π,32π,2π,再求出x 的值,这样才能得到确定图象的五个关键点,而不是先确定x 的值,后求“ωx +φ”的值. 2.由函数y =A sin(ωx +φ)的部分图象确定解析式关键在于确定参数A ,ω,φ的值. (1)一般可由图象上的最大值、最小值来确定|A |.(2)因为T =2πω,所以往往通过求得周期T 来确定ω,可通过已知曲线与x 轴的交点从而确定T ,即相邻的最高点与最低点之间的距离为T2;相邻的两个最高点(或最低点)之间的距离为T .(3)从寻找“五点法”中的第一个零点⎝⎛⎭⎫-φω,0(也叫初始点)作为突破口,以y =A sin(ωx +φ)(A >0,ω>0)为例,位于单调递增区间上离y 轴最近的那个零点最适合作为“五点”中的第一个点.3.在研究y =A sin(ωx +φ)(A >0,ω>0)的性质时,注意采用整体代换的思想,如函数在ωx +φ=π2+2k π(k ∈Z )时取得最大值,在ωx +φ=3π2+2k π(k ∈Z )时取得最小值. 4.函数()sin y A x ωϕ=+的性质⑴ 周期性:函数()sin y A x ωϕ=+(其中A ωϕ,,为常数,且00A ω≠>,)的周期仅与自变量的系数有关.最小正周期为2πT ω=.⑵ 值域:[]A A -,教材要点学科素养 学考 高考 考法指津高考考向1.用五点法画出函数)sin(ϕ+=wx A y 的图像直观想象 水平1 水平11.继续加深理解“五点法”的应用,特别是一些特殊点:端点和对应五点。
2.掌握正余型弦函数以及正切型函数性质的处理方法。
【考查内容】正弦型函数的伸缩变换和平移变换; 利用三角函数的图像变换求解析式。
【考查题型】选择题、填空题【分值情况】5--12分2.正弦型函数与正弦函数的图像直接的关系直观想象 水平2 水平 23.正弦型函数的振幅、周期 数学抽象 水平1 水平14.正弦型函数的频率、相位、和初相数学抽象 水平1 水平1 第五讲 函数)sin(ϕ+=wx A y 的图像 知识通关⑶ 奇偶性:当()π k k ϕ=∈Z 时,函数()sin y A x ωϕ=+为奇函数;当()ππ 2k k ϕ=+∈Z 时,函数()sin y A x ωϕ=+为偶函数. ⑷ 单调区间:求形如()sin y A ωx φ=+或()cos y A ωx φ=+(其中0A ≠,0ω>)的函数的单调区间可以通过图象的直观性求解,或根据解不等式的方法去解答,列不等式的原则是:①把“()0ωx φω+>”视为一个“整体”.②0A >()0A <时,所列不等式的方向与()sin y x x =∈R 、()cos y x x =∈R 的单调区间对应的不等式的方向相同(反).⑸ 对称轴方程:0x x =,其中()0ππ 2x k k ωϕ+=+∈Z . ⑹ 对称中心:()00x ,,其中()0π x k k ωϕ+=∈Z . 5、A ωϕ、、对函数()sin y A x ωϕ=+的图象的影响 ⑵ ϕ对()sin y x ϕ=+的图象的影响.函数()sin y x ϕ=+(0)ϕ≠的图象,可以看做是把sin y x =图像上的各点向左(0)ϕ>或向右(0)ϕ<平移ϕ个单位而得到的.(可简记为左""+右""-) 即sin y x=00ϕϕ>−−−−−−→<时向左时向右平移ϕ个单位得()sin y x ϕ=+⑵ω对()sin y x ϕ=+的图象的影响.函数sin y x ω=(01)ωω>≠,的图象,可以看做是把sin y x =的图象上的各点的横坐标都缩短(1)ω>或伸长(01)ω<<到原来的1ω倍(纵坐标不变)而得到的.即sin y x =的横坐标101ωω>−−−−−−−→<<时缩短时伸长到原来的1ω倍得sin y x ω=. ⑵A (0)A >对()sin y A x ωϕ=+的图象的影响函数sin y A x =(0A >且1A ≠)的图象,可以看做是sin y x =的图象上各点的纵坐标都伸长(1)A > 或缩短(01)A <<到原来的A 倍(横坐标不变)而得到的.即sin y x =的纵坐标101A A >−−−−−−−→<<时伸长时缩短到原来的A 倍得sin y A x =.题型一 平移变换例1 将函数y =sin 2x 的图象向左平移π8个单位长度,所得图象的函数解析式为( ) A .y =sin ⎝⎛⎭⎫2x +π4 B .y =sin ⎝⎛⎭⎫2x -π4 C .y =sin ⎝⎛⎭⎫2x +π8 D .y =sin ⎝⎛⎭⎫2x -π8题型五 图象变换的综合应用例5 下图是函数()sin y A x xωϕ=+∈R ,在区间π5π66⎡⎤-⎢⎥⎣⎦,上的图象.为了得到这个函数的图象,只要将()sin y x x =∈R 的图象上所有的点( )A .向左平移3个单位长度,再把所得点的横坐标缩短到原来的12倍,纵坐标不变B .向左平移π3个单位长度,再把所得点的横坐标伸长到原来的2倍,纵坐标不变C .向左平移π6个单位长度,再把所得点的横坐标缩短到原来的12倍,纵坐标不变D .向左平移π6个单位长度,再把所得点的横坐标伸长到原来的2倍,纵坐标不变解析:由图象知,1A =,2ππω=,解得2ω=; 故sin(2)y x ϕ=+π5π736π212+=,7sin 2π112ϕ⎛⎫⋅+=- ⎪⎝⎭,从73π2ππ()62k k ϕ+=+∈Z . 故π2π3k ϕ=+()k ∈Z .此函数的解析式为πsin 23y x ⎛⎫=+ ⎪⎝⎭.答案 A变式训练5 将函数y =2sin ⎝⎛⎭⎫x +π3的图象向左平移m (m >0)个单位长度后,所得图象对应的函数为偶函数,则m 的最小值为( ) A.π12 B.π6 C.π3 D.5π6解析: 因为函数y =2sin ⎝⎛⎭⎫x +π3的图象向左平移m 个单位长度,所得图象对应的函数为y =2sin ⎝⎛⎭⎫x +π3+m ,所以π3+m =k π+π2,k ∈Z ,即m =k π+π6,k ∈Z .又m >0,所以m 的最小值为π6,答案 B题型六 函数y =A sin ()ωx +φ,|φ|<π2性质的应用例6 设函数f (x )=sin(2x +φ)(-π<φ<0), 函数y =f (x )的图象的一条对称轴是直线x =π8.(1) 求φ的值;(2) 求函数y =f (x )的单调区间及最值. 解析: (1)由2x +φ=k π+π2,k ∈Z ,得x =k π2+π4-φ2,k ∈Z ,(1)求函数y=f(x)的解析式;一、选择题1.将函数y =2sin ⎝⎛⎭⎫2x +π6的图象向右平移14个周期后,所得图象对应的函数为( ) A .y =2sin ⎝⎛⎭⎫2x +π4 B .y =2sin ⎝⎛⎭⎫2x +π3 C .y =2sin ⎝⎛⎭⎫2x -π4 D .y =2sin ⎝⎛⎭⎫2x -π3 解析: 函数y =2sin ⎝⎛⎭⎫2x +π6的周期为T =2π2=π,向右平移14个周期,即向右平移π4个单位长度后,得到图象对应的函数为y =2sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π4+π6=2sin ⎝⎛⎭⎫2x -π3,故选D. 答案 D2.把函数y =sin ⎝⎛⎭⎫2x -π4的图象向右平移π8个单位长度,所得图象对应的函数是( ) A .非奇非偶函数 B .既是奇函数又是偶函数 C .奇函数 D .偶函数解析: y =sin ⎝⎛⎭⎫2x -π4的图象向右平移π8个单位得到y =sin ⎣⎡⎦⎤2⎝⎛⎭⎫x -π8-π4=sin ⎝⎛⎭⎫2x -π2=-cos 2x 的图象, y =-cos 2x 是偶函数. 答案 D4.若函数f (x )=sin ⎝⎛⎭⎫ωx +π6-1(ω>0)的周期为2π3,则函数f (x )图象的对称轴方程为( ) A .x =k π+π3(k ∈Z )B .x =k π-π3(k ∈Z )C .x =k π3+π9(k ∈Z )D .x =k π3-π9(k ∈Z )解析: 由函数y =sin ⎝⎛⎭⎫ωx +π6-1的周期为2π3,知2π|ω|=2π3,又ω>0,所以ω=3, 则对称轴方程为3x +π6=π2+k π,k ∈Z ,即x =π9+k π3,k ∈Z .答案 C5.下列表示函数y =sin ⎝⎛⎭⎫2x -π3在区间⎣⎡⎦⎤-π2,π上的简图正确的是( )解析: 将y =sin x 的图象上所有点的横坐标缩短为原来的12,再将所有点向右平移π6个单位长度即可得到y =sin ⎝⎛⎭⎫2x -π3的图象,依据此变换过程可得到A 中图象是正确的.也可以分别令2x -π3=0,π2,π,3π2,2π得到五个关键点,描点连线即得函数y =sin ⎝⎛⎭⎫2x -π3的图象. 答案 A6.把函数f (x )=2cos(ωx +φ)(ω>0,0<φ<π)的图象上每一点的横坐标伸长到原来的2倍,纵坐标不变,然后再向左平移π6个单位长度,得到一个最小正周期为2π的奇函数g (x ),则ω和φ的值分别为( )A .1,π3B .2,π3 C.12,π6 D.12,π3解析: 依题意得f (x )第一次变换得到的函数解析式为m (x )=2cos ⎝⎛⎭⎫ω2x +φ, 则函数g (x )=2cos ⎝⎛⎭⎫ωx 2+ωπ12+φ. 因为函数的最小正周期为2π,所以ω=2, 则g (x )=2cos ⎝⎛⎭⎫x +π6+φ. 又因为函数为奇函数,所以φ+π6=k π+π2,k ∈Z ,又0<φ<π,则φ=π3.答案 B8.要得到y =tan 2x 的图象,只需把y =tan ⎝⎛⎭⎫2x -π6的图象( ) A .向左平移π6个单位得到B .向左平移π12个单位得到C .向右平移π12个单位得到D .向右平移π6个单位得到解析: 设向左平移φ个单位得到y =tan 2x 的图象,y =tan ⎣⎡⎦⎤2(x +φ)-π6=tan ⎝⎛⎭⎫2x +2φ-π6,∴2φ-π6=0,∴φ=π12, ∴向左平移π12个单位得到.答案 B9.已知将函数()cos4f x x =的图象向右平移()0ϕϕ>个单位长度后所得的图象关于y 轴对称,则ϕ的值可能为( )A .6π B .3π C .8π D .4π 解析:将函数()cos4f x x =的图象向右平移()0ϕϕ>个单位长度后,得到()cos 44y x ϕ=-的图象,由题意,得()4k k ϕπ=∈Z ,则()4k k πϕ=∈Z ,取1k =,得4πϕ=. 答案 D10.若函数()sin()f x A x ωϕ=+(其中0A >,||)2πϕ<图象的一个对称中心为(3π,0),其相邻一条对称轴方程为712x π=,该对称轴处所对应的函数值为1-,为了得到()cos2g x x =的图象,则只要将()f x 的图象( )A .向右平移6π个单位长度 B .向左平移12π个单位长度 C .向左平移6π个单位长度 D .向右平移12π个单位长度解析:根据已知函数()()sin f x A x ωϕ=+(其中0A >,)2πϕ<的图象过点,03π⎛⎫ ⎪⎝⎭,7,112π⎛⎫-⎪⎝⎭, 可得1A =,1274123πππω⋅=-,解得:2ω=.再根据五点法作图可得23πϕπ⋅+=,可得:3πϕ=, 可得函数解析式为:()sin 2.3f x x π⎛⎫=+ ⎪⎝⎭故把()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移12π个单位长度, 可得sin 2cos236y x x ππ⎛⎫=++= ⎪⎝⎭的图象,故选B . 答案 B二、填空题11.将函数y =sin(-2x )的图象向左平移π4个单位长度,所得函数图象的解析式为________.解析: y =sin(-2x )――――――――――→左移π4个单位长度y =sin ⎣⎡⎦⎤-2⎝⎛⎭⎫x +π4, 即y =sin ⎝⎛⎭⎫-2x -π2=-sin ⎝⎛⎭⎫2x +π2=-cos 2x .答案 y =3sin ⎝⎛⎭⎫13x -114.已知函数()()()sin 0,0,f x A x A ωϕωϕπ=+>><是奇函数,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若()g x 的最小正周期为2π,且4g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭______. 解析: 函数()()()sin 0,0,f x A x A ωϕωϕπ=+>><是奇函数,所以()00f =,代入可得0ϕ=,()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x . 则()1sin 2g x A x ω⎛⎫= ⎪⎝⎭,()g x 的最小正周期为2π,则2212ππω= ,解得2ω=,所以()sin g x A x =,因为4g π⎛⎫=⎪⎝⎭sin 4A π=,解得2A =,所以()2sin 2f x x =,则2sin 33882f ππ⨯⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭答案三、解答题15.使函数y =f (x )的图象上的每一点的纵坐标保持不变,横坐标缩短到原来的12倍,然后再将其图象沿x轴向左平移π6个单位长度得到的曲线与y =sin 2x 的图象相同,求f (x )的表达式.解析:方法一 (正向变换)y =f (x )―――――→横坐标缩短到原来的12倍y =f (2x )――――――→沿x 轴向左平移π6个单位长度 y =f ⎝⎛⎭⎫2⎝⎛⎭⎫x +π6,即y =f ⎝⎛⎭⎫2x +π3, ∴f ⎝⎛⎭⎫2x +π3=sin 2x . 令2x +π3=t ,则2x =t -π3,∴f (t )=sin ⎝⎛⎭⎫t -π3,即f (x )=sin ⎝⎛⎭⎫x -π3. 方法二 (逆向变换)根据题意,y =sin 2x ―――――→沿x 轴向右平移π6个单位长度 y =sin 2⎝⎛⎭⎫x -π6=sin ⎝⎛⎭⎫2x -π3――――――→横坐标伸长到原来的2倍纵坐标不变y =sin ⎝⎛⎭⎫x -π3.16.函数y =A sin(ωx +φ)⎝⎛⎭⎫A >0,ω>0,0≤φ≤π2在x ∈(0,7π)内只取到一个最大值和一个最小值,且当x =π时,y max =3;当x =6π时,y min =-3.(1)求此函数的解析式; (2)求此函数的单调递增区间.解析: (1)由题意得A =3,12T =5π,所以T =10π,所以ω=2πT =15,则y =3sin ⎝⎛⎭⎫15x +φ.因为点(π,3)在此函数图象上, 则3sin ⎝⎛⎭⎫π5+φ=3. 又因为0≤φ≤π2,有φ=π2-π5=3π10,所以y =3sin ⎝⎛⎭⎫15x +3π10.(2)当-π2+2k π≤15x +3π10≤π2+2k π,k ∈Z ,即-4π+10k π≤x ≤π+10k π,k ∈Z 时, 函数y =3sin ⎝⎛⎭⎫15x +3π10单调递增.所以此函数的单调递增区间为[-4π+10k π,π+10k π](k ∈Z ).18.已知定义在区间⎣⎡⎦⎤-π,23π上的函数f (x )=A sin(ωx +φ)(A >0,ω>0,0<φ≤π)的图象关于直线x =-π6对称,当x ∈⎣⎡⎦⎤-π6,2π3时,f (x )的图象如图1-5-5所示.图1-5-5(1)求f (x )在⎣⎡⎦⎤-π,23π上的解析式; (2)求方程f (x )=22的解. 解析: (1)由题图知:A =1,T =4⎝⎛⎭⎫2π3-π6=2π,则ω=2πT =1, 在x ∈⎣⎡⎦⎤-π6,2π3时,将⎝⎛⎭⎫π6,1代入f (x )得, f ⎝⎛⎭⎫π6=sin ⎝⎛⎭⎫π6+φ=1,因为0<φ≤π,所以φ=π3, 所以在x ∈⎣⎡⎦⎤-π6,2π3时,f (x )=sin ⎝⎛⎭⎫x +π3. 同理在x ∈⎣⎡⎦⎤-π,-π6时, f (x )=sin ⎝⎛⎭⎫x -23π. 综上,f (x )=⎩⎨⎧sin ⎝⎛⎭⎫x +π3,x ∈⎣⎡⎦⎤-π6,2π3,sin ⎝⎛⎭⎫x -23π,x ∈⎣⎡⎦⎤-π,-π6.(2)由f (x )=22在区间⎣⎡⎦⎤-π6,2π3内可得x 1=5π12,x 2=-π12. 因为y =f (x )关于x =-π6对称,有x 3=-π4,x 4=-3π4.则f (x )=22的解为-π4,-3π4,5π12,-π12.一、选择题1.要得到y =sin ⎝⎛⎭⎫x 2+π3的图象,只要将函数y =sin x2的图象( ) A .向左平移π3个单位长度B .向右平移π3个单位长度C .向左平移2π3个单位长度D .向右平移2π3个单位长度答案 C2.函数f (x )=sin(ωx +φ)的图象上所有的点向左平移π2个单位长度.若所得图象与原图象重合,则ω的值不可能等于( )A .4B .6C .8D .12解析: 对于B 选项,f (x )=sin(6x +φ)的图象向左平移π2个单位长度,得y =sin ⎣⎡⎦⎤6⎝⎛⎭⎫x +π2+φ=sin(6x +φ+π)=-sin(6x +φ)的图象. 答案 B图1-5-3 A .y =sin ⎝⎛⎭⎫x +π6 B .y =sin ⎝⎛⎭⎫2x -π6 C .y =cos ⎝⎛⎭⎫4x -π3 D .y =cos ⎝⎛⎭⎫2x -π6 解析: 由图象知,14T =π12-⎝⎛⎭⎫-π6=π4,∴T =π=2πω,∴ω=2,把y =cos 2x 的图象向右平移π12个单位即得所给图象,∴所求函数为y =cos 2⎝⎛⎭⎫x -π12=cos ⎝⎛⎭⎫2x -π6. 答案 D5.若将函数y =2sin 2x 的图象向左平移π12个单位长度,则平移后图象的对称轴为( )A .x =k π2-π6(k ∈Z )B .x =k π2+π6(k ∈Z )C .x =k π2-π12(k ∈Z )D .x =k π2+π12(k ∈Z )解析: 由题意将函数y =2sin 2x 的图象向左平移π12个单位长度后得到函数的解析式为y =2sin ⎝⎛⎭⎫2x +π6, 由2x +π6=k π+π2,k ∈Z ,得函数的对称轴为x =k π2+π6(k ∈Z ),故选B.答案 B6.函数f (x )=cos(ωx +φ)的部分图象如图所示,则f (x )的单调递减区间为( )A.⎝⎛⎭⎫k π-14,k π+34,k ∈Z B.⎝⎛⎭⎫2k π-14,2k π+34,k ∈Z C.⎝⎛⎭⎫k -14,k +34,k ∈Z D.⎝⎛⎭⎫2k -14,2k +34,k ∈Z 解析: 由图象知,周期T =2⎝⎛⎭⎫54-14=2, ∴2πω=2,∴ω=π. 由π×14+φ=π2+2k π,k ∈Z ,不妨取φ=π4,∴f (x )=cos ⎝⎛⎭⎫πx +π4. 由2k π<πx +π4<2k π+π,k ∈Z ,得2k -14<x <2k +34,k ∈Z ,∴f (x )的单调递减区间为⎝⎛⎭⎫2k -14,2k +34,k ∈Z . 故选D. 答案 D8.已知函数()sin(),(0)6f x x ωω=+> 图象上相邻两条对称轴的距离为2,把()f x 图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的图象向右平移53π个单位长度,得到函数()g x 的图象,则( )A .()cos 4g x x =-B .()cos 4g x x =C .()cos g x x =-D .()cos g x x =解析:依题意,22T π=,所以T π=,所以2ππω=,解得2ω=,所以()sin(2)6f x x π=+.把()f x 图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到曲线sin()6y x π=+,再把曲线sin()6y x π=+向右平移53π个单位长度,得到曲线5sin()36y x ππ=-+,即cos y x =,故()cos g x x =。
正弦型函数解析式

正弦型函数解析式:y=Asin(ωx+φ)+b各常数值对函数图像的影响:φ:决定波形与X轴位置关系或横向移动距离(左加右减)ω:决定周期(最小正周期T=2π/∣ω∣)A:决定峰值(即纵向拉伸压缩的倍数)b:表示波形在Y轴的位置关系或纵向移动距离(上加下减)两角和差公式两角和与差的三角函数公式sin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ-cosαsinβcos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβtan(α+β)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)二倍角公式二倍角的正弦、余弦和正切公式(升幂缩角公式)sin2α=2sinαcosαcos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan2α=2tanα/[1-tan^2(α)]半角公式半角的正弦、余弦和正切公式(降幂扩角公式)sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)另也有tan(α/2)=(1-cosα)/sinα=sinα/(1+cosα)万能公式万能公式sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]万能公式推导附推导:sin2α=2sinαcosα=2sinαcosα/(cos^2(α)+sin^2(α))......*,(因为cos^2(α)+sin^2(α)=1)再把*分式上下同除cos^2(α),可得sin2α=2tanα/(1+tan^2(α))然后用α/2代替α即可。
三角函数(正弦函数与余弦函数)图像的变换及三角函数解析式的求法

1、(安徽卷文8)函数sin(2)3y x π=+图像的对称轴方程可能是( )A .6x π=-B .12x π=-C .6x π=D .12x π=2、(广东卷文5)已知函数2()(1cos 2)sin ,f x x x x R =+∈,则()f x 是( ) A 、最小正周期为π的奇函数 B 、最小正周期为2π的奇函数 C 、最小正周期为π的偶函数 D 、最小正周期为2π的偶函数 3、(全国Ⅰ卷文6)2(sin cos )1y x x =--是( ) A .最小正周期为2π的偶函数B .最小正周期为2π的奇函数C .最小正周期为π的偶函数D .最小正周期为π的奇函数4、(湖南卷理6)函数2()sin cos f x x x x =+在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是( )A.1C. 325、(天津卷文6)把函数sin ()y x x =∈R 的图象上所有的点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数是( )A .sin 23y x x π⎛⎫=-∈ ⎪⎝⎭R ,B .sin 26x y x π⎛⎫=+∈ ⎪⎝⎭R ,C .sin 23y x x π⎛⎫=+∈ ⎪⎝⎭R ,D .sin 23y x x 2π⎛⎫=+∈ ⎪⎝⎭R ,6、(全国Ⅰ卷文9)为得到函数πcos 3y x ⎛⎫=+ ⎪⎝⎭的图象,只需将函数sin y x =的图像( )A .向左平移π6个长度单位B .向右平移π6个长度单位 C .向左平移5π6个长度单位D .向右平移5π6个长度单位7、(全国Ⅰ卷理8)为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像,只需将函数sin 2y x =的图像( )A .向左平移5π12个长度单位 B .向右平移5π12个长度单位 C .向左平移5π6个长度单位D .向右平移5π6个长度单位1.(安徽卷文8)函数sin(2)3y x π=+图像的对称轴方程可能是( )A .6x π=-B .12x π=-C .6x π=D .12x π=解:sin(2)3y x π=+的对称轴方程为232x k πππ+=+,即212k x ππ=+,0,12k x π==2.(广东卷文5)已知函数2()(1cos 2)sin ,f x x x x R =+∈,则()f x 是( ) A 、最小正周期为π的奇函数 B 、最小正周期为2π的奇函数 C 、最小正周期为π的偶函数 D 、最小正周期为2π的偶函数 【解析】222211cos 4()(1cos 2)sin 2cos sin sin 224xf x x x x x x -=+===,选D.9.(全国Ⅰ卷文6)2(sin cos )1y x x =--是( ) A .最小正周期为2π的偶函数B .最小正周期为2π的奇函数C .最小正周期为π的偶函数D .最小正周期为π的奇函数sinx cosx,2sinxcosx 2y=1sin 2x 1=sin 2x T D2ππ±解析:本题主要考查了三角函数的化简,主要应用了与的关系,同时还考查了二倍角公式和函数的奇偶性和利用公式法求周期。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据正弦型函数的图象求其解析式(一)课前系统部分1、设计思想建构主义强调,学生并不是空着脑袋走进教室的。
在日常生活中,在以往的学习中,他们已经形成了丰富的经验,小到身边的衣食住行,大到宇宙、星体的运行,从自然现象到社会生活,他们几乎都有一些自己的看法。
而且,有些问题即使他们还没有接触过,没有现成的经验,但当问题一旦呈现在面前时,他们往往也可以基于相关的经验,依靠他们的认知能力,形成对问题的某种解释。
而且,这种解释并不都是胡乱猜测,而是从他们的经验背景出发而推出的合乎逻辑的假设。
所以,教学不能无视学生的这些经验,另起炉灶,从外部装进新知识,而是要把学生现有的知识经验作为新知识的生长点,引导学生从原有的知识经验中“生长”出新的知识经验。
为此我们根据“用已知知识去探讨新知识”的教学方式,沿着“复习已知知识--提出由简单到复杂的问题--解决问题--反思解决过程”这条主线,把从情境中探索和提出数学问题作为教学的出发点,以“问题”为红线组织教学,形成以提出问题与解决问题相互引发携手并进的“情境--问题”学习链,使学生真正成为提出问题和解决问题的主体,成为知识的“发现者”和“创造者”,使教学过程成为学生主动获取知识、发展能力、体验数学的过程。
根据上述精神,做出了如下设计:创设一个现实问题情境作为提出问题的背景,并且用示波器演示电压的图形,让学生对数学的学习产生形象直观的感觉,逐步将现实问题转化、抽象成过渡性数学问题,并使学生产生进一步探索解决问题的动机。
然后引导学生抓住问题的数学实质。
2、课标及教材分析“根据正弦型函数的图象求其解析式”是职高教科书数学第一册第七章第三节的延展内容,它是在学习好正弦函数,正弦型函数后的一个升华内容,是三角函数图象知识的高层次运用,也是解决生活实际问题的一个重要思想方法,因此具有一定的应用价值。
布鲁纳指出,学生不是被动的、消极的知识的接受者,而是主动的、积极的知识的探究者。
教师的作用是创设学生能够独立探究的情境,引导学生去思考,参与知识获得的过程。
因此,做好“根据正弦型函数的图象求解析式”的教学,不仅能复习巩固旧知识,使学生掌握新的有用的知识,体会联系、发展等辩证观点,而且能培养学生的应用意识和实践操作能力,以及提出问题、解决问题等研究性学习的能力。
3、学情分析在近几年教学实践中我们发现这样的怪现象:绝大多数学生认为数学很重要,但很难;学得很苦、太抽象、太枯燥,要不是升学,我们才不会去理会,况且将来用数学的机会很少;许多学生完全依赖于教师的讲解,不会自学,不敢提问题,也不知如何提问题。
这说明了学生一是不会学数学,二是对数学有恐惧感,没有信心,这样的心态怎能对数学有所创新呢?即使有所创新那与学生们所花代价也不成比例,其间扼杀了他们太多的快乐和个性特长。
建构主义提倡情境式教学,认为多数学习应与具体情境有关,只有在解决与现实世界相关联的问题中,所建构的知识才将更丰富、更有效和易于迁移。
4、教学目标通过本节课的学习,能够让学生更加深刻的理解到正弦型函数sin y x =与正弦型函数sin()y A x ωϕ=+的变换关系,并且能通过正弦型函数的图象用平移法求出其解析式,从而对函数图象的平移与五点作图法有更深刻的了解,对于接受能力强的,能够掌握五点法就比较成功了。
5、重点难点重难点都是正弦型函数sin()y A x ωϕ=+各参数求法,尤其是字母ϕ的求法,因些在本节课中介绍了两种解法,着重讲解平移法,最后介绍五点法求解,只要求学生能了解。
6、教学策略与手段本节课的内容很有层次感,有简单的,有提高的,对每一类同学都会有所得。
主要采用启发性讲述法、试验法和采用多媒体手段教学方法。
7、教学用具及课前准备教师:借一个物理上用的学生示波器。
并把课堂练习题印在一张试卷上。
让学生在课堂上直接做在试卷上。
学生:在课前应该对正弦函数变换到正弦型函数的图象的过程相当熟悉,特别是对初相位ϕ的作用。
另外对五点法作正弦型函数的图象的过程比较了解。
这将为五点法找函数的解析式提供不少方便。
(二)课堂系统部分——教学过程1、课前探究:同学们,我们对现在使用的市电还是比较熟悉的,都知道是220V ,然而大家可能不知道市电的电压并不是稳定于220V 不变,而是随着时间改变电压不断改变的,并且电压随时间变化的图象就是一个正弦型函数的图象,现在我们做一个实验,请大家观察一下电压变化情况。
用示波器演示电压变化图。
2、新课导入部分正弦型函数的图象广泛地存在于我们的生活中,比如说,刚才做实验发现的市电的电压,电流值,以及物理学的简谐振动等等都可以看成是一种正弦型函数。
如果我们能把这个函数的图象表达式求出来,那么我们就能更加深刻的了解这种变化关系,因此在这一堂课中,我们将学习如何通过正弦型函数的图象求解析式。
请大家先回答我几个问题。
(1)由正弦函数sin y x =的图象变到sin()y A x ωϕ=+的图象,要分几部,哪几步?(2)正弦型函数解析式中的几个参数A ,ω,ϕ的作用分别是什么。
(3)五点法作函数型函数的图象时,是如何列表的。
3、新课内容:(1)平移法求正弦型函数的图象请大家观察PPT 中的几个简单的正弦型函数的图象,并说出他的解析式。
图1 图2 图3这三个问题这简单了,一般都拦不住大家,下面我们研究有点难度的图象,比如说这个 例1:根据所给正弦型函数的图象,求出其表达式。
(1)请一位同学分析出,这个函数的图象的最值问题:最大值为2,最小值为-2,因此得出A =2(2)请一位同学观察得出这个函数的周期:T=5()66πππ--=,并且用自己的话说明正弦型函数的图象何为一个周期。
并能计算出22w Tπ==, (3)再请一位同学分析平移量的问题:向左平移了6π个单位,根据以前学的函数平移知识(左加右减,上加下减),得出公式,但要强调是在x 后面加还是在wx 后面加。
得出表达式为2sin[2()]6y x π=+,即2sin()3y x π=+练习1:请同学们完成试卷上面的习题,根据正弦型函数的图象求其表达式。
习题1:(1)函数的最大值是____,最小值是______,因此A=________(2)函数的一个周期T=___________,因此w =___________(3)函数的图象向_____平移了_________个单位,综上得出此函数图象的表达式为_____________习题2这个例题要分析透彻,特别是平移量为什么应该加上X 上面,对于有系数的,一定(1)函数的最大值是____,最小值是______,因此A=________(2)函数的一个周期T=___________,因此w =___________(3)函数的图象向_____平移了_________个单位,综上得出此函数图象的表达式为_____________例2:根据所给正弦型函数的图象,求出其表达式。
xyO 12π65π22-(1)请一位同学分析出,这个函数的图象的最值问题:最大值为2,最小值为-2,因此得出A =2(2)请同学们分析周期的问题,从12π到56π是34个周期。
因此354612T ππ=-,从而计算出T=π,由2w Tπ=得出2w =。
(3)关于平移量的问题,先要计算五点中的第一个点的坐标,通过周期与第五个点的坐标不难计算出第一个点的坐标为6π-,因此是向左平移了6π个单位,从而得出表达式2sin[2()]6y x π=+,即2sin(2)3y x π=+练习2:请同学们完成试卷上面的习题,根据正弦型函数的图象求其表达式。
习题3:(1)函数的最大值是____,最小值是______,因此A=________(2)函数的一个周期T =___________,因此w =___________(3)函数图象五个点中的第一个点的坐标为____________,因此函数的图象向_____平移了__________个单位,综上得出此函数图象的表达式为____________________(2)探究用五点法来求正弦型函数图象的表达式例3:根据所给正弦型函数的图象,求出其表达式。
xy O 12π65π22-从图象容易观察出(,2)12π为五点作图法中的第二个点,5(,0)6π为第五个点,因此由作图时列举时的五点计算公式,容易计算出w ϕ和。
从而得出函数表达式。
练习3:请同学们完成试卷上面的习题,根据正弦型函数的图象求其表达式。
习题4:4、板书设计5、小结:这堂课我们学习了如何利用正弦型函数的图象求其解析式的方法:平移法,五点法。
6、作业设计(1)已知函数13()2sin()543f x xπ=+-,它的最小正周期是()(A)134π(B)413π(C)813π(D)138π(2)已知函数13()2sin()43f x xπ=+,它的最大值是()(A)2 (B)-2 (C)134(D)3π一、复习回顾1、正弦型函数解析式:y=Asin(ωx+φ) A:决定峰值(即纵向拉伸压缩的倍数)ω:决定周期(最小正周期T=2π/∣ω∣)φ:决定波形与X轴位置关系或横向移动距离(左加右减)2、函数图象的平移(左加右减,上加下减)3、五点法作正弦型函数的图象xωx+φ02ππ23ππ2y=Asin(ωx+φ)0 A 0 -A 0二、例题分析…………………………………………………………………………(3)已知函数()2sin()3f x wx π=+的周期是3π,则w =( ) (A )3π (B )6 (C )3 (D )2 (4)请根据正弦型函数的图象求出解析式(最好用两种方法求解):(5)已知函数sin()y A wx b ϕ=++ (0,0,A w x R >>∈)在一个周期内的图象如图示,求直线3y =与函数()f x 图象的所有交点的坐标。
(三)课后系统部分——教学后记这堂课在第一个班上时,感觉不太成功,首先,正弦型函数的图象这部分内容知识点较繁琐,并且难度很大,对学生的要求较高,而我们的学情是学生基础差,底子薄,理解、计算能力不强;其次,涉及到作图问题,我们的学生动手能力和积极性都很差。
这两方面都给我教学环节的设计和教学语言的组织带来了困难。
如何提升他们的学习兴趣,科学有效地引导他们,使他们“听得懂,学得会”,是我面临的最大问题,在得到组内老师的大力帮助下,确定了这堂课的主线:先让学生知道正弦型函数的图象广泛存在于我的生活中,明确研究图象写表达式的意义,然后用几何画板演示出三个参数对图象的作用,最终解决问题。
吸取了这个教训之后,在第二个班上取得了比较好的效果。
自我感觉这节课的亮点有以下几个方面: 1、从生活出发的教学让学生感受到学习的快乐,向同学展示了交流电的电压与电流以512πx及沙摆运动图象恰恰是我们的正弦型函数的图象。
