2020届高三数学一轮复习强化训练精品――几何证明选讲
2020届高三数学一轮复习强化训练精品――几何概型

14 分
因此∠ ACC′= 180 30 =75°, 2
A =90-75=15 , Ω =90,因此, P〔D〕= 15 = 1 . 90 6
例 5 甲、乙两人约定在 6 时到 7 时之间在某处会面,并约定先到者应等候另一人一刻钟,过时即可离 去. 求两人能会面的概率 .
解 以 x 轴和 y 轴分不表示甲、 乙两人到达约定地点的时刻, 那么两人能够会面的充要条件是 | x- y| ≤15. 在如下图平面直
1 000
记事件 B:〝取 30 毫升种子含有带麦锈病的种子〞 .
9分
那么 P〔 B〕= 30 =0.03 ,即取 30 毫升种子含有带麦锈病的种子的概率为 1 000
0.03.
例 4 在 Rt△ ABC中,∠ A=30°,过直角顶点 C 作射线 CM交线段 AB于 M,求使 | AM| >| AC| 的概率 . 解 设事件 D〝作射线 CM,使 | AM| >| AC| 〞. 在 AB上取点 C′使 | AC′|=| AC| ,因为△ ACC′是等腰三角形,
的距离不大于 1 的点构成的区域,向 D 中随机投一点,那么落入 E 中的概率为
.
2 的点构成的区域, E 是到原点
答案 16
3. 如下图,有一杯 2 升的水,其中含有 1 个细菌,用一个小杯从这杯水中取出 0.1 升水,求小杯水中含有那个细菌的概率 .
解 记〝小杯水中含有那个细菌〞为事件 A,那么事件 A 的概率只与取出的水的体积有关,符合几何概型的条件
角坐标系下,〔x, y〕的所有可能结果是边长为 60 的正方形区域,而事件 A〝两人能够会面〞的可能结果由图中的阴影部
分表示 . 由几何概型的概率公式得:
P〔A〕 = SA = 602 452 = 3 600 2 025 = 7 .
(广东专用)高考数学一轮复习第十三章13.1几何证明选讲课件文

4×(3+2+4)=36, ∴PA=6.
题型分类·深度剖析
题型二
圆的切割线定理的应用
【例 2】 如图所示,已知 PA 与 解析
答案 思维升华
⊙O 相切,A 为切点,PBC 为 在与圆有关的问题中,或在特殊的几
割线,D 为⊙O 上一点,AD, 何图形中,常利用“四定理”及三角形
BC 相交于点 E.
相似等知识来证明线段相等或线段
【例 1】 如图,△ABC 中,D
解析
答案 思维升华
是 AC 的中点,E 是 BC 延长 利用平行线分线段成比例定理
线上一点,过 A 作 AH∥BE. 及推论证明比例式应注意:
连接 ED 并延长交 AB 于 F, (1)作出图形,观察图形及已知条 交 AH 与 H.如果 AB=4AF, 件,寻找合适的比例关系;
基础知识·自主学习
要点梳理
知识回顾 理清教材
6.圆的切线的性质及判定定理 (1)性质 性质定理:圆的切线垂直于经过切点的 半径 . 推论 1:经过圆心且垂直于切线的直线必经过 切点 . 推论 2:经过切点且垂直于切线的直线必经过 圆心 . (2)判定定理:经过半径的外端并且垂直于这条半径的直线是 圆的 切线 .
成比例等问题.
一般地,涉及圆内的两条相交弦时首
先考虑相交弦定理,涉及两条割线时
若 F 为 CE 上 一 点 且 使 得 要想到割线定理,涉及切线和割线时
∠EDF=∠P,已知 EF=1, 要注意应用切割线定理,要注意相交
EB=2,PB=4,则 PA 的长为 弦定理中线段之间的关系与切割线
__6______.
题型分类·深度剖析
题型三
圆的有关性质的综合应用
解析
答案 思维升华
2020届一轮复习苏教版几何证明选讲学案

选修4-1几何证明选讲A第1讲相似三角形的判定及有关性质[最新考纲]了解平行线等分线段定理和平行截割定理;掌握相似三角形的判定定理及性质定理;理解直角三角形射影定理.知识梳理1.平行截割定理(1)平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.(2)平行线分线段成比例定理①定理:三条平行线截两条直线,所得的对应线段成比例.②推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.2.相似三角形的判定与性质(1)相似三角形的判定定理①两角对应相等的两个三角形相似.②两边对应成比例并且夹角相等的两个三角形相似.③三边对应成比例的两个三角形相似.(2)相似三角形的性质定理①相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.②相似三角形周长的比等于相似比.③相似三角形面积的比等于相似比的平方.3.直角三角形的射影定理直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.如图,在Rt△ABC中,CD是斜边上的高,则有CD2=AD·BD,AC2=AD·AB,BC2=BD·AB.诊断自测1. 如图,已知a∥b∥c,直线m,n分别与a,b,c交于点A,B,C和A′,B′,C′,如果AB=BC=1,A′B′=32,则B′C′=________.解析由平行线等分线段定理可直接得到答案.答案3 22.如图,△ABC∽△AFE,EF=8,且△ABC与△AFE的相似比是3∶2,则BC 等于________.解析∵△ABC∽△AFE,∴BC EF =3 2.又EF=8,∴BC=12.答案123. (2018·揭阳模拟)如图,BD⊥AE,∠C=90°,AB=4,BC=2,AD=3,则EC =________.解析 在Rt △ADB 中, DB =AB 2-AD 2=7,依题意得,△ADB ∽△ACE ,∴DB EC =AD AC ,可得EC =DB ·ACAD =27. 答案 274.如图,∠C =90°,∠A =30°,E 是AB 中点,DE ⊥AB 于E ,则△ADE 与△ABC 的相似比是________.解析 ∵E 为AB 中点,∴AE AB =12,即AE =12AB ,在Rt △ABC 中,∠A =30°,AC =32AB ,又∵Rt △AED ∽Rt △ACB ,∴相似比为AE AC =13.故△ADE 与△ABC 的相似比为1∶ 3.答案 1∶ 35. (2018·湛江模拟)如图,在△ABC 中,D 是AC 的中点,E 是BD 的中点,AE 交于BC 于F ,则BFFC =________.解析 如图,过点D 作DG ∥AF ,交BC 于点G ,易得FG =GC ,又在△BDG 中,BE =DE ,即EF 为△BDG 的中位线,故BF =FG ,因此BFFC =12.答案 12考点一 平行截割定理的应用【例1】 如图,在△ABC 中,DE ∥BC ,EF ∥CD ,若BC=3,DE =2,DF =1,则AB 的长为________.解析由⎩⎪⎨⎪⎧DE ∥BC ,EF ∥CD ,BC =3,DE =2⇒AE AC =AF AD =DE BC =23,又DF =1,故可解得AF =2,∴AD =3, 又AD AB =23,∴AB =92.答案 92规律方法 利用平行截割定理解决问题,特别注意被平行线所截的直线,找准成比例的线段,得到相应的比例式,有时需要进行适当的变形,从而得到最终的结果.【训练1】 如图,在梯形ABCD 中,AB ∥CD ,AB =4,CD =2.E ,F 分别为AD ,BC 上的点,且EF =3,EF ∥AB ,则梯形ABFE 与梯形EFCD 的面积比为________.解析 如图,延长AD ,BC 交于一点O ,作OH ⊥AB 于点H . ∴x x +h 1=23,得x =2h 1,x +h 1x +h 1+h 2=34,得h 1=h 2. ∴S 梯形ABFE =12×(3+4)×h 2=72h 2, S 梯形EFCD =12×(2+3)×h 1=52h 1, ∴S 梯形ABFE ∶S 梯形EFCD =7∶5. 答案 7∶5考点二 相似三角形的判定及性质【例2】 如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,E 为AC 的中点, ED 、CB 延长线交于一点F . 求证:FD 2=FB ·FC .证明 ∵E 是Rt △ACD 斜边中点, ∴ED =EA ,∴∠A =∠1, ∵∠1=∠2,∴∠2=∠A ,∵∠FDC =∠CDB +∠2=90°+∠2,∠FBD =∠ACB +∠A =90°+∠A ,∴∠FBD =∠FDC ,∵∠F 是公共角,∴△FBD ∽△FDC , ∴FB FD =FDFC ,∴FD 2=FB ·FC .规律方法 判定两个三角形相似要注意结合图形性质灵活选择判定定理,特别要注意对应角和对应边.证明线段乘积相等的问题一般转化为有关线段成比例问题.(2)相似三角形的性质可用来证明线段成比例、角相等;可间接证明线段相等. 【训练2】 (2018·陕西卷)如图,AB 与CD 相交于点E ,过E 作BC 的平行线与AD的延长线交于点P,已知∠A=∠C,PD=2DA=2,则PE=________.解析∵PE∥BC,∴∠C=∠PED,又∠C=∠A,则有∠A=∠PED,又∠为公共角,所以△PDE∽△PEA,PD PE=PEP A,即PE2=PD·P A=2×3=6,故PE= 6.答案 6考点三直角三角形射影定理及其应用【例3】如图所示,AD、BE是△ABC的两条高,DF⊥AB,垂足为F,直线FD 交BE于点G,交AC的延长线于H,求证:DF2=GF·HF.证明∵∠H+∠BAC=90°,∠GBF+∠BAC=90°,∴∠H=∠GBF.∵∠AFH=∠GFB=90°,∴△AFH∽△GFB.∴HFBF=AFGF,∴AF·BF=GF·HF.因为在Rt△ABD中,FD⊥AB,∴DF2=AF·BF,所以DF2=GF·HF.规律方法(1)在使用直角三角形射影定理时,要注意将“乘积式”转化为相似三角形中的“比例式”.(2)证题时,要注意作垂线构造直角三角形是解决直角三角形问题时常用的方法.【训练3】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=4,sin∠ACD=45,则CD=______,BC=______.解析 在Rt △ADC 中,AD =4,sin ∠ACD =AD AC =45,得AC =5,CD =AC 2-AD 2=3,又由射影定理AC 2=AD ·AB ,得AB =AC 2AD =254.∴BD =AB -AD =254-4=94,由射影定理BC 2=BD ·AB =94×254,∴BC =154.答案 3 154三角形相似与圆的交汇问题【典例】 如图所示,⊙O 和⊙O ′相交于A ,B 两点,过A 作两圆的切线分别交两圆于C ,D 两点,连接DB 并延长交⊙O 于点E ,证明:(1)AC ·BD =AD ·AB ; (2)AC =AE .[审题视点] (1)根据待证等式可将各边回归到△ACB ,△DAB 中,再证两三角形相似;(2)本问可先证明△EAD ∽△ABD ,再结合第(1)问结论得证. 证明 (1)由AC 与⊙O ′相切于A ,得∠CAB =∠ADB , 同理∠ACB =∠DAB ,所以△ACB ∽△DAB . 从而AC AD =AB BD ,即AC ·BD =AD ·AB .(2)由AD 与⊙O 相切于A ,得∠AED =∠BAD .又∠ADE =∠BDA ,得△EAD ∽△ABD . 从而AE AB =ADBD ,即AE ·BD =AD ·AB . 综合(1)的结论知,AC =AE .[反思感悟] 1.易失分点:(1)证明本题第(2)问时,想不到证明△EAD ∽△ABD ,从而无法解答.(2)证明本题第(2)问时,没有应用第(1)问的结论从而无法证明结论成立. 2.防范措施:(1)证明等积式成立,应先把它写成比例式,找出比例式中给出的线段所在三角形是否相似,若不相似,则进行线段替换或等比替换.(2)在有多个结论的题目中,如果结论带有普遍性,已经证明的结论,可作为证明下一个结论成立的条件使用. 【自主体验】(2018·江苏卷)如图,AB 和BC 分别与圆O 相切于点D ,C ,AC 经过圆心O ,且BC =2OC .求证:AC =2AD证明 连接OD ,因为AB 和BC 分别与圆O 相切于点D ,C , 所以∠ADO =∠ACB =90°.又因为∠A =∠A ,所以Rt △ADO ∽Rt △ACB . 所以AD AC =OD BC . 又BC =2OC =2OD , 故AC =2AD .第2讲直线与圆[最新考纲]1.理解圆周角定理及其推论;掌握圆的切线的判定定理及性质定理;理解弦切角定理及其推论.2.掌握相交弦定理、割线定理、切割线定理;理解圆内接四边形的性质定理与判定定理.知识梳理1.圆周角定理与圆心角定理(1)圆周角定理及其推论①定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.②推论:(i)推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.(ii)推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.(2)圆心角定理:圆心角的度数等于它所对弧的度数.2.弦切角的性质弦切角定理:弦切角等于它所夹的弧所对的圆周角.3.圆的切线的性质及判定定理(1)定理:圆的切线垂直于经过切点的半径.(2)推论:①推论1:经过圆心且垂直于切线的直线必经过切点.②推论2:经过切点且垂直于切线的直线必经过圆心.4.与圆有关的比例线段基本图形条件结论应用P AB、PCD是⊙O的割线(1)P A·PB=PC·PD(2)△P AC∽△PDB(1)求线段P A、PB、PC(2)应用相似求AC、BDP A切⊙O于A,PBC是⊙O的割线(1)P A2=PB·PC(2)△P AB∽△PCA(1)已知P A、PB、PC知一(2)求解AB、ACP A、PB是⊙O的切线(1)P A=PB(2)∠OP A=∠OPB(1)证线段相等,已知P(2)求角(1)圆内接四边形的性质定理①定理1:圆内接四边形的对角互补.②定理2:圆内接四边形的外角等于它的内角的对角.(2)圆内接四边形的判定定理及推论①判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点共圆.②推论:如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.诊断自测1.如图,△ABC中,∠C=90°,AB=10,AC=6,以AC为直径的圆与斜边交于点P,则BP长为________.解析连接CP.由推论2知∠CP A=90°,即CP⊥AB,由射影定理知,AC2=AP·AB.∴AP=3.6,∴BP=AB-AP=6.4.答案 6.42.如图,AB 、AC 是⊙O 的两条切线,切点分别为B 、C ,D 是优弧上的点,已知∠BAC =80°, 那么∠BDC =______.解析 连接OB 、OC ,则OB ⊥AB ,OC ⊥AC ,∴∠BOC =180°-∠BAC =100°, ∴∠BDC =12∠BOC =50°. 答案 50°3.如图,四边形ABCD 是圆O 的内接四边形,延长AB 和DC 相交 于点P .若PB =1,PD =3,则BCAD 的值为________.解析 ∵ABCD 为圆内接四边形,∴∠PBC =∠ADP ,又∠P =∠P ,∴△BCP ∽△DAP ,∴BC AD =PB PD =13. 答案 134. (2018·广州调研)如图,四边形ABCD 内接于⊙O ,BC 是直径,MN 与⊙O 相切,切点为A ,∠MAB =35°,则∠D =________.解析 连接BD ,由题意知,∠ADB =∠MAB =35°,∠BDC =90°,故∠ADC =∠ADB +∠BDC =125°. 答案 125°5.如图所示,过点P的直线与⊙O相交于A,B两点.若P A=1,AB=2,PO =3,则⊙O的半径r=________.解析设⊙O的半径为r(r>0),∵P A=1,AB=2,∴PB=P A+AB=3.延长PO交⊙O于点C,则PC=PO+r=3+r.设PO交⊙O于点D,则PD=3-r.由圆的割线定理知,P A·PB=PD·PC,∴1×3=(3-r)(3+r),则r= 6.答案 6考点一圆周角、弦切角及圆的切线问题【例1】如图所示,⊙O的直径为6,AB为⊙O的直径,C为圆周上一点,BC =3,过C作圆的切线l,过A作l的垂线AD,AD分别与直线l、圆交于D、E.(1)求∠DAC的度数;(2)求线段AE的长.解(1)由已知△ADC是直角三角形,易知∠CAB=30°,由于直线l与⊙O相切,由弦切角定理知∠BCF=30°,由∠DCA+∠ACB+∠BCF=180°,又∠ACB=90°,知∠DCA=60°,故在Rt△ADC中,∠DAC=30°.(1)(2)法一连接BE,如图(1)所示,∠EAB=60°=∠CBA,则Rt△ABE≌Rt△BAC,所以AE=BC=3.法二连接EC,OC,如图(2)所示,则由弦切角定理知,∠DCE=∠CAE=30°,又∠DCA=60°,故∠ECA=30°,(2)又因为∠CAB=30°,故∠ECA=∠CAB,从而EC∥AO,由OC⊥l,AD⊥l,可得OC∥AE,故四边形AOCE是平行四边形,又因为OA=OC,故四边形AOCE是菱形,故AE=AO=3.规律方法(1)圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系,从而证明三角形全等或相似,可求线段或角的大小.(2)涉及圆的切线问题时要注意弦切角的转化;关于圆周上的点,常作直径(或半径)或向弦(弧)两端画圆周角或作弦切角.【训练1】如图,△ABC的角平分线AD的延长线交它的外接圆于点E.(1)证明:△ABE∽△ADC;(2)若△ABC的面积S=12AD·AE,求∠BAC的大小.(1)证明由已知条件,可得∠BAE=∠CAD. 因为∠AEB与∠ACD是同弧所对的圆周角.所以∠AEB =∠ACD .故△ABE ∽△ADC .(2)解 因为△ABE ∽△ADC ,所以AB AD =AEAC ,即AB ·AC =AD ·AE 又S =12AB ·AC sin ∠BAC ,且S =12AD ·AE , 故AB ·AC sin ∠BAC =AD ·AE ,则sin ∠BAC =1.又∠BAC 为△ABC 的内角, 所以∠BAC =90°.考点二 与圆有关的比例线段【例2】 如图,P A 切⊙O 于点A ,割线PBC 交⊙O 于点B ,C ,∠APC 的角平分线分别与AB 、AC 相交于点D 、E ,求证:(1)AD =AE ; (2)AD 2=DB ·EC .证明 (1)∠AED =∠EPC +∠C , ∠ADE =∠APD +∠P AB .因PE 是∠APC 的角平分线,故∠EPC =∠APD . 又P A 是⊙O 的切线,故∠C =∠P AB . 所以∠AED =∠ADE .故AD =AE .(2)⎭⎬⎫∠PCE =∠P AD ∠CPE =∠APD ⇒△PCE ∽△P AD ⇒EC AD =PCP A ;⎭⎬⎫∠PEA =∠PDB ∠APE =∠BPD ⇒△P AE ∽△PBD ⇒AE DB =P APB .又P A 是切线,PBC 是割线⇒P A 2=PB ·PC ⇒P A PB =PCP A . 故EC AD =AEDB ,又AD =AE ,故AD 2=DB ·EC .规律方法涉及与圆有关的等积线段或成比例的线段,常利用圆周角或弦切角证明三角形相似,在相似三角形中寻找比例线段;也可以利用相交弦定理、切割线定理证明线段成比例,在实际应用中,一般涉及两条相交弦应首先考虑相交弦定理,涉及两条割线就要想到割线定理,见到切线和割线时要注意应用切割线定理.【训练2】(2018·天津卷)如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD与BC交于点F.若AB =AC,AE=6,BD=5,则线段CF的长为________.解析由切割线定理得AE2=EB·ED,解得EB=4.因为AB=AC,所以∠ABC=∠ACB=∠ADB.由弦切角定理得∠EAB=∠EDA,所以∠EAB=∠ABC,则AE∥BC,因为AC∥BD,所以四边形AEBC是平行四边形.所以AE=BC=6,AC=EB=4,又由题意可得△CAF∽△CBA,所以CACB=CF CA,CF=CA2CB=83.答案83考点三圆内接四边形的判定及应用【例3】(2018·银川一中月考)如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在∠P AC的内部,点M是BC的中点.(1)证明:A、P、O、M四点共圆;(2)求∠OAM+∠APM的大小.(1)证明连接OP,OM,因为AP与⊙O相切于点P,所以OP⊥AP.因为M是⊙O的弦BC的中点,所以OM⊥BC,于是∠OP A+∠OMA=180°.由圆心O在∠P AC的内部,可知四边形APOM的对角互补,所以A、P、O、M四点共圆.(2)解由(1)得A、P、O、M四点共圆,所以∠OAM=∠OPM,由(1)得OP⊥AP,因为圆心O在∠P AC的内部,所以∠OPM+∠APM=90°,所以∠OAM+∠APM=90°.规律方法(1)如果四点与一定点距离相等,那么这四点共圆;(2)如果四边形的一组对角互补,那么这个四边形的四个顶点共圆;(3)如果四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆.【训练3】如图,已知△ABC的两条角平分线AD和CE相交于点H,∠ABC=60°,F在AC上,且AE=AF.求证:(1)B、D、H、E四点共圆;(2)CE平分∠DEF.证明(1)在△ABC中,∵∠ABC=60°,∴∠BAC+∠BCA=120°.∵AD,CE分别是△ABC的角平分线,∴∠HAC+∠HCA=60°,∴∠AHC=120°.∴∠EHD=∠AHC=120°.∴∠EBD+∠EHD=180°.∴B,D,H,E四点共圆.(2)连接BH,则BH为∠ABC的平分线,∴∠EBH=∠HBD=30°.由(1)知B,D,H,E四点共圆,∴∠CED=∠HBD=30°,∠HDE=∠EBH=30°.∴∠HED=∠HDE=30°.∵AE=AF,AD平分∠BAC,∴EF⊥AD.又∠EHA=∠HDE+∠CED=60°,∴∠CEF=30°.∴CE平分∠DEF.关于圆的综合应用【典例】如图所示,已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1,⊙O2于点D,E,DE与AC 相交于点P.(1)求证:AD∥EC;(2)若AD是⊙O2的切线,且P A=6,PC=2,BD=9,求AD的长.[审题视点](1)连接AB,在⊙O1中使用弦切角定理,在⊙O2中使用圆周角定理,即可证明∠D=∠E;(2)根据切割线定理,只要求出BE的长度即可,在⊙O2中根据相交弦定理可得BP·PE,根据(1)中△ADP∽△CEP,又可得BP,PE的一个方程,解方程组求出BP ,PE 的长度即可. (1)证明 连接AB ,如图所示.∵AC 是⊙O 1的切线,∴∠BAC =∠D . 又∵∠BAC =∠E .∴∠D =∠E .∴AD ∥EC . (2)解 设BP =x ,PE =y , ∵P A =6,PC =2,∴xy =12.① ∵根据(1),可得△ADP ∽△CEP , ∴DP EP =APCP ,即9+x y =62,②由①②,可得⎩⎪⎨⎪⎧ x =3,y =4或⎩⎪⎨⎪⎧x =-12,y =-1.(负值舍去)∴DE =9+x +y =16.∵AD 是⊙O 2的切线,∴AD 2=DB ·DE =9×16. ∴AD =12.[反思感悟] 在平面几何的有关计算中往往要使用比例线段,产生比例线段的一个主要根据是两三角形相似,本题中使用三角形的相似把⊙O 2中两条待求的线段联系起来,发挥了相似三角形的桥梁作用.在涉及两圆的公共弦时,通常是作出两圆的公共弦,如果有过公共点的切线就可以使用弦切角定理,在两个圆内实现角的等量代换,这是解决两个圆相交且在交点处有圆的切线问题的基本思考方向.【自主体验】如图,梯形ABCD 内接于⊙O ,AD ∥BC ,过B 引⊙O 的切线分别交DA 、CA 的延长线于E 、F .(1)求证:AB 2=AE ·BC ;(2)已知BC =8,CD =5,AF =6,求EF 的长. (1)证明 ∵BE 切⊙O 于B , ∴∠ABE =∠ACB .又AD ∥BC ,∴∠EAB =∠ABC , ∴△EAB ∽△ABC , ∴AE AB =AB BC . ∴AB 2=AE ·BC .(2)解 由(1)△EAB ∽△ABC ,∴BE AC =AB BC . 又AE ∥BC ,∴EF AF =BE AC ,∴AB BC =EF AF. 又AD ∥BC ,∴,∴AB =CD ,∴CD BC =EF AF ,∴58=EF6, ∴EF =308=154.。
【走向高考】2020年高考数学总复习 13-1几何证明选讲课后作业 北师大版
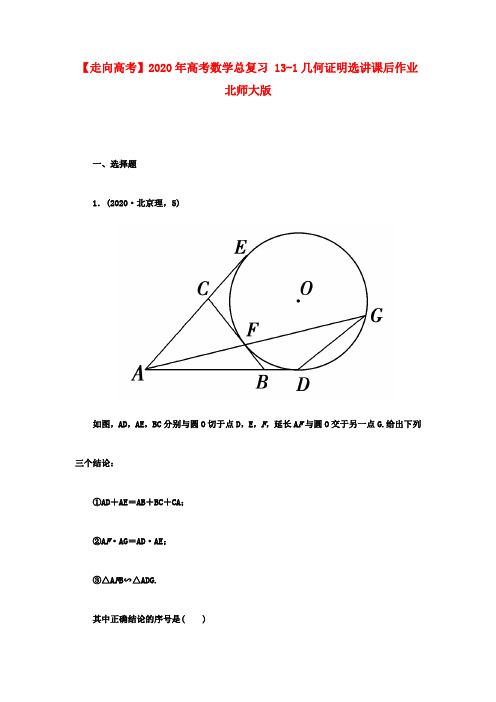
【走向高考】2020年高考数学总复习 13-1几何证明选讲课后作业北师大版一、选择题1.(2020·北京理,5)如图,AD,AE,BC分别与圆O切于点D,E,F,延长A F与圆O交于另一点G.给出下列三个结论:①AD+AE=AB+BC+CA;②A F·AG=AD·AE;③△A F B∽△ADG.其中正确结论的序号是( )A.①② B.②③C.①③ D.①②③[答案] A[解析]本题主要考查了圆的切线及有关定理.依题意:①正确,由圆的切线可知:BC=B F+F C=BD+CE,∴AD+AE=AB+BC+CA.②正确,∵A F·AG=AD2且AD=AE,∴A F·AG=AD·AE.③错误.若△A F B∽△ADG,则ABAG=A FAD,即A F·AG=AB·AD.这与A F·AG=AD2矛盾,故选A.2.自圆O外一点P引圆的切线,切点为A,M为PA的中点,过M引圆的割线交圆于B,C两点,且∠BM P=100°,∠BPC=40°,则∠MPB的大小为( )A.10°B.20°C.30°D.40°[答案] B[解析]因为PA与圆相切于点A,所以AM2=MB·MC.而M为PA的中点,所以PM=MA,则PM2=MB·MC,∴PMMC =MB PM.又∠BMP=∠PMC,所以ΔBMP∽△PMC,所以∠MPB=∠MCP,在△PMC中,由∠CMP+∠MPC +∠MCP=180°,即∠CMP+∠BPC+2∠MPB=180°,所以100°+40°+2∠MPB=180°,从而∠MPB=20°.二、填空题3.(2020·天津理,12)如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且D F=C F=2,A F:F B:B E=4:2:1.若CE与圆相切,则线段CE的长为______.[答案]7 2[解析]本题主要考查切割定理及相交弦定理,设每份为a,则A F=4a,F B=2a,BE=a,根据相交弦定理:D F·F C=A F·F B,则2=8a2,∴a2=14,由切割定理:EC2=BE·AE=7a2,∴EC2=74,∴EC=72.4.(2020·湖南理)如图所示,过⊙O 外一点P 作一条直线与⊙O 交于A ,B 两点.已知PA =2,点P 到⊙O的切线长PT =4,则弦AB 的长为________.[答案] 6[解析] 根据切线长定理:PT 2=PA·PB,PB =PT 2PA =162=8.所以AB =PB -PA =8-2=6.5.(2020·徐州模拟)如图,在梯形ABCD 中,AD∥BC,BD 与AC 相交于点O ,过点O 的直线分别交AB ,CD 于E ,F ,且E F ∥BC,若AD =12,BC =20,则E F =________.[答案] 15[解析] ∵AD∥BC,∴OB OD =BC AD =2012=53,∴OB BD =58, ∵OE∥AD,∴OE AD =OB BD =58, ∴OE=58AD =58×12=152,同理可求得O F =38BC =38×20=152,∴E F =OE +O F =15.6.(2020·湘潭模拟)如图,已知⊙O 的直径AB =5,C 为圆周上一点,BC =4,过点C作⊙O 的切线l ,过点A 作l 的垂线AD ,垂足为D ,则CD =________.[答案]12 5[解析]易得△BCA为直角三角形,且∠BCA=90°,∴AC=AB2-BC2=52-42=3.又∠DCA=∠CBA,∴Rt△BCA∽Rt△CDA,∴BABC=CACD,∴CD=CA·BCBA=3×45=125.三、解答题7.(2020·江苏,21A) 如图,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2).圆O1的弦AB交圆O2于点C(O1不在AB上).求证:AB:AC为定值.[解析]证明:连接AO 1,并延长分别交两圆于点E 和点D ,连结BD ,CE.因为圆O 1与圆O 2内切于点A ,所以点O 2在AD 上.故AD ,AE 分别为圆O 1,圆O 2的直径.从而∠ABD=∠ACE=π2.所以BD∥CE,于是AB AC =AD AE =2r 12r 2=r 1r 2.所以AB:AC 为定值.8.如图所示,已知⊙O 1与⊙O 2相交于A 、B 两点,过点A 作⊙O 1的切线交⊙O 2于点C ,过点B 作两圆的割线,分别交⊙O 1、⊙O 2于点D 、E ,DE 与AC 相交于点P.(1)求证:AD∥EC;(2)若AD 是⊙O 2的切线,且PA =6,PC =2,BD =9,求AD 的长.[解析] (1)∵AC 是⊙O 1的切线,∴∠BAC=∠D,又∵∠BAC=∠E,∴∠D=∠E,∴AD∥EC.(2)设BP =x ,PE =y ,∵PA=6,PC =2,∴xy=12(1)∵AD∥EC,∴PD PE =AP PC ,∴9+x y =62(2) 由(1)、(2)解得⎩⎪⎨⎪⎧x =3y =4 (∵x>0,y>0)∴DE=9+x +y =16,∵AD 是⊙O 2的切线,∴AD 2=DB·DE=9×16,∴AD=12.一、选择题1.如图,AB 是两圆的交点,AC 是小圆的直径,D 和E 分别是CA 和CB 的延长线与大圆的交点,已知AC =4,BE =10,且BC =AD ,则DE =( )A .6 3B .6C .8D .6 2[答案] A[解析]设CB=AD=x,则由割线定理,得CA·CD=CB·CE,即4(4+x)=x(x+10),化简得x2+6x-16=0,解得x=2或x=-8(舍去),即CD=6,CE=12,因为CA为直径,所以∠CBA=90°,即∠ABE=90°,则由圆的内接四边形对角互补,得∠D=90°,则CD2+DE2=CE2(勾股定理)∴62+DE2=122,∴DE=6 3.[点评] 本题关键是设出CB=AD=x,利用割线定理,通过解一元二次方程求出x.2.如图所示,矩形ABCD中,AB=12,AD=10,将此矩形折叠使点B落在AD边的中点E处,则折痕F G的长为( )A.13 B.63 5C.656D.636[答案] C[解析]过A作AH∥F G交DG于H,则四边形A F GH为平行四边形.∴AH=F G. ∵折叠后B点与E点重合,折痕为F G,∴B与E关于F G对称.∴BE⊥F G,∴BE⊥AH.∴∠ABE=∠DAH,∴Rt△ABE∽Rt△DAH.∴BEAB=AHAD.∵AB=12,AD=10,AE=12AD=5,∴BE=122+52=13,∴F G=AH=BE·ADAB=656.二、填空题3.(2020·湖南,11)如图,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则A F的长为________.[答案]23 3[解析]本小题考查内容为几何证明——圆与三角形相似.如图,连结AE,OA,OE,∠AOB=60°,OA=2,∴AD= 3.又∵△A F E∽△O F B,∴A FF O=AEBO,AE=2,BD=1,∴A F3-A F=2,∴A F =233.4.(2020·北京理)如图,⊙O 的弦ED ,CB 的延长线交于点A ,若BD⊥AE,AB =4,BC=2,AD =3,则DE =______;CE =________.[答案] 5 27[解析] 首先由割线定理不难知道AB·AC=AD·AE,于是AE =8,DE =5,又BD⊥AE,故BE 为直径,因此∠C=90°,由勾股定理可知CE 2=AE 2-AC 2=28,故CE =27.5.(2020·广东文)如图,在直角梯形ABCD 中,DC∥AB,CB⊥AB,AB =AD =a ,CD =a2,点E ,F 分别为线段AB 、AD 的中点,则E F =__________.[答案]a 2[解析]本题考查了最常规的平面几何知识,如图连接DE,BE綊CD,∴CDEB为矩形,∴DE⊥AB,DE又为中线,∴AD=DB=a,E F为中位线,∴E F=a2 .6.(文)(2020·广东文,15)如右图,在梯形ABCD 中,AB∥CD,AB =4,CD =2,E ,F 分别为AD ,BC 上点,且E F =3,E F ∥AB,则梯形AB F E 与梯形E F CD 的面积比为________.[答案] 7∶5[解析] 本题主要考查平面解析几何.利用面积公式.将线段AD 与BC 延长交于点H(如图所示),根据相似三角形面积之比等于相似比的平方,可得S △HCD S △HE F =49,S △HCD S △HAB =416,故梯形AB F E 与梯形E F CD 的面积比为7∶5.(理)(2020·广东理,15)如图,过圆O 外作一点P 分别作圆的切线和割线交圆于A ,B ,且PB =7,C 是圆上一点使得BC =5,∠BAC=∠APB,则AB =________.[答案]35[解析] 本题考查圆、圆的切线、相似三角形等平面几何知识.由圆的切线性质可知∠PAB=∠ACB,又∠APB=∠BAC,所以△PAB∽△ACB,所以AB BC =PB AB ,而BC =5,PB =7,∴AB 5=7AB,∴AB 2=35,AB =35.三、解答题7.(2020·新课标理,22)如图,D、E分别为△ABC的边AB、AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.(1)证明:C、B、D、E四点共圆;(2)若∠A=90°,且m=4,n=6,求C、B、D、E所在圆的半径.[解析](1)证明:如图,连接DE,在△ADE和△ACB中,AD·AB=mn=AE·AC,即ADAC =AEAB.又∠DAE=∠CAB,从而△ADE∽△ACB.因此∠ADE=∠ACB.所以C,B,D,E四点共圆.(2)m=4,n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.故AD=2,AB=12.如图,取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂直,两垂线相交于H 点,连接DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.由于∠A=90°,故GH∥AB,H F∥AC.从而H F=AG=5,D F=12(12-2)=5.故C,B,D,E四点所在圆的半径为5 2.8.(2020·辽宁理,22)如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.(1)证明:CD∥AB;(2)延长CD到F,延长DC到G,使得E F=EG,证明:A,B,G,F四点共圆.[解析](1)因为EC=ED,所以∠EDC=∠ECD.因为A,B,C,D四点在同一圆上,所以∠EDC=∠EBA.故∠ECD=∠EBA.所以CD∥AB.(2)由(1)知,AE=BE.因为E F=EG,故∠E F D=∠EGC,从而∠F ED=∠GEC.连结A F,BG,则△E F A≌△EGB,故∠F AE=∠GBE.又CD∥AB,∠EDC=∠ECD,所以∠F AB=∠GBA.所以∠A F G+∠GBA=180°.故A,B,G,F四点共圆.。
20届高考数学一轮复习讲义(提高版) 专题6.3 几何概型(解析版)

6.3 几何概型1.几何概型设D 是一个可度量的区域(例如线段、平面图形、立体图形等),每个基本事件可以视为从区域D 内随机地取一点,区域D 内的每一点被取到的机会都一样;随机事件A 的发生可以视为恰好取到区域D 内的某个指定区域d 中的点.这时,事件A 发生的概率与d 的测度(长度、面积、体积等)成正比,与d 的形状和位置无关.我们把满足这样条件的概率模型称为几何概型. 2.几何概型的概率计算公式一般地,在几何区域D 中随机地取一点,记事件“该点落在其内部一个区域d 内”为事件A ,则事件A 发生的概率P (A )=d 的测度D 的测度.3.要切实理解并掌握几何概型试验的两个基本特点 (1)无限性:在一次试验中,可能出现的结果有无限多个; (2)等可能性:每个结果的发生具有等可能性. 4.随机模拟方法(1)使用计算机或者其他方式进行的模拟试验,以便通过这个试验求出随机事件的概率的近似值的方法就是模拟方法.(2)用计算器或计算机模拟试验的方法为随机模拟方法.这个方法的基本步骤是①用计算器或计算机产生某个范围内的随机数,并赋予每个随机数一定的意义;②统计代表某意义的随机数的个数M 和总的随机数个数N ;③计算频率f n (A )=M N作为所求概率的近似值.考向一 长度【例1】某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是________.【修炼套路】---为君聊赋《今日诗》,努力请从今日始【套路秘籍】---千里之行始于足下【答案】12【解析】如图所示,画出时间轴.小明到达的时间会随机的落在图中线段AB 中,而当他的到达时间落在线段AC 或DB 上时,才能保证他等车的时间不超过10分钟,根据几何概型,得所求概率P =10+1040=12.【举一反三】1.在区间[0,5]上随机地选择一个数p ,则方程x 2+2px +3p -2=0有两个负根的概率为________. 【答案】 23【解析】 方程x 2+2px +3p -2=0有两个负根,则有⎩⎪⎨⎪⎧Δ≥0,x 1+x 2<0,x 1x 2>0,即⎩⎪⎨⎪⎧4p 2-4(3p -2)≥0,-2p <0,3p -2>0,解得p ≥2或23<p ≤1,又p ∈[0,5],则所求概率为P =3+135=1035=23.2.在区间[0,2]上随机地取一个数x ,则事件“-1≤121log ()2x +≤1”发生的概率为_______.【答案】 34【套路总结】求解与长度、角度有关的几何概型的方法求与长度(角度)有关的几何概型的概率的方法是把题中所表示的几何模型转化为长度(角度),然后求【解析】 由-1≤121log ()2x +≤1,得12≤x +12≤2,得0≤x ≤32.由几何概型的概率计算公式,得所求概率P =32-02-0=34.考向二 面积【例2】(1)一只蚂蚁在边长分别为6,8,10的△ABC 区域内随机爬行,则其恰在到顶点A 或顶点B 或顶点C 的距离小于1的地方的概率为________.(2)设不等式组⎩⎪⎨⎪⎧y ≤x ,y ≥-x ,2x -y -4≤0所表示的平面区域为M ,x 2+y 2≤1所表示的平面区域为N ,现随机向区域M 内抛一粒豆子,则豆子落在区域N 内的概率为________.【答案】(1)π48 (2)3π64【解析】(1)蚂蚁活动的范围是在三角形的内部,三角形的边长为6,8,10,是直角三角形,∴面积为12×6×8=24,而“恰在离三个顶点距离都小于1”正好是一个半径为1的半圆,面积为12π×12=π2,∴根据几何概型的概率公式可知其到三角形顶点的距离小于1的地方的概率为π224=π48.(2)画出两不等式组表示的平面区域,则图中阴影部分为两不等式组的公共部分,易知A (4,4),B ⎝ ⎛⎭⎪⎫43,-43,OA ⊥OB ,平面区域M 的面积S △AOB =12×423×42=163,阴影部分的面积S =14×π×12=π4.由几何概型的概率计算公式,得P=SS △AOB =π4163=3π64【举一反三】1.已知P 是△ABC 所在平面内一点,PB →+PC →+2PA →=0,现将一粒黄豆随机撒在△ABC 内,则黄豆落在△PBC 内的概率是________. 【答案】 12【解析】 以PB ,PC 为邻边作平行四边形PBDC ,则PB →+PC →=PD →,因为PB →+PC →+2PA →=0, 所以PB →+PC →=-2PA →,得PD →=-2PA →,由此可得,P 是△ABC 边BC 上的中线AO 的中点,点P 到BC 的距离等于A 到BC 距离的12,所以S △PBC =12S △ABC ,所以将一粒黄豆随机撒在△ABC 内,黄豆落在△PBC内的概率为S △PBCS △ABC=12. 2.在区间[1,5]和[2,4]上分别各取一个数,记为m 和n ,则方程x 2m 2+y 2n2=1表示焦点在x 轴上的椭圆的概率是________. 【答案】 12【解析】 ∵方程x 2m 2+y 2n2=1表示焦点在x 轴上的椭圆,∴m >n .【套路总结】求解与面积有关的几何概型时,关键是弄清某事件对应的面积,必要时可根据题意构造两个变量,把变量看成点的坐标,找到全部试验结果构成的平面图形,以便求解.如图,由题意知,在矩形ABCD 内任取一点Q (m ,n ),点Q 落在阴影部分的概率即为所求的概率,易知直线m =n 恰好将矩形平分,∴所求的概率为P =12.考向三 体积【例3】(1)在棱长为2的正方体ABCD —A 1B 1C 1D 1中,点O 为底面ABCD 的中心,在正方体ABCD —A 1B 1C 1D 1内随机取一点P ,则点P 到点O 的距离大于1的概率为________.(2)如图,在一个棱长为2的正方体鱼缸内放入一个倒置的无底圆锥形容器,圆锥的底面圆周与鱼缸的底面正方形相切,圆锥的顶点在鱼缸的缸底上,现在向鱼缸内随机地投入一粒鱼食,则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是________.【答案】(1)1-π12 (2)1-π4【解析】(1)记“点P 到点O 的距离大于1”为A ,P (A )=23-12×43π×1323=1-π12. (2)鱼缸底面正方形的面积为22=4,圆锥底面圆的面积为π.所以“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是1-π4.【举一反三】1.如图,在长方体ABCD—A1B1C1D1中,有一动点在此长方体内随机运动,则此动点在三棱锥A—A1BD内的概率为______.【答案】16【解析】因为1A A BDV-=1A ABDV-=13AA1×S△ABD=16×AA1×S矩形ABCD=16V长方体,故所求概率为1A A BDVV-长方体=16.考向四角度【例4】如图,四边形ABCD为矩形,AB=3,BC=1,在∠DAB内任作射线AP,则射线AP与线段BC有公共点的概率为________.【答案13【解析】因为在∠DAB内任作射线AP,所以它的所有等可能事件所在的区域H是∠DAB,当射线AP与线段BC有公共点时,射线AP落在∠CAB内,则区域H为∠CAB,所以射线AP与线段BC有公共点的概率为∠CAB∠DAB=30°90°=13.【举一反三】【套路总结】对于与体积有关的几何概型问题,关键是计算问题的总体积(总空间)以及事件的体积(事件空间),对于某些较复杂的也可利用其对立事件去求.1.在Rt △ABC 中,∠A =30°,过直角顶点C 作射线CM 交线段AB 于点M ,则AM >AC 的概率为________. 【答案】 16【解析】 设事件D 为“作射线CM ,使AM >AC ”.在AB 上取点C ′使AC ′=AC , 因为△ACC ′是等腰三角形,所以∠ACC ′=180°-30°2=75°,事件D 发生的区域μD =90°-75°=15°,构成事件总的区域μΩ=90°,所以P (D )=μD μΩ=15°90°=16.1.如图所示的长方形内,两个半圆均以长方形的一边为直径且与对边相切,在长方形内随机取一点,则此点取自阴影部分的概率是( )A .34π- B .332π-C .334π-D .33π-【答案】C【解析】如下图所示:【运用套路】---纸上得来终觉浅,绝知此事要躬行设长方形的长为4,宽为2,则120AOB ∠=∴阴影部分的面积21182223123323S ππ⎛⎫=⨯⨯-⨯⨯=- ⎪⎝⎭∴所求概率为:823334234p ππ-==-⨯本题正确选项:C2.最近各大城市美食街火爆热开,某美食店特定在2017年元旦期间举行特大优惠活动,凡消费达到88元以上者,可获得一次抽奖机会.已知抽奖工具是一个圆面转盘,被分为6个扇形块,分别记为1,2,3,4,5,6,其面积成公比为3的等比数列(即扇形块2是扇形块1面积的3倍),指针箭头指在最小的1区域内时,就中“一等奖”,则一次抽奖抽中一等奖的概率是( )A .140B .1121C .1364D .11093【答案】C 【解析】由题意,可设1,2,3,4,5,6 扇形区域的面积分别为,3,9,27,81,243x x x x x x ,则由几何概型得,消费88 元以上者抽中一等奖的概率1392781243364x P x x x x x x ==+++++ ,故选C.3.已知在椭圆方程22221x y a b+=中,参数,a b 都通过随机程序在区间()0,t 上随机选取,其中0t >,则椭圆的离心率在3,12⎛⎫⎪ ⎪⎝⎭之内的概率为( ) A .12 B .13 C .14 D .23【答案】A【解析】当a b > 时2223142a b a b a -<<⇒< ,当a b < 时,同理可得2ba <,则由下图可得所求的概率21121222t tP t ⨯⨯== ,故选A.4.在区间[]1,4-上随机选取一个数x ,则1x ≤的概率为( )A .25 B .35 C .15 D .23【答案】A【解析】因为()5,112D d ==--=,所以由几何概型的计算公式可得25d P D ==,应选答案A 。
.【学科精品】2020届高考数学一轮复习人教B版 选修4-1 几何证明选讲 .doc

选修4-1 几何证明选讲1.平行线截割定理与相似三角形了解平行线截割定理,理解相似三角形的判定和性质定理,了解直角三角形射影定理.2.圆的初步(1)理解圆周角定理,理解圆的切线的判定和性质定理及弦切角定理.(2)理解相交弦定理、割线定理、切割线定理.(3)理解圆内接四边形的判定与性质定理.知识点一平行线截割定理与相似三角形1.平行线的截割定理(1)平行线等分线段定理定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.推论1:经过三角形一边的中点与另一边平行的直线必平分第三边.推论2:经过梯形一腰的中点,且与底边平行的直线平分另一腰.(2)平行线分线段成比例定理定理:三条平行线截两条直线,所得的对应线段成比例.推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.2.相似三角形的判定定理(1)判定定理1:两角对应相等,两三角形相似.(2)判定定理2:两边对应成比例且夹角相等,两三角形相似.(3)判定定理3:三边对应成比例,两三角形相似. 3.相似三角形的性质定理(1)性质定理:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.(2)推论:相似三角形外接圆的直径比、周长比等于相似比,外接圆的面积比等于相似比的平方.4.直角三角形相似的判定定理(1)判定定理1:如果两个直角三角形有一个锐角对应相等,那么它们相似. (2)判定定理2:如果两个直角三角形的两条直角边对应成比例,那么它们相似. (3)判定定理3:如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.5.直角三角形射影定理直角三角形斜边上的高是两直角边在斜边上射影的比例中项;两直角边分别是它们在斜边上射影与斜边的比例中项.易误提醒1.在使用平行线截割定理时易出现对应边的对应顺序混乱,导致错误. 2.在解决相似三角形的判定或应用时易出现对应边和对应角的对应失误.3.射影定理是直角三角形中的一个重要结论,其实质就是三角形的相似.但要注意满足直角三角形射影定理结论的三角形不一定是直角三角形,所以要搞清楚定理中的条件和结论之间的关系,不能乱用.[自测练习]1.(2018·鞍山模拟)如图,在▱ABCD 中,E 是BC 上一点,BE ∶EC =2∶3,AE 交BD 于点F ,则BF ∶FD 的值为________.解析:因为AD =BC ,BE ∶EC =2∶3,所以BE ∶AD =2∶5,因为AD ∥BC ,所以BF ∶FD =BE ∶AD =2∶5,即BF ∶FD =25.答案:252.如图,D ,E 分别是△ABC 的边AB ,AC 上的点,DE ∥BC 且ADDB=2,那么△ADE 与四边形DBCE 的面积比是________.解析:∵DE ∥BC ,∴△ADE ∽△ABC , ∴S △ADE S △ABC =AD2AB2.∵AD DB =2,∴AD AB =23, ∴S △ADE S △ABC =49,故S △ADE S 四边形DBCE =45.答案:453.在Rt △ACB 中,∠C =90°,CD ⊥AB 于D ,若BD ∶AD =1∶9,则tan ∠BCD 的值为________.解:由射影定理得CD 2=AD ·BD , 又BD ∶AD =1∶9, 令BD =x ,则AD =9x (x >0). ∴CD 2=9x 2,CD =3x . Rt △CDB 中 ,tan ∠BCD =BD CD =x 3x =13. 答案:13知识点二 圆的初步 1.圆周角(1)定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半. (2)推论1:①同弧或等弧所对的圆周角相等; ②同圆或等圆中,相等的圆周角所对的弧也相等. (3)推论2:①半圆(或直径)所对的圆周角是直角; ②90°的圆周角所对的弦是直径. 2.圆的切线(1)判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. (2)性质定理:圆的切线垂直于经过切点的半径.(3)切线长定理:从圆外一点引圆的两条切线,切线长相等,圆心和这一点的连线平分两条切线的夹角.3.弦切角定理及其推论(1)定理:弦切角的度数等于它所夹的弧的度数的一半. (2)推论:弦切角等于它所夹的弧所对的圆周角. 4.圆中的比例线段(1)相交弦定理:圆内的两条相交弦,每条弦被交点分成的两条线段长的积相等. (2)割线定理:从圆外一点引圆的两条割线,该点到每条割线与圆的交点的两条线段长的积相等.(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.易误提醒1.解决圆周角、圆心角及弦切角问题时,要注意角之间关系,易于混淆导致错误. 2.使用相交弦定理与切割线定理时,注意对应线段成比例及相似三角形知识的应用.[自测练习]4.如图所示,CD 是圆O 的切线,切点为C ,点B 在圆O 上,BC =2,∠BCD =30°,则圆O 的面积为________.解析:过B 作⊙O 的直径BA ,连接AC (图略),则∠ACB =90°.又由弦切角定理得∠CAB =∠BCD =30°,∴AB =2BC =4.∴半径OA =2,∴S =πr 2=4π.答案:4π5.如图所示,已知⊙O 的割线P AB 交⊙O 于A ,B 两点,割线PCD 经过圆心,若P A =3,AB =4,PO =5,则⊙O 的半径为________.解析:设⊙O 的半径为r .由割线定理得P A ·PB =PC ·PD,3×7=(PO -r )(PO +r ),即21=25-r 2,∴r 2=4,∴r =2.答案:2考点一 平行线分线段成比例定理的应用|1.如图,等边三角形DEF 内接于△ABC ,且DE ∥BC ,已知AH ⊥BC 于点H ,BC =4,AH =3,求△DEF 的边长.解:设DE =x ,AH 交DE 于点M ,显然MH 的长度与等边三角形DEF 的高相等,又DE ∥BC ,则DEBC =AM AH =AH -MH AH ,所以x 4=3-32x 3=2-x 2,解得x =43. 2.如图,在△ABC 中,点D 是AC 的中点,点E 是BD 的中点,AE 交BC 于点F ,求BFFC的值.解:如图,过点D 作DM ∥AF 交BC 于点M . ∵点E 是BD 的中点,∴在△BDM 中,BF =FM . 又点D 是AC 的中点, ∴在△CAF 中,CM =MF , ∴BF FC =BF FM +MC =12.平行线分线段成比例定理及推论的应用(1)利用平行线分线段成比例定理来计算或证明,首先要观察平行线组,再确定所截直线,进而确定比例线段及比例式,同时注意合比性质、等比性质的运用.(2)解决此类问题往往需要作辅助的平行线,要结合条件构造平行线组,再应用平行线分线段成比例定理及其推论转化比例式解题.考点二 相似三角形的判定及性质|1.如图,AD ,BE 是△ABC 的两条高,DF⊥AB ,垂足为F ,交BE 于点G ,交AC 的延长线于H ,求证:DF 2=GF ·HF .证明:在△AFH 与△GFB 中,因为∠H +∠BAC =90°,∠GBF +∠BAC =90°,所以∠H =∠GBF . 因为∠AFH =∠BFG =90°,所以△AFH ∽△GFB ,所以HF BF =AFGF ,所以AF ·BF =GF ·HF .因为在Rt △ABD 中,FD ⊥AB ,所以DF 2=AF ·BF .所以DF 2=GF ·HF .2.如图,M 是平行四边形ABCD 的边AB 的中点,直线l 过点M 分别交AD ,AC 于点E ,F ,交CB 的延长线于点N .若AE =2,AD =6,求AFAC的值. 解:∵AD ∥BC ,∴△AEF ∽△CNF , ∴AF CF =AE CN ,∴AF AF +CF =AE AE +CN. ∵M 为AB 的中点,∴AE BN =AMBM =1,∴AE =BN ,∴AF AC =AF AF +CF =AE AE +BN +BC =AE 2AE +BC. ∵AE =2,BC =AD =6,∴AF AC =22×2+6=15. 3.如图所示,CD 垂直平分AB ,点E 在CD 上,DF ⊥AC ,DG ⊥BE ,F ,G 分别为垂足.求证:AF ·AC =BG ·BE . 证明:因为CD 垂直平分AB , 所以∠ADC =∠BDC =90°,AD =DB .在Rt △ADC 中,因为DF ⊥AC ,所以AD 2=AF ·AC .同理BD 2=BG ·BE .所以AF ·AC =BG ·BE .1.证明相似三角形的一般思路 (1)先找两对内角对应相等;(2)若只有一个角对应相等,再判定这个角的两邻边是否对应成比例; (3)若无角对应相等,就要证明三边对应成比例. 2.注意射影定理的其他变式.考点三 圆中有关定理及推论的应用|(1)(2018·高考湖北卷)如图,P A 是圆的切线,A 为切点,PBC 是圆的割线,且BC =3PB ,则ABAC=________.[解析] 因为P A 是圆的切线,A 为切点,PBC 是圆的割线,由切割线定理,知P A 2=PB ·PC =PB (PB +BC ).因为BC =3PB ,所以P A 2=4PB 2,即P A =2PB .由△P AB ∽△PCA ,所以AB AC =PB PA =12.[答案]1 2(2)(2018·高考全国卷Ⅰ)如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.①若D为AC的中点,证明:DE是⊙O的切线;②若OA=3CE,求∠ACB的大小.[解]①证明:如图,连接AE,由已知得,AE⊥BC,AC⊥AB.在Rt△AEC中,由已知得,DE=DC,故∠DEC=∠DCE.连接OE,则∠OBE=∠OEB.又∠ACB+∠ABC=90°,所以∠DEC+∠OEB=90°,故∠OED=90°,DE是⊙O的切线.②设CE=1,AE=x,由已知得AB=23,BE=12-x2.由射影定理可得,AE2=CE·BE,所以x2=12-x2,即x4+x2-12=0.可得x=3,所以∠ACB=60°.(1)涉及圆的切线问题时要注意弦切角的转化;关于圆周上的点,常作直径(或半径)或向弦(弧)两端作圆周角或弦切角.(2)与圆有关的比例线段解题思路:①见到圆的两条相交弦就要想到相交弦定理.②见到圆的两条割线就要想到割线定理.③见到圆的切线和割线就要想到切割线定理.1.(2018·高考重庆卷)如图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若P A =6,AE=9,PC=3,CE∶ED=2∶1,则BE=________.解析:由切割线定理,知P A2=PC·PD,即62=3PD,解得PD=12,所以CD=PD-PC=9,所以CE=6,ED=3.由相交弦定理,知AE·BE=CE·ED,即9BE=6×3,解得BE =2.答案:22.如图所示,已知D 为△ABC 的BC 边上一点,⊙O 1经过点B ,D ,交AB 于另一点E ,⊙O 2经过点C ,D ,交AC 于另一点F ,⊙O 1与⊙O 2的另一交点为G .(1)求证:A 、E 、G 、F 四点共圆;(2)若AG 切⊙O 2于G ,求证:∠AEF =∠ACG .证明:(1)如图,连接GD ,四边形BDGE ,CDGF 分别内接于⊙O 1,⊙O 2, ∴∠AEG =∠BDG ,∠AFG =∠CDG , 又∠BDG +∠CDG =180°, ∴∠AEG +∠AFG =180°, ∴A 、E 、G 、F 四点共圆.(2)∵A 、E 、G 、F 四点共圆,∴∠AEF =AGF ,∵AG 与⊙O 2相切于点G ,∴∠AGF =∠ACG ,∴∠AEF =∠ACG .32.四点共圆的证明方法【典例】如图,AB 是⊙O 的直径,弦BD ,CA 的延长线相交于点E ,EF 垂直BA 的延长线于点F .(1)求证:BE ·DE +AC ·CE =CE 2;(2)若D 是BE 的中点,证明E ,F ,C ,B 四点共圆.[思路点拨] (1)利用割线定理易证;(2)本题已知AB 是⊙O 的直径,可得到线段相等,利用四个点到一定点的距离相等证明四点共圆.[解] (1)证明:由割线定理得EA ·EC =DE ·BE , 所以BE ·DE +AC ·CE =EA ·CE +AC ·CE =CE 2, 所以BE ·DE +AC ·CE =CE 2. (2)连接CB ,CD ,FD . 因为AB 是⊙O 的直径, 所以∠ECB =90°, 所以CD =12EB .因为EF ⊥BF ,所以FD =12BE .所以E ,F ,C ,B 四点到点D 的距离相等. 所以E ,F ,C ,B 四点共圆. [方法点评] 四点共圆的证明方法:(1)若四个点到一定点的距离相等,则这四个点共圆.(2)若一个四边形的一组对角的和等于180°,则这个四边形的四个顶点共圆. (3)若一个四边形的一个外角等于它的内对角,则这个四边形的四个顶点共圆. (4)若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线段的两个端点共圆.(5)若AB ,CD 两线段相交于点P ,且P A ·PB =PC ·PD ,则A ,B ,C ,D 四点共圆. (6)若AB ,CD 两线段延长后相交于点P ,且P A ·PB =PC ·PD ,则A ,B ,C ,D 四点共圆. (7)若四边形两组对边乘积的和等于对角线的乘积,则四边形的四个顶点共圆. [跟踪练习] 如图,点F 是△ABC 外接圆上BC的中点,点D ,E 在边AC 上,使得AD =AB ,BE =EC .证明:B ,E ,D ,F 四点共圆.证明:如图,连接FC ,FB ,则FC =FB .连接EF ,则△CEF ≌△BEF ,所以∠BFE =∠CFE .因为A ,B ,F ,C 共圆,所以∠CAB +∠CFB =180°,所以∠CAB +2∠BFE =180°.连接BD ,因为AB =AD ,所以∠ABD =∠ADB ,所以∠CAB +2∠ADB =180°.所以∠ADB =∠BFE .所以B ,E ,D ,F 四点共圆.A 组 考点能力演练1.(2018·大连模拟)如图,已知D 为△ABC 中AC 边的中点,AE ∥BC ,ED 交AB 于G ,交BC 延长线于F ,若BG ∶GA =3∶1,BC =8,求AE 的长.解:因为AE ∥BC ,D 为AC 的中点,所以AE =CF ,AE BF =AG BG =13.设AE =x ,又BC =8,所以x x +8=13,3x =x +8,所以x =4.所以AE =4. 2.(2018·洛阳模拟)如图,AB 为圆O 的直径,CD 为垂直于AB 的一条弦,垂足为E ,弦BM 与CD 交于点F .(1)证明:A ,E ,F ,M 四点共圆; (2)证明:AC 2+BF ·BM =AB 2.证明:(1)连接AM (图略),则∠AMB =90°. ∵AB ⊥CD ,∴∠AEF =90°.∴∠AMB +∠AEF =180°,即A ,E ,F ,M 四点共圆. (2)连接AC ,CB (图略).由A ,E ,F ,M 四点共圆, 得BF ·BM =BE ·BA .在Rt △ACB 中,BC 2=BE ·BA ,AC 2+CB 2=AB 2,∴AC 2+BF ·BM =AB 2. 3.已知:如图,在△ABC 中,AB =AC ,∠BAC =90°,D ,E ,F 分别在AB ,AC ,BC 上,AE =13AC ,BD =13AB ,且CF =13BC .求证:(1)EF ⊥BC ; (2)∠ADE =∠EBC . 证明:设AB =AC =3a , 则AE =BD =a ,CF =2a . (1)CE CB =2a 32a =23,CF CA =2a 3a =23. 又∠C 为公共角,故△BAC ∽△EFC , 由∠BAC =90°得∠EFC =90°,故EF ⊥BC . (2)由(1)得EF =FC AC ·AB =2a ,故AE EF =a 2a =22,AD BF =2a 22a =22,∴AE EF =AD BF, ∴△ADE ∽△FBE ,所以∠ADE =∠EBC .4.(2018·兰州双基)如图,在正△ABC 中,点D ,E 分别在BC ,AC 上,且BD =13BC ,CE =13CA ,AD ,BE 相交于点P .求证: (1)四点P ,D ,C ,E 共圆;(2)AP ⊥CP .证明:(1)在正△ABC 中,由BD =13BC ,CE =13CA ,知:△ABD ≌△BCE , ∴∠ADB =∠BEC ,即∠ADC +∠BEC =π,∴四点P ,D ,C ,E 共圆.(2)连接DE (图略),在△CDE 中,CD =2CE ,∠ACD =60°,由正弦定理知∠CED =90°, 由四点P ,D ,C ,E 共圆知,∠DPC =∠DEC ,∴AP ⊥CP .5.如图,设AB 为⊙O 的任一条不与直线l 垂直的直径,P 是⊙O 与l 的公共点,AC ⊥l ,BD ⊥l ,垂足分别为C ,D ,且PC =PD .(1)求证:l 是⊙O 的切线;(2)若⊙O 的半径OA =5,AC =4,求CD 的长.解:(1)证明:连接OP ,∵AC ⊥l ,BD ⊥l ,∴AC ∥BD .又OA =OB ,PC =PD ,∴OP ∥BD ,从而OP ⊥l .∵点P 在⊙O 上,∴l 是⊙O 的切线.(2)由(1)可知OP =12(AC +BD ), ∴BD =2OP -AC =10-4=6.过点A 作AE ⊥BD ,垂足为E ,则BE =BD -AC =6-4=2.∴在Rt △ABE 中,AE =AB2-BE2=102-22=4 6.∴CD =4 6.B 组 高考题型专练1.(2018·高考新课标全国卷Ⅰ)如图,四边形ABCD 是⊙O 的内接四边形,AB 的延长线与DC 的延长线交于点E ,且CB =CE .(1)证明:∠D =∠E ;(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.证明:(1)由题设知A,B,C,D四点共圆,所以∠D=∠CBE.由已知得∠CBE=∠E,故∠D=∠E.(2)如图,设BC的中点为N,连接MN,则由MB=MC知MN⊥BC,故O在直线MN上.又AD不是⊙O的直径,M为AD的中点,故OM⊥AD,即MN⊥AD.所以AD∥BC,故∠A=∠CBE.又∠CBE=∠E,故∠A=∠E.由(1)知,∠D=∠E,所以△ADE为等边三角形.2.(2018·高考湖南卷)如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F.证明:(1)∠MEN+∠NOM=180°;(2)FE·FN=FM·FO.证明:(1)如图所示.因为M,N分别是弦AB,CD的中点,所以OM⊥AB,ON⊥CD,即∠OME=90°,∠ENO=90°,因此∠OME+∠ENO=180°.又四边形的内角和等于360°,故∠MEN+∠NOM=180°.(2)由(1)知,O,M,E,N四点共圆,故由割线定理即得FE·FN=FM·FO.3.(2018·高考陕西卷)如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.(1)证明:∠CBD=∠DBA;(2)若AD=3DC,BC=2,求⊙O的直径.解:(1)证明:因为DE为⊙O的直径,则∠BED+∠EDB=90°,又BC⊥DE,所以∠CBD+∠EDB=90°,从而∠CBD=∠BED.又AB切⊙O于点B,得∠DBA=∠BED,所以∠CBD =∠DBA .(2)由(1)知BD 平分∠CBA ,则BA BC =AD CD=3,又BC =2,从而AB =3 2. 所以AC =AB2-BC2=4,所以AD =3.由切割线定理得AB 2=AD ·AE ,即AE =AB2AD=6,故DE =AE -AD =3,即⊙O 的直径为3.4.(2018·高考全国卷Ⅱ)如图,O 为等腰三角形ABC 内一点,⊙O 与△ABC 的底边BC 交于M ,N 两点,与底边上的高AD 交于点G ,且与AB ,AC 分别相切于E ,F 两点.(1)证明:EF ∥BC ;(2)若AG 等于⊙O 的半径,且AE =MN =23,求四边形EBCF 的面积.解:(1)证明:由于△ABC 是等腰三角形,AD ⊥BC ,所以AD 是∠CAB 的平分线. 又因为⊙O 分别与AB ,AC 相切于点E ,F ,所以AE =AF ,故AD ⊥EF .从而EF ∥BC .(2)由(1)知,AE =AF ,AD ⊥EF ,故AD 是EF 的垂直平分线.又EF 为⊙O 的弦,所以O 在AD 上.连接OE ,OM ,则OE ⊥AE .由AG 等于⊙O 的半径得AO =2OE ,所以∠OAE =30°.因此△ABC 和△AEF 都是等边三角形.因为AE =23,所以AO =4,OE =2.因为OM =OE =2,DM =12MN =3,所以OD =1. 于是AD =5,AB =1033. 所以四边形EBCF 的面积为12×⎝⎛⎭⎫10332×32-12×(23)2×32=1633.。
2020届一轮复习人教A版 几何证明选讲 课时作业
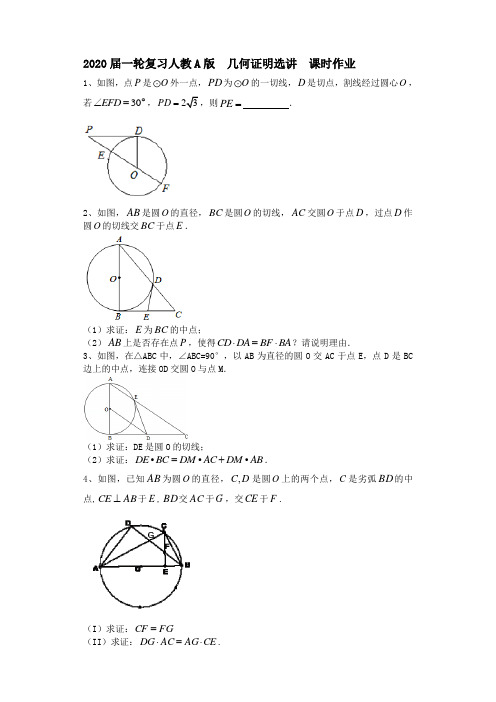
2020届一轮复习人教A 版 几何证明选讲 课时作业1、如图,点P 是O 外一点,PD 为O 的一切线,D 是切点,割线经过圆心O ,若30EFD ∠=︒,23PD =,则PE = .2、如图,AB 是圆O 的直径,BC 是圆O 的切线,AC 交圆O 于点D ,过点D 作圆O 的切线交BC 于点E .(1)求证:E 为BC 的中点;(2)AB 上是否存在点P ,使得CD DA BF BA ⋅=⋅?请说明理由.3、如图,在△ABC 中,∠ABC=90°,以AB 为直径的圆O 交AC 于点E ,点D 是BC 边上的中点,连接OD 交圆O 与点M .(1)求证:DE 是圆O 的切线;(2)求证:•••DE BC DM AC DM AB =+.4、如图,已知AB 为圆O 的直径,D C ,是圆O 上的两个点,C 是劣弧BD 的中点,AB CE ⊥于E ,BD 交AC 于G ,交CE 于F .(I )求证:FG CF =(II )求证:CE AG AC DG ⋅=⋅.5、如图,已知AB 为圆O 的直径,D C ,是圆O 上的两个点,C 是劣弧BD 的中点,AB CE ⊥于E ,BD 交AC 于G ,交CE 于F .(I )求证:FG CF =(II )求证:CE AG AC DG ⋅=⋅.6、如图,AC 是圆O 的直径,ABCD 是圆内接四边形,BE DE ⊥于点E ,且BE 与圆O 相切于点B .(1)求证:CB 平分ACE ∠;(2)若6,3AB BE ==,求AD 的长.7、如图,AC 是圆O 的直径,ABCD 是圆内接四边形,BE DE ⊥于点E ,且BE 与圆O 相切于点B .(1)求证:CB 平分ACE ∠;(2)若6,3AB BE ==,求AD 的长.8、如图,AB 为圆O 的一条弦,C 为圆O 外一点.CA ,CB 分别交圆O 于D ,E 两点. 若AB =AC ,EF ⊥AC 于点F ,求证:F 为线段DC 的中点.9、如图,圆周角BAC ∠的平分线与圆交于点D ,过点D 的切线与弦AC 的延长线交于点E ,AD 交BC 于点F .(1)求证://BC DE ;(2)若,,,D E C F 四点共圆,且AC BC =,求BAC ∠.10、已知AD 是ABC ∆的外角EAC ∠的平分线,交BC 的延长线于点D ,延长DA 交ABC ∆的外接圆于点F ,连接,FB FC .(1)求证:FB FC =;(2)若AB 是ABC ∆外接圆的直径,120EAC ∠=,33BC =,求AD 的长.11、如图,圆M 与圆N 交于,A B 两点,以A 为切点作两圆的切线分别交圆M 和圆N 于,C D 两点,延长DB 交圆M 于点E ,延长CB 交圆N 于点F ,已知5,10BC DB ==.(1)求AB 的长;(2)求CF DE. 12、如图,四边形ABCD 外接于圆,AC 是圆周角BAD ∠的角平分线,过点C 的切线与AD 延长线交于点E ,AC 交BD 于点F .(1)求证://BD CE ;(2)若AB 是圆的直径,4,1AB DE ==,求AD 的长.13、如图,ABC∆的外接圆为O,延长CB至Q,再延长QA至P,使得22QC QA BA QC-=⋅.(1)求证:QA为O的切线;(2)若AC恰好为BAP∠的平分线,6,12AB AC==,求QA的长度.14、如图,P是圆O外一点,PA是圆O的切线,A 为切点,割线PBC与圆O交于B,C,PAPC2=,D为PC中点,AD的延长线交圆O于点E,证明:OPED CBA(Ⅰ)ECBE=;(Ⅱ)22PBDEAD=⋅.15、如图,已知圆O是ABC∆的外接圆,,AB BC AD=是BC边上的高,AE是圆O的直径,过点C作圆O的切线交BA的延长线于点F.(1)求证:AC BC AD AE=;(2)若2,2AF CF==AE的长.16、如图所示,PQ为O的切线,切点为Q,割线PEF过圆心O,且QM QN=.(Ⅰ)求证:PF QN PQ NF =; (Ⅱ)若3QP QF ==,求PF 的长.17、如图所示,PQ 为O 的切线,切点为Q ,割线PEF 过圆心O ,且QM QN =.(Ⅰ)求证:PF QN PQ NF =;(Ⅱ)若3QP QF ==,求PF 的长.18、如图,已知:C 是以AB 为直径的半圆O 上一点,CH AB ⊥于点H ,直线AC 与过B 点的切线相交于点,D F 为BD 中点,连接AF 交CH 于点E .(1)求证:FC 是O 的切线;(2)若,FB FE O =2,求FC .19、如图AB 是圆O 的一条弦,过点A 作圆的切线AD ,作BC AC ⊥,与该圆交于点D ,若23AC =2CD =.(1)求圆O 的半径;(2)若点E 为AB 中点,求证,,O E D 三点共线.20、如图,四边形ABCD 内接于⊙O ,过点A 作⊙O 的切线EP 交CB 的延长线于P ,已知EAD PCA ∠=∠.证明:(1)AD AB =;(2)2DA DC BP =⋅.参考答案1、答案:2连接,DE EF ,依题意可知90PDO EDF ∠=∠=,而30EFD ∠=︒,故在Rt PDO ∆中,30,4cos30P PO ∠===,且E 为PO 中点,所以2PE =. 【考点】几何证明选讲.2、答案:(1)证明见解析;(2)存在点F 使得CD DA BF BA ⋅=⋅.试题分析:(1)先由弦切角定理DBE BDE ∠=∠,进而C EDC ∠=∠,EC DE =,可得BE EC =,可得结论;(2)由射影定理2BD CD DA =⋅,作DF AB ⊥于点F ,由弦切角定理得2BD BF BA =⋅,即存在点F 使得CD DA BF BA ⋅=⋅.试题(1)连接BD ,∵AB 是圆O 的直径,∴90ADB ∠=︒,又BC 、DE 是圆O 的切线,∴BE DE =,∴DBE BDE ∠=∠,又∵DBE ∠与C ∠互余,BDE ∠与EDC ∠互余,∴C EDC ∠=∠,∴EC DE =,∴BE EC =,因而E 为BC 的中点.(2)在直角三角形ABC 中,2BD CD DA =⋅,作DF AB ⊥于点F ,则在直角三角形ABD 中,2BD BF BA =⋅,因而CD DA BF BA ⋅=⋅,则存在点F 使得CD DA BF BA ⋅=⋅.【考点】1、弦切角定理的应用;2、射影定理的应用.3、答案:试题分析:(1)由点D 是BC 中点,点O 是AB 中点⇒1//2OD AC ⇒,A BOD AEO EOD ∠=∠∠=∠,OA OE =⇒A AEO ∠=∠⇒BOD EOD ∠=∠⇒EOD BOD ∆≅∆⇒090OED OBD ∠=∠=⇒OE ED ⊥⇒DE 是圆O 的切线;(2)延长DO 交圆O 于点F ,由(1)知DE 是圆O 的切线,而DF 是圆O 的割线⇒2DE DM DF =⇒222DM DF DE DE BC ==⇒DM AC DM AB DM +=()()222AC AB DM OD OF DM DF +=+=.试题(1)连结OE , 点D 是BC 中点,点O 是AB 中点,∴1//2OD AC ,∴,A BOD AEO EOD ∠=∠∠=∠, OA OE =,∴A AEO ∠=∠,∴BOD EOD ∠=∠,在EOD ∆和BOD ∆中, OE OB =,∴EOD BOD ∆≅∆,∴090OED OBD ∠=∠=,即OE ED ⊥.E 是圆O 上一点,∴DE 是圆O 的切线(2)延长DO 交圆O 于点F ,()()222DM AC DM AB DM AC AB DM OD OF DM DF +=+=+=,由(1)知DE 是圆O 的切线,而DF 是圆O 的割线,∴2DE DM DF =,由(1)知EOD BOD ∆≅∆,∴DE DB =,点D 是BC 的中点,∴2BC DB =.∴222DM DF DE DE BC ==【考点】1、三角形的全等;2、切割线定理;3、切线的定义.4、答案:试题分析:(I )在同一三角形中证明线段相等,一般利用对应两角相等,而等弧对应角相等,即DAC CAB ∠=∠,其余角也相等即DGA ACE ∠=∠,又CGF DGA ∠=∠,所以CGF ACE ∠=∠,即FG CF =(II )证明线段成比例,一般利用三角形相似,易得ADG RT ∆∽AEC RT ∆,所以AC CE AG DG =,即CE AG AC DG ⋅=⋅ 试题(I )C 是劣弧BD 的中点CAB DAC ∠=∠∴在AEC RT ADG RT ∆∆与中, 90=∠=∠AEC ADBACE DGA ∠=∠∴,又CGF DGA ∠=∠,所以CGF ACE ∠=∠.从而,在CGF ∆中,FG CF =.(II )在AEC RT ADG RT ∆∆与中,,CAB DAC ∠=∠因此,ADG RT ∆∽AEC RT ∆,由此可得AC CE AG DG =,即CE AG AC DG ⋅=⋅【考点】三角形相似【名师名师点评】1.解决与圆有关的成比例线段问题的两种思路(1)直接应用相交弦、切割线定理及其推论;(2)当比例式(等积式)中的线段分别在两个三角形中时,可转化为证明三角形相似,一般思路为“相似三角形→比例式→等积式”.在证明中有时还要借助中间比来代换,解题时应灵活把握.2.应用相交弦定理、切割线定理要抓住几个关键内容:如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等.5、答案:试题分析:(I )在同一三角形中证明线段相等,一般利用对应两角相等,而等弧对应角相等,即DAC CAB ∠=∠,其余角也相等即DGA ACE ∠=∠,又CGF DGA ∠=∠,所以CGF ACE ∠=∠,即FG CF =(II )证明线段成比例,一般利用三角形相似,易得ADG RT ∆∽AEC RT ∆,所以AC CE AG DG =,即CE AG AC DG ⋅=⋅ 试题(I )C 是劣弧BD 的中点CAB DAC ∠=∠∴在AEC RT ADG RT ∆∆与中, 90=∠=∠AEC ADB ACE DGA ∠=∠∴,又CGF DGA ∠=∠,所以CGF ACE ∠=∠.从而,在CGF ∆中,FG CF =.(II )在AEC RT ADG RT ∆∆与中,,CAB DAC ∠=∠因此,ADG RT ∆∽AEC RT ∆,由此可得AC CE AG DG =,即CE AG AC DG ⋅=⋅【考点】三角形相似【名师名师点评】1.解决与圆有关的成比例线段问题的两种思路(1)直接应用相交弦、切割线定理及其推论;(2)当比例式(等积式)中的线段分别在两个三角形中时,可转化为证明三角形相似,一般思路为“相似三角形→比例式→等积式”.在证明中有时还要借助中间比来代换,解题时应灵活把握.2.应用相交弦定理、切割线定理要抓住几个关键内容:如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等.6、答案:(1)证明见解析;(2)6.试题分析:(1)要证CB 平分ACE ∠,只要证ACB ECB ∠=∠,由已知这两个角是两个直角三角形中的锐角,因此只要证其余角相等,即CAB CBE ∠=∠,这两个角是同弧所对的圆周角和弦切角,它们显然相等,结论得证;(2)由(1)的证明知ABC BEC ∆∆,从而有12BC AC =,这样在直角ABC ∆中,可得出30CAB ∠=︒,也有30CBE ∠=︒,这两个三角形,ABC BEC ∆∆中的所有边长都可求出,可利用切割线定理求出CD ,从而由勾股定理得AD .(此题可由60ACB ∠=︒得60BCE ∠=︒,从而60ACD ∠=︒,由三角形全等就可得AD 长)试题(1)证明:BE 与圆O 相切于点B ,∴CBE BAC ∠=∠.①BE DE ⊥∴90BCE CBE ∠=-∠②AC 是圆O 的直径,∴90BCA BAC ∠=-∠③由①②③得BCA ∠=BCE ∠,即CB 平分ACE ∠.(2)由(1)知,ABC BEC ∆∆6,3,AB BE ∴==1,2BC BE AC AB ∴==即1sin ,2CAB ∠=30,CBE CAB ∴∠=∠=故AC=CB =CE =由切割线定理得223EB EC ED ED =⋅⇒=⇒=6CD AD ∴=∴=.【考点】弦切角定理,切割线定理,相似三角形的判定与性质.7、答案:(1)证明见解析;(2)6.试题分析:(1)要证CB 平分ACE ∠,只要证ACB ECB ∠=∠,由已知这两个角是两个直角三角形中的锐角,因此只要证其余角相等,即CAB CBE ∠=∠,这两个角是同弧所对的圆周角和弦切角,它们显然相等,结论得证;(2)由(1)的证明知ABC BEC ∆∆,从而有12BC AC =,这样在直角ABC ∆中,可得出30CAB ∠=︒,也有30CBE ∠=︒,这两个三角形,ABC BEC ∆∆中的所有边长都可求出,可利用切割线定理求出CD ,从而由勾股定理得AD .(此题可由60ACB ∠=︒得60BCE ∠=︒,从而60ACD ∠=︒,由三角形全等就可得AD 长)试题(1)证明:BE 与圆O 相切于点B ,∴CBE BAC ∠=∠.①BE DE ⊥∴90BCE CBE ∠=-∠②AC 是圆O 的直径,∴90BCA BAC ∠=-∠③由①②③得BCA ∠=BCE ∠,即CB 平分ACE ∠.(2)由(1)知,ABC BEC ∆∆6,3,AB BE ∴==1,2BC BE AC AB ∴==即1sin ,2CAB ∠=30,CBE CAB ∴∠=∠=故AC=CB =CE =由切割线定理得223EB EC ED ED =⋅⇒=⇒=6CD AD ∴=∴=.【考点】弦切角定理,切割线定理,相似三角形的判定与性质.8、答案:试题分析:要证F 为线段DC 的中点,由于EF ⊥AC ,因此只要证ED EC =,也即只要证EDC ECD ∠=∠,而这两个角都可与ABC ∠相等,因此结论得证.试题证明:因为点A 、D 、E 、B 在圆O 上,即四边形ADEB 是圆内接四边形,所以∠B =∠EDC 。
2020届高考数学大一轮复习 第十二章 几何证明选讲课件 文 北师大版

(1)证明:EF∥BC; (2)若AG等于⊙O的半径,且AE=MN=2 3 ,求四边形EBCF 的面积.
解:(1)证明:由于△ABC是等腰三角形,AD⊥BC, 所以AD是∠CAB的平分线. 又因为⊙O分别与AB,AC相切于点E,F,所以AE=AF,即 △AEF也是等腰三角形. 故AD⊥EF.从而EF∥BC.
1.(2015· 高考课标卷Ⅰ)如图,AB是⊙O的直径,AC是⊙O 的切线,BC交⊙O于点E.
(1)若D为AC的中点,证明:DE是⊙O的切线; (2)若OA= 3CE,求∠ACB的大小.
解:(1)证明:如图,连接AE,由已知得AE⊥BC,AC⊥AB.
在Rt△AEC中,由已知得DE=DC,故∠DEC=∠DCE. 连接OE,则∠OBE=∠OEB.
3.直角三角形的射影定理
直角三角形斜边上的高是两直角边在斜边上射影的比例中 项;两直角边分别是它们在斜边上射影与斜边的比例中项. 如图,在Rt△ABC中,CD是斜边AB上的高,则有CD2= AD· BD,AC2=AD· AB,BC2=BD· AB.
1.(2015· 高考课标卷Ⅱ)如图,O为等腰三角形ABC内一点,⊙ O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点 G,且与AB,AC分别相切于E,F两点.
考点二 命题点 圆周角定理
圆中的相关定理与有关线段
1.圆周角定理与圆心角定理 第十二章 几何证明选讲(1)圆周角定理及其推论
①定理:圆上一条弧所对的圆周角等于它所对的圆心角的一 半.
②推论: (ⅰ)推论1:同弧或等弧所对的圆周角相等;同圆或等圆中, 相等的圆周角所对的弧也相等. (ⅱ)推论2:半圆(或直径)所对的圆周角是直角;90° 的圆周角 所对的弦是直径. (2)圆心角定理:圆心角的度数等于它所对弧的度数.
高考数学一轮复习 几何证明选讲 第1课时 相似三角形的判定及有关性质课件 理(选修41)

另一腰.
平分
• 2.平行线分线段成比例定理 • 三条平行线截两条直线,所得的___对__应线段成比例. • 推论:平行于三角形一边的直线截其他两边(或两边的延长
线)所得的对应线段成_______. • 3.相似三角形的判定 比例 • 判定定理1:两角对应_____,两三角形相似. • 判定定理2:两边对应___相__等___且夹角______,两三角形相 • 似判.定定理3:三边对应___成__比__例_,两三角形相相等似.
【解析】 (1)证明:∵OE∥BC, ∴AAEB=AAOC.又∠BAC=∠CAB,∴△EAO∽△BAC. ∴OBCE=AAEB,同理OBCF=DDCF. ∵AD∥EF∥BC,∴AABE=DDCF,∴OBCE=OBCF. ∴OE=OF.
(2)∵OE∥AD,∴BBOD=BBEA,∴△EBO∽△ABD. ∴OADE=BBOD,同理OBCE=AAOC. 又 AD∥BC,∴BBOD=CAOC,∴OADE+OBCE=CAOC+AAOC=1. • 【答案】 (1)略 (2)1
• 答案 6
解析 由直角三角形射影定理,得 AC2=AD·AB. ∴AB=AACD2=422=8,∴BD=AB-AD=8-2=6.
授人以渔
题型一 平行线分线成比例
例1 如图,在梯形 ABCD 中,AD∥BC,EF 经过梯形对角线 的交点 O,且 EF∥AD. (1)求证:OE=OF; (2)求OADE+OBCE的值.
即6-3x=3
x
,所以 3
x2-6x+9=0,解得
x=3.
(2)若△ADP∽△BCP,则ABDC=BAPP,
即 3
33=6-x x,解得 x=23.
2019-2020年高三数学一轮复习第十三篇几何证明选讲第2节直线与圆的位置关系课件理

解析:由切割线定理得 PA2=PC·PD,
得 PD= PA 2 = 6 2 =12,
PC
3
所以 CD=PD-PC=12-3=9,即 CE+ED=9,
因为 CE∶ED=2∶1,所以 CE=6,ED=3.
由相交弦定理得 AE·EB=CE·ED,
即 9EB=6×3,得 EB=2.
所以 CH⊥AD.又 AB 为圆的直径,
所以∠ACB=90°,
所以 CB2=BH·BA. 因为∠BCF=∠CAB=∠D,
所以△BCF∽△BDC,所以 BC = BF
BD
BC
,
所以 BC2=BF·BD,所以 BH·BA=BF·BD.
审题点拨
关键点
所获信息
AC 是☉O1 的切线,割线 DE 与 AC 交于点 P
定义、定理 及推论
内容
定义 判定定理
如果一条直线与一个圆有唯一公共点,则这条直线叫做这 个圆的切线,公共点叫做切点 经过半径的外端并且 垂直于 这条半径的直线是圆的切线
性质定理
性质定理 的推论
圆的切线 垂直于 经过切点的半径 经过圆心且垂直于切线的直线必经过 切点 . 经过切点且垂直于切线的直线必经过 圆心 .
(2)若AB=4,AE=2,求CD的长.
【例 2】 (2015 沈阳一模)如图,已知 AB 是圆 O 的直径,C,D 是圆 O 上的两 个点,CE⊥AB 于 E,BD 交 AC 于 G,交 CE 于 F,CF=FG. (1)求证:C 是劣弧 BD的中点;
证明:(2)因为∠GBC= π -∠CGB,∠FCB= π -∠GCF, 22
(B)①②④
(C)③⑤
(D)①③⑤
解析:①错误,若弧不一样,则圆心角与圆周角的关系不确定;②错误,只有在同 圆或等圆中,相等的圆周角所对的弧才相等;③正确,可以推出等腰梯形的对角 互补,所以有外接圆;④错误,弦切角等于它所夹的弧所对的圆周角,所夹的弧 的度数等于该弧所对圆心角的度数,所以弦切角所夹弧的度数等于弦切角度 数的2倍;⑤正确,圆内接四边形ABCD的对角互补.
【名师推荐资料】新2020版高考数学一轮复习 第一部分 基础与考点过关 几何证明选讲学案 选修4-1

选修41 几何证明选讲1. 如图,四边形ABCD 是圆O 的内接四边形,已知∠BOD=100°,求∠BCD.解:由题设∠BAD=12∠BOD =50°,则∠BCD=180°-∠BAD=130°.2. 如图,AB 是圆O 的直径,MN 与圆O 相切于点C ,AC =12BC ,求sin ∠MCA 的值.解:由弦切角定理得,∠MCA =∠ABC,sin ∠ABC =AC AB =AC AC 2+BC 2=AC 5AC =55. 故sin ∠MCA =55. 3. 已知△ABC 内接于圆O ,BE 是圆O 的直径,AD 是BC 边上的高.求证:BA·AC=BE·AD.证明:连结AE.∵ BE 是圆O 的直径,∴ ∠BAE =90°,∴ ∠BAE =∠ADC.∵ ∠BEA =∠ACD,∴ Rt △BEA ∽Rt △ACD. ∴ BE BA =ACAD,∴ BA ·AC =BE·AD. 4. 如图,在圆O 中,M ,N 是弦AB 的三等分点,弦CD ,CE 分别经过点M ,N.若CM =2,MD =4,CN =3,求线段NE 的长.解:设AM =a ,由相交弦定理可知,CM ·MD =AM·MB,CN ·NE =AN·NB,即2×4=a×2a,3×NE =2a×a,消去a 解得NE =83.5. 如图,EA 与圆O 相切于点A ,D 是EA 的中点,过点D 引圆O 的割线,与圆O 相交于点B ,C ,连结EC.求证:∠DEB=∠DCE.证明:∵ EA 与圆O 相切于点A ,由切割线定理得DA 2=DB·DC. ∵ D 是EA 的中点,∴ DA =DE.∴ DE 2=DB·DC.∴ DE DC =DB DE.∵ ∠EDB =∠CDE,∴ △EDB ∽△CDE ,∴ ∠DEB =∠DCE.1. 圆周角定理(1) 圆周角定理:圆周角的度数等于其所对弧的度数的一半.(2) 推论1:同弧(或等弧)所对的圆周角相等.同圆或等圆中,相等的圆周角所对的弧相等.(3) 推论2:半圆(或直径)所对的圆周角等于90°.反之,90°的圆周角所对的弧为半圆(或弦为直径).2. 圆的切线(1) 圆的切线的性质与判定① 相关定义:当直线与圆有2个公共点时,直线与圆相交;当直线与圆有且只有1个公共点时,直线与圆相切,此时直线是圆的切线,公共点称为切点;当直线与圆没有公共点时,直线与圆相离.② 切线的判定定理:过半径外端且与这条半径垂直的直线是圆的切线.③切线的性质定理:圆的切线垂直于经过切点的半径.④切线长定理:从圆外一点引圆的两条切线,切线长相等.(2)弦切角①定义:顶点在圆上,一边与圆相切,另一边与圆相交的角称为弦切角.②弦切角定理:弦切角的度数等于其所夹弧的度数的一半.③推论:同弧(或等弧)上的弦切角相等,同弧(或等弧)上的弦切角与圆周角相等.3. 相交弦定理相交弦定理:圆的两条相交弦,每条弦被交点分成的两条线段长的积相等.4. 切割线定理(1)割线定理:从圆外一点引圆的两条割线,该点到每条割线与圆的交点的两条线段长的积相等.(2)切割线定理:从圆外一点引圆的一条割线与一条切线,切线长是这点到割线与圆的两个交点的线段长的等比中项.5. 圆内接四边形(1)圆内接四边形性质定理:圆内接四边形的对角互补.(2)圆内接四边形判定定理:如果四边形的对角互补,则此四边形内接于圆.[备课札记], 1圆周角与弦切角定理及应用), 1) (2017·苏锡常镇一模)如图,圆O的直径AB=6,C为圆上一点,BC=3,过点C作圆的切线l,过点A作l的垂线AD,AD分别与直线l、圆交于点D,E.求∠DAC的大小与线段AE的长.解:如图,连结OC,BE,因为BC=OB=OC=3,所以∠CBO=60°.因为∠DCA=∠CBO,所以∠DCA=60°.又AD⊥DC得∠DAC=30°.因为∠ACB=90°,得∠CAB=30°,所以∠EAB=60°,从而∠ABE=30°,所以AE =12AB =3.变式训练如图,CP 是圆O 的切线,P 为切点,直线CO 交圆O 于A ,B 两点,AD ⊥CP ,垂足为D.求证:∠DAP=∠BAP.证明:∵ CP 与圆O 相切,∴ ∠DPA =∠PBA. ∵ AB 为圆O 的直径,∴ ∠APB =90°, ∴ ∠BAP =90°-∠PBA.∵ AD ⊥CP ,∴ ∠DAP =90°-∠DPA, ∴ ∠DAP =∠BAP., 2 圆的切线的判定与性质), 2) 如图,∠PAQ 是直角,圆O 与射线AP 相切于点T ,与射线AQ 相交于B ,C 两点.求证:BT 平分∠OBA.∵ AT 是切线,∴ OT ⊥AP.∵ ∠PAQ 是直角,即AQ⊥AP,∴ AB∥OT, ∴ ∠TBA =∠BTO.又OT =OB ,∴ ∠OTB =∠OBT,∴ ∠OBT =∠TBA,即BT 平分∠OBA. 备选变式(教师专享)如图,AC 切圆O 于D ,AO 的延长线交圆O 于B ,BC 切圆O 于B ,若AD∶AC=1∶2,求AOOB的值.∵ AD ∶AC =1∶2,∴ D 为AC 的中点. 又AC 切圆O 于D ,∴ OD ⊥AC.∴OA =OC. ∴ △AOD ≌△COD ,∴ ∠1=∠2. 又△OBC ≌△ODC ,∴ ∠3=∠2.∴ ∠1=∠2=∠3=60°,∴ OC =2OB.∴ OA =2OB ,即AOOB=2., 3 圆内接四边形的判定与性质), 3) (2017·南通、扬州、泰州模拟)如图,已知AB 为圆O 的一条弦,点P 为弧AB 的中点,过点P 任作两条弦PC ,PD ,分别交AB 于点E ,F.求证:PE·PC=PF·PD.因为∠PAB=∠PCB,点P 为弧AB 的中点, 所以∠PAB=∠PBA, 所以∠PCB =∠PBA.又∠DCB=∠DPB,所以∠PFE=∠PBA+∠DPB=∠PCB+∠DCB=∠PCD,所以E,F,D,C四点共圆.所以PE·PC=PF·PD.备选变式(教师专享)如图,已知AP是圆O的切线,P为切点,AC是圆O的割线,与圆O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.(1)求证:A,P,O,M四点共圆;(2)求∠OAM+∠APM的大小.(1)证明:连结OP,OM,因为AP与圆O相切于点P,所以OP⊥AP.因为M是圆O的弦BC的中点,所以OM⊥BC,于是∠OPA+∠OMA=180°.由圆心O在∠PAC的内部,可知四边形APOM的对角互补,所以A,P,O,M四点共圆.(2)解:由(1)得A,P,O,M四点共圆,所以∠OAM=∠OPM.因为AP是圆O的切线,P为切点,所以OP⊥AP,所以∠OPM+∠APM=90°,所以∠OAM+∠APM=90°., 4相交弦定理、割线定理及切割线定理的应用), 4) (2017·苏州暑期检测)如图,△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=60°,且PD =1,PB=9,求EC.解:∵ 弦切角∠PAE=∠ABC=60°,又PA=PE,∴△PAE为等边三角形.由切割线定理有PA2=PD·PB=9,∴ AE=EP=PA=3,ED=EP-PD=2,EB=PB-PE=6,由相交弦定理有EC·EA=EB·ED=12, ∴ EC =12÷3=4. 变式训练(2017·南京、盐城期末)如图,AB 是半圆O 的直径,点P 为半圆O 外一点,PA ,PB 分别交半圆O 于点D ,C.若AD =2,PD =4,PC =3,求BD 的长.解:由割线定理得PD·PA=PC·PB, 则4×(2+4)=3×(3+BC ),解得BC =5.又AB 是半圆O 的直径,故∠ADB=π2.则在Rt △PDB 中有BD =PB 2-PD 2=64-16=4 3.1. (2017·苏州期末)如图,点E 是圆O 内两条弦AB 和CD 的交点,过AD 延长线上一点F 作圆O 的切线FG ,G 为切点,已知EF =FG.求证:EF∥CB.证明:由切割线定理得FG 2=FA·FD.又EF =FG ,所以EF 2=FA·FD,即EF FA =FD EF.因为∠EFA=∠DFE,所以△DEF∽△EAF, 所以∠FED=∠FAE.因为∠FAE=∠DAB=∠DCB,所以∠FED=∠BCD, 所以EF∥CB.2. 如图所示,△ABC 是圆O 的内接三角形,且AB =AC ,AP ∥BC ,弦CE 的延长线交AP于点D.求证:AD 2=DE·DC.证明:连结AE ,则∠AED=∠B.∵ AB =AC ,∴ ∠ACB =∠B,∴ ∠ACB=∠AED. ∵ AP ∥BC ,∴ ∠ACB =∠CAD,∴ ∠CAD =∠AED.又∠ADC=∠EDA,∴ △ACD ∽△EAD. ∴ CD AD =AD ED,即AD 2=DE·DC.3. (2017·南京、盐城模拟)△ABC 的顶点A ,C 在圆O 上,B 在圆O 外,线段AB 与圆O 交于点M.(1) 如图①,若BC 是圆O 的切线,且AB =8,BC =4,求线段AM 的长; (2) 如图②,若线段BC 与圆O 交于另一点N ,且AB =2AC ,求证:BN =2MN.(1) 解:因为BC 是圆O 的切线,故由切割线定理得BC 2=BM·BA. 设AM =t ,因为AB =8,BC =4,所以42=8(8-t ),解得t =6,即线段AM 的长度为6. (2) 证明:因为四边形AMNC 为圆内接四边形, 所以∠A=∠MNB.又∠B=∠B,所以△BMN∽△BCA,所以BN BA =MN CA.因为AB =2AC ,所以BN =2MN.4. (2017·常州期末)如图,过圆O 外一点P 作圆O 的切线PA ,切点为A ,连结OP 与圆O 交于点C ,过点C 作AP 的垂线,垂足为D.若PA =25,PC ∶PO =1∶3,求CD 的长.解:延长PO 交圆O 于点B ,连结OA. 设PC =x (x >0),则由PC∶PO=1∶3, 得PO =3x ,则PB =5x. 因为PA 是圆O 的切线,所以PA 2=PC·PB,即(25)2=x·(5x ),解得x =2. 故OA =OC =4.因为PA 是圆O 的切线,所以OA⊥PA.又CD⊥PA,则OA∥CD,因此CD OA =PC PO =13.又OA =4,所以CD =43.1. (2017·苏北四市期末)如图,AB 为半圆O 的直径,点D 为弧BC 的中点,点E 为BC 的中点.求证:AB·BC=2AD·BD.证明:因为D 为弧BC 的中点, 所以∠DBC=∠DAB,DC =DB.因为AB 为半圆O 的直径,所以∠ADB=90°. 又E 为BC 的中点,所以EC =EB ,所以DE⊥BC, 所以△ABD∽△BDE.所以AB AD =BD BE =2BDBC ,所以AB·BC=2AD·BD.2. 如图,AB 为圆O 的切线,A 为切点,C 为线段AB 的中点,过C 作圆O 的割线CED ,求证:∠CBE=∠BDE.证明:因为CA 为圆O 的切线,所以CA 2=CE·CD.又CA =CB ,所以CB 2=CE·CD,即CB CE =CD CB.又∠ECB=∠BCD,所以△BCE ∽△DCB , 所以∠CBE=∠BDE.3. 如图,AB 是圆O 的直径,弦BD ,CA 的延长线相交于点E ,EF 垂直于BA ,交BA 的延长线于点F. 求证:(1) ∠DEA=∠DFA;(2) AB 2=BE·BD-AE·AC.证明:(1) 连结AD ,因为AB 为圆O 的直径, 所以∠ADB=90°.又EF⊥AB,∠EFA =90°, 所以A ,D ,E ,F 四点共圆. 所以∠DEA=∠DFA.(2) 由(1)知,BD ·BE =BA·BF, 连结BC.又△ABC∽△AEF, ∴ AB AE =ACAF,即AB·AF=AE·AC. ∴ BE ·BD -AE·AC=BA·BF-AB·AF=AB (BF -AF )=AB 2.4. 如图,直线AB 与圆O 相切于点B ,直线AO 交圆O 于D ,E 两点,BC ⊥DE ,垂足为C ,且AD =3DC ,BC =2,求圆O 的直径.解:因为DE 是圆O 的直径,则∠BED+∠EDB=90°. 又BC⊥DE,所以∠CBD+∠EDB=90°. 又AB 切圆O 于点B ,得∠ABD=∠BED, 所以∠CBD=∠DBA.即BD 平分∠CBA,则AB BC =ADCD =3.又BC =2,从而AB =32,所以AC =AB 2-BC 2=4, 所以AD =3.由切割线定理得AB 2=AD·AE,即AE =AB 2AD=6,故DE =AE -AD =3,即圆O 的直径为3.与圆有关的辅助线的五种作法 (1) 有弦,作弦心距;(2) 有直径,作直径所对的圆周角; (3) 有切点,作过切点的半径; (4) 两圆相交,作公共弦; (5) 两圆相切,作公切线.。
高三数学第一轮复习强化训练 22.1《几何证明选讲》新人教版必修2

22.1几何证明选讲【考纲要求】1.几何证明选讲(1)了解平行线截割定理,会证明并应用直角三角形射影定理.(2)会证明并应用圆周角定理、圆的切线的判定定理及性质定理.(3)会证明并应用相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理.(4)了解平行投影的含义,通过圆柱与平面的位置关系了解平行投影;会证平面与圆柱面的截线是椭圆(特殊情形是圆).(5)了解下面定理:定理在空间中,取直线为轴,直线与相交于点 O ,其夹角为α, 围绕旋转得到以 O 为顶点,为母线的圆锥面,任取平面π,若它与轴交角为β(π与平行,记β=0),则:①β>α,平面π与圆锥的交线为椭圆;②β=α,平面π与圆锥的交线为抛物线;③β<α,平面π与圆锥的交线为双曲线.(6)会利用丹迪林(Dandelin)双球(如图所示,这两个球位于圆锥的内部,一个位于平面π的上方,一个位于平面π的下方,并且与平面π及圆锥面均相切,其切点分别为F、E)证明上述定理①情形:当β>α时,平面π与圆锥的交线为椭圆.(图中上、下两球与圆锥面相切的切点分别为点B和点C,线段BC与平面π相交于点A.)(7)会证明以下结果:①在(6)中,一个丹迪林球与圆锥面的交线为一个圆,并与圆锥的底面平行,记这个圆所在平面为π';②如果平面π与平面π'的交线为m,在(5)①中椭圆上任取一点A,该丹迪林球与平面π的切点为F,则点A到点F的距离与点A到直线m的距离比是小于1的常数e.(称点F为这个椭圆的焦点,直线m为椭圆的准线,常数e为离心率.)(8)了解定理(5)③中的证明,了解当β无限接近α时,平面π的极限结果.【基础知识】1、平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等。
推理1:经过三角形一边的中点与另一边平行的直线必平分第三边。
推理2:经过梯形一腰的中点,且与底边平行的直线平分另一腰。
2、平分线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例。
高考数学一轮复习课件:几何证明选讲

返回目录
6.直线与圆的位置关系 圆 相如离果;圆与直线没有公共点,这种情况我们说直线与
如果圆心到一条直线的距离小于半径 , 则这条直线 和该圆一定相交于两点,这时我们说直线与圆相交,这条 直线叫做 圆的割线 ;
如果一条直线与圆只有一个公共点,则这条直线叫 做这个圆的切线,公共点叫做切点.
7.圆切线的判定定理、性质及推论. 8.圆周角、圆周角定理及推论. 9.弦切角、弦切角定理及推论. 10.圆的切线、内接四边形、弦切角、比例线段.
返回目录
题型分析
考点一 计算问题 如图所示,圆O的直径AB=6,C 为圆周上一点,BC=3,过C作圆 的切线l,过A作l的垂线AD,AD 分别与直线l、圆交于点D,E,则 ∠DAC= ,线段AE的长为 .
返回目录
【分析】本题主要考查直线与圆的关系及平面几何基本 知识. 【解析】如图所示:∵OC⊥l,AD⊥l,∴AD∥OC. ∵BC=3, ∴△OBC为等边三角形,∠B=60°, ∴∠CAB=30°,∴∠ACO=30°, ∴∠DAC=30°.∴∠EAO=60°.连结OE, ∴∠OAE为等边三角形.∴AE=3.
线NB垂直于直线ON,且 交圆O于B点. 过B点的切 线交直线ON于K.证明:∠OKM=90°.
【分析】利用射影定理、圆的切线性质解题是关键.
返回目录
【证明】(1)因为MA是圆O的切线,所以OA⊥AM.
又因为AP⊥OM,在Rt△OAM源自,由射影定理知,OA2=OM·OP.
(2)因为BK是圆O的切线,BN⊥OK,
1.射影定理的内容及其证明; 2.圆周角与弦切角定理的内容及其证明; 3.圆幂定理的内容及其证明; 4.圆内接四边形的性质与判定; 5.平行投影的性质与圆锥曲线的统一定义.
2020年高三理科数学一轮复习试题选编31:几何证明(教师版)

2020年高三理科数学一轮复习试题选编31:几何证明姓名____________班级___________学号____________分数______________一、选择题1 .(北京市海淀区2013届高三上学期期末考试数学理试题 )如图,PC 与圆O 相切于点C ,直线PO 交圆O 于,A B 两点,弦CD 垂直AB 于E . 则下面结论中,错误..的结论是 A.BEC ∆∽DEA ∆ B .ACE ACP ∠=∠C .2DE OE EP =⋅D .2PC PA AB =⋅【答案】D解:由切割线定理可知2PC PA PB =⋅,所以D 错误,所以选 D .2 .(北京市顺义区2013届高三第一次统练数学理科试卷(解析))如图,AC AB ,分别与圆O 相切于点ADE C B ,,是⊙O 的割线,连接CE BE BD CD ,,,.则( )A .DE AD AB ⋅=2B .CE AC DE CD ⋅=⋅C .CE BD CD BE ⋅=⋅ D .CD BD AE AD ⋅=⋅【答案】答案C 由切线长定理知2ABAD AE =⋅,所以A 错误.选C .3 .(2012北京理)5.如图. ∠ACB=90º,CD ⊥AB 于点D,以BD 为直径的圆与BC 交于点E.则 ( )A .CE ·CB=AD ·DBB .CE ·CB=AD ·ABC .AD ·AB=CD ² D .CE ·EB=CD ²【答案】【解析】在ACB ∆中,∠ACB=90º,CD ⊥AB 于点D,所以DB AD CD∙=2,由切割线定理的BCB CE CD ∙=2,所以CE ·CB=AD ·DB .【答案】A4 .(北京市石景山区2013届高三一模数学理试题)如图,直线AM 与圆相切于点M, ABC 与ADE 是圆的两条割线,且BD ⊥AD,连接M D .EC .则下面结论中,错误..的结论是( )A .∠ECA = 90oB .∠CEM=∠DMA+∠DBAC .AM 2= AD·AED .AD·DE =AB·BC 【答案】D5 .(北京市东城区普通校2013届高三3月联考数学(理)试题 )如图,已知AB 是⊙O 的一条弦,点P 为AB 上一点, PC OP ⊥,PC 交⊙O 于C ,若4AP =,2PB =,则PC 的长是( )A .3B. C .2 DAB COP【答案】B6 .(2011年高考(北京理))如图,,,AD AE BC 分别于圆O 切于点,,D E F ,延长AF 与圆O 交于点G ,给出下列三个结论:①AD AE AB BC CA +=++;②AF AG AD AE ⋅=⋅; ③AFB ∆∽ADG ∆其中正确的结论的序号是 ( ) A .①② B .②③ C .①③ D .①②③ 【答案】A【命题立意】本题考查了平面几何问题,圆以及圆的切线问题的研究,通过圆的切线所具有的性质反映出平面几何中的转化思想以及三角形的相似关系.【解析】因为,,AD AE BC 都是圆的切线,所以B D B E =,CE CF =,所以A BBC C A A++=+++,所以①正确;因为,,AD AE BC 都是圆的切线,所以AD AE =,由切割线定理得2AF AG AD AD AE ⋅==⋅,所以②正确; 由切线定理知ACD BDF BFD ∠=∠=∠,ABF BDF BFD ∠=∠+∠,所以③错误,选择 ( )A .7 .(2013北京房山二模数学理科试题及答案)如图,,,,A B C D 是⊙O 上的四个点,过点B 的切线与DC 的延长线交于点E .若110BCD ︒∠=,则DBE ∠=( )A .75︒B .70︒C .60︒D .55︒【答案】B .二、填空题8 .(2013届北京海滨一模理科)如图,AP 与O 切于点A ,交弦DB 的延长线于点P ,过点B 作圆O 的切线交AP 于点C . 若90ACB ∠=︒,3,4BC CP ==,则弦DB 的长为_______.D CB PAO【答案】2459 .(2013北京丰台二模数学理科试题及答案)如图,已知⊙O 的弦AB 交半径OC 于点D,若AD=4,BD=3,OC=4,则CD 的长为______.【答案】 2;10.(北京市东城区普通高中示范校2013届高三3月联考综合练习(二)数学(理)试题 )如图,是圆O 的切线,切点为A ,D 点在圆内,DB 与圆相交于C ,若3BC DC ==,2=OD ,6AB =,则圆O 的半径为 .CA BOD【答案】11.(北京市通州区2013届高三上学期期末考试理科数学试题 )如图,已知5AD =,8DB =,AO =则圆O 的半径OC 的长为 .A【答案】5【 解析】取BD 的中点,连结OM ,则O M B D ⊥,因为8BD =,所以4,549DM MB AM ===+=,所以22290819OM AO AM =-=-=,所以半径5OB ====,即5OC =。
高考数学课程一轮复习 第67课时 几何证明选讲

相交弦定理割线定理切割线定理切线长定理选修4-1几何证明选讲(理)第67课时几何证明选讲【考点点知】知己知彼,百战不殆相似三角形考点主要集中在利用平面三角形的相似及直角三角形求解线段之比,线段的长等具有一定的探究性的问题.圆的考题题源相当的丰富,主要热点集中于圆的切线与割线,求解角度及线段长度等题型.考点1:相似三角形(1)平行线截割定理:三条平行线截两条直线,所得的对应线段成比例.(2)相似三角形的判定①相似三角形的定义:对应角相等,对应边成比例的两个多边形叫做相似多边形(对应边的比值叫做相似比).②相似三角形的判定(特例为两个直角三角形的相似判定):判定1: AA;判定2:SAS;判定3: SSS.(“SAS”为两边对应成比例,夹角相等).(3)相似三角形的性质:性质1:对应高(中线、角平分线、周长、外接(内切)圆的半径、外接(内切)圆的周长)的比等于相似比;性质2: 对应面积(外接圆、内切圆)的比等于相似比的平方.(4)直角三角形的射影定理:在Rt△ABC中,90C∠= ,CD AB⊥.①2CD AD BD=⋅;②2AC AD AB=⋅;③2BC BD AB=⋅.考点2:圆(1)圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.①圆心角定理:圆心角的度数等于它所对弧的度数.②推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.③半圆(或直径)所对的圆周角是直角;90 的圆周角所对的弦是直径.(2)圆的切线的判定及性质:①圆的切线的判定定理;②圆的切线的性质定理:圆的切线垂直于经过切点的半径.(3)圆幂定理:PA PB PC PD⋅=⋅(4)圆内接四边形的性质与判定:①性质1,对角互补;性质2,外角等于它的内角的对角.②判定定理:一个四边形的对角互补⇒四个顶点共圆.(推论:一个外角=它的内对角,⇒四个顶点共圆).ABCDO(5)平面与圆柱面的截线是椭圆(特例是圆).离心率cos ce aβ==(β是平面与圆柱的轴线的交角).(6)平面与圆锥面的截线,离心率cos cos c e a βα==(α是圆锥母线与轴线的交角,β是平面与圆锥的轴线的交角).【小题热身】明确考点,自省反思1.(2010朝阳期末)如图,已知O 的直径5AB =, C 为圆周上一点,4BC =,过点C 做O 的切线l ,过点A 作l 的垂线AD ,垂足为D ,则CD = .2.(2010湖南卷)如图1所示,过⊙O 外一点P 作一 直线与⊙O 交于A ,B 两点.已知PA=2,点P 到⊙O 的切 线长PT=4,则弦AB 的长为 .3. (2010广东卷)如图3,在直角梯形ABCD 中,//DC AB ,CB AB ⊥,AB AD a ==,2a CD =, 点,E F 分别是线段,AB AD 的中点,则EF = .【考题点评】分析原因,醍醐灌顶例 1.如图所法,圆O 的直径6=AB ,C 为圆周上一点,3=BC ,过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分别与直线l 、圆交于点D 、E ,则∠DAC = ,线段AE 的长为 .思路透析: 由已知条件可得090ACB ∠=, BC=3, AB=6 , 则AC=060ABC ∠=.∵直线l 为圆O 上过点C 的切线, ∴060DCA ABC ∠=∠=, 又∵AD l ⊥,∴09030DAC DCA ∠=-∠=,且09sin 6022AD AC ===, 01cos602DC AC ===,∵2DC DE AD =⋅, ∴22734922DC DE AD ===, 93322AE AD DE =-=-=.例2.如图,ABC ∆中,E D ,分别是BC 边与AC 边上的点, BC AD AC AB ⊥⊥,,8,6,===AC AB EC BE . 求BE 的长.思路透析: ∵8,6,==⊥AC AB AC AB ,∴10=BC .又∵BC AD ⊥,∴5322==BC AC CD . 作EF //AD 交BC 于F 点, ∵EC BC =,∴5==BF CF , 从而42553285=⨯=⋅==CD CA CF EC BE . 例3.如图,已知AP 是O 的切线,P 为切点,AC 是O 的割线,与O 交于B C ,两点,圆心O 在PAC ∠的内部,点M 是BC 的中点.(Ⅰ)证明AP O M ,,,四点共圆; (Ⅱ)求OAM APM ∠+∠的大小. 思路透析:(Ⅰ)证明:连结OP OM ,. 因为AP 与O 相切于点P ,所以OP AP ⊥.因为M 是O 的弦BC 的中点,所以OM BC ⊥. 于是180OPA OMA ∠+∠=°. 由圆心O 在PAC ∠的内部,可知四边形APOM 的对角互补,所以AP O M ,,,四点共圆. (Ⅱ)解:由(Ⅰ)得AP O M ,,,四点共圆,所以OAM OPM ∠=∠. 由(Ⅰ)得OP AP ⊥.由圆心O 在PAC ∠的内部,可知90OPM APM ∠+∠=°. 所以90OAM APM ∠+∠=°.例4.如图1,在正方形ABCD 中,点E,F 分别为边BC,CD 的中点,AF,DE 相交于点G ,则可得结论:①AF=DE ;②AF ⊥DE .(不需要证明)(Ⅰ)如图2,若点E ,F 不是正方形ABCD 的边BC ,CD 的中点,但满足CE=DF ,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)(Ⅱ)如图3,若点E ,F 分别在正方形ABCD 的边CB 的延长线和DC 的延长线上,且CE=DF ,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.(Ⅲ)如图4,在(2)的基础上,连接AE 和EF ,若点M ,N ,P ,Q 分别为AE ,EF ,FD ,AD 的中点,请判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种?A A并写出证明过程.思路透析:(Ⅰ)成立;(Ⅱ)成立. 四边形ABCD 是正方形,90ADF DCE ∴== ∠∠,AD CD =. 又EC DF = ,ADF DCE ∴△≌△. E F AF DE ∴==,∠∠.又90E CDE +=∠∠,90F CDE ∴+=∠∠.90FGD ∴= ∠,AF DE ∴⊥.(Ⅲ)正方形.证明:AM ME AQ DQ == ,,12MQ ED MQ ED ∴=,∥, 同理12NP ED NP ED =,∥,MQ NP ∴∥. ∴四边形MNPQ 是平行四边形.又ME MANE NF == ,,12MN AF MN AF ∴=,∥. 又AF ED = ,MQ MN ∴=.∴平行四边形MNPQ 是菱形.AF ED MQ ED AF MQ ⊥∴⊥ ,,∥.又MN AF ∥,MN MQ ∴⊥.90QMN ∴=∠,∴菱形MNPQ 是正方形. 【即时测评】学以致用,小试牛刀1. (2010广东卷)如图,,AB CD 是半径为a 的圆O 的两条弦,它们相较于AB 的中点P ,23a PD =, 30OAP ∠= ,则CP =( )B E G F A DC 图1BE GF A D C图2BEG F A DC图3BEG FADC图4N M P QEABCMNA.a 89 B. 58a C. 2a D. a 2. 在矩形ABCD 中,3,10AB BC ==, 点F 在AD 边上,:2:3AF FD =,BF CE ⊥交BF 的延长线于点E ,交AD 于点G , 则BE CE +=( )A. 13B. 14C. 15D. 163. (2010陕西卷)如图,已知Rt △ABC 的两条 直角边AC ,BC 的长分别为3cm ,4cm ,以AC 为直径 的圆与AB 交于点D ,则BD =( ) cm.A. 3B. 165C.95D. 24. 如图,ΔABC 内接于⊙O ,AB =AC ,直 线MN 切⊙O 于点C ,BE ∥MN 交AC 于点E . 若AB =6,BC =4,则AE =( )A. 52B. 103C. 3D. 4【课后作业】学练结合,融会贯通一、填空题:1. 如右图所示,圆O 上一点C 在直径AB 上的射影为D ,4,8CD BD ==,则圆O 的半径长为 .2. (2010海淀期中)如图,AB 为O 的直径,且AB=8, P 为OA 的中点,过点P 作O 的弦CD ,且:3:4,CP PD = 则弦CD 的长度为 .3.(2010天津卷)如图,四边形ABCD 是圆O 的内接 四边形,延长AB 和DC 相交于点P .若1PB =,3PD =. 则BCAD的值为 .B CDABCOP4. (2010东城综合)如图,已知AB 是⊙O 的一条弦, 点P 为AB 上一点, PC OP ⊥,PC 交⊙O 于C , 若4AP =,2PB =,则PC 的长是 .5. 在ABC ∆中,已知CM 是ACB ∠的平分线,AMC ∆ 的外接圆O 交BC 于点N ;若AB AC 31=,求证:BN MN= .6.(2010北京卷)如图,O 的弦ED ,CB 的延长线 交于点A .若BD ⊥AE ,AB =4, BC =2, AD =3,则DE = ;CE = . 二、解答题:7.(2010江苏卷)AB 是⊙O 的直径,D 为⊙O 上一点,过点D 作⊙O 的切线交AB 延长线于C ,若DA=DC ,求证:AB=2BC .8.(2010宁夏海南卷)如图:已知圆上的弧AC BD =,过C 点的圆的切线与BA 的延长线交于 E 点,证明:(Ⅰ)ACE ∠=BCD ∠. (Ⅱ)2BC =BE ·CD .第67课时 选修4-1几何证明选讲参考答案【小题热身】1. 1252. 63.2a【即时测评】1. A2. B3. B4. B【课后作业】一、填空题:1. 52. 73. 134. 5. 3 6. 二、解答题:7. 证明:连OD ,则:OD ⊥DC ,又OA=OD ,DA=DC ,所以∠DAO=∠ODA=∠DCO , ∠DOC=∠DAO+∠ODA=2∠DCO , 所以∠DCO=300,∠DOC=600,所以OC=2OD ,即OB=BC=OD=OA ,所以AB=2BC .8. 解析:(Ⅰ)因为 AC BD=, 所以BCD ABC ∠=∠.又因为EC 与圆相切于点C ,故ACE ABC ∠=∠所以ACE BCD ∠=∠. (Ⅱ)因为ECB CDB ∠=∠,EBC BCD ∠=∠, 所以BDC ∆∽ECB ∆,故BC CDBE BC=. 即2BC BE CD =⨯.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020届高三数学一轮复习强化训练精品――几何证明选讲基础自测1.如下图,在△ABC 中,∠C=90°,正方形DEFC内接于△ABC ,DE ∥AC ,EF ∥BC ,AC =1,BC =2,那么AF ∶FC = .答案212.从不在⊙O 上的一点A 作直线交⊙O 于B 、C ,且AB ·AC =64,OA =10,那么⊙O 的半径等于 .答案241或63.设P 为△ABC 内一点,且AP =52AB +51AC ,那么△ABP 的面积与△ABC 的面积之比等于 . 答案514.如下图,AC 为⊙O 的直径,BD ⊥AC 于P ,PC =2,PA =8,那么CD 的长为,cos ∠ACB = .答案25555.如下图,PA 与圆O 相切于A ,PCB 为圆O 的割线,同时只是圆心O ,∠BPA =30°,PA =23,PC =1,那么圆O 的半径等于 .答案 7 例1 :如下图,以梯形ABCD 的对角线AC 及腰AD 为邻边作平行四边形ACED ,连接EB ,DC 的延长线交BE 于F . 求证:EF =BF .证明连接AE 交DC 于O .∵四边形ACED 为平行四边形,∴O 是AE 的中点〔平行四边形对角线互相平分〕.∵四边形ABCD 是梯形,∴DC ∥AB .在△EAB 中,OF ∥AB ,O 是AE 的中点,∴F 是EB 的中点,即EF =BF .例2如下图,在△ABC 中,AD 为BC 边上的中线,F 为AB上任意一点,CF 交AD 于点E .求证:AE ·BF =2DE ·AF .证明过点D 作AB 的平行线DM 交AC 于点M ,交FC 于点N.在△BCF 中,D 是BC 的中点,DN ∥BF ,∴DN =21BF .∵DN ∥AF ,∴△AFE ∽△DNE ,∴AF AE=DN DE . 又DN =21BF ,∴AF AE =BF DE 2,即AE ·BF =2DE ·AF .例3〔2018·苏、锡、常、镇三检〕自圆O 外一点P 引切线与圆切于点A ,M 为PA 的中点,过M 引割线交圆于B ,C 两点.求证:∠MCP =∠MPB .证明∵PA 与圆相切于A ,∴MA 2=MB ·MC ,∵M 为PA 中点,∴PM =MA ,∴PM 2=MB ·MC ,∴MC PM=PM MB.∵∠BMP =∠PMC ,∴△BMP ∽△PMC ,∴∠MCP =∠MPB .例4〔14分〕如下图,AB 是⊙O 的直径,G 为AB 延长线上的一点,GCD 是⊙O 的割线,过点G 作AB 的垂线,交AC 的延长线于点E ,交AD 的延长线于点F ,过G 作⊙O 的切线,切点为H .求证:〔1〕C ,D ,F ,E 四点共圆;〔2〕GH 2=GE ·GF .证明〔1〕连接BC .∵AB 是⊙O 的直径,∴∠ACB =90°.∵AG ⊥FG ,∴∠AGE =90°.又∠EAG =∠BAC ,∴∠ABC =∠AEG .又∠FDC =∠ABC ,∴∠FDC =∠AEG .∴∠FDC +∠CEF =180°.∴C ,D ,F ,E 四点共圆. 7分〔2〕∵GH 为⊙O 的切线,GCD 为割线,∴GH 2=GC ·GD .由C ,D ,F ,E 四点共圆,得∠GCE =∠AFE ,∠GEC =∠GDF .∴△GCE ∽△GFD .∴GF GC =GD GF ,即GC ·GD =GE ·GF .∴CH 2=GE ·GF . 14分例5〔2018·徐州三检〕如下图,圆O 是△ABC 的外接圆,过点C 的切线交AB 的延长线于点D ,CD =27,AB =BC =3.求BD 以及AC 的长.解由切割线定理得:DB ·DA =DC 2,即DB 〔DB +BA 〕=DC 2,DB 2+3DB -28=0,得DB =4.∵∠A =∠BCD ,∴△DBC ∽△DCA ,∴CA BC=DC DB,得AC =DB DCBC ?=273. 1.:如下图,从R t △ABC 的两直角边AB ,AC 向外作正方形ABFG 及ACDE ,CF ,BD 分不交AB ,AC 于P ,Q .求证:AP =AQ .证明∵∠BAC +∠BAG =90°+90°=180°,∴C ,A ,G 三点共线.同理B ,A ,E 三点共线.∵AB ∥GF ,AC ∥ED ,∴GF AP =CG CA ,ED AQ =BE BA ,即AP =CG GFCA ?,AQ =BE EDBA ?.又∵CA =ED =AE ,GF =BA =AG ,∴CG =CA +AG =AE +BA =BE .∴AP =AQ .2.如下图,△ABC 是⊙O 的内接三角形,且AB =AC ,AP 是∠BAC 的外角的平分线,弦CE 的延长线交AP 于点D.求证:AD 2=DE ·DC .证明连接AE ,那么∠AED =∠B . ∵AB =AC ,∴∠B=∠ACB .∵∠QAC =∠B +∠ACB ,又∠QAP =∠PAC ,∴∠DAC =∠B =∠AED .又∠ADE =∠CDA ,∴△ACD ∽△EAD ,从而ADCD=DE AD ,即AD 2=DE ·DC .3.〔2018·南京第二次质检〕如下图,圆O 的两弦AB 和CD 交于点E ,EF ∥CB ,EF 交AD 的延长线于点F ,FG 切圆O 于点G .〔1〕求证:△DFE ∽△EFA ;〔2〕假如EF =1,求FG 的长.〔1〕证明∵EF ∥CB ,∴∠DEF =∠DCB .∵∠DCB =∠DAB ,∴∠DEF =∠DAB .∵∠DFE =∠EFA ,∴△DFE ∽△EFA .〔2〕解∵△DFE ∽△EFA ,∴FA EF =EFFD .∴EF 2=FA ·FD .∵FG 切圆于G ,∴FG 2=FA ·FD .∴EF 2=FG 2.∴EF =FG .∵EF =1,∴FG =1.4.:如下图,在△ABC 中,AB =AC ,O是△ABC 的外心,延长CA 到P ,再延长AB到Q ,使AP =BQ .求证:O ,A ,P ,Q 四点共圆.证明连接OA ,OC ,OP ,OQ .∵O 是△ABC 的外心,∴OA =OC .∴∠OCP =∠OAC .由于等腰三角形的外心在顶角的平分线上,∴∠OAC =∠OAQ ,从而∠OCP =∠OAQ ,在△OCP 和△OAQ 中,由CA =AB ,AP =BQ ,∴CP =AQ .又OC =OA ,∠OCP =∠OAQ ,∴△OCP ≌△OAQ ,∴∠CPO =∠AQO ,∴O ,A ,P ,Q 四点共圆.5.〔2018·徐州模拟〕如下图,D 为△ABC 的BC 边上一点,⊙O 1通过点B ,D ,交AB 于另一点E ,⊙O 2通过点C ,D ,交AC 于另一点F ,⊙O 1与⊙O 2交于点G .〔1〕求证:∠EAG =∠EFG ;〔2〕假设⊙O 2的半径为5,圆心O 2到直线AC 的距离为3,AC =10,AG 切⊙O 2于G ,求线段AG 的长.〔1〕证明连接GD ,因为四边形BDGE ,CDGF 分不内接于⊙O 1,⊙O 2,∴∠AEG =∠BDG ,∠AFG =∠CDG ,又∠BDG +∠CDG =180°,∴∠AEG +∠AFG =180°.即A ,E ,G ,F 四点共圆,∴∠EAG =∠EFG .〔2〕解因为⊙O 2的半径为5,圆心O 2到直线AC 的距离为3,因此由垂径定理知FC =22235=8,又AC =10,∴AF =2,∵AG 切⊙O 2于G ,∴AG 2=AF ·AC=2×10=20,AG =25.一、填空题1.如下图,在△ABC 中,AD 是高线,CE 是中线,DC =BE ,DG ⊥CE 于G ,EC 的长为8,那么EG = .答案 42.如下图,△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,BE 的延长线交AC 于点F ,那么AF = AC .答案313.如下图,在半圆O 中,AB 为直径,CD ⊥AB ,AF 平分∠CAB交CD 于E ,交CB 于F ,那么图中相似三角形一共有对.答案 54.(2018·广东理,15)PA 是圆O 的切线,切点为A ,PA =2,AC 是圆O 的直径,PC 与圆O 交于点B ,PB =1,那么圆O 的半径R = .答案35.如下图,矩形ABCD 中,AB =12,AD =10,将此矩形折叠使点B 落在AD 边上的中点E 处,那么折痕FG 的长为 .答案6656.如下图,AP 是圆O 的切线,P 为切点,AC 是圆O的割线,与圆O 交于B ,C 两点,圆心O 在∠PAC 的内部,点M 是BC 的中点.那么∠OAM +∠APM 的大小为 .答案 90°7.如下图,圆O 的直径AB =6,C 为圆周上一点,BC =3.过C 作圆的切线l ,过A 作l 的垂线AD ,AD 分不与直线l 、圆交于点D 、E ,那么∠DAC = ,线段AE 的长为 .答案 30° 38.〔2018·徐州质检〕如下图,锐角△ABC 内接于⊙O ,∠ABC =60°,∠BAC =36°,作OE ⊥AB 交劣弧于点E ,连结EC ,那么∠OEC = .答案 12°二、解答题9.:如下图,在△ABC 中,D 是BC 的中点,F 是BA 延长线上的点,FD 与AC 交于点E .求证:AE ·FB =EC ·FA .证明过A 作AG ∥BC ,交DF 于G 点.∵AG ∥BD ,∴FB FA=BD AG.又∵BD =DC ,∴FB FA =DC AG.∵AG ∥CD ,∴DC AG=EC AE.∴FB FA =ECAE .∴AE ·FB =EC ·FA .10.:如下图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于D ,DE ⊥AC 于E ,DF ⊥BC 于F.求证:AE ·BF ·AB =CD 3.证明∵∠ACB =90°,CD ⊥AB ,∴CD 2=AD ·BD ,故CD 4=AD 2·BD 2.又∵R t △ADC 中,DE ⊥AC ,R t △BDC 中,DF ⊥BC ,∴AD 2=AE ·AC ,BD 2=BF ·BC .∴CD 4=AE ·BF ·AC ·BC .又∵AC ·BC =AB ·CD ,∴CD 4=AE ·BF ·AB ·CD ,即AE ·BF ·AB =CD 3.11.〔2018·苏南四市二检〕从⊙O 外一点P 引圆的两条切线PA ,PB 及一条割线PCD ,A ,B 为切点.求证:BC AC =BDAD .证明∵PA 为⊙O 的切线,∴∠PAC =∠PDA ,而∠APC =∠DPA ,∴△PAC ∽△PDA ,那么AD AC=PD PA.同理BD BC=PDPB. ∵PA =PB ,∴AD AC=BD BC.∴BC AC=BD AD .12.〔2018·宁夏〕如下图,过圆O 外一点M 作它的一条切线,切点为A ,过A 点作直线AP 垂直于直线OM ,垂足为P . 〔1〕证明:OM ·OP =OA 2;〔2〕N 为线段AP 上一点,直线NB 垂直于直线ON ,且交圆O 于B 点.过B 点的切线交直线ON 于K. 证明:∠OKM =90°.证明 (1)因为MA 是圆O 的切线,因此OA ⊥AM .又因为AP ⊥OM ,在Rt △OAM 中,由射影定理知,OA 2=OM ·OP .〔2〕因为BK 是圆O 的切线,BN ⊥OK ,同〔1〕,有OB 2=ON ·OK ,又OB =OA ,因此OP ·OM =ON ·OK ,即OP ON =OK OM . 又∠NOP =∠MOK ,因此△ONP ∽△OMK ,故∠OKM =∠OPN =90°.13.〔2018·江苏〕如下图,设△ABC 的外接圆的切线AE 与BC 的延长线交于点E ,∠BAC 的平分线与BC 交于点D .求证:ED 2=EC ·EB .证明如下图,因为AE 是圆的切线,因此∠ABC =∠CAE .又因为AD 是∠BAC 的平分线,因此∠BAD =∠CAD .从而∠ABC +∠BAD =∠CAE +∠CAD .因为∠ADE =∠ABC +∠BAD ,∠DAE =∠CAE +∠CAD ,因此∠ADE =∠DAE ,故EA =ED .因为EA 是圆的切线,因此由切割线定理知,EA 2=EC ·EB ,而EA =ED ,因此ED 2=EC ·EB .14.:如下图,△ABC 内接于⊙O ,过点A 的切线交BC的延长线于点P ,D 为AB 的中点,DP 交AC 于M .求证:22PCPA =MC AM . 证明如下图,过点B 作BN ∥CM ,交PD 的延长线于点N ,那么∠N =∠AMD ,∠NBD =∠DAM .又AD =DB ,∴△BND ≌△AMD .∴BN =AM . ∵CM ∥BN ,∴CM BN =CP BP . ∴PC BP=MC AM .由切割线定理,得PA 2=PC ·PB .∴22PC PA =2PC PB PC =PC BP ,故22PC PA =MC AM .。
