初中数学经典练习题汇总
初中数学经典试题及答案

初中数学经典试题及答案一、选择题(每题3分,共30分)1. 下列哪个选项是偶数?A. 3B. 5C. 8D. 72. 如果一个数的相反数是它本身,那么这个数是:A. 0B. 1C. -1D. 23. 一个数的绝对值是它本身,那么这个数是:A. 正数B. 负数C. 非负数D. 非正数4. 计算下列算式的结果:(2x - 3) + (3x + 4) =A. 5x + 1B. 5x - 1C. 2x + 1D. 2x - 15. 下列哪个选项是方程的解?A. x + 2 = 5,x = 3B. x - 2 = 5,x = 3C. 2x + 3 = 7,x = 2D. 3x - 4 = 5,x = 36. 一个三角形的三个内角之和是:A. 90°B. 180°C. 360°D. 270°7. 一个圆的直径是10厘米,那么它的半径是:A. 5厘米B. 10厘米C. 20厘米D. 15厘米8. 下列哪个选项是不等式的解集?A. x > 5B. x < 5C. x = 5D. x ≠ 59. 一个数的立方是它本身,那么这个数是:A. 0B. 1C. -1D. 以上都是10. 一个数的平方等于它本身,那么这个数是:A. 0B. 1C. -1D. 以上都是二、填空题(每题4分,共20分)11. 一个数的平方根是它本身,那么这个数可以是______。
12. 如果一个数的绝对值是5,那么这个数可以是______。
13. 一个数的倒数是它本身,那么这个数是______。
14. 一个数的相反数是它本身,那么这个数是______。
15. 一个数的立方等于它本身,那么这个数可以是______。
三、解答题(每题5分,共50分)16. 解方程:2x - 5 = 9。
17. 计算:(3x + 2)(2x - 3)。
18. 证明:在一个直角三角形中,斜边的平方等于两直角边的平方和。
数学初中经典试题及答案

数学初中经典试题及答案一、选择题(每题3分,共30分)1. 已知一个数的平方等于36,这个数可能是:A. 6B. -6C. 6或-6D. 以上都不是2. 一个三角形的两边长分别为3和5,第三边长为:A. 2B. 4C. 6D. 83. 计算下列表达式的值:\((-3) \times (-2)\)A. 6B. -6C. 3D. -34. 一个圆的半径为5厘米,那么它的面积是:A. 78.5平方厘米B. 25平方厘米C. 78.5平方分米D. 25平方分米5. 以下哪个是等腰三角形?A. 三边长分别为3, 4, 5B. 三边长分别为5, 5, 5C. 三边长分别为2, 3, 4D. 三边长分别为1, 2, 36. 一个数的绝对值是5,这个数可能是:A. 5B. -5C. 5或-5D. 以上都不是7. 计算下列表达式的值:\((-2)^2\)A. 4B. -4C. 2D. -28. 一个直角三角形的两条直角边长分别为6和8,那么斜边长为:A. 10B. 14C. 16D. 209. 一个数的立方等于-64,这个数是:A. 4B. -4C. 2D. -210. 计算下列表达式的值:\((-1)^3\)A. 1B. -1C. 3D. -3二、填空题(每题2分,共20分)1. 一个数的相反数是-7,这个数是________。
2. 一个数的倒数是\(\frac{1}{3}\),这个数是________。
3. 一个数的平方根是4,这个数是________。
4. 一个数的立方根是2,这个数是________。
5. 一个等差数列的首项是2,公差是3,那么第5项是________。
6. 一个等比数列的首项是3,公比是2,那么第3项是________。
7. 一个直角三角形的斜边长是10,一个直角边长是6,那么另一个直角边长是________。
8. 一个圆的直径是10厘米,那么它的周长是________厘米。
9. 一个数的绝对值是8,这个数是________或________。
初中数学经典试题及答案

初中数学经典试题及答案初中数学是学生学习数学的基础阶段,也是打好数学基础的关键时期。
下面是一些初中数学经典试题及答案,供学生们参考。
一、代数与方程1. 已知一个数的三倍加上8等于25,求此数。
解:设这个数为x,根据题意可得方程:3x + 8 = 25。
解方程得:3x = 25 - 8,即3x = 17。
再将两边除以3得:x = 17 ÷ 3 = 5 余 2。
所以,这个数为5。
2. 解方程:4(x - 3) = 2(2x - 5)。
解:先化简方程两边的括号,得:4x - 12 = 4x - 10。
然后我们发现方程两边的变量项一样,所以这个方程没有解。
二、几何与图形1. 长方形ABCD中,AB = 8cm,BC = 6cm。
若AC的垂直平分线与BC交于点E,请问AE的长度是多少?解:由于AC的垂直平分线与BC交于点E,所以AE是AC 的中位线。
根据中位线的性质可知,AE = 1/2AC。
则AE =1/2(8 + 6) = 1/2 × 14 = 7cm。
2. 在⭕O中,AB是直径,AC是弧BC的切线,且OB = 10cm,AC = 6cm。
请问BC的度数是多少?解:由于AC是弧BC的切线,所以直径AB与切线AC垂直。
根据垂径定理可知,切线与直径的夹角等于其对应的弧的度数的一半。
则BC度数为2×∠BAC = 2×∠BAC = 2×6 = 12度。
三、数与运算1. 甲、乙两个小贩卖菜,甲当天卖出的菜较多,乙卖出的菜数是甲卖出的菜数的2/3。
如果甲卖出的菜数是乙卖出的菜数的1-1/2倍,问两个小贩卖出的菜分别是多少?解:设甲卖出的菜数为x,乙卖出的菜数为y。
根据题意可得以下方程:y = 2/3xx = (1-1/2)y解这个方程组,得:x = 4,y = 6。
所以甲卖出的菜数为4,乙卖出的菜数为6。
2. 一个两位数,十位数与个位数之和为12,如果把十位数和个位数交换,得到一个数比原来的数大18,求原来的两位数。
初中数学解一元二次方程经典练习题(含答案)

初中数学解一元二次方程经典练习题(含答案)解下列解一元二次方程:1、x2=121;2、(2x+3)2=9;3、3(4x+5)2-147=0;4、(2x−7)2+9 =6(2x-7);5、7x(x-6)=3(12-2x);6、(3x-5)(2x+5)= x+7;7、3(3x-4)+ x(4-3x)=0;8、x(2x+5)=4(2x-1)+3;9、(x−3)2+4=5(3-x);10、4x2+7x +1=0;11、512x2+ 13= x;12、(x−1)(x−2)2 -1 = (x+1)(x−3)3;13、14[12(x+1)+13(x+2)+2] =x2;14、(x+1)(x+2)+(x+3)(x+4)=(x+2)(x+3)+32;15、x= 2(0.3x+21)3 - (0.2x−1)(x+2)2;16、x2+(1+ 2√5)x +( 4+√5)=0;参考答案1、x2=121;解:x2=121等式两边同时开平方x= 11故原方程的根是:x1=11,x2= -112、(2x +3)2=9;解:(2x +3)2=9等式两边同时开平方(2x +3)=±3令2x +3 = 3,即2x=0,解得x=0令2x +3 =-3,即2x=-6,解得x=-3故原方程的根是:x 1=0,x 2=-33、3(4x +5)2-147=0;解:3(4x +5)2-147=03(4x +5)2=147等式两边同时除以3(4x +5)2= 49等式两边同时开平方4x+5=±7令4x+5=7, 解得x= 12 令4x+5= -7,解得x=-3故原方程的根是:x 1= 12,x 2=-34、(2x −7)2+9 =6(2x-7);解:(2x −7)2 +9 =6(2x-7)右边的项移到等号左边(2x−7)2-6(2x-7)+9 =0(2x−7)2 -2・3・(2x-7)+32=0[(2x−7)−3 ]2=0令(2x−7)−3 =0,解得 x=5故原方程的根是:x1=x2=55、7x(x-6)=3(12-2x);解:7x(x-6)=3(12-2x)等号左边提取-27x(x-6)=-6(x-6)右边的项移到等号左边7x(x-6)+6(x-6)=0提取公因式(x-6)(x-6)(7x+6)=0令x-6=0,解得x=6令7x+6=0,解得x= - 67故原方程的根是:x1=6,x2=- 676、(3x-5)(2x+5)= x+7;解(3x-5)(2x+5)= x+7等号左边去括号6x2+15x-10x-25 =x+76x2+5x-25=x+76x2+4x-32=03x2+2x-16=0(3x+8)(x-2)=0令3x+8=0,解得x= - 83令x-2 =0,解得x=2故原方程的根是:x1=- 8,x2=237、3(3x-4)+ x(4-3x)=0;解:3(3x-4)+ x(4-3x)=0 3(3x-4)- x(3x-4)=0 提取公因式(3x-4)(3x-4)(3- x)=0令3x-4=0,解得x= 43令3- x =0,解得x=3,x2=3 故原方程的根是:x1= 438、x(2x+5)=4(2x-1)+3;解:x(2x+5)=4(2x-1)+3 2x2 +5x =8x-4+32x2 +5x =8x-12x2 -3x +1=0(2x-1)(x-1)=0令2x-1=0,解得x= 12 令x-1=0,解得x=1故原方程的根是:x 1= 12 ,x 2=19、(x −3)2 +4=5(3-x );解:(x −3)2 +4= 5(3-x )等号左边提取-1(x −3)2 +4= -5(x-3)右边的项移到等号左边(x −3)2 +5(x-3)+4=0[(x -3)+1][(x-3)+4]=0(x-2)(x+1)=0令x-2=0,解得x=2令x+1=0,解得x=-1故原方程的根是:x 1=2,x 2=-110、4x 2+7x +1=0;解:4x 2+7x +1=0判别式△=72 -4×4×1 =33x= −7 ±√332×4 = −7 ±√338故原方程的根是:x 1=−7 +√338,x 2=−7 −√33811、512x 2 + 13 = x ; 解:512x 2 + 13 = x等式两边同时乘以125x 2 +4 =12x5x 2 +4 -12x =0(5x-2)(x-2)=0令5x-2=0,解得x= 25 令x-2=0,解得x=2故原方程的根是:x 1= 25,x 2=212、(x−1)(x−2)2-1 = (x+1)(x−3)3 ; 解:(x−1)(x−2)2 -1 = (x+1)(x−3)3 等式两边分子去括号x 2−3x+22 -1 = x 2−2x−33等式两边同时乘以63(x 2−3x +2)-6 =2(x 2−2x −3) 3x 2 -9x+6 -6= 2x 2 -4x −6x 2 -5x +6=0(x-2)(x-3)=0令x-2=0,解得x=2令x-3=0,解得x=3故原方程的根是:x 1=2,x 2=313、 14[12(x+1)+13(x+2)+2] =x 2;解:14[12(x+1)+13(x+2)+2] =x 2等号两边同时乘以412(x+1)+13(x+2)+2 =4x 2等号两边同时乘以63(x+1)+2(x+2)+12 =24x 23x+3+2x+4+12=24x 224x 2-5x-19=0(24x+19)(x-1)=0令24x+19=0,解得x= −1924令x-1=0,解得x= 1故原方程的根是:x 1=−1924,x 2= 114、(x+1)(x+2)+(x+3)(x+4)=(x+2)(x+3)+32;解:(x+1)(x+2)+(x+3)(x+4)=(x+2)(x+3)+32 等号两边去括号x 2+3x+2+x 2+7x+12 =x 2+5x+6+32整理得x 2+5x-24=0(x+8)(x-3)=0令x+8=0,解得x= -8令x-3=0,解得x= 3故原方程的根是:x 1=-8,x 2= 315、x=2(0.3x+21)3 - (0.2x−1)(x+2)2 ; 解:x= 2(0.3x+21)3 - (0.2x−1)(x+2)2等号两边同时乘以66x=4(0.3x+21)-3(0.2x-1)(x+2) 去括号6x=1.2x+84-0.6x 2+1.8x+6整理得0.6x 2+3x-90=0等号两边同时乘以10,然后再除以6 x 2+5x-150=0(x+15)(x-10)=0令x+15=0,解得x= -15令x-10=0,解得x= 10故原方程的根是:x 1= -15,x 2= 1016、x 2+(1+ 2√5)x +( 4+√5)=0; 解:x 2+(1+ 2√5)x +( 4+√5)=0 判别式△=(1+ 2√5)2-4・1・( 4+√5)=1+4√5+20-16-4√5=5x= −(1+ 2√5)±√52∙1即x= −(1+ 2√5)+√52=−(1+ √5)2或 x= −(1+ 2√5)−√52=−(1+3 √5)2故原方程的根是:x1=−(1+ √5)2,x2= −(1+3 √5)2。
初中数学练习题及答案

初中数学练习题及答案【练习题一】题目:已知一个直角三角形的两条直角边分别为3厘米和4厘米,求斜边的长度。
【答案】根据勾股定理,直角三角形的斜边长度可以通过以下公式计算:\[ c = \sqrt{a^2 + b^2} \]其中,\( a \) 和 \( b \) 分别是直角三角形的两条直角边,\( c \) 是斜边。
将题目中的数值代入公式:\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]所以,斜边的长度是5厘米。
【练习题二】题目:一个圆的半径是7厘米,求这个圆的面积。
【答案】圆的面积可以通过以下公式计算:\[ A = \pi r^2 \]其中,\( r \) 是圆的半径。
将题目中的数值代入公式:\[ A = \pi \times 7^2 = 49\pi \]如果使用圆周率的近似值3.14,那么面积为:\[ A \approx 49 \times 3.14 = 153.86 \]所以,这个圆的面积约为153.86平方厘米。
【练习题三】题目:一个长方体的长、宽、高分别是5厘米、4厘米和3厘米,求这个长方体的体积。
【答案】长方体的体积可以通过以下公式计算:\[ V = l \times w \times h \]其中,\( l \) 是长,\( w \) 是宽,\( h \) 是高。
将题目中的数值代入公式:\[ V = 5 \times 4 \times 3 = 60 \]所以,这个长方体的体积是60立方厘米。
【练习题四】题目:一个分数是\( \frac{3}{4} \),如果分子增加9,新的分数是多少?【答案】分数的分子增加9后,新的分数的分子变为:\[ 3 + 9 = 12 \]分母不变,所以新的分数是:\[ \frac{12}{4} \]这个分数可以化简为:\[ \frac{12}{4} = 3 \]所以,新的分数是3。
【练习题五】题目:一个数的\( \frac{1}{3} \) 等于12,求这个数。
经典初中数学试题及答案

经典初中数学试题及答案一、选择题(每题2分,共10分)1. 下列哪个选项是二次方程的解?A. \(x = 2\)B. \(x = -3\)C. \(x = 4\)D. \(x = \frac{1}{2}\)答案:D2. 一个圆的半径是5厘米,那么这个圆的周长是多少?A. 10π厘米B. 20π厘米C. 30π厘米D. 40π厘米答案:B3. 如果一个数的相反数是-7,那么这个数是多少?A. 7B. -7C. 0D. 14答案:A4. 一个等腰三角形的底边长为6厘米,两腰长为5厘米,那么这个三角形的周长是多少?A. 16厘米B. 21厘米C. 26厘米D. 31厘米答案:B5. 一个数的绝对值是5,这个数可能是?A. 5B. -5C. 5或-5D. 0答案:C二、填空题(每题2分,共10分)1. 一个数的平方是36,这个数是________。
答案:±62. 如果一个三角形的内角和为180°,其中一个角是90°,另外两个角的度数之和是________。
答案:90°3. 一个数除以3余2,除以5余3,除以7余2,这个数最小是________。
答案:534. 一个长方体的长、宽、高分别是10厘米、8厘米、5厘米,那么这个长方体的体积是________立方厘米。
答案:4005. 一个分数的分子是15,分母是30,这个分数化简后是________。
答案:\(\frac{1}{2}\)三、解答题(每题15分,共30分)1. 已知一个二次方程 \(ax^2 + bx + c = 0\) 的两个解是 \(x_1 =2\) 和 \(x_2 = -3\),求出 \(a\)、\(b\)、\(c\) 的值。
答案:根据韦达定理,我们有 \(x_1 + x_2 = -\frac{b}{a}\) 和\(x_1 \cdot x_2 = \frac{c}{a}\)。
将 \(x_1 = 2\) 和 \(x_2 = -3\) 代入,得到 \(-1 = -\frac{b}{a}\) 和 \(-6 = \frac{c}{a}\)。
初中数学练习题题库

初中数学练习题题库初中数学练习题题库包含了各种类型的题目,旨在帮助学生巩固和提升数学知识。
以下是一些精选的练习题,涵盖了初中数学的主要知识点。
1. 有理数的加减法计算下列有理数的和:(1) 3 + (-2)(2) -5 + 72. 一元一次方程解下列一元一次方程:(1) 2x + 3 = 7(2) 4x - 5 = 33. 几何图形的认识判断下列几何图形的性质:(1) 正方形的对角线相等且互相垂直。
(2) 圆的半径是圆心到圆周上任意一点的距离。
4. 代数式的求值计算下列代数式的值:(1) 当a=2,b=3时,求2a + b的值。
(2) 当m=-1,n=4时,求mn - 2n的值。
5. 多项式的运算进行下列多项式的运算:(1) (2x^2 + 3x - 1) + (x^2 - 4x + 5)(2) (3x^2 - 2x + 1) - (x^2 + 5x - 3)6. 概率的计算计算下列事件发生的概率:(1) 抛掷一枚公平的硬币,正面朝上的概率。
(2) 抛掷一个公平的六面骰子,得到偶数的概率。
7. 函数的图像和性质分析下列函数的图像和性质:(1) y = 2x + 1(2) y = x^2 - 4x + 48. 统计图表的解读根据下列统计图表回答问题:(1) 某班级学生身高分布图,求平均身高。
(2) 某地区月平均气温变化图,求最热和最冷的月份。
这些练习题覆盖了初中数学的基础和进阶知识点,通过练习可以加深对数学概念的理解,提高解题能力。
建议学生在完成每道题目后,仔细检查答案,确保理解每个步骤的逻辑和原理。
七年级数学经典例题

七年级数学经典例题一、有理数运算。
1. 计算:(-2)+3-(-5)- 解析:- 根据有理数的运算法则,减去一个数等于加上这个数的相反数。
- 所以(-2)+3 - (-5)=(-2)+3+5。
- 先计算(-2)+3 = 1,再计算1 + 5=6。
2. 计算:-2^2-( - 3)^3÷(-1)^2023- 解析:- 先计算指数运算。
-2^2=-4(这里注意指数运算的优先级,先计算指数2^2 = 4,再加上负号)。
- (-3)^3=-27,(-1)^2023=-1。
- 则原式=-4-(-27)÷(-1)。
- 接着计算除法-27÷(-1) = 27。
- 最后计算-4 - 27=-31。
二、整式的加减。
3. 化简:3a + 2b - 5a - b- 解析:- 合并同类项,同类项是指所含字母相同,并且相同字母的指数也相同的项。
- 对于a的同类项3a和-5a,合并得3a-5a=-2a。
- 对于b的同类项2b和-b,合并得2b - b=b。
- 所以化简结果为-2a + b。
4. 先化简,再求值:(2x^2 - 3xy + 4y^2)-3(x^2 - xy+(5)/(3)y^2),其中x = - 2,y = 1- 解析:- 先去括号,根据去括号法则,括号前是正号,去掉括号不变号;括号前是负号,去掉括号要变号。
- 原式=2x^2-3xy + 4y^2-3x^2 + 3xy-5y^2。
- 再合并同类项,2x^2-3x^2=-x^2,4y^2-5y^2=-y^2,-3xy+3xy = 0。
- 化简结果为-x^2-y^2。
- 当x=-2,y = 1时,代入得-(-2)^2-1^2=-4 - 1=-5。
三、一元一次方程。
5. 解方程:3x+5=2x - 1- 解析:- 移项,把含有x的项移到等号一边,常数项移到等号另一边,移项要变号。
- 得到3x - 2x=-1 - 5。
- 合并同类项得x=-6。
初中数学经典试题及答案

初中数学经典试题及答案1. 试题一:求平方根将以下数分别求出它们的平方根:a) 9b) 16c) 25d) 36答案及解析:a) √9 = 3b) √16 = 4c) √25 = 5d) √36 = 6解析:平方根的定义是与一个数乘积为该数的平方的非负数。
对于给定的数,我们可以通过求平方根来找到它的平方根。
例如,在本题中,9的平方根是3,因为3乘以3等于9。
同样地,16的平方根是4,25的平方根是5,36的平方根是6。
2. 试题二:等差数列求和求下列等差数列的前n项和:2, 5, 8, 11, ...我们首先观察到该等差数列的公差为3,即每一项与前一项之间的差为3。
因此,我们可以将等差数列通项公式应用于该题目。
通项公式:a_n = a_1 + (n-1)d其中,a_n表示第n项,a_1表示第1项,d表示公差。
根据题目给定的等差数列,我们可以得到:a_1 = 2d = 3我们接下来使用前n项和公式求解,该公式为:S_n = n/2 * (a_1 + a_n)将题目给定的数值代入公式:S_n = n/2 * (2 + (2 + (n-1)*3))简化得到:S_n = n/2 * (4 + 3n)所以,该等差数列的前n项和为:S_n = n/2 * (4 + 3n)3. 试题三:比例与百分数计算现有一本数学书,共有300页。
其中,60%的页数为练习题。
请问该书练习题页数有多少?将60%转化为小数形式,即:60% = 0.60。
我们可以使用百分数与数值的乘法来计算题目中的要求。
题目中给出的总页数为300页,我们用该总页数乘以0.60即可得到练习题页数:练习题页数 = 300 * 0.60 = 180页所以,该数学书的练习题页数为180页。
4. 试题四:解方程求解以下方程:3x + 7 = 22答案及解析:我们可以通过移项与化简的方法求解该方程。
首先,我们将方程中的常数项7移到另一侧,得到:3x = 22 - 7继续计算得到:3x = 15最后,我们将方程两边同时除以系数3,即可求解出x的值:x = 15/3x = 5解答:方程3x + 7 = 22的解为x = 5。
初二数学经典题100道

答案:42.一个三角形的两个内角分别是35度和65度,求第三个内角的度数。
答案:80度3.解方程:2x - 5 = 15。
答案:x = 104.一个长方形的长是10厘米,宽是4厘米,求它的面积。
答案:40平方厘米5.一个圆的半径是7厘米,求它的周长(取π=3.14)。
答案:43.96厘米6.一个数除以4余2,这个数可能是多少?答案:10,14,18,22等7.一个班级有40名学生,其中女生占全班的55%,求女生的人数。
答案:22人8.一个数的1/3加上10等于20,求这个数。
答案:309.一个三角形的底是8厘米,高是5厘米,求它的面积。
答案:20平方厘米10.一个数的5倍减去15等于30,求这个数。
答案:911.一个圆的直径是14厘米,求它的面积(取π=3.14)。
答案:153.86平方厘米12.一个数的2/5是12,求这个数。
答案:3013.一个数的3倍减去18等于9,求这个数。
答案:914.一个长方体的长、宽、高分别是8厘米、6厘米和4厘米,求它的体积。
答案:192立方厘米15.一个数的4倍加上20等于60,求这个数。
答案:1016.一个数的1/4加上5等于10,求这个数。
答案:1517.一个数的3/5是18,求这个数。
答案:3018.一个数的2倍减去10等于14,求这个数。
答案:1219.一个数的5倍加上10等于40,求这个数。
答案:620.一个数的1/2加上12等于22,求这个数。
答案:2021.一个数的3倍加上15等于30,求这个数。
答案:522.一个数的4倍减去20等于20,求这个数。
10答案:4524.一个数的2倍加上6等于18,求这个数。
答案:625.一个数的5倍减去25等于25,求这个数。
答案:1026.一个数的1/4加上10等于15,求这个数。
答案:2027.一个数的3倍减去9等于15,求这个数。
答案:828.一个数的4倍加上12等于36,求这个数。
答案:629.一个数的1/5加上4等于6,求这个数。
初中经典数学题目

初中经典数学题目
1. 求解一元一次方程。
2. 计算圆的面积和周长。
3. 解析几何的基础题目。
4. 公式变化和运算。
5. 利用勾股定理解决问题。
6. 解决直角三角形的面积问题。
7. 解决等边三角形的面积和周长问题。
8. 利用坐标确定点的位置。
9. 利用二元一次方程解决问题。
10. 利用比例的定义解决问题。
11. 利用百分比解决问题。
12. 利用概率的定义解决问题。
13. 利用数据分析解决问题。
14. 利用统计中的平均数解决问题。
15. 二次函数的图象和性质问题解决。
16. 利用图形的旋转解决问题。
17. 利用图形的平移解决问题。
18. 利用数据的规律解决问题。
19. 我们使用公式a²-b²解决问题。
20. 利用方程的解集解决问题。
初中数学经典试题100题
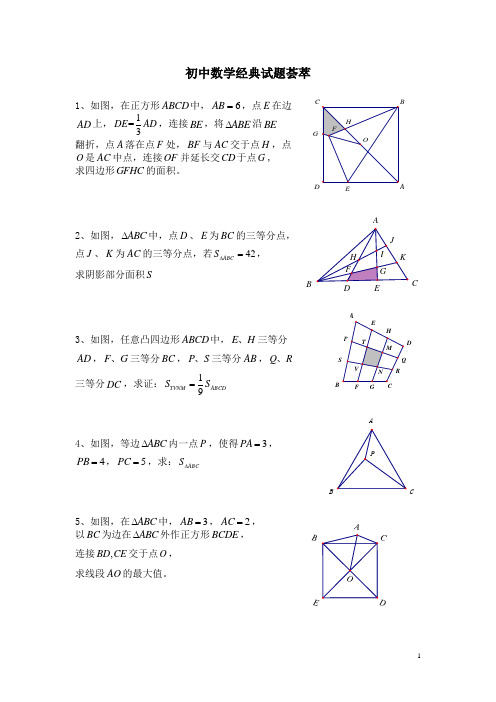
FG BDCBAGECDABCA初中数学经典试题荟萃1、如图,在正方形ABCD 中,6AB =,点E 在边AD 上,1=3DE AD ,连接BE ,将ABE ∆沿BE翻折,点A 落在点F 处,BF 与AC 交于点H ,点 O 是AC 中点,连接OF 并延长交CD 于点G , 求四边形GFHC 的面积。
2、如图,ABC ∆中,点D 、E 为BC 的三等分点, 点J 、K 为AC 的三等分点,若42ABC S ∆=, 求阴影部分面积S3、如图,任意凸四边形ABCD 中,E H 、三等分AD ,F G 、三等分BC ,P S 、三等分AB ,Q R 、 三等分DC ,求证:19TVNMABCD S S =4、如图,等边ABC ∆内一点P ,使得3PA =,4PB =,5PC =,求:ABC S ∆5、如图,在ABC ∆中,3AB =,2AC =, 以BC 为边在ABC ∆外作正方形BCDE , 连接,BD CE 交于点O , 求线段AO 的最大值。
D EFADEFABAB CDBAC6、如图,等边ABC ∆中,120BDC ∠=︒, DC GD =,AG 交CD 延长线于点E 。
求证:AE EG =7、如图,分别以锐角ABC ∆的三边为斜边 向外作等腰Rt DAB ∆、等腰Rt EBC ∆、 等腰Rt FAC ∆。
求证:①AE DF = ②AE DF ⊥8、如图,四边形ABCD 中,E F 、分别 是AB CD 、的中点,P 为对角线AC 延长线上任意一点,PF 交AD 于M ,PE 交BC 于N ,EF 交MN 于K ,求证:K 点平分线段MN9、如图,ABCD 中,E F 、分别是AB BC 、上 的点,DE 交AC 于M ,AF 交BD 于N ,若AF 平分BAC ∠,DE AF ⊥,DE 与AF 交于P ,记BE x OM =,BN y ON =,CF z BF =,试比较x y z 、、的大小关系。
初中数学练习题及答案

初中数学练习题及答案1. 代数基础问题:如果一个数的平方等于该数本身,这个数是什么?答案:这个数是0或1。
2. 方程求解问题:解方程 \( x + 5 = 10 \)。
答案:将5从等式的两边减去,得到 \( x = 5 \)。
3. 因式分解问题:将 \( 2x^2 - 6x \) 因式分解。
答案:提取公因数 \( 2x \),得到 \( 2x(x - 3) \)。
4. 几何问题问题:如果一个直角三角形的两条直角边分别为3和4,求斜边的长度。
答案:根据勾股定理,斜边长度 \( c = \sqrt{3^2 + 4^2} = 5 \)。
5. 比例问题问题:如果 \( \frac{a}{b} = \frac{c}{d} \),且 \( b = 4 \),\( c = 6 \),求 \( a \) 和 \( d \)。
答案:根据比例的性质,\( a = \frac{6}{4} \times b =\frac{3}{2} \times 4 = 6 \),\( d = \frac{b}{c} \times d =\frac{4}{6} \times 6 = 4 \)。
6. 函数图像问题:如果函数 \( y = 2x + 3 \),当 \( x = 1 \) 时,求\( y \) 的值。
答案:将 \( x = 1 \) 代入函数,得到 \( y = 2 \times 1 + 3= 5 \)。
7. 统计问题问题:一组数据为 2, 4, 6, 8, 10,求这组数据的平均数和中位数。
答案:平均数是所有数值的总和除以数值的数量,即\( \frac{2+4+6+8+10}{5} = 6 \)。
中位数是数据排序后位于中间的数,即6。
8. 应用题问题:一个班级有30名学生,其中15名学生喜欢数学,12名学生喜欢英语,5名学生既喜欢数学又喜欢英语。
求只喜欢数学的学生人数。
答案:根据容斥原理,只喜欢数学的学生人数为 \( 15 - 5 = 10 \)。
数学初一经典试题及答案

数学初一经典试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是正数?A. -3B. 0C. 5D. -0.5答案:C2. 绝对值等于4的数是:A. 4B. -4C. 4或-4D. 0答案:C3. 有理数的加法法则中,同号两数相加,取相同的符号,并把绝对值相加,下列哪个选项符合这个法则?A. 3 + 2 = 5B. -3 + 2 = -1C. 3 + (-2) = 1D. -3 + (-2) = -5答案:D4. 一个数的相反数是它本身,这个数是:A. 1B. -1C. 0D. 2答案:C5. 下列哪个选项是不等式?A. 3x + 2 = 7B. 2x - 3 < 5C. 4y = 8D. 5z + 7答案:B6. 一个数的立方等于它本身,这个数是:A. 1B. -1C. 0D. 1或-1答案:C7. 一个数的平方等于9,这个数是:A. 3B. -3C. 3或-3D. 9答案:C8. 下列哪个选项是单项式?A. 3x + 2B. 5x^2 - 3x + 1C. 7x^3D. x/2答案:C9. 下列哪个选项是多项式?A. 4xB. 2x^2 + 3x - 5C. 6D. x^2 - 4/x答案:B10. 下列哪个选项是等式?A. 2x + 3 > 5B. 4y - 6 = 0C. 7z - 2 ≠ 3D. 5w答案:B二、填空题(每题4分,共40分)11. 计算:2 + (-3) = _______。
答案:-112. 计算:-4 × (-2) = _______。
答案:813. 计算:(-3)^2 = _______。
答案:914. 计算:|-7| = _______。
答案:715. 计算:(-5) + (-5) = _______。
答案:-1016. 计算:3 × 2^2 = _______。
答案:1217. 计算:(-2)^3 = _______。
答案:-818. 计算:(1/2) × (-4) = _______。
初中数学解一元一次方程经典练习题(含答案)

初中数学解一元一次方程经典练习题(含答案)解下列一元一次方程:1、3x+7 =2x+14;2、59 x + 2.5 = 23 x + 2.4;3、6(x+1)+7(x+2)= 8(x+3);4、x=2−x 3 + 2+x 4 ;5、2x +3(21+x )=6x +5(9+x );6、5−x 3 + 6-x = 1−x 2 + 20+x 4 ;7、23 [ x - 15( x +1)]= 14(x+14);8、4+3x−10.7 =2- 2x−30.5 ;9、5(x-2)+6x= 0.8(x+4)-3;10、3x+4(x+1)+5(x+2)=50;11、 13 - 15(16 x -1;12、1= x + x 2 + x 4 + x 6 + x12 ;参考答案1、3x+7=2x+14;解:3x+7=2x+143x-2x=14-7x=7故原方程的解是:x=72、59 x + 2.5 = 23 x + 2.4; 解:59 x + 2.5 = 23 x + 2.4 59 x - 23 x =2.4-2.5 5−2×39 x= -0.1 −19x= -0.1x= -0.9故原方程的解是:x= -0.93、6(x+1)+7(x+2)= 8(x+3);解:6(x+1)+7(x+2)= 8(x+3)6x+6+7x+14 =8x+2413x+20 =8x+2413x-8x=24-205x= 4x= 45故原方程的解是:x= 454、x= 2−x3 + 2+x4;解:x= 2−x3 + 2+x412x =4(2-x)+3(2+x)12x=8-4x+6+3x12x=14-x12x+x =1413x=14x= 1413故原方程的解是:x= 14135、2x +3(21+x)=6x +5(9+x);解:2x +3(21+x)=6x +5(9+x)2x+63+3x =6x+45+5x5x+63 =11x+455x-11x=45-63-6x= -18x=3故原方程的解是:x=36、5−x3 + 6-x = 1−x2+ 20+x4;解:5−x3 + 6-x = 1−x2+ 20+x4等式两边同时乘以124(5-x)+12(6-x)=6(1-x)+3(20+x)20-4x+72-12x =6-6x+60+3x-16x+92 =-3x+66-16x+3x =-92+66-13x= -26x=2故原方程的解是:x=27、23[ x - 15( x +1)]=14(x+14);解:23[ x - 15( x +1)]=14(x+14)等式两边同时乘以128 [ x - 15( x +1)]=3(x+14)8x- 85( x +1)=3x+42- 85( x +1)= 3x-8x+42- 85( x +1)= -5x+42等式两边同时乘以5-8(x+1)=5(-5x+42)-8x-8 =-25x+21025x-8x=210+817x=218x= 21817故原方程的解是:x=218178、4+ 3x−10.7 =2- 2x−30.5 ;解:4+ 3x−10.7 =2- 2x−30.5等式两边同时乘以0.7×0.54×0.7×0.5 +0.5(3x-1)=2×0.7×0.5 -0.7(2x-3)1.4+1.5x-0.5= 0.7-1.4x+2.10.9+1.5x= -1.4x+2.81.5x+1.4x=2.8-0.92.9x= 1.9x= 1929 故原方程的解是:x= 19299、5(x -2)+6x= 0.8(x+4)-3;解:5(x -2)+6x= 0.8(x+4)-35x-10+6x =0.8x+3.2-35x+6x-0.8x =3.2-3+10(5+6-0.8)x=10.210.2x=10.2x=1故原方程的解是:x=110、3x+4(x+1)+5(x+2)=50; 解:3x+4(x+1)+5(x+2)=503x+4x+4+5x+10=503x+4x+5x= 50-4-10(3+4+5)x= 3612x= 36x= 3故原方程的解是:x=311、 13 - 15(16 x -1;解: 13 - 15(16 x -1等号两边同时乘以15 - 15(16 x -1)] = x 等号左边去中括号(16 x -1)=x 等号左边去小括号- 16 x +1=x等号两边同时乘以2430x-4x+24=24x26x+24=24x2x= -24x= -12故原方程的解是:x= -1212、1= x + x2 + x4+ x6+ x12;解:1= x + x2 + x4+ x6+ x12等式两边同时乘以12 12=12x+6x+3x+2x+x12=24xx= 12故原方程的解是:x= 12。
初中数学习题练习题库

初中数学习题练习题库第一节:整式与因式分解1. 将下列各式因式分解,并写出各因式的次数:(1) x^2 - 4y^2(2) a^3 - b^3(3) 4x^2 + 12xy + 9y^22. 将下列各式化简并求值:(1) 3(2x + 5) - 2(3 - x)(2) 4(2a - b) + 2(3a + b) - 5(3a - 2b)第二节:线性方程与一元一次方程组1. 解下列方程:(1) 3x - 5 = 2x + 9(2) 2(x - 3) = 4x + 10(3) 5x + 2 = 2(x + 3)2. 解下列一元一次方程组:(1) {2x + 3y = 7{x - 2y = -4(2) {3a - 2b = 8{2a + 5b = -1第三节:百分数与分数1. 将下列百分数转化为分数并进行化简:(1) 25%(2) 75%(3) 120%2. 将下列分数转化为百分数并写成百分数形式:(1) 3/5(2) 7/10(3) 5/8第四节:平面图形与立体几何1. 计算下列各图形的面积:(1) 正方形,边长为8cm(2) 长方形,长为12cm,宽为5cm(3) 圆的半径为4cm2. 计算下列各图形的体积:(1) 正方体,边长为6cm(2) 长方体,长为8cm,宽为4cm,高为3cm(3) 球的半径为5cm第五节:数据统计与概率1. 根据给定的数据,计算下列各项统计量:(1) 平均数:5, 9, 12, 15, 18(2) 中位数:7, 9, 14, 16, 20(3) 众数:3, 5, 5, 7, 9, 9, 92. 计算下列事件的概率:(1) 从一副扑克牌中抽出一张红色的牌(2) 抛一枚骰子,点数为2或4以上是初中数学练习题库的一部分,希望能够对你的数学学习有所帮助。
完成练习题可以提高数学能力和解题能力,同时为将来的应试考试打下基础。
祝你成功!。
初中数学练习题

初中数学练习题一、代数部分1. 计算:(3a 2b)+(4a + 5b)2. 计算:5x 3(2x 4)3. 化简:4x^2 2x + 7x 3x^24. 解方程:2(x 3) = 3(x + 1)5. 解方程:5(2x 1) 3(3x + 2) = 76. 计算下列各式的值:a = 3, b = 2 时,2a^2 3ab + 4b^27. 已知 x + y = 5,x y = 1,求 x 和 y 的值。
二、几何部分1. 计算下列图形的周长和面积:(1)长方形,长为8cm,宽为5cm(2)正方形,边长为6cm(3)圆形,半径为4cm2. 下列各图中,哪些是平行四边形?哪些是梯形?(请画出图形)3. 已知直角三角形的两个直角边分别为3cm和4cm,求斜边的长度。
4. 在直角坐标系中,点A(2, 3)和点B(3, 1),求线段AB的长度。
5. 已知等边三角形的边长为6cm,求其面积。
三、应用题部分1. 某商店进行打折促销,原价为200元的商品,打8折后售价为多少元?2. 一辆汽车以60km/h的速度行驶,行驶了2.5小时后,行驶了多少千米?3. 甲、乙两人共同完成一项工作,甲单独完成需要10天,乙单独完成需要15天。
两人合作完成这项工作需要多少天?4. 一桶水重100千克,用去一半后,剩下的水重多少千克?5. 小明买了3本书,每本书的价格分别为18元、25元和22元,小明一共花了多少钱?四、选择题部分1. 下列选项中,哪一个不是代数式?A. 5x + 3B. x^2 y^2C. √a + bD. 1/22. 在直角三角形中,若一个锐角的度数为30°,则另一个锐角的度数是?A. 30°B. 45°C. 60°D. 90°3. 下列各数中,哪个数是有理数?A. √2B. πC. 3.14D. √14. 下列图形中,对称轴最多的是?A. 长方形B. 正方形C. 等边三角形D. 圆形5. 一辆汽车行驶200km,速度为80km/h,行驶时间为?A. 2小时B. 2.5小时C. 3小时D. 4小时五、填空题部分1. 若 a = 4,那么 3a 2 的值是 _______。
初中数学好用的练习题

初中数学好用的练习题一、选择题(每题2分,共10分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 22. 一个数的平方根是它本身,这个数可能是:A. 0B. 1C. -1D. 23. 一个圆的半径为5厘米,那么它的直径是:A. 10厘米B. 15厘米C. 20厘米D. 25厘米4. 如果一个角的度数是90度,那么它是:A. 锐角B. 直角C. 钝角D. 平角5. 一个数的绝对值是它本身,那么这个数:A. 一定是正数B. 一定是负数C. 可以是0D. 可以是任何数二、填空题(每题2分,共10分)6. 一个数的立方是-27,这个数是______。
7. 如果一个三角形的两边长分别是3和4,第三边的长x满足1<x<7,则这个三角形是______三角形。
8. 一个长方体的长宽高分别是2厘米、3厘米和4厘米,它的体积是______立方厘米。
9. 一个数的相反数是-5,那么这个数是______。
10. 一个圆的周长是2π厘米,那么它的半径是______厘米。
三、计算题(每题5分,共20分)11. 计算下列表达式的值:(1) (-3)^2 - √16 + 3π(2) √(2^2 + 3^2)12. 已知一个直角三角形的两条直角边分别是6厘米和8厘米,求斜边的长度。
13. 一个长方体的长是10厘米,宽是5厘米,高是3厘米,求它的表面积。
14. 已知一个圆的面积是π平方厘米,求这个圆的半径。
四、解答题(每题15分,共30分)15. 一个班级有40名学生,其中男生人数是女生人数的两倍。
求这个班级男生和女生各有多少人。
16. 某工厂生产了一种产品,每件产品的成本是10元,销售价格是15元。
如果工厂希望获得的利润是成本的40%,那么每件产品的销售价格应该是多少?五、应用题(每题25分,共50分)17. 某学校为了美化校园,决定在操场的四周种植树木。
操场是一个长方形,长100米,宽50米。
如果每棵树之间的间隔是2米,那么需要种植多少棵树?18. 某公司为了奖励员工,决定发放奖金。
12篇初一数学练习题

练习题 1一、选择题1. 下列各数中,是负数的是()A. -(-5)B. |-5|C. (-5)²D. -52. 若 a 与 -3 互为相反数,则 a 的值是()A. 3B. -3C. 1/3D. -1/3二、填空题1. 比较大小:-3____ -5(填“>”“<”或“=”)2. 绝对值小于 4 的所有整数的和为____。
三、计算1. 计算:(-2) + 3 - 52. 计算:(-4) × 5 ÷ (-5)四、解答题1. 已知有理数 a,b 在数轴上的位置如图所示,化简:|a - b| - |b|。
2. 某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负。
某天自 A 地出发到收工时所走路线(单位:千米)为:+10,-3,+4,+2,-8,+13,-2,+12,+8,+5。
问收工时距 A 地多远?练习题 2一、选择题1. 下列式子中,是单项式的是()A. x + yB. -3x²C. x² + 1D. 1/x2. 下列计算正确的是()A. 3a + 2b = 5abB. 5y² - 3y² = 2C. 7a + a = 7a²D. 3x²y - 2yx² = x²y二、填空题1. 单项式 -2πab²/5 的系数是____,次数是____。
2. 多项式 3x² - 2x - 5 是____次____项式。
三、计算1. 化简:3x² - [7x - (4x - 3) - 2x²]2. 先化简,再求值:5(3a²b - ab²) - (ab² + 3a²b),其中 a = 1/2,b = -1。
四、解答题1. 已知 A = 2x² + 3xy - 2x - 1,B = -x² + xy - 1,且 3A + 6B 的值与 x 无关,求 y 的值。
初中数学化简求值经典练习题(含答案)

初中数学化简求值经典练习题(含答案)先化简再求值: 1.(1+ 1x +1x+1)÷x (x+1)+2(x+1)−1x 2−1-1,其中:x=√2-1 ;2.1-(1x−1-1)( 1x-1),其中:x=√5+2 ;3.25x -12x−3y ·(4x 2-9y 2+4x−6y 5x),其中:x=√3+12,y= √3−13;4.2(x-2y )+3(2x-3y )-4(3x-4y ),其中:x= - 34,y= 23;5.7x 3-2x (3x-5)-(4+5x-6x 2+7x 3),其中:x=2;6.(x+1)(x-3)+3x 2- 2〔2(x-2)(x+1)+(5x+4〕),其中:x= 34 ;7.x (x-1)-(x-2)(x+3)+6[32(6+x )+ 13(5-x )],其中x= -1.2 ;8.x−9x 2−9·x 2−6x+99−x+(4x−142x 2−x−21+3),其中x=√3-3 ;9.x−2y 3x+4y ÷(x +−2xy+4y 2x−2y)·3x 2+7xy+4y 2x 2−y 2,其中:x=√5-1,y=√3-1 ;10.12(2x+4)(x-2)+x−5x 2−10x+25·(x 2-x-20),其中:x 是大于3且小于6的自然数; 11.(4x+31x−5+x+5)-x 2−9x−5·x−2x+3,其中:x 满足|x |=4 ;12.(x+3)÷ x 2+x−6x 2−6x+8-x−1x+1×2x 2−x−3x−1,其中:x=2sin60°-1 ;参考答案1.(1+ 1x +1x+1)÷x (x+1)+2(x+1)−1x 2−1-1,其中:x=√2-1 ; 解:(1+ 1x + 1x+1)÷x (x+1)+2(x+1)−1x 2−1-1=(x+1x+ 1x+1)÷x 2+x+2x+2−1(x+1)(x−1)-1=x 2+3x+1x (x+1)÷x 2+3x+1(x+1)(x−1)-1 = x 2+3x+1x (x+1) ·(x+1)(x−1)x 2+3x+1-1=x−1x-1=1 - 1x-1 = - 1x将x=√2-1代入 原式= - √2−1= -√2+1(√2−1)(√2+1)= -√2−1故当 x=√2-1时原代数式的值是:-√2−1 2. 1-(1x−1-1)( 1x-1),其中:x=√5+2 ;解:1-(1x−1 -1)( 1x-1)=1-(1x−1-x−1x−1)( 1x- xx)=1- −x+2x−1 ·1−xx=1-x−2x=1-(1- 2x) = 2x将x=√5+2代入 原式= √5+2=√5−2(√5+2)(√5−2)=2√5-4故当 x=√5+2时原代数式的值是:2√5-4 3.25x -12x−3y ·(4x 2-9y 2+4x−6y5x ),其中:x= √3+12,y= √3−13 ; 解:25x - 12x−3y (4x 2-9y 2+4x−6y 5x)= 25x -12x−3y〔(2x+3y )(2x-3y ) +2(x−3y )5x〕= 25x - 〔(2x+3y )+ 25x〕 = -(2x+3y ) = -2x-3y将x= √3+12,y= √3−13代入原式= -2·√3+12 -3·√3−13= -(√3+1)-(√3−1)=2√3故当x= √3+12,y= √3−13时原代数式的值是:2√34.2(x-2y)+3(2x-3y)-4(3x-4y),其中:x= - 34,y= 23;解:2(x-2y)+3(2x-3y)-4(3x-4y) =2x-4y+6x-9y-12x+16y= -4x+3y将x= - 34,y= 23代入原式= -4·(- 34)+3·23=3+2=5故当 x=2时原代数式的值是:55. 7x3-2x(3x-5)-(4+5x-6x2+7x3),其中:x=2;解:7x3-2x(3x-5)-(4+5x-6x2+7x3)=7x3-6x2+10x-4-5x+6x2-7x3=5x-4将x=2代入原式=5·2-4=6故当 x=2时原代数式的值是:66.(x+1)(x-3)+3x 2- 2〔2(x-2)(x+1)+(5x+4〕),其中:x= 34 ;解:(x+1)(x-3)+3x 2- 2〔2(x-2)(x+1)+(5x+4〕) = x 2-2x-3+3x 2-2〔2(x 2-x-2)+(5x+4〕) =4x 2-2x-3-2〔2x 2-2x-4+5x+4) =4x 2-2x-3-2(2x 2+3x ) =4x 2-2x-3-4x 2-6x = -8x-3 将x= 34 代入原式= -8·34-3= -9故当 x= 34 时原代数式的值是:-97.x (x-1)-(x-2)(x+3)+6[32(6+x )+ 13(5-x )],其中x= -1.2 ;解:x (x-1)-(x-2)(x+3)+6[32(6+x )+ 13(5-x )]=x 2-x-(x 2+x-6)+ [6*32(6+x )+ 6*13(5-x )]=-2x+6+[9(6+x )+ 2(5-x )] =6-2x+(54+9x+10-2x ) =6-2x+(64+7x )=70+5x 将x= -1.2代入 原式=70+5×(-1.2)=64故当x= -1.2时原代数式的值是:64 8.x−9x 2−9·x 2−6x+99−x+(4x−142x 2−x−21+3),其中x=√3-3 ; 解:x−9x 2−9·x 2−6x+99−x +(4x−142x 2−x−21 +3)=x−9(x+3)(x−3)·(x−3)2−(x−9)+〔2(2x−7)(2x−7)(x+3)+3〕= - x−3x+3+2x+3+3= 5−x x+3+3= 5−x+3x+9x+3= 2x+14x+3=(2x+6)+8x+3=2+8x+3将x=√3-3代入 原式=2+(√3−3)+3=2+8√33故当x=√3-3时原代数式的值是:2+ 8√339.x−2y 3x+4y÷(x +−2xy+4y 2x−2y)·3x 2+7xy+4y 2x 2−y 2,其中:x=√5-1,y=√3-1;解:x−2y3x+4y ÷(x + −2xy+4y2x−2y)·3x2+7xy+4y2x2−y2= x−2y3x+4y ÷x2−4xy+4y2x−2y·(3x+4y)(x+y)(x+y)(x−y)=x−2y3x+4y ÷(x−2y)2x−2y·3x+4yx−y=x−2y3x+4y ·1x−2y·3x+4yx−y= 1x−y将x=√5-1,y=√3-1代入原式=(√5−1)−(√3−1)=√5−√3= √5+√3(√5−√3)(√5+√3)= √5+√35−3= √5+√32故当x=√5-1,y=√3-1时原代数式的值是:√5+√3210.12(2x+4)(x-2)+ x−5x2−10x+25·(x2-x-20),其中:x是大于3且小于6的自然数;解:12(2x+4)(x-2)+ x−5x2−10x+25·(x2-x-20)=(x+2)(x-2)+ x−5(x−5)2·(x+4)(x-5)=x2 -4 +x+4=x2 +xx是大于3且小于6的自然数那么x 是自然数4或5,但是当x=5时,分式 x−5x 2−10x+25的分母等于0,故x 不能为5,所以x 只能是自然数4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(2009•河南)如图,在Rt △ABC 中,∠ACB=90°,∠B=60°,BC=2.点O 是AC 的中点,过点O 的直线l 从与AC 重合的位置开始,绕点O 作逆时针旋转,交AB 边于点D ,过点C 作CE ∥AB 交直线l 于点E ,设直线l 的旋转角为α.
(1)①当α= 度时,四边形EDBC 是等腰梯形,此时AD 的长为 ; ②当α= 度时,四边形EDBC 是直角梯形,此时AD 的长为 ; (2)当α=90°时,判断四边形EDBC 是否为菱形,并说明理由.
2.)如图,在平面直角坐标系中,已知点D 为函数y=
x
18
(x >0)上 的一点,四边形ABCD 是直角梯形(点B 在坐标原点处),AD ∥BC ,∠B=90°,A (0,3),C (4,0),点P 从A 出发,以3个单位/秒的速度沿直线AD 向右运动,点Q 从点C 同时出发,以1个单位/秒的速度沿直线CB 向左运动. (1)求点D 的坐标;
(2)从运动开始,经过多少时间以点P 、Q 、C 、D 为顶点的四边形为平行四边形? (3)当运动时间t=
3
2
秒时,在y 轴上找一点M ,使得△PCM 是以.PC ..为底..的等腰三角形时,请求出点M 的坐标.
5.(7分)3月12日“植树节”这天,某校组织师生到距学校20千米的公路旁植树,甲班师生骑自行车先走,45分钟后,乙班师生乘汽车出发,结果两班师生同时到达,已知汽车的速度是自行车速度的2.5倍,求两种车的速度各是多少?
3.如图直线y =kx +2k (k ≠0)与x 轴交于点B ,与双曲线y =(m +5)x 2m +1
交于点A 、C ,其中点A
在第一象限,点C 在第三象限.
(1)求双曲线的解析式;(2)求B 点的坐标; (3)若S △AOB =2,求A 点的坐标;
(4)在(3)的条件下,在x 轴上是否存在点P , 使△AOP 是等腰三角形?若存在,请写出P 点的坐标; 若不存在,请说明理由.
4.如图所示在直角梯形ABCD 中,AD//BC ,∠A =90°,AB =12,BC =21,AD=16.动点P 从点B 出发,沿射线BC 的方向以每秒2个单位长的速度运动,动点Q 同时从点A 出发,在线段AD 上以每秒1个单位长的速度向点D 运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t (秒).
(1)设△DPQ 的面积为S ,求S 与t 之间的函数关系式; (2)t 为何值时,△DPQ 的面积是60.
(3)当t 为何值时,四边形PCDQ 是平行四边形? (4)当t 为何值时, PD =PQ.
6.(7分)如图,已知一次函数y=k 1x+b 的图象与反比例函数y=x
k 2
的图象交于A (1,-3),B (3,m )两点,连接OA 、OB .
(1)求两个函数的解析式; (2)求△ABC 的面积.
A B O
x
y
7.(8分)如图,以△ABC 的三边为边,在BC 的同侧作三个等边△ABD 、△BEC 、△ACF .
(1)判断四边形ADEF 的形状,并证明你的结论;
(2)当△ABC 满足什么条件时,四边形ADEF 是菱形?是矩形? 8.(8分)
为了缓解用电紧张的矛盾,某电力公司特制定了新的用户用电收费标准,每月用电量x (度)与应付电费y (元)的关系如图所示.
(1)根据图象,请分别求出当500≤≤x 和x >50时,y 关于x 的函数关系式;
(2)请回答:
当每月用电量不超过50度时,收费标准是________________; 当每月的用电量越过50度时,收费标准是________________. 9.(本题满分10分)
如图,△ABC 中,AD ⊥BC 于D 点,E 为BD 上的一点,EG ∥AD ,分别交AB 和CA 的延长线于F 、G 两点,∠AFG=∠AGF (1)求证:△ABD ≌△ACD .
(2)若∠ABC=40°,求∠GAF 的大小.
A F
E
D
C
B
20.(本小题8分)已知,一张矩形纸片ABCD的边长
分别为9cm和3cm,把顶点A和C叠合在一起,得折
痕EF(如图).
(1)猜想四边形AECF是什么四边形,并证明你
的猜想.
(2)求折痕EF的长.
23.(本小题10分) 我区浙江中国花木城组织10辆汽车装运完A、B、C三种不同品质的苗木共100吨到外地销售,按计划10辆汽车都要装满,且每辆汽车只能装同一种苗木,由信息解答以下问题:
苗木品种 A B C
每辆汽车运载量(吨)12 10 8
每吨苗木获利(万元) 3 4 2
(1)设装A种苗木车辆数为x,装运B种苗木的车辆数为y,求y与x之间的函数关系式;(2)若装运每种苗木的车辆都不少于2辆,则车辆安排方案有几种?写出每种安排方案;(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润。
24.(本小题12分)如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=16cm,AB=12cm,BC=21cm,动点P从点B出发,沿射线BC的方向以每秒2cm的速度运动,动点Q从点A出发,在线段AD上以每秒1cm的速度向点D运动,点P,Q分别从点B,A同时出发,当点Q 运动到点D时,点P随之停止运动,设运动的时间为t(秒).
(1)当t为何值时,四边形PQDC是平行四边形.
(2)当t为何值时,以C,D,Q,P为顶点的梯形面积等于
60cm2?
(3)是否存在点P,使△PQD是等腰三角形?若存在,请求
第24题
出所有满足要求的t的值,若不存在,请说明理由.
19、码头工人以每天30吨的速度往一艘船上装载货物,把轮船装完毕恰好用了8天时间。
(1) 轮船到达目的地后开始卸货,卸货速度V (单位:吨/天)与卸货时间t (单位:
天)之间有怎样的函数关系?
(2) 由于遇到紧急情况,船上货物必须在不超过5日内卸载完毕,那么平均每天至
少要卸多少吨货物?
20、如图,一块直角三角形的纸片,两直角边AC =6㎝,BC =8㎝,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合。
求DE 的长
21、先化简,再求值:23331
111x x x x x -÷-+--,其中x 是不等式⎪⎩⎪⎨⎧≤-
<--3132
10)2(43x x x x 的整数解。
23、如图,已知A(n ,-2),B(1,4)是一次函数y=kx+b 的图象和反比例函数y=
x
m
的图象的两个交点,直线AB 与y 轴交于点C . (1)求反比例函数和一次函数的关系式; (2)求△AOC 的面积; (3)求不等式kx+b-x
m
<0的解集(直接写出答案).
A
C
D
B
E
第20题图
25、为了进一步优化普洱市中心城区的城市功能,提升城市品质,思茅区对振兴大道、思茅路的人行道地转、花池、排水管道等公用设施全面更新改造,根据市政建设的需要须在60天内完成工程.现在甲、乙两个工程队有能力承包这个工程.经调查知道:乙队单独完成此项工程的时间是甲队单独完成的1.5倍,甲、乙两队合作完成工程需要30天,甲队每天的工程费用2500元,乙队每天的工程费用2000元.根据以上信息可设计几个施工方案?你觉得哪一种方案节省工程款?请说明理由
26.如图所示,在正方形ABCD中,E、F分别是AB、CD上的两点, AB=6cm,动点P从E点出
发以1cm/s的速度沿E—B-C-D-A-E运动,设P点运动的时间为t秒。
(1)若AE=CF=2cm ,当P运动到BC上时,试用t的代数式表示BP、CP的长。
(2)若AE=CF=2cm是否存在点P使△PEF是等腰三角形?若存在求出此时t的所有值。
(至少写出四个点)
(3)当线段BE、CF、BC满足什么条件时,是否一定存在点P使△PEF是等腰直角三角形?若存在请直接写出这个关系式,若不存在请说明理由。
