平行线四大模型(归纳总结)
初中数学知识归纳平行线与平行四边形的判定

初中数学知识归纳平行线与平行四边形的判定平行线与平行四边形是初中数学中的重要概念,学好这部分知识对于解决几何问题非常关键。
在本文中,将对平行线与平行四边形的判定方法进行归纳总结,帮助初中生更好地理解和掌握这一知识点。
一、平行线的判定方法1. 同位角相等法同位角是指两条直线被一条截线所切割而形成的内、外两对对应角,若两条直线被同一条截线所截,而同位角相等,则这两条直线是平行的。
这是平行线判定中常用的一种方法。
2. 内错角相等法内错角指两条平行线被一条直线所切割而形成的两个相对的内角,若这两个内角相等,则这两条直线是平行的。
3. 单位判定法若直线AB与直线CD分别与第三条直线EF相交,使得∠AFE=∠EFD,则可以判定AB和CD平行。
4. 平行线定理平行线定理是欧几里得几何中的基本定理,它指出:如果一条直线与两条平行线相交,那么这两条平行线之间的对应角都相等。
二、平行四边形的判定方法1. 对角线互相平分法如果一个四边形的对角线互相平分,即使两条对角线分别在中点重合,那么这个四边形是平行四边形。
2. 邻边角相等法邻边角指平行四边形中两个相邻的内角,如果两个邻边角相等,则这个四边形是平行四边形。
3. 对边对角相等法对边对角指平行四边形中两对相对的内角,如果对边对角相等,则这个四边形是平行四边形。
4. 对顶角相等法对顶角指平行四边形中两对相对的对角,如果对顶角相等,则这个四边形是平行四边形。
总结归纳了平行线和平行四边形的判定方法后,让我们来看几个例题加深理解。
例题一:已知直线AB与直线CD向同一方向做射线,且∠EAF = 90°,EF是直线AB的垂线,垂足为F。
若∠ECD = ∠BAF,证明AB∥CD。
解析:根据题目中的信息可得:∠EAF = 90°,EF是AB的垂线。
又∠ECD = ∠BAF。
根据垂直线上的角相等定理可知∠EAF = ∠BAF。
综上所述,根据同位角相等法可知AB∥CD。
平行线的性质归纳总结

平行线的性质归纳总结平行线是几何学中一个重要的概念,它们具有一系列独特的性质和规律。
在本文中,我们将对平行线的性质进行归纳总结。
一、平行线的定义和符号表示平行线是指在同一个平面内永不相交的两条直线。
我们可以用符号"||" 表示平行线。
二、平行线的性质1. 垂直的平行线若一条直线与另外两条不同的直线相交,且与其中一条直线垂直,那么另外两条直线是平行的。
例如:若直线l与直线m相交,直线l与直线n垂直,那么直线m与直线n是平行的。
2. 平行线的性质1:同向性若两条平行线与同一直线相交,折角之间的关系保持不变。
例如:若直线l与直线m平行,直线m与直线n相交,则角A与角B是对应角,角A与角C是内错角。
3. 平行线的性质2:内角性质当两条平行线被一条截线所切分时,内错角互补,即它们的和等于180度。
180度。
4. 平行线的性质3:外角性质当两条平行线被一条截线所切分时,外错角相等。
例如:若直线l与直线m平行,直线n为截线,则角A = 角C。
5. 平行线的性质4:同位角当两条平行线被一条截线所切分时,同位角相等。
例如:若直线l与直线m平行,直线n为截线,则角A = 角D。
6. 平行线的性质5:内错角当两条平行线被一条截线所切分时,内错角相等。
例如:若直线l与直线m平行,直线n为截线,则角B = 角C。
7. 平行线的性质6:同旁内角当两条平行线被一条截线所切分时,同旁内角互补,即它们的和等于180度。
例如:若直线l与直线m平行,直线n为截线,则角B + 角D = 180度。
8. 平行线的性质7:同旁外角当两条平行线被一条截线所切分时,同旁外角相等。
9. 平行线的性质8:错综对应角若两条平行线被多条截线所切分,那么对应角相等。
例如:若直线l与直线m平行,直线n和直线p均为截线,则角A = 角E,角B = 角F,角C = 角G。
10. 平行线的性质9:平行线之间的距离两条平行线之间的距离是恒定的,且等于它们之间任意一点到两条平行线的距离。
平行线中的常考模型,掌握这三个考察方向,多拿4—12分

平行线中的常考模型,掌握这三个考察方向,多拿4—12分在平行线这一部分,有三个重要的模型。
这三个模型分别是:铅笔模型猪脚模型鹰嘴模型(1)鹰嘴模型(2)因为这三个模型相通的,(1)都是两条平行线和平行线之外的一个点;(2)都是三个角∠B 、∠D 、∠E 之间的关系;(3)证明方法都可以过平行线外的这个点做已知直线的平行线;(4)考查方向也基本一样。
所以把它们们合并在一起给大家介绍。
希望通过这次讲解,能让孩子达到举一反三的目的。
模型的主要考查方向是:一、考证明方法在考试当中,一般会考到这三个模型的证明方法。
都可以通过平行线外面的点做已知直线的平行线,然后通过角度转化,来证明角度之间的关系。
1.铅笔模型:证明:过点E作射线EF,使EF //AB∵AB//CD∴EF//CD∴∠FED+∠D=180°∵EF//AB∴∠FEB+∠B=180°∴∠BED+∠B+∠D=∠FED+FEB+∠B+∠D=∠FED+∠D+∠FEB+∠B=180°+180°=360°即∠BED+∠B+∠D= 360°(总结:铅笔顶端的三个角的和是360°)2.模型猪脚:证明:过点E作射线EF,使EF //AB∵AB//CD∴EF//CD∴∠FED=∠D∵EF//AB∴∠FEB=∠B∴∠BED= ∠FED+∠FEB =∠B+∠D(总结:两个脚趾尖儿的度数和等于趾缝处的度数)3. 鹰嘴模型(1)提示:对七年级的孩子,不适用外角的定理去证明该题。
证明:过点E作射线EF,使EF //AB∵AB//CD∴EF//CD∴∠FED=∠D∵EF//AB∴∠FEB=∠B∴∠D=∠FED=∠BED+∠FEB=∠BED+∠B即:∠BED=∠D-∠B(总结:鹰嘴度数等于大角减去小角)4. 鹰嘴模型(2)提示:对七年级的孩子,不适用外角的定理去证明该题。
证明:过点E作射线EF,使EF //AB∵AB//CD∴EF//CD∴∠FED=∠D∵EF//AB∴∠FEB=∠B∴∠B=∠FEB=∠BED+∠FED=∠BED+∠D即:∠BED=∠B-∠D(总结:鹰嘴度数等于大角减去小角)一、考结论的应用这一类考题主要是需要同学们把三个模型的结论记住。
平行线拐点问题六种模型题型

平行线常见四种易错题型分析七年级下学期,平行线常见四种易错题型分析:过拐点作已知直线的平行线。
本篇内容,我们接着介绍平行线中常见的六种易错题型,早掌握避免遇到时出错。
平行线间拐点问题基本模型有三种: 第一种铅笔模型;第二种M型;第三种猪手模型。
我们还介绍了平行线四大拐点模型:“铅笔”模型、“猪蹄”模型、“臭脚”模型、“骨折”模型,这四类模型的共通点是需要做辅助线,做辅助线的方法比较多,通用的方法为:过拐点作已知直线的平行线。
一、性质定理与判定定理的区分要分清它们,只要注意:(1)由角得到直线平行,是判定定理,选择①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行,这三个定理之一。
(2)由平行的直线得到角的关系,是性质定理,选择①两直线平行,同位角相等;②两直线平行,内错角相等;③两直线平行,同旁内角互补,这三个定理之一。
【分析】先由垂直的定义得到:∠2=∠3,然后由同位角相等,两直线平行得到:EF∥BD,再由两直线平行,同位角相等得到:∠4=∠5,然后根据等量代换得到:∠1=∠5,再根据内错角相等,两直线平行得到:DG∥BC,最后由两直线平行,同位角相等即可证∠ADG=∠C.二、三线八角理解不透彻很多学生遇到两条平行线被第三条直线所截时,会找同位角、内错角、同旁内角,但是遇到两条相交线被第三条直线所截时,却不会找了,主要原因就是对“三线八角”理解不透彻。
要想准确地解决这类问题,首先要明确三种角的位置特点,在前一篇文章中我们特地介绍过,七年级下学期,三线八角、平行线的性质与判定定理,掌握解题诀窍其次要搞清楚被哪条直线所截。
【分析】∠A与∠B的共边线为直线AB,那么直线AB为截线,即直线AC与直线BC被第三条直线AB所截,那么∠A与∠B是同旁内角,正确;∠1与∠2是邻补角,错误;∠2与∠A的共边线为直线AC,是同位角,错误;∠2与∠3是内错角,错误。
三、对平行线的概念理解不透彻例题3:判断题:同一平面内不相交的两条线,叫做平行线.【分析】这句话,乍看没有问题,但是细看的话,与定义有出入。
初中数学平行线知识点归纳总结(二)2024

初中数学平行线知识点归纳总结(二)【引言】平行线是初中数学的重要知识点之一,它主要涉及到平行线的定义、性质以及与角、相交线等几何图形的关系。
本文将对初中数学平行线知识点进行归纳总结,帮助同学们更好地理解和掌握这一内容。
【正文】1. 平行线的定义- 两条直线在同一平面内,且不相交,那么它们就是平行线。
- 平行线符号:∥2. 平行线的性质- 平行线上的任意两条线段之间的距离是相等的。
- 平行线与一个非其上的点连线所得的所有角都相等。
- 平行线与另一直线的相交角之和等于180°。
- 平行线与平行线之间的夹角相等。
3. 平行线与角的关系- 对顶角与平行线:若平行线被一条横截线所截,那么所截得的对顶角是相等的。
- 同位角与平行线:若平行线被一条横截线所截,那么所截得的同位角是相等的。
- 内错角与平行线:若平行线被两条横截线所截,那么所截得的内错角互补(和为180°)。
- 相间角与平行线:若平行线被两条横截线所截,那么所截得的相间角互补(和为180°)。
4. 平行线与相交线的关系- 同位线与平行线:若两条平行线被一条横截线所截,那么所截得的同位线互相平行。
- 辅助线与平行线:在解决几何问题时,我们可以通过引入辅助线的方式来利用平行线的性质进行推导和求解。
5. 平行线的简单应用- 利用平行线的性质证明几何关系。
- 利用平行线的性质求解几何问题,如长度比较、面积计算等。
【总结】初中数学中的平行线知识点主要包括平行线的定义、性质以及与角、相交线的关系。
掌握这些知识点,能够帮助我们更好地解决几何问题,进行证明和计算。
通过本文的归纳总结,希望能对同学们的学习和理解有所帮助。
(完整版)七年级数学培优-平行线四大模型

平行线四大模型平行线的判定与性质l、平行线的判定根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行,但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行,这就需要更简单易行的判定方法来判定两直线平行.判定方法l:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称:同位角相等,两直线平行.判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称:内错角相等,两直线平行,判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称:同旁内角互补,两直线平行,如上图:若已知∠1=∠2,则AB∥CD(同位角相等,两直线平行);若已知∠1=∠3,则AB∥CD(内错角相等,两直线平行);若已知∠1+ ∠4= 180°,则AB∥CD(同旁内角互补,两直线平行).另有平行公理推论也能证明两直线平行:平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.2、平行线的性质利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果已知两条直线平行,当它们被第三条直线所截,得到的同位角、内错角、同旁内角也有相应的数量关系,这就是平行线的性质.性质1:两条平行线被第三条直线所截,同位角相等.简称:两直线平行,同位角相等性质2:两条平行线被第三条直线所截,内错角相等.简称:两直线平行,内错角相等性质3:两条平行线被第三条直线所截,同旁内角互补.简称:两直线平行,同旁内角互补本讲进阶平行线四大模型模型一“铅笔”模型点P在EF右侧,在AB、CD内部“铅笔”模型结论1:若AB∥CD,则∠P+∠AEP+∠PFC=3 60°;结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD.模型二“猪蹄”模型(M模型)点P在EF左侧,在AB、CD内部“猪蹄”模型结论1:若AB∥CD,则∠P=∠AEP+∠CFP;结论2:若∠P=∠AEP+∠CFP,则AB∥CD.模型三“臭脚”模型点P在EF右侧,在AB、CD外部“臭脚”模型结论1:若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;结论2:若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD.模型四“骨折”模型·点P在EF左侧,在AB、CD外部“骨折”模型结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.巩固练习平行线四大模型证明(1)已知AE // CF ,求证∠P +∠AEP +∠PFC = 360°.(2)已知∠P=∠AEP+∠CFP,求证AE∥CF.(3)已知AE∥CF,求证∠P=∠AEP-∠CFP.(4)已知∠P= ∠CFP -∠AEP,求证AE //CF.模块一平行线四大模型应用例1(1)如图,a∥b,M、N分别在a、b上,P为两平行线间一点,那么∠l+∠2+∠3= .(2)如图,AB∥CD,且∠A=25°,∠C=45°,则∠E的度数是.(3)如图,已知AB∥DE,∠ABC=80°,∠CDE =140°,则∠BCD= .(4) 如图,射线AC∥BD,∠A= 70°,∠B= 40°,则∠P= .练(1)如图所示,AB∥CD,∠E=37°,∠C= 20°,则∠EAB的度数为.(2) 如图,AB∥CD,∠B=30°,∠O=∠C.则∠C= .例2如图,已知AB ∥DE ,BF 、 DF 分别平分∠ABC 、∠CDE ,求∠C 、 ∠F 的关系.练如图,已知AB ∥DE ,∠FBC =n 1∠ABF ,∠FDC =n1∠FDE . (1)若n =2,直接写出∠C 、∠F 的关系 ; (2)若n =3,试探宄∠C 、∠F 的关系;(3)直接写出∠C 、∠F 的关系 (用含n 的等式表示).例3如图,已知AB ∥CD ,BE 平分∠ABC ,DE 平分∠ADC .求证:∠E = 2 (∠A +∠C ) .练如图,己知AB ∥DE ,BF 、DF 分别平分∠ABC 、∠CDE ,求∠C 、∠F 的关系.例4如图,∠3==∠1+∠2,求证:∠A+∠B+∠C+∠D= 180°.练(武昌七校2015-2016 七下期中)如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠l+∠2= 90°,M、N分别是BA、CD的延长线上的点,∠EAM和∠EDN的平分线相交于点F则∠F的度数为().A. 120°B. 135°C. 145°D. 150°模块二平行线四大模型构造例5如图,直线AB∥CD,∠EF A= 30°,∠FGH= 90°,∠HMN=30°,∠CNP= 50°,则∠GHM= .练如图,直线AB∥CD,∠EFG =100°,∠FGH =140°,则∠AEF+ ∠CHG= .例6 已知∠B =25°,∠BCD=45°,∠CDE =30°,∠E=l0°,求证:AB∥EF.练已知AB∥EF,求∠l-∠2+∠3+∠4的度数.(1)如图(l),已知MA1∥NA n,探索∠A1、∠A2、…、∠A n,∠B1、∠B2…∠B n-1之间的关系.(2)如图(2),己知MA1∥NA4,探索∠A1、∠A2、∠A3、∠A4,∠B1、∠B2之间的关系.(3)如图(3),已知MA1∥NA n,探索∠A1、∠A2、…、∠A n之间的关系.如图所示,两直线AB∥CD平行,求∠1+∠2+∠3+∠4+∠5+∠6.。
平行线四大模型

平行线四大模型1、平行线的判定根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行,但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行,这就需要更简单易行的判定方法来判定两直线平行.判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称:同位角相等,两直线平行.判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称:内错角相等,两直线平行,判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称:同旁内角互补,两直线平行,如上图:若已知∠1=∠2,则AB∥CD(同位角相等,两直线平行);若已知∠1=∠3,则AB∥CD(内错角相等,两直线平行);若已知∠1+∠4=180°,则AB∥CD(同旁内角互补,两直线平行).另有平行公理推论也能证明两直线平行:平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.2、平行线的性质利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果已知两条直线平行,当它们被第三条直线所截,得到的同位角、内错角、同旁内角也有相应的数量关系,这就是平行线的性质.性质1:两条平行线被第三条直线所截,同位角相等.简称:两直线平行,同位角相等性质2:两条平行线被第三条直线所截,内错角相等.简称:两直线平行,内错角相等性质3:两条平行线被第三条直线所截,同旁内角互补.简称:两直线平行,同旁内角互补平移3.平移是指在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移(translation),简称平移。
4.平移的性质经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等;平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形)。
(1)图形平移前后的形状和大小没有变化,只是位置发生变化;(2)图形平移后,对应点连成的线段平行且相等(或在同一直线上)(3)多次平移相当于一次平移。
平行线中的四大经典模型(浙教版)(解析版)
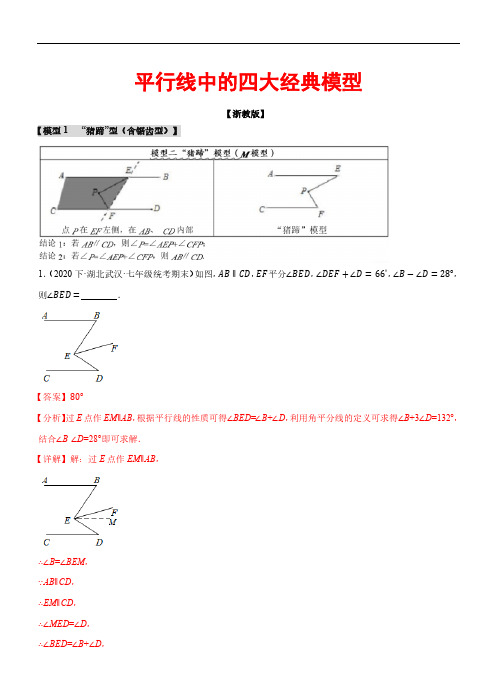
平行线中的四大经典模型【浙教版】【模型1 “猪蹄”型(含锯齿型)】1.(2020下·湖北武汉·七年级统考期末)如图,AB∥CD,EF平分∠BED,∠DEF+∠D=66°,∠B−∠D=28°,则∠BED=.【答案】80°【分析】过E点作EM∥AB,根据平行线的性质可得∠BED=∠B+∠D,利用角平分线的定义可求得∠B+3∠D=132°,结合∠B-∠D=28°即可求解.【详解】解:过E点作EM∥AB,∴∠B=∠BEM,∵AB∥CD,∴EM∥CD,∴∠MED=∠D,∴∠BED=∠B+∠D,∵EF平分∠BED,∴∠DEF=1∠BED,2∵∠DEF+∠D=66°,∠BED+∠D=66°,∴12∴∠BED+2∠D=132°,即∠B+3∠D=132°,∵∠B-∠D=28°,∴∠B=54°,∠D=26°,∴∠BED=80°.故答案为:80°.【点睛】本题主要考查平行线的性质,角平分线的定义,作出辅助线证出∠BED=∠B+∠D是解题的关键.2.(2023上·辽宁鞍山·七年级统考期中)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,∠BCD=n°,则∠BED的度数为.(用含n的式子表示)n°【答案】40°+12【分析】首先过点E作EF∥AB,由平行线的传递性得AB∥CD∥EF,再根据两直线平行,内错角相等,得n°,∠EDC=40°,再由出∠BCD=∠ABC=n°,∠BAD=∠ADC=80°,由角平分线的定义得出∠ABE=12两直线平行,内错角相等得出∠BEF=∠ABE=1n°∠FED=∠EDC=40°,由∠BED=∠BEF+∠FED即可2得出答案.【详解】解:如图,过点E作EF∥AB,则AB∥CD∥EF,∵AB∥CD,∴∠BCD=∠ABC=n°,∠BAD=∠ADC=80°,又∵BE平分∠ABC,DE平分∠ADC,∴∠ABE=12∠ABC=12n°,∠EDC=12∠ADC=12×80°=40°,∵AB∥EF∥CD,∴∠BEF=∠ABE=12n°,∠FED=∠EDC=40°,∴∠BED=∠FED+∠BEF=40°+12n°,故答案为:40°+12n°.【点睛】本题考查平行线的性质,角平分线的定义,解题关键是作出正确的辅助线,掌握平行线的性质和角平分线的定义.3.(2023下·广东河源·七年级河源市第二中学校考期中)已知直线l1∥l2,A是l1上的一点,B是l2上的一点,直线l3和直线l1,l2交于C和D,直线CD上有一点P.(1)如果P点在C,D之间运动时,问∠PAC,∠APB,∠PBD有怎样的数量关系?请说明理由.(2)若点P在C,D两点的外侧运动时(P点与C,D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?(请直接写出答案,不需要证明)【答案】(1)∠PAC+∠PBD=∠APB(2)当点P在直线l1上方时,∠PBD−∠PAC=∠APB;当点P在直线l2下方时,∠PAC−∠PBD=∠APB.【分析】(1)过点P作PE∥l1,由“平行于同一条直线的两直线平行”可得出PE∥l1∥l2,再由“两直线平行,内错角相等”得出∠PAC=∠APE、∠PBD=∠BPE,再根据角与角的关系即可得出结论;(2)按点P的两种情况分类讨论:①当点P在直线l1上方时;②当点P在直线l2下方时,同理(1)可得∠PAC=∠APE、∠PBD=∠BPE,再根据角与角的关系即可得出结论.【详解】(1)解:∠PAC+∠PBD=∠APB.过点P作PE∥l1,如图1所示.∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠APE+∠BPE,∴∠PAC+∠PBD=∠APB.(2)解:结论:当点P在直线l1上方时,∠PBD−∠PAC=∠APB;当点P在直线l2下方时,∠PAC−∠PBD=∠APB.①当点P在直线l1上方时,如图2所示.过点P作PE∥l1.∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠BPE−∠APE,∴∠PBD−∠PAC=∠APB.②当点P在直线l2下方时,如图3所示.过点P作PE∥l1.∵PE∥l1,l1∥l2,∴PE∥l1∥l2,∴∠PAC=∠APE,∠PBD=∠BPE,∵∠APB=∠APE−∠BPE,∴∠PAC−∠PBD=∠APB.【点睛】本题考查了平行线的性质以及角的计算,解题的关键是根据“两直线平行,内错角相等”找到相等的角.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质得出相等(或互补)的角是关键.4.(2023下·山东聊城·七年级统考阶段练习)已知直线AB//CD,EF是截线,点M在直线AB、CD之间.(1)如图1,连接GM,HM.求证:∠M=∠AGM+∠CHM;(2)如图2,在∠GHC的角平分线上取两点M、Q,使得∠AGM=∠HGQ.试判断∠M与∠GQH之间的数量关系,并说明理由.【答案】(1)证明见详解(2)∠GQH=180°−∠M;理由见详解【分析】(1)过点M作MN∥AB,由AB∥CD,可知MN∥AB∥CD.由此可知:∠AGM=∠GMN,∠CHM=∠HMN,故∠AGM+∠CHM=∠GMN+∠HMN=∠M;(2)由(1)可知∠AGM+∠CHM=∠M.再由∠CHM=∠GHM,∠AGM=∠HGQ,可知:∠M=∠HGQ+∠GHM,利用三角形内角和是180°,可得∠GQH=180°−∠M.【详解】(1)解:如图:过点M作MN∥AB,∴MN∥AB∥CD,∴∠AGM=∠GMN,∠CHM=∠HMN,∵∠M=∠GMN+∠HMN,∴∠M=∠AGM+∠CHM.(2)解:∠GQH=180°−∠M,理由如下:如图:过点M作MN∥AB,由(1)知∠M=∠AGM+∠CHM,∵HM平分∠GHC,∴∠CHM=∠GHM,∵∠AGM=∠HGQ,∴∠M=∠HGQ+∠GHM,∵∠HGQ+∠GHM+∠GQH=180°,∴∠GQH=180°−∠M.【点睛】本题考查了利用平行线的性质求角之间的数量关系,正确的作出辅助线是解决本题的关键,同时这也是比较常见的几何模型“猪蹄模型”的应用.5.(2023下·福建莆田·七年级莆田第二十五中学校考阶段练习)如图,AB//CD,点E在直线AB,CD内部,且AE⊥CE.(1)如图1,连接AC,若AE平分∠BAC,求证:CE平分∠ACD;(2)如图2,点M在线段AE上,①若∠MCE=∠ECD,当直角顶点E移动时,∠BAE与∠MCD是否存在确定的数量关系?并说明理由;∠ECD(n为正整数),当直角顶点E移动时,∠BAE与∠MCD是否存在确定的数量关系?并②若∠MCE=1n说明理由.【答案】(1)见解析;(2)①∠BAE +12∠MCD =90°,理由见解析;②∠BAE +n n+1∠MCD =90°,理由见解析.【分析】(1)根据平行的性质可得∠BAC +∠DCA =180°,再根据AE ⊥CE 可得∠EAC +∠ECA =90°,根据AE 平分∠BAC 可得∠BAE =∠EAC ,等量代换可得∠ECD +∠EAC =90°,继而求得∠DCE =∠ECA ;(2)①过E 作EF ∥AB ,先利用平行线的传递性得出EF ∥AB ∥CD ,再利用平行线的性质及已知条件可推得答案;②过E 作EF ∥AB ,先利用平行线的传递性得出EF ∥AB ∥CD ,再利用平行线的性质及已知条件可推得答案.【详解】(1)解:因为AB//CD ,所以∠BAC +∠DCA =180°,因为AE ⊥CE ,所以∠EAC +∠ECA =90°,因为AE 平分∠BAC ,所以∠BAE =∠EAC ,所以∠BAE +∠DCE =90°,所以∠EAC +∠DCE =90°,所以∠DCE =∠ECA ,所以CE 平分∠ACD ;(2)①∠BAE 与∠MCD 存在确定的数量关系:∠BAE +12∠MCD =90°, 理由如下: 过E 作EF ∥AB ,∵AB∥CD,∴EF∥AB∥CD,∴∠BAE=∠AEF,∠FEC=∠DCE,∵∠E=90°,∴∠BAE+∠ECD=90°,∵∠MCE=∠ECD,∴∠BAE+12∠MCD=90°;②∠BAE与∠MCD存在确定的数量关系:∠BAE+nn+1∠MCD=90°,理由如下:过E作EF∥AB,∵AB∥CD,∴EF∥AB∥CD,∴∠BAE=∠AEF,∠FEC=∠DCE,∵∠E=90°,∴∠BAE+∠ECD=90°,∵∠MCE=1n∠ECD,∴∠BAE+nn+1∠MCD=90°.【点睛】本题主要考查平行线的性质和角平分线的定义,解决本题的关键是要添加辅助线利用平行性质. 6.(2023·全国·七年级专题练习)(1)如图1,已知AB//CD,∠ABF=∠DCE,求证:∠BFE=∠FEC(2)如图2,已知AB//CD,∠EAF=14∠EAB,∠ECF=14∠ECD,求证:∠AFC=34∠AEC【答案】(1)见解析;(2)见解析【分析】(1)如图:延长BF、DC相较于E,由AB//CD可得∠ABF=∠E,再结合∠ABF=∠DCE可得∠DCE=∠E,即可得当BE//DE,最后运用两直线平行、内错角相等即可证明结论;(2)如图2:连接AC,设∠EAF=x,∠ECF=y,∠EAB=4x,∠ECD=4y,根据平行线性质得出∠BAC+∠ACD=180°,求出∠CAE+∠ACE=180°-(4x+4y),再求出∠AEC和∠AFC,最后比较即可得到结论.【详解】(1)证明:如图:延长BF、DC相较于G∵AB//CD∴∠ABF=∠G∵∠ABF=∠DCE∴∠DCE=∠G∴BG//CE∴∠BFE=∠FEC;(2)如图2:连接AC,设∠EAF=x,∠ECF=y,∠EAB=4x,∠ECD=4y,∵AB//CD,∴∠BAC+∠ACD=180°∴∠CAE+4x+∠ACE+4y=180°∴∠CAE+∠ACE=180°-(4x+4y),∠F AC+∠FCA=180°-(3x+3y),∴∠AEC=180°-(∠CAE+∠ACE)=180°-[80°-(4x+4y)]=4x+4y=4(x+y)∠AFC=180°-(∠F AC+∠FCA)=180°-[180°-(3x+3y))]=3x+3y=3(x+y),∴∠AFC=34∠AEC.【点睛】本题主要考查了平行线的判定与性质、三角形内角和定理的应用等知识点,灵活应用平行线的判定与性质以及三角形内角和定理正确的表示角成为解答本题的关键.7.(2017下·湖北武汉·七年级统考期中)如图1,已知AB∥CD,∠B=30°,∠D=120°;(1)若∠E=60°,则∠F=;(2)请探索∠E与∠F之间满足的数量关系?说明理由;(3)如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.【答案】(1)90°(2)∠F=∠E+30°,理由见解析(3)15°【分析】(1)如图1,分别过点E,F作EM//AB,FN//AB,根据平行线的性质得到∠B=∠BEM=30°,∠MEF=∠EFN,∠D+∠DFN=180°,代入数据即可得到结论;(2)如图1,根据平行线的性质得到∠B=∠BEM=30°,∠MEF=∠EFN,由AB//CD,AB//FN,得到CD//FN,根据平行线的性质得到∠D+∠DFN=180°,于是得到结论;(3)如图2,过点F作FH//EP,设∠BEF=2x°,则∠EFD=(2x+30)°,根据角平分线的定义得到∠PEF=1 2∠BEF=x°,∠EFG=12∠EFD=(x+15)°,根据平行线的性质得到∠PEF=∠EFH=x°,∠P=∠HFG,于是得到结论.【详解】(1)解:如图1,分别过点E,F作EM//AB,FN//AB,∴EM//AB//FN,∴∠B=∠BEM=30°,∠MEF=∠EFN,又∵AB//CD,AB//FN,∴CD//FN,∴∠D+∠DFN=180°,又∵∠D=120°,∴∠DFN=60°,∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,∴∠EFD=∠MEF+60°∴∠EFD=∠BEF+30°=90°;故答案为:90°;(2)解:如图1,分别过点E,F作EM//AB,FN//AB,∴EM//AB//FN,∴∠B=∠BEM=30°,∠MEF=∠EFN,又∵AB//CD,AB//FN,∴CD//FN,∴∠D+∠DFN=180°,又∵∠D=120°,∴∠DFN=60°,∴∠BEF=∠MEF+30°,∠EFD=∠EFN+60°,∴∠EFD=∠MEF+60°,∴∠EFD=∠BEF+30°;(3)解:如图2,过点F作FH//EP,由(2)知,∠EFD=∠BEF+30°,设∠BEF=2x°,则∠EFD=(2x+30)°,∵EP平分∠BEF,GF平分∠EFD,∴∠PEF=12∠BEF=x°,∠EFG=12∠EFD=(x+15)°,∵FH//EP,∴∠PEF=∠EFH=x°,∠P=∠HFG,∵∠HFG=∠EFG−∠EFH=15°,∴∠P=15°.【点睛】本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质定理是解题的关键.8.(2020下·浙江绍兴·七年级统考期末)问题情境:如图1,已知AB∥CD,∠APC=108°.求∠PAB+∠PCD 的度数.经过思考,小敏的思路是:如图2,过P作PE∥AB,根据平行线有关性质,可得∠PAB+∠PCD=360°−∠APC=252°.问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.(1)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系.(3)问题拓展:如图4,MA1∥NA n,A1−B1−A2−⋯−B n−1−A n是一条折线段,依据此图所含信息,把你所发现的结论,用简洁的数学式子表达为.【答案】(1)∠CPD=∠α+∠β,理由见解析(2)∠CPD=∠β-∠α或∠CPD=∠α-∠β(3)∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠B n−1【分析】(1)过P作PE∥AD,根据平行线的判定可得PE∥AD∥BC,再根据平行线的性质即可求解;(2)过P作PE∥AD,根据平行线的判定可得PE∥AD∥BC,再根据平行线的性质即可求解;(3)问题拓展:分别过A2,A3…,An-1作直线∥A1M,过B1,B2,…,Bn-1作直线∥A1M,根据平行线的判定和性质即可求解.【详解】(1)∠CPD=∠α+∠β,理由如下:如图,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β;(2)当P在BA延长线时,∠CPD=∠β-∠α;理由:如图,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE-∠DPE=∠β-∠α;当P在BO之间时,∠CPD=∠α-∠β.理由:如图,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE-∠CPE=∠α-∠β.(3)问题拓展:分别过A2,A3…,An-1作直线∥A1M,过B1,B2,…,Bn-1作直线∥A1M,由平行线的性质和角的和差关系得∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠B n−1.故答案为:∠A1+∠A2+…+∠An=∠B1+∠B2+…+∠B n−1.【点睛】本题主要考查了平行线的判定和性质的应用,主要考查学生的推理能力,第(2)问在解题时注意分类思想的运用.9.(2020下·重庆九龙坡·七年级统考期末)已知,AB∥CD.点M在AB上,点N在CD上.(1)如图1中,∠BME、∠E、∠END的数量关系为:;(不需要证明)如图2中,∠BMF、∠F、∠FND的数量关系为:;(不需要证明)(2)如图3中,NE平分∠FND,MB平分∠FME,且2∠E+∠F=180°,求∠FME的度数;(3)如图4中,∠BME=60°,EF平分∠MEN,NP平分∠END,且EQ∥NP,则∠FEQ的大小是否发生变化,若变化,请说明理由,若不变化,求出∠FEQ的度数.【答案】(1)∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND;(2)120°;(3)不变,30°【分析】(1)过E作EH∥AB,易得EH∥AB∥CD,根据平行线的性质可求解;过F作FH∥AB,易得FH∥AB∥CD,根据平行线的性质可求解;(2)根据(1)的结论及角平分线的定义可得2(∠BME+∠END)+∠BMF-∠FND=180°,可求解∠BMF=60°,进而可求解;(3)根据平行线的性质及角平分线的定义可推知∠FEQ=1∠BME,进而可求解.2【详解】解:(1)过E作EH∥AB,如图1,∴∠BME=∠MEH,∵AB∥CD,∴HE∥CD,∴∠END=∠HEN,∴∠MEN=∠MEH+∠HEN=∠BME+∠END,即∠BME=∠MEN﹣∠END.如图2,过F作FH∥AB,∴∠BMF=∠MFK,∵AB∥CD,∴FH∥CD,∴∠FND=∠KFN,∴∠MFN=∠MFK﹣∠KFN=∠BMF﹣∠FND,即:∠BMF=∠MFN+∠FND.故答案为∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.(2)由(1)得∠BME=∠MEN﹣∠END;∠BMF=∠MFN+∠FND.∵NE平分∠FND,MB平分∠FME,∴∠FME=∠BME+∠BMF,∠FND=∠FNE+∠END,∵2∠MEN +∠MFN =180°,∴2(∠BME +∠END )+∠BMF ﹣∠FND =180°,∴2∠BME +2∠END +∠BMF ﹣∠FND =180°,即2∠BMF +∠FND +∠BMF ﹣∠FND =180°,解得∠BMF =60°,∴∠FME =2∠BMF =120°;(3)∠FEQ 的大小没发生变化,∠FEQ =30°.由(1)知:∠MEN =∠BME +∠END ,∵EF 平分∠MEN ,NP 平分∠END ,∴∠FEN =12∠MEN =12(∠BME +∠END ),∠ENP =12∠END ,∵EQ ∥NP ,∴∠NEQ =∠ENP ,∴∠FEQ =∠FEN ﹣∠NEQ =12(∠BME +∠END )﹣12∠END =12∠BME ,∵∠BME =60°,∴∠FEQ =12×60°=30°.【点睛】本题主要考查平行线的性质及角平分线的定义,作平行线的辅助线是解题的关键.10.(2023下·辽宁大连·如图,AB//CD ,点O 在直线CD 上,点P 在直线AB 和CD 之间,∠ABP =∠PDQ =α,PD 平分∠BPQ .(1)求∠BPD 的度数(用含α的式子表示);(2)过点D 作DE//PQ 交PB 的延长线于点E ,作∠DEP 的平分线EF 交PD 于点F ,请在备用图中补全图形,猜想EF 与PD 的位置关系,并证明;(3)将(2)中的“作∠DEP的平分线EF交PD于点F”改为“作射线EF将∠DEP分为1:3两个部分,交PD于点F”,其余条件不变,连接EQ,若EQ恰好平分∠PQD,请直接写出∠FEQ=__________(用含α的式子表示).【答案】(1)∠BPD=2α;(2)画图见解析,EF⊥PD,证明见解析;(3)45°−α2或45°−32α【分析】(1)根据平行线的传递性推出PG//AB//CD,再利用平行线的性质进行求解;(2)猜测EF⊥PD,根据PD平分∠BPQ,∠BPD=2α,推导出∠BPD=∠DPQ=2α,再根据DE//PQ、EF平分∠DEP,通过等量代换求解;(3)分两种情况进行讨论,即当∠PEF:∠DEF=1:3与∠DEF:∠PEF=1:3,充分利用平行线的性质、角平分线的性质、等量代换的思想进行求解.【详解】(1)过点P作PG//AB,∵AB//CD,PG//AB,∴PG//AB//CD,∴∠BPG=∠ABP=α,∠DPG=∠PDQ=α,∴∠BPD=∠BPG+∠DPG=2α.(2)根据题意,补全图形如下:猜测EF⊥PD,由(1)可知:∠BPD=2α,∵PD平分∠BPQ,∠BPD=2α,∴∠BPD=∠DPQ=2α,∵DE//PQ,∴∠EDP=∠DPQ=2α,∴∠DEP=180°−∠BPD−∠EDP=180°−4α,又EF平分∠DEP,∠PEF=12∠DEP=90°−2α,∴∠EFD=180°−∠PEF−∠BPD=90°,∴EF⊥PD.(3)①如图1,∠PEF:∠DEF=1:3,由(2)可知:∠EPD=∠DPQ=∠EDP=2α,∠DEP=180°−4α,∵∠PEF:∠DEF=1:3,∴∠PEF=14∠DEP=45°−α,∠DEF=34∠DEP=135°−3α,∵DE//PQ,∴∠DEQ=∠PQE,∠EDQ+∠PQD=180°,∵∠EDP=2α,∠PDQ=α,∴∠EDQ=∠EDP+∠PDQ=3α,∠PQD=180°−∠EDQ=180°−3α,又EQ平分∠PQD,∴∠PQE=∠DQE=∠DEQ=12∠PQD=90°−32α,∴∠FEQ=∠DEF−∠DEQ=135°−3α−(90°−32α)=45°−32α;②如图2,∠DEP=180°−4α,∠PQD=180°−3α(同①);若∠DEF:∠PEF=1:3,则有∠DEF=14∠DEP=14×(180°−4α)=45°−α,又∠PQE=∠DQE=12∠PQD=12×(180°−3α)=90°−32α,∵DE//PQ,∴∠DEQ=∠PQE=90°−32α,∴∠FEQ=∠DEQ−∠DEF=45°−12α,综上所述:∠FEQ=45°−32α或45°α2,故答案是:45°−α2或45°−32α.【点睛】本题考查了平行线的性质、角平分线、三角形内角和定理、垂直等相关知识点,解题的关键是掌握相关知识点,作出适当的辅助线,通过分类讨论及等量代换进行求解.【模型2 “铅笔”型】1.(2012下·广东茂名·七年级统考期中)如图,AB∥ED,∠B+∠C+∠D=()A.180°B.360°C.540°D.270°【答案】B【分析】过C点作直线CF∥AB,根据平行线的性质可得∠B+∠BCF=180°,∠FCD+∠D=180°,然后再计算∠B+∠C+∠D即可.【详解】如图,过C点作直线CF∥AB,∵AB∥ED,∴CF∥ED,∴∠B+∠BCF=180°,∠FCD+∠D=180°,∴∠B+∠BCF+∠FCD+∠D=360°,即∠B+∠BCD+∠D=360°.故选:B【点睛】本题主要考查了平行线的性质,熟练掌握平行线的性质是解题的关键.2.(2012·江苏常州·七年级统考期中)一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=.【答案】270°【分析】过B作BF∥AE,则CD∥BF∥AE.根据平行线的性质即可求解.【详解】过B作BF∥AE,∵CD∥AE,则CD∥BF∥AE,∴∠BCD+∠1=180°,又∵AB⊥AE,∴AB⊥BF,∴∠ABF=90°,∴∠ABC+∠BCD=90°+180°=270°.故答案为:270.【点睛】本题主要考查了平行线的性质,两直线平行,同旁内角互补.正确作出辅助线是解题的关键.3.(2023下·陕西西安·七年级西安市第八十三中学校联考期中)如图1所示的是一个由齿轮、轴承、托架2所示的是手动变速箱托架工作时某一时刻的示意图,已知AB∥CD,CG∥EF,∠BAG=150°,∠DEF=130°,则∠AGC的度数是.【答案】80°【分析】过点F作FM∥CD,因为AB∥CD,所以AB∥CD∥FM,再根据平行线的性质可以求出∠MFA,∠EFM,进而可求出∠EFA,再根据平行线的性质即可求得∠AGC.【详解】解:如图,过点F作FM∥CD,∵AB∥CD,∴AB∥CD∥FM,∴∠DEF+∠EFM=180°,∠MFA+∠BAG=180°,∵∠BAG=150°,∠DEF=130°,∴∠MFA=30°,∠EFM=50°,∴∠EFA=∠EFM+∠AFM=80°,∵CG∥EF,∴∠AGC=∠EFA=80°.故答案为80°.【点睛】本题考查平行线的性质,解题关键是结合图形利用平行线的性质进行角的转化和计算.4.(2023下·广东东莞·七年级东莞市长安实验中学校考期中)如图,已知AB∥CD.(1)如图1所示,∠1+∠2=;(2)如图2所示,∠1+∠2+∠3=;并写出求解过程.(3)如图3所示,∠1+∠2+∠3+∠4=;(4)如图4所示,试探究∠1+∠2+∠3+∠4+⋯+∠n=.【答案】(1)180°;(2)360°;(3)540°;(4)(n-1)×180°【分析】(1)由两直线平行,同旁内角互补,可得答案;(2)过点E作AB的平行线,转化成两个图1,同理可得答案;(3)过点E,点F分别作AB的平行线,转化成3个图1,可得答案;(4)由(2)(3)类比可得答案.【详解】解:(1)如图1,∵AB∥CD,∴∠1+∠2=180°(两直线平行,同旁内角互补).故答案为:180°;(2)如图2,过点E作AB的平行线EF,∵AB∥CD,∴AB∥EF,CD∥EF,∴∠1+∠AEF=180°,∠FEC+∠3=180°,∴∠1+∠2+∠3=360°;(3)如图3,过点E,点F分别作AB的平行线,类比(2)可知∠1+∠2+∠3+∠4=180°×3=540°,故答案为:540°;(4)如图4由(2)和(3)的解法可知∠1+∠2+∠3+∠4+…+∠n=(n-1)×180°,故答案为:(n-1)×180°.【点睛】此题考查了平行线的性质.注意掌握辅助线的作法是解此题的关键.5.(2020下·江苏淮安·七年级统考期末)问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC 的度数.思路点拨:小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可分别求出∠APE、∠CPE的度数,从而可求出∠APC的度数;小丽的思路是:如图3,连接AC,通过平行线性质以及三角形内角和的知识可求出∠APC的度数;小芳的思路是:如图4,延长AP交DC的延长线于E,通过平行线性质以及三角形外角的相关知识可求出∠APC 的度数.问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算,你求得的∠APC的度数为°;问题迁移:(1)如图5,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD、∠α、∠β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.【答案】110;(1)∠CPD=∠α+∠β,理由见解析;(2)∠CPD=∠β−∠α或∠CPD=∠a−∠β,理由见解析【分析】小明的思路是:过P作PE∥AB,构造同旁内角,利用平行线性质,可得∠APC=110°.(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠a=∠DPE,∠β=∠CPE,即可得出答案;(2)画出图形(分两种情况:①点P在BA的延长线上,②点P在AB的延长线上),根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.【详解】解:小明的思路:如图2,过P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠APE=180°−∠A=50°,∠CPE=180°−∠C=60°,∴∠APC=50°+60°=110°,故答案为:110;(1)∠CPD=∠α+∠β,理由如下:如图5,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠a=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠a+∠β;(2)当P在BA延长线时,∠CPD=∠β−∠α;理由:如图6,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠CPE−∠DPE=∠β−∠α;当P在BO之间时,∠CPD=∠a−∠β.理由:如图7,过P作PE∥AD交CD于E,∵AD∥BC,∴AD∥PE∥BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE−∠CPE=∠α−∠β.【点睛】本题考查了三角形的内角和定理,平行线的判定和性质,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.6.(2020下·内蒙古·七年级校考期中)综合与探究:(1)问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.小明想到一种方法,但是没有解答完:如图2,过P作PE∥AB,∴∠APE+∠PAB=180°.∴∠APE=180°−∠PAB=180°−130°=50°.∵AB∥CD.∴PE∥CD.…………请你帮助小明完成剩余的解答.(2)问题探究:请你依据小明的思路,解答下面的问题:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.当点P在A,B两点之间时,∠CPD,∠α,∠β之间有何数量关系?请说明理由.【答案】(1)110°;(2)∠CPD=∠α+∠β,理由见解析【分析】(1)过P作PE//AB,构造同旁内角,通过平行线性质,可得∠APC=50°+60°=110°.(2)过P作PE//AD交CD于E,推出AD//PE//BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.【详解】解:(1)过P作PE∥AB,∴∠APE+∠PAB=180°,∴∠APE=180°−∠PAB=180°−130°=50°.∵AB∥CD,∴PE∥CD.∴∠CPE+∠PCD=180°,∴∠CPE=180°−120°=60°,∴∠APC=50°+60°=110°.(2)∠CPD=∠α+∠β,如图3,过P作PE//AD交CD于E,∵AD//BC,∴AD//PE//BC,∴∠α=∠DPE,∠β=∠CPE,∴∠CPD=∠DPE+∠CPE=∠α+∠β;【点睛】本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.7.(2020下·天津滨海新·七年级统考期末)如图1,四边形MNBD为一张长方形纸片.(1)如图2,将长方形纸片剪两刀,剪出三个角(∠BAE、∠AEC、∠ECD),则∠BAE+∠AEC+∠ECD=__________°.(2)如图3,将长方形纸片剪三刀,剪出四个角(∠BAE、∠AEF、∠EFC、∠FCD),则∠BAE+∠AEF+∠EFC+∠FCD=__________°.(3)如图4,将长方形纸片剪四刀,剪出五个角(∠BAE、∠AEF、∠EFG、∠FGC、∠GCD),则∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=___________°.(4)根据前面探索出的规律,将本题按照上述剪法剪n刀,剪出(n+1)个角,那么这(n+1)个角的和是____________°.【答案】(1)360;(2)540;(3)720;(4)180n.【分析】(1)过点E作EH∥AB,再根据两直线平行,同旁内角互补即可得到三个角的和等于180°的2倍;(2)分别过E、F分别作AB的平行线,根据两直线平行,同旁内角互补即可得到四个角的和等于180°的三倍;(3)分别过E、F、G分别作AB180°的三倍;(4)根据前三问个的剪法,剪n刀,剪出n+1个角,那么这n+1个角的和是180n度.【详解】(1)过E作EH∥AB(如图②).∵原四边形是长方形,∴AB∥CD,又∵EH∥AB,∴CD∥EH(平行于同一条直线的两条直线互相平行).∵EH∥AB,∴∠A+∠1=180°(两直线平行,同旁内角互补).∵CD∥EH,∴∠2+∠C=180°(两直线平行,同旁内角互补).∴∠A+∠1+∠2+∠C=360°,又∵∠1+∠2=∠AEC,∴∠BAE+∠AEC+∠ECD=360°;(2)分别过E、F分别作AB的平行线,如图③所示,用上面的方法可得∠BAE+∠AEF+∠EFC+∠FCD=540°;(3)分别过E、F、G分别作AB的平行线,如图④所示,用上面的方法可得∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=720°;(4)由此可得一般规律:剪n刀,剪出n+1个角,那么这n+1个角的和是180n度.故答案为:(1)360;(2)540;(3)720;(4)180n.【点睛】本题主要考查了多边形的内角和,作平行线并利用两直线平行,同旁内角互补是解本题的关键,总结规律求解是本题的难点.8.(2023下·浙江·七年级期末)已知AB//CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一动点P.(1)如图1所示时,试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?并说明理由.(2)除了(1)的结论外,试问∠AEP,∠EPF,∠PFC还可能满足怎样的数量关系?请画图并证明(3)当∠EPF满足0°<∠EPF<180°,且QE,QF分别平分∠PEB和∠PFD,①若∠EPF=60°,则∠EQF=__________°.②猜想∠EPF与∠EQF的数量关系.(直接写出结论)【答案】(1)∠AEP+∠PFC=∠EPF)∠AEP+∠EPF+∠PFC=360°;(3)①150°或30;②∠EPF+2∠EQF=360°或∠EPF=2∠EQF【分析】(1)由于点P是平行线AB,CD之间有一动点,因此需要对点P的位置进行分类讨论:如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为:∠EPF=∠AEP+∠PFC;(2)当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为:∠AEP+∠EPF+∠PFC=360°;(3)①若当P点在EF的左侧时,∠EQF=∠BEQ+∠QFD=150°;当P点在EF的右侧时,可求得∠BEQ+∠QFD=30°;②结合①可得∠EPF=180°−2∠BEQ+180°−2∠DFQ=360°−2(∠BEQ+∠PFD),由∠EQF=∠BEQ+∠DFQ,得出∠EPF+2∠EQF=360°;可得EPF=∠BEP+∠PFD,由∠BEQ+∠DFQ=∠EQF,得出∠EPF= 2∠EQF.【详解】解:(1)如图1,过点P作PG//AB,∵PG//AB,∴∠EPG=∠AEP,∵AB//CD,∴PG//CD,∴∠FPG=∠PFC,∴∠AEP+∠PFC=∠EPF;(2)如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为:∠AEP+∠EPF+∠PFC=360°;过点P作PG//AB,∵PG//AB,∴∠EPG+∠AEP=180°,∵AB//CD,∴PG//CD,∴∠FPG+∠PFC=180°,∴∠AEP+∠EPF+∠PFC=360°;(3)①如图3,若当P点在EF的左侧时,∵∠EPF=60°,∴∠PEB+∠PFD=360°−60°=300°,∵EQ,FQ分别平分∠PEB和∠PFD,∴∠BEQ=12∠PEB,∠QFD=12∠PFD,∴∠EQF=∠BEQ+∠QFD=12(∠PEB+∠PFD)=12×300°=150°;如图4,当P点在EF的右侧时,∵∠EPF=60°,∴∠PEB+∠PFD=60°,∴∠BEQ+∠QFD=12(∠PEB+∠PFD)=12×60°=30°;故答案为:150°或30;②由①可知:∠EQF=∠BEQ+∠QFD=12(∠PEB+∠PFD)=12(360°−∠EPF),∴∠EPF+2∠EQF=360°;∠EQF=∠BEQ+∠QFD=12(∠PEB∠PFD)=12∠EPF,∴∠EPF=2∠EQF.综合以上可得∠EPF与∠EQF的数量关系为:∠EPF+2∠EQF=360°或∠EPF=2∠EQF.【点睛】本题主要考查了平行线的性质,平行公理和及推论等知识点,作辅助线后能求出各个角的度数,是解此题的关键.9.(2023下·浙江宁波·七年级统考期中)如图,AB//CD,定点E,F分别在直线AB,CD上,在平行线AB,CD之间有一个动点P,满足0°<∠EPF<180°.(1)试问:∠AEP,∠EPF,∠PFC满足怎样的数量关系?解:由于点P是平行线AB,CD之间一动点,因此需对点P的位置进行分类讨论.如图1,当点P在EF的左侧时,易得∠AEP,∠EPF,∠PFC满足的数量关系为∠AEP+∠PFC=∠EPF;如图2,当点P在EF的右侧时,写出∠AEP,∠EPF,∠PFC满足的数量关系_________.(2)如图3,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.①若∠EPF=100°,则∠EQF的度数为______;②猜想∠EPF与∠EQF的数量关系,并说明理由;③如图4,若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3,以此类推,则∠EPF与∠EQ2020F满足怎样的数量关系?(直接写出结果)【答案】(1)∠AEP+∠EPF+∠PFC=360°;(2)①130°;②∠EPF+2∠EQF=360°,见解析;③∠EPF+22021∠EQ2020F=360°【分析】(1)过点P作PH//AB,利用平行线的性质即可求解;(2)根据(1)的结论结合角平分线的定义,平角的定义,运用整体思想即可求解.【详解】解:(1)如图2,当点P在EF的右侧时,过点P作PM//AB,则PM//CD,∴∠AEP+∠EPM=180°,∠PFC+∠MPF=180°,∴∠AEP+∠EPM+∠PFC+∠MPF=360°,即:∠AEP+∠EPF+∠PFC=360°;故答案为:∠AEP+∠EPF+∠PFC=360°;(2)①由(1)得:∠DFQ+∠BEQ=∠EQF,∠PEA+∠PFC=∠EPF,∵∠EPF=100°,∴∠PEA+∠PFC=100°,∵QE,QF分别平分∠PEB和∠PFD,∴∠DFP=2∠DFQ,∠BEP=2∠BEQ,∵∠PFC+∠DFP=180°,∠PEA+∠BEP=180°,∴∠PFC+2∠DFQ=180°,∠PEA+2∠BEQ=180°,∴∠PFC+2∠DFQ+∠PEA+2∠BEQ=360°,∴100°+2∠DFQ+2∠BEQ=360°,∴∠DFQ+∠BEQ=130°,∴∠EQF=∠DFQ+∠BEQ=130°,故答案为:130°;②∠EPF+2∠EQF=360°,理由如下:∵QE,QF分别平分∠PEB和∠PFD,∴∠DFP=2∠DFQ,∠BEP=2∠BEQ,∵∠PFC+∠DFP=180°,∠PEA+∠BEP=180°,∴∠PFC+2∠DFQ=180°,∠PEA+2∠BEQ=180°,∴∠PFC+2∠DFQ+∠PEA+2∠BEQ=360°,∴∠PFC+∠PEA +2(∠DFQ +∠BEQ)=360°,∵由(1)得:∠DFQ+∠BEQ=∠EQF,∠PEA+∠PFC=∠EPF,∴∠EPF +2∠EQF=360°;③∵Q1E,Q1F分别平分∠QEB和∠QFD,∴∠DFP=2∠DFQ=22∠DFQ1,∠BEP=2∠BEQ=22∠BEQ1,∵∠PFC+∠DFP=180°,∠PEA+∠BEP=180°,∴∠PFC+22∠DFQ1=180°,∠PEA+22∠BEQ1=180°,∴∠PFC+22∠DFQ1+∠PEA+22∠BEQ1=360°,∴∠PFC+∠PEA +22(∠DFQ1 +∠BEQ1)=360°,∵由(1)得:∠DFQ1+∠BEQ1=∠EQ1F,∠PEA+∠PFC=∠EPF,∴∠EPF +22∠EQ1F=360°;同理可得:∠EPF +23∠EQ2F=360°,∠EPF +24∠EQ3F=360°,……∴∠EPF+22021∠EQ2020F=360°.【点睛】本题主要考查了平行线的性质,平行公理及推论,角平分线的定义等知识点,作辅助线后能求出各个角的度数,利用整体思想解决第(2)问是解此题的关键.10.(2020下·辽宁大连·七年级统考期末)阅读下面材料,完成(1)~(3)题.数学课上,老师出示了这样—道题:如图1,已知AB//CD,点E,F分别在AB,CD上,EP⊥FP,∠1=60°.求∠2的度数.同学们经过思考后,小明、小伟、小华三位同学用不同的方法添加辅助线,交流了自己的想法:小明:“如图2,通过作平行线,发现∠1=∠3,∠2=∠4,由已知EP⊥FP,可以求出∠2的度数.”小伟:“如图3这样作平行线,经过推理,得∠2=∠3=∠4,也能求出∠2的度数.”小华:∵如图4,也能求出∠2的度数.”(1)请你根据小明同学所画的图形(图2),描述小明同学辅助线的做法,辅助线:______;(2)请你根据以上同学所画的图形,直接写出∠2的度数为_________°;老师:“这三位同学解法的共同点,都是过一点作平行线来解决问题,这个方法可以推广.”请大家参考这三位同学的方法,使用与他们类似的方法,解决下面的问题:(3)如图,AB//CD,点E,F分别在AB,CD上,FP平分∠EFD,∠PEF=∠PDF,若∠EPD=a,请探究∠CFE与∠PEF 的数量关系((用含α的式子表示),并验证你的结论.【答案】(1)过点Р作PQ//AC;(2)30;(3)∠CFE−2∠PEF=180∘−a.【分析】(1)根据图中所画虚线的位置解答即可;(2)过点Р作PQ//AC,根据平行线的性质可得∠1=∠3,∠2=∠4,由EP⊥FP可得∠3+∠4=90°,即可得出∠1+∠2=90°,进而可得答案;(3)设∠CFE=x,∠PEF=∠PDF=y,过点P作PQ//AB,根据平行线的性质可得∠BEP+∠EPQ= 180°,∠CFE=∠FEB=x,∠PDF=∠DPQ,进而根据角的和差关系即可得答案.【详解】(1)由图中虚线可知PQ//AC,∴小明同学辅助线的做法为过点Р作PQ//AC,故答案为:过点Р作PQ//AC(2)如图2,过点Р作PQ//AC,∵AB//CD,∴PQ//AB//CD,∴∠1=∠3,∠2=∠4,∵EP⊥FP,∴∠EPF=∠3+∠4=90°,∴∠1+∠2=90°,∵∠1=60°,∴∠2=30°,故答案为:30(3)如图,设∠CFE=x,∠PEF=∠PDF=y,过点P作PQ//AB,∴∠BEP+∠EPQ=180°,∠CFE=∠FEB=x∵AB//CD,∴PQ//CD,∴∠PDF=∠DPQ∴∠DPQ=∠EHF=∠PDF=y∵∠CFE=∠FEB=x=∠FEP+∠BEP∴x=y+(180−a+y)∴x−2y=180−α,即∠CFE−2∠PEF=180∘−a.【点睛】本题考查平行线的性质,两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;正确作出辅助线,熟练掌握平行线的性质是解题关键.【模型3 “鸡翅”型】1.(2023下·湖南株洲·七年级统考期末)①如图1,AB∥CD,则∠A+∠E+∠C=360°;②如图2,AB ∥CD,则∠P=∠A−∠C;③如图3,AB∥CD,则∠E=∠A+∠1;④如图4,直线AB∥CD∥EF,点O在直线EF上,则∠α−∠β+∠γ=180°.以上结论正确的个数是()A.1个B.2个C.3个D.4个【答案】C【分析】①过点E作直线EF∥AB,由平行线的性质:两直线平行,同旁内角互补,即可得出结论;②如图2,先根据三角形外角的性质得出∠1=∠C+∠P,再根据两直线平行,内错角相等即可作出判断;③如图3,过点E作直线EF∥AB,由平行线的性质可得出∠A+∠AEC﹣∠1=180°,即得∠AEC=180°+∠1﹣∠A;④如图4,根据平行线的性质得出∠α=∠BOF,∠γ+∠COF=180°,再利用角的关系解答即可.【详解】解:①如图1,过点E作直线EF∥AB,∵AB∥CD,∴AB∥CD∥EF,∴∠A+∠1=180°,∠2+∠C=180°,∴∠A+∠1+∠2+∠C=360°,∴∠A+∠AEC+∠C=360°,故①正确;②如图2,∵∠1是△CEP的外角,∴∠1=∠C+∠P,∵AB∥CD,∴∠A=∠1,即∠P=∠A﹣∠C,故②正确;③如图3,过点E作直线EF∥AB,∵AB∥CD,∴AB∥CD∥EF,∴∠A+∠3=180°,∠1=∠2,∴∠A+∠AEC﹣∠1=180°,即∠AEC=180°+∠1﹣∠A,故③错误;④如图4,∵AB∥EF,∴∠α=∠BOF,∵CD∥EF,∴∠γ+∠COF=180°,∵∠BOF=∠COF+∠β,∴∠COF=∠α﹣∠β,∴∠γ+∠α﹣∠β=180°,故④正确;综上结论正确的个数为3,故选:C.【点睛】本题考查的是平行线的性质及三角形外角的性质,熟练掌握平行线的性质,根据题意作出辅助线是解答此题的关键.2.(2023上·七年级课时练习)(1)已知:如图(a),直线DE∥AB.求证:∠ABC+∠CDE=∠BCD;(2)如图(b),如果点C在AB与ED之外,其他条件不变,那么会有什么结果?你还能就本题作出什么新的猜想?【答案】(1)见解析;(2)当点C在AB与ED之外时,∠ABC−∠CDE=∠BCD,见解析【分析】(1)由题意首先过点C作CF∥AB,由直线AB∥ED,可得AB∥CF∥DE,然后由两直线平行,内错角相等,即可证得∠ABC+∠CDE=∠BCD;(2)根据题意首先由两直线平行,内错角相等,可得∠ABC=∠BFD,然后根据三角形外角的性质即可证得∠ABC-∠CDE=∠BCD.【详解】解:(1)证明:过点C作CF∥AB,∵AB∥ED,∴AB∥ED∥CF,∴∠BCF=∠ABC,∠DCF=∠EDC,∴∠ABC+∠CDE=∠BCD;(2)结论:∠ABC-∠CDE=∠BCD,证明:如图:∵AB∥ED,∴∠ABC=∠BFD,在△DFC中,∠BFD=∠BCD+∠CDE,∴∠ABC=∠BCD+∠CDE,∴∠ABC-∠CDE=∠BCD.若点C在直线AB与DE之间,猜想∠ABC+∠BCD+∠CDE=360°,。
平行线四大模型(完整版+培优)

平行线四大模型(完整版+培优)平行线四大模型模型一:铅笔模型当点P在EF右侧,在AB、CD内部时,有以下结论:1.若AB∥CD,则∠P+∠AEP+∠PFC=360°;2.若∠P+∠AEP+∠PFC=360°,则AB∥CD.模型二:猪蹄模型当点P在EF左侧,在AB、CD内部时,有以下结论:1.若AB∥CD,则∠P=∠AEP+∠CFP;2.若∠P=∠AEP+∠CFP,则AB∥CD.模型三:臭脚模型当点P在AB、CD之间时,有以下结论:1.若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;2.若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD.模型四:骨折模型当点P在EF右侧,在AB、CD外部时,有以下结论:1.若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;2.若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.当点P在EF左侧,在AB、CD外部时,有以下结论:1.若AB∥CD,则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;2.若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.应用:例1:1.∠l+∠2+∠3=180°;2.∠E=110°;3.∠BCD=40°;4.∠P=70°.练:1.∠EAB的度数为17°;2.∠C=30°;3.∠P=30°+n×20°.例2:BF、DF分别平分∠ABC、∠XXX,则∠C、∠F的关系为∠ABF=∠XXX∠XXX.练:1.∠XXX∠BDE;2.当n=2时,∠C=∠F;3.∠C=n×∠F.1.如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,要证明∠E=2(∠A+∠C)。
2.如图,已知AB∥DE,BF、DF分别平分∠ABC、∠XXX,要求出∠C、∠F的关系。
相交线与平行线常见的四大类6种模型

相交线与平行线的概念还可以与其他数学分支如代数、数论等相结合,产生新的交叉应 用和研究领域。
THANKS
感谢观看
相交线与平行线常见的四大类6种模 型
目录
• 引言 • 相交线模型 • 平行线模型 • 角的性质与判定 • 距离与长度的计算 • 模型的应用与拓展
01
引言
目的和背景
理解和掌握相交线与 平行线的基本概念和 性质
培养空间观念和推理 能力,为进一步学习 几何知识打下基础
分析和解决与相交线 与平行线相关的实际 问题
性质
平行线间距离相等;平行线同位角 相等,内错角相等。
判定
同位角相等,两直线平行;内错角 相等,两直线平行;同旁内角互补, 两直线平行。
直线与平面平行
定义
一条直线与一个平面没有交点, 则称这条直线与该平面平行。
性质
直线与平面平行,则该直线上任 意一点到平面的距离相等;直线 与平面平行,过该直线的平面与 已知平面的交线与该直线平行。
面积法
通过构造三角形或平行四边形等图形,利用面积公式间接求出点 到直线的距离。
向量法
在平面直角坐标系中,利用向量的数积和模长公式计算点到直 线的距离。
平行线间的距离
垂线段法
在两条平行线间作垂线段,该垂线段的长度即为平行线间的距离。
斜率截距法
已知平行线的斜率和截距,通过公式直接计算平行线间的距离。
四大类6种模型概述
斜交线
两条直线在同一平面内,但不平行 也不垂直,它们的交角不等于90度。
垂直线
两条直线在同一平面内,它们之间 的交角等于90度。
四大类6种模型概述
同位角相等
两条平行线被一条横截线所截,同位 角相等。
(完整版)平行线知识点+四大模型

平行线四大模型平行线的判定与性质l、平行线的判定根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行,但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行,这就需要更简单易行的判定方法来判定两直线平行.判定方法l:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称:同位角相等,两直线平行.判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称:内错角相等,两直线平行,判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称:同旁内角互补,两直线平行,如上图:若已知∠1=∠2,则AB∥CD(同位角相等,两直线平行);若已知∠1=∠3,则AB∥CD(内错角相等,两直线平行);若已知∠1+ ∠4= 180°,则AB∥CD(同旁内角互补,两直线平行).另有平行公理推论也能证明两直线平行:平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.2、平行线的性质利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果已知两条直线平行,当它们被第三条直线所截,得到的同位角、内错角、同旁内角也有相应的数量关系,这就是平行线的性质.性质1:两条平行线被第三条直线所截,同位角相等.简称:两直线平行,同位角相等性质2:两条平行线被第三条直线所截,内错角相等.简称:两直线平行,内错角相等性质3:两条平行线被第三条直线所截,同旁内角互补.简称:两直线平行,同旁内角互补本讲进阶平行线四大模型模型一“铅笔”模型点P在EF右侧,在AB、CD内部“铅笔”模型结论1:若AB∥CD,则∠P+∠AEP+∠PFC=3 60°;结论2:若∠P+∠AEP+∠PFC= 360°,则AB∥CD.模型二“猪蹄”模型(M模型)点P在EF左侧,在AB、CD内部“猪蹄”模型结论1:若AB∥CD,则∠P=∠AEP+∠CFP;结论2:若∠P=∠AEP+∠CFP,则AB∥CD.模型三“臭脚”模型点P在EF右侧,在AB、CD外部“臭脚”模型结论1:若AB∥CD,则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP;结论2:若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP,则AB∥CD.模型四“骨折”模型·点P在EF左侧,在AB、CD外部“骨折”模型结论结论2:若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP,则AB∥CD.巩固练习平行线四大模型证明(1)已知AE // CF ,求证∠P +∠AEP +∠PFC = 360°. (2)已知∠P=∠AEP+∠CFP,求证AE∥CF.(3)已知AE∥CF,求证∠P=∠AEP-∠CFP.(4)已知∠P= ∠CFP -∠AEP,求证AE //CF.模块一平行线四大模型应用例1(1)如图,a∥b,M、N分别在a、b上,P为两平行线间一点,那么∠l+∠2+∠3= .(2)如图,AB∥CD,且∠A=25°,∠C=45°,则∠E的度数是.(3)如图,已知AB∥DE,∠ABC=80°,∠CDE =140°,则∠BCD= .(4) 如图,射线AC∥BD,∠A= 70°,∠B= 40°,则∠P= .练(1)如图所示,AB∥CD,∠E=37°,∠C= 20°,则∠EAB的度数为.(2) 如图,AB∥CD,∠B=30°,∠O=∠C.则∠C= .例2如图,已知AB ∥DE ,BF 、 DF 分别平分∠ABC 、∠CDE ,求∠C 、 ∠F 的关系.练如图,已知AB ∥DE ,∠FBC =n 1∠ABF ,∠FDC =n1∠FDE . (1)若n =2,直接写出∠C 、∠F 的关系 ; (2)若n =3,试探宄∠C 、∠F 的关系;(3)直接写出∠C 、∠F 的关系 (用含n 的等式表示).例3如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC.求证:∠E= 2 (∠A+∠C) .练如图,己知AB∥DE,BF、DF分别平分∠ABC、∠CDE,求∠C、∠F的关系.例4如图,∠3==∠1+∠2,求证:∠A+∠B+∠C+∠D= 180°.练(武昌七校2015-2016 七下期中)如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠l+∠2= 90°,M、N分别是BA、CD的延长线上的点,∠EAM和∠EDN的平分线相交于点F则∠F的度数为().A. 120°B. 135°C. 145°D. 150°模块二平行线四大模型构造例5如图,直线AB∥CD,∠EF A= 30°,∠FGH= 90°,∠HMN=30°,∠CNP= 50°,则∠GHM= .练如图,直线AB∥CD,∠EFG=100°,∠FGH=140°,则∠AEF+ ∠CHG= .例6 已知∠B =25°,∠BCD=45°,∠CDE =30°,∠E=l0°,求证:AB∥EF.练已知AB∥EF,求∠l-∠2+∠3+∠4的度数.(1)如图(l),已知MA1∥NA n,探索∠A1、∠A2、…、∠A n,∠B1、∠B2…∠B n-1之间的关系.(2)如图(2),己知MA1∥NA4,探索∠A1、∠A2、∠A3、∠A4,∠B1、∠B2之间的关系.(3)如图(3),已知MA1∥NA n,探索∠A1、∠A2、…、∠A n之间的关系.如图所示,两直线AB∥CD平行,求∠1+∠2+∠3+∠4+∠5+∠6.。
部编数学七年级下册专题03平行线四大模型与动态角度问题专题讲练(解析版)含答案

专题03 平行线四大模型与动态角度问题专题讲练平行线与动态角度问题在初中数学几何模块中属于基础工具类问题,也是学生必须掌握的一块内容,该份资料就平行线的四大模型(铅笔模型、猪蹄模型、拐弯模型、“5”字模型)和动态角度问题(翻折、旋转、动点)进行梳理及对应试题分析,方便掌握。
模型1:铅笔头模型【解题技巧】如图,①已知:AB∥CD,结论:∠PAB+∠APB+∠PCD=360°;②已知:∠PAB+∠APB+∠PCD=360°,结论:AB∥CD.图①、图②图③③已知:AB∥CD,结论:∠1+∠2+…+∠n=180(n-1).例1、(2021.河北七年级月考)如图,已知:AB∥CD,求证:∠PAB+∠APB+∠PCD=360°;【解析】方法一(破角):过点P作PQ∥AB则AB∥CD∥PQ∴∠BAP+∠APQ=180°,∠CPQ+∠PCD=180°∴∠BAP+∠APQ+∠CPQ+∠PCD=360° 即∠PAB+∠APB+∠PCD=360°.方法二(添角):连接AC,易知,∠1+∠4=180°,∠2+∠3+∠P=180°∴∠1+∠4+∠2+∠3+∠P=360°即∠PAB +∠APB +∠PCD =360°.变式1.(2021·河南·七年级期中)如图,直线12l l P ,130Ð=°,则23Ð+Ð=( )A .150°B .180°C .210°D .240°【答案】C 【分析】根据题意作直线l 平行于直线l 1和l 2,再根据平行线的性质求解即可.【解析】解:作直线l 平行于直线l 1和l 212////l l l Q 1430;35180°°\Ð=Ð=Ð+Ð=245Ð=Ð+ÐQ 2+3=4+5+3=30180210°°°\ÐÐÐÐÐ+= 故选C.【点睛】本题主要考查平行线的性质,关键在于等量替换的应用,两直线平行同旁内角互补,两直线平行内错角相等.变式2.(2021·黑龙江·哈尔滨市第四十七中学七年级期中)如图,已知直线l 1∥l 2,∠A =125°,∠B =85°,且∠1比∠2大4°,那么∠1=______.【答案】17°【分析】延长AB ,交两平行线与C 、D ,根据平行线的性质和领补角的性质计算即可;【详解】延长AB ,交两平行线与C 、D ,∵直线l 1∥l 2,∠A =125°,∠B =85°,∴4285Ð+Ð=°,13125Ð+Ð=°,34180Ð+Ð=°,∴852*******°-Ð+°-Ð=°,∴1230Ð+Ð=°,又∵∠1比∠2大4°,∴2=14ÐÐ-°,∴2134Ð=°,∴117Ð=°;故答案是17°.【点睛】本题主要考查了平行线的性质应用,准确计算是解题的关键.例2.(2021·福建泉州七年级期末)问题情境:我市某中学班级数学活动小组遇到问题:如图1,AB ∥CD ,∠PAB =130°,∠PCD =120°,求∠APC 的度数.经过讨论形成的思路是:如图2,过P 作PE ∥AB ,通过平行线性质,可求得∠APC 的度数.(1)按该数学活动小组的思路,请你帮忙求出∠APC 的度数;(2)问题迁移:如图3,AD ∥BC ,点P 在A 、B 两点之间运动时, ADP a Ð=,BCP βÐ=.请你判断CPD Ð、a 、 β之间有何数量关系?并说明理由;(3)拓展应用:如图4,已知两条直线AB ∥CD ,点P 在两平行线之间,且BEP Ð的平分线与 ∠DFP 的平分线相交于点Q ,求2P Q Ð+Ð的度数.【答案】(1)110°;(2)∠CPD =α+β,见解析;(3)360°.【解析】解:(1)过点P 作PE ∥AB ,∵AB ∥CD , ∴PE ∥AB ∥CD .∴∠A +∠APE =180°,∠C +∠CPE =180°∵∠PAB =130°,∠PCD =120°,∴∠APE =50°,∠CPE =60°,∴∠APC =∠APE +∠CPE =110°.(2)∠CPD =α+β,理由如下:过P 作PE ∥AD 交CD 于E .∵AD ∥BC ,∴AD ∥PE ∥BC ,∴∠DPE =α,∠CPE =β,∴∠CPD =∠DPE +∠CPE =α+β.(3)由(1)可得,∠P +∠BEP +∠DFP =360° 又∵QE 平分∠PEB ,QF 平分∠PFQ∴∠BEP =2∠BEQ ,∠DFP =2∠DFQ ∴∠P +2∠Q =∠P +2(∠BEQ +∠DFQ )=∠P +∠BEP +∠DFP =360°.变式3.(2021·佛山顺德区月考)问题情境1:如图1,AB ∥CD ,P 是ABCD 内部一点,P 在BD 的右侧,探究∠B ,∠P ,∠D 之间的关系?小明的思路是:如图2,过P 作PE ∥AB ,通过平行线性质,可得∠B ,∠P ,∠D 之间满足 关系.(直接写出结论)问题情境2:如图3,AB ∥CD ,P 是AB ,CD 内部一点,P 在BD 的左侧,可得∠B ,∠P ,∠D 之间满足 关系.(直接写出结论)问题迁移:请合理的利用上面的结论解决以下问题:已知AB ∥CD ,∠ABE 与∠CDE 两个角的角平分线相交于点F (1)如图4,若∠E =80°,求∠BFD 的度数;(2)如图5中,∠ABM =13∠ABF ,∠CDM =13∠CDF ,写出∠M 与∠E 之间的数量关系并证明你的结论.(3)若∠ABM =1n ∠ABF ,∠CDM =1n∠CDF ,设∠E =m °,用含有n ,m °的代数式直接写出∠M = .【答案】问题情境1:∠B +∠BPD +∠D =360°,∠P =∠B +∠D ;(1)140°;(2)16∠E +∠M =60°(3)360m 2nM °°-Ð=.【解析】(1)∵BF 、DF 分别是∠ABE 和∠CDE 的平分线,∴∠EBF =12∠ABE ,∠EDF =12∠CDE ,由问题情境1得:∠ABE +∠E +∠CDE =360°,∵∠E =80°,∴∠ABE +∠CDE =280°,∴∠EBF +∠EDF =140°,∴∠BFD =360°﹣80°﹣140°=140°;(2)16∠E +∠M =60°,理由是:设∠ABM =x ,∠CDM =y ,则∠FBM =2x ,∠EBF =3x ,∠FDM =2y ,∠EDF =3y ,由问题情境1得:∠ABE +∠E +∠CDE =360°,∴6x +6y +∠E =360°,即16∠E =60﹣x ﹣y ,∵∠M +∠EBM +∠E +∠EDM =360°,∴6x +6y +∠E =∠M +5x +5y +∠E ,∴∠M =x +y ,∴16∠E +∠M =60°;(3)设∠ABM =x ,∠CDM =y ,则∠FBM =(n ﹣1)x ,∠EBF =nx ,∠FDM =(n ﹣1)y ,∠EDF =ny ,由问题情境1得:∠ABE +∠E +∠CDE =360°,∴2nx +2ny +∠E =360°,∴x +y =360m 2n°°-,∵∠M +∠EBM +∠E +∠EDM =360°,∴2nx +2ny +∠E =∠M +(2n ﹣1)x +(2n ﹣1)y +∠E ,∴∠M =360m 2n °°-;故答案为:∠M =360m 2n°°-.变式4.(2021·洛阳市期中)已知:如图1,12180°Ð+Ð=,Ð=ÐAEF HLN .(1)判断图中平行的直线,并给予证明;(2)如图2,2Ð=ÐPMQ QMB ,2Ð=ÐPNQ QND ,请判断P Ð与Q Ð的数量关系,并证明.【答案】(1)AB ∥CD ,EF ∥HL ,见解析;(2)∠P =3∠Q ,见解析.【解析】解:(1)AB∥CD,EF∥HL,∵∠1=∠AMN,∴∠1+∠2=180°,∴∠AMN+∠2=180°,∴AB∥CD;延长EF交CD于F1,∵AB∥CD,∴∠AEF=∠EF1L,∵∠AEF=∠HLN,∴∠EF1L=∠HLN,∴EF∥HL;(2)∠P=3∠Q,由(1)得AB∥CD,作QR∥AB,PL∥AB,∴∠RQM=∠QMB,RQ∥CD,∴∠RQN=∠QND,∴∠MQN=∠QMB+∠QND,∵AB∥CD,PL∥AB,∴AB∥CD∥PL,∴∠MPL=∠PMB,∠NPL=∠PND,∴∠MPN=∠PMB+∠PND,∵∠PMQ=2∠QMB,∠PNQ=2∠QND,∴∠PMB=3∠QMB,∠PND=3∠QND,∴∠MPN=3∠MQN,即∠P=3∠Q.例3.(2021·西安七年级月考)下列各图中的MA1与NA n平行.(1)图①中的∠A1+∠A2= 度,图②中的∠A1+∠A2+∠A3= 度,图③中的∠A1+∠A2+∠A3+∠A4= 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度,…,第⑩个图中的∠A1+∠A2+∠A3+…+∠A10= 度(2)第n个图中的∠A1+∠A2+∠A3+…+∠A n= .【答案】(1)180;360;540;720;1620;(2)180°(n﹣1).【解析】解:(1)∵MA1∥NA2,∴∠A1+∠A2=180°,如图,分别过A2、A3、A4作MA1的平行线,图②中的∠A1+∠A2+∠A3=360°,图③中的∠A1+∠A2+∠A3+∠A4=540°,图④中的∠A1+∠A2+∠A3+∠A4+∠A5=720°,…,第⑩个图中的∠A1+∠A2+∠A3+…+∠A10=1620°;(2)第n个图中的∠A1+∠A2+∠A3+…+∠A n=180°(n﹣1).故答案为180,360,540,720,1620;180°(n﹣1).变式5.(2021·全国初二课时练习)如图①:MA1∥NA2,图②:MA11NA3,图③:MA1∥NA4,图④:MA1∥NA5,……,则第n个图中的∠A1+∠A2+∠A3+…+∠A n+1______.(用含n的代数式表示)n【答案】n180°分析:分别求出图①、图②、图③中,这些角的和,探究规律后,理由规律解决问题即可.【解析】如图①中,∠A1+∠A2=180∘=1×180∘,如图②中,∠A1+∠A2+∠A3=360∘=2×180∘,如图③中,∠A1+∠A2+∠A3+∠A4=540∘=3×180∘,…,n,故答案为180n°.第n个图,∠A1+∠A2+∠A3+…+∠A n+1学会从=n180°点睛:平行线的性质.模型2:猪蹄模型(M型)【解题技巧】如图,①已知:AB∥CD,结论:∠APC=∠A+∠C;②已知:∠APC=∠A+∠C,结论:AB∥CD.图①、图②图③③已知:AB ∥CD ,结论:∠A +∠P 2+∠C =∠P 1+∠P 3. 例1、(2022.广东省初一月考)如图所示,已知:AB ∥CD ,求证:∠APC =∠A +∠C ;【解析】方法一(破角):过点P 作PQ ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥PQ ∴∠1=∠2,∠3=∠4∴∠APC =∠2+∠3=∠1+∠4.方法二(添角): 连接AC ,∵AB ∥CD ∴∠1+∠3+∠2+∠4=180°,又∠2+∠3+∠APC =180° ∴∠APC =∠1+∠4.变式1.(2021·山东青岛期末)如图,//AB CD ,点E 在AC 上,110A Ð=°,15D Ð=°,则下列结论正确的个数是( )(1)AE EC =;(2)85AED Ð=°;(3)A CED D Ð=Ð+Ð;(4)45BED Ð=°A .1个B .2个C .3个D .4个【答案】B .【解析】解:过点E 作EF ∥AB ,(1)无法判断;(2)∵AB //CD ,AB //EF ,∴EF //CD ,∴∠AEF =70°,∠DEF =15°,∴∠AED =85°,正确;(3)由(2)得:∠A =∠CEF =∠CED +∠DEF ,∠DEF =∠D ∴∠A =∠CED +∠D ,正确;(4)无法判断;故答案为:B .变式2.(2021.湖北七年级期中)如图,//AB EF ,90C Ð=°,则a Ð,βÐ,g Ð之间的关系是( )A .βa gÐ=Ð+ÐB .180a βg Ð+Ð+Ð=°C .90a βg Ð+Ð-Ð=°D .90βg a Ð+Ð-Ð=°【答案】C .【解析】解:分别过C 、D 作AB 的平行线CM 和DN ,则AB ∥CM ∥DN ∥EF ∴∠α=∠BCM ,∠DCM =∠CDN ,∠NDE =∠γ而∠β=∠CDN +∠NDE =∠DCM +∠γ=90°-∠BCM +∠γ=90°-∠α+∠γ.即∠α+∠β-∠γ=90°,故答案为:C .例2.(2021·浙江杭州七年级期中)如图(1)所示是一根木尺折断后的情形,你可能注意过,木尺折断后的断口一般是参差不齐的,那么请你深入考虑一下其中所包含的一类数学问题,我们不妨取名叫“木尺断口问题”.(1)如图(2)所示,已知//AB CD ,请问B Ð,D Ð,E Ð有何关系并说明理由;(2)如图(3)所示,已知//AB CD ,请问B Ð,E Ð,D Ð又有何关系并说明理由;(3)如图(4)所示,已知//AB CD ,请问E G +∠∠与B F D ++∠∠∠有何关系并说明理由.【答案】见解析.【解析】解:(1)∠E =∠B +∠D ,理由如下:过点E 作直线a ∥AB ,则a ∥AB ∥CD ,则∠B =∠1,∠D =∠2,∴∠BED =∠1+∠2=∠B +∠D .(2)∠E +∠B +∠D =360°,理由如下:过点E 作直线b ∥AB ,则b ∥AB ∥CD ∴∠B +∠3=180°,∠4+∠D =180°∴∠B +∠3+∠4+∠D =360°即∠E +∠B +∠D =360°.(3)∠B +∠F +∠D =∠E +∠G ,理由如下:过点E ,F ,G 作直线c ∥AB ,d ∥AB ,e ∥AB ,则c ∥AB ∥d ∥e ∥CD ,则∠B =∠5,∠6=∠7,∠8=∠9,∠10=∠D∴∠B +∠EFG +∠D =∠5+∠7+∠8+∠10=∠5+∠6+∠9+∠10=∠BEF +∠FGD .变式3.(2021·山西八年级期末)综合与探究问题情境:综合实践课上,王老师组织同学们开展了探究三角之间数量关系的数学活动.(1)如图1,//EF MN ,点,A B 分别为直线,EF MN 上的一点,点P 为平行线间一点且130,120PAF PBN Ð=°Ð=°,求APB Ð度数;问题迁移:(2)如图2,射线OM 与射线ON 交于点O ,直线//m n ,直线m 分别交,OM ON于点,A D ,直线n 分别交,OM ON 于点,B C ,点P 在射线OM 上运动.①当点P 在,A B (不与,A B 重合)两点之间运动时,设,ADP BCP a βÐ=ÐÐ=Ð.则,,CPD a βÐÐÐ之间有何数量关系?②若点P 不在线段AB 上运动时(点P 与点,,A B O 三点都不重合),请你直接写出,,CPD a βÐÐÐ间的数量关系.【答案】(1)110°;(2)①∠CPD =α+β;②当P 在BA 延长线时,∠CPD =β-α;;当P 在OB 之间时,∠CPD =α-β.【解析】解:(1)过P 作PG ∥EF ,则PG ∥EF ∥MN ,∴∠PAF +∠GPA =180°,∠PBN +∠GPB =180°∴∠GPA =180°-130°=50°,∠GPB =180°-∠PBN =60°∴∠APB =∠GPA+∠GPB =50°+60°=110°.(2)①∠CPD =∠α+∠β. ②当P 在BA 延长线时,∠CPD =β-α.过P 作PE ∥AD 交AD 于E ,∵AD ∥BC ,∴∠DPE =α,∠CPE =β ∴∠CPD =β-α.当P 在OB 之间时,∠CPD =α-β 过P 作PE ∥AD 交CD 于E ,同理,得:∠CPD =α-β.变式4.(2021·河南七年级期末)把一块含60°角的直角三角尺()0090,60EFG EFG EGF Ð=Ð=放在两条平行线,AB CD 之间.(1)如图1,若三角形的60°角的顶点G 放在CD 上,且221Ð=Ð,求1Ð的度数;(2)如图2,若把三角尺的两个锐角的顶点,E G 分别放在AB 和CD 上,请你探索并说明AEF Ð与FGC Ð间的数量关系;(3)如图3,若把三角尺的直角顶点F 放在CD 上,30°角的顶点E 落在AB 上,请直接写出AEG Ð与CFG Ð的数量关系.【答案】(1)40°;(2)∠AEF +∠FGC =90°;(3)∠AEG +∠CFG =300°.【解析】解:(1)∵AB ∥CD ,∴∠1=∠EGD ,∵∠2+∠FGE +∠EGD =180°,∠2=2∠1,∴2∠1+60°+∠1=180°,∴∠1=40°;(2)过点F 作FP ∥AB ,∵CD ∥AB ,∴FP ∥AB ∥CD ,∴∠AEF =∠EFP ,∠FGC =∠GFP .∴∠AEF +∠FGC =∠EFP +∠GFP =∠EFG ,∵∠EFG =90°,∴∠AEF +∠FGC =90°;(3) ∠AEG +∠CFG =300°,理由如下:∵AB ∥CD ,∴∠AEF +∠CFE =180°,即∠AEG −30°+∠CFG −90°=180°,整理得:∠AEG +∠CFG =300°.模型3:拐弯模型【解题技巧】类型1(鸟嘴形):如图,已知AB ∥CD ,结论:∠1=∠2+∠3.类型2(骨折形):如图,AB ∥CD ,结论:∠2=∠1+∠3.例1.(2021.广东省七年级期中)如图,已知AB ∥CD ,求证:∠1=∠2+∠3.【解析】证法1(添角):过点P 作PQ ∥AB ,则AB ∥CD ∥PQ∴∠2+∠3+∠4=180°,∠1+∠4=180°∴∠1=∠2+∠3.证法2:延长AB交PD于Q,则∠2=∠4,∠1+∠5=180°,∠5+∠3+∠4=180°∴∠1=∠3+∠4=∠2+∠3.例2. (2021·忠县七年级月考)如图,已知直线l1//l2,l3、和l1、l2分别交于点A、B、C、D,点P在直线l3或上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明;(4)若点P在线段DC延长线上运动时,请直接写出∠1、∠2、∠3之间的关系.【答案】(1)见详解;(2)∠3=∠2﹣∠1;(3)∠3=360°﹣∠1﹣∠2;(4)∠3=360°﹣∠1﹣∠2.【解析】(1)证明:过P作PQ∥l1,则PQ∥l1∥l2,∴∠1=∠QPE、∠2=∠QPF∵∠EPF=∠QPE+∠QPF,∴∠EPF=∠1+∠2.(2)∠3=∠2﹣∠1;过P 作PQ ∥l 1,则PQ ∥l 1∥l 2,则:∠1=∠QPE 、∠2=∠QPF ∵∠EPF =∠QPF ﹣∠QPE ,∴∠EPF =∠2﹣∠1.(3)∠3=360°﹣∠1﹣∠2.过P 作PQ ∥l 1,则PQ ∥l 1∥l 2,∴∠EPQ +∠1=180°,∠FPQ +∠2=180°,∵∠EPF =∠EPQ +∠FPQ ;∴∠EPQ +∠FPQ +∠1+∠2=360°,即∠EPF =360°﹣∠1﹣∠2;(4)点P 在线段DC 延长线上运动时,∠3=∠1﹣∠2.过P 作PQ ∥l 1,则PQ ∥l 1∥l 2,∴∠1=∠QPE 、∠2=∠QPF ;∵∠QPE ﹣∠QPF=∠EPF ;∴∠3=∠1﹣∠2.变式3.(2021·余干县期末)如图1,AD //BC ,BAD Ð的平分线交BC 于点G ,90BCD Ð=°.(1)求证:BAG BGA Ð=Ð;(2)如图2,若50ABC Ð=°,BCD Ð的平分线交AD 于点E ,交射线GA 于点F ,AFC Ð的度数.【答案】(1)见解析;(2)20°.【解析】解:(1)∵DA ∥BC ∴∠DAG =∠AGB∵AC 平分∠BAD ∴∠BAG =∠DAG ∴∠BAG =∠AGB .(2)∵∠ABC =50°∴∠BGA =∠BAG =65°,∴∠AGC =115°∵CE 平分∠DCB ∴∠ECB =45°,∴∠AFC =180°-∠AGC -∠ECB =20°.变式4.(2021·福建三明七年级期中)问题情境:在综合与实践课上,老师让同学们以“两条平行线AB ,CD 和一块含60°角的直角三角尺()90,60EFG EFG EGF Ð=Ð=o o ”为主题开展数学活动.操作发现:(1)如图1,小明把三角尺的60o 角的顶点G 放在CD 上,若221Ð=Ð,求1Ð的度数;(2)如图2,小颖把三角尺的两个锐角的顶点E 、G 分别放在AB 和CD 上,请你探索并说明AEF Ð与FGC Ð之间的数量关系;结论应用:(3)如图3,小亮把三角尺的直角顶点F 放在CD 上,30o 角的顶点E 落在AB 上.若AEG a Ð=,求CFG Ð的度数(用含a 的式子表示).图1 图2 图3【答案】(1)40°;(2)∠AEF +∠FGC =90°;(3)∠CFG =60°-α.【解析】解:(1)∵AB ∥CD ,∴∠1=∠EGD .又∵∠2=2∠1,∴∠2=2∠EGD .又∵∠FGE =60°,∴∠EGD =13(180°﹣60°)=40°,∴∠1=40°;(2)∵AB ∥CD ,∴∠AEG +∠CGE =180°,即∠AEF +∠FEG +∠EGF +∠FGC =180°.又∵∠FEG +∠EGF =90°,∴∠AEF +∠FGC =90°;(3)∵AB ∥CD ,∴∠AEF +∠CFE =180°,即∠AEG +∠FEG +∠EFG +∠GFC =180°.又∵∠GFE =90°,∠GEF =30°,∠AEG =α,∴∠GFC =180°﹣90°﹣30°﹣α=60°﹣α.模型4:“5”字模型基本模型:如图,AB ∥CD ,结论:∠1+∠3-∠2=180°.例1.(2021.浙江七年级期中)如图,AB ∥CD ,求证:∠1+∠3-∠2=180°.【解析】过P作PQ∥AB,则AB∥CD∥PQ∴∠1+∠4=180°,∠4+∠5=∠3,∠5=∠2 ∴∠1+∠3-∠2=180°.变式1.(2021.北京七年级期中)如图,已知AB∥CD, EF∥CD,则下列结论中一定正确的是( )A.∠BCD= ∠DCE;B.∠ABC+∠BCE+∠CEF=360°;C.∠BCE+∠DCE=∠ABC+∠BCD;D.∠ABC+∠BCE -∠CEF=180°.【分析】根据平行线的性质,找出图形中的同旁内角、内错角即可判断.【解析】延长DC到H。
七年级平行线知识点归纳

七年级平行线知识点归纳
平行线是初中数学中的重要知识点,学好平行线对后续学习几何知识有很大帮助。
下面是对七年级平行线知识点的归纳总结。
一、平行线和垂直线的基本概念
1.两条不在同一平面内的直线没有交点,称为异面直线。
2.两条在同一平面内的直线,若它们不在同一点相交,则称它们为平行的。
3.两条平行直线之间的距离是相等的。
4.两条垂直直线之间的角度为90度。
二、判定平行线的方法
1.同位角相等定理:当一条直线被另外两个直线截断时,同位角相等的两条直线平行。
2.内错角、外错角定理:两条直线被一条横截线截断时,同侧内错角之和等于180度,同侧外错角之和等于180度。
3.平行线的性质之一:一条直线与两条平行直线相交时,所作的内角和为180度。
三、平行线的性质
1.平行线与平面的交线上所有的角都相等。
2.同位角互相等价,即对应的同位角互相相等。
3.被平行线截断的两条直线所夹角相等。
4.平行四边形的对角线互相平分。
四、平面内角和公式
1.三角形的内角和为180度。
2.四边形的内角和为360度。
3.n边形的内角和为(n-2)×180度。
以上是七年级平行线知识点的归纳总结,希望对你的学习有帮助。
同时还需要多做练习,加深理解和熟练掌握。
苏版七年级平行线和全等三角形模型(拓展提优)

平面图形(二)&全等三角形模型汇编平行线四大模型:结论1: 若AB// CD 贝P+Z AEF+Z PFC3 60 ° 结论2:若Z P+Z AEF+Z PFC 360。
,则AB// CD结论1:若AB// CD 则Z P=Z AEF+Z CFP 结论2:若Z P=Z AEP+Z CFP 贝U AB// CD结论1: 若AB// CD 贝UZ P=Z AEP Z CFP或Z P=Z CFP Z AEP 结论 2 :若Z P=Z AEP Z CFP或Z P=Z CFP Z AEP 贝U AB// CD结论1:若AB// CD 则Z P=Z CFP Z AEP或Z P=Z AEP Z CFP 结论 2 :若Z P=Z CFP Z AEP或Z P=Z AEP Z CFP贝U AB// CD 巩固练习平行线四大模型证明(1) 已知AE// CF,求证Z P+ Z AEP+ Z PFC= 360(2) 已知Z P=Z AEP Z CFP 求证AE// CF.(3) 已知AE// CF,求证Z P=Z AEP Z CFP(4) 已知Z P= Z CFP- Z AEP,求证AE// CF.模块一平行线四大模型应用例1(1)如图,a// b, M N分别在a、b上,P为两平行线间一点,那么Z l +Z 2+Z 3= ___________⑵如图,AB// CD且/ A=25°,/C=45°,则/E的度数是_____________ .⑶如图,已知AB// DE / ABC80°,/CDE=140 °,则/BCD •⑷如图,射线AC/ BD / A= 70 ° ,Z B= 40。
,则/P= __________________练如图所示,AB// CD / E=37°,/C= 20。
,则/EAB的度数为_____________(七一中学2015-2016七下3月月考)如图,AB// CD / B=30°,Z O=Z C.则/ C= .例2如图,已知AB// DE BF DF分别平分/ ABC / CDE求/ C / F的关系•练如图,已知AB// DE / FB(=1 / ABF / FD(=丄 / FDEn n(1)若n=2,直接写出/ C / F的关系______________________ ;⑵若n=3,试探宄/ C、/ F的关系;⑶直接写出/ C / F的关系_____________________ (用含n的等式表示)例3如图,已知AB// CD BE平分/ ABC DE平分/ ADC 求证:/ E= 2 ( / A+/C).练如图,己知AB// DE BF DF分别平分/ ABC / CDE求/ C / F的关系.例 4 如图,/ 3==/ 1 + / 2,求证:/ A+/ B+/ C+/ D= 180练(武昌七校2015-2016 七下期中)如图,ABL BC AE平分/ BAD交BC于E, AE1 DE / l +/2= 90°, M N分别是BA CD的延长线上的点,/ EAM和/ EDN勺平分线相交于点F则/ F的度数为().A 120 °B 135 C. 145 D 150模块二平行线四大模型构造例5 如图,直线AB// CD / EFA= 30 °,/FGH 90 ° ,Z HMN30°,/CNP 50。
平行线四大模型

E
A
B
C
D
FA
B
C
D
典例练习
(1)如图,a∥b,M、N 分别在 a、b 上,P 为两平行线间一点,那么∠l+∠2+∠3=
.
典例练习
如图,AB∥CD,且∠A=25°,∠C=45°,则∠E的度数是
.
典例练习
如图,已知AB∥DE,∠ABC=80°,∠CDE =140°,则∠BCD=
典例练习
如图,射线AC∥BD,∠A= 70°,∠B= 40°,则∠P=
剖析三 猪脚模型与铅笔模型的变形
【例 4】如图,已知 AB∥DE,∠ABC=50°,∠CDE=150°,则∠BCD 的值为( )
A
B
D
E
A.20° 【答案】A
B.50°
C.40°
C D.30°
041
“骨折”模型
剖析四 臭脚模型
条件:点P在EF左侧,在AB、 CD外部
结论1:若AB∥CD, ∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP;
A
B
F MC
P
D
E
021
“铅笔”模型
剖析二 铅笔模型
条件:点P在EF右侧,在AB、 CD内部
结论1:若AB∥CD, 则∠P+∠AEP+∠PFC=360°
结论2:若∠P+∠AEP+∠PFC= 360° 则AB∥CD.
A
E
A
B
A
E1
P E2
C
F
图1
C
D
图2
C 图3
B
A
E1 E2
E3
D
C 图4
B E1 E2 E3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点 P 在 EF 左侧,在 AB、 CD 外部
“骨折”模型
结论 1:若 AB∥CD,则∠P=∠CFP-∠AEP 或∠P=∠AEP-∠CFP;
结论 2:若∠P=∠CFP-∠AEP 或∠P=∠AEP-∠CFP,则 AB∥CD.
【发散思维】
图 1: 180
图 2: 180
图 3: 180
“猪蹄”模型
模型三“臭脚”模型(“鸡翅”模型)
点 P 在 EF 右侧,在 AB、 CD 外部
“臭脚”模型
结论 1:若 AB∥CD,则∠P=∠AEP-∠CFP 或∠P=∠CFP-∠AEP;
结论 2:若∠P=∠AEP-∠CFP 或∠P=∠CFP-∠AEP,则 AB∥CD.
模型四“骨折”模型(“鹰嘴”模型)
图 4: 180
图 5: 180 图 6: 180
【探索发现】
思考 1:
1 +2 ++ n 与 1+2 ++ n1 的关系?
思考 2:
1+2 ++ n =
.
平行线四大模型 模、 CD 内部 结论 1:若 AB∥CD,则∠P+∠AEP+∠PFC=3 60°; 结论 2:若∠P+∠AEP+∠PFC= 360°,则 AB∥CD.
“铅笔”模型
模型二“猪蹄”模型(M 模型)
点 P 在 EF 左侧,在 AB、 CD 内部 结论 1:若 AB∥CD,则∠P=∠AEP+∠CFP; 结论 2:若∠P=∠AEP+∠CFP,则 AB∥CD.
