数据分析实验二
商务大数据分析报告实验任务2

武汉纺织大学《商务数据分析》实验报告
指导教师:侯德林
实验时间: 06 年 5 月 44 日
实验二数据方差、相关和回归分析
一、实验目的
1.掌握使用SPSS软件进行方差分析。
2.掌握使用SPSS软件进行相关分析。
3.掌握使用SPSS软件进行回归分析。
二、实验内容
1.根据数据样本,运用SPSS进行数据的方差分析,包括单因素、多因素和
协方差分析。
2.根据数据样本,进行数据的相关分析,包括二元定距和定序变量相关分析、
偏相关和距离相关分析。
3.根据数据样本,运用SPSS进行数据的回归分析,包括一元和多元回归、
非线性回归、时间序列和含虚拟自变量回归、逻辑回归分析等。
三、操作步骤
1. 方差分析单因素
多因素
协方差分析
2根据数据样本,进行数据的相关分析二元定距
定序变量相关分析
偏相关
距离相关分析
3.根据数据样本,运用SPSS进行数据的回归分析,包括
一元和多元回归、
非线性回归、
时间序列
含虚拟自变量回归、
逻辑回归分析等。
四、实验收获和建议。
实验2 分析数据流和绘制数据流图

实验报告课程名称_软件工程导论__________学院____计算机工程学院_________班级14软件1班学号2014144141姓名秦川2016年11月8日批阅教师时间实验成绩课程名称软件工程学号2014144141姓名秦川实验日期2016.11.8实验名称实验2分析数据流和绘制数据流图实验目的:1、掌握数据流的分析方法2、掌握数据流图的绘制实验内容:任务一绘制数据流图任务二分析数据流和绘制数据流图案例一:总务办公管理系统案例二:火车票预订系统实验原理:数据流图(DFD)是软件系统系统的逻辑模型,仅仅描绘数据在软件中流动(从输入移动到输出)的过程中所经受的变换(即加工处理)。
数据流图的绘制方法:根据数据流图的四种成分:源点或终点,处理,数据存储和数据流,从问题描述中提取数据流图的四种成分;然后依据“自顶向下、从左到右、由粗到细、逐步求精”的基本原则进行绘制。
基本符号如下:实验过程与结果:1.运行Microsoft Office Visio2007运行Microsoft Office Visio2007 2.选择“软件和数据库”中的“数据流模型图”模板选中数据流模型图模板3.用鼠标选拉图标进行绘图任务一绘制数据流图试绘制工资管理系统的数据流图,根据数据流图的符号说明仔细理解下图含义:这是学校教职工工资管理系统,教师根据课时表,职工根据任务表来确定个人工资情况,数据按以下方向传递:首先,对课时表或任务表进行审核,审核后的数据经排序形成专用表格;再进行一系列额外计算,包括个人所得说、住房公积金、保险费得出具体所发工资,并将工资表发给银行;然后,向教职工展示工资所得明细;最后,形成编制报表,更新分类表后,交于会计。
其中,人事科负责人事数据,教师与职工的工资由银行发放,会计做好报表的统计。
任务二分析数据流和绘制数据流图案例一:总务办公管理系统系统简介:某单位准备开发一个购买办公用品和设备的总务办公管理系统。
数值分析实验报告--实验2--插值法

1 / 21数值分析实验二:插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时, 是否也更加靠近被逼近的函数。
龙格(Runge )给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分,分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。
实验要求:(1) 选择不断增大的分点数目n=2, 3 …. ,画出原函数f(x)及插值多项式函数()n L x 在[-1,1]上的图像,比较并分析实验结果。
(2) 选择其他的函数,例如定义在区间[-5,5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。
(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式,比较其结果,试分析2 / 21原因。
1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上,根据拉格朗日插值多项式编写Matlab 脚本,其中把拉格朗日插值部分单独编写为f_lagrange.m 函数,方便调用。
1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20,画出原函数和拉格朗日插值函数的图像,如图1所示。
Matlab 脚本文件为Experiment2_1_1fx.m 。
可以看出,当n 较小时,拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x),即插值效果越来越好。
数据导入与预处理 实验二

信息工程学院《数据导入与预处理》课程实验报告实验二实验名称:分析某时期人口数据特征间的关系实验性质:综合型b=pd.Series(data=a)plt.scatter(b.values,values[:,1], marker='o') ## 绘制散点图plt.scatter(b.values,values[:,2], marker='_',c='r')## 绘制散点plt.scatter(b.values,values[:,3], marker='D',c='b')## 绘制散点plt.scatter(b.values,values[:,4], marker='v',c='y')## 绘制散点plt.scatter(b.values,values[:,5], marker='.',c='y')## 绘制散点# plt.ylabel('生产总值(亿元)')## 添加纵轴标签# plt.title('2000-2017年各产业季度生产总值散点图')## 添加图表标题plt.legend(['年末总人口','男性人口','女性人口','城镇人口','乡村人口'])## 添加图例p.add_subplot(2,1,2)plt.plot(b.values,values[:,1],'b-',b.values,values[:,2],'r-.',b.values,values[:,3],'g--',b.values,values[:,4],'b--',b.values,values[:,5],'y--')## 绘制折线图# plt.ylabel('生产总值(亿元)')## 添加纵轴标签# plt.title('2000-2017年各产业季度生产总值折线图')## 添加图表标题plt.legend(['年末总人口','男性人口','女性人口','城镇人口','乡村人口'])## 添加图例4plt.savefig('1.png')plt.show()5、有图可以看到:随着时间的增长年末总人口,城镇人口有明显的下降趋势,乡村人口。
头歌实践教学平台实验二(3篇)

第1篇一、实验目的1. 熟悉头歌实践教学平台的基本操作。
2. 掌握Python编程语言的基本语法。
3. 学习使用Python进行简单的数据分析。
二、实验环境1. 头歌实践教学平台2. Python编程环境三、实验内容本次实验将使用Python进行简单的数据分析,主要包括以下步骤:1. 数据导入2. 数据清洗3. 数据分析4. 结果展示四、实验步骤1. 数据导入首先,我们需要导入实验所需的数据。
本次实验使用的是CSV格式的数据,可以通过以下代码实现:```pythonimport pandas as pd读取CSV文件data = pd.read_csv("data.csv")```2. 数据清洗数据清洗是数据分析过程中的重要环节,主要是对数据进行处理,使其符合分析要求。
以下是一些常见的数据清洗方法:(1)删除缺失值```python删除缺失值data.dropna(inplace=True)```(2)删除重复值```python删除重复值data.drop_duplicates(inplace=True)```(3)数据类型转换```python将字符串类型转换为整数类型data['column_name'] = data['column_name'].astype(int)```3. 数据分析在数据清洗完成后,我们可以对数据进行各种分析。
以下是一些常见的分析方法:(1)描述性统计```python计算描述性统计describe = data.describe()print(describe)```(2)分组统计```python分组统计grouped_data = data.groupby('column_name').mean()print(grouped_data)```(3)相关性分析```python计算相关性correlation = data.corr()print(correlation)```4. 结果展示最后,我们需要将分析结果展示出来。
实验二 数据统计

实验二数据统计引言概述:数据统计是一种重要的研究方法,它通过收集、整理和分析数据来揭示事物的规律和趋势。
在科学研究、市场调查、社会调查等领域中,数据统计被广泛应用。
本文将从数据收集、数据整理、数据分析和数据展示四个方面,详细介绍实验二中的数据统计方法。
一、数据收集:1.1 选择合适的样本:在进行数据统计之前,首先需要选择合适的样本。
样本的选择应该具有代表性,能够反映整体的特征。
可以通过随机抽样、分层抽样等方法来选择样本。
1.2 数据收集工具:根据实验的需要,选择合适的数据收集工具。
常见的数据收集工具包括问卷调查、观察记录、实验测量等。
根据实验的目的和数据类型选择合适的工具,确保数据的准确性和可靠性。
1.3 数据收集过程:在进行数据收集时,需要确保数据的完整性和一致性。
要制定清晰的数据收集流程,明确每个环节的责任和要求。
同时,要注意保护被调查者的隐私权,确保数据的合法性和保密性。
二、数据整理:2.1 数据清洗:在数据收集之后,需要对数据进行清洗。
清洗数据可以去除异常值、缺失值等干扰因素,保证数据的准确性和可靠性。
可以使用数据清洗工具或编程语言来进行数据清洗。
2.2 数据编码:对于定性数据,需要将其转化为定量数据进行统计分析。
可以使用编码规则将定性数据转化为数字编码,便于后续的数据分析。
2.3 数据整合:在数据整理过程中,需要将多个数据源的数据进行整合。
可以使用数据集成工具或编程语言来进行数据整合,确保数据的一致性和完整性。
三、数据分析:3.1 描述性统计分析:描述性统计分析是对数据进行整体和个体的描述。
可以通过计算均值、中位数、标准差等指标来对数据进行描述,揭示数据的分布和变异情况。
3.2 推论性统计分析:推论性统计分析是通过样本数据对总体进行推断。
可以使用假设检验、置信区间等方法来进行推论性统计分析,揭示样本数据对总体的代表性和差异性。
3.3 相关性分析:相关性分析是研究变量之间关系的方法。
可以使用相关系数、回归分析等方法来分析变量之间的相关性,揭示变量之间的关联程度和影响因素。
科研作图与数据分析

实验报告实验二科研作图与数据分析一、实验目的意义作图是科研基本素养之一,科研绘图不仅是美学作品,更是卓越科研成果的凝练结晶。
图形是高效的可视化信息交流方式,清晰准确的图片可以快速而有效传递和帮助理解文字信息,加强与文章的整体联系;数据分析是指用适当的统计分析方法对收集来的大量数据进行分析,提取有用信息和形成结论而对数据加以详细研究和概况总结的过程,是为了寻求问题的答案而实施的有计划、有步骤的行为。
通过实验,理解与重视科研作图的重要性,了解主要作图软件并掌握常用作图方法。
实验二分为两节,此次实验主要通过对所给数据的分析,掌握利用方差分析2012软件进行方差分析的步骤,提高自身的结果分析能力与文字表达能力,逐步为科研论文写作打下基础。
本次实验还应掌握一些查阅文献的方法,通过查阅有关小麦密度试验的英文文献,并将摘要翻译成中文的过程,达到提高自身文献阅读能力,熟悉文献查找方式与写作格式的目的。
二、实验工具软件:方差分析2012三、实验步骤1、选择多点二因素随机区组实验:年数为2,A处理数4个-免耕、旋耕、翻耕、深松耕作,B因素处理数2个-覆盖和不覆盖,实验重复数为3次,然后进行方差分析,将分析结果以表格形式表达。
2、选择两因素随机区组实验:分别对每年进行分析。
A处理数4个-免耕、旋耕、翻耕、深松耕作,B因素处理数2个-覆盖和不覆盖,实验重复数为3次,然后进行方差分析,将分析结果以表格形式表达。
3、登录Web of science 网页,选择数据库为“Web of science 核心合集”,在检索框中依次输入“wheat”和“density”,进行检索时可自行设置其他检索依据,选择一篇文献并将其摘要翻译成英文。
四、结果分析与讨论1、不同年份、耕作方式、覆盖方式对小麦有效穗数、穗粒数、千粒重、理论产量和实际产量的影响表1 产量性状方差分析(F值)Table 1 Analysis of variance (F value)变异来源Source of variation有效穗数(个/m2)Number of productive ear穗粒数(个/穗)Number of grains per ear千粒重(g)1000-grain weight理论产量(Kg/hm2)Theoretical yield实际产量(Kg/hm2)Y 0.0ns0.0ns0.0ns0.0ns0.0A 14.4** 6.8**31.4**25.4**82.7**B 2.0ns 2.2ns0.3ns0.3ns12.6**Y×A 0.0ns0.0ns0.0ns0.0ns0.0Y×B 0.2ns25.6**114.1**0.1ns31.8**A×B 2.0ns 2.2ns0.3ns0.3ns12.6**Y×A×B 10.5**9.0**23.9**9.5**8.3**注:Y、A和B分别表示年、耕作方式和覆盖率。
实验二 数据统计

实验二数据统计引言概述:数据统计是实验过程中非常重要的一环,通过对实验数据的统计分析,可以匡助研究人员更好地理解实验结果、发现规律、做出结论。
本文将详细介绍实验二中数据统计的相关内容,包括数据采集、数据处理、数据分析、结果展示和结论总结。
一、数据采集1.1 实验数据的采集方式:在实验过程中,应该明确数据的采集方式,例如手动记录、传感器采集、仪器仪表采集等。
1.2 数据的记录和整理:在数据采集过程中,要确保数据的准确性和完整性,及时记录数据并整理成统一的格式,方便后续的数据处理和分析。
1.3 数据的存储和备份:为了防止数据丢失或者损坏,应该将数据存储在安全可靠的地方,并定期进行备份,以确保数据的完整性和可靠性。
二、数据处理2.1 数据清洗:在进行数据分析之前,需要对数据进行清洗,包括去除异常值、缺失值处理、数据格式转换等,以确保数据的准确性和可靠性。
2.2 数据归一化:对于不同类型的数据,需要进行归一化处理,将数据转换为统一的标准,方便后续的数据分析和比较。
2.3 数据抽样:在数据量较大的情况下,可以进行数据抽样,选取代表性的样本进行分析,以节省时间和提高效率。
三、数据分析3.1 描述统计分析:通过描述统计方法,可以对数据进行整体的描述和分析,包括均值、中位数、标准差等指标,匡助研究人员更好地理解数据的特征和规律。
3.2 统计判断分析:通过统计判断方法,可以对数据进行判断和预测,包括假设检验、方差分析、回归分析等,匡助研究人员做出科学的结论。
3.3 数据可视化分析:通过数据可视化的方式,如图表、图象等,可以直观地展示数据的分布和趋势,匡助研究人员更直观地理解数据的含义和结论。
四、结果展示4.1 结果呈现方式:在展示实验结果时,可以选择适合的呈现方式,如表格、图表、图象等,以清晰、简洁的方式展示数据和结论。
4.2 结果解读和分析:在展示结果的同时,需要对结果进行解读和分析,说明数据的含义和结论,匡助读者更好地理解实验结果。
数据挖掘实验二数据立方体与联机分析处理

数据挖掘实验二数据立方体与联机分析处理简介数据挖掘是一种从大量数据中发现隐藏模式、关联和趋势的技术。
在实际应用中,数据挖掘常常需要对数据进行预处理和转换,以便更好地挖掘数据中的信息和知识。
本文将介绍数据挖掘实验中的数据立方体和联机分析处理技术。
一、数据立方体数据立方体是一种以多维数组的形式组织数据的方法,通过将数据按照不同维度进行分类、聚合和计算,可以更好地理解和分析数据。
数据立方体通常包含多个维度和度量。
1. 维度维度是指数据的描述性属性或者类别。
在数据立方体中,维度用于对数据进行分类和分组。
例如,在销售数据中,维度可以是时间、地点和产品等。
2. 度量度量是指可以进行计算的数值型属性。
在数据立方体中,度量用于对数据进行聚合和计算。
例如,在销售数据中,度量可以是销售额、销售量和利润等。
3. 数据立方体的构建数据立方体的构建包括数据清洗、分组、聚合和计算等过程。
首先,需要对原始数据进行清洗,去除重复数据、缺失数据和异常值。
然后,根据维度进行数据分组,将数据划分为不同的类别。
接下来,对每个类别的数据进行聚合和计算,计算出相应的度量值。
最后,将聚合后的数据组织成多维数组形式,构建数据立方体。
4. 数据立方体的使用数据立方体可以通过多维数据分析工具进行查询和分析。
通过选择不同的维度和度量,可以进行针对性的数据探索和分析。
例如,可以通过选择时间维度和销售额度量,分析不同时间段内的销售情况。
数据立方体的使用可以帮助用户更深入地了解数据,发现隐藏的规律和趋势。
二、联机分析处理。
数据分析与数据挖掘--实验二 异常值检校实验

实验报告封面课程名称:数据分析与数据挖掘课程代码:任课老师:周化实验指导老师: 周化实验报告名称:异常值检校实验学生姓名:学号:教学班:递交日期:签收人:我申明,本报告内的实验已按要求完成,报告完全是由我个人完成,并没有抄袭行为。
我已经保留了这份实验报告的副本。
申明人(签名):实验报告评语与评分:评阅老师签名:一、实验名称:异常值检校实验二、实验日期:2015年9月22日三、实验目的:(1)熟悉和巩固数据预处理中的缺失值、时序值、异常值的处理方法;(2)能够使用数据分析工具完成异常值检校;(3)对工具分析而得的异常值能够根据所学知识进行修正;四、实验用的仪器和材料:硬件:PC电脑一台;配置:内存,2G及以上硬盘250G及以上软件环境:操作系统windows server 2003数据库环境:Microsoft SQL SERVER 2005五、实验内容:1)利用SQL2008数据挖掘外接工具完成MOVIECLICK数据集中相应数据表单的异常值校验(找出异常值),对特征属性的设置,阈值的设置进行多种尝试(特征属性=2,阈值=75%)、(特征属性=3,阈值=85%或65%)、(特征属性大于3,阈值=75%),分别观察所校验的异常值结果,并予以记录第一组条件:特征值类型特征值数量阈值异常数对异常值的描述第二组条件:特征值类型特征值数量阈值异常数对异常值的描述第三组条件:特征值类型特征值数量阈值异常数对异常值的描述2)能够根据大课所学,借鉴缺失值补偿方法对部分异常值进行修正,并给出修正后结果或策略。
(3)一个24小时(每小时测量一次数据)的时间相关数据集X用作训练数据集,预测3小时后的值。
已知数据集是X={7,8,9,10,9,8,7,9,11,13,15,17,16,15,14,13,12,11,10,9,7,5,3,1}计算出时间窗=6,MA=5的所有根据测量用移动平均数法预测出的T(1)至T(5)。
spss实验二、实验步骤
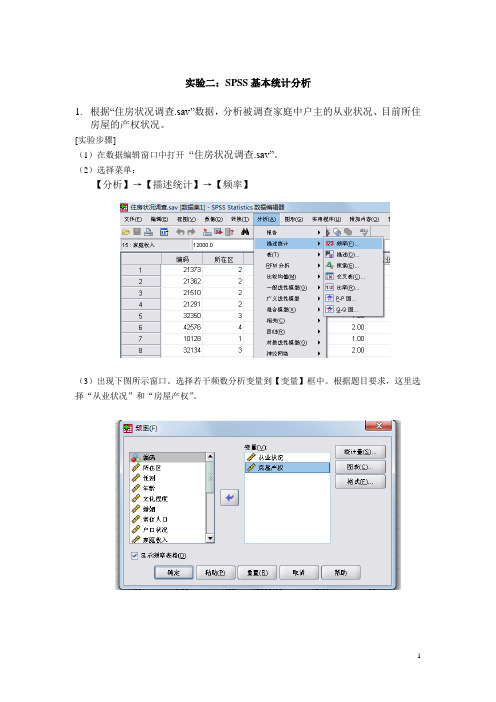
实验二:SPSS基本统计分析1.根据“住房状况调查.sav”数据,分析被调查家庭中户主的从业状况、目前所住房屋的产权状况。
[实验步骤](1)在数据编辑窗口中打开“住房状况调查.sav”。
(2)选择菜单:【分析】→【描述统计】→【频率】(3)出现下图所示窗口。
选择若干频数分析变量到【变量】框中。
根据题目要求,这里选择“从业状况”和“房屋产权”。
(4)按【图表】按钮选择绘制统计图形,出现如下所示的窗口。
在【图表类型】框中选择要输出的图表类型,这里分别选择条形图。
在【图表值】框中选择图表中值的含义,如频率或百分比,这里选择频率。
(5)按【格式】按钮,调整频数分布表中数据的输出顺序。
这里选择“按计数的降序排序”。
(6)按【继续】,完成操作。
2.根据“住房状况调查.sav”数据,对人均住房面积计算基本描述统计量,并分别对本市户口和外地户口家庭进行比较。
分析:这里,由于进行本市户口和外地户口家庭的比较,因此,应首先按照“户口状况”对数据进行拆分,然后计算“人均面积”的基本描述统计量。
(1)在数据编辑窗口中打开“住房状况调查.sav”。
(2)选择菜单:【数据】→【拆分文件】(3)出现下图所示窗口。
选择拆分变量“户口状况”到【分组方式】框中,选择“比较组”。
(4)选择菜单:【分析】→【描述统计】→【描述】(5)出现下图所示窗口。
选择需计算的数值型变量到【变量】框中。
根据题目要求,这里选择“人均面积”。
(6)按【选项】按钮指定计算哪些基本描述统计量,选择相应的项,出现下图所示的窗口。
(7)按【继续】按钮,完成操作。
数据整理与分析实验报告(二)

引言概述:数据整理与分析是现代科学研究中不可或缺的一环。
随着科技的快速发展和数据的爆炸式增长,如何对大量的数据进行整理和分析已成为许多研究人员所面临的重要问题。
本实验报告(二)旨在通过具体案例,介绍数据整理与分析的一般步骤和常用方法。
正文内容:一、数据收集与整理1.确定数据收集的目标和范围2.针对目标设定适当的数据采集方式3.清洗数据,去除异常值和缺失值4.对数据进行预处理,如归一化、标准化等5.建立数据集,方便后续的分析和挖掘二、数据探索与可视化1.利用统计方法,对数据的分布和关系进行分析2.绘制直方图、散点图等可视化图形,进行数据的可视化展示3.运用统计软件工具,进行数据的探索性分析4.利用数据挖掘技术,挖掘出数据中的潜在规律和关联性5.进一步深入分析数据,探索数据中的异常点和趋势三、数据建模与预测1.选择适当的数据建模方法,如回归分析、决策树、聚类分析等2.建立模型,并进行模型的训练和验证3.利用模型对未知数据进行预测和分类4.对模型的效果进行评估和优化5.利用模型的结果,为决策者提供决策支持四、数据分析与解释1.利用统计分析方法,对数据进行分析和解释2.运用统计学的假设检验方法,对数据的差异性进行检验3.利用相关性分析、因子分析等方法,分析数据之间的关系4.运用预测模型,对数据的趋势和未来发展进行分析5.结合领域知识,对数据的分析结果进行解释并给出建议五、数据报告与分享1.撰写数据报告,将整理和分析的过程进行详细描述2.在报告中,将重点呈现关键的实验结果和发现3.使用数据可视化工具,将分析结果以图表的形式展示出来4.向相关人员和团队分享数据和分析结果,促进合作和共享5.根据反馈和评审,不断完善数据整理和分析的流程总结:数据整理与分析是科学研究不可或缺的重要环节,它能够帮助研究人员从庞杂的数据中提取有用的信息和规律。
本实验报告(二)通过具体的步骤和方法,介绍了数据整理与分析的过程。
从数据收集与整理,到数据探索与可视化,再到数据建模与预测,最后到数据分析与解释,通过系统地进行数据整理和分析,我们能够更好地理解数据,发现数据中的规律与趋势,并为决策者提供科学的决策支持。
数据分析实验报告

数据分析实验报告实验⼀SAS系统的使⽤【实验类型】(验证性)【实验学时】2学时【实验⽬的】使学⽣了解SAS系统,熟练掌握SAS数据集的建⽴及⼀些必要的SAS语句。
【实验内容】1. 启动SAS系统,熟悉各个菜单的内容;在编辑窗⼝、⽇志窗⼝、输出窗⼝之间切换。
2. 建⽴数据集表1Name Sex Math Chinese EnglishAlice f908591Tom m958784Jenny f939083Mike m808580Fred m848589Kate f978382Alex m929091Cook m757876Bennie f827984Hellen f857484Wincelet f908287Butt m778179Geoge m868582Tod m898484Chris f898487Janet f8665871)通过编辑程序将表1读⼊数据集sasuser.score;2)将下⾯记事本中的数据读⼊SAS数据集,变量名为code name scale shareprice:000096 ⼴聚能源8500 0.059 1000 13.27000099 中信海直6000 0.028 2000 14.2000150 ST麦科特12600 -0.003 1500 7.12000151 中成股份10500 0.026 1300 10.08000153 新⼒药业2500 0.056 2000 22.753)将下⾯Excel表格中的数据导⼊SAS数据集work.gnp;name x1 x2 x3 x4 x5 x6 北京190.33 43.77 7.93 60.54 49.01 90.4 天津135.2 36.4 10.47 44.16 36.49 3.94 河北95.21 22.83 9.3 22.44 22.81 2.8 ⼭西104.78 25.11 6.46 9.89 18.17 3.25 内蒙古128.41 27.63 8.94 12.58 23.99 3.27 辽宁145.68 32.83 17.79 27.29 39.09 3.47 吉林159.37 33.38 18.37 11.81 25.29 5.22 ⿊龙江116.22 29.57 13.24 13.76 21.75 6.04 上海221.11 38.64 12.53 115.65 50.82 5.89 江苏144.98 29.12 11.67 42.6 27.3 5.74 浙江169.92 32.75 21.72 47.12 34.35 5 安徽153.11 23.09 15.62 23.54 18.18 6.39 福建144.92 21.26 16.96 19.52 21.75 6.73 江西140.54 21.59 17.64 19.19 15.97 4.94 ⼭东115.84 30.76 12.2 33.1 33.77 3.85 河南101.18 23.26 8.46 20.2 20.5 4.3 湖北140.64 28.26 12.35 18.53 20.95 6.23 湖南164.02 24.74 13.63 22.2 18.06 6.04 ⼴东182.55 20.52 18.32 42.4 36.97 11.68 ⼴西139.08 18.47 14.68 13.41 20.66 3.85 四川137.8 20.74 11.07 17.74 16.49 4.39 贵州121.67 21.53 12.58 14.49 12.18 4.57 云南124.27 19.81 8.89 14.22 15.53 3.03 陕西106.02 20.56 10.94 10.11 18 3.29 ⽢肃95.65 16.82 5.7 6.03 12.36 4.49 青海107.12 16.45 8.98 5.4 8.78 5.93 宁夏113.74 24.11 6.46 9.61 22.92 2.53新疆123.24 38 13.72 4.64 17.77 5.753. 将sasuser.score数据集的内容复制到⼀个临时数据集test,要求只包含变量name, sex, math。
实验5数据的描述性分析(二)

实验5数据的描述性分析(二)一、实验目的:1.掌握定量数据的描述性统计分析中常用的指标(1)集中趋势:众数、中位数median()、四分位数、百分位数quantile()、(加权)平均数(weigthted.)mean()(2)分散程度:极差range()、半极差、方差var()、标准差sd()、变异系数、标准误(3)分布形态:偏度系数、峰度系数2.掌握R语言绘直方图、茎叶图和箱线图的方法。
二、实验内容:练习:要求:①完成练习并粘贴运行截图到文档相应位置(截图方法见下),并将所有自己输入文字的字体颜色设为红色(包括后面的思考及小结),②回答思考题,③简要书写实验小结。
④修改本文档名为“本人完整学号姓名1”,其中1表示第1次实验,以后更改为2,3,...。
如文件名为“1305543109张立1”,表示学号为1305543109的张立同学的第1次实验,注意文件名中没有空格及任何其它字符。
最后连同数据文件、源程序文件等(如果有的话,本次实验没有),一起压缩打包发给课代表,压缩包的文件名同上。
截图方法:法1:调整需要截图的窗口至合适的大小,并使该窗口为当前激活窗口(即该窗口在屏幕最前方),按住键盘Alt键(空格键两侧各有一个)不放,再按键盘右上角的截图键(通常印有“印屏幕”或“Pr Scrn”等字符),即完成截图。
再粘贴到word文档的相应位置即可。
法2:利用QQ输入法的截屏工具。
点击QQ输入法工具条最右边的“扳手”图标,选择其中的“截屏”工具。
)1.自行完成教材中相应的例题。
2.(习题3.7)画出习题3.3中小鸡增重的直方图(1) 小区间的宽度为0.lg,起点为3.55g,终点为4.95g。
纵坐标是频数,并将频数标在直方图的上方(类似图3.6(a));(1)源代码:hist(x,col="lightblue",borde="red",+ xlab="小鸡增重量(g)",breaks=14,+ labels=TRUE,xlim=c(3.55,4.55))运行结果或截图:(2)将(1)中直方图的纵坐标改为频率,并将数据的概率密度曲线和正态分布密度曲线同时画在直方图上(类似图 3.6(b))。
实验二:描述性分析实验报告

数据分析及优化设计实验指导书(实验报告)实验名称描述性分析实验实验目的1、熟练掌握利用MATLAB软件计算均值、方差、协方差、相关系数、标准差与变异系数、偏度与峰度、中位数、分位数、三均值、四分位极差与极差。
2、熟练掌握jbtest与kstest关于一维数据的正态性检验。
3、掌握统计作图方法。
4、掌握多维数据的数字特征与相关矩阵的处理方法。
实验题答案实验一:1998年到2020年,我国汽车产量相关统计数据如表所示,解决以下问题:1)计算各项指标的平均值、标准差、变异系数、三均值、偏度与峰度;对数据进行读取,并计算各个指标的平均值、标准差、变异系数、三均值、偏度与峰度,代码如下:1.A=xlsread('第二章数据 experiment2_1.xlsx');=["生产产量(万吨)","金属切削机床产量(万台)","汽车产量(万辆)"]3.M=mean(A); %计算各指标(即各列)的均值4.SD=std(A); %计算各指标标准差5.V=SD./abs(M); %计算各指标变异系数6.SM=[0.25,0.5,0.25]*prctile(A,[25;50;75]); %计算各指标(即各列)的三均值7.pd=skewness(A,0); %计算每列数据的偏度8.fd=kurtosis(A,0)-3; %计算每列数据的峰度9.OUT=["数据名称",NAME;"平均值",M;"标准差",SD;"变异系数",V;"三均值",SM;"偏度",pd;"峰度",fd]在编辑器中输入代码,并保存为.m文件,在命令行窗口中输出各个计算结果如下图所示:2)各项指标是否服从正态分布?若服从正态分布,计算概率为1%时的生铁产量、金属切削机床产量及汽车产量;若不服从正态分布,利用Box-Cox 变换将数据进行变换,对变换后的数据进行相应的分析;对各项指标进行JB检验、KS检验和改进KS检验(即Lilliefors检验),并结合QQ图进行分析判断各项对应指标是否服从正态分布,Matlab中代码如下:1.%%-------------------------------绘图-------------------------------%%2.a1=A(:,[1]); %生铁产量(万吨)3.a2=A(:,[2]); %金属切削机床产量(万台)4.a3=A(:,[3]); %汽车产量(万辆)5.subplot(1,3,1),qqplot(a1),title('生铁产量');6.subplot(1,3,2),qqplot(a2),title('金属切削机床产量');7.subplot(1,3,3),qqplot(a3),title('汽车产量');8.h1=jbtest(X); %JB检验9.h2=kstest(X); %KS检验10.h3=lillietest(X); %改进KS检验11.H=[h1;h2;h3];各列指标检验结果如下:可以看出,生铁产量、金属切削机床产量、汽车产量三项指标都满足h1=0,h2=1,h3=0,表示JB检验和Lilliefors检验支持生铁产量、金属切削机床产量、汽车产量三项指标都服从正态分布,KS检验不支持生铁产量、金属切削机床产量、汽车产量三项指标服从正态分布。
数据挖掘实验报告(两篇)2024

引言概述:数据挖掘是一项广泛应用于各个行业的技术,通过对大数据的处理和分析,可以发现隐藏在数据中的有价值信息。
本文是数据挖掘实验报告(二),将对具体的数据挖掘实验进行详细的阐述和分析。
本实验主要聚焦于数据预处理、特征选择、模型建立和评估等关键步骤,以增加对实验过程和结果的理解,提高实验的可靠性和准确性。
通过实验结果的分析和总结,可以帮助读者更好地理解数据挖掘的方法和技术,并为实际应用提供参考和指导。
正文内容:1. 数据预处理在进行数据挖掘之前,首先需要对原始数据进行预处理。
数据预处理的目的是清洗数据、处理缺失值和异常值等数据问题,以确保数据的质量和准确性。
在本实验中,我们采用了多种方法对数据进行预处理。
其中包括数据清洗、缺失值处理和异常值检测等。
具体的操作包括了数据去重、数据标准化、缺失值的填补和异常值的处理等。
2. 特征选择特征选择是数据挖掘的关键步骤之一,它的目的是从原始数据中选择出对问题解决有价值的特征。
在本实验中,我们通过使用相关性分析、方差选择和递归特征消除等方法,对原始数据进行特征选择。
通过分析特征与目标变量之间的关系,我们可以得出最有价值的特征,从而减少计算复杂度和提高模型准确性。
3. 模型建立模型建立是数据挖掘实验的核心步骤之一。
在本实验中,我们采用了多种模型进行建立,包括决策树、支持向量机、朴素贝叶斯等。
具体而言,我们使用了ID3决策树算法、支持向量机算法和朴素贝叶斯算法等进行建模,并通过交叉验证和网格搜索等方法选择最佳的模型参数。
4. 模型评估模型评估是对建立的模型进行准确性和可靠性评估的过程。
在本实验中,我们采用了多种评估指标进行模型评估,包括准确率、召回率、F1分数等。
通过对模型的评估,我们可以得出模型的准确性和可靠性,并进一步优化模型以达到更好的效果。
5. 结果分析与总结总结:本文是对数据挖掘实验进行详细阐述和分析的实验报告。
通过对数据预处理、特征选择、模型建立和评估等关键步骤的分析和总结,我们得出了对数据挖掘方法和技术的深入理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据分析上机实验二
班别:信计101班学号:
一:题目:在习题1.4表1.8中,列出了各地区居民消费水平,设对应于全体居民、农村居民、城镇居民的数据变量分别为x1,x2,x3。
取公共因子数为1,对x1,x2,x3迚行因子分析,并迚行解释,对公共因子F1得分从小到大迚行排序,并迚行分析解释。
答:第一个表主要是共同度,并对此迚行标准化,也就是原始数据标准化,以消除变量间在数量级和量纲上的不同。
由第二个表可知,所求得的特征值r1=2.945,r2=0.038,r3=0.016,各主成分的贡献率分别为98.175%,1.275%,0.55%,第一个主成分的贡献率已经达到98.175%,故在实际应用中只取第一个主成分,通过第三个图
Y1=0.994x1+0.989x2+0.989x3
Y1是全体居民(x1),农村居民(x2),城镇居民(x3)的加权和,一个地区的消费水平越高的时候,Y1较大,因此Y1放映的是一个地区消费水平高低的一个综合指标,也就是我们成为的“大小因子”。
对公共因子F1得分从小到大进行排序并分析解释
排序后的结果
答:由上面的Y1=0.994x1+0.989x2+0.989x3,反应的是各地区的消费水平的指标,由这些数据经过由小到大排序后可以看出,地区总得分比较高的是上海,北京,浙江,可认为就是该地区消费水平比较高,经济发展水平也高,而西藏,贵州等地总得分比较低,可认为就是该地区消费水平,发展也地。
由上面的得分数据也可以看出,就是我们国家的地区发展水平,消费水平是不均衡的,沿海地区发展好,消费高,而一些西部地区消费水平地,发展也很滞后。
二:取公共因子数为2,采用方差最大正交旋转进行因子分析,对公共因子F1得得分从小到大进行排序,在对公共因子F1,F2进行解释。
Total Variance Explained
图表数据分析:
答:-----(1)第一个表示共同度的情况,从几个数据的大小可以看出,他们经过初始化后还是挺相近的。
对第二个表迚行总方差分析,由表可知,此表选择了连个因子迚行分析,通过表可知r1=2.945,r2=0.038,r3=0.016,各主成分的贡献率分别为98.175%,1.275%,0.55%,第一个主成分的贡献率已经达到99.450%.其共同度矩阵的线性表示为
Y1=0.994x1+0.989x2+0.989x3
Y2=-0.009x1-0.133x2+0.143x3
---------(2)迚过方差最大旋转之后发现其得线性表示为
Y3=0.715x1+0.798x2+0.604x3
Y4=0.692x1+0.600x2+0.796x3
通过最大方差旋转后发现,系数都变为正的了,而且就是系数之间相差都比较小,可认为就是解析比较好,可以很好地反应各地区的消费消费水平的高低。
由表四的变换矩阵,可得到一个线性表示
Y6=0.712X4-0.702X5
Y7=0.702X4+0.712X5
其中Y6表示的是迚行方差最大旋转之前的得分综合评判指标
其中Y6表示的是迚行方差最大旋转之后的得分综合评判指标
对比发现Y7模拟的较好。
答:通过方差最大旋转之前与方差最大旋转后之后,再由小到大进行各地区的得分情况进行排序相比可知。
方差最大旋转之前,得分最高的是前三名是上海,北京、浙江,得分最小的后三位是西藏、贵州、甘肃;而方差最大旋转之后的得分最高的是上海、北京、江苏;最低的是贵州、广东、陕西。
方差最大旋转之前的得分情况,主要反映的是总体得分情况,也即是地区的总体消费水平,而没有能够很好地反映城乡之间的消费的差别。
而通过方差最大能够很好地解决这个问题,不仅反映了总体的消费水平,而且能够反映城乡之间的消费水平。
如在方差最大旋转之前,广东的得分是很高的,但是方差最大旋转之后,广东的得分就变低了,也就是说,广东的总体消费水平是很高的,但是城乡之间的消费水平是存在很大的差异的,也就是城乡发展不平衡。
