数字信号处理上机作业
《数字信号处理》课后上机题#优选.

subplot(2,2,2);stem(n,sn1,'.')
title('(b)系统1的单位阶跃响应');
xlabel('n');ylabel('s(n)')
%系统2
xn=[1,zeros(1,30)];
%xn=单位脉冲序列,长度N=31
xi=filtic(B2,A2,ys);
实验报告
第一章:时域离散信号和时域离散系统
*16.已知两个系统的差分方程分别为
(1) y(n)=0.6y(n-1)-0.08y(n-2)+x(n)
(2) y(n)=0.7y(n-1)-0.1y(n-2)+2x(n)-x(n-2)
分别求出所描述的系统的单位脉冲响应和单位阶跃响应.
解:(可附程序)
(1)系统差分方程的系数向量为
subplot(2,2,1);stem(n,hn1,'.')
title('(a)系统1的系统单位脉冲响应');
xlabel('n');ylabel('h(n)')
xn=ones(1,30);
%xn=单位阶跃序列,长度N=31
sn1=filter(B1,A1,xn,xi);
%调用filter解差分方程,求系统输出信号sn1
%设差分方程(2)系数向量
%系统1
xn=[1,zeros(1,30)];
ys=0;
%xn=单位脉冲序列,长度N=31
xi=filtic(B1,A1,ys);
%由初始条件计算等效初始条件输入序列xi
hn1=filter(B1,A1,xn,xi);
西安电子科技大学数字信号处理上机作业

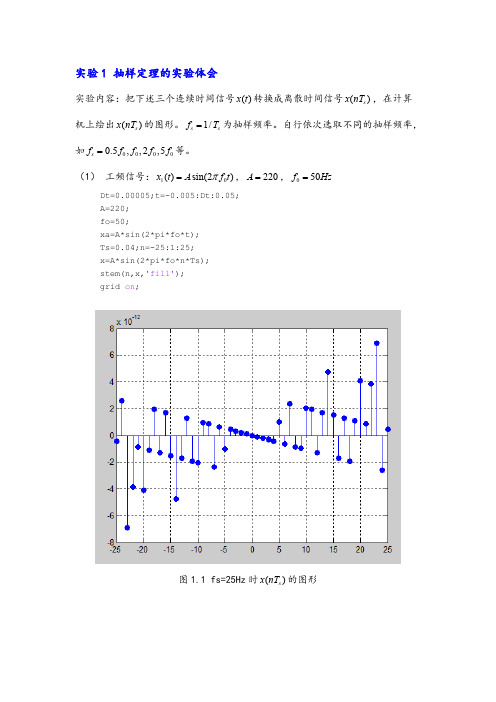
数字信号处理MATLAB上机作业M 2.21.题目The square wave and the sawtooth wave are two periodic sequences as sketched in figure ing the function stem. The input data specified by the user are: desired length L of the sequence, peak value A, and the period N. For the square wave sequence an additional user-specified parameter is the duty cycle, which is the percent of the period for which the signal is positive. Using this program generate the first 100 samples of each of the above sequences with a sampling rate of 20 kHz ,a peak value of 7, a period of 13 ,and a duty cycle of 60% for the square wave.2.程序% 用户定义各项参数参数A = input('The peak value =');L = input('Length of sequence =');N = input('The period of sequence =');FT = input('The desired sampling frequency =');DC = input('The square wave duty cycle = ');% 产生所需要的信号t = 0:L-1;T = 1/FT;x = A*sawtooth(2*pi*t/N);y = A*square(2*pi*(t/N),DC);% Plotsubplot(2,1,1)stem(t,x);ylabel('幅度');xlabel('n');subplot(2,1,2)stem(t,y);ylabel('幅度');xlabel('n');3.结果4.结果分析M 2.41.题目(a)Write a matlab program to generate a sinusoidal sequence x[n]= Acos(ω0 n+Ф) and plot thesequence using the stem function. The input data specified by the user are the desired length L, amplitude A, the angular frequency ω0 , and the phase Фwhere 0<ω0 <pi and 0<=Ф<=2pi. Using this program generate the sinusoidal sequences shown in figure 2.15. (b)Generate sinusoidal sequences with the angular frequencies given in Problem 2.22.Determine the period of each sequence from the plot and verify the result theoretically. 2.程序%用户定义的参数L = input('Desired length = ');A = input('Amplitude = ');omega = input('Angular frequency = ');phi = input('Phase = ');%信号产生n = 0:L-1;x = A*cos(omega*n + phi);stem(n,x);xlabel('n');ylabel('幅度');title(['\omega_{o} = ',num2str(omega)]);3.结果(a)ω0=0ω0=0.1πω0=0.8πω0=1.2π(b)ω0=0.14πω0=0.24πω0=0.34πω0=0.68πω0=0.75π4.结果分析M 2.51.题目Generate the sequences of problem 2.21(b) to 2.21(e) using matlab.2.程序(b)n = 0 : 99;x=sin(0.6*pi*n+0.6*pi);stem(n,x);xlabel('n');ylabel('幅度');(c)n = 0 : 99;x=2*cos(1.1*pi*n-0.5*pi)+2*sin(0.7*pi*n);stem(n,x);xlabel('n');ylabel('幅度');(d)n = 0 : 99;x=3*sin(1.3*pi*n-4*cos(0.3*pi*n+0.45*pi));stem(n,x);xlabel('n');ylabel('幅度');(e)n = 0 : 99;x=5*sin(1.2*pi*n+0.65*pi)+4*sin(0.8*pi*n)-cos(0.8*pi*n);stem(n,x);xlabel('n');ylabel('幅度');(f)n = 0 : 99;x=mod(n,6);stem(n,x);xlabel('n');ylabel('幅度');3.结果(b)(c)(d)(e)(f)4.结果分析M 2.61.题目Write a matlab program to plot a continuous-time sinusoidal signal and its sampled version and verify figure 2.19. You need to use the hold function to keep both plots.2.程序%用户定义的参数fo = input('Frequency of sinusoid in Hz = ');FT = input('Samplig frequency in Hz = ');%产生信号t = 0:0.001:1;g1 = cos(2*pi*fo*t);plot(t,g1,'-')xlabel('时间t');ylabel('幅度')holdn = 0:1:FT;gs = cos(2*pi*fo*n/FT);plot(n/FT,gs,'o');hold off3.结果4.结果分析M 3.11.题目Using program 3_1 determine and plot the real and imaginary parts and the magnitude and phase spectra of the following DTFT for various values of r and θ:G(e jω)=1, 0<r<1.1−2r(cosθ)e−jω+r2e−2jω2.程序%program 3_1%discrete-time fourier transform computatition%k=input('Number of frequency points = ');num=input('Numerator coefficients= ');den=input('Denominator coefficients= ');%computer the frequency responsew=0:pi/k:pi;h=freqz(num,den,w);%plot the frequency responsesubplot(221)plot(w/pi,real(h));gridtitle('real part')xlabel('\omega/\pi');ylabel('Amplitude') subplot(222)plot(w/pi,imag(h));gridtitle('imaginary part')xlabel('\omega/\pi');ylabel('Amplitude') subplot(223)plot(w/pi,abs(h));gridtitle('magnitude spectrum')xlabel('\omega/\pi');ylabel('magnitude') subplot(224)plot(w/pi,angle(h));gridtitle('phase spectrum')xlabel('\omega/\pi');ylabel('phase,radians')3.结果(a)r=0.8 θ=π/6(b)r=0.6 θ=π/34.结果分析M 3.41.题目Using matlab verify the following general properties of the DTFT as listed in Table 3.2:(a) Linearity, (b) time-shifting, (c) frequency-shifting, (d) differentiation-in-frequency, (e) convolution, (f) modulation, and (g) Parseval’s relation. Since all data in matlab have to be finite-length vectors, the sequences to be used to verify the properties are thus restricted to be of finite length.2.程序%先定义两个信号N = input('The length of the sequence = ');k = 0:N-1;%g为正弦信号g = 2*sin(2*pi*k/(N/2));%h为余弦信号h = 3*cos(2*pi*k/(N/2));[G,w] = freqz(g,1);[H,w] = freqz(h,1);%*************************************************************************%% 线性性质alpha = 0.5;beta = 0.25;y = alpha*g+beta*h;[Y,w] = freqz(y,1);figure(1);subplot(211),plot(w/pi,abs(Y));xlabel('\omega/\pi');ylabel('|Y(e^j^\omega)|');title('线性叠加后的频率特性');grid;% 画出Y 的频率特性subplot(212),plot(w/pi,alpha*abs(G)+beta*abs(H));xlabel('\omega/\pi');ylabel('\alpha|G(e^j^\omega)|+\beta|H(e^j^\omega)|');title('线性叠加前的频率特性');grid;% 画出alpha*G+beta*H 的频率特性%*************************************************************************% % 时移性质n0 = 10;%时移10个的单位y2 = [zeros([1,n0]) g];[Y2,w] = freqz(y2,1);G0 = exp(-j*w*n0).*G;figure(2);subplot(211),plot(w/pi,abs(G0));xlabel('\omega/\pi');ylabel('|G0(e^j^\omega)|');title('G0的频率特性');grid;% 画出G0的频率特性subplot(212),plot(w/pi,abs(Y2));xlabel('\omega/\pi');ylabel('|Y2(e^j^\omega)|');title('Y2的频率特性');grid;% 画出Y2 的频率特性%*************************************************************************% % 频移特性w0 = pi/2; % 频移pi/2r=256; %the value of w0 in terms of number of samplesk = 0:N-1;y3 = g.*exp(j*w0*k);[Y3,w] = freqz(y3,1);% 对采样的512个点分别进行减少pi/2,从而生成G(exp(w-w0))k = 0:511;w = -w0+pi*k/512;G1 = freqz(g,1,w);figure(3);subplot(211),plot(w/pi,abs(Y3));xlabel('\omega/\pi');ylabel('|Y3(e^j^\omega)|');title('Y3的频率特性');grid;% 画出Y3的频率特性subplot(212),plot(w/pi,abs(G1));xlabel('\omega/\pi');ylabel('|G1(e^j^\omega)|');title('G1的频率特性');grid;% 画出G1 的频率特性%*************************************************************************% % 频域微分k = 0:N-1;y4 = k.*g;[Y4,w] = freqz(y4,1);%在频域进行微分y0 = ((-1).^k).*g;G2 = [G(2:512)' sum(y0)]';delG = (G2-G)*512/pi;figure(4);subplot(211),plot(w/pi,abs(Y4));xlabel('\omega/\pi');ylabel('|Y4(e^j^\omega)|');title('Y4的频率特性');grid;% 画出Y4的频率特性subplot(212),plot(w/pi,abs(delG));xlabel('\omega/\pi');ylabel('|delG(e^j^\omega)|');title('delG的频率特性');grid;% 画出delG的频率特性%*************************************************************************% % 相乘性质y5 = conv(g,h);%时域卷积[Y5,w] = freqz(y5,1);figure(5);subplot(211),plot(w/pi,abs(Y5));xlabel('\omega/\pi');ylabel('|Y5(e^j^\omega)|');title('Y5的频率特性');grid;% 画出Y5的频率特性subplot(212),plot(w/pi,abs(G.*H));%频域乘积xlabel('\omega/\pi');ylabel('|G.*H(e^j^\omega)|');title('G.*H的频率特性');grid;% 画出G.*H的频率特性%*************************************************************************% % 帕斯瓦尔定理y6 = g.*h;%对于freqz函数,在0到2pi直接取样[Y6,w] = freqz(y6,1,512,'whole');[G0,w] = freqz(g,1,512,'whole');[H0,w] = freqz(h,1,512,'whole');% Evaluate the sample value at w = pi/2% and verify with Y6 at pi/2H1 = [fliplr(H0(1:129)') fliplr(H0(130:512)')]';val = 1/(512)*sum(G0.*H1);% Compare val with Y6(129) i.e sample at pi/2 % Can extend this to other points similarly% Parsevals theoremval1 = sum(g.*conj(h));val2 = sum(G0.*conj(H0))/512;% Comapre val1 with val23.结果(a)(b)(c)(d)(e)4.结果分析M 3.81.题目Using matlab compute the N-point DFTs of the length-N sequences of Problem 3.12 for N=3, 5, 7, and 10. Compare your results with that obtained by evaluating the DTFTs computed in Problem 3.12 at ω= 2pik/N, k=0, 1,……N-1.2.程序%用户定义N的长度N = input('The value of N = ');k = -N:N;y1 = ones([1,2*N+1]);w = 0:2*pi/255:2*pi;Y1 = freqz(y1, 1, w);%对y1做傅里叶变换Y1dft = fft(y1);k = 0:1:2*N;plot(w/pi,abs(Y1),k*2/(2*N+1),abs(Y1dft),'o');grid;xlabel('归一化频率');ylabel('幅度');(a)clf;N = input('The value of N = ');k = -N:N;y1 = ones([1,2*N+1]);w = 0:2*pi/255:2*pi;Y1 = freqz(y1, 1, w);Y1dft = fft(y1);k = 0:1:2*N;plot(w/pi,abs(Y1),k*2/(2*N+1),abs(Y1dft),'o');xlabel('Normalized frequency');ylabel('Amplitude');(b)%用户定义N的长度N = input('The value of N = ');k = -N:N;y1 = ones([1,2*N+1]);y2 = y1 - abs(k)/N;w = 0:2*pi/255:2*pi;Y2 = freqz(y2, 1, w);%对y1做傅里叶变换Y2dft = fft(y2);k = 0:1:2*N;plot(w/pi,abs(Y2),k*2/(2*N+1),abs(Y2dft),'o');grid;xlabel('归一化频率');ylabel('幅度');(c)%用户定义N的长度N = input('The value of N = ');k = -N:N;y3 =cos(pi*k/(2*N));w = 0:2*pi/255:2*pi;Y3 = freqz(y3, 1, w);%对y1做傅里叶变换Y3dft = fft(y3);k = 0:1:2*N;plot(w/pi,abs(Y3),k*2/(2*N+1),abs(Y3dft),'o');grid;xlabel('归一化频率');ylabel('幅度');3.结果(a)N=3N=5 N=7N=10 (b)N=3N=5 N=7N=10 (c)N=3N=5 N=7N=104.结果分析M 3.191.题目Using Program 3_10 determine the z-transform as a ratio of two polynomials in z-1 from each of the partial-fraction expansions listed below:(a)X1(z)=−2+104+z−1−82+z−1,|z|>0.5,(b)X2(z)=3.5−21−0.5z−1−3+z−11−0.25z−2,|z|>0.5,(c)X3(z)=5(3+2z−1)2−43+2z−1+31+0.81z−2,|z|>0.9,(d)X4(z)=4+105+2z−1+z−16+5z−1+z−2,|z|>0.5.2.程序% Program 3_10% Partical-Fraction Expansion to rational z-Transform %r = input('Type in the residues = ');p = input('Type in the poles = ');k = input('Type in the constants = ');[num, den] = residuez(r,p,k);disp('Numberator polynominal coefficients');disp(num) disp('Denominator polynomial coefficients'); disp(den)4.结果分析M 4.61.题目Plot the magnitude and phase responses of the causal IIR digital transfer functionH(z)=0.0534(1+z−1)(1−1.0166z−1+z−2) (1−0.683z−1)(1−1.4461z−1+0.7957z−2).What type of filter does this transfer function represent? Determine the difference equation representation of the above transfer function.2.程序b=[0.0534 -0.00088644 -0.00088644 0.0534];a=[1 -2.1291 1.7833863 -0.5434631];figure(1)freqz(b,a);figure(2)[H,w]=freqz(b,a);plot(w/pi,abs(H)),grid;xlabel('Normalized Frequency (\times\pi rad/sample)'),ylabel('Magnitude');幅度化成真值之后:4.结果分析H(z)=0.0534−0.00088644z−1−0.00088644z−2+0.0534z−31−2.1291z−1+1.7833863z−2−0.5434631z−3M 4.71.题目Plot the magnitude and phase responses of the causal IIR digital transfer functionH(z)=(1−z−1)4(1−1.499z−1+0.8482z−2)(1−1.5548z−1+0.6493z−2).2.程序b=[1 -4 6 -4 1];a=[1 -3.0538 3.8227 -2.2837 0.5472]; figure(1)freqz(b,a);figure(2)[H,w]=freqz(b,a);plot(w/pi,abs(H)),grid;xlabel('Normalized Frequency (\times\pi rad/sample)'), ylabel('Magnitude');3.结果4.结果分析。
数字信号上机作业
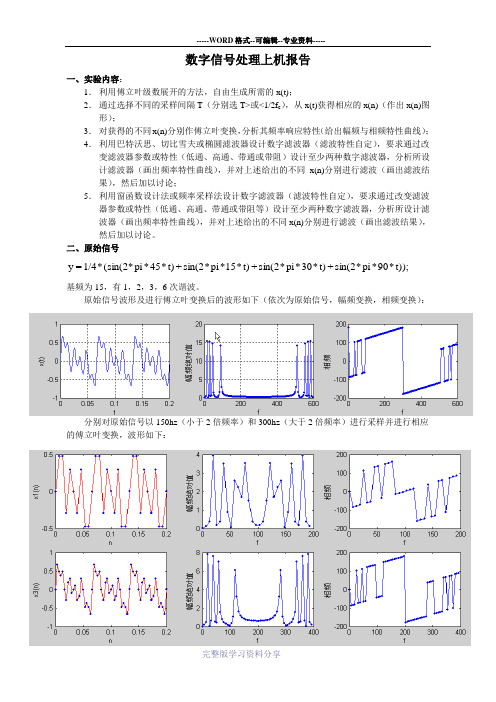
数字信号处理上机报告一、实验内容:1.利用傅立叶级数展开的方法,自由生成所需的x(t);2.通过选择不同的采样间隔T(分别选T>或<1/2f c),从x(t)获得相应的x(n)(作出x(n)图形);3.对获得的不同x(n)分别作傅立叶变换,分析其频率响应特性(给出幅频与相频特性曲线);4.利用巴特沃思、切比雪夫或椭圆滤波器设计数字滤波器(滤波特性自定),要求通过改变滤波器参数或特性(低通、高通、带通或带阻)设计至少两种数字滤波器,分析所设计滤波器(画出频率特性曲线),并对上述给出的不同x(n)分别进行滤波(画出滤波结果),然后加以讨论;5.利用窗函数设计法或频率采样法设计数字滤波器(滤波特性自定),要求通过改变滤波器参数或特性(低通、高通、带通或带阻等)设计至少两种数字滤波器,分析所设计滤波器(画出频率特性曲线),并对上述给出的不同x(n)分别进行滤波(画出滤波结果),然后加以讨论。
二、原始信号45*+t)**pisin(2y1/4=15*(sin(2pi***pi***90t));*+sin(2t)+t)*sin(2*30pi基频为15,有1,2,3,6次谐波。
原始信号波形及进行傅立叶变换后的波形如下(依次为原始信号,幅频变换,相频变换):分别对原始信号以150hz(小于2倍频率)和300hz(大于2倍频率)进行采样并进行相应的傅立叶变换,波形如下:三、数字滤波器数字滤波器采用了巴特沃思滤波器和切比雪夫滤波器。
1、巴特沃思滤波器:巴特沃思滤波器为3阶,采样频率300hz,低通截至频率40hz,带通为40~60hz,高通为60hz。
低通的幅频和相频特性如下图所示:带通的幅频和相频特性如下图所示:高通的幅频和相频特性如下图所示:原始信号经过滤波后,波形如下所示:经过滤波后,感觉高通滤波后的信号似乎不够平滑,但是,调整了很多次,总不能令人满意。
高通滤波的幅频特性感觉不是很好,但是,试了很多次,也没有找到一个好的办法,请老师批评指正。
《数字信号处理》上机实验指导

《数字信号处理》上机实验指导《数字信号处理》上机实验指导实验一、Z 变换及离散时间系统分析(一)、实验目的1、通过本实验熟悉Z 变换在离散时间系统分析中的地位和作用。
2、掌握并熟练使用有关离散系统分析的MATLAB 调用函数及格式,以深入理解离散时间系统的频率特性。
(二)、实验内容及步骤对于一个给定的LSI 系统,其转移函数H(z)习惯被定义为H(z)=B(z)/A(z),即:abn a n b z n a z a z a z n b z b z b A B H ------++++++++++==)1(...)3()2(1)1(...)3()2()1(b )z ()z ()z (2121 公式中b n 和an 分别是H(Z)分子与分母多项式的阶次,在有关MATLAB 的系统分析的文件中,分子和分母的系数被定义为向量,即)]1(),...,2(),1([)]1(),...,2(),1([+=+=a b n a a a a n b b b b并要求)1(a =1,如果)1(a ≠1,则程序将自动的将其归一化为1。
1、系统的阶跃响应调用格式为:y=filter(b,a,x),其中x,y,a,b 都是向量。
例1 令4321432155075.02925.28291.30544.31001836.0007374.0011 016.0007344.0001836.0)z (--------+-+-++++=z z z z z z z z H 求该系统的阶跃响应(y (n ))。
实现该任务的程序如下:clear;x=ones(100);% x(n)=1,n=1~100;t=1:100;% t 用于后面的绘图;b=[.001836,.007344,.011016,.007374,.001836]; % 形成向量b ;a=[1,-3.0544,3.8291,-2.2925,.55075]; % 形成向量a ;y=filter(b,a,x);% 求所给系统的输出,本例实际上是求所给系统的阶跃响应;plot(t,x,'r.',t,y,'k-');grid on;% 将x(n)(绿色)y(n)(黑色)画在同一个%图上;ylabel('x(n) and y(n)')xlabel('n')2、单位抽样响应h(n)调用格式为:h=impz(b ,a ,N) 或 [h ,t]=impz(b ,a ,N)其中N 是所需的h(n)的长度,前者绘图时n 从1开始,而后者从0开始。
数字信 处理上机作业

数字信号处理上机作业学院:电子工程学院班级:021215组员:实验一:信号、系统及系统响应1、实验目的(1) 熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定理的理解。
(2) 熟悉时域离散系统的时域特性。
(3) 利用卷积方法观察分析系统的时域特性。
(4) 掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。
2、实验原理与方法(1) 时域采样。
(2) LTI系统的输入输出关系。
3、实验内容及步骤(1) 认真复习采样理论、离散信号与系统、线性卷积、序列的傅里叶变换及性质等有关内容,阅读本实验原理与方法。
(2) 编制实验用主程序及相应子程序。
①信号产生子程序,用于产生实验中要用到的下列信号序列:a. xa(t)=A*e^-at *sin(Ω0t)u(t)b. 单位脉冲序列:xb(n)=δ(n)c. 矩形序列: xc(n)=RN(n), N=10②系统单位脉冲响应序列产生子程序。
本实验要用到两种FIR系统。
a. ha(n)=R10(n);b. hb(n)=δ(n)+2.5δ(n-1)+2.5δ(n-2)+δ(n-3)③有限长序列线性卷积子程序用于完成两个给定长度的序列的卷积。
可以直接调用MATLAB语言中的卷积函数conv。
conv用于两个有限长度序列的卷积,它假定两个序列都从n=0 开始。
调用格式如下:y=conv (x, h)4、实验结果分析①分析采样序列的特性。
a. 取采样频率fs=1 kHz,,即T=1 ms。
b. 改变采样频率,fs=300 Hz,观察|X(e^jω)|的变化,并做记录(打印曲线);进一步降低采样频率,fs=200 Hz,观察频谱混叠是否明显存在,说明原因,并记录(打印)这时的|X(e^jω)|曲线。
程序代码如下:close all;clear all;clc;A=50;a=50*sqrt(2)*pi;m=50*sqrt(2)*pi;fs1=1000;fs2=300;fs3=200;T1=1/fs1;T2=1/fs2;T3=1/fs3;N=100;n=[0:N-1];x1=A*exp(-a*n*T1).*sin(m*n*T1);x2=A*exp(-a*n*T2).*sin(m*n*T2);x3=A*exp(-a*n*T3).*sin(m*n*T3);w=linspace(-pi,pi,10000);X1=x1*exp(-j*n'*w);X2=x2*exp(-j*n'*w);X3=x3*exp(-j*n'*w);figure(1)subplot(1,3,1)plot(w/pi,abs(X1));xlabel('\omega/π');ylabel('|H(e^j^\omega)|')title('采样频率为1000Hz时的频谱图');subplot(1,3,2)plot(w/pi,abs(X2));xlabel('\omega/π');ylabel('|H(e^j^\omega)|')title('采样频率为300Hz时的频谱图');subplot(1,3,3)plot(w/pi,abs(X3));xlabel('\omega/π');ylabel('|H(e^j^\omega)|')title('采样频率为200Hz时的频谱图');②时域离散信号、系统和系统响应分析。
数字信号处理上机实验 作业结果与说明 实验三、四、五

上机频谱分析过程及结果图 上机实验三:IIR 低通数字滤波器的设计姓名:赵晓磊 学号:赵晓磊 班级:02311301 科目:数字信号处理B一、实验目的1、熟悉冲激响应不变法、双线性变换法设计IIR 数字滤波器的方法。
2、观察对实际正弦组合信号的滤波作用。
二、实验内容及要求1、分别编制采用冲激响应不变法、双线性变换法设计巴特沃思、切贝雪夫I 型,切贝雪夫II 型低通IIR 数字滤波器的程序。
要求的指标如下:通带内幅度特性在低于πω3.0=的频率衰减在1dB 内,阻带在πω6.0=到π之间的频率上衰减至少为20dB 。
抽样频率为2KHz ,求出滤波器的单位取样响应,幅频和相频响应,绘出它们的图,并比较滤波性能。
(1)巴特沃斯,双线性变换法Ideal And Designed Lowpass Filter Magnitude Responsefrequency in Hz|H [e x p (j w )]|frequency in pi units|H [ex p (j w )]|Designed Lowpass Filter Phase Response in radians frequency in pi unitsa r g (H [e x p (j w )](2)巴特沃斯,冲激响应不变法(3)切贝雪夫I 型,双线性变换法(4)切贝雪夫Ⅱ型,双线性变换法综合以上实验结果,可以看出,使用不同的模拟滤波器数字化方法时,滤波器的性能可能产生如下差异:使用冲击响应不变法时,使得数字滤波器的冲激响应完全模仿模拟滤波器的冲激响应,也就是时域逼急良好,而且模拟频率和数字频率之间呈线性关系;但频率响应有混叠效应。
frequency in Hz|H [e x p (j w )]|Designed Lowpass Filter Magnitude Response in dBfrequency in pi units|H [e x p (j w )]|frequency in pi unitsa r g (H [e x p (j w )]Ideal And Designed Lowpass Filter Magnitude Responsefrequency in Hz|H [e x p (j w )]|frequency in pi units|H [e xp (j w )]|frequency in pi unitsa r g (H [e x p (j w )]Ideal And Designed Lowpass Filter Magnitude Responsefrequency in Hz|H [e x p (j w )]|frequency in pi units|H [ex p (j w )]|Designed Lowpass Filter Phase Response in radiansfrequency in pi unitsa r g (H [e x p (j w )]使用双线性变换法时,克服了多值映射的关系,避免了频率响应的混叠现象;在零频率附近,频率关系接近于线性关系,高频处有较大的非线性失真。
中国科学院刘艳老师现代数字信号处理第二章上机作业

rxx=xcorr(x,x,'unbiased'); %观测信号的自相关函数 Rxx rxsx=xcorr(x,sx,'unbiased'); %观测信号与期望信号的互相关函数 Rxdx bx=sx*(sx)'/N; %期望信号均方值 for Lx=2:N %确定滤波器长度 for i=1:Lx %确定观测信号的自相关函数矩阵 for j=1:Lx if i<=j Rxx(i,j)=rxx(N+j-i); else Rxx(i,j)=rxx(N+i-j); end end end Rxx=inv(Rxx); %求逆矩阵 Rxsx=(rxsx(N:N+Lx-1))'; %截取相同长度向量以便可以进行矩阵乘法 hx=Rxx*Rxsx; %滤波器单位脉冲响应 hopt=Rxx-1Rxsx ex=bx-(Rxsx)'*hx; %均方误差 if ex<1e-2 %判断均方误差是否最小 (以 1%作为衡量度) break; end end ax=[1 zeros(1,Lx-1)]'; %确定滤波器系数 fx=filter(hx,ax,x); %滤波 %y 方向上的信号% vy=normrnd(0,0.06.^0.5,1,N); %噪声 sy=sin(0.004*pi*n); %期望信号 y=sy+vy; %观测信号 ryy=xcorr(y,y,'unbiased'); % 观 测 信 号 的 自 相 关 函 数 rysy=xcorr(y,sy,'unbiased'); %观测信号与期望信号的互相关函数 by=sy*(sy)'/N; %期望信号均方值 for Ly=2:N %确定滤波器长度 for i=1:Ly %确定观测信号的自相关函数矩阵 for j=1:Ly if i<=j Ryy(i,j)=ryy(N+j-i); else Ryy(i,j)=ryy(N+i-j); end end end Ryy=inv(Ryy); %求逆矩阵 Rysy=(rysy(N:N+Ly-1))'; %截取相同长度向量 hy=Ryy*Rysy; %滤波器单位脉冲响应 ey=by-(Rysy)'*hy; %均方误差
数字信号处理上机实验
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力通根保1据过护生管高产线中工敷资艺设料高技试中术卷资0配不料置仅试技可卷术以要是解求指决,机吊对组顶电在层气进配设行置备继不进电规行保范空护高载高中与中资带资料负料试荷试卷下卷问高总题中体2资2配,料置而试时且卷,可调需保控要障试在各验最类;大管对限路设度习备内题进来到行确位调保。整机在使组管其高路在中敷正资设常料过工试程况卷中下安,与全要过,加度并强工且看作尽护下可关都能于可地管以缩路正小高常故中工障资作高料;中试对资卷于料连继试接电卷管保破口护坏处进范理行围高整,中核或资对者料定对试值某卷,些弯审异扁核常度与高固校中定对资盒图料位纸试置,卷.编保工写护况复层进杂防行设腐自备跨动与接处装地理置线,高弯尤中曲其资半要料径避试标免卷高错调等误试,高方要中案求资,技料编术试写5交、卷重底电保要。气护设管设装备线备置4高敷、调动中设电试作资技气高,料术课中并3试、中件资且卷管包中料拒试路含调试绝验敷线试卷动方设槽技作案技、术,以术管来及架避系等免统多不启项必动方要方式高案,中;为资对解料整决试套高卷启中突动语然过文停程电机中气。高课因中件此资中,料管电试壁力卷薄高电、中气接资设口料备不试进严卷行等保调问护试题装工,置作合调并理试且利技进用术行管,过线要关敷求运设电行技力高术保中。护资线装料缆置试敷做卷设到技原准术则确指:灵导在活。分。对线对于盒于调处差试,动过当保程不护中同装高电置中压高资回中料路资试交料卷叉试技时卷术,调问应试题采技,用术作金是为属指调隔发试板电人进机员行一,隔变需开压要处器在理组事;在前同发掌一生握线内图槽部纸内 故资,障料强时、电,设回需备路要制须进造同行厂时外家切部出断电具习源高题高中电中资源资料,料试线试卷缆卷试敷切验设除报完从告毕而与,采相要用关进高技行中术检资资查料料和试,检卷并测主且处要了理保解。护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
23春-数字信号处理-在线作业

23春-数字信号处理-在线作业交卷时间2023-05-14 12:28:41一、单选题(每题3分,共20道小题,总分值60分)1.由模拟信号进行采样得到时域离散信号时,同样要满足定理,(3分)采样位移反折对称正确答案A您的答案是A回答正确展开2.序列x(n)的部分x e(n)对应着X(e jω)的实部X R(e jω)。
(3分)对称共轭对称反对称共轭反对称正确答案B您的答案是D回答错误展开3.栅栏效应的存在,有可能漏掉的频谱分量。
(3分)大小高低正确答案A您的答案是A回答正确展开4.如果信号的自变量和函数值均取离散值,则称为。
(3分)模拟信号数字信号离散信号抽样信号正确答案B您的答案是C回答错误展开5.采用按时间抽取的基-2 FFT算法计算N=8点DFT,需要计算______次复数乘法(3分)8165664正确答案D您的答案是D回答正确展开6.因果(可实现)系统其系统函数H(z)的收敛域一定包含点。
(3分)12∞正确答案D您的答案是D回答正确展开7.如果信号的自变量和函数值都取连续值,则称这种信号为或者称为时域连续信号,例如语言信号、温度信号等(3分)模拟信号数字信号离散信号抽样信号正确答案A您的答案是A回答正确展开8.由傅里叶变换理论知道,若信号的频谱有限宽,则其持续时间必然为。
(3分)有限长无限长不确定正确答案B您的答案是B回答正确展开9.序列x(n)的部分x o(n)对应着X(e jω)的虚部(包括j)。
(3分)对称共轭对称反对称共轭反对称正确答案D您的答案是D回答正确展开10.对连续信号进行谱分析时,首先要对其采样,变成时域后才能用DFT(FFT)进行谱分析。
(3分)模拟信号数字信号离散信号抽样信号正确答案C您的答案是A回答错误展开11.维持Fs不变,为提高可以增加采样点数N。
(3分)频率周期频率分辨率数字分辨率正确答案C您的答案是C回答正确展开12.离散序列x(n)只在n为时有意义。
(3分)自然数整数实数复数正确答案B您的答案是B回答正确展开采用按时间抽取的基-2 FFT算法计算N=8点DFT,需要计算______次复数加法(3分)8165664正确答案C您的答案是D回答错误展开14.所谓信号的谱分析,就是计算信号的。
数字信号处理第一次上机

数字信号处理第一次上机作业1. p13 1.10代码:dt=0.0001;%连续函数时域步长tf=6;t=0:dt:tf;xa=sqrt(t)+cos(t);T=0.5;%采样间隔n=0:1:tf/T;x=sqrt(n*T)+cos(n*T);deltax=0.5;xq=deltax*round(x/deltax);subplot(1,2,1);plot(t,xa,':'),hold on,grid on;%连续时间信号,绘制点线plot(n*T,x,'o');%离散时间信号,绘制圆圈stem(n*T,xq,'*'),grid on;%数字信号,绘制星号legend('连续时间信号xa','离散时间信号x','数字信号xq') subplot(1,2,2)stairs(n*T,xq),grid onlegend('数字信号采样保持')set(gcf,'color','w')运行结果:2. 输出以下三种信号:1)x(t)=sin(1.25πt+0.25π),t∈[0,10];连续信号。
2)对x(t)采样,采样频率f_s=0.5Hz;离散时间信号。
3)对x(t)采样,采样频率f_s=2.5Hz;离散时间信号。
4)对x(t)采样,采样频率f_s=4Hz;离散时间信号。
代码:clearn1=0:2:10;x1=sin(1.25*pi*n1+0.25*pi);subplot(4,1,1)stem(n1,x1);xlabel('n1');ylabel('x1');n2=0:0.4:10;x2=sin(1.25*pi*n2+0.25*pi);subplot(4,1,2)stem(n2,x2);xlabel('n2');ylabel('x2');n3=0:0.25:10;x3=sin(1.25*pi*n3+0.25*pi); subplot(4,1,3)stem(n3,x3);xlabel('n3');ylabel('x3');t=0:0.01:10;x=sin(1.25*pi*t+0.25*pi); subplot(4,1,4)plot(t,x);xlabel('t');ylabel('x');结果3. 计算习题2.13(b)中两个离散信号的线性卷积(书面作业题中的一道)。
中国科学院刘艳老师现代数字信号处理第四章上机作业

1、假设一平稳随机信号为()()()0.81x n x n w n =−+,其中)(n w 是均值为0,方差为1的白噪声,数据长度为1024。
(1)、产生符合要求的)(n w 和)(n x ;(2)、给出信号x(n)的理想功率谱;(3)、编写周期图谱估计函数,估计数据长度N=1024及256时信号功率谱,分析估计效果。
(4)、编写Bartlett 平均周期图函数,估计当数据长度N=1024及256时,分段数L 分别为2和8时信号)(n x 的功率谱,分析估计效果。
一、一、解题思路解题思路w(n)可以通过随机序列randn(1,N)来产生,x(n)可以通过对w(n)滤波产生(由递推式可得系统的传递函数),也可以直接由递推式迭代产生。
由于线性系统的输出功率谱等于输入功率谱乘以传递函数模的平方,X(n)可以看做w(n)通过一线性系统的输出,H(z)=1/(1-0.8z)。
所以x(n)的理想功率谱P(ejw)=σw2|H(ejw)|2。
周期图方法:直接对观测数据做FFT变换,变换的结果取模的平方再除以数据长度,作为估计的功率谱。
256个观测点时可以对原观测数据以4为间隔提取得到。
Bartlett法:将L组独立的观测数据分别求周期图,再将L个周期图求平均作为信号的功率谱估计。
L组数据可以通过对原观测数据以L为间隔提取得到。
二、二、MATLAB MATLAB MATLAB实现程序及注解实现程序及注解clear all;clear;close all;Fs=500;%采样率N=1024;%观测数据w=sqrt(1)+randn(1,N);%0均值,方差为1的白噪声,长度1024x=[w(1)zeros(1,N-1)];%初始化x(n),长度1024,x(1)=w(1)for i=2:Nx(i)=0.8*x(i-1)+w(i);%迭代产生观测数据x(n)end%%%%%%%%%%%%%%%%%%%%%理想功率谱%%%%%%%%%%%%%%%%%%%%[h,w1]=freqz(x);figure,plot(w1*500/(2*pi),10*log10(abs(h).^2));grid on;title('理想功率谱');xlabel('频率');ylabel('功率db');%%%%%%%%%%%%%%%%%%%%%周期图法%%%%%%%%%%%%%%%%%%%%%%1024个观测点Pxx=abs(fft(x)).^2/N;%周期图公式Pxx=10*log10(Pxx(index+1));%化为dbfigure;plot(k,Pxx);grid on;title('周期图1024点');xlabel('频率');ylabel('功率db');%周期图256个观测点x1=x(1:4:N);Pxx1=abs(fft(x1,1024)).^2/N;figure;plot(k,Pxx1);grid on;title('周期图256点');xlabel('频率');ylabel('功率db');%%%%%%%%%%%%%%%Bartlett平均周期图,N=1024%%%%%%%%%%%%%%%%%%%分段L=2L=2;x_21=x(1:L:N);x_22=x(2:L:N);Pxx_21=abs(fft(x_21,1024)).^2/length(x_21);Pxx_22=abs(fft(x_22,1024)).^2/length(x_22);Pxx_2=(Pxx_21+Pxx_22)/L;figure;subplot(2,2,1),plot(k,10*log10(Pxx_2(index+1)));grid on;title('N=1024,L=2');xlabel('频率');ylabel('功率db');%分段L=8L1=8;x3=zeros(L1,N/L1);%产生L1行,N/L1列的矩阵用以存储分组的数据for i=1:L1x3(i,:)=x(i:L1:N);%将原始数据分为8组endPxx3=zeros(L1,1024);%产生L1行,1024列矩阵用以存储分组的周期图for i=1:L1Pxx3(i,:)=abs(fft(x3(i,:),1024)).^2/length(x3(i,:));%分别求周期图,结果保存在Pxx3中,FFT长度为1024endfor i=1:1024Pxx3_m(i)=sum(Pxx3(:,i))/L1;%求平均endsubplot(2,2,2),plot(k,10*log10(Pxx3_m(index+1)));grid on;title('N=1024,L=8');xlabel('频率');ylabel('功率db');%%%%%%%%%%%%%%%Bartlett平均周期图,N=256,求法同上%%%%%%%%%%%%%%分段L=2,分别计算周期图,再取平均x=x(1:4:N);L2=2;x_31=x(1:L2:length(x));x_32=x(2:L2:length(x));Pxx_31=abs(fft(x_31,1024)).^2/length(x_31);Pxx_32=abs(fft(x_32,1024)).^2/length(x_32);Pxx_3=(Pxx_31+Pxx_32)/L2;subplot(2,2,3),plot(k,10*log10(Pxx_3(index+1)));grid on;title('N=256,L=2');xlabel('频率');ylabel('功率db');%分段L=8L3=8;x4=zeros(L3,length(x)/L3);for i=1:L3x4(i,:)=x(i:L3:length(x));%将原始数据分为8组endPxx4=zeros(L3,1024);for i=1:L3Pxx4(i,:)=abs(fft(x4(i,:),1024)).^2/length(x4(i,:));%分别求周期图,FFT长度为1024endfor i=1:1024Pxx4_m(i)=sum(Pxx4(:,i))/L3;%求平均endsubplot(2,2,4),plot(k,10*log10(Pxx4_m(index+1)));grid on;title('N=256,L=8');xlabel('频率');ylabel('功率db');三、实验结果理想功率谱图如图1-1所示图1-1理想功率谱图1024点的周期图以及256点的周期图分别如图1-2、1-3所示图2-21024点的周期图图2-3256点的周期图Bartlett平均周期图法的相应图像如图1-4所示图1-4Bartlett平均周期图法的相应图像四、实验结果分析由图1-2、1-3可以看出,周期图法得到的功率谱估计,谱线的起伏较大,即估计所得的均方误差较大。
数字信号处理上机实验报告

数字信号处理上机实验报告实验一熟悉MATLAB环境一、实验目的1、熟悉 MATLAB的主要操作命令。
2、学会简单的矩阵输入和数据读写。
3、掌握简单的绘图命令。
4、用 MATLAB编程并学会创建函数。
5、观察离散系统的频率响应。
二、实验容认真阅读本章附录,在MATLAB环境下重新做一遍附录中的例子,体会各条命令的含义。
在熟悉 MATLAB基本命令的基础上,完成以下实验。
上机实验容:1、数组的加减乘除和乘方运算,输入A1234,B3456,求C A B ,D A B,E A. B,F A./ B,G A.^ B ,并用stem语句画出A、 B、C、 D、 E、F、 G。
程序:>> A=[1 2 3 4];B=[3 4 5 6];C=A+B; D=A-B; E=A.*B; F=A./B; G=A.^B;subplot(2,4,1);stem(A,'.'); subplot(2,4,2);stem(B,'.');subplot(2,4,3);stem(C,'.'); subplot(2,4,4);stem(D,'.');subplot(2,4,5);stem(E,'.'); subplot(2,4,6);stem(F,'.');subplot(2,4,7);stem(G,'.')2、用MATLAB实现下列序列。
a)x(n)0.8n0n15b) x(n)e(0. 2 3 j ) n0n 15c)x(n)3cos(0.125 n0.2 ) 2sin(0.25 n 0.1 ) 0 n 15程序:A)clear;clc;n=[0:15];x1=0.8.^n;subplot(3,1,1),stem(x1)title('x1=0.8^n')xlabel('n'); ylabel('x1');B)clear;clc;n=[0:15];x2=exp((0.2+3j)*n);subplot(3,1,1),stem(x2)title('x2=exp((0.2+3j)*n)')xlabel('n'); ylabel('x2');C)clear;clc;n=[0:15];x3=3*cos(0.125*pi*n+0.2*pi)+2*sin(0.25*pi*n+0.1*pi); subplot(3,1,1),stem(x3)title('x3=3*cos(0.125*pi*n+0.2*pi)+2*sin(0.25*pi*n+0.1*pi)') xlabel('n'); ylabel('x3');3、绘出下列时间常数的图形,对x 轴,y轴以及图形上方均须加上适当的标注:a)x(t )sin( 2 t )0t10sb)x(t )cos(100t )sin(t )0 t 4s>>m=0:0.01:10;n=0:0.01:4;x1t=sin(2*pi*m);x2t=cos(100*pi*n).*sin(pi*n);subplot(2,1,1);plot(m,x1t);subplot(2,1,2);plot(n,x2t);4、给定一因果系统 H(z)=(1+ 2z- 1z-2)/( 1- 0.67z 1z 2),求出并绘制H(z)的幅频响应与相频响应。
数字信号处理上机答案(含程序及图片)第三版高西全著

数字信号处理上机答案(含程序及图片)第三版高西全丁玉美著数字信号处理实验一内容一a=0.8;ys=0;A=[1,-0.9];B=[0.05,0.05];xn=[1,zeros(1,50)];x1n=[1 1 1 1 1 1 1 1 zeros(1,50)];x2n=ones(1,128);xi=filtic(B,A,ys);hn=filter(B,A,xn,xi)n=0:length(hn)-1;subplot(2,2,1);stem(n,yn,'.')title('(a) 系统单位脉冲响应h(n)');xlabel('n');ylabel(hn);y1n=filter(B,A,x1n,xi);n=0:length(y1n)-1;subplot(2,2,2);y='y1(n)'; stem(n,y1n,'.')title('(b) 系统对R8(n)的响应y1(n)');xlabel('n');ylabel(yn);y2n=filter(B,A,x2n,xi);n=0:length(y2n)-1;subplot(2,2,4);y='y2(n)'; stem(n,y2n,'.')title('(c) 系统对u(n)的响应y2(n)');xlabel('n');ylabel(yn);20400.020.040.060.080.1nh (n )(a) 系统单位脉冲响应h(n)020400.20.40.6ny 1(n )(b) 系统对R8(n)的响应y1(n)501000.20.40.60.81ny 2(n )(c) 系统对u(n)的响应y2(n)内容二x1n=[1 1 1 1 1 1 1 1 ];h1n=[ones(1,10) zeros(1,10)]; h2n=[1 2.5 2.5 1 zeros(1,10)]; y21n=conv(h1n,x1n); y22n=conv(h2n,x1n); M1=length(y21n)-1; M2=length(y22n)-1; n1=0:1:M1; n2=0:1:M2;n11=0:length(h1n)-1; n22=0:length(h2n)-1;subplot(2,2,1); tstem(n11,h1n); title('(d) 系统单位脉冲响应h1(n)'); xlabel('n');ylabel(h1(n));subplot(2,2,2); stem(n1,y21n,'fill'); title('(e) h1(n)与R8(n)的卷积y21(n)'); xlabel('n');ylabel(y21(n));subplot(2,2,3); tstem(n22,h2n); title('(f) 系统单位脉冲响应h2(n)'); xlabel('n');ylabel(h2(n));subplot(2,2,4); stem(n1,y22n,'fill'); title('(g) h2(n)与R8(n)的卷积y22(n)'); xlabel('n');ylabel(y22(n));5101500.51nh 1(n )(d) 系统单位脉冲响应h1(n)010202468ny 21(n )(e) h1(n)与R8(n)的卷积y21(n)510123nh 2(n )(f) 系统单位脉冲响应h2(n)510152002468ny 22(n )(g) h2(n)与R8(n)的卷积y22(n)内容三谐振器对u(n)的响应a=0.8;ys=0;xn=[1,zeros(1,250)];B=[1/100.49,-1/100.49];A=[1,-1.8237,0.9801]; xi=filtic(B,A,ys); yn=filter(B,A,xn,xi) n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,'.')谐振器对正弦信号的响应a=0.8;ys=0;xsin=sin(0.014*n)+sin(0.4*n);B=[1/100.49,-1/100.49];A=[1,-1.8237,0.9801]; xi=filtic(B,A,ys); yn=filter(B,A,xsin,xi) n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,'.')50100150200250-0.01-0.008-0.006-0.004-0.00200.0020.0040.0060.0080.0150100150200250-0.5-0.4-0.3-0.2-0.100.10.20.30.40.5数字信号处理实验三实验(1)x1n=[ones(1,4)]; X1k8=fft(x1n,8); X1k16=fft(x1n,16); N=8;f=2/N*(0:N-1); figure(1);subplot(1,2,1);stem(f,abs(X1k8),'.'); title('(la) 8µãDFT[x_1(n)]');xlabel('\omega/\pi¡¯);ylabel(¡®|(e^j^\omega)|'); N=16;f=2/N*(0:N-1);subplot(1,2,2);stem(f,abs(X1k16),'.'); title('(la) 16µãDFT[x_1(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|');实验(1-2,1-3)M=8;xa=1:(M/2);xb=(M/2):-1:1;x2n=[xa,xb];x3n=[xb,xa];X2k8=fft(x2n,8);X2k16=fft(x2n,16);X3k8=fft(x3n,8);X3k16=fft(x3n,16);figure(2);N=8;f=2/N*(0:N-1);subplot(2,2,1);stem(f,abs(X2k8),'.');title('(2a) 8µãDFT[x_2(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|'); subplot(2,2,3);stem(f,abs(X3k8),'.');title('(3a) 8µãDFT[x_3(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|'); N=16;f=2/N*(0:N-1);subplot(2,2,2);stem(f,abs(X2k16),'.');title('(2a) 16µãDFT[x_2(n)]');xlabel('');ylabel('');subplot(2,2,4);stem(f,abs(X3k16),'.');title('(3a) 16µãDFT[x_3(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|');实验(2-1,2-2)N=8;n=0:N-1;x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k8=fft(x4n,8);X4k16=fft(x4n,16);X5k8=fft(x5n,8);X5k16=fft(x5n,16);figure(3);N=8;f=2/N*(0:N-1);subplot(2,2,1);stem(f,abs(X4k8),'.');title('(4a) 8µãDFT[x_4(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|'); subplot(2,2,3);stem(f,abs(X5k8),'.');title('(5a) 8µãDFT[x_5(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|'); N=16;f=2/N*(0:N-1);subplot(2,2,2);stem(f,abs(X4k16),'.');title('(4a) 16µãDFT[x_4(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|'); subplot(2,2,4);stem(f,abs(X5k16),'.');title('(5a) 16µãDFT[x_5(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|');实验(3)Fs=64;T=1/Fs;N=16;n=0:N-1;nT=n*T;x8n=cos(8*pi*nT)+cos(16*pi*nT)+cos(20*pi*nT); X8k16=fft(x8n,16);N=16;f=2/N*(0:N-1);figure(4);subplot(2,2,1);stem(f,abs(X8k16),'.');title('(8a) 16µãDFT[x_8(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|'); N=32;n=0:N-1;nT=n*T;x8n=cos(8*pi*nT)+cos(16*pi*nT)+cos(20*pi*nT); X8k32=fft(x8n,32);N=32;f=2/N*(0:N-1);figure(4);subplot(2,2,2);stem(f,abs(X8k32),'.');title('(8a) 32µãDFT[x_8(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|'); N=64;n=0:N-1;nT=n*T;x8n=cos(8*pi*nT)+cos(16*pi*nT)+cos(20*pi*nT); X8k64=fft(x8n,64);N=64;f=2/N*(0:N-1);figure(4);subplot(2,2,3);stem(f,abs(X8k64),'.');title('(8a) 64µãDFT[x_8(n)]');xlabel('\omega/\pi');ylabel('|(e^j^\omega)|');数字信号处理实验四内容一function st=mstgN=800Fs=10000;T=1/Fs;Tp=N*T; t=0:T:(N-1)*T;k=0:N-1;f=k/Tp; fc1=Fs/10; fm1=fc1/10; fc2=Fs/20; fm2=fc2/10; fc3=Fs/40; fm3=fc3/10;xt1=cos(2*pi*fm1*t).*cos(2*pi*fc1*t); xt2=cos(2*pi*fm2*t).*cos(2*pi*fc2*t); xt3=cos(2*pi*fm3*t).*cos(2*pi*fc3*t); st=xt1+xt2+xt3; fxt=fft(st,N); subplot(3,1,1)plot(t,st);grid;xlabel('t/s');ylabel('s(t)');axis([0,Tp/8,min(st),max(st)]);title('(a) s(t)的波形') subplot(3,1,2)stem(f,abs(fxt)/max(abs(fxt)),'.');grid;title('(b) s(t)的频谱') axis([0,Fs/5,0,1.2]);xlabel('f/Hz');ylabel('幅度')0.0010.0020.0030.0040.0050.0060.0070.0080.0090.01-10123t/ss (t )(a) s(t)的波形20040060080010001200140016001800200000.51(b) s(t)的频谱f/Hz幅度内容二Fs=10000;T=1/Fs;st=mstg;%低通滤波器设计与实现fp=280;fs=450;wp=2*fp/Fs;ws=2*fs/Fs;rp=0.1;rs=60;[N,wp]=ellipord(wp,ws,rp,rs);[B,A]=ellip(N,rp,rs,wp);y1t=filter(B,A,st);figure(2);subplot(3,1,1);[H,w]=freqz(B,A,1000);m=abs(H);plot(w/pi,20*log(m/max(m)));grid on;title('低通滤波损耗函数曲线'); xlabel('w/pi ');ylabel('幅度'); axis([0,1,0,1.2*max(H)])yt='y1(t)'; subplot(3,1,2); plot(t,y1t);title('低通滤波后的波形');xlabel('t/s');ylabel(y1(t));%带通滤波器设计与实现fpl=440;fpu=560;fsl=275;fsu=900;wp=[2*fpl/Fs,2*fpu/Fs];ws=[2*fsl/Fs,2*fsu/Fs];rp=0.1;rs=60;[N,wp]=ellipord(wp,ws,rp,rs);[B,A]=ellip(N,rp,rs,wp);y2t=filter(B,A,st);figure(3);subplot(3,1,1);[H,w]=freqz(B,A,1000);m=abs(H);plot(w/pi,20*log(m/max(m)));grid on;title('带通滤波损耗函数曲线'); xlabel('w/pi ');ylabel('幅度'); axis([0,1,0,1.2*max(H)])yt='y2(t)'; subplot(3,1,2); plot(t,y2t);title('带通滤波后的波形');xlabel('t/s');ylabel(y2(t));%高通滤波器设计与实现fp=890;fs=600;wp=2*fp/Fs;ws=2*fs/Fs;rp=0.1;rs=60;[N,wp]=ellipord(wp,ws,rp,rs);[B,A]=ellip(N,rp,rs,wp,'high');y3t=filter(B,A,st);figure(4);subplot(3,1,1);[H,w]=freqz(B,A,1000);m=abs(H);plot(w/pi,20*log(m/max(m)));grid on;title('高通滤波损耗函数曲线'); xlabel('w/pi ');ylabel('幅度'); axis([0,1,0,1.2*max(H)])yt='y3(t)'; subplot(3,1,2); plot(t,y3t);title('高通滤波后的波形');xlabel('t/s');ylabel(y3(t));低通滤波器损耗函数及其分离出的调幅信号y1(t)带通滤波器损耗函数及其分离出的调幅信号y2(t)高通滤波器损耗函数及其分离出的调幅信号y3(t)数字信号处理实验五1、function xt=xtg(N)Fs=1000;T=1/Fs;Tp=N*T;t=0:T:(N-1)*T;fc=Fs/10;f0=fc/10;mt=cos(2*pi*f0*t);ct=cos(2*pi*fc*t);xt=mt.*ct;nt=2*rand(1,N)-1;fp=150; fs=200;Rp=0.1;As=60;fb=[fp,fs];m=[0,1];dev=[10^(-As/20),(10^(Rp/20)-1)/(10^(Rp/20)+1)];[n,fo,mo,W]=remezord(fb,m,dev,Fs);hn=remez(n,fo,mo,W);yt=filter(hn,1,10*nt);xt=xt+yt;fst=fft(xt,N);k=0:N-1;f=k/Tp;subplot(3,1,1);plot(t,xt);grid;xlabel('t/s');ylabel('x(t)');axis([0,Tp/5,min(xt),max(xt)]);title('(a) 信号加噪声波形')subplot(3,1,2);plot(f,abs(fst)/max(abs(fst)));grid;title('(b) 信号加噪声的频谱')axis([0,Fs/2,0,1.2]);xlabel('f/Hz');ylabel('幅度')2、xt=xtg;N=1000;Fs=1000;T=1/Fs;Tp=N*T;k=0:N-1;f=k/Tp;t=0:T:(N-1)*T;fp=120;fs=150;Rp=0.1;As=60;Fs=1000;wc=(fp+fs)/Fs;B=2*pi*(fs-fp)/Fs;M=ceil(11*pi/B);hn=fir1(M-1,wc,blackman(M));Hw=abs(fft(hn,N));ywt=fftfilt(hn,xt,N);figure;subplot(2,1,1);plot(f,20*log10(Hw)/max(Hw));grid onxlabel('f/Hz');ylabel('幅度(dB )');title('(a)低通滤波器的幅频特性')axis([0,500,-160,5]);subplot(2,1,2);plot(t,ywt);grid onxlabel('t/s');ylabel('y_1(t)');title('(b)滤除噪声后的信号波形')050100150200250300350400450500-150-100-500f/Hz幅度(d B )(a)低通滤波器的幅频特性00.10.20.30.40.50.60.70.80.91-1-0.50.51t/s y 1(t )(b)滤除噪声后的信号波形。
数字信号处理上机实验及答案(第三版,第十章)

第十章上机实验数字信号处理是一门理论和实际密切结合的课程,为深入掌握课程内容,最好在学习理论的同时,做习题和上机实验。
上机实验不仅可以帮助读者深入的理解和消化基本理论,而且能锻炼初学者的独立解决问题的能力。
本章在第二版的基础上编写了六个实验,前五个实验属基础理论实验,第六个属应用综合实验。
实验一系统响应及系统稳定性。
实验二时域采样与频域采样。
实验三用FFT对信号作频谱分析。
实验四IIR数字滤波器设计及软件实现。
实验五FIR数字滤波器设计与软件实现实验六应用实验——数字信号处理在双音多频拨号系统中的应用任课教师根据教学进度,安排学生上机进行实验。
建议自学的读者在学习完第一章后作实验一;在学习完第三、四章后作实验二和实验三;实验四IIR数字滤波器设计及软件实现在。
学习完第六章进行;实验五在学习完第七章后进行。
实验六综合实验在学习完第七章或者再后些进行;实验六为综合实验,在学习完本课程后再进行。
10.1 实验一: 系统响应及系统稳定性1.实验目的(1)掌握求系统响应的方法。
(2)掌握时域离散系统的时域特性。
(3)分析、观察及检验系统的稳定性。
2.实验原理与方法在时域中,描写系统特性的方法是差分方程和单位脉冲响应,在频域可以用系统函数描述系统特性。
已知输入信号可以由差分方程、单位脉冲响应或系统函数求出系统对于该输入信号的响应,本实验仅在时域求解。
在计算机上适合用递推法求差分方程的解,最简单的方法是采用MA TLAB语言的工具箱函数filter函数。
也可以用MATLAB语言的工具箱函数conv函数计算输入信号和系统的单位脉冲响应的线性卷积,求出系统的响应。
系统的时域特性指的是系统的线性时不变性质、因果性和稳定性。
重点分析实验系统的稳定性,包括观察系统的暂态响应和稳定响应。
系统的稳定性是指对任意有界的输入信号,系统都能得到有界的系统响应。
或者系统的单位脉冲响应满足绝对可和的条件。
系统的稳定性由其差分方程的系数决定。
数字信号处理上机题15,16,17,18
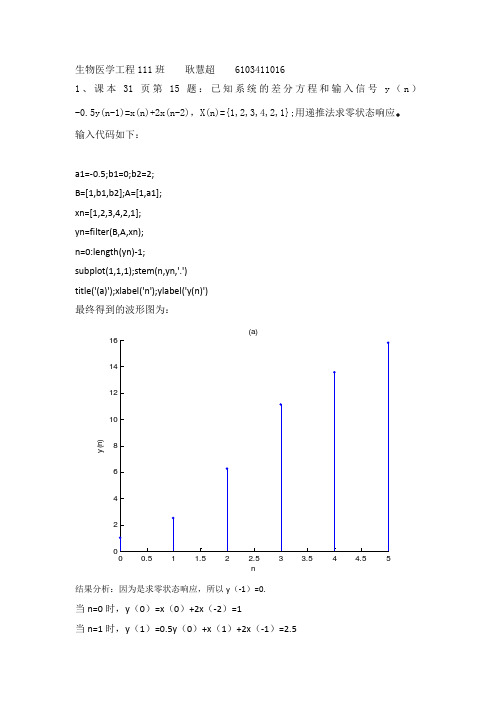
生物医学工程111班 耿慧超 61034110161、课本31页第15题:已知系统的差分方程和输入信号y (n )-0.5y(n-1)=x(n)+2x(n-2),X(n)={1,2,3,4,2,1};用递推法求零状态响应。
输入代码如下:a1=-0.5;b1=0;b2=2; B=[1,b1,b2];A=[1,a1]; xn=[1,2,3,4,2,1]; yn=filter(B,A,xn); n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,'.') title('(a)');xlabel('n');ylabel('y(n)') 最终得到的波形图为:00.51 1.522.533.544.55(a)ny (n )结果分析:因为是求零状态响应,所以y (-1)=0.当n=0时,y (0)=x (0)+2x (-2)=1当n=1时,y (1)=0.5y (0)+x (1)+2x (-1)=2.5当n=2时,y(2)=0.5y(1)+x(2)+2x(0)=6.25当n=3时,y(3)=0.5y(2)+x(3)+2x(1)=11.125当n=4时,y(4)=0.5y(3)+x(4)+2x(2)=13.5625当n=5时,y(5)=0.5y(4)+x(5)+2x(3)=15.78125因为后面一个数都是在前面的基础上加正值,所以结果会越来越大,但是增加的幅度变小。
2、课本31页第16题:已知两个系统的差分方程分别为(1)Y(n)=0.6y(n-1)-0.08y(n-2)+x(n)(2)y(n)=0.7y(n-1)-0.1y(n-2)+2x(n)-x(n-2)分别求出所描述的系统的单位脉冲响应和单位阶跃响应。
(1)输入代码如下:ys=0;xn=[1,zeros(1,30)];B=1;A=[1,-0.6,0.08];xi=filtic(B,A,ys);yn=filter(B,A,xn,xi);n=0:length(yn)-1;subplot(2,1,1);stem(n,yn,'.')title('(a)');xlabel('n');ylabel('y(n)')ys=0;xn=[1,ones(1,30)];B=1;A=[1,-0.6,0.08];xi=filtic(B,A,ys);yn=filter(B,A,xn,xi);n=0:length(yn)-1;subplot(2,1,2);stem(n,yn,'.')title('(a)');xlabel('n');ylabel(' h(n)')最终得到的波形图为:051015202530(a)n y (n )51015202530(a)nh (n )结果分析:单位冲激响应:y (0)=0.6y(-1)-0.08y(-2)+x(0)=1 y (1)=0.6y(0)-0.08y(-1)+x(1)=0.6 y (2)=0.6y(1)-0.08y(0)+x(2)=0.28 y (3)=0.6y(2)-0.08y(1)+x(3)=0.12 y (4)=0.6y(3)-0.08y(2)+x(4)=0.0496 y (5)=0.6y(4)-0.08y(3)+x(5)=0.02016 单位阶跃响应:y (0)=0.6y(-1)-0.08y(-2)+x(0)=1 y (1)=0.6y(0)-0.08y(-1)+x(1)=1.6 y (2)=0.6y(1)-0.08y(0)+x(2)=1.88 y (3)=0.6y(2)-0.08y(1)+x(3)=2 y (4)=0.6y(3)-0.08y(2)+x(4)=2.0496 y (5)=0.6y(4)-0.08y(3)+x(5)=2.06976由结果可以看出与图形相符,说明程序是正确的,在n=5之前y (n )所取的值变化大,之后就几乎不变这是由单位采样序列 (n )或单位阶跃序列u (n )本身的性质决定的。
数字信号处理(MATLAB版)上机实验操作

实验一离散时间信号与系统一、实验目的:1、熟悉常见离散时间信号的产生方法;2、熟悉离散时间系统的单位脉冲响应和单位阶跃响应的求解方法;3、熟悉离散时间信号经过离散时间系统的响应的求解方法。
二、实验内容:已知离散时间系统差分方程为y(n)-0.5y(n-1)+0.06y(n-2)=x(n)+x(n-1),求1、该系统的单位脉冲响应并绘图;2、该系统的单位阶跃响应并绘图;3、已知x(n)=可自己指定用filter函数经过系统的响应并绘图;4、用conv_m函数求系统响应并绘图。
三、实验平台:MA TLAB集成系统四、设计流程:此处写个人自己的设计流程五、程序清单:此处写程序内容六、调试和测试结果:此处写程序的执行结果和实验过程中的调试经过、出现的错误和对应的解决方法七、教师评语与成绩评定此处由老师填写上机操作:实验一离散时间信号与系统实验内容:1.脉冲响应>> b =[1,1]; a = [1,-0.5,0.06];n = [-10:25];>> impz(b,a,n);>> title('Impulse Response'); xlabel('n'); ylabel('h(n)')2.单位阶跃响应>> x = stepseq(0,-10,25); s = filter(b,a,x);Warning: Function call stepseq invokes inexact match d:\MATLAB7\work\STEPSEQ.M.>> stem(n,s)>> title('Step Response'); xlabel('n');ylabel('s(n)')3.>> a=[1,-0.5,0.06];b=[1,1];>> n=-20:120;>> x1=exp(-0.05*n).*sin(0.1*pi*n+pi/3);>> s1=filter(b,a,x1);>> stem(n,s1);;xlabel('n');ylabel('s1(n)');4.>> a=[1,-0.5,0.06];b=[1,1];>> n=-20:120;>> h=impz(b,a,n);>> x1=exp(-0.05*n).*sin(0.1*pi*n+pi/3);>> [y,m]=conv_m(x1,n,h,n);Warning: Function call conv_m invokes inexact match d:\MATLAB7\work\CONV_M.M. >> stem(m,y);title('系统响应');xlabel('m');ylabel('y(m)');实验二离散信号与系统的连续频域分析一、实验目的:1、掌握离散时间信号的DTFT的MATLAB实现;2、掌握离散时间系统的DTFT分析;3、掌握系统函数和频率相应之间的关系。
数字信号处理第二章上机作业

第二章上机作业1、ljdt(A,B)函数定义function ljdt(A,B)p=roots(A);q=roots(B);p=p';q=q';x=max(abs([p q 1]));x=x+0.1;y=x;clfhold onaxis([-x x -y y])w=0:pi/300:2*pi;t=exp(i*w);plot(t)axis('square')plot([-x x],[0 0])plot([0 0],[-y y])text(0.1,x,'jIm[z]')text(y,1/10,'Re[z]')plot(real(p),imag(p),'x')plot(ral(q),imag(q),'o')title('pole-zero diagram for discrete system') hold off例2.26a=[3 -1 0 0 0 1];b=[1 1];ljdt(a,b)p=roots(a)q=roots(b)pa=abs(p)程序运行结果如下:P=0.7255+0.4633i0.7255+0.4633i-0.1861+0.7541i-0.1861-0.7541i-0.7455q=-1pa=0.86080.86080.77680.77680.7455例2.27b=[0 1 2 1];a=[1 -0.5 -0.005 0.3];subplot 311zplane(b,a);xlabel('实部');ylabel('虚部'); num=[0 1 2 1];den=[1 -0.5 -0.005 0.3];h=impz(num,den);subplot 312stem(h);xlabel('k');title('单位脉冲响应'); [H,w]=freqz(num,den);subplot 313plot(w/pi,abs(H));xlabel('频率\omega');title('频率响应')例2.28a=[1,-1];b=[1];subplot 321impz(b,a);a1=[1,-0.8];b1=[1];subplot 322impz(b1,a1,10);a2=[1,-2];b2=[1];subplot 323impz(b2,a2,10);a3=[1,-2*0.8*cos(pi/4),0.8^2];b3=[1];subplot 324impz(b3,a3,20);a4=[1,-2*0.8*cos(pi/8),1];b4=[1];subplot 325impz(b4,a4,20);a5=[1,-2*1.2*cos(pi/4),1.2^2];b5=[1];subplot 326impz(b5,a5,20);例2.29b=[1,0,-1];a=[1,0,-0.81];figure(1)subplot(2,1,1);dimpulse(b,a,50);ylabel('h(n)'); subplot(2,1,2);dstep(b,a,50);ylabel('g(n)'); figure(2)w=[0:1:500]*pi/500; freqz(b,a,w)例2.30b=[1,0,0,0,0,0,0,0,-1];a0=1;a1=[1,0,0,0,0,0,0,0,-(0.8)^8];a2=[1,0,0,0,0,0,0,0,-(0.9)^8];a3=[1,0,0,0,0,0,0,0,-(0.98)^8];[H,w]=freqz(b,a0);[H1,w1]=freqz(b,a1);[H2,w2]=freqz(b,a2);[H3,w3]=freqz(b,a3);subplot(4,2,1);zplane(b,a0);xlabel('实部');ylabel('虚部');title('FIR梳状滤波器零点图')subplot(4,2,2);zplane(b,a1);xlabel('实部');ylabel('虚部');title('IIR梳状滤波器零点图a=0.8')subplot(4,2,3);plot(w/pi,abs(H));title('FIR梳状滤波器幅频响应曲线') subplot(4,2,4);plot(w/pi,abs(H1));title('IIR梳状滤波器幅频响应曲线a=0.8')subplot(4,2,5);zplane(b,a2);xlabel('实部');ylabel('虚部');title('IIR梳状滤波器零极点图a=0.9')subplot(4,2,6);zplane(b,a3);xlabel('实部');yalbel('虚部')title('IIR梳状零极点图a=0.98')a4=[1,0,0,0,0,0,0,0,-(0.9)^8];a5=[1,0,0,0,0,0,0,0,-(0.98)^8];[H4,W4]=freqz(b,a4);[H5,W5]=freqz(b,a5);subplot(4,2,7);plot(w/pi,abs(H4));title('IIR梳状滤波器频幅响应曲线a=0.9')subplot(4,2,8);plot(w/pi,abs(H5));title('IIR梳状滤波器零极点图a=0.98')例2.31num=[0.45 0.4 -1];den=[1 -0.4 -0.45];x0=[1 2];y0=[0 1];N=50;n=[0:N-1]';x=0.8.^n;Zi=filtic(num,den,y0,x0);[y,Zf]=filter(num,den,x,Zi);plot(n,x,'r-',n,y,'b--');title('响应');xlabel('n');ylabel('x(n)-y(n)'); legend('输入x','输入y',1);grid;例2.32num=[18];den=[18 3 -4 -1];[r,p,k]=residuez(num,den) 程序运行结果如下:r =0.36000.24000.4000p =0.5000-0.3333-0.3333k =[](1)f=sym('cos(a*k)');F=ztrans(f)程序运行结果如下:F =(z-cos(a))*z/(z^2-2*z*cos(a)+1) (2)F=sym('a*z/(z-a)^2');f=iztrans(F)程序运行结果如下:f =a^n*n例2.34(1)f=sym('a^n')F=ztrans(f)程序运行结果如下:f =a^nF =-z/(a - z)(2)f=sym('1');F=ztrans(f)程序运行结果如下F =z/(z - 1)b=1;a=poly([0.9 0.9 -0.9]);[r,p,k]=residuez(b,a)程序运行结果如下:r =0.25000.50000.2500p =0.90000.9000-0.9000k =[]例2.36x1=[1,2,3];n1=-1:1;x2=[2,4,3,5];n2=-2:1;[y,n]=conv_m(x1,n1,x2,n2);运行结果如下:y =2 8 17 23 19 15。
西电数字信号处理上机实验
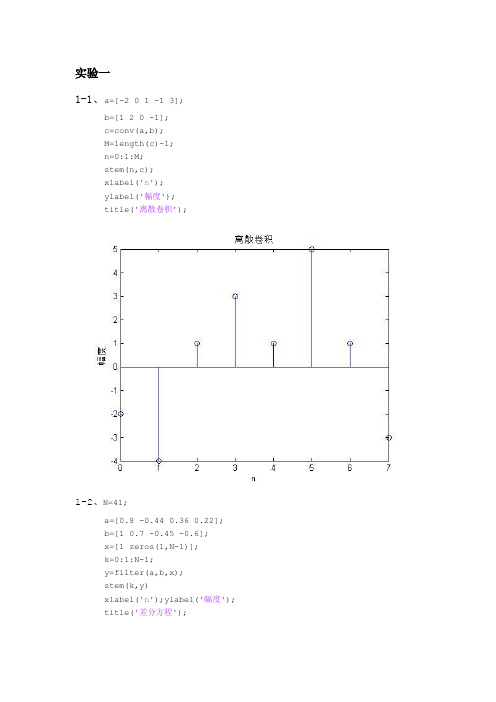
实验一1-1、a=[-2 0 1 -1 3];b=[1 2 0 -1];c=conv(a,b);M=length(c)-1;n=0:1:M;stem(n,c);xlabel('n');ylabel('幅度');title('离散卷积’);1-2、N=41;a=[0.8 -0.44 0.36 0.22]; b=[1 0.7 -0.45 -0.6];x=[1 zeros(1,N-1)];k=0:1:N-1;y=filter(a,b,x);stem(k,y)xlabel('n');ylabel('幅度'); title('差分方程');1-3、k=256;num=[0.8 -0.44 0.36 0.02];den=[1 0.7 -0.45 -0.6];w=0:pi/k:pi;h=freqz(num,den,w);subplot(2,2,1);plot(w/pi,real(h));gridtitle('实部');xlabel('\omega/\pi');ylabel('幅度'); subplot(2,2,2);plot(w/pi,imag(h));gridtitle('虚部');xlabel('\omega/\pi');ylabel('Amplitude'); subplot(2,2,3);plot(w/pi,abs(h));gridtitle('幅度谱');xlabel('\omega/\pi');ylabel('幅值'); subplot(2,2,4);plot(w/pi,angle(h));gridtitle('相位谱');xlabel('\omega/\pi');ylabel('弧度');实验二2-1、N=16;n=0:1:15;p=8;q=4;a=0.1;f=0.0625;xa=exp(-((n-p).^2)./q);figure(1)stem(n, xa,'.');title('xa(n)序列')xlabel('n')ylabel('xa(n)')grid on[H, w] = freqz(xa, 1, [], 'whole', 1); Hamplitude = abs(H);Hphase = angle(H);Hphase = unwrap(Hphase);figure(2)subplot(2, 1, 1)plot(w, Hamplitude)title('幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|') grid onsubplot(2, 1, 2)plot(w, Hphase)title('相频响应')xlabel('w/(2*pi)')ylabel('fai(H(exp(jw)))') grid on2-2、n=0:1:15;a=0.1;f1=0.0625;f2=0.04375;f3=0.05625;xb1=exp(-a*n).*sin(2*pi*f1*n);figuresubplot(3,2,1)stem(n, xb1,'.');title('f=0.0625的时域特性')xlabel('n')ylabel('xb1(n)')grid on[H, w] = freqz(xb1, 1, [], 'whole', 1); Hamplitude = abs(H);subplot(3,2,2)plot(w, Hamplitude)title('f=0.0625的幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|')grid onxb2=exp(-a*n).*sin(2*pi*f2*n);subplot(3,2,3)stem(n, xb2,'.');title('f=0.04375的时域特性')xlabel('n')ylabel('xb2(n)')grid on[H, w] = freqz(xb2, 1, [], 'whole', 1); Hamplitude = abs(H);subplot(3,2,4)plot(w, Hamplitude)title('f=0.04375的幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|')grid onxb3=exp(-a*n).*sin(2*pi*f3*n);subplot(3,2,5)stem(n, xb3,'.');title('f=0.05625的时域特性')xlabel('n')ylabel('xb3(n)')grid on[H, w] = freqz(xb3, 1, [], 'whole', 1); Hamplitude = abs(H);subplot(3,2,6)plot(w, Hamplitude)title('f=0.05625的幅频响应')xlabel('w/(2*pi)')ylabel('|H(exp(jw))|')grid on2-3、n1=0:1:3;xc1=n1+1;n2=4:7;xc2=8-n2;xc=[xc1,xc2];n =[n1,n2];figurestem(n,xc);xlabel('n'); ylabel('xc');title('三角序列');n1=0:1:3;xd1=4-n1;n2=4:7;xd2=n2-3;xd=[xd1,xd2];n =[n1,n2];figurestem(n,xd);xlabel('n'); ylabel('xd');title('反三角序列');N = 16;[H1,w1] = freqz(xc,1, 256, 'whole', 1); Hamplitude1 = abs(H1);figureplot(2*w1, Hamplitude1)title('xc幅频响应')xlabel('w/pi')ylabel('|H(exp(jw))|')grid on[H2,w2] = freqz(xd,1, 256, 'whole', 1); Hamplitude2 = abs(H2);figureplot(2*w2, Hamplitude2)title('xd幅频响应')xlabel('w/pi')ylabel('|H(exp(jw))|')grid on[H3, w3] = freqz(xc, 1, N, 'whole', 1); Hamplitude3 = abs(H3);figuresubplot(2, 1, 1)h3 = stem(2*w3, Hamplitude3, '*');title('xc幅频响应进行N点FFT’);xlabel('n')ylabel('|H(exp(jw))|')grid on[H4, w4] = freqz(xd, 1, N, 'whole', 1); Hamplitude4 = abs(H4);subplot(2, 1, 2)h4 = stem(2*w4, Hamplitude4, '*');title('xd幅频响应进行N点FFT');xlabel('n')ylabel('|H(exp(jw))|')grid on2-4、N = 128;f1 = 1/16;n = 0:N-1;xn = sin(2*pi*0.125.*n)+ cos(2*pi*(0.125+f1).*n); figurestem(n,xn);figuresubplot(2,1,1),plot(n,abs(fft(xn)));title('f =1/16 幅频响应');f2 = 1/64;xn = sin(2*pi*0.125.*n)+ cos(2*pi*(0.125+f2).*n); subplot(2,1,2),plot(n,abs(fft(xn)));title('f =1/64 幅频响应');2-5、N=16;n=0:1:15;p=8;q=2;a=0.1;f=0.0625;xa=exp(-((n-p).^2)./q);xb=exp(-a*n).*sin(2*pi*f*n);%线性卷积x=conv(xa,xb);XDft= fft(x, 32);XDftR = abs(XDft);XDftPhase = angle(XDft);XDftPhase = unwrap(XDftPhase);figure(1);stem(x,'.');title('x(n)序列');xlabel('n')ylabel('x(n)')grid onfigure(2)subplot(2, 1, 1)stem(XDftR, '.');title('X(k)的幅度’);xlabel('k')ylabel('|X(k)|')grid onsubplot(2, 1, 2)stem(XDftPhase, '.');title('X(k)的相角')xlabel('k')ylabel('fai((X(k)))')grid on%圆周卷积XDft161 = fft(xa, N);XDft16R1 = abs(XDft161);XDft16Phase1 = angle(XDft161);XDft16Phase1 = unwrap(XDft16Phase1); XDft162 = fft(xb, N);XDft16R2 = abs(XDft162);XDft16Phase2 = angle(XDft162);XDft16Phase2 = unwrap(XDft16Phase2); XDft16=XDft161.*XDft162;XDft16R=XDft16R1.*XDft16R2;XDft16Phase=XDft16Phase2 +XDft16Phase1 ; x = ifft(XDft16, N);figure(3)stem(x,'.')title('x(n)序列')xlabel('n')ylabel('x(n)')grid onfigure(4)subplot(2, 1, 1)t= 0 : 1 : N - 1;stem(t, XDft16R, '.');title('X(k)的幅度')xlabel('k')ylabel('|X(k)|')grid onsubplot(2, 1, 2)stem(t,XDft16Phase, '.');title('X(k)的相角')xlabel('k')ylabel('fai((X(k)))')grid on2-6、xe=rand(1,512);n1=0:1:3;xc1=n1+1;n2=4:7;xc2=8-n2;xc=[xc1,xc2];%重叠相加法yn=zeros(1,519);for j=0:7xj=xe(64*j+1:64*(j+1));xak=fft(xj,71);xck=fft(xc,71);yn1=ifft(xak.*xck);temp=zeros(1,519);temp(64*j+1:64*j+71)=yn1; yn=yn+temp;end;n=0:518;figure(1)subplot(2,1,1);plot(n,yn);xlabel('n');ylabel('y(n)');title('xc(n)与xe(n)的线性卷积的时域波形-重叠相加法'); subplot(2,1,2);plot(n,abs(fft(yn)));xlabel('k');ylabel('Y(k)');axis([0,600,0,300]);title('xc(n)Óëxe(n)的线性卷积的幅频特性-重叠相加法'); %重叠保留法k=1:7;xe1=k-k;xe_1=[xe1,xe];yn_1=zeros(1,519);for j=0:7xj_1=xe_1(64*j+1:64*j+71);xak_1=fft(xj_1);xck_1=fft(xc,71);yn1_1=ifft(xak_1.*xck_1);temp_1=zeros(1,519);temp_1(64*j+1:64*j+64)=yn1_1(8:71);yn_1=yn_1+temp_1;end;n=0:518;figure(2)subplot(2,1,1);plot(n,yn_1);xlabel('n');ylabel('y(n)');title(' xc(n)的线性卷积的时域波形-重叠保留法'); subplot(2,1,2);plot(n,abs(fft(yn_1)));xlabel('k');ylabel('Y(k)');axis([0,600,0,300]);title('xc(n)Óëxe(n)的线性卷积的幅频特性-重叠保留法');实验三3-1、Wp=0.3;Ws=0.2;Rp=0.8;Rs=20;[N,Wpo]=cheb1ord(Wp,Ws,Rp,Rs);[Bz,Az]=cheby1(N,Rp,Wpo,'high');w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('Chebyshev高通滤波器');3-2、Wp=0.2;Ws=0.3;Rp=1;Rs=25;[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bs,As]=butter(N,Wc,'s');[Bz,Az]=impinvar(Bs,As);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(211);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('脉冲响应不变法')[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(212);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('双线性变换法')3-3、Wp=1.2/8;Ws=2/8;Rp=0.5;Rs=40;[N,Wpo]=cheb1ord(Wp,Ws,Rp,Rs);[Bz,Az]=cheby1(N,Rp,Wpo);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(311);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('切比雪夫')[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(312);plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('巴特沃斯')[N,Wpo]=ellipord(Wp,Ws,Rp,Rs);[Bz,Az]=ellip(N,Rp,Rs,Wpo);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));subplot(313);plot(w/pi,H),grid ontitle('椭圆')xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB')3-4、Wp1=2/15;Wpu=0.2;Ws1=0.1;Wsu=0.4;Rp=3;Rs=20;Wp=[Wp1,Wpu];Ws=[Ws1,Wsu];[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc);w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);H=20*log10(abs(H));plot(w/pi,H),grid onxlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB') title('双线性变换法Butterworth型数字带通滤波器')。
《数字信号处理》课后上机题

%系统1
xn=[1,zeros(1,30)];
ys=0;
%xn=单位脉冲序列,长度N=31
xi=filtic(B1,A1,ys);
%由初始条件计算等效初始条件输入序列xi
hn1=filter(B1,A1,xn,xi);
%调用filter解差分方程,求系统输出信号hn1
n=0:length(hn1)-1;
11111111
x3n=
12344321
第五章:时域离散系统的网络结构
*19.假设滤波器的系统函数为
在单位圆上采样六点,选择r=0.95,试画出它的频率采样结构,并在计算机上用DFT求出频率采样结构中的有关系数.
解:(可附程序)
hn=[5,5,5,3,3,3];
r=0.95;
Hk=fft(hn,6);
n=0:length(sn1)-1;
subplot(2,2,2);stem(n,sn1,'.')
title('(b)系统1的单位阶跃响应');
xlabel('n');ylabel('s(n)')
%系统2
xn=[1,zeros(1,30)];
%xn=单位脉冲序列,长度N=31
xi=filtic(B2,A2,ys);
B1=1,A1=[1,-0.6,0.08]
(2)系统差分方程的系数向量为
B2=[2,0,-1],A2=[1,-0.7,0.1]
调用MATLAB函数filter计算两个系统的单位脉冲响应和单位阶跃响应的程序%B1=1;A1=[1,-0.6,0.08];
%设差分方程(1)系数向量
B2=[2,0,-1];A2=[1,-0.7,0.1];
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字信号处理上机作业学院:电子工程学院班级:021215组员:页脚内容1实验一:信号、系统及系统响应1、实验目的(1) 熟悉连续信号经理想采样前后的频谱变化关系,加深对时域采样定理的理解。
(2) 熟悉时域离散系统的时域特性。
(3) 利用卷积方法观察分析系统的时域特性。
(4) 掌握序列傅里叶变换的计算机实现方法,利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。
2、实验原理与方法(1) 时域采样。
(2) LTI系统的输入输出关系。
3、实验内容及步骤(1) 认真复习采样理论、离散信号与系统、线性卷积、序列的傅里叶变换及性质等有关内容,阅读本实验原理与方法。
(2) 编制实验用主程序及相应子程序。
①信号产生子程序,用于产生实验中要用到的下列信号序列:页脚内容2a. xa(t)=A*e^-at *sin(Ω0t)u(t)b. 单位脉冲序列:xb(n)=δ(n)c. 矩形序列:xc(n)=RN(n), N=10②系统单位脉冲响应序列产生子程序。
本实验要用到两种FIR系统。
a. ha(n)=R10(n);b. hb(n)=δ(n)+2.5δ(n-1)+2.5δ(n-2)+δ(n-3)③有限长序列线性卷积子程序用于完成两个给定长度的序列的卷积。
可以直接调用MATLAB语言中的卷积函数conv。
conv用于两个有限长度序列的卷积,它假定两个序列都从n=0 开始。
调用格式如下:y=conv (x, h)4、实验结果分析①分析采样序列的特性。
a. 取采样频率fs=1 kHz,,即T=1 ms。
b. 改变采样频率,fs=300 Hz,观察|X(e^jω)|的变化,并做记录(打印曲线);进一步降低采样频率,fs=200 Hz,观察频谱混叠是否明显存在,说明原因,并记录(打印)这时的|X(e^jω)|曲线。
程序代码如下:close all;clear all;clc;A=50;页脚内容3a=50*sqrt(2)*pi;m=50*sqrt(2)*pi;fs1=1000;fs2=300;fs3=200;T1=1/fs1;T2=1/fs2;T3=1/fs3;N=100;n=[0:N-1];x1=A*exp(-a*n*T1).*sin(m*n*T1);x2=A*exp(-a*n*T2).*sin(m*n*T2);x3=A*exp(-a*n*T3).*sin(m*n*T3);w=linspace(-pi,pi,10000);X1=x1*exp(-j*n'*w);X2=x2*exp(-j*n'*w);X3=x3*exp(-j*n'*w);页脚内容4figure(1)subplot(1,3,1)plot(w/pi,abs(X1));xlabel('\omega/π');ylabel('|H(e^j^\omega)|')title('采样频率为1000Hz时的频谱图');subplot(1,3,2)plot(w/pi,abs(X2));xlabel('\omega/π');ylabel('|H(e^j^\omega)|')title('采样频率为300Hz时的频谱图');subplot(1,3,3)plot(w/pi,abs(X3));xlabel('\omega/π');ylabel('|H(e^j^\omega)|')title('采样频率为200Hz时的频谱图');页脚内容5②时域离散信号、系统和系统响应分析。
a. 观察信号xb(n)和系统hb(n)的时域和频域特性;利用线性卷积求信号xb(n)通过系统hb(n)的响应y(n),比较所求响应y(n)和hb(n)的时域及频域特性,注意它们之间有无差别,绘图说明,并用所学理论解释所得结果。
b. 观察系统ha(n)对信号xc(n)的响应特性。
程序代码如下:close all;clear all;clc;xbn=[1];xcn=ones(1,10);han=ones(1,10);hbn=[1,2.5,2.5,1];页脚内容6yn=conv(xbn,hbn);n1=0:length(xbn)-1;n2=0:length(hbn)-1;subplot(2,1,1);stem(n1,xbn,'.')xlabel('n');ylabel('xb(n)')title('xb(n)的时域特性曲线')subplot(2,1,2);stem(n2,hbn,'.')xlabel('n');ylabel('hb(n)')title('hb(n)的时域特性曲线')figure(2)subplot(2,1,1);n1=[0:length(xbn)-1];w=linspace(-pi,pi,10000);Xbn=xbn*exp(-j*n1'*w);subplot(2,1,1);plot(w/pi,abs(Xbn));页脚内容7xlabel('\omega/π');ylabel('幅度')title('DTFT[xb[n]的频谱');n2=[0:length(hbn)-1];w=linspace(-pi,pi,10000);Hb=hbn*exp(-j*n2'*w);subplot(2,1,2);plot(w/pi,abs(Hb));xlabel('\omega/π');ylabel('幅度')title('DTFT[hb(n)]的频谱');figure(3)n1=0:length(yn)-1;n2=0:length(hbn)-1;subplot(2,1,1);stem(n1,yn,'.')xlabel('n');ylabel('y(n)')title('y(n)的时域特性曲线')subplot(2,1,2);stem(n2,hbn,'.')页脚内容8xlabel('n');ylabel('hb(n)')title('hb(n)的时域特性曲线')figure(4)subplot(2,1,1);n1=[0:length(yn)-1];w=linspace(-pi,pi,10000);Y=yn*exp(-j*n1'*w);subplot(2,1,1);plot(w/pi,abs(Y));xlabel('\omega/π');ylabel('幅度')title('DTFT[y(n)]的频谱');n2=[0:length(hbn)-1];w=linspace(-pi,pi,10000);Hb=hbn*exp(-j*n2'*w);subplot(2,1,2);plot(w/pi,abs(Hb));页脚内容9xlabel('\omega/π');ylabel('幅度')title('DTFT[hb(n)]的频谱');zn=conv(xcn,han);%以下为%系统ha(n)对信号xc(n)的频率响应特性的分析figure(5)n3=[0:length(zn)-1];w=linspace(-pi,pi,10000);Z=zn*exp(-j*n3'*w);subplot(2,1,1);plot(w/pi,abs(Z));xlabel('\omega/π');ylabel('幅度')title('DTFT[zn]的幅度谱');subplot(2,1,2);plot(w/pi,angle(Z));xlabel('\omega/π');ylabel('相位')title('DTFT[zn]的相位谱');页脚内容10图一:xb(n)与hb(n)时域曲线的对比图二:xb(n)与hb(n)频谱函数的对比页脚内容11图三:y(n)与hb(n)时域曲线的对比页脚内容12图四:y(n)与hb(n)频谱函数的对比页脚内容13图五:系统ha(n)对信号xc(n)的频率响应特性的分析包含z(n)幅度谱和相位谱页脚内容14③卷积定理的验证。
(如下程序中Y1为直接线性卷积所得结果做DTFT,Y2为各自的DTFT相乘后所得的结果)程序代码如下:close all;clear all;clc;x1=[1,3,4,0,2];x2=[3,2,0,0,1,5];n1=0:length(x1)-1;n2=0:length(x2)-1;页脚内容15y1=conv(x1,x2);m1=0:length(y1)-1;w=linspace(-pi,pi,10000);X1=x1*exp(-j*n1'*w);X2=x2*exp(-j*n2'*w);Y1=y1*exp(-j*m1'*w);Y2=X1.*X2;subplot(2,1,1);plot(w/pi,abs(Y1));xlabel('\omega/π');ylabel('幅度')title('DTFT[y1(n)]的特性曲线');subplot(2,1,2);plot(w/pi,abs(Y2));xlabel('\omega/π');ylabel('幅度')title('DTFT[y2(n)]的特性曲线');页脚内容165、思考题(1)在分析理想采样序列特性的实验中,采样频率不同时,相应理想采样序列的傅里叶变换频谱的数字频率度量是否都相同?它们所对应的模拟频率是否相同?为什么?答:数字频率度量不相同,但他们所对应的模拟频率相同。
由w=Ω*Ts得,采样间隔变化时模拟频率对应的数字频率会有相应的变化,故其度量会有所变化。
(2)在卷积定理验证的实验中,如果选用不同的频域采样点数M值,例如,选M=10和M=20,分别做序列的傅里叶变换,求得的结果有无差异?答:有差别。
DFT相当于序列频谱的等间隔采样,当取点少时,DFT包含序列频谱的信息会少,与序列频谱的误差会增大。
取点多时,DFT会反映更多的频谱信息,误差会小,减轻了栅栏效应。
