平面概念定理
平面几何的著名定理
平面几何的著名定理一、毕达格拉斯定理(即勾股定理)在任何一个直角三角形中,两条直角边的长的平方和等于斜边长的平方,这就叫做勾股定理。
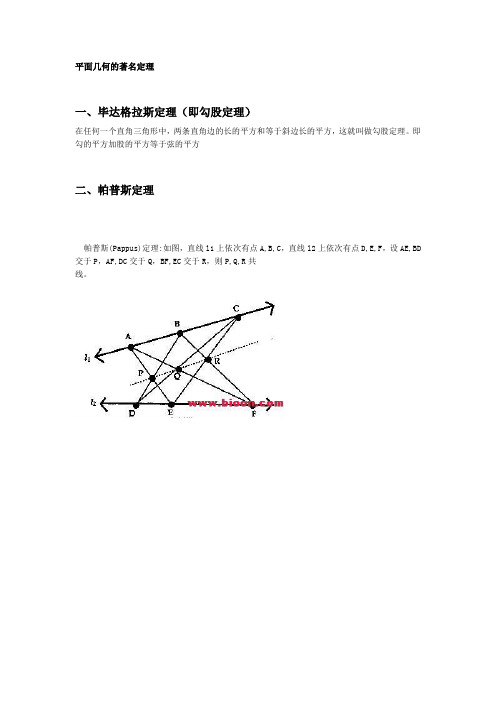
即勾的平方加股的平方等于弦的平方二、帕普斯定理帕普斯(Pappus)定理:如图,直线l1上依次有点A,B,C,直线l2上依次有点D,E,F,设AE,BD 交于P,AF,DC交于Q,BF,EC交于R,则P,Q,R共线。
三、影射定理(与相似三角形和比例有关)直角三角形射影定理(又叫欧几里德(Euclid)定理):直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
公式Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:(1)(AD)^2;=BD·DC,(2)(AB)^2;=BD·BC ,(3)(AC)^2;=CD·BC 。
等积式 (4)ABXAC=BCXAD(可用面积来证明)四、梅涅劳斯定理梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 。
证明一过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , CE/EA=DC/AG。
三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1它的逆定理也成立:若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上,且满足(AF/FB)×(BD/DC)×(CE/EA)=1,则F、D、E三点共线。
关于平面几何的61条著名定理

关于平面几何的61条著名定理一些平面几何的著名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、三角形的三条高线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s,s为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形。
平面几何的基本概念和定理

平面几何的基本概念和定理1. 基本概念1.1 点平面几何的研究对象是由点、线、面组成的。
点是几何图形的基本元素,用来表示位置。
在平面几何中,点没有大小和形状,只有位置。
我们通常用大写字母来表示点,如A、B、C等。
1.2 直线直线是由无数个点连成的,它在平面内延伸无穷远。
我们通常用一个小写字母加上箭头表示直线,如直线AB、CD等。
直线上的点可以用小写字母表示,如点P、Q、R等。
1.3 射线射线是由一个起点开始,延伸到一个方向上的直线。
我们通常用一个小写字母加上箭头表示射线,如射线AB、CD等。
射线上的点可以用小写字母表示,如点P、Q、R等。
1.4 线段线段是由两个端点确定的直线部分,具有有限的长度。
我们通常用两个端点的大写字母表示线段,如线段AB、CD等。
1.5 平面平面是由无数个点组成的二维空间。
在平面几何中,我们通常用大写字母I表示平面,如平面ABCD等。
1.6 角角是由两条射线的公共端点和这两条射线的延伸部分组成的图形。
我们通常用一个小写字母表示角的顶点,如角A、B、C等。
角的度量单位是度(°),用符号°表示。
1.7 三角形三角形是由三条线段组成的平面图形,具有三个顶点和三个内角。
我们通常用三个顶点的大写字母表示三角形,如三角形ABC等。
1.8 四边形四边形是由四条线段组成的平面图形,具有四个顶点和四个内角。
我们通常用四个顶点的大写字母表示四边形,如四边形ABCD等。
1.9 圆圆是由平面上所有与给定点(圆心)距离相等的点组成的图形。
我们通常用圆心和半径的大写字母表示圆,如圆O(半径为r)。
2. 基本定理2.1 欧几里得几何公理欧几里得几何公理是平面几何的基础,包括以下五个公理:1.任意两点之间存在唯一的直线。
2.直线上的点可以按任意顺序排列。
3.任意两点确定一条直线。
4.直线上的点与直线外的点确定一条直线。
5.平面上任意一点到平面上任意一点的直线是唯一的。
2.2 平行线公理平行线公理是指:如果两条直线在平面内不相交,那么这两条直线是平行的。
平面与平面平行的判定定理的证明

平面与平面平行的判定定理的证明大家好,今天我们要聊的是平面与平面平行的判定定理。
别看它名字长,实际内容并不复杂。
让我们用简单的方式来搞懂它。
首先,我们得明白,两个平面平行是啥意思。
平行平面就像两块纸,始终在同一个方向上移动,但永远不会相交。
记住这一点,我们就能深入探讨它们是如何“默契”地保持平行的。
1. 定理概述1.1. 先来个大概念,平面与平面平行的判定定理说的就是如何判断两个平面是否平行。
这里有一个简单的规则:如果两个平面之间的距离始终相等,那么这两个平面就是平行的。
这就好比你拿着两张照片,用同样的距离在墙上挂起来,不管怎么摆,都不会有交点,它们就是平行的。
1.2. 再深入一点,我们可以用线来帮忙判断平面平行。
如果在一个平面上的一条直线和另一个平面上的一条直线分别与第三个平面平行,那么这两个平面也一定是平行的。
这就像你有两根同样长度的棍子,在地上竖起来,只要它们都跟地面平行,它们在任何角度下也会互相平行。
2. 定理证明2.1. 说到证明,那就得进入“牛刀小试”的阶段了。
我们先拿一张纸当平面A,再拿一张纸当平面B。
要证明这两个平面平行,我们可以用一个小技巧。
假设你有一个第三个平面C,把A、B分别跟C对比。
如果A上的任何一条直线都跟C平行,而B上的任何一条直线也跟C平行,那么根据定义,A和B就是平行的。
2.2. 更简单的方法是考虑两个平面之间的交线。
如果平面A和B分别与平面C相交,且交线平行,那么A和B之间的距离也就一直保持不变,这样它们就平行了。
这种情况下,想象一下两个书架,书架上的书总是保持在相同的高度,那么这两个书架一定是平行的。
用这种方式来理解平面之间的关系,就会觉得容易多了。
3. 实际应用3.1. 在现实中,平面平行的判定定理其实是非常实用的。
比如,在建筑工程中,设计师需要保证建筑物的墙壁是平行的,这样才能让房间看起来整洁而且空间感更好。
想象一下,如果墙壁不平行,那整个房间就像斜着的船舱,让人住进去真是“岂曰无衣”呀。
平面几何基本定理

定义:通过构造新的图形或对象来证明定理的方法 特点:直观、易于理解,能够将复杂问题转化为简单问题 应用:在平面几何中广泛应用于证明各种定理和性质 示例:通过构造辅助线来证明三角形的一些性质和定理
定义:通过代 数运算和逻辑 推理来证明平 面几何定理的
方法
特点:基于代 数方程和不等 式的推导,可 以证明一些较 为抽象和复杂
欧几里得几何定理 非欧几里得几何定理 解析几何定理 射影几何定理
计算机图形学:用于生成二 维图形和动画
物理学:用于描述物体运动 轨迹和力的作用
航空航天:用于设计和分析 飞行器的结构和性能
建筑学:用于设计和分析建 筑物的结构和稳定性
平行线性质: 平行线之间的
距离相等
角平分线性质: 角平分线将一 个角分为两个
计算机图形学中的应用:平面几何定理在计算机图形学中也有着重要的应用,例如在绘制二维图形、三维 模型等方面,需要利用平面几何定理进行计算和推导。
经济学中的应用:在经济学中,平面几何定理也被广泛应用,例如在分析市场供需关系、预测商品价格走 势等方面,需要利用平面几何定理进行数据分析和模型构建。
生物学中的应用:在生物学中,平面几何定理也被应用于一些领域,例如生态学中研究生物种群分 布、行为学中研究动物运动轨迹等方面,需要利用平面几何定理进行数据分析和模型构建。
的几何定理、三 角形的余弦定
理等
实例:通过代 数方法证明勾 股定理的过程
欧几里得几何定理:公元前300年左右,欧几里得在《几何原本》中提出了平面几何 的基本定理,奠定了平面几何的基础。
非欧几里得几何定理:19世纪,高斯、黎曼等数学家提出了非欧几里得几何,突破 了欧几里得几何的限制,进一步推广了平面几何定理。
定理在计算机图形学 中的应用:在制作动 画、游戏等计算机图 形学领域中,平面几 何定理被广泛应用。
直线平行平面的判定定理

直线平行平面的判定定理直线和平面是空间解析几何中的基本概念,它们的位置关系有着重要的几何性质。
在空间中,当一条直线与一个平面满足特定条件时,我们可以根据直线和平面的性质来判断它们是否平行。
本文将介绍直线平行平面的判定定理,以及相关的推导和应用。
一、在空间中,判定一条直线与一个平面是否平行,可以根据以下定理进行判断:定理1:如果直线上的任意一点到平面的距离为定值k,那么这条直线与这个平面平行。
证明:设直线L上任意一点为P(x,y,z),平面为α,平面上一点为Q(a,b,c)。
根据直线上任意一点到平面的距离公式,有:d(P, α) = |ax + by + cz + d| / √(a^2 + b^2 + c^2)其中,α的一般方程为ax + by + cz + d = 0。
因为直线L上的任意一点P(x,y,z)到平面α的距离为定值k,所以有:|ax + by + cz + d| / √(a^2 + b^2 + c^2) = k即:|ax + by + cz + d| = k√(a^2 + b^2 + c^2)根据绝对值的性质,得到:ax + by + cz + d = ± k√(a^2 + b^2 + c^2)由于k为定值,√(a^2 + b^2 + c^2)也为定值,因此左侧和右侧都是一个常数等式,表示一个平面β。
所以,直线L和平面β平行,即直线L与平面α平行。
经过推导和证明,我们得出了判定直线平行平面的定理,即直线与平面上的一点到平面的距离为定值,那么这条直线和这个平面是平行的。
二、直线平行平面的应用直线平行平面的判定定理在解决空间几何问题时具有重要的应用价值。
下面通过几个具体的例子来说明其应用。
例1:已知平面α的一般方程为2x - 3y + 4z - 5 = 0,直线L上的一点为P(1, 2, -1),求直线L与平面α的位置关系。
解:由直线平行平面的判定定理可知,如果点P到平面α的距离为定值,那么直线L与平面α平行。
初中平面几何--概念、定理、解析

初中几何概念、定理平面几何1.两点之间的所有连线中,线段最短。
2.两点之间线段的长度叫做这两点之间的距离。
3.经过两点有一条直线,并且只有一条直线。
4.将一个角分成相等的两部分的射线叫做这个角的角平分线。
5.如果两个角的和是一个直角,这两个角叫做互为余角。
简称互余,其中的一个角叫做另一个角的余角。
6.如果两个角的和是一个平角,这两个角叫做互为补角。
简称互补,其中的一个角叫做另一个角的补角。
7.同角(或等角)的余角相等。
8.同角(或等角)的补角相等。
9.对顶角相等。
10.在同一平面内,不相交的两条直线叫做平行线。
11.经过直线外一点,有且只有一条直线与已知直线平行。
12.如果两条直线都与第三条直线平行,那么这两条直线相互平行。
13.如果两条直线相交成直角,那么这两条直线互相垂直。
互相垂直的两条直线的交点叫做垂足。
14.当两条直线互相处置时,其中一条直线叫做另一条直线的垂线。
15.经过一点有且只有一条直线与已知直线垂直。
16.直线外一点到直线上各点连接的所有线段中,垂线段最短。
17.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
18.同位角相等,两直线平行。
19.内错角相等,两直线平行。
20.同旁内角互补,两直线平行。
21.两直线平行,同位角相等。
22.两直线平行,内错角相等。
23.两直线平行,同旁内角互补。
24.在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做图形的平移。
平移不改变图形的形状、大小。
25.如果两条直线互相平行,那么其中一条直线上任意两点到另一直线的距离相等,这个距离称为平行线之间的距离。
26.三角形的任意两边之和大于第三边。
27.在三角形中,从一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高。
28.在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
29.在三角形中链接一个顶点与它对边中点的线段,叫做三角形的中线。
平面几何的60条著名定理

平面几何的60条著名定理一些平面几何的著名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、三角形的三条高线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s,s为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD ×BC=AC×BD20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和△DEF都是正三角形,则由线段AD、BE、CF的中心构成的三角形也是正三角形。
平面几何的26个定理

高一数学竞赛班二试讲义第1讲 平面几何中的26个定理班级 姓名一、知识点金1. 梅涅劳斯定理:若直线l 不经过ABC ∆的顶点,并且与ABC ∆的三边,,BC CA AB 或它们的延长线分别交于,,P Q R ,则1BP CQ AR PC QA RB⋅⋅= 注:梅涅劳斯定理的逆定理也成立(用同一法证明)2. 塞瓦定理: 设,,P Q R 分别是ABC ∆的三边,,BC CA AB 或它们的延长线上的点,若,,AP BQ CR 三线共点,则1BP CQ AR PC QA RB⋅⋅= 注:塞瓦定理的逆定理也成立3. 托勒密定理:在四边形ABCD 中,有AB CD BC AD AC BD ⋅+⋅≥⋅,并且当且仅当四边形ABCD 内接于圆时,等式成立。
AB AE AC ADBC ED AC AD==⇒又4. 西姆松定理:若从ABC ∆外接圆上一点P 作,,BC AB CA 的垂线,垂足分别为,,D E F ,则,,D E F 三点共线。
西姆松定理的逆定理:从一点P 作,,BC AB CA 的垂线,垂足分别为,,D E F 。
若,,D E F 三点共线,则点P 在ABC ∆的外接圆上。
5. 蝴蝶定理:圆O 中的弦PQ 的中点M ,过点M 任作两弦AB ,CD ,弦AD 与BC 分别交PQ 于X ,Y ,则M 为XY 之中点。
证明:过圆心O 作AD 与BC 的垂线,垂足为S 、T ,,OY ,OM ,SM ,MT 。
∴AM/CM=AD/BC∵AS=1/2AD,BT=1/2BC ∴AM/CM=AS/CT又∵∠A=∠C ∴△AMS∽△CMT∴∠MSX=∠MTY∴∠OMX+∠OSX=180°∴O,S ,X ,M同理,O ,T ,∴∠MTY=∠MOY,∠MSX=∠MOX∴∠MOX=∠MOY , ∵OM⊥PQ ∴XM=YM注:把圆换成椭圆、抛物线、双曲线蝴蝶定理也成立6. 坎迪定理:设AB 是已知圆的弦,M 是AB 上一点,弦,CD EF 过点M ,连结,CF ED ,分别交AB 于,L N ,则1111LM MN AM MB-=-。
平面平行平面的判定定理

平面平行平面的判定定理平面平行平面的判定定理,听起来有点高大上,但其实它也没那么复杂,咱们可以轻松聊聊。
你想象一下,一个平面就像是一块大桌子,坐在上面的东西都是在这块平面上。
平行呢,就是说有两个这样的桌子,它们永远不会碰到一起,哪怕你再怎么挪动它们。
这就很有意思了,生活中有很多事情都像这样,比如说你和朋友一起排队,大家站得整整齐齐,虽然你们在不同的平面上,但依旧不妨碍彼此。
如何判定这两个平面是不是平行呢?简单来说,就是得看它们的角度。
想象一下,如果你把两块桌子放在同一个房间,它们的高度差不多,但一个偏左一个偏右,嘿,它们就是平行的。
这就像咱们生活中的一些好朋友,虽然性格不同,但始终保持着一种默契,永远不会走到一起。
这种感觉,真的很奇妙,不是吗?就像是两条永不相交的路,永远朝着同一个方向走去。
在几何的世界里,有个重要的概念叫做“法线”。
法线就像是平面上的一根铅笔竖着放着,直直的指向天空。
要是有两个平面,它们的法线也平行,那么这两个平面绝对也是平行的。
这就有点像是你和你的室友,虽然各自的生活方式大相径庭,但你们的价值观却不谋而合,彼此的关系自然就稳稳的。
生活中有时候就是这样,许多看似复杂的事情,其实都能用一种简单的方式去理解。
假如你碰到两个平面,想要判断它们是否平行,你首先可以看看它们的法线。
如果它们的法线方向一致,那就基本可以认定这两个平面是平行的了,没错,这就像是看一个人的眼神。
如果眼神闪烁,肯定有猫腻,但如果目光坚定,那就可以放心了。
这种直观的判断法,在生活中也常常适用,别再被那些复杂的公式给搞晕了,平常心,简单点,就能看得更清楚。
还有一种情况,如果有一条直线与这两个平面都相交,那么这条线就会在两个平面上形成两个角。
这两个角如果相等,那么这两个平面也是平行的。
这就好比说你和好朋友一起打麻将,虽然你们的手牌不一样,但打出来的点数如果相同,那你们就是心有灵犀。
这种时候,大家就能心照不宣,一拍即合,这就是生活的乐趣所在。
平面解析几何的基本概念与定理总结

平面解析几何的基本概念与定理总结平面解析几何是几何学和分析学的结合,研究平面中点、线、圆等几何图形的性质和相互关系。
本文将总结平面解析几何中的基本概念与定理。
一、基本概念1. 点:平面上的一个位置,用大写字母表示,如点A、点B等。
2. 坐标系:平面上的一个坐标系由两个相互垂直的坐标轴组成,分别是x轴和y轴。
3. 坐标:用有序实数对(x, y)表示平面上的点,x为横坐标,y为纵坐标。
如点A的坐标为(x1, y1)。
4. 距离公式:平面上两点A(x1, y1)和B(x2, y2)之间的距离d可以通过以下公式计算:d = √((x2 - x1)² + (y2 - y1)²)5. 中点公式:平面上两点A(x1, y1)和B(x2, y2)的中点M的坐标可以通过以下公式计算:M = ((x1 + x2)/2, (y1 + y2)/2)二、基本定理1. 距离定理:平面上两点A(x1, y1)和B(x2, y2)之间的距离d满足以下性质:a) d ≥ 0b) d = 0 当且仅当A和B重合c) d = d(B, A) (对称性)d) d(A, B) + d(B, C) ≥ d(A, C) (三角不等式)2. 斜率概念:直线L通过两点A(x1, y1)和B(x2, y2),其斜率k可以通过以下公式计算:k = (y2 - y1)/(x2 - x1)3. 直线的方程:直线L的方程可以通过以下形式表示:a) 一般式:Ax + By + C = 0(A、B和C为实数)b) 斜截式:y = kx + b(k为斜率,b为截距)4. 两直线关系定理:设直线L1和L2的方程分别为:L1: A1x + B1y + C1 = 0L2: A2x + B2y + C2 = 0则L1与L2的关系可以通过以下性质判断:a) L1与L2平行:A1/A2 = B1/B2 ≠ C1/C2b) L1与L2垂直:A1A2 + B1B2 = 0c) L1与L2重合:A1/A2 = B1/B2 = C1/C25. 圆的方程:圆C的方程可以通过以下形式表示:(x - h)² + (y - k)² = r²其中(h, k)为圆心的坐标,r为半径。
认识平面几何的61个著名定理

【认识平面几何的61个著名定理,自行画出图形来学习,★部分要求证明出来】★1、勾股定理(毕达哥拉斯定理)★2、射影定理(欧几里得定理)★3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线和两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
★6、三角形各边的垂直平分线交于一点。
★7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC 的外心为O ,垂心为H ,从O 向BC 边引垂线,设垂足不L ,则AH=2OL9、三角形的外心,垂心,重心在同一条直线上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇大上定理:(圆内接四边形的九点圆) 圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
★13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式: ()()()s c s b s a s r ---=,s 为三角形周长的一半★14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC分成m和n两段,则有n×AB2+m×AC2=BC×(AP2+mn)17、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E 的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上★19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD★20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和△DEF都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
关于平面几何的60条著名定理

关于平面几何的60条著名定理 一些平面几何的著名定理1、勾股定理〔毕达哥拉斯定理〕2、射影定理〔欧几里得定理〕3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、三角形的三条高线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,那么AH=2OL9、三角形的外心,垂心,重心在同一条直线〔欧拉线〕上。
10、〔九点圆或欧拉圆或费尔巴赫圆〕三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线〔欧拉线〕上12、库立奇*大上定理:〔圆内接四边形的九点圆〕圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、〔内心〕三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s,s为三角形周长的一半14、〔旁心〕三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:〔巴布斯定理〕设三角形ABC的边BC的中点为P,那么有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,那么有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n〔值不为1〕的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,那么有AB×CD+AD×BC=AC×BD20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,那么△DEF是正三角形,21、爱尔可斯定理1:假设△ABC和△DEF都是正三角形,那么由线段AD、BE、CF的中心构成的三角形也是正三角形。
关于平面几何的60条著名定理

关于平面几何的60条著名定理关于平面几何的 60 条著名定理些平面几何的著名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1 的两部分4、四边形两边中心的连线的两条对角线中心的连线交于5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、三角形的三条高线交于一点&设三角形ABC的外心为0,垂心为H 从0向BC边引垂线,设垂足为L,则AH=20L9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s , s 为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点中线定理:(巴布斯定理)设三角形ABC的边BC的中点15、为P,则有AB2+AC2=2(AP2+BP2) 16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,贝U有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD勺对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B 的距离之比为定比m:n (值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD 20、以任意三角形ABC 的边BC CA AB为底边,分别向外作底角都是30度的等腰^ BDC △CEA △ AFB则^ DEF是正三角形,21、爱尔可斯定理1:若^ ABC和^ DEF都是正三角形,则由线段AD BE、CF的中心构成的三角形也是正三角形。
平面几何基本定理

一.平面几何1. 勾股定理(毕达哥拉斯定理)(广义勾股定理)(1)锐角对边的平方,等于其他两边之平方和,减去这两边中的一边和另一边在这边上的射影乘积的两倍. (2)钝角对边的平方等于其他两边的平方和,加上这两边中的一边与另一边在这边上的射影乘积的两倍. 2. 射影定理(欧几里得定理)3. 中线定理(巴布斯定理)设△ABC 的边BC 的中点为P ,则有)(22222BP AP AC AB +=+;中线长:222222a c b m a -+=4. 垂线定理:2222BD BC AD AC CD AB -=-⇔⊥高线长:C b B c A abcc p b p a p p a h a sin sin sin ))()((2===---=5. 角平分线定理:三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例.如△ABC 中,AD 平分∠BAC ,则AC AB DC BD =;(外角平分线定理)角平分线长:2cos 2)(2Ac b bc a p bcp c b t a +=-+=(其中p 为周长一半)6. 正弦定理:R CcB b A a 2sin sin sin ===,(其中R 为三角形外接圆半径) 7. 余弦定理:C ab b a ccos 2222-+=8. 角定理:ABDAC AC BAD AD BAC ∠+∠=∠sin sin sin9. 斯特瓦尔特(Stewart )定理:设已知△ABC 及其底边上B 、C两点间的一点D ,则有AB 2·DC +AC 2·BD -AD 2·BC =BC ·DC ·BD10. 圆周角定理:同弧所对的圆周角相等,等于圆心角的一半.(圆外角如何转化?)11. 弦切角定理:弦切角等于夹弧所对的圆周角12. 圆幂定理:(相交弦定理:垂径定理:切割线定理(割线定理):切线长定理:)13. 布拉美古塔(Brahmagupta )定理: 在圆接四边形ABCD中,AC ⊥BD ,自对角线的交点P 向一边作垂线,其延长线必平分对边14. 点到圆的幂:设P 为⊙O 所在平面上任意一点,PO =d ,⊙O的半径为r ,则d 2-r 2就是点P 对于⊙O 的幂.过P 任作一直线与⊙O 交于点A 、B ,则PA·PB = |d 2-r 2|.“到两圆等幂的点的轨迹是与此二圆的连心线垂直的一条直线,如果此二圆相交,则该轨迹是此二圆的公共弦所在直线”这个结论.这条直线称为两圆的“根轴”.三个圆两两的根轴如果不互相平行,则它们交于一点,这一点称为三圆的“根心”.三个圆的根心对于三个圆等幂.当三个圆两两相交时,三条公共弦(就是两两的根轴)所在直线交于一点.15. 托勒密(Ptolemy )定理:圆接四边形对角线之积等于两组对边乘积之和,即AC ·BD =AB ·CD +AD ·BC ,(逆命题成立) .(广义托勒密定理)AB ·CD +AD ·BC ≥AC ·BD16. 蝴蝶定理:AB 是⊙O 的弦,M 是其中点,弦CD 、EF 经过点M ,CF 、DE 交AB 于P 、Q ,求证:MP =QM .17. 费马点:定理1等边三角形外接圆上一点,到该三角形较近两顶点距离之和等于到另一顶点的距离;不在等边三角形外接圆上的点,到该三角形两顶点距离之和大于到另一点的距离.定理2 三角形每一角都小于120°时,在三角形必存在一点,它对三条边所的角都是120°,该点到三顶点距离和达到最小,称为“费马点”,当三角形有一角不小于120°时,此角的顶点即为费马点18. 拿破仑三角形:在任意△ABC 的外侧,分别作等边△ABD 、△BCE 、△CAF ,则AE 、AB 、CD 三线共点,并且AE =BF =CD ,这个命题称为拿破仑定理. 以△ABC 的三条边分别向外作等边△ABD 、△BCE 、△CAF ,它们的外接圆⊙C 1 、⊙A 1 、⊙B 1的圆心构成的△——外拿破仑的三角形,⊙C 1 、⊙A 1 、⊙B 1三圆共点,外拿破仑三角形是一个等边三角形;△ABC 的三条边分别向△ABC 的侧作等边△ABD 、△BCE 、△CAF ,它们的外接圆⊙C 2 、⊙A 2 、⊙B 2的圆心构成的△——拿破仑三角形,⊙C 2 、⊙A 2 、⊙B 2三圆共点,拿破仑三角形也是一个等边三角形.这两个拿破仑三角形还具有相同的中心19. 九点圆(Nine point round 或欧拉圆或费尔巴赫圆):三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,九点圆具有许多有趣的性质,例如:(1)三角形的九点圆的半径是三角形的外接圆半径之半 (2)九点圆的圆心在欧拉线上,且恰为垂心与外心连线的中点(3)三角形的九点圆与三角形的切圆,三个旁切圆均相切〔费尔巴哈定理〕20. 欧拉(Euler )线:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上.21. 欧拉(Euler )公式:设三角形的外接圆半径为R ,切圆半径为r ,外心与心的距离为d ,则d 2=R 2-2Rr .22. 锐角三角形的外接圆半径与切圆半径的和等于外心到各边距离的和.23. 重心:三角形的三条中线交于一点,并且各中线被这个点分成2:1的两部分;)3,3(C B A C B A y y y x x x G ++++重心性质:(1)设G 为△ABC 的重心,连结AG 并延长交BC 于D ,则D 为BC 的中点,则1:2:=GD AG ;(2)设G为△ABC的重心,则ABC ACG BCG ABG S S S S ∆∆∆∆===31(3)设G 为△ABC 的重心,过G 作DE ∥BC 交AB 于D ,交AC 于E ,过G 作PF ∥AC 交AB 于P ,交BC 于F ,过G 作HK ∥AB 交AC 于K ,交BC 于H ,则2;32=++===ABKHCA FP BC DE AB KH CA FP BC DE (4)设G 为△ABC 的重心,则222222333GC AB GB CA GA BC +=+=+)(31222222CA BC AB GC GB GA ++=++22222223PG GC GB GA PC PB PA +++=++(P 为△ABC 任意一点);④到三角形三顶点距离的平方和最小的点是重心,即222GC GB GA ++最小;⑤三角形到三边距离之积最大的点是重心;反之亦然(即满足上述条件之一,则G 为△ABC 的重心).24. 垂心:三角形的三条高线的交点;)cos cos cos cos cos cos ,cos cos cos cos cos cos (Cc B b A a y C c y B b y A a C c B b A a x C c x B b x A a H CB AC B A ++++++++垂心性质:(1)三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍(2)垂心H 关于△ABC 的三边的对称点,均在△ABC 的外接圆上;(3)△ABC 的垂心为H ,则△ABC ,△ABH ,△BCH ,△ACH 的外接圆是等圆;(4)设O ,H 分别为△ABC 的外心和垂心,HCA BCO ABH CBO HAC BAO ∠=∠∠=∠∠=∠,,25. 心:三角形的三条角分线的交点—接圆圆心,即心到三角形各边距离相等),(cb a cy by ayc b a cx bx ax I CB AC B A ++++++++心性质:(1)设I 为△ABC 的心,则I 到△ABC 三边的距离相等,反之亦然 (2)设I为△ABC的心,则C AIB B AIC A BIC ∠+︒=∠∠+︒=∠∠+︒=∠2190,2190,2190(3)三角形一角平分线与其外接圆的交点到另两顶点的距离与到心的距离相等;反之,若A ∠平分线交△ABC 外接圆于点K ,I 为线段AK 上的点且满足KI=KB ,则I 为△ABC 的心(4)设I 为△ABC 的心,,,,c AB b AC a BC ===A∠平分线交BC 于D ,交△ABC 外接圆于点K ,则acb KD IK KI AK ID AI +=== (5)设I 为△ABC 的心,,,,c AB b AC a BC ===I 在AB AC BC ,,上的射影分别为F E D ,,,切圆半径为r ,令)(21c b a p ++=①pr S ABC =∆;②c p CD CE b p BF BD a p AF AE -==-==-==;;;③CI BI AI p abcr ⋅⋅⋅=.26. 外心:三角形的三条中垂线的交点——外接圆圆心,即外心到三角形各顶点距离相等;2sin 2sin 2sin 2sin ,2sin 2sin 2sin 2sin 2sin 2sin (B A By AyC B A Cx Bx Ax O BA CB A +++++++外心性质:(1)外心到三角形各顶点距离相等(2)设O 为△ABC 的外心,则A BOC ∠=∠2或A BOC ∠-︒=∠2360(3)∆=S abc R 4;(4)锐角三角形的外心到三边的距离之和等于其切圆与外接圆半径之和27. 旁心:一角平分线与两外角平分线交点——旁切圆圆心;设△ABC 的三边,,,c AB b AC a BC ===令)(21c b a p ++=,分别与AB AC BC ,,外侧相切的旁切圆圆心记为C B A I I I ,,,其半径分别记为C B A r r r ,,旁心性质:(1),21,2190A C BI C BI A C BI C B A ∠=∠=∠∠-︒=∠(对于顶角B ,C 也有类似的式子) (2))(21C A I I I C B A ∠+∠=∠ (3)设A AI 的连线交△ABC 的外接圆于D ,则DC DB DI A ==(对于C B CI BI ,有同样的结论)(4)△ABC 是△I A I B I C 的垂足三角形,且△I A I B I C 的外接圆半径'R 等于△ABC 的直径为2R . 28. 三角形面积公式C B A R Rabc C ab ah S a ABC sin sin sin 24sin 21212====∆)cot cot (cot 4222C B A c b a ++++=))()((c p b p a p p pr ---==,其中a h 表示BC 边上的高,R 为外接圆半径,r 为切圆半径,)(21c b a p ++=29. 三角形中切圆,旁切圆和外接圆半径的相互关系;2sin 2cos 2cos 4,2cos 2sin 2cos 4,2cos 2cos 2sin 4;2sin 2sin 2sin4CB A R rC B A R r C B A R r C B A R r c b a ====.1111;2tan2tan ,2tan 2tan ,2tan 2tan r r r r B A r r C A r r C B r r c b a c b a =++===30. 梅涅劳斯(Menelaus )定理:设△ABC 的三边BC 、CA 、AB或其延长线和一条不经过它们任一顶点的直线的交点分别为P 、Q 、R 则有1=⋅⋅RBARQA CQ PC BP .(逆定理也成立) 31. 梅涅劳斯定理的应用定理1:设△ABC 的∠A 的外角平分线交边CA 于Q ,∠C 的平分线交边AB 于R ,∠B 的平分线交边CA 于Q ,则P 、Q 、R 三点共线32. 梅涅劳斯定理的应用定理2:过任意△ABC 的三个顶点A 、B 、C 作它的外接圆的切线,分别和BC 、CA 、AB 的延长线交于点P 、Q 、R ,则P 、Q 、R 三点共线33. 塞瓦(Ceva )定理:设X 、Y 、Z 分别为△ABC 的边BC 、CA 、AB 上的一点,则AX 、BY 、CZ 所在直线交于一点的充要条件是AZ ZB ·BX XC ·CY Y A=1 34. 塞瓦定理的应用定理:设平行于△ABC 的边BC 的直线与两边AB 、AC 的交点分别是D 、E ,又设BE 和CD 交于S ,则AS 一定过边BC 的中点M 35. 塞瓦定理的逆定理:(略)36. 塞瓦定理的逆定理的应用定理1:三角形的三条中线交于一点,三角形的三条高线交于一点,三角形的三条角分线交于一点37. 塞瓦定理的逆定理的应用定理2:设△ABC 的切圆和边BC 、CA 、AB 分别相切于点R 、S 、T ,则AR 、BS 、CT 交于一点. 38. 西摩松(Simson )定理:从△ABC 的外接圆上任意一点P向三边BC 、CA 、AB 或其延长线作垂线,设其垂足分别是D 、E 、R ,则D 、E 、R 共线,(这条直线叫西摩松线Simson line ) 39. 西摩松定理的逆定理:(略)40. 关于西摩松线的定理1:△ABC 的外接圆的两个端点P 、Q关于该三角形的西摩松线互相垂直,其交点在九点圆上 41. 关于西摩松线的定理2(安宁定理):在一个圆周上有4点,以其中任三点作三角形,再作其余一点的关于该三角形的西摩松线,这些西摩松线交于一点42. 史坦纳定理:设△ABC 的垂心为H ,其外接圆的任意点P ,这时关于△ABC 的点P 的西摩松线通过线段PH 的中心. 43. 史坦纳定理的应用定理:△ABC 的外接圆上的一点P 的关于边BC 、CA 、AB 的对称点和△ABC 的垂心H 同在一条(与西摩松线平行的)直线上.这条直线被叫做点P 关于△ABC 的镜象线.44. 牛顿定理1:四边形两条对边的延长线的交点所连线段的中点和两条对角线的中点,三点共线.这条直线叫做这个四边形的牛顿线. 45. 牛顿定理2:圆外切四边形的两条对角线的中点,及该圆的圆心,三点共线. 46. 笛沙格定理1:平面上有两个三角形△ABC 、△DEF ,设它们的对应顶点(A 和D 、B 和E 、C 和F )的连线交于一点,这时如果对应边或其延长线相交,则这三个交点共线. 47. 笛沙格定理2:相异平面上有两个三角形△ABC 、△DEF ,设它们的对应顶点(A 和D 、B 和E 、C 和F )的连线交于一点,这时如果对应边或其延长线相交,则这三个交点共线. 48. 波朗杰、腾下定理:设△ABC 的外接圆上的三点为P 、Q 、R ,则P 、Q 、R 关于△ABC 交于一点的充要条件是:弧AP +弧BQ +弧CR =0(mod2π) .49. 波朗杰、腾下定理推论1:设P 、Q 、R 为△ABC 的外接圆上的三点,若P 、Q 、R 关于△ABC 的西摩松线交于一点,则A 、B 、C 三点关于△PQR 的的西摩松线交于与前相同的一点. 50. 波朗杰、腾下定理推论2:在推论1中,三条西摩松线的交点是A 、B 、C 、P 、Q 、R 六点任取三点所作的三角形的垂心和其余三点所作的三角形的垂心的连线段的中点. 51. 波朗杰、腾下定理推论3:考查△ABC 的外接圆上的一点P的关于△ABC 的西摩松线,如设QR 为垂直于这条西摩松线该外接圆的弦,则三点P 、Q 、R 的关于△ABC 的西摩松线交于一点.52. 波朗杰、腾下定理推论4:从△ABC 的顶点向边BC 、CA 、AB 引垂线,设垂足分别是D 、E 、F ,且设边BC 、CA 、AB 的中点分别是L 、M 、N ,则D 、E 、F 、L 、M 、N 六点在同一个圆上,这时L 、M 、N 点关于关于△ABC 的西摩松线交于一点 53. 卡诺定理:通过△ABC 的外接圆的一点P ,引与△ABC 的三边BC 、CA 、AB 分别成同向的等角的直线PD 、PE 、PF ,与三边的交点分别是D 、E 、F ,则D 、E 、F 三点共线. 54. 奥倍尔定理:通过△ABC 的三个顶点引互相平行的三条直线,设它们与△ABC 的外接圆的交点分别是L 、M 、N ,在△ABC 的外接圆上取一点P ,则PL 、PM 、PN 与△ABC 的三边BC 、CA 、AB 或其延长线的交点分别是D 、E 、F ,则D 、E 、F 三点共线.55. 清宫定理:设P 、Q 为△ABC 的外接圆的异于A 、B 、C 的两点,P 点的关于三边BC 、CA 、AB 的对称点分别是U 、V 、W ,这时,QU 、QV 、QW 和边BC 、CA 、AB 或其延长线的交点分别是D 、E 、F ,则D 、E 、F 三点共线.56. 他拿定理:设P 、Q 为关于△ABC 的外接圆的一对反点,点P 的关于三边BC 、CA 、AB 的对称点分别是U 、V 、W ,这时,如果QU 、QV 、QW 和边BC 、CA 、AB 或其延长线的交点分别是D 、E 、F ,则D 、E 、F 三点共线.(反点:P 、Q 分别为圆O 的半径OC 和其延长线的两点,如果OC 2=OQ ×OP 则称P 、Q 两点关于圆O 互为反点)57. 朗古来定理:在同一圆周上有A 1、B 1、C 1、D 1四点,以其中任三点作三角形,在圆周取一点P ,作P 点的关于这4个三角形的西摩松线,再从P 向这4条西摩松线引垂线,则四个垂足在同一条直线上.58. 从三角形各边的中点,向这条边所对的顶点处的外接圆的切线引垂线,这些垂线交于该三角形的九点圆的圆心 59. 一个圆周上有n 个点,从其中任意n -1个点的重心,向该圆周的在其余一点处的切线所引的垂线都交于一点 60. 康托尔定理1:一个圆周上有n 个点,从其中任意n -2个点的重心向余下两点的连线所引的垂线共点.61. 康托尔定理2:一个圆周上有A 、B 、C 、D 四点及M 、N 两点,则M 和N 点关于四个三角形△BCD 、△CDA 、△DAB 、△ABC 中的每一个的两条西摩松线的交点在同一直线上.这条直线叫做M 、N 两点关于四边形ABCD 的康托尔线. 62. 康托尔定理3:一个圆周上有A 、B 、C 、D 四点及M 、N 、L三点,则M 、N 两点的关于四边形ABCD 的康托尔线、L 、N 两点的关于四边形ABCD 的康托尔线、M 、L 两点的关于四边形ABCD 的康托尔线交于一点.这个点叫做M 、N 、L 三点关于四边形ABCD 的康托尔点.63. 康托尔定理4:一个圆周上有A 、B 、C 、D 、E 五点及M 、N 、L 三点,则M 、N 、L 三点关于四边形BCDE 、CDEA 、DEAB 、EABC 中的每一个康托尔点在一条直线上.这条直线叫做M 、N 、L 三点关于五边形A 、B 、C 、D 、E 的康托尔线. 64. 费尔巴赫定理:三角形的九点圆与切圆和旁切圆相切. 65. 莫利定理:将三角形的三个角三等分,靠近某边的两条三分角线相得到一个交点,则这样的三个交点可以构成一个正三角形.这个三角形常被称作莫利正三角形.66. 布利安松定理:连结外切于圆的六边形ABCDEF 相对的顶点A 和D 、B 和E 、C 和F ,则这三线共点.67. 帕斯卡(Paskal )定理:圆接六边形ABCDEF 相对的边AB和DE 、BC 和EF 、CD 和FA 的(或延长线的)交点共线. 68. 阿波罗尼斯(Apollonius )定理:到两定点A 、B 的距离之比为定比m :n (值不为1)的点P ,位于将线段AB 分成m :n 的分点C 和外分点D 为直径两端点的定圆周上.这个圆称为阿波罗尼斯圆.69. 库立奇*大上定理:(圆接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆接四边形的九点圆.70. 密格尔(Miquel )点: 若AE 、AF 、ED 、FB 四条直线相交于A 、B 、C 、D 、E 、F 六点,构成四个三角形,它们是△ABF 、△AED 、△BCE 、△DCF ,则这四个三角形的外接圆共点,这个点称为密格尔点.71. 尔刚(Gergonne )点:△ABC 的切圆分别切边AB 、BC 、CA于点D 、E 、F ,则AE 、BF 、CD 三线共点,这个点称为尔刚点.72. 欧拉关于垂足三角形的面积公式:O 是三角形的外心,M 是三角形中的任意一点,过M 向三边作垂线,三个垂足形成的三角形的面积,其公式: 222ABC D 4||R d R S S EF -=∆∆.二.集合1.元素与集合的关系U x A x C A ∈⇔∉,U x C A x A ∈⇔∉.2.德摩根公式();()U U U U U U C A B C A C B C A B C A C B==3.包含关系A B A A B B=⇔=U U A B C B C A ⇔⊆⇔⊆U A C B ⇔=ΦU C A B R ⇔=4.集合12{,,,}n a a a 的子集个数共有2n 个;真子集有2n –1个;非空子集有2n–1个;非空的真子集有2n–2个.5.集合A 中有M 个元素,集合B 中有N 个元素,则可以构造M*N 个从集合A 到集合B 的映射;6.容斥原理()()card A B cardA cardB card A B =+-()()card A B C cardA cardB cardC card A B =++-()()()()card A B card B C card CA card ABC ---+.三.二次函数,二次方程 1·二次函数的解析式的三种形式(1)一般式2()(0)f x ax bx c a =++≠;(2)顶点式2()()(0)f x a x h k a =-+≠;(3)零点式12()()()(0)f x a x x x x a =--≠. 2·解连不等式()N f x M <<常有以下转化形式()N f x M <<⇔[()][()]0f x M f x N --<⇔|()|22M N M Nf x +--<⇔()0()f x N M f x ->- ⇔11()f x N M N>--. 3·方程0)(=x f 在),(21k k 上有且只有一个实根,与0)()(21<k f k f 不等价,前者是后者的一个必要而不是充分条件.特别地, 方程)0(02≠=++a c bx ax 有且只有一个实根.在),(21k k ,等价于0)()(21<k f k f ,或0)(1=k f 且22211k k a bk +<-<,或0)(2=k f 且22122k abk k <-<+. 4·闭区间上的二次函数的最值 二次函数)0()(2≠++=a c bx ax x f 在闭区间[]q p ,上的最值只能在abx 2-=处及区间的两端点处取得,具体如下:(1)当a>0时,若[]q p abx ,2∈-=,则{}min max max ()(),()(),()2bf x f f x f p f q a =-=;[]q p abx ,2∉-=,{}max max ()(),()f x f p f q =,{}min min ()(),()f x f p f q =.(2)当a<0时,若[]q p abx ,2∈-=,则{}min ()min (),()f x f p f q =,若[]q p abx ,2∉-=,则{}max ()max (),()f x f p f q =,{}min ()min (),()f x f p f q =.5·一元二次方程的实根分布依据:若()()0f m f n <,则方程0)(=x f 在区间(,)m n 至少有一个实根 .设q px x x f ++=2)(,则(1)方程0)(=x f 在区间),(+∞m 有根的充要条件为0)(=m f 或2402p q pm ⎧-≥⎪⎨->⎪⎩; (2)方程0)(=x f 在区间(,)m n 有根的充要条件为()()0f m f n <或2()0()0402f m f n p q p m n>⎧⎪>⎪⎪⎨-≥⎪⎪<-<⎪⎩或()0()0f m af n =⎧⎨>⎩或()0()0f n af m =⎧⎨>⎩; (3)方程0)(=x f 在区间(,)n -∞有根的充要条件为()0f m <或2402p q p m ⎧-≥⎪⎨-<⎪⎩ .6·定区间上含参数的二次不等式恒成立的条件依据(1)在给定区间),(+∞-∞的子区间L (形如[]βα,,(]β,∞-,[)+∞,α不同)上含参数的二次不等式(,)0f x t ≥(t 为参数)恒成立的充要条件是min (,)0()f x t x L ≥∉.(2)在给定区间),(+∞-∞的子区间上含参数的二次不等式(,)0f x t ≥(t 为参数)恒成立的充要条件是(,)0()man f x t x L ≤∉.(3))(24>++=c bx ax x f 恒成立的充要条件是00a b c ≥⎧⎪≥⎨⎪>⎩或2040a b ac <⎧⎨-<⎩.四.简易逻辑1·真值表234·充要条件(1)充分条件:若p q ⇒,则p 是q 充分条件.(2)必要条件:若q p ⇒,则p 是q 必要条件.(3)充要条件:若p q ⇒,且q p ⇒,则p 是q 充要条件.注:如果甲是乙的充分条件,则乙是甲的必要条件;反之亦然.五.函数1· 函数的单调性(1)设[]2121,,x x b a x x ≠∈⋅那么[]1212()()()0x x f x f x -->⇔[]b a x f x x x f x f ,)(0)()(2121在⇔>--上是增函数;[]1212()()()0x x f x f x --<⇔[]b a x f x x x f x f ,)(0)()(2121在⇔<--上是减函数.(2)设函数)(x f y =在某个区间可导,如果0)(>'x f ,则)(x f 为增函数;如果0)(<'x f ,则)(x f 为减函数.2·如果函数)(x f 和)(x g 都是减函数,则在公共定义域,和函数)()(x g x f +也是减函数; 如果函数)(u f y =和)(x g u =在其对应的定义域上都是减函数,则复合函数)]([x g f y =是增函数.3·奇偶函数的图象特征奇函数的图象关于原点对称,偶函数的图象关于y 轴对称;在对称区间上,奇函数的单调性相同,欧函数相反;,如果一个函数的图象关于原点对称,那么这个函数是奇函数;如果一个函数的图象关于y 轴对称,那么这个函数是偶函数,如果一个奇函数的定义域包括0,则必有f(0)=0;4若函数)(x f y =是偶函数,则)()(a x f a x f --=+;若函数)(a x f y +=是偶函数,则)()(a x f a x f +-=+. 5· 对于函数)(x f y =(R x ∈),)()(x b f a x f -=+恒成立,则函数)(x f 的对称轴是函数2ba x +=;两个函数)(a x f y +=与)(x b f y -= 的图象关于直线2ba x +=对称. 6·若)()(a x f x f +--=,则函数)(x f y =的图象关于点)0,2(a对称; 若)()(a x f x f +-=,则函数)(x f y =为周期为a 2的周期函数.7 多项式函数110()n n n n P x a x a xa --=+++的奇偶性 多项式函数()P x 是奇函数⇔()P x 的偶次项(即奇数项)的系数全为零.多项式函数()P x 是偶函数⇔()P x 的奇次项(即偶数项)的系数全为零. 8函数()y f x =的图象的对称性 (1)函数()y f x =的图象关于直线x a=对称()()f a x f a x ⇔+=- (2)()f a x f x ⇔-=.(2)函数()y f x =的图象关于直线2a b x +=对称()()f a mx f b mx ⇔+=-()()f a b mx f mx ⇔+-=.9两个函数图象的对称性 (1)函数()y f x =与函数()y f x =-的图象关于直线0x =(即y 轴)对称.(2)函数()y f mx a =-与函数()y f b mx =-的图象关于直线2a bx m+=对称.(3)函数)(x f y =和)(1x f y -=的图象关于直线y=x 对称.10 若将函数)(x f y =的图象右移a 、上移b 个单位,得到函数b a x f y +-=)(的图象;若将曲线0),(=y x f 的图象右移a 、上移b 个单位,得到曲线0),(=--b y a x f 的图象.11 互为反函数的两个函数的关系a b f b a f =⇔=-)()(1.12若函数)(b kx f y +=存在反函数,则其反函数为])([11b x f ky -=-,并不是)([1b kx f y +=-,而函数)([1b kx f y +=-是])([1b x f ky -=的反函数.13 几个常见的函数方程 (1)正比例函数()f x cx =,()()(),(1)f x y f x f y f c +=+=. (2)指数函数()x f x a =,()()(),(1)0f x y f x f y f a +==≠. (3)对数函数()log a f x x =,()()(),()1(0,1)f xy f x f y f a a a =+=>≠.(4)幂函数()f x x α=,'()()(),(1)f xy f x f y f α==. (5)余弦函数()cos f x x =,正弦函数()sin g x x =,()()()()()f x y f x f y g x g y -=+,0()(0)1,lim 1x g x f x→==.14 几个函数方程的周期(约定a>0)(1))()(a x f x f +=,则)(x f 的周期T=a ; (2)0)()(=+=a x f x f ,或)0)(()(1)(≠=+x f x f a x f ,或1()()f x a f x +=-(()0)f x ≠,或[]1(),(()0,1)2f x a f x =+∈,则)(x f 的周期T=2a ;(3))0)(()(11)(≠+-=x f a x f x f ,则)(x f 的周期T=3a ;(4))()(1)()()(212121x f x f x f x f x x f -+=+且1212()1(()()1,0||2)f a f x f x x x a =⋅≠<-<,则)(x f 的周期T=4a ;(5)()()(2)(3)(4)f x f x a f x a f x a f x a +++++++()()(2)(3)(4)f x f x a f x a f x a f x a =++++,则)(x f 的周期T=5a ; (6))()()(a x f x f a x f +-=+,则)(x f 的周期T=6a.六 指数与对数1·分数指数幂(1)m na=(0,,a m n N*>∈,且1n >).(2)1m nm naa-=(0,,am n N *>∈,且1n >).2·根式的性质(1)n a =.(2)当na =;当n,0||,0a a a a a ≥⎧==⎨-<⎩.3·有理指数幂的运算性质(1) (0,,)r s r s a a a a r s Q +⋅=>∈.(2)()(0,,)r s rs a a a r s Q =>∈.(3)()(0,0,)rr r ab a b a b r Q =>>∈.注: 若a >0,p 是一个无理数,则a p 表示一个确定的实数.上述有理指数幂的运算性质,对于无理数指数幂都适用. 4·指数式与对数式的互化式log b a N b a N =⇔=(0,1,0)a a N >≠>.5·对数的换底公式log log log m a m N N a=(0a >,且1a ≠,0m >,且1m ≠,0N >).推论 log log m na anb b m=(0a >,且1a >,,0m n >,且1m ≠,1n ≠, 0N >).6·对数的四则运算法则若a >0,a ≠1,M >0,N >0,则(1)log ()log log a a a MN M N=+;(2)log log log a a a M M N N=-;(3)log log ()na a M n M n R =∈.7·设函数)0)((log )(2≠++=a c bx ax x f m ,记ac b 42-=∆.若)(x f 的定义域为R ,则0>a ,且0<∆;若)(x f 的值域为R ,则0>a ,且0≥∆.对于0=a 的情形,需要单独检验.8·对数换底不等式及其推广若0a>,0b >,0x >,1x a ≠,则函数log ()ax y bx = (1)当a b >时,在1(0,)a 和1(,)a+∞上log ()ax y bx =为增函数.,(2)当a b <时,在1(0,)a 和1(,)a +∞上log ()ax y bx =为减函数.推论:设1n m >>,0p >,0a >,且1a ≠,则(1)log ()log m p m n p n++<.(2)2log log log 2a a a m nm n +<. 9·平均增长率的问题如果原来产值的基础数为N ,平均增长率为p ,则对于时间x 的总产值y ,有(1)x y N p =+.39.数列的同项公式与前n 项的和的关系11,1,2n n n s n a s s n -=⎧=⎨-≥⎩( 数列{}n a 的前n 项的和为12n n s a a a =+++).七 数列1·等差数列的通项公式*11(1)()n a a n d dn a d n N =+-=+-∈;其前n项和公式为1()2n n n a a s +=1(1)2n n na d -=+211()22d n a d n =+-. 2·等比数列的通项公式1*11()n nna a a q q n N q-==⋅∈; 其前n 项的和公式为11(1),11,1n n a q q s q na q ⎧-≠⎪=-⎨⎪=⎩或11,11,1n n a a qq q s na q -⎧≠⎪-=⎨⎪=⎩.3·等比差数列{}n a :11,(0)n n a qa d a b q +=+=≠的通项公式为1(1),1(),11n n n b n d q a bq d b q d q q -+-=⎧⎪=+--⎨≠⎪-⎩;其前n 项和公式为(1),(1)1(),(1)111n n nb n n d q s d q db n q q q q +-=⎧⎪=-⎨-+≠⎪---⎩.八 三角函数1·常见三角不等式(1)若(0,)2x π∈,则sin tan x x x <<.(2) 若(0,)2x π∈,则1sin cos x x <+≤(3) |sin ||cos |1x x +≥.2·同角三角函数的基本关系式22sin cos 1θθ+=,tan θ=θθcos sin ,tan 1cot θθ⋅=.3·正弦、余弦的诱导公式212(1)sin ,sin()2(1)s ,nn n co απαα-⎧-⎪+=⎨⎪-⎩212(1)s ,s()2(1)sin ,nn co n co απαα+⎧-⎪+=⎨⎪-⎩;tan tan tan()1tan tan αβαβαβ±±=.22sin()sin()sin sin αβαβαβ+-=-(平方正弦公式);22cos()cos()cos sin αβαβαβ+-=-.sin cos a b αα+=)αϕ+(辅助角ϕ所在象限由点(,)a b 的象限决定,tan baϕ= ).5·半角正余切公式:sin sin tan ,cot 21cos 1cos αααααα==+- 6·二倍角公式sin 2sin cos ααα=.2222cos 2cos sin 2cos 112sin ααααα=-=-=-.22tan tan 21tan ααα=-. 7·最简单的三角不等式及其解集sin (||1)(2arcsin ,2arcsin ),x a a x k a k a k Z πππ>≤⇔∈++-∈sin (||1)(2arcsin ,2arcsin ),x a a x k a k a k Z πππ<≤⇔∈--+∈cos (||1)(2arccos ,2arccos ),x a a x k a k a k Zππ>≤⇔∈-+∈cos (||1)(2arccos ,22arccos ),x a a x k a k a k Zπππ<≤⇔∈++-∈tan ()(arctan ,),2x a a R x k a k k Zπππ>∈⇒∈++∈tan ()(,arctan ),2x a a R x k k a k Z πππ<∈⇒∈-+∈角的变形:2()()2()()()ααβαββαβαβααββ=-++=+--=+-8·三倍角公式3sin 33sin 4sin 4sin sin()sin()33ππθθθθθθ=-=-+3cos34cos 3cos 4cos cos()cos()33ππθθθθθθ=-=-+323tan tan tan 3tan tan()tan()13tan 33θθππθθθθθ-==-+-9·三角函数的周期公式函数sin()y x ωϕ=+,x ∈R 及函数cos()y x ωϕ=+,x ∈R(A,ω,ϕ为常数,且A ≠0,ω>0)的周期2T πω=;函数tan()y x ωϕ=+,,2x k k Z ππ≠+∈(A,ω,ϕ为常数,且A ≠0,ω>0)的周期T πω=.10·正弦定理 2sin sin sin a b cR A B C===.11余弦定理2222cos a b c bc A =+-;2222cos b c a ca B=+-;2222cos c a b ab C =+-.12·面积定理(1)111222a b c Sah bh ch ===(a b c h h h 、、分别表示a 、b 、c 边上的高).(2)111sin sin sin 222Sab C bc A ca B ===. (3)OABS ∆=.13·在三角形中有下列恒等式:①sin()sin A B C +=② tan tan tan tan .tan .tan A B C A B C ++=14·简单的三角方程的通解sin (1)arcsin (,||1)kx a x k a k Z a π=⇔=+-∈≤. s 2arccos (,||1)co x a x k a k Z a π=⇔=±∈≤.tan arctan (,)x a x k a k Z a R π=⇒=+∈∈.特别地,有sin sin (1)()k k k Z αβαπβ=⇔=+-∈. s cos 2()co k k Z αβαπβ=⇔=±∈.tan tan ()k k Z αβαπβ=⇒=+∈.15·三角形角和定理在△ABC 中,有()A B C C A B ππ++=⇔=-+222C A Bπ+⇔=-222()C A B π⇔=-+八 向量1·实数与向量的积的运算律设λ、μ为实数,那么(1) 结合律:λ(μa )=(λμ)a ;(2)第一分配律:(λ+μ)a =λa +μa;(3)第二分配律:λ(a +b )=λa +λb .2·向量的数量积的运算律:(1) a ·b= b ·a (交换律);(2)(λa )·b=λ(a ·b )=λa ·b = a ·(λb );(3)(a +b )·c= a ·c +b ·c. 3·平面向量基本定理如果e 1、e 2是同一平面的两个不共线向量,那么对于这一平面的任一向量,有且只有一对实数λ1、λ2,使得a=λ1e 1+λ2e 2.不共线的向量e 1、e 2叫做表示这一平面所有向量的一组基底. 4·向量平行的坐标表示 设a =11(,)x y ,b =22(,)x y ,且b≠0,则a b(b ≠0)12210x y x y ⇔-=.5·a 与b 的数量积(或积)a ·b =|a ||b |cos θ. 6·a ·b 的几何意义数量积a ·b 等于a 的长度|a |与b 在a 的方向上的投影|b |cos θ的乘积.7·平面向量的坐标运算(1)设a =11(,)x y ,b =22(,)x y ,则a+b=1212(,)x x y y ++. (2)设a =11(,)x y ,b =22(,)x y ,则a-b=1212(,)x x y y --.(3)设A11(,)x y ,B22(,)x y ,则2121(,)AB OB OA x x y y =-=--.(4)设a =(,),x y R λ∈,则λa=(,)x y λλ.(5)设a =11(,)x y ,b =22(,)x y ,则a ·b=1212()x x y y +.8·两向量的夹角公式cos θ=(a =11(,)x y ,b =22(,)x y ).9·平面两点间的距离公式,A Bd =||AB AB AB =⋅=11(,)x y ,B 22(,)x y ).10·向量的平行与垂直设a =11(,)x y ,b =22(,)x y ,且b ≠0,则A ||b ⇔b =λa12210x y x y ⇔-=.a ⊥b(a ≠0)⇔a ·b=012120x x y y ⇔+=.11·线段的定比分公式设111(,)P x y ,222(,)P x y ,(,)P x y 是线段12PP 的分点,λ是实数,且12PP PP λ=,则121211x x x y y y λλλλ+⎧=⎪⎪+⎨+⎪=⎪+⎩⇔121OP OP OP λλ+=+ ⇔12(1)OP tOP t OP =+-(11t λ=+). 12·三角形的重心坐标公式△ABC 三个顶点的坐标分别为11A(x ,y )、22B(x ,y )、33C(x ,y ),则△ABC 的重心的坐标是123123(,)33x x x y y y G ++++.13·点的平移公式''''x x h x x h y y k y y k⎧⎧=+=-⎪⎪⇔⎨⎨=+=-⎪⎪⎩⎩''OP OP PP ⇔=+ . 注:图形F 上的任意一点P(x ,y)在平移后图形'F 上的对应点为'''(,)Px y ,且'PP 的坐标为(,)h k .14·“按向量平移”的几个结论(1)点(,)P x y 按向量a =(,)h k 平移后得到点'(,)P x h y k ++.(2) 函数()y f x =的图象C 按向量a =(,)h k 平移后得到图象'C ,则'C 的函数解析式为()y f x h k =-+.(3) 图象'C 按向量a =(,)h k 平移后得到图象C ,若C 的解析式()y f x =,则'C 的函数解析式为()y f x h k =+-. (4)曲线C :(,)0f x y =按向量a =(,)h k 平移后得到图象'C ,则'C 的方程为(,)0f x h y k --=.(5) 向量m =(,)x y 按向量a =(,)h k 平移后得到的向量仍然为m =(,)x y .15·三角形五“心”向量形式的充要条件设O 为ABC ∆所在平面上一点,角,,A B C 所对边长分别为,,a b c ,则(1)O 为ABC ∆的外心222OA OB OC ⇔==.(2)O 为ABC ∆的重心0OA OB OC ⇔++=. (3)O 为ABC ∆的垂心OA OB OB OC OC OA ⇔⋅=⋅=⋅.(4)O 为ABC ∆的心0aOA bOB cOC ⇔++=. (5)O 为ABC ∆的A ∠的旁心aOA bOB cOC ⇔=+.九 不等式1·常用不等式:(1),a b R ∈⇒222a b ab +≥(当且仅当a =b 时取“=”号).(2),a b R +∈⇒2a b+≥(当且仅当a =b 时取“=”号).(3)3333(0,0,0).ab c abc a b c ++≥>>>(4)柯西不等式22222()()(),,,,.a b c d ac bd a b c d R ++≥+∈(5)b a b a b a +≤+≤-.2·极值定理已知y x ,都是正数,则有(1)若积xy 是定值p ,则当y x =时和y x +有最小值p 2;(2)若和y x +是定值s ,则当y x =时积xy 有最大值241s . 推广 已知R y x ∈,,则有xy y x y x 2)()(22+-=+(1)若积xy 是定值,则当||y x -最大时,||y x +最大; 当||y x -最小时,||y x +最小.(2)若和||y x +是定值,则当||y x -最大时, ||xy 最小;当||y x -最小时, ||xy 最大.3·一元二次不等式20(0)ax bx c ++><或2(0,40)a b ac ≠∆=->,如果a 与2axbx c ++同号,则其解集在两根之外;如果a 与2ax bx c ++异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.121212()()0()x x x x x x x x x <<⇔--<<; 121212,()()0()x x x x x x x x x x <>⇔--><或.4·含有绝对值的不等式当a> 0时,有22x a x a a x a <⇔<⇔-<<.22x a x a x a >⇔>⇔>或x a <-.75.无理不等式(1()0()0()()f x g x f x g x ≥⎧⎪>⇔≥⎨⎪>⎩.(2)2()0()0()()0()0()[()]f x f x g x g x g x f x g x ≥⎧≥⎧⎪>⇔≥⎨⎨<⎩⎪>⎩或.(32()0()()0()[()]f x g x g x f x g x ≥⎧⎪<⇔>⎨⎪<⎩. 5·指数不等式与对数不等式(1)当1a >时,()()()()f x g x a a f x g x >⇔>;()0log ()log ()()0()()a a f x f x g x g x f x g x >⎧⎪>⇔>⎨⎪>⎩.(2)当01a <<时,()()()()f x g x a a f x g x >⇔<;()0log ()log ()()0()()a a f x f x g x g x f x g x >⎧⎪>⇔>⎨⎪<⎩十 直线方程1·斜率公式①2121y y kx x -=-(111(,)P x y 、222(,)P x y ).② k=tanα(α为直线倾斜角)2·直线的五种方程(1)点斜式 11()y y k x x -=- (直线l 过点111(,)P x y ,且斜率为k ).(2)斜截式y kx b =+(b 为直线l 在y 轴上的截距). (3)两点式 112121y y x x y y x x --=--(12y y ≠)(111(,)P x y 、222(,)P x y (12x x ≠)).(4)截距式 1x ya b+=(a b 、分别为直线的横、纵截距,0a b ≠、)(5)一般式 0Ax By C ++=(其中A 、B 不同时为0).5·两条直线的平行和垂直(1)若111:l y k x b =+,222:l y k x b =+ ①121212||,l l k k b b ⇔=≠;②12121l l k k ⊥⇔=-.(2)若1111:0l A x B y C ++=,2222:0l A x B y C ++=,且A 1、A 2、B 1、B 2都不为零,①11112222||A B C l l A B C ⇔=≠;②两直线垂直的充要条件是12120A A B B +=;即:12l l ⊥⇔12120A A B B +=6·夹角公式(1)2121tan ||1k k k k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-)(2)12211212tan ||A B A B A A B B α-=+.(1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠).直线12l l ⊥时,直线l 1与l 2的夹角是2π. 7·1l 到2l 的角公式(1)2121tan 1k k k k α-=+.(111:l y k x b =+,222:l y k x b =+,121k k ≠-)(2)12211212tan A B A B A A B B α-=+.(1111:0l A x B y C ++=,2222:0l A x B y C ++=,12120A A B B +≠).直线12l l ⊥时,直线l 1到l 2的角是2π.8·四种常用直线系方程(1)定点直线系方程:经过定点000(,)P x y 的直线系方程为00()y y k x x -=-(除直线0x x =),其中k是待定的系数; 经过定点000(,)P x y 的直线系方程为00()()0A x x B y y -+-=,其中,A B 是待定的系数.(2)共点直线系方程:经过两直线1111:0l A x B y C ++=,2222:0l A x B y C ++=的交点的直线系方程为111222()()0A x B y C A x B y C λ+++++=(除2l ),其中λ是待定的系数.(3)平行直线系方程:直线y kx b =+中当斜率k 一定而b 变动时,表示平行直线系方程.与直线0Ax By C ++=平行的直线系方程是0Ax By λ++=(0λ≠),λ是参变量.(4)垂直直线系方程:与直线0Ax By C ++= (A ≠0,B ≠0)垂直的直线系方程是0Bx Ay λ-+=,λ是参变量.9·点到直线的距离d =(点00(,)P x y ,直线l:0Ax By C ++=).10·0Ax By C ++>或0<所表示的平面区域设直线:0l Ax By C ++=,若A>0,则在坐标平面从左至右的区域依次表示 0Ax By C ++<,0Ax By C ++>,若A<0,则在坐标平面从左至右的区域依次表示0Ax By C ++>,0Ax By C ++<,可记为“x 为正开口对,X 为负背靠背“。
关于平面几何的60条著名定理

关于平面几何的 60 条著名定理些平面几何的著名定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1 的两部分4、四边形两边中心的连线的两条对角线中心的连线交于5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、三角形的三条高线交于一点&设三角形ABC的外心为0,垂心为H 从0向BC边引垂线,设垂足为L,则AH=20L9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s , s 为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点中线定理:(巴布斯定理)设三角形ABC的边BC的中点15、为P,则有AB2+AC2=2(AP2+BP2) 16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,贝U有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD勺对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B 的距离之比为定比m:n (值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD 20、以任意三角形ABC 的边BC CA AB为底边,分别向外作底角都是30度的等腰^ BDC △ CEA △ AFB则^ DEF是正三角形,21、爱尔可斯定理1:若^ ABC和^ DEF都是正三角形,则由线段AD BE、CF的中心构成的三角形也是正三角形。
直线与平面平行判定定理

直线与平面平行判定定理一、引言直线与平面平行判定定理是解析几何中的重要定理之一,它可以帮助我们判断一条直线与一个平面是否平行。
本文将介绍直线与平面平行判定定理的基本概念、证明过程以及应用。
二、直线与平面平行判定定理的基本概念1. 直线:直线是由无数个点连成的轨迹,它没有宽度和厚度,可以延伸到无穷远。
2. 平面:平面是由无数个点组成的一个平面图形,它是无厚度的,可以延伸到无穷远。
3. 平行线:如果两条直线在同一个平面内,且没有交点,我们称这两条直线是平行线。
4. 平行面:如果两个平面没有交线,我们称这两个平面是平行面。
三、直线与平面平行判定定理的证明过程直线与平面平行判定定理的证明过程相对复杂,这里我们简要介绍一下基本思路。
我们需要明确定理的前提条件:直线和平面在同一个三维空间中。
然后,我们假设直线与平面不平行,即直线与平面有交点。
接下来,我们通过推理和运用几何知识来推导出矛盾的结论。
最后,我们得出结论:如果直线与平面有交点,则直线与平面不平行。
通过反证法的证明过程,我们可以得到直线与平面平行判定定理。
四、直线与平面平行判定定理的应用直线与平面平行判定定理在解析几何中有广泛的应用。
以下是一些常见的应用场景:1. 证明平行四边形:利用直线与平面平行判定定理,可以证明两对边分别平行的四边形是平行四边形。
2. 证明角平分线平行:利用直线与平面平行判定定理,可以证明角的平分线与平面平行。
3. 证明线段平行:利用直线与平面平行判定定理,可以证明两个线段平行。
4. 证明三角形平行边:利用直线与平面平行判定定理,可以证明三角形中的某两边平行。
五、总结直线与平面平行判定定理是解析几何中的重要定理,它可以帮助我们判断一条直线与一个平面是否平行。
通过证明过程,我们可以深入理解该定理的原理和应用。
在解析几何的学习和实际问题中,我们可以灵活运用直线与平面平行判定定理,解决各种与平行相关的几何问题。
通过不断的练习和应用,我们可以提高解析几何的能力,更好地理解和应用直线与平面平行判定定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
证明(: 存在性)∵A a , 在a上任取两点B、C,
∴过不共线的三点A,B,C有一个平面 (公理3)
∵B∈ ,C∈ ∴a (公理1)
∴过点A和直线a有一个平面
(唯一性)
又由公理3,经过不共线的三点A、B、C的平面
只有一个 ∴经过a和点A的平面只有一个.
推论2: 经过两条相交直线有且只有一个 平面。
a
α
b
a ∥ b 有且只有一个平面, 使得a ,b
另法:两条平行直线确定一个平面。
已知:直线a、b且a∥b.
求证:经过直线a、b有且只有一个平面.
证明:(1)存在性.
a
∵a∥b,由平行线的定义,
a、b在同一平面内,
α
B•
b
∴过直线a、b有一个平面α.
(2)唯一性。
在直线b上任取一点B,则B a(否则与a∥b 矛盾)
二、简单几何体 (1)棱柱 (2)棱锥 (3)多面体与正多面体 (4)球
今天,我们先来学习
“平面”的知识!
1.平面
概念:平面无大小、无厚度、无边界无面积, 是无限延伸的.
几何画法:通常用一个角为 45o平行四边形来表示平面.
符号表示:通常用希腊字母 , , 等来表 示,如:平面 也可用表示平行四边形的两个 相对顶点的字母来表示,如:平面AC.aLeabharlann a αa // α
a α =A a b=A α β= a
集合 (直线)
与集合 (平面) 之间的
关系
公理一:如果一条直线上的两点在一个平面内, 那么这条直线上的所有点都在这个平面内
符号语言ΑΑ α l ΒΒαl l
应用:
1.判断点或直线在平 面内的依据; 2.检查物体表面是否平整 α A
面上升到三维空间,因此,需要我们在学习过程中通过严
密的逻辑推理把三维空间图形问题转化为二维平面图形问
题,这也是学好立体几何的一个重要方法.
• 土木建筑、机械设计、航行测绘等大量的实际问题,
都要涉及对立体图形的研究。因此,学好立体几何对我们
的日常生产和生活非常重要。
一、空间直线和平面 (1)平面(2)空间直线与直线 (3)直线与平面(4)平面与平面
A● a
A● α
●A α
Aa
Aα
A α
元素 (点) 与集合 (直线 或平面) 之间的 关系
5、直线和平面的位置关系:
直线a在平面α内(或 平面α经过直线a) 直线a与平面α平行
直线a与平面α相交 与点A
a α
a
α a
α ●A
直线a与直线b相交 与点A
平面α与平面β相交 与直线a
Aa
●
α
b
β
α
1.判定两个平面相交
2.判定点共线
3.两平面两个公共点的连线就是它们的交线
例 2 . 正 方 体 A C1中 ,对 角 线 A1C 和 平 面 B D C1
交于O,AC与BD交于点M求, 证:点C1、O、
M共线.
D1
C1
A1
B1
•O
D
C
A
M B
D1 A1
C1 B1
•O
D
C
A
M
证明: C1、O、M 面BDC1,
课题:
平面
观察下面图形
• 同学们比较图(1)和图(2)有什么不同?
(1)
平面几何图形
(2)
立体几何图形
引言
•
以往我们所学的几何是平面几何,研究的是平面图形
的性质、画法、计算、应用.今天我们开始学习一门新的
学科——立体几何.立体几何的研究对象是空间图形的性
质、画法、计算及应用.它使得我们的学习内容从二维平
有时也可以用其他平面图形来表示,如:
(1)
(2)
(3)
表示两平面相交的画法
3.观察下面图形,说明它们的摆放位置不同.
4、点和直线的位置关系:
点A在直线a上(或
A
直线a经过点A)
●
a
A a
点A在直线a外 (或直线a不经 过点A)
点A在平面α内 (或平面α经过点
A)
点A在平面a外 (或平面a不经 过点A)
且B、a在过a、b的平面α内。
又由推论1,过点B和直线a的平面只有一个,
∴过直线a、b的平面只有一个。
由(1)(2),可知经过两条平行直线的平面
有且只有一个。
l
P
=a且
Pa
公理3
经过不在同一条直线 上的三点, ,有且只 有一个平面。
αA ●
C ● ●
B
A、B、C三点不共线
有且只有一个平面α,
使A∈α,B ∈α,C ∈α.
推论1:经过一条直线和直线外一点,有
且只有一个平面.
已知:点A a
A
a
BC
求证:过点A和直线a有且只有一个平面.
又A ,
AP ,即a
经过相交直线a、b有平面.
(2)唯一性。 ∵经过直线a、b的平面一定经过点A和直线b,
而A b。
根据推论1,经过点A和直线b的平面只有一个. ∴经过a、b的平面只有一个.
由(1)(2),可知经过两条相交直线 有且只有一个平面。
推论3:经过两条平行直线有且只有一个 平面。
Aa
•b
α
a b P 存在唯一的平面 , 使得a ,b
另法:两相交直线确定一个平面。
已知:直线a、b且a∩b=P.
求证:过a、b有且只有一个平面。
证明:(1)存在性
在直线a上取不同于点P的点A
则点A直线b.
α
C
Pa
•
•b
•A
根据推论1,过点A和直线b有一个平面α。
b , P b, P
l B
公理二:如果两个平面有一个公共点,那么它
们还有其它公共点,这些公共点的集合是一条
经过这个公共点的直线。
如果两个平面有一条公共
β
直线,则称这两个平面相
交,这条公共直线叫做这 P
两个平面的交线。
l
α
符号语言: P l且P l
应用:判定两个平面有交线及交线位置的依据
B
又C1、O、M 面A1 ACC1,
由公理2知,
点C1、O、M在平面BDC1与平面A1 ACC1的交线上, C 、O、M三点共线。
公理三:经过不在一条直线上的三点有且只有一 个平面
即:不共线的三点确定一个平面
过A,B,C三点的平面可记作:平面ABC
B
应用:确定平面的依据
A
α
C
判定点或线的共面;
8、平面的基本性质的三种语言描述:
语言 公理
公理1
文字语言
如果一条直线上的两 点在一个平面内,那 么这条直线上的所有 点都在这个平面内。
图形语言
●
A
●
B
l
如果两个平面有一个公
公理2
共点,那么它们还有其 他的公共点,且所有这
β
●P
些公共点的集合是一条
α
a
过这个公共点的直线
符号语言
Al,B l, A ,B
