交流电的有效值和平均值

有效值与平均值

交流电的有效值和平均值交流电流的有效值按电流的热效应来规定，定义为：因此，有效值也叫均方根值．有效值的意义是：在一个周期的时间内，交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等．或者说，就电流通过电阻产生的热量说，（变化）与（稳定）等效．类似地，交流电压、交流电动势的有效值定义为：不同波形的交流电，有效值与最大值的关系不同．对正弦交流电，，由定义得：=即正弦交流电的有效值等于最大值被除．对下图所示的方波说，由定义显然可得有效值与最大值相等．对下图所示的三角波和锯齿波说，由定义可得有效值等于最大值被除．．交流电在一个周期内的平均值为零，而技术上应用的交流电的平均值是指在一个周期内交流电的绝对值的平均值．也等于交流电在正半个周期内的平均值．即：= ，= ，=不同波形的交流电，平均值与最大值的关系不同．对正弦交流电，由定义得：= = = 0×637Im正弦交流电的有效值与平均值之比为：．对于方波：对于三角波、锯齿波，由定义得：=交流电的有效值与平均值是两个不同的概念，一般说，有效值比平均值大．实用上用得最多的交流电是正弦交流电．交流电的最大值、有效值、平均值中，有效值用得最多．这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念．对正弦交流电，设：，则：= ==所以：==由此可见，从计算交流电的平均功率上看，交流电的有效值与稳恒电流的值相当．我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度．对单向脉动电流说，指针偏转角度正比于电流的平均值．在磁电式电表上加接整流二极管用来测量交流电流时，电表真正测量的是交流电流的平均值．因为有效值用得最多，几乎所有的交流电表的表盘都是按“有效值”来刻度的，这一点我们应该特别注意．电磁式电表指针偏转的角度正比于电流的平方，这是与磁电式电表不同的地方．。

交流电的瞬时值最大值有效值和平均值e

根据定义，这两个电流所产生的热量应相等，即
将代入上式i=Imsinωt
4．平均值：交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值。对于某一段时间或某一过程，其平均感应电动势：
=ቤተ መጻሕፍቲ ባይዱ=
二、正弦交流电的“四值〞之间的关系
1、正弦交流电的有效值与最大值的关系： U= ，I=
注：I U是电流、电压的有效值，Im、Um是电流、电压的最大值
2、正弦交流电的平均值与最大值和有效值的关系：，，，
注：Ip、Up是电流、电压的平均值
三、“四值〞解题方法小结：
交变电流有四值，即有效值、平均值、最大值和瞬时值．各值何时应用，对照如下情况确定：
〔1〕在研究电容器是否被击穿时，要用峰值〔最大值〕．因电容器上标明的电压是它在直流电源下工作时所承受的最大值．
〔2〕在研究交变电流的功率和产生的热量时，只能用有效值．
〔3〕在求解某一时刻线圈受到的磁力矩时，只能用瞬时值．
〔4〕在求交变电流流过导体的过程中通过导体截面积的电量时，要用平均值．
一、准确把握概念
1. 瞬时值：交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。瞬时值随时间的变化而变化。不同时刻，瞬时值的大小和方向均不同。交流电的瞬时值取决于它的周期、幅值和初相位。以正弦交流电为例〔从中性面开始计时〕。那么有：
其瞬时值为：e=Emsinωt
i=Imsinωt u=Umsinωt
2．最大值：交变电流的最大值是指交变电流在一个周期内所能到达的最大值，它可以用来表示交变电流的强弱或电压的上下。以正弦交流电为例。那么有：
Em=nBωS，此时电路中的电流强度及用电器两端的电压都具有最大值，即Im= ，Um=ImR。
3．有效值：交变电流的有效值是根据电流的热效应来定义的，让交变电流和恒定电流通过相同阻值的电阻，如果在相同的时间内产生的热量相等，我们就把这一恒定电流的数值叫做这一交变电流的有效值。

交流电的有效值和平均值定义与计算

交流电的有效值和平均值交流电流的有效值按电流的热效应来规定，定义为：因此，有效值也叫均方根值．有效值的意义是：在一个周期的时间，交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等．或者说，就电流通过电阻产生的热量说，（变化）与（稳定）等效．类似地，交流电压、交流电动势的有效值定义为：不同波形的交流电，有效值与最大值的关系不同．对正弦交流电，，由定义得：=即正弦交流电的有效值等于最大值被除．对下图所示的方波说，由定义显然可得有效值与最大值相等．对下图所示的三角波和锯齿波说，由定义可得有效值等于最大值被除．．交流电在一个周期的平均值为零，而技术上应用的交流电的平均值是指在一个周期交流电的绝对值的平均值．也等于交流电在正半个周期的平均值．即：= ，= ，=不同波形的交流电，平均值与最大值的关系不同．对正弦交流电，由定义得：= = = 0×637Im正弦交流电的有效值与平均值之比为：．对于方波：对于三角波、锯齿波，由定义得：=交流电的有效值与平均值是两个不同的概念，一般说，有效值比平均值大．实用上用得最多的交流电是正弦交流电．交流电的最大值、有效值、平均值中，有效值用得最多．这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念．对正弦交流电，设：，则：= ==所以：==由此可见，从计算交流电的平均功率上看，交流电的有效值与稳恒电流的值相当．我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度．对单向脉动电流说，指针偏转角度正比于电流的平均值．在磁电式电表上加接整流二极管用来测量交流电流时，电表真正测量的是交流电流的平均值．因为有效值用得最多，几乎所有的交流电表的表盘都是按“有效值”来刻度的，这一点我们应该特别注意．电磁式电表指针偏转的角度正比于电流的平方，这是与磁电式电表不同的地方．。

交流电的瞬时值、最大值、有效值和平均值

交流电的瞬时值、最大值、有效值和平均值之青柳念文创作交变电流的大小和方向都随时间作周期性变更，所以要准确描绘交变电流的发生的效果，需要用到“最大值、有效值、瞬时值、平均值”四个物理量.交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”.这四个近似但又有区此外物理量，容易造成混乱，懂得好“四值”对于学习交流电有极大的帮忙.一、准确掌控概念1. 瞬时值：交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值.瞬时值随时间的变更而变更.分歧时刻，瞬时值的大小和方向均分歧.交流电的瞬时值取决于它的周期、幅值和初相位.以正弦交流电为例（从中性面开端计时）.则有：其瞬时值为：e=E m sinωti=I m sinωt u=U m sinωt2．最大值：交变电流的最大值是指交变电流在一个周期内所能达到的最大值，它可以用来暗示交变电流的强弱或电压的高低.以正弦交流电为例.则有：E m =nBωS，此时电路中的电流强度及用电器两头的电压都具有最大值，即I m =r R E m， U m =I m R.3．有效值：交变电流的有效值是根据电流的热效应来定义的，让交变电流和恒定电畅通过相同阻值的电阻，如果在相同的时间内发生的热量相等，我们就把这一恒定电流的数值叫做这一交变电流的有效值.交流电的有效值是根据它的热效应确定的.交流电流i 通过电阻R 在一个周期内所发生的热量和直流电流I 通过同一电阻R 在相同时间内所发生的热量相等, 则这个直流电流I 的数值叫做交流电流i 的有效值, 用大写字母暗示, 如I 、 U 等.一个周期内直流电通过电阻R 所发生的热量为：交流电通过同样的电阻R ，在一个周期内所发生热量：根据定义，这两个电流所发生的热量应相等，即将代入上式i=I m sinωt4．平均值：交变电流的平均值是指在某一段时间内发生的交变电流对时间的平均值.对于某一段时间或某一过程，其平均感应电动势：I t N E 平均电流→∆∆•=φ=U rR E 平均电压→+=I R • 二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系： U=m mU U 707.02=，I=m m I I 707.02=注：I U 是电流、电压的有效值，I m 、U m 是电流、电压的最大值2、正弦交流电的平均值与最大值和有效值的关系：m m P I I I 637.02==π，m m P U U U 637.02==π，I I P 90.0=，U U P 90.0=注：I p 、U p 是电流、电压的平均值三、“四值”解题方法小结：交变电流有四值，即有效值、平均值、最大值和瞬时值．各值何时应用，对照如下情况确定：（1）在研究电容器是否被击穿时，要用峰值（最大值）．因电容器上标明的电压是它在直流电源下工作时所承受的最大值．（2）在研究交变电流的功率和发生的热量时，只能用有效值．（3）在求解某一时刻线圈受到的磁力矩时，只能用瞬时值．（4）在求交变电流流过导体的过程中通过导体截面积的电量时，要用平均值．。

有效值与平均值

有效值与平均值
有效值：让一个交流电流和一个直流电流分别通过阻值相同的电阻，如果在相同时间内产生的热量相等，那么就把这一直流电的数值叫做这一交流电的有效值。

平均值：正弦交流电的波形是对称于横轴的，在一个周期内的平均值恒等零，所以一般所说平均值是指半个周期内的平均值。

交流电流表和交流电压表测量的值都是有效值。

在选取晶闸管额定电压、电流的时候考滤的是最大值。

最大值也称为幅值或峰值。

最大值=跟号2倍的有效值
平均值=0.637倍的最大值
对于正弦交流,有效值等于1.1倍平均值,等于0.707倍峰值.
对于任意波形(包括直流),有效值满足均方根关系.即:瞬间电压的平方在一个周期内的积分的平方根再除以时间.
如果它的峰峰值是Upp的话那么有效值就是它除以2倍根号2，如果它的幅值是Um的话就除以根号2。

交流电的瞬时值、最大值、有效值和平均值

交流电的瞬时值、最大值、有效值和平均值交变电流的大小和方向都随时间作周期性变化，所以要准确描述交变电流的产生的效果，需要用到“最大值、有效值、瞬时值、平均值”四个物理量。

交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”。

这四个类似但又有区别的物理量，容易造成混乱，理解好“四值”对于学习交流电有极大的帮助。

一、准确把握概念1. 瞬时值：交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值。

瞬时值随时间的变化而变化。

不同时刻，瞬时值的大小和方向均不同。

交流电的瞬时值取决于它的周期、幅值和初相位。

以正弦交流电为例（从中性面开始计时）。

则有：其瞬时值为：e=Emsinωti=Imsinωt u=Umsinωt2．最大值：交变电流的最大值是指交变电流在一个周期内所能达到的最大值，它可以用来表示交变电流的强弱或电压的高低。

以正弦交流电为例。

则有：Em=nBωS，此时电路中的电流强度及用电器两端的电压都具有最大值，即Im=， Um=ImR。

3．有效值：交变电流的有效值是根据电流的热效应来定义的，让交变电流和恒定电流通过相同阻值的电阻，如果在相同的时间内产生的热量相等，我们就把这一恒定电流的数值叫做这一交变电流的有效值。

交流电的有效值是根据它的热效应确定的。

交流电流i通过电阻R在一个周期内所产生的热量和直流电流I通过同一电阻R在相同时间内所产生的热量相等, 则这个直流电流I的数值叫做交流电流i的有效值, 用大写字母表示, 如I、 U等。

一个周期内直流电通过电阻R所产生的热量为：交流电通过同样的电阻R，在一个周期内所产生热量：根据定义，这两个电流所产生的热量应相等，即将代入上式i=Imsinωt4．平均值：交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值。

对于某一段时间或某一过程，其平均感应电动势：==二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系： U=，I=注：I U 是、的，Im、Um是电流、电压的最大值2、正弦交流电的与最大值和有效值的关系：，，，注：Ip、Up是电流、电压的平均值三、“四值”解题方法小结：交变电流有四值，即有效值、平均值、最大值和瞬时值．各值何时应用，对照如下情况确定：（1）在研究电容器是否被击穿时，要用峰值（最大值）．因电容器上标明的电压是它在直流电源下工作时所承受的最大值．（2）在研究交变电流的功率和产生的热量时，只能用有效值．（3）在求解某一时刻线圈受到的磁力矩时，只能用瞬时值．（4）在求交变电流流过导体的过程中通过导体截面积的电量时，要用平均值．。

交流电的瞬时值最大值有效值和平均值

交流电的瞬时值、最大值、有效值和平均值交变电流的大小和方向都随时间作周期性变化,所以要准确描述交变电流的产生的效果,需要用到“最大值、有效值、瞬时值、平均值”四个物理量;交流电的“最大值、有效值、瞬时值、平均值”常称为交流电的“四值”;这四个类似但又有区别的物理量,容易造成混乱,理解好“四值”对于学习交流电有极大的帮助;一、准确把握概念1. 瞬时值：交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值;瞬时值随时间的变化而变化;不同时刻,瞬时值的大小和方向均不同;交流电的瞬时值取决于它的周期、幅值和初相位;以正弦交流电为例从中性面开始计时;则有：其瞬时值为：e=E m sinωti=I m sinωt u=U m sinωt2．最大值：交变电流的最大值是指交变电流在一个周期内所能达到的最大值,它可以用来表示交变电流的强弱或电压的高低;以正弦交流电为例;则有：E m =nB ωS,此时电路中的电流强度及用电器两端的电压都具有最大值,即I m =r R E m , U m =I m R;3．有效值：交变电流的有效值是根据电流的热效应来定义的,让交变电流和恒定电流通过相同阻值的电阻,如果在相同的时间内产生的热量相等,我们就把这一恒定电流的数值叫做这一交变电流的有效值;交流电的有效值是根据它的热效应确定的;交流电流i通过电阻R在一个周期内所产生的热量和直流电流I通过同一电阻R在相同时间内所产生的热量相等, 则这个直流电流I 的数值叫做交流电流i的有效值, 用大写字母表示, 如I、U 等;一个周期内直流电通过电阻R所产生的热量为：交流电通过同样的电阻R,在一个周期内所产生热量：根据定义,这两个电流所产生的热量应相等,即将代入上式i=I m sinωt4．平均值：交变电流的平均值是指在某一段时间内产生的交变电流对时间的平均值;对于某一段时间或某一过程,其平均感应电动势：I tN E 平均电流→∆∆•=φ=U r R E 平均电压→+=I R •二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最大值的关系： U=m mU U 707.02=,I=m m I I 707.02= 注：I U 是、的,I m 、U m 是电流、电压的最大值2、正弦交流电的与最大值和有效值的关系：m m P I I I 637.02==π,m m P U U U 637.02==π,I I P 90.0=,U U P 90.0= 注：I p 、U p 是电流、电压的平均值三、“四值”解题方法小结：交变电流有四值,即有效值、平均值、最大值和瞬时值．各值何时应用,对照如下情况确定：1在研究电容器是否被击穿时,要用峰值最大值．因电容器上标明的电压是它在直流电源下工作时所承受的最大值．2在研究交变电流的功率和产生的热量时,只能用有效值．3在求解某一时刻线圈受到的磁力矩时,只能用瞬时值．4在求交变电流流过导体的过程中通过导体截面积的电量时,要用平均值．。

浅谈交流电的有效值和平均值

浅谈交流电的有效值和平均值电工技术, 电阻, 交流电, 平均值, 绝对值一、基本概念：交流电的有效值：在相同的电阻上分别通以直流电流和交流电流，经过一个交流周期的时间，如果它们在电阻上所损失的电能相等的话，则把该直流电流（电压）的大小作为交流电流（电压）的有效值，正弦电流（电压）的有效值等于其最大值(幅值)的0.707倍。

交流电的平均值：对于交流电来说，数学上的平均值是0（因为是正负是对称的）。

但电工技术上我们关心的是其量值（绝对值）的大小。

所以电工技术上的平均值指的是电流（电压）的绝对值在一个周期内的平均值。

二、例子：1、10V的直流电压加在10Ω电阻的两端，电阻的发热功率是多少？这个答案很简单，坛里所有的朋友都会：P=U×U/R=10V×10V/10Ω=10W2、如果把上面的10V直流电压改成下图±10V的方波呢，电阻的发热功率又是多少？答案是否也不难？因为负半周时电压的平方和正半周时是一样的，所以功率也和上面一样还是10W!(电压是负的功率还是正的，也就是功率和电压的正负无关)图中红色部分是正半周做的功，蓝色部分是负半周作的功问：这个±10V的方波电压的平均值是多少？有效值是多少？峰值是多少？根据上面的定义，很明显:①平均值是10V（其电压的绝对值在一个周期内的平均值是10V）;②有效值是10V（发热功率相同的等效直流电压是10V）;③峰值是10V3、如果把上面的方波去掉负半周部分（也就是+10V方波），那电阻上的功率又会是多少呢？很明显，只有一半时间在做功，从宏观上看其平均功率只有一半了，也就是5W!同问：这个+10V的方波电压的平均值是多少？有效值是多少？峰值是多少？根据上面的定义，很明显：①平均值是5V（其电压的绝对值在一个周期内的平均值是5V）;②有效值是7.07V：（发热功率相同的等效直流电压是：U^2=PR=5W×10Ω，U=根号50≈7.07V）；③峰值是10V可见：去掉负半周后其电压的平均值是原来的一半，而有效值并不是原来的一半，而是原来的0.707倍！峰值不变以上为了便于理解，用了方波做例子计算（如果用正弦波，那么就需要有高等数学的微积分知识，对于某些朋友可能理解困难。

交流电平均值、瞬时值、最大值、有效值的区别

交流电平均值、瞬时值、最大值、有效值的区别高中分校林永德在交流电教学中，历届学生对交流电的瞬时值、最大值、有效值、平均值的理解容易出错，有的乱用方式，有的忽视条件，如果在教学中注意以下两个方面，可以有效地防止学生所出的错误。

1．以交流发电模式为主体，揭示概念的实值。

① 发电模式：N 匝线圈，其面积为S ，总电阻为r ，在一匀强磁场中（磁感应强度为B ），绕垂直于B 的轴，以角速度ω匀速转动；即构成交流电源；交流电源通过滑环和电刷引到外电路，即构成交流全电路。

② 概念的理解：A 、最大值，当线圈平面与磁场平行时，出现最大值。

最大电动势Em=NB ωS 最大电流Im=rR Em +，R 两端的最大电压Um=I m ·R 。

B 、瞬时值:交流全路中，其电动势、电流、电压、均随时间发生周期性变化，如从中性面开始计时，其瞬时值分别为：e=Emsin ωt i=Imsin ωt u=Umsin ωtC 、有效值：对于正弦（或余弦）交流电，有效值=2最大值。

即 E=2EmI=2ImU=2UmD 、平均值：对于某一段时间或某一过程，其平均感应电动势： I t NE 平均电流→∆∆∙=φ=U rR E 平均电压→+=I R ∙ 2、学生容易出现的错误：（1）有效值的理解：有效值=2最大值，学生容易把条件“正弦或余弦”交流电忽视，对于非正弦或余弦交流电，学生很难建立起电流热效应方程，以求解有效值。

如：求以下交流电的有效值。

学生容易出现以下几种答案： a : U=25, b : U=23c: U=28正确的解法：建立电流热效应方程： 2.01.031.05222⨯=⨯+⨯RU R R 即： U=17 （V ）（2）平均值的理解：如：交流发电模式中，从中性面开始，转过060，求此过程的平均电动势。

学生容易出现以下错误，把平均电动势理解为电动势的平均值，即E =S NB Em e e ω43260sin 02021=+=+ 正确的解法： E =N πωωπφ2326160cos 0S NB BS BS N t =∙-=∆∆ （3）求解功率或电热用交流电源给外电路供电，在求解功率或电热问题的时候，学生很容易把平均值与有效值混淆。

交流电的有效值和平均值定义和计算

交流电的有效值和平均值交流电流的有效值按电流的热效应来规定，定义为：因此，有效值也叫均方根值．有效值的意义是：在一个周期的时间内，交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等．或者说，就电流通过电阻产生的热量说，（变化）与（稳定）等效．类似地，交流电压、交流电动势的有效值定义为：不同波形的交流电，有效值与最大值的关系不同．对正弦交流电，，由定义得：=即正弦交流电的有效值等于最大值被除．对下图所示的方波说，由定义显然可得有效值与最大值相等．对下图所示的三角波和锯齿波说，由定义可得有效值等于最大值被除．．交流电在一个周期内的平均值为零，而技术上应用的交流电的平均值是指在一个周期内交流电的绝对值的平均值．也等于交流电在正半个周期内的平均值．即：= ，= ，=不同波形的交流电，平均值与最大值的关系不同．对正弦交流电，由定义得：= = = 0×637Im正弦交流电的有效值与平均值之比为：．对于方波：对于三角波、锯齿波，由定义得：=交流电的有效值与平均值是两个不同的概念，一般说，有效值比平均值大．实用上用得最多的交流电是正弦交流电．交流电的最大值、有效值、平均值中，有效值用得最多．这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念．对正弦交流电，设：，则：= ==所以：==由此可见，从计算交流电的平均功率上看，交流电的有效值与稳恒电流的值相当．我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度．对单向脉动电流说，指针偏转角度正比于电流的平均值．在磁电式电表上加接整流二极管用来测量交流电流时，电表真正测量的是交流电流的平均值．因为有效值用得最多，几乎所有的交流电表的表盘都是按“有效值”来刻度的，这一点我们应该特别注意．电磁式电表指针偏转的角度正比于电流的平方，这是与磁电式电表不同的地方．。

如何理解交流电的有效值和平均值

如何理解交流电的有效值和平均值交流电是指电流和电压在周期性变化的情况下，正负方向反复交替的电信号。

在交流电中，我们常常涉及到有效值和平均值的概念。

理解这两个概念对于电路分析和计算电功率等方面非常重要。

首先，我们来理解交流电的有效值。

有效值也被称为均方根值，用来表示交流电的大小。

对于周期为T的交流电信号I(t)，其有效值Irms定义为在一个周期内该信号的电流值的平方平均值在T的长度上的开平方。

同样地，对于周期为T的交流电压信号V(t)，其有效值Vrms定义为在一个周期内该信号的电压值的平方平均值在T的长度上的开平方。

有效值的物理意义是在电阻上产生相同功率时所需的直流电流值或电压值。

换句话说，当电阻电流为Irms时，在电路中会发生与交流电流Irms相同的热耗散功率。

因此，我们可以把有效值视为交流电中电流或电压信号的"等效"直流值。

对于正弦波交流电而言，其有效值通常等于其峰值的1/√2倍。

其次，我们来理解交流电的平均值。

平均值也被称为直流值或直流等效值，用来表示交流电的平均大小。

对于周期为T的交流电信号I(t)，其平均值Iavg定义为在一个周期内该信号的电流值的平均值。

对于周期为T的交流电压信号V(t)，其平均值Vavg定义为在一个周期内该信号的电压值的平均值。

平均值的物理意义是交流电信号在一个周期内正半周期所产生的热耗散功率与负半周期所吸收的热耗散功率的平均值。

平均值计算时不考虑信号的正负情况，而只计算信号的大小平均值。

对于正弦波交流电而言，其平均值为0，因为正半周期的功率与负半周期的功率相互抵消。

在实际应用中，有效值和平均值经常被用来计算电路中的功率和能量消耗。

电功率是电流和电压的乘积，可以通过使用有效值计算。

对于交流电，电功率通常定义为乘积的时间平均值，即有效值乘以平均值的结果。

这是因为交流电的功率是随着时间的变化而变化的，通过取乘积的时间平均值可以得到一个稳定的功率值。

综上所述，交流电的有效值和平均值是描述其大小的两个重要指标。

交流电的瞬时值、最大值、有效值和平均值

交流电的瞬时值、最年夜值、有效值和平均值之迟辟智美创作交变电流的年夜小和方向都随时间作周期性变动，所以要准确描述交变电流的发生的效果，需要用到“最年夜值、有效值、瞬时值、平均值”四个物理量.交流电的“最年夜值、有效值、瞬时值、平均值”常称为交流电的“四值”.这四个类似但又有区另外物理量，容易造成混乱，理解好“四值”对学习交流电有极年夜的帮手.一、准确掌控概念1. 瞬时值：交流电流、电压、电动势在某一时刻所对应的值称为它们的瞬时值.瞬时值随时间的变动而变动.分歧时刻，瞬时值的年夜小和方向均分歧.交流电的瞬时值取决于它的周期、幅值和初相位.以正弦交流电为例（从中性面开始计时）.则有：其瞬时值为：e=E m sinωti=I m sinωt u=U m sinωt2．最年夜值：交变电流的最年夜值是指交变电流在一个周期内所能到达的最年夜值，它可以用来暗示交变电流的强弱或电压的高低.以正弦交流电为例.则有： E m =nBωS ，此时电路中的电流强度及用电器两真个电压都具有最年夜值，即I m =r R E m， U m =I m R.3．有效值：交变电流的有效值是根据电流的热效应来界说的，让交变电流和恒定电流通过相同阻值的电阻，如果在相同的时间内发生的热量相等，我们就把这一恒定电流的数值叫做这一交变电流的有效值.交流电的有效值是根据它的热效应确定的.交流电流i 通过电阻R 在一个周期内所发生的热量和直流电流I 通过同一电阻R 在相同时间内所发生的热量相等, 则这个直流电流I 的数值叫做交流电流i 的有效值, 用年夜写字母暗示, 如I 、 U 等.一个周期内直流电通过电阻R 所发生的热量为：交流电通过同样的电阻R ，在一个周期内所发生热量：根据界说，这两个电流所发生的热量应相等，即将代入上式i=I m sinωt4．平均值：交变电流的平均值是指在某一段时间内发生的交变电流对时间的平均值.对某一段时间或某一过程，其平均感应电动势：I t N E 平均电流→∆∆•=φ=U rR E 平均电压→+=I R • 二、正弦交流电的“四值”之间的关系1、正弦交流电的有效值与最年夜值的关系： U=m mU U 707.02=，I=m m I I 707.02=注：I U 是电流、电压的有效值，I m 、U m 是电流、电压的最年夜值2、正弦交流电的平均值与最年夜值和有效值的关系：m m P I I I 637.02==π，m m P U U U 637.02==π，I I P 90.0=，U U P 90.0=注：I p 、U p 是电流、电压的平均值三、“四值”解题方法小结：交变电流有四值，即有效值、平均值、最年夜值和瞬时值．各值何时应用，对比如下情况确定：（1）在研究电容器是否被击穿时，要用峰值（最年夜值）．因电容器上标明的电压是它在直流电源下工作时所接受的最年夜值．（2）在研究交变电流的功率和发生的热量时，只能用有效值．（3）在求解某一时刻线圈受到的磁力矩时，只能用瞬时值．（4）在求交变电流流过导体的过程中通过导体截面积的电量时，要用平均值．。

平均值、有效值经典解释

（1）交流电的有效值为“平方-平均-平方根”值，简称“方均根”值。

英文里电工书上或电器说明书上就叫做“r m s”，如电压的有效值记作 Vrms,.....。

“r m s”为“root-mean-square”三个单词的打头字母，按照英文单词的顺序就是“根-均-方”，中文里应当颠倒顺序翻译，因为先平方，接着求平均，然后开平方。

曾经一度有人翻译成“均方根”，这种译法与实际运算步骤不一致，还是译成“方均根”比较恰当。

英文里不用与中文的“有效值”相对应的单词。

（2）从等效热效应得到的直接关系是，在阻值相等的电阻上功率等效，或者如果加上时间就是放出的热量（能量）等效。

由此得出电流或者电压的平方等效。

紧接着要计算电流（或电压）平方的平均值，决不是像楼上网友所说的那样电流（或电压）一次方的平均值！很显然，正弦函数在一个周期内的平均值为零。

如果正弦函数与横轴之间的面积都算作正值，那么，就是绝对值函数 | sin x | 的平均值，它应该等于2/π = 0.6366 根本不等于根号 2 分之1。

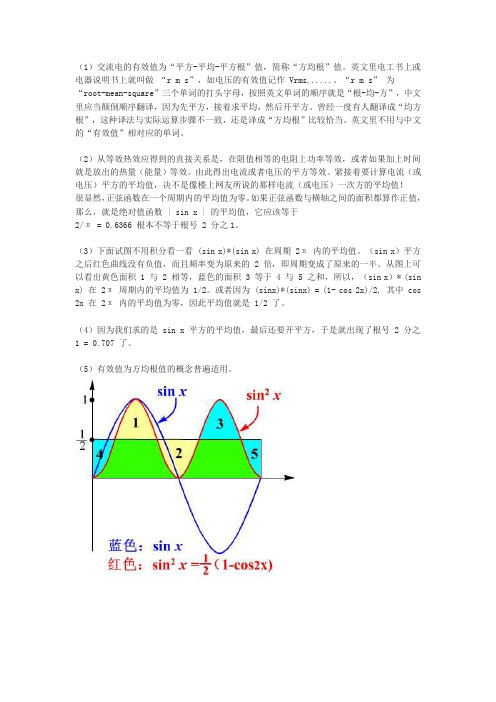
（3）下面试图不用积分看一看 (sin x)*(sin x) 在周期 2π内的平均值。

（sin x）平方之后红色曲线没有负值，而且频率变为原来的 2 倍，即周期变成了原来的一半。

从图上可以看出黄色面积 1 与 2 相等，蓝色的面积 3 等于 4 与 5 之和，所以，（sin x）* (sin x) 在 2π周期内的平均值为 1/2。

或者因为 (sinx)*(sinx) = (1- cos 2x)/2, 其中 cos 2x 在 2π内的平均值为零，因此平均值就是 1/2 了。

（4）因为我们求的是 sin x 平方的平均值，最后还要开平方，于是就出现了根号 2 分之1 = 0.707 了。

（5）有效值为方均根值的概念普遍适用。