信号可视化及时域运算课程设计(常用连续信号及信号的时移、反褶、尺度变换)(1)
信号与系统实验一连续时间信号分析实验报告

实验一 连续时间信号分析一、实验目的(一)掌握使用Matlab 表示连续时间信号1、学会运用Matlab 表示常用连续时间信号的方法2、观察并熟悉常用信号的波形和特性(二)掌握使用Matlab 进行连续时间信号的相关运算1、学会运用Matlab 进行连续时间信号的时移、反褶和尺度变换2、学会运用Matlab 进行连续时间信号微分、积分运算3、学会运用Matlab 进行连续时间信号相加、相乘运算4、学会运用Matlab 进行连续时间信号卷积运算二、实验条件装用Matlab R2015a 的电脑。
三、实验内容1、利用Matlab 命令画出下列连续信号的波形图。
(1))4/3t (2cos π+ 程序:t=-3:0.01:3; ft=2*cos(3*t+pi/4); plot(t,ft)图像:(2))t (u )e 2(t--程序:t=-6:0.01:6; ut=(t>=0);ft=(2-1*exp(-t)).*ut; plot(t,ft)图像:(3))]2()(u )][t (cos 1[--+t u t π 程序:t=-6:0.01:6; ut=(t>=0); ut2=(t>=2);ft=(1+cos(pi*t)).*(ut-ut2); plot(t,ft)图像:2、利用Matlab 命令画出复信号)4/t (j 2e )t (f π+=的实部、虚部、模和辐角。
程序:t=0:0.01:20;ft=2*exp(1j*(t+pi/4));subplot(2,2,1);plot(t,real(ft));title('ʵ²¿');axis([-0.5,20,-2.5,2.5]); subplot(2,2,2);plot(t,imag(ft));title('Ð鲿');axis([-0.5,20,-2.5,2.5]); subplot(2,2,3);plot(t,abs(ft));title('Ä£');axis([-0.5,20,-0.5,2.5]); subplot(2,2,4);plot(t,angle(ft));title('·ø½Ç');axis([-0.5,20,-3.5,3.5]);图像:3、已知信号的波形如下图所示:试用Matlab 命令画出()()()()2332----t f t f t f t f ,,,的波形图。
实验一信号的表示、可视化及时域运算

实验一信号的表示、可视化及时域运算实验一信号的表示、可视化及时域运算一、实验目的:熟悉MATLAB 软件的使用,学会信号的表示及用MATLAB 来产生信号,实现信号的可视化。
二、实验时数:2学时三、实验内容:信号按照自变量的取值是否连续可分为连续时间信号和离散时间信号。
信号与系统的仿真运算对信号与系统课程的学习有着重要意义。
MATLAB 以其科学与技术计算通用的交互系统和编程语言,具有良好的交互数学计算和易于使用的集成图形,编程简单,功能连贯,成为信号与系统的仿真运算首选。
本次实验完成以下内容:1.熟悉MATLAB 语言。
A )双击快捷图标,启动MATLAB 。
B )了解界面功能。
主界面包括标题栏、菜单栏、工具栏和输入输出区等。
C )简单的信号处理可以通过在Command Window 中输入相关指令按Enter 键执行来达到处理目的。
复杂的信号处理可以通过编写M 文件,执行M 文件达到处理目的。
M 文件的编写类似于Word 文档编写。
选中命令窗口File 菜单中M-File 打开M 文件编辑器或单击命令窗口工具栏中New M-File 图标编辑M-文件。
D )M-文件可以在命令窗口输入已保存的M-文件名回车执行,也可使用M-文件编辑器窗口中选择Debug 菜单中的RUN 运行M-文件。
2.连续信号的表示与可视化。
MATLAB 提供了大量的生成基本信号的函数,一种常用的方法是调用相关函数及运算通过向量形式来表示信号,用适当的MATLAB 语句表示信号后,可以利用MATLAB 的绘图命令绘制出直观的信号波形。
本次实验完成指数信号at Ae ,正弦信号)sin(0?ω+t A ,)cos(0?ω+t A ,抽样函数tt t Sa ππ)sin()(=,矩形脉冲函数(产生以t=o 为中心的宽度为width 的矩形波)),(width t rectpuls ,三角波脉冲函数),,(skew width t tripuls 。
信号与系统课设 常用连续时间信号的可视化及微积分运算

成绩评定表课程设计任务书目录一、引言 (1)二、Matlab入门 (2)2.1 Matlab7.0介绍 (2)2.2利用Matlab7.0编程完成习题设计 (3)三、Matlab7.0实现连续时间信号微积分运算的设计 (4)3.1常用连续时间信号的类别及原理 (4)3.2编程设计及实现 (4)3.3运行结果及其分析 (7)四、结论 (16)五、参考文献 (17)一、引言人们之间的交流是通过消息的传播来实现的,信号则是消息的表现形式,消息是信号的具体内容。
《信号与系统》课程是一门实用性较强、涉及面较广的专业基础课,该课程是将学生从电路分析的知识领域引入信号处理与传输领域的关键性课程,对后续专业课起着承上启下的作用. 该课的基本方法和理论大量应用于计算机信息处理的各个领域,特别是通信、数字语音处理、数字图像处理、数字信号分析等领域,应用更为广泛。
近年来,计算机多媒体教序手段的运用逐步普及,大量优秀的科学计算和系统仿真软件不断涌现,为我们实现计算机辅助教学和学生上机实验提供了很好的平台。
通过对这些软件的分析和对比,我们选择MATLAB语言作为辅助教学工具,借助MATLAB强大的计算能力和图形表现能力,将《信号与系统》中的概念、方法和相应的结果,以图形的形式直观地展现给我们,大大的方便我们迅速掌握和理解老师上课教的有关信号与系统的知识。
MATLAB是当前最优秀的科学计算软件之一,也是许多科学领域中分析、应用和开发的基本工具。
MATLAB全称是Matrix Laboratory,是由美国Mathworks公司于20世纪80年代推出的数学软件,最初它是一种专门用于矩阵运算的软件,经过多年的发展,MATLAB已经发展成为一种功能全面的软件,几乎可以解决科学计算中的所有问题。
而且MATLAB编写简单、代码效率高等优点使得MATLAB在通信、信号处理、金融计算等领域都已经被广泛应用。
它具有强大的矩阵计算能力和良好的图形可视化功能,为用户提供了非常直观和简洁的程序开发环境,因此被称为第四代计算机语言。
MATLAB在常用信号时域变换与运算中的及可视化(毕业论文)

引言摘要MATLAB是目前世界上最流行的、应用最广泛的工程计算和仿真软件,它将计算、可视化和编程等功能同时集中于一个易于开发的环境。
MA TLAB主要应用于数学计算、系统建模与仿真、数学分析与可视化、科学与工程绘图和用户界面设计等。
MATLAB是Matrix Laboratory的缩写,是由MathWorks公司于1984年推出的一个交互式开发系统,其基本数据要素是矩阵。
MA TLAB的语法规则简单,适用于专业科技人员的思维方式和书写习惯;而且MATLAB可适用于多种平台,随着计算机软、硬件的更新而及时升级,使得编程和调试效率大大提高。
目前,MA TLAB已经成为应用代数、自动控制理论、数理统计、数字信号处理、动态系统仿真和金融等专业的基本数学工具,各国的高等学校纷纷将MATLAB正式列入本科生和研究生课程的数学计划中,成为学生必须掌握的基本软件之一。
本文首先对MATLAB的功能进行简单介绍,再利用一些常用信号作为实验对象,对其时域运算与变换进行猜想和理论分析,再使用MATLAB的各功能对猜想和分析进行验证,同时将这些常用信号的波形用MATLAB的制图功能绘制出来,即利用MATLAB进行对常用信号的可视化。
关键词:MA TLAB、常用信号、时域运算与变化、可视化I电子科技大学成都学院专科毕业设计论文AbstractMATLAB is the world's most popular, the most widely used engineering calculation and simulation software, it will calculate, visualization and programming focused on an easy development environment. MATLAB is mainly used in mathematical calculations, system modeling and simulation, mathematical analysis and visualization, science and engineering graphics and user interface design. MA TLAB Matrix Laboratory, is an interactive development system introduced in 1984 by The MathWorks, the basic data elements of the matrix. The MATLAB syntax rules apply to the way of thinking and writing habits of professional scientific and technical personnel; and MATLAB applicable to a variety of platforms, with the timely upgrade of the computer software and hardware updates, making programming and debugging efficiency is greatly improved. , MATLAB has become the application of algebra, automatic control theory, mathematical statistics, digital signal processing, dynamic system simulation, and financial and other professional basic mathematical tools, the national institutions of higher learning have MA TLAB officially included in the mathematical program of undergraduate and graduate courses students must master to become one of the basic software.MATLAB function simple, use some common computing and transform its time-domain signal as subjects, conjecture and theoretical analysis, and then use the MATLAB function to verify the conjecture and analysis, while commonly used in signal waveform draw with the graphics capabilities of MATLAB using MA TLAB visualization of the common signal.Key words: MATLAB、common signal、the time domain algorithms、visualizationAbstract目录Abstract ............................................................................................................................II 引言................................................................................................... 错误!未定义书签。
实验十五信号的可视化和信号的时域运算

syms t;
%定义符号变量 函数体用单引号括起;
f=sym(‘sin(t-1)/(t-1)’); %定义符号函数f1=sin(t-1)/(t-1); f1=subs(f,t,-t); %将反褶得f1(t)=f(-t),即将f函数中的t
替换为-t ;
f2=subs(f1,t,2*t); %将f1函数中的t替换为2t;即压缩或
subplot(4,1,3), plot(t, f3), hold on; %同时显示f3和f1 plot(t, f1, ‘--’) ; axis([-5 5 -2.3 2.3]), grid on set(gca, 'xtick', [-4 -2 0 2 4]), set(gca, 'ytick', [-2 0 2]); subplot(4,1,4), plot(t, f4), hold on plot(t, f1, ‘--’), plot(t, -f1 ,‘--’); 点 上画虚线 axis([-5 5 -1.2 1.2]), grid on set(gca, 'xtick', [-4 -2 0 2 4]), set(gca, 'ytick', [-1 0 1]) ‘--’表示在相应的 %在相应的线上画虚线
• 在command windows下,输入:
t=1:10回车后,显示t=1,2,……t=10 如换成:t=1:10; 后,则不显示 (多分号) 若换成:t=1:0.01:10; • 如画余弦波形: (0.01为步长)
t=1:0.01:10;
plot(t,cos(t)); 若间隔较大, t=1:0.1:10; plot(t,cos(t)); • 以上命令不能保存 %波形感觉平滑
信号表示及变换课程设计

信号表示及变换课程设计一、课程目标知识目标:1. 学生能理解并掌握信号表示的基本概念,包括连续信号和离散信号的分类及特点。
2. 学生能够描述信号的时域和频域特性,并运用数学表达式进行表示。
3. 学生能够掌握常见信号变换的原理,如傅里叶变换、拉普拉斯变换和Z变换,并了解它们在信号处理中的应用。
技能目标:1. 学生能够运用数学工具绘制并分析简单信号的波形。
2. 学生能够运用傅里叶变换等方法将时域信号转换到频域,并分析信号的频谱特性。
3. 学生能够通过实例练习,掌握信号变换的基本操作,解决实际问题。
情感态度价值观目标:1. 学生通过本课程的学习,培养对信号处理科学的兴趣,增强探索科学和技术问题的热情。
2. 学生能够认识到信号表示及变换在工程技术和日常生活中的重要性,增强学习的责任感。
3. 学生在小组合作学习中培养团队协作意识,学会尊重他人意见,提高沟通与解决问题的能力。
课程性质分析:本课程属于电子信息学科的基础课程,通过理论教学与实例分析相结合的方式,使学生掌握信号处理的基本概念和方法。
学生特点分析:考虑到学生所在年级的特点,他们对基础数学知识和物理概念已有一定了解,但对信号处理的高阶概念尚属初识。
因此,课程设计应注重由浅入深,循序渐进。
教学要求:1. 教学中注重理论与实践相结合,强调学生的动手操作能力。
2. 通过问题驱动的教学方法,引导学生主动思考,提高解决问题的能力。
3. 教学评估关注学生在知识掌握、技能运用和情感态度价值观方面的全面发展。
二、教学内容本课程教学内容主要包括以下几部分:1. 信号的分类及表示方法- 连续信号与离散信号的区分及特点- 时域信号与频域信号的分析方法- 数学表达式和波形图的绘制2. 常见信号变换原理及操作- 傅里叶变换原理及其应用- 拉普拉斯变换和Z变换的基本概念- 信号变换在实际工程中的应用案例分析3. 教学实例与实验操作- 选取典型信号进行分析,如正弦信号、方波信号等- 通过实验操作,观察信号变换前后的波形变化- 结合实际问题,运用所学知识解决信号处理问题教学大纲安排:第一周:信号分类及表示方法第二周:时域信号与频域信号分析第三周:傅里叶变换原理及操作第四周:拉普拉斯变换和Z变换基本概念第五周:教学实例与实验操作教材章节关联:本课程教学内容与教材中以下章节相关:- 第三章 信号的分类与表示- 第四章 信号变换原理- 第七章 信号变换的应用教学内容确保科学性和系统性,以帮助学生扎实掌握信号表示及变换相关知识。
实验一--连续时间信号在Matlab中的运算

实验一连续时间信号在Matlab 中的运算一、实验目的1、学会运用Matlab 进行连续时间信号的时移、反褶和尺度变换。
2、学会运用Matlab 进行连续时间信号相加、相乘、微分、积分和卷积运算。
3、观察并熟悉这些信号的波形和特性。
二、实验原理1、连续时间信号的表示连续信号的表示方法有两种:符号推理法和数值法。
从严格意义上讲,Matlab 数值计算的方法不能处理连续时间信号。
然而,可利用连续信号在等时间间隔点的取样值来近似表示连续信号,即当取样时间间隔足够小时,这些离散样值能被Matlab 处理,并且能较好地近似表示连续信号。
2、信号的时移、反褶和尺度变换信号的平移、反转和尺度变换是针对自变量时间而言的,其数学表达式和波形变换中存在着一定的变化规律。
从数学表达式上来看,信号的上述所有计算都是自变量的替换过程。
所以在使用Matlab 进行连续时间信号的运算时,只需要进行相应的变量代换即可完成相关工作。
3、连续时间信号的微分和积分连续时间信号的微分运算,可使用diff 命令函数来完成,其语句格式为:diff(function, ‘variable ',n) 。
其中,function 表示需要进行求导运算的函数,或者被赋值的符号表达式;variable 为求导运算的独立变量;n 为求导阶数,默认值为一阶导数。
连续时间信号积分运算可以使用int 命令函数来完成,其语句格式为:int(function, ‘variable ',a, b) 。
其中,function 表示被积函数,或者被赋值的符号表达式;variable为积分变量;a为积分下限,b为积分上限,a和b默认时则求不定积分。
4、信号的相加和相乘运算信号的相加和相乘是信号在同一时刻取值的相加和相乘。
因此Matlab 对于时间信号的相加和相乘都是基于向量的点运算。
5、连续信号的卷积运算卷积积分是信号与系统时域分析的重要方法之一。
定义为:f (t) f1(t) f2 (t) -f1( )f2(t )dMatlab 进行卷积计算可通过符号运算方法和数值计算方法实现。
实验1 信号的时域描述与运算
实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB 表示及其可视化方法。
2. 掌握信号基本时域运算的MATLAB 实现方法。
3. 利用MATLAB 分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB 表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB 中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB 并不能处理连续时间信号,在MATLAB 中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
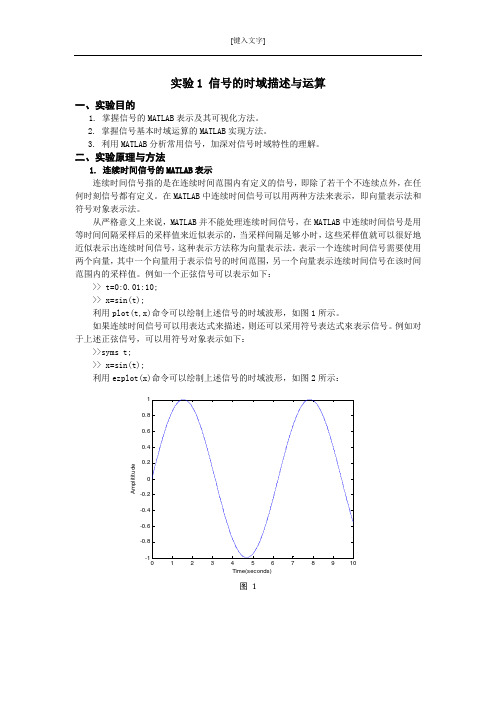
例如一个正弦信号可以表示如下:>> t=0:0.01:10; >> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>>syms t; >> x=sin(t);利用ezplot(x)命令可以绘制上述信号的时域波形,如图2所示:图 1Time(seconds)A m p l i t i t u d e图表 2matlab 提供了一些函数用于常用信号的产生,例如阶跃信号、脉冲信号、指数信号、正弦信号等,表中列出了一些常用的基本函数。
常用的信号产生函数2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
1)相加和相乘信号相加和相乘指两信号对应时刻的值相加和相乘,对于两个采用向量表示的可以直接使用算术运算的运算符“+”和“*”来计算,此时要求表示两信号的向量时间范围和采样间隔相同。
沈阳理工大学信号与系统课程设计 常用连续时间信号的可视化及信号的尺度、奇偶分解运算

成绩评定表课程设计任务书摘要MATLAB目前已发展成为由MATLAB语言、MATLAB工作环境、MATLAB图形处理系统、MATLAB数学函数库和MATLAB应用程序接口五大部分组成的集数值计算、图形处理、程序开发为一体的功能强大的系统。
本次课程设计则在深入研究连续时间信号傅里叶级数分析理论知识的基础上,利用MATLAB强大的图形处理功能、符号运算功能以及数值计算功能,通过MATLAB编程进行图形功能仿真,从而实现连续时间周期信号频域分析的仿真波形,包括以下内容:用MATLAB实现常用连续时间信号的时域波形;用MATLAB实现信号的时域运算;用MATLAB实现信号的时域变换;用MATLAB实现信号简单的时域分解;用MATLAB实现连续时间系统的卷积积分的仿真波形;用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形;用MATLAB 实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形。
关键词:MATLAB;图形处理;连续时间信号;目录1.MATLAB简介 (1)2.常用连续时间信号的波形 (2)2.1 常用连续时间信号的基本原理 (2)2.2 编程设计及实现 (2)2.3 运行结果及其分析 (5)3.常用连续时间信号的尺度变换 (8)3.1编程设计及实现 (8)3.1.1矩形波—尺度变换 (8)3.1.2三角波—尺度变换 (8)3.2运行结果及其分析 (10)4.常用连续时间信号的奇偶分解 (11)4.1 信号的奇偶分解原理 (11)4.2 编程设计及实现 (12)4.2.1对信号进行奇偶分解 (12)4.2.2将奇偶分量合并为原信号 (12)4.3运行结果及其分析 (13)4.3.1对信号进行奇偶分解 (13)4.3.2将奇偶分量合并为原信号 (14)5.结论 (15)6.参考文献 (16)1、 MATLAB简介1.1 MATLAB语言功能MATLAB是一个高精度的科学计算语言,它将计算、可视化编程结合在一个容易使用的环境中,在这个环境中,用户可以把提出的问题和解决问题的办法用熟悉的数学符号表示出来,它的典型使用包括:(1)数学和计算;(2)运算法则;(3)建模、仿真;(4)数值分析、研究和可视化;(5)科学的工程图形;(6)应用程序开发,包括创建图形用户接口。
信号与系统实验报告连续时间信号的时域分析

连续时间信号的时域分析一、 实验目的1、 掌握连续时间信号时域运算的基本方法;2、 掌握相关格式的调用格式及作用;3、 掌握连续信号的基本运算;4、 掌握利用计算机进行卷积的运算的原理和方法;5、 熟悉连续信号卷积运算函数conv 的应用;二、 实验原理信号的基本运算包括信号的相加(减)和相乘(除。
信号的时域变换包括信号的平移、翻转、倒相尺度变换等,由以下公式所描述:1、 相加(减):12(t)f (t)f (t)f =±2、 乘:12f(t)f (t)f (t)=⨯3、 延时或平移:0f(t)f(t t )→-,0t 0>时右移,0t 0<时左移4、 翻转:→f(t)f(-t)5、 尺度变换:()()f t f at →,1a >时尺度缩小,1a <时尺度放大,0a <时还必须包含翻转6、 标量相乘:()()f t af t →7、 倒相:()()f t f t →-8、 微分:()()df t f t dt→ 9、 积分:()()tf t f d ττ-∞→⎰10、 卷积:12()()*()f t f t f t =三、 验证性实验1、 连续信号的相加>> clear all;>> t=0:0.0001:3;>> b=3;>> t0=1;u=stepfun(t,t0);>> n=length(t);>>fori=1:nu(i)=b*u(i)*(t(i)-t0);end>> y=sin(2*pi*t);>> f=y+u;>>plot(t,f);>>xlabel('时间(t)');ylabel('幅值f(t)');title('连续信号的相加');2、 连续信号的相乘>> clear all;>>t=0:0.0001:5;>>b=3;>>t0=1;u=stepfun(t,t0);>>n=length(t);>>for i=1:n>>u(i)=b*u(i)*(t(i)-t0);>>end>>y=sin(2*pi*t);>> f=y.*u;>>plot(t,f)>>xlabel(‘时间(t)’);ylabel(‘幅值f(t)’);title(‘连续信号的相乘’);3、 移位>> clear all;>> t=0:0.0001:2;>> y=sin(2*pi*t);>> y1=sin(2*pi*(t-0.2));>>plot(t,y,'-',t,y1,'--')4、 尺度变换>> clear all;>>t=0:0.0001:1;>>a=2;>>y=sin(2*pi*t);>>y1=sin(2*a*pi*t);>>subplot(2,1,1);>>plot(t,y);>>ylabel('y(t)');xlabel('t');>> title('尺度变换');>>subplot(2,1,2)>>plot(t,y1);>>ylabel('y1(t)');xlabel('t');四、 设计性实验1、 已知信号1f (t)(t 4)[U(t)U(t 4)]=-+--,2(t)sin(2t)f π=,用MATLAB 绘出下列信号的时域波形。
时域连续信号的表示及运算实验报告

姓名: 周强 班级: 电信1004班 学号: 201004135136实验1 时域连续信号的表示及运算一、 实验目的1.掌握常用时域连续信号的MA TLAB 表示方法。
2.掌握连续信号的基本运算,包括信号相加与相乘、微分与积分、平移、反转、尺度变换、奇偶分解、卷积积分等。
二、 实验原理及方法MATLAB 利用连续信号在等时间间隔点的采样值来近似表示连续信号。
三、 实验内容及步骤1. 利用MATLAB 命令画出下列连续信号的波形图。
(1))()2(t u e t--源代码 (1 ) )()2(t u e t -- 图像 t=0:0.001:8;y=(2-exp(-t)).*heaviside(t);plot(t,y);grid onaxis([0 8 1 2])波形图(2))(cos t u源代码:t=0:0.01:2*pi;y=heaviside(cos(t));plot(t,y);grid onaxis([0 2*pi 0 1])波形图(3)产生幅度为1、周期为1、占空比为0.5的周期矩形信号。
源代码t=0:0.01:8; 波形图y=heaviside(sin(2*pi*t));plot(t,y);grid onaxis([0 4 0 1.2]);2. 已知)(t f 的波形如图1-15所示,做出)()(t f t f +、)()(t f t f ⋅、)(t f 的微分、)(t f 的积分、)43(t f -的波形。
)(t f 的图像代码syms t yy=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);ezplot(t ,y);grid onaxis([0 4 -1.5 1.5]))(t f 的图像t )(t f 01121-图1-15)()(t f t f +源代码syms t y y1y1=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);y=y1+y1; )()(t f t f +波形图ezplot(t,y);grid onaxis([0 4 -2.1 2.1]))()(t f t f ⋅源代码syms t yy=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);ezplot(t ,y*y);grid onaxis([0 4 -2.1 2.1])波形图)(t f 的微分syms t y fy=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);f=diff(y,'t');t=0:0.01:4; )(tf的微分波形图ezplot(f,t);grid onf的积分)(t源代码syms t y f y1y=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);f=int(y,'t');t=0:0.01:4;ezplot(f,t);grid on波形图3(tf4)源代码syms t y1 yy1=t*(heaviside(t)-heaviside(t-1))+heaviside(t-2)-heaviside(t-1);y=subs(y1,t,3-4*t);ezplot(t ,y);grid onaxis([0 1.2 -1.2 1.2])波形图实验心得与小结:(1)学会了单位阶跃函数heaviside()的使用,掌握了用matlab画一些连续信号的波形图(2)掌握了对一些基本的函数求微分,积分,翻转,平移的方法,还有一些符号变量的使用(3)学会了如何利用三角函数的周期性画出周期性的单位阶跃函数体会:在学习的过程中只有不断的尝试,才能从其中学到一些东西,在上机的过程中,我们不能只会画几个图像就以为学会了,从理解到自己能熟练运用还有一段距离,只有不断的从实验中发现错误才能提高自己,才能有收获。
课程设计--连续时间信号和系统时域分析及MATLAB实现

课程设计任务书题目:连续时间信号和系统时域分析及MATLAB实现课题内容:一、用MATLAB实现常用连续时间信号的时域波形(通过改变参数,分析其时域特性)。
二、用MATLAB实现信号的时域运算三、用MATLAB实现信号的时域变换(参数变化,分析波形变化)1、反转,2、使移(超时,延时),3、展缩,4、倒相,5、综合变化四、用MATLAB实现信号简单的时域分解1、信号的交直流分解,2、信号的奇偶分解五、用MATLAB实现连续时间系统的卷积积分的仿真波形给出几个典型例子,对每个例子,要求画出对应波形。
六、用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形。
给出几个典型例子,四种调用格式。
七、利用MATLAB实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形。
给出几个典型例子,要求可以改变激励的参数,分析波形的变化。
时间安排:学习MATLAB语言的概况第1天学习MATLAB语言的基本知识第2、3天学习MATLAB语言的应用环境,调试命令,绘图能力第4、5天课程设计第6-9天答辩第10天指导教师签名:年月日目录摘要 (Ⅰ)1.绪论 (1)2.对课题内容的分析 (2)2.1连续时间信号概述 (2)2.2采样定理 (2)2.3总体思路 (2)3.设计内容 (2)3.1用MATLAB实现常用连续时间信号的时域波形 (2)3.1.1单位阶跃信号和单位冲击信号 (2)3.1.2正弦信号 (4)3.1.3指数信号 (5)3.1.4实指数信号和虚指数信号 (6)3.2用MATLAB实现信号的时域运算 (7)3.2.1相加 (7)3.2.2相乘 (8)3.2.3数乘 (9)3.2.4微分 (10)3.2.5积分 (12)3.3用MATLAB实现信号的时域变换 (13)3.4用MATLAB实现信号简单的时域分解 (15)3.4.1 交直流分解 (15)3.4.2 奇偶分解 (16)3.5用MATLAB实现连续时间系统的卷积积分的仿真波形 (18)3.6用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形 (19)3.7利用MATLAB实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形 (20)4.心得体会 (22)5.参考文献 (23)摘要本文介绍了基于MATLAB的连续时间信号与系统时域分析。
实验三 连续时间信号的时域基本运算

ቤተ መጻሕፍቲ ባይዱ
程序如下: syms t f=sym('(t/2+1)*(heavisi
de(t+2)-heaviside(t-2))') subplot(2,3,1) ezplot(f,[-3,3]) y1=subs(f,t,t+2) subplot(2,3,2) ezplot(y1,[-5,1]) y2=subs(f,t,t-2) subplot(2,3,3) ezplot(y2,[-1,5]) y3=subs(f,t,-t)
f (t), f1(t), f2 (t)
均为符号表达式, t 为符号变量。
上一页 下一页
1、加法 f (t) f1 (t) f 2 (t) 用符号运算命令来实现两个连续信号的
相加,并用ezplot命令绘制其结果波形。 Matlab的实现命令如下:
s=symadd(f1,f2) 或者s=f1+f2 ezplot(s)
上一页 下一页
6、倒相 即:将信号f(t)以横轴为对称轴对折得到
-f(t)。 Matlab的实现命令如下:
y= -f ezplot(y)
上一页 下一页
已知信号 f (t) (1 t ) [ (t 2) (t 2)]
2
分别求出下式数学表达式,并绘制其时 域波形。
f (t 2), f (t 2), f (t), f (2t), f (t)
上一页 下一页
实验要求 在计算机中输入程序,验证实验结果,
并将实验结果存入指定存储区域。 对于程序设计实验,要求通过对验证性
实验的练习,自行编制完整实验程序, 实现对信号的模拟,并得出实验结果。 在实验报告中写出完整的自编程序,并 给出实验结果
信号系统ppt课件

u(t- t0 )
1
0
t
t0
21
u(t)的性质:单边特性,即: 某些脉冲信号可以用阶跃信号来表示。
22
例1:
E
E
E
t
t
因为 所以,矩形脉冲G(t)可表示为
G1(t)
t0
t
23
例2: f(t)
1
1
1
0
1t
0
1t 0
1t
信号加窗或取单边
f(t)
t t0
24
符号函数
定义 可用阶跃表示
-1 0 1
2
t
证明
两边积分,
比例
由f ( 2 t )
f(t)
13
二、微分和积分
1、微分
1
1
t
20 1
34
0
1
4 01 3
t
0
-1
t
t
14
2、积分 f(t)
0
t f(t)=
0
t
积分运算可削弱毛刺噪声的影响
15
三 . 信号相加或相乘
1、相加:
t 0
t 0 t 0
t
t
t
16
2、相乘:
t
t
3、幅度变化
先平移后反转
f (t t0 )
1 20
f (t t0 )
1 20
1
-2
01 t
先反转后平移
1
1
-1 0
2t
0 t0-1 t0
2+t0
6
练习2:已知f(t)如图所示,求 y(t)=f(-3t+6)的波形。
实验二 连续时间信号在MATLAB中的运算

电子信息工程系实验报告课程名称:信号与系统实验项目名称:连续时间信号在MATLAB 中的运算 实验时间:2013-11-22班级:电信112班 姓名: 学号:一、实 验 目 的:1、学会运用MATLAB 进行连续信号的时移、反折和尺度变换;2、学会运用MATLAB 进行连续信号的相加、相乘运算;3、学会运用MATLAB 数值计算方法求连续信号的卷积。
二、实 验 环 境:1、Windows 72、MATLAB 7.1三、实 验 原 理:2.1信号的时移、反折和尺度变换信号的时移、反折和尺度变换是针对自变量时间而言的,其数学表达式与波形变换之间存在一定的变换规律。
信号的时移就是将信号数学表达式中的用替换,其中为正实数。
因此,()f t t 0t t ±0t 波形的时移变换是将原来的波形在时间轴上向左或者向右移动。
为波形()f t 0()f t t +()f t 向左移动;为波形向右移动。
信号的反折就是将表达式中的自变0t 0()f t t -()f t 0t ()f t 量用替换,即变换后的波形是原波形的y 轴镜像。
信号的尺度变换就是将表达式t t -()f t 中的自变量用替换,其中,为正实数。
对应于波形的变换,则是将原来的的波t at a ()f t 形以原点为基准压缩()至原来的,或者扩展()至原来的。
1a >1/a 01a <<1/a 上述可以推广到的情况。
0()f at t ± 2.2 MATLAB 数值计算法求连续时间信号的卷积用MATLAB 分析连续时间信号,可以通过时间间隔取足够小的离散时间信号的数值计算方法来实现。
可调用MATLAB 中的conv( )函数近似地数值求解连续信号的卷积积分。
如果对连续时间信号和进行等时间间隔均匀抽样,则和分别变为离散1()f t 2()f t t ∆1()f t 2()f t 序列和。
其中为整数。
当足够小时,和即为连1()f m t ∆2()f m t ∆m t ∆1()f m t ∆2()f m t ∆续时间信号和。
信号与系统第1章

1.2.2 典型信号 下面,我们将给出一些典型信号的表达式和波 形。 一、指数信号 指数信号的表达式为
f (t ) = K eα t
f (t )
Keα t (α > 0)
K
K e α t (α = 0 )
Keα t (α < 0)
0
t
二、正弦信号
正弦信号和余弦信号二者仅在相位上相差 2 ,统称为 正弦信号,一般写作 f(t)
冲激偶的性质 (1)冲激偶是奇函数,即
δ '(− t) = − δ '(t)
(2) (3)
f (t)δ (t) = f (0)δ (t) − f (0)δ(t)
' ' '
∫
( ∞ 2 ' ' δ (t) f (t)dt= − f (0) ) −∞
∞ ' −∞ ∞ 0
∫ δ (t −t ) f (t)dt=−f (t )
S E=1V
+ -
+ C
vc (t )
-
例:图中假设S、E、C都是理想元件 (内阻为0),当 t = 0 时S闭合,求电 容C上的电压。 解:由于S、E、C 都是理想元件,所 以,回路无内阻,当S 闭合后,C上的 电压会产生跳变,从而形成阶跃电 压。即: ⎧0 t < 0
vc (t ) = ⎨ ⎩1
例1:G (t )
E
f1 (t )
f 2 (t )
E
=
−
−
−
E
τ
2
τ
2
τ
2
t
τ
2
t
t
因为 f1 (t ) = Eu (t + ),
连续信号的时域描述与运算

续信号的时域描述与运算信号与系统课程实验报告1. 实验名称: 连续信号的时域描述与运算2. 实验目的1、通过绘制典型信号的波形,了解这些信号的基本特征。
2、通过绘制信号运算结果的波形,了解这些信号运算对信号所起的作用。
3. 实验原理1、如果一个信号在连续时间范围内有定义,则称该信号为连续时间信号,简称为连续信号。
从严格意义上来讲,MATLAB数值计算方法并不能处理连续信号,但是可利用连续信号在等时间间隔点的采样值来近似表示覅连续信号,即当采样间隔足够小时,这些离散采样值能够被MATLAB处理,并且能较好的近似表示连续信号一种方法是向量表示法,定义两个行向量f和t,当时间间隔取得足够小时,就可以得到f(t)的近似波形。
在这种方法中,主要的绘图函数是plot(t,y)另一种方法是符号运算表示法。
如果信号可以用一个符号表达式来表示,则可用ezplot命令绘制出信号的波形。
可以用sym()来产生符号表达式2、记住一些常用连续信号的MATLAB表示,并且用连续信号的基本运算产生需要信号如单位阶跃函数u(t),在MATLAB中用Heaviside()表示f1和f2的卷积运算,用conv(f1,f2)来产生。
4. 实验内容与仿真4.1 实验内容第一小节利用MATLAB命令画出下列信号的波形图。
(1)(t e-2)u(t)代码与波形图:(2)u(cost)代码与波形图:(3)周期矩形信号:幅度为1,周期为1,占空比为0.5代码与波形图:4.2实验内容第二小节已知f(t)波形,作出以下波形:1)f(t)+f(t)、f(t)*f(t)、f(t)微分、f(t)积分;代码:syms t ff=t.*(heaviside(t)-heaviside(t-1))-heaviside(t-1)+heaviside(t-2); subplot(221);h=ezplot(t,f+f);set(h,'LineWidth',3,'color','r');grid onsubplot(222);h=ezplot(t,f.*f);set(h,'LineWidth',3,'color','r');grid onsubplot(223);h=ezplot(t,diff(f,'t',1));set(h,'LineWidth',3,'color','r');grid on subplot(224);h=ezplot(t,int(f,'t'));set(h,'LineWidth',3,'color','r');grid on波形:2)f(3-4t)、f(1-t/1.5)、f(t)奇偶分量代码:波形:3)f(t)*f(3-4t) 代码:波形:5. 思考题答1)不一定相同,f(t+t0)可以是函数f(t)向左平移t0;而函数f(-t+t0)可以是函数f(t)向左平移t0后再反转,也可以是f(t)反转后再向右平移t0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成绩评定表课程设计任务书目录一、引言 (1)二、Matlab入门 (2)2.1 Matlab7.0介绍 (2)2.2利用Matlab7.0编程完成习题设计 (3)三、Matlab7.0实现连续时间信号时移、反褶、尺度变换的设计 (4)3.1常用连续时间信号的类别及原理 (4)3.2编程设计及实现 (4)3.3运行结果及其分析 (6)四、结论 (17)五、参考文献 (18)一、引言近年来,计算机多媒体教序手段的运用逐步普及,大量优秀的科学计算和系统仿真软件不断涌现,为我们实现计算机辅助教学和学生上机实验提供了很好的平台。
通过对这些软件的分析和对比,我们选择MATLAB语言作为辅助教学工具,借助MATLAB强大的计算能力和图形表现能力,将《信号与系统》中的概念、方法和相应的结果,以图形的形式直观地展现给我们,大大的方便我们迅速掌握和理解老师上课教的有关信号与系统的知识。
MATLAB是当前最优秀的科学计算软件之一,也是许多科学领域中分析、应用和开发的基本工具。
MATLAB全称是Matrix Laboratory,是由美国Mathworks公司于20世纪80年代推出的数学软件,最初她是一种专门用于矩阵运算的软件,经过多年的发展,MATLAB已经发展成为一种功能全面的软件,几乎可以解决科学计算中的所有问题。
而且MATLAB编写简单、代码效率高等优点使得MATLAB在通信、信号处理、金融计算等领域都已经被广泛应用。
它具有强大的矩阵计算能力和良好的图形可视化功能,为用户提供了非常直观和简洁的程序开发环境,因此被称为第四代计算机语言。
MATLAB 强大的图形处理功能及符号运算功能,为我们实现信号的可视化及系统分析提供了强有力的工具。
MATLAB 强大的工具箱函数可以分析连续信号、连续系统,同样也可以分析离散信号、离散系统,并可以对信号进行各种分析域计算,如相加、相乘、移位、反折、傅里叶变换、拉氏变换、Z 变换等等多种计算。
人们之间的交流是通过消息的传播来实现的,信号则是消息的表现形式,消息是信号的具体内容。
《信号与系统》课程是一门实用性较强、涉及面较广的专业基础课,该课程是将学生从电路分析的知识领域引入信号处理与传输领域的关键性课程,对后续专业课起着承上启下的作用. 该课的基本方法和理论大量应用于计算机信息处理的各个领域,特别是通信、数字语音处理、数字图像处理、数字信号分析等领域,应用更为广泛。
作为信号与系统的基本分析软件之一,利用MATLAB进行信号与系统的分析与设计是通信以及信息工程学科的学生所要掌握的必要技能之一。
通过学习并使用MATLAB语言进行编程实现课题的要求,对学生能力的培养极为重要。
尤其会提高综合运用所学理论知识进行分析问题、解决问题的能力,也便于将理论知识与实践相结合,并得以更好地掌握信号分析与处理的基本方法与实现。
这也将为后续相关的课程学习打下一定的基础,从而在以后相关课程设计与分析的时候达到对MATLAB的熟练应用与融会贯通。
二、Matlab入门2.1 Matlab7.0介绍Matlab7.0是美国Mathworks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。
它比Matlab的老版本提供了更多更强的新功能和更全面、更方便的联机帮助信息。
当然也比以前的版本对于软件、硬件提出了更高的要求。
MATLAB7.0提供了丰富的库函数(称为M文件),既有常用的基本库函数,又有种类齐全、功能丰富多样的的专用工具箱Toolbox函数。
函数即是预先编制好的子程序。
在编制程序时,这些库函数都可以被直接调用。
无疑,这会大大提高编程效率。
MATLAB7.0的基本数据编程单元是不需要指定维数的复数矩阵,所以在MATLAB环境下,数组的操作都如数的操作一样简单方便。
而且,MATLAB7.0界面友好,用户使用方便。
首先,MATLAB 具有友好的用户界面与易学易用的帮助系统。
用户在命令窗里通过help命令可以查询某个函数的功能及用法,命令的格式极为简单。
其次,MATLAB程序设计语言把编辑、编译、连接、执行、调试等多个步骤融为一体,操作极为简单。
除此之外,MATLAB7.0还具有强大的图形功能,可以用来绘制多姿多彩的图形,直观而形象。
在国内外Matlab 已经经受了多年的考验。
Matlab7.0功能强大,适用范围很广。
其可以用来线性代数里的向量、数组、矩阵运算,复数运算,高次方程求根,插值与数值微商运算,数值积分运算,常微分方程的数值积分运算、数值逼近、最优化方法等,即差不多所有科学研究与工程技术应用需要的各方面的计算,均可用Matlab来解决。
综上所述,在进行信号的分析与仿真时,MATLAB7.0无疑是一个强大而实用的工具。
尤其对于信号的分析起到了直观而形象的作用,非常适合与相关课题的研究与分析。
2.2利用Matlab7.0编程完成习题设计在熟悉了MATLAB7.0的基本界面之后,可以通过简单的编程与相关函数的调用,实现一些常用时间信号的可视化操作。
例如:编程实现正弦波的仿真。
程序如下,直接在命令窗口键入如下程序:t=0:0.001:2*pi;w0=2;phi=0;ft1=sin(w0*t+phi);plot(t,ft1)仿真图形如下:图a三、Matlab7.0实现连续时间信号时移、反褶、尺度变换的设计3.1常用连续时间信号的类别及原理在信号与系统中,常用的连续时间信号有三角波信号、指数信号、正余弦信号、抽样信号、单位阶跃信号、冲击信号等。
这些信号的归类都是按照函数取值的连续性与离散性划分的。
即如果在讨论的的时间间隔内,除若干不连续点之外,对于任意时间值都可以给出确定的函数值,此信号就称为连续信号。
在连续时间信号的时域运算中,信号的时移、反褶以及尺度变换都是常见的运算。
这些运算的方法都是直接对函数中的自变量t进行相应的变换,各变换的方法如下:(1)时移: t→t±a, 当a大于等于0时,t左移a个单位; 当a小于0时,t右移a个单位。
(2)反褶:t→-t, 函数沿纵轴反转180°。
(3)尺度变换:t→a*t,(a不等于0) t变为原来的1/a倍,a小于1时变宽,a大于1时变窄,等于1时保持不变。
在编写程序过程中,可以通过冒号运算符产生一个行向量定义自变量的取值范围,通过相关语句定义坐标的纵轴与横轴取值,通过调用plot或者ezplot函数可以实现相关运算的图形可视化及其仿真。
3.2编程设计及实现1.矩形波:t=-4:0.001:4;T=2;ft=rectpuls(t,T);plot(t,ft)axis([-4,4,-0.5,1.5])2.三角波:t=-3:0.001:3;ft=tripuls(t,4,0.5);plot(t,ft)3.阶跃函数:syms t yy=heaviside(t);t=-4:0.01:4;ezplot(y,t);grid on4.指数函数:t=0:001:10;A=1;a=0.4;ft=A*exp(a*t);plot(t,ft)5.抽样函数:syms t y fy=sinc(2*t);t=0:0.01:pi;ezplot(y,t);grid on6.正弦波:t=0:0.001:2*pi;w0=2;phi=0;ft1=sin(w0*t+phi);plot(t,ft1)7.余弦波:t=0:0.001:2*pi;w0=2;phi=0;ft1=cos(w0*t+phi);plot(t,ft1)3.3运行结果及其分析对应以上七个相关程序以及其中两个函数(含程序)相关运算的可视化及其仿真图如下:1:矩形波信号图12:三角波信号图2 3:阶跃函数信号图34:指数函数信号图4 5:抽样信号图56:正弦波图6 7:余弦波图78.1:三角波—时移 t→t-1图8.1程序如下:t=-3:0.001:3;ft=tripuls(t-1,4,0.5);plot(t,ft)8.2:三角波—反褶 t→-t图8.2程序如下:t=-3:0.001:3;ft=tripuls(-t,4,0.5);plot(t,ft)8.3:三角波—尺度变换 t→2t图8.3程序如下:t=-3:0.001:3;ft=tripuls(2*t,4,0.5);plot(t,ft)9.1:矩形波—时移 t→t+1图9.1程序如下:t=-4:0.001:4;T=2;ft=rectpuls(t+1,T);plot(t,ft)axis([-4,4,-0.5,1.5])9.2:矩形波—反褶 t→-t图9.2程序如下:t=-4:0.001:4;T=2;ft=rectpuls(-t,T);plot(t,ft)axis([-4,4,-0.5,1.5])9.3:矩形波—尺度变换 t→0.5*t图9.3程序如下:t=-4:0.001:4;T=2;ft=rectpuls(0.5*t,T);plot(t,ft)axis([-4,4,-0.5,1.5])四、结论本次课程设计过程中,使我<<对信号与系统>>这门课有了更深入的了解,也学会了使用MATLAB软件。
通过查阅了相关资料,我了解了通过使用rectpuls可以产生以零为中心的方波,tripuls(t、w、s)制定三角波的宽度为w斜率为s(-1<s<1),由于是第一次做信号与系统的课程设计,对于相关设计过程和分析方法以及MATLAB软件的使用并不大熟练。
但功夫不负有心人,最终还算顺利完成,这对我以后学习相关的课程以及进行更高层次的信号与系统设计都奠定了一定的基础。
设计过程中出现了一些问题,通过咨询老师和同学都得到了解决,这些都锻炼了我自主解决问题的能力。
但是我掌握了研究这类问题的方法,即问题解决的过程就是要从问题所表现出来的情况出发,通过反复推敲,作出相应判断,逐步找出问题的症结所在,从而一举击破。
在这次信号与系统课程设计过程中,尤其在使用MATLAB软件进行相关信号的仿真与分析时,这种分析解决问题的能力就更为重要。
学习任何知识,仅从理论上去求知,而不去实践、探索是不够的。
通过为期数天的MATLAB课程设计,我对MATLAB这个仿真软件有了更进一步的认识和了解。
在这数天时间里,我通过自己摸索,查阅资料,并且在指导老师的指导下完成了常用连续时间信号的编程与仿真;并最终将课程设计报告总结完毕。
在整个设计过程中我懂得了许多东西,也培养了独立思考和设计的能力,树立了对知识应用的信心,相信会对今后的学习工作和生活有非常大的帮助,并且提高了自己的动手实践操作能力,使自己充分体会到了在设计过程中的成功喜悦。
虽然这个设计做的不是太成功,但是在设计过程中所学到的东西是这次课程设计的最大收获和财富,使我终身受益。
