混凝土【结构设计】原理单筋截面承载力计算[001]方案
单筋梁截面承载力计算

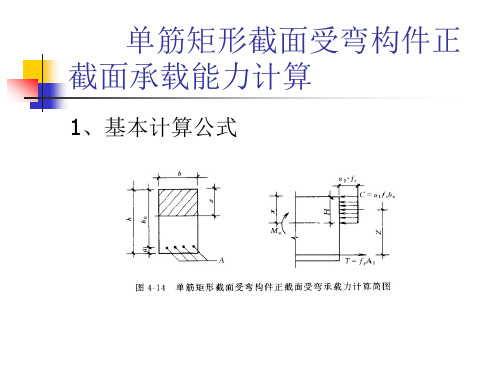
基本构件计算:单筋矩形梁正截面承载力计算一、计算简图二、基本公式1.公式法的三个基本公式:单筋矩形梁正截面受弯承载力计算的三个基本公式:s y c A f bx f =1α⎪⎭⎫ ⎝⎛-=≤201x h bx f M M c u α⎪⎭⎫ ⎝⎛-=≤20x h A f M M s y u式中 M —— 弯矩设计值;M u —— 受弯承载力设计值,即破坏弯矩设计值;c f 1α—— 混凝土等效矩形应力图的应力值; y f —— 钢筋抗拉强度设计值; s A —— 受拉钢筋截面面积; b —— 梁截面宽度; x —— 混凝土受压区高度;h 0 —— 截面有效高度,即截面受压边缘到受拉钢筋合力点的距离,h 0=h-a ; a —— 受拉钢筋合力点到梁受拉边缘的距离,当受拉钢筋为一排时,a =c+d/2; c —— 混凝土保护层厚度; d —— 受拉钢筋直径。
2.系数法的基本公式(1)系数的公式).(s ξ-ξ=α501(4-21)s αξ211--= (4-25)ξ-=α-+=γ5012211.ss (4-26)(2)基本公式 21201)5.01(bh f bh f M c s c ααξξα=-=0h A f M s s y γ=三、基本公式的适用条件1)防止超筋破坏b ξξ≤ 或 b ρρ≤ 或 0h x b ξ≤2)防止少筋破坏bh A A s s min min ,ρ=≥四、计算方法1.截面选择(设计题)按已知的荷载设计值作用下的弯矩M 设计截面时,常遇到下列两种情形: 情形1 : 已知:M 、混凝土强度等级及钢筋等级;构件截面尺寸b 及h 。
求:所需的受拉钢筋截面面积A s 。
[解](1)确定基本数据c f ;y f ;a h h -=0(2)计算有关系数21bh f Mc s αα=s αξ211--=ξ-=α-+=γ5012211.ss(3)计算受拉钢筋 0h f MA s y s γ=或 01bh f f A ycs αξ=(4)根据求得的受拉钢筋A s ,按照有关构造要求从附表20中选用钢筋直径和根数 (5)验算适用条件1)适用条件:b ξ≤ξ;2)若b ξ>ξ:需加大截面,或提高混凝土强度等级,或改用双筋矩形截面 3)验算bh A A m in m in ,s s ρ=≥。
单筋矩形截面正截面承载力计算方法

2 0
=91.0㎜< ξ b h0 < 不属超筋梁. 不属超筋梁.
2 × 80 × 10 6 = 415 415 1.0 × 11.9 × 200
2
=0.518×415=215.0mm
3. 计算 s ,并判断是否为少筋梁 计算A
As = α 1 f c bx f y
【 解 】 查 表 得 fc=9.6N/mm2 , ft =1.10N/mm2 , fy =300N/mm2 , ξb=0.550 , α1=1.0 , 结 构 重 要 性 系 数 γ0=1.0,可变荷载组合值系数Ψc=0.7 ,可变荷载组合值系数 计算弯矩设计值M 1. 计算弯矩设计值 钢筋混凝土重度为25kN/m3 ,故作用在梁上的恒荷载 钢筋混凝土重度为 标准值为 gk=10+0.25×0.55×25=13.438kN/m × × 简支梁在恒荷载标准值作用下的跨中弯矩为 Mgk=gk l02/8=13.438×62/8=60.471kN. m ×
对少筋梁,应将其受弯承载力降低使用(已建成工程) 对少筋梁,应将其受弯承载力降低使用(已建成工程) 或修改设计. 或修改设计. ④判断截面是否安全 则截面安全. 若M≤Mu,则截面安全. 【例3.2.1】 某钢筋混凝土矩形截面简支梁,跨中弯矩 】 某钢筋混凝土矩形截面简支梁, 设计值M=80kNm, 梁的截面尺寸 ×h=200×450mm, , 梁的截面尺寸b× 设计值 × , 采用C25级混凝土,HRB400级钢筋.试确定跨中截面纵 采用 级混凝土, 级钢筋. 级混凝土 级钢筋 向受力钢筋的数量. 向受力钢筋的数量.
则不属超筋梁.否则为超筋梁, 若x≤ξbh0,则不属超筋梁.否则为超筋梁,应加大截 面尺寸,或提高混凝土强度等级,或改用双筋截面. 面尺寸,或提高混凝土强度等级,或改用双筋截面. ③计算钢筋截面面积As,并判断是否属少筋梁
单筋T形裁面承载力计算时

单筋T形裁面承载力计算时
首先,我们需要了解一些相关的术语和性质:
1.截面面积:T形截面中,除去梁体部分后,单根筋材所占的横截面积。
2.配筋率:截面面积与整个截面面积的比值。
3.抗压面积:截面中钢筋的抗压面积,即配筋率乘以截面面积。
4.混凝土的抗压强度:表示混凝土在受压状态下能够承受的最大应力。
现在我们开始计算单筋T形裁面的承载力。
步骤1:计算抗压面积
首先确定截面中的钢筋数量及其直径,并计算出配筋率。
然后乘以截
面面积,得到抗压面积。
步骤2:计算混凝土的承载力
根据混凝土的抗压强度,可以计算出混凝土的承载力,即混凝土抗压
强度乘以抗压面积。
步骤3:计算钢筋的承载力
钢筋的承载力即为其受拉强度,可以根据钢筋的材料特性进行计算。
步骤4:比较混凝土和钢筋的承载力
将混凝土的承载力与钢筋的承载力进行比较,取较小值作为单筋T形
裁面的承载力。
需要注意的是,在实际工程中,还需要考虑混凝土和钢筋的粘结性能、受力状态等因素,以确定更加准确的结果。
实际计算中,还需要采用临界
状态法、弹性线性平衡法等方法进行计算。
请注意,上述步骤只是单筋T形裁面承载力计算的基本方法。
在实际
工程中,为了保证结构的安全性和稳定性,还需要进行更加复杂的计算和
分析,并参考相关的设计规范和标准。
单筋矩形截面正截面承载力计算方法

单筋矩形截面正截面承载力计算方法
在计算单筋矩形截面的承载力时,我们需要考虑两种主要的受力情况:剪力和弯矩。
以下是单筋矩形截面承载力计算的详细方法。
1.剪力承载力计算:
首先,计算纵向筋的贡献:
Vr = φ × As × fy /γs
其中,Vr为纵向筋的承载力,φ为抗剪强度折减系数,一般取0.75,As为纵向筋的截面面积,fy为纵向筋的抗拉强度设计值,γs为安全系数,一般取1.15
然后,计算混凝土的贡献:
Vc = φ × b × x × fcd /γc
其中,Vc为混凝土的承载力,b为矩形截面的宽度,x为截面混凝土
受剪应力点至受拉纵筋的距离,fcd为混凝土的抗压强度设计值,γc为
混凝土安全系数,一般取1.5
最终,剪力承载力为:
V=Vr+Vc
2.弯矩承载力计算:
首先,计算纵向筋的承载力:
Mr = φ × (As × fy) × (d - a/2) / γs
其中,Mr为纵向筋的弯矩承载力,d为矩形截面的有效高度,a为纵向筋至受压边缘的距离,As为纵向筋的截面面积,fy为纵向筋的抗拉强度设计值,γs为安全系数。
3.组合效应计算:
在实际情况中,剪力和弯矩通常是同时作用于单筋矩形截面的。
根据极限状态设计原则,剪力和弯矩的组合效应需要考虑。
计算组合效应时,可以根据相应的超信度进行组合,采用相应的抗风定额规定即可。
综上所述,单筋矩形截面的承载力计算主要包括剪力承载力和弯矩承载力的计算,并根据实际受力情况考虑组合效应。
详细的计算公式和参数需要根据具体情况进行设计和选择,以确保梁的安全可靠性。
混凝土截面正截面承载力计算方法

混凝土截面正截面承载力计算方法嘿,咱今儿就来说说这混凝土截面正截面承载力计算方法。
你想想啊,这混凝土就好比是建筑的脊梁骨,那承载力可太重要啦!要是没算好,这房子不就跟纸糊的似的,能安全吗?计算这混凝土截面正截面承载力,就像是走一条有点崎岖但又必须走对的路。
首先得搞清楚各种参数,就像你出门得知道带啥东西一样。
混凝土的强度等级啦,钢筋的规格啦,这些都得心里有数。
然后呢,根据不同的情况选择合适的计算方法。
这就好比你去不同的地方得选不同的交通工具,去近的地方走路就行,远的地方就得坐车或者坐飞机啦。
比如说单筋矩形截面,那计算起来可得仔细着点。
要考虑混凝土受压区的高度,钢筋的应力等等。
这可不能马虎,就跟你做饭放调料似的,多一点少一点味道可就差远了。
再说说双筋矩形截面,这就更复杂一些啦。
就像解一道很难的数学题,得一步一步来,稍有不慎就全错啦。
还有其他形状的截面呢,那计算方法又不一样啦。
你说这神奇不神奇?就好像每个人都有自己的脾气性格一样。
咱在计算的时候,可不能马马虎虎,得像对待宝贝一样小心翼翼。
你说要是算错了,那后果得多严重啊!房子倒了可不是闹着玩的。
这就好像你搭积木,要是底层没搭好,上面再怎么漂亮也得塌呀!所以啊,一定要把这混凝土截面正截面承载力计算准确了,才能让我们住的房子安心、放心。
那怎么才能算得准呢?这就得靠我们的知识和经验啦。
多学习,多实践,就像练功一样,时间久了自然就厉害啦。
你说这计算方法是不是很重要?咱可不能小瞧了它呀!不然到时候出了问题,那可就傻眼咯!大家可得重视起来呀,这可是关乎我们生活安全的大事呢!你说对不对?。
单筋矩形正截面受弯承载力计算公式

单筋矩形正截面受弯承载力计算公式根据图1和截面内力平衡条件,并满足承载能力极限状态计算表达式的要求,可得出如下基本计算公式:图1 单筋矩形截面梁板正截面受弯承载力计算简图∑x=0 f c bx=f y A s(1)∑M=0 KM≤f c bx(h0−)(2)式中M——弯矩设计值(N·mm);f c——混凝土轴心抗压强度设计值(N/mm2),按附表1–2取用;b——矩形截面宽度(mm);x——混凝土受压区计算高度(mm);h0——截面有效高度(mm);f y——受拉钢筋的强度设计值(N/mm2),按附表1–5取用;A s——受拉钢筋的截面面积(mm2);K——承载力安全系数, 按表1–7取用。
利用基本公式进行截面计算时,必须求解方程组,比较麻烦。
为简化计算,将式(1)、(2)改写如下:将ξ=x/h0代入公式(1)、(2),并引入截面抵抗矩系数αs,令αs =ξ(1–ξ)(3)则基本公式改写为:f c bξh0=f y A s(4)KM≤αs f c bh02(5)由式(4)可得:ρ= ξf c/f y基本公式是根据适筋破坏的情况推导出来的。
因此,它的适用条件为:(1)ρ≤ρmax或x ≤ξb h0或ξ≤ξb,以防止发生超筋破坏,ρmax=ξb f c/f y;基本公式是依据适筋构件破坏时的应力图形情况推导的,当受拉钢筋屈服的同时,受压区混凝土也达到极限压应变εcu,梁发生的临界破坏状态,就是适筋梁与超筋梁的界限。
但为了结构的安全,更有效地防止发生超筋破坏,,应用基本公式和由它派生出来的公式计算时,必须符合此条件。
(2)ρ≥ρmin,以防止发生少筋破坏钢筋混凝土梁板构件破坏时承担的弯矩等于同截面素混凝土梁板构件所能承担的弯矩时的受力状态,为适筋破坏与少筋破坏的分界。
这时梁板的配筋率应是适筋梁板的最小配筋率。
《规范》不仅考虑了这种“等承载力”原则,而且还考虑了混凝土的性质和工程经验等。
因此,基本公式应符合此条件。
单筋受弯构件正截面承载力计算

3.2 例题例4-1: 一钢筋砼矩形截面简支梁,计算跨度l 0=6.0m ,截面尺寸: b ×h =250mm ×600mm ,承受均布荷截标准值g k =15kN/m(不含自重),均布活截标准值q k =18KN/m ,一类环境,试确定该梁的配筋并给出配筋图。
解:1.选择材料,确定计算参数选用 C25级砼: f C =11.9N/mm 2 α1=1.0钢筋:HRB335级 f y =300N/mm 2 取C=25 ξb =0.55 a s =35 h 0=600-35=5652.确定荷载设计值,据《荷载规范》 取:γG =1.2 γQ =1.4恒载设计值:G =γG (g k +b ×h ×γ)=1.2(15+0.25×0.6×25)=22.5KN/m 活载设计值:Q =γQ ×q k =1.4×18=25.2kN/m3.确定梁跨中截面弯矩设计值M =()228181l Q G ql +=m KN .65.2140.67.47812=⨯⨯= 4.确定构件重要性系数0γ据《规范》:一般构件0γ=1.05.求受压区高度x由∑x=0 f y A s =1αf c bx ∑M =0 M=α1f c bx(h o -2x ) 联立求解可得:mm b f M h h x C 76.1462509.110.11065.2140.125655652621020=⨯⨯⨯⨯⨯--=--=αγ6.求受拉钢筋的面积A sA s =2137.145530076.1462509.110.1mm f bxf y C =⨯⨯⨯=α5.求截面抵抗矩系数αs226.05652509.110.11065.21426201=⨯⨯⨯⨯==bh f M C s αα 6.求ξ, A sξ=260.0226.0211211=⨯--=--s α 或查表:αs=0.26 → ξ=0.260 γs =0.87A s =26145687.0.5653001065.214mm r h f M so y =⨯⨯= 7.选择钢筋据《规范》附录B ,选用22,As=1520mm 钢筋净距: s =25373224252250>=⨯-⨯- 8.验算适用条件,据《规范7.2.1》x =147.76<75.31056555.00=⨯=h b ξ 或55.026.0=<=b ξξ据《规范9.5.1》, A s =1520 > ρmin bh 0=0.002×250×600=300ρmin =45f t /f y =45×1.27/300=0.0019=0.19% 均满足要求。
(word完整版)混凝土结构设计原理单筋截面承载力计算

单筋矩形截面承载力计算分为截面设计和截面复核。
一、截面设计已知:M 、混凝土和钢筋材料强度、截面尺寸b ×h 求:As计算步骤:1、获得as 、h 0、f y 、f c 、 ξb(as 估计:绑扎骨架1层取40mm,两层取65mm ,板取20mm 等) 2、由公式1c 0=b h -2xM f x α(),求x (解一元二次方程)3、判断是否为超筋: 0b b x x h ξ≤=4、由公式1c b y s f x f A α=,求As5、选配钢筋6、看是否为少筋。
具体计算公式:min max 0.2%, 45%?ty f f ρ⎧⎫⎪⎪⎨⎬⎪⎪⎩⎭== 00min ??s A hbh h ρρ= >==7、配筋,画配筋图习题3-1:梁截面尺寸=250500b h mm ⨯⨯,一类环境,HRB335钢筋,混凝土强度等级C25,M=125kN.m 。
计算受拉钢筋截面面积并绘图。
解:查表得11.9, 1.27,300,0.55c t y b f MPa f MPa f MPa ξ==== 假设钢筋按一层布置,则040,50040460s a mm h mm ==-=1)求受压区高度由公式1c 0=b h -2x M f x α()得: 612510=1.011.9250460-2xx ⨯⨯⨯⨯⨯()整理得:2920840340x x -+=120817,1030.55460253b x mm x mm h mmξ==<=⨯=大于梁高,舍去不超筋2)求受拉钢筋面积由公式1c b y s f x f A α=得:21c b 1.011.92501031021300s yf xA mm f α⨯⨯⨯===选择钢筋4(As=1256mm 2)或220+2(As=1137mm 2)最小配筋率:min 0.2%1.27max 0.2%, 45%max 0.2%, 45%300ty f f ρ⎧⎫⎧⎫⎪⎪⎪⎪=⎨⎬⎨⎬⎪⎪⎩⎭⎪⎪⎩⎭==⨯00min 12560.217%250465s A hbh h ρρ= =1.08% >⨯==不少筋3)配筋图实际的as=20+10+10=40mm,和假设一样,不必重新计算钢筋净距=(250—20*2-10*2-20*4)/3=37mm>25mm,满足要求二、截面复核已知:截面尺寸b 、h,M d ,材料强度,配筋As求:M u 或校核承载力: u M M >或u M M <求解步骤:1、获得as 、h 0、f y 、f c 、 ξb2、如有配筋图,校核钢筋布置,及验算是否少筋3、由公式1c b y s f x f A α=,求x ,4、判断是否超筋:0b b x x h ξ≤=5、由公式1c 0=b h -2u x M f x α()或y s 0=h -2u xM f A ()求M u ,校核是否能安全承载:,u u M M M M ><截面安全,截面不安全习题3—2:梁截面尺寸=200500b h mm ⨯⨯,一类环境,受拉钢筋采用2根直径为18的HRB335钢筋,As=509mm 2,混凝土强度等级C25,M=125kN 。
钢筋混凝土受弯构件正截面承载力计算—单筋矩形截面梁计算

受压混凝土的应力-应变关系
计算原则
2)等效矩形应力图
简化原则:受压区混凝土的合力大小不变;受压区混凝土的合力作用点不变。
等效矩形应力图形的混凝土受压区高度 x 1xn ,等效矩形应力图形的应力值 为 1 fc, 1、1 的值见下表。
表 1、1 值
混凝土强 度等级
≤C50
C55
C60
C65
C70
C75
(2)求跨中截面的最大弯矩设计值。
因仅有一个可变荷载,故弯矩设计值应有取下列两者中的较大值:
M 1 1.2g 1.4q l 2
8
1 1.2 5 1.4 10 5.02 62.5
8
M 1 1.35g 1.4 0.7q l 2
8
1 1.35 5 1.4 0.7 10 5.02 51.7
需要加固、补强
计算原则
1)基本假定
01 平截面假定。
02
钢筋的应力 s 等于钢筋应变 s 与其弹性模量 Es 的乘积,但不得大
于其强度设计值 fy,即
s sEs fv
03 不考虑截面受拉区混凝土的抗拉强度。
计算原则
04
受压混凝土采用理想化的应力-应变关系,当混凝土强度等级为
C50及以下时,混凝土极限压应变 cu=0.0033。
(1)受拉钢筋为4 25,As=1964 mm2; (2)受拉钢筋为3 18,As=763 mm²。
单筋矩形截面梁计算
解 查表得:
fc 9.6N/mm2
ft 1.10N/mm2
f y 300N/mm2 c 1.0
b 0.550
c 30mm
单筋矩形截面梁计算
(1)
d
25
h0 h c 2 450 30 2 408
单筋梁截面承载力计算

单筋梁截面承载力计算单筋梁是一种常见的钢结构梁,在计算其承载力时,需要考虑两种极限状态,即弯曲极限状态和局部破坏极限状态。
首先,我们来看弯曲极限状态的计算。
单筋梁在弯曲时,主要靠材料的受拉能力来承载荷载。
弯曲截面的受拉区域称为筋部,受压区域称为翼缘或者是受拉钢筋的折减后的面积。
在计算弯曲承载力时,需要考虑以下几个参数:1.混凝土的强度:一般使用混凝土的抗压强度来计算,在计算承载力时,一般假定混凝土为强度等级为C30的材料。
2.钢筋的强度:钢筋的强度也需要考虑,在计算承载力时,一般假定钢筋的强度等级为HRB3353.截面形状:单筋梁的截面形状可以是矩形、T形或者是箱形等,根据不同截面形状,计算方法也会有所不同。
4.截面尺寸:截面尺寸包括截面的宽度和高度,需要根据实际情况进行测量或者计算。
在计算弯曲承载力时,一般采用以下公式:M = αβfc*b*h^2/6其中,M为截面所受弯矩,α为混凝土强度参数,取值范围为0.5-0.95,β为形状系数,根据不同截面形状取不同值,fc为混凝土的抗压强度,b为截面的宽度,h为截面的高度。
下面我们来看局部破坏极限状态的计算。
局部破坏主要发生在梁的支座区域。
梁的支座区域受到的压力较大,容易出现局部压力过大而破坏的情况。
在计算局部破坏承载力时1.支座宽度:支座宽度是一个重要参数,在计算局部破坏时需要考虑。
2.支座深度:支座深度也是一个重要参数,需要根据实际情况进行测量或者计算。
3.材料强度:在计算局部破坏承载力时,需要考虑材料的强度,包括混凝土和钢筋的强度。
计算局部破坏承载力时,一般采用以下公式:N = γfcb*bhd其中,N为局部破坏时截面所受力的分力,γ为混凝土局部破坏的形状参数,取值范围为0.25-0.8,fcb为混凝土的抗压强度,b为支座宽度,h为支座深度,d为混凝土的有效高度。
综上所述,单筋梁截面承载力的计算涉及到材料的强度、截面形状及尺寸等参数。
通过以上的公式及参数计算,可以评估单筋梁的承载能力,为工程设计提供依据。
《混凝土结构设计原理》钢筋和混凝土受弯构件正截面承载力计算

《混凝土结构设计原理》钢筋和混凝土受弯构件正截面承载力计算钢筋和混凝土受弯构件正截面承载力计算是混凝土结构设计中的一项重要内容。
正截面承载力是指构件在弯曲荷载作用下所能承受的最大力。
本文将介绍正截面承载力的计算方法。
首先,钢筋和混凝土受弯构件的截面主要由混凝土和钢筋两部分组成。
混凝土的承载能力主要通过压应力进行传递,而钢筋则主要通过拉应力进行传递。
因此,在计算正截面承载力时,需要分别考虑混凝土和钢筋的承载能力。
对于混凝土的承载能力计算,一般采用极限平衡法或材料应力-应变关系来进行。
在极限平衡法中,混凝土的弯曲承载能力可以通过下式计算:Mrd = φ × α × W × z × (d - α/z)其中,Mrd表示混凝土的弯曲承载能力;φ为混凝土材料的折减系数,考虑了实际使用中存在的各种因素;α为混凝土抗压区高度与截面有效高度之比;W为混凝土抗压区的受压区面积;z为抗压区重心到截面受拉边缘的距离;d为截面的有效高度。
对于钢筋的承载能力计算,可以通过以下公式进行:Md = As × fy × (d - a/2)其中,Md表示钢筋的弯曲承载能力;As为钢筋的截面面积;fy为钢筋的屈服强度;d为截面的有效高度;a为混凝土抗压区高度。
当混凝土和钢筋的弯曲承载能力相等时,构件达到破坏状态。
因此,可以根据混凝土和钢筋的承载能力计算结果,来确定构件的正截面承载力。
需要注意的是,以上计算过程中涉及到的参数如α、z、d、a等都需要根据具体情况进行确定。
这些参数的取值与构件的几何形状、材料特性、受力状态等密切相关。
因此,在进行正截面承载力计算时,需要进行充分的分析和计算,并根据相关规范和标准进行校核。
总结来说,钢筋和混凝土受弯构件正截面承载力的计算是一个综合考虑混凝土和钢筋材料特性、构件几何形状和受力状态的过程。
通过合理的参数选择和计算方法,可以得到结构构件的正截面承载力,为混凝土结构设计提供依据。
单筋T形梁正截面承载力计算

单筋T形梁正截面承载力计算首先,单筋T形梁的截面形状决定了其抗弯性能。
截面一般包括上翼缘、下翼缘和腹板三个部分。
上翼缘主要承担拉力,下翼缘和腹板主要承担压力。
根据材料的强度和构件尺寸,可以计算出单筋T形梁的截面性能指标,如截面面积、截面惯性矩、截面模量等。
其次,单筋T形梁的承载力计算还要考虑由荷载引起的应力。
常见的荷载包括自重、活载、风载和地震载等。
这些荷载可以综合考虑,并转化为梁的等效荷载作用于梁上。
根据不同的受力情况,可以采用弹性理论或塑性理论进行计算。
弹性理论假设材料的应力和应变满足胡克定律,可以解析地计算出梁的最大应力和变形情况。
而塑性理论假设材料达到屈服应变时,应力保持不变,可以通过平衡条件和塑性转化准则进行计算。
在设计和计算中,还需要考虑梁的安全性。
常见的安全系数包括抗弯强度安全系数、极限状态安全系数和服务状态安全系数等。
抗弯强度安全系数是指梁的抗弯强度与设计荷载之比,一般要求大于1.5、极限状态安全系数是指梁在极限状态下的荷载与承载力之比,要求大于1.0。
而服务状态安全系数是指梁在使用过程中的荷载与承载能力之比,要求大于 1.0。
最后,计算单筋T形梁的承载力还需要考虑构件的受限状况。
单筋T形梁的受限状态一般有局部屈曲、整体侧扭和挤压等。
这些受限状态会影响梁的承载能力。
为了确保梁的良好工作性能,需要对梁的限制状态进行合理的分析和计算。
综上所述,单筋T形梁的承载力计算是一个综合考虑材料、截面形状、荷载、安全性和受限状况等多个因素的过程。
只有在合理选择计算方法和参数的基础上,才能保证梁的设计符合规范,并能满足工程实际需求。
因此,在设计和计算单筋T形梁的承载力时,需要根据具体情况进行详细分析,并结合相关理论和规范进行计算,以保证构件的安全可靠性。
钢筋混凝土梁的正截面承载力计算课件

目录
• 钢筋混凝土梁的基本知识 • 钢筋混凝土梁的正截面承载力计算方法 • 实际工程案例分析
PART 01
引言
课程背景
钢筋混凝土梁是土木工程中常用的结构形式,其正截面承载力是保证结构安全的重 要因素。
随着建筑行业的不断发展,对钢筋混凝土梁的正截面承载力计算提出了更高的要求。
钢筋混凝土的组成和特性
混凝土
钢筋混凝土梁
混凝土是一种建筑材料,由骨料(沙、 石)和水泥等材料混合而成,具有较 高的抗压强度和良好的耐久性。
钢筋混凝土梁是由混凝土和钢筋共同 组成的复合材料,具有较高的抗压和 抗拉强度,广泛应用于建筑结构中。
钢筋
钢筋是钢材的一种,用于增强混凝土 的抗拉强度和韧性,提高梁的承载能 力。
启示
实际工程中应充分考虑各种因素 对梁承载力的影响,加强监测和 维护,确保结构安全和稳定
PART 05
课程总结与展望
课程内容的回顾
钢筋混凝土梁的基本概念
正截面承载力的定义
钢筋混凝土梁是一种常见的建筑结构构件, 由混凝土和钢筋组成,具有较高的承载能 力和耐久性。
正截面承载力是指梁在垂直荷载作用下, 原理,通 过梁的正截面受力分析,推导 出承载力的计算公式。
考虑混凝土和钢筋的应力应变 关系,将混凝土和钢筋的承载 力进行整合,得到总承载力。
引入安全系数,考虑施工误差、 材料变异等因素,对计算结果 进行修正。
计算步骤和注意事项
根据受力情况,选 择合适的计算模型。
按照步骤进行计算, 注意公式的适用范 围和限制条件。
02
正截面承载力是梁设计中的重要 参数,直接关系到梁的承载能力 和安全性。
PART 03
钢筋混凝土受弯构件正截面承载力计算-混凝土结构设计原理

1 /171第四章 钢筋混凝土受弯构件正截面承载力计算本章学习要点:1、掌握单筋矩形截面、双筋矩形截面和T 形截面承载力的计算方法;2、了解配筋率对受弯构件破坏特征的影响和适筋受弯构件在各阶段的受力特点;3、熟悉受弯构件正截面的构造要求。
§4-1 概述一、受弯构件的定义同时受到弯矩M 和剪力V 共同作用,而轴力N 可以忽略的构件(图4—1). 梁和板是土木工程中数量最多,使用面最广的受弯构件。
梁和板的区别:梁的截面高度一般大于其宽度,而板的截面高度则远小于其宽度。
受弯构件常用的截面形状如图4-2所示。
图4-1二、受弯构件的破坏特性正截面受弯破坏:沿弯矩最大的截面破坏,破坏截面与构件的轴线垂直。
斜截面破坏:沿剪力最大或弯矩和剪力都较大的截面破坏。
破坏截面与构件轴线斜交。
进行受弯构件设计时,要进行正截面承载力和斜截面承载力计算。
2 /172图4—3 受弯构件的破坏特性§4—2 受弯构件正截面的受力特性一、配筋率对正截面破坏性质的影响配筋率:为纵向受力钢筋截面面积A s 与截面有效面积的百分比.sA bh 式中 s A —-纵向受力钢筋截面面积。
b -—截面宽度,0h —-截面的有效高度(从受压边缘至纵向受力钢筋截面重心的距离)。
构件的破坏特征取决于配筋率、混凝土的强度等级、截面形式等诸多因素,但配筋率的影响最大。
受弯构件依配筋数量的多少通常发生如下三种破坏形式: 1、 少筋破坏当构件的配筋率低于某一定值时,构件不但承载力很低,而且只要其一开裂,裂缝就急速开展,裂缝处的拉力全部由钢筋承担,钢筋由于突然增大的应力而屈服,构件立即发生破坏。
图4—4 受弯构件正截面破坏形态2、适筋破坏当构件的配筋率不是太低也不是太高时,构件的破坏首先是受拉区纵向钢筋屈服,然后压区砼压碎。
钢筋和混凝土的强度都得到充分利用.破坏前有明显的塑性变形和裂缝预兆。
3、超筋破坏当构件的配筋率超过一定值时,构件的破坏是由于混凝土被压碎而引起的。
单筋矩形截面受弯构件正截面承载能力计算精选全文
h
' f
h0
h
' f
2
的计算区别 5)在现浇混凝土楼盖体系中如何确定翼缘
的宽度
实际结构设计时,首先应根据楼(屋) 盖的布置,确定翼缘的宽度。
T型截面的设计
T型截面与矩形截面的差异: 形状上:T型截面有宽大的翼缘; 受力上:T型截面的受压区高度小; 受压区高度:在翼缘内,在翼缘外; 两种不同的受压区高度如何处理; 配筋形式:单筋、双筋等 配筋率如何计算
两种T型截面梁
受压区在翼缘内 受压区在翼缘外 受压区在翼缘内同矩形梁(已经解决,b'f ) 受压区在翼缘外,把它分解成T型梁计算
关键问题: 如何判别 如何分解
判别问题
判别问题的实质,是求受压区高度是否
超过了
h
' f
设计题判别:用弯矩平衡
校核题判别:用内力平衡
f y As
1
f
c
b
' f
h
' f
Mu
1
f
c
b
' f
h
' f
h0
h
' f
2
第一类型的计算公式
同矩形截面
第二类型的计算公式
1 fc
b
' f
b
h
' f
1 fcbx
f y As
M
1 fc
b
' f
b
h
' f
h0
h
' f
2
1
f
c
bx
h0
x 2
适用条件同矩形截面
M1
1 fc
《混凝土结构设计原理》钢筋和混凝土受弯构件正截面承载力计算

《混凝土结构设计原理》钢筋和混凝土受弯构件正截面承载力计算钢筋和混凝土受弯构件正截面承载力计算是结构设计中的一个重要部分,在实际工程中有着广泛的应用。
本文将介绍钢筋和混凝土受弯构件正截面承载力计算的原理和方法。
首先,正截面承载力计算主要涉及到两个方面:混凝土的承载力和钢筋的承载力。
混凝土的承载力主要包括混凝土本身的抗压强度和抗拉强度两个方面;钢筋的承载力主要包括钢筋的抗拉强度和屈服强度两个方面。
其次,正截面承载力计算的常用方法有弯矩优化法和极限平衡法。
弯矩优化法是指通过假设截面内部的混凝土和钢筋承受的应力分布,推导出正截面承载力的理论公式,并通过求解该公式来确定正截面承载力。
极限平衡法是指通过假设截面处于极限破坏状态,利用平衡方程推导出正截面承载力的上限,并通过比较上限值和实际载荷的大小来确定正截面承载力。
最后,具体进行正截面承载力计算时,需要根据受力情况确定正截面的受力模式。
一般情况下,正截面的受力模式可分为受压模式和受拉模式。
在受压模式下,混凝土为主要受力构件,钢筋主要起到约束混凝土的作用;在受拉模式下,钢筋为主要受力构件,混凝土主要起到传递受拉力的作用。
在受压模式下,可以通过计算混凝土的抗压承载力和钢筋的抗压承载力来确定正截面的承载力。
混凝土的抗压承载力可以通过抗压强度和截面积计算得到;钢筋的抗压承载力可以通过抗压强度和受压区域的钢筋面积计算得到。
在受拉模式下,可以通过计算混凝土和钢筋的抗拉承载力来确定正截面的承载力。
混凝土的抗拉承载力可以通过抗拉强度和截面积计算得到;钢筋的抗拉承载力可以通过抗拉强度和受拉区域的钢筋面积计算得到。
在实际工程中,还需要考虑正截面的变形性能。
正截面的变形性能主要包括截面的抗裂性能和抗挠性能。
抗裂性能可以通过计算混凝土和钢筋的抗裂承载力来进行评估;抗挠性能可以通过计算混凝土和钢筋的抗挠承载力来进行评估。
总结起来,钢筋和混凝土受弯构件正截面承载力的计算是一个综合考虑混凝土和钢筋两者抗压、抗拉承载力及变形性能的过程。
《混凝土结构基本原理》钢筋和混凝土受拉构件的截面承载力计算22页PPT

35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
谢谢!
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
《混凝土结构基本原理》钢 筋和混凝土受拉构件ቤተ መጻሕፍቲ ባይዱ截面
承载力计算
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单筋矩形截面承载力计算
分为截面设计和截面复核。
一、截面设计
已知:M 、混凝土和钢筋材料强度、截面尺寸b ×h 求:As
计算步骤:1、获得as 、h 0、f y 、f c 、 ξb
(as 估计:绑扎骨架1层取40mm ,两层取65mm ,板取20mm 等) 2、由公式1c 0=b h -2
x
M f x α(),求x (解一元二次方程) 3、判断是否为超筋: 0b b x x h ξ≤= 4、由公式1c b y s f x f A α=,求As
5、选配钢筋
6、看是否为少筋。
具体计算公式:
min max 0.2%, 45%?t y f f ρ⎧⎫⎪⎪⎨
⎬⎪⎪⎩
⎭
== 00
min ??s A h bh h ρρ= >=
=
7、配筋,画配筋图
习题3-1:梁截面尺寸=250500b h mm ⨯⨯,一类环境,HRB335钢筋,混凝土强度等级C25,M=125kN.m 。
计算受拉钢筋截面面积并绘图。
解:查表得11.9, 1.27,300,0.55c t y b f MPa f MPa f MPa ξ==== 假设钢筋按一层布置,则040,50040460s a mm h mm ==-= 1)求受压区高度
由公式1c 0=b h -2
x M f x α()得:
612510=1.011.9250460-2x x ⨯⨯⨯⨯⨯() 整理得:2920840340x x -+=
120817,1030.55460253b x mm x mm h mm ξ==<=⨯=大于梁高,舍去
不超筋
2)求受拉钢筋面积 由公式1c b y s f x f A α=得:
21c b 1.011.9250103
1021300
s y
f x
A mm f α⨯⨯⨯=
=
=
选择钢筋4
20(As=1256mm 2)或2
20+2
18(As=1137mm 2)
最小配筋率:
min 0.2%1.27max 0.2%, 45%max 0.2%, 45%300t
y f f ρ⎧⎫⎧⎫⎪⎪⎪
⎪=⎨
⎬⎨⎬⎪⎪⎩⎭⎪⎪⎩⎭
=
=⨯
00
min 12560.217%250465s A h
bh h ρρ= =1.08% >⨯=
=
不少筋 3)配筋图
实际的as=20+10+10=40mm ,和假设一样,不必重新计算
钢筋净距=(250-20*2-10*2-20*4)/3=37mm>25mm ,满足要求
二、截面复核
已知:截面尺寸b 、h ,M d ,材料强度,配筋As
求:M u 或校核承载力: u M M >或u M M <
求解步骤:1、获得as 、h 0、f y 、f c 、 ξb
2、如有配筋图,校核钢筋布置,及验算是否少筋
3、由公式1c b y s f x f A α=,求x ,
4、判断是否超筋:0b b x x h ξ≤=
5、由公式1c 0=b h -2
u x
M f x α()或y s 0=h -2
u x M f A ()求M u ,校核是否能安全承载:
,u u M M M M ><截面安全,截面不安全
习题3-2:梁截面尺寸=200500b h mm ⨯⨯,一类环境,受拉钢筋采用2根直
径为18的HRB335钢筋,As=509mm 2,混凝土强度等级C25,M=125kN.m 。
验算截面上承受弯矩为M=80kN.m 时是否安全?
解:查表得11.9,300,=1.27,0.55c y t b f MPa f MPa f MPa ξ=== 假设箍筋采用直径为6的钢筋
020+6+9=35,50035465s a mm h mm ==-=
min max 0.2%, 0.450.2%t y f f ρ⎧⎫⎪⎪
⎨⎬⎪⎪⎩⎭
==
min
005095000.55%=0.2%=0.215%200465465
s A h bh h ρρ===>⨯
由公式1c b y s f x f A α=得:
01300509
64.160.554652561.011.9200
y s
b c f A x mm h mm f b
ξα⨯=
=
=<=⨯=⨯⨯
则:
1c 0=b h -2
64.162u x
M f x M α⨯⨯⨯⨯()
=1.011.920064.16(465-)=66.11kN<=80kN
或
因此该梁截面不安全。
