实验模态分析
实验模态分析简介

工程振动与测试
(1)幅频图识别步骤如下:
c、由共振峰值Hm和阻
尼比求得刚度为
k
1
2Hm 1 2
d、由固有频率和刚度求 得质量为
m=k/ n2
Testing Techniques
工程振动与测试
(2)相频图 识别步骤如下:
a、由()=
-/2点确定系统的 共振频率pd,其位 置与阻尼无关,由
此n=pd 。
Testing Techniques
工程振动与测试
(1)幅频图识别步骤如下: a、由共振峰极值Hm求得半功率点幅值为
HP=0.707Hm,由半功率点HP的带宽求得衰减系 数近似值为
n (2 1)
2
b、由峰值位置得共振 频率pd,固有频率为
n pd2 n2
则
n
n
Testing Techniques
工程振动与测试
第15章 实验模态分析简介
模态分析实质上是一种坐标变换。其目的在于 把原物理坐标系统中描述的相应向量转换到“模态 坐标系统”中来描述。
在物理坐标系统中,弹性力和阻尼力往往和两 座标的相对位移与相对速度有关,即对应的矩阵为 非对角阵,对于有成千上万自由度的系统,解非对 角阵(或耦合方程)既费时又会产生很大误差,向 量并不一定正交。
幅频实部曲线和幅频虚部曲线表达式与幅频特性 曲线和相频特性曲线表达式的关系为
H ( ) [H R( )]2 [H I ( )]2
( )
H 1( ) H R ( )
arctg
2 1 2
Testing Techniques
工程振动与测试
测单 频自 响由 特度 性系 曲统 线的
实
这些特性曲线主要应用于参数识别。
模态分析实验报告

模态分析实验报告1.引言模态分析是一种常用的结构动力学方法,旨在研究结构在不同频率下的振动特性,对于结构设计和加固具有重要意义。
本实验旨在通过模态分析方法,研究一个简单的结构体系的固有频率和振型。
2.实验目标通过实验测量和计算,得到结构的第一、第二和第三固有频率,并利用模态分析方法绘制结构的振型图。
同时,通过实验结果对比,验证模态分析方法的有效性。
3.实验材料和方法(1)材料:实验所用的结构是一个简单的桥梁模型,由若干根长木棒组成。
(2)方法:悬挂测频仪对结构进行激振,通过麦克风捕捉振动信号,并用计算机进行分析和处理。
4.实验过程(1)组装结构体系:根据实验设计要求,组装简单桥梁模型,确保结构的稳定性和一致性。
(2)悬挂测频仪:将测频仪正确安装在结构体系的一侧,并调整好位置和角度。
(3)激振:根据测频仪的说明书,调节激振源的频率和幅值,使结构产生振动。
(4)数据记录:用麦克风将振动信号转化为电信号,并通过计算机采集和记录数据。
(5)模态分析:利用采集的数据,进行模态分析,计算结构的固有频率和振型。
(6)数据处理:整理和分析实验结果,绘制振型图并与理论值进行比较。
5.结果分析通过实验和数据处理,得到结构的第一、第二和第三固有频率分别为f1、f2和f3、根据模态分析方法,绘制结构的振型图。
将实验结果与理论值进行比较,进行误差分析、灵敏度分析等。
6.结论本实验利用模态分析方法,研究了一个简单的结构体系的固有频率和振型,并通过实验结果与理论值的比较,验证了模态分析方法的有效性。
通过本实验,我们更深入地理解了结构振动的基本原理和方法,具备了一定的模态分析实验技能。
7.实验总结本实验通过模态分析方法研究了结构的振动特性,对于结构设计和加固具有重要意义。
在实验过程中,我们遇到了一些困难和问题,通过积极探索和思考,取得了一定的实验成果。
但我们也发现了许多不足之处,如实验设计和数据处理的精确性等,需要进一步改进和完善。
第3章 实验模态分析的基本理论

实验模态分析第三章:实验模态分析的基本理论振动系统的特性可以用模态来描述:固有频率、固有振型(主振型)、模态质量、模态刚度和模态阻尼等。
建立用模态参数表示的振动系统的运动方程并确定其模态参数的过程使称为模态分析。
—种理解可以认为,振动系统的物理模型、物理参数和以物理参数表示的运动方程都是已知的,引入模态参数、建立模态方程的目的是为了简化计算,解除方程耦合,缩减自由度。
另一种理解可以认为,通过对实际结构的振动测试,识别振动系统的模态参数,从而建立起系统的以模态参数表示的运动方程,供各种工程计算应用。
试验模态分析指的是后一种过程,即通过振动测试(称模态试验),识别模态参数,建立以模态参数表示的运动方程这样一个过程。
1 多自由度系统振动基础回顾&&&++=M x C x K x f t []{}[]{}[]{}{()} 2实模态理论一个n 自由度线性定常振动系统,其运动方程可以如下表示:现对两端作付氏变换得:[]{}[]{}[]{}{()}M x C xK x f t ++=&&&2([][][]){()}{()}M j C K X F ωωωω−++=式中和分别是x(t)和F(t)的付氏变换,并有()X ω()F ω()()j t X x t e dt ωω+∞−−∞=∫()()j t F f t e dtωω+∞−−∞=∫(){()}{()}Z X F ωωω=111212122212()()()()()()()()()()n n n n nn Z Z Z Z Z Z Z Z Z Z ωωωωωωωωωω⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦L L L L L L L 1()[()]{()}{()}{()}X Z F H F ωωωωω−==2[][][]K M j C ωω=−+阻抗矩阵中各元素值无法在实际振动测试中获得,因为人们不可能在实际结构上固定其它坐标,令其不动,仪留下J坐标,待其作出响应;也不可能仅使某个坐标运动,在其余坐标上测量力。
模态分析方法与步骤

模态分析方法与步骤下面我将从模态分析的定义、方法、步骤和案例实践等方面进行详细介绍。
一、模态分析的定义模态分析是指通过对系统的不同动态模态(如结构模态、振动模态等)进行分析和评估,以揭示系统的特性、行为和潜在问题。
其目的是为了更好地了解系统的功能、性能、稳定性等,并为系统的优化提供依据。
二、模态分析的方法1.实验方法:通过实际测试和测量,获取系统的模态参数(如固有频率、阻尼比、模态形态等),从而分析系统的动态特性。
2.数值模拟方法:利用数学建模和计算机仿真技术,建立系统的动力学模型,并进行模拟分析,以获取系统的模态响应和模态特性。
3.统计分析方法:通过对大量历史数据或采样数据的分析,探索系统的模态变化规律和概率分布情况。
三、模态分析的步骤1.确定分析目标:明确需要进行模态分析的对象、目的和要求。
例如,是为了定位系统的故障、评估系统的稳定性、优化系统的结构等。
2.数据采集和处理:根据分析目标,确定所需的数据类型和采集方法,例如使用传感器进行采集或获取历史数据。
然后对采集到的数据进行处理,如滤波、时域变换、频域分析等。
3.建立模型:根据已有的数据和系统特性,建立适当的模型。
例如,对其中一结构物进行模态分析时,可以建立结构的有限元模型。
4.分析模态特性:利用实验、仿真或统计方法,分析系统的模态特性,如固有频率、振型等。
可以绘制频谱图、振型图等,以便直观地展示结果。
5.识别问题和改进方案:基于对系统模态特性的分析,识别潜在问题,并提出相应的改进方案。
例如,如果发现其中一模态频率太低,可能意味着系统存在过度振动或共振问题,需要采取相应的措施来改进。
6.验证和优化:对改进方案进行验证和优化,以确保其有效性和可行性。
可以通过迭代分析和实验评估来逐步完善方案。
四、模态分析的案例实践1.桥梁的模态分析:对大跨度桥梁的模态分析可以帮助提前发现潜在的共振问题,并优化桥梁的设计和结构。
例如,可以通过数值模拟方法对桥梁的振动特性进行分析,以确定固有频率和振型,并预测桥梁在不同外界激励下的动态响应。
模态分析实验报告一

实验一用不测力模态分析法测量简支梁的模态参数、实验目的(1)学习不测力实验模态分析方法的原理(2)掌握用不测力模态分析法测量结构固有频率、模态振型、模态阻尼比的方法、实验系统框图三、实验原理所谓不测力法就是在试验过程中不需要测量激励力的方法。
工程中的的大量结构和机器都是很难人工施加激励力的。
其结构的响应主要由环境激励引起的,而这些环境激励是既不可控又难以测量的。
不测力法只能利用系统的响应数据对固有频率、模态振型、模态阻尼或阻尼比这几个模态参数进行估计,而这几个模态参数已经能够满足绝大多数工程中结果动力特性分析的要求。
不测力法模态软件利用测量得到相应的自功率谱、互功率谱、传递率和相干函数进行模态参数估计。
前述的运行模态分析法(OMA属于不测力模态分析法。
不测力法也可分为解析法和图解法两种类型。
使用范围与测力法一致。
图解法也可选用自互功率谱综合法或传递函数法,解析法可选用随机子空间法(SSI)。
四、实验步骤简支梁的几何尺寸为:长(x向)625mm宽(y向)50mm使用不测力法做其z方向的的振动模态,实验过程如下。
1. 测点的确定可以将简支梁分出八等分,即九个结点,去掉两端的两个节点以及2号节点,共选取6个测点,如图所示。
实验时,将传感器放置于每一个等分点处。
2. 连接仪器将两个测量用的加速度传感器分别接入采集器的的通道1和通道23. 测量设置打开仪器电源,启动分析软件,选择频谱分析模式。
新建4个窗口,分别显示通道1和通道2的时间波形以及通道1和通道2的平均谱,平衡清零后,即可开始采样。
4. 参数设置(1)系统参数设置:采样频率:2kH z;采样方式:连续;触发方式:自由采集;平均方式:线性平均;平均次数:100次;时域点数:2048点;窗类型:海宁窗•(2)通道参数设置:参考通道:通道1。
工程单位和灵敏度:参考实验十。
本实验中,两个传感器的灵敏度必须设置正确。
模态参数:编写测点号和方向。
实验时,将其中一个传感器放置在参考点处,并在整个测试过程中该传感器位置不变,其通道的“几何参数(模态参数)”栏中“参考标识”打“V”,其余通道的“参考标识”打“X”;移动另外一个传感器进行测量,在每一批次的测试过程结束之后,都要对通道2的测点编号进行设置,具体做法与测力模态分法相似。
模态分析的应用及它的试验模态分析

模态分析的应用及它的试验模态分析模态分析是一种通过分析系统的模态特性来预测和改善系统性能的方法。
它可以应用于各种领域,包括机械工程、土木工程、航空航天工程、电力系统等。
在机械工程中,模态分析可以帮助设计人员了解结构的振动特性,以及在不同条件下结构的自然频率和振型。
这对于避免共振现象、减少结构疲劳和保证结构稳定性非常重要。
模态分析还可以用来优化设计,改善结构的刚度和减轻结构的重量。
在土木工程中,模态分析可以用来评估建筑物、桥梁和其他结构的振动响应。
通过模态分析,可以确定结构的临界风速、车辆通过时的振动响应等,以确保结构的安全性和使用寿命。
在航空航天工程中,模态分析可以帮助设计人员了解飞机、火箭等飞行器的自由振动特性。
通过模态分析,可以确定飞行器的固有振动频率和振动模态,并优化设计以减少结构的振动响应和降低噪音。
在电力系统中,模态分析可以用来评估系统的稳定性和动态响应。
通过模态分析,可以确定系统中存在的低频振荡模态,以及可能导致系统瓦解的致命模态。
这有助于设计人员优化系统的控制策略和改善系统的稳定性。
试验模态分析是通过实验测量来获取结构的模态参数,以进行模态分析的方法。
试验模态分析通常分为激励法和反馈法两种方法。
在激励法中,实验过程中对结构施加激励信号,并通过测量系统的响应信号来获取结构的模态参数。
常用的激励信号包括冲击信号和正弦信号。
通过分析结构响应信号的频谱特性,可以确定结构的自然频率和阻尼比。
在反馈法中,通过测量系统的响应信号,然后根据经验公式或模态参数识别算法,反推出结构的模态参数。
反馈法不需要对结构进行外部激励,因此更加方便实用,但也存在一定的理论假设和误差。
试验模态分析可以用于实际结构的模态识别和评估,因为它可以直接测量结构的实际响应,避免了理论模态分析中的近似和假设。
然而,试验模态分析需要在实际工程环境中进行,受到环境噪声、传感器布置等因素的影响,所以需要合理设计实验方案和选择适当的仪器设备。
Abaqus模态分析报告实验报告材料

Abaqus模态分析报告实验报告材料一、引言模态分析是结构动力学中的重要分析方法,它用于确定结构的固有频率和振型。
Abaqus 作为一款功能强大的有限元分析软件,为模态分析提供了高效、准确的解决方案。
本报告将详细介绍使用 Abaqus 进行模态分析的实验过程、结果以及相关分析。
二、实验目的本次实验的主要目的是通过 Abaqus 软件对给定的结构进行模态分析,获取其固有频率和振型,评估结构的动态特性,并为后续的结构设计和优化提供依据。
三、实验模型实验所分析的结构为一个简单的悬臂梁,其几何尺寸为长1000mm,宽 100mm,高 50mm。
材料属性为弹性模量 E = 21×10^11 Pa,泊松比ν = 03,密度ρ = 7800 kg/m³。
四、实验步骤1、模型建立在Abaqus/CAE 中创建部件,使用草图工具绘制悬臂梁的截面形状,然后通过拉伸操作生成三维实体模型。
定义材料属性,将弹性模量、泊松比和密度等参数输入到材料定义中。
划分网格,采用合适的网格类型和尺寸,以保证计算精度和效率。
2、边界条件设置在悬臂梁的固定端设置完全固定约束,即限制所有自由度。
3、分析步设置创建模态分析步,指定分析的模态阶数。
4、求解提交作业进行求解计算。
五、实验结果1、固有频率求解完成后,得到了悬臂梁的前 5 阶固有频率,分别为:一阶固有频率:f1 = 5234 Hz二阶固有频率:f2 = 31567 Hz三阶固有频率:f3 = 78912 Hz四阶固有频率:f4 = 125678 Hz五阶固有频率:f5 = 187534 Hz2、振型各阶固有频率对应的振型如下:一阶振型:悬臂梁在垂直方向上的弯曲振动,固定端振幅为 0,自由端振幅最大。
二阶振型:悬臂梁在水平方向上的弯曲振动,固定端振幅为 0,自由端振幅最大。
三阶振型:悬臂梁的扭转振动,固定端扭转角为 0,自由端扭转角最大。
四阶振型:悬臂梁在垂直和水平方向上的复合弯曲振动,振幅分布较为复杂。
试验模态分析范文

试验模态分析范文试验模态分析是指在试验条件下对被试个体的心理状态进行分析,通过对被试在不同条件下的行为和反应进行观察和记录,得出被试个体的心理特征和状态。
本文将从试验模态分析的定义、应用领域、研究方法和意义等方面展开论述。
试验模态分析是实验心理学中的一种重要研究方法,主要用于探究人的心理机制和心理过程,并进一步了解人的行为和反应规律。
在试验条件下,研究者可以对被试进行情绪、注意力、运动、学习、记忆等多个方面的测试,从而获取更准确的心理测量数据,深入分析人的心理特征和心理状态。
试验模态分析广泛应用于实验心理学的各个领域。
在人格心理学研究中,可以通过试验模态分析测量被试个体的人格特征,了解其个性特点和心理特质。
在认知心理学研究中,可以通过试验模态分析测量被试在不同认知任务中的注意力、记忆、思维等心理过程,探究人的认知机制和认知能力。
在发展心理学研究中,可以通过试验模态分析测量不同年龄段儿童在学习、记忆、情绪等方面的差异,揭示儿童心理发展的规律和特点。
试验模态分析有多种研究方法,常用的方法包括自我报告、行为观察、生理测量和脑电图记录等。
自我报告是最常用的方法之一,通过让被试回答问卷或进行口头陈述,了解其主观感受和意识体验。
行为观察是对被试的行为和反应进行直接观察和记录,可以了解被试的动作、交流和表情等行为特征。
生理测量是通过测量被试的生理指标,如心率、皮肤电导等,来揭示其心理状态。
脑电图记录是通过记录被试的脑电波,研究其脑部活动和神经机制。
试验模态分析具有重要的研究意义。
首先,它可以帮助研究者更准确地了解被试的心理特征和心理状态,揭示人的行为和反应之背后的心理机制和原因。
其次,试验模态分析可以为实验心理学的其他研究方法提供基础和依据,进一步深入研究人的心理过程和行为规律。
最后,试验模态分析还可以为心理疾病的诊断和治疗提供参考依据,帮助临床医生更准确地了解患者的心理状态和病情。
总之,试验模态分析是一种在试验条件下对被试个体心理状态进行分析的重要研究方法,广泛应用于实验心理学的各个领域。
结构模态分析实验报告

一、实验目的1. 理解结构模态分析的基本原理和方法;2. 掌握结构模态分析实验步骤和数据处理方法;3. 培养动手能力和分析问题的能力;4. 提高对结构动力性能的认识。
二、实验原理结构模态分析是研究结构在受到外部激励时,其自由振动特性的过程。
结构模态分析主要包括以下几个步骤:1. 建立结构模型:根据结构的特点,建立相应的力学模型;2. 划分单元:将结构划分为若干个单元,如梁、板、壳等;3. 单元刚度矩阵:根据单元的几何尺寸和材料特性,计算单元刚度矩阵;4. 总刚度矩阵:将单元刚度矩阵组装成总刚度矩阵;5. 求解特征值和特征向量:求解总刚度矩阵的特征值和特征向量,得到结构的固有频率和振型。
三、实验内容1. 实验设备:结构模态分析实验台、计算机、传感器、数据采集系统等;2. 实验材料:实验台结构、传感器、数据采集卡等;3. 实验步骤:(1)搭建实验台:将实验台结构固定在实验台上,确保结构稳定;(2)安装传感器:在实验台结构上安装传感器,用于测量结构的振动响应;(3)连接数据采集系统:将传感器与数据采集系统连接,设置采集参数;(4)进行实验:对实验台结构施加激励,采集结构的振动数据;(5)数据处理:对采集到的数据进行处理,计算结构的固有频率和振型。
四、实验结果与分析1. 实验数据:实验过程中,采集到实验台结构的振动数据,包括位移、速度、加速度等;2. 数据处理:对实验数据进行处理,计算结构的固有频率和振型;3. 结果分析:(1)固有频率:实验结果表明,实验台结构的固有频率分别为f1、f2、f3、f4、f5等;(2)振型:实验结果表明,实验台结构的振型分别为第1阶振型、第2阶振型、第3阶振型等;(3)分析:根据实验结果,分析实验台结构的动力性能,如刚度、稳定性等。
五、结论1. 通过本次实验,掌握了结构模态分析的基本原理和方法;2. 学会了结构模态分析实验步骤和数据处理方法;3. 提高了动手能力和分析问题的能力;4. 对结构动力性能有了更深入的认识。
实验模态分析

•Hale Waihona Puke 动力学优化设计方法实施过程
Ⅰ. 目标函数 1. 结构系统的频率特性: 为了避免共振,必须使结构的固有频率 避开激振力的频率(频 带 )。特别是对最低的前几阶频率。设结构前m阶频率是 i ,要 求经过动力学设计后相应频率的目标值是 i* ,按其偏差的加权平 方和最小来构造如下的目标函数:
J f (Pr ) Wi(ωi ωi* )2
最优解数学描述:
1 F (t , d ) max (1 f1 2 f 2 3 f 3 4 f 4 ) 4 s.t. W W0 , 10m m s2 20m m t d T1 tu , td T3 tu , d 0 D d1
式中, 分别为第1~4阶固有频率的加权系数,分别取
实验模态分析
第一个假设可以通过调节力幅比较频响曲线 第二个假设考虑激振与传感器附加质量对系统频响 函数影响 第三个假设是对响应测点布置的数量 第四个假设是测量频响函数的对比(A/B)(B/A)
实验模态分析 模态试验的基本过程
建模 频响 设别 验证
实验模态分析
实验模态分析
频响函数的定义H1 H2 Hv 频响函数原始定义H1是输出响应(如位移)频谱除以输入力频谱H1(ω) = X(ω) / F(ω),它不能用平均减少噪声,改为 H2(ω) = X(ω)·F(ω)* / F(ω)·F(ω)*= Pxf / Pff Hv(ω) = X(ω)·X(ω)* / F(ω)·X(ω)*= Pxx / Pfx
实验模态分析的实现方法及应用场合
实验模态分析的实现方法及应用场合
• 不测力法适用于桥梁及大型建筑、运行状态的机械设备、不易实现人 工激励结构的实验模态分析; • 单点拾振法和单点激励法适用于中小型结构及大型结构缩比模型的实 验模态分析; • 单点激励多点响应法(SIMO)适用于中小型结构及大型结构缩比模型的 精确实验模态分析;
桥梁模态分析实验报告(3篇)

第1篇一、实验目的本次实验旨在通过桥梁模态分析,了解桥梁结构的动力特性,包括自振频率、振型和阻尼比等。
通过实验,加深对桥梁结构动力响应分析的理解,为桥梁设计、维护和检测提供理论依据。
二、实验原理桥梁模态分析是研究桥梁结构动力响应的一种方法,通过分析桥梁结构的振动特性,可以了解其在受到外部激励时的响应情况。
实验原理主要包括以下几个方面:1. 振动方程:根据牛顿第二定律,桥梁结构的振动方程可以表示为:\[ m\ddot{u} + c\dot{u} + ku = F(t) \]其中,\( m \) 为质量矩阵,\( c \) 为阻尼矩阵,\( k \) 为刚度矩阵,\( u \) 为位移向量,\( F(t) \) 为外部激励。
2. 特征值问题:桥梁结构的振动方程是一个齐次方程,当外部激励为零时,解的形式为:\[ m\ddot{u} + c\dot{u} + ku = 0 \]通过求解该齐次方程的特征值问题,可以得到桥梁结构的自振频率和振型。
3. 模态参数识别:在实际工程中,由于测量误差和外界因素的影响,无法直接得到桥梁结构的自振频率和振型。
因此,需要通过实验手段进行模态参数识别。
常用的方法包括时域分析法、频域分析法和时频分析法等。
三、实验设备1. 桥梁模型:本次实验采用一根简支梁作为桥梁模型,长度为3米,截面尺寸为100mm×100mm。
2. 激振器:用于施加外部激励,产生桥梁结构的振动。
3. 传感器:用于测量桥梁结构的振动响应,包括加速度传感器和位移传感器。
4. 数据采集系统:用于采集传感器信号,并进行实时处理和分析。
四、实验步骤1. 搭建实验模型:将简支梁固定在实验平台上,确保其稳定。
2. 安装传感器:在桥梁模型的适当位置安装加速度传感器和位移传感器。
3. 激振:通过激振器对桥梁模型施加正弦激励,产生桥梁结构的振动。
4. 采集数据:使用数据采集系统采集加速度传感器和位移传感器的信号。
5. 数据处理:对采集到的信号进行滤波、去噪等预处理,然后进行时域分析、频域分析和时频分析,识别桥梁结构的模态参数。
实验模态分析与参数识别报告

2022年春季学期讨论生课程考核(读书报告、讨论报告)考核科目:试验模态分析同学所在院(系):同学所在学科:学生姓名:学号:学生类别:考核结果阅卷人试验模态分析与参数识别报告模态分析可分为试验模态分析与工作模态分析等。
模态分析的最终目标是识别出系统的模态参数,为结构系统的振动分析、振动故障诊断和预报、结构动力特性的优化设计供应依据。
模态是机械结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。
这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。
1、模态分析原理模态分析的过程是将线性时不变系统振动微分方程组中的物理坐标变换为模态坐标,使方程组解耦,成为一组以模态坐标及模态参数描述的独立方程,坐标变换的变换矩阵为振型矩阵,其每列即为各阶振型。
[M]{X}÷[C]{X}+[K]{X}={F(∕)}⑴其中:[M]—质量矩阵,[K]一刚度矩阵,[C]一粘性阻尼矩阵,{尸⑺}一激励力的列阵。
振动模态是弹性结构固有的、整体的特性。
假如通过模态分析方法搞清晰了结构物在某一易受影响的频率范围内,各阶主要模态的特性,就可能预知结构在此频段内,在外部或内部各种振源作用下实际振动响应,而且一旦通过模态分析知道模态参数并赐予验证,就可以把这些参数用于设计过程,优化系统动态特性,或者讨论把该结构连接到其他结构上时所产生的影响。
方程(1)经傅氏变换,可得频域内的振动方程:(-√ [ M] + j∖∖[q +[ ∕C]) {X(ιv)} = {F(w)}(2)对应于固有频率叼的固有振型或模态向量以幅值最大点为参考点的表达式为:M={X(叫)}∕X(叫)厘。
它们亦即简谐自由振动的主振型,满意以下关系式:([K]^[M])[∣ }z=O(3)此代数方程组的系数行列式等于零,即为特征方程式:[M], [K]为实数对称矩阵,[M] 正定,[K]为非负定,其特征值域和对应的特征向量为实数。
实验模态分析方法与应用概论

实验模态分析方法与应用概论引言:实验模态分析是一种用于研究结构动力学特性的方法,通过实验测量和数据分析,可以确定结构的固有频率、阻尼比以及模态形态等参数。
实验模态分析方法包括模态参数识别、模态不确定度评估和模型修正三个步骤。
本文将介绍实验模态分析方法的基本原理和常用应用。
一、实验模态分析方法的基本原理1.1模态分析的基本思想1.2模态参数识别在模态参数识别过程中,需要选择合适的激励信号和测量点位置,通过对结构的振动响应信号进行分析,得到结构的固有频率、阻尼比和模态振型等参数。
常用的模态参数识别方法包括傅里叶变换法、自相关法、互谱法和最小二乘法等。
1.3模态形态绘制在模态形态绘制过程中,通常需要在结构上布置加速度传感器或激光测振仪等测量设备,测量结构的振动响应信号。
然后,通过信号处理和数据分析技术,将实际测量的振动响应数据转化为结构的模态振型,并绘制成图像。
二、实验模态分析方法的应用2.1结构健康监测实验模态分析方法可以用于结构健康监测,通过定期对结构进行振动测试和模态分析,可以及时发现结构的损伤和变形等问题,为结构的维护和修复提供参考。
例如,在桥梁结构的健康监测中,可以通过模态分析方法来确定桥梁的固有频率和模态形态,从而判断桥梁的结构安全状况。
2.2结构参数识别实验模态分析方法还可以用于结构参数的识别。
通过对结构在不同工况下的振动响应信号进行测量和分析,可以确定结构的质量、刚度和阻尼等参数。
例如,在机械系统中,可以通过模态分析方法来识别机械系统的转子和轴系的质量和刚度参数,从而评估系统的性能和可靠性。
2.3结构优化设计实验模态分析方法还可以用于结构的优化设计。
通过对不同结构参数和材料的改变进行模态分析和比较,可以评估结构的动力特性,并选择最佳的设计方案。
例如,在汽车工程中,可以通过模态分析方法来优化汽车底盘的结构,提高汽车的悬挂系统和减震器的性能。
总结:实验模态分析方法是一种研究结构动力学特性的重要手段,通过实验测量和数据分析,可以确定结构的固有频率、阻尼比和模态振型等参数。
实验模态分析基础

实验模态分析基础实验模态分析是一种因果推断方法,它可以确定不同变量之间的因果关系。
它通常用于实验研究中,其中研究人员对一组受试者进行操作,在不同处理条件下观察和测量结果变量。
通过比较不同处理条件下的结果变量,研究人员可以确定不同变量之间的关系。
实验模态分析包括几个主要步骤。
首先,研究人员需要设计实验研究,以确定不同的处理条件和结果变量。
然后,研究人员将受试者随机分配到不同的处理条件中,并在每个处理条件下测量结果变量。
接下来,研究人员使用分析方法来确定主效应和相互作用效应。
最后,研究人员对结果进行解释和解读。
主效应和相互作用效应实验模态分析的目标是确定主效应和相互作用效应。
主要效应是指一个变量对结果变量的直接影响。
相互作用效应是指两个或多个变量之间的交互作用对结果变量的影响。
通过分析主效应和相互作用效应,研究人员可以确定变量之间的关系。
实验模态分析使用统计学方法来确定主效应和相互作用效应。
通常使用方差分析(ANOVA)来进行分析。
方差分析将总变差分解为组内变差和组间变差。
组内变差反映了随机误差的影响,而组间变差反映了处理条件的影响。
通过比较组内变差和组间变差,可以确定主效应和相互作用效应。
实验模态分析可以广泛应用于各个领域的研究中。
例如,在医学研究中,实验模态分析可以用来研究药物和治疗的效果。
在农业研究中,实验模态分析可以用来研究不同肥料对作物产量的影响。
在教育研究中,实验模态分析可以用来研究不同教学方法的效果。
总结实验模态分析是一种统计学方法,用于研究和解释不同变量之间的关系。
通过实验模态分析,我们可以确定主效应和相互作用效应,从而更好地理解变量之间的相互关系。
实验模态分析可以应用于各个领域的研究中,并为实践提供建议和决策。
7.6实验模态分析过程及案例

工程振动测试技术实验模态分析过程及案例实验模态分析主要是通过模态实验,测量系统的振动响应信号,或同时测量系统的激励信号、响应信号,从测量到的信号中,识别描述系统动力特征的有关参数。
主要内容有:物理参数识别:质量矩阵刚度矩阵阻尼矩阵主要内容有:模态参数识别:固有频率衰减系数模态矢量模态刚度模态阻尼实验模态分析模态分析系统一般由三部分组成1、激振系统2、测量系统3、分析系统有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)模态实验流程图基本步骤如下:1、确定实验模型,将实验结构支撑起来,(边界条件的确定)2、模态实验,激励实验结构(一般用锤击法),记录激励、响应的时间历程。
3、时间历程的数字处理,FFT求出传递(频响)函数。
4、参数识别(固有频率、衰减系数(阻尼比)、振型等)。
5、动画显示。
动画显示获得了模态矢量式后,实验结构各自由度的主振动就知道了,例如,在单一的第r 阶模态振动中,各自由度的响应为{}sin()r n t r r dr r x B e t −=ω+θA 12r ,,,N=动画显示如果将一个振动周期等分成若干个时间间隔(一般为40等分),在每一个时间间隔,各自由度的相互位置构成一幅画面,即主振型在此瞬时的形态,在屏幕上连续显示这些画面,可观察到一个连续运动的动画图形,这就是实验结构第r阶主振型的动画图形。
龙洗的实验模态分析艺术观赏龙洗和鱼洗是一种铜制圆盆,盆内铸有龙形花纹的称龙洗,铸有鱼形花纹者称鱼洗。
四点“喷水”盆边有双耳,当盆内盛水,双耳被搓动时,盆发出悦耳嗡呜。
四(六、八、十、十二)股珠泉喷起,可高达一尺有余。
洗的制作者恰好将盆内龙或鱼的嘴对准这四(六、八、十、十二)个点,珠泉似从龙或鱼口中喷出。
四点“喷水”十点“喷水”在进行龙洗的搓振运动分析中,要用到固有频率和模态的数据。
龙洗高为11.5cm,最大半径20cm,厚度约2mm,耳高4.5cm。
盆上测点共244个,布置在沿z向分布的五个圆周上,每个圆周均布48点,每个耳的上部有两个测点,如图所示。
试验模态分析实验报告
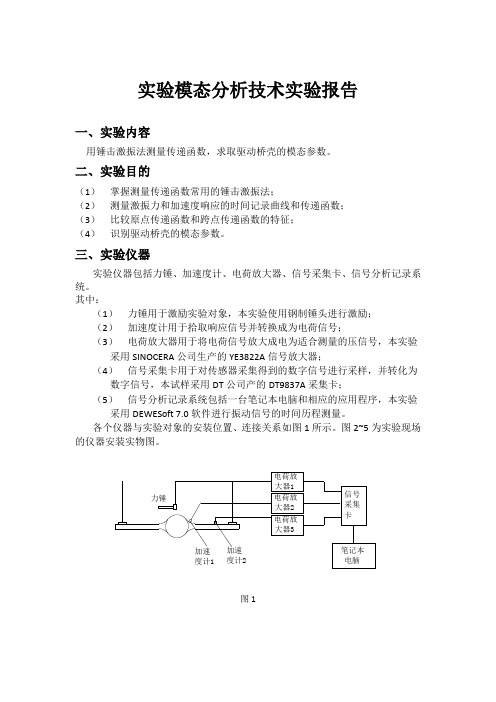
实验模态分析技术实验报告一、实验内容用锤击激振法测量传递函数,求取驱动桥壳的模态参数。
二、实验目的(1)掌握测量传递函数常用的锤击激振法;(2)测量激振力和加速度响应的时间记录曲线和传递函数;(3)比较原点传递函数和跨点传递函数的特征;(4)识别驱动桥壳的模态参数。
三、实验仪器实验仪器包括力锤、加速度计、电荷放大器、信号采集卡、信号分析记录系统。
其中:(1)力锤用于激励实验对象,本实验使用钢制锤头进行激励;(2)加速度计用于拾取响应信号并转换成为电荷信号;(3)电荷放大器用于将电荷信号放大成电为适合测量的压信号,本实验采用SINOCERA公司生产的YE3822A信号放大器;(4)信号采集卡用于对传感器采集得到的数字信号进行采样,并转化为数字信号,本试样采用DT公司产的DT9837A采集卡;(5)信号分析记录系统包括一台笔记本电脑和相应的应用程序,本实验采用DEWESoft 7.0软件进行振动信号的时间历程测量。
各个仪器与实验对象的安装位置、连接关系如图1所示。
图2~5为实验现场的仪器安装实物图。
力锤加速度计1加速度计2电荷放大器1电荷放大器2电荷放大器3信号采集卡笔记本电脑图1图2图3图4图5四、实验数据采集过程用安装有加速度传感器的力锤敲击实验对象上的某一点。
加速度传感器拾取激励力的信号。
安装在实验对象的某一观测点上的加速度计拾取响应信号,经电荷放大器后输入信号采集系统。
(1)仪器操作要点如下:a)锤子上的加速度传感器信号必须接入信号采集器的第一通道,响应信号依次接入信号采集器的其他通道;b)在信号采集分析系统上设置适当的参数,首先设置采集参数,如实验名(ASCⅡ码)、试验号(数字)、数据路径、结果路径、采样类型(多次触发)、单位类型(可变)、设置工程单位和标定值;c)采样菜单中选用多次触发,设置相应的参数,开始采样。
(2)敲击传感器附近的测点,测量原点传递函数;(3)敲击远离传感器的其他测点,测量跨点传递函数。
实验模态分析范文

实验模态分析范文实验模态分析是一种用于分析和测量人类认知过程的工具和方法。
它通过实验室实验和观察来研究人们在处理信息和做出决策时的心理模式和策略。
实验模态分析的目的是为了揭示人类认知的本质,以便更好地理解我们的思维和行为方式。
实验模态分析可以运用于许多领域,如心理学、认知科学、人机交互等。
在心理学中,实验模态分析可以帮助研究人员了解人们在特定条件下的思维方式和行为模式,揭示认知过程中的规律和原则。
在认知科学中,实验模态分析可以帮助科学家研究人类的信息处理机制,揭示认知系统的结构和功能。
实验模态分析通常包括以下步骤:实验设计、实验实施、数据收集和数据分析。
在实验设计阶段,研究人员需要确定实验的目的和研究问题,并制定相应的实验假设和方法。
在实验实施阶段,研究人员需要根据实验设计的要求进行实验操作,收集相关数据。
在数据收集阶段,研究人员可以使用各种手段和工具来收集数据,如心理测量、行为观察等。
在数据分析阶段,研究人员需要对收集到的数据进行整理和分析,以获取有关实验结果的信息和结论。
实验模态分析的关键是实验设计和数据分析。
在实验设计中,研究人员需要选择合适的实验条件和方法,并且确保实验结果的可靠性和有效性。
在数据分析中,研究人员需要使用统计方法和分析技术来处理和解释数据,以揭示人类认知过程中的模式和规律。
实验模态分析可以帮助我们更好地理解人类的思维和行为方式,对于改善教学、提高工作效率、优化人机交互等方面有着重要的意义。
它可以帮助我们发现认知瓶颈和误差,优化决策和问题解决过程,提高思维效率和创造力。
同时,实验模态分析也可以帮助我们设计更好的人机界面和交互系统,提升用户体验和满意度。
然而,实验模态分析也存在一些局限性。
首先,实验模态分析通常是在实验室条件下进行的,因此可能无法完全反映现实生活中的认知过程。
其次,实验模态分析依赖于研究对象的自述和行为观察,可能存在主观误差和偏差。
此外,实验模态分析需要具备一定的研究技能和专业知识,对研究人员的要求较高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、频响函数的测量
3 试件及激振器的支撑 激振器: 1.固支在结构物外。 2.悬挂在结构物外(低频)。 因使激振器悬挂系统的频率远低于结构的激励和弹性体共振频率。必 要时可在激振器上附加大的质量块以进一步降低悬挂频率。 3.采用隔振悬挂在结构物内部。
二、频响函数的测量
二、频响函数的测量
4 测点布置与激振点的选择 测点布置 1.能够较好地反映结构物的构型 2.能够充分显示结构的模态振型 例:一个梁单元无法求解简支梁的10个模态。计算上一般要求至 少20个单元,计算出的20阶模态,只有前10阶准确。 激励点 应避开节点节线。多点激励进行校合。 激励力的选择 在不破坏试件的情况下,尽可能大的激励力,有助于提高信噪 比。 不同大小的激励力,可以定性考查结构非线性的程度
三、曲线拟合方法
频域方法:基于FRFs数据的方法 经典方法,分析仪厂商自65年起开发。如美国HP系列分析 仪:3560、35665、35670、3565s、5423等;丹麦 B&K公 司的模拟分析仪;SISO、SIMO、MIMO识别方法; 最小二乘频域法LSFD 结构系统参数识别ISSPA 复模态指数函数CMIF 利用输入和输出数据进行模态参数识别: 单输入/单输出识别法(SISO) 单输入/单输出识别法(SIMO) 多输入/多输出识别法(MIMO)
二、频响函数的测量
3 试件及激振器的支撑 2.固支支承(Fixed-Fixed Support)。又称地面支承。 理论上容易实现,仿真计算时只需要将有关自由度约束即可。但 实现起来有困难。由于实现固支条件的结构不可能是刚性的,有弹 性。因此要实现固支支承,就必须要求支承结构的最低弹性体频率远 高于试验结构的最高分析频率。因此要实现高频模态的固支支承是很 困难的,一般情况下,中小结构能够实现的固支频率大约是400Hz, 特殊条件下小结构固支有可能超过1000Hz,但对大结构要实现固支 支承很困难。 3.实际工作状态支承。
二、频响函数的测量
2.3 随机激励(Random Excitation) 纯随机(Random),应采用汉宁窗(Hanning Window),难免泄漏 (Leakage) 伪随机(Pseudo Random周期随机),矩形窗(Rectangular),可 无泄漏 猝发随机(Burst Random),占空比(10%-100%)可调,与 阻尼比有关。矩形窗, 可无泄漏。
1 测试系统及设备 频响函数是结构系统的固有 特性,但它可以通过作用于 系统的激励和对应的响应来 描述
二、频响函数的测量
二、频响函数的测量
1 测试系统及设备
试验结构 激励系统 测量系统 分析系统 输出和记录系统
二、频响函数的测量
1.1 试验结构(Structure under Test) 线性条件下,被测试的结构的动特性是结构固有的。而我 们要测试的FRFs只是结构固有特性的一个近似模型。 结构可以用不同的数学模型描述,至少可表现为测试方案 的不同选取: (1)激励点的位置、激励方式和个数不同; (2)测量点的分布和个数。 测试方案不同,对结构特性的描述模型(自由度数、参数 等)也不同,但这些模型均是对结构特征值的近似表示。 关键在于解决实验模型和结构实际特性之间的近似程度问 题。
第8章 实验模态分析初步2
结构动特性的建模方法
理论建模:动力学仿真分析 耦合的力平衡方程 通过有限元离散模型,采用模态分析理论、特征值求解 技术和矩阵变换技术获得结构的动力学特性:频率、阻尼 和振型;建立结构完整模态模型(一组解耦的方程组)、 系统的传递特性(传递函数或频响函数),进一步建立结 构的频域响应计算模型和时域响应计算模型。 通过网格调整和模型的缩减技术,可以建立与实测模型 具有比对意义的分析模型。用于进行实验研究的指导和分 析模型的修改。对实验研究的指导作用主要表现在:确定 传感器和激励设备的配置方案、传感器类型、频响、灵敏 度、线性范围、温度特性等的要求。
结构动特性的建类 实验建模是通过系统的输入信号和输出响应之一或全部来 确定系统动特性模型的方法。因此又可称为辨识过程。辨识 的方法可分为: 系统辨识:模型的形式、阶次、参数均未知; 参数辨识:模型的形式已知,阶次和参数待定;或仅参数待 定;
结构动特性的建模方法
二、频响函数的测量
1.2 激励系统(Excitation System) (1) 稳态激励(Stationary Excitation): 信号发生器(Source、Function Generator)、功放 (Power Amplifier)、激振器(Shaker、Actuator) 信号发生器:正弦(Sinusoidal)、随机(Random)、 瞬态(Transient) 激振器:无台面、小推力。有台面的激振器通常称为振 动台。
一、基本概念
模态分析理论的基本假设
线性假设 时不变假设 可观测性假设 系统满足: 线性叠加性 一致性 互易性
一、基本概念
一、基本概念
一、基本概念
模态试验的过程: (1) 频响函数的测量 (2) 曲线拟合 (3) 模态参数计算 (4) 结果输出、动画显示 (5) 结果验证 …
二、频响函数的测量
二、频响函数的测量
Matlab:支持AD板,但未提供各主要数采和分析硬件制造商的硬件驱动 程序。可视化图标式编程(Icon-based Pragramming)、科学计算、 数学仿真、控制算法、神经网络等功能强大。SD公司的Siglab HP-VEE虚拟试验方案:美国HP公司产品。支持VXI总线(工业标准) 的硬件,但该总线硬件种类较少,非标准设备无法集成,如振动台。 是系统集成商级的虚拟软件平台。 DasyLab虚拟设备集成平台:德国Iotech公司产品。1996年左右在中国 推出。有配套的硬件设备,软硬件价格均较低,性能较高,同时支持 多家数采系统硬件,与MatLab、VC、VB兼容。非标准设备无法集 成。是用户级的虚拟软件平台。 LabView:美国NI公司产品。功能强大,是系统集成商级的虚拟软件平 台。与MatLab、VC、VB兼容。NI公司是虚拟设备标准的倡导者和制 订者。目前在国内外均有大量用户。 DiaDem:奥地利产品。1999推出到中国,目前用户较少。
结构动特性的建模方法
实验建模:实验模态分析方法 1 采用实验建模的原因 (1) 实际结构太复杂,难以采用理论简化和进行精确的动力 学仿真分析 组成部件多,连接关系复杂,甚至有刚体、柔性体及机构 耦合; 包含间隙、摩擦等非线性; 包含大位移和大变形等几何非线性; 结构强度、构形、边界条件和受力条件时变; 受复杂风载、运动载荷、热环境条件等共同作用;如发电 机组、大桥
结构动特性的建模方法
实验建模:实验模态分析方法 1 采用实验建模的原因 (2)动力学仿真分析的结果需要得到实验验证; 原型试验(Prototype Experiment) 全尺寸模型试验(Full Scale Model Experiment) 缩尺动力学相似模型试验(Scale Model Experiment) 部件试验(Component Experiment)
二、频响函数的测量
压电陶瓷(Piezo-Ceramic)激振器:小型、高频(通常可高达 60kHz-180kHz)、推力(Force)小、行程(Stroke)小,位移和波形 (waveform)控制精确(微米级); 电动式(Electrical):频带宽(0-5.5kHz)、能量较大,推力可达吨 级,行程一般可达1至2英寸、位移和波形控制较精确(标准台失真 (distortion)可控制在10%以下),但特大推力困难,出于技术垄断和 军事目的20吨以上推力振动台美国限制对华出口; 电液伺服式(Hydro-Electric Servo):频带窄(0-500 Hz)、能量 大、推力大、行程大; 机械式(Mechanical):频带窄(10-100Hz)、行程一般数毫米、 噪音大、位移和波形控制不精确;
二、频响函数的测量
(2) 冲击激励(Impact Excitation): 力锤(Hammer),适用于小阻尼线性结构。还有夯锤、 落锤、摆式冲击锤、小火箭等; (3) 脉动等(Enviromental Excitation): 利用大地、地震、人工爆炸模拟地震风等条件引起的振 动。
二、频响函数的测量
1.3 测量系统(Measurement System): 传感器+放大器(Transducer+Amplifier) ICP传感器(内装IC放大电路) (Integrated Circuit Piezoelectric)
二、频响函数的测量
1.4 分析系统: (1) 毫伏表、相位计、示波器、滤波器、频率计 (2) 频谱分析仪(模拟式、数字式):HP35665A、 HP3567A、HP3565S (3) 虚拟设备(PC-Based软件和硬件集成,可视化虚拟分析 仪和显示仪表):
振动的测量 * 基本知识
一、基本概念
一、基本概念
什么是实验模态分析EMA
通过实验的方法(获取频率响应FRF),然后模态估计和识别 方法,得到系统的模态参数。
动力学仿真分析FEM
根据结构的几何形状、边界条件和材料特性,进行建模,获取 M、C、K,然后计算模态参数。
一、基本概念
模态分析理论的基本假设
二、频响函数的测量
2.4 冲击激励(Impact Excitation) 激励频率:DC~ 。 激励的时域波形近似半正弦,频谱为
二、频响函数的测量
3 试件及激振器的支撑 1.自由支承(Free-Free Support)。 无约束条件对仿真计算容易实现,但需要进行移频处理。试验实现真 正自由支承的方法有:气悬浮、磁悬浮、太空无重力环境、自由下落 (失重)。 实际支承的最高刚体频率小于结构最低弹性频率的 ,即可减少基础模 态(悬挂系统)对结构模态的影响,实现近似自由支承。因此对于低 频模态(小于1Hz)要实现自由支承很困难,但对高频模态实现自由 支承很容易。主要方法有: 橡胶绳悬挂。要求橡胶绳足够长、足够软。 软弹簧支承。 海绵垫、橡胶垫支承。 空气弹簧。
