九年级数学圆复习专题课件
合集下载
九年级上册24圆复习(共17张PPT)

九年级上册
圆 单元复习(1)
圆外 圆内
相切
圆上
相离
相交
同(等)弧所对的 圆周角相等,都等 于圆心角的一半
圆心角等、弧等、 弦等知一得二
点与圆
直径所对的圆周角 是直角,圆内接四 边形对角互补
同圆或等圆中
圆周角定理
直线与圆
正多边形 与圆
圆心角等
等分 圆周
弦等 弧等
中心、外接圆
正多边形
半径R外
中心角 360 n
(弧BC=弧BD,则弦BC=弦BD)
4. 证弧等:AB过圆心,AB⊥CD 则弧BC=弧BD,弧AC=弧AD)
练习1在⊙O中,AB为直径,C为⊙O上一点. 如图D为弧AC 上一点,且OD经过AC的中点E,连接DC并延长,与AB的延 长线相交于点P,若∠CAB=10°,求∠P的大小.
D
C E
A
P
O
B
练习2
旋转不变性
弧弦圆心 角的关系
圆的
轴对称性 定理知
垂直于弦 的直径
性质
二得三
圆的基本概念
半径、弦心距、
弦的一半构成 Rt△
圆弧 弦
圆
弧长与扇 形面积
边心距R内 计算解直角△
圆锥侧面积 与全面积
s n R2 360
l n R 180
圆心 半径知识脉络树 Nhomakorabea诊断练习
1.如图,A,B,C,D四个点均在圆上,∠AOD=50°,
B
AAA
BBB
D
圆
的 弧、弦、圆心角之间的关系
有
关
性
圆周角与圆心角的关系
质 圆周角
圆周角与弧是关系
圆周角与直径的关系
圆 单元复习(1)
圆外 圆内
相切
圆上
相离
相交
同(等)弧所对的 圆周角相等,都等 于圆心角的一半
圆心角等、弧等、 弦等知一得二
点与圆
直径所对的圆周角 是直角,圆内接四 边形对角互补
同圆或等圆中
圆周角定理
直线与圆
正多边形 与圆
圆心角等
等分 圆周
弦等 弧等
中心、外接圆
正多边形
半径R外
中心角 360 n
(弧BC=弧BD,则弦BC=弦BD)
4. 证弧等:AB过圆心,AB⊥CD 则弧BC=弧BD,弧AC=弧AD)
练习1在⊙O中,AB为直径,C为⊙O上一点. 如图D为弧AC 上一点,且OD经过AC的中点E,连接DC并延长,与AB的延 长线相交于点P,若∠CAB=10°,求∠P的大小.
D
C E
A
P
O
B
练习2
旋转不变性
弧弦圆心 角的关系
圆的
轴对称性 定理知
垂直于弦 的直径
性质
二得三
圆的基本概念
半径、弦心距、
弦的一半构成 Rt△
圆弧 弦
圆
弧长与扇 形面积
边心距R内 计算解直角△
圆锥侧面积 与全面积
s n R2 360
l n R 180
圆心 半径知识脉络树 Nhomakorabea诊断练习
1.如图,A,B,C,D四个点均在圆上,∠AOD=50°,
B
AAA
BBB
D
圆
的 弧、弦、圆心角之间的关系
有
关
性
圆周角与圆心角的关系
质 圆周角
圆周角与弧是关系
圆周角与直径的关系
人教版九年级上册教材数学:圆复习课件演示
圆的定义(集合观点)
• 圆是到定点的距离等于定长的点的集合。 – 圆上各点到定点(圆心)的距离都等于定长 (半径); – 到定点的距离等于定长的点都在圆上。
• 一个圆把平面内的所有点 分成了多少类?
• 你能模仿圆的集合定义思 想,说说什么是圆的内部 和圆的外部吗?
人教版九年级上册教材数学:圆复习 课件演 示
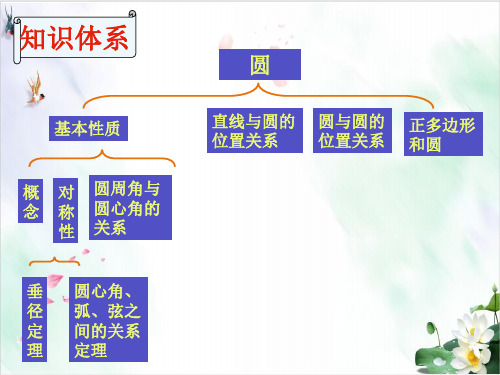
知识体系
基本性质
概 对 圆周角与 念 称 圆心角的
性 关系
垂 圆心角、 径 弧、弦之 定 间的关系 理 定理
圆
直线与圆的 圆与圆的 正多边形 位置关系 位置关系 和圆
圆的定义(运动观点)
在一个平面内,线段OA绕它固 定的一个端点O旋转一周,另一 个端点A随之旋转所形成的图形 叫做圆。
固定的端点O叫做圆心,线段 OA叫做半径,以点O为圆心的圆, 记作☉O,读作“圆O”
B
人教版九年级上册教材数学:圆复习 课件演 示
A
人教版九年级上册教材数学:圆复习 课件演 示
C
O
C O
B
A B
B A
A
C
O
圆周角:顶点在圆上,并且两边都和圆相 交的角。 圆心角: 顶点在圆心的角.
人教版九年级上册教材数学:圆复习 课件演 示
人教版九年级上册教材数学:圆复习 课件演 示
画图:同一条弧所对的圆周角和圆心角 之间可能出现哪几种不同的位置关系?
人教版九年级上册教材数学:圆复习 课件演 示
A
AO=BO=CO=DO,
侧想半一弧=圆想弧A会D:B有=D将。什弧一么B个C关,圆系弧沿?A着C任一C 条直径O 对折D ,两
性A质O:=B圆O是=C轴O对=D称O图,形,任何B 一条直A 径所在
九年级数学《圆-复习课》课件

(2)若AB=x,CD=y,求x,y的关系式。 (3若AB、CD是⊙O的两条平行切线,BD与AB、CD分别相交 于B. D两点,且BO⊥OD.求证:BD与⊙O相切。
CD
(Ⅱ)如图②,连接AA′、BB′,设△ACA′和△BCB′的面积分别 为S1、S2.求证:S1:S2=1:3;
(Ⅲ)如图③,设AC的中点为E,A′B′的中点为P,AC=a,连接EP. 求当θ为何值时,EP的长度最大,并写出EP的最大值 (直接 写出结果即可).
圆中分类讨论 1已知,△ABC内接于⊙O,BC=4 3 半径为4,则∠A=___
3 如图,四边形ABCD是平行四边形,以AB为直径的O经过点 D,E是O上一点,且∠AED=45∘.(1)试判断CD与O的位置关系, 并说明理由;(2)若O的半径为3cm,AE=5cm,求sin∠ADE.
4 已知:△ABC中,E是内心,∠A的平分线和△ABC的外 接圆相交于点D,求证:DE=DB=DC
5 如图,圆O为△ABC的内切圆,切点为E,F,G,∠C=90°, AO的延长线交BC于点D,AC=4,CD=1,求圆的半径.
第3 题
第4 题
第5题
二 旋转性质的运用 1.在△ABC中,∠ACB=90∘,∠ABC=30∘,将△ABC绕顶点C 顺时针旋转,旋转角为θ (0∘<θ<180∘),得到△A′B′C.(Ⅰ)如 图①,当AB∥CB′时,设A′B′与CB相交于点D. 证明:△A′CD 是等边三角形;
3 如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上 一点,延长DA至点E,使CE=CD. (1)求证:AE=BD;(2)若AC⊥BC,求证:AD+BD=2√CD.
4已知:如图,AB、CD是⊙O的两条平行切线,A. C是切点, ⊙O的另一条切线BD与AB、CD分别相交于B. D两点。 (1)求证:BO⊥OD.
CD
(Ⅱ)如图②,连接AA′、BB′,设△ACA′和△BCB′的面积分别 为S1、S2.求证:S1:S2=1:3;
(Ⅲ)如图③,设AC的中点为E,A′B′的中点为P,AC=a,连接EP. 求当θ为何值时,EP的长度最大,并写出EP的最大值 (直接 写出结果即可).
圆中分类讨论 1已知,△ABC内接于⊙O,BC=4 3 半径为4,则∠A=___
3 如图,四边形ABCD是平行四边形,以AB为直径的O经过点 D,E是O上一点,且∠AED=45∘.(1)试判断CD与O的位置关系, 并说明理由;(2)若O的半径为3cm,AE=5cm,求sin∠ADE.
4 已知:△ABC中,E是内心,∠A的平分线和△ABC的外 接圆相交于点D,求证:DE=DB=DC
5 如图,圆O为△ABC的内切圆,切点为E,F,G,∠C=90°, AO的延长线交BC于点D,AC=4,CD=1,求圆的半径.
第3 题
第4 题
第5题
二 旋转性质的运用 1.在△ABC中,∠ACB=90∘,∠ABC=30∘,将△ABC绕顶点C 顺时针旋转,旋转角为θ (0∘<θ<180∘),得到△A′B′C.(Ⅰ)如 图①,当AB∥CB′时,设A′B′与CB相交于点D. 证明:△A′CD 是等边三角形;
3 如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上 一点,延长DA至点E,使CE=CD. (1)求证:AE=BD;(2)若AC⊥BC,求证:AD+BD=2√CD.
4已知:如图,AB、CD是⊙O的两条平行切线,A. C是切点, ⊙O的另一条切线BD与AB、CD分别相交于B. D两点。 (1)求证:BO⊥OD.
人教版九年级上册数学精品教学课件 第24章 圆 第二十四章 小结与复习

二、 圆的基本性质 1. 圆的对称性
圆是轴对称图形,它的任意一条_直__径__所在的直线都是 它的对称轴.圆也是中心对称图形,圆心即为对称中心.
2. 有关圆心角、弧、弦的性质 (1) 在同圆中,如果圆心角相等,那么 它们所对的弧相等,所对的弦也相等;
(2) 在同圆或等圆中,如果两个圆心角、 两条弧和两条弦中有一组量相等,那么
A
O
BP
又∵∠COB = 2∠PCB,∴∠ACO =∠PCB.
∵ AB 是⊙O 的直径,∴∠ACO +∠OCB = 90°.
∴∠PCB +∠OCB = 90°,即 OC⊥CP.
∵ OC 是⊙O 的半径,∴ PC 是⊙O 的切线.
针对训练 7. 如图,点 D 是∠AOB 的平分线 OC 上任
意一点,过 D 作 DE⊥OB 于 E,以 DE 为半径作⊙D.
12. 正多边形的相关概念 (1) 中心:正多边形外接圆和内切圆有公共的圆心,称 其为正多边形的中心. (2) 半径:外接圆的半径叫做正多边形的半径. (3) 边心距:中心到正多边形一边的距离叫做正多边形 的边心距.
(4) 中心角:正多边形每一条边所对的外接圆的圆心角 都相等,叫做正多边形的中心角.
它们所对应的其余各组量都分别相等.
三、与圆有关的位置关系
1. 点与圆的位置关系 判断点与圆的位置关系可由点到圆心的距离 d 与
圆的半径 r 比较得到.
设☉O 的半径是 r,点 P 到圆心的距离为 d ,则有
d<r
点 P 在圆内;[以注转意化]为点点与到圆圆的心位的置距关系离可与
d=r
点 P 在圆上;半径之间的大小关系;反过
S 1 nar 1 Cr. 其中 C 为正 n 边形的周长.
圆 初三 ppt课件ppt课件ppt

圆的性质
01
圆的直径是半径的两倍 ,半径是直径的一半。
02
圆内接正多边形的所有 边都相等,所有内角也 都相等。
03
圆的外切正多边形的所 有边都相等,所有内角 也都相等。
04
圆的周长和面积都随着 半径的增加而增加。
圆的度量
圆的周长公式
C = 2πr,其中r是圆的半径。
圆的面积公式
A = πr^2,其中r是圆的半径。
圆弧的长度公式
圆内接多边形的周长和面积公式
L = θ/360° × 2πr,其中θ是圆心角的大小 ,r是圆的半径。
P = nπr/180,A = nr^2/4,其中n是多边 形的边数,r是圆的半径。
02 圆的对称性
圆的中心对称性
总结词
圆关于其圆心对称
详细描述
圆关于其圆心具有中心对称性 ,即任意一点关于圆心的对称 点也在圆上。
• 总结词:掌握圆的综合问题需要理解圆的性质和定理,以 及与其他几何知识的结合。
圆的综合问题 圆的综合问题
圆的综合题解题思路 利用圆的性质和定理解决实际问题。
结合其他几何知识,如三角形、四边形等,进行解题。
圆的综合问题 圆的综合问题
运用代数、方程等数学方法进行求解。 圆的综合题解题方法
观察题目,分析已知条件和未知量。
C = 2πr,其中r是圆的半 径,π是一个常数约等于 3.14159。
周长计算方法
使用圆的半径计算出周长 ,可以通过公式直接计算 ,也可以使用计算器或图 形计算软件进行计算。
周长计算实例
假设一个圆的半径为5厘 米,那它的周长就是 31.4厘米。
圆在几何作图中的应用
圆规作图
圆规是用来画圆的工具,通过固定半径长度,可以在纸上 画出标准的圆形。
第24章 圆的复习-九年级数学上册教学课件(人教版)

原 所示,则这个小圆孔的宽口AB的长度为 8 mm.
理
C
精
炼
O
8mm
A
B
提
D
升
与圆有关的概念
典 1.圆:平面内到定点的距离等于定长的所有点组成的图形.
例 2.弦:连结圆上任意两点的线段.
3.直径:经过圆心的弦是圆的直径,直径是最长的弦.
原 4.劣弧:小于半圆周的圆弧.
理 5.优弧:大于半圆周的圆弧.
炼 【注意】(1)三角形的外心是三角形三边的垂直平分线的交点.
(2)一个三角形的外接圆是唯一的.
提
(3)三角形的内心是三角形三条角平分线的交点.
升
(4)一个三角形的内切圆是唯一的.
点与圆的位置关系
典 1.在△ABC中,∠C=90º,AC=1,BC=2,M是AB的中点,以点C为圆 例 心,1为半径作⊙C,则( C )
原 2.垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦, 理 并且平分这条弦所对的两条弧;
精 3.垂径定理的推论:平分弧的直径垂直平分这条弧所对的弦. 炼
提 升
圆的基本性质
典 1.圆的对称性: 例 圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
原 2.有关圆心角、弧、弦的性质:
理
在同圆或等圆中,如果两个圆心角、
° 精 炼
提 升
典 6.如图,已知A、B、C、D是⊙O上的四点,延长DC,AB相交于点 例 E.若BC=BE.求证:△ADE是等腰三角形.
原 理
精 炼
提 升
典 7.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 例 (1)若∠CBD=39º,求∠BAD的度数; 原 (2)求证:∠1=∠2. 理
圆 初三 ppt课件ppt课件

CHAPTER
06
圆的综合题解题思路
圆的综合题解题方法
利用圆的性质
根据圆的性质,如圆周 角定理、垂径定理等, 推导出其他相关条件或
结论。
数形结合
将圆的性质与代数方程 相结合,通过代数运算
解决问题。
构造辅助线
在解题过程中,根据需 要构造辅助线,以连接 圆上的点或与其他图形
建立联系。
运用相似三角形
在解题过程中,通过构 造相似三角形,利用相 似三角形的性质解决问
THANKS
感谢观看
详细描述
圆的一般方程是$x^{2} + y^{2} + Dx + Ey + F = 0$,其中$D, E, F$是三个系数 。这个方程表示所有满足这个方程的点都在圆上。通过解这个方程,可以得到圆 上三个点的坐标。
圆的参数方程
总结词
圆的参数方程是一种基于三角函数的描述圆的方式,它通过 角度和半径来描述圆上的点。
题。
圆的综合题解题技巧
寻找隐含条件
在题目中寻找隐含条件,这些条件可 能对解题起到关键作用。
化复杂为简单
将复杂的问题分解为多个简单的问题 ,逐一解决,最后再综合起来。
利用特殊到一般的思路
先考虑特殊情况,再推广到一般情况 ,这样有助于找到解题思路。
注意图形的变化
在解题过程中,注意图形的变化,如 角度、长度等的变化,并利用这些变 化解决问题。
VS
详细描述
根据圆的对称性质,我们可以利用已知圆 上的任意一点或直径两端点来作出一个与 已知圆相切或重合的新圆。具体操作包括 通过圆心和已知圆上一点作圆,以及通过 两个已知圆的中心和它们之间的距离作圆 。
利用已知点作圆
人教版数学九年级上册第24章圆章节复习课件(共38张)

( (
并且AC与BD的度数分别是96 °和36 °,动点P是AB上的任意一
点,则PC+PD的最小值是
3.
C
D
A
B PO P
D’
图b
3 与圆有关的位置关系
【例3】如图, O为正方形对角线上一点,以点O 为圆心,OA长为
半径的☉O与BC相切于点M.
(1)求证:CD与☉O相切;
(1)证明:过点O作ON⊥CD于N.连接OM ∵BC与☉O相切于点M, ∴ ∠OMC=90 °, ∵四边形ABCD是正方形,点O在AC上. ∴AC是∠BCD的角平分线, ∴ON=OM, ∴ CD与☉O相切.
二、与圆有关的位置关系 1.点与圆的位置关系 判断点与圆的位置关系可由点到圆心的距离d与圆的半径r比较
得到.
设☉O的半径是r,点P到圆心的距离为d,则有
d<r d=r d>r
点P在圆内; 点P在圆上; 点P在圆外.
【注意】点与圆的位置关系可以转化为 点到圆心的距离与半径之间的关系;反 过来,也可以通过这种数量关系判断点 与圆的位置关系.
2.扇形面积公式 半径为R,圆心角为n°的扇形面积S= _n_3_6R_0_2_或__12__l_R_. 3.弓形面积公式
弓形的面积=扇形的面积±三角形的面积
4.圆锥的侧面积 (1)圆锥的侧面展开图是一个 扇形 . (2)如果圆锥母线长为l,底面圆的半径为r,那么这个扇形的半径为 l ,
扇形的弧长为 2 r .
点C作☉O的切线交AB的延长线于点E,则∠E等于 50° .
2 垂径定理
【例2】工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的
直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点,E为OD延长线上一点,且∠CAE=2∠C,AC与BD交于点H,与OE交于点F.
(1)求证:AE是⊙O的切线; 3
(1)证明:∵D是 的中点,
(2)若DH=9,tan C=4 ,求直径AB的长. ∴OE⊥AC,∴∠AFE=90°,
∴∠E+∠EAF=90°.
∵∠AOE=2∠C,∠CAE=2∠C,
∴∠CAE=∠AOE,
考点一 圆心角、弧、弦之间的关系
例1 (2018·青岛中考)如图,点A,B,C,D在⊙O上,∠AOC=140°,点B
是 的中点,则∠D的度数是( )
如图,连接OB.∵点B是 的中点,
∴∠AOB= 1∠AOC=70°,
2 由圆周角定理得∠D=
1∠AOB=35°.
2
故选D.A.70° B.55° C.35.5°
考点四 切线的性质与判定 (5年5考)
命题角度❶ 切线的性质
例4(2018·泰安中考)如图,BM与⊙O相切于点B,若∠MBA=140°,则
∠ACB的度数为(
)
【分析 】连接 OA ,OB ,由切线的性 质知 ∠OBM=90° ,从而得
∠ABO=∠BAO=50°,由内角和定理知∠AOB=80°,根据圆周角定
.(2019·泰安中考)如图,△ABC是⊙O的内接三角形,∠A=119°,过 点C的圆的切线交BO于点P,则∠P的度数为( )
A.32° B.31° C.29° D.61°
小结: 常做的辅助线 见切线,连半 径
命题角度2 切线的判定
.(2019·济宁中考)如图,AB是⊙O的直径,C是⊙O上一点,D是的中
D.35°
利用圆心角、弧、弦的关系求角度
(1)在同圆或等圆中
(2)同一圆中半径处处相等,可构造等腰三角形实现“等边对等角”. (3)作辅助线法 遇到弦时:①过圆心作弦的垂线,再连接过弦的端点的半径,构造直角三 角形; ②连接圆心和弦的两个端点,构造等腰三角形,或连接圆周上一点和弦的 两个端点.
.如图,P是⊙O外一点,PA,PB分别交⊙O于C,D两点,已知 弧AB,弧CD的 度数分别为88°,32°,则∠P的度数为( )
为.
【分析】连接OC,作CH⊥OB于
H,根据直角三角形的性质求出
AB,根据勾股定理求出BD,证明
△AOC为等边三角形,得到∠AOC
=60°,∠COB=30°,根据扇形
面积公式、三角形面积公式计算
A.26° C.30°
B.28° D.32°
考点二 垂径定理 (5年2考)
例2 (2015·泰安中考)如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半 径为4,则AC的长等于( )
【分析】首先连接OA,OC,过点O作OD⊥AC于点D,利用圆周角定理、 垂径 定理求解AC的长即可. 【自主解答】 如图,连接OA,OC,过点O作OD⊥AC于点D. ∵∠AOC=2∠B=120°,OA=OC, ∴∠OCD=∠OAC=30°. 在Rt△COD中,OC=4,∠2OC3D=30°, ∴CD=OC·cos3 30°=4× =2, ∴A小C结=:2C涉D及=弦4 时.故,选一A般.先作辅助线,构造垂径定理的应用环境
考点五 与弧长,扇形面积有关的计算 (5年1考)
例5 (2019·泰安中考)如图,将⊙O沿弦AB折叠, 恰好经过圆心O,若 ⊙O的半径为3,则 的长为( )
A. 1 π 2
C.2π
B.π D.3π
【分析】连接OA,OB,作OC⊥AB于C,根据翻转变换的性质得到O1C= 2
OA,根据等腰三角形的性质、三角形内角和定理求出∠AOB的度数,根 据弧长公式计算即可. 【自主解答】 如图,连接OA,OB,作OC⊥AB于C, 由题意得OC=1 OA,
(2019·德州中考)如图,CD为⊙O的直径,弦AB⊥CD,垂足为E,
CE=1,AB=6,则弦AF的长度为
.
【分析】连接OC,由圆周角定理可求得∠及其推论 (5年3考)
形的性质即可求得∠OBC的度数. 例3 (2017·泰安中考)如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于
2 ∴∠OAC=30°. ∵OA=OB,∴∠OBA=∠OAC=30°, ∴∠AOB=120°, ∴ 的长= =2π.故选C.
命题角度 求不规则图形的面积
例6 (2019·泰安中考)如图,∠AOB=90°,∠B=30°,以点O为圆心,
OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影部分的面积
5
设HF=3x,DF=4x, 则DH=5x=9,
∵AF2+4O8 F2 =OA2, ∴( )25+(y- )2=
∵∠C=∠FDH,∠DFH=∠CFD,∴△DFH∽△CFD,y2,36
5
解得y=10,
∴OA=10,∴直径AB
的长为20.
切线的判定方法
(1)“连半径,证垂直”:若直线与圆有公共点,则连接圆心与交点得到 半径,证明半径与直线垂直. (2)“作垂直,证等径”:若未给出直线与圆的公共点,则过圆心作直线 的垂线段,证明垂线段的长等于半径.在判定时,必须说明“是半径”或 “点在圆上”,这是最容易犯错的地方.
理得出
A.40° B.50° C.60° D.70°
【 自 主 解 答 】 如 图 , 连 接 OA , OB , 则 OB⊥BM , ∴ ∠ BAO = ∠ ABO =
∠MBA- ∠OBM=1140°-90°=50°,∴∠AOB=180°-50°×2=80°, ∴∠ACB= 2∠AOB=40°.故选A.
∴∠E+∠AOE=90°,
∴∠EAO=90°,
∴AE是⊙O的切线.
2)若DH=9,tan C= 3 ,求直径AB的长 4
(2)解:∵OD=OB,∴∠B=∠ODB.
∵∠C=∠B,∴∠ODB=∠C,
AF=CF=48 . 5
设 OA = OD = y ,
∴tan C=tan∠ODB=
∴OF3=6 y- .
(
)
A.180°-2α
连接OC.
B.2α
∵△ABC内接于⊙O,∠A=α,
C.90°+α
∴∠BOC=2∠A=2α.
D.90°-α
∵OB=OC,
∴∠OBC=∠OCB=
=90°-
α.故选D.
(2018·济宁中考)如图,点B,C,D在⊙O上,若∠BCD=130°,则 ∠BOD的度数是( )
A.50° B.60° C.80° D.100°
