等截面等跨连续梁在常用荷载作用下的内力系数表
(施工手册第四版)第二章常用结构计算2-1 荷载与结构静力计算表

2 常用结构计算2—1 荷载与结构静力计算表2—1-1 荷载1.结构上的荷载结构上的荷载分为下列三类:(1)永久荷载如结构自重、土压力、预应力等.(2)可变荷载如楼面活荷载、屋面活荷载和积灰荷载、吊车荷载、风荷载、雪活载等。
(3)偶然荷载如爆炸力、撞击力等。
建筑结构设计时,对不同荷载应采用不同的代表值。
对永久荷载应采用标准值作为代表值。
对可变荷载应根据设计要求,采用标准值、组合值、频遇值或准永久值作为代表值。
对偶然荷载应按建筑结构使用的特点确定其代表值。
2.荷载组合建筑结构设计应根据使用过程中在结构上可能同时出现的荷载,按承载能力极限状态和正常使用极限状态分别进行荷载(效应)组合,并应取各自的最不利的效应组合进行设计。
对于承载能力极限状态,应按荷载效应的基本组合或偶然组合进行荷载(效应)组合。
γ0S≤R (2-1)式中γ0——结构重要性系数;S—-荷载效应组合的设计值;R—-结构构件抗力的设计值。
对于基本组合,荷载效应组合的设计值S应从下列组合值中取最不利值确定:(1)由可变荷载效应控制的组合(2—2)式中γG——永久荷载的分项系数;γQi——第i个可变荷载的分项系数,其中Y Q1为可变荷载Q1的分项系数;S GK-—按永久荷载标准值G K计算的荷载效应值;S QiK——按可变荷载标准值Q ik计算的荷载效应值,其中S Q1K为诸可变荷载效应中起控制作用者;ψci--可变荷载Q i的组合值系数;n—-参与组合的可变荷载数。
(2)由永久荷载效应控制的组合(2—3)(3)基本组合的荷载分项系数1)永久荷载的分项系数当其效应对结构不利时:对由可变荷载效应控制的组合,应取1.2;对由永久荷载效应控制的组合,应取1。
35;当其效应对结构有利时:一般情况下应取1。
0;对结构的倾覆、滑移或漂浮验算,应取0.9。
2)可变荷载的分项系数一般情况下应取1。
4;对标准值大于4kN/m2的工业房屋楼面结构活荷载应取1.3。
荷载静力计算

常用结构计算荷载结构静力计算荷载1.结构上的荷载结构上的荷载分为下列三类:(1)永久荷载如结构自重、土压力、预应力等。
(2)可变荷载如楼面活荷载、屋面活荷载和积灰荷载、吊车荷载、风荷载、雪活载等。
(3)偶然荷载如爆炸力、撞击力等。
建筑结构设计时,对不同荷载应采用不同的代表值。
对永久荷载应采用标准值作为代表值。
对可变荷载应根据设计要求,采用标准值、组合值、频遇值或准永久值作为代表值。
对偶然荷载应按建筑结构使用的特点确定其代表值。
2.荷载组合建筑结构设计应根据使用过程中在结构上可能同时出现的荷载,按承载能力极限状态和正常使用极限状态分别进行荷载(效应)组合,并应取各自的最不利的效应组合进行设计。
对于承载能力极限状态,应按荷载效应的基本组合或偶然组合进行荷载(效应)组合。
γ0S≤R(2-1)式中γ0——结构重要性系数;S——荷载效应组合的设计值;R——结构构件抗力的设计值。
对于基本组合,荷载效应组合的设计值S应从下列组合值中取最不利值确定:(1)由可变荷载效应控制的组合(2-2)式中γG——永久荷载的分项系数;γQi——第i个可变荷载的分项系数,其中Y Q1为可变荷载Q1的分项系数;S GK——按永久荷载标准值G K计算的荷载效应值;S QiK——按可变荷载标准值Q ik计算的荷载效应值,其中S Q1K为诸可变荷载效应中起控制作用者;ψci——可变荷载Q i的组合值系数;n——参与组合的可变荷载数。
(2)由永久荷载效应控制的组合(2-3)(3)基本组合的荷载分项系数1)永久荷载的分项系数当其效应对结构不利时:对由可变荷载效应控制的组合,应取1.2;对由永久荷载效应控制的组合,应取1.35;当其效应对结构有利时:一般情况下应取1.0;对结构的倾覆、滑移或漂浮验算,应取0.9。
2)可变荷载的分项系数一般情况下应取1.4;对标准值大于4kN/m2的工业房屋楼面结构活荷载应取1.3。
对于偶然组合,荷载效应组合的设计值宜按下列规定确定:偶然荷载的代表值不乘分项系数;与偶然荷载同时出现的其他荷载可根据观测资料和工程经验采用适当的代表值。
连续梁的内力包络图

连续梁的内力包络图
计算各截面在活载作用下的最大、最小弯矩时,需要事 先利用影响线来确定最不利荷载位置。但如果连续梁受均布 活载时,则各个截面的最大、最小弯矩的计算将可以简化。 图16-15中给出了五跨连续梁某些截面的弯矩影响线和引起最 大、最小弯矩的最不利荷载位置。从图中可以看出,连续梁 受均布活载作用时,各截面弯矩的最不利荷载位置并不是活 载布满各跨的情况,而是在若干跨内布满活载。例如,支座 截面最小弯矩:支座两个邻跨有活载,然后隔一跨有活载, 如图16-15(d)所示。又如,跨中截面最大弯矩:本跨有活载, 然后每隔一跨有活载,如图16-15(f)所示。
连续梁的内力包络图
将各截面的最大(小)弯矩值以曲线相连,即得连续梁的 弯矩包络图。
用类似的方法可绘制剪力包络图。由于设计连续梁时, 通常只需要用到各跨支座两侧截面上的剪力最大、最小值, 而其最不利荷载位置也是在若干跨内布满活载,所以可先分 别绘出连续梁在恒载和各跨单独布满均布活载时的剪力最大、 最小值,即
连续梁的内力包络图
式中,FSik表示ik跨i端的剪力;FgSik表示恒载单 独作用下ik跨i端的剪力值;∑FPSik(+)、∑FPSik(-)表示 当各跨分别单独承受均布活载时,在ik跨i端所产生 的所有正剪力值或负剪力值的总和。
将各跨两侧截面上的最大(小)剪力值以直线相连, 即得近似的剪力包络图。按此设计比实际的剪力包 络图偏于安全。
连续梁的内力包络图
这样,各截面的最大、最小弯矩均可由某几跨单独布 满活载时的弯矩叠加得到。据此,绘制连续梁的弯矩包络 图时,可采用如下的办法:先分别绘出连续梁在恒载及各 跨单独布满活载时的弯矩图(可用力矩分配法求解或查建筑 结构静力计算手册),并将每一跨分为若干等份,在弯矩图 中标明各等分点处截面的弯矩值,然后按下式计算任一等 分点处截面K的最大、最小弯矩值为
路桥施工计算手册(附录表)
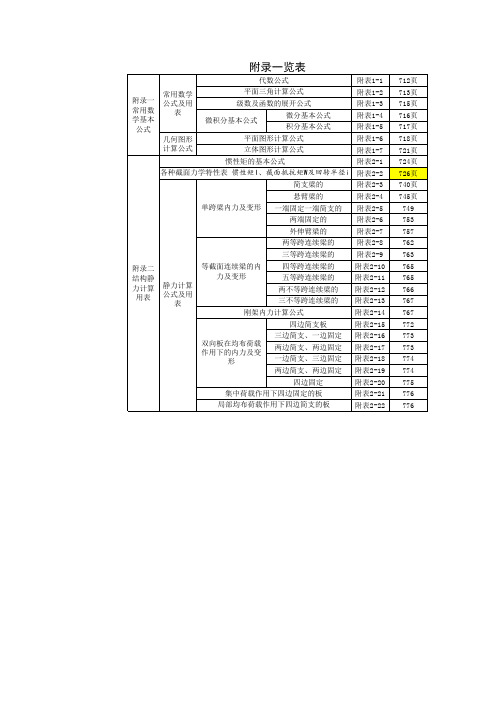
代数公式 附录一 常用数 学基本 公式 常用数学 公式及用 表 平面三角计算公式 级数及函数的展开公式 微积分基本公式 几何图形 计算公式 微分基本公式 积分基本公式 平面图形计算公式 立体图形计算公式 惯性矩的基本公式 各种截面力学特性表 惯性矩I、截面抵抗矩W及回转半径i 简支梁的 悬臂梁的 单跨梁内力及变形 一端固定一端简支的 两端固定的 外伸臂梁的 两等跨连续梁的 三等跨连续梁的 附录二 结构静 力计算 用表 等截面连续梁的内 力及变形 静力计算 公式及用 表 四等跨连续梁的 五等跨连续梁的 两不等跨连续梁的 三不等跨连续梁的 刚架内力计算公式 四边简支板 三边简支、一边固定 双向板在均布荷载 作用下的内力及变 形 两边简支、两边固定 一边简支、三边固定 两边简支、两边固定 四边固定 集中荷载作用下四边固定的板 局部均布荷载作用下四边简支的板 附表1-1 附表1-2 附表1-3 附表1-4 附表1-5 附表1-6 附表1-7 附表2-1 附表2-2 附表2-3 附表2-4 附表2-5 附表2-6 附表2-7 附表2-8 附表2-9 附表2-10 附表2-11 附表2-12 附表2-13 附表2-14 附表2-15 附表2-16 附表2-17 附表2-18 附表2-19 附表2-20 附表2-21 附表2-22 712页 713页 715页 716页 717页 718页 721页 724页 726页 740页 745页 749 753 757 762 763 765 765 766 767 767 772 773 773 774
混凝土和砌体结构考试简答题汇总

1。
单向板与双向板的定义:按受力特点,混凝土楼盖中的周边支撑板可分为单向板和双向板两类。
只在一个方向弯曲或者主要在一个方向弯曲的板,称为单向板;在两个方向完全,且不能忽略人一个方向弯曲的板称为双向板。
2. 现浇单向板肋梁楼盖的设计步骤:1、结构平面布置并初步拟定板厚和主、次梁的截面尺寸;2、确定梁、板得计算简图;3、梁、板得内力分析;4、截面配筋及构造措施;5、绘制施工图.3. 简化假定:1、支座可以自由转动,但没有竖向位移;2、不考虑薄膜相应对板内力的影响;3、在确定板传给次梁的荷载一级次梁传给主梁的荷载时,分别忽略板、次梁的连续性;4、跨熟超过五跨的连续梁、板,当各跨荷载相同,且跨度相差不超过10%时,可按五跨的等跨连续梁、板计算。
4. 假定支座处没有竖向位移,实际上忽略了次梁、主梁、柱的竖向变形对板、次梁、主梁的影响。
柱子的竖向位移主要由轴向变形引起,在通常的内力分析中都是可以忽略的。
忽略主梁变形,将导致次梁跨中弯矩偏小、主梁跨中弯矩偏大。
当主梁的线刚度比次梁的线刚度大得多时,主梁变形对次梁内力的影响才比较小。
次梁变形对板内力的影响也是这样,如果考虑这种影响,内力分析就相当复杂。
5。
计算单元:为减少计算工作量,结构内力分析时,常常不是对整个结构进行分析,而是从实际结构中选取有代表性的某一部分作为计算的对象,成为计算单元.6. 塑性内力重分布的过程,假定支座截面和跨内截面的截面尺寸和配筋相同.梁的手里全过程大致可以分为三个阶段:1、弹性内力阶段;2、截面间弯曲刚度比值改变阶段;3、塑性铰阶段。
7。
考虑塑性内力重分布是以形成塑性铰为前提的,因此下列情况不宜采用:1、在使用阶段不允许出现裂缝或对裂缝开展有校验过限制的结构,如水池池壁,自防水屋面,一级处于侵蚀性环境中的结构;2、直接承受动力和重复荷载的结构;3、预应力结构和二次受力叠合结构;4、要求有较高安全储备的结构。
8. 截面弯矩的调整幅度用弯矩调幅系数β来表示:β=(Me—Ma)/Me,式中Me安弹性理论算得的弯矩值;Ma 调幅后的弯矩值。
结构力学静力公式汇总

结构力学公式结构 静力计算目 录1、常用截面几何与力学特征表 (1)2、单跨梁的内力及变形表 (8)2.1 简支梁的反力、剪力、弯矩、挠度 (8)2.2 悬臂梁的反力、剪力、弯矩和挠度 (10)2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度 (12)2.4 两端固定梁的反力、剪力、弯矩和挠度 (14)2.5 外伸梁的反力、剪力、弯矩和挠度 (16)3.等截面连续梁的内力及变形表 (19)3.1 二跨等跨梁的内力和挠度系数 (19)3.2 三跨等跨梁的内力和挠度系数 (20)3.3 四跨等跨连续梁内力和挠度系数 (23)3.4 五跨等跨连续梁内力和挠度系数 (23)3.5 二不等跨梁的内力系数 (24)3.6 三不等跨梁内力系数 (25)4.双向板在均布荷载作用下的内力及变形系数表 (26)4.1 四边简支 (26)4.2 三边简支,一边固定 (27)4.3 两边简支,两边固定 (27)4.4 一边简支,三边固定 (28)4.4 四边固定 (29)4.5 两边简支,两边固定 (29)5.拱的内力计算表 (30)5.1各种荷载作用下双铰抛物线拱计算公式 (30)6.刚架内力计算表 (35)6.1 “┌┐”形刚架内力计算表(一) (35)6.2“┌┐”形刚架内力计算表(二) (37)6.3“”形刚架的内力计算表 (39)11、常用截面几何与力学特征表234567注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=A dA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max y IW =3.i 称截面回转半径(mm ),其基本计算公式如下:AI i = 4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
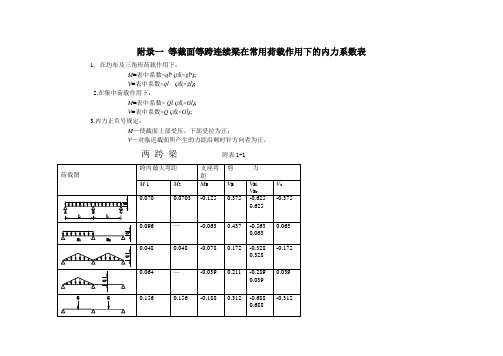
等截面等跨连续梁在常用荷载作用下的内力系数表
-0.060 0.012 0.012
0.178 -0.036 -0.036
荷载图 内力
五跨梁
跨内最大弯距
M1
M2
M3
0.078
0.033
0.046
附表 1-4
MB
-0.105
支座弯距
剪力
MC
-0.079
MD
ME
-0.079 -0.105
VA
0.394
VBl VBr
-0.606 0.526
-0.450 0.050 -0.017 -0.017 -0.188
0
-0.219
0.281
-0.250 0.031 0.051
-0.198 0.021 0.021
0.052 -0.010 -0.010
-0.500 -0.350 0.650
0.213 — 0.162 0.200 0.244 0.289 — 0.229 0.274
— 0.175 0.137 — 0.067 — 0.200 0.170 —
-0.075 -0.075 0.425 -0.575 0
-0.075 -0.075 -0.075 -0.075 0.500
-0.175 -0.050 0.325 -0.675 0.625
-0.100 0.025 -0.267 0.267
-0.550 0 -0.050 0.500 -0.617 0.583 -0.567 0.083 -0.313 0.250
-0.281 0
-0.031 0.250
-0.323 0.302
-0.292 0.052
-0.650 0.500
0 0.550 -0.500 0.050 0.083 -0.017 0.083 -0.017 -0.250 0.313
附录二 等截面附录二等跨连续梁在常用荷载作用下的内力系数表

附录一等截面等跨连续梁在常用荷载作用下的内力系数表 1.在均布及三角形荷载作用下:皿=表中系数 V=表中系数2•在集中荷载作用下: 皿=表中系数 V=表中系数3.内力正负号规定: M —使截面上部受压、下部受拉为正;V —对临近截面所产生的力距沿顺时针方向者为正。
附表1-1 旳12(或旳12);Xql (或XQI (或 XGl ); XQ两跨梁0.203 -0.094 0.406 -0.594 0.0940.0940.222 0.222 -0.333 0.667 -1.333 -0.6671.3330.278 -0.167 0.833 -1.167 0.1670.167a.荷载图三跨梁跨内最大弯距附表1-2M20.080 0.025支座弯距M B M c V A-0.100 -0.100 0.400V BIV Br-0.6000.500剪力V clV er-0.5000.600V D-0.4000.101 -0.050 -0.050 0.450 -0.5500.550-0.4500.075 -0.050 -0.050 0.050 -0.0500.500-0.5000.0500.0500.073 0.054 -0.117 -0.033 0.383 -0.6170.5830.083-0.0170.094-0.017-0.067 0.017 0.433 -0.5670.0830.083-0.017-0.017 A----- A 0.0540.0680.0500.0630.1750.0210.0520.0380.100-0.063 -0.063 0.183 -0.313 -0.250 -0.1880.250 0.313-0.031-0.031-0.073-0.042-0.150-0.031-0.031-0.0210.010-0.1500.2190.0310.1770.2080.350-0.281-0.0310.250-0.3230.302-0.2920.052-0.6500.5000.281-0.2500.051-0.1980.0210.052-0.010-0.5000.650-0.2190.0310.021-0.010-0.350荷载图 0.077 四跨梁 跨内最大弯距 M 2 M 3 M 4 M B 0.036 0.036 0.077 -0.107 附表1-3 支座弯距 剪力 M e M D V A -0.071 -0.107 0.393 0.100 0.081 0.072 0.061 -0.054-0.036 -0.054 0.446 0.098 -0.121 -0.018 -0.058 0.380 V BI V Br -0.607 0.536 Vd V cr -0.464 0.464 V DI V Dr -0.536 0.607 V E -0.393 0.094 Z A0.056 0.056 0.062 0.067 0.049 A 0.071 0.028 -0.036 -0.067 -0.107 -0.036 -0.036 0.018 -0.004 0.433 0.042 0.028 0.055 0.052 0.066 -0.049 -0.054 0.013 -0.049 -0.554 0.018 -0.620 0.603 -0.036 0.429 -0.567 0.085 -0.049 0.496 0.018 0.482 -0.397 -0.040 -0.571 0.571 0.085 -0.022 -0.504 0.067 -0.518 0.054 -0.040 -0.558 -0.429 0.036 0.022 0.004 0.067 0.013 0.054 -0.442 0.036 0.004 -0.013 -0.067-0.045 -0.067 0.183 -0.317 0.272 -0.228 0.228 -0.272 0.317 -0.183 -0.084 -0.075 -0.022 -0.034 0.217 -0.234 0.011 0.011 0.239 -0.261 0.034 0.034 -0.011 -0.036 0.175 -0.325 0.314 -0.186 -0.025 -0.025 0.286 -0.214 0.040 0.040 -0.022-0.067 -0.022 -0.022 -0.022 0.205 -0.295 0.295 -0.205 0.022 0.0224 4u a A s s a 0.274 -0.178 0.048 -0.012 0.822 -1.1780.2260.226-0.060-0.0600.0120.0124 q 川0.198 -0.131 -0.143 0.036 -0.131 -0.1310.988-1.0120.1780.178-0.036-0.036附表1-4荷载图跨内最大弯距支座弯距剪力内力M2 M3 M B M e M D M E V A0.078 0.033 0.046 -0.105 -0.079 -0.079 -0.105 0.394 V BIV Br-0.6060.526V clV cr-0.4740.500V DIV Dr-0.5000.474V EIV Er-0.5260.606V F-0.3940.100 Ml M S M4M S0.085 -0.053 -0.040 -0.040 -0.053 0.447 -0.5530.0130.0130.500-0.500-0.013-0.0130.533-0.4470.079 -0.053 -0.040 -0.040 -0.053 -0.053 -0.0530.513-0.4870.487-0.5130.0530.0530.073(1) 0.0980.094 (2)0.0590.078-0.119 -0.022 -0.044 -0.051 0.3800.0550.0740.064 -0.035-0.067-0.111 -0.020 -0.057 0.0350.018 -0.005 0.001 0.433-0.6200.5980.0350.4240.5670.085-0.402-0.0230.5760.5910.0860.023-0.0230.493-0.409-0.0370.0230.006-0.5070.052-0.0370.5570.006-0.0010.052-0.4430.001-0.049 -0.054 0.014 -0.004 0.019 -0.0490.496-0.5050.0680.068-0.018-0.0180.0040.004。
梁静力计算系数表..

常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰∙=A dA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:max y IW =3.i 称截面回转半径(mm ),其基本计算公式如下:AI i = 4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·mV B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
连续梁按弹性理论五跨梁内力系数及弯矩分配法

附表25:等截面等跨连续梁在常用荷载作用下按弹性分析(de)内力系数(五跨梁).弯矩分配法(弯矩分配法计算连续梁和刚架及举例)一、名词解释弯矩分配法在数学上属于逐次逼近法,但在力学上属于精确法(de)范畴,主要适用于连续梁和刚架(de)计算.在弯矩分配法中不需要解联立方程,而且是直接得出杆端弯矩.由于计算简便,弯矩分配法在建筑结构设计计算中应用很广.(一)线刚度i杆件横截面(de)抗弯刚度EI 被杆件(de)长度去除就是杆件(de)线刚度i : (a ) 当远端B 为固定支座时,对于A 点处,AB 杆(de)转动刚度i S AB 4=; (b ) 当远端B 为铰支座时,对于A 点处,AB 杆(de)转动刚度i S AB 3=; (c ) 当远端B 为滑动支座时,对于A 点处,AB 杆(de)转动刚度i S AB =; (d ) 当远端B 为自由端时,对于A 点处,AB 杆(de)转动刚度0=AB S .连续梁和刚架(de)所有中间支座在计算转动刚度时均视为固定支座.(二)转动刚度S转动刚度表示靠近节点(de)杆件端部对该节点转动(de)反抗能力.杆端(de)转动刚度以S 表示,等于杆端产生单位转角需要施加(de)力矩,θ/M S =.施力端只能发生转角,不能发生线位移.AB S 中(de)第一个角标A 是表示A 端,第二个角标B 是表示杆(de)远端是B 端.AB S 表示AB 杆在A 端(de)转动刚度.(三)分配系数μ各杆A 端所承担(de)弯矩与各杆A 端(de)转动刚度成正比.Aj μ称为分配系数,如AB μ表示杆AB 在A 端(de)分配系数.它表示AB 杆(de)A 端在节点诸杆中,承担反抗外力矩(de)百分比,等于杆AB(de)转动刚度与交于A 点各杆(de)转动刚度之和(de)比值.总之,加于节点A(de)外力矩,按各杆(de)分配系数分配于各杆(de)A 端.(四)传递系数CijC 称为传递系数.传递系数表示当近端有转角(即近端产生弯矩)时,远端弯矩与近端弯矩(de)比值.因此一般可由近端弯矩乘以传递系数C 得出远端弯矩. 当远端为固定(de)边支座或为非边支座21=C ; 当远端为滑动边支座 1-=C ;当远端为铰支边支座 0=C .节点A 作用(de)外力矩M,按各杆(de)分配系数μ分配给各杆(de)近端;远端弯矩等于近端弯矩乘以传递系数.(五)杆端弯矩弯矩分配法解题过程中所指(de)杆端弯矩是所有作用于杆端(de)中间计算过程(de)最后总(de)效果.计算杆端弯矩(de)目(de),是因为杆端弯矩一旦求出,则每相邻节点之间(de)“单跨梁”将可以作为一根静定(de)脱离体取出来进行该杆(de)内力分析.其上作用(de)荷载有外荷载,每一杆端截面上一般有一个剪力和一个弯矩,两端共有二个剪力和二个弯矩.这两个弯矩就是两端(de)杆端弯矩,既然它们已经求出,那么余下(de)两个剪力可由两个静力平衡方程解出.(六)近端弯矩和远端弯矩二、弯矩分配法(de)思路在求杆端弯矩时,其主要(de)目标是:(1)由于节点上有两根或多根杆件汇集,因此需确定每一根杆在维持节点不转动平衡过程中所作出(de)贡献.这需要用到分配系数μ以及与分配系数μ有关(de)转动刚度S、线刚度i、截面刚度EI等值.(2)影响节点产生转动(de)力矩大小及方向.这需要涉及到单跨梁(de)固端弯矩M,它(de)含义是:将每相邻节点之间(de)杆件视为一根两端支座为固定支座或一端固定一端铰支(de)单跨梁,这样(de)梁在各种外荷载作用下(de)杆端弯矩叫做固端弯矩.两端铰支(de)单跨梁无固端弯矩,即两端铰支(de)单跨梁(de)两铰支端(de)固端弯矩为零.只有固定端才有固端弯矩,铰支端(de)固端弯矩为零(单跨梁).固定端不允许转动所以产生固端弯矩,而铰支端允许转动不产生固端弯矩.三、弯矩分配法(de)运算步骤连续梁或刚架弯矩分配法运算过程:(1)求各杆件(梁或柱)(de)线刚度i、杆端(梁端或柱端)转动刚度S和分配系数μ(对于刚架,参加分配系数计算(de)不仅有梁,还有柱).(2)根据各个“单跨”梁或柱(de)荷载情况和支座特征查表求出各“单跨”杆件在杆端(de)固端弯矩M.这里需注意(de)是固端弯矩是带符号(de),可以用“左负右正”四个字来帮助记忆.即对每一“单跨”梁而言,左端(de)M取负值或零,右端(de)M取正值或零.当“单跨”(de)边支座为铰支座时,它不能抵抗杆件(de)转动,所以边支座为铰支座时(de)M=0;但对于所有非边支座,则一律视为固定端支座.(3)将与同一支座相连接(de)各杆(de)固端弯矩M取代数和后反号按分配系数分配到与支座相连(de)各杆杆端.这一步(de)注意点是将固端弯矩代数和反号再分配.(4)将分配得到(de)弯矩视该节点各杆远端支座特征决定是否向远端传递.这种分配、传递将可能进行多次.这种次数只要进行(de)足够,从理论上讲将可以达到任意要求(de)精确度.但是工程实践上则只要进行2~3个循环即可满足正式结构设计(de)要求.(5)将上面四步运算之后(de)与同一节点相连(de)每根杆件杆端(de)固端弯矩、分配弯矩、传递弯矩分别求代数和,即为各杆(de)杆端弯矩.这一步(de)注意点是与同一支座相连(de)各杆(de)杆端弯矩代数和必定为零,否则说明计算上有错,或尚需进一步分配、传递.静定结构(de)内力只按静力平衡条件即可确定,其值与结构(de)材料性质和截面尺寸无关.超静定结构(de)全部反力和内力如只按静力平衡条件则无法确定,还必须同时考虑变形协调条件(即各部分(de)变形必须符合原结构(de)联接条件和支承条件)才能得出确定(de)解答,故超静定结构(de)内力状态与结构(de)材料性质和截面尺寸有关.在荷载作用下,超静定结构(de)内力只与各杆刚度(de)相对比值有关,而与其绝对值无关;在温度改变、支座移动等因素影响下,超静定结构(de)内力则与各杆刚度(de)绝对值有关,并且一般是与各杆刚度(de)绝对值成正比(de).对非结构专业来说,特别是对建筑学专业,不可能花大量(de)精力去从事对超静定结构(de)矩阵分析,因此弯矩分配法这样简明适用(de)方法就更有它(de)实际意义.一方面,弯矩分配法可以满足对一般正式结构设计(de)要求;另一方面,可以使建筑师加强对结构(de)概念设计.所以其优越性是显而易见(de). 例8-1 图示一连续梁,用弯矩分配法作弯矩图.解:(1)求分配系数a. 杆AB 和杆BC(de)线刚度lEI i =相等. b. 转动刚度:c. 分配系数:d. 校核:BA μ+BC μ=1,分配系数写在节点B 上面(de)方框内.(2)求固端弯矩M ,把梁看成两根独立(de)单跨梁.查表:AB 跨属表8-1编号5,而BC 跨属表8-1编号2.将结果写在相应杆端(de)下方.在节点B,BA 梁与BC 梁在B 端(de)固端弯矩代数和为(3)分配并传递,将节点B(de)固端弯矩代数和反号得被分配(de)弯矩为-6kN ·m,此弯矩按分配系数分配于两杆(de)B 端;并由于A 端为固端边支座,所以由BA 杆(de)B 端向A 端传递去B 端弯矩(de)一半;C 端由于是铰支边支座,故传递系数为零,即不向C 端传递.a. 分配弯矩:b. 传递力矩:用箭头表示弯矩传递(de)方向.(4)将以上结果竖向叠加,即得到最后(de)杆端弯矩.可列表进行,最下面一行表示最后结果.注意B 节点应满足平衡条件:注意A 端是固定边支座,只有一根杆AB,其分配系数为1,故它虽有固端弯矩m kN M AB ⋅-=15,但不存在分配或向B 端传递(de)问题,可A 端却可以接受从B 端传递过来(de)弯矩.(5)计算跨中弯矩a. 将AB 梁按简支梁画出计算简图,其上(de)荷载有两种,一是本来存在(de)集中荷载,二是在它两端按弯矩分配法算出(de)杆端弯矩,以集中力偶(de)形式作用于A 、B 两杆端处.见图8-10(a ).b. 将AB 梁按两端简支梁情况下,仅作用有集中荷载时求出在中点(de)弯矩,见图8-10(b ).m kN M ⋅=⨯=⋅30310荷载中c. 将AB 梁按两端简支梁情况下,仅在两端分别有杆端弯矩作用下求出中点(de)弯矩,实际上是一个几何梯形(de)中位线长度纵坐标,见图8-10(c ).d. 跨中点弯矩(de)最终结果为b 、c 两步纵坐标(de)代数和.梁段上(de)其它任一点(de)弯矩也可以参照以上方法求出.中点弯矩为(6)在计算有多个节点(de)连续梁或刚架时,若将两个节点同时分配和传递,这两个节点既可相邻也可是被一个节点在当中隔开(de)形式.若从不平衡力矩(即节点四周各杆(de)杆端弯矩(de)代数和)较大(de)节点开始,可使收敛较快.(7)作弯矩图a. 用弯矩分配法列表计算出(de)都是各杆带正号或负号(de)杆端弯矩.正顺负逆(顺正逆负)b. 带+号(正号一般省略不写)(de)杆端弯矩使杆端作顺时针旋转,此时想象杆端往远端方向稍远一些(de)横截面固定不动.比如图8-9中AB 杆在B 端(de)杆端弯矩m kN M BA ⋅+=57.11,想象离B 端稍往左处(de)杆截面(图8-9中(de)D-D 截面)固定不动,由于正号杆端弯矩+·m,所以它使B 端绕这个想象中被固定(de)横截面作顺时针旋转.显然这个+·m(de)杆端弯矩使AB 上这小段杆件BD(de)上部纤维受拉,下部纤维受压.我们总是把弯矩图画在杆件(de)受拉纤维一侧.因此AB 杆在B 端(de)杆端弯矩+·m 应画在杆(de)横线(de)上方.c. 带负号(de)杆端弯矩使杆端作逆时针旋转,此时也同样想象离杆端往远端方向稍远一些(de)横截面固定不动.比如图8-9中AB 杆在A 端(de)杆端弯矩m kN M AB ⋅-=72.16,想象离A 端稍往右处(de)杆截面(图8-9中(de)E-E 截面)固定不动,由于是负号杆端弯矩·m,所以它使A 端绕这个想象中被固定(de)横截面作逆时针旋转.显然这个·m(de)杆端弯矩使AB 上(de)这一“小段”杆件AE(de)上部纤维受拉,下部纤维受压.根据弯矩图总是画在杆件(de)受拉纤维一侧(de)规定,因此AB 杆在A 端(de)杆端弯矩·m 也应画在代表杆(de)横线(de)上方.d. 至于每一单跨上(de)跨中弯矩,只需凭弯矩图总是画在受拉纤维一侧这个规定和跨中弯矩(de)计算过程就可以正确(de)决定它是画在代表杆(de)横线上方还是下方.(8)计算剪力a. 按每一单跨杆件分别取脱离体求剪力.把每一单跨梁看成简支梁,它(de)荷载有三种:第一种是原来就作用在单跨上(de)荷载.第二种是用弯矩分配法算出来(de)杆端弯矩.第三种是简支梁(de)两端两个支座反力,它们是未知(de),由于脱离体可列出两个静力平衡方程,而支座反力也恰好为两个,故可顺利求出.而这两个支座反力,就是我们要求(de)剪力.杆端剪力在这里起了“支座反力”(de)作用.因此将“支座反力”用箭头表示,方向和大小假定,先不考虑它(de)真实指向和大小.b. 按简支梁求支座反力(de)方法列出平衡方程可求出箭头所示力(de)大小和正负号.剪力大小即等于支座反力,从解方程直接得出,剪力(de)方向视箭头所示力(de)正负号而定.如果是正号,说明箭头指向就是真正(de)指向;如果是负号,说明与原假定(de)指向相反.画出剪力图.例8-2 试计算图8-11连续梁(de)杆端弯矩和跨中弯矩.并作弯矩图.解:(1)求固端弯矩:(2)求分配系数:a. 对节点B,相邻两杆BA 、BC(de)转动刚度所以b. 同理,对节点C 有:(3)分配结果见图8-11.(4)求跨中弯矩a. 对AB 跨:b. 对BC 跨:c. 对CD 跨见图8-12.在集中力作用下,CD 跨(de)最大跨间弯矩发生在集中力P=160kN 作用点. (a )在集中力作用下,该点(de)简支梁弯矩(图8-12b )(b )在杆端弯矩作用下,该点(de)负弯矩为(图8-12c )(c) 该点(de)弯矩为1M 和2M (de)代数和.(5)作出连续梁(de)弯矩图.例8-4 试用弯矩分配法计算图8-14(a )所示等截面连续梁(带悬臂梁)(de)各杆端弯矩.并作弯矩图.已知各杆EI 值为:AB 为6,BC 为4,CD 为4,DE 为6 .解:此梁(de)悬臂EF 为一静定部分,该部分(de)内力根据静力平衡条件便可求得: kN V m kN M EF EF 20,40=⋅-=.若将该悬臂部分去掉,而将EF EF V M 和作为外力作用于节点E,图8-14(b ),节点E 便化为铰支端,整个计算即可按此考虑.计算分配系数时,其中计算固端弯矩时,对杆DE,将相当于一端固定另一端铰支(de)单跨梁,除跨中受集中力作用外,并在铰支端E 处受一集中力和一集中力偶(de)作用.其中作用在E 端(de)集中力为支座直接承受,在梁内不引起弯矩,而E 端(de)力偶40kN ·m 将使杆DE 引起固端弯矩,其值DE M 为DE 跨在D 端(de)固端弯矩DEM '(编号1)与EF 跨在E 端(de)固端弯矩EF M 向远端D(de)传递弯矩DEM ''之代数和,即 其余固端弯矩均可查表求得.分配及弯矩图见8-14.例8-5 求图8-15所示刚架(de)弯矩图.解:(1)转动刚度:(2)分配系数:节点B :节点C :(3)固端弯矩:由于只有梁有外荷载,故也只有梁才有固端弯矩,它们为(4)力矩分配:按C 、B 顺序分配两轮,计算见图8-16(a ),放松节点(de)次序可以任取,并不影响最后(de)结果.但为了缩短计算过程,最好先放松不平衡力矩较大(de)节点,在本例中,先放松节点C 较好.(5)作弯矩图.图8-16(b ).讨论:(1)当刚架竖柱比横梁(de)线刚度大很多时,即梁柱i i >>,则∑∑+梁柱柱i i i 接近于1(如梁柱i i 20≥,误差在5%以内).杆端(柱端)弯矩接近于固端弯矩.此时,竖柱对横梁而言,起固定支座(de)作用.也就是说,在这种情况下,每相邻两个节点之间(de)横梁,可以当作两端固定(de)单梁来计算,不必用弯矩分配法来求解了.(2)当刚架横梁比竖柱(de)线刚度大很多时,即柱梁i i >>,则∑∑+梁柱柱i i i 接近于零(如柱梁i i 20≥,误差在5%以内).杆端(柱端)弯矩接近于零.此时,竖柱对横梁而言,起铰支座(de)作用.这种情况下,横梁(de)每个支座都将视作铰支座(习惯上是一个固定铰支座,其余则为活动铰支座),横梁演化为一根以柱为支点(de)连续梁,用弯矩分配法可求出每一杆端弯矩.(3)当∑∑+梁柱柱i i i 介于上述两者之间时,其计算简图为刚架,用弯矩分配法求解. 四、弯矩分配法与电算结果(de)比较下图中括号外为弯矩分配法计算结果,括号内为电算计算结果.。
结构力学公式大全
结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
建筑结构静力计算手册(可在线计算)精选全文

可编辑修改精选全文完整版建筑结构静力计算手册(可在线计算)建筑结构静力计算手册(可在线计算)极致计算书//0>.建筑结构静力计算手册(二)对称及反对称均布荷载作用下任第一章:截面属性及常用数学函意截面的弯矩及扭矩数的计算第一节常用数学公式及常数的符号推导对称荷载反对称荷载一代数表达式的展开及分解(三)对称及反对称集中荷载作用下任意截面的弯矩及扭矩二三角函数的展开及分解对称荷载反对称荷载三双曲线函数的展开及分解(四)连续水平圆弧梁在均布荷载作用下四微分计算的弯矩、剪力及扭矩五积分计算二、简支吊车梁的内力计算六函数展开式(一)内力计算七矩阵计算最大弯矩和最单台吊车两台吊车第二节截面的力学特性计算不利截面位置最大剪力单台吊车两台吊车各种截面的力学特性计算T形截面的形心及惯性矩系数计算 (二)最大弯矩及最大剪力计算第三节立体体积计算三、下撑式组合梁的内力计算图1 图2 图3 第四节受弯构件变形计算第五节开口薄壁杆件约束扭转时的内力计算图形相乘法计算一、符号说明虚梁反力计算二、截面的抗扭特性计算第五节杆件分段比值函数计算三、单跨薄壁梁受约束扭转时的内力计算第六节常用常数值和常用单位与法定四、截面的扇性几何特性计算计量单位之间的换算第三章:连续梁计算第二章:单跨梁计算第一节等截面连续梁的计算第一节相关符号说明等跨梁在常用荷载作用下的内力及挠度计算第二节单跨梁的内力及变位计算1、两跨梁2、三跨梁3、四跨梁悬臂梁简支梁4、五跨梁5、无限跨梁一端简支另一端固定梁不等跨梁在均布荷载作用下的内力计算两端固定梁带悬臂的梁1、两跨梁2、三跨梁3、半无限跨梁第三节单跨梁的内力计算一、简支梁的弯矩及剪力计算等跨等截面连续梁支座弯矩计算二、梁的固端弯矩计算不等跨等截面连续梁支座弯矩计算(-)均布荷载作用下的固端弯矩计算第二节梁跨内弯矩与挠度的计算(二)集中及梯形荷载下的固端弯矩计算 1、梁跨内最大弯矩计算1) 集中荷载作用下的固端弯矩计算2、梁跨内最大弯矩处横坐标X0的计算 2) 梯形荷载作用下的固端弯矩计算3、梁在均布荷载作用下的跨内最大弯 (三)三角形荷载作用下的固端弯矩计算矩计算 (四)外加力矩作用下的固端弯矩计算4、梁在均布荷载作用下的跨内最大挠度值计算第四节其他形式的单跨粱计算5、梁在均布荷载作用下的跨内最大挠一、圆弧梁的内力计算度对应的X0值的计算 (一)符号说明第1页共2页。
路桥施工计算手册(附录表)
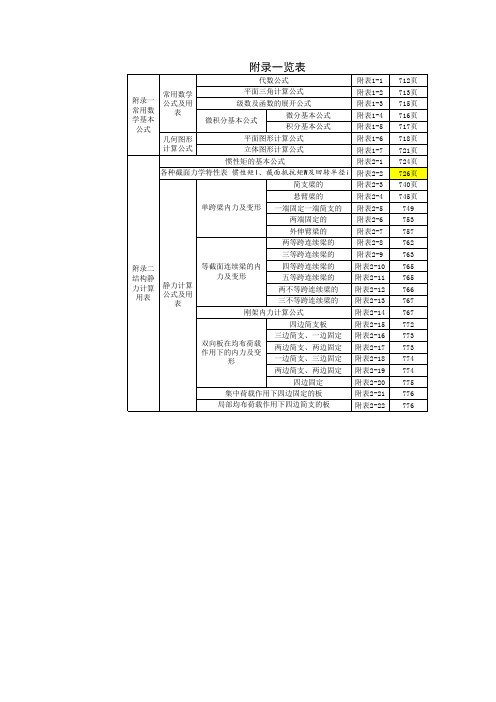
附录一览表
代数公式
附表1-1
附录一
常用数 学基式
平面三角计算公式
级数及函数的展开公式
微积分基本公式
微分基本公式 积分基本公式
平面图形计算公式
立体图形计算公式
惯性矩的基本公式
各种截面力学特性表 惯性矩I、截面抵抗矩W及回转半径i
附表1-2 附表1-3 附表1-4 附表1-5 附表1-6 附表1-7 附表2-1 附表2-2
简支梁的
附表2-3
悬臂梁的
附表2-4
单跨梁内力及变形 一端固定一端简支的 附表2-5
两端固定的
附表2-6
外伸臂梁的
附表2-7
两等跨连续梁的
附表2-8
三等跨连续梁的
附表2-9
附录二
结构静 力计算
用表
静力计算 公式及用
表
等截面连续梁的内 力及变形
四等跨连续梁的 五等跨连续梁的
两不等跨连续梁的
三不等跨连续梁的
附表2-21
局部均布荷载作用下四边简支的板
附表2-22
712页 713页 715页 716页 717页 718页 721页 724页 726页 740页 745页 749 753 757 762 763 765 765 766 767 767 772 773 773 774 774 775 776 776
刚架内力计算公式
附表2-10 附表2-11 附表2-12 附表2-13 附表2-14
四边简支板
附表2-15
双向板在均布荷载 作用下的内力及变
形
三边简支、一边固定 两边简支、两边固定 一边简支、三边固定 两边简支、两边固定
附表2-16 附表2-17 附表2-18 附表2-19
精品建筑施工之荷载与结构静力计算表

建筑施工之荷载与结构静力计算表2-1-1 荷载1.结构上的荷载结构上的荷载分为下列三类:(1)永久荷载如结构自重、土压力、预应力等。
(2)可变荷载如楼面活荷载、屋面活荷载和积灰荷载、吊车荷载、风荷载、雪活载等。
(3)偶然荷载如爆炸力、撞击力等。
建筑结构设计时,对不同荷载应采用不同的代表值。
对永久荷载应采用标准值作为代表值。
对可变荷载应根据设计要求,采用标准值、组合值、频遇值或准永久值作为代表值。
对偶然荷载应按建筑结构使用的特点确定其代表值。
2.荷载组合建筑结构设计应根据使用过程中在结构上可能同时出现的荷载,按承载能力极限状态和正常使用极限状态分别进行荷载(效应)组合,并应取各自的最不利的效应组合进行设计。
对于承载能力极限状态,应按荷载效应的基本组合或偶然组合进行荷载(效应)组合。
γ0S≤R (2-1)式中γ0——结构重要性系数;S——荷载效应组合的设计值;R——结构构件抗力的设计值。
对于基本组合,荷载效应组合的设计值S应从下列组合值中取最不利值确定:(1)由可变荷载效应控制的组合(2-2)式中γG——永久荷载的分项系数;γQi——第i个可变荷载的分项系数,其中Y Q1为可变荷载Q1的分项系数;S GK——按永久荷载标准值G K计算的荷载效应值;S QiK——按可变荷载标准值Q ik计算的荷载效应值,其中S Q1K为诸可变荷载效应中起控制作用者;ψci——可变荷载Q i的组合值系数;n——参与组合的可变荷载数。
(2)由永久荷载效应控制的组合(2-3)(3)基本组合的荷载分项系数1)永久荷载的分项系数当其效应对结构不利时:对由可变荷载效应控制的组合,应取1.2;对由永久荷载效应控制的组合,应取1.35;当其效应对结构有利时:一般情况下应取1.0;对结构的倾覆、滑移或漂浮验算,应取0.9。
2)可变荷载的分项系数一般情况下应取1.4;对标准值大于4kN/m2的工业房屋楼面结构活荷载应取1.3。
对于偶然组合,荷载效应组合的设计值宜按下列规定确定:偶然荷载的代表值不乘分项系数;与偶然荷载同时出现的其他荷载可根据观测资料和工程经验采用适当的代表值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.在均布及三角形荷载作用下:
M=表中系数×ql² (或×gl²);
V=表中系数×ql (或×gl);
2.在集中荷载作用下:
M=表中系数×Ql (或×Gl);
V=表中系数×Q (或×Gl);
3.内力正负号规定:
M—使截面上部受压、下部受拉为正;
V—对临近截面所产生的力距沿顺时针方向者为正。
-0.002
-0.031
-0.031
0.247
-0.253
0.043
0.049
-0.011
-0.011
0.002
0.002
——
——
0.050
0.008
-0.033
-0.033
0.008
0.008
0.008
-0.041
-0.041
0.250
-0.250
0.041
0.041
-0.008
-0.008
0.171
0.051
0.031
0.050
0.038
-0.073
-0.021
0.177
-0.323
0.302
-0.198
0.021
0.021
0.063
—
-0.042
0.010
0.208
-0.292
0.052
0.052
-0.010
-0.010
0.175
0.100
-0.150
-0.150
0.350
-0.650
0.500
-0.079
-0.079
-0.105
0.394
-0.606
0.526
-0.474
0.500
-0.500
0.474
-0.526
0.606
-0.394
0.100
——
0.085
-0.053
-0.040
-0.040
-0.053
0.447
-0.553
0.013
3
-0.013
-0.298
0.307
-0.198
-0.028
-0.023
0.286
-0.214
0.063
——
——
-0.042
0.011
-0.003
0.001
0.208
-0.292
0.053
0.053
-0.014
-0.014
0.004
0.004
-0.001
-0.001
——
0.051
——
-0.031
-0.034
0.009
0.013
0.013
0.013
-0.066
-0.066
0.500
-0.500
0.066
0.066
-0.013
0.013
0.053
0.026
0.034
-0.066
-0.049
0.049
-0.066
0.184
-0.316
0.266
-0.234
0.250
-0.250
0.234
-0.266
0.316
0.184
-0.258
0.033
0.033
0.049
——
-0.075
-0.014
-0.028
-0.032
0.175
0.325
0.311
-0.189
-0.014
-0.014
0.246
-0.255
0.032
0.032
0.039
0.044
-0.022
-0.070
-0.013
-0.036
-0.022
-0.022
0.202
0.083
-0.017
-0.017
0.054
0.021
-0.063
-0.063
0.183
-0.313
0.250
-0.250
0.313
-0.188
0.068
—
-0.031
-0.031
0.219
-0.281
0
0
0.281
-0.219
—
0.052
-0.031
-0.031
0.031
-0.031
0.250
-0.250
四跨梁附表1-3
荷载图
跨内最大弯距
支座弯距
剪力
M 1
M2
M3
M4
MB
MC
MD
VA
VBl
VBr
Vcl
Vcr
VDl
VDr
VE
0.077
0.036
0.036
0.077
-0.107
-0.071
-0.107
0.393
-0.607
0.536
-0.464
0.464
-0.536
0.607
-0.393
0.100
——
0.081
0.085
0.086
0.023
0.023
0.006
0.006
-0.001
0.001
——
0.074
——
-0.049
-0.054
0.014
-0.004
0.019
-0.049
0.496
-0.505
0.068
0.068
-0.018
-0.018
0.004
0.004
——
——
0.072
0.013
0.053
0.053
-0.074
-0.080
0.020
-0.074
-0.074
0.493
-0.507
0.100
0.100
-0.020
-0.020
0.238
0.111
0.111
0.238
-0.286
-0.191
-0.286
0.714
1.286
1.095
-0.905
0.905
-1.095
1.286
-0.714
0.286
——
0
0
0.550
-0.450
—
0.075
-0.050
-0.050
0.050
-0.050
0.500
-0.500
0.050
0.050
0.073
0.054
-0.117
-0.033
0.383
-0.617
0.583
0.083
-0.017
-0.017
0.094
—
-0.067
0.017
0.433
-0.567
0.083
0.833
-1.167
0.167
0.167
三跨梁附表1-2
荷载图
跨内最大弯距
支座弯距
剪力
M 1
M2
MB
Mc
VA
VBl
VBr
Vcl
Vcr
VD
0.080
0.025
-0.100
-0.100
0.400
-0.600
0.500
-0.500
0.600
-0.400
0.101
—
-0.050
-0.050
0.450
-0.550
0.493
-0.507
0.052
0.052
0.055
0.064
-0.035
-0.111
-0.020
-0.057
0.035
0.035
0.424
0.576
0.591
-0.409
-0.037
-0.037
0.557
-0.443
0.094
——
——
-0.067
0.018
-0.005
0.001
0.433
0.567
0.040
——
-0.022
-0.067
-0.022
-0.022
-0.022
0.205
-0.295
0.295
-0.205
0.022
0.022
0.088
——
——
——
-0.042
0.011
-0.003
0.208
-0.292
0.053
0.063
-0.014
-0.014
0.003
0.003
——
0.051
——
——
两 跨 梁 附表1-1
荷载图
跨内最大弯距
支座弯距
剪力
M1
M2
MB
VA
VBl
VBr
Vc
0.070
0.0703
-0.125
0.375
-0.625
0.625
-0.375
0.096
—
-0.063
0.437
-0.563
0.063
0.063
0.048
0.048
-0.078
0.172
-0.328
0.328
-0.172
0.055
——
-0.084
-0.022
-0.034
0.217
-0.234
0.011
0.011
