专题03 全等三角形及其判定核心知识解读(解析版)
(完整版)全等三角形知识点梳理,推荐文档

(完整版)全等三角形知识点梳理,推荐文档第十二章全等三角形2018.9 杨1.全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.对应边相等。
2.全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.对应角相等。
证明三角形全等基本思路:三角形全等的判定(1)三边分别相等的两个三角形全等,简写成边边边或SSS .1.如图,AB =AD ,CB =CD ,求证:(1)△ABC≌△ADC;(2)∠B =∠D.证明:(1)中,2.已知在四边形ABCD 中,AB=CD,AD=BC,,求证AD//BC做辅助线,连接AC ,利用SSS 证明全等,得到∠DAC=∠ACB ,从而证明平行三角形全等的判定(2)两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或“SAS”).两边和其中一边的对角对应相等的两个三角形不一定全等.1.如图,将两个一大、一小的等腰直角三角尺拼接(A ,B ,D 三点共线,AB =CB ,EB =DB ,∠ABC=∠EBD=90°),连接AE ,CD ,试确定AE 与CD 的关系,并证明你的结论.解:结论:AE =CD ,AE⊥CD.证明:延长AE 交CD 于F ,在△ABE 与△CBD 中,{AB =CB ,∠ABE =∠CBD ,BE =BD ,)∴△ABE≌△CBD(SAS ),∴AE=CD ,∠EAB=∠DCB,∵∠DCB+∠CDB=90°,∴∠EAB+∠CDB=90°,∴∠AFD=90°,∴AE⊥CD.2.在△ABC 和△CDE 中,CA=CB,CD=CE,∠ACB=∠DCE=90°,AE 与BD 交与点F (1)求证:△ACE≌△BCD(2)求证:AE⊥BD1,利用SAS 证明全等,AC=BC DC=EC ∠BCD=∠ACE2,全等得到角相等∠CAE=∠DCB∠CAB+∠EAB+∠ABC=90°∠DCB∠EAB+∠ABC=90°三角形全等的判定(3)两角和它们的夹边分别对应相等的两个三角形全等,简称角边角或ASA .两个角和其中一个角的对边分别相等的两个三角形全等,简称角角边或AAS .求证:三角形一边的两端点到这边的中线或中线延长线的距离相等.如图,AD 为△ABC 的中线,且CF⊥AD 于点F ,BE⊥AD,交AD 的延长线于点E ,求证:BE =CF.证法1:∵AD 为△ABC 的中线,∴BD=CD.∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°.在△BED 与△CFD 中{∠BED =∠CFD ,∠BDE =∠CDF ,BD =CD ,)F∴△BED≌△CFD(AAS ),∴BE=CF.证法2:∵S △ABD =AD·BE ,S △ACD =AD·C F ,1212且S △ABD =S △ACD (等底同高的两个三角形面积相等),∴AD·BE =AD·CF ,∴BE=CF.1212三角形全等的判定(4)斜边和一条直角边分别对应相等的两个直角三角形全等,简称“斜边、直角边”或“HL ”.如图,E ,F 分别为线段AC 上的两点,且DE⊥AC 于点E ,BF⊥AC 于点F ,若AB =CD ,AE =CF ,BD 交AC 于点M. 求证:BM =DM ,ME =MF.证明:∵AE=CF ,∴AE+EF =CF +EF∴AF=CE.在Rt △ABF与Rt △CDE 中{AB =CD ,AF =CE ,)∴Rt △ABF≌Rt △CDE(HL ),∴BF=DE.∵DE⊥AC,BF⊥AC,∴∠DEM=∠BFM=90°.在△BFM 与△DEM 中{∠BFM =∠DEM ,∠BMF =∠DME ,BF =DE ,)∴△BFM≌△DEM(AAS ),∴BM=DM ,ME =MF.角的平分线的性质角平分线的性质:角的平分线上的点到角的两边的距离相等.文字命题的证明方法:a .明确命题中的已知和求证;b .根据题意,画出图形,并用数学符号表示已知和求证;c .经过分析,找出由已知推出要证的结论的途径,写出证明过程.方法总结:(1)角平分线的性质是证明线段相等的另一途径.(2)在已知角平分线的条件下,也可想到翻折构造全等的方法.角平分线的性质是证线段相等的常用方法之一,角平分线的性质与判定通常是交叉使用,作角的平分线或过角的平分线上一点作角两边的垂线段是常用的辅助线.1.在△ABC 中,AD 是△ABC 的角平分线,E ,F 分别是AB ,AC 上一点,并且有∠EDF+∠EAF=180°.试判断DE 和DF的大小关系并说明理由.建议收藏下载本文,以便随时学习!解:结论:DE =DF.证明:过点D 作DG⊥AB 于点G ,作DH⊥AC 于点C ,∵AD 是△ABC 的角平分线,∴DG=DH.∵∠DGA=∠DHA=90°,∴∠GDH+∠BAC=180°,∵∠EDF+∠EAF=180°,∴∠GDH=∠EDF,∴∠GDH-∠EDH=∠EDF-∠EDH,∴∠GDE=∠FDH.在△DGE 与△DHF 中,{∠DGE =∠DHF =90°,DG =DH ,∠GDE =∠HDF ,)∴△DGE≌△DHF(ASA ),∴DE=DF 2.如图,在△ABC 中,D 是BC 边上一点,连接AD ,过点B 作BE ⊥AD 于点E ,过点C 作CF ⊥AD 交AD 的延长线于点F ,且BE =CF.求证:AD 是△ABC 的中线.利用AAS 证明全等∠BDE=∠F∠BDE=∠CDFBE=CF利用全等证明垂直此类题目中必有垂直,利用垂直角度和是90°,再根据全等转换一个角,达到另外的两个角度和是90°,得到第三个角是90°,进一步证明线的垂直关系。
全等三角形(知识点讲解)

全等三角形(知识点讲解)全等三角形(知识点讲解)全等三角形是初中数学中的重要概念,也是几何学中的核心内容之一。
在这篇文章中,我们将从定义、判定全等三角形的条件以及全等三角形的性质等方面进行讲解。
一、全等三角形的定义全等三角形指的是具有完全相同的三边和三角的三角形。
简而言之,在几何学中,当两个三角形的对应边长相等、对应角度相等时,我们称这两个三角形是全等的。
二、全等三角形的判定条件为了判断两个三角形是否全等,我们有以下几个常用的判定条件:1. SSS判定法:即边-边-边判定法。
当两个三角形的三条边分别相等时,它们就是全等的。
2. SAS判定法:即边-角-边判定法。
当两个三角形的一对夹角和夹角两边分别相等时,它们就是全等的。
3. ASA判定法:即角-边-角判定法。
当两个三角形的一对夹角和夹角对边分别相等时,它们就是全等的。
4. AAS判定法:即角-角-边判定法。
当两个三角形的两对夹角和一个非夹角边分别相等时,它们就是全等的。
需要注意的是,这些判定条件是相互独立的,即只要满足其中一种条件,就可以判定两个三角形是全等的。
三、全等三角形的性质全等三角形具有以下重要性质:1. 对应边对应角相等性质:全等三角形的对应边对应角相等。
即若∆ABC≌∆DEF,那么 AB = DE, AC = DF, BC = EF,并且∠A = ∠D,∠B = ∠E, ∠C = ∠F。
2. 全等三角形的任意一角都与对应角相等:即若∆ABC≌∆DEF,那么∠A = ∠D, ∠B = ∠E, ∠C = ∠F。
3. 全等三角形的任意一边都与对应边相等:即若∆ABC≌∆DEF,那么 AB = DE, AC = DF, BC = EF。
4. 全等三角形的外角相等:即若∆ABC≌∆DEF,那么∠BAC =∠EDF, ∠ABC = ∠DEF, ∠ACB = ∠DFE。
通过以上性质,我们可以进行全等三角形的各种推理和计算。
四、全等三角形的应用全等三角形在几何学的应用非常广泛。
专题03 全等三角形及其判定核心知识解读(解析版)

专题03 全等三角形及其判定核心知识解读一、基础知识点综述1. 全等形能够完全重合的两个图形叫作全等形. 满足两个条件:形状相同、大小相等.得到全等形常用变换:平移、翻折、旋转.2. 全等三角形相关概念能够完全重合的两个三角形叫作全等三角形.将两个全等三角形重合在一起,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.全等符号“≌”.3. 常用技巧对应边、对应角的找法:(1)有对顶角的,对顶角是对应角;(2)有公共角的,公共角是对应角;(3)有公共边的,公共边是对应边;(4)全等三角形对应边所对的角是对应角,对应角所对的边是对应边;(5)两个全等三角形中一对最长边(最大角)一定是对应边(角);两个全等三角形中一对最短边(最小角)一定是对应边(角).4. 对应边(角)与对边(角)的区别对应边(角)是相对于两个三角形而言的,是指两条边(两个角)之间的关系;对边(角)是在同一个三角形中而言的,对边是指三角形中某个内角(顶点)所对的边,对角是指三角形中某个边所对的角.在书写时通常将对应顶点写在相同的位置上.5. 全等三角形性质(1)对应边、对应角相等;(2)对应角的平分线,对应边的中线,对应边上的高分别对应相等;(3)全等三角形的面积相等,周长相等.6. 几个常用图形中的全等三角形(1)平移型(2)翻折型(3)旋转型7. 全等三角形判断定理(1)SSS ——三边分别对应相等的两个三角形全等.在≌ABC 和≌DEF 中,AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩,≌≌ABC ≌≌DEF (SSS ).(2)SAS ——两边和它们的夹角分别对应相等的两个三角形全等.在≌ABC 和≌DEF 中,AB DE B E BC EF =⎧⎪=⎨⎪=⎩∠∠,≌≌ABC ≌≌DEF (SAS ).BCE F(3)ASA ——两角和它们的夹边分别对应相等的两个三角形全等.在≌ABC 和≌DEF 中,A D AB DE B E =⎧⎪=⎨⎪=⎩∠∠∠∠,≌≌ABC ≌≌DEF (ASA ).(4)AAS ——两角和其中一个角的对边分别对应相等的两个三角形全等.在≌ABC 和≌DEF 中,A DB E AC DF =⎧⎪=⎨⎪=⎩∠∠∠∠,≌≌ABC ≌≌DEF (AAS ).(5)HL ——斜边和一条直角边分别相等的两个直角三角形全等.在Rt ≌ABC 和Rt ≌DEF 中,AB DE AC DF =⎧⎨=⎩,≌≌ABC ≌≌DEF (HL ).注意:一般三角形的全等判断定理(SSS 、SAS 、ASA 、AAS )同样适用于直角三角形全等的判定,即直角三角形全等的判定定理有5个.二、典型例题精讲例1. (2019·广东期末)圣母大学计算机系的史戈宇教授带一家人去旅行,途中汽车被劫走报警911,而警察毫无作为,马自达汽车上安装的MMS 系统,虽然可以提示汽车与手机APP 之间的直线距离,但方位不准确,且不能实时提供数据. 史教授利用“贪心算法”将被抢车辆定位在了一块区域内,这是芝加哥一个BE以暴乱和枪击文明的地区.如下图所示,当史教授与同伴开车从点E向A点方向行驶时,汽车与手机APP之间直线距离逐渐变小,从A点驶向F点时,距离逐渐变大. 当史教授与同伴开车从点F向B点方向行驶时,汽车与手机APP之间直线距离逐渐变小,从B点驶向G点时,距离逐渐变大.史教授再次报警后,警察根据史教授确定的被盗汽车的位置,很快找到了被盗汽车,根据你学的数学知识,在图中画出被盗汽车的位置.【分析】所谓“贪心算法”是指仅知道一动点与一不动点之间的直线距离而不知道方位时,怎么找到不动点的方法. 也就是先沿着一个方向走,直到距离不再明显变小(这是说明我们前进的方向已经几乎垂直于我们和目标之间连线),就转到垂直方向再继续搜寻.【答案】见解析.【解析】解:如图所示,连接EF,GF,过点A作AN≌EF,过点B作BM≌GF,直线AN、BM的交点即为P点位置.例2. (2019·辽宁期末)在≌ABC中,≌C=90°,AC=BC,BP是≌ABC的角平分线,过点P作PD≌AB 于点D,将≌EPF绕点P旋转,使≌EPF的两边交直线AB于点E,交直线BC于点F,请解答下列问题:当≌EPF绕点P旋转到如图1的位置,点E在线段AD上,点F在线段BC上,且满足PE=PF.≌请判断CP、CF、AE之间的数量关系,并加以证明.≌求出≌EPF的度数.图1 图2【答案】见解析.【解析】解:≌CP=CF+AE,理由如下:≌在≌ABC中,≌C=90°,AC=BC,≌AC=BC,≌A=≌ABC=45°,AC≌BC,≌PD≌AB,≌≌APD=45°,即PD=AD,≌BP平分≌ABC,PD≌AB,PC≌BC,≌PC=PD,≌PE=PF,≌Rt≌PED≌Rt≌PFC,≌DE=CF,≌CP=PD=AD=AE+ED=AE+CF;≌由≌知:≌DPE=≌CPF,≌≌EPF=≌DPC,≌≌ABC=45°,在四边形DPCB中,≌DPC=360°-90°-90°-45°=135°,即≌EPF=135°.例3. (2019·山东期末)如图,B、E、F、C在同一条直线上,AF≌BC于点F,DE≌BC于E,AB=DC,BE=CF,求证:AB≌CD.【答案】见解析.【解析】证明:≌AF≌BC,DE≌BC,≌≌DEC=≌AFB=90°,≌BE=CF,≌BE+EF=CF+EF,即BF=CE,在Rt≌ABF和Rt≌DCE中,AB=CD,BF=CE,≌Rt≌ABF≌Rt≌DCE,≌≌B=≌C,≌AB≌DC.例4. (2019·淄博月考)已知:如图所示,在≌ABC、≌ADE中,≌BAC=≌DAE=90°,AB=AC,AD=AE,点D、C、E三点共线,连接BD.求证:(1)≌BAD≌≌CAE;(2)BD≌CE.【答案】见解析.【解析】证明:(1)≌≌BAC=≌DAE=90°,≌≌BAC+≌CAD=≌DAE+≌CAD,即≌BAD=≌CAE,在≌BAD和≌CAE中,≌AB=AC,≌BAD=≌CAE,AD=AE,≌≌BAD≌≌CAE;(2)由(1)知,BD=CE,≌≌BAD≌≌CAE,≌≌ABD=≌ACE,由≌ABD+≌DBC=45°,得≌ACE+≌DBC=45°,≌≌DBC+≌DCB=90°,即BD≌CE.例5. 已知直线CD≌AB于点O,≌EOF=90°,射线OP平分≌COF.(1)如图1,≌EOF在直线CD的右侧,且点E在点F的上方.≌若≌COE=30°,求≌BOF和≌POE的度数;≌请判断≌POE与≌BOP之间存在怎样的数量关系?并说明理由.(2)如图2,≌EOF在直线CD的左侧,且点E在点F的下方.≌请直接写出≌POE与≌BOP之间存在怎样的数量关系.≌请直接写出≌POE与≌DOP之间存在怎样的数量关系.图1 图2【答案】见解析.【解析】解:(1)≌≌CD≌AB,≌≌COB=90°,≌≌EOF=90°,≌≌COE+≌BOE=≌BOE+≌BOF,即≌COE=≌BOF=30°,≌≌COF=120°,又≌OP平分≌COF,≌≌COP=60°,≌≌POE=30°;≌由≌知,≌COE=≌BOF,≌COP=≌POF,≌≌POE=90°+≌POF,≌BOP=90°+≌COP,≌≌POE=≌BOP.(2)≌由上知,≌COP=≌POF,≌≌POE=90°+≌POF,≌BOP=90°+≌COP,≌≌POE=≌BOP.≌≌≌POE=≌BOP,≌DOP+≌BOP=270°,≌≌POE+≌DOP=270°.例6. (2019·山东期末)在等腰≌ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD 为一边在AD的右侧作≌ADE,使得AD=AE,≌DAE=≌BAC,连接CE.(1)如图1,当点D在线段BC上,如果≌BAC=90°,求≌BCE的度数;(2)如图2,当点D在线段BC上,如果≌BAC=60°,求≌BCE的度数;(3)设≌BAC=α,≌BCE=β,≌如图3,当点D在线段BC上移动,则α、β之间有怎么样的数量关系?请说明理由.≌当点D在线段BC的反向延长线上移动时,α、β之间有怎么样的数量关系?请说明理由.【答案】见解析.【解析】解:(1)≌≌BAC=≌DAE,≌≌BAC-≌DAC=≌DAE-≌DAC,即≌BAD=≌CAE,在≌ADB和≌AEC中,≌AB=AC,≌BAD=≌CAE,AD=AE,≌≌ADB≌≌AEC,≌≌B=≌ACE,≌≌B+≌ACB=≌ACE+≌ACB,即≌BCE=≌B+≌ACB,又≌≌BAC=90°,≌≌BCE=90°.(2)≌≌BAC=60°,≌≌DAE=≌BAC=60°,≌AB=AC,AD=AE,≌≌B=≌ACB=60°,≌ADE=≌AED=60°,≌≌B=≌ACE=60°,≌≌BCE=120°.(3)≌α+β=180°,理由如下:≌≌BAC=≌DAE,≌≌BAC+≌DAC=≌DAE+≌DAC,即≌BAD=≌CAE,在≌ADB和≌AEC中,≌AB=AC,≌BAD=≌CAE,AD=AE,≌≌ADB≌≌AEC,≌≌B=≌ACE,≌≌B+≌ACB=≌ACE+≌ACB,即≌B+≌ACB=β,又≌α+≌B+≌ACB=180°,≌α+β=180°.≌α=β,理由如下:在≌ADB和≌AEC中,≌AB=AC,≌BAD=≌CAE,AD=AE,≌≌ADB≌≌AEC,≌≌ABD=≌ACE,≌≌ABD=≌BAC+≌ACB,≌ACE=≌BCE+≌ACB,≌≌BAC=≌BCE,即α=β.例7. (2019·内蒙古月考)已知≌ABC的高AD所在直线与高BE所在直线相交于点F.(1)如图1,若≌ABC为锐角三角形,且≌ABC = 45°,过点F作F G//BC,交直线AB于点G.试说明:F G + DC = AD.图1(2)如图2,若≌ABC= 135°,过点F作FG//BC,交直线AB于点G,直接写出F G,DC,AD之间满足的数量关系.图2【答案】见解析.【解析】解:(1)证明:≌≌ADB=90°,≌ABC=45°,≌≌BAD=≌ABC=45°,≌AD=BD,≌≌BEC=90°,≌≌CBE+≌C=90°,≌≌DAC+≌C=90°,≌≌CBE=≌DAC,≌≌FDB≌≌CDA≌GF≌BD,≌≌AGF=≌ABC=45°,≌≌AGF=≌BAD,≌F A=FG,≌FG+DC=F A+DF=AD;(2)FG-DC=AD;由(1)知,AF=FG,≌BFD=≌ACD,AD=BD,≌FDB=≌ADC=90°,≌≌FDB≌≌CDA.≌DC=DF,≌FG-DC=AD.。
三角形的全等知识点总结

三角形的全等知识点总结在几何学中,全等是一个重要的概念,它意味着两个或多个图形在形状和大小上完全相同。
在三角形中,全等三角形是非常常见的,它们具有相等的边和角。
本文将对三角形的全等知识点进行总结,以帮助读者更好地理解和掌握这一概念。
一、全等三角形的定义全等三角形的定义是:如果两个三角形的对应边相等,对应角相等,那么这两个三角形是全等的。
二、全等三角形的判定条件1. SSS判定法(边边边):如果两个三角形的三条边分别相等,则这两个三角形是全等的。
2. SAS判定法(边角边):如果两个三角形的一条边和这个边上的两个角分别与另一个三角形的一条边和这个边上的两个角相等,则这两个三角形是全等的。
3. ASA判定法(角边角):如果两个三角形的一条角和这个角对应的两边分别与另一个三角形的一条角和这个角对应的两边相等,则这两个三角形是全等的。
4. RHS判定法(直角边斜边):如果两个直角三角形的一条直角边和斜边分别与另一个直角三角形的一条直角边和斜边相等,则这两个直角三角形是全等的。
三、全等三角形的性质1. 全等三角形的对应角相等,即对应顶点的角是相等的。
2. 全等三角形的对应边相等,即对应边的长度是相等的。
3. 全等三角形的对应高线相等。
4. 全等三角形的周长和面积完全相同。
四、全等三角形的性质运用利用全等三角形的性质可以进行各种几何推理和证明。
1. 利用全等三角形可以证明两条线段相等。
2. 利用全等三角形可以证明两个角相等。
3. 利用全等三角形可以证明两个三角形全等。
4. 利用全等三角形可以证明两个四边形全等。
五、全等三角形的应用全等三角形的知识在实际生活和工程中具有广泛的应用。
1. 在建筑工程中,利用全等三角形可以计算高楼房屋的高度,简化测量过程。
2. 在地图测量中,利用全等三角形可以计算两地的距离和高度。
3. 在设计中,利用全等三角形可以保证建筑物的比例和对称性。
4. 在计算机图形学中,利用全等三角形可以进行图形变换和模型重建。
全等三角形常见模型知识点总结和重难点精析

全等三角形常见模型知识点总结和重难点精析一、概述全等三角形是八年级数学中的重要内容,它涉及到三角形的边、角以及它们的性质和定理。
全等三角形的定义、性质和应用场景对于学生来说是非常重要的基础知识。
在实际问题中,全等三角形常常被用来解决几何问题,例如测量、建筑设计等。
二、基础知识点1、全等三角形的定义:能够完全重合的两个三角形称为全等三角形。
2、全等三角形的性质:a) 全等三角形的对应边相等;b) 全等三角形的对应角相等;c) 全等三角形的周长和面积都相等。
3、全等三角形的判定方法:a) 边边边(SSS):三边对应相等的两个三角形全等;b) 边角边(SAS):两边及其夹角对应相等的两个三角形全等;c) 角边角(ASA):两角及其夹边对应相等的两个三角形全等;d) 角角边(AAS):两角及其一角的对边对应相等的两个三角形全等。
三、重难点精析1、易错点:在实际应用中,学生常常会忽视全等三角形的对应关系,导致解题错误。
因此,在应用全等三角形时,一定要明确对应关系。
2、难点解析:对于一些较为复杂的几何问题,如何准确找到全等三角形并选择合适的判定方法进行证明,是学生的难点。
这种情况下,需要学生通过多练习、多思考来提高解题能力。
四、例题精选例1:已知△ABC≌△DEF,其中AB=DE,∠A=∠D,∠B=∠E,则第三组对应边为____,对应角为____。
解析:根据全等三角形的性质,可知第三组对应边为AC=DF,对应角为∠ACB=∠F。
例2:在△ABC中,AB=AC,点D在BC上,且AD=BD,AC=CD,求△ABC各角的度数。
解析:设∠BAC=x,∵AB=AC,∴∠B=∠C=90°-x/2.又∵AD=BD,∴∠BAD=∠BDA=90°-x/4.∵AC=CD,∴∠CAD=∠CDA=90°-x/2.∵∠BAC+∠B+∠C=180°,∴x+3×(90°-x/2)=180°,解得x=45°。
三角形全等知识点归纳

三角形全等知识点归纳一、全等三角形的定义全等三角形就是能够完全重合的两个三角形。
就像两个一模一样的双胞胎,它们的形状和大小完全相同。
这里要注意哦,全等用符号“≌”来表示。
二、全等三角形的性质1. 全等三角形的对应边相等。
比如说一个三角形的三条边分别是3cm、4cm、5cm,那么和它全等的三角形的三条边也一定是3cm、4cm、5cm。
2. 全等三角形的对应角相等。
如果一个三角形的三个角分别是30°、60°、90°,那它全等的三角形的三个角也是30°、60°、90°。
三、全等三角形的判定方法1. SSS(边边边)如果两个三角形的三条边对应相等,那么这两个三角形全等。
这就好比我们搭积木,如果三根积木的长度都一样,那搭出来的形状肯定是一样的。
2. SAS(边角边)当两个三角形的两条边及其夹角对应相等时,这两个三角形全等。
可以想象一下,有两条边固定了长度和它们之间的夹角,那这个三角形的形状也就确定了。
3. ASA(角边角)两个三角形的两个角及其夹边对应相等,这两个三角形全等。
就像我们知道了两个角的大小和它们中间那条边的长度,这个三角形也就确定下来了。
4. AAS(角角边)两个角和其中一个角的对边对应相等的两个三角形全等。
这个可能稍微难理解一点,但是只要记住它也是一种判定方法就好啦。
5. HL(斜边、直角边)这是直角三角形特有的判定方法哦。
如果两个直角三角形的斜边和一条直角边对应相等,那么这两个直角三角形全等。
四、全等三角形的应用1. 证明线段相等当我们要证明两条线段相等的时候,如果能找到包含这两条线段的两个全等三角形,那么根据全等三角形对应边相等的性质,就可以证明这两条线段相等啦。
2. 证明角相等同理,要证明两个角相等,也可以通过找到包含这两个角的全等三角形,利用全等三角形对应角相等的性质来证明。
全等三角形的知识点虽然有点多,但是只要我们理解了定义、性质和判定方法,并且多做一些练习题,就一定能掌握得很好哦。
三角形全等的判定(6种题型)-2023年新八年级数学核心知识点与常见题型(浙教版)(解析版)
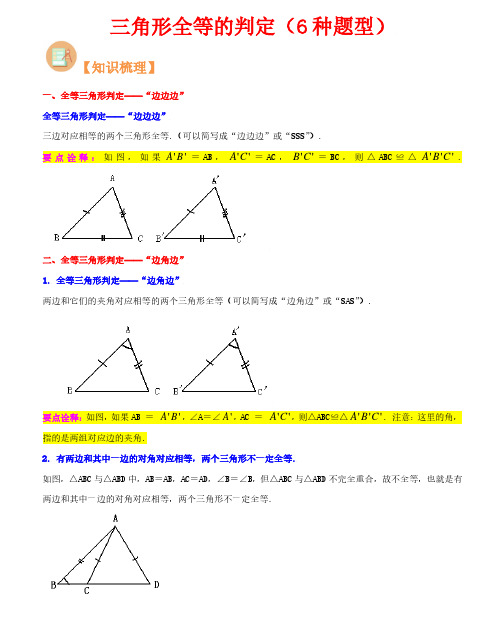
三角形全等的判定(6种题型)【知识梳理】一、全等三角形判定——“边边边”全等三角形判定——“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).要点诠释:如图,如果''A B =AB ,''A C =AC ,''B C =BC ,则△ABC ≌△'''A B C .二、全等三角形判定——“边角边”1. 全等三角形判定——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).要点诠释:如图,如果AB = ''A B ,∠A =∠'A ,AC = ''A C ,则△ABC ≌△'''A B C . 注意:这里的角,指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB =AB ,AC =AD ,∠B =∠B ,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.三、垂直平分线:1.定义:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.2.性质定理:线段垂直平分线上的点到线段两端的距离相等四、全等三角形判定——“角边角”全等三角形判定——“角边角”两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”).要点诠释:如图,如果∠A =∠'A ,AB =''A B ,∠B =∠'B ,则△ABC ≌△'''A B C .五、全等三角形判定——“角角边” 1.全等三角形判定——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”)要点诠释:由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等,也就是说,用角边角条件可以证明角角边条件,后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图,在△ABC 和△ADE 中,如果BC ,那么∠ADE =∠B ,∠AED =∠C ,又∠A =∠A ,但△ABC 和△ADE 不全等.这说明,三个角对应相等的两个三角形不一定全等.六、角平分线的性质定理:角平分线上的点到角两边的距离相等.【考点剖析】题型一、全等三角形的判定——“边边边”例1、已知:如图,△RPQ 中,RP =RQ ,M 为PQ 的中点.求证:RM 平分∠PRQ .【思路点拨】由中点的定义得PM =QM ,RM 为公共边,则可由SSS 定理证明全等.【答案与解析】证明:∵M 为PQ 的中点(已知),∴PM =QM在△RPM 和△RQM 中,()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边 ∴△RPM ≌△RQM (SSS ).∴ ∠PRM =∠QRM (全等三角形对应角相等).即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到,如:公共边、公共角、对顶角等条件隐含在题目或图形之中. 用全等三角形的性质和判定.【变式】已知:如图,AD =BC ,AC =BD.试证明:∠CAD =∠DBC.【答案】证明:连接DC ,在△ACD 与△BDC 中()AD BC AC BDCD DC ⎧=⎪=⎨⎪=⎩公共边 ∴△ACD≌△BDC(SSS )∴∠CAD =∠DBC (全等三角形对应角相等)【变式2】、如图,在△ABC 和△ADE 中,AB =AC ,AD =AE ,BD =CE ,求证:∠BAD =∠CAE.【答案与解析】证明:在△ABD 和△ACE 中,AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACE (SSS )∴∠BAD =∠CAE (全等三角形对应角相等).【总结升华】把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等,综合应用全等三角形的判定和性质. 要证∠BAD =∠CAE ,先找出这两个角所在的三角形分别是△BDA 和△CAE ,然后证这两个三角形全等.题型二、全等三角形的判定——“边角边”例2、已知:如图,AB =AD ,AC =AE ,∠1=∠2.求证:BC =DE .【思路点拨】由条件AB =AD ,AC =AE ,需要找夹角∠BAC 与∠DAE ,夹角可由等量代换证得相等.【答案与解析】证明: ∵∠1=∠2∴∠1+∠CAD =∠2+∠CAD ,即∠BAC =∠DAE在△ABC 和△ADE 中AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADE (SAS )∴BC =DE (全等三角形对应边相等)【总结升华】证明角等的方法之一:利用等式的性质,等量加等量,还是等量.【变式】如图,将两个一大、一小的等腰直角三角尺拼接 (A 、B 、D 三点共线,AB =CB ,EB =DB ,∠ABC =∠EBD =90°),连接AE 、CD ,试确定AE 与CD 的位置与数量关系,并证明你的结论.【答案】AE =CD ,并且AE ⊥CD证明:延长AE 交CD 于F ,∵△ABC 和△DBE 是等腰直角三角形∴AB =BC ,BD =BE在△ABE 和△CBD 中90AB BC ABE CBD BE BD =⎧⎪∠=∠=︒⎨⎪=⎩∴△ABE ≌△CBD (SAS )∴AE =CD ,∠1=∠2又∵∠1+∠3=90°,∠3=∠4(对顶角相等)∴∠2+∠4=90°,即∠AFC =90°∴AE ⊥CD例3、如图,AD 是△ABC 的中线,求证:AB +AC >2AD .【思路点拨】延长AD 到点E ,使AD =DE ,连接CE .通过证全等将AB 转化到△CEA 中,同时也构造出了2AD .利用三角形两边之和大于第三边解决问题.【答案与解析】证明:如图,延长AD 到点E ,使AD =DE ,连接CE .在△ABD 和△ECD 中,AD DE ADB EDC BD CD ⎧⎪∠∠⎨⎪⎩===.∴△ABD ≌△ECD (SAS ).∴AB =CE .∵AC +CE >AE ,∴AC +AB >AE =2AD .即AC +AB >.【总结升华】证明边的大小关系主要有两个思路:(1)两点之间线段最短;(2)三角形的两边之和大于第三边.要证明AB +AC >2AD ,如果归到一个三角形中,边的大小关系就是显然的,因此需要转移线段,构造全等三角形是转化线段的重要手段.可利用旋转变换,把△ABD 绕点D 逆时针旋转180°得到△CED ,也就把AB 转化到△CEA 中,同时也构造出了2AD .若题目中有中线,倍长中线,利用旋转变换构造全等三角形是一种重要方法.例4、已知,如图:在△ABC 中,∠B =2∠C ,AD ⊥BC ,求证:AB =CD -BD .【思路点拨】在DC 上取一点E ,使BD =DE ,则△ABD ≌△AED ,所以AB =AE ,只要再证出EC =AE 即可.【答案与解析】证明:在DC 上取一点E ,使BD =DE∵ AD ⊥BC ,∴∠ADB =∠ADE在△ABD 和△AED 中,BD DE ADB=ADE AD AD ⎧⎪⎨⎪⎩=∠∠=∴△ABD ≌△AED (SAS ).∴AB =AE ,∠B =∠AED .又∵∠B =2∠C =∠AED =∠C +∠EAC .∴∠C =∠EAC .∴AE =EC .∴AB =AE =EC =CD —DE =CD —BD .【总结升华】此题采用截长或补短方法.上升到解题思想,就是利用翻折变换,构造的全等三角形,把条件集中在基本图形里面,从而使问题加以解决.如图,要证明AB =CD -BD ,把CD -BD 转化为一条线段,可利用翻折变换,把△ABD 沿AD 翻折,使线段BD 运动到DC 上,从而构造出CD -BD ,并且也把∠B 转化为∠AEB ,从而拉近了与∠C 的关系.【变式】已知,如图,在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于E ,并且AE =12(AB +AD ), 求证:∠B +∠D =180°. AE D CB【答案】证明:在线段AE 上,截取EF =EB ,连接FC ,∵CE ⊥AB ,∴∠CEB =∠CEF =90°在△CBE 和△CFE 中,CEB CEF EC =EC EB EF =⎧⎪∠=∠⎨⎪⎩∴△CBE 和△CFE (SAS )∴∠B =∠CFE∵AE =12(AB +AD ),∴2AE = AB +AD ∴AD =2AE -AB∵AE =AF +EF ,∴AD =2(AF +EF )-AB =2AF +2EF -AB =AF +AF +EF +EB -AB =AF +AB -AB ,即AD =AF在△AFC 和△ADC 中(AF AD FAC DAC AC AC =⎧⎪∠=∠⎨⎪=⎩角平分线定义)∴△AFC ≌△ADC (SAS )∴∠AFC =∠D∵∠AFC +∠CFE =180°,∠B =∠CFE.∴∠AFC +∠B =180°,∠B +∠D =180°.题型三、全等三角形的判定——“角边角”例5、已知:如图,E ,F 在AC 上,AD ∥CB 且AD =CB ,∠D =∠B .求证:AE =CF .【答案与解析】证明:∵AD ∥CB∴∠A =∠C在△ADF 与△CBE 中A C AD CB D B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADF ≌△CBE (ASA )∴AF =CE ,AF +EF =CE +EF故得:AE =CF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】(2022•长安区一模)已知:点B 、E 、C 、F 在一条直线上,AB ∥DE ,AC ∥DF ,BE =CF .求证:△ABC ≌△DEF .【分析】先利用平行线的性质得到∠B=∠DEF,∠ACB=∠F,再证明BC=EF,然后根据“ASA”可判断△ABC≌△DEF.【解答】证明:∵AB∥DE,∴∠B=∠DEF,∵AC∥DF,∴∠ACB=∠F,∵BE=CF,∴BE+EC=CF+EC,即BC=EF,在△ABC和△DEF中,{∠B=∠DEF BC=EF∠ACB=∠F,∴△ABC≌△DEF(ASA).5种判定方法是解决问题的关键.选用哪一种判定方法,取决于题目中的已知条件.例6、如图,G是线段AB上一点,AC和DG相交于点E.请先作出∠ABC的平分线BF,交AC于点F;然后证明:当AD∥BC,AD=BC,∠ABC=2∠ADG时,DE=BF.【思路点拨】通过已知条件证明∠DAC=∠C,∠CBF=∠ADG,则可证△DAE≌△BCF【答案与解析】证明:∵AD∥BC,∴∠DAC=∠C∵BF平分∠ABC∴∠ABC=2∠CBF∵∠ABC=2∠ADG∴∠CBF=∠ADG在△DAE 与△BCF 中⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BCAD CBF ADG ∴△DAE≌△BCF(ASA )∴DE=BF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下:(1)找到以待证角(线段)为内角(边)的两个三角形;(2)证明这两个三角形全等;(3)由全等三角形的性质得出所要证的角(线段)相等.【变式】已知:如图,在△MPN 中,H 是高MQ 和NR 的交点,且MQ =NQ .求证:HN =PM.【答案】证明:∵MQ 和NR 是△MPN 的高,∴∠MQN =∠MRN =90°,又∵∠1+∠3=∠2+∠4=90°,∠3=∠4∴∠1=∠2在△MPQ 和△NHQ 中,12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ (ASA )∴PM =HN题型四、全等三角形的判定——“角角边”例7.(2021秋•苏州期末)如图,在四边形ABCD 中,E 是对角线AC 上一点,AD ∥BC ,∠ADC =∠ACD ,∠CED +∠B =180°.求证:△ADE ≌△CAB .【分析】由等角对等边可得AC=AD,再由平行线的性质可得∠DAE=∠ACB,由∠CED+∠B=180°,∠CED+∠AED=180°,得∠AED=∠B,从而利用AAS可判定△ADE≌△CAB.【解答】证明:∵∠ADC=∠ACD,∴AD=AC,∵AD∥BC,∴∠DAE=∠ACB,∵∠CED+∠B=180°,∠CED+∠AED=180°,∴∠AED=∠B,在△ADE与△CAB中,{∠DAE=∠ACB ∠AED=∠BAD=AC,∴△ADE≌△CAB(AAS).【点评】本题主要考查全等三角形的判定,解答的关键是由已知条件得出相应的角或边的关系.例8、已知:如图,AB⊥AE,AD⊥,∠E=∠B,DE=CB.求证:AD=AC.【思路点拨】要证AC=AD,就是证含有这两个线段的三角形△BAC≌△EAD.【答案与解析】证明:∵AB⊥AE,AD⊥AC,∴∠CAD=∠BAE=90°∴∠CAD+∠DAB=∠BAE+∠DAB ,即∠BAC=∠EAD在△BAC和△EAD中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC ≌△EAD (AAS )∴AC =AD【总结升华】我们要善于把证明一对角或线段相等的问题,转化为证明它们所在的两个三角形全等. 题型五:线段的垂直平分线 例9.(2023秋·浙江杭州·八年级校考开学考试)如图所示,在ABC 中,8AC =,5BC =,AB 的垂直平分线DE 交AB 于点D ,交AC 于点E ,则BCE 的周长为( )A .13B .18C .10.5D .21【答案】A 【分析】根据线段垂直平分线的性质得到AE BE =,再将BCE 的周长转化为AC BC +的长,即可求解.【详解】解:DE 是AB 的垂直平分线,∴AE BE =,∴BCE 的周长为BE EC BC AE EC BC AC BC ++=++=+,8AC =,5BC =,∴BCE 的周长为8513AC BC +=+=,故选:A .【点睛】本题主要考查的是线段垂直平分线的性质,掌握线段垂直平分线的性质是解题的关键.【变式1】(2022秋·浙江温州·八年级校考期中)如图,点D 是ABC 边AC 的中点,过点D 作AC 的垂线交BC 于点E ,已知6AC =,ABC 的周长为14,则ABE 的周长是( )A .6B .14C .8D .20【答案】C 【分析】由题意可知:ED 垂直平分AC ,故EA EC =,结合6AC =,ABC 的周长为14,即可得出答案.【详解】解:∵点D 是ABC 边AC 的中点, ED AC ⊥,∴ED 垂直平分AC ,∴EA EC =,∵6AC =,ABC 的周长为14,∴1468AB BC +=−=,∴8AB BC AB BE EC AB BE AE +=++=++=,∴ABE 的周长是8.故选:C .【点睛】此题考查了垂直平分线的性质和判定,掌握垂直平分线的性质和判定是解题的关键.【答案】C 【分析】根据垂直平分线的性质可知,到A ,B ,C 表示三个居民小区距离相等的点,是AC ,BC 两边垂直平分线的交点,由此即可求解.【详解】解:如图所示,分别作AC ,BC 两边垂直平分线MN ,PQ 交于点O ,连接OA,OB,OC,∵MN,PQ是AC,BC两边垂直平分线,==,∴OA OB OC∴点O是到三个小区的距离相等的点,即点O是AC,BC两边垂直平分线的交点,故选:C.【点睛】本题主要考查垂直平分线的性质,掌握垂直平分线的性质是解题的关键.八年级专题练习)如图,在ABC中,是ABC外的一点,且【分析】根据到线段两端距离相等的点在线段的垂直平分线上,即可证明A、D都在BC的垂直平分线上,由此即可证明结论.AB AC,【详解】证明:∵=∴点A在BC的垂直平分线上,BD CD,∵=∴点D在BC的垂直平分线上,∴A、D都在BC的垂直平分线上,∴AD垂直平分BC.【点睛】本题主要考查了线段垂直平分线的判定,熟知线段垂直平分线的判定条件是解题的关键.【变式】.(2022秋·浙江·八年级专题练习)如图,点E是△ABC的边AB的延长线上一点,∠BCE=∠A+∠ACB,求证:点E在BC的垂直平分线上.【分析】由三角形的外角性质得到∠EBC=∠A+∠ACB,结合已知推出∠BCE=∠EBC,得到BE=CE,即可得到结论.【详解】证明:∵∠BCE=∠A+∠ACB,∠EBC=∠A+∠ACB,∴∠BCE=∠EBC,∴BE=CE,∴点E在BC的垂直平分线上.【点睛】本题考查了三角形的外角性质,线段垂直平分线的判定,用到的知识点:到线段两端点的距离相等的点在线段的垂直平分线上.题型六:角平分线【答案】A【分析】根据角平分线上的点到两边的距离相等即可解答.【详解】根据题意要使集贸市场到三条公路的距离相等即集贸市场应建在三个角的角平分线的交点.故本题选A .【点睛】本题考查了角平分线的性质,熟记角平分线的性质是解答本题的关键. 的中点,ABC ,则BED 的面积为( 【答案】C【分析】作DF AC ⊥于F ,DM AB ⊥于点M ,根据角平分线的性质求出DM ,根据三角形的面积公式计算即可.【详解】解:作DF AC ⊥于F ,DM AB ⊥于点MAD 是ABC 的角平分线DF AC ⊥于F ,DM AB ⊥,112122AC DF AB DM ∴⋅+⋅=,112122AC DM AB DM ⋅+⋅=∴即:3421DM DM +=得3DM =8AB =, E 是AB 的中点,142BE AB ∴== 1143622BEDS BE DM ∴=⋅=⨯⨯= 故选:C .【点睛】本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键. 例12.(2022秋·浙江·八年级专题练习)已知:如图,90B C ∠=∠=,M 是BC 的中点,DM 平分ADC ∠.(1)若连接AM ,则AM 是否平分BAD ∠?请你证明你的结论;(2)线段DM 与AM 有怎样的位置关系?请说明理由.【答案】(1)AM 平分BAD ∠,证明见解析(2)DM AM ⊥,理由见解析【分析】(1)过点M 作ME AD ⊥,垂足为E ,证明ME MC MB ==即可得证.(2)利用两直线平行,同旁内角互补,证明1390∠+∠=.【详解】(1)AM 平分BAD ∠,理由为:证明:过点M 作ME AD ⊥,垂足为E ,∵DM 平分ADC ∠,∴12∠=∠,∵ME AD ⊥,MC CD ⊥∴MC ME =(角平分线上的点到角两边的距离相等),又∵MC MB =,∴ME MB =,∵MB AB ⊥,ME AD ⊥,∴AM 平分BAD ∠(到角的两边距离相等的点在这个角的平分线上).(2)DM AM ⊥,理由如下:∵90B C ∠=∠=,∴,DC CB AB CB ⊥⊥,∴DC AB ∥(垂直于同一条直线的两条直线平行),∴180DAB CDA ∠+∠=(两直线平行,同旁内角互补)又∵111,322CDA DAB ∠=∠∠=∠(角平分线定义) ∴2123180∠+∠=,∴1390∠+∠=,∴90AMD ∠=.即DM AM ⊥.【点睛】本题考查了角平分线的性质定理和判定定理,平行线的性质,熟练掌握以上的知识是解题的关键. 【变式1】(2023秋·浙江台州·八年级统考期末)如图 90B C ∠=∠=︒,E 为BC 上一点,AE 平分BAD ∠,DE 平分CDA ∠.(1)求AED ∠的度数;(2)求证:E 是BC 的中点.【答案】(1)90︒(2)见解析.【分析】(1)利用已知条件可以得到180BAD CDA ∠+∠=︒,想要求AED ∠的度数,只需要根据三角形内角和定理和角平分线的性质即可得到结论.(2)过点E 做EF AD ⊥,根据角平分线上的点到角的两边距离相等即可得结论.【详解】(1)解:∵90B C ∠=∠=︒,∴DC AB ∥,∴180BAD CDA ∠+∠=︒,∵AE 平分BAD ∠,DE 平分CDA ∠, ∴12EAD BAD ∠=∠,12EDA CDA ∠=∠, ∴1()902EAD EDA BAD CDA ∠+∠=∠+∠=︒,∴180()90AED EAD EDA ∠=︒−∠+∠=︒;(2)证明:过点E 作EF AD ⊥于点F ,∵AE 平分BAD ∠,90B Ð=°,EF AD ⊥,∴EF EB =.∵DE 平分CDA ∠,90C ∠=︒,EF AD ⊥,∴EF EC =.∴EB EC =,即E 是BC 的中点.【点睛】本题考查了平行线的判定与性质,以及角平分线上的点到角两边距离相等的性质,熟记性质和定理并做出辅助线是解题的关键.【变式2】.(2022秋·浙江杭州·八年级校考期中)如图,在ABC 外作两个大小不同的等腰直角三角形,其中90DAB CAE ∠=∠=︒,AB AD =,AC AE =.连接DC 、BE 交于F 点.(1)求证:DAC BAE ≌△△; (2)直线DC 、BE 是否互相垂直,试说明理由;(3)求证:AF 平分DFE ∠.【答案】(1)见解析(2)DC BE ⊥,理由见解析(3)见解析【分析】(1)由题意可得AD AB =,AC AE =,由90DAB CAE ∠=∠=︒,可得到DAC BAE ∠=∠,从而可证DAC BAE ≌△△;(2)由(1)可得ACD AEB ∠=∠,再利用直角三角形的性质及等量代换即可得到结论;(3)作AM DC ⊥于M ,AN BE ⊥于N ,利用全等三角形的面积相等及角平分线的判定即可证得结论.【详解】(1)证明:∵90DAB CAE ∠=∠=︒,∴DAB BAC CAE BAC ∠+∠=∠+∠,即DAC BAE ∠=∠,又∵AD AB =,AC AE =,∴()SAS DAC BAE ≌△△;(2)解:DC BE ⊥,理由如下;∵DAC BAE ≌△△, ∴ACD AEB ∠=∠,∵90AEB AOE ∠+∠= ,AOE FOC ∠=∠,∴90FOC ACD ∠+∠=,∴90EFC ∠=,∴DC BE ⊥;(3)证明:作AM DC ⊥于M ,AN BE ⊥于N ,∵DAC BAE ≌△△, ∴DAC BAE S S ∆∆=,DC BE =, ∴1122DC AM BE AN ⋅=⋅,∴AM AN =,∴AF 平分DFE ∠.【点睛】本题主要考查全等三角形的判定和性质,及直角三角形的性质,角平分线的判定,熟练掌握判定和性质是解决本题的关键.【变式3】(2023春·浙江金华·八年级浙江省义乌市后宅中学校考阶段练习)已知:OP 平分MON ∠,点A ,B 分别在边OM ,ON 上,且180OAP OBP ∠∠+=︒.(1)如图1,当90OAP ∠=︒时,求证:OA OB =;(2)如图2,当90OAP ∠<︒时,作PC OM ⊥于点C .求证:①PA PB =;②请直接写出OA ,OB ,AC 之间的数量关系 .【答案】(1)见解析(2)①见解析;②2OA OB AC −=【分析】(1)证明()AAS OPA OPB ≌,即可得证;(2)①作PD ON ⊥于点D ,证明()AAS PAC PBD ≌,即可得证; ②证明()AAS OCP ODP ≌,得出OD =,根据AC BD =,即可得证.【详解】(1)证明:180OAP OBP ∠∠+=︒,且90OAP ∠=︒,90OAP OBP ∠∠∴==︒,OP 平分MON ∠,POA POB ∠∠∴=,OP OP =,()AAS OPA OPB ∴≌,OA OB ∴=;(2)证明:①如图2,作PD ON ⊥于点D ,PC OM ⊥于点C ,PC PD ∴=,90PCA PDB OCP ∠∠∠===︒,180OAP OBP ∠∠+=︒,180DBP OBP ∠∠+=︒,OAP DBP ∠∠∴=,在PAC 和PBD 中,CAP DBP PCA PDBPC PD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()AAS PAC PBD ∴≌, PA PB ∴=;②结论:2OA OB AC −=.理由:在OCP 和ODP 中,OCP ODP COP DOP OP OP ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS OCP ODP ∴≌,OC OD ∴=,OA AC OB BD ∴−=+,AC BD =,2OA OB AC BD AC ∴−=+=.故答案为:2OA OB AC −=.【点睛】本题考查了角平分线的性质,全等三角形的性质与判定,掌握全等三角形的性质与判定是解题的关键.【过关检测】一、单选题 1.(2022秋·浙江·八年级专题练习)如图,在ABC 中,90A ∠=︒,点D 是边AC 上一点,3DA =,若点D 到BC 的距离为3,则下列关于点D 的位置描述正确的是( )A .点D 是AC 的中点B .点D 是B ∠平分线与AC 的交点 C .点D 是BC 垂直平分线与AC 的交点D .点D 与点B 的距离为5【答案】B 【分析】作DE BC ⊥于E ,连接BD ,利用角平分线的判定定理可证明BD 是ABC ∠的角平分线,即可作答.【详解】解:如图所示:作DE BC ⊥于E ,连接BD ,∵3DA =,点D 到BC 的距离为3,∴=AD DE ,∵90A ∠=︒,∴DA BA ⊥,∵DE BC ⊥,∴BD 是ABC ∠的角平分线,即点D 是ABC ∠的角平分线与AC 的交点,故B 项正确;其余选项,利用现有条件均无法得出,故选:B .【点睛】本题主要考查了角平分线的判定定理,作出辅助线,证明BD 是ABC ∠的角平分线,是解答本题的关键. 2.(2023·浙江·九年级专题练习)如图,已知BF DE =,AB ∥DC ,要使ABF CDE ≅△△,添加的条件可以是( )A.BE DF =B .AF CE =C .AB CD = D .B D ∠=∠【答案】C 【分析】根据AB ∥DC ,可得B D ∠=∠,又BF DE =,所以添加AB CD =,根据SAS 可证ABF CDE ≅△△.【详解】解:应添加AB DC =,理由如下:AB ∥DC ,B D ∴∠=∠.在ABF △和CDE 中,AB CD B DBF DE =⎧⎪∠=∠⎨⎪=⎩,(SAS)ABF CDE ∴≅,故选:C .【点睛】本题主要考查了平行线的性质以及全等三角形的判定,熟练掌握全等三角形的判定是解题的关键.3.(2023·浙江金华·统考二模)如图,ABC 和DEF 中,AB DE ∥,A D ∠=∠,点B ,E ,C ,F 共线,添加一个条件,不能判断ABC DEF ≌△△的是( )A .AB DE =B .ACB F ∠=∠C .BE CF =D .AC DF =【答案】B 【分析】根据AB DE ∥可得B DEF ∠=∠,加上A D ∠=∠,可知ABC 和DEF 中两组对角相等,因此一组对边相等时,即可判断ABC DEF ≌△△. 【详解】解:AB DE ∥,∴B DEF ∠=∠, 又A D ∠=∠,∴ABC 和DEF 中两组对角相等,当AB DE =时,根据ASA 可证ABC DEF ≌△△,故A 选项不合题意; 当ACB F ∠=∠时,ABC 和DEF 中,三组对角相等,不能判断ABC DEF ≌△△,故B 选项符合题意; 当BE CF =时,BC EF =,根据AAS 可证ABC DEF ≌△△,故C 选项不合题意; 当AC DF =时,根据AAS 可证ABC DEF ≌△△,故D 选项不合题意; 故选B .【点睛】本题考查添加条件使三角形全等,解题的关键是熟练掌握全等三角形的各种判定方法..ABC 的三条中线的交点.ABC 三边的垂直平分线的交点.ABC 三条角平分线的交点.ABC 三条高所在直线的交点【答案】C【分析】角平分线上的点到角的两边的距离相等,由此可解.【详解】解:要使凉亭到草坪三条边的距离相等,∴凉亭应在ABC 三条角平分线的交点处.故选C .【点睛】本题考查了角平分线的性质,解题的关键是注意区分三角形中线的交点、高的交点、垂直平分线的交点以及角平分线的交点之间的区别. 5.(2020秋·浙江·八年级期末)如图,AD 是ABC 中BAC ∠的平分线,DE AB ⊥交AB 于点E ,DF AC ⊥交AC 于点F ,若7ABC S =△,2DE =,4AB =,则AC 的长为( )A .3B .4C .5D .6【答案】A 【分析】先根据角平分线的性质得到2DF DE ==,再利用三角形面积公式得到11242722AC ⨯⨯+⨯⨯=,然后解关于AC 的方程即可.【详解】解:∵AD 是BAC ∠的平分线,DE AB ⊥,DF AC ⊥,2DE =,∴2DF DE ==,∵7ABC S =△,4AB =,又∵ABD ACD ABC S S S +=△△△,∴111124272222AB DE DF AC AC ⋅+⋅=⨯⨯+⨯⨯=,∴3AC =.故选:A .【点睛】本题考查角平分线的性质:角的平分线上的点到角的两边的距离相等.理解和掌握角平分线的性质是解题的关键.本题也考查了三角形的面积及等积变换.6.(2022秋·浙江·八年级专题练习)如图,用B C ∠=∠,12∠=∠,直接判定ABD ACD ≌△△的理由是( )A .AASB .SSSC .ASAD .SAS【答案】A 【分析】根据三角形全等的判定方法判定即可.【详解】解:在ABD △和ACD 中,12B CAD AD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()AAS ABD ACD ≌,故A 正确. 故选:A .【点睛】本题主要考查三角形全等的判定,解题的关键是掌握证明全等三角形的几种证明方法:AAS 、ASA 、SSS 、SAS 、HL .A .2B .【答案】C 【分析】由FC AB ∥,得F ADE ∠=∠,FCE A ∠=∠,即可根据全等三角形的判定定理“AAS”证明CFE ADE ≅,则4CF AD AB BD ==−=.【详解】解:FC AB ∥,F ADE ∴∠=∠,FCE A ∠=∠,在CFE 和ADE V 中,F ADE FCE AFE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,()AAS CFE ADE ∴≅, CF AD ∴=,5AB =,1BD =,514AD AB BD ∴=−=−=,4CF ∴=,CF ∴的长度为4.故选:C .【点睛】此题重点考查平行线的性质、全等三角形的判定与性质等知识,正确地找到全等三角形的对应边和对应角并且证明CFE ADE ≅是解题的关键.A .SSS【答案】B 【分析】根据已知条件两边,及两边的夹角是对顶角解答.【详解】解:在AOB 和COD △中,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩,()AOB COD SAS ∴≌. 故选:B .【点睛】本题考查了全等三角形的应用,准确识图判断出两组对应边的夹角是对顶角是解题的关键. 9.(2022秋·浙江嘉兴·九年级校考期中)在联欢会上,有A 、B 、C 三名选手站在一个三角形的三个顶点位置上,他们在玩“抢凳子”游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放在ABC 的( )A .三边垂直平分线的交点B .三杂中线的交点C .三条角平分线的交点D .三条高所在直线的交点【答案】A【分析】根据题意可知,当木凳所在位置到A 、B 、C 三个顶点的距离相等时,游戏公平,再由线段垂直平分线的性质即可求解.【详解】解:由题意可得:当木凳所在位置到A 、B 、C 三个顶点的距离相等时,游戏公平,∵线段垂直平分线上的点到线段两端的距离相等,∴木凳应放的最适当的位置是在ABC 的三边垂直平分线的交点,故选:A .【点睛】本题考查线段垂直平分线的性质的应用,掌握线段垂直平分线的性质是解题的关键. )可说明ABC 与△ 【答案】A 【分析】先根据垂直的定义可得90ACB ADB ∠=∠=︒,再根据角平分线的定义可得CAB DAB ∠=∠,然后根据AAS 定理即可得.【详解】解:,BC AC BD AD ⊥⊥,90ACB ADB ∴∠=∠=︒,AB 平分CAD ∠,CAB DAB ∴∠=∠,在ABC 和ABD △中,90ACB ADB CAB DABAB AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()AAS ABC ABD ∴≌,故选:A . 【点睛】本题主要考查了三角形全等的判定,熟练掌握三角形全等的判定方法是解题关键.二、填空题【答案】CA FD =,B E ∠=∠,A D ∠=∠,AB DE ∥等【分析】可选择CA FD =添加条件后,能用SAS 进行全等的判;也可选择B E ∠=∠添加条件后,能用ASA 进行全等的判定;也可选择A D ∠=∠添加条件后,能用AAS 进行全等的判定;也可选择AB DE ∥添加条件后,能用ASA 进行全等的判定即可;【详解】解:添加CA FD =,∵12∠=∠,BC EF =,∴()SAS ABC DEF ≌△△,故答案为:CA FD =;或者添加B E ∠=∠,∵BC EF =,12∠=∠,∴()ASA ABC DEF ≌△△,故答案为:B E ∠=∠;或者添加A D ∠=∠,∵12∠=∠,BC EF =,∴()AAS ABC DEF ≌△△,故答案为:A D ∠=∠;或者添加AB DE ∥,∵AB DE ∥,∴B E ∠=∠,∵12∠=∠,BC EF =,∴()AAS ABC DEF ≌△△,故答案为:AB DE ∥.【点睛】本题考查了全等三角形的判定,解答本题关键是掌握全等三角形的判定定理,本题答案不唯一.【答案】AB DC =【分析】添加条件AB DC =,利用SAS 证明ABC DCB △≌△即可.【详解】解:添加条件AB DC =,理由如下:在ABC 和DCB △中,AB DC ABC DCBBC CB =⎧⎪∠=∠⎨⎪=⎩, ∴()SAS ABC DCB △≌△, 故答案为:AB DC =.【点睛】本题主要考查了全等三角形的判定,熟知全等三角形的判定定理是解题的关键,全等三角形的判定定理有SSS SAS AAS ASA HL ,,,,. 13.(2023秋·浙江湖州·八年级统考期末)如图,已知AC DB =,要使得ABC DCB ≅,根据“SSS”的判定方法,需要再添加的一个条件是_______.【答案】ABDC =【分析】要使ABC DCB ≅,由于BC 是公共边,若补充一组边相等,则可用SSS 判定其全等.【详解】解:添加AB DC =.在ABC 和DCB △中AB DC BC CB AC BD =⎧⎪=⎨⎪=⎩, ∴()ABC DCB SSS ≅△△, 故答案为:AB DC =.【点睛】本题考查三角形全等的判定方法;判定两个三角形全等的一般方法有:SSS 、SAS 、ASA 、AAS 、HL .添加时注意:AAA 、SSA 不能判定两个三角形全等,不能添加,根据已知结合图形及判定方法选择添加的条件是正确解答本题的关键.14.(2022秋·浙江丽水·八年级统考期末)如图,在ABC 中,CD 是边AB 上的高,BE 平分ABC ∠,交CD 于点E ,6BC =,若BCE 的面积为9,则DE 的长为______.【答案】3【分析】过E 作EF BC ⊥于F ,根据角平分线性质求出EF DE =,根据三角形面积公式求出即可.【详解】解:过E 作EF BC ⊥于F ,CD 是AB 边上的高,BE 平分ABC ∠,交CD 于点E ,DE EF ∴=,192BCE S BC EF =⋅=,1692EF ∴⨯⨯=,3EF DE ∴==,故答案为:3.【点睛】本题考查了角平分线性质的应用,能根据角平分线性质求出3EF DE ==是解此题的关键,注意:在角的内部,角平分线上的点到角的两边的距离相等. 八年级期末)如图,在ABC 中, 【答案】4【分析】根据线段垂直平分线的性质得到2AD BD ==,则4CD AC AD =−=.【详解】解:∵AB 的垂直平分线交AB 于点E ,交AC 于点D ,∴2AD BD ==,∵6AC =,∴4CD AC AD =−=,故答案为:4.【点睛】本题主要考查了线段垂直平分线的性质,熟知线段垂直平分线上的点到线段两端的距离相等是解题的关键. 16.(2022秋·浙江温州·八年级校联考期中)如图,在ABC 中,DE 是AC 的中垂线,分别交AC ,AB 于点D ,E .已知BCE 的周长为9,4BC =,则AB 的长为______.【答案】5【分析】先利用三角形周长得到5CE BE +=,再根据线段垂直平分线的性质得到EC EA =,然后利用等线段代换得到AB 的长.【详解】解:∵BCE 的周长为9,9CE BE BC ∴++=,又4BC =,5CE BE ∴+=,又DE 是AC 的中垂线,EC EA ∴=,5AB AE BE CE BE ∴=+=+=;故答案为:5.【点睛】本题考查了垂直平分线的性质:垂直平分线上任意一点,到线段两端点的距离相等.17.(2023秋·浙江杭州·八年级校考开学考试)如图,已知12∠=∠,要说明ABC BAD ≌,(1)若以“SAS ”为依据,则需添加一个条件是__________;(2)若以“ASA ”为依据,则需添加一个条件是__________.【答案】 BC AD = BAC ABD ∠=∠【分析】(1)根据SAS 可添加一组角相等,故可判定全等;(2)根据ASA 可添加一组角相等,故可判定全等;【详解】解:(1)已知一组角相等和一个公共边,以“SAS ”为依据,则需添加一组角,即BC AD =故答案为:BC AD =;(2)已知一组角相等,和一个公共边,以“ASA ”为依据,则需添加一组角,即BAC ABD ∠=∠. 故答案为:BAC ABD ∠=∠.【点睛】本题主要考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS SAS ASA AAS HL 、、、、.添加时注意:AAA SSA 、不能判定两个三角形全等. 18.(2019秋·浙江嘉兴·八年级校考阶段练习)如图,点B 、E 、C 、F 在一条直线上,AB ∥DE ,AB=DE ,BE=CF ,AC=6,则DF=________【答案】6.【分析】根据题中条件由SAS 可得△ABC ≌△DEF ,根据全等三角形的性质可得AC=DF=6.【详解】∵AB ∥DE ,∴∠B=∠DEF∵BE=CF ,∴BC=EF ,在△ABC 和△DEF 中,AB DE B DEFBC EF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ),∴AC=DF=6.考点:全等三角形的判定与性质.。
八年级数学上册《全等三角形》知识点解析

八年级数学上册《全等三角形》知识点解析八年级数学上册《全等三角形》知识点解析在现实学习生活中,相信大家一定都接触过知识点吧!知识点有时候特指教科书上或考试的知识。
为了帮助大家掌握重要知识点,下面是店铺收集整理的八年级数学上册《全等三角形》知识点解析,欢迎大家分享。
八年级数学上册《全等三角形》知识点解析1一、定义1.全等形:形状大小相同,能完全重合的两个图形.2.全等三角形:能够完全重合的两个三角形.二、重点1.平移,翻折,旋转前后的图形全等.2.全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.3.全等三角形的判定:SSS三边对应相等的两个三角形全等【边边边】SAS两边和它们的夹角对应相等的两个三角形全等【边角边】ASA两角和它们的夹边对应相等的两个三角形全等【角边角】AAS两个角和其中一个角的对边开业相等的两个三角形全等【边角边】HL斜边和一条直角边对应相等的两个三角形全等【斜边,直角边】4.角平分线的性质:角的平分线上的点到角的两边的距离相等.5.角平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上.八年级数学上册《全等三角形》知识点解析2全等三角形定义:能够完全重合的两个三角形叫做全等三角形。
理解:①全等三角形形状与大小完全相等,与位置无关;②一个三角形经过平移、翻折、旋转可以得到它的全等形;③三角形全等不因位置发生变化而改变。
通过上面对全等三角形知识点的讲解学习,相信同学们对全等三角形的知识已经能很好的掌握了吧,后面我们进行更多知识点的巩固学习。
初中数学知识点总结:平面直角坐标系下面是对平面直角坐标系的内容学习,希望同学们很好的掌握下面的内容。
平面直角坐标系平面直角坐标系:在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为x轴或横轴,竖直的数轴称为y轴或纵轴,两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素:①在同一平面②两条数轴③互相垂直④原点重合三个规定:①正方向的规定横轴取向右为正方向,纵轴取向上为正方向②单位长度的规定;一般情况,横轴、纵轴单位长度相同;实际有时也可不同,但同一数轴上必须相同。
全等三角形知识点详细解析

全等三角形知识点详细解析今天小编为大家精心整理了一篇有关数学的相关内容,以供大家阅读,更多信息请关注学习方法网!一、知识网络二、基础知识梳理(一)、基本概念1、“全等”的理解全等的图形必须满足:(1)形状相同的图形;(2)大小相等的图形;即能够完全重合的两个图形叫全等形。
同样我们把能够完全重合的两个三角形叫做全等三角形。
2、全等三角形的性质(1)全等三角形对应边相等;(2)全等三角形对应角相等;3、全等三角形的判定方法(1)三边对应相等的两个三角形全等。
(2)两角和它们的夹边对应相等的两个三角形全等。
(3)两角和其中一角的对边对应相等的两个三角形全等。
(4)两边和它们的夹角对应相等的两个三角形全等。
(5)斜边和一条直角边对应相等的两个直角三角形全等。
4、角平分线的性质及判定性质:角平分线上的点到这个角的两边的距离相等判定:到一个角的两边距离相等的点在这个角平分线上(二)灵活运用定理证明两个三角形全等,必须根据已知条件与结论,认真分析图形,准确无误的确定对应边及对应角;去分析已具有的条件和还缺少的条件,并会将其他一些条件转化为所需的条件,从而使问题得到解决。
运用定理证明三角形全等时要注意以下几点。
1、判定两个三角形全等的定理中,必须具备三个条件,且至少要有一组边对应相等,因此在寻找全等的条件时,总是先寻找边相等的可能性。
2、要善于发现和利用隐含的等量元素,如公共角、公共边、对顶角等。
3、要善于灵活选择适当的方法判定两个三角形全等。
(1)已知条件中有两角对应相等,可找:①夹边相等(ASA)②任一组等角的对边相等(AAS)(2)已知条件中有两边对应相等,可找①夹角相等(SAS)②第三组边也相等(SSS)(3)已知条件中有一边一角对应相等,可找①任一组角相等(AAS或ASA)②夹等角的另一组边相等(SAS)三、疑点、易错点1、对全等三角形书写的错误在书写全等三角形时一定要把表示对应顶点的字母写在对应的位置上。
《全等三角形》讲义(完整版)

全等三角形讲义一、知识点总结全等三角形定义:形状大小相同,并且能够完全重合的两个三角形叫做全等形三角形。
补充说明:重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角。
全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等 全等三角形判定定理:(1)边边边定理:三边对应相等的两个三角形全等。
(简称SSS ) (2)边角边定理:两边和它们的夹角对应相等的两个三角形全等。
(简称SAS) (3)角边角定理:两角和它们的夹边对应相等的两个三角形全等。
(简称ASA ) (4)角角边定理:两个角和其中一个角的对边对应相等的两个三角形全等。
(简称AAS ) (5)斜边、直角边定理:斜边和一条直角边对应相等的两个直角三角形全等。
(简称HL ) 角平分线的性质:在角平分线上的点到角的两边的距离相等.∵OP 平分∠AOB ,PM ⊥OA 于M ,PN ⊥OB 于N , ∴PM=PN角平分线的判定:到角的两边距离相等的点在角的平分线上.∵PM ⊥OA 于M ,PN ⊥OB 于N ,PM=PN ∴OP 平分∠AOB三角形的角平分线的性质:三角形三个内角的平分线交于一点,并且这一点到三边的距离等。
二、典型例题举例A BC PMNO A BC PMNO例1、如图,△ABN ≌△ACM,∠B 和∠C 是对应角,AB 与AC 是对应边,写出其他对应边和对应角.例2、如图,△ABC 是一个钢架,AB=AC ,AD 是连结点A 与BC 中点D 的支架.求证:△ABD ≌△ACD .例3、已知:点A 、F 、E 、C 在同一条直线上, AF =CE ,BE ∥DF ,BE =DF . 求证:△ABE ≌△CDF .例4、如图:D 在AB 上,E 在AC 上,AB =AC ,∠B =∠C .求证AD =AE .例5、如图:∠1=∠2,∠3=∠4 求证:AC=AD例6、如图,B 、E 、F 、C 在同一直线上,AF ⊥BC 于F ,DE ⊥BC 于E ,AB=DC ,BE=CF ,你认为AB 平行于CD 吗?说说你的理由D CB ACADB123 4例7、如图1,△ABC 的边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ,连结EG ,试判断△ABC 与△AEG 面积之间的关系,并说明理由.例8、如图,OC 是∠AOB 的平分线,P 是OC 上的一点,PD ⊥OA 交OA 于D ,PE ⊥OB 交OB 于E ,F 是OC 上的另一点,连接DF ,EF ,求证DF =EF例9、如图,△ABC 中,AD 是它的角平分线,P 是AD 上的一点,PE ∥AB 交BC 于E ,PF ∥AC 交BC 于F ,求证:D 到PE 的距离与D 到PF 的距离相等例10、如图,在△ABC 中,AD 为∠BAC 的平分线,DE ⊥AB 于E ,DF ⊥AC 于F ,△ABC 面积是282cm ,AB =20cm ,AC =8cm ,求DE 的长.AGF C BDE图1AEB DCFAB CDE D C EFBA 例10、已知:BE ⊥CD ,BE =DE ,BC =DA ,求证:① △BEC ≌△DAE ;②DF⊥BC .例11、如图,已知:E 是∠AOB 的平分线上一点,EC ⊥OB ,ED ⊥OA ,C ,D 是垂足,连接CD ,求证:(1)∠ECD=∠EDC ;(2)OD=OC ;(3)OE 是CD 的中垂线.三、专题版块专题一: 全等三角形的判定和性质的应用例1、如图,在△ABC 中,AB=AC , BAC=40°,分别以AB 、AC 为边作两个等腰三角形ABD 和ACE ,使∠BAD=∠CAE=90°.(1)求∠DBC 的度数.(2)求证:BD=CE.例2、如图,A B ∥CD,AF ∥DE,BE=CF,求证:AB=CD.例3、如图在△ABC 中,BE 、CF 分别是AC 、AB 边上的高,在BE 延长线上截取BM =AC ,在CF 延长线上截到CN =AB ,求证:AM =AN 。
全等三角形判定方式和解释

全等三角形判定方式和解释一、全等三角形的基础概念全等三角形是指两个三角形能够完全重合,它们的形状和大小都相等。
全等关系是三角形的一种重要性质,它在几何学中有广泛的应用。
二、全等三角形的判定方式1. 边边边(SSS)判定法如果两个三角形的三边长度分别相等,则这两个三角形全等。
数学表示为:如果△ABC ≌△DEF,当且仅当AB = DE, BC = EF, AC = DF。
解释:这个判定法是基于三角形的定义和性质。
在平面几何中,三角形的定义是一个由三条边和三个角构成的闭合二维多边形。
因此,如果两个三角形的三条边长度相等,那么它们的角度一定相等,从而它们的形状和大小都相等。
2. 边角边(SAS)判定法如果两个三角形的两边长度相等,并且这两边所夹的角相等,则这两个三角形全等。
数学表示为:如果△ABC ≌△DEF,当且仅当AB = DE, BC = EF, 且∠BAC = ∠DEF。
解释:这个判定法也基于三角形的性质。
在一个三角形中,任何一边的长度都受到与其所夹的两个角的影响。
因此,如果两个三角形的两条边长度相等,并且这两条边所夹的角相等,那么它们的形状和大小一定相等。
3. 角边角(ASA)判定法如果两个三角形的两个角相等,并且这两个角所夹的一边相等,则这两个三角形全等。
数学表示为:如果△ABC ≌△DEF,当且仅当∠A = ∠D, ∠B = ∠E, 且AB = DF。
解释:这个判定法同样基于三角形的性质。
在一个三角形中,任何一角的度数都受到与其所夹的两边长度的影响。
因此,如果两个三角形的两个角相等,并且这两个角所夹的一边长度相等,那么它们的形状和大小一定相等。
4. 角角边(AAS)判定法如果两个三角形的两个角相等,并且其中一个角所对的一边相等,则这两个三角形全等。
数学表示为:如果△ABC ≌△DEF,当且仅当∠A = ∠D, ∠B = ∠E, 且AC = DF。
解释:这个判定法也是基于三角形的性质。
在一个三角形中,任何一角的度数都受到与其所夹的两边长度的影响。
初二数学全等三角形知识点解析

一.定义1.全等形:形状大小相同,能完全重合的两个图形.2.全等三角形:能够完全重合的两个三角形.二.重点1.平移,翻折,旋转前后的图形全等.2.全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.3.全等三角形的判定:SSS三边对应相等的两个三角形全等[边边边]SAS两边和它们的夹角对应相等的两个三角形全等[边角边]ASA两角和它们的夹边对应相等的两个三角形全等[角边角]AAS两个角和其中一个角的对边开业相等的两个三角形全等[边角边]HL斜边和一条直角边对应相等的两个三角形全等[斜边,直角边]4.角平分线的性质:角的平分线上的点到角的两边的距离相等.5.角平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上.全等三角形的方法举例SSS(边边边)即三边对应相等的两个三角形全等.举例:如下图,AC=BD,AD=BC,求证∠A=∠B.证明:在△ACD与△BDC中{AC=BD,AD=BC,CD=CD.∴△ACD≌△BDC.(SSS)∴∠A=∠B.(全等三角形的对应角相等)SAS(边角边)即三角形的其中两条边对应相等,且两条边的夹角也对应相等的两个三角形全等.[2]举例:如下图,AB平分∠CAD,AC=AD,求证∠C=∠D.证明:∵AB平分∠CAD.∴∠CAB=∠BAD.在△ACB与△ADB中{AC=AD,∠CAB=∠BAD,AB=AB.∴△ACB≌△ADB.(SAS)∴∠C=∠D.(全等三角形的对应角相等)ASA(角边角)即三角形的其中两个角对应相等,且两个角夹边也对应相等的两个三角形全等.[3]举例:如下图,AB=AC,∠B=∠C,求证△ABE≌△ACD.证明:在△ABE与△ACD中{∠A=∠A,AB=AC,∠B=∠C.∴△ABE≌△ACD.(ASA)AAS(角角边)即三角形的其中两个角对应相等,且对应相等的角所对应的边也对应相等的两个三角形全等.[3]举例:如下图,AB=DE,∠A=∠E,求证∠B=∠D.证明:在△ABC与△EDC中{∠A=∠E,∠ACB=∠DCE,AB=DE.∴△ABC≌△EDC.(AAS)∴∠B=∠D.(全等三角形的对应角相等)HL(斜边、直角边)即在直角三角形中一条斜边和一条直角边对应相等的两个直角三角形全等.[3]举例:如下图,Rt△ADC与Rt△BCD,AC=BD,求证AD=BC.证明:在Rt△ADC与Rt△BCD中{AC=BD,CD=CD.∴Rt△ADC≡Rt△BCD.(HL)∴AD=BC.(全等三角形的对应边相等)全等三角形解法的用途因为多边形可由多个三角形组成,所以利用此方法,亦可验证其它全等的多边形。
初一数学:全等三角形的性质和判定(含解析)

B′ 、 C′ 对应.
注意:寻找全等三角形的对应角、对应边的一般规律是:
⑴把其中一个图形通过平移、翻折或旋转,能与另一个图形完全 重合,则重合的边就是对应边,重合的角就是对应角,表示两
C
C'
个三角形全等时,要把对应字母写在对应位置上.
⑵有公共边时,则公共边为对应边;有公共角时,则公共角为对 A
B A'
∴ AC − BC = DB − BC (等量减等量差相等),即 AB = CD , CE ∥ BF (内错角相等,两直线平行). ∵ AD = AC + BD − BC , ∴ 2AC = AD + BC = 8+ 2= 10 , ∴ AC = 5 .
板块二 全等三角形的常用判定方法
知识导航
三角形全等的判定: 1.如果两个三角形的三条边分别对应相等,那么这两个三角形全等,简记为 SSS. 2.如果两个三角形的两边及这两边的夹角对应相等,那么这两个三角形全等,简记为 SAS. 3.如果两个三角形的两个角及这两个角的夹边对应相等,那么这两个三角形全等,简记为 ASA. 4.如果两个三角形的两个角及其中的一个角所对的边对应相等,那么这两个三角形全等,简记为 AAS. 5.如果两个直角三角形的斜边及一条直角边分别对应相等,那么这两个直角三角形全等,简记为 HL.
注:三角形全等的判定条件中必须是三个元素,并且一定有一组对应边相等.
为了理解记忆三角形全等的判定条件,现归纳如下表:
已知条件 三边
是否全等 是
图形(或反例)
形式结论 SSS
两边及夹角
是
SAS
两边一角
两边及对非直角
否
无
两边及对直角
是
HL
全等三角形的性质及判定(经典讲义)

全等三角形的性质及判定知识要点1、全等三角形概念:两个能完全重合的三角形叫做全等三角形.2、全等三角形性质:(1)两全等三角形的对应边相等,对应角相等.(2)全等三角形的对应边上的高相等,对应边上的中线相等,对应角的平分线相等.(3)全等三角形的周长、面积相等.3、全等三角形判定方法:(1)全等判定一:三条边对应相等的两个三角形全等(SSS)(2)全等判定二:两角和它们的夹边对应相等的两个三角形全等(ASA)(3)全等判定三:两角及其中一个角的对边对应相等的两个三角形全等(AAS) (4)全等判定四:两边和它们的夹角对应相等的两个三角形全等(SAS)专题一、全等图形的性质——全等图形的对应边(对应中线、角平分线、高线)、对应角、对应周长、对应面积相等例题1:下列说法,正确的是()A.全等图形的面积相等B.面积相等的两个图形是全等形C.形状相同的两个图形是全等形D.周长相等的两个图形是全等形例题2:如图1,折叠长方形ABCD ,使顶点D 与BC 边上的N 点重合,如果AD=7 cm ,DM=5 c m,∠DAM=39°,则AN =____cm,NM =____cm,NAB =.A DCEMDB 图3AB 图1 CN 图2 图 4【仿练1】如图2,已知ABC ADE ,AB AD ,BC DE ,那么与BAE 相等的角是.【仿练2】如图3,ABC ADE ,则AB= ,∠E= _ .若∠BAE=120°,∠BAD=40°,则∠BAC= .、三角形全等的判定一(SSS)相关几何语言考点C AE CFM BA∵AE=CF∵CM 是△的中线∴_____________( ) ∴____________________∴__________()或A B ∵AC=EF∴____________________∴__________()AB=AB ()A DB CE F在△ABC和△DEF中_________∵__________________∴△ABC≌△DEF()A例1.如图,AB=AD,CB=CD.△ABC与△ADC全等吗?为什么?CBDCDB E2例3.如图,点B,E,C,F 在一条直线上,AB=DE,AC=DF,BE=CF.求证∠A=∠D.习练1..如图,AB=CD,AD=CB,那么下列结论中错误的是()A.∠A=∠C B.AB=AD C.AD∥BC D.AB∥CD2、如图所示,在△ABC中,AB=AC,BE=CE,则由“S SS”可以判定()A.△ABD≌△ACD B.△BDE≌△CDEC.△ABE≌△ACE D.以上都不对3.如图,AB=AC,BD=CD,则△ABD≌△ACD的依据是()A.SSS B.SAS C.AASD.HL4.如图,AB=AC,D为B C 的中点,则△ABD ≌_________.5.如图,已知A B=DE,BC=EF,若要使△ABC≌△DEF,那么还要需要一个条件,这个条件可以是:.2.如图,AB=AC,BD=DC,∠BAC=36°,则∠BAD 的度数是°.7、.如图,AB=AE,AC=AD,BD=CE,求证:△ABC≌ADE。
(完整版)八上《全等三角形》全等三角形的判定知识点整理

12.2全等三角形的判定一、知识要点1、两个三角形全等的条件【重点】(1)判定1——边边边公理三边对应相等的两个三角形全等,简写成“边边边”或“SSS”。
“边边边”公理的实质:三角形的稳定性(用三根木条钉三角形木架)。
注意:边边边是三条边都相等,并且在书写时边与边要对应书写。
在已知两边相等的情况下优先考虑。
(2)判定2——边角边公理两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”。
注意:边角边中,角是指两对应边的夹角,如上图中,同样在书写时对应边角对准。
比如上图中正确的写法是:△ABC≌△A'B'C'(3)判定3——角边角公理两角和它们的夹边对应相等的两个三角形全等。
简写为“角边角”或“ASA”。
注意:角边角中,边是两个角中间时,才能描述为角边角,否则就是下面的角角边。
(4)判定4——角角边推论两角和其中一角的对边对应相等的两个三角形全等。
简称“角角边”或“AAS”。
如图,是一个屋顶钢架,AB=AC ,D 是BC 中点。
求证: 分析:要证明,就必须证出∠1=∠2,才能知道∠1=∠2=90︒,可得。
怎么才能证出∠1=∠2呢,从题目条件可看出,只要证出和全等即可,分析一下这两个三角形全等条件够吗?显然可利用“边边边”公理可证。
证明:在和中()()()⎪⎩⎪⎨⎧===已知公共边已知DC BD AD AD AC AB ∴≌ACD ∆(SSS )∴∠1=∠2(全等三角形对应角相等) ∴(平角定义) ∴(垂直定义)(5)直角三角形全等的判定——斜边直角边公理斜边和一条直角边对应相等的两个直角三角形全等。
简写成“斜边直角边”或“HL”。
判定直角三角形全等的方法: ①一般三角形全等的判定方法都适用; ②斜边-直角边公理2、证明三角形全等一般有以下步骤: (1)读题:明确题中的已知和求证;(2)要观察待证的线段或角,在哪两个可能全等的三角形中(3)、分析要证两个三角形全等,已有什么条件,还缺什么条件。
第03讲 全等三角形(解析版)

第03讲全等三角形一、全等图形形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫做全等图形.要点:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.两个全等形的周长相等,面积相等.二、全等三角形能够完全重合的两个三角形叫全等三角形.三、对应顶点,对应边,对应角1.对应顶点,对应边,对应角定义两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.要点:在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.2.找对应边、对应角的方法(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;(3)有公共边的,公共边是对应边;(4)有公共角的,公共角是对应角;(5)有对顶角的,对顶角一定是对应角;(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.四、全等三角形的性质全等三角形的对应边相等;全等三角形的对应角相等;要点:全等三角形对应边上的高相等,对应边上的中线相等,周长相等,面积相等.全等三角形的性质是今后研究其它全等图形的重要工具.例1.下列所给的图形中,是全等图形的是()A.对应边相等的五边形B.对应角相等的三角形C.同一底片印出的同样尺寸的照片D.两本书【解析】根据全等形的概念:能够完全重合的两个图形叫做全等形求解即可.【解析】A 、对应边相等的五边形对应角不一定相等,即图形不一定能完全重合,故本选项错误;B 、对应角相等的三角形对应边不一定相等,即图形不一定能完全重合,故本选项错误;C 、同一底片印出的同样尺寸的照片,形状相同,大小相等,即图形能完全重合,是全等形,故本选项正确;D 、两本书的形状不一定相同,大小也不一定相等,即图形不一定能完全重合,故本选项错误.故选:C .【点睛】本题考查了全等形的概念,所谓能够完全重合,是指两个图形的形状相同,大小相等.理解定义是解题的关键.例2.如图,图中的两个三角形全等,则α∠等于()A .50︒B .71︒C .58︒D .59︒【答案】D 【分析】由全等三角形的对应角相等,结合三角形内角和定理即可得到答案.【解析】解:由全等三角形的性质可知,两幅图中边长为a 、b 的夹角对应相等,∴180507159α∠=︒-︒-︒=︒,故选D .【点睛】本题考查了全等三角形的性质以及三角形内角和定理,解题的关键是掌握全等三角形的对应角相等.例3.下列说法中正确的是()A .两个面积相等的图形,一定是全等图形B .两个等边三角形是全等图形C .两个全等图形的面积一定相等D .若两个图形周长相等,则它们一定是全等图形【解析】根据全等图形的判定和性质,对每个选项进行判断,即可得到答案.【解析】解:A、两个面积相等的图形不一定是全等图形,故A错误;B、两个等边三角形不一定是全等图形,故B错误;C、两个全等图形的面积一定相等,正确;D、若两个图形的周长相等,则它们不一定是全等形,故D错误;故选:C.【点睛】本题考查了全等图形的判定和性质,解题的关键是熟记全等图形的判定和性质进行判断.例4.全等三角形是()A.面积相等的三角形B.角相等的三角形C.周长相等的三角形D.完全重合的三角形【答案】D【解析】根据全等三角形的定义即可求解.【解析】解:全等三角形是指能够完全重合的三角形.故选:D【点睛】本题考查了全等三角形的定义,熟知全等三角形的定义是解题的关键.例5.如图,两个三角形全等,则α∠等于()A.72︒B.60︒C.58︒D.50︒【答案】C【解析】根据全等三角形的性质解答即可.【解析】解:∵两个三角形全等,且α∠是b 、c 两边的夹角,∴α∠=58°故选:C .【点睛】本题考查了全等三角形的性质,正确识图、掌握全等三角形的性质是关键.例6.如图,若DEF ABC ≅ ,点B 、E 、C 、F 在同一条直线上,9BF =,5EC =,则CF 的长为()A .1B .2C .2.5D .3【答案】B【解析】根据全等三角形的对应边相等得到BE=CF ,计算即可.【解析】解:∵△DEF ≌△ABC ,∴BC=EF ,∴BE+EC=CF+EC ,∴BE=CF ,又∵BF=BE+EC+CF=9,EC=5∵CF=12(BF-EC)=12(9-5)=2.故选:B .【点睛】本题考查了全等三角形的性质,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.例7.在△ABC 中,∠C=∠B ,与△ABC 全等的三角形有一个角是100°,那么△ABC 中与这个角对应的角是()A .∠B B .∠A C .∠C D .∠B 或∠C【答案】B【解析】根据三角形的内角和等于180°可知,∠C 与∠B 不可能为100°,根据全等三角形的性质可得∠A 为所求角.【解析】解:假设=100C B ∠=∠ , =200C B ∠+∠ ,与=180C B A ∠+∠+∠ 矛盾,∴假设不成立,则100A ∠=o ,故答案为B.【点睛】本题考查了全等三角形的基本性质和三角形内角和定理,满足内角和定理的前提下找到对应角是解题关键.例8.如图,ABC 与BAD 全等,可表示为________,C ∠与D ∠是对应角,AC 与BD 是对应边,其余的对应角是________,其余的对应边是________.【答案】ABC BAD≌CAB ∠与DBA ∠,ABC ∠与BAD ∠AB 与BA ,BC 与AD【解析】由ABC BAD ≌,结合图形可得其余的对应角与对应边.【解析】解:ABC BAD ≌,C ∠与D ∠是对应角,AC 与BD 是对应边,∴其余的对应角是CAB ∠与DBA ∠,ABC ∠与BAD ∠;其余的对应边是AB 与BA ,BC 与AD .故答案为:ABC BAD ≌,CAB ∠与DBA ∠,ABC ∠与BAD ∠,AB 与BA ,BC 与AD【点睛】本题考查的是三角形全等的表示,全等三角形的对应边与对应角的理解,掌握以上知识是解题的关键.例9.如图所示,已知△ABC ≌△ADE ,∠C =∠E ,AB =AD ,则另外两组对应边为________,另外两组对应角为________.【答案】BC=DE 、AC=AE ,∠B=∠ADE 、∠BAC=∠DAE【解析】由已知△ABC ≌△ADE ,∠C=∠E ,AB=AD 得C 点与点E ,点B 与点D 为对应点,然后根据全等三角形的性质可得答案.解答:解:∵△ABC ≌△ADE ,∠C=∠E ,AB=AD ,∴AC=AE ,BC=DE ;∴∠BAC=∠DAE ,∠B=∠ADE.例10.如图,AD=AB ,∠C=∠E,∠CDE=55︒,则∠ABE=______.【答案】125°【解析】试题解析:∵在△ADC 和△ABE 中,{C EA A AD AB∠∠∠∠===,∴△ADC ≌△ABE (AAS ),∴∠ADC=∠ABE ,∵∠CDE=55°,∴∠ADC=125°,∴∠ABE=125°.一、单选题1.下列各组图形中,属于全等图形的是()A.B.C .D .【答案】C【分析】根据全等图形的定义(能够完全重合的两个图形叫做全等形)逐项判断即可得.【解析】解:A 、两个图形的大小不相同,不能够完全重合,不是全等图形,则此项不符合题意;B 、两个图形的大小不相同,不能够完全重合,不是全等图形,则此项不符合题意;C 、两个图形能够完全重合,是全等图形,则此项符合题意;D 、两个图形的形状不相同,不能够完全重合,不是全等图形,则此项不符合题意;故选:C .【点睛】本题考查了全等图形,熟记定义是解题关键.2.下列不是全等三角形的性质的是()A .全等三角形的面积相等B .全等三角形的周长相等C .全等三角形的对应边相等D .全等三角形的角相等【答案】D【分析】根据全等三角形的性质逐一判断即可.【解析】A 、全等三角形的面积相等,是全等三角形的性质,不符合题意;B 、全等三角形的周长相等,是全等三角形的性质,不符合题意;C 、全等三角形的对应边相等,是全等三角形的性质,不符合题意;D 、全等三角形的对应角相等,故原说法不是全等三角形的性质,符合题意故选:D.【点睛】本题考查了全等三角形的性质,属于应知应会知识点,熟知全等三角形的性质是关键.3.如图,ABC EBD ≌△△,4cm AB =,7cm BD =,则CE 的长度为()A .4cmB .3.5cmC .3cmD .2cm【答案】C 【分析】根据全等三角形对应边相等,可得7cm BC BD ==,4cm AB BE ==,再根据CE BC CE =-,即可进行解答.【解析】解:∵ABC EBD ≌△△,∴7cm BC BD ==,4cm AB BE ==,∴()743cm CE BC BE =-=-=,故选:C .【点睛】本题主要考查了全等三角形的性质,解题的关键是掌握全等三角形对应边相等.4.如图,图中的两个三角形是全等三角形,其中一些角和边的大小如图所示,那么x 的值是()A .30︒B .36︒C .65︒D .79︒【答案】C 【分析】根据全等三角形对应角相等,可以求得x 的值.【解析】解: 图中的两个三角形是全等三角形,∴两个三角形中边长为4和7的边的夹角相等,∴65x F =∠=︒,故选:C .【点睛】本题考查全等三角形的性质,解答本题的关键是明确题意,利用全等三角形的性质解答.5.已知图中的两个三角形全等,AD 与CE 是对应边,则A 的对应角是()A .BCE∠B .E ∠C .ACD ∠D .B∠【答案】A 【分析】观察图形,AD 与CE 是对应边,根据对应边去找对应角.【解析】观察图形知,AD 与CE 是对应边∴∠B 与∠ACD 是对应角又∠D 与∠E 是对应角∴∠A 与∠BCE 是对应角.故选:A .【点睛】本题考查了全等三角形的性质,正确的识别图形是解题的关键.6.如图,,40,30ABD CDB ABD CBD ∠=︒∠=︒ ≌,则C ∠等于()A .20︒B .100︒C .110︒D .115︒【答案】C 【分析】利用全等三角形的性质得到∠CDB =∠ABD ,再结合三角形内角和计算即可.【解析】∵ABD CDB △≌△,∴40CDB ABD ∠=∠=︒,∴1801803040110C CBD CDB ∠=︒-∠-∠=︒-︒-︒=︒故选C .【点睛】本题考查全等三角形的性质,特别基础,熟记全等三角形对应角相等是解题的关键.7.如图,△ABC ≌△ADE ,如果AB =5cm ,BC =7cm ,AC =6cm ,那么DE 的长是()A .6cmB .5cmC .7cmD .无法确定【答案】C 【分析】根据全等三角形的性质计算即可;【解析】∵△ABC ≌△ADE ,∴BC DE =,∵BC =7cm ,∴7DE cm =;故答案选C .【点睛】本题主要考查了全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.8.已知△ABC ≌△DEF ,BC =EF =6cm ,△ABC 的面积为18cm 2,则EF 边上的高是()A .6cmB .7cmC .8cmD .9cm 【答案】A【分析】利用全等三角形的性质找出同一个三角形的底边长及面积,代入面积公式即可求解三角形的高.【解析】解:设△DEF 的面积为s ,边EF 上的高为h ,A.αβ=置上.故答案为:对应顶点;对应边;对应角;对应顶点.【点睛】此题主要考查了全等形及相关概念,属于基本概念题,是需要识记的内容.12.如图,ABC 与BAD 全等,可表示为________,C ∠与D ∠是对应角,AC 与BD 是对应边,其余的对应角是________,其余的对应边是________.【答案】ABC BAD ≌CAB ∠与DBA ∠,ABC ∠与BAD ∠AB 与BA ,BC与AD 【分析】由ABC BAD ≌,结合图形可得其余的对应角与对应边.【解析】解:ABC BAD ≌,C ∠与D ∠是对应角,AC 与BD 是对应边,∴其余的对应角是CAB ∠与DBA ∠,ABC ∠与BAD ∠;其余的对应边是AB 与BA ,BC 与AD .故答案为:ABC BAD ≌,CAB ∠与DBA ∠,ABC ∠与BAD ∠,AB 与BA ,BC 与AD【点睛】本题考查的是三角形全等的表示,全等三角形的对应边与对应角的理解,掌握以上知识是解题的关键.13.如图,四边形ABCD ≌四边形A ′B ′C ′D ′,则∠A 的大小是______.【答案】95°【分析】根据两个多边形全等,则对应角相等,利用四边形内角和为360°即可求解.【解析】∵四边形ABCD ≌四边形A ′B ′C ′D ′∴∠D =∠D ′=130゜∵四边形ABCD 的内角和为360゜∴∠A =360゜-∠B -∠C -∠D =95゜故答案为:95゜【点睛】本题考查了多边形全等的性质、多边形的内角和定理,掌握多边形全等的性质是关键.14.如果,60,40ABC DEF B C ∠=︒∠=︒≌ ,那么F ∠=___________.【答案】40︒/40度【分析】根据全等三角形的对应角相等,即可求解.【解析】解:∵,60,40ABC DEF B C ∠=︒∠=︒≌ ,∴40F C ∠=∠=︒.故答案为:40︒【点睛】本题主要考查了全等三角形的性质,熟练掌握全等三角形的对应角相等是解题的关键.15.如图,△EFG ≌△NMH ,△EFG 的周长为15cm ,HN=6cm ,EF=4cm ,FH=1cm ,则HG=______.【答案】4cm【分析】首先根据全等三角形对应边相等可得MN=EF=4cm ,FG=MH ,△HMN 的周长=△EFG 的周长=15cm ,再根据等式的性质可得FG-HG=MH-HG ,即GM=FH ,进而可得答案.【解析】解:∵△EFG ≌△NMH ,∴MN=EF=4cm ,FG=MH ,△HMN 的周长=△EFG 的周长=15cm ,∴FG-HG=MH-HG ,即FH=GM=1cm ,∵△EFG 的周长为15cm ,∴HM=15-6-4=5cm ,∴HG=5-1=4cm .故答案为4cm .【点睛】本题考查全等三角形的性质,解题关键是掌握全等三角形对应边相等.16.如图,,125,25,ABC ADE EAB CAD BAC ∠=︒∠=︒∠ ≌的度数为___________.【答案】75︒【分析】根据全等三角形的性质求出∠EAD =∠CAB ,求出∠DAB =∠EAC =50°,即可得到∠BAC 的度数.【解析】解:∵ ABC ≌ ADE ,∴∠EAD =∠CAB ,∴∠EAD ﹣∠CAD =∠CAB ﹣∠CAD ,【答案】1s或7s 4【分析】分两种情况解决:①若AP BP=,建立方程求得答案即可.【解析】解:分两种情况:①若ACP BPQ△≌△,则572t=-,解得:1st=,②若ACP BQP△≌△,则AP272t t=-,解得7s4t=.故答案为1s或7s 4.【点睛】此题考查全等三角形的判定与性质,注意分类讨论思想的渗透.三、解答题19.找出下列图形中的全等图形.【答案】(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形【分析】根据能够完全重合的两个图形是全等形即可判断出答案.【解析】解:由题意得:(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形.【点睛】本题考查了全等形的定义,属于基础题,注意掌握全等形的定义.20.如图,OCA OBD ≌,点C 和点B ,点A 和点D 是对应顶点.说出这两个三角形中相等的边和角.【答案】AC DB =,OA OD =,OC OB =;A D ∠=∠,C B ∠=∠,AOC DOB ∠=∠.【分析】根据全等三角形的性质得出即可.【解析】解:∵O C A O B D ≌,∴两个三角形中相等的边为AC DB =,OA OD =,OC OB =;两个三角形中相等的角为A D ∠=∠,C B ∠=∠,AOC DOB ∠=∠.【点睛】本题考查了三角形的性质的应用,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应边相等,对应角相等.21.如图,,12,5ACF ADE AD AE ∆≅∆==,求DF 的长,【答案】7.【分析】先由全等三角形的性质得到AF=AE=4,继而根据DF=AD-AF 进行求解即可.【解析】∵△ACF ≌△ADE ,∴AF=AE ,∵AE=5,∴AF=5,∵DF=AD-AF ,AD=12,∴DF=12-5=7.【点睛】本题考查了全等三角形的性质,熟练掌握全等三角形的对应边相等是解题的关键.22.如图:ABC DBC ≌ ,且A ∠和D ∠,ABC ∠和DBC ∠是对应角,请写出三组对应边:【答案】48︒【分析】根据全等三角形的性质得出内角和定理求得AEC ∠【解析】解:∵ABC △∴,AC AE DAE =∠=∠∴12AEC ACE ∠=∠=∵AEC ∠是ADE V 的一个外角,∴D AEC DAE ∠=∠-∠∴48B D ∠=∠=︒.【点睛】本题考查了全等三角形的性质,三角形外角的性质,三角形内角和定理,掌握以上知识是解题的关键.24.如图,ABC ≌一、单选题1.(2020·山东淄博·统考中考真题)如图,若△ABC≌△ADE,则下列结论中一定成立的是()A .AC =DEB .∠BAD =∠CAEC .AB =AED .∠ABC =∠AED【答案】B 【分析】根据全等三角形的性质即可得到结论.【解析】解:∵△ABC ≌△ADE ,∴AC =AE ,AB =AD ,∠ABC =∠ADE ,∠BAC =∠DAE ,∴∠BAC ﹣∠DAC =∠DAE ﹣∠DAC ,即∠BAD =∠CAE .故A ,C ,D 选项错误,B 选项正确,故选:B .【点睛】本题考查了全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.二、填空题2.(2013·广西柳州·中考真题)如图,△ABC ≌△DEF ,请根据图中提供的信息,写出x =___.【答案】20【分析】先利用三角形的内角和定理求出70A ∠=︒,然后根据全等三角形对应边相等解答.【解析】解:如图,180506070A ∠=︒-︒-︒=︒,ABC DEF ∆≅∆ ,20EF BC ∴==,即20x =.故答案为:20.【点睛】本题考查了全等三角形的性质,根据角度确定出全等三角形的对应边是解题的关键.3.(2010·江苏南京·中考真题)已知点A 、B 的坐标分别为(2,0),(2,4),以A 、B 、P为顶点的三角形与△ABO全等,写出一个符合条件的点P的坐标:__________【答案】(4,0);(0,4);(4,4)(只要写出一个即可)【分析】画出图形,根据全等三角形的性质和坐标轴与图形的性质可求点P的坐标.【解析】解:如图∵△ABO≌△ABP,∴①OA=AP1,点P1的坐标:(4,0);②OA=BP2,点P2的坐标:(0,4);③OA=BP3,点P3的坐标:(4,4).故填:(4,0),(0,4),(4,4).【点睛】本题考查三角形全等和坐标轴与图形的性质.正确标出位置,熟练掌握三角形全等是解题的关键.。
2021-2022学年八年级数学上册《 三角形全等的判定3》知识讲解

专题12.7 三角形全等的判定3(知识讲解)【要点梳理】要点一、判定直角三角形全等的一般方法由三角形全等的条件可知,对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,这两个直角三角形就全等了.这里用到的是“AAS”,“ASA”或“SAS”判定定理.要点二、判定直角三角形全等的特殊方法——斜边,直角边定理在两个直角三角形中,有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).这个判定方法是直角三角形所独有的,一般三角形不具备.特别说明:(1)“HL”从顺序上讲是“边边角”对应相等,由于其中含有直角这个特殊条件,所以三角形的形状和大小就确定了.(2)判定两个直角三角形全等的方法共有5种:SAS、ASA、AAS、SSS、HL.证明两个直角三角形全等,首先考虑用斜边、直角边定理,再考虑用一般三角形全等的证明方法.(3)应用“斜边、直角边”判定两个直角三角形全等的过程中要突出直角三角形这个条件,书写时必须在两个三角形前加上“Rt”.【典型例题】类型一、直角三角形全等的判定——“HL”1、如图,已知:AB⊥BD,ED⊥BD,AB=CD,AC=CE.(1)AC与CE有什么位置关系?(2)请证明你的结论.举一反三:【变式】如图,Rt⊥ABC中,⊥ACB=90°,D是AB上的一点,过D作DE⊥AB交AC于点E,CE=DE.连接CD交BE于点F.(1)求证:BC=BD;(2)若点D为AB的中点,求⊥AED的度数.2、 如图,在∆ABC 中, AC = BC ,直线l 经过顶点C ,过 A , B 两点分别作l 的垂线 AE , BF , E , F 为垂足. AE = CF ,求证: ∠ACB = 90︒ .举一反三:【变式】 如图,Rt ABC 与Rt DEF △的顶点A ,F ,C ,D 共线,AB 与EF 交于点G ,BC 与DE 相交于点H ,90B E ∠=∠=︒,AF CD =,AB DE =.(1)求证:Rt ABC Rt DEF ≌;(2)若1GF =,求线段HC 的长.【变式1】已知:如图,AB =CD ,DE ⊥AC ,BF ⊥AC ,E ,F 是垂足,DE BF =.求证:(1)AF CE =;(2)AB CD ∥.【变式2】如图,⊥A=⊥D=90°,AB=DE,BF=EC.求证:Rt⊥ABC⊥Rt⊥DEF.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题03 全等三角形及其判定核心知识解读一、基础知识点综述1. 全等形能够完全重合的两个图形叫作全等形. 满足两个条件:形状相同、大小相等.得到全等形常用变换:平移、翻折、旋转.2. 全等三角形相关概念能够完全重合的两个三角形叫作全等三角形.将两个全等三角形重合在一起,重合的顶点叫作对应顶点,重合的边叫作对应边,重合的角叫作对应角.全等符号“≌”.3. 常用技巧对应边、对应角的找法:(1)有对顶角的,对顶角是对应角;(2)有公共角的,公共角是对应角;(3)有公共边的,公共边是对应边;(4)全等三角形对应边所对的角是对应角,对应角所对的边是对应边;(5)两个全等三角形中一对最长边(最大角)一定是对应边(角);两个全等三角形中一对最短边(最小角)一定是对应边(角).4. 对应边(角)与对边(角)的区别对应边(角)是相对于两个三角形而言的,是指两条边(两个角)之间的关系;对边(角)是在同一个三角形中而言的,对边是指三角形中某个内角(顶点)所对的边,对角是指三角形中某个边所对的角.在书写时通常将对应顶点写在相同的位置上.5. 全等三角形性质(1)对应边、对应角相等;(2)对应角的平分线,对应边的中线,对应边上的高分别对应相等;(3)全等三角形的面积相等,周长相等.6. 几个常用图形中的全等三角形(1)平移型(2)翻折型(3)旋转型7. 全等三角形判断定理(1)SSS ——三边分别对应相等的两个三角形全等.在≌ABC 和≌DEF 中,AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩,≌≌ABC ≌≌DEF (SSS ).(2)SAS ——两边和它们的夹角分别对应相等的两个三角形全等.在≌ABC 和≌DEF 中,AB DE B E BC EF =⎧⎪=⎨⎪=⎩∠∠,≌≌ABC ≌≌DEF (SAS ).BCE F(3)ASA ——两角和它们的夹边分别对应相等的两个三角形全等.在≌ABC 和≌DEF 中,A D AB DE B E =⎧⎪=⎨⎪=⎩∠∠∠∠,≌≌ABC ≌≌DEF (ASA ).(4)AAS ——两角和其中一个角的对边分别对应相等的两个三角形全等.在≌ABC 和≌DEF 中,A DB E AC DF =⎧⎪=⎨⎪=⎩∠∠∠∠,≌≌ABC ≌≌DEF (AAS ).(5)HL ——斜边和一条直角边分别相等的两个直角三角形全等.在Rt ≌ABC 和Rt ≌DEF 中,AB DE AC DF =⎧⎨=⎩,≌≌ABC ≌≌DEF (HL ).注意:一般三角形的全等判断定理(SSS 、SAS 、ASA 、AAS )同样适用于直角三角形全等的判定,即直角三角形全等的判定定理有5个.二、典型例题精讲例1. (2019·广东期末)圣母大学计算机系的史戈宇教授带一家人去旅行,途中汽车被劫走报警911,而警察毫无作为,马自达汽车上安装的MMS 系统,虽然可以提示汽车与手机APP 之间的直线距离,但方位不准确,且不能实时提供数据. 史教授利用“贪心算法”将被抢车辆定位在了一块区域内,这是芝加哥一个BE以暴乱和枪击文明的地区.如下图所示,当史教授与同伴开车从点E向A点方向行驶时,汽车与手机APP之间直线距离逐渐变小,从A点驶向F点时,距离逐渐变大. 当史教授与同伴开车从点F向B点方向行驶时,汽车与手机APP之间直线距离逐渐变小,从B点驶向G点时,距离逐渐变大.史教授再次报警后,警察根据史教授确定的被盗汽车的位置,很快找到了被盗汽车,根据你学的数学知识,在图中画出被盗汽车的位置.【分析】所谓“贪心算法”是指仅知道一动点与一不动点之间的直线距离而不知道方位时,怎么找到不动点的方法. 也就是先沿着一个方向走,直到距离不再明显变小(这是说明我们前进的方向已经几乎垂直于我们和目标之间连线),就转到垂直方向再继续搜寻.【答案】见解析.【解析】解:如图所示,连接EF,GF,过点A作AN≌EF,过点B作BM≌GF,直线AN、BM的交点即为P点位置.例2. (2019·辽宁期末)在≌ABC中,≌C=90°,AC=BC,BP是≌ABC的角平分线,过点P作PD≌AB 于点D,将≌EPF绕点P旋转,使≌EPF的两边交直线AB于点E,交直线BC于点F,请解答下列问题:当≌EPF绕点P旋转到如图1的位置,点E在线段AD上,点F在线段BC上,且满足PE=PF.≌请判断CP、CF、AE之间的数量关系,并加以证明.≌求出≌EPF的度数.图1 图2【答案】见解析.【解析】解:≌CP=CF+AE,理由如下:≌在≌ABC中,≌C=90°,AC=BC,≌AC=BC,≌A=≌ABC=45°,AC≌BC,≌PD≌AB,≌≌APD=45°,即PD=AD,≌BP平分≌ABC,PD≌AB,PC≌BC,≌PC=PD,≌PE=PF,≌Rt≌PED≌Rt≌PFC,≌DE=CF,≌CP=PD=AD=AE+ED=AE+CF;≌由≌知:≌DPE=≌CPF,≌≌EPF=≌DPC,≌≌ABC=45°,在四边形DPCB中,≌DPC=360°-90°-90°-45°=135°,即≌EPF=135°.例3. (2019·山东期末)如图,B、E、F、C在同一条直线上,AF≌BC于点F,DE≌BC于E,AB=DC,BE=CF,求证:AB≌CD.【答案】见解析.【解析】证明:≌AF≌BC,DE≌BC,≌≌DEC=≌AFB=90°,≌BE=CF,≌BE+EF=CF+EF,即BF=CE,在Rt≌ABF和Rt≌DCE中,AB=CD,BF=CE,≌Rt≌ABF≌Rt≌DCE,≌≌B=≌C,≌AB≌DC.例4. (2019·淄博月考)已知:如图所示,在≌ABC、≌ADE中,≌BAC=≌DAE=90°,AB=AC,AD=AE,点D、C、E三点共线,连接BD.求证:(1)≌BAD≌≌CAE;(2)BD≌CE.【答案】见解析.【解析】证明:(1)≌≌BAC=≌DAE=90°,≌≌BAC+≌CAD=≌DAE+≌CAD,即≌BAD=≌CAE,在≌BAD和≌CAE中,≌AB=AC,≌BAD=≌CAE,AD=AE,≌≌BAD≌≌CAE;(2)由(1)知,BD=CE,≌≌BAD≌≌CAE,≌≌ABD=≌ACE,由≌ABD+≌DBC=45°,得≌ACE+≌DBC=45°,≌≌DBC+≌DCB=90°,即BD≌CE.例5. 已知直线CD≌AB于点O,≌EOF=90°,射线OP平分≌COF.(1)如图1,≌EOF在直线CD的右侧,且点E在点F的上方.≌若≌COE=30°,求≌BOF和≌POE的度数;≌请判断≌POE与≌BOP之间存在怎样的数量关系?并说明理由.(2)如图2,≌EOF在直线CD的左侧,且点E在点F的下方.≌请直接写出≌POE与≌BOP之间存在怎样的数量关系.≌请直接写出≌POE与≌DOP之间存在怎样的数量关系.图1 图2【答案】见解析.【解析】解:(1)≌≌CD≌AB,≌≌COB=90°,≌≌EOF=90°,≌≌COE+≌BOE=≌BOE+≌BOF,即≌COE=≌BOF=30°,≌≌COF=120°,又≌OP平分≌COF,≌≌COP=60°,≌≌POE=30°;≌由≌知,≌COE=≌BOF,≌COP=≌POF,≌≌POE=90°+≌POF,≌BOP=90°+≌COP,≌≌POE=≌BOP.(2)≌由上知,≌COP=≌POF,≌≌POE=90°+≌POF,≌BOP=90°+≌COP,≌≌POE=≌BOP.≌≌≌POE=≌BOP,≌DOP+≌BOP=270°,≌≌POE+≌DOP=270°.例6. (2019·山东期末)在等腰≌ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD 为一边在AD的右侧作≌ADE,使得AD=AE,≌DAE=≌BAC,连接CE.(1)如图1,当点D在线段BC上,如果≌BAC=90°,求≌BCE的度数;(2)如图2,当点D在线段BC上,如果≌BAC=60°,求≌BCE的度数;(3)设≌BAC=α,≌BCE=β,≌如图3,当点D在线段BC上移动,则α、β之间有怎么样的数量关系?请说明理由.≌当点D在线段BC的反向延长线上移动时,α、β之间有怎么样的数量关系?请说明理由.【答案】见解析.【解析】解:(1)≌≌BAC=≌DAE,≌≌BAC-≌DAC=≌DAE-≌DAC,即≌BAD=≌CAE,在≌ADB和≌AEC中,≌AB=AC,≌BAD=≌CAE,AD=AE,≌≌ADB≌≌AEC,≌≌B=≌ACE,≌≌B+≌ACB=≌ACE+≌ACB,即≌BCE=≌B+≌ACB,又≌≌BAC=90°,≌≌BCE=90°.(2)≌≌BAC=60°,≌≌DAE=≌BAC=60°,≌AB=AC,AD=AE,≌≌B=≌ACB=60°,≌ADE=≌AED=60°,≌≌B=≌ACE=60°,≌≌BCE=120°.(3)≌α+β=180°,理由如下:≌≌BAC=≌DAE,≌≌BAC+≌DAC=≌DAE+≌DAC,即≌BAD=≌CAE,在≌ADB和≌AEC中,≌AB=AC,≌BAD=≌CAE,AD=AE,≌≌ADB≌≌AEC,≌≌B=≌ACE,≌≌B+≌ACB=≌ACE+≌ACB,即≌B+≌ACB=β,又≌α+≌B+≌ACB=180°,≌α+β=180°.≌α=β,理由如下:在≌ADB和≌AEC中,≌AB=AC,≌BAD=≌CAE,AD=AE,≌≌ADB≌≌AEC,≌≌ABD=≌ACE,≌≌ABD=≌BAC+≌ACB,≌ACE=≌BCE+≌ACB,≌≌BAC=≌BCE,即α=β.例7. (2019·内蒙古月考)已知≌ABC的高AD所在直线与高BE所在直线相交于点F.(1)如图1,若≌ABC为锐角三角形,且≌ABC = 45°,过点F作F G//BC,交直线AB于点G.试说明:F G + DC = AD.图1(2)如图2,若≌ABC= 135°,过点F作FG//BC,交直线AB于点G,直接写出F G,DC,AD之间满足的数量关系.图2【答案】见解析.【解析】解:(1)证明:≌≌ADB=90°,≌ABC=45°,≌≌BAD=≌ABC=45°,≌AD=BD,≌≌BEC=90°,≌≌CBE+≌C=90°,≌≌DAC+≌C=90°,≌≌CBE=≌DAC,≌≌FDB≌≌CDA≌GF≌BD,≌≌AGF=≌ABC=45°,≌≌AGF=≌BAD,≌F A=FG,≌FG+DC=F A+DF=AD;(2)FG-DC=AD;由(1)知,AF=FG,≌BFD=≌ACD,AD=BD,≌FDB=≌ADC=90°,≌≌FDB≌≌CDA.≌DC=DF,≌FG-DC=AD.。
