合工大电磁场与电磁波第6章答案
电磁场与电磁波课后习题及答案六章习题解答

第六章时变电磁场有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场之中,如题图所示。
滑片的位置由确定,轨道终端接有电阻,试求电流i.解穿过导体回路abcda的磁通为故感应电流为一根半径为a的长圆柱形介质棒放入均匀磁场中与z轴平行。
设棒以角速度绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解介质棒内距轴线距离为r处的感应电场为故介质棒内的极化强度为极化电荷体密度为极化电荷面密度为则介质体积内和表面上同单位长度的极化电荷分别为平行双线传输线与一矩形回路共面,如题图所示。
设、、,求回路中的感应电动势。
解由题给定的电流方向可知,双线中的电流产生的磁感应强度的方向,在回路中都是垂直于纸面向内的。
故回路中的感应电动势为式中故则有一个环形线圈,导线的长度为l,分别通过以直流电源供应电压U0和时变电源供应电压U(t)。
讨论这两种情况下导线内的电场强度E。
解设导线材料的电导率为,横截面积为S,则导线的电阻为而环形线圈的电感为L,故电压方程为当U=U0时,电流i也为直流,。
故此时导线内的切向电场为当U=U(t)时,,故即求解此微分方程就可得到。
一圆柱形电容器,内导体半径为a,外导体内半径为b,长为l。
设外加电压为,试计算电容器极板间的总位移电流,证明它等于电容器的传导电流。
解当外加电压的频率不是很高时,圆柱形电容器两极板间的电场分布与外加直流电压时的电场分布可视为相同(准静态电场),即故电容器两极板间的位移电流密度为则式中,是长为l的圆柱形电容器的电容。
流过电容器的传导电流为可见由麦克斯韦方程组出发,导出点电荷的电场强度公式和泊松方程。
解点电荷q产生的电场满足麦克斯韦方程和由得据散度定理,上式即为利用球对称性,得故得点电荷的电场表示式由于,可取,则得即得泊松方程试将麦克斯方程的微分形式写成八个标量方程:(1)在直角坐标中;(2)在圆柱坐标中;(3)在球坐标中。
解(1)在直角坐标中(2)在圆柱坐标中(3)在球坐标系中已知在空气中,求和。
电磁场与电磁波课后习题及答案六章习题解答

第六章 时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mT z e t ω=B 之中,如题6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.解 穿过导体回路abcda 的磁通为5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为 00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为0000()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m =、0.1m b c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。
电磁场与电磁波课后习题及答案六章习题解答

第六章 时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mT z e t ω=B 之中,如题 6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.解 5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰g g B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为00()(P r r r a e r σεεωε==⋅=-⋅=-P n B e 则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m=、0.1m b c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。
解 由题给定的电流方向可知,双线中的电流产生的磁感应强度的方向,在回路中都是垂直于纸面向内的。
合工大电磁场与电磁波习题答案

(2) ∇ ⋅ A = 4 − 2x + 2z , ∇ ⋅ A M (1,1,3) = 8 ;
( ) (3) A = xyzr = xyz xex + yey + zez = x2 yzex + xy2 zey + xyz2ez
= f ' (r) r ×r
r =0
(3) ∇ × ⎡⎣ f (r )C ⎤⎦ = ∇f (r )× C
= f ' (r )∇r ×C = f ' (r) r×C
r
(4) ∇i⎡⎣r × f (r )C ⎤⎦ = f (r )C ⋅[∇ × r] − ri⎡⎣∇ ×( f (r )C )⎤⎦
=
−r − sinθ cosϕey − cosθ ez
∂ = −e∂ r
( ) ∂ er =
ϕ
∂
ϕ
sinθ cosϕex + sinθ sin ϕey + cosθ ez
= − sinθ sinϕex + sinθ cosϕey
( ) = sinθ − sinϕex + cosϕey
f
(r)
=
C r3
( ) 1-13 求 矢 量 场 A = xyz ex + ey + ez 在 点 M (1, 3, 2) 的 旋 度 以 及 在 这 点 沿 方 向
n = ex + 2ey + 2ez 的环量面密度。
e∂x e∂y e∂z
解: ∇ × A M = ∂ x
∂ y
∂ z
6 电磁场与电磁波 第六章 答案

6.2 自由空间中一均匀平面波的磁场强度为)cos()(0x wt H a a H z y π-+= m A /求:(1)波的传播方向;(2)波长和频率;(3)电场强度; (4)瞬时坡印廷矢量。
解:)cos()(0x wt H a a H z y π-+=m A /(1) 波沿+x 方向传播(2) 由题意得:k=π rad/m , 波长m k 22==πλ , 频率Hz c f 8105.1⨯==λ (3))cos(120)(0x wt H a a a H E z y x ππη--=⨯= m v / (4))(cos 24020x wt H a H E S x ππ-=⨯= 2/m w 6.3无耗媒质的相对介电常数4=r ε,相对磁导率1=r μ,一平面电磁波沿+z 方向传播,其电场强度的表达式为)106cos(80z t E a E y β-⨯=求:(1)电磁波的相速;(2)波阻抗和β;(3)磁场强度的瞬时表达式;(4)平均坡印廷矢量。
解:(1)s m cv r r p /105.118⨯===εμμε(2))(6000Ω===πεεμμεμηrr , m r a d c w w r r /4===εμμεβ (3))4106cos(60180z t E a E a H x z -⨯-=⨯=πη m A / (4)π120]Re[2120*E a H E S z av =⨯= 2/m w6.4一均匀平面波从海水表面(x=0)沿+x 方向向海水中传播。
在x=0处,电场强度为m v t a E y /)10cos(1007π =,若海水的80=r ε,1=r μ,m s /4=γ。
求:(1)衰减常数、相位常数、波阻抗、相位速度、波长、趋肤深度;(2)写出海水中的电场强度表达式;(3)电场强度的振幅衰减到表面值的1%时,波传播的距离;(4)当x=0.8m 时,电场和磁场得表达式;(5)如果电磁波的频率变为f=50kHz ,重复(3)的计算。
合工大电磁场与电磁波第6章答案

第6章习题答案6-1在r 1、 r 4、0的媒质中,有一个均匀平面波,电场强度是E(z,t) E m sin( t kz —)3若已知f 150 MHz ,波在任意点的平均功率流密度为0.265卩w/m 2,试求:(1) 该电磁波的波数 k ?相速V p ?波长?波阻抗 ?(2)t 0, z 0的电场 E(0,0)?(3) 时间经过0.1 之后电场E(0,0)值在什么地方?(4) 时间在t 0时刻之前0.1 口 s ,电场E(0,0)值在什么地方?—2 f —解:(1) k .——.r 2 (rad/m) cv p c/. r 1.5 108(m/s)k 1(m)(4)在O 点左边15 m 处6-2 一个在自由空间传播的均匀平面波,电场强度的复振幅是—4 j 20 z— 4 j(520 z)八、,、[/ E 10 e je x 10 ee y 伏 / 米试求:(1)电磁波的传播方向?(2) 电磁波的相速V p ?波长 ?频率f ? (3) 磁场强度H ?(4) 沿传播方向单位面积流过的平均功率是多少?=12060 (Q )(2): S a vE m0 60.265 10E m 1.00 10■. 0 r2(V/m)E(0,0)(3)往右移E m sin 8.66 103z v p t 15 m3(V/m )解:(1)电磁波沿z方向传播。
(2)自由空间电磁波的相速v p c 3 108 m/s••• k —20c20 c f —10c3 109Hz217j(20 z )z(3) H ^e z E 26510 7(e 2 e x e j20 z e y )(A/m)*(4)S av ^Re(EH *)^-^e z2.65 10 11e z (W/m 2)226-3证明在均匀线性无界无源的理想介质中,不可能存在 磁波。
证•/ EjkE °e jkz 0,即不满足Maxwell 方程不可能存在E E °e jkz e z 的均匀平面电磁波。
电磁场与电磁波理论第6章习题解答

第6章习题解答已知空气中存在电磁波的电场强度为 ()80cos 6π102πy E e E t z =⨯+r rV /m试问:此波是否为均匀平面波传播方向是什么求此波的频率、波长、相速以及对应的磁场强度H r。
解:均匀平面波是指在与电磁波传播方向相垂直的无限大平面上场强幅度、相位和方向均相同的电磁波。
电场强度瞬时式可以写成复矢量j 0e kzy E e E -=r r &。
该式的电场幅度为0E ,相位和方向均不变,且0z E e ⋅=r r ⇒z E e ⊥r r ,此波为均匀平面波。
传播方向为沿着z -方向。
由时间相位86π10t t ω=⨯ ⇒ 86π10ω=⨯ 波的频率Hz 1038⨯=f 波数2πk =波长2π 1 m k λ== 相速p 310 m/s v kω==⨯ 由于是均匀平面波,因此磁场为j 0w w1() e kz z x EH e E e Z Z -=-⨯=r r r v &&有一频率为600MHz 的均匀平面波在无界理想介质(r r 4,1εμ==)中沿x +方向传播。
已知电场只有y 分量,初相位为零,且010t t ==s 时,1x =m 处的电场强度值为800kV/m 。
试写出E v 和H v的瞬时表达式。
解:根据题意,角频率812π10ω=⨯,r r 0028πk cωεμεμεμ====,因此 80cos(12π108π)y E e E t x =⨯-r r由s 10=t ,m 1=x 处的电场强度值为kV /m 800,可以得到kV/m 8000=E8800cos(12π108π) kV/m y E e t x =⨯-r r根据电场的瞬时表达式可以写出电场的复矢量为j8π800e kV/m x y E e -=r r&波阻抗为()0r w r 060π ΩZ μμμεεε===。
因此磁场强度复矢量为 j8πw 140() e kA/m 3πx x z H e E e Z -=⨯=r r r r &&因此,磁场的瞬时表达式为840cos(12π108π)3πz H e t x =⨯-r r在无界理想介质中,均匀平面波的电场强度为 ()80sin 2π102πx E e E t z =⨯-r rV /m已知介质的r 1μ=,试求其r ε,并写出H r的表达式。
合工大电磁场与电磁波第6章规范标准答案

第6章习题答案6-1在r 1、 r 4、0的媒质中,有一个均匀平面波,电场强度是 E(z,t) E m sin( t kz —)3若已知f 150 MHz ,波在任意点的平均功率流密度为 0.265卩w/m 2,试求:(1)该电磁波的波数 k ?相速V p ?波长 ?波阻抗 ?(2) t 0 , z 0 的电场 E(0,0) ?(3) 时间经过0.1 之后电场E(0,0)值在什么地方?(4) 时间在t 0时刻之前0.1 口 s ,电场E(0,0)值在什么地方?—2 f —解:(1) k ..——r 2 (rad/m)cv p c/. r 1.5 108(m/s)k 1(m)6-2 一个在自由空间传播的均匀平面波,电场强度的复振幅是—4 j 20 z — 4 j(520 z)八、,、[/E 10 e je x 10 ee y 伏 / 米试求:(1)电磁波的传播方向?(2) 电磁波的相速V p ?波长 ?频率f ? (3) 磁场强度H ?(4) 沿传播方向单位面积流过的平均功率是多少?=12060 (Q )(2): Sa vE m0 60.265 10E m1.00 10 \0 r2 (V/m) E m sin 8.66 10 3z v p t 15 m(4)在O 点左边15 m 处E(0,0)3(V/m)(3)往右移解:(1)电磁波沿z方向传播。
(2)自由空间电磁波的相速v p c 3 108 m/s••• k — 20c 20 cf —10c 3 109Hz217j(20 z )z(3) H ^e z E265 10 7(e 2e x e j20 z e y )(A/m)*(4)S av ^Re(EH *)^-^e z2.65 10 11e z (W/m 2)2 26-3证明在均匀线性无界无源的理想介质中, 不可能存在E E °e jkze z 的均匀平面电磁波。
证•/ E jkE °e jkz0,即不满足Maxwell 方程.不可能存在E E °e jkze z 的均匀平面电磁波。
电磁场与电磁波(第4版)第6章部分习题参考解答

G ex
Erm
cos(ωt
+
β1
z
)
=
G ex
Eim
cos(2πft
+
β1
z
)
= =
eGxGηη22
−η1 + η1
−ex18.37
100 cos(2π ×109t + 20.93z) cos(2π ×109t + 20.93z) V/m
G H1r
(
z,
t
)
= =
1 ηG 1 ey
G (−ez × E1r ) = 0.049 cos(2π
距离导体平面最近的合成波电场 G
E1
为
0
的位置;(5) 距离导体平面最近的合成波磁场 H1 为 0 的位置。
解:(1) ω = 2πf = 2π ×108 rad/s
β
=
ω c
=
2π ×108 3 ×108
=
2 3
π
rad/m
η1 = η0 =
μ0 = 120π Ω ε0
G
G
则入射波电场 Ei 和磁场 Hi 的复矢量分别为
G Ei (x)
=
G
− j2 πx
ey10e 3
G V/m , Hi (x)
=1 η1
G ex
G × Ei (x)
G = ez
1
− j2 πx
e3
12π
A/m
G
G
(2) 反射波电场 Er 和磁场 Hr 的复矢量分别为
G Er (x) =
G
j2 πx
−ey10e 3
G V/m , Hr (x)
电磁场与电磁波 习题6

www×
⎡ ⎢ ⎢⎣
−
10−4
sin(ωt − 120π
20πz
)evx
+
10−4
cos(ωt − 120π
20πz)evy
)
⎤ ⎥ ⎥⎦
=
10−8 120π
evz
(W/m2 )
v S av
=
1
Re[
v E
×
v H
*
]
2
86
课后答案网
《电磁场与电磁波》——习题详解
=
1 2
课后答案网
《电磁场与电磁波》——习题详解
第六章 平面电磁波
6-1 理想媒质中一平面电磁波的电场强度矢量为
v E
(t
)
=
evx
5
cos
2π
(108
t
−
z
)
(V/m)
(1) 求媒质及自由空间中的波长。
(2) 已知媒质 µ = µ0 , ε = ε 0ε r ,求媒质的 ε r 。
v
m H
=1 η
evz
×
v E
=1 η0
(evy
+
jevx )10−4 e− j20π z
课 后 答 案 网
o = 10−4e− j20π z (jevx + evy ) (A/m) c 120π
(3) 电磁波的瞬时值为
. v
E(t)
=
v Re[E
e
jω
t
]
w = evx10−4 cos(ω t − 20π z) + evy10−4 sin(ω t − 20π z) (V/m)
(mV/m) (mA/m)
工程电磁场与电磁波_丁君版_答案第六章习题答案

6-1.解:E矢量为y 方向,电磁波沿-z 方向传播,)2106cos(7.37)2(8222z t z E y πππ+⨯⨯-=∂∂)2106cos(7.37)106(82822z t tE y πππ+⨯⨯⨯-=∂∂又π2=k ,μεω22=k ,8106⨯=πω 2222222228222)106()2(tE t E k t E z E y y y y ∂∂=∂∂=∂∂⋅⨯=∂∂∴μεωππ )2106cos(7.378z t E y ππ+⨯=∴符合均匀平面波的一维波动方程,所以它属于均匀平面波。
6-2.解:;10328Hz f ⨯==πω π2=k ;m k 12==πλ;s m kv P /1038⨯==ω;m uE H 1.0/77.3/===εη 波沿-z 轴传播;由右手螺旋法则,H 在x 方向上振动。
6-3. 解: (1)Hz vf 881092.461.0103⨯=⨯==λ (2)91003.2/1⨯==f T s (3)3.1061.022===πλπk (4)12.2377/800/===ηE HA/m 方向为y aˆ 6-4.解:由E 和 H的关系可知:y m x m a az t H aaz t H H ˆ)sin(ˆ)sin(-+--=ωωy m x m a az t E aaz t E ˆ)sin(/ˆ)sin(/00-⋅+-⋅-=ωηωη H E S⨯=z m m z m m a az t E az t E aaz t E az t E ˆ)sin(/)sin(ˆ)sin(/)sin(00-⋅⋅-+-⋅⋅-=ωηωωηω z m a az t E ⋅-=022/)(sin 2ηω6-5 解:Hz U f 98000105.212.0103⨯=⨯==λ5001.050111===H E η 又rrrru u u επεεη120001==πε120500=rru(1)在均匀媒质中有:11v v P = rr u Cf ελ=1 2981108105.2103-⨯⨯⨯⨯==∴λεf C u r r (2)由式(1)、(2)得 99.1=r u 13.1=r ε6-6 解:m V a a aE z y x 310)ˆ2ˆˆ4(⨯+-=1)333310)ˆ78ˆ24ˆ33(3186********ˆˆˆ⨯++-=-⨯-⨯=⨯z y x z y x a a aaaaH E322231078243310)ˆ78ˆ24ˆ33(ˆ⨯++⨯++-=z y x a a aaz y x a a a ˆ89.0ˆ27.0ˆ37.0++= 2)3ˆˆˆ(42)10jkr x y z E aa a e -=-+⨯ˆˆˆ(6183)jkr x y z H aa a e -=+-*311ˆˆˆRe[](332478)1022av x y z S E H aa a =⨯=-++⨯3)HE ur r ==επη1201 5.2=∴r ε6-7解: 1)不失一般性,可假设两圆极化波左旋:)ˆˆ(101y x jkz a j ae E E +=-右旋:)ˆˆ(202y x jkz a j ae E E -=-合成波:21E E E+==y jkz x jkz a e j E E a e E E ˆ)(ˆ)(20102010---++ =y jkz jx jkzae e E E aeE E ˆ)(ˆ)(220102010---++πy x E E+=y x E E ≠ 2πϕϕ-=-y xx E 与y E 振幅不等,相位相差2π为一个椭圆极化波故椭圆极化波可分解为一个左旋圆极化波和一个右旋圆极化波。
电磁场与电磁波第六章答案

v
20
则位移电流的瞬时表达式为: J D
a x 5 10 7 cos(6 10 9 t 20z ) 2
3.海水的电导率约为 0.4ms / m ,其相对介电常数为 81。求海水中位移电流密度等于传导 电流密度时的界限频率。 3 解答:
5 1 时的频率为界限频率。则得 f 8.9 10 Hz
6.若空气的磁感应强度如题 2 所示,求磁场强度和电场强度的复数形式、坡印廷矢量的 瞬时值及平均值。
6 解答
1 j 20z H aye
0
,E
1 a x e j 20z , c
1 S EH a z cos 2 (6 109 t 20z ) , 0c
7 解答:由 E j 0 H
得H
0 0 E ym e jkz a x E xm e jkz a y 0 0
瞬时形式为: H
0 0 E ym cos(t kz)a x E xm cos(t kz)a y 0 0
1 1 S av Re E H az 2 2 0 c
(c
3 108 m / s)
7.在空气中,已知电场强度 E Exm cos(t kz)ax E ym cos(t kz)a y 。求坡印廷矢 量的瞬时值 S 及平均值 S av 。
j ( kz 0 )
,其中
0 为常数, k 2 2 0 0 。①求两个波的坡印廷矢量的平均值 S av1 和 S av2 ;②证明空间
中总的 Sav Sav1 Sav2 。 11 解答:1)由 E j 0 H ,得
电磁场与电磁波_章六习题答案

电磁场与电磁波_章六习题答案第6章平⾯电磁波点评:1、6-8题坡印廷⽮量单位,2W m ,这⾥原答案有误!2、6-13题第四问应为右旋圆极化波。
3、6-19题第三问和第四问,原答案错误。
这⾥在介质⼀中,z<0。
4、⽮量书写⼀定引起重视,和标量书写要分清,结果若是确切的数值则单位⼀定要标清楚。
5、马上期末考试,那些对参考答案借鉴过多的同学务必抓紧时间把每道题⽬弄懂!本章是考试重点,⼤家务必弄懂每道题。
6-1、已知正弦电磁场的电场瞬时值为()()88,0.03sin 100.04cos 10 3x x z t t kz t kz V m πππ?=-+--E e e试求:⑴电场的复⽮量;⑵磁场的复⽮量和瞬时值。
解:(1)()8,0.03cos 102x z t t kz ππ?=--E e +80.04cos 103x t kz ππ?--e所以电场的复⽮量为32()0.030.04 j j jkz x z e e e V m ππ---??=+E e(2) 由复数形式的麦克斯韦⽅程,得到磁场的复⽮量3200054321()0.030.04 7.610 1.0110j j jkz x y yj j jkz y E j kz e e e j z k e e e A mππππωµωµωµ--------=-??==+??=?+?H E e e e磁场的瞬时值则为()5848(,)7.610sin 101.0110cos 103y z t k t kz t kz πππ--=-+--H e6-2、真空中同时存在两个正弦电磁场,电场强度分别为1110jk z x E e -=E e ,2220jk z y E e -=E e ,试证明总的平均功率流密度等于两个正弦电磁场的平均功率流密度之和。
解:由麦克斯韦⽅程11111001()jk z xyy E jk E e j zωµ-==-=-?E e e H 可得111100jk z yk E e ωµ-=H e故2*11011101Re 22zk E ωµ??=?=S E H e 同理可得22222002()y jk z xx E jk E e j zωµ-=-=--=-?E e e H222200jk z xk E e ωµ-=-H e2*22022201Re 22zk E ωµ??=?=S E H e 另⼀⽅⾯,因为12=+E E E0y x x y E Ej z zωµ=-+=-??E e e H所以212120100jk z jk z xyk k E e E e ωµωµ--=-+H e e22*110220120011Re 22z k E k E ωµωµ=?=+=+ ?S E H e S S6-5、已知在⾃由空间中球⾯波的电场为0sin cos()E t kr r θθω?? =-E e ,求H 和k 。
电磁场与电磁波:第六章作业答案

都是实数,故 也是实数。
反射波的电场为
可见,反射波的电场的两个分量的振幅仍相等,相位关系与入射波相比没有变化,故反射波仍然是圆极化波。但波的传播方向变为-z方向,故反射波变为右旋圆极化波,而入射波是沿+z方向传播的左旋圆极化波。
透射波的电场为
式中, 是媒质2中的相位常数。可见,透射波是沿+z方向传播的左旋圆极化波。
(1)求每一区域中的波阻抗和传播常数;
(2)分别求两区域中的电场、磁场的瞬时形式。
解(1)波阻抗
得
对于无损耗介质
得
(2) 区的入射波为
反射波为
故合成波为
Ⅱ区只有透射波
6.9一圆极化波自空气中垂直入射于一介质板上,介质板的本征阻抗为 。入射波电场为 。求反射波与透射波的电场,它们的极化情况如何?
解设媒质1为空气,其本征阻抗为 ,故分界面上的反射系数和透射系数分别为
V/m
(1)应用麦克斯韦方程求相伴的磁场 ;
(2)若在波传播方向上 处放置一无限大的理想导体板,求 区域中的合成波电场 和磁场 ;
(3)求理想导体板表面的电流密度。
解(1)将已知的电场写成复数形式
由 得
写成瞬时值表示式
(2)均匀平面波垂直入射到理想导体平面上会产生全反射,反射波的电场为
即 区域内的反射波电场为
(1)入射波的频率 与波长 ;
(2) 和 的瞬时表达式
(3)入射角 ;
(4)反射波的 和 ;
(5)总场的 和 。
解(1)由已知条件知入射波的波矢量为
故波长为
频率为
(2)入射波传播方向的单位矢量为
入射波的磁场复数表示式为
其瞬时表示式
而电场的瞬时表示式为
《电磁场与电磁波》第4版(谢处方 编)课后习题答案 高等教育出版社六章习题解答
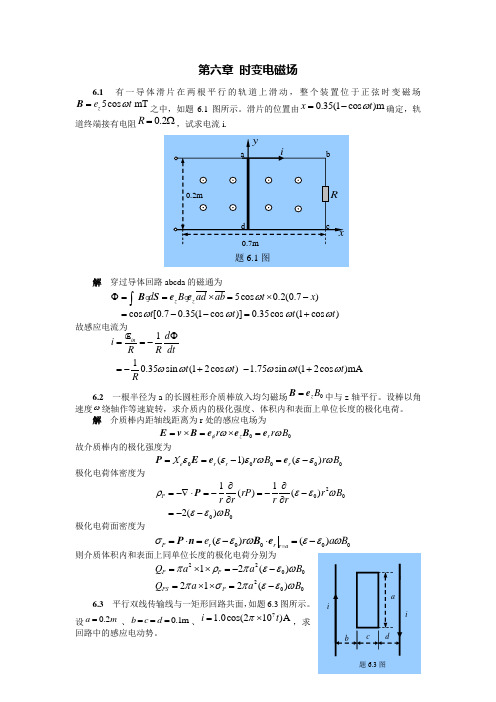
第六章 时变电磁场6.1 有一导体滑片在两根平行的轨道上滑动,整个装置位于正弦时变磁场5cos mT z e t ω=B 之中,如题6.1图所示。
滑片的位置由0.35(1cos )m x t ω=-确定,轨道终端接有电阻0.2R =Ω,试求电流i.解 穿过导体回路abcda 的磁通为5cos 0.2(0.7)cos [0.70.35(1cos )]0.35cos (1cos )z z d B ad ab t x t t t t ωωωωωΦ==⨯=⨯-=--=+⎰ B S e e故感应电流为110.35sin (12cos ) 1.75sin (12cos )mAin d i R R dt t t t t R ωωωωωωΦ==-=-+-+E6.2 一根半径为a 的长圆柱形介质棒放入均匀磁场0z B =B e 中与z 轴平行。
设棒以角速度ω绕轴作等速旋转,求介质内的极化强度、体积内和表面上单位长度的极化电荷。
解 介质棒内距轴线距离为r 处的感应电场为 00z r r r B φωω=⨯=⨯=E v B e e B e故介质棒内的极化强度为 00000(1)()e r r r r B r B εεεωεεω==-=-P E e e X极化电荷体密度为2000011()()2()P rP r B r r r rB ρεεωεεω∂∂=-∇⋅=-=--∂∂=--P极化电荷面密度为0000()()P r r r a e r a B σεεωεεω==⋅=-⋅=-P n B e则介质体积内和表面上同单位长度的极化电荷分别为220020012()212()P P PS P Q a a B Q a a B πρπεεωπσπεεω=⨯⨯=--=⨯⨯=-6.3 平行双线传输线与一矩形回路共面,如题6.3图所示。
设0.2a m =、0.1m b c d ===、71.0cos(210)A i t π=⨯,求回路中的感应电动势。
电磁场与电磁波课后习题答案(杨儒贵编着)(第二版)第6章

第六章 电磁感应6-1 一个半径为a 的导体圆盘位于均匀恒定磁场0B 中,恒定磁场0B 的方向垂直于圆盘平面,若该圆盘以角速度ω绕其轴线旋转,求圆盘中心与边缘之间的电压。
解 将导体圆盘分割为很多扇形条,其半径为a ,弧长为φd a 。
当导体圆盘旋转时,扇形条切割磁力线产生的电动势等于圆盘中心与边缘之间的电压。
根据书中式(6-1-11),在离圆盘中心为r ,长度为r d 的线元中产生的电动势为0d d B v l ⋅⨯=e r r B d 0ω=因此,圆盘中心与边缘之间的电压为2000 21d a B r r Be aωω==⎰ 6-2 一个面积为b a ⨯的矩形 线圈位于双导线之间,位置 如习题图6-2所示。
两导线 中电流方向始终相反,其变 化规律为A )102sin(10921t I I ⨯==π, 试求线圈中感应电动势。
习题图6-2解 建立的坐标如图6-2所示。
在c b x c +<<内,两导线产生的磁感应强度为()x d c b I x I zz-+++=πμπμ222010e e Β 则穿过回路的磁通量为s Β⎰⋅=sm d Φx a x d c b x I z cb czd 11210e e ⋅⎪⎭⎫⎝⎛-+++=⎰+πμ ()()cdd b c b a I ++=ln 210πμ 则线圈中的感应电动势为te md d Φ-=()()t I cd d b c b a d d ln 210++-=πμ()()()V 10ln 102cos 1090⨯⎥⎦⎤⎢⎣⎡++⨯-=cd d b c b t a πμ 6-3 设带有滑条AB 的两根平行导线的终端并联电阻Ω2.0=R ,导线间距为0.2m ,如习题图6-3所示。
若正弦电磁场t B z sin 5ωe =垂直穿过该回路,当滑条AB 的位置以m ) cos 1(35.0t x ω-=规律变化时,试求回路中的感应电流。
解 建立的坐标如图6-3所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章习题答案6-1 在1=r μ、4=r ε、0=σ的媒质中,有一个均匀平面波,电场强度是)3sin(),(πω+-=kz t E t z E m若已知MHz 150=f ,波在任意点的平均功率流密度为2μw/m 265.0,试求:(1)该电磁波的波数?=k 相速?=p v 波长?=λ波阻抗?=η (2)0=t ,0=z 的电场?)0,0(=E(3)时间经过μs 1.0之后电场)0,0(E 值在什么地方?(4)时间在0=t 时刻之前μs 1.0,电场)0,0(E 值在什么地方? 解:(1))rad/m (22πεπμεω===r cfk)m/s (105.1/8⨯==r p c v ε)m (12==kπλ )Ω(60120πεμπη=rr= (2)∵ 6200210265.02121-⨯===m rm av E E S εεμη∴ (V/m)1000.12-⨯=m E)V/m (1066.83sin)0,0(3-⨯==πm E E(3) 往右移m 15=∆=∆t v z p(4) 在O 点左边m 15处6-2 一个在自由空间传播的均匀平面波,电场强度的复振幅是米伏/1010)202(j 420j 4yx e e E z zeeπππ----+=试求: (1)电磁波的传播方向?(2)电磁波的相速?=p v 波长?=λ频率?=f (3)磁场强度?=H(4)沿传播方向单位面积流过的平均功率是多少?解:(1) 电磁波沿z 方向传播。
(2)自由空间电磁波的相速m/s 1038⨯==c v p)m (1.02022===πππλk ∵ πω20==ck∴ c πω20=∴ Hz 1031029⨯===c f πω(3))A/m )((10652120j )220(j 7y z x z z e e.e e E e H πππη-+--+⨯=⨯=(4))W/m (106522)Re(21211*z z av .e e H E S *-⨯=⋅=⨯=ηE E6-3 证明在均匀线性无界无源的理想介质中,不可能存在z e E kz e E j 0-=的均匀平面电磁波。
证 ∵ 0j j 0≠-=⋅∇-kz e kE Ε,即不满足Maxwell 方程∴ 不可能存在z e E kz e E j 0-=的均匀平面电磁波。
6-4在微波炉外面附近的自由空间某点测得泄漏电场有效值为1V/m ,试问该点的平均电磁功率密度是多少?该电磁辐射对于一个站在此处的人的健康有危险吗?(根据美国国家标准,人暴露在微波下的限制量为10-2W/m 2不超过6分钟,我国的暂行标准规定每8小时连续照射,不超过3.8×10-2W/m 2。
)解:把微波炉泄漏的电磁辐射近似看作是正弦均匀平面电磁波,它携带的平均电磁功率密度为2302W/m 1065.23771-⨯===ηe av E S 可见,该微波炉的泄漏电场对人体的健康是安全的。
6-5 在自由空间中,有一波长为12cm 的均匀平面波,当该波进入到某无损耗媒质时,其波长变为8cm ,且此时m /V 41.31=E ,m /A 125.0=H 。
求平面波的频率以及无损耗媒质的r ε和r μ。
解:因为r r εμλλ/0=,所以4/9)8/12(2==r r εμ又因为r r H E εμπ120=,所以4443.01202=⎪⎭⎫⎝⎛=H E r r πεμ 1=r μ,25.2=r ε6-6 若有一个点电荷在自由空间以远小于光速的速度v 运动,同时一个均匀平面波也沿v 的方向传播。
试求该电荷所受的磁场力与电场力的比值。
解:设v 沿z 轴方向,均匀平面波电场为E ,则磁场为 E e H ⨯=z 01η电荷受到的电场力为E F q e =其中q 为点电荷电量,受到的磁场力为E E H e B vF 00000εμημμqv vq v q q z m -=-=⨯=⨯=E cqv -= 故电荷所受磁场力与电场力比值为cv F F e m =6-7 一个频率为GHz 3=f ,y e 方向极化的均匀平面波在5.2=r ε,损耗角正切值为10-2的非磁性媒质中,沿正x e 方向传播。
(1)求波的振幅衰减一半时,传播的距离; (2)求媒质的波阻抗,波的相速和波长;(3)设在0=x 处的y t e E ⎪⎭⎫⎝⎛+⨯=3106sin 509ππ,写出),(t x H 的表示式。
解:(1)210tan -==ωεσψ,这是一个低损耗媒质,平面波的传播特性,除了有微弱的损耗引起的衰减之外,和理想介质的相同。
其衰减常数为497.01035.2210321021028922=⨯⨯⨯⨯==≈--πμεωεμσα 因为2/1=-ieα,所以m 40.12ln ==αl(2)对低损耗媒质,Ω4.2385.2/120/==≈πεμη 相速m/s 1090.15.2103188⨯=⨯==μεv波长(cm)32.6(m)0632.0/===f v λ (3)3.991035.210689=⨯⨯⨯=≈πμεωβ(A/m))33.99106sin(21.0)3106sin(50),(95.095.0zx zx x t e x t e t x e e H πππβπη+-⨯=+-⨯=--6-8微波炉利用磁控管输出的2.45GHz 频率的微波加热食品,在该频率上,牛排的等效复介电常数)j 3.01(40~-=rε。
求: (1)微波传入牛排的穿透深度δ,在牛排内8mm 处的微波场强是表面处的百分之几?(2)微波炉中盛牛排的盘子是发泡聚苯乙烯制成的,其等效复介电常数=rε~ )103.0j 1(03.14-⨯-。
说明为何用微波加热时,牛排被烧熟而盘子并没有被毁。
解:(1)20.8mm m 0208.011211212==⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛+==-ωεσμεωαδ%688.20/8/0===--e e E E z δ(2)发泡聚苯乙烯的穿透深度(m)1028.103.1103.01045.22103212213498⨯=⨯⨯⨯⨯⨯⨯⨯=⎪⎭⎫ ⎝⎛===-πμεωεσωμεσαδ可见其穿透深度很大,意味着微波在其中传播的热损耗极小,所以不会被烧毁。
6-9 已知海水的1,81S /m 4===r r μεσ,,在其中分别传播MHz 100=f 或kHz 10=f 的平面电磁波时,试求:????====λβαp v解:当MHz 1001=f 时,888.=ωεσ当kHz 102=f 时,41088⨯=.ωεσ故kHz 102=f 时,媒质可以看成导体,可以采用近似公式ωμσβα21≈≈ 而MHz 1001=f 时媒质是半电介质,不能采用上面的近似公式。
(1) 当MHz 1001=f 时(Nep/m)5.371)(12221=-+=ωεσμεωα (rad/m)0.421)(12221=++=ωεσμεωβ (m/s)101490811⨯==.βωυp (m)1490211.==βπλ(2) 当kHz 102=f 时 39702122.=≈≈ωμσβα ∴ (Nep/m)39702.≈α(rad/m)39702.≈β(m/s)1058.1522⨯==βωυp (m)815222.==βπλ6-10 证明电磁波在良导电媒质中传播时,场强每经过一个波长衰减54.54dB 。
证:在良导体中,βα≈,故απβπλ22==因为 l le E eE E α2π00--==所以经过一个波长衰减 54.57(dB))lg(20lg2020=-=--πe E E6-11 为了得到有效的电磁屏蔽,屏蔽层的厚度通常取所用屏蔽材料中电磁波的一个波长,即πδ2=d式中δ是穿透深度。
试计算(1)收音机内中频变压器的铝屏蔽罩的厚度。
(2)电源变压器铁屏蔽罩的厚度。
(3)若中频变压器用铁而电源变压器用铝作屏蔽罩是否也可以? (铝:S /m 1072.37⨯=σ,1=r ε,1=r μ;铁:S/m 107=σ,1=r ε,410=r μ,f =465kHz 。
)解: ωμσππδ222==d(1)铝屏蔽罩厚度为0.76(mm)(m)1060710723104104652224773=⨯=⨯⨯⨯⨯⨯⨯=--.. πππd (2)铁屏蔽罩厚度为(mm)41.1(m)1041.11010104502223747=⨯=⨯⨯⨯⨯⨯=-- πππd (3) m)(741(m)1047110101041046522257473μπππ..=⨯=⨯⨯⨯⨯⨯⨯=-- 铁d(mm)73(m)103371072310450222277=⨯=⨯⨯⨯⨯⨯=--.. πππ铝d 用铝屏蔽50Hz 的电源变压器需屏蔽层厚73mm ,太厚,不能用。
用铁屏蔽中周变压器需屏蔽层厚m 714μ.,故可以选用作屏蔽材料。
6-12 在要求导线的高频电阻很小的场合通常使用多股纱包线代替单股线。
证明,相同截面积的N 股纱包线的高频电阻只有单股线的N1。
证:设N 股纱包中每小股线的半径为r ,单股线的半径为R ,则22r N R ππ=,即r N R =单股线的高频电阻为 δπσR R 211⋅=其中σ为电导率,δ为趋肤深度。
N 股纱包线的高频电阻为 δπσrN R N 21⋅=∴NrN r N rN R R R N 11===6-13 已知群速与相速的关系是ββd dv v v p p g +=式中β是相移常数,证明下式也成立λλd dv v v p p g -=证:由λπβ2=得λλπλπβd d d 22)1(2-==∴ λλλλπλπd dv v d dv v v p p p p g -=-⋅+=)2(226-14 判断下列各式所表示的均匀平面波的传播方向和极化方式 (1)y x e e E kz kz e E e jE j 1j 1j +=(2)z kx y kx e H e H e e H j 2j 1--+= (021≠≠H H ) (3)y x e e E kz kze E eE j 0j 0j ---=(4))(j 00j y x e e E ϕe AE E e kz +=- (A 为常数,πϕ±≠,0)(5))j (j j z x e e H ky mky me E e E --+=ηη(6)y m x m kz t E kz t E t z e e E )cos()sin(),(-+-=ωω(7)y m x m kz t E kz t E t z e e E )4cos()4sin(),(πωπω--++-= 解:(1)—z 方向,直线极化。
(2)+x 方向,直线极化。
(3)+z 方向,右旋圆极化。
(4)+z 方向,椭圆极化。
