《计算机图形学》实验报告——区域填充和剪裁

实验报告模板
《计算机图形学》实验报告
区域填充算法、裁剪算法
一、实验目的及要求
上机用所学的算法来填充多边形区域，在所给的区域里面剪裁所给出的线段。

二、理论基础
区域填充：区域填充所采用的算法是种子天填充算法。

算法的主要思想是在所给定的区域类取一点作为种子，然后向种子坐标的上下左右，或者上下左右，左上，左下，右上，右下八个方向进行填充，从而达到填充整个区域的目地。

但是由于在上述的算法中其他的新种子呀进行入栈，就会使得很多用过的种子从新入栈，使效率不高。

所以重新设计了一下算法，采用取一点先横向填充，即(x0,y0)y0,不变x0++或者x0--,在所给定的范围之类填充完了之后再采用y+1，y-1.上下两个方向进行填充。

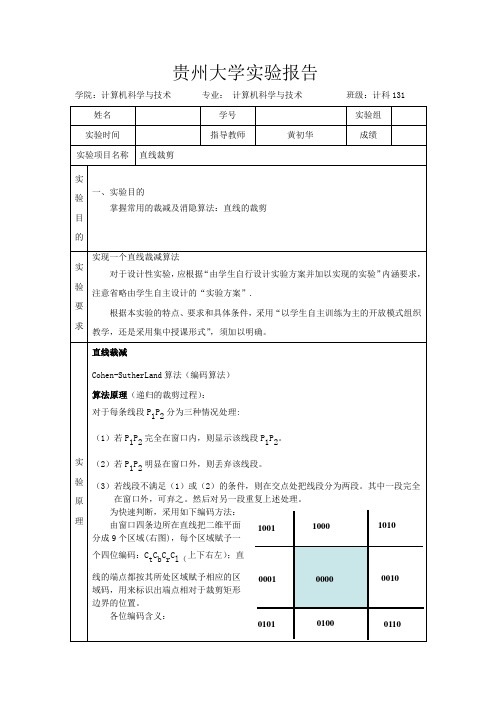
剪裁:选用了Cohe-SutherLand算法，剪裁算法的主体思想是先将整个区域分成9个区域。

如图所示
1001 1000 1010
0001 0000 0010
0101 0100 0110
其中0000里面是所需要的剪裁的部分。

在一条直线在这个区域里面。

它的两个端点将会落在上面的区域中的任何一个区域中。

1) 当线段完全在框里面，取这个两个端点；2) 当这条直线明显在区域外面，则抛弃；3) 如果不满足上面的2个条件，则把线段分成两段，其中一段在外面，则放弃，在里面则保留。

通过上面的标记来判断端点是否在区域里面。

三、算法设计与分析
剪裁：
void COpenglForMFCView::OnAreaCut()
{
// TODO: Add your command handler code here
m_bClip = !m_bClip ;
if( !m_bClip )
return ;
// 直线端点集合数组一定为端点对偶数个点坐标和裁剪准备时数据一致
int nvLines[8][2] = {{0,0},{100,100},{10,201},{-200,-50},{-50,-140},{-50,140},{-80,10},{240,270}};
// 裁剪窗口边界坐标上下左右
int nvClip[4] = {100,-100,-100,100};
// 加入裁剪代码得到最终的直线端点代码存入裁剪后数据集
// 存入的数据位nvLineFinal
int nvLineFinal[8][2] ; //存入最终的剪裁的坐标
// 处理过程
// AfxMessageBox(_T("Please Insert The Clip Code!") );
// 保存过程
vLineFinal.clear() ;
int i = 0 ;
int nValidLineNum = 0 ; // 有效直线端点对数目根据实际情况修改有效坐标Point2D oPtTmp ;
////////////////////////算法填写位置///////////////////////////////////////////////
float x0,y0,x1,y1,left,right,bottom,top,x,y;
int code1,code2,code;
//将存入边界的上下左右的信息
top = nvClip[0];
bottom =nvClip[1];
left = nvClip[2];
right = nvClip[3];
for (i=0;i<8;i+=2)
{
x0 = nvLines[i][0]; //存入任意直线的起点与终点坐标
y0 = nvLines[i][1];
x1 = nvLines[i+1][0];
y1 = nvLines[i+1][1];
encode(x0,y0,&code1,top,right,bottom,left);
encode(x1,y1,&code2,top,right,bottom,left);
while(code1<<1>0||code2<<1>0)
{
if ((code1&code2)<<1>0) break;
code = code1;
if(code1==0) code = code2;
if ((1&code)<<1>0) //1是左边线段与左边界相交
{
x = left;
y = y0 + (y1 - y0)*(left - x0)/(x1-x0);
}
else if((2&code)<<1>0) //2是右边界线段与右边界相交
{
x = right;
y = y0 + (y1 - y0)*(right - x0)/(x1-x0);
}
else if ((4&code)<<1>0) //4是底边界线段与底边界相交
{
y = bottom;
x = x0 + (x1-x0)*(bottom - y0)/(y1-y0);
}
else if ((8&code)<<1>0) //8是顶边界线段与顶边界相交
{
y = top;
x = x0 + (x1-x0)*(top - y0)/(y1-y0);
}
if (code == code1)
{
x0 = x;
y0 = y;
encode(x0,y0,&code1,top,right,bottom,left);
}
else
{
x1 = x;
y1 = y;
encode(x1,y1,&code2,top,right,bottom,left);
}
}
/*oPtTmp.x=x0;
oPtTmp.y=y0;
vLineFinal.push_back(oPtTmp) ;
oPtTmp.x=x1;
oPtTmp.y=y1;
vLineFinal.push_back(oPtTmp) ; */
//if
((x0>left&&x0<right)&&(x1>left&&x1<right)&&(y0>bottom&&y0<top)&&(y1>bottom&&y1<top) )
{
nvLineFinal[nValidLineNum][0] = x0; //将最终的坐标存入数组
nvLineFinal[nValidLineNum][1] = y0;
nvLineFinal[nValidLineNum+1][0] = x1;
nvLineFinal[nValidLineNum+1][1] = y1;
nValidLineNum += 2;
}
}
/////////////////////////////////////////////////////////////////////////////
for( i = 0 ; i < nValidLineNum ; ++i )
{
oPtTmp.x = nvLineFinal[i][0] ;
oPtTmp.y = nvLineFinal[i][1] ;
vLineFinal.push_back(oPtTmp) ;
}
// 将裁剪窗口边界信息保存
vClipWnd.clear() ;
// 左上
oPtTmp.x = nvClip[2] ;
oPtTmp.y = nvClip[0] ;
vClipWnd.push_back(oPtTmp) ;
// 左下
oPtTmp.y = nvClip[1] ;
vClipWnd.push_back(oPtTmp) ;
// 右下
vClipWnd.push_back(oPtTmp) ;
oPtTmp.x = nvClip[3] ;
vClipWnd.push_back(oPtTmp) ;
// 右上
vClipWnd.push_back(oPtTmp) ;
oPtTmp.y = nvClip[0] ;
vClipWnd.push_back(oPtTmp) ;
// 左上
vClipWnd.push_back(oPtTmp) ;
oPtTmp.x = nvClip[2] ;
vClipWnd.push_back(oPtTmp) ;
return ;
}
四、程序调试及结果的分析
五、实验心得及建议
在实验过程中，将画线分成了几个部分。

分别是k为无穷的时候，0<k<=1,k>1,-1<=k<0,k<-1.这几种情况。

采用了分而治之的思想，各个击破。

但是在算法实现中还是遇到了一些困难。

例如对c++的不了解，花费了大量的时间在阅读程序上，还有就不问题考虑的不过全面。

花费了很多时间去了调试，另一个是在细节方面处理得不够好，所画的直线有些地方还是有“折”样。

评语：。