BPSK系统仿真及误码率计算源程序
现代通信原理BPSK仿真实验

通信原理BPSK仿真实验一、实验题目利用仿真软件实现BPSK的调制解调,并仿真分析其在高斯信道下的误码性能。
二、实验原理调制过程:信号的产生采用键控法。
原理:用二进制单极性脉冲控制开关选择0相位载波和π相位载波的输出。
解调过程:相干解调。
必须采用相干解调的方式,从接收到的已调信号中提取本地载波,与信号相乘后通过低通滤波器,抽样判决后得到基带信号。
三、实验仿真1、实验系统2、各模块设置系统时钟设置:Sample Rate:5000Hz Stop Time=1{系统中使用的滤波器为巴特沃斯滤波器}(一)以下四个模块为调制过程,产生BPSK信号。
●模块0:产生频率为50Hz的单极性脉冲,控制开关。
●模块1:开关由单极性脉冲控制对两种相位的正弦波进行选择。
(Gate delay=0 Ctrl thresh=1 ) ●模块2和3:生成正弦波,作为载波。
(二)以下模块主要为从接收到的已调信号中提取本地载波。
●模块25:高斯白噪声(Mean=0v Std Dev=1v)●模块30:放大器:增益Gain=-30dB●模块24:带通滤波器,设置在解调之前。
通带为430-570Hz。
●模块23:幂函数,次数为2,将接收到的以调信号平方。
●模块11:带通滤波器(998-1002Hz;BP Filter Order=3)为获取1000Hz的正弦波●模块10:分频器对输入信号进行2分频,为获取500Hz的正弦波●模块15:带通滤波器(490-510Hz;BP Filter Order=3)为获取500Hz的正弦波作为本地载波。
(三)解调过程和抽样判决●模块9和17:组成解调器。
BPSK信号与本地载波通过乘法器,在经过低通滤波器(60Hz恢复数字基带信号对应的模拟信号。
●模块19:非门,判决作用。
●模块20:采样器,采样频率为50Hz。
●模块21:保持器,采样后经保持器得到恢复的波形。
(四)误码性能分析●模块27:误码率图标(Trails=1000)●模块29:终止符(误码=6个)●模块31:终值显示符●模块32:数字延迟器(Delay:20000)3、系统波形分析及相关参数分析模块4:输入波形模块26:BPSK信号可以看到键控法产生的BPSK信号,第一张图中竖着的白线为相位反相点,在第二张放大后的图中可以清晰的看到信号相位相反的地方。
BPSK通信系统(2024版)

BPSK解 调/判决
低通 滤波
26
接收信号的pdf函数
当发射+1与-1的概率相同时的接收信号pdf函数为:
误码区间
正确判决区间
27
BPSK信号的误码率
发送正信号时,接收信号为
prs1 1N0exp rN 1 02
发送负信号时,接收信号为
prs2 1N0ex prN 0 12
此时判决门限为0
28
判决准则: •发送“+1”信号(记为s1),接收为负信号 接收信号错误 •发送“-1”信号(记为s2) ,接收为正信号 接收信号错误 •否则判决为接收正确
8
成型滤波器:将输入脉冲信号变为Sinc函数输出
sinc函数: g(t) sin(t /T) t /T
t
1.2
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-10
-5
g(t)=sin(pi*t/T)/(pi*t/T)
t
0
5
10
9
成型滤波器:将输入脉冲信号变为Sinc函数输出
sinc函数:
n
信号幅度
sinc函 数 1
0.8
0.6
0.4
0.2
0
-0.2
-0.4 -50 -40 -30 -20 -10
0
10
20
30
40
50
样点
10
实际系统操作-生成脉冲序列
1 0.8 0.6 0.4 0.2
0 -0.2 -0.4 -0.6 -0.8
-1
10
20
30
40
50
60
70
2PSK误码率程序及仿真图讲课教案

clear all;close all;clcframe=10000;t=0:pi/180:2*pi;source_code=randint(1,500);SNR=0:0.25:10;carrier1=sin(2*pi*t);carrier2=sin(2*pi*t+pi);Carrier=[carrier1carrier2];snr=10.^(SNR./10);for loop=1:length(source_code)if source_code(loop)==1modulated_signal(loop,:)=carrier1;elsemodulated_signal(loop,:)=carrier2;endendModulated=reshape(modulated_signal',1,loop*length(carrier1)); Modulated_Information=2*source_code-1;for iteration=1:length(SNR)error=0;for i=1:frameadd_noise=awgn(Modulated_Information,SNR(iteration));for address=1:length(add_noise)if add_noise(address)>0demodulated(address)=1;elsedemodulated(address)=0;endif demodulated(address)~=source_code(address)error=error+1;endendendPe(iteration)=error/frame/length(source_code);Pe_theor=(erfc(sqrt(snr))).*(1-0.5*erfc(sqrt(snr)));endfigure(1)semilogy(SNR,Pe_theor,'Marker','o','Color','r');grid on;hold on; semilogy(SNR,Pe,'Marker','*','Color','b')% axis([snrdB_min snrdB_max 0.0001 1]);xlabel('信噪比');ylabel('误码率');title('BPSK信号最佳接收误码率曲线');legend('理论值','实际值');图4-2 BPSK信号误码率的仿真图function [enc_comp]=cm_dpske(E,M,mapping,sequence);k=log2(M);N=length(sequence);reminder=rem(N,k);if(reminder~=0),for i=N+1:N+k-reminder,sequence(i)=0;end;N=N+k-reminde;endtheta=0;for i=1:k:N,index=0;for j=i:i+k-1,index=2*index+sequence(j);endindex=index+1;theta=mod(2*pi*mapping(index)/M+theta,2*pi);enc_comp((i+k-1)/k,1)=sqrt(E)*cos(theta);enc_comp((i+k-1)/k,2)=sqrt(E)*sin(theta);end============================================== function [p]=cm_sm35(SNRindB)N=2000;E=1;snr=10^(SNRindB/10);sgma=sqrt(E/(4*snr));for i=1:2*N;temp=rand;if(temp<0.5),dsource(i)=0;elsedsource(i)=1;endendmapping=[0 1 3 2];M=4;[diff_enc_output]=cm_dpske(E,M,mapping,dsource);for i=1:N,[gsrv1,gsrv2]=gngauss(sgma);r(i,:)=diff_enc_output(i,:)+[gsrv1,gsrv2];endprev_theta=0;numoferr=0;for i=1:N,theta=angle(r(i,1)+j*r(i,2));delta_theta=mod(theta-prev_theta,2*pi);if((delta_theta<pi/4)|(delta_theta>7*pi/4)),decis=[0 0];elseif(delta_theta<3*pi/4),decis=[0 1];elseif(delta_theta<5*pi/4),decis=[1 1];elsedecis=[1 0];endprev_theta=theta;if((decis(1)~=dsource(2*i-1))|(decis(2)~=dsource(2*i))), numoferr=numoferr+1;end;end;p= numoferr/N;=======================================echo onSNRindB1=0:2:12;SNRindB2=0:0.1:12;for i=1:length(SNRindB1),[pe]=cm_sm35(SNRindB1(i));smld_bit_err_prb(i)=pe;echo off;end;echo on;for i=1:length(SNRindB2),SNR=exp(SNRindB2(i)*log(10)/10);theo_err_prb(i)=Qfunct(sqrt(2*SNR));echo off;end;semilogy(SNRindB2,theo_err_prb);hold onsemilogy(SNRindB1,smld_bit_err_prb,'*');。
bpsk 误码率 matlab

bpsk 误码率 matlab以bpsk误码率为标题的Matlab文章引言:误码率是衡量数字通信系统性能的重要指标之一。
在数字通信中,调制技术起着至关重要的作用,而二进制相移键控(BPSK)调制是最常用的一种调制方式之一。
本文将使用Matlab来计算BPSK调制的误码率,并通过实际案例说明其应用。
一、BPSK调制简介BPSK调制是一种基本的数字调制技术,它将二进制数字序列映射到正弦波的相位上。
在BPSK调制中,二进制1和0分别对应于正弦波的两个不同相位。
具体而言,二进制1对应于正弦波的0度相位,而二进制0对应于正弦波的180度相位。
二、BPSK调制的误码率计算方法误码率是指在接收端解调过程中,接收到的比特错误的概率。
在BPSK调制中,误码率的计算可以通过理论公式或仿真方法来实现。
本文将介绍使用Matlab进行仿真计算的方法。
1.生成随机二进制数据序列我们需要生成随机的二进制数据序列,以模拟实际通信环境中的数据传输。
在Matlab中,可以使用randi函数生成指定长度的随机二进制数据序列。
2.进行BPSK调制生成的随机二进制数据序列需要经过BPSK调制,将其映射到正弦波的相位上。
在Matlab中,可以使用pskmod函数实现BPSK调制。
3.添加高斯噪声为了模拟实际通信环境中的噪声干扰,我们需要向BPSK调制后的信号中添加高斯噪声。
在Matlab中,可以使用awgn函数实现高斯噪声的添加。
4.进行BPSK解调接收端收到经过噪声干扰的信号后,需要进行BPSK解调,将其恢复为二进制数据序列。
在Matlab中,可以使用pskdemod函数实现BPSK解调。
5.计算误码率经过BPSK解调后得到的二进制数据序列与发送端的原始数据序列进行比较,即可计算误码率。
在Matlab中,可以使用biterr函数实现误码率的计算。
三、实例演示下面通过一个实例演示如何使用Matlab计算BPSK调制的误码率。
假设我们要传输长度为10000的二进制数据序列,传输信道为高斯信道。
qpsk、bpsk蒙特卡洛仿真matlab代码

qpsk、bpsk的蒙特卡洛仿真是一种用于测试和验证通信系统性能的重要工具。
通过模拟大量的随机输入数据,并对系统进行多次仿真运算,可以对系统的性能进行全面评估,包括误码率、信噪比要求等。
在matlab中,我们可以通过编写相应的仿真代码来实现qpsk、bpsk 的蒙特卡洛仿真。
下面将分别介绍qpsk和bpsk的蒙特卡洛仿真matlab代码。
一、qpsk的蒙特卡洛仿真matlab代码1. 生成随机的qpsk调制信号我们需要生成一组随机的qpsk调制信号,可以使用randi函数生成随机整数序列,然后将其映射到qpsk符号点上。
2. 添加高斯白噪声在信号传输过程中,会受到各种干扰,其中最主要的干扰之一就是高斯白噪声。
我们可以使用randn函数生成高斯白噪声序列,然后与调制信号相加,模拟信号在传输过程中受到的噪声干扰。
3. 解调和判决接收端需要进行解调和判决操作,将接收到的信号重新映射到qpsk符号点上,并判断接收到的符号与发送的符号是否一致,从而判断是否发生误码。
4. 统计误码率通过多次仿真运算,记录错误判决的次数,从而可以计算出系统的误码率。
二、bpsk的蒙特卡洛仿真matlab代码1. 生成随机的bpsk调制信号与qpsk相似,我们需要先生成一组随机的bpsk调制信号,然后模拟信号传输过程中的噪声干扰。
2. 添加高斯白噪声同样使用randn函数生成高斯白噪声序列,与bpsk调制信号相加。
3. 解调和判决接收端对接收到的信号进行解调和判决,判断接收到的符号是否与发送的符号一致。
4. 统计误码率通过多次仿真运算,记录错误判决的次数,计算系统的误码率。
需要注意的是,在编写matlab代码时,要考虑到信号的长度、仿真次数、信噪比的范围等参数的选择,以及仿真结果的统计分析和可视化呈现。
qpsk、bpsk的蒙特卡洛仿真matlab代码可以通过以上步骤实现。
通过对系统性能进行全面评估,可以帮助工程师优化通信系统设计,提高系统的可靠性和稳定性。
AWGN信道中BPSK调制系统的BER仿真计算

AWGN信道中BPSK调制系统的BER仿真计算AWGN信道中的BPSK(Binary Phase Shift Keying)调制系统的BER (Bit Error Rate)是通过使用仿真计算来估计误码率的。
在这个系统中,0和1两种不同的数字比特被编码成不同的相位,然后通过AWGN信道传输。
在接收端,使用最大似然检测来解调接收到的信号,并将其解调成0或1首先,我们需要确定系统的各个参数。
这些参数包括:1.调制阶数:在BPSK系统中,调制阶数为2,即只有两种可能的相位。
2.信噪比(SNR):SNR是信号功率和噪声功率之间的比值。
在AWGN信道中,SNR可以表示为信号功率与噪声功率之比。
信噪比通常以分贝(dB)表示。
3.误码率(BER):BER是指接收到的比特与发送的比特之间不匹配的概率。
接下来,我们可以通过以下步骤进行BER仿真计算:1.生成随机比特序列:使用随机数生成器来生成0和1的比特序列。
比特序列的长度应与仿真中所希望获得的误码率有关。
2.比特到相位的转换:将生成的比特序列转换为相位序列。
在BPSK系统中,0表示一个相位(例如0度),1表示另一个相位(例如180度)。
3.信号的发送:将相位序列转换为正弦信号,并将其通过AWGN信道发送。
4.加入噪声:在接收端,我们需要给接收信号添加高斯白噪声。
噪声的功率由信噪比决定。
5.信号的接收:接收到的信号将通过最大似然检测进行解调。
解调后的结果将与发送的比特进行比较,并计算错误的个数。
6.误码率计算:通过比较接收到的比特和发送的比特,计算误码率。
将错误的比特数除以总的比特数,即可得到误码率。
在仿真过程中,我们可以通过改变SNR的值来观察BER的变化。
通常,随着SNR的增加,误码率会减小。
这是因为较高的信噪比意味着更强的信号和较少的噪声,从而更容易准确地检测到发送的比特。
最后,我们可以通过绘制BER曲线来直观地表示误码率与SNR之间的关系。
在绘制曲线时,通常使用对数坐标来显示SNR的范围。
BPSK的误比特率性能进行了仿真

本代码对BPSK的误比特率性能进行了仿真,给出了Mente Carlo仿真结果与理论分析结果的对比。
以下是源代码和仿真结果图:%-------------------------------------------------------------------------% Main Program lavabin 2006.07.25%-------------------------------------------------------------------------% % This program is used to get the BPSK BER curve under AWGN condition % % Assuming that Eb = 0% % Theoretical BER = Q(sqrt(2*Eb/No))%-------------------------------------------------------------------------echo offclcclear allclose alltic% ---------------------------------------------------coefNum = 2^16;SNR_in_dB = [0:0.1:10];signalTx = rand(1, coefNum);signalTx(find(signalTx <= 0.5)) = -1;signalTx(find(signalTx > 0.5)) = +1;[Pe] = BPSK_AWGN_Pe(signalTx, SNR_in_dB);for i = 1:length(SNR_in_dB)SNR(i) = 10^(SNR_in_dB(i)/10);Pe_theoretical(i) = qfunc(sqrt(2*SNR(i)));end% ---------------------------------------------------figure(1);grid onsemilogy(SNR_in_dB, Pe,'go-');hold onsemilogy(SNR_in_dB, Pe_theoretical,'r*-');legend('Pe Actual','Pe Theoretical');title('BPSK BER Performance Evaluation');xlabel('Eb/No');ylabel('BPSK BER');% ---------------------------------------------------echo onsimulation_time = toc%-------------------------------------------------------------------------% End of Function%-------------------------------------------------------------------------%--------------------------------------------------------------------------%% Avetis Ioannisyan% 10/26/05%--------------------------------------------------------------------------% Given desired SNR and the input signal, function outputs prob of error % occuring in AWGN environment such that N(0, No/2). The input signal is% modulated digital using ASK with amplitude -1 and +1%% Example:% coefNum = 2^17;% SNR = [0:0.1:10];%% signalTx = rand(1, coefNum);% signalTx(find(signalTx <= 0.5)) = -1;% signalTx(find(signalTx > 0.5)) = +1;%% [Pe] = BPSK_AWGN_Pe(signalTx, SNR);%% semilogy(SNR, Pe);%-------------------------------------------------------------------------% lavabin 2006.07.25%-------------------------------------------------------------------------function [Pe] = BPSK_AWGN_Pe(signalTx, SNR)% number of coef to generate (length)coefNum = length(signalTx);N0=[]; AWGN=[]; Pe=[]; signalRx=[];% create white noise N(0, 0.5)randn('state',sum(100*clock));% % Reset randomizer% % ------------------------------------------------------------% % Return RANDN to its default initial state.% % randn('state',0)% % ------------------------------------------------------------% % Initialize RANDN to a different state each time.% % randn('state',sum(100*clock))% % ------------------------------------------------------------ AWGN = randn(length(SNR), coefNum);% Construction of AWGN Matrixfor i = 1:length(SNR)% make noise level from specified SNR: No = 1/(10^(SNR/10)) assuming Eb=1N0(i) = 1/(10^(SNR(i)/10)); %generate No, or, sqrt(variance) = No for the WGN noise% adjust for the desired N(0,No/2) => X = mue + sqrt(var)*N(0, 0.5) AWGN(i,:) = sqrt(N0(i)./2) .* AWGN(i,:);% produce received signalsignalRx(i,:) = signalTx + AWGN(i,:);% perform signal detectionsignalRx(i, find(signalRx(i,:) <= 0)) = -1;signalRx(i, find(signalRx(i,:) > 0)) = +1;% estimate error probabilityerror = length(find(signalRx(i,:)-signalTx));Pe(i) = error / coefNum;end%-------------------------------------------------------------------------% End of Function%-------------------------------------------------------------------------下面是图形结果:。
BPSK调制解调及误码率的计算

BPSK调制解调及误码率的计算BPSK (Binary Phase Shift Keying) 是一种基本的数字调制技术,常用于数字通信系统中。
它通过将数字信号映射为相位上的两个值来进行调制,并使用相干解调器进行解调。
本文将介绍BPSK调制解调的原理以及如何计算误码率。
1.BPSK调制原理:在BPSK调制中,每个二进制位(0或1)被映射为两个可能的相位值:0对应于0度相位,1对应于180度相位。
这种相位差可以通过正弦和余弦函数来实现。
-二进制信息序列被输入到调制器中。
-调制器将二进制位转换为相位值,0对应于0度相位,1对应于180度相位。
-经过调制的信号通过信道传输。
2.BPSK解调原理:BPSK解调器的任务是将传输信号恢复为原始的二进制序列。
当信号通过信道传输后,可能会受到噪声和其他干扰的影响,从而导致误码的产生。
BPSK解调的过程如下:-接收到的信号经过信道传输后,会受到噪声和其他干扰的影响,使信号的相位发生随机的偏移。
-解调器使用相干解调的方法测量接收信号的相位。
-根据测量到的相位值,解调器将信号恢复为原始的二进制序列。
3.误码率的计算方法:误码率是衡量通信系统性能的重要指标,它表示在传输过程中发生误码的概率。
对于BPSK调制,误码率的计算可以通过理论分析或仿真实验进行。
理论分析方法:在BPSK调制中,误码率的理论计算可以使用误码率表达式得到。
对于理想的信道,没有噪声和干扰,误码率的表达式为:P_e = Q(sqrt(2*Eb/N0))其中,Eb/N0表示信噪比,Q(x)为高斯函数。
对于有噪声和干扰的实际信道,可以根据信号接收的信噪比进行实际误码率的计算。
仿真实验方法:使用计算机仿真软件,可以模拟BPSK调制解调系统,并通过对大量的二进制序列进行模拟传输和解调,统计接收到的误码数量来计算误码率。
误码率的计算通过测量接收信号中发生错误的比特数与总传输的比特数之比得到。
它通常以对数的形式表示,即以dB为单位。
2PSK误码率程序及仿真图

close all;clcframe=10000;t=0:pi/180:2*pi;source_code=randint(1,500);SNR=0:0.25:10;carrier1=sin(2*pi*t);carrier2=sin(2*pi*t+pi);Carrier=[carrier1carrier2];snr=10.^(SNR./10);for loop=1:length(source_code)if source_code(loop)==1modulated_signal(loop,:)=carrier1;elsemodulated_signal(loop,:)=carrier2;endendModulated=reshape(modulated_signal',1,loop*length(carrier1)); Modulated_Information=2*source_code-1;for iteration=1:length(SNR)error=0;for i=1:frameadd_noise=awgn(Modulated_Information,SNR(iteration));for address=1:length(add_noise)if add_noise(address)>0demodulated(address)=1;elsedemodulated(address)=0;endif demodulated(address)~=source_code(address)error=error+1;endendPe(iteration)=error/frame/length(source_code);Pe_theor=(erfc(sqrt(snr))).*(1-0.5*erfc(sqrt(snr)));endfigure(1)semilogy(SNR,Pe_theor,'Marker','o','Color','r');grid on;hold on; semilogy(SNR,Pe,'Marker','*','Color','b')% axis([snrdB_min snrdB_max 0.0001 1]);xlabel('信噪比');ylabel('误码率');title('BPSK信号最佳接收误码率曲线');legend('理论值','实际值');图4-2 BPSK信号误码率的仿真图function [enc_comp]=cm_dpske(E,M,mapping,sequence);k=log2(M);N=length(sequence);reminder=rem(N,k);if(reminder~=0),for i=N+1:N+k-reminder,sequence(i)=0;end;N=N+k-reminde;endtheta=0;for i=1:k:N,index=0;for j=i:i+k-1,index=2*index+sequence(j);endindex=index+1;theta=mod(2*pi*mapping(index)/M+theta,2*pi);enc_comp((i+k-1)/k,1)=sqrt(E)*cos(theta);enc_comp((i+k-1)/k,2)=sqrt(E)*sin(theta);end============================================== function [p]=cm_sm35(SNRindB)N=2000;E=1;snr=10^(SNRindB/10);sgma=sqrt(E/(4*snr));for i=1:2*N;temp=rand;if(temp<0.5),dsource(i)=0;elsedsource(i)=1;endendmapping=[0 1 3 2];M=4;[diff_enc_output]=cm_dpske(E,M,mapping,dsource);for i=1:N,[gsrv1,gsrv2]=gngauss(sgma);r(i,:)=diff_enc_output(i,:)+[gsrv1,gsrv2];endprev_theta=0;numoferr=0;for i=1:N,theta=angle(r(i,1)+j*r(i,2));delta_theta=mod(theta-prev_theta,2*pi);if((delta_theta<pi/4)|(delta_theta>7*pi/4)),decis=[0 0];elseif(delta_theta<3*pi/4),decis=[0 1];elseif(delta_theta<5*pi/4),decis=[1 1];elsedecis=[1 0];endprev_theta=theta;if((decis(1)~=dsource(2*i-1))|(decis(2)~=dsource(2*i))), numoferr=numoferr+1;end;end;p= numoferr/N;=======================================echo onSNRindB1=0:2:12;SNRindB2=0:0.1:12;for i=1:length(SNRindB1),[pe]=cm_sm35(SNRindB1(i));smld_bit_err_prb(i)=pe;echo off;end;echo on;for i=1:length(SNRindB2),SNR=exp(SNRindB2(i)*log(10)/10);theo_err_prb(i)=Qfunct(sqrt(2*SNR));echo off;end;semilogy(SNRindB2,theo_err_prb);hold onsemilogy(SNRindB1,smld_bit_err_prb,'*');。
PSK理论误码率与实际误码率MATLAB仿真程序

PSK理论误码率与实际误码率MATLAB仿真程序%%pskclc;clear all;close all;nsymbol = 1e6;%%每种信噪比下符号数的发送符号数data = randint(1,nsymbol,[0,1]);%%产生1行,nsymbol列均匀分布的随机数0,1bpsk_mod = 2*data-1;%%调制,0转化为-1;1转化为1spow = norm(bpsk_mod).^2/nsymbol;%%求每个符号的平均值,其中norm是求向量2范数函数SNR_dB = 1:10;%%%信噪比dB形式SNR = 10.^(SNR_dB/10);%%信噪比转化为线性值for loop= 1:length(SNR)sigma = sqrt(spow/(2*SNR(loop)));%%%根据符号功率求噪声功率s_receive = bpsk_mod+sigma*(randn(1,length(bpsk_mod))+j*randn(1,lengt h(bpsk_mod)));%%添加复高斯白噪声bpsk_demod = (real(s_receive)>0);%%%解调data_receive=double(bpsk_demod);%%接收数据,转化为[err,ser(loop)] = symerr(data,data_receive);%误码率endser_theory = qfunc(sqrt(2*SNR));%理论误码率,注意Q函数和误差函数的对应关系semilogy(SNR_dB,ser,'-k*',SNR_dB,ser_theory,'-bo');title('BPSK信号在AWGN信道下的性能');xlabel('信噪比/dB');ylabel('误码率');legend('误码率','理论误码率');grid on;。
(完整版)PSK理论误码率与实际误码率MATLAB仿真程序

%%pskclc;clear all;close all;nsymbol = 1e6;%%每种信噪比下符号数的发送符号数data = randint(1,nsymbol,[0,1]);%%产生1行,nsymbol列均匀分布的随机数0,1bpsk_mod = 2*data-1;%%调制,0转化为-1;1转化为1spow = norm(bpsk_mod).^2/nsymbol;%%求每个符号的平均值,其中norm是求向量2范数函数SNR_dB = 1:10;%%%信噪比dB形式SNR = 10.^(SNR_dB/10);%%信噪比转化为线性值for loop= 1:length(SNR)sigma = sqrt(spow/(2*SNR(loop)));%%%根据符号功率求噪声功率s_receive = bpsk_mod+sigma*(randn(1,length(bpsk_mod))+j*randn(1,length(bpsk_mod)));%%添加复高斯白噪声bpsk_demod = (real(s_receive)>0);%%%解调data_receive=double(bpsk_demod);%%接收数据,转化为[err,ser(loop)] = symerr(data,data_receive);%误码率endser_theory = qfunc(sqrt(2*SNR));%理论误码率,注意Q函数和误差函数的对应关系semilogy(SNR_dB,ser,'-k*',SNR_dB,ser_theory,'-bo');title('BPSK信号在AWGN信道下的性能');xlabel('信噪比/dB');ylabel('误码率');legend('误码率','理论误码率');grid on;。
完整word版,PSK理论误码率与实际误码率MATLAB仿真程序

%%pskclc;clear all;close all;nsymbol = 1e6;%%每种信噪比下符号数的发送符号数data = randint(1,nsymbol,[0,1]);%%产生1行,nsymbol列均匀分布的随机数0,1bpsk_mod = 2*data-1;%%调制,0转化为-1;1转化为1spow = norm(bpsk_mod).^2/nsymbol;%%求每个符号的平均值,其中norm是求向量2范数函数SNR_dB = 1:10;%%%信噪比dB形式SNR = 10.^(SNR_dB/10);%%信噪比转化为线性值for loop= 1:length(SNR)sigma = sqrt(spow/(2*SNR(loop)));%%%根据符号功率求噪声功率s_receive = bpsk_mod+sigma*(randn(1,length(bpsk_mod))+j*randn(1,length(bpsk_mod)));%%添加复高斯白噪声bpsk_demod = (real(s_receive)>0);%%%解调data_receive=double(bpsk_demod);%%接收数据,转化为[err,ser(loop)] = symerr(data,data_receive);%误码率endser_theory = qfunc(sqrt(2*SNR));%理论误码率,注意Q函数和误差函数的对应关系semilogy(SNR_dB,ser,'-k*',SNR_dB,ser_theory,'-bo');title('BPSK信号在AWGN信道下的性能');xlabel('信噪比/dB');ylabel('误码率');legend('误码率','理论误码率');grid on;。
实验4-BPSK调制解调仿真精选全文完整版

可编辑修改精选全文完整版实验四BPSK调制解调仿真【实验目的】加深移动通信系统中调制解调的理解;能够使用 Matlab(或者 C 语言)进行通信系统调制解调基带仿真,并进行性能分析;【实验内容】使用 Matlab (或者 C 语言)仿真 BPSK调制解调(只能相干解调)过程;比较发送端星座图以及不同信噪比下接收端星座图的不同;仿真 AWGN 信道下 BPSK的误码率;【实验设备】一台PC机【实验步骤】1.产生发送信息比特;2.对信息比特进行 BPSK调制;3.将 BPSK调制后的发送信号经过 AWGN 信道,从而获得接收信号波形;4.比较发送端星座图以及不同信噪比下接收端星座图的不同;5.对接收信号进行 BPSK解调;6.通过蒙特卡洛方法,仿真系统误码率,画出 BPSK调制解调误码率曲线。
【实验报告】按照要求完成实验报告。
实验报告中要求给出不同信噪比条件下(信噪比分别为-5dB,0dB,5dB,10dB)接收端的星座图。
画出AWGN 信道下 BPSK调制解调误码率曲线。
一、仿真程序及说明clc;clear all ;n=1000;SNR=[-5 0 5 10];source=randint(1,n);In_BPSK=source*2-1;for i=1:length(SNR)Y(i,:)=AWGN(In_BPSK,SNR(i));endY_RE=Y;Y_RE(find(Y>0))=1;Y_RE(find(Y<0))=0;for i=1:length(SNR)Y_ERRO(i,:)=abs(Y_RE(i,:)-source)Y_BIT(i)=sum(Y_ERRO(i,:))/n/误码率 = 错误码元数 / 传输总码元数endsemilogy(SNR,Y_BIT);grid on ;title(' 误码率' );figuresubplot(4,1,1);plot(Y(1,:),0,'*');title('SNR=-5dB');subplot(4,1,2);plot(Y(2,:),0,'*');title('SNR=0dB');subplot(4,1,3);plot(Y(3,:),0,'*');title('SNR=5dB')subplot(4,1,4);plot(Y(4,:),0,'*');title('SNR=10dB');二、总结通过这次试验,巩固的BPSK调制解调以及星座图的知识,也让我们对于不同性噪比下系统性能的优异有了更深的认识。
BPSK系统仿真—MATLAB

程序代码:主程序:%基带信号s(t)clear allclose allclcnum=10; %码元个数tnum=200;%码元长度N=num*tnum;a=randint(1,num,2); %产生1行num列的矩阵,矩阵内0和1随机出现fc=0.1; %载波频率t=0:0.05:9.99;s=[];c=[];for i=1:numif(a(i)==0)A=zeros(1,tnum);elseA=ones(1,tnum);ends=[s A];cs=sin(2*pi*fc*t);c=[c cs]; %产生载波信号endfigure(1);subplot(4,1,1);plot(s);grid on;xlabel('基带信号s(t)');axis([0 N -2 2]);%BPSK已调信号。
采用模拟调制方法s_NRZ=[];for i=1:numif(a(i)==0)A=ones(1,tnum);elseA=-1*ones(1,tnum);ends_NRZ=[s_NRZ,A];ende=s_NRZ.*c;figure(1);subplot(4,1,2);plot(e);grid on;xlabel('BPSK调制信号');axis([0 N -2 2]);%加高斯噪声am=0.7; %输入信号经信道后振幅由1衰减为0.7SNR=5;snr=10^(SNR/10);N0=(am*am)/2/snr;%计算噪声功率N0_db=10*log10(N0);%将噪声功率转换为dBWni=wgn(1,N,N0_db);% 产生1行N列的高斯噪声yi=e+ni;%BSK已调信号中加入白噪声,输入信噪比为SNRfigure(1);subplot(4,1,3);plot(yi);grid on;xlabel('加入高斯白噪声的已调信号yi(t)');% %带通滤波器[b1,a1] = BUTTER(3,[2*pi*0.0001,2*pi*0.01]);%计算带通滤波器的H(z)系数y=filter(b1,a1,yi);%对信号yi进行滤波,得到信号yfigure(1);subplot(4,1,4);plot(y);grid on;xlabel('经带通滤波器后信号');%与恢复载波相乘x1=2*c.*y;figure(2);subplot(4,1,1);plot(x1);grid onxlabel('与恢复载波相乘后的信号x1(t)');%低通滤波器[b2,a2]=butter(2,0.005); %计算H(z)系数,频率为(1/200)x=filter(b2,a2,x1); %对信号x1滤波,得到信号xfigure(2);subplot(4,1,2);plot(x);grid onaxis([0 N -2 2]);xlabel('经低通滤波器后信号波形')x=fun_panjue(x);%调用函数,进行抽样判决figure(2);subplot(4,1,3);plot(x);grid on;xlabel('加噪后解调信号x(t)');axis([0 N -2 2]);x=fun_yanc(x); %调用函数,进行消除延迟figure(2);subplot(4,1,4);plot(x);grid on;xlabel('加噪后去掉延迟的解调信号x(t)');axis([0 N -2 2]);%误码率计算Err1=length(find(x~=s))%计算解调信号中错误码元个数Pe_test1=Err1/N%计算实际误码率Pe1=(1/2)*erfc(sqrt(snr))%计算系统理论误码率%% 理论误码率曲线Pe=[];for SNR=1:10am=0.7; %输入信号经信道后振幅由1衰减为0.7E=am*am/2;snr=10^(SNR/10);N0=(am*am)/(2*snr);no=N0/(2*200); %计算噪声功率N0_db=10*log10(N0);%将噪声功率转换为dBWni=wgn(1,N,N0_db);% 产生1行N列的高斯噪声yi=e+ni; %BSK已调信号中加入白噪声,输入信噪比为SNRy=filter(b1,a1,yi);%对yi进行滤波(带通滤波器),得到信号yx1=2*c.*y; %与恢复载波相乘xx=filter(b2,a2,x1); %经低通滤波器滤波xx=fun_panjue(xx);%抽样判决xx=fun_yanc(xx); %消除延迟snr=10^(SNR/10);Pe=[Pe,(1/2)*erfc(sqrt(snr))];%计算理论误码率endPe;figure;SNR=1:10;semilogy(SNR,Pe,'b--');hold on %以log10(Pe)为纵坐标画图grid on子程序一:抽样判决(由于存在“倒pi”现象,故以0为基准进行判决,大于0,判为0;小于0,判为1)function w=fun_panjue(w)N=length(w);if w(100)>0w(1:100)=0;elsew(1:100)=1;endfor i=101:Nif w(i)>0;w(i)=0;elsew(i)=1;endend子函数二:消除延迟(由于抽样判决后会产生延迟,故认为对解调信号进行时移,以减小甚至消除延迟,便于与基带信号进行比较,计算实际误码率)function m=fun_yanc(m)N=length(m);leng=0;for i=1:Nif m(i)==1leng=i;break;endendelsefor i=1:Nif m(i)==0leng=i;break;endendendleng1=leng-(floor(leng/200))*200; for i=1:(N-leng1)m(i)=m(i+leng1);endfor i=(N-leng1):Nm(i)=m(N-200+10);end输入信噪比为5 dB时,计算的错误码元,实际误码率,理论误码率Err1 =15Pe_test1 =0.0075Pe1 =0.0060各波形图如下所示:。
BPSK扩频误码率matlab仿真
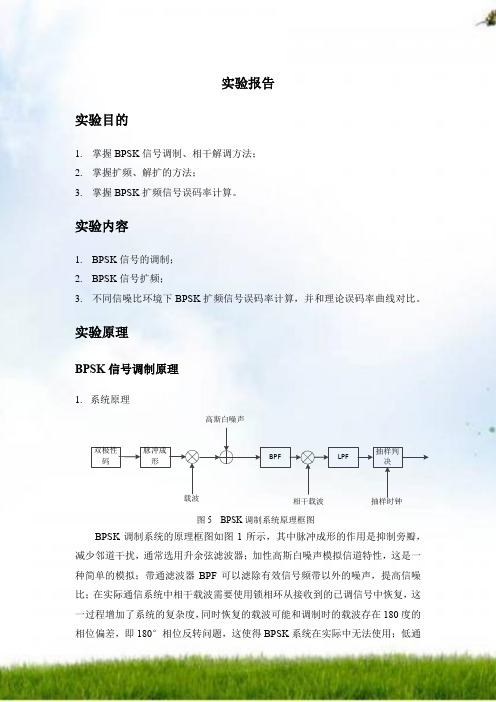
实验报告实验目的1.掌握BPSK信号调制、相干解调方法;2.掌握扩频、解扩的方法;3.掌握BPSK扩频信号误码率计算。
实验内容1.BPSK信号的调制;2.BPSK信号扩频;3.不同信噪比环境下BPSK扩频信号误码率计算,并和理论误码率曲线对比。
实验原理BPSK信号调制原理1.系统原理双极性码脉冲成形BPF LPF抽样判决载波高斯白噪声图5 BPSK调制系统原理框图BPSK调制系统的原理框图如图1所示,其中脉冲成形的作用是抑制旁瓣,减少邻道干扰,通常选用升余弦滤波器;加性高斯白噪声模拟信道特性,这是一种简单的模拟;带通滤波器BPF可以滤除有效信号频带以外的噪声,提高信噪比;在实际通信系统中相干载波需要使用锁相环从接收到的已调信号中恢复,这一过程增加了系统的复杂度,同时恢复的载波可能和调制时的载波存在180度的相位偏差,即180°相位反转问题,这使得BPSK系统在实际中无法使用;低通滤波器LPF 用于滤除高频分量,提高信噪比;抽样判决所需的同步时钟需要从接收到的信号中恢复,即码元同步,判决门限跟码元的统计特性有关,但一般情况下都为0。
2. 参数要求码元速率1000波特,载波频率4KHz ,采样频率为16KHz 。
BPSK 信号扩频原理通信理论和通信技术的研究,是围绕着通信系统的有效性和可靠性这两个基本问题展开的,所以有效性和可靠性是设计和评价一个通信系统的主要性能指标。
通信系统的有效性,是指通信系统传输信息效率的高低。
这个问题是讨论怎样以最合理、最经济的方法传输最大数量的信息。
在模拟通信系统中,多路复用技术可提高系统的有效性。
显然,信道复用程度越高,系统传输信息的有效性就越好。
在数字通信系统中,由于传输的是数字信号,因此传输的有效性是用传输速率来衡量的。
通信系统的可靠性,是指通信系统可靠地传输信息。
由于信息在传输过程中受到干扰,收到的信息和发出的信息并不完全相同。
可靠性就是用来衡量收到信息和发出信息的符合程度。
BPSK调制解调及误码率的计算

%随机产生码元clcclear allnum=10;%码元个数ek=round(rand(1,num,1));%产生载波t=0:2*pi/999:2*pi;%周期num1=1000;%个数len=length(t);c=-sin(t);%调制ektemp=[];ctemp=[];for n=1:numif ek(n)==0ctemp=[ctemp,-c];a=zeros(1,len);ektemp=[ektemp,a];elseif ek(n)==1ctemp=[ctemp,c];a=ones(1,len);ektemp=[ektemp,a];endendsubplot(2,1,1); %分别画出原信号、已调信号示意plot(ektemp,'LineWidth',1.5);title('原码元');grid on;axis([0 num1*num -2.5 2.5]);subplot(2,1,2);plot(ctemp,'LineWidth',1.5);title('已调信号');grid on;axis([0, num1*num, -2.5, 2.5]);%相干解调%本地载波loca=[];for n=1:numloca=[loca,c];%此处c的正负决定解调后是否倒pi endlocb=loca;%相乘locc=2*ctemp.*locb;%低通滤波器[b,a] = BUTTER(3,2*pi*0.0003,'low'); %信号频率为0.001locd=filter(b,a,locc);%低通滤波后的信号figure;subplot(2,1,1); %相乘后的波形plot(locc,'LineWidth',1.5);title('相乘后的信号');grid on;axis([0 num1*num -2.5 2.5 ]);dd=locd+randn(1,10000);%低通滤波后的信号波形图subplot(2,1,2);plot(dd,'LineWidth',1.5);title('低通滤波后的信号');grid on;axis([0 num1*num -2.5 2.5 ]);%抽样判决for i=1:num1*numif(locd(i)>0) %判决,得到解调结果locd(i)=1;elselocd(i)=-1;endendfigure;subplot(2,1,1); %分别画出原信号、解调后信号示意plot(ektemp,'LineWidth',1.5);title('原码元')grid on;axis([0 num1*num -2.5 2.5]);subplot(2,1,2);plot(locd,'LineWidth',1.5);title('解调后的信号');grid on;axis([0 num1*num -2.5 2.5 ]);p=symerr(ektemp,locd)/10 %误码率%误码率曲线figure(4)r=0:2:10;rr=10.^(r/10);pe1=1/2*exp(-rr);%相干解调的误码率曲线hold onplot(r,pe1,'r');grid on;pe2=(1-1/2*erfc(sqrt(rr))).*erfc(sqrt(rr));%差分相干解调的误码率曲线plot(r,pe2,'b');xlabel('bpsk,dpsk误码率曲线'); set(gca,'XTick',-6:3:18);。
