GMM_EM_混合高斯模型及其求解应用
高斯混合模型中的参数估计与EM算法详解

高斯混合模型中的参数估计与EM算法详解高斯混合模型(Gaussian Mixture Model,GMM)是一种常用的概率统计模型,用于描述由多个高斯分布构成的数据集。
在实际应用中,参数估计是使用GMM的关键步骤之一,而期望最大化(Expectation Maximization,EM)算法是一种常用的参数估计方法。
本文将详细介绍GMM的参数估计方法与EM算法的原理。
首先,我们需要理解高斯混合模型。
GMM是由多个高斯分布组合而成的概率分布模型。
每个高斯分布称为一个分量,是由均值、方差和权重组成的。
其中,均值表示分量的中心位置,方差表示分量的散布程度,权重表示每个分量在整个数据集中的相对重要性。
在GMM中,参数估计的目标是通过已知的数据集,估计出每个分量的均值、方差和权重。
而EM算法是实现这一目标的一种迭代优化算法。
EM算法的基本思想是通过迭代更新,不断提高参数估计的准确性。
具体而言,EM算法包含两个主要步骤:E步和M步。
在E步中,我们根据当前估计的参数值,计算每个样本属于各个分量的概率。
这个过程可以通过贝叶斯公式计算得到。
具体地,对于每个样本,我们根据当前的均值、方差和权重计算它属于每个分量的概率,并将其归一化,以保证所有样本在各个分量上的概率和为1。
在M步中,我们利用已经计算得到的样本属于各个分量的概率,更新参数的值。
具体而言,我们首先计算每个分量所占的样本的比例,即权重的估计值。
然后,对于每个分量,我们根据样本的加权平均值和方差来估计其均值和方差。
这里的权重就是E步中计算得到的样本属于各个分量的概率。
通过反复执行E步和M步,可以逐渐提高参数估计的准确性,直到满足停止准则为止。
通常情况下,停止准则可以是迭代次数达到一定阈值,或是参数变化的绝对值小于某个设定的阈值。
在实际应用中,选择适当的初始参数值对于EM算法的收敛至关重要。
一种常用的初始化方法是使用K-means算法来得到初始的均值估计。
具体而言,我们先用K-means算法将数据集聚类成K个簇,然后使用每个簇的中心作为每个分量的初始均值。
EM算法用于高斯混合模型

EM算法用于高斯混合模型高斯混合模型(Gaussian Mixture Model,简称GMM)是一种常用的概率密度估计方法,其基本思想是将数据分解为由多个高斯分布组成的混合模型。
每个高斯分布对应于数据中的一个潜在类别,而混合系数则表示每个类别的权重。
GMM的参数估计通常使用期望最大化(Expectation Maximization,简称EM)算法来进行。
EM算法是一种迭代优化算法,用于求解含有隐变量的最大似然估计问题。
GMM中,EM算法被用来最大化对数似然函数,从而估计GMM的参数。
EM算法的基本思想是,在每一次迭代中,先进行E步(Expectation),计算隐变量在给定参数下的后验概率。
然后进行M步(Maximization),通过极大化对数似然函数来估计参数。
重复执行E步和M步,直到收敛为止。
在GMM中,E步计算的是隐藏变量对应的后验概率,即每个样本属于每个高斯分布的概率。
这个概率可以使用贝叶斯公式计算得到。
假设有N个样本,K个高斯分布,那么对于每个样本i和高斯分布j,可以计算其后验概率:$$w_{ij} = \frac{\pi_j \cdot \mathcal{N}(x_i,\mu_j,\Sigma_j)}{\sum_{k=1}^{K} \pi_k \cdot \mathcal{N}(x_i,\mu_k,\Sigma_k)}$$其中,$w_{ij}$表示样本i属于高斯分布j的后验概率,$\pi_j$表示高斯分布j的混合系数,$\mathcal{N}(x_i,\mu_j,\Sigma_j)$表示高斯分布j的概率密度函数。
在M步中,需要利用E步计算得到的后验概率,更新GMM的参数。
更新过程分两步进行:首先,根据后验概率的加权平均来更新混合系数,即每个高斯分布对应的权重;然后,根据后验概率的加权平均来更新高斯分布的均值和协方差矩阵。
混合系数的更新可以通过对每个高斯分布的后验概率求平均得到:$$\pi_j = \frac{1}{N} \sum_{i=1}^{N} w_{ij}$$高斯分布的均值和协方差矩阵的更新可以通过将样本加权平均来得到:$$\mu_j = \frac{1}{\sum_{i=1}^{N} w_{ij}} \sum_{i=1}^{N} w_{ij} \cdot x_i$$$$\Sigma_j = \frac{1}{\sum_{i=1}^{N} w_{ij}} \sum_{i=1}^{N}w_{ij} \cdot (x_i - \mu_j)(x_i - \mu_j)^T$$重复执行E步和M步,直到收敛为止。
机器学习算法总结(六)——EM算法与高斯混合模型

机器学习算法总结(六)——EM算法与⾼斯混合模型 极⼤似然估计是利⽤已知的样本结果,去反推最有可能(最⼤概率)导致这样结果的参数值,也就是在给定的观测变量下去估计参数值。
然⽽现实中可能存在这样的问题,除了观测变量之外,还存在着未知的隐变量,因为变量未知,因此⽆法直接通过最⼤似然估计直接求参数值。
EM算法是⼀种迭代算法,⽤于含有隐变量的概率模型的极⼤似然估计,或者说是极⼤后验概率估计。
1、经典的三硬币模型 引⼊⼀个例⼦来说明隐变量存在的问题。
假设有3枚硬币,分别记作A,B,C。
这些硬币正⾯出现的概率分别是π,p,q。
我们的实验过程如下,先投掷硬币A,根据其结果选出硬币B和硬币C,正⾯选B,反⾯选C;然后投掷选出的硬币,此时出现正⾯记作1,出现反⾯记作0。
在这个例⼦中我们观察到的变量只是B或者C的结果,⽽对A的结果并不知道,在这⾥A的结果也就是我们的隐变量。
A的结果对最终的结果是有影响的,因此在估计参数时必须将A的结果考虑进去。
1、EM算法 我们将观测变量表⽰为Y = (Y1,Y2,....,Y n),隐变量表⽰为Z = (Z1,Z2,....,Z n),则观测数据的似然函数可以表⽰为 在这⾥P(Y|θ) 是P(Y, Z|θ) 的边缘概率,通过转换后可以表⽰成右边的形式,我们将其转换成对数形式,这样便于求联合概率 然⽽对于这样的式⼦直接根据极⼤化求θ的值是很困难的,因为这⾥还存在隐变量Z,在这⾥引⼊EM算法,通过迭代求解,假设在第i 次迭代后θ的估计值为θ(i)。
我们希望新估计值能是L(θ)增加,通过迭代逐步的达到最⼤值。
为此我们考虑第i+1步迭代后两者的差: 利⽤Jensen不等式将上述式⼦展开并得到其下界(对数函数是凹函数): 令 则有 在这⾥B(θ, θ(i)) 是L(θ) 的⼀个下界,⽽且由的表达式可知 因此任何能使得B(θ, θ(i)) 增⼤的θ,也能使得L(θ) 增⼤。
因此求θ值使得B(θ, θ(i)) 增⼤就可以转变成求θ使得L(θ) 增⼤,即求 将上述式⼦展开可得(在这⾥去掉常数项,因为常数项不会影响最终的结果) 因此问题就演变成了求Q函数的极⼤化。
EM算法用于高斯混合模型

EM算法用于高斯混合模型EM算法(Expectation-Maximization algorithm)是一种迭代算法,用于估计含有隐变量的概率模型参数。
它被广泛应用于高斯混合模型(Gaussian Mixture Model,GMM)的参数估计。
GMM 是一种概率模型,它由若干个高斯分布组成,每个高斯分布对应数据的一个分量。
具体来说,EM算法包含两个步骤:E步骤(Expectation step)和M步骤(Maximization step)。
在E步骤中,给定当前参数估计,我们计算隐变量的期望值。
而在M步骤中,根据这些隐变量的期望值,我们重新估计参数。
这两个步骤会反复迭代,直到参数收敛为止。
首先,我们来看E步骤。
在GMM中,每个观测值都可以由多个高斯分布生成。
我们需要计算每个数据点属于每个高斯分布的后验概率。
这个后验概率可以表示为每个高斯分布生成一些数据点的概率除以所有高斯分布生成这个数据点的概率之和。
这个后验概率即为数据点属于每个高斯分布的权重。
计算后验概率的方法是使用贝叶斯公式。
然后,我们来看M步骤。
在M步骤中,我们根据E步骤计算得到的后验概率,重新估计高斯分布的参数。
具体来说,对于每个高斯分布,我们计算其均值和协方差矩阵。
均值可以通过将数据点乘以其对应的后验概率,再除以所有后验概率之和来计算。
协方差矩阵可以通过计算每个数据点与对应高斯分布的均值之间的差的外积,再乘以其对应的权重,最后除以所有权重之和来计算。
在每次迭代中,E步骤和M步骤会交替进行,直到算法收敛。
算法的收敛条件可以选择参数变化的很小或达到一定的迭代次数。
在每次迭代中,EM算法会逐渐提高对数据的拟合程度,也就是逐渐改善参数的估计。
EM算法有很多优点。
首先,它是一种通用的算法,适用于各种类型的概率模型估计。
其次,EM算法在估计参数时可以有很大的灵活性,可以根据需求自定义参数的个数和选择去模型每个分量的数据。
此外,EM 算法收敛到局部最优,而跳出局部最优通常需要全局优化方法。
高斯混合模型(转)

⾼斯混合模型(转)混合⾼斯模型的原理说⽩了就⼀句话:任意形状的概率分布都可以⽤多个⾼斯分布函数去近似。
换句话说,⾼斯混合模型(GMM)可以平滑任意形状的概率分布。
其参数求解⽅法⼀般使⽤极⼤似然估计求解,但使⽤极⼤似然估计法往往不能获得完整数据(⽐如样本已知,但样本类别(属于哪个⾼斯分布)未知),于是出现了EM(最⼤期望值)求解⽅法。
虽然上⾯说的简单,但是混合⾼斯模型和EM求解的理论还是⽐较复杂的,我把我所找到的我认为能够快速掌握⾼斯混合模型的资料打包到了附件中,⼤家可以去下载,了解混合⾼斯模型以及EM的完整推导过程。
附件下载地址:⼤致抽取下⾼斯混合模型的重要概念:1)任意数据分布可⽤⾼斯混合模型(M个单⾼斯)表⽰((1)式)(1)其中:(2)(3)表⽰第j个⾼斯混合模型2)N个样本集X的log似然函数如下:(4)其中:参数:,(5)下⾯具体讲讲基于EM迭代的混合⾼斯模型参数求解算法流程:1)初始参数由k-means(其实也是⼀种特殊的⾼斯混合模型)决定:function [Priors, Mu, Sigma] = EM_init_kmeans(Data, nbStates)% Inputs -----------------------------------------------------------------% o Data: D x N array representing N datapoints of D dimensions.% o nbStates: Number K of GMM components.% Outputs ----------------------------------------------------------------% o Priors: 1 x K array representing the prior probabilities of the% K GMM components.% o Mu: D x K array representing the centers of the K GMM components.% o Sigma: D x D x K array representing the covariance matrices of the% K GMM components.% Comments ---------------------------------------------------------------% o This function uses the 'kmeans' function from the MATLAB Statistics% toolbox. If you are using a version of the 'netlab' toolbox that also% uses a function named 'kmeans', please rename the netlab function to% 'kmeans_netlab.m' to avoid conflicts.[nbVar, nbData] = size(Data);%Use of the 'kmeans' function from the MATLAB Statistics toolbox[Data_id, Centers] = kmeans(Data', nbStates);Mu = Centers';for i=1:nbStatesidtmp = find(Data_id==i);Priors(i) = length(idtmp);Sigma(:,:,i) = cov([Data(:,idtmp) Data(:,idtmp)]');%Add a tiny variance to avoid numerical instabilitySigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));endPriors = Priors ./ sum(Priors);2)E步(求期望)求取:(7)其实,这⾥最贴切的式⼦应该是log似然函数的期望表达式事实上,3)中参数的求取也是⽤log似然函数的期望表达式求偏导等于0解得的简化后的式⼦,⽽这些式⼦⾄于(7)式有关,于是E步可以只求(7)式,以此简化计算,不需要每次都求偏导了。
GMM和EM算法

帧序列的同一像素
I(x,y,1)
I(x,y,2)
I(x,y,3)
I(x,பைடு நூலகம்,t)
满足混合高斯模型
6/33
基于混合高斯的运动目标检测
是否存在一个更好的模型? 在标准测试集I2R上设计实验,分析动态像素分布规律
场景分布具有代表 性
动态特性具有代表性 包含室内室外两种环境,涵盖校园、餐厅、 商场、机场、喷泉、湖面、教室、办公大厅 等,每个场景都具有代表性; 既有背景变动强烈的场景如电梯、校园、喷 泉和湖面,又有背景变动较为温和的场景如 机场、商店等,场景的动态性分布比较全面 包含光照剧烈变化的场景和多个光照对比明 显的场景,对光照条件的考察比较到位
由贝叶斯公式
后验概率
31
国家精品课程网上资源的可用性研究/***
求解混合高斯模型
公式继续推:
最终目标函数:
32
国家精品课程网上资源的可用性研究/***
求解混合高斯模型
33
国家精品课程网上资源的可用性研究/***
求解混合高斯模型
EM求解GMM流程
EXPECTATION! MAXMIZATION!
求解混合高斯模型
简化问题的参数表达式:
其中:
29
国家精品课程网上资源的可用性研究/***
求解混合高斯模型
问题并未结束!znk在实际情况中往往是不知道的! 问题的解决:利用znk的期望E[znk] 去估计znk!
30
国家精品课程网上资源的可用性研究/***
求解混合高斯模型
求期望 公式推推推
I ( x , y , l , f ) k ( x, y , l , f
EM算法推导与GMM的训练应用
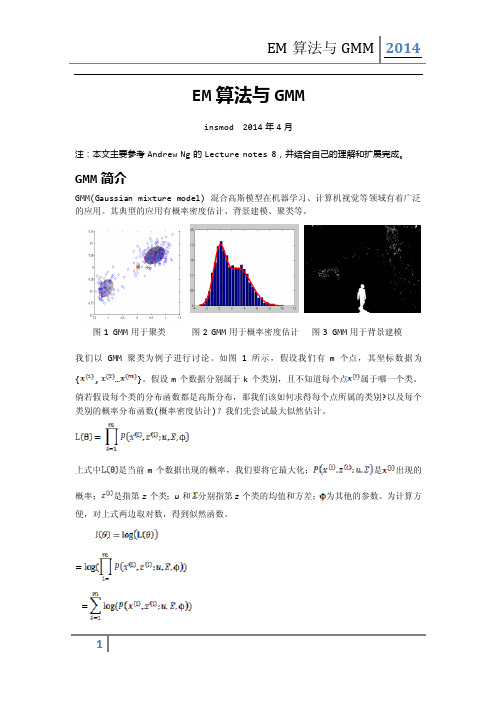
itetation = 0; while( itetation < ite_cnt )
% init papameters w0 = zeros(1, data_len); % Qi, postprior w1 = zeros(1, data_len);
% E-step, update Qi/w to get a tight lower bound for k1=1:data_len
Jensen 不等式
若实函数 存在二阶导 且有
,则 为凸函数(convex function)。
的值域为 ,则对于
有以下不等式成立: 此不等式的几何解释如下
2
EM 算法与 GMM 2014
需要说明的是,若
则不等式的方向取反。对Leabharlann 式进行推广,便可得到 Jensen
不等式(Jensen’s Inequality)。倘若有 为凸函数,且
上式中 x 和 z 为自变量;
为需要估计的参数。
为高斯分布,我们可
以写出解析式,但是
的形式是未知的。所以如果我们不能直接对 求偏导取极值。
考虑到 z 是不能直接观测到的,我们称为隐藏变量(latent variable)。为了求解
我们引入 EM 算法(Expectation-Maximization)。我们从 Jensen 不等式开始讨论 EM 算 法。
概率密度函数,有
且
。现在对 的表达式进行一定得处理,先乘以一
个 再除以一个 ,有
3
EM 算法与 GMM 2014
我们把
看做是 的函数;
为概率密度,则有
考虑到 log 函数为凹函数,利用 Jensen 不等式有
此时我们找到了 的一个下界。而且这个下界的选取随着 到了一组下界。用下图来简单描述
GMM算法及其应用

引入K维的随机变量z,并且z使用1-of-K表示。zk 1 表示 第k类被选中的概率,即:
pzk 1 k
z k 需要满足以下两个条件:
和
(2)
关于z有:
GMM原始公式推导
每一类数据都服从正态分布,用条件概率可以表示为
GMM原始公式推导
每一类数据都服从正态分布,用条件概率可以表示为 上式可以改写为:
从而可以求出p(x):
例子
GMM模型的在二维空间的示意图
GMM原始公式推导
采用Bayes规则,数据点x属于第k个类的概率可以用后验 概率表示为:
GMM—参数最大似然估计
GMM
K
px k N x k , k k 1
有三组参数需要估计:
GMM—参数最大似然估计
对上式取对数,再对均值 求令导数为0,可得
GMM
使用一个高斯模型拟合分布
GMM
使用两个高斯模型拟合分布
GMM-例子
GMM
原始形式
K
px k N x k , k k 1
权重 k可以看成使第k类被选中的概率。
GMM
原始形式
K
px k N x k , k k 1
权重 k可以看成使第k类被选中的概率。
GMM原始形式推导
主要任务
输入视频
背景
j 1
3.M步骤:通过下列重估共识修正参数
new k
1 Nk
N
(znk )xn
n1
new k
Nk N
new k
1 Nk
N
(znk )(xn k new )(xn k new )T
n1
EM算法
4.检验是否收敛
EM
gmm高斯模型推导

gmm高斯模型推导全文共四篇示例,供读者参考第一篇示例:GMM (Gaussian Mixture Model)高斯混合模型是一种常用的概率模型,用于对数据进行聚类和密度估计。
它假设数据是由若干个高斯分布组成的混合分布生成的,每个高斯分布对应一个聚类,每个数据点的生成过程由各个高斯分布按一定概率加权组成。
本文将从GMM 的基本理论出发,逐步推导GMM的EM算法,以及参数的估计和模型的选择。
GMM的基本理论包括数学描述和模型假设。
假设我们有N个数据点x_1, x_2, \cdots, x_N,每个数据点有D个维度。
GMM假设这些数据由K个高斯分布组成,每个高斯分布对应一个聚类,表示为\{ \pi_k, \mu_k, \Sigma_k \}_{k=1}^{K},其中\pi_k是第k个高斯分布的混合系数,\mu_k是第k个高斯分布的均值向量,\Sigma_k 是第k个高斯分布的协方差矩阵。
GMM模型的概率密度函数定义如下:p(x) = \sum_{k=1}^{K} \pi_k \mathcal{N}(x|\mu_k, \Sigma_k)其中\mathcal{N}(x|\mu, \Sigma)表示多维高斯分布的概率密度函数。
每个高斯分布的参数需要满足以下条件:\mu_k \in \mathbb{R}^D, \Sigma_k \in \mathbb{R}^{D\times D}, \Sigma_k \succ 0接下来我们将推导GMM的EM算法。
EM算法是一种迭代优化算法,用于估计含有隐变量的概率模型的参数。
GMM中的隐变量是数据点的类别,即数据点属于哪一个高斯分布的概率最大。
EM算法的基本思路是通过迭代优化求解下面的似然函数极大化问题:具体来说,EM算法分为两步:E步和M步。
在E步中,我们计算数据点属于各个高斯分布的后验概率,即第n个数据点属于第k个高斯分布的概率:迭代E步和M步直到模型参数收敛,即对数似然函数的收敛差值小于一个给定的阈值。
GMM_EM_混合高斯模型及其求解应用

k N( xi | k , k )
E-step
N( x | ,
j 1 j i j
K
1 N k E (zik) ( xi k )( xi k )T N k i 1
j
)
M-step
k
E(z
i 1
N
N
ik
)
N
i 1
f ( I xy ,t ) xy ,k ,t N ( I xy ,t , xy ,k ,t , xy ,k ,t ),
k 1 K
k 1
K
xy , k ,t
1
Ixy,t 表示t时刻图像I中的xy位置的像素特征。
模型主要步骤:
1,模型初始化; 2,背景描述; 3,前景判决; 4,模型更新。
N
(z ) ( x )( x ) E
ik
k
E(z
i 1
ik
)
N
N i 1
Nk N
N k E ( zik )
GMM参数学习
• 进一步解释
1 N k E ( zik ) xi N k i 1 1 N k E (zik) ( xi k )( xi k )T N k i 1
z
i 1 k 1
ik
{ln k ln N ( xi | k , k )}
1 Nk
N
1 k Nk 1 k Nk
N
zik xi
i 1 N
Nzi 1 Nhomakorabeaik
( xi k )( xi k )
T
k
z
i 1
N
gmm的基本原理和应用

gmm的基本原理和应用1. 基本原理高斯混合模型(GMM)是一种常用的概率模型,用于对多个高斯分布进行加权混合。
它是一种非监督学习算法,常用于聚类、数据建模和异常检测等任务。
GMM的基本原理包括以下几个方面:1.1 高斯分布高斯分布也称为正态分布,是一种连续型概率分布。
它可以用均值和方差来描述,具有钟形曲线的特点。
高斯分布的概率密度函数可以表示为:$$ f(x) = \\frac{1}{\\sqrt{2 \\pi \\sigma^2}} \\cdot e^{-\\frac{(x - \\mu)^2}{2 \\sigma^2}} $$其中,$\\mu$ 是均值,$\\sigma$ 是标准差。
1.2 高斯混合模型高斯混合模型是将多个高斯分布加权混合得到的模型。
假设我们有K个高斯分布,每个分布对应一个权重 $\\pi_k$,满足以下两个条件:1.$\\pi_k \\geq 0$ 且 $\\sum_{k=1}^{K} \\pi_k = 1$2.每个高斯分布都可以用均值 $\\mu_k$ 和协方差矩阵 $\\Sigma_k$ 来表示则高斯混合模型的概率密度函数可以表示为:$$ f(x) = \\sum_{k=1}^{K} \\pi_k \\cdot \\frac{1}{\\sqrt{2 \\pi \\sigma_k^2}} \\cdot e^{-\\frac{(x - \\mu_k)^2}{2 \\sigma_k^2}} $$其中,$\\sum_{k=1}^{K} \\pi_k$ 表示对所有的高斯分布进行加权求和。
1.3 模型参数估计在实际应用中,我们需要从数据中估计出高斯混合模型的参数。
常用的方法是最大似然估计(Maximum Likelihood Estimation,简称MLE)。
MLE的思想是使观测数据发生的概率最大化。
对于高斯混合模型,MLE的目标是找到最优的参数 $\\Theta = \\{\\pi_k,\\mu_k, \\Sigma_k\\}$,使得观测数据 $X = \\{x_1, x_2, ..., x_N\\}$ 的概率最大。
多元高斯混合模型 em算法 工况-概述说明以及解释

多元高斯混合模型em算法工况-概述说明以及解释1.引言1.1 概述在编写文章的概述部分时,需要对主题进行简要介绍,并提供相关背景信息。
这里是关于多元高斯混合模型(Gaussian Mixture Model, GMM)及其在工况(engineering conditions)中的应用的概述。
多元高斯混合模型是一种常见的统计模型,它是由多个高斯分布组成的概率密度函数的线性组合。
在实际问题中,很多数据的分布无法被单个高斯分布完全描述,而是由多个高斯分布混合而成。
多元高斯混合模型通过将这些高斯分布加权组合,能够更好地近似复杂数据的分布情况。
EM算法是一种常用于估计多元高斯混合模型参数的迭代算法。
通过EM算法,我们可以根据观测数据来估计出模型中每个高斯分布的均值、协方差和权重等参数,从而得到最优的模型拟合结果。
EM算法的基本思想是通过交替迭代的方式,通过E步骤计算隐变量(即数据来自于哪个高斯分布),再通过M步骤更新模型参数,不断优化模型,直到收敛到最优解。
在工况中,多元高斯混合模型及EM算法的应用非常广泛。
工况通常涉及到多个不同的条件和变量,而且这些条件和变量之间往往存在复杂的关联关系。
通过使用多元高斯混合模型,可以更好地对这些变量的分布进行建模和描述,进而提供更准确的分析和预测结果。
无论是在工程领域的故障诊断、质量控制还是金融领域的风险分析等应用场景中,多元高斯混合模型都发挥着重要的作用。
总而言之,本文将针对多元高斯混合模型及其在工况中的应用展开详细探讨。
通过介绍多元高斯混合模型的基本原理和EM算法的实现方式,以及探讨其在工况中的应用案例,旨在提供一种全面的分析方法和工具,以帮助读者更好地理解和应用该模型解决实际问题。
1.2文章结构文章结构部分的内容可以包括以下内容:本文将从以下几个方面进行论述:多元高斯混合模型、EM算法以及它们在工况中的应用。
首先,我们将介绍多元高斯混合模型的基本概念和原理。
通过对多元高斯分布和混合模型的介绍,读者将了解到多元高斯混合模型在数据建模和聚类分析中的重要性及应用场景。
高斯混合模型的理解和应用

高斯混合模型的理解和应用作者:张鹂沣来源:《课程教育研究》2018年第48期【摘要】本文主要介绍了人工智能的核心——机器学习中的无监督学习算法中的高斯混合模型。
研究了使用EM算法对高斯混合模型进行参数估计。
其次讨论了高斯混合模型和K-means算法作为聚类算法上的异同。
最后介绍了现阶段高斯混合模型在实际中的应用。
【关键词】高斯混合模型 K-means算法无监督学习【中图分类号】G63 【文献标识码】A 【文章编号】2095-3089(2018)48-0218-02前段时间Alpha go横扫世界高手的人机大战成为一时热点,而这反映出近年来发展最为迅速而引人注目绝对非人工智能莫属了。
人工智能是研究学习人类智能的方法并发展为完整的应用系统的一门前沿的技术科学。
人工智能的核心是机器学习,它是一门涉及数学、统计学、计算机科学等专业学科的多领域交叉学科。
具体而言,机器学习由数据样本出发应用不同的算法“学习”出规律,进而可以应用于新的数据样本上。
众多的机器学习算法可以从不同的维度进行分类。
其中一种分类方式是依据数据是否有或仅有部分的标记或分类标签而分为监督学习和无监督学习,或半监督学习。
聚类分析是将已有的对象根据“学习的规律”而分组,每组中由具有相同性质或属性的对象组成。
这属于典型的无监督学习。
不论是越来越多可得的海量数据,还是机器学习算法的进一步发展和完善,人工智能都有了更广阔的应用场景,展现了更惊人的发展潜力。
在不远的未来,人工智能必将能满足更多的科技和生产提出的新要求,带来方方面面的革新。
1.高斯混合模型1.1 高斯混合模型的定义当p=1时,闵可夫斯基距离即为欧氏距离;当P=2时,闵可夫斯基距离此时即为常用的曼哈顿距离。
在不同的情形下,适用于不同的距离度量,选择更合适的距离度量有益于得到更好的模型效果。
2.2 高斯混合模型与K-Means模型的异同高斯混合模型与K-Means模型都属于机器学习算法中无监督学习中的聚类算法模型——都是通过对无已知标记或分类的样本数据通过算法根据数据的分布结构或性质进行分类的过程。
高斯混合模型em算法

高斯混合模型em算法高斯混合模型(Gaussian Mixture Model,简称GMM)是一种概率模型,它能够将多个高斯分布组合在一起,从而更好地对数据进行建模和描述。
EM算法(Expectation-Maximization Algorithm,期望最大化算法)是一种常用于GMM参数估计的迭代算法。
本文将重点介绍GMM和EM算法,并对EM算法的具体步骤进行详细解释。
1. 高斯混合模型(Gaussian Mixture Model)高斯混合模型通过同时拟合多个高斯分布的线性组合来对数据进行建模。
设X为观测数据,其概率密度函数可以表示为:P(X) = Σk=1 to K (πk * N(x|μk, Σk))其中,N(x|μk, Σk)表示高斯分布的概率密度函数,πk为每个分布的权重,并满足Σk=1 to K πk = 1。
通过最大化似然函数,可以估计出每个高斯分布的参数μk和Σk。
2. EM算法(Expectation-Maximization Algorithm)EM算法是一种迭代算法,用于求解含有隐变量的概率模型参数估计问题。
EM算法通过交替进行E步和M步来迭代地逼近模型参数的最大似然估计。
- E步(Expectation Step):在E步中,通过当前的模型参数估计隐变量的期望。
对于GMM,E步的目标是计算每个样本属于每个高斯分布的后验概率。
- M步(Maximization Step):在M步中,根据E步计算得到的隐变量的期望,更新模型参数。
对于GMM,M步的目标是最大化对数似然函数,从而估计出每个高斯分布的参数μk和Σk。
具体的EM算法步骤如下:(1) 初始化参数,包括高斯分布的个数K、每个高斯分布的权重πk、每个高斯分布的均值μk和协方差矩阵Σk。
(2) 进行E步,计算每个样本属于每个高斯分布的后验概率。
根据当前的参数估计后验概率如下:γij = πj * N(xi|μj, Σj) / Σk=1 to K (πk * N(xi|μk, Σk))(3) 进行M步,更新模型参数。
EM算法与GMM的训练应用

EM算法与GMM的训练应用EM算法(Expectation Maximization algorithm)是一种用于参数估计的迭代算法,主要应用于概率模型和统计推断中。
GMM(Gaussian Mixture Model)是一种常用的概率模型,通过将数据分解为多个高斯分布的线性组合来描述数据的分布。
EM算法在GMM的训练中有着广泛的应用。
下面将从EM算法和GMM的基本原理、EM算法在GMM训练中的应用以及相关案例等方面进行详细阐述。
首先,我们来了解一下EM算法和GMM的基本原理。
EM算法通过迭代的方式,求解含有隐变量的概率模型的参数估计。
其步骤包括:初始化模型的参数,然后通过E步(Expectation)计算隐变量的期望值,再通过M步(Maximization)估计模型的参数。
重复进行E步和M步,直到参数收敛。
GMM是一种概率密度模型,用于描述数据的分布情况。
它假设数据是由多个高斯分布的线性组合生成的。
GMM的参数包括每个分量的均值、方差和每个分量对整体生成的权重。
EM算法在GMM训练中有着广泛的应用。
具体而言,EM算法通过最大似然估计的方法,从给定的数据中估计GMM的参数。
它可以有效地识别数据中的潜在分布,并将数据分解成多个高斯分布的线性组合。
EM算法在GMM训练中的应用可以概括为以下几个步骤:1.初始化GMM的参数,包括每个分量的均值、方差和权重。
2.E步骤:根据当前的参数估计,计算每个数据点属于每个分量的后验概率。
3.M步骤:根据E步骤的结果,估计新的参数值,包括每个分量的均值、方差和权重。
4.重复进行E步和M步,直到参数收敛。
5.得到收敛后的参数估计结果,即为GMM模型的训练结果。
EM算法在GMM训练中的应用可以帮助我们识别和分析数据的分布情况。
例如,可以用于图像分割、文本分类、异常检测等领域。
以图像分割为例,假设我们有一张包含物体的图像,我们希望将图像中的物体和背景分割开来。
我们可以将图像中的每个像素看作是数据点,通过GMM训练得到每个像素属于物体和背景的概率。
GMM高斯混合模型的EM算法参数估计matlab仿真

GMM高斯混合模型的EM算法参数估计matlab仿真1.算法仿真效果matlab2022a仿真结果如下:2.算法涉及理论知识概要GMM,高斯混合模型,也可以简写为MOG。
高斯模型就是用高斯概率密度函数(正态分布曲线)精确地量化事物,将一个事物分解为若干的基于高斯概率密度函数(正态分布曲线)形成的模型。
GMMs已经在数值逼近、语音识别、图像分类、图像去噪、图像重构、故障诊断、视频分析、邮件过滤、密度估计、目标识别与跟踪等领域取得了良好的效果。
高斯混合模型(GMM) 是一种机器学习算法。
它们用于根据概率分布将数据分类为不同的类别。
高斯混合模型可用于许多不同的领域,包括金融、营销等等!这里要对高斯混合模型进行介绍以及真实世界的示例、它们的作用以及何时应该使用GMM。
高斯混合模型(GMM) 是一个概率概念,用于对真实世界的数据集进行建模。
GMM是高斯分布的泛化,可用于表示可聚类为多个高斯分布的任何数据集。
高斯混合模型是一种概率模型,它假设所有数据点都是从具有未知参数的高斯分布的混合中生成的。
高斯混合模型可用于聚类,这是将一组数据点分组为聚类的任务。
GMM 可用于在数据集中可能没有明确定义的集群中查找集群。
此外,GMM 可用于估计新数据点属于每个集群的概率。
高斯混合模型对异常值也相对稳健,这意味着即使有一些数据点不能完全适合任何集群,它们仍然可以产生准确的结果。
这使得 GMM 成为一种灵活而强大的数据聚类工具。
它可以被理解为一个概率模型,其中为每个组假设高斯分布,并且它们具有定义其参数的均值和协方差。
GMM 由两部分组成——均值向量(μ) 和协方差矩阵(Σ)。
高斯分布被定义为呈钟形曲线的连续概率分布。
高斯分布的另一个名称是正态分布。
这是高斯混合模型的图片:它可以被理解为一个概率模型,其中为每个组假设高斯分布,并且它们具有定义其参数的均值和协方差。
GMM 由两部分组成——均值向量(μ) 和协方差矩阵(Σ)。
EM算法及其应用实例

EM算法及其应用实例EM算法(Expectation-Maximization algorithm)是一种迭代算法,用于解决含有隐变量的概率模型的参数估计问题。
EM算法被广泛应用于许多领域,如机器学习、数据挖掘、自然语言处理等。
EM算法的主要思想是通过迭代的方式,交替进行两个步骤:E步骤(expectation)和M步骤(maximization)。
在每一次迭代中,E步骤用于计算模型在当前参数下对观测数据的期望,M步骤则用于更新模型参数,使得模型的对数似然函数得到最大化。
通过不断重复这两个步骤,最终获得模型的最优参数估计。
EM算法的应用实例有很多,下面以两个典型的应用实例进行说明。
1.高斯混合模型(GMM):高斯混合模型是一种概率密度模型,由多个高斯分布组成。
每个高斯分布对应一个隐藏变量,表示观测数据来自于哪个分布。
因此,高斯混合模型包含两部分参数:高斯分布的参数和隐藏变量的分布。
EM算法可以用于估计高斯混合模型的参数。
在E步骤中,根据当前参数,计算每个观测数据来自于每个高斯分布的概率。
在M步骤中,根据E步骤得到的概率,更新高斯混合模型的参数。
通过不断迭代E步骤和M步骤,最终可以得到高斯混合模型的最优参数估计。
2.隐马尔可夫模型(HMM):隐马尔可夫模型是一种概率图模型,用于描述时间序列数据的生成过程。
隐马尔可夫模型由两部分参数组成:状态转移概率和观测概率。
EM算法可以用于估计隐马尔可夫模型的参数。
在E步骤中,根据当前参数,计算观测数据在每个时间步上处于每个隐藏状态的概率。
在M步骤中,根据E步骤得到的概率,更新隐马尔可夫模型的参数。
通过不断迭代E步骤和M步骤,最终可以得到隐马尔可夫模型的最优参数估计。
除了高斯混合模型和隐马尔可夫模型,EM算法还可以应用于其他概率模型的参数估计问题,如朴素贝叶斯分类器、混合朴素贝叶斯分类器等。
总之,EM算法是一种有效的参数估计算法,广泛应用于各个领域。
它通过迭代的方式,交替进行E步骤和M步骤,不断更新模型参数,最终得到模型的最优参数估计。
高斯混合模型em算法

高斯混合模型 (Gaussian Mixture Model, GMM) 和 EM 算法1. 引言高斯混合模型 (Gaussian Mixture Model, GMM) 是一种常见的概率模型,用于对数据进行聚类和密度估计。
它假设数据是由多个高斯分布组成的混合体,每个高斯分布称为一个分量。
EM 算法是一种迭代优化算法,用于估计 GMM 的参数。
在本文中,我们将介绍 GMM 和 EM 算法的基本概念,并详细解释 EM 算法在估计 GMM 参数时的工作原理。
2. 高斯混合模型 (GMM)高斯混合模型是一种生成模型,用于描述多变量数据的概率分布。
它假设数据是由 K 个高斯分布组成的混合体,每个高斯分布具有自己的均值向量和协方差矩阵。
对于一个 K 维随机变量 X ,其概率密度函数可以表示为:p (X )=∑πk Kk=1⋅N (X|μk ,Σk )其中 πk 是第 k 个高斯分布的权重(满足 ∑πk K k=1=1),N (X|μk ,Σk ) 是第 k 个高斯分布的概率密度函数。
GMM 的参数包括每个高斯分布的权重 πk 、均值向量 μk 和协方差矩阵 Σk 。
3. EM 算法EM 算法是一种迭代优化算法,用于估计概率模型的参数。
在 GMM 中,EM 算法被广泛应用于估计模型的参数。
EM 算法的基本思想是通过迭代优化两步来逐步改进参数估计:E 步(Expectation Step )和 M 步(Maximization Step )。
E 步(Expectation Step )在 E 步中,我们根据当前参数的估计值,计算每个样本属于每个高斯分布的后验概率。
这些后验概率被称为责任(responsibility )。
γ(z nk )=πk ⋅N (x n |μk ,Σk )∑πj K j=1⋅N(x n |μj ,Σj )其中 z nk 表示第 n 个样本属于第 k 个高斯分布的责任。
M 步(Maximization Step)在 M 步中,我们使用 E 步中计算得到的责任,重新估计模型的参数。
高斯混合模型em算法

高斯混合模型em算法高斯混合模型与EM算法高斯混合模型(Gaussian Mixture Model,GMM)是一种常用的概率模型,用于对多元数据进行建模和分析。
它可以描述一个数据集中包含的多个潜在的高斯分布,并通过EM算法来对模型参数进行估计。
本文将介绍高斯混合模型和EM算法的基本原理以及它们在实际应用中的一些例子。
高斯混合模型是由多个高斯分布组成的概率分布模型。
对于一个具有N个样本的数据集,高斯混合模型假设这些样本是由K个高斯分布组成的,每个高斯分布对应着数据集中的一个潜在成分。
每个样本点的生成过程可以表示为:```x = w_1 * N(mu_1, sigma_1^2) + w_2 * N(mu_2, sigma_2^2) + ... + w_K *N(mu_K, sigma_K^2)```其中,`x`为一个样本点,`N(mu_i, sigma_i^2)`表示一个高斯分布,`w_i`表示对应的样本点属于第i个高斯分布的概率。
高斯混合模型的目标是通过拟合样本数据,估计出每个高斯分布的参数以及每个样本点属于不同高斯分布的概率。
EM算法(Expectation-Maximization algorithm)是一种常用的估计高斯混合模型参数的方法。
EM算法的基本思路是通过迭代的方式,交替进行两个步骤:E步骤(Expectation)和M步骤(Maximization)。
具体每次迭代的过程如下:1. 初始化高斯混合模型的参数:包括每个高斯分布的参数(均值和方差)以及每个样本点属于不同高斯分布的概率。
2. E步骤:根据当前模型参数,计算每个样本点属于每个高斯分布的概率。
这个概率可以使用贝叶斯定理和高斯分布的概率密度函数得到。
3. M步骤:根据E步骤的计算结果,更新高斯分布的参数以及每个样本点属于不同高斯分布的概率。
通常使用最大似然估计的方法进行参数的更新。
4. 重复步骤2和步骤3,直到模型收敛或达到设定的迭代次数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p( xi | zik 1; ) N ( xi | k , k )
• 从而得到
p ( xi | Z i ; ) N ( xi | k , k )
k 1 K zik
注意:这里zik只有0和1的选择
GMM参数学习
• 在简化问题中,我们实际的观察变量是{X,Z},根 据一下两个公式
Nk 1 ln N ( X | k , k ) k ( xi k ) k,可以得到
1 k Nk
Nk
x
i 1 i
Nk
i
1 k Nk
(x
i 1
k
)( xi k )T
GMM参数学习
• 在zik已知的情况下,我们求出了高斯函数的数值 解:
k 1
K
L K k 1 0 k 1
L i 1 k
zik N
i 1 k 1
N
K
zik
N
0
k
z
i 1
N
ik
N
Nk N
GMM参数学习
• 引入隐变量Z后,我们得到了最大化目标函数的 N K 结果
ln p(X, Z; )
1 k Nk 1 k Nk
z
i 1 N i 1
N
ik i
x
z
ik
( xi k )( xi k )T
其中
N k zik
i 1 N
GMM参数学习
L ln p (X, Z; ) ( k 1)
k 1
K
z
i 1 k 1
N
K
ik
{ln k ln N ( xi | k , k )} ( k 1)
f ( I xy ,t ) xy ,k ,t N ( I xy ,t , xy ,k ,t , xy ,k ,t ),
k 1 K
k 1
K
xy , k ,t
1
Ixy,t 表示t时刻图像I中的xy位置的像素特征。
模型主要步骤:
1,模型初始化; 2,背景描述; 3,前景判决; 4,模型更新。
Nk N
N k E ( zik )
GMM参数学习
• 算法流程
GMM参数学习
• GMM,K=2
原始数据 K-meams初始化 迭代过程
迭代过程
迭代过程
迭代结果
高斯混合模型(GMM)
• GMM的表达式
• GMM参数计算
• GMM应用举例
GMM应用:背景建模
• 背景模型:对图像中的场景进行建模,从而进行 运动检测。
GMM应用:背景建模
• 前景判决(2/2)
M xy ,t 1 arg min{mxy , k ,t 1 ( I xy ,t 1 ) 0}
k
前景判决:
if M xy ,t 1 B, 前景 else 背景
GMM应用:背景建模
• 模型更新(1/2)更新模型,使其适应场景的变化
更新所有高斯模型的权重,并重新归一化:
GMM应用:背景建模
• 模型初始化(1/3)
xy ,k ,t
I xy ,t 0
k 1 k 1
0 k K
GMM应用:背景建模
• 模型初始化(2/3)
2 xy , k ,t var
k 1, 2,..., K
GMM应用:背景建模
• 模型初始化(3/3)
xy ,k ,t
• 为了最大化上式,由于zik已知,我们可以把上式 按观察到的(x,z) 分为K组,即按照所属的高斯函 数进行分组
ln p(X, Z; )
iC1
(ln
iCK
1
ln N ( xi | 1 , 1 )) (ln 2 ln N ( xi | 2 , 2 ))
iC2
n 1 k 1 K
N
K
=
z
n 1 k 1
N
ik
{ln k ln N ( xi | k , k )}
• 后者的ln直接作用于正态分布,使正态分布由乘 的e指数形式变为加的简单形式
GMM参数学习
ln p(X, Z; )
z
i 1 k 1
N
K
ik
{ln k ln N ( xi | k , k )}
xy,k ,t 1 (1 ) xy,k ,t mxy,k,t 1
N ( I xy ,t 1; xy , M xy ,t 1 ,t , xy ,M xy ,t 1 ,t ) xy , M xy ,t 1 ,t 1 (1 ) xy , M xy ,t 1 ,t I xy ,t 1
2 2 2 xy , M xy ,t 1 ,t (1 ) xy , M xy ,t 1 ,t ( I xy ,t xy , M xy ,t 1 ,t )
GMM应用:背景建模
• 模型更新(2/2)
(1)更新前k-1个模型的权重:
xy,i,t 1 (1 Winit )( xy,i,t 1
i 1 i 1 k 1 N N K
• 可以看出目标函数是和的对数,优化问题麻烦, 简化的问题:某混合高斯分布一共有K个分布, 对于每一个观察到的x,如果我们同时还知道它 是属于K中哪一个分布的,则可以直接求解出各 个高斯分布的参数。 • 因此引入隐变量Z,用于表示样本{x}输入哪一个 高斯分布
E ( zik | ) =
k N( xi | k , k )
E-step
N( x | ,
j 1 j i j
K
1 N k E (zik) ( xi k )( xi k )T N k i 1
j
)
M-step
k
E(z
i 1
N
N
ik
)
N
i 1
现在的问题转化为如何求解E{zik}?
k
E(z
i 1
N
ik
)
N
N i 1
Nk N
N k E ( zik )
E{zik}
EM算法
GMM参数学习
GMM参数学习
E ( zik | ) z zik p ( zik | xn , ) = z zik p ( zik | xi , )
Zik只有 0、1取值
p ( zik 1| ) p ( xi | zik 1, ) = p ( xi | ) =
k N( xi | k , k )
N( x | ,
j 1 j i j
K
j
)
公式展开
GMM参数学习
• 小结
1 N k E ( zik ) xi N k i 1
GMM参数学习
• 比较原问题和简化问题
ln( p( X ; )) ln p( xi ; ) ln( k N ( xi ; k , k ))
i 1 i 1 k 1
zik
N
N
K
ln p (X, Z; ) ln{ kzik N ( xi | k , k ) }
高斯混合模型(GMM)
• 公式表达:
参数空间:
高斯混合模型(GMM)
• GMM的表达式
• GMM参数计算
• GMM应用举例
GMM参数学习
*注意:对于观察集{x}中的各个观察值x ,这里认为相互之间独立。 i
GMM参数学习
• 对目标函数取对数:
ln( p( X ; )) ln p( xi ; ) ln( k N ( xi ; k , k ))
N
(z ) ( x )( x ) E
ik
k
E(z
i 1
ik
)
N
N i 1
Nk N
N k E ( zik )
GMM参数学习
• 进一步解释
1 N k E ( zik ) xi N k i 1 1 N k E (zik) ( xi k )( xi k )T N k i 1
高斯混合模型(GMM)
高斯混合模型(GMM)
• GMM的表
• GMM参数计算
• GMM应用举例
高斯混合模型(GMM)
• GMM的表达
• GMM参数计算
• GMM应用举例
高斯模型
• 是一种参数化模型,用高斯密度函数估计目标的 分布
• 单高斯(Single Gaussian Model)
• 高斯混合模型(Gaussian mixture model)
z
i 1 k 1
ik
{ln k ln N ( xi | k , k )}
1 Nk
N
1 k Nk 1 k Nk
N
zik xi
i 1 N
N
z
i 1
ik
( xi k )( xi k )
T
k
z
i 1
N
ik
N
i 1
N k N
N k zik
GMM参数学习
• 定义Zi={zi1,…, ziK}, zik表示xi是否属于第k个高斯 函数,zik只有两个取值0、1,即zik=1表示xi属于 第k个高斯函数, zik=0表示xi不属于第k个高斯函 数。 • 那么,有:
z
k 1
K
ik
1
K
p( Z i ) kzik
k 1
GMM参数学习
ik
N
