8.7 泰勒级数和麦克劳林级数 托马斯微积分
常用Taylor公式(即Maclaurin级数)合集(超全二十六个,收藏前先点赞同,谢谢)

注:第三条e^x的展开式,在“1”和“+½x^2”之间添上一个“+x”。
1.\begin{aligned}\frac{1}{1-x}=\sum_{n=0}^\inftyx^n=1+x+x^2+x^3+\omicron(x^3),x\in(-1,1).\end{aligned}2.\begin{aligned}\frac{1}{1+x}=\sum_{n=0}^\infty (-1)^nx^n=1-x+x^2-x^3+\omicron(x^3),x\in(-1,1).\end{aligned}3.\begin{aligned}e^x=\sum_{n=0}^\infty\frac{x^n}{n!}=1+\frac{1}{2}x^2+\frac{1}{6}x^3+\omicron(x^3),x\in(-\infty,+\infty).\end{aligned}4.\begin{aligned}\sin x=\sum_{n=0}^\infty(-1)^n\frac{x^{2n+1}}{(2n+1)!}=x-\frac{x^3}{6}+\omicron(x^3),x\in(-\infty,+\infty).\end{aligned}5.\begin{aligned}\cos x=\sum_{n=0}^\infty(-1)^n\frac{x^{2n}}{(2n)!}=1-\frac{x^2}{2}+\frac{x^4}{24}+\omicron(x^4),x\in(-\infty,+\infty).\end{aligned}6.\begin{aligned}\tan x=\sum_{n=0}^\infty\frac{B_{2n}(-4)^n(1-4^n)}{(2n)!}x^{2n-1}=x+\frac{x^3}{3}+\omicron(x^3),x\in(-\frac{\pi}{2},\frac{\pi}{2}).\end{aligned}其中 B_{2n}是 \mathrm{Bernoulli}数,定义为\begin{aligned}B_n=\lim_{x\rightarrow0}\frac{d^n}{dx^n}[\frac{x}{e^x-1}].\end{aligned}7.\begin{aligned}\arcsin x=\sum_{n=0}^\infty\frac{(2n)!}{4^n(n!)^2}\times\frac{x^{2n+1}}{2n+1}=x+\frac{x^3}{6}+\omicron (x^3),x\in[-1,1]\end{aligned}8.\begin{aligned}\arccos x=\frac{\pi}{2}-\arcsin x=\frac{\pi}{2}-\sum_{n=0}^\infty\frac{(-1)^nx^{2n+1}}{2n+1}=\frac{\pi}{2}-x-\frac{x^3}{6}+\omicron(x^3),x\in[-1,1].\end{aligned}注:一般的Taylor公式表里面没有标注 \arccos x的原因是, \arccos x+\arcsin x=\frac{\pi}{2},也就是说,根据 \arcsin x的Taylor公式,就可以直接推出 \arccos x的Taylor了。
泰勒级数_中文

┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊外文文献翻译泰勒级数出自维基百科,自由的百科全书,对于其他系列扩展概念,见系列(数学)。
在数学中,泰勒级数是一个具有代表性的利用单点的导数来实现无穷计算的函数。
泰勒级数的概念是由英国数学家布鲁克·泰勒在1715年正式提出。
如果泰勒级数在零点展开,则该级数称为麦克劳林级数。
科林·麦克劳林是苏格兰数学家,他在18世纪针对该级数做了广泛的使用,泰勒级数便以他的名字命名。
一般,通过使用其泰勒级数的有限项来逼近一个函数。
泰勒定理给出针对该逼近的误差估计。
一个函数的任何有限数量的泰勒级数被称为泰勒多项式。
一个函数的泰勒级数是该函数的泰勒多项式的无限逼近。
一个函数可能不等于它的泰勒级数,即使在每一个点其泰勒级数都收敛。
如果一个函数等于其在一个开放的区间(或在复平面上的盘)的泰勒级数,则它是已知的解析函数。
定义泰勒级数的实(复)函数()f x在实(复)数a的领域上是无限可微的幂级数:Λ+-+-+-+332)(!3)()(!2)('')(!1)(')(axafaxafaxafaf这也可以写成更简洁的形式:nnnaxnaf)(!)()(-∑∞=其中!n表示n的阶乘,)()(af n表示f在a点的n阶导数。
f的零阶导数是它本身,)(ax-和!0的值都为1,在0=a的情况下,该级数也称为麦克劳林级数。
例子对于任何多项式的麦克劳林级数都是该多项式本身。
1)1(--x,1||<x的麦克劳林级数就是如下的集合级数:Λ++++321xxx因此1x-在1a=上的泰勒级数为:Λ+---+--32)1()1()1(1xxx对上面的麦克劳林级数积分,得到)1log(x-(log为自然对数的符号)的麦克劳林级数为:Λ-----432413121xxxx而log()x在1a=上对应的泰勒级数就为:Λ+---+---432)1(41)1(31)1(21)1(xxxx指数函数x e在0a=处的泰勒级数为:┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊ΛΛ++++++=++++++12024621!5!4!3!2!11543254321xxxxxxxxxx上面的展开式成立,因为x e的导数关于x仍为x e而且10=e,这使得项nx)0(-以!n为分母的项,在无穷项和式中每一项式子都成立。
泰勒级数与麦克劳林级数

泰勒级数与麦克劳林级数在微积分中,泰勒级数和麦克劳林级数是常见的数学工具。
它们被广泛应用于近似计算和函数展开等领域。
本文将介绍泰勒级数和麦克劳林级数的定义、性质以及实际应用。
1. 泰勒级数泰勒级数是一种将任意函数表示为无穷级数的方法。
给定一个函数f(x),在某个点a处连续可导,泰勒级数可以表达为:f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + f'''(a)(x-a)^3/3! + ...其中,f(a)为函数f(x)在点a处的函数值,f'(a)为f(x)在点a处的导数,f''(a)为f(x)在点a处的二阶导数,以此类推。
这个级数可以无限展开,收敛于f(x)。
泰勒级数的应用非常广泛。
通过截取前n项,我们可以得到一个函数在某个点附近的近似表达式。
这对于计算复杂的函数或者求解方程有着重要的作用。
2. 麦克劳林级数麦克劳林级数是泰勒级数的一种特殊形式,即在泰勒级数中取a=0。
这样,泰勒级数变为:f(x) = f(0) + f'(0)x + f''(0)x^2/2! + f'''(0)x^3/3! + ...麦克劳林级数是常用的近似函数展开形式之一,也是泰勒级数中最简单的形式。
通过截取麦克劳林级数的前n项,我们可以得到一个函数在原点附近的近似表达式。
3. 应用案例泰勒级数和麦克劳林级数在实际问题中有着广泛的应用。
以下是一些常见的应用案例:3.1 物理学中的近似计算在物理学中,许多复杂的物理现象可以使用泰勒级数或麦克劳林级数进行近似计算。
例如,在光学中,我们可以使用麦克劳林级数来近似计算透镜的光焦度和成像规律。
这些近似计算可以大大简化问题,使得物理学研究更加便捷。
3.2 工程领域中的函数逼近在工程领域,函数逼近是一种常见的问题。
通过使用泰勒级数或麦克劳林级数,我们可以将一个复杂的函数表示为一系列简单的数学形式。
泰勒级数的微积分应用

泰勒级数的微积分应用泰勒级数是微积分中的一个重要概念,它能够将一个函数在某一点附近展开成无限项的多项式函数。
这个概念在数学、物理和工程学等领域都有广泛的应用。
本文将讨论泰勒级数在微积分应用中的重要性。
一、泰勒级数的定义泰勒级数是指将一个函数$f(x)$在$x=a$处展开成多项式函数的无限级数,它的一般形式为:$f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n$其中$f^{(n)}(a)$表示$ f(x)$的$n$阶导数在$x=a$处的值。
这个展开式的意义在于将一个复杂的函数$f(x)$用一个简单的多项式函数来近似表示。
二、泰勒级数的应用2.1. 函数近似泰勒级数广泛应用于函数近似的问题中,尤其在工程学和物理学中。
这些学科中需要处理许多涉及复杂函数的问题,而泰勒级数提供了一种有效的方式将这些函数近似成多项式函数。
例如,在计算机图形学中,背景图像和物体是由复杂函数来描述的,但由于计算机内存的限制,需要将这些函数近似成多项式函数。
泰勒级数是这些近似计算的理论基础。
2.2. 误差分析泰勒级数的另一个重要应用就是误差分析。
假设我们要计算一个函数$f(x)$在点$x=a$处的值,在计算机中我们不能真正得到一个无限的级数,只能计算级数中的前几项。
如果我们截断级数,这就会产生一个误差。
泰勒级数的误差可以通过残差项来表示,残差项是由级数中剩余未计算的项组成的。
残差项的取值可以用一个精确的上限来计算,这个上限取决于级数中被截断的项的数量和级数的光滑度。
2.3. 极值和方程求解泰勒级数也可以用来解决极值和方程求解问题,在微积分中,求解极值和方程的过程通常是优化问题。
泰勒级数可以被用来优化复杂多项式函数展开式的求解。
对于一个极值问题,可以使用泰勒级数展开式来确定局部极值点的位置和一些相关的信息。
这些信息可以告诉我们有关函数行为的重要特征,例如函数的单调性和凸性等。
8个常见的麦克劳林级数

8个常见的麦克劳林级数
麦克劳林级数是数学中的重要工具,它可以把一个函数表示为一系列具有特定形式的多项式之和。
这些多项式都是基函数的伸缩版本,基函数通常是一些简单的函数,我们会在下面的 8 个常见麦克劳林级数中看到。
1. 指数函数级数
指数函数级数是指按指数幂展开的级数,形式如下:
$$\mathrm{e}^{x} = \sum_{n=0}^{\infty} \frac{x^n}{n!}$$
这个级数在数学和物理中都具有广泛的应用。
它可以描述一些与指数和生长率有关的现象,例如放射性衰变和人口增长模型。
这个级数在计算机图形学和信号处理中非常常见,可以用来生成平滑的波形。
和正弦函数级数一样,这个级数也在计算机图形学和信号处理中广泛应用。
4. 自然对数级数
这个级数在微积分和复杂度分析中经常用到,也可以用来计算财务中的复利。
这个级数可以用来计算逆正切函数的值,也可以用来计算某些积分。
6. 二项式级数
7. 超几何级数
这个级数在统计学、计算物理学和量子力学中都有广泛应用。
这个级数在电磁学、光学和声学中经常用到,可以用来描述环形波浪等现象。
总结
这八个麦克劳林级数是数学中的基础工具,具有广泛的应用。
它们可以用来描述各种现象,从指数增长到正弦波形到离散概率分布。
了解这些级数的基本形式和应用,对于学习数学和科学学科都非常有帮助。
托马斯微积分课件8.7 Taylor and Maclaurin Series

Analysis.
1 1 1 n 1 2 f x 2 x 2 3 x 2 n 1 x 2 2 2 2 2 12 1 x2 1 x 0, 4 1 x 2 2 x 2
n
1 n 1 2 n 1
1 1 2 x 1,1 , x , . 2 2
1 n 1 n n n 1 1 n f x x 2 x 1 2 x , x , . 3 n 0 2 2 n 0 3 n 0
目录
上页
下页
返回
结束
Solution. The Taylor series generated by f at 0 is
The Taylor polynomial is
目录
上页
下页
返回
结束
Two questions: 1. How accurately do a function’s Taylor polynomial approximate the function on a given interval?
Step 3. Draw a conclusion.
目录 上页 下页 返回 结束
Example 5.
Solution.
目录
上页
下页
返回
结束
Example 6.
Solution.
目录
上页
下页
返回
结束
Example 7.
Solution.
目录
上页
下页
返回
结束
Example 10.
Solution.
x
电路理论:Taylor级数

n!
n0 n!
2)
1
1 z z2 zn zn,
( z 1)
1 z
n0
3)
1
1 z z2 (1)n zn (1)n zn,
1 z
n0
( z 1)
4) sin z z z3 z5 (1)n z2n1 ,
3! 5!
(2n 1)! ( z )
5) cos z 1 z2 z4 (1)n z2n ,
n0
设 C 为收敛圆z 1内从 0 到 z 的曲线,
( z 1)
将展开式两端沿 C 逐项积分, 得
z 1 dz z (1)n zndz
01 z
0 n0
即 ln(1 z) z z2 z3 (1)n zn1 z 1
23
n1
例3 把函数 f ( z ) 1 展开成 z 的幂级数. 3z 2
2! 4!
(2n)!
( z )
6) ln(1 z) z z2 z3 (1)n zn1 ,
23
n1
(1)n zn1
n0
n1
( z 1)
7)(1 z) 1 z ( 1) z2 ( 1)( 2) z3
2!
3!
( 1)( n 1) zn , ( z 1)
中的 Rn( x ) 0 ( n ).
如果函数 f ( z ) 在区域 D内解析,则 f ( z )在D 内有任意阶导数,
问题:在什么条件下,解析函数能表示成幂级数呢?
二、Taylor级数展开定理
定理 设 f (z) 在区域 D内解析, z0为 D内的一
点, 则对任何 z0 D , 及使得 U(z0 , ) D 的 0都有
f (z) cn(z z0 )n
泰勒级数

1.在数学中,泰勒级数(Taylor series)用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。
泰勒级数是以于1715年发表了泰勒公式的英国数学家布鲁克·泰勒(Sir Brook Taylor)来命名的。
通过函数在自变量零点的导数求得的泰勒级数又叫做迈克劳林级数,以苏格兰数学家科林·麦克劳林的名字命名。
拉格朗日在1797年之前,最先提出了带有余项的现在形式的泰勒定理。
实际应用中,泰勒级数需要截断,只取有限项,可以用泰勒定理估算这种近似的误差。
一个函数的有限项的泰勒级数叫做泰勒多项式。
一个函数的泰勒级数是其泰勒多项式的极限(如果存在极限)。
即使泰勒级数在每点都收敛,函数与其泰勒级数也可能不相等。
开区间(或复平面开片)上,与自身泰勒级数相等的函数称为解析函数。
定义在数学上,一个在实数或复数a邻域上的无穷可微实变函数或复变函数ƒ(x)的泰勒级数是如下的幂级数:这里,n! 表示n的阶乘而表示函数f在点a处的n阶导数。
如果a = 0,那么这个级数也可以被称为麦克劳伦级数。
解析函数柯西在1823年指出函数e−1/x²在x = 0处不解析。
如果泰勒级数对于区间(a-r, a+r)中的所有x都收敛并且级数的和等于f(x),那么我们就称函数f(x)为解析的(analytic)。
当且仅当一个函数可以表示成为幂级数的形式时,它才是解析的。
为了检查级数是否收敛于f(x),通常采用泰勒定理估计级数的余项。
上面给出的幂级数展开式中的系数正好是泰勒级数中的系数。
泰勒级数的重要性体现在以下三个方面:1幂级数的求导和积分可以逐项进行,因此求和函数相对比较容易。
2一个解析函数可被延伸为一个定义在复平面上的一个开片上的解析函数,并使得复分析这种手法可行。
3泰勒级数可以用来近似计算函数的值。
对于一些无穷可微函数f(x)虽然它们的展开式收敛,但是并不等于f(x)。
例如,分段函数,当x≠ 0且f (0) = 0,则当x = 0所有的导数都为零,所以这个f(x)的泰勒级数为零,且其收敛半径为无穷大,虽然这个函数f仅在x= 0处为零。
泰勒级数与麦克劳林公式

泰勒级数与麦克劳林公式泰勒级数和麦克劳林公式是微积分中非常重要的概念和工具。
它们在数学和物理学中广泛应用,能够将一个函数在某个点附近进行展开,从而简化复杂的计算。
本文将介绍泰勒级数和麦克劳林公式的定义、推导和应用,并探讨它们的异同点。
1. 泰勒级数泰勒级数是一种用无穷级数表示的函数展开式。
通过泰勒级数,我们可以用一个多项式来近似表示任意可微的函数。
设函数f的n阶导数在某个点a处存在,那么关于点a的泰勒级数展开式可以表示为:f(x) = f(a) + f’(a)(x-a) + f’‘(a)(x-a)²/2! + f’’’(a)(x-a)³/3! + …其中,f’(a)表示f在点a处的一阶导数,f’’(a)表示f在点a处的二阶导数,以此类推。
这个展开式是一个无穷级数,它的每一项都依赖于函数在点a处的导数。
泰勒级数的重要性在于它可以将一个任意复杂的函数表示成一个无穷级数,使得对该函数的研究和计算变得简单。
通过截取无穷级数的前n项,可以得到一个多项式函数,从而近似表示原函数。
当n越大时,这个多项式的逼近效果越好。
2. 泰勒级数的推导泰勒级数可以通过函数的n阶导数来推导得到。
考虑一个函数f(x)在点a处的泰勒级数展开:f(x) = f(a) + f’(a)(x-a) + f’‘(a)(x-a)²/2! + f’’’(a)(x-a)³/3! + …要得到泰勒级数的具体形式,我们需要计算函数f在点a处的各阶导数。
将f(x)在点a处展开为泰勒级数的前n项,我们只需要计算f在点a处的n阶导数。
对f(x)进行n次求导,并将x替换为a,我们可以得到f在点a处的n阶导数f⁽ⁿ⁾(a)。
将f⁽ⁿ⁾(a)代入泰勒级数的展开式中,就可以得到泰勒级数展开的n阶近似。
3. 麦克劳林公式麦克劳林公式是泰勒级数的一个特例,它是将泰勒级数展开到最低阶的情况。
麦克劳林公式将一个函数在零点附近进行泰勒展开,公式为:f(x) = f(0) + f’(0)x + f’‘(0)x²/2! + f’’’(0)x³/3! + …这里,f⁽ⁿ⁾(0)表示函数f在零点处的n阶导数。
微积分二知识点总结

微积分二知识点总结引言微积分是数学中的重要分支,用于研究函数的变化和曲线的性质。
微积分可以分为微分学和积分学两个部分。
本文将总结微积分二中的一些重要知识点,包括泰勒展开、泰勒级数、函数的傅里叶级数展开、常微分方程等内容。
泰勒展开和泰勒级数泰勒展开是函数在某一点附近用幂级数逼近的方法。
假设函数f(x)在x=a处具有n阶导数,那么泰勒展开可以表示为:f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2! + ... + f^n(a)(x-a)^n/n! + Rn(x)其中Rn(x)为余项,它表示当n趋向于无穷大时的误差。
泰勒级数是泰勒展开的一种特殊情况,当a=0时,泰勒展开可以简化为泰勒级数:f(x) = f(0) + f'(0)x + f''(0)x^2/2! + ... + f^n(0)x^n/n! + Rn(x)泰勒级数的应用非常广泛,可以用来近似计算各种函数的值。
傅里叶级数展开傅里叶级数展开是一种将周期函数表示为正弦和余弦函数的线性组合的方法。
假设f(x)是一个周期为2π的函数,傅里叶级数展开可以表示为:f(x) = a0/2 + Σ(an*cos(nx) + bn*sin(nx))其中a0、an和bn为函数f(x)的系数。
傅里叶级数展开的基本思想是将一个周期函数分解成多个简单的正弦和余弦函数的叠加。
这种表示方法在信号处理和频谱分析中非常有用。
常微分方程常微分方程是描述函数的变化规律与函数本身及其导数之间的关系的方程。
常微分方程可以分为一阶和二阶常微分方程。
一阶常微分方程可以表示为:dy/dx = f(x, y)其中f(x, y)为已知函数。
二阶常微分方程可以表示为:d^2y/dx^2 = f(x, y, dy/dx)常微分方程在物理学、工程学和经济学等领域中都有着广泛的应用。
总结微积分二是微积分的进阶课程,涵盖了泰勒展开、泰勒级数、函数的傅里叶级数展开、常微分方程等重要知识点。
微积分-泰勒级数
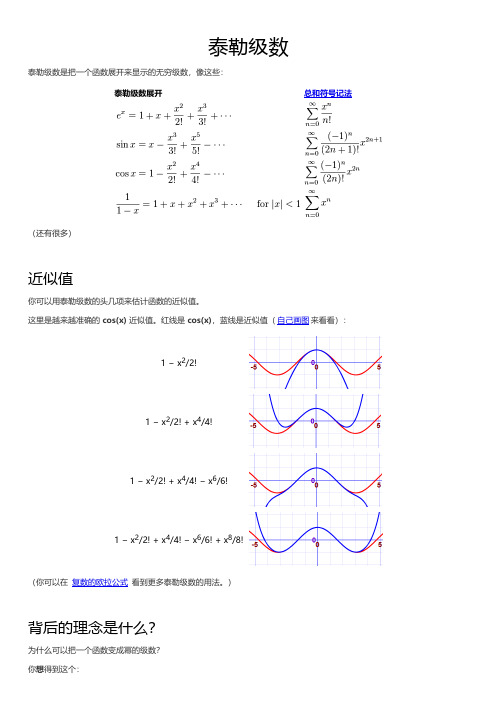
泰勒级数泰勒级数是把一个函数展开来显示的无穷级数,像这些:泰勒级数展开总和符号记法(还有很多)近似值你可以用泰勒级数的头几项来估计函数的近似值。
这里是越来越准确的 cos(x) 近似值。
红线是 cos(x),蓝线是近似值(自己画图来看看):1 − x2/2!1 − x2/2! + x4/4!1 − x2/2! + x4/4! − x6/6!1 − x2/2! + x4/4! − x6/6! + x8/8!(你可以在 复数的欧拉公式 看到更多泰勒级数的用法。
)背后的理念是什么?为什么可以把一个函数变成幂的级数?你想得到这个:f(x) = c0 + c1(x-a) + c2(x-a)2 + c3(x-a)3 + ……选一个 "a" 的值来求这些: c0、c1、c2、等等……这是用导数算出来的……简短回顾:导数告诉我们函数在任何一点的坡度。
你需要知道函数 f(x) 的导数和这些 导数基本规律:常数 的导数是 0x 的导数是 1x n 的导数是 nx n-1 (例子:x3 的导数是 3x2)我们用这个符号 ’ 来代表 "的导数"。
好,开始:求 c0:以 x=a,所有 (x-a) ,剩下的是:f(a) = c0 的项都等于零所以 c0 = f(a)求 c1:取f(x) 的导数:f’(x) = c1 + 2c2(x-a) + 3c3(x-a)2 + ……设 x=a,所有 (x-a) 的项都是零:f’(a) = c1所以 c1 = f’(a)求 c2:再取导数:f’’(x) = 2c2 + 3×2×c3(x-a) + ……设 x=a,所有 (x-a) 的项都等于零:f’’(a) = 2c2所以 c2 = f’’(a)/2看到规律了吗?每项是高一个阶的导数…………除以在这项以下所有的指数的积(我们可以用 阶乘记号 来写,例如 3! = 3×2×1)结果是:这便是求泰勒级数每一项的规律:取导数,除以 n!。
微积分中的泰勒级数

泰勒级数是微积分中的一个重要概念,由数学家布鲁诺·约瑟夫·泰勒于18世纪提出。
它在数学和物理学中具有广泛的应用,并为我们理解和解决问题提供了有力的工具。
泰勒级数是将某个函数表示成无限多项式的形式。
具体而言,给定一个函数f(x),如果该函数在某个点a处的各阶导数均存在,那么可以将f(x)展开成该点处的泰勒级数。
泰勒级数可以看作是对函数在某点附近进行多项式逼近的一种方法,它的表达式如下:f(x)=f(a)+f'(a)(x-a)+f''(a)(x-a)²/2!+f'''(a)(x-a)³/3!+...其中f'(a)表示f(x)在x=a处的一阶导数,f''(a)表示二阶导数,以此类推。
这个级数可以展开到无穷多项,表示了函数f(x)在点a附近的无限阶导数的信息。
泰勒级数的使用可以帮助我们进行函数的近似计算。
通过选择合适的近似点a,我们可以用泰勒级数来逼近函数的值,并且可以根据需要选择级数展开的项数来控制逼近的准确度。
当我们只需要获得一个近似值时,通常只需要保留级数展开的前几项即可。
泰勒级数的应用十分广泛。
在数学中,泰勒级数可以用来研究函数的性质,例如函数的最大值、最小值、凸凹性等。
它可以用来证明一些重要的数学定理,如拉格朗日中值定理和柯西中值定理。
在物理学中,泰勒级数被广泛应用于微分方程的求解和物理量的近似计算。
例如,在牛顿力学中,我们可以利用泰勒级数来求解运动方程,并在小的位移范围内进行物体运动的近似计算。
虽然泰勒级数是一个有用的工具,但是我们需要注意其使用的条件和限制。
首先,泰勒级数适用于在某个点附近的局部近似,不能用于全局表达。
其次,在使用泰勒级数进行逼近时,我们需要保证函数在展开点附近的所有阶导数存在。
还需要注意选择合适的展开点,以获得较好的逼近效果。
总之,泰勒级数是微积分中的一个重要概念,定义了函数的级数展开形式。
泰勒级数的定义和应用

泰勒级数的定义和应用1. 泰勒级数的概念泰勒级数(Taylor series)是一种在数学分析中常用的工具,它是一个函数在某一点的邻域内的无穷级数展开式。
其目的在于用一组多项式来逼近一个连续函数,使得在给定误差范围内,该多项式与原函数的值尽可能接近。
2. 泰勒级数的表达式设函数f(x)在点a处可导,且导数在该点连续,那么函数f(x)在点a处的泰勒级数可以表示为:[ f(x) = f(a) + f’(a)(x-a) + (x-a)^2 + (x-a)^3 + + (x-a)^n + R_n(x) ]其中,( f^{(n)}(a) )表示f(x)在点a处的第n阶导数,n为正整数;( R_n(x) )表示余项,表示泰勒级数中余项部分的误差。
当n趋于无穷大时,如果余项趋于0,则泰勒级数收敛于函数f(x)。
3. 泰勒级数的性质(1)收敛性:泰勒级数的收敛性与余项密切相关。
如果余项满足一定的条件,例如幂级数展开的余项为( R_n(x) (x-a)^{n+1} ),其中M为常数,则泰勒级数收敛。
(2)唯一性:在某一区间内,一个函数的泰勒级数是唯一的,除非该函数在该区间内具有多个极值点。
(3)对称性:如果函数f(x)是偶函数,则其泰勒级数在原点对称;如果函数f(x)是奇函数,则其泰勒级数关于原点对称。
4. 泰勒级数的应用泰勒级数在数学、物理、工程等领域有着广泛的应用,以下列举几个典型例子:(1)求解微分方程:泰勒级数可以用来求解许多微分方程,特别是那些形式复杂的非线性微分方程。
通过将方程两边展开成泰勒级数,可以简化方程求解过程。
(2)数值计算:在计算机计算中,为了提高计算精度,常常需要将函数在某一点附近展开成泰勒级数,然后利用级数的前几项进行数值计算。
(3)泰勒级数在物理学中的应用:在物理学中,许多自然现象可以用泰勒级数来描述,例如正弦函数、余弦函数等。
通过将物理量展开成泰勒级数,可以研究其在不同条件下的变化规律。
数学物理方法泰勒级数

数学物理方法泰勒级数小伙伴们!今天咱来聊聊数学物理方法里的泰勒级数哈。
一、泰勒级数是啥玩意儿。
泰勒级数啊,其实就是一种用多项式来逼近函数的方法。
想象一下哈,有些函数可能特别复杂,我们不太好直接去研究它的各种性质啥的。
这时候呢,泰勒级数就闪亮登场啦!它就像是一个神奇的工具,能把一个复杂的函数表示成一系列多项式的和。
比如说,对于一个在某点x_0附近有足够好性质的函数f(x),它的泰勒级数展开式大概长这样:f(x)=∑_n = 0^∞frac{f^(n)(x_0)}{n!}(x x_0)^n=f(x_0)+f'(x_0)(x x_0)+(f''(x_0))/(2!)(x x_0)^2+(f'''(x_0))/(3!)(x x_0)^3+·s这里面的f^(n)(x_0)表示函数f(x)在x_0点的n阶导数哦。
是不是看着有点晕乎?没关系,咱慢慢理解。
二、泰勒级数的作用。
泰勒级数的作用那可真是不小哈。
1. 函数近似计算。
有时候我们遇到一些复杂的函数,要计算它在某个点的值可能特别麻烦。
这时候呢,我们就可以用泰勒级数把它展开,然后只取前面有限的几项来近似计算函数的值。
比如说,计算sin x在x = 0.1的值,我们知道sin x的泰勒级数展开式是sin x = x-(x^3)/(3!)+(x^5)/(5!)-(x^7)/(7!)+·s。
如果我们只取前两项,那sin(0.1)≈ 0.1-((0.1)^3)/(6)= 0.1 0.000167≈0.09983,和真实值很接近啦。
2. 分析函数性质。
通过泰勒级数展开,我们还能更好地了解函数在某点附近的性质。
比如说,看它的导数情况,通过展开式中各项的系数,我们能知道函数在这一点的变化快慢等信息。
就像从一个函数的泰勒级数展开式中,我们可以看出它在展开点附近是单调递增还是递减,是凸的还是凹的。
3. 求解微分方程。
泰勒级数及其应用

泰勒级数及其应用张伯顺(湖北工业大学 武汉市 430068)摘要:泰勒级数是一种重要的数学工具,在诸多场合有着广泛的应用。
下文针对其在近似计算、极限计算、级数与广义积分的敛散性、说明无穷小的阶、不等式的证明及中值定理的证明等方面的应用展开论述与分析。
关键词:泰勒级数;近似;极限;敛散性;不等式;中值定理泰勒级数是我们应用较多的一种数学工具,在这里对其做一个简要的介绍,并论述一些它的应用。
1.泰勒级数的定义若函数)(0x f 在点0x 的某一临域内具有直到)1(+n 阶导数,则在该邻域内)(x f 的n 阶泰勒公式为:)()(!)()(!2)())(()()(00)(200''00'0x R x x n x f x x x f x x x f x f x f n n n +-++-+-+=其中, )(x R n 为余项,有两种形式:皮亚诺余项及拉格朗日余项。
在应用泰勒级数时,应选择不同的形式,一般是做近似计算时采用朗格朗日余项,做极限时采用皮亚诺余项。
以上函数展开式称为泰勒级数。
2.泰勒级数的应用2.1近似计算目前解决解决非线性问题的一种有效工具是泰勒级数,即利用泰勒展开式一阶近似,将非线性问题线性化,达到近似求解的目的。
如若一阶近似达不到近似精度标准的话,还可以在泰勒级数展开式中取更高的阶,在实际问题中我们经常会使用级数的二阶多项式求复杂问题的近似解。
例如:在我们日常生活中的路面结构中,路面结构是在不断遭受载荷的重压而产生振动,以致遭受破坏的,研究发现其振动是以非线性的形式进行的。
我们已知的线性振动形式为:kx x F =)(对于非线性振动负荷和变形的关系为:)()(x f x F =因为这里的)(x f 未知,所以我们可以借助于泰勒级数,将上式展开为:x kx F β±=,使其成为线性函数,进而分析出符合硬弹簧特性,经验证拟合水泥振动特性,达到了令人满意的效果。
常用泰勒级数

常用泰勒级数一、什么是泰勒级数?泰勒级数是一种用无限多个项的幂函数表示一个函数的方法,也被称为泰勒展开式。
它可以将任何光滑函数表示为一个无穷级数的形式,使得在某个区间内该级数收敛于原函数。
二、为什么要使用泰勒级数?使用泰勒级数可以将复杂的函数转化为简单的形式,从而更容易进行计算和分析。
此外,泰勒级数也可以用于近似计算,例如在物理学中常用于求解微积分方程或差分方程。
三、常用泰勒级数1. 正弦函数正弦函数可以表示为以下形式的泰勒级数:sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...其中“!”表示阶乘运算。
2. 余弦函数余弦函数可以表示为以下形式的泰勒级数:cos(x) = 1 - x^2/2! + x^4/4! - x^6/6! + ...同样地,“!”表示阶乘运算。
3. 指数函数指数函数可以表示为以下形式的泰勒级数:e^x = 1 + x + x^2/2! + x^3/3! + ...在这种情况下,“!”表示阶乘运算。
4. 自然对数函数自然对数函数可以表示为以下形式的泰勒级数:ln(1+x) = x - x^2/2 + x^3/3 - x^4/4 + ...其中x的值必须满足|x| < 1。
5. 反正切函数反正切函数可以表示为以下形式的泰勒级数:arctan(x) = x - x^3/3 + x^5/5 - x^7/7 + ...其中x的值必须满足|x| < 1。
四、总结泰勒级数是一种重要的数学工具,可以用于将复杂的函数转化为简单的形式,并且在计算和分析中具有广泛应用。
常用的泰勒级数包括正弦函数、余弦函数、指数函数、自然对数函数和反正切函数等。
熟练掌握这些常用泰勒级数对于理解高等数学和物理学等领域中许多重要概念非常有帮助。
数学史话之级数双子星泰勒和麦克劳林

数学史话之级数双⼦星泰勒和麦克劳林说了这么多⼤⽜了,今天科普君要说两个并不那么有名,但是只要学过⾼等数学⼜都知道的⼈,他们就是级数双⼦星--泰勒和麦克劳林。
布鲁克·泰勒于1685年出⽣在英国的埃德蒙顿,1701年进⼊剑桥⼤学学习,1714年获得法学博⼠学位。
不过他在⼤学期间也学习数学,师从梅钦(就是发明梅钦公式的那个⼈,梅钦公式是⽤来计算π值的实际可⽤的公式)。
1712年泰勒被选为英国皇家学会会员,并进⼊了仲裁⽜顿和莱布尼茨发明微积分优先权的委员会,后来因为健康原因离职了。
布鲁克·泰勒泰勒最早提出了"马步遍历棋盘问题",即在64格的棋盘上,每格只跳⼀次,怎么⾛完整个棋盘。
这个问题最终由欧拉进⾏了科学的处理。
1714年到1719年,泰勒完成了两部极其重要的数学著作:《正和反的增量法》和《直线透视》。
⽽泰勒真正闻名于世的就是他在微积分学中的将函数展开成⽆穷级数的定理:函数在⼀个点的邻域内的值可以⽤函数在该点的值和各阶导数值组成的⽆穷级数表现出来:泰勒级数然⽽,在半个世纪⾥,数学家们并没有认识到泰勒定理的重⼤价值,直到拉格朗⽇才真正地发现了它的价值所在。
拉格朗⽇认为这个定理是微积分的基本定理,并且给出了它的余项表达式(拉格朗⽇余项,就是上⾯那个公式⾥⾯等号前⾯的那三个点…),⽽泰勒定理的严格证明是由⼀个世纪之后的柯西来完成的。
拉格朗⽇余项泰勒的著作《正和反的增量法》为⾼等数学添加了⼀个新的分⽀,今天这个⽅法被称为有限差分⽅法。
它使任何单变量函数都可展成幂级数;同时亦使泰勒成了有限差分理论的奠基者。
泰勒在书中还讨论了微积分对⼀系列物理问题之应⽤,其中以有关弦的横向振动之结果尤为重要。
他透过求解⽅程导出了基本频率公式,开创了研究弦振问题之先河。
此外,此书还包括了他在数学上的其他创造性⼯作,如论述常微分⽅程的奇异解,曲率问题之研究等。
泰勒于1731年就不幸离世了。
泰勒对数学的贡献要⽐⼀条以他命名的定理⼤得多,但是由于不喜欢明确和完整地把他的思路写下来,因此他的许多证明没有遗留下来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例7. 将
展成 x-1 的幂级数.
1 1 解: 2 x 4 x 3 ( x 1)( x 3)
x 1 2 x 1 4
2
( x 1 2 )
n
x 1 ( x 1) n ( x 1) (1) 1 2 n 2 2 2
机动 目录 上页 下页 返回 结束
思考与练习
1. 函数 数” 有何不同 ? 处 “有泰勒级数” 与 “能展成泰 勒级
n
提示: 后者必需证明 lim Rn ( x) 0, 前者无此要求.
2. 如何求
的幂级数 ?
1 1 1 1 n 1 提示: y cos 2 x (1) 2 2 2 2 n 0 ( 2n) !
由泰勒级数理论可知, 函数 f ( x) 展开成幂级数的步
骤如下 :
第一步 求函数及其各阶导数在 x = 0 处的值 ; 第二步 写出麦克劳林级数 , 并求出其收敛半径 R ;
第三步 判别在收敛区间(-R, R) 内 lim Rn ( x) 是否为 0.
n
机动
目录
上页
下页
返回
结束
例1. 将函数
例5. 将函数
展开成 x 的幂级数.
上式右端的幂级数在 x =1 收敛 , 而 ln(1 x) 在 x 1 有 定义且连续, 所以展开式对 x =1 也是成立的, 于是收敛 区间为 利用此题可得
机动
目录
上页
下页
返回
结束
例6. 将
展成
的幂级数.
解: sin x sin ( x ) 4 4
) 1 cos( x ) sin( x 4 4
2
) cos sin( x ) sin cos( x 4 4 4 4
1 3 1 5 ( x ) ( x ) ( x ) 4 5! 4 4 3! 1 1 2 1 3 1 ( x ) ( x ) ( x ) 2 4 2! 4 3! 4
随着n变大,更近似,局部范围
还有什么办法可以从上式推出这个式子?
机动 目录 上页 下页 返回 结束
截断误差
3 n x x x ex 1 x Rn ( x) 2 ! 3! n! 2
其中
当n =9 时
机动
目录
上页
下页
返回
结束
2. 间接展开法 利用已知函数的展开式及幂级数的运算性质,
f ( n 1) ( ) Rn ( x) ( x x0 ) n 1 ( 在 x 与 x0 之间) (n 1) ! 称为拉格朗日余项 . f ( x) Pn ( x) Rn ( x)
机动 目录 上页 下页 返回 结束
若函数
的某邻域内具有任意阶导数 ) 2 f ( x0 ) f ( x0 )( x x0 ) 2! f ( n ) ( x0 ) ( x x0 ) n n! 为f (x) 的泰勒 (Taylor)级数.
将所给函数展开成 幂级数.
例4. 将函数
展开成 x 的幂级数.
解: 因为 1 2 n n 1 x x (1) x ( 1 x 1 ) 1 x
把 x 换成 x 2 , 得 1 2 4 n 2n 1 x x ( 1 ) x 2 1 x
展开成 x 的幂级数.
解: f ( n) ( x) e x , f ( n) (0) 1 (n 0 ,1,), 故得级数 1 n 1 2 1 3 1 x x 3! x x n! 2! 1 1 R lim 其收敛半径为 n n ! ( n 1) ! 对任何有限数 x , 其余项满足
机动 目录 上页
( 1 x 1 )
下页 返回 结束
1 解: f ( x) (1) n x n ( 1 x 1 ) 1 x n 0 从 0 到 x 积分, 得 x n ( 1 ) ln(1 x) (1) n x n d x x n 1 , 1 1 x x 1 1 n 0 n 0 n 1 0
n 1 4 (1) n x 2n , 2 n 1 ( 2n) !
x ( , )
机动
目录
上页
下页
返回
结束
作业
P703 从1到33的单数题
第五节 目录
上页
下页
返回
结束
备用题 1. 将下列函数展开成 x 的幂级数
解:
(1) n x 2 n ,
n 0
x (1,1)
第七节 函数的泰勒级数
第八章
一个幂级数的和函数在其收敛区间内是任意阶可导的, 反问题: 函数在一个区间上任意阶可导,如何将其表示 成为幂级数; 这个幂级数收敛吗?此级数的和函数与 这个函数相等吗? 求和 展开 和函数
用处:用多项式逼近一般函数,近似计算。
机动 目录 上页 下页 返回 结束
一、泰勒 ( Taylor ) 级数
sin( (n 1) ) 2
(n 1)!
x
n 1
n
1 x 3 1 x 5 (1) n 1 1 x 2n 1 sin x x 3 ! 5! ( 2n 1) !
机动 目录 上页 下页 返回 结束
P701 例9
机动
目录
上页
下页
返回
结束
类似的,可推出: 1 2 1 4 n 1 1 2n cos x 1 x x (1) x 2! 4! ( 2n) !
a0 f (0) a1 f (0)
f ( x) a1 2a2 x nan x n 1 ;
1 f (0) f ( x) 2!a2 n(n 1)an x n 2 ; a 2 2 !
f
( n)
( x ) n ! an ;
n 0
n x 2n (1) x 0
(1) n 2 n 1 x d x n 0 2n 1
x=±1 时, 此级数条件收敛, f (0)
4
, 因此
(1) n 2n 1 f ( x) x , x [1, 1] 4 n 0 2n 1
机动
目录
上页
若函数 该邻域内有 : 的某邻域内具有 n + 1 阶导数, 则在
f f ( x) f ( x0 ) f ( x0 )( x x0 ) ( x0 ) ( x x0 ) 2 2! (n) f ( x0 ) n ( x x0 ) Rn ( x) n! 此式称为 f (x) 的 n 阶泰勒公式 , 其中
n
n
f ( x) S n 1 ( x) Rn ( x)
n
lim Rn ( x) lim f ( x) S n 1 ( x) 0 ,
n
机动 目录
x ( x0 )
上页 下页 返回 结束
定理2. 若 f (x) 能展成 x 的幂级数, 则这种展开式是 唯一的 , 且与它的麦克劳林级数相同. 证: 设 f (x) 所展成的幂级数为 则
1 f ( n ) (0) an n !
显然结论成立 .
机动 目录 上页 下页 返回 结束
泰勒(中值)定理 :
时, 有 f ( x0 ) f ( x0 ) f ( x0 )( x x0 ) ( x x0 ) 2 2! (n) f ( x0 ) n ( x x0 ) Rn ( x) ① n! 其中 Rn ( x) 阶的导数 , 则当
f ( x) limn Pn ( x)
定理1 . 设函数 f (x) 在点 x0 的某一邻域
内具有
各阶导数, 则 f (x) 在该邻域内能展开成泰勒级数的充要 条件是 f (x) 的泰勒公式中的余项满足: lim Rn ( x) 0 .
f ( n ) ( x0 ) n f ( x ) ( x x ) , x ( x0 ) 证明: n! 0 n 0 f ( k ) ( x0 ) k ( x x0 ) 令 S n 1 ( x) k! k 0
e n n 1 x x e (n 1)! ( 在0与x 之间) 1 1 1 x 2 3 故 e 1 x x x x n , 2! 3! n!
机动 目录 上页 下页 返回 结束
例2. 将
解: f
(n)
展开成 x 的幂级数.
( x)
f
(n)
1 8
(1)
n 0 n
1 2
n2
1 2
2n 3
( x 1) n
机动
( 1 x 3 )
目录 上页 下页 返回 结束
内容小结
1. 函数的幂级数展开法 (1) 直接展开法 — 利用泰勒公式 ; (2) 间接展开法 — 利用幂级数的性质及已知展开 式的函数 . 2. 常用函数的幂级数展开式 1 2 1 n x e 1 x x x , 2! n!
x ( , )
n ( 1 ) ln(1 x) x 1 x 2 1 x 3 1 x 4 x n 1 n 1 2 3 4 x (1, 1]
机动 目录 上页 下页 返回 结束
2 n 1 x3 x5 x7 x n ( 1 ) sin x x 3! 5! 7 ! (2n 1) ! x ( , ) 2n x2 x 4 x6 x n ( 1 ) cos x 1 2 ! 4 ! 6! ( 2n) ! x ( , ) m(m 1) 2 m (1 x) 1 m x x 2! m(m 1) (m n 1) n x x (1, 1) n! 当 m = –1 时 1 1 x x 2 x 3 (1) n x n , x (1, 1) 1 x
