青岛版五年级下册数学版 第7单元 长方体和正方体 习题课件 7.9长方体和正方体体积的统一公式
五年级下册数学单元衔接题-七、包装盒——长方体和正方体 青岛版(含答案)

第七单元长方体和正方体1.一块长方形铁皮如图所示,剪掉四个角上所有阴影部分的正方形(每个正方形都相同)后,沿虚线折起来,做成没有盖子的长方体铁盒,该铁盒的长是()cm,宽是()cm,高是()cm,表面积是()cm2,容积是()cm3(铁皮厚度不计)解析:结合题意观察图形可知,这个铁盒的长、宽、高分别是(40-5×2)厘米、(20-5×2)厘米、5厘米,再利用长方体的表面积公式和长方体的体积公式分别计算即可。
在计算表面积时应注意是5个面的面积。
解答:30,10,5,700,1 500。
2.用一根48厘米的铁丝焊接成一个最大的正方体框架,这个框架的每条边应该是多少厘米?解析:根据正方体的特征,它的12条棱长都相等,把48厘米平均分成12份,每份就是一条棱的长度。
解答:48÷12=4(厘米)答:这个框架的每条边应该是4厘米.3.用棱长1厘米的小正方体摆成稍大一些的正方体,至少需要多少个小正方体?解析:题目要求至少要多少个棱长为1厘米的小正方体,那么拼成的棱长应尽量小,所以应该考虑棱长为2的立方体,体积是8立方厘米,所以要8个。
解答:2×2×2=8(个)答:至少需要8个小正方体。
4.一个长方体的容器(如图),里面的水深5cm,把这个容器盖紧后竖放,使长10cm、宽8cm的面朝下,这时里面的水深是多少厘米?解析:首先根据长方体的体积(容积)公式求出容器中水的体积,然后用水的体积除以竖放后以长10cm、宽8cm的面作为底面时的底面积(10×8),即可求出水深。
解答:20×10×5÷(10×8)=12.5(厘米)。
答:这时里面的水深是12.5厘米。
5.将下面的硬纸板按照虚线折成一个立方体,哪个面与哪个面相对?解析:通过实验可以看到带有标号的面7与10,面8与11,面9与12是相对的面。
解答:面7与10,面8与11,面9与12是相对的面。
五年级下册数学单元测试-7.长方体和正方体 青岛版(六三)(含答案)

五年级下册数学单元测试-7.长方体和正方体一、单选题1.下图中有________个长方体。
( )A. 1B. 2C. 3D. 42.一个西瓜的体积大约是8()A. 立方厘米B. 立方分米C. 立方米D. 立方毫米3.正方体是特殊的()。
A. 长方体B. 圆柱体C. 球D. 圆锥体4.如图,沿虚线把长方体木料刚好锯成2个同样的正方体,这样表面积比原长方体增加了32cm2。
原来长方体木料的表面积是()cm。
A. 64B. 128C. 160D. 3205.求做一个抽屉要用的木板的面积,是要求这个抽屉的()A. 表面积.B. 上、下、左、前、后5个面的面积.C. 前、后、左、右、下5个面的面积.二、判断题6.长、宽、高相等的长方体是正方体.7.一个正方体木料,加工成一个最大的圆锥,圆锥的体积是正方体体积的.()8.这两个长方体的体积相等,所以它们的表面积也相等。
9.在长方体上,我们可以找到两条既不平行也不相交的线段。
10.一个长方体有四个面完全一样,它的另外两个面一定是正方形。
三、填空题11.棱长7厘米的正方体,表面积是________12.填空(1)正方体有________个面,每个面都是面积相等的________;(2)正方体有________条棱,每条棱的长度________;(3)正方体有________个顶点,从一个顶点出发的三条棱都叫做正方体的________.正方体也可以说是长、宽、高都相等的________.13.一个长方体,表面积是,底面积是,底面周长是36cm.这个长方体的体积是________ .14.一个长方体,表面全部涂成红色后,被分割成若干个体积都等于1立方厘米的小正方体,如果在这些小正方体中,不带红色的小正方体的个数是8.两面带红色的小正方体的个数至多为________.15.用一根铁丝刚好可以焊接成一个棱长是6cm的正方体柜架,如果用这根铁丝焊接成一个长4cm,宽3cm 的长方体,它的高是________ cm.四、解答题16.一个正方体,每个面上分别写着数字1~6,有一个人从不同的角度观察到下图的情况,问这个正方体上相对的两个面上的数字各是几?17.一个长方体玻璃缸,从里面量,长10dm,宽8dm,高5dm,里面水深4.5dm。
五年级下数学(课课练)第7单元第1课时-长方体和正方体的认识青岛版

青岛版(2014秋)五年级下数学(课课练)第7单元第1课时-长方体和正方体的认识一、填空。
1.长方体有()个面,一般都是()形,也可能有相对的两个面是()形,相对的两个面的面积();有()条棱,相对的()条棱的长度相等;有()个顶点。
2.正方体有()个面,每个面都是()形,它们的面积都(),有()条棱,长度都(),有()个顶点。
3.两个面相交的()叫做棱。
三条棱相交的()叫做顶点。
4. 相交于一点的三条棱分别叫做长方体的()、()、()。
5. 正方体是长、宽、高都相等的(),它是一种特殊的()。
6. 一个长方体,它的长、宽、高分别是9厘米、3厘米和2.5厘米。
它上面的面长()厘米,宽()厘米,左边的面长()厘米,宽()厘米,相交于一个顶点的三条棱长之和是()厘米。
7. 一个长方体的棱长和是36厘米,从一个顶点出发的三条棱的和是()厘米。
8. 用一根24厘米长的铁丝焊成一个正方体框架,这个正方体框架的棱长是()厘米。
9. 一个正方体的棱长是5厘米,它的表面积与底面积的比是()∶(),比值是()。
10. 一个长方体的底面积是0.2平方分米,高是8分米,它的体积是()立方分米。
11. 表面积是54平方厘米的正方体,它的体积是()立方厘米。
12. 一个长方体的棱长总和是120厘米,长、宽、高的比是5∶3∶2,这个长方体的体积是()立方厘米。
13. 长方体的长、宽各扩大2倍,高不变,体积将扩大()倍。
于一点的三条棱分别叫做长方体的()、()、()。
14. 一个棱长是3m的正方体,它的棱长总和是()m,其中一个面的面积是()㎡。
15. 一个正方体的棱长之和是84dm,这个正方体的一条棱长()dm。
16. 一根长96厘米的铁丝围成一个正方体,这个正方体的棱长是()厘米。
17. 一个长方体的棱长总和是80厘米,长10厘米,宽是7厘米。
高是()厘米。
18. 至少需要()厘米长的铁丝,才能做一个底面周长是18厘米,高3厘米的长方体框架。
青岛版五年级数学下册课件第7单元长方体和正方体

50cm
= 6200(平方厘米) 答:至少需要6200平方厘米的纸板。
二、合作探索
根据刚才的解题过程,你能总结出长方体的表面积计算公式吗?
前、后面: 50×30×2 = 3000(平方厘米) 左、右面: 20×30×2 = 1200(平方厘米) 上、下面: 50×20×2 = 2000(平方厘米)
三、自主练习
1.下面的平面图哪些可以折成长方体或正方体?
长方体
长方体
长方体
正方体
三、自主练习
2.右图是一个长方体。
(1)上面的面积是( 24 )平方厘米; (2)前面的面积是( 30 )平方厘米;
(3)右面的面积是( 20 )平方厘米;
(4)表面积是( 148 )平方厘米。
三、自主练习
3. 计算下面图形的表面积。
的占地面积是多少,列式为
20×20
辨析:不能正确区分求物体的占地面积还是表面积。
三、自主练习
9.计算下面图形的表面积。
答:12×8×4+8×8×2=512(cm2)
辨析:易把特殊长方体(有2个面是正方形)当作
=34(米)
答:至少需要34米铝条。
下面:5×0.5=2.5(平方米)
答:前面是15平方米、右面 是1.5平方米、下面是2.5平
方米。
三、自主练习
4.哪几个面可以围成一个长方体?
① ③ ⑦
⑤
②
④
⑥
⑧
三、自主练习
5. 用12个棱长是1厘米的小正方体拼成一个长方体,有几种不
同的拼法?拼成的长方体的长、宽、高各是多少?
情境导入 合作探索 自主练习 回顾反思 课后作业
青岛版五年级下册《第7章_长方体、正方体》小学数学-有答案-单元测试卷(2)

青岛版五年级下册《第7章长方体、正方体》2014年单元测试卷(2)一、想一想,算一算,填一填.(每空1分,共30分)1. 长方体有________个顶点,有________条棱,有________个面。
相交于长方体一个顶点的三条棱的长度分别叫做它的________、________和________.2. 一个长方体的长、宽、高分别是7厘米、6厘米和5厘米,它的棱长总和是________ 厘米。
做这样一个无盖的长方体盒子,需要________平方厘米材料。
3. 在横线里填上适当的数。
9020立方厘米=________升 4.07立方分米=________立方厘米3.02立方米=________立方分米9.08立方分米=________毫升。
4. 一个长方体的金鱼缸,长是8分米,宽是5分米,高是6分米,不小心前面的玻璃被打坏了,修理时配上的玻璃的面积是________平方分米。
5. 把3升盐水装入容积是250毫升的盐水瓶里,能装________瓶。
6. 挖一个长和宽都是5米的长方体菜窖,要使菜窖的容积是50立方米,应该挖________米深。
7. 在横线里填上适当的单位名称。
8. 一块长25厘米,宽12厘米的,厚8厘米的砖,所占的空间是________立方厘米,占地面积最大是________平方厘米。
9. 正方体的棱长扩大3倍,棱长总和扩大________倍,表面积扩大________倍,体积扩大________倍。
10. 一个长方体平均分成两个正方体(如图),正方体的棱长是4米,则这个长方体的侧面积是________,体积是________.二、判断对错(每题1分,共5分)把一个正方体的橡皮泥揉捏成一个长方体,它的体积和表面积都不变。
________(判断对错)长方体中相邻的两个面不可能是正方形。
________.(判断对错)棱长是6厘米的正方体,它的表面积和体积相等。
________.(判断对错)把一块正方体橡皮泥捏成一个长方体后,虽然它的形状变了,但是它所占有的空间大小不变。
五年级下册数学习题课件-3长方体和正方体人教版(共47张PPT)

每个面的面积:_2_×__2_=__4_(_d_m_2_)_____。 正方体的表面积:__4_×__6_=__2_4_(_d_m_2)______。
五年级下册数学习题课件-3 长方体和正方体 人教版(共47张PPT)
4. 一个不锈钢花瓶的形状是正方体,棱长和是36 cm,制作这个花瓶至少需要 不锈钢板多少平方厘米? 36÷12=3(cm) 3×3×6=54(cm2)
20×30×2+8×30×2+20×8=1840(cm2)
3. 一个长方体包裹,它的长、宽、高分别是5 dm,4 dm,2 dm。如果实际用纸 是表面积的1.4倍,那么包装这个包裹至少要用多少平方分米的包装纸? (5×4+5×2+4×2)×2×1.4=106.4(dm2)
4. 小区门前的水池的形状是长方体,它的宽是6 m,长是宽的1.5倍,深1.2 m。 如果把水池的四周和底面贴上瓷砖,那么贴瓷砖的面积是多少平方米? 长:6×1.5=9(m) 9×6+9×1.2×2+6×1.2×2=90(m2)
3 长方体和正方体
第1课时 长 方 体
1. 仔细想,认真填。 (1) 同学们正在用一些小棒和橡皮泥拼搭长方体的框架。
① 上图是小明已经拼搭好的部分,他还需要( 5 )个橡皮泥小球、( 1 ) 根9 cm小棒、( 2 )根5 cm小棒、( 3 )根3 cm小棒,就可以拼搭成一个长 ( 9 )cm、宽( 5 )cm、高( 3 )cm的长方体框架。 ② 长方体框架上面是( 长方 )形,长是( 9 )cm,宽是( 5 )cm。 ③ 长方体框架( 左 )面和( 右 )面的长是5 cm,宽是3 cm。 ④ 把长方体框架的所有棱都粘上胶带,至少需要( 68 )cm长的胶带。 (2) 在长、宽、高不全相等的长方体中,最多可以有( 2 )个面是正方形。 在这样的长方体中,有( 4 )个长方形的面相同。
青岛版小学数学 五年级下册《第七单元 长方体和正方体:7.9 长方体和正方体体积的统一公式》练习课件PPT

提升点2 用操作法解决长方体的容积问题
7.一块长方形纸板,长为30 cm,宽为20 cm,先在 纸板的四个角上分别剪掉一个边长为5 cm的小正 方形,再沿虚线折成一个无盖纸盒。这个纸盒的 容积是多少?(纸板的厚度忽略不计) (30-5×2)×(20-5×2)×5=1000(cm3) 答:这个纸盒的容积是1000 cm3。
七 包装盒——长方体和正方体
第9课时 长方体和正方体体积的统一公式
QD 五年级下册
习题课件
提示:点击 进入习题
1
2
3
4
5
6
7
8
知 识 点 长方体和正方体体积的统一公式
1.填一填。 (1)长方体或正方体底面的面积叫作( 底面积 )。 (2)长方体(或正方体)的体积=( 底面积 )×( 高 ),用
字母可以表示为V=( Sh )。
提升点1 运用长(正)方体的体积公式解决问题
5. 把一个长12 cm、宽10 cm、高9 cm的长方体削成一 个最大的正方体。这个正方体的体积是多少?
9×9×9=729(cm3) 答:这个正方体的体积是729 cm3。
6.一个长方体鱼缸,从里面量长25 cm,宽12 cm,高 16 cm。往里面倒入3 L水,水深多少厘米?
0.3×0.3×5×500=225(m3) 答:这些方木一共有225 m3。
易 错 点 计算一个数的立方和平方时理解有误
4.计算。
63=( 216 )
52=( 25 )
23=( 8 )
32=( 9 )
x+x+x=( 3x )
x•x•x=( x3 )
辨析:一个数的立方表示3个这样的数相乘, 一个数的平方表示2个这样的数相乘。
青岛版五下数学第七单元讲解

青岛版五下数学第七单元讲解同学们,咱们现在来讲讲青岛版五年级下册数学的第七单元啊。
一、单元主题与总体印象。
这个单元啊,就像是一个充满挑战的小王国,里面有很多有趣的数学知识在等着咱们去探索呢。
这一单元主要是关于长方体和正方体的内容,这俩家伙在咱们的生活里可到处都是影子,像咱们住的房子,有的房间就是长方体形状的,还有那些小盒子,很多都是正方体或者长方体的。
二、长方体和正方体的认识。
1. 面、棱、顶点。
咱们先来说说长方体。
长方体就像一个有六个面的小盒子,这六个面啊,还分成三组相对的面,每组相对的面都长得一模一样呢。
就好比你有三对双胞胎朋友,每对双胞胎都长得很像。
而且长方体还有棱,棱就是面与面相交的那条线,一共有12条棱。
这些棱也不是随便长的,它们分成三组,每组里的四条棱长度是相等的。
还有顶点,就是三条棱相交的那个点,长方体有8个顶点。
正方体就更有意思啦,正方体可以说是长方体的特殊情况。
正方体的六个面啊,那是完全一样的正方形,12条棱的长度也都相等,它的8个顶点也和长方体一样,规规矩矩地待在那儿。
2. 长、宽、高。
对于长方体来说,相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
你可以想象一下,长就像长方体躺在地上时最长的那条棱,宽就是比较短的那条横向的棱,高呢,就是直直往上的那条棱。
不过呢,这长、宽、高可不是固定不变的,如果把长方体换个方向放,原来的宽可能就变成高了,就像你把盒子转个方向,它的各个边的“身份”也跟着变了。
三、长方体和正方体的表面积。
表面积啊,就像是给长方体或者正方体穿的一层衣服的面积。
比如说,你要给一个长方体的盒子包上一层漂亮的纸,那这层纸的大小就是这个长方体的表面积。
长方体的表面积就是它六个面的面积之和。
正方体因为六个面都一样,所以它的表面积就更好算啦,就是一个面的面积乘以6,因为正方体一个面的面积 = 棱长×棱长,那它的表面积就是棱长×棱长×6。
青岛版五年级数学下册第七单元 长方体和正方体附答案

青岛版五年级数学下册单元培优测试卷第七单元长方体和正方体一、填空。
(每空1分,共17分)1.300 mL=( )L 1.05 m3=( )dm34500 cm3=( )dm3=( )L2.右图是一个无盖的正方体纸盒展开图(每个小正方形边长2厘米)。
与①相对的面是( ),该正方体纸盒的容积为( )立方厘米。
(盒壁厚度忽略不计)3.晓丽家有两块长8分米、宽5分米和两块长5分米、宽4分米的长方形玻璃,爸爸想用这几块玻璃做一个无盖的长方体玻璃缸,还需要一块长( )分米、宽( )分米的长方形玻璃,做这个玻璃缸一共需要( )平方分米玻璃,它最多可盛水( )立方米。
4.聪聪用一根36 dm长的铁丝做成了一个正方体框架,这个框架的棱长是( )dm。
如果在这个框架的表面糊一层纸,至少需要( )dm2的纸,得到的正方体的体积是( )dm3。
5.在一个长9 dm、宽6 dm、高8 dm 盛有水的长方体水槽中,放入一块珊瑚石(完全浸没在水中,水未溢出),水面升高了4 cm,这块珊瑚石的体积是( )dm3。
(水槽壁厚度忽略不计)6.一个长方体的棱长之和是92厘米,已知长是10厘米,宽是7厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
7.一根长方体木材,长4.5 米,沿横截面截成若干段长0.9 米的小长方体,表面积增加了3.2 平方分米,原长方体木材的体积是( )立方分米。
二、判断。
( 对的打“√”,错的打“×”)(每小题2分,共10分)1.当长方体有两个相对的面是正方形时,另外四个面是完全相同的长方形。
( )2.两个棱长总和相等的长方体和正方体,它们的体积也相等。
( ) 3.正方体的棱长扩大到原来的3倍,体积就扩大到原来的27倍,表面积扩大到原来的3倍。
( )4.一个容积是50升的微波炉,它的体积一定大于50立方分米。
( ) 5.把一个棱长1 dm的正方体切成棱长1 cm的小正方体,可以切成100 个。
青岛版五年级下册数学教案:07-4-2(长方体和正方体的容积)

青岛版五年级下册数学教案:07-4-2(长方体和正方体的容积)教学目标
1.了解长方体和正方体的特性和区别;
2.学会计算长方体和正方体的容积;
3.能够应用所学知识解决实际问题。
教学重点和难点
1.计算长方体和正方体的体积;
2.培养学生的数学思维和应用能力。
教学内容
1.长方体和正方体的特性和区别;
2.计算长方体和正方体的体积;
3.实际问题练习。
教学过程
导入(5分钟)
1.引出本课要学习的内容,介绍长方体和正方体的特性和区别;
2.通过图片、实物等方式让学生感受长方体和正方体的不同。
讲解(20分钟)
1.讲解长方体和正方体的定义、特性、公式;
2.通过教材例题和讲解,引导学生掌握计算长方体和正方体体积的方法;
3.发现并讲解学生容易出错的点,帮助学生建立正确的思维模式。
实践(25分钟)
1.发放练习册,进行课堂练习;
2.引导学生根据实际问题,应用所学知识,计算长方体和正方体的体积;
3.督促学生在练习中发现并解决问题。
拓展(10分钟)
1.通过引导,让学生关注长方体和正方体的应用;
2.谈论应用长方体和正方体的好处。
总结(5分钟)
1.总结本节课的内容;
2.督促学生巩固所学知识;
3.复习重点难点。
教学评估
1.课堂练习成绩;
2.教师观察;
3.自我评估和互评。
教学反思
1.教学目标设置是否明确;
2.讲课方式是否生动;
3.教材例题是否充分;
4.练习册是否合理;
5.学生是否理解得到。
小学数学五年级下册7.4-长方体和正方体(长方体和正方体体积)-青岛版

三、自主练习
1. 你知道它们的体积各是多少吗?
42
27
三、自主练习
2.计算下面图形的体积。
5×8×5=200(cm3)4×4×4=64(dm3)20×4×5=400(m3)
三、自主练习
3. 一段长3米的方木,横截面是一个边长0.2米的正方 形。50根这样的方木,体积是多少立方米?
0.2×0.2×3 = 0.12(立方米)
0.12×50 = 6(立方米) 答:50根这样的方木,体积是 6 立方米。
三、自主练习
4. 右图是一瓶清洁剂。瓶的形状近似长方体,它的长是 7.3厘米,宽4厘米,高22厘米。这瓶清洁剂的容积 是多少毫升?(瓶壁厚度忽略不计)
怎样求饮料箱的体积呢?啤 酒箱呢?
桃汁饮料盒能盛多少 升饮料呢?
二、合作探究
怎样求饮料箱的体积呢? 求饮料箱的体积,就是求长方体和正方体的体积。 我们借助学具来研究求长方体和正方体体积的方法。
3cm 6cm 2cm
2cm 4cm
5cm
3cm 3cm 3cm
二、合作探究
怎样求长方体和正方体的体积呢?
7.3×4×22 = 642.4(立方厘米)
624.4立方厘米 = 642.4毫升 答:这瓶清洁剂的容积是 642.4 毫升。
5cm
5×4×2=40(立方厘米)
长方体的体积是40立方厘米。
二、合作探究
摆一个长棱是3厘米的正方体,并算出它的体积是多少立 方厘米。
木块总数:
3cm
3×3×3=27(个)
体积:
青岛版六三制五年级下册数学单元测试卷第七单元 包装盒——长方体和正方体(含答案)
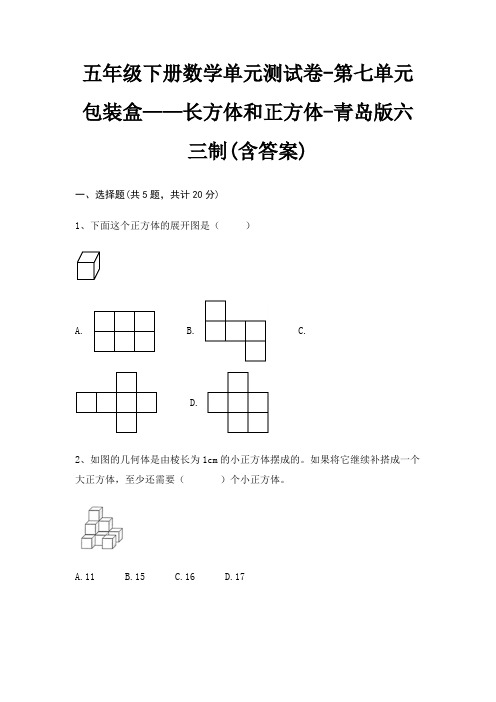
五年级下册数学单元测试卷-第七单元包装盒——长方体和正方体-青岛版六三制(含答案)一、选择题(共5题,共计20分)1、下面这个正方体的展开图是()A. B. C.D.2、如图的几何体是由棱长为1cm的小正方体摆成的。
如果将它继续补搭成一个大正方体,至少还需要()个小正方体。
A.11B.15C.16D.173、一种长方体盒装纯牛奶,外包装上标着“净含量600ml“,从外面测量长8厘米,宽5厘米,高15厘米.根据以上数据,你认为“净含量”的标注是()A.真实的B.虚假的C.无法确定4、一个正方体的棱长扩大2倍,它的体积扩大()倍。
A.2B.4C.8D.165、一个正方体,棱长是55分米,它的体积是()立方米。
A.166375B.166.375C.18150D.18.15二、填空题(共8题,共计24分)6、一个正方体的棱长和是48厘米,这个正方体的棱长是________厘米.7、还缺几块?缺________块8、做一个长8分米,宽4分米,高3分米的鱼缸,用角钢做它的框架,至少需要角钢________米,至少需要玻璃________,最多可装水________。
.9、将2升水倒入下图中的两个长方体水槽中,使它们水面高度相等,这个高度是________厘米。
(单位:厘米)10、一个长方体,长8cm,宽6cm,高2cm,它的棱长和是________,表面积是________,体积是________。
11、如下图,把长方体木块截成两段后,表面积增加36dm2,原来木块的体积是________dm3。
12、一个正方体的棱长总和是36分米,这个正方体的表面积和体积各是________.13、一个正方体的棱长扩大为原来的2倍,那么正方体的棱长之和就会扩大为原来的________倍,底面积就会扩大为原来的________倍,侧面积就扩大为原来的________倍,体积就扩大为原来的________倍.三、判断题(共4题,共计8分)14、用4个同样大小的小正方体能拼成一个大正方体。
最新版本新青岛版数学五年级下册《长方体、正方体的体积》ppt课件

棱长 棱长 棱长
正 长方体的体积 = 棱长 长 × 棱长 宽 × 棱长 高
a 棱长
棱长 a 棱长 a
V = a a a 棱长 棱长 长方体的体积 = 棱长 长 × 宽 × 高 V = a3
一块正方体石料,棱长 是6dm,这块石料的体 积是多少立方分米? V = a3 =63 =6×6×6 =216(dm3)
5 5 5 9
2 1.5
填一填
一根长方体木料,长5m,横截面的面积 是0.06m2。这根木料的体积是多少?
0.06m2
建筑工地要挖一个长50m,宽30m,深 50cm的长方体土坑,控出多少方的土?
一块棱长30cm的正方体冰块, 它的体积是多少立方厘米?
挖一个长和宽都是 5米的长方体菜窖, 要使菜窖的窖是50 立方米,应挖多少 米深?
答:少7立方分米。
※2、一个长方体长8厘米、宽 5厘米,
160÷8÷5=4(厘米) 答:它的高是4厘米。
※3、一个长方体的长是6厘米 宽5厘米,高4厘米,如果把高 截去1厘米,它的体积减少了 多少立方厘米? 6×5×1=30(立方厘米)
答:它的体积减少了30立方厘米。
答:这块石料的体积是216 dm3。
底面Leabharlann 底面长方体或正方体底面的面积叫底面积。
h
a
b
底面积
长方体的体积=长×宽×高
V = sh
a
a
a
底面积
正方体的体积=棱长×棱长×棱长
V = sh
底面
底面
长方体(或正方体)的体积=底面积×高
V = sh
努 力 吧 !
计算下面立体图形的表面积和体积。 (单位:分米)
五年级数学下册《长方体、正方体表面积和体积的比较》课件 人教新课标版

长方体(或正方体)的表面积是指
长方体(正方体)6个面 的总面积。
长方体(或正方体)的体积是指
长方体(正方体)所占空 间的大小。
表面积的计量单位是
平方厘米 平方分米 平方米
体积的计量单位是
立方厘米 立方分米 立方米
要计算一个长方体的表面积, 需要测量哪些长度?
长 宽
高
要计算它的体积呢?
长 宽 高
平方厘米。体积是27立方厘米
4、一本书的长是20cm,宽是10cm, 高是1cm,请问给这本书包书皮, 最少用多少平方分米的纸?这本书 的体积是多少立方分米?
5、一种汽车油箱,从里面量长4分米, 宽和高都是2分米。油箱的容积是多少升? 如果用铁皮做这个油箱,至少要用多少铁 皮?如果一天用掉1升油,一箱油能用几 天?
• 6、由3个同样的长为1厘米,宽 为2厘米,高为3厘米的小长方体, 拼成一个大长方体,可能有几种 不同的拼法?如果用包装纸把他 们包起来,哪种情况最省包装纸?
注意:要想让最后的大长方体表 面积最小,就要让最大的面尽量 多的重合。
判断:
• 体积一定的情况下,表面积不一定 一样。
思考题 从一个长方体上截下一个体积是32立方 厘米的小长方体后,剩下的部分正好是 一个棱长为4厘米的正方体。原长方体的 表面积是多少平方厘米?
怎样计算长方体的表面积?
(长×宽+长×高+宽×高)×2
怎样计算长方体的体积?
长×宽×高
怎样计算正方体的表面积
棱长×棱长×6
怎样计算正方体的体积?棱源自×棱长×棱长类别意义
计量单位 计算方法 条件
(长×宽+长×高 +宽×高)×2
表 长方体 6 个面 平方厘米 面 平方分米 的总面 积 正方体 平方米 积
青岛版6年制数学五年级下册《七、包装盒——长方体和正方体》练习题含答案
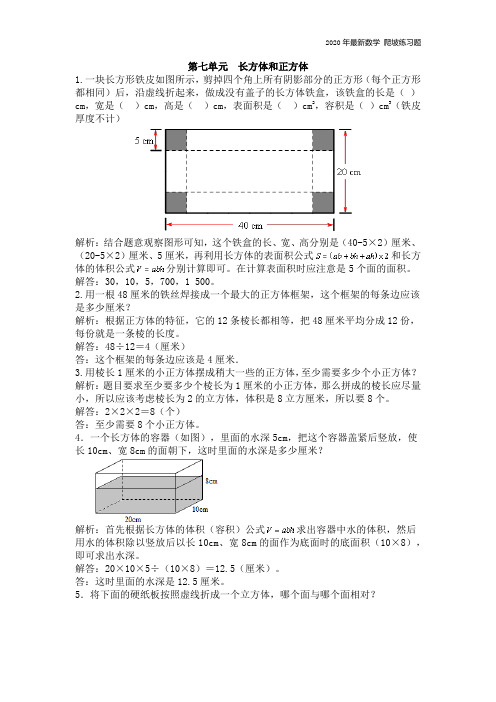
第七单元长方体和正方体1.一块长方形铁皮如图所示,剪掉四个角上所有阴影部分的正方形(每个正方形都相同)后,沿虚线折起来,做成没有盖子的长方体铁盒,该铁盒的长是()cm,宽是()cm,高是()cm,表面积是()cm2,容积是()cm3(铁皮厚度不计)解析:结合题意观察图形可知,这个铁盒的长、宽、高分别是(40-5×2)厘米、(20-5×2)厘米、5厘米,再利用长方体的表面积公式和长方体的体积公式分别计算即可。
在计算表面积时应注意是5个面的面积。
解答:30,10,5,700,1 500。
2.用一根48厘米的铁丝焊接成一个最大的正方体框架,这个框架的每条边应该是多少厘米?解析:根据正方体的特征,它的12条棱长都相等,把48厘米平均分成12份,每份就是一条棱的长度。
解答:48÷12=4(厘米)答:这个框架的每条边应该是4厘米.3.用棱长1厘米的小正方体摆成稍大一些的正方体,至少需要多少个小正方体?解析:题目要求至少要多少个棱长为1厘米的小正方体,那么拼成的棱长应尽量小,所以应该考虑棱长为2的立方体,体积是8立方厘米,所以要8个。
解答:2×2×2=8(个)答:至少需要8个小正方体。
4.一个长方体的容器(如图),里面的水深5cm,把这个容器盖紧后竖放,使长10cm、宽8cm的面朝下,这时里面的水深是多少厘米?解析:首先根据长方体的体积(容积)公式求出容器中水的体积,然后用水的体积除以竖放后以长10cm、宽8cm的面作为底面时的底面积(10×8),即可求出水深。
解答:20×10×5÷(10×8)=12.5(厘米)。
答:这时里面的水深是12.5厘米。
5.将下面的硬纸板按照虚线折成一个立方体,哪个面与哪个面相对?解析:通过实验可以看到带有标号的面7与10,面8与11,面9与12是相对的面。
解答:面7与10,面8与11,面9与12是相对的面。
五年级数学下册试题 《7.长方体和正方体》-单元测试1 青岛版 含答案

青岛版五年级数学下册《7.长方体和正方体》-单元测试1一、单选题(总分:40分本大题共8小题,共40分)1.(本题5分)棱长是8厘米的正方体与另一个长方体的体积相等,如果长方体的高是16厘米,那么它的底面积是()A.0.5cm2B.4cm2C.32cm22.(本题5分)一个长6dm,宽4dm,高4dm的长方体盒子,最多能放()个棱长为2dm 的正方体木块.A.12B.13C.14D.153.(本题5分)一根长方体的木料的体积是80立方分米,横截面积是4平方分米,木料长是()A.20分米B.320分米C.80分米4.(本题5分)一个长方体的长、宽、高分别是acm,bcm,hcm.如果高增加2cm,体积比原来增加()立方厘米.A.abh+22B.2abhC.(h+2)abD.2ab5.(本题5分)一个正方体棱长扩大到原来的2倍,体积扩大到原来的()A.2倍B.8倍C.16倍D.10倍6.(本题5分)下面的图形经过折叠不能围成一个长方体的是()A.B.C.D.7.(本题5分)正方体的棱长扩大4倍,它的表面积会扩大()倍.A.4B.16C.648.(本题5分)一个长方体正好切成3个一样的正方体,切开后每个正方体的表面积是12平方厘米,那么原来这个长方体的表面积是()A.36平方厘米B.30平方厘米C.28平方厘米二、填空题(总分:25分本大题共5小题,共25分)9.(本题5分)一个长方体纸盒高1.2米,它底面是边长0.8米的正方形,它的体积是____立方米.10.(本题5分)一个长方体长acm,宽bcm,高hcm,如果它的高增加3cm,那么体积比原来增加____立方厘米.11.(本题5分)一种小汽车上的油箱,里面长5dm,宽4dm,高3dm,这个油箱可以装汽油____L.12.(本题5分)正方体的表面中有可能有长方形.…____.(判断对错)13.(本题5分)一个正方体的底面积是25平方分米,它的表面积是____,体积是____.三、解答题(总分:35分本大题共5小题,共35分)14.(本题7分)小红放学后给鱼缸内的金鱼换水,她把20升清水倒入一个长5分米,宽4分米,高4分米的金鱼缸内,金鱼缸内的水深是厘米?15.(本题7分)挖一个长50米,宽30米,深2米的游泳池,需要挖土多少方?挖成后,给这个游泳池的四壁贴上瓷砖,贴瓷砖的面积是多少?16.(本题7分)0.75立方厘米=____升68立方厘米=____立方分米4.05立方分米=____升=____毫升____mL=75L1350立方厘米=____升____毫升____公顷=2500平方米.17.(本题7分)计算下列正方体、长方体的表面积和体积.(单位是cm)18.(本题7分)丁丁家要做一个长5分米,宽4分米,高6分米的无盖玻璃鱼缸.丁丁最少要准备多少平方分米玻璃?青岛版五年级数学下册《7.长方体和正方体》-单元测试1参考答案与试题解析1.【答案】:C;【解析】:解:8×8×8÷16=512÷16=32(平方厘米),答:长方体的底面积是32 平方厘米.故选:C.2.【答案】:A;【解析】:解:6×4×4÷23=96÷8=12(个)答:最多能放12个棱长为2dm的正方体木块.故选:A.3.【答案】:A;【解析】:解:80÷4=20(分米),答:木料的长是20分米.故选:A.4.【答案】:D;【解析】:解:增加的部分的体积为:a×b×2=2ab(立方厘米).答:新的长方体的体积比原来增加2ab立方厘米.故选:D.5.【答案】:B;【解析】:解:根据正方体的体积公式v=a3,一个正方体的棱长扩大到原来的2倍,体积扩大到原来的2×2×2=8倍;故选:B.6.【答案】:B;【解析】:解:A、C、D、都能围成长方体,不符合题意;B、图形折叠起来后,能围成长方体的2个底面,侧面重复,不能围成长方体,符合题意.故选:B.7.【答案】:B;【解析】:解:正方体的表面积=棱长×棱长×6,根据积的变换规律可知,棱长扩大4倍表面积就扩大4×4=16.故选:B.8.【答案】:C;【解析】:解:12×3-12÷6×4=36-8=28(平方厘米)答:原来这个长方体的表面积是28平方厘米.故选:C.9.【答案】:0.768;【解析】:解:0.8×0.8×1.2=0.768(立方米),答:它的体积是0.768立方米.故答案为:0.768.10.【答案】:3ab;【解析】:解:a×b×3=3ab(立方厘米),答:那么体积比原来增加3ab立方厘米.故答案为:3ab.11.【答案】:60;【解析】:解:5×4×3=60(立方分米)60立方分米=60升答:这个油箱可以装汽油60升.故答案为:60.12.【答案】:x;【解析】:解:正方体的6个面都是正方形,所以正方体的表面中有可能有长方形.这种说法是错误的.故答案为:×.13.【答案】:150平方分米;125立方分米;【解析】:解:因为正方体的底面积是25平方分米,且5×5=25,所以这个正方体的棱长是5分米,则表面积是5×5×6=150(平方分米),体积是:5×5×5=125(立方分米),答:这个正方体的表面积是150平方分米,体积是125立方分米.故答案为:150平方分米,125立方分米.14.【答案】:解:20升=20立方分米,20÷(5×4),=20÷20,=1(分米),=10厘米;答:金鱼缸内的水深是10厘米.;【解析】:根据长方体的体积公式:v=sh,用水的体积除以鱼缸的底面积即可求出高.15.【答案】:解:50×30×2=1500×2=3000(方);50×30+(50×2+30×2)×2=1500+(100+60)×2=1500+160×2=1500+320=1820(平方米);答:需要挖土3000方,贴瓷砖的面积是1820平方米.;【解析】:求挖土多少方,根据长方体的体积公式:v=abh,把数据代入公式解答;求贴瓷砖的面积,由于游泳池是无盖的,所以只一个底面和4个侧面的总面积,根据长方体的表面积公式解答即可.16.【答案】:0.000750.068;4.05;4050;75000;1;350;0.25;【解析】:解:0.75立方厘米=0.00075升68立方厘米=0.068立方分米4.05立方分米=4.05升=4050毫升75000mL=75L1350立方厘米=1升 350毫升0.25公顷=2500平方米故答案为:0.00075,0.068,4.05,4050,75000,1,350,0.25.17.【答案】:解:(1)5×5×6=150(平方厘米)5×5×5=125(立方厘米)答:表面积是150平方厘米,体积是125立方厘米.(2)(8×3+8×2+3×2)×2=(24+16+6)×2=46×2=92(平方厘米)8×3×2=48(立方厘米)答:它的表面积是92平方厘米,体积是48立方厘米.;【解析】:(1)已知正方体的棱长是5厘米,根据正方体的表面积公式:S=6a2可求出它的表面积,正方体的体积公式V=a3可求出它的体积.(2)已知长方体的长是8厘米,宽是2厘米,高是3厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2可求出它的表面积,长方体的体积公式:V=abh可求出它的体积是多少,据此解答.18.【答案】:解:5×4+(5×6+4×6)×2,=20+108,=128(平方分米);答:丁丁最少要准备128平方分米玻璃.;【解析】:由于鱼缸是无盖的,缺少的是上面,所以只求它的5个面的总面积即可,根据长方体的表面积公式进行解答.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高
Sh
(3)填出下表中长方体或正方体的相关数据。
36 dm2
120 cm3
40.5 m
624 m3
2.计算下列图形的体积。
50×4.8=240(cm3)
0.36×0.6=0.216(dm3)
9×9=81(m3)
3. 某装饰公司订购500根方木,每根方木长5 m,横 截面是一个边长为0.3 m的正方形。这些方木一共 有多少立方米?
3 L=3000 cm3 3000÷(25×12)=10(cm) 答:水深10 cm。
提升点2 用操作法解决长方体的容积问题
7.一块长方形纸板,长为30 cm,宽为20 cm,先在 纸板的四个角上分别剪掉一个边长为5 cm的小正 方形,再沿虚线折成一个无盖纸盒。这个纸盒的 容积是多少?(纸板的厚度忽略不计)
(30-5×2)×(20-5×2)×5=1000(cm3) 答:这个纸积分别是35 cm2、 15 cm2和21 cm2,如果长、宽、高都是质数,那么 这个长方体的体积是多少立方厘米?
35=7×5 15=5×3 21=3×7 7×5×3=105(cm3) 答:这个长方体的体积是105 cm3。
0.3×0.3×5×500=225(m3) 答:这些方木一共有225 m3。
易 错 点 计算一个数的立方和平方时理解有误
4.计算。
63=( ) 216
23=( ) x+x+x=8 ( )
52=( ) 25
32=( )
x•x•x=( 9 )
3x
x3
辨析:一个数的立方表示3个这样的数相乘, 一个数的平方表示2个这样的数相乘。
七 包装盒——长方体和正方体
第9课时 长方体和正方体体积的统一公式
QD 五年级下册
提示:点击 进入习题
1
2
3
4
5
6
7
8
知 识 点 长方体和正方体体积的统一公式
1.填一填。
(1)长方体或正方体底面的面积叫作( 底面积 )。
(2)长方体(或正方体)的体积=(
)×( ),用
字母可以表示为V=(
)。底面积
提升点1 运用长(正)方体的体积公式解决问题
5. 把一个长12 cm、宽10 cm、高9 cm的长方体削成一 个最大的正方体。这个正方体的体积是多少?
9×9×9=729(cm3) 答:这个正方体的体积是729 cm3。
6.一个长方体鱼缸,从里面量长25 cm,宽12 cm,高 16 cm。往里面倒入3 L水,水深多少厘米?
