工程力学中的张量分析(刘建林编著)PPT模板
合集下载
【张量分析ppt课件】张量分析课件第二章2 矢量函数PPT共47页

【张量分析ppt课件】张量分析课件第 二章2 矢量函数
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事, 只想现 在的事 。现在 有成就 ,以后 才能更 辉煌。
18、敢于向黑暗宣战的人,心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前,莽撞的 人只能 引为烧 身,只 有真正 勇敢的 人才能 所向披 靡。
谢谢你的阅路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
张量分析TensorAnalysisppt课件

的切线方向。矢量 r 可以取作曲线坐标系的基矢量(协变基矢量):
xi
gi
r xi
zj xi
ij
注意:对于在曲线坐标系中的每一点,都有三个基 矢量。
ቤተ መጻሕፍቲ ባይዱ
基矢量一般不是单位矢量,彼此也不正交;
基矢量可以有量纲,但一点的三个基矢量的量纲可以不同;
基矢量不是常矢量,它们的大小和方向依赖于它们所在点的坐标。
利用克罗内克符号,上式可写成:
ds2 ijdxidxj
克罗内克符号的一些常用性质:
ijxi xj
x j xi
j i
ijki kj
D) 置换符号
置换符号eijk=eijk定义为:
1
e ijk
e ijk
1
0
当i,j,k是1,2,3的偶置换(123,231,312) 当i,j,k是1,2,3的奇置换(213,132,321) 当i,j,k的任意二个指标相同
i,j,k的这些排列分别叫做循环排列、逆循环排列和非循环排列。
D) 置换符号(续)
置换符号主要可用来展开三阶行列式:
a11 a1 2 a3 1 aa12 a22 a32 a11a22a33a12a23a3 1a13a1 2a32
a13 a23 a33 a11a23a32 a12a1 2a33 a13a1 2a32
量 Ai ,在坐标系yi中有三个分量 Âi ,它们由以下的变换法则相联系;
AˆiyAjxxyij
逆变矢量用上标表示;因此上标也称为逆变指标。
(3) 协变矢量(一阶协变张量)
一个量被称为协变矢量或一阶协变张量,若它在坐标系 xi 中有三个分 量 Ai ,在坐标系yi中有三个分量 Âi ,其变换法则相为;
【张量分析ppt课件】张量分析课件第二章 矢量代数与矢量分析

(2.1-3)
在矢量的加法和减法运算中定义单位元素为:
o 0 i1 0 i2 0 i3
同时长度为1的矢量称为单位矢量。 应当注意单位矢量元素和单位矢量的区别。
例2 : 图 2-4 所示具有坐标系的矢空间 V 中 矢量a、 b。试求 2a +1.5b在{o;i1, i2 }中的表示。 a (3 1) i 1 (1 0) i 2 2 i 1 i 2 解:
a b ( ai i i ) (b j i j ) ai b j ij ai bi b a ; a , b V
(2.1-4) (2.1-5)
1 ; i j i i i j ij 0 ; i j
其中δij称为Kronecker符号。 定义矢量积
例6 :
证明e—δ恒等式: eijk eimn jm kn jn km 证: 由(2.1-12)式有:i j ik e jkiii eijkii
im in emne ie eemn ie
eijkeemn ii ie (i j ik ) (im in ) (eijkii ) (eemnie ) (i j ik ) (im in ) eijkeemn ie (i j ik ) (im in )
X2
x2
x r2 o r1 x1 (a ) X1
x2 i2 x i1 x1 X1
X2
(b )
图2-3
设V的坐标系为{o;i1,i2,i3},V中矢量的加法和矢量与 数量的标量积按(1.1-3)和(1.1-4)定义,即对x,y ∈ V;α,β ∈F有 x y xi yi
i i i i
( xi yi ) ii
【张量分析ppt课件】张量分析课件第三章 张量代数

按§2.5节三中(g)式面积矢量记法有:
dH 0 r u(r ) (r )dV
试证明物体 Ω 对o点的动量矩为:
H0 J ω
Ω
式中 称为物体 Ω 对o点的二阶惯性矩张量(注:J 不是四阶单位张量。但 J表达式中的 I是二阶单位张量)。 u (r ) ω r 证: H (r u) dV r (ω r ) dV (r r )ω (r ω)r ) dV
I u (ii ii ) (u j i j ) u j iiij ui ii u
设存在另一二阶张量 I ,且满足 u I I u 。则: u I u I o ; uo ∵ I I O ; I I (唯一性) ∴ 3.
A : J ( Amn imin ) : (ii i j ii i j ) Amnmi jn ii i j Amn imin A
二阶张量与二阶张量的(一)点乘:
A B (Aij ii i j) ( Bmn imin) (Aij Bmn )ii (i j im )in Aij Bjn ii in
二阶张量与二阶张量的(双)点乘:
A : B ( Aij ii i j ) : ( Bmn imin ) ( Aij Bmn )(ii im )(i j in ) Aij Bij
A P2 A P2
A0 P2 Φ0 P4
Φ0 P4
(3.1-11)
A : Φ0 A
0 0
的 n ; A ; A ; ; 分别称为一阶单位张量、二阶单位张量和四 阶单位张量。 上式定义的一阶、二阶和四阶单位张量具有性质: u u V n 1. u A0 A0 ii ii ij ii i j (3.1-12) 2. I 为单位二阶张量。 ii i j 且记 A ; A 为 I 。即 I ii ii ij。并称
【张量分析ppt课件】张量分析课件第三章3 二阶张量特征值与特征方向

设V中标准正交坐标系为 {i1, i2, i3} 。则二阶张量 A和矢量 u可表示为:
A Aij ii i j ; u ui ii A u u ; ( A I ) u o
可分别写成: 或
u A u
;
u ( A I ) o
( Aij ii i j ij ii i j ) (umim ) o ; (umim ) ( Aij ii i j ij ii i j ) o A12 A13 u1 0 A11 A u 0 A A 22 23 2 21 (3.4-3) A32 A33 A31 u 3 0
det(A I ) 0 ( a) det(A* I ) 0 ( b)
∵ ∴ (a)、(b)两式是关于λ的三次相同的代数方程。也就是说 A的右特征值和左特征值相同。由 (a)式或 (b)式得: ∵
[( A I ) a ] [( A I ) b][( A I ) c ] 0 a (b c ) [( A I ) a ] [( A I ) b][( A I ) c ] det( A I )
; ∴
u ai 2
u1 0 u 2 a u 0 3
(a是任意实数)
是方程组(1)的非零解。
A u (i1i3 i2i1 i2i2 i3i1 ) (ai2 ) ai2 1u
因此 u = a i2是 A的λ1 = 1特征值对应的右特征矢量。 左特征矢量: ∵
(detet Q) det(Q I ) det(Q I )
2 det(Q I ) 0 ∴ 因此得出结论: 正交二阶张量 Q,当det Q =1时存在右特征矢量 r。其对应 的特征值λ = 1。且:
工程力学pptPowerPointTemplate

1.4 20世纪,量子力学与相对论力学得到较快发展。
PPT文档演模板
工程力学pptPowerPointTemplate
第二节 理论力学的研究内容 :
2.1 理论力学所研究的内容是以牛顿三大定律为基础的古典力学(宏观物体 的运动速度小于光速-3×105km/s):
2.2 理论力学包括:静力学、运动学和动力学:
1.2 力使物体的运动状态发生变化的效应,称为力的外效应(运动):力使 物体发生变形的效应,为力的内效应。理论力学只研究力的外效应(假定 为刚体),而材料力学才研究力的内效应。
1.3 力的三要素:大小、方向和作用点:
PPT文档演模板
工程力学pptPowerPointTemplate
第二节 静力学公理 :
PPT文档演模板
工程力学pptPowerPointTemplate
第四章 平面任意力系:
4-2 平面任意力系向一点简化 平面力系简化的最后结果:
平面任意力系一般可以通过简化中心,简化为一个力F‘R和一个力偶 Mo,在此基础上,还可以进一步简化为一个合力(力的平移定理); 4-3 平面任意力系的平衡条件: 平面任意力系平衡的充要条件是力系各力在平面上两个正交轴上投影 的代数和分别等于零,力系各力对平面上任一点之矩的代数和等于零;
PPT文档演模板
工程力学pptPowerPointTemplate
第四章 平面任意力系:
4-2 平面任意力系向一点简化 根据力的可传性和力的平移定理,平面力系中任一力,向作用平面 内任一点移动(纵移和平移),在该点形成原作用力和一附加力偶矩, 各力和各力偶的矢量和,分别为主力矢(主矢)和主力偶矢(主矩); 力系向任何一点简化其主矢都等于力系诸力的矢量和,主矢与简化 中心位置的选择无关,而主矩一般与简化中心的选择有关; 固定端的约束:不仅限制了物体的移动,还限制了物体的转动,通 过平面力系的简化,可以为简化为固定端的约束力和约束力偶;
PPT文档演模板
工程力学pptPowerPointTemplate
第二节 理论力学的研究内容 :
2.1 理论力学所研究的内容是以牛顿三大定律为基础的古典力学(宏观物体 的运动速度小于光速-3×105km/s):
2.2 理论力学包括:静力学、运动学和动力学:
1.2 力使物体的运动状态发生变化的效应,称为力的外效应(运动):力使 物体发生变形的效应,为力的内效应。理论力学只研究力的外效应(假定 为刚体),而材料力学才研究力的内效应。
1.3 力的三要素:大小、方向和作用点:
PPT文档演模板
工程力学pptPowerPointTemplate
第二节 静力学公理 :
PPT文档演模板
工程力学pptPowerPointTemplate
第四章 平面任意力系:
4-2 平面任意力系向一点简化 平面力系简化的最后结果:
平面任意力系一般可以通过简化中心,简化为一个力F‘R和一个力偶 Mo,在此基础上,还可以进一步简化为一个合力(力的平移定理); 4-3 平面任意力系的平衡条件: 平面任意力系平衡的充要条件是力系各力在平面上两个正交轴上投影 的代数和分别等于零,力系各力对平面上任一点之矩的代数和等于零;
PPT文档演模板
工程力学pptPowerPointTemplate
第四章 平面任意力系:
4-2 平面任意力系向一点简化 根据力的可传性和力的平移定理,平面力系中任一力,向作用平面 内任一点移动(纵移和平移),在该点形成原作用力和一附加力偶矩, 各力和各力偶的矢量和,分别为主力矢(主矢)和主力偶矢(主矩); 力系向任何一点简化其主矢都等于力系诸力的矢量和,主矢与简化 中心位置的选择无关,而主矩一般与简化中心的选择有关; 固定端的约束:不仅限制了物体的移动,还限制了物体的转动,通 过平面力系的简化,可以为简化为固定端的约束力和约束力偶;
[工学]第一章 张量分析初步
![[工学]第一章 张量分析初步](https://img.taocdn.com/s3/m/6e564091fd0a79563c1e72c5.png)
2 x j
(
xi
)
两个特殊符号
两个特殊符号
为书写的方便,可以使用kronecker符号和排列符号简化书 写。
kronecker符号
定义
1 i j ij 0 i j
11 22 33 1 12 21 13 31 23 32 0
例题
Qii, S展开? 步骤:分析i,指标类型?字母类型?再展开 2. 写出a=Aijbicj的展开式。
1. 3. 4.
5.
写出 ti ji n j 的展开式。 写出 bik b jk ij 的展开式。 u j 的展开式。 ?写出 1 ui
eij
6.
1 ?写出 w 2 ij eij 的展开式。
第一章 张量分析初步
第一章 张量分析初步
本章学习目的 引入最基本的张量概念,为今后学习应变张量、 应力张量、广义虎克定律和弹性波方程等专业概 念及运算做准备。是本门课的数学基础。 ? 1 已学习过的物理量
标量? 向量?
a11 x1 a12 x2 a13 x3 b1 a 21 x1 a 22 x2 a23 x3 b2 a31 x1 a32 x2 a33 x3 b3
2
有了标量和向量是否足够描述自然现象?
如何用一个最简单 的式子来表示?
用矩阵? 还有更简单的表示方法吗? aij x j bi 可总结为: aij, xj, bi是些什么量?
§1.1 指标记号及两个特殊符号
指标记号
空间有个坐标系OXYZ,P (x, y, z)是其中的一点,坐 z 标为:x, y ,z P(x, y, z) 直角坐标系中的基向量:
张量分析第6章精品PPT课件

du(t) Dui gi dt Dt
全导数
Dui Dt
dui dt
umvk imk
分量的指标升降
Dui gij Du j
Dt
Dt
➢ 质点的加速度
du(t) dt
dui
dt
umvk imk
gi
Dui Dt
gi
dv(t) dt
dvi
dt
vmvk imk
gi
Dvi Dt
gi
Gˆ = G
dG = d
dt dt
gˆij gˆ i gˆ j
dgˆij dt
gˆ i gˆ j
gˆij
gˆ i
dgˆ j dt
dgˆ i dt
gˆ j
2d gˆij
gˆ i
gˆ
j
vˆ
ˆ v
gˆ
i
gˆ
j
2d gˆij gˆi gˆ j vˆ ˆ v gˆij gˆi gˆ j
dgˆi
dt
gˆi
ˆ v
vˆ
gˆi
v vˆ = d +
dgˆi
dt
vˆ
gˆi d gˆi gˆi
dgˆi
dt
ˆ v
gˆ i d gˆi gˆi
➢ Euler基矢量的物质导数
gi gi x j k ,t
dgi dt
gi x j
dx j dt
ˆ jvˆi ˆ ivˆ j
配上相应的逆变基矢量后,定义应变率张量为:
dˆ
dˆij gˆ i gˆ
j
1 2
d dt
gˆij
gˆ i gˆ
j
1 2
ˆ vˆ vˆˆ
张量分析课件-1.6 张量的基本概念

T ij βki βl jT kl
T
i j
Tij βik β ljTkl
j k j l T β β i i l T k
β β T
l j
i k
k l
同一坐标系内,张量的逆变、协变、混变分量之间 满足指标升降关系。m 阶张量可以有 nm 种分量的集合。 n 维空间中 m 个矢量分量进行并乘运算所得到 nm 个数的集合可构成 m 阶张量。例如:
t Tijk βir β s β j k Trst
T
ij k
β β β T
t k
i r
j s
rs t
t r T i jk βri β s β T j k st
1.6.2.1 张量的实体表示法(并矢表示法)
j i T T ij gi g j Tij g i g j T i j gi g j T i g gj k i j k T T ijk gi g j gk Tijk g i g j g k T ij g g g T g g g k i j jk i
基张量(基矢量的并矢)线性无关。
在张量的实体表示法中,分量指标的排列顺序和相配 基矢量的排列顺序是一一对应的,不能随意更换。例如
T T gi g j T g j gi T gi g j T g j gi
ij ji ji ij
1.6.3
度量张量
G g ij gi g j gij g i g j δ ij gi g j δi j g iT
st i
T
ij
β β T rs
r i s j rs s j r s s r
张量分析ppt课件张量分析课件第五章5协变基底矢量导数

r2
r1
22 1
r2
22 2
3 22
r3
rr2
r2 x3
r2 z
r1
23 1
r2
23 2
3 23
r3
o
r3 x1
r3 r
r1
31 1
r2
31 2
r3
31 3
o
r3 x2
r3
r1
32 1
r2
32 2
3 32
r3
o
例11: 试求球坐标:
r3 x3
r3 z
r1
33 1
r2
33 2
r3
33 3
o
x1 r sin cos
2
x3
2 2
1
[r2 cos2 cos2 r2 cos2 sin2 r2 sin2 )2 r
1
h3
x1
2
x2
2
x3
2
2
1
(r2 sin2 sin2 r2 sin2 cos2 0)2 r sin
由(5.3-154)式得,除 1h2、 1h3、 2h3 偏导数分别为 1、sin、r cos、 外,其余的偏导数均为零。
jri ( jri ) r k rk
(5.3-3)
式中 ( jri ) r k 是矢量 j ri 在协变基矢量rk上的线性表示系数( 或称为 rk 上的坐标)。同理, j ri 也可以在逆变基底上线性
表示为:
jri ( jri ) rk rk
(5.3-4)
定义:
k ij
k
i
3 22
h2 (h3 )2 3h2
1 33
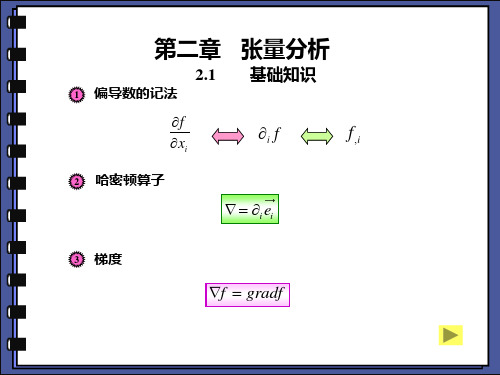
第二章 张量分析
P也可用另外三个变量 x,1' x,2' 来x 表3' 示,即
P P x1' , x 2' , x 3' P x i'
这种坐标系记为 xi。' 这两组变量
x1 , 和x 2 , x 3 表示x同1' 一, x空2' , x 3'
间点的位置。两者由下列坐标变换联系起来:
xi xi xi'
aigi a jg j aia j gi g j
aiaj 0
令
gij gi g j
g ij g i g j
gi j gi g j g j gi
它们分别称为协变度量张量、逆变度量张量和混合度量张量
考虑到矢量a的任意性 g ji gi g j i j
可知:基矢量 g与i 是g i 正交的,它们称为互逆基矢量 互逆基矢量间具有下列关系:
gig j g k gi g j g k gig j g k eijk
这两个量定义为爱丁顿(Eddington)张量并分别记为 和ijk 。ijk
由此定义可知
123 g1g 2g3
123 g1g 2g3
对于矢量 a 0 ,则有
a 2 a a a i g i a j g j a i a j g i g j ai gi a j g j ai a j gi g j
(ii) x 2' (常 数 C)为2 通过z轴的平面; (iii) x3' (常z 数 C)3为垂直于z轴的平面;
和坐标曲线:
(i) x1' 和r C1 x的2' 交线 (zC线2 )是直线; (ii) x 2' 和 C2 的x3'交线z (r线C3)是直线;
P P x1' , x 2' , x 3' P x i'
这种坐标系记为 xi。' 这两组变量
x1 , 和x 2 , x 3 表示x同1' 一, x空2' , x 3'
间点的位置。两者由下列坐标变换联系起来:
xi xi xi'
aigi a jg j aia j gi g j
aiaj 0
令
gij gi g j
g ij g i g j
gi j gi g j g j gi
它们分别称为协变度量张量、逆变度量张量和混合度量张量
考虑到矢量a的任意性 g ji gi g j i j
可知:基矢量 g与i 是g i 正交的,它们称为互逆基矢量 互逆基矢量间具有下列关系:
gig j g k gi g j g k gig j g k eijk
这两个量定义为爱丁顿(Eddington)张量并分别记为 和ijk 。ijk
由此定义可知
123 g1g 2g3
123 g1g 2g3
对于矢量 a 0 ,则有
a 2 a a a i g i a j g j a i a j g i g j ai gi a j g j ai a j gi g j
(ii) x 2' (常 数 C)为2 通过z轴的平面; (iii) x3' (常z 数 C)3为垂直于z轴的平面;
和坐标曲线:
(i) x1' 和r C1 x的2' 交线 (zC线2 )是直线; (ii) x 2' 和 C2 的x3'交线z (r线C3)是直线;
第2章-张量分析(清华大学张量分析-你值得拥有)PPT课件

• 负整数次幂
G T 0 T 1(1) T 1 T 1 T T 1
T 2 T 1 T 1
T m T 1 T 1 T 1 T 1
几种特殊的二阶张量
➢ 正张量:N>0的对称二阶张量
uN u 0
➢ 非负张量:N≥0的对称二阶张量 u N u 0
对称二阶张量总可以化为:
N N1e1e1 N2e2e2 N3e3e3
能量密度。而大变形情况会出现高度非线性,则不能 用加法分解,而要用乘法分解。
• 最简单的坐标变换
y y
x cos sin x
y
sin
cos
y
x
• 椭圆曲线的坐标变换
x
正交变换可使椭圆曲线的方程由以下一般形式
ax2 bxy cy2 d 0
变换为最简形式,即两主轴坐标系下形式。
x a
2
y b
2
1
几种特殊的二阶张量
➢ 正交张量Q
• 正交张量的定义和性质
可证: Q e3 e3
Q e1 cos e1 sin e2 Q e2 cos e2 sin e1
e1, e2 整体绕轴向旋转一个角度
几种特殊的二阶张量
• 正交张量对应的正交变换的特性
① 保内积性质 ② 保长度性质 ③ 保角度性质
(Q u) (Q v) u v
(Q u) (Q u) u u
l i
Tii
J2
1 2!
T T ij l
lm i
m j
1 2
(TiiTll
TliTil )
J3
1 3!
T T ijk l
lmn i
Tm n
j k
det(T )
【张量分析ppt课件】张量分析课件第一章 线性空间-50页精选文档

(2)∵ x y z ( x 1 y 1 ) z 1 , , ( x n y n ) z n
( x 1 y 1 z 1 , ,x n y n z n )
x ( y z ) ( x 1 ( y 1 z 1 ) , , ( x n ( y n z n ))
( x 1 y 1 z 1 , ,x n y n z n )
∴ x + (y + z )= ( x + y )+ z = x + y + z (4)∵ o(0, ,0)V0 x o (x 1 0 , x n 0 )(x1, ,xn)
∴ xox
(5)∵ ()x ()(x 1 , ,xn) (()x 1 , ,()xn)
∴
(x 1 , ,xn) (x 1 ), ,)xn)
第一章 线性空间
若记实数集合为F,F中的元素记为a、b、c、…。
则加法法则将F中的任意两个元素 a, bF ; c F
+ (a, b)c
abc
乘法法则将F中的任意两个元素 a, bF ; c F
× (a, b)c
abc
显然具有加法法则和乘法则所确定的实数集中元
素间确定关系使得实数集构成一个空间。并记为:
所有以x点为起点的矢量按:
u x yu x z(y 1 x 1 , ,y n x n ) (z 1 x 1 , ,z n x n )
(y 1 ( x 1 ) (z 1 x 1 ) ,,(y n x n ) (z n x n ))
u xy (y1x1, ,ynxn) ((y1x1) ,,(ynxn)) F
a, b,xF
(6) (a b ) x a x b x
a, b,xF
【张量分析ppt课件】张量分析课件第二章2 矢量函数共46页PPT资料

o
解:v ()vc o si1 vs ini2 (0 .5 c o s 0 .2 5 c o s 2)i1
(0 .5 s in 0 .2 5 s inc o s)i2 ; 0 /2 0 :v 0 .2 5 m / s ; 1 5 :v 0 .2 5 9 m / s
3 0 :v 0 .2 8 3 m / s ; 4 5 :v 0 .3 2 3 m / s
,b]区间的不同取值x (t)位置矢量平面描绘一条曲线。
对矢量函数: x x (t1 ,t2 ) x 1 (t1 ,t2 )i1 x 2 (t1 ,t2 )i2
t2
x2
当t = b 时: 2 2
x x (t1 ,b 2 ) x 1 (t1 ,b 2 )i1 x 2 (t1 ,b 2 )i2
a2
更一般地有:对矢量函数 x(t)的终点所描绘的曲线称为矢
端曲线或称为 x(t)的图形。而(2.3-1)式称为矢量方程。
ቤተ መጻሕፍቲ ባይዱ例12:
x2
已知小球在四分之一圆弧轨道中运动。圆弧
轨道半径R=50cm,小球运动速度的大小 v φ
0.51cos(m。/s)试求小球速度矢量方程;并在图
4
中画出小球速度的矢端曲线。
程。参数方程在 {o;i1,i2,i3} 中描绘的曲线称为矢端曲 线(面)。
具有一个参数的矢量函数矢端曲线(二维映射分析):
设x = x (t) , b≤t≤a。在平面坐标系{o;i1,i2}中,矢量x
随t的变化,且: xx1(t)i1x2(t)i2
x2
x完全由x1(t), x2(t)的变化确定。
t*
xx(t1, ,tn)
(2.3-3)
x x 1 ( t 1 ,, t n ) i 1 x 2 ( t 1 ,, t n ) i 2 x 3 ( t 1 ,, t n ) i 3 x i ( t 1 ,, t n ) i i
张量分析课件-3.4 二阶张量的二阶张量函数

上式存在极限的条件是: (1)当T 的特征根= 时, H 的特征根= 。 1 2 (2)极限 lim 存在,因而k0,k1,k2 也接近于相应 2 1 1 2 极限。 III. T 的特征方程具有三重根 1=2=3 具有三重根的能化为对角型标准形的张量只能是球形张量, 故T 为球形张量,考虑→,2→ 的极限过程,H=f (T )表
于三个特征值的集合,与特征值得排序无关。特征值的集合取
T T T , J2 , J3 决于特征方程的系数 J1 ),因此 k0,k1,k2是主不变
T T T , J2 , J3 量 J1 函数,从而H 是 T 的各向同性函数。
II. T 的特征方程具有二重根 1=2≠3
2 1
lim
T 3G 1 2 f T lim T 2G T 1G
3.4.3 同时化为对角型标准形的函数
设二阶张量T 的二阶张量函数 H=f (T ),当T 在某一组基
矢量中化为对角型标准形时,H 在同一组基矢量中也化为对 角型标准形,并设 H 的特征根 i(i=1,2,3)为T 的特征根 i(i=1,2,3)的函数,而与T 的其他性质无关,即
i i j i 1 , 2 , 3
H f T 1 2 1 1 2 2 3 3 1 3 1 2 T 2 1 3 3 1 2 1 3 2
2 2 G 1 2 2 T 3 2 1 3 2
T
i j
3 2 1 J11 J 21 J 3 T 0 0 O
3 2J J J J J
2 2 1 3
【张量分析ppt课件】张量分析课件第五章 曲线坐标.ppt

一、逆变基底
对给定的曲线坐标:
xi xi (x1, x 2 , x 3) ; (i 1, 2, 3)
令:
ri
x xi
xj xi
ij
;
r1 r1 r1 r2
g r2 r1 r2 r2
r3 r1 r3 r2
(i 1, 2,3)
r1 r3 r2 r3 r3 r3
定义:
r1
1 g
x x1
x x2
x x3
xj x1
xk x2
xl x3
ij
(ik
il )
x1 x2 x3
x1 x1 x1
x j xk xl x1 x2 x3 ejkl x1 x 2 x 3 x 2 x 2 x 2
x1 x2 x3 x3 x3 x3
由于 xi xi (x1, x 2, x3) ; i 1, 2,3 是一一对应的函数。因此有:
为 x1, x 2 , x 3曲线坐标线。
设{o;i1, i2, i3}是三维 Euclid 矢量空间的标准正交坐标系;
是曲线坐标; x1(x1, x2 , x3 ) , x 2 (x1, x2 , x3) , x 3(x1, x2, x3)
r1(x1, x2 , x3 ) , r2 (x1, x2 , x3)
x1 x1 sin x 2 cos x 3 ; x2 x1 sin x 2 sin x 3 ; x3 x1 cos x 2
是一一对应的三个实函数,其反函数存在。且:
x1
( x1 )2
(x2 )2
1
(x3 )2 2
x2
arctg
(
x1
)
2
(x2 )2 x3
1
2
对给定的曲线坐标:
xi xi (x1, x 2 , x 3) ; (i 1, 2, 3)
令:
ri
x xi
xj xi
ij
;
r1 r1 r1 r2
g r2 r1 r2 r2
r3 r1 r3 r2
(i 1, 2,3)
r1 r3 r2 r3 r3 r3
定义:
r1
1 g
x x1
x x2
x x3
xj x1
xk x2
xl x3
ij
(ik
il )
x1 x2 x3
x1 x1 x1
x j xk xl x1 x2 x3 ejkl x1 x 2 x 3 x 2 x 2 x 2
x1 x2 x3 x3 x3 x3
由于 xi xi (x1, x 2, x3) ; i 1, 2,3 是一一对应的函数。因此有:
为 x1, x 2 , x 3曲线坐标线。
设{o;i1, i2, i3}是三维 Euclid 矢量空间的标准正交坐标系;
是曲线坐标; x1(x1, x2 , x3 ) , x 2 (x1, x2 , x3) , x 3(x1, x2, x3)
r1(x1, x2 , x3 ) , r2 (x1, x2 , x3)
x1 x1 sin x 2 cos x 3 ; x2 x1 sin x 2 sin x 3 ; x3 x1 cos x 2
是一一对应的三个实函数,其反函数存在。且:
x1
( x1 )2
(x2 )2
1
(x3 )2 2
x2
arctg
(
x1
)
2
(x2 )2 x3
1
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
03
第2章张量
第2章张量
2.1张量的定义 2.2张量的运算 2.3特殊张量 2.4张量分解 习题
04
第3章张量函数及场方程
第3章张 量函数及 场方程
3.1张量函数 3.2张量函数的导数 3.3张量场方程 习题
05
第4章曲线坐标系
第4章曲线坐 标系
0 1 4.1基矢量的导数
0 2 4.2张量场函数对矢径的导数 0 3 4.3矢量和张量场函数分量对坐标的
工程力学中的张量分析 (刘建林编著)
演讲人
2 0 2 X - 11 - 11
目录
01. 前言 03. 第2章张量 05. 第4章曲线坐标系
02. 第1章一阶张量——矢量 04. 第3章张量函数及场方程 06. 参考文献
01
前言
前言
02
第1章一阶张量——矢量
第1章一阶张量— —矢量
1.1矢量 1.2矢量的特殊运算 1.3坐标变换 习题
协变导数
0 4 4.4张量场函数的散度与旋度
0 5 4.5非完整系
06
4.6正交曲线坐标系中的物理分 量
第4章曲线坐标系
习题
06
参考文献
参考文献
感谢聆听
