熊伟运筹学课后习题答案1-4章
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
运筹学课后习题答案

第一章 线性规划1、由图可得:最优解为2、用图解法求解线性规划: Min z=2x 1+x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤≥+≤+-01058244212121x x x x x x解:由图可得:最优解x=1.6,y=6.4Max z=5x 1+6x 2⎪⎩⎪⎨⎧≥≤+-≥-0,23222212121x x x x x x解:由图可得:最优解Max z=5x 1+6x 2, Max z= +∞Maxz = 2x 1 +x 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤0,5242261552121211x x x x x x x由图可得:最大值⎪⎩⎪⎨⎧==+35121x x x , 所以⎪⎩⎪⎨⎧==2321x xmax Z = 8.1212125.max 23284164120,1,2maxZ .jZ x x x x x x x j =+⎧+≤⎪≤⎪⎨≤⎪⎪≥=⎩如图所示,在(4,2)这一点达到最大值为26将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≥-=++-≥+-≤++无约束321321321321,0,052327x x x x x x x x x x x x解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’⎪⎪⎩⎪⎪⎨⎧≥≥≥≥≥≥-=++-=--+-=+-++0,0,0'',0',0,05232'''7'''5433213215332143321x x x x x x x x x x x x x x x x x x x7将线性规划模型化为标准形式Min Z =x 1+2x 2+3x 3⎪⎪⎩⎪⎪⎨⎧≥≤-=--≥++-≤++无约束,321321321321,00632442392-x x x x x x x x x x x x解:令Z ’ = -z ,引进松弛变量x 4≥0,引进剩余变量x 5≥0,得到一下等价的标准形式。
运筹学版熊伟编著习题答案

运筹学(第3版)习题答案P36 P74 P88 P105 P142 P173 P195 P218 P248 P277 P304 品P343 P371全书420页第1章 线性规划工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-23所示.产品 资源 A B C 资源限量 材料(kg) 4 2500 设备(台时) 3 1400 利润(元/件)101412310和130.试建立该问题的数学模型,使每月利润最大.【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量,则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 建筑公司需要用5m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格及数量如表1-24所示:型号A 型号B 每套窗架需要材料长度(m ) 数量(根)长度(m) 数量(根)A 1:2 2B 1: 2 A 2:3 B 2:23需要量(套)300400问怎样下料使得(1)用料最少;(2)余料最少. 【解 方案 一 二 三 四 五 六 七 八 九 十 需要量 B1 2 1 1 1 0 0 0 0 0 0 800 B2 2 0 1 0 0 2 1 1 0 0 0 1200 A1 2 0 0 1 0 0 1 0 2 1 0 600 A2120 2 3 900 余料(m) 0 1 1 1 01设x j (j =1,2,…,10)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为10112342567368947910min 28002120026002239000,1,2,,10jj j Z x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩∑ (2)余料最少数学模型为2345681012342567368947910min 0.50.50.52800212002*********0,1,2,,10j Z x x x x x x x x x x x x x x x x x x x x x x x x j =++++++⎧+++≥⎪+++≥⎪⎪+++≥⎨⎪+++≥⎪⎪≥=⎩某企业需要制定1~6月份产品A 的生产与销售计划。
运筹学第三版课后习题答案 (2)

运筹学第三版课后习题答案第一章:引论1.1 课后习题习题1a)运筹学是一门应用数学的学科,旨在解决实际问题中的决策和优化问题。
它包括数学模型的建立、问题求解方法的设计等方面。
b)运筹学可以应用于各个领域,如物流管理、生产计划、流程优化等。
它可以帮助组织提高效率、降低成本、优化资源分配等。
c)运筹学主要包括线性规划、整数规划、指派问题等方法。
习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。
它可以帮助制定最佳的生产计划,优化供应链管理,提高运输效率等。
运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题,优化医疗资源分配等。
1.2 课后习题习题1运筹学方法可以应用于各个领域,如物流管理、生产计划、供应链管理、流程优化等。
在物流管理中,可以使用运筹学方法优化仓储和运输的布局,提高货物的运输效率。
在生产计划中,可以使用运筹学方法优化产品的生产数量和生产周期,降低生产成本。
在供应链管理中,可以使用运筹学方法优化订单配送和库存管理,提高供应链的效率。
在流程优化中,可以使用运筹学方法优化业务流程,提高整体效率。
习题2在物流管理中,可以使用运筹学方法优化车辆的调度和路线规划,以提高运输效率和降低成本。
在生产计划中,可以使用运筹学方法优化生产线的安排和产品的生产量,以降低生产成本和提高产能利用率。
在供应链管理中,可以使用运筹学方法优化供应链各个环节的协调和调度,以提高整体效率和减少库存成本。
在流程优化中,可以使用运筹学方法优化业务流程的排布和资源的分配,以提高流程效率和客户满意度。
第二章:线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法,用于解决包含线性约束和线性目标函数的优化问题。
其一般形式为:max c^T*xs.t. Ax <= bx >= 0其中,c是目标函数的系数向量,x是决策变量向量,A是约束矩阵,b是约束向量。
习题2使用线性规划方法可以解决许多实际问题,如生产计划、供应链管理、资源分配等。
运筹学1至6章习题参考答案

-0.25
1
1.5
2
C(j)-Z(j)
-1.75
0
0
1.25
0
-12.5
X1
-3
1
0
2
-1
0
2
M
X2
-5
0
1
-0.5
0.5
0
2
4
X5
0
0
0
-1.5
[0.5]
1
0
0
C(j)-Z(j)
0
0
3.5
-0.5
0
-16
X1
-3
1
0
-1
0
2
2
X2
-5
0
1
1
0
-1
2
X4
0
0
0
-3
1
2
0
C(j)-Z(j)
0
0
2
0
1
【解】设xj、yj(j=1,2,…,6)分别为1~6月份的生产量和销售量,则数学模型为
(1)
(2)目标函数不变,前6个约束右端常数800改为1000,第7~11个约束右端常数200改为0,第12个约束“≤200”改为“=-200”。
1.4某投资人现有下列四种投资机会,三年内每年年初都有3万元(不计利息)可供投资:
0
0
0
R. H. S.
Ratio
Basis
C(i)
X1
X2
X3
X4
X5
X6
X4
0
-1
2
3
1
0
0
4
M
X5
0
[4]
熊伟编《运筹学》习题四详细解答

习题四4.1工厂生产甲、乙两种产品,由A、E二组人员来生产。
A组人员熟练工人比较多,工作效率高,成本也高;E组人员新手较多工作效率比较低,成本也较低。
例如,A组只生产甲产品时每小时生产10件,成本是50元有关资料如表4.21所示。
表 4.21二组人员每天正常工作时间都是8小时,每周5天。
一周内每组最多可以加班10小时,加班生产的产品每件增加成本5元。
工厂根据市场需求、利润及生产能力确定了下列目标顺序:P1:每周供应市场甲产品400件,乙产品300件P2:每周利润指标不低于500元P3:两组都尽可能少加班,如必须加班由A组优先加班建立此生产计划的数学模型。
4.1【解】解法一:设X1, X2分别为A组一周内正常时间生产产品甲、乙的产量,X3, X4分别为A组一周内加班时间生产产品甲、乙的产量;X5, X6分别为B组一周内正常时间生产产品甲、乙的产量,X7, X8分别为B组一周内加班时间生产产品甲、乙的产量。
总利润为80(X1 X3 X5 X7) (5055X3 45X5 50X7)75(X2 X X6 X s) (45X2 50X4 40X6 45x030X1 30X2 25X3 25X4 35X5 35X6 30X7 30X8生产时间为A 组:0.1捲0.125X20.1X30.125X4B 组:0.125x50.2X60.125X70.2沧数学模型为:min Z p1(d1d2) P2d3 P3(d 4 d5) P4(d6 2d?)X1 X3 X5 X7 d1 d1 400X2 X4 X6 X8 d2 d2 30030为30X225X325X435X535X630X730XS d3500400.1X10.125X2 d4d4400.125X5 0.2X6 d5d50.1X3 0.125x4 d6d6 100.125X70.2X8 d7d7 10X j 0,d i ,d i 0,i 1,2丄,7; j 1,2,L ,8解法二:设X1, X2分别为A组一周内生产产品甲、乙的正常时间,X3, X4分别为A组一周内生产产品甲、乙的加班时间;X5, X6分别为B组一周内生产产品甲、乙的正常时间,X7, X8分别为B组一周内生产产品甲、乙的加班时间。
运筹学课后习题答案 熊伟(第二版)
【解】虚拟一个发点和一个收点
T6.11-1
得到流量v=22的最小费用流,最小费用为271。求解过程参看第4章PPT文档习题答案。
T6.11-13
最小费用最大流如下图,最大流量等于27,总费用等于351。
6.12如图6-43所示,(1)求解旅行售货员问题;(2)求解中国邮路问题。
图6-43
【解】(1)旅行售货员问题。
总费用最小的设备更新方案为:第一种方案,第1年购置一台设备使用到第5年年末;第二种方案,第1年购置一台设备使用到第2年年末,第3年年初更新后使用到第5年年末。总费用为11.5万元。
6.8图6-43是世界某6大城市之间的航线,边上的数字为票价(百美元),用Floyd算法设计任意两城市之间票价最便宜的路线表。
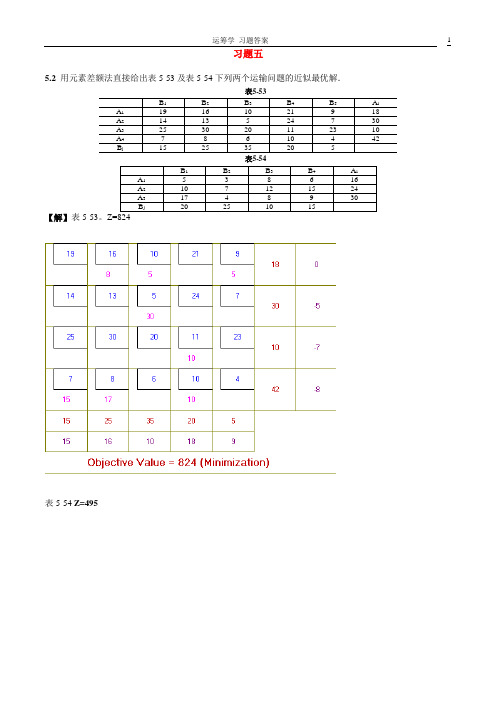
表5-56
B1
B2
B3
B4
Ai
A1
9
15
4
8
10
A2
3
1
7
6
30
A3
2
10
13
4
20
A4
4
5
8
3
43
bj
20
15
50
15
【解】(1)
(2)
5.4求下列运输问题的最优解
(1)C1目标函数求最小值;(2)C2目标函数求最大值
15 45 20 40 60 30 50 40
(3)目标函数最小值,B1的需求为30≤b1≤50, B2的需求为40,B3的需求为20≤b3≤60,A1不可达A4,B4的需求为30.
【解】(1)
(2)
(3)先化为平衡表
B11
B12
B2
B31
B32
熊伟运筹学(第2版)1-3章参考答案

运筹学(第2版)习题答案1--3习题一1.1 讨论下列问题:(1)在例1.2中,如果设x j (j=1,2,…,7)为工作了5天后星期一到星期日开始休息的营业员,该模型如何变化.(2)在例1.3中,能否将约束条件改为等式;如果要求余料最少,数学模型如何变化;简述板材下料的思路. (3)在例1.4中,若允许含有少量杂质,但杂质含量不超过1%,模型如何变化.(4)在例1.6中,假定同种设备的加工时间均匀分配到各台设备上,要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1小时,模型如何变化.(5)在单纯形法中,为什么说当00(1,2,,)k ik a i m λ>≤=并且时线性规划具有无界解。
1.2 工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-23所示.根据市场需求,试建立该问题的数学模型,使每月利润最大.【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量,则数学模型为1.3 建筑公司需要用6m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格及数量如表1-24所示:问怎样下料使得(1【解】 设x j (j =1,2,…,14)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为用单纯形法求解得到两个基本最优解X (1)=( 50 ,200 ,0 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=534 X (2)=( 0 ,200 ,100 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,150 ,0 ,0 );Z=534 (2)余料最少数学模型为用单纯形法求解得到两个基本最优解X (1)=( 0 ,300 ,0 ,0,50 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0,用料550根 X (2)=( 0 ,450 ,0 ,0,0 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0,用料650根 显然用料最少的方案最优。
运筹学(第五版) 习题答案

非基变量 的检验数 =0,所以有无穷多最优解。
(3)解:大M法
加入人工变量,化成标准型:
Max z=10 +15 +12 +0 +0 +0 -M
s.t. 5 +3 + + =9
-5 +6 +15 + =15
2 + + - + =5
, , , , , , 0
当 0,目标函数在原点最大值。
k= 时, , 同号。
当 0时,目标函数在BC线断上任一点有最大值
当 0时,目标函数在原点最大值。
k=0时, =0
当 0时,目标函数在A点有最大值
当 0,目标函数在OC线断上任一点有最大值
(2)当 =0时,max z=
0时,目标函数在C点有最大值
0时,目标函数在OA线断上任一点有最大值
(i=1,2,3…,n)
0, 0, (i=1,2,3…n; k=1,2….,m)
M是任意正整数
初始单纯形表:
-M
-M
…
-M
…
…
…
b
…
…
…
…
-M
1
1
0
…
0
1
1
…
…
0
0
…
0
-M
1
0
1
…
0
0
…
…
0
0
…
0
…
…
…
…
…
…
…
…
…
…
…
…
…
运筹学课后习题答案

第一章线性规划及单纯形法1用X j (j=1.2…5)分别代表5中饲料的采购数,线性规戈肪莫型:min Z = 0.2x1+0.7x2 +0.4x3 +0.3X4 +0.8X5st 3为+2x2 +X3 +6% +18x5 > 700为+ 0.5x2 +0.2X3+2X4 +x5 > 300.5x1 +x^0.2x3+2x4> 0.8x5 > 100X j(j =1,234,5,6) >02.解:设X1X2X3X4X5X6x表示在第i个时期初开始工作的护士人数,Z表示所需的总人数,贝Umi nz=M +X2 +X3 + X4 +X5+X6st. x^i + X e >60X+x2 >70X2 +X3 >60X3 +& >50& +X5 >20X5 +X6 >30为(i =1,2.3.4.5.6)>03.解:设用i=1 , 2, 3分别表示商品A , B, C, j=1 , 2, 3分别代表前,中,后舱,Xij表示装于j舱的i种商品的数量,Z表示总运费收入则:max Z =1000(X11 +X12 +为3)+ 700(X21 +X22 +X23) +600区1 +心 +怡3)st. +為2 +为3 兰600X21 + X22 +X23 兰1000X31 +X32 +X33 兰80010X11 +5X21 +7X31 <40010X12 +5X22 +7X32 兰540010^3 +5X23 +7X33 兰15008x11 +6x21 +5x31 兰20008x12 +6x22 +5x32 兰30008为3 +6X23 +5X33 兰15008X11 +6X21 +5X31 兰0 158x12 十6x22 十5X328X13 +6X23 + 5X33 ^0 158X12+6X22 +5X328片1 +6X21 +5x31 兰0 18X13+6X23+5X33Xj 3 0(i =1,2.3 .j =1,2,3)5 . (1)(2)max z = X j + X2st. 6X1+10X2 <120N + X2 汐O5 <为 >1O3<X2 >8解:如图:由图可得:X =(10,6)T ; Z =16* T 即该问题具有唯一最优解x =(10,6)z =5% +6X22X] - X2 - 2-2X4 + 3X2 兰2X i, x^ 0XI无可行解⑷maxst.如图:由图知,该问题具有无界解。
运筹学课后习题答案

运筹学课后习题答案第一章线性规划1、由图可得:最优解为2、用图解法求解线性规划:Min z=2x1+x2解:由图可得:最优解x=1.6,y=6.43用图解法求解线性规划:Max z=5x1+6x2解:由图可得:最优解Max z=5x1+6x2, Max z= +4用图解法求解线性规划:Maxz = 2x 1 +x 2 由图可得:最大值==+35121x x x ,所以==2321x xmax Z = 8.6将线性规划模型化成标准形式:Min z=x 1-2x 2+3x 3 解:令Z ’=-Z,引进松弛变量x 4≥0,引入剩余变量x 5≥0,并令x 3=x 3’-x 3’’,其中x 3’≥0,x 3’’≥0Max z ’=-x 1+2x 2-3x 3’+3x 3’’7将线性规划模型化为标准形式Min Z =x1+2x2+3x3解:令Z’ = -z,引进松弛变量x4≥0,引进剩余变量x5≥0,得到一下等价的标准形式。
x2’=-x2 x3=x3’-x3’’Z’ = -min Z = -x1-2x2-3x39用单纯形法求解线性规划问题:Max Z =70x1+120x2解: Max Z =70x1+120x2单纯形表如下Max Z =3908.11.解:(1)引入松弛变量X4,X5,X6,将原问题标准化,得max Z=10X1+6X2+4X3X1+X2+X3+X4=10010 X1+4X2+5X3+X5=6002 X1+2X2+6X3+X6=300X1,X2,X3,X4,X5,X6≥0得到初始单纯形表:(2)其中ρ1 =C1-Z1=10-(0×1+0×10+0×2)=10,同理求得其他根据ρmax =max{10,6,4}=10,对应的X1为换入变量,计算θ得到,θmin =min{100/1,600/10,300/2}=60,X5为换出变量,进行旋转运算。
(3)重复(2)过程得到如下迭代过程ρj≤0,迭代已得到最优解,X*=(100/3,200/3,0,0,0,100)T,Z* =10×100/3+6×200/3+4×0 =2200/3。
熊伟运筹学课后习题答案1-4章

目录教材习题答案 ................................................................................................... 错误!未定义书签。
习题一 ...................................................................................................................................... 1 习题二 .................................................................................................................................... 27 习题三 .................................................................................................................................... 37 习题四 .................................................................................................................................... 39 习题五 ....................................................................................................... 错误!未定义书签。
习题六 ....................................................................................................... 错误!未定义书签。
运筹学第3版熊伟编著习题答案

求没有限制,由于仓库容量有限,仓库最多库存产品 A1000 件,1 月初仓库库存 200 件。1~
6 月份产品 A 的单件成本与售价如表 1-25 所示。
表 1-25
月份
1
2
3
4
5
6
产品成本(元/件)
300 330 320 360
360
300
销售价格(元/件)
350 340 350 420
410
340
(1)1~6 月份产品 A 各生产与销售多少总利润最大,建立数学模型;
(2)当 1 月初库存量为零并且要求 6 月底需要库存 200 件时,模型如何变化。
【解】设 xj、yj(j=1,2,…,6)分别为 1~6 月份的生产量和销售量,则数学模型为
最新精品文档,知识共享!
max Z 300x1 350 y1 330x2 340 y2 320x3 350 y3 360x4
第1章 线性规划
1.1 工厂每月生产 A、B、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源
限量及单件产品利润如表 1-23 所示.
表1-23
产品 资源
A
B
C
资源限量
材料(kg)
1.5
1.2
4
2500
设备(台时)
3
1.6
1.2
利润(元/件)
10
14
12
1400
根据市场需求,预测三种产品最低月需求量分别是 150、260 和 120,最高月需求是 250、310 和 130.试建立该问题的数学模型,使每月利润最大. 【解】设 x1、x2、x3 分别为产品 A、B、C 的产量,则数学模型为
xj 0, j 1, 2, ,10
运筹学答案(熊伟)上汇总

部分有图形的答案附在各章PPTபைடு நூலகம்档的后面,请留意。
第1章线性规划
第2章线性规划的对偶理论第3章整数规划第4章目标规划
第5章运输与指派问题第6章网络模型第7章网络计划第8章动态规划第9章排队论第10章存储论第11章决策论第12章对策论
习题一
1.1讨论下列问题:
(1)在例1.1中,假定企业一周内工作5天,每天8小时,企业设备A有5台,利用率为0.8,设备B有7台,利用率为0.85,其它条件不变,数学模型怎样变化.
1.4 A、B两种产品,都需要经过前后两道工序加工,每一个单位产品A需要前道工序1小时和后道工序2小时,每一个单位产品B需要前道工序2小时和后道工序3小时.可供利用的前道工序有11小时,后道工序有17小时.
每加工一个单位产品B的同时,会产生两个单位的副产品C,且不需要任何费用,产品C一部分可出售赢利,其余的只能加以销毁.
maxZ=3x 1+7x 2+2x 3-x 4⎧x 1+2x 2≤11⎪2x +3x ≤1712⎪⎪
⎨-2x 2+x 3+x 4=0⎪x ≤13⎪3⎪⎩x j ≥0, j =1, 2, , 4
1.5某投资人现有下列四种投资机会,三年内每年年初都有3万元(不计利息)可供投资:方案一:在三年内投资人应在每年年初投资,一年结算一次,年收益率是20%,下一年可继续将本息投入获利;
⎪-1.5x 12-1.2x 21+x 31+x 34≤30000⎪⎪
⎨x 12≤20000⎪x ≤15000⎪23
⎪x 34≤10000⎪⎪⎩x ij ≥0, i =1, ,3; j =1, 4
最优解X=(30000,0,66000,0,109200,0;Z=84720
运筹学第三版熊伟课后习题答案

填空题答案线性规划1.(决策变量、目标函数和约束条件;目标函数是决策变量的线性函数并且求最大值或最小值、约束条件是决策变量的线性不等式组)2.(-2)3.(-4/3)4.(7,3)5.(6,2),(26)6.(-M),(M)7.(-4,12)8.(0,11/3,5)9.(MR x x x Z -+-=3212m ax ), (2+M,-1+2M,1+M,0,-M,0)10.(R w =min ),(-1,-2,-1,0,1,0)11.(非基变量) (0)12.(1)3,0,021-<≥≥a b b (2)120,0,3,(2,0,0,0)b b a λ≥≥=-=-13.某个λk >0且a ik ≤0(i =1,2,…,m )14.目标函数值大于零线性规划的对偶理论15.(4,-1)16.(0,0)17.(无可行解)18.(80),(3,0,1)19.(-∞,-λj +c j )20.[2,4],[8,16]21.B -1的第i 列22.(10,15)23.≤,≤整数规划24. ⎪⎪⎪⎩⎪⎪⎪⎨⎧==≥++-+≤+-+≤---≥+3,2,1101)1(305)1(184)1(52221321221121j y y y y M y x x M y x x M y x x j ,或25. ⎪⎪⎪⎩⎪⎪⎪⎨⎧=--≥+≤-->+≤10)1(54)1(662211或y M y x yM x M y x yM x26.(分枝定界法和割平面法)27.(x 1≤3),(x 1≥4)28.(s -5x 4-5x 5=-1)或(s -5/8x 4-5/8x 5=-1/8)29.(1,1)目标规划30.(不低于目标值),(恰好等于目标值)31. -+-++=22111)(m in d p d d p Z32.(0,3)及(1,2)33.(9,0,2,0)34.(G 4>G 1>G 3>G 2>G 5)运输与指派问题35.(1,2,3,2,6),(4,1,2,2) 36.(1)550,010********=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Z X (2) 580,101010510152=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Z X (3) 550,010********=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=Z X (4) X 1,X 3最接近最优解37.(闭回路法),(位势法)38.(mn ),(m+n),(m+n -1)39. (不包含任何闭回路)40.(线性规划)41.(求最小值、效率非负、工作数等于人数)42.(B )43.(最少直线数等于m )44. (m+n -1)45.11,30网络模型46.(连通)47.(所有点)48.(破圈法和加边法)49.(发点v i 到点v j 的最短路长),(b (j )+w ij )50.(Floyd 算法)51.(使最大服务距离达到最小、使总运量最小)52.(单位时间内弧的最大通过能力)53.(最大流)54.(f ij <c ij ),(f ij >0)55.(费用)TOP网络计划56.i <j57.前道工序58.用节点表示事件用箭条表示工序59.用箭条表示事件用节点表示工序60.最乐观时间、最可能时间、悲观时间61.4()6ij ij ijij a m b E t ++=,2()6ij ij ij b a D t -⎛⎫= ⎪⎝⎭62.是指紧前工序的最早可能完工时间的最大值,)},(),({max ),(i t i T j i T ES j i ES θθθ+=<<63.是指为了不影响紧后工序如期开工,工序最迟必须开工的时间),()},({min )},(),({min ),(j i t j T j i t j T j i T LS j i LS j i LS -=-=<<<<ϕϕϕϕ64. ),(),(),(),(),(),(),(),(j i t j i T j i T j i T j i T j i T j i T j i S ES LF EF LF ES LS --=-=-=65.在不影响紧后工序的最早开始时间的条件下,工序(i ,j ) 的开始时间可以推迟的时间 动态规划66.状态67.s k 、x k68.13 (注:加上终端条件)69.阶段、状态、决策与策略、状态转移方程及指标函数70.逆序,顺序排队论71.负指数72.2573.1/μ74.顾客的到达过程是泊松过程;服务时间服务负指数分布,3个服务台、队长无限制、顾客源有限、先到先服务75.λ/μ,1-λ/μ存储论76.将单位时间分成n 等分的时间区间t ,在每个区间开始订购或生产相同的货物量 77.1078.173.2,10.38,10079.C o =C -S +H ,C u =P -C +B ,供过于求时单位产品总成本,供不应求时单位产品总成本80.0()Qu u oC f x dx C C =+⎰ 决策论81.悲观主义准则、乐观主义准则、最小机会损失准则、等可能准则、折衷准则82.收益期望值最大、后悔期望值最小83.决策点、策略点、每个方案在相应自然状态的效益值、表述该方案被删除掉84.马尔可夫85.离散,有限的多属性决策86.效益型、成本型、固定型、区间型87.minmax max j j ij jij x x x x y --=88.规范化方法、线性比例方、标准化方法、 归一化方法、单位化方法89.1,090.(-3,3)91.592.n93.(期望值法、方程组法、算术平均法、几何平均法、特征值法及最小平方法),(最大方差法、熵值法,主分量分析法),(加权集成法、乘法集成法、两阶段赋权法)94.计算法则与矩阵乘法相同,但元素之间的乘法运算换成元素取最小运算∧,元素之间的加法运算换成元素取最大运算∨95.目标层、准则层及方案层博弈论96.局中人,策略集,得益函数97.**max min min max j i ij ij ij j i a a a == 98. 11122122(,)789E x y x y x y x y x y =+++,11122122(,)789E x y x y x y x y x y =+++(与局中人相同)99.16/3 (由期望值函数11122122(,)7256E x y x y x y x y x y =+++得到)100.12312312312123min 5716551741,,0z x x x x x x x x x x x x x x =++++≥⎧⎪++≥⎪⎨+≥⎪⎪≥⎩,12312312312123max 6715541751,,0w y y y y y y y y y y y y y y =++++≤⎧⎪++≤⎪⎨+≤⎪⎪≥⎩, **(0.143,0.857,0),(0.4287,0,0.5713)x y ==,G V =4.4287。
运筹学第3版熊伟编著习题答案

运筹学第3版熊伟编著习题答案在学习运筹学的过程中,熊伟编著的第 3 版教材中的习题对于我们理解和掌握这门学科的知识起到了至关重要的作用。
下面,我将为大家详细呈现这些习题的答案。
首先,让我们来看第一章的习题。
在这部分习题中,主要涉及到了运筹学的基本概念和一些简单的数学模型构建。
例如,有一道关于线性规划的题目,给定了一些生产条件和资源限制,要求我们求出最优的生产方案。
对于这道题,我们需要先建立线性规划的数学模型,设定决策变量、目标函数和约束条件。
然后,通过图解法或者单纯形法来求解。
经过一系列的计算和分析,我们得出最优的生产方案是生产某种产品_____个,另一种产品_____个,从而实现利润最大化。
在第二章的习题中,重点考察了整数规划的相关知识。
整数规划相较于线性规划,多了决策变量必须为整数的限制条件,这使得问题的求解变得更加复杂。
有一道题目是关于背包问题的,给定了不同物品的价值和重量,以及背包的容量限制,要求找出能够装入背包且价值最大的物品组合。
对于这类问题,我们可以采用分支定界法或者割平面法来求解。
通过逐步缩小可行解的范围,最终确定最优的物品组合。
第三章的习题主要围绕动态规划展开。
动态规划是解决多阶段决策问题的一种有效方法。
比如,有一个资源分配的问题,在多个阶段中,如何合理分配有限的资源以达到最优的效果。
我们通过建立递推关系式,从最后一个阶段逐步向前推导,最终找到整个过程的最优策略。
第四章是关于图与网络分析的内容。
这部分的习题常常涉及到最短路径问题、最大流问题等。
例如,在一个交通网络中,要求找出从起点到终点的最短路径。
我们可以运用迪杰斯特拉算法或者弗洛伊德算法来解决。
对于最大流问题,则可以使用福特富尔克森算法来求得最大流量。
第五章的习题聚焦于存储论。
存储论主要研究在不同需求情况下,如何确定最佳的存储策略,以平衡存储成本和缺货成本。
例如,有一道关于确定经济订货批量的题目,给定了年需求量、单位订货成本和单位存储成本等参数,我们可以通过公式计算出经济订货批量为_____。
运筹学熊伟 第二版第三长答案

运筹学熊伟第二版第三长答案运筹学熊伟第二版第三长答案练习33.1[解决方案]设置XJ参数1.投资项目?0不投资J项目maxz?30x1?40x2?20x3?15x4?30x5?5x1?4x2?5x3?7x4?8x5?30? 十、7x?9x?5倍?6x?252345?1.8x1?2x2?6x3?2x4?9x5?30? XJ=0或1,J?1.5.,模型为最优解x=(1,1,1,0,1),z=110万元,即当选择项目1、2、3和5时,总收入最大。
三点二【解】设xj为投资第j个点的状态,xj=1或0,j=1,2,…,12麦克斯?400x1?500x2?450x3400x12?900x1?1200x2?1000x3850x11?1000x12?9000? 44771212? 十、2,x?3,x?1,x?2,x?3,x?4.Jjjjjjj?1j?1j?5j?5j?8j?8.十、1还是0,J?1.12? J最优解:X1=X5=X12=0,其余XJ=1,总收入z=3870万元,实际完成投资8920万元。
三点三【解】设xj为装载第j件货物的状态,xj=1表示装载第j件货物,xj=0表示不装载第j件货物,有麦克斯?5x1?8x2?4x3?6x4?7x5?3x6?6x1?5x2?3x3?4x4?7x5?2x6?20??3x1?7x2?4x3?5x4?6x5?2x6?56?? x4?x5?0 x?十、12? 1.xj?0或13.4【解】设xij(i=1,2,…,5;j=1,2,3,4)为第i人参赛j项目的状态,即1xij0我参加了j活动第i人不参赛j项目54记第i人参赛j项目的成绩为cij,,目标函数麦克斯cijxiji?1j?1每个运动员最多只能参加3个项目并且每个项目只能参赛一次,约束条件:xi1?xi2?xi3?xi4?3i?1,2,?, 5.每项活动必须至少参加一次,总人数为10人。
限制条件:x1j?x2j?x3j?x4j?x5j?1j?1,2,3,4一xi?1j?154ij?10数学模型是maxzcijxiji?1j?154?xi1?xi2?xi3?xi4?3i?1,2,?,5?x?x?x?x?x?1j?1,2,3,42j3j4j5j?1j?54xij?10?i?1j?1??xij?1或0,i?1,2,?,5;j?1,2,3,43.5x1?2x2?8.y1m?x1?5.嗯??十、5.(1?y)m?x1?2y1?4y2?6y3?8y4?4x1?x2?10? y2m1[解决方案](1)?2x1?6x2?18? y3m(2)?十、10? ym(3)?y1?y2?y3?y4?1.2.YYY1.YJ、还是0?1,2,3,4? 十、8.(1?y)m1222?Jy?0或1?yj?0或1,j?1,2,33.6.明兹?10y1?6x1?15y2?10x2?x1?y1m;x2?y2m?十、8.ym3?1.x2?6.(1?y3)米??x1?x2?0y4?4y5?4y6?8y7?8y8[解决方案]??y4?y5?y6?y7?y8?1.x1?2x2?20? 900万日元?2x1?x2?20? 1000万日元??x1?x2?20? 110万日元?YYY21011? 911?? x1?0,x2?0 yj?0还是1,J?1,2,?,3.7[溶液](1)x=(1,2)或x=(0,3)z=3(2)x=(5,0),z=53.8二条件(1)条件(2)条件(3)条件(4)[溶液](1)x=(3,3),z=15(2)x=(5,2),z=163.9.【解】(1)x=(1,1,1),z=8(2) x=(1,1,1,0),z=43.10[溶液](1)x=(1,0,1,1),z=8(2)x=(1,1,0,0,0),z=-2三。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录教材习题答案 ................................................. 错误!未定义书签。
习题一 ................................................... 错误!未定义书签。
习题二 ................................................... 错误!未定义书签。
习题三 ................................................... 错误!未定义书签。
习题四 ................................................... 错误!未定义书签。
习题五 ................................................... 错误!未定义书签。
习题六 ................................................... 错误!未定义书签。
习题七 ................................................... 错误!未定义书签。
习题八 ................................................... 错误!未定义书签。
部分有图形的答案附在各章PPT文档的后面,请留意。
习题一讨论下列问题:(1)在例中,假定企业一周内工作5天,每天8小时,企业设备A有5台,利用率为,设备B有7台,利用率为,其它条件不变,数学模型怎样变化.(2)在例中,如果设x j(j=1,2,…,7)为工作了5天后星期一到星期日开始休息的营业员,该模型如何变化.(3)在例中,能否将约束条件改为等式;如果要求余料最少,数学模型如何变化;简述板材下料的思路.(4)在例中,若允许含有少量杂质,但杂质含量不超过1%,模型如何变化.(5)在例中,假定同种设备的加工时间均匀分配到各台设备上,要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1小时,模型如何变化.工厂每月生产A、B、C三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1-22所示.表1-22130.试建立该问题的数学模型,使每月利润最大.【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量,则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 建筑公司需要用6m 长的塑钢材料制作A 、B 两种型号的窗架.两种窗架所需材料规格及数量如表1-23所示:表1-23 窗架所需材料规格及数量问怎样下料使得(1【解】 第一步:求下料方案,见下表。
设x j (j =1,2,…,14)为第j 种方案使用原材料的根数,则 (1)用料最少数学模型为14112342567891036891112132347910121314min 2300322450232400232346000,1,2,,14jj j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪++++++≥⎪⎪++++++≥⎨⎪++++++++≥⎪⎪≥=⎩∑ 用单纯形法求解得到两个基本最优解X (1)=( 50 ,200 ,0 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=534 X (2)=( 0 ,200 ,100 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,150 ,0 ,0 );Z=534 (2)余料最少数学模型为134131412342567891036891112132347910121314min 0.60.30.70.40.82300322450232400232346000,1,2,,14j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =+++++⎧+++≥⎪++++++≥⎪⎪++++++≥⎨⎪++++++++≥⎪⎪≥=⎩ 用单纯形法求解得到两个基本最优解X (1)=( 0 ,300 ,0 ,0,50 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0,用料550根 X (2)=( 0 ,450 ,0 ,0,0 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0,用料650根 显然用料最少的方案最优。
A 、B 两种产品,都需要经过前后两道工序加工,每一个单位产品A 需要前道工序1小时和后道工序2小时,每一个单位产品B 需要前道工序2小时和后道工序3小时.可供利用的前道工序有11小时,后道工序有17小时.每加工一个单位产品B 的同时,会产生两个单位的副产品C ,且不需要任何费用,产品C 一部分可出售赢利,其余的只能加以销毁.出售单位产品A 、B 、C 的利润分别为3、7、2元,每单位产品C 的销毁费为1元.预测表明,产品C 最多只能售出13个单位.试建立总利润最大的生产计划数学模型.【解】设x 1,x 2分别为产品A 、B 的产量,x 3为副产品C 的销售量,x 4为副产品C 的销毁量,有x 3+x 4=2x 2,Z 为总利润,则数学模型为123412122343maxZ=3+7+2211231720130,1,2,,4j x x x x x x x x x x x x x j -+≤⎧⎪+≤⎪⎪-++=⎨⎪≤⎪≥=⎪⎩某投资人现有下列四种投资机会, 三年内每年年初都有3万元(不计利息)可供投资:方案一:在三年内投资人应在每年年初投资,一年结算一次,年收益率是20%,下一年可继续将本息投入获利;方案二:在三年内投资人应在第一年年初投资,两年结算一次,收益率是50%,下一年可继续将本息投入获利,这种投资最多不超过2万元;方案三:在三年内投资人应在第二年年初投资,两年结算一次,收益率是60%,这种投资最多不超过万元; 方案四:在三年内投资人应在第三年年初投资,一年结算一次,年收益率是30%,这种投资最多不超过1万元.投资人应采用怎样的投资决策使三年的总收益最大,建立数学模型. 【解】是设x ij 为第i 年投入第j 项目的资金数,变量表如下数学模型为112131122334111211212312213134122334max 0.20.20.20.50.60.3300001.2300001.5 1.2300002000015000100000,1,,3;1,4ij Z x x x x x x x x x x x x x x x x x x x i j =+++++⎧+≤⎪-++≤⎪⎪--++≤⎪⎪≤⎨⎪≤⎪⎪≤⎪≥==⎪⎩最优解X=(30000,0,66000,0,109200,0);Z =84720IV 发展公司是商务房地产开发项目的投资商.公司有机会在三个建设项目中投资:高层办公楼、宾馆及购物中心,各项目不同年份所需资金和净现值见表1-24.三个项目的投资方案是:投资公司现在预付项目所需资金的百分比数,那么以后三年每年必须按此比例追加项目所需资金,也获得同样比例的净现值.例如,公司按10%投资项目1,现在必须支付400万,今后三年分别投入600万、900万和100万,获得净现值450万.公司目前和预计今后三年可用于三个项目的投资金额是:现有2500万,一年后2000万,两年后2000万,三年后1500万.当年没有用完的资金可以转入下一年继续使用.IV 公司管理层希望设计一个组合投资方案,在每个项目中投资多少百分比,使其投资获得的净现值最大.表1-24【解】以1%为单位,计算累计投资比例和可用累计投资额,见表(2)。
表(2)设x j 为j 项目投资比例,则数学模型:123123123123123max 457050408090025001001601404500190240160650020031022080000,1,2,3j Z x x x x x x x x x x x x x x x x j =++⎧++≤⎪++≤⎪⎪++≤⎨⎪++≤⎪⎪≥=⎩ 最优解X =(0,,);Z=万元年份实际投资项目1比例:0项目2比例:项目3比例:累计投资(万元) 00102030净现值0图解下列线性规划并指出解的形式:(1)12 121212max2131,0Z x x x xx xx x=-++≥⎧⎪-≥-⎨⎪≥⎩【解】最优解X=(1/2,1/2);最优值Z=-1/2(2)12 121212min3 22 23120,0Z x xx xx xx x=---≥-⎧⎪+≤⎨⎪≥≥⎩【解】最优解X=(3/4,7/2);最优值Z=-45/4(3)12 1212121212min32211410 2731,0Z x x x xx xx xx xx x=-++≤⎧⎪-+≤⎪⎪-≤⎨⎪-≤⎪⎪≥⎩【解】最优解X=(4,1);最优值Z=-10(4) 121212112max 3812223,0Z x x x x x x x x x =++≤⎧⎪+≤⎪⎨≤⎪⎪≥⎩ 【解】最优解X =(3/2,1/4);最优值Z=7/4(5) ⎪⎪⎩⎪⎪⎨⎧≥≤≥≥-+=0,6322min 21212121x x x x x x x x Z 【解】最优解X =(3,0);最优值Z=3(6) ⎪⎪⎩⎪⎪⎨⎧≥≤≥≥-+=0,6322max 21212121x x x x x x x x Z【解】无界解。
(7)12121212min 25262,0Z x x x x x x x x =-+≥⎧⎪+≤⎨⎪≥⎩【解】无可行解。
(8)12 1211212max 2.52 280.5 1.5210,0Z x x x xxx xx x=++≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩【解】最优解X=(2,4);最优值Z=13将下列线性规划化为标准形式 (1)123123123123123max 423205743103650,0,Z x x x x x x x x x x x x x x x =+-++≤⎧⎪-+≥⎪⎨++≥-⎪⎪≥≥⎩无限制【解】(1)令654''3'33,,,x x x x x x -=为松驰变量 ,则标准形式为'''1233'''12334'''12335'''12336'''1233456max 42332057443103665,,,,,,0Z x x x x x x x x x x x x x x x x x x x x x x x x x x =--+⎧++-+=⎪-+--=⎪⎨---++=⎪⎪≥⎩ (2) 123123112123min 935|674|205880,0,0Z x x x x x x x x x x x x =-++-≤⎧⎪≥⎪⎨+=-⎪⎪≥≥≥⎩ 【解】(2)将绝对值化为两个不等式,则标准形式为123123412351612123456max 9356742067420588,,,,,0Z x x x x x x x x x x x x x x x x x x x x x '=-+-+-+=⎧⎪--++=⎪⎪-=⎨⎪--=⎪⎪≥⎩ (3)1211212max 231510,0Z x x x x x x x =+≤≤⎧⎪-+=-⎨⎪≥≥⎩【解】方法1:121314121234max 23151,,,0Z x x x x x x x x x x x x =+-=⎧⎪+=⎪⎨-=⎪⎪≥⎩ 方法2:令111111,1,514x x x x x '''=-+≤-=有= 1211212max 2(1)34(1)1,0Z x x x x x x x '=++'≤⎧⎪'-++=-⎨⎪≥⎩则标准型为121312123max 22340,,0Z x x x x x x x x x '=++'+=⎧⎪'-+=⎨⎪'≥⎩(4) 12123123123123123max min(34,)2304215965,0Z x x x x x x x x x x x x x x x x x =+++++≤⎧⎪-+≥⎪⎨++≥-⎪⎪≥⎩无约束、【解】令1212311134,,y x x y x x x x x x '''≤+≤++=-,线性规划模型变为11211231123112311231123max 3()42304()2159()65,,0Z yy x x x y x x x xx x x x x x x x x x x x x x x x ='''≤-+⎧⎪'''≤-++⎪⎪'''-++≤⎪⎨'''--+≥⎪⎪'''-++≥-⎪'''≥⎪⎩、 标准型为112411235112361123711238112345678max 33400230442159965,,,,,,,,0Z yy x x x x y x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ='''-+-+=⎧⎪'''-+--+=⎪⎪'''-+++=⎪⎨'''--+-=⎪⎪'''-+--+=⎪'''≥⎪⎩设线性规划⎪⎩⎪⎨⎧=≥=+-=+++=4,,1,06024503225max 42132121 j x x x x x x x x x Z j取基11322120(P )4041B B ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,P 、=,分别指出B B 12和对应的基变量和非基变量,求出基本解,并说明B B 12、是不是可行基.【解】B 1:x 1,x 3为基变量,x 2,x 4为非基变量,基本解为X=(15,0,20,0)T,B 1是可行基。
