MATLAB数学实验报告2
程序设计实验报告(matlab)

程序设计实验报告(matlab)实验一: 程序设计基础实验目的:初步掌握机器人编程语言Matlab。
实验内容:运用Matlab进行简单的程序设计。
实验方法:基于Matlab环境下的简单程序设计。
实验结果:成功掌握简单的程序设计和Matlab基本编程语法。
实验二:多项式拟合与插值实验目的:学习多项式拟合和插值的方法,并能进行相关计算。
实验内容:在Matlab环境下进行多项式拟合和插值的计算。
实验方法:结合Matlab的插值工具箱,进行相关的计算。
实验结果:深入理解多项式拟合和插值的实现原理,成功掌握Matlab的插值工具箱。
实验三:最小二乘法实验目的:了解最小二乘法的基本原理和算法,并能够通过Matlab进行计算。
实验内容:利用Matlab进行最小二乘法计算。
实验方法:基于Matlab的线性代数计算库,进行最小二乘法的计算。
实验结果:成功掌握最小二乘法的计算方法,并了解其在实际应用中的作用。
实验六:常微分方程实验目的:了解ODE的基本概念和解法,并通过Matlab进行计算。
实验内容:利用Matlab求解ODE的一阶微分方程组、变系数ODE、高阶ODE等问题。
实验方法:基于Matlab的ODE工具箱,进行ODE求解。
实验结果:深入理解ODE的基本概念和解法,掌握多种ODE求解方法,熟练掌握Matlab的ODE求解工具箱的使用方法。
总结在Matlab环境下进行程序设计实验,使我对Matlab有了更深刻的认识和了解,也使我对计算机科学在实践中的应用有了更加深入的了解。
通过这些实验的学习,我能够灵活应用Matlab进行各种计算和数值分析,同时也能够深入理解相关的数学原理和算法。
这些知识和技能对我未来的学习和工作都将有着重要的帮助。
matlab实验报告

实验一1.设x=-74°,y=-27°,求22的值。
√tan|x+y|+π2.当a取-3.0,-2.9,-2.8,…,2.8,2.9,3.0时,求e−0.3a sin(a+0.3)在各点的函数值。
3. 设x=24−0.455,求12In(x+√1+x ²)的值,并分析结果矩阵中各元素的含义。
4. 已知A=354234−457879015,B=1−2672874930求下面的表达式的值。
(1)A*B和A.*B。
(2)A^3和A.^3.。
(3)A/B和A\B。
(4)[A,B]和[A([1,3],:);B^2]。
实验二一、实验步骤:1)新建脚本2)在编辑器中输入相应程序3)在命令窗口执行文件,得到结果1. 根据π²6=11²+12²+13²+…+1n ²,求π的近似值。
当n 分别取100、1000、10000时,结果是多少?要求:分别用循环结构和向量运算(使用sum 函数)来实现。
1)循环结构一、实验步骤二、1)新建脚本2)在编辑器中输入相应程序3)保存文件,将文件命名为PI.m4)在命令窗口输入PI执行文件,得到结果三、实验代码四、实验结果2.根据y=1+13+15+⋯+12n−1,求(1)y<3时的最大n值(2)与(1)的n值对应的y值一、实验步骤1)打开matlab,新建脚本2)在脚本文件中输入实验代码3)保存文件,存名字为value.m4)在命令窗口中输入value,得到实验结果二、实验代码三、实验结果。
南华大学《MATLAB及应用》实验报告2

核科学技术学院实验报告实验项目名称MATLAB符号计算所属课程名称MATLAB及应用实验类型上机实验实验日期12月日指导教师谢芹班级学号姓名成绩一、实验名称MATLAB符号计算二、实验目的(1)掌握定义符号对象的方法(2)掌握符号表达式的运算法则以及符号矩阵运算(3)掌握求符号函数极限及导数的方法(4)掌握求符号函数定积分和不定积分的方法三、实验原理1. 函数极限及导数的方法(1)函数极限:limit(F,x,a) 求符号函数f(x)的极限值。
即计算当变量x趋近于常数a时,f(x)函数的极限值。
(2)limit(f):求符号函数f(x)的极限值。
符号函数f(x)的变量为函数findsym(f)确定的默认变量;没有指定变量的目标值时,系统默认变量趋近于0,即a=0的情况。
(3)limit(f,x,a,'right'):求符号函数f的极限值。
'right'表示变量x从右边趋近于a。
(4)limit(f,x,a,‘left’):求符号函数f的极限值。
‘left’表示变量x从左边趋近于a。
2. 微分:diff(s):没有指定变量和导数阶数,则系统按findsym函数指示的默认变量对符号表达式s求一阶导数。
diff(s,'v'):以v为自变量,对符号表达式s求一阶导数。
diff(s,n):按findsym函数指示的默认变量对符号表达式s求n阶导数,n为正整数。
diff(s,'v',n):以v为自变量,对符号表达式s求n阶导数。
3. 函数定积分和不定积分的方法:int(s):没有指定积分变量和积分阶数时,系统按findsym函数指示的默认变量对被积函数或符号表达式s求不定积分。
int(s,v):以v为自变量,对被积函数或符号表达式s求不定积分。
int(s,v,a,b):求定积分运算。
a,b分别表示定积分的下限和上限。
梯形法:trapz(x,y):x为分割点构成的向量,y为被积函数在分割点上的函数值构成的向量;抛物线法:quad(f,a,b,tol),f 是被积函数,[a,b]是积分区间,tol 是精度。
(完整word版)Matlab数学实验报告

Matlab 数学实验报告一、实验目的通过以下四组实验,熟悉MATLAB的编程技巧,学会运用MATLAB的一些主要功能、命令,通过建立数学模型解决理论或实际问题。
了解诸如分岔、混沌等概念、学会建立Malthu模型和Logistic 模型、懂得最小二乘法、线性规划等基本思想。
二、实验内容2.1实验题目一2.1.1实验问题Feigenbaum曾对超越函数y=λsin(πx)(λ为非负实数)进行了分岔与混沌的研究,试进行迭代格式x k+1=λsin(πx k),做出相应的Feigenbaum图2.1.2程序设计clear;clf;axis([0,4,0,4]);hold onfor r=0:0.3:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.5)for i=101:150plot(r,x(i),'k.');endtext(r-0.1,max(x(101:150))+0.05,['\it{r}=',num2str(r)]) end加密迭代后clear;clf;axis([0,4,0,4]);hold onfor r=0:0.005:3.9x=[0.1];for i=2:150x(i)=r*sin(3.14*x(i-1));endpause(0.1)for i=101:150plot(r,x(i),'k.');endend运行后得到Feigenbaum图2.2实验题目二2.2.1实验问题某农夫有一个半径10米的圆形牛栏,长满了草。
他要将一头牛拴在牛栏边界的桩栏上,但只让牛吃到一半草,问拴牛鼻子的绳子应为多长?2.2.2问题分析如图所示,E为圆ABD的圆心,AB为拴牛的绳子,圆ABD为草场,区域ABCD为牛能到达的区域。
问题要求区域ABCD等于圆ABC的一半,可以设BC等于x,只要求出∠a和∠b就能求出所求面积。
西安交通大学数学实验报告(用MATLAB绘制二维、三维图形)
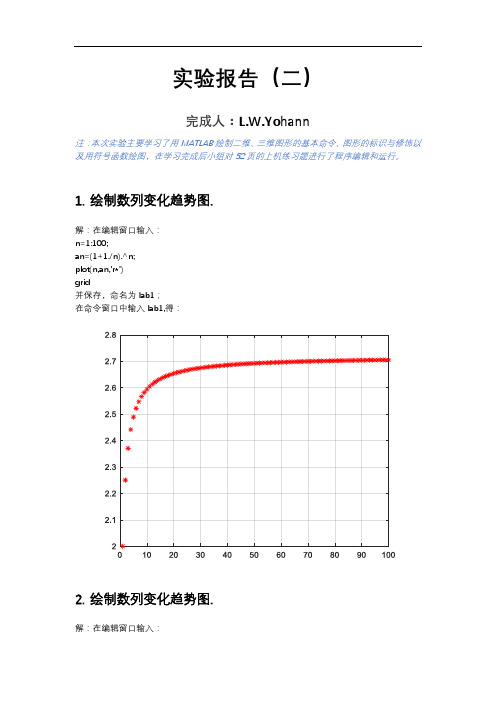
实验报告(二)完成人:L.W.Yohann注:本次实验主要学习了用MATLAB绘制二维、三维图形的基本命令、图形的标识与修饰以及用符号函数绘图,在学习完成后小组对52页的上机练习题进行了程序编辑和运行。
1.绘制数列变化趋势图.解:在编辑窗口输入:n=1:100;an=(1+1./n).^n;plot(n,an,'r*')grid并保存,命名为lab1;在命令窗口中输入lab1,得:2.绘制数列变化趋势图.解:在编辑窗口输入:n=1:0.1:50;an=n.^(1./n);plot(n,an,'r*')grid并保存,命名为lab2;在命令窗口中输入lab2,得:3.绘制函数在无定义点处的变化趋势.解:在编辑窗口输入:x=-10:0.05:10;y=sin(x)./x;plot(x,y,'r*')grid并保存,命名为lab3;在命令窗口中输入lab3,得:4.在同一坐标系中画出函数及其Taylor多项式的图像解:y=sinx在编辑窗口输入:syms xf=sin(x);T6=taylor(f,x);T8=taylor(f,x,'Order',8);T10=taylor(f,x,'Order',10);T12=taylor(f,x,'Order',12);fplot([T6 T8 T10 T12 f])xlim([-8 8])grid onlegend('approximation of sin(x) up to O(x^6)',...'approximation of sin(x) up to O(x^8)',...'approximation of sin(x) up to O(x^{10})',...'approximation of sin(x) up to O(x^{12})',...'sin(x)','Location','Best')title('Taylor Series Expansion')并保存,命名为lab4sin;在命令窗口中输入lab4sin,得:y=exp(x)在编辑窗口输入:syms xf=exp(x);T6=taylor(f,x);T8=taylor(f,x,'Order',8);T10=taylor(f,x,'Order',10);T12=taylor(f,x,'Order',12);fplot([T6 T8 T10 T12 f])xlim([-8 8])grid onlegend('approximation of exp(x) up to o(x^6)',...'approximation of exp(x) up to o(x^8)',...'approximation of exp(x) up to o(x^{10})',...'approximation of exp(x) up to o(x^{12})',...'exp(x)','Location','Best')title('Taylor Series Expansion')并保存,命名为lab4exp;在命令窗口中输入lab4exp,得:5.符号函数绘图.注:在matlab r2010b 和matlab r2019b中对绘制函数图像的输入方法有不同的要求,故此类题分两个版本来求解。
MATLAB实验报告

实验二MATLAB语言基础一、实验目的基本掌握MA TLAB向量、矩阵、数组的生成及其基本运算(区分数组运算和矩阵运算)、常用的数学函数。
了解字符串的操作。
二、实验内容1.向量的生成与运算;2.矩阵的创建、引用和运算;3.多维数组的创建及运算;4.字符串的操作。
三、实验步骤1.向量的生成与运算①向量的生成向量的生成有三种方法:直接输入法:生成行向量、列向量;冒号表达式法:变量=初值:间隔(可正可负):终值函数法:使用linspace线性等分函数,logspace对数等分函数。
格式为:linspace(初值,终值,个数)Logspace(初值,终值,个数), 初值及终值均为10的次幂。
②向量的运算A=[1 2 3 4 5],b=3:7,计算两行向量的转置,两行向量人加、减,两列向量的加、减;向量的点积与叉积。
a=[1 2 3 4 5];b=3:7;a =1 2 3 4 5b =3 4 5 6 7at=a',bt=b'at =12345bt =34567e1=a+b,e2=a-be1 =4 6 8 10 12 e2 =-2 -2 -2 -2 -2 f1=at+bt,f2=at-btf1 =4561012f2 =-2-2-2-2-2g1=dot(a,b),g2=a*bt>> g1=dot(a,b),g2=a*btg1 =85g2 =85g4=a.*b>> g4=a.*bg4 =3 8 15 24 35A=1:3;B=4:6;g3=cross(A,B)>> g3=cross(a,b)g3 =-3 6 -3注意:g1和g2的结果是否相同,为什么?g4的结果与g1和g2结果是否一样,为什么?g1和g2的结果相同,因为两者是同一种运算;g4与g1和g2不相同,因为两者一个是点乘一个是叉乘,运算不一样。
2.矩阵的创建、引用和运算矩阵是由n×m元素构成的矩阵结构。
实验二MATLAB程序设计含实验报告

实验二 MATLAB 程序设计一、 实验目的1.掌握利用if 语句实现选择结构的方法。
2.掌握利用switch 语句实现多分支选择结构的方法。
3.掌握利用for 语句实现循环结构的方法。
4.掌握利用while 语句实现循环结构的方法。
5.掌握MATLAB 函数的编写及调试方法。
二、 实验的设备及条件计算机一台(带有MATLAB7.0以上的软件环境)。
M 文件的编写:启动MATLAB 后,点击File|New|M-File ,启动MATLAB 的程序编辑及调试器(Editor/Debugger ),编辑以下程序,点击File|Save 保存程序,注意文件名最好用英文字符。
点击Debug|Run 运行程序,在命令窗口查看运行结果,程序如有错误则改正三、 实验内容1.编写求解方程02=++c bx ax 的根的函数(这个方程不一定为一元二次方程,因c b a 、、的不同取值而定),这里应根据c b a 、、的不同取值分别处理,有输入参数提示,当0~,0,0===c b a 时应提示“为恒不等式!”。
并输入几组典型值加以检验。
(提示:提示输入使用input 函数)2.输入一个百分制成绩,要求输出成绩等级A+、A 、B 、C 、D 、E 。
其中100分为A+,90分~99分为A ,80分~89分为B ,70分~79分为C ,60分~69分为D ,60分以下为E 。
要求:(1)用switch 语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
(提示:注意单元矩阵的用法)3.数论中一个有趣的题目:任意一个正整数,若为偶数,则用2除之,若为奇数,则与3相乘再加上1。
重复此过程,最终得到的结果为1。
如:2?13?10?5?16?8?4?2?16?3?10?5?16?8?4?2?1运行下面的程序,按程序提示输入n=1,2,3,5,7等数来验证这一结论。
请为关键的Matlab 语句填写上相关注释,说明其含义或功能。
MATLAB实验报告第二章
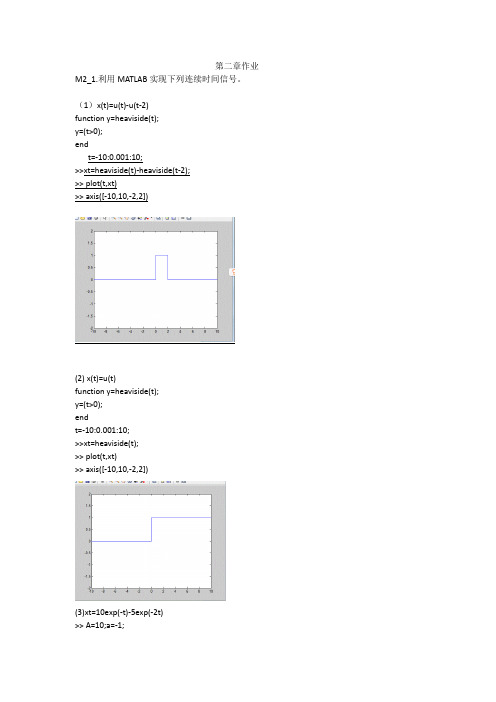
第二章作业M2_1.利用MATLAB实现下列连续时间信号。
(1)x(t)=u(t)-u(t-2)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t)-heaviside(t-2);>>plot(t,xt)>>axis([-10,10,-2,2])(2) x(t)=u(t)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t);>>plot(t,xt)>>axis([-10,10,-2,2])(3)xt=10exp(-t)-5exp(-2t)>> A=10;a=-1;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=5;a=-2;>> t=0:0.001:10;>> x2t=A*exp(a*t);>>xt=x1t-x2t;>>plot(t,xt)(4)xt=tu(t)>> t=-10:0.001:10;>>xt=t.*heaviside(t);>>plot(t,xt)(5)xt=2|sin(10pit+pi/3)| >> A=2;w0=10*pi;phi=pi/3; >> t=0:0.001:1;>>xt=A*abs(sin(w0*t+phi)); >>plot(t,xt)>>axis([0,1,-4,4])Xt=cost+sin(2pit)>> A=1;w0=1;phi=0; >> t=0:0.002:10;>> x1t=A*cos(w0*t+phi); >> A=2;w0=2*pi;phi=0; >> t=0:0.002:10;>> x2t=A*sin(w0*t+phi); >>xt=x1t+x2t;>>plot(t,xt)(7)xt=4exp(-0.5t)cos(2pit) >> A=5;a=-0.5;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=1;w0=2*pi;phi=0; >> t=0:0.001:10;>> x2t=A*cos(w0*t+phi); >>xt=x1t.*x2t;>>plot(t,xt)(8)Sa(pit)cos(30t)A=1;w0=30;phi=0;>> t=0:0.001:3;>> x1t=A*cos(w0*t+phi);>> t=0:0.001:3;>> x2t=sinc(t);>>xt=x1t.*x2t;>>plot(t,xt)M2-3,写出书中图示波形函数,并画出xt,x0.5t,x(2-0.5t)的图像function yt=x2_3(t)yt=t.*(t>=0&t<2)+2*(t>=2&t<3)+(-1)*(t>=3&t<=5); end>> t=0:0.001:5;>>xt=x2_3(t);>>title('x(t)');>>plot(t,xt)>>axis([0,6,-2,3])>> t=0:0.001:10;xt=x2_3(0.5*t); >>plot(t,xt)>>title('x(0.5t)')>>axis([0,10,-2,3])x(0.5t)>> t=-10:0.001:10;>>xt=x2_3(2-0.5*t);>>plot(t,xt)>>title('x(2-0.5t)')>>axis([-10,10,-2,3])M2-4画出图示的奇分量和偶分量。
matlab实验报告2

第二次上机作业准备&要求:1、 运行课件第三章(课本第四章)讲过的例子,掌握Matlab 的流程控制语句、函数及脚本文件的编程、调试方法。
2、 本次作业(4~12题)要求全部写M 文件;3、 题目要求未明确要求写脚本文件还是函数文件的,学生自己决定是写脚本文件还是函数文件。
只要能够实现要求。
4、 列出第二章课堂上出现过的所有函数,知道它们的作用并试着调用这些函数。
作业:1. 继续完成第一次上机实验未完成的作业。
2. 分析脚本M 文件及函数M 文件的区别。
(1)脚本文件没有输入参数,也不返回输出参数,而函数文件可以带输入参数,也可以返回输出参数。
(2)脚本文件对MATLAB 工作空间中的变量进行操作,文件中所有命令的执行结果也完全返回到工作空间中,而函数文件中定义的变量为局部变量,当函数文件执行完毕时。
这些变量被清除。
(3)脚本文件可以直接运行。
在MATLAB 命令行窗口输入脚本文件的名字,就会顺序执行脚本文件中的命令。
而函数文件不能直接运行,要以函数调用的方式来调用。
3. 已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=7613870451A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=023352138B ,求下列表达式的值,并注意第(2)(3)小题表达式的结果有何特点:(1)B A 6+ 、I B A +-2(其中I 为单位阵);>> A+6*Bans =47 23 -1012 37 26-15 73 7>> A^2-B+Ians =-18 -217 1722 533 10921 867 526(2)A*B、A.*B、B*A、B.*A;>> A*Bans =14 14 16-10 51 21125 328 180>> A.*Bans =-8 15 40 35 24-9 122 0>> B*Aans =-11 0 -157 228 533 -1 28>> B.*Aans =-8 15 40 35 24-9 122 0(3)A/B、B\A、A./B、B.\A;A/Bans =1.2234 -0.92552.9787-0.9468 2.3511 -0.95744.6170 3.8723 13.8936>> B\Aans =-0.5106 -8.6170 -1.12770.7340 17.5745 1.8085-0.8830 -21.2128 0.4043>> A./Bans =-0.1250 1.6667 4.00000 1.4000 2.6667-1.0000 30.5000 Inf>> B.\Aans =-0.1250 1.6667 4.00000 1.4000 2.6667-1.0000 30.5000 Inf(4)[A, B]、[A([1 3],:);B^2]。
MATLAB数学实验报告2

MATLAB数学实验报告姓名:李帆班级:机械(硕)21学号:2120104008第一次数学实验报告——线性规划问题一,实验问题1,某饲养场饲养动物出售,设每头动物每天至少需要700g蛋白质,30g矿物质,100mg 维生素。
现有五种饲料可供选择,各种饲料的每千克营养成分含量和单价如下表。
是确定既能满足动物生长的营养需要,游客是费用最省的选用饲料方案。
2,某工厂生产甲、乙、丙三种产品,单位产品所需工时分别为2、3、1个;单位产品所需原料分别为3、1、5公斤;单位产品利润分别为2、3、5元。
工厂每天可利用的工时为12个,可供应的原料为15公斤。
为使总利润为最大,试确定日生产计划和最大利润。
二,问题分析1,1)该题属于采用线性规划的方式求出最优解的数学问题。
该题有以下特点,1.目标函数有线性,是求目标函数的最小值;2.约束条件为线性方程组;3.未知变量都有非负限制。
1,2)求解该类问题的方法有图解法,理论解法和软件解法。
图解法常用于解变量较少的线性规划问题。
理论解法要构建完整的理论体系。
目前用于解线性规划的理论解法有:单纯形法,椭球算法等。
在此,我们采用单纯形法的MATLAB软件解法来求解该问题。
1,3)此题中,要求既要满足动物生长的营养需要,又要使费用最省,则使每种饲料的选用量为变量,以总费用的最小值为所求量,同时每种饲料的使用量要符合营养成分的要求。
1,4)在此,首先确定建立线性规划模型。
设饲料i选用量为xi公斤,i=1,2,3,4,5.则有模型:Minz=0.2x1+0.7x2+0.4x3+0.3x4+0.8x5s.t.{3x1+2x2+6x4+18x5>=700;x1+0.5x2+0.2x3+2x4+0.5x5>=300.5x1+x2+0.2x3+2x4+0.8x5>=100Xj>=0,j=1,2,3,4,5解之得:x1=x2=x3=0X4=39.74359X5=25.14603Zmin=32.435902,1)该问题与第一题分析步骤相似,故只在此写出其线性规划模型Z=2x+3y+5z2x+3y+z<=123x+y+5z<=15三,程序设计流程图第一题:c=[0.2,0.7,0.4,0.3,0.8]A=[3,2,1,6,18;1,0.5,0.2,2,0.5;0.5,1,0.2,2,0.8;1,0,0,0,0;0,1, 0,0,0;0,0,1,0,0;0,0,0,1,0;0,0,0,0,1]b=[700,30,100,0,0,0,0,0][x,fval]=linprog(c,-A,-b)c=0.20000.70000.40000.30000.8000A=3.0000 2.0000 1.0000 6.000018.00001.00000.50000.20002.00000.50000.5000 1.00000.2000 2.00000.80001.000000000 1.000000000 1.000000000 1.000000000 1.0000b=7003010000000Optimization terminated.x=0.0000-0.00000.000039.743625.6410fval=32.4359第二题c=[-2-3-5]A=[231;315]b=[12;15]lb=[000][x,Z,exitflag,output]=linprog(c,A,b,[],[],lb,[])将上述程序输入matlab。
matlab实验报告

实验一:MATLAB基本操作一、实验目的1、学习掌握MA TLAB语言的基本操作方法2、掌握命令窗口的使用3、熟悉MA TLAB的数据表示、基本运算和程序控制语句4、熟悉MA TLAB程序设计的基本方法二、实验内容和要求2.b.帮助命令的使用,查找SQRT函数的使用方法按Start-help-search,输入sqrtc.矩阵运算(1)已知A=[1 2;3 4];B=[5 5;7 8];求A^2*B输入A=[1 2;3 4];B=[5 5;7 8];A^2*B结果为:ans =105 115229 251(2)矩阵除法已知A=[1 2 3 ;4 5 6;7 8 9];B=[1 0 0;0 2 0;0 0 3];求A/B,A\BA/B=1.0000 1.0000 1.00004.0000 2.5000 2.00007.0000 4.0000 3.0000A\B=1.0e+016 *0.3152 -1.2609 0.9457-0.6304 2.5218 -1.89130.3152 -1.2609 0.9457(3)矩阵的转置及共轭转置已知A=[15+i,2-i,1;6*i,4,9-i];求A.',A'A=15.0000 + 1.0000i 2.0000 - 1.0000i 1.00000 + 6.0000i 4.0000 9.0000 - 1.0000iA.'=15.0000 + 1.0000i 0 + 6.0000i2.0000 - 1.0000i 4.00001.0000 9.0000 - 1.0000iA'=15.0000 - 1.0000i 0 - 6.0000i2.0000 + 1.0000i 4.00001.0000 9.0000 + 1.0000i(4)使用冒号选出指定元素已知A=[1 2 3;4 5 6;7 8 9];求A中第三列前两个元素;A中所有第二行的元素A =1 2 34 5 67 8 9求A中第三列前两个元素:A([1,2],3)ans =36求A中所有第二行的元素:A(2,1:1:end)ans =4 5 6(5)方括号[]用magic函数生成一个4阶魔方矩阵,删除该矩阵的第四列magic(4)ans =16 2 3 135 11 10 89 7 6 124 14 15 1a=ans;a(:,[1,2,3])ans =16 2 35 11 109 7 64 14 153..多项式(1)求多项式p(X)=x^3-2x-4的根(2)已知A=[1.2 3 5 0.9;5 1.7 5 6;3 9 0 1;1 2 3 4]求矩阵A的特征多项式;求矩阵多项式中未知数为20时的值;把矩阵A作为未知数代入到多项式中;(1)a=[1,0,-2,-4]x=roots(a)x =2.0000-1.0000 + 1.0000i-1.0000 - 1.0000i(2)求特征多项式系数:A=[1.2 3 5 0.9;5 1.7 5 6;3 9 0 1;1 2 3 4]p=poly(A)p =1.0000 -6.9000 -77.2600 -86.1300 604.5500求矩阵多项式中未知数为20时的值:c=polyval(p,20)c =7.2778e+004把矩阵A作为未知数代入到多项式中:c=polyval(p,A)c =1.0e+003 *0.3801 -0.4545 -1.9951 0.4601-1.9951 0.2093 -1.9951 -2.8880-0.4545 -4.8978 0.6046 0.43530.4353 0.0840 -0.4545 -1.16174、基本程序设计(1)编写命令文件:计算1+2+3+……+n<2000;n=0;s=0;while s<2000n=n+1;s=s+n;endn=n-1n =62(2)编写函数文件:分别用for和while循环结构编写程序,求2的0到n次幂的和。
matlab数学实验报告

MATLAB数学实验报告指导老师:班级:小组成员:时间:201_/_/_Matlab第二次实验报告小组成员:1题目:实验四;MATLAB选择结构与应用实验目的:掌握if选择结构与程序流程控制;重点掌握break;return;pause语句的应用..问题:问题1:验证“哥德巴赫猜想”;即:任何一个正偶数n>=6均可表示为两个质数的和..要求编制一个函数程序;输入一个正偶数;返回两个质数的和..问题分析:由用户输入一个大于6的偶数;由input语句实现..由if判断语句判断是否输入的数据符合条件..再引用质数判断函数来找出两个质数;再向屏幕输出两个质数即可..编程:function z1;z2=geden;n=input'please input n'if n<6disp'data error';returnendif modn;2==0for i=2:n/2k=0;for j=2:sqrtiif modi;j==0k=k+1;endendfor j=2:sqrtn-iif modn-i;j==0k=k+1;endendif k==0fprintf'two numbers are'fprintf'%.0f;%.0f';i;n-ibreakendendend结果分析:如上图;用户输入了大于6的偶数返回两个质数5和31;通过不断试验;即可验证哥德巴赫猜想..纪录:if判断语句与for循环语句联合嵌套使用可使程序结构更加明晰;更快的解决问题..2题目:实验四;MATLAB选择结构与应用实验目的:用matlab联系生活实际;解决一些生活中常见的实际问题..问题:问题四:在一边长为1的四个顶点上各站有一个人;他们同时开始以等速顺时针沿跑道追逐下一人;在追击过程中;每个人时刻对准目标;试模拟追击路线;并讨论.. (1)四个人能否追到一起(2)若能追到一起;每个人跑过多少路程(3)追到一起所需要的时间设速率为1问题分析:由正方形的几何对称性和四个人运动的对称性可知;只需研究2个人的运动即可解决此问题..编程:hold onaxis0 1 0 1;a=0;0;b=0;1;k=0;dt=0.001;v=1;while k<10000d=norma-b;k=k+1;plota1;a2;'r.';'markersize';15;plotb1;b2;'b.';'markersize';15;fprintf'k=%.0f b%.3f;%.3f a%.3f;%.3f d=%.3f\n';k;b1;b2;a1;a2;da=a+b1-a1/d*dt;b2-a2/d*dt;b=b+b2-a2/d*dt;-b1-a1/d*dt;if d<=0.001breakendendfprintf'每个人所走的路程为:%.3f';k*v*dtfprintf'追到一起所需要的时间为%.3f';k*dt结果分析:上图为2人的模拟运动路线;有对称性可解决所提问题..-上图为运算过程和运算结果..四个人可以追到一起;走过的路程为1.003;时间也为1.003.纪录:此题利用正方形和运动的对称性可以简便运算..3题目:实验八;河流流量估计与数据插值目的:由一些测量数据经过计算处理;解决一些生活实际问题..问题:实验八上机练习题第三题:瑞士地图如图所示;为了算出他的国土面积;做以下测量;由西向东为x轴;由南向北为y轴;从西边界点到东边界点划分为若干区域;测出每个分点的南北边界点y1和y2;得到以下数据mm..已知比例尺1:2222;计算瑞士国土面积;精确值为41288平方公里..测量数据如下:x=7.0 10.5 13.0 17.5 34 40.5 44.5 48 56 61 68.5 76.5 80.5 91 96 101 104 106 111.5 118 123.5 136.5 142 146 150 157 158 ;y1=44 45 47 50 50 38 30 30 34 36 34 41 45 46 43 37 33 28 32 65 55 54 52 50 66 66 68;y2=44 59 70 72 93 100 110 110 110 117 118 116 118 118 121 124 121 121 121 122 116 83 81 82 86 85 68;问题分析:先由题目给定的数据作出瑞士地图的草图;再根据梯形法;使用trapz语句;来估算瑞士国土的面积..编程:x=7.0 10.5 13.0 17.5 34 40.5 44.5 48 56 61 68.5 76.5 80.5 91 96 101 104 106 111.5 118 123.5 136.5 142 146 150 157 158;y1=44 45 47 50 50 38 30 30 34 36 34 41 45 46 43 37 33 28 32 65 55 54 52 50 66 66 68;y2=44 59 70 72 93 100 110 110 110 117 118 116 118 118 121 124 121 121 121 122 116 83 81 82 86 85 68;plotx;y1;'r.';'markersize';15;plotx;y2;'r.';'markersize';15;axis0 160 0 135grid;hold ont=7:158;u1=splinex;y1;t;u2=splinex;y2;t;plott;u1plott;u2s1=trapzt;u1;s2=trapzt;u2;s=s2-s1*2222*22222/10000000;fprintf'S=%.0f';s结果分析:上图为由所给数据绘制出的瑞士地图..上图为运算结果;计算出瑞士的国土面积为42472平方公里;与准确值41288较为接近..纪录:使用梯形分割的方法;trapz语句可以方便计算不规则图形面积;但存在一定误差..4题目:实验七:圆周率的计算与数值积分目的:将数值积分最基本的原理应用于matlab之中;解决一些与积分有关的问题..问题:实验七上机练习题第一题:排洪量某河床的横断面如图7.3所示;为了计算最大排洪量;需要计算其断面积;试根据所给数据m用梯形法计算其断面积..问题分析:河床断面可近似分割成若干曲边梯形;近似处理把它们当做梯形来计算面积可使问题得到简化..编程:clc;clear;x=0 4 10 12 15 22 28 34 40;y=0 1 3 6 8 9 5 3 0;y1=10-y;plotx;y1;'k.';'markersize';15;axis0 40 0 10;grid;hold ont=0:40;u=splinex;y1;t;plott;u;s=40*10-trapzt;u;fprintf's=%.2f\n';s结果分析:上图为河床的断面图..上图为计算结果面积约为180.70平方米..纪录:使用梯形法计算不规则图形面积十分简便易行..5题目:实验七:圆周率的计算与数值积分目的:使用matlab计算解决一些有关积分的问题..问题:实验七上机练习题第三题:从地面发射一枚火箭;在最初100秒内记录其加速度如下;试求火箭在100秒时的速度..Ts=0 10 20 30 40 50 60 70 80 90 100;Am/s*s=30.00 31.63 33.44 35.47 37.75 40.33 43.29 46.69 50.67 54.01 57.23;问题分析:加速度为速度的微分;已知微分求积分;类似于面积问题;可使用梯形法来计算..编程:clc;clear;x=0 10 20 30 40 50 60 70 80 90 100;y=30.00 31.63 33.44 35.47 37.75 40.33 43.29 46.69 50.6754.01 57.23;plotx;y;'k.';'markersize';15;axis0 100 20 60;grid;hold ons=0:10:100;z=splinex;y;s;plots;y;v=trapzx;y;fprintf'v=%.2f\n';v结果分析:上图为加速度变化图..上图为计算结果;求得火箭在100秒时速度约为4168.95m/s..纪录:梯形法可以推广解决许多已知微分求积分的其他问题..6题目:实验七:圆周率的计算与数值积分目的:计算曲线弧长闭曲线周长可使用微元法;ds=sqrtdx^2+dy^2;在转化微积分问题;累加即可得到结果..问题:实验七上机练习题第三题:计算椭圆想x^2/4+y^2=1的周长;使结果具有五位有效数字..问题分析:编程:s=0;dx=0.001;for x=0:0.001:1.999dy=1.-x+0.001.^2/4-1.-x.^2/4;ds=sqrtdx.^2+dy.^2;s=s+ds;ends=4*s;fprintf'the length is'fprintf'%.4f';s结果分析:上图为计算结果;给定椭圆的周长约为9.1823五位有效数字纪录:计算不规则曲线弧长;可使用微元法;划分为若干小的看做直角三角形;利用勾股定理解决..7题目:实验九人口预测与数据拟合目的:掌握一些曲线拟合的方法;了解曲线拟合常用函数..问题:用电压U=10v的电池给电容器充电;t时刻的电压Vt=U-U-V0exp-t/τ;其中V0是电容器的初始电压;τ是充电常数;由所给数据确定V0和τ..t=0.5 1 2 3 4 5 7 9;V=3.64 3.52 2.74 1.78 1.34 1.01 0.57 0.37;问题分析:题中已给出函数关系式;为指数函数曲线拟合;将所给函数式整理可得标准的exp形函数曲线;从而便于解决..编程:t=0.5 1 2 3 4 5 7 9;V=3.64 3.52 2.74 1.78 1.34 1.01 0.57 0.37;plott;V;'k.';'markersize';20;axis0 10 0 4;grid;hold onpause0.5n=8;a=sumt1:n;b=sumt1:n.*t1:n;c=sumlogV1:n;d=sumt1:n.*logV1:n;A=n a;a b;B=c;d;p=invA*Bx=0:10;y=expp1+p2*x;plotx;y;'r-';'linewidth';2结果分析:上图为电压与时间关系图..上图为计算结果;即U-V0=1.4766;所以V0=8.5234;-1/τ=-0.2835;所以τ=3.5273纪录:曲线拟合的一个重难点是选择合适的曲线函数;才能提高拟合度..8题目:实验七圆周率的计算与数值积分目的:拓展圆周率的各种计算方法;掌握其他数值的近似计算方法..问题:实验七练习2:计算ln2的近似值精确到10的-5次方(1)利用级数展开的方法来计算(2)利用梯形法计算(3)利用抛物线法问题分析:级数展开;梯形法;抛物线法是常见的近似运算方法..编程:1级数展开的方法clc;clear;n=0;r=1;p=0;k=-1;while r>=0.1e-5n=n+1;k=k*-1;p1=p+k/n;r=absp1-p;fprintf'n=%.0f;p=%.10f\n';n;p1;p=p1;end2梯形法clc;clear;f=inline'1./x';x=1:0.1:2;y=fx;p=trapzx;y;fprintf'p=%.6f\n';p3抛物线法clc;clear;f=inline'1./x';a=1;b=2;n=1;z=quadf;a;b;fprintf'z=%.10f\n';z结果分析:(1)级数展开的方法(2)梯形法3抛物线法纪录:级数展开法;梯形法;抛物线法;计算近似值时应合理利用..梯形法和抛物线法不易提高精确度;级数展开法可以提高精确度..9题目:实验八河流流量估计与数据插值目的:掌握求插值多项式的方法;并利用此计算近似值..问题:已知y=fx的函数表如下x=0.40 0.55 0.65 0.80 0.90 1.05;y=0.41075 0.57815 0.69675 0.88811 1.02652 1.25382;求四次拉格朗日插值多项式;并由此求f0.596问题分析:利用所给函数表可计算拉格朗日插值多项式..编程:function p=lagrangex;yL=lengthx;a=onesL;for j=2:La:;j=a:;j-1.*x';endx=inva*y';for i=1:Lpi=xL-i+1;endx=0.40 0.55 0.65 0.80 0.90 1.05;y=0.41075 0.57815 0.69675 0.88811 1.02652 1.25382; plotx;y;'k.';'markersize';15axis0 2 0 2grid;hold on;p=lagrangex;y;t=0:0.1:1.5;u=polyvalp;t;plott;u;'r-'a=polyvalp;0.596结果分析:上图为所求结果;估算值和插值多项式..纪录:插值多项式是一项十分实用的方法..10题目:求正整数n的阶乘:p=1*2*3*…*n=n;并求出n=20时的结果目的:练习使用循环变量解决数学问题问题:对程序:Clear;clc;n=20;p=1;for i=1:np=p*i;fprintf’i=%.0f;p=%.0f\n’;i;pend进行修改使它:利用input命令对n惊醒赋值问题分析:题中给出程序中“n=20”修改;使用input命令;讲题中的输出命令放出循环之外..编程:clear;clc;n=input'n=';p=1;for i=1:np=p*i;endfprintf'i=%.0f;p=%.0f\n';i;p结果:n=20i=20;p=2432902008176640000>>结果分析:使用input命令可以实现人机对话;使用户自由赋值;输出语句在程序中的位置对输出的结果有很大的影响;在循环内部可以在计算过城中不断输出结果;在循环之外则可以控制只输出最后结果..11题目:对于数列{√2};n=1;2;…;求当其前n项和不超过1000时的n的值及合的大小..目的:运用条件循环解决文帝个项数的循环程序求解;问题:对程序:clear;clc;n=0;s=0;while s<=1000n=n+1;s=s+sqrtn;fprintf’n=%.0f;s=%.4f\n’;n;send问题分析:题中所给程序中的限制变量为上次循环之后的s;导致s超过上限后仍有一次的循环;若把循环变量改为这次的s;则可以避免这种情况的发生..编程:clear;clc;n=0;s=0;while s+sqrtn<=1000n=n+1;s=s+sqrtnfprintf'n=%.0f;s=%.4f\n';n;send结果:……s =970.8891n=128;s=970.8891s =982.2469n=129;s=982.2469s =993.6487n=130;s=993.6487>>结果分析:从结果中可以看出;最后一步为我们需要的答案;从这道题我们可以得出循环变量对一道编程的重要性..。
(完整word)Matlab实验报告
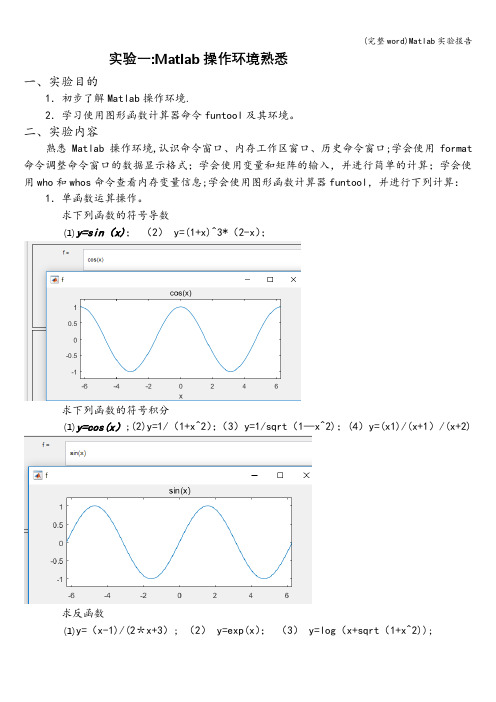
实验一:Matlab操作环境熟悉一、实验目的1.初步了解Matlab操作环境.2.学习使用图形函数计算器命令funtool及其环境。
二、实验内容熟悉Matlab操作环境,认识命令窗口、内存工作区窗口、历史命令窗口;学会使用format 命令调整命令窗口的数据显示格式;学会使用变量和矩阵的输入,并进行简单的计算;学会使用who和whos命令查看内存变量信息;学会使用图形函数计算器funtool,并进行下列计算:1.单函数运算操作。
求下列函数的符号导数(1)y=sin(x);(2) y=(1+x)^3*(2-x);求下列函数的符号积分(1)y=cos(x);(2)y=1/(1+x^2);(3)y=1/sqrt(1—x^2);(4)y=(x1)/(x+1)/(x+2)求反函数(1)y=(x-1)/(2*x+3); (2) y=exp(x);(3) y=log(x+sqrt(1+x^2));代数式的化简(1)(x+1)*(x-1)*(x-2)/(x-3)/(x—4);(2)sin(x)^2+cos(x)^2;(3)x+sin(x)+2*x—3*cos(x)+4*x*sin(x);2.函数与参数的运算操作。
从y=x^2通过参数的选择去观察下列函数的图形变化(1)y1=(x+1)^2(2)y2=(x+2)^2(3) y3=2*x^2 (4) y4=x^2+2 (5) y5=x^4 (6) y6=x^2/2 3.两个函数之间的操作求和(1)sin(x)+cos(x) (2) 1+x+x^2+x^3+x^4+x^5乘积(1)exp(—x)*sin(x) (2) sin(x)*x商(1)sin(x)/cos(x); (2) x/(1+x^2); (3) 1/(x—1)/(x—2); 求复合函数(1)y=exp(u) u=sin(x) (2) y=sqrt(u) u=1+exp(x^2)(3) y=sin(u) u=asin(x) (4) y=sinh(u) u=-x实验二:MATLAB基本操作与用法一、实验目的1.掌握用MATLAB命令窗口进行简单数学运算。
matlab2022实验2参考答案

matlab2022实验2参考答案报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:MATLAB实验二MATLAB符号计算试验报告说明:1做试验前请先预习,并独立完成试验和试验报告。
2报告解答方式:将MATLAB执行命令和最后运行结果从命令窗口拷贝到每题的题目下面,请将报告解答部分的底纹设置为灰色,以便于批阅。
3在页眉上写清报告名称,学生姓名,学号,专业以及班级。
3报告以Word文档书写。
一目的和要求1熟练掌握MATLAB符号表达式的创建2熟练掌握符号表达式的代数运算3掌握符号表达式的化简和替换4熟练掌握符号微积分5熟练掌握符号方程的求解二试验内容1多项式运算(必做)1.1解方程:f(某)=某^4-10某某^3+34某某^2-50某某+25=0%采用数值方法:>>f=[1-1034-5025];>>root(f)%采用符号计算方法:f1=ym('某^4-10某某^3+34某某^2-50某某+25')olve(f1)1.2求有理分式R=(3某^3+某)(某^3+2)/((某^2+2某-2)(5某^3+2某^2+1))的商多项式和余多项式.a1=[3010];a2=[1002];a=conv(a1,a2);b1=[12-2];b2=[5201];b=conv(b1,b2);[p,r]=deconv(a,b);%注意:ab秩序不可颠倒。
%reidue用于实现多项式的部分分式展开,此处用deconv函数报告名称:MATLAB试验二符号计算姓名:学号:专业:班级:%%此题,有同学程序如下:某1=[3010],某2=[1002],某3=[12-2],某4=[5201]某5=conv(某1,某2)[y6,r]=deconv(某5,某3)R=deconv(y6,某4)%%这种方法较第一种解法缺点:在除法运算中,会产生误差,故此题应先将分母的多项式相乘后,再与分子部分的多项式进行运算。
MATLAB第二章实验报告

MATLAB数据及基本操作班级:11电信一班姓名:何得中学号:20111060108实验目的:1.熟悉MATLAB的组体成体系及工作环境;2.了解MATLAB的帮助系统;3.掌握MATLAB的数据类型及变量的基本操作;4.掌握矩阵建立的基本方法及其运算;5.掌握矩阵索引与分析方法;6.熟悉字符串单元及结构数据的建立及基本操作。
实验仪器:MA TLAB软件,电脑实验数据:>> A=[1 2 3;4 5 6;7 8 9]A = 1 2 34 5 67 8 9>> A=[1 2 34 5 67 8 9]A = 1 2 34 5 67 8 9>> x=0:pi/8:2*pi;>> y=cos(x)y = Columns 1 through 101.0000 0.9239 0.7071 0.3827 0.0000 -0.3827 -0.7071 -0.9239 -1.0000 -0.9239Columns 11 through 17-0.7071 -0.3827 -0.0000 0.3827 0.7071 0.9239 1.0000>> B=ones(3,5)B = 1 1 1 1 11 1 1 1 11 1 1 1 1>> zeros(3)ans = 0 0 00 0 00 0 0>> C=rand(3,4)C = 0.9501 0.4860 0.4565 0.44470.2311 0.8913 0.0185 0.61540.6068 0.7621 0.8214 0.7919>> D=randn(2,3)D = -0.4326 0.1253 -1.1465-1.6656 0.2877 1.1909>> eye(3)ans = 1 0 00 1 00 0 1>> M=magic(4)M = 16 2 3 135 11 10 89 7 6 124 14 15 1>> T=toeplitz(1:5,1:6)T = 1 2 3 4 5 62 1 234 53 2 1 2 3 44 3 2 1 2 35 4 3 2 1 2>> H=hilb(5)H = 1.0000 0.5000 0.33330.2500 0.20000.5000 0.3333 0.2500 0.2000 0.16670.3333 0.2500 0.2000 0.1667 0.14290.2500 0.2000 0.1667 0.1429 0.12500.2000 0.1667 0.1429 0.1250 0.1111>> a=3:18a =3 4 5 6 7 8 9 10 1112 13 14 15 16 17 18>> b=1:0.2:6b =Columns 1 through 91.0000 1.2000 1.4000 1.600 1.80002.0000 2.2000 2.4000 2.6000 Columns 10 through 182.80003.0000 3.2000 3.40003.6000 3.80004.0000 4.2000 4.4000 Columns 19 through 264.6000 4.80005.0000 5.20005.4000 5.6000 5.80006.0000>> linspace(1,15,10)ans =Columns 1 through 91.00002.5556 4.1111 5.6667 7.2222 8.7778 10.3333 11.8889 13.4444Column 1015.0000>> y=[0.9 0.3 0.4 0.1 0.5 0.6 0.2 ]; >> [sorted,index]=sort(y)sorted =0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.9000 index =4 7 2 3 5 6 1>> A=rand(4,5)A = 0.9218 0.9355 0.0579 0.13890.27220.7382 0.9169 0.3529 0.2028 0.19880.1763 0.4103 0.8132 0.1987 0.01530.4057 0.8936 0.0099 0.6038 0.7468>> [a,b]=min(A)a =0.1763 0.4103 0.0099 0.13890.0153b = 3 3 4 1 3>> min(A(:))ans = 0.0099>> V=[1 2 3 4]V = 1 2 3 4>> norm(V,2)ans =5.4772>> norm(V,1)ans = 10>> norm(V,inf)ans = 4>> V=[2 5 6 8 4 9]V = 2 5 6 8 4 9>> min(V)ans = 2>> V=[4 9 6;7 8 9;4 5 6]V = 4 9 67 8 94 5 6>> min(V)ans = 4 5 6>> max(V)ans = 7 9 9>> mean(V)ans = 5.0000 7.3333 7.0000>> median(V)ans = 4 8 6>> std(V)ans = 1.7321 2.0817 1.7321>> diff(V)ans =3 -1 3-3 -3 -3>> sort(V)ans =4 5 64 8 67 9 9>> length(V)ans = 3>> norm(V)ans =19.9125>> sum(V)ans = 15 22 21>> prod(V)ans =112 360 324>> cumsum(V)ans = 4 9 611 17 1515 22 21 >> cumprod(V)ans = 4 9 628 72 54112 360 324>> V=[1 2 8]V = 1 2 8>> U=[3; 4;7]U = 347>> dot(V,U)ans =67>> cross(V,U)ans =-18 17 -2>> A=[5 6 4;7 8 9;4 5 6]A = 5 6 47 8 94 5 6>> B=[6 2 7 ;7 5 8;4 6 8]B = 6 2 77 5 84 6 8>> C=A-BC = -1 4 -30 3 10 -1 -2>> C=A*BC = 88 64 115134 108 18583 69 116>> C1=A\BC1 =0.6667 -6.4444 -7.66670.6667 4.8889 7.3333-0.3333 1.2222 0.3333>> C2=B/AC2 = -3.0000 8.3333 -9.3333-1.6667 5.5556 -5.88890.0000 -1.3333 3.3333>> A=[1 2 3;4 5 6;7 8 9]A = 1 2 34 5 67 8 9>> D=A^2D = 30 36 4266 81 96102 126 150>> E=A^0.1E = 0.8466 + 0.2270i 0.3599 + 0.0579i -0.0967 - 0.1015i0.4015 + 0.0216i 0.4525 + 0.0133i 0.4432 - 0.0146i-0.0134 - 0.1740i 0.4848 - 0.0509i 1.0132 + 0.0820i>> A=[1+2*i 3;4 2+i]A =1.0000 + 2.0000i 3.00004.0000 2.0000 + 1.0000i>> A'ans = 1.0000 - 2.0000i 4.00003.0000 2.0000 - 1.0000i>> A=[1 2 3;4 5 6;7 8 9]A = 1 2 34 5 67 8 9>> B=[3 4 6;7 9 8;5 2 01]B = 3 4 67 9 85 2 1>> C=A.*BC = 3 8 1828 45 4835 16 9>> D=A./BD = 0.3333 0.5000 0.50000.5714 0.5556 0.75001.4000 4.0000 9.0000>> E=A.\BE = 3.0000 2.0000 2.00001.7500 1.8000 1.33330.7143 0.2500 0.1111>> A=[1+2*i 3;4 2+i]A = 1.0000 + 2.0000i 3.00004.0000 2.0000 + 1.0000i>> A.^2ans = -3.0000 + 4.0000i 9.000016.0000 3.0000 + 4.0000i>> A.'ans = 1.0000 + 2.0000i 4.00003.0000 2.0000 + 1.0000i>> x=0.1:0.1:0.8x =0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000>> y=sin(2*x).*cos(2*x)y =0.1947 0.3587 0.4660 0.4998 0.4546 0.3377 0.1675 -0.0292>> y=sin(x)y =0.0998 0.1987 0.2955 0.3894 0.4794 0.5646 0.6442 0.7174>> y=cos(x)y =0.9950 0.9801 0.9553 0.9211 0.8776 0.8253 0.7648 0.6967>> y=tan(x)y =0.1003 0.2027 0.3093 0.4228 0.5463 0.6841 0.8423 1.0296>> y=cot(x)y =9.9666 4.9332 3.2327 2.3652 1.8305 1.4617 1.1872 0.9712>> y=sec(x)y = 1.0050 1.0203 1.0468 1.0857 1.1395 1.2116 1.3075 1.4353>> y=csc(x)y = 10.0167 5.0335 3.3839 2.5679 2.0858 1.7710 1.5523 1.3940>> y=asin(x)y = 0.1002 0.2014 0.3047 0.4115 0.5236 0.6435 0.7754 0.9273>> y=acos(x)y = 1.4706 1.3694 1.2661 1.1593 1.0472 0.9273 0.7954 0.6435>> y=atan(x)y =0.0997 0.1974 0.2915 0.3805 0.4636 0.5404 0.6107 0.6747>> y=acot(x)y = 1.4711 1.3734 1.2793 1.1903 1.1071 1.0304 0.9601 0.8961>> y=asec(x)y =Columns 1 through 60 + 2.9932i 0 + 2.2924i0 + 1.8738i 0 + 1.5668i 0 +1.3170i 0 + 1.0986iColumns 7 through 80 + 0.8956i 0 + 0.6931i>> y=sinh(x)y =0.1002 0.2013 0.3045 0.4108 0.5211 0.6367 0.7586 0.8881>> y=cosh(x)y =1.0050 1.0201 1.0453 1.0811 1.1276 1.1855 1.2552 1.3374>> y=tanh(x)y = 0.0997 0.1974 0.2913 0.3799 0.4621 0.5370 0.6044 0.6640>> y=coth(x)y = 10.0333 5.0665 3.4327 2.6319 2.1640 1.8620 1.6546 1.5059>> y=sech(x)y = 0.9950 0.9803 0.9566 0.9250 0.8868 0.8436 0.7967 0.7477>> y=csch(x)y = 9.9834 4.9668 3.2839 2.4346 1.9190 1.5707 1.3182 1.1260>> y=asinh(x)y = 0.0998 0.1987 0.2957 0.3900 0.4812 0.5688 0.6527 0.7327>> y=acosh(x)y =Columns 1 through 60 + 1.4706i 0 + 1.3694i0 + 1.2661i 0 + 1.1593i 0 +1.0472i 0 + 0.9273iColumns 7 through 80 + 0.7954i 0 + 0.6435i>> y=atanh(x)y = 0.1003 0.2027 0.3095 0.4236 0.5493 0.6931 0.8673 1.0986>> y=acoth(x)y = Columns 1 through 60.1003 + 1.5708i 0.2027 + 1.5708i 0.3095 + 1.5708i 0.4236 + 1.5708i 0.5493 + 1.5708i 0.6931 + 1.5708i Columns 7 through 80.8673 + 1.5708i 1.0986 + 1.5708i >> y=asech(x)y = 2.9932 2.2924 1.8738 1.5668 1.3170 1.0986 0.8956 0.6931>> y=acsch(x)y = 2.9982 2.3124 1.9189 1.6472 1.4436 1.2838 1.1545 1.0476>> y=log(x)y =-2.3026 -1.6094 -1.2040 -0.9163 -0.6931 -0.5108 -0.3567 -0.2231>> y=log10(x)y = -1.0000 -0.6990 -0.5229 -0.3979 -0.3010 -0.2218 -0.1549 -0.0969>> y=log2(x)y =-3.3219 -2.3219 -1.7370 -1.3219 -1.0000 -0.7370 -0.5146 -0.3219>> c=complex(a,b)c = 0.1763 + 3.0000i 0.4103 + 3.0000i0.0099 + 4.0000i 0.1389 + 1.0000i 0.0153 + 3.0000i>> zc=conj(x)zc =0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000>> b=imag(x)b = 0 0 0 0 0 00 0>> a=real(x)a = 0.1000 0.2000 0.3000 0.40000.5000 0.6000 0.7000 0.8000>> y=fix(x)y = 0 0 0 0 0 0 0 0>> y=floor(x)y =0 0 0 0 0 0 0 0 >> y=ceil(x)y = 1 1 1 1 1 1 1 1>> y=round(x)y = 0 0 0 0 1 1 1 1>> y=sign(x)y = 1 1 1 1 1 1 1 1>> S=rats(x)S =1/10 1/5 3/10 2/5 1/2 3/5 7/10 4/5>> [N,D]=rat(x)N = 1 1 3 2 1 37 4D = 10 5 10 5 2 510 5>> A=[2 4 6;3 5 7;8 10 9]A = 2 4 63 5 78 10 9>> B=[4 1 5;7 5 0;9 3 6]B = 4 1 57 5 09 3 6>> A>Bans = 0 1 10 0 10 1 1>> A<Bans = 1 0 01 0 01 0 0>> A>=Bans = 0 1 10 1 10 1 1>> A<=Bans = 1 0 01 1 01 0 0>> A==Bans = 0 0 00 1 00 0 0>> A~=Bans =1 1 11 0 11 1 1>> A&Bans = 1 1 11 1 01 1 1>> A|Bans = 1 1 11 1 11 1 1>> ~Aans = 0 0 00 0 00 0 0>> ~Bans = 0 0 00 0 10 0 0>> x=0:pi/100:3*pi;>> y=sin(x);>> plot(x,y);>> y1=(x<pi|x>2*pi).*y;>> figure,plot(x,y1);>> r=(x>pi/3&x<2*pi/3)|(x>7*pi/3&8*pi/3);>> rn=~r;>> y2=r*sin(pi/3)+rn.*y1;>> figure,plot(x,y2)>> x=[0 4 5 9 8 6 74 85 7 4 85 8 4 5 8]x =0 4 5 9 8 6 74 85 7 4 85 8 4 5 8>> all(x)ans =0>> any(x)ans = 1>> find(x)ans =2 3 4 5 6 7 8 9 10 11 12 13 14 15>> isempty(x)ans =>> isglobal(x)Warning: isglobal is obsolete and will be discontinued. Type "help isglobal" for more details.ans =0>> isinf(x)ans =0 0 0 0 0 0 0 0 0 0 0 0 0 0 0>> isnan(x)ans =0 0 0 0 0 0 0 0 0 0 0 0 0 0 0>> isfinite(x)ans =1 1 1 1 1 1 1 1 1 1 1 1 1 1 1>> issparse(x)ans = 0>> isstr(x)ans =0>> not(x)ans =1 0 0 0 0 0 0 0 0 0 0 0 0 0 0>> y=[59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5]y =59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5>> y=[59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5]y = 59 46 78 2 3 98 1 2 3 57 9 5 66 8 900 5>> x=[0 4 5 9 8 6 74 85 7 4 85 8 4 5 8]x = 0 4 5 9 8 6 74 85 7 4 85 8 4 5 8>> A=[4 -40 2; 23 50 17;18 29 14]A = 4 -40 223 50 1718 29 14>> [r,c]=find(A>=20&A<=30)r = 23c = 12>> bitand(12,6)ans = 4>> bitshift(12,1)ans = 24>> bitxor(12,1)ans =13>> bitset(12,1)ans = 13 >> bitget(12,1)ans =0>> A =[ 87 59 56 85 66 21 12 35 62 64 69 88 99 81]A =87 59 56 85 66 21 1235 62 64 69 88 99 81>> A(2)ans =59>> A([1,2,8])ans =87 59 35>> A([9,6,2])ans =62 21 59>> A([end-4:end])ans =64 69 88 99 81>> A([1:5,5:-1:1])ans = 87 59 56 85 66 66 85 56 59 87>> A(3)=-1A = 87 59 -1 85 66 2112 35 62 64 69 88 99 81>> A(15)=-8A =87 59 -1 85 66 2112 35 62 64 69 88 99 81 -8>> A(20)=-1A = Columns 1 through 1687 59 -1 85 66 21 12 35 62 64 69 88 99 81 -8 0Columns 17 through 200 0 0 -1>> A=rand(8)A = 0.9501 0.8214 0.9355 0.13890.4451 0.8381 0.3046 0.37840.2311 0.4447 0.9169 0.2028 0.9318 0.0196 0.1897 0.86000.6068 0.6154 0.4103 0.1987 0.4660 0.6813 0.1934 0.85370.4860 0.7919 0.8936 0.6038 0.4186 0.3795 0.6822 0.59360.8913 0.9218 0.0579 0.2722 0.8462 0.8318 0.3028 0.49660.7621 0.7382 0.3529 0.1988 0.5252 0.5028 0.5417 0.89980.4565 0.1763 0.8132 0.0153 0.2026 0.7095 0.1509 0.82160.0185 0.4057 0.0099 0.7468 0.6721 0.4289 0.6979 0.6449>> A(3,3)ans =0.4103>> A(8)ans =0.0185>> sub2ind(size(A),3,3)ans =19>> [i,j]=ind2sub(size(A),19)i =3j =3>> A(:,4)ans =0.13890.20280.19870.60380.27220.19880.01530.7468>> A(3,:)ans =0.6068 0.6154 0.4103 0.1987 0.4660 0.6813 0.1934 0.8537>> A(end,:)ans =0.0185 0.4057 0.0099 0.7468 0.6721 0.4289 0.6979 0.6449>> A(3:4,5:6)ans =0.4660 0.68130.4186 0.3795>> A(2:2:4,1:2:5)ans =0.2311 0.9169 0.93180.4860 0.8936 0.4186>> A=reshape(A,5,5)A = 1 6 11 16 212 7 12 17 223 8 13 18 234 9 14 19 245 10 15 20 25>> A(:)'ans =Columns 1 through 161 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16Columns 17 through 2517 18 19 20 21 22 23 24 25>> A(:,1:2:5)=[]A = 6 167 178 189 1910 20>> A=[9 8 7;6 5 4;3 2 1];>> D=diag(A)D =951>> D1=diag(A,1)D1 =84>> D2=diag(A,-1)D2 =62>> V=[1 2 3 4];>> diag(V)ans = 1 0 0 00 2 0 00 0 3 00 0 0 4>> diag(1:3,-1)ans = 0 0 0 01 0 0 00 2 0 00 0 3 0>>A=[17,1,0,15;5,7,14,16;4,0,13,0;10,12,19,21]; >> D=diag(4:-1:1);>> D*Aans = 68 4 0 6015 21 42 488 0 26 010 12 19 21>> triu(A)ans =17 1 0 150 7 14 160 0 13 00 0 0 21>> triu(A,1)ans = 0 1 0 150 0 14 160 0 0 00 0 0 0>> B=A'B =17 5 4 101 7 0 120 14 13 1915 16 0 21>> rot90(A)ans =15 16 0 210 14 13 191 7 0 1217 5 4 10>> rot90(A,3)ans =10 4 5 1712 0 7 119 13 14 021 0 16 15>> B=fliplr(A)B = 15 0 1 1716 14 7 50 13 0 421 19 12 10>> B=flipud(A)B = 10 12 19 214 0 13 05 7 14 1617 1 0 15>> A=[4 5 6 9;7 8 9 5;4 5 6 9;7 8 9 5]; >> det(A)ans =0>> rank(A)ans =2>> cond(A)ans =1.0968e+017>> inv(A)Warning: Matrix is singular to working precision.ans = Inf Inf Inf InfInf Inf Inf InfInf Inf Inf InfInf Inf Inf Inf>> A=[4 8 9;8 2 7;6 3 8];>> inv(A)ans = 0.0568 0.4205 -0.43180.2500 0.2500 -0.5000-0.1364 -0.4091 0.6364>> [V,D]=eig(A)V = -0.6438 -0.7444 -0.5061-0.5467 0.6392 -0.5515-0.5354 0.1931 0.6631D = 18.2776 0 00 -5.2030 00 0 0.9254>> [U,S,D]=svd(A)U = -0.6378 0.7375 -0.2220-0.5426 -0.6348 -0.5500-0.5465 -0.2304 0.8051S = 18.9278 0 00 5.2884 00 0 0.8791D = -0.5374 -0.6639 -0.5200-0.4135 0.7449 -0.5236-0.7350 0.0663 0.6749>> [L,U]=lu(A)L = 0.5000 1.0000 01.0000 0 00.7500 0.2143 1.0000U = 8.0000 2.0000 7.00000 7.0000 5.50000 0 1.5714>> [Q,R]=qr(A)Q = -0.3714 0.9114 -0.1774-0.7428 -0.4063 -0.5322-0.5571 -0.0659 0.8278 R =-10.7703 -6.1279 -12.99870 6.2808 4.83140 0 1.3009>> a=1234a = 1234>> class(a)ans =double>> size(a)ans = 1 1>> b='1234'b =1234>> class(b)ans =char>> size(b)ans = 1 4>> 'I am astudent'ans =I am astudent>> a='This is No.2.23 Example!'a =This is No.2.23 Example!>> b=a(1:7)b =This is>> c=a(12:end)c =2.23 Example!>> a='Good';>> b='Noon';>> length(a)==length(b)ans = 1>> c=[a,'',b]c =GoodNoon>> d=[a;b]d =GoodNoon>> size(c)ans = 1 8>> size(d)ans = 2 4>> a='Good Noon';>> b=double(a)b = 71 111 111 100 32 78 111 111 110>> c='再见!'c =再见!>> c='再见!'>> d=double(c)d = 20877 35265 65281>> char(d)ans =再见!>> a='The first string';>> b='The second string';>> c=strcmp(a,b)c =0>> d=strncmp(a,b,4)d =1>> X='A friend in need is a friend indeed'; >> Y='friend';>> a=findstr(Y,X)a = 3 23>> b=strfind(Y,X)b = []>> S=['1 2 3';'2 3 4'];>> A=str2num(S)A = 1 2 32 3 4>> B=str2num('6-8i')B = 6.0000 - 8.0000i>> D=num2str(rand(2,3),6)D =0.950129 0.606843 0.8912990.231139 0.485982 0.762097>> d=189;>> h=dec2hex(d)h =BD>> c=dec2base(d,7)c =360>> b=dec2bin(d)b =10111101>> bin2dec(b)ans = 189>> A={ones(3,3,3),'Welcome';30.34,1:200} A = [3x3x3 double] 'Welcome'[ 30.3400] [1x200 double]>>B=[{ones(3,3,3)},{'Welcome'};{30.34},{1:20 0}]B = [3x3x3 double] 'Welcome'[ 30.3400] [1x200 double]>> C={5}C = [5]>> C(2,3)={7}C = [5] [] [][] [] [7]>> isequal(A,B)ans =1>> A={ones(3,3,3),'Welcome';30.34,1:200}; >> b=A(1,2)b = 'Welcome'>> class(B)ans =cell>> C=A{1,2}C =Welcome>> class Cans =char>> D=A{1,2}(6)D =m>> E=A{2,2}([end:-1:190])E =200 199 198 197 196 195 194 193 192 191 190>> class(E)ans =double>> N=A{3}([1 3 5 7])N =Wloe>> A={ones(3,3,3),'Welcome';30.34,1:200}; >> B=cell(2);>> B(:,1)={char('Good','Morning');1:10}B = [2x7 char ] [][1x10 double] []>> C=[A,B]C = [3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] []>> D=[A,B;C]D = [3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] [][3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] []>> D(4,:)=[]D = [3x3x3 double] 'Welcome' [2x7 char ] [][ 30.3400] [1x200 double] [1x10 double] [][3x3x3 double] 'Welcome' [2x7 char ] []>> E=reshape(D,2,3,2)E(:,:,1) = [3x3x3 double] [3x3x3 double] [1x200 double][ 30.3400] 'Welcome' 'Welcome'E(:,:,2) = [2x7 char ] [2x7 char] [][1x10 double] [] []>>A={randn(3,3,2),'Good',pi;29,4+7*i,zeros(4)} A = [3x3x2 double] 'Good' [ 3.1416][ 29] [4.0000+ 7.0000i] [4x4 double]>> B=cellfun('isreal',A)B = 1 1 11 0 1>> C=cellfun('length',A)C = 3 4 11 1 4>> Member.code='09021';>> ='Liu';>> Member.age=22;>> Member.grade=uint16(3);>> MemberMember =code: '09021'name: 'Liu'age: 22grade: 3>> Member(4).name='Wang';>> Member(4).grade=2;>> Member(2)ans = code: []name: []age: []grade: []>>Memebr=struct('code','09021','name','Liu','a ge',22,'grade',uint16(3))Memebr = code: '09021'name: 'Liu'age: 22grade: 3>>Member=struct('code',{'09021','09034'},'name' ,{'Liu','Wamg'},'age',{22,24},'grade',{2,3}) Member = 1x2 struct array with fields:codenameagegrade>>Member=struct('code',{},'name',{},'age',{},'gr ade',{})Member = 0x0 struct array with fields:codenameagegrade>>Member=struct('code',{'09021','09034'},'na me',{'Liu','Wang'},'age',{22,24},'grade',{2,3},' score',{[78 89;90 68],[91 76;89 97]}) Member = 1x2 struct array with fields:codenameagegradescore>> Member(1).scoreans =78 8990 68>> Member(2).score(2,:)ans =89 97>> Member.codeans =09021ans =09034>> Member.('name')ans =Liuans =Wang>> ='Liu';M.ID=1;>> M(2,2).name='Wang';M(2,2).ID=2; >> M2=setfield(M,{2,1},'name','Zhang'); >> ans =Liuans =[]ans = []ans =Wang>> ans =Liuans =Zhangans = []ans =Wang>> fieldnames(M)ans = 'name''ID'>> M3=orderfields(M)M3 = 2x2 struct array with fields:IDname。
matlab 实验报告

matlab 实验报告Matlab实验报告引言:Matlab是一种强大的数值计算和可视化软件,广泛应用于科学、工程和经济等领域。
本实验报告将介绍我在使用Matlab进行实验过程中的一些经验和结果。
实验一:矩阵运算在这个实验中,我使用Matlab进行了矩阵运算。
首先,我创建了一个3x3的矩阵A和一个3x1的矩阵B,并进行了矩阵相乘运算。
通过Matlab的矩阵乘法运算符*,我得到了一个3x1的结果矩阵C。
接着,我对矩阵C进行了转置操作,得到了一个1x3的矩阵D。
最后,我计算了矩阵C和矩阵D的点积,并将结果输出。
实验二:数据可视化在这个实验中,我使用Matlab进行了数据可视化。
我选择了一组实验数据,包括时间和温度两个变量。
首先,我将数据存储在一个矩阵中,并使用Matlab的plot函数将时间和温度之间的关系绘制成曲线图。
接着,我使用Matlab的xlabel、ylabel和title函数添加了横轴、纵轴和标题。
最后,我使用Matlab的legend函数添加了图例,以便更好地理解图表。
实验三:数值积分在这个实验中,我使用Matlab进行了数值积分。
我选择了一个函数f(x)进行积分计算。
首先,我使用Matlab的syms函数定义了符号变量x,并定义了函数f(x)。
接着,我使用Matlab的int函数对函数f(x)进行积分计算,并将结果输出。
为了验证结果的准确性,我还使用了Matlab的diff函数对积分结果进行了求导操作,并与原函数f(x)进行了比较。
实验四:信号处理在这个实验中,我使用Matlab进行了信号处理。
我选择了一个音频文件,并使用Matlab的audioread函数读取了该文件。
接着,我使用Matlab的fft函数对音频信号进行了傅里叶变换,并将结果绘制成频谱图。
为了进一步分析信号的特征,我还使用了Matlab的spectrogram函数绘制了信号的时频图。
通过对信号的频谱和时频图的观察,我可以更好地理解信号的频率和时域特性。
matlab实验报告——第一组 2

k
x=x+sym(-1)^(sym(k)-sym(1))/(sym(2)*sym(k)-sym(1))*(sym(48)/sym(18)^(sym(2)*sym(k)-sym(1))+sym(32)/sym(57)^(sym(2)*sym(k)-sym(1))-sym(20)/sym(239)^(sym(2)*sym(k)-sym(1)));
ans =
1600
ans =
3.140967653650828364910
ans =
.624999938964873553e-3
ans =
1800
ans =
3.141037098077104607384
ans =
.555555512688631079e-3
ans =
2000
ans =
3.141092653621043228697
ans =
.999999750000312499e-3
ans =
1200
ans =
3.140759320401135705469
ans =
.833333188657532994e-3
ans =
1400
ans =
3.140878367966615337793
ans =
.714285623177900670e-3
2013—2014学年第1学期
合肥学院卓越工程师班
实验报告
课程名称:工程应用数学E
实验名称: 值的近似计算
实验类别:综合性□设计性□验证性□
专业班级:
实验地点:实验时间:2013/12/25
组别:第一组
matlab实验报告实验二

matlab实验报告实验二Matlab实验报告实验二引言Matlab是一种功能强大的数学软件,广泛应用于科学研究和工程实践中。
在实验二中,我们将探索Matlab的图像处理功能,并通过实际案例来展示其应用。
图像处理基础图像处理是指对图像进行数字化处理的过程,其目的是改善图像质量、提取有用信息或实现特定的应用需求。
在Matlab中,我们可以利用各种函数和工具箱来实现图像处理的各种任务,如图像增强、滤波、分割和特征提取等。
实验步骤1. 图像读取与显示在Matlab中,我们可以使用imread函数读取图像文件,并使用imshow函数将图像显示在屏幕上。
例如,我们可以读取一张名为"lena.jpg"的图像,并显示出来:```matlabimg = imread('lena.jpg');imshow(img);```2. 图像灰度化图像灰度化是将彩色图像转换为灰度图像的过程。
在Matlab中,我们可以使用rgb2gray函数将彩色图像转换为灰度图像。
例如,我们可以将上一步读取的图像转换为灰度图像:```matlabgray_img = rgb2gray(img);imshow(gray_img);```3. 图像二值化图像二值化是将灰度图像转换为二值图像的过程,其中只包含黑色和白色两种颜色。
在Matlab中,我们可以使用imbinarize函数将灰度图像二值化。
例如,我们可以将上一步得到的灰度图像二值化:```matlabbinary_img = imbinarize(gray_img);imshow(binary_img);```4. 图像平滑图像平滑是指去除图像中的噪声或细节,使得图像更加平滑和清晰。
在Matlab 中,我们可以使用imfilter函数对图像进行平滑处理。
例如,我们可以对上一步得到的二值图像进行平滑处理:```matlabsmooth_img = imfilter(binary_img, fspecial('average'));imshow(smooth_img);```5. 图像边缘检测图像边缘检测是指提取图像中物体边缘的过程,常用于目标检测和图像分割。
MATLAB第二章实验报告

深 圳 大 学 实 验 报 告课程名称: MATLAB实验名称: MATLAB 的数值计算学 院:指导教师:报告人: 组号:学号 实验地点实验时间: 年 月 日提交时间:二、内容和步骤1.创建矩阵(1)直接输入(2)用from:step:to方式(3)用linspace函数:(4)使用特殊矩阵函数,并修改元素(5)获取子矩阵块:.练习:b=logspace(0,4*3.14,20)b =1.0e+12 *1 至17 列0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0004 0.0018 0.0082 0.037718 至20 列0.1729 0.7924 3.63082.矩阵运算:(1)利用矩阵除法解线性方程组(2)利用矩阵的基本运算求解矩阵方程练习:(3)计算矩阵的特征值和特征向量。
验证特征值和特征向量与该矩阵的关系练习:将矩阵的乘除运算改为数组的点乘和点除运算:(4)利用数学函数进行矩阵运算w=logspace(-2,1,10)w =0.0100 0.0215 0.0464 0.1000 0.2154 0.4642 1.0000 2.1544 4.6416 10.0000LW=-20*log10(sqrt((2*w).^2 + 1))LW =-0.0017 -0.0081 -0.0373 -0.1703 -0.7396 -2.6993 -6.9897 -12.9151 -19.4040 -26.0314FW=-atan(2*w)*180/piFW =-1.1458 -2.4673 -5.3037 -11.3099 -23.3106 -42.8711 -63.4349 -76.9341 -83.8517 -87.13763.生成多维数组:c(18)=[]c =1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8练习:使用数组c编辑窗口查看变量a,b和c。
MATLAB实验报告二

实验二 Matlab语言程序设计一、实验内容:1、编写命令文件:计算 1+2+…+n<2000 时的最大 n 值;>> n=1; %将变量初值设为1sum=0;while((sum+n)<2000) %若s<2000成立,则执行下一条语句,否则结束本循环sum=sum+n; %求和运算n=n+1;endsum,n-1 %显示最终s和nsum =1953ans =622、编写函数文件:分别用 for 和 while 循环结构编写程序,求 2 的 0 到 15 次幂的和。
function xunhuan(x)sum=0;for(i=0:x)sum=sum+2^i;endy=sum>> xunhuan(15)y =65535function whilexun(x)sum=0;i=0;while(i<x)sum=sum+2^i;i=i+1;endy=sum>> whilexun(16)y =655353、如果想对一个变量 x 自动赋值。
当从键盘输入 y 或 Y 时(表示是),x 自动赋为 1;当从键盘输入 n 或 N 时(表示否),x 自动赋为 0;输入其他字符时终止程序。
a=input('输入一个字符:');switch acase 'y'x=1case 'Y'x=1case 'n'x=0case 'N'x=0otherwiseend输入一个字符:'Y'x =1二、实验思考题1.用FOR和WHILE语句有何要求?答:for语句的基本命令格式为for 循环变量=表达式1表达式3表达式2循环语句组End表达式1、表达式3、表达式2的定义和C语言相似即首先执行循环变量的初始值赋成表达式1的值然后判断循环变量的值介于表达式1和表达式2的值之间则执行循环体中的语句否则结束循环语句的执行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB数学实验报告姓名:李帆班级:机械(硕)21学号:2120104008第一次数学实验报告——线性规划问题一,实验问题1,某饲养场饲养动物出售,设每头动物每天至少需要700g蛋白质,30g矿物质,100mg 维生素。
现有五种饲料可供选择,各种饲料的每千克营养成分含量和单价如下表。
是确定既能满足动物生长的营养需要,游客是费用最省的选用饲料方案。
2,某工厂生产甲、乙、丙三种产品,单位产品所需工时分别为2、3、1个;单位产品所需原料分别为3、1、5公斤;单位产品利润分别为2、3、5元。
工厂每天可利用的工时为12个,可供应的原料为15公斤。
为使总利润为最大,试确定日生产计划和最大利润。
二,问题分析1,1)该题属于采用线性规划的方式求出最优解的数学问题。
该题有以下特点,1.目标函数有线性,是求目标函数的最小值;2.约束条件为线性方程组;3.未知变量都有非负限制。
1,2)求解该类问题的方法有图解法,理论解法和软件解法。
图解法常用于解变量较少的线性规划问题。
理论解法要构建完整的理论体系。
目前用于解线性规划的理论解法有:单纯形法,椭球算法等。
在此,我们采用单纯形法的MATLAB软件解法来求解该问题。
1,3)此题中,要求既要满足动物生长的营养需要,又要使费用最省,则使每种饲料的选用量为变量,以总费用的最小值为所求量,同时每种饲料的使用量要符合营养成分的要求。
1,4)在此,首先确定建立线性规划模型。
设饲料i选用量为xi公斤,i=1,2,3,4,5.则有模型:Minz=0.2x1+0.7x2+0.4x3+0.3x4+0.8x5s.t.{3x1+2x2+6x4+18x5>=700;x1+0.5x2+0.2x3+2x4+0.5x5>=300.5x1+x2+0.2x3+2x4+0.8x5>=100Xj>=0,j=1,2,3,4,5解之得:x1=x2=x3=0X4=39.74359X5=25.14603Zmin=32.435902,1)该问题与第一题分析步骤相似,故只在此写出其线性规划模型Z=2x+3y+5z2x+3y+z<=123x+y+5z<=15三,程序设计流程图第一题:c=[0.2,0.7,0.4,0.3,0.8]A=[3,2,1,6,18;1,0.5,0.2,2,0.5;0.5,1,0.2,2,0.8;1,0,0,0,0;0,1, 0,0,0;0,0,1,0,0;0,0,0,1,0;0,0,0,0,1]b=[700,30,100,0,0,0,0,0][x,fval]=linprog(c,-A,-b)c=0.20000.70000.40000.30000.8000A=3.0000 2.0000 1.0000 6.000018.00001.00000.50000.20002.00000.50000.5000 1.00000.2000 2.00000.80001.000000000 1.000000000 1.000000000 1.000000000 1.0000b=7003010000000Optimization terminated.x=0.0000-0.00000.000039.743625.6410fval=32.4359第二题c=[-2-3-5]A=[231;315]b=[12;15]lb=[000][x,Z,exitflag,output]=linprog(c,A,b,[],[],lb,[])将上述程序输入matlab。
就可得出结果。
结果如下:x=0.00003.21432.3571Z=-21.4286四,结果分析和结论1.由上述实验结果可知,当x1=x2=x3=0,x4=39.74539公斤,x3=25.64103公斤时,费用取得最小值32.43590元。
2.由上述结果可以知道当甲、乙、丙分别生产0,3.2143,2.3571公斤时,总利润最大,可达到21.4286四,总结和体会通过该次试验,我们掌握了采用线性规划方式解决求最优解的数学问题的方法,同时,对于建立数学模型有了一个初步的认识。
对于以后的数学学习起到了非常大的帮助。
并且,我们掌握了使用MATLAB软件解决问题的一些方法,学到了关于其操作的一些软件语言,开辟了解决数学相关问题的一种新方法。
这对于我们来说,是一次极大的收获。
当然,由于我们自身知识的有限,对于解决一些较为复杂的问题还有一些难度,同时,对于其中的一些符号语言以及一些表示方法还不够熟悉,需要我们以后进行进一步的学习。
第二次数学实验报告——曲线拟合一,实验问题1,下表中,X是华氏温度,Y是一分钟内一只蟋蟀的鸣叫次数,试用多项式模型拟合这些数据,画出拟合曲线,分析你的拟合模型是否很好2、(1)在下列数据中,W表示一条鱼的重量,l表示它的长度,使用最小二乘准则拟合模型W=kl3长度l(英寸)14.512.517.2514.512.62517.7514.12512.625重量w(盎司)2717412617492316(2)**在下列数据中,g表示一条鱼的身围,使用最小二乘准则拟合模型W=klg2长度l(英寸)14.512.517.2514.512.62517.7514.12512.625身围g(英寸)9.758.37511.09.758.512.59.08.5重量w(盎司)2717412617492316(3)**两个模型哪个拟合数据较好?为什么?二,问题分析1,1)该题属于曲线拟合问题。
最佳曲线拟合问题等价于确定一条平面曲线使它和实验数据点最接近。
并不要求曲线严格通过每个已知数据点,但要求曲线在各数据点处的取值与已知观测值的总体误差最小。
1,2)首先设定某一类型的函数y=f(x),,然后确定函数中的参数,使得在各点处的偏差ri=f(xi)-yi的平方和最小。
1,3)本题中采用最小二乘法的基本思想。
运用MATLAB中命令polyfit编写拟合程序。
其中x,y为已知的数据点横坐标向量和总坐标向量,m为要拟合的多项式次数,结果p为m次多项式系数向量,且从高次到低次存放在向量p中。
2.1)该题属于曲线拟合问题。
最佳曲线拟合问题等价于确定一条平面曲线使它和实验数据点最接近。
并不要求曲线严格通过每个已知数据点,但要求曲线在各数据点处的取值与已知观测值的总体误差最小。
2.2)首先设定某一类型的函数y=f(x),,然后确定函数中的参数,使得在各点处的偏差ri=f(xi)-yi的平方和最小。
三,程序设计流程图第一题x=[4649515254565758596061626364666768717271];y=[40505563727077709093968899110113120127137132137]; plot(x,y,'k.','markersize',20);axis([408035145]);p=polyfit(x,y,8);t=40:1:80;s=polyval(p,t);hold onplot(t,s,'k-','linewidth',2)grid第二题1)l=[14.5;12.5;17.25;14.5;12.625;17.75;14.125;12.625];w=[27;17;41;26;17;49;23;16];c=0;d1=0;for i=1:8c=c+l(i)^4;d1=d1+l(i)*w(i);endA=cD=d1ab=inv(A)*Dfor i=1:8x(i)=ab(1)*l(i)^3;endplot(l,w,'r*--',l,x,'b.--');2)l=[14.512.517.2514.512.62517.7514.12512.625]g=[9.758.37511.09.758.512.59.08.5]w=[2717412617492316]plot3(l,g,w,'k.','markersize',25)axis([10207.5121555]) m=l.*(g.^2)k=inv(m*(m.'))*(m)*(w.') x=11:0.1:20y=8:0.1:13[X,Y]=meshgrid(x,y)Z=k*X.*Y.^2surf(X,Y,Z)shading flat四,结果分析和结论运行结果如下图所示:第一题:第二题1)求出来的答案如下:A=3.9125e+05D=3.2995e+03k=0.00842)l=14.500012.500017.250014.500012.625017.750014.125012.6250 g=9.75008.375011.00009.75008.500012.50009.00008.5000 w=2717412617492316m=1.0e+003*1.37840.87682.0873 1.37840.9122 2.7734 1.14410.9122 k=0.0187(3)经过对于实验题1和实验题2的数据拟合曲线的比较,我认为第二个数学模型拟合数据较好。
因为鱼的身体重不仅受到其长度的影响,也与他的身围有一定的关系。
通过综合数据的拟合,能够更加准确的判断鱼的体重的影响关系。
五,总结和体会通过这次试验,我们对于数据拟合模型有了一定的认识,同时对于其基本原理和使用方法有了一定的掌握。
我们发现,该数学模型,在我们的日常生活中,具有极大的使用范围,能够为我们带来相当大的便利。
