MIT(麻省理工)信号与系统讲义-lecture7
合集下载
美国MIT信号与系统课程的基本结构
MIT 2009 年秋季学期信号与系统课程教学日程表 Wednesday / Recitation 备注 教学内容 Thursday / Lecture 教学内容 L1 ： Signals and Systems L3 ： Feedback， Cycles and Modes L5 ： Feedback Control Schemes L7 ： Laplace Transforms and Z Friday / Recitation 教学内容 R2 ： Difference Equations R4 ： Feedback， Cycles and Modes R6 ： Feedback Control Schemes R8 ： Laplace Transforms and Z
பைடு நூலகம்
由 S． Mahajan 和 D． Freeman 于 2009 年编著的《离 。教 学 内 容 涵 盖 了 散时间 信 号 与 系 统： 算 子 法 》 Oppenheim著作的全部主要内容。 此外， 还包括补充
表1 日期 / 课型 周次 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Tuesday / Lecture 教学内容 （ Registration Day） L2 ： DT Systems L4 ： Feedback and Position Control L6 ： CT Systems，Difference Eqs． L8 ： CT Operator Representations （ For Columbus Day） L11 ： Frequency sponse ReHW1 due HW2 due HW3 due EX4 HW5 due HW6 due EX7 HW8 due HW9 due EX10 HW11 due HW12 due EX13
信号与系统课件第七章(电子)
虚轴上的极点：
单极点
p0
p1,2
j
A t
Acost t
响应函数幅度不随时间变化。
r重极点
Ajt j t 或 Ajt j cos t j t
j 0,1,2,, 1
响应随t的增大而增大。
右半开平面的极点：
单极点
p 0
p1,2
j
0
Aet t Ae t cost t
左半开平面
H(s)的极点，在s平面的位置
虚轴
左半开平面的极点：
右半开平面
单极点
p 0
p1,2
j
0
Aet t
Ae t cost t
重极点
Ajt jet t 或 Ajt je t cos t j t
j 0,1,2,, 1
响应函数是衰减的， 当t→∞时，响应趋近于零。
j-pi
j
H ( j ) H (s) s j
j 1 n
( j pi )
pi
n1
0
对于任意极点 p和i 零点 ，j 令
j pi j j
Aie Bje
ji j
j
于是
pi
H ( j )
bm B1B2 Bme j( 1 2 m )
A A A e 1 2
j (1 2 n )
n
H ( j ) e j ( )
单位圆外的极点
单极点
pa a 1
Aak (k)
p1,2
ae j
a 1
Aak cos(k ) (k)
如有重极点，其所对应的响应也随k的增加而增大。
由以上讨论可得如下结论:(因果)
H(z)在单位圆内的极点所对应的响应序列都是 衰减的，当k趋于无限时，响应趋于零。
信号与系统课程介绍课件
详细描述
线性是指系统的输出与输入成正比关系，满 足叠加原理；时不变性是指系统的特性不随 时间的变化而变化；因果性是指系统的输出 只与过去的输入有关，与未来的输入无关； 稳定性是指系统在受到一定程度的干扰后能 够恢复到原来的状态。了解这些基本特性有
助于更好地理解和分析系统的行为。
04
信号与系统的关系
系统的定义与分类是系统基础知识的重要组成部分，它有助于理解系统的基本概念和性 质。
详细描述
系统是指由相互关联、相互作用的元素组成的集合，这些元素之间相互作用，共同完成 特定的功能或目标。根据不同的分类标准，系统可以分为线性系统、非线性系统、时不
变系统、时变系统等。
系统的数学模型
总结词
系统的数学模型是描述系统行为的重要工具，它可以通过数学方程来描述系统 的输入和输出之间的关系。
实验报告撰写规范
实验目的与意义
学生需在报告中明确实验目的和意义，阐述实验 的重要性。
实验步骤与结果
学生需详细记录实验步骤和实验结果，包括数据 记录、图表绘制等。
ABCD
实验原理
学生需简要介绍实验所涉及的原理和方法，为实 验操作提供理论依据。
分析与结论
学生对实验结果进行分析和讨论，得出结论，并 指出实验中存在的问题和改进方向。
信号的数学表示方法
总结词
信号可以用各种数学工具进行表示和分析，如时间域和频域表示法。
详细描述
在时间域中，信号可以表示为随时间变化的函数，通过导数、积分等数学运算可 以分析信号的形状、幅度、频率等特性。在频域中，信号可以表示为频谱或傅里 叶级数，通过分析频谱可以了解信号的频率成分和频率特性。
信号的基本特性
第三周
系统的稳定性、性 能分析和优化方法 。
信号与系统讲稿
信号与系统讲稿第一讲：引言授课时数学时学习目标了解信号的传递学习重点、难点、通信系统的组成关键点学习模式视觉模式，听觉模式讲授过程学习讲授内容体系设计预备知识引题材料移动通信技术可以说从无线电通信发明之日就产生了。
1897年，M·G·马可尼所完成的无线通信试验就是在固定站与一艘拖船之间进行的，距离为18海哩。
而现代移动通信技术的发展始于上世纪20年代，大致经历了五个发展阶段。
35年前，谁也无法想象有一天每个人身上都有一部电话，被连接到这个世界。
如今，人们可以通过手机进行通讯，智能手机更如同一款随身携带的小型计算机，通过3G等移动通讯网络实现无线网络接入后，可以方便的实现个人信息管理及查阅股票、新闻、天气、交通、商品信息、应用程序下载、音乐图片下载等。
下让我们来回顾一下移动通信网络技术的发展简史。
第一阶段从上世纪20年代至40年代，为早期发展阶段。
在这期间，首先在短波几个频段上开发出专用移动通信系统，其代表是美国底特律市警察使用的车载无线电系统。
该系统工作频率为2MHz，到40年代提高到30～40MHz,可以认为这个阶段是现代移动通信的起步阶段，特点是专用系统开发，工作频率较低。
1946年10月贝尔电话公司启动车载无线电话服务第二阶段从上世纪40年代中期至60年代初期。
在此期间内，公用移动通信业务开始问世。
1946年，根据美国联邦通信委员会(FCC)的计划，贝尔系统在圣路易斯城建立了世界上第一个公用汽车电话网，称为‚城市系统‛。
当时使用三个频道，间隔为120kHz，通信方式为单工，随后，西德(1950年)、法国(1956年)、英国(1959年)等国相继研制了公用移动电话系统。
美国贝尔实验室完成了人工交换系统的接续问题。
这一阶段的特点是从专用移动网向公用移动网过渡，接续方式为人工，网的容量较小。
人工交换台第三阶段从上世纪60年代中期至70年代中期。
在此期间，美国推出了改进型移动电话系统(IMTS)，使用150MHz和450MHz频段，采用大区制、中小容量，实现了无线频道自动选择并能够自动接续到公用电话网。
MIT(麻省理工)信号与系统讲义-lecture2
Signals and Systems
Fall 2003 Lecture #2
9 September 2003 1) Some examples of systems 2) System properties and examples a) Causality b) Linearity c) Time invariance
11
CAUSAL OR NONCAUSAL
depends on causal
noncausal
depends on future
depends on future
noncausal
depends on
causal
12
TIME-INVARIANCE (TI)
Informally, a system is time-invariant (TI) if its behavior does not depend on what time it is. • Mathematically (in DT): A system x[n] → y[n] is TI if for any input x[n] and any time shift n0, If x[n] →y[n] then x[n -n0] →y[n -n0] •Similarly for a CT time-invariant system, If x(t) →y(t) then x(t -to) →y(t -to) .
• This system detects changes in signal slope
7
Observations
1)A very rich class of systems (but by no means all systems of interest to us) are described by differential and difference equations. 2)Such an equation, by itself, does not completely describe the input-output behavior of a system: we need auxiliary conditions (initial conditions, boundary conditions). 3)In some cases the system of interest has time as the natural independent variable and is causal. However, that is not always the case. 4)Very different physical systems may have very similar mathematical descriptions.
Fall 2003 Lecture #2
9 September 2003 1) Some examples of systems 2) System properties and examples a) Causality b) Linearity c) Time invariance
11
CAUSAL OR NONCAUSAL
depends on causal
noncausal
depends on future
depends on future
noncausal
depends on
causal
12
TIME-INVARIANCE (TI)
Informally, a system is time-invariant (TI) if its behavior does not depend on what time it is. • Mathematically (in DT): A system x[n] → y[n] is TI if for any input x[n] and any time shift n0, If x[n] →y[n] then x[n -n0] →y[n -n0] •Similarly for a CT time-invariant system, If x(t) →y(t) then x(t -to) →y(t -to) .
• This system detects changes in signal slope
7
Observations
1)A very rich class of systems (but by no means all systems of interest to us) are described by differential and difference equations. 2)Such an equation, by itself, does not completely describe the input-output behavior of a system: we need auxiliary conditions (initial conditions, boundary conditions). 3)In some cases the system of interest has time as the natural independent variable and is causal. However, that is not always the case. 4)Very different physical systems may have very similar mathematical descriptions.
信号与系统全套课件
滤波器设计和应用
滤波器的概念和分类
根据滤波器的频率响应特性，可分为低通、高通、带通和带阻滤 波器等。
滤波器设计方法
包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等设计方法， 以及数字滤波器的设计等。
滤波器的应用
在通信、音频处理、图像处理等领域广泛应用，如信号去噪、平 滑处理、频率选择性传输等。
04 信号与系统复频域分析
状态变量分析法概述
1
状态变量分析法是一种基于系统内部状态变量描 述系统动态行为的方法。
2
它适用于线性时不变系统，可以方便地分析系统 的稳定性、能控性、能观性等重要特性。
3
状态变量分析法通过引入状态变量的概念，将高 阶微分方程转化为一阶微分方程组，从而简化系 统分析和设计的复杂性。
状态方程和输出方程建立
系统函数的性质
系统函数具有因果性、稳定性、频率 响应等性质，这些性质决定了系统的 基本特性和性能指标。
稳定性判据和稳态误差分析
稳定性判据
通过系统函数的极点分布来判断系统的 稳定性，常用的稳定性判据有劳斯判据 、奈奎斯特判据等。
VS
稳态误差分析
稳态误差是指系统对输入信号响应的稳态 分量与期望输出之间的差值，通过分析系 统函数和输入信号的特性，可以对系统的 稳态误差进行定量评估。
信号与系统全套课件
目 录
• 信号与系统基本概念 • 信号与系统时域分析 • 信号与系统频域分析 • 信号与系统复频域分析 • 离散时间信号与系统分析 • 状态变量分析法在信号与系统中的应用
01 信号与系统基本概念
信号定义与分类
信号定义
信号是传递信息的函数，它可以是时间的函数，也可以是其 他独立变量的函数。在信号处理中，通常将信号表示为时间 的函数，即s(t)。
信号与系统7精品PPT课件
图7.1－1
12
例子:反因果序列
例7.1－2 求反因果序列f(k)=-akε(-k-1)的Z变换及其收敛域
（式中a
解 k≥0时f(k)=0,故其单边Z变换等于零。f(k)的双边Z变
换为
1
1
F (z) [ak (k 1)]zk (ak )zk (a1z)k
k
k
k
令m=-k,代入上式，得
F(z)是z的有理函数,与拉普拉斯变换类似，可以用它的零 点和极点来表征。本例中，F(z)具有一个零点z=0和一个极 点z=a,在图7.1－1(a)中分别用符号“○”和“×”表示。
求得因果序列与其双边Z变换的对应关系为:
a k (k) z , z | a |
za
(7.1－10)
11
因果序列f(k) 的收敛域
系统分析方法如下表
分析方法
连 时域法 续 系 频域法 统 S 域法
基本 信号
(t)
e jt
e st
响应计算
数学工具
y f (t ) h(t ) f (t ) 卷积积分
Y f ( j ) H ( j ) F ( j ) 傅氏变换
Yf (s) H(s) F(s)
拉氏变换
离 时域法 (k )
5
利用柯西公式推导Z逆变换
将式(7.1－3)两端乘以zn-1,n为任一整数，并在收敛域中进行积分，得
F (z)z n1dz z n1[ f (k)z k ]dz
C
C
f (k ) z nk1dz C
k
k
(7.1－6)
上面,积分路径C是复平面上环绕坐标原点沿逆时针方向的围线。
根据复变函数理论中的柯西公式，当n-k-1=-1,即k=n时，上式右
12
例子:反因果序列
例7.1－2 求反因果序列f(k)=-akε(-k-1)的Z变换及其收敛域
（式中a
解 k≥0时f(k)=0,故其单边Z变换等于零。f(k)的双边Z变
换为
1
1
F (z) [ak (k 1)]zk (ak )zk (a1z)k
k
k
k
令m=-k,代入上式，得
F(z)是z的有理函数,与拉普拉斯变换类似，可以用它的零 点和极点来表征。本例中，F(z)具有一个零点z=0和一个极 点z=a,在图7.1－1(a)中分别用符号“○”和“×”表示。
求得因果序列与其双边Z变换的对应关系为:
a k (k) z , z | a |
za
(7.1－10)
11
因果序列f(k) 的收敛域
系统分析方法如下表
分析方法
连 时域法 续 系 频域法 统 S 域法
基本 信号
(t)
e jt
e st
响应计算
数学工具
y f (t ) h(t ) f (t ) 卷积积分
Y f ( j ) H ( j ) F ( j ) 傅氏变换
Yf (s) H(s) F(s)
拉氏变换
离 时域法 (k )
5
利用柯西公式推导Z逆变换
将式(7.1－3)两端乘以zn-1,n为任一整数，并在收敛域中进行积分，得
F (z)z n1dz z n1[ f (k)z k ]dz
C
C
f (k ) z nk1dz C
k
k
(7.1－6)
上面,积分路径C是复平面上环绕坐标原点沿逆时针方向的围线。
根据复变函数理论中的柯西公式，当n-k-1=-1,即k=n时，上式右
MIT 公开课程 信号与系统 Lecture 2
6.003:Signals and SystemsDiscrete-Time SystemsFebruary4,2010Discrete-Time SystemsWe start with discrete-time(DT)systems because they•are conceptually simpler than continuous-time systems•illustrate same important modes of thinking as continuous-time•are increasingly important(digital electronics and computation)From Samples to SignalsLumping all of the(possibly infinite)samples into a single object—the signal—simplifies its manipulation.This lumping is an abstraction that is analogous to•representing coordinates in three-space as points•representing lists of numbers as vectors in linear algebra•creating an object in PythonLet Y=R X.Which of the following is/are true:1.y[n]=x[n]for all n2.y[n+1]=x[n]for all n3.y[n]=x[n+1]for all n4.y[n−1]=x[n]for all n5.none of the aboveOperator ApproachApplies your existing expertise with polynomials to understand block diagrams,and thereby understand systems.Example: AccumulatorThese systems are equivalent in the sense that if each is initially atrest, they will produce identical outputs from the same input.(1 −R ) Y 1 = X 1⇔ ?Y 2 =(1+ R + R 2+ R 3+ ···) X 2Proof: Assume X 2 = X 1:Y 2 =(1+ R+ R 2 + R 3 + ···) X 2 =(1+ R + R 2 + R 3 + ···) X 1 = (1+ R + R 2 + R 3 + ···)(1 −R ) Y 1= ((1 + R + R 2 + R 3 + ···) −(R + R 2 + R 3 + ···)) Y 1 = Y 1It follows that Y 2 = Y 1.It also follows that (1 −R) and (1 + R + R 2 + R 3 + ···) are reciprocals .Example: AccumulatorThe reciprocal of 1−R can also be evaluated using synthetic division.1+R +R 2 +R 3 + ···1 −R 11 −RRR −R 2R 2R 2 −R 3R 3R 3 −R 4···Therefore1=1+ R + R 2 + R 3 + R 4 + ··· 1 −RAnalysis of Cyclic Systems:Geometric GrowthIf traversing the cycle decreases or increases the magnitude of the signal,then the fundamental mode will decay or grow,respectively.If the response decays toward zero,then we say that it converges. Otherwise,we it diverges.M IT OpenCourseWare6.003 Signals and SystemsSpring 2010For information about citing these materials or our Terms of Use, visit: /terms.。
《信号与系统》课程讲义课件
《信号与系统》课程讲义 课件
这份课程讲义课件为大家提供了关于《信号与系统》的详细介绍，让您轻松 了解这一重要学科。
课程简介
这门课程涵盖了数字信号处理和系统分析的基础知识，旨在让学生了解信号的特性、表示和处理 方法，以及在实际应用中的相关工具和技能。
1 信号分析
了解不同类型的信号及其特性，如周期信号、离散信号和非周期信号等
1
分析总结
对意见和反馈进行深入分析和总结
3
改进课程
针对性改进课程和教学方法
作业和考核方式
为了评估学生对课程知识的掌握程度，我们采用以下方式进行作业和考核：
作业
• 每周一次作业 • 包括习题集、实验和项目作业等 • 占总评成绩的30%
考试
• 期中、期末闭卷考试 • 包括理论和实践题目 • 占总评成绩的70%
课程反馈和改进
我们非常重视您的反馈，它将帮助我们不断改进课程和教学方法。请通过学校邮件系统或班级论坛，随 时提出您的意见和建议。
数字信号处理应用
掌握数字信号处理相关的技 术和应用，如音频处理和图 像处理等
课程大纲
第一章 第二章 第三章 第四章 第五章 第六章
信号与系统的基本概念 时域分析方法 傅里叶分析方法 滤波器 离散信号的频域分析 离散信号的滤波器设计
教学方法
为了帮助学生更好的掌握课程内容，我们采用了以下教学方法：
小组讨论
2 系统分析
掌握系统的基本概念，如线性时不变系统、滤波器和傅立叶变换等
3 信号处理方法
学会数字信号处理的基本方法，如离散傅立叶变换、数字滤波器和采样等
课程目标
通过本课程，学生将获得以下核心能力:
分析信号
了解信号的特性并进行分析， 从而为实际应用提供解决方 案
这份课程讲义课件为大家提供了关于《信号与系统》的详细介绍，让您轻松 了解这一重要学科。
课程简介
这门课程涵盖了数字信号处理和系统分析的基础知识，旨在让学生了解信号的特性、表示和处理 方法，以及在实际应用中的相关工具和技能。
1 信号分析
了解不同类型的信号及其特性，如周期信号、离散信号和非周期信号等
1
分析总结
对意见和反馈进行深入分析和总结
3
改进课程
针对性改进课程和教学方法
作业和考核方式
为了评估学生对课程知识的掌握程度，我们采用以下方式进行作业和考核：
作业
• 每周一次作业 • 包括习题集、实验和项目作业等 • 占总评成绩的30%
考试
• 期中、期末闭卷考试 • 包括理论和实践题目 • 占总评成绩的70%
课程反馈和改进
我们非常重视您的反馈，它将帮助我们不断改进课程和教学方法。请通过学校邮件系统或班级论坛，随 时提出您的意见和建议。
数字信号处理应用
掌握数字信号处理相关的技 术和应用，如音频处理和图 像处理等
课程大纲
第一章 第二章 第三章 第四章 第五章 第六章
信号与系统的基本概念 时域分析方法 傅里叶分析方法 滤波器 离散信号的频域分析 离散信号的滤波器设计
教学方法
为了帮助学生更好的掌握课程内容，我们采用了以下教学方法：
小组讨论
2 系统分析
掌握系统的基本概念，如线性时不变系统、滤波器和傅立叶变换等
3 信号处理方法
学会数字信号处理的基本方法，如离散傅立叶变换、数字滤波器和采样等
课程目标
通过本课程，学生将获得以下核心能力:
分析信号
了解信号的特性并进行分析， 从而为实际应用提供解决方 案
MIT 信号与系统 Lecture 19
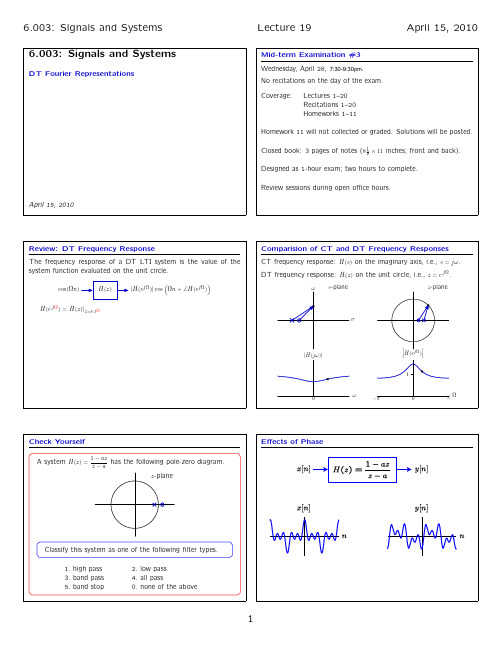
April 15, 2010
Homework 11 will not collected or graded. Solutions will be posted. Closed book: 3 pages of notes (8 1 2 × 11 inches; front and back). Designed as 1-hour exam; two hours to complete. Review sessions during open office hours. April 15, 2010
ω s-plane z -plane
H (e j Ω ) = H (z )|z =e j Ω
σ
|H (jω )|
H (ej Ω )
1
0
ω
−π
0
πΩ
Check Yourself
A system H (z ) = 1 − az has the following pole-zero diagram. z−a z -plane
x[7]
Number of multiples increases as N 2 .
8 × 8 = 64 multiplications
FFT
Divide into two 4-point series (divide and conquer). Even-numbered entries ⎡ ⎤ ⎡ 0 0 a0 W4 W 4 ⎢a ⎥ ⎢W0 W1 ⎢ 1⎥ ⎢ 4 4 ⎢ ⎥=⎢ 0 2 ⎣ a2 ⎦ ⎣ W4 W4 0 3 a3 W4 W4 Odd-numbered entries ⎡ ⎤ ⎡ 0 0 W4 W4 b0 ⎢b ⎥ ⎢W0 W1 ⎢ 1⎥ ⎢ 4 4 ⎢ ⎥=⎢ 0 2 ⎣ b2 ⎦ ⎣ W 4 W 4 0 3 W4 W4 b3 in x[n]:
MIT(麻省理工)信号与系统讲义-lecture8
b) x(t) real and odd
Purely imaginary &
c) For real
Properties of the CT Fourier Transform
1) Linearity
2) Time Shifting Proof: FT magnitude unchanged
Linear change i源自 FT phaseProperties (continued)
3) Conjugate Symmetry
— All the energy is concentrated in one frequency — ωo
More generally
Example #4:
“Line spectrum”
Example #5:
— Sampling function
Same function in the frequency-domain! Note: (period in t) T ⇔ (period in ω) 2π/T Inverse relationship again!
Fourier’s Derivation of the CT Fourier Transform
•
• •
x(t) - an aperiodic signal - view it as the limit of a periodic signal as T → ∞
For a periodic signal, the harmonic components are spaced ω0 = 2π/T apart ... As T → ∞, ω0 → 0, and harmonic components are spaced closer and closer in frequency
《信号与系统教案》课件
信号与系统分析方法
介绍了信号与系统分析的常用方法，如时域分析、频域分析、复频域 分析等。
信号与系统的应用
列举了一些信号与系统的实际应用案例，如通信系统、控制系统等， 以展示信号与系统在工程实践中的重要性。
未来发展方向与展望
信号处理的新技术
介绍了一些新兴的信号处理技 术，如深度学习在信号处理中 的应用、稀疏信号处理等，并 探讨了这些技术对未来信号处 理领域的影响。
详细描述
信号是信息传输的载体，它可以表示声音、图像、文字等不同形式的信息。信号具有时间、幅度、相 位等特征，这些特征在不同类型的信号中有所不同。根据不同的特征和用途，信号可以分为连续信号 和离散信号、确定信号和随机信号、模拟信号和数字信号等类型。
系统的定义与分类
总结词
系统是实现特定功能的整体，由相互关联的元素组成，可以分为线性系统和非线性系统、时不变系统和时变系统 等类型。
信号与系统是信息传输和处理的基础，广泛应用于通 信、图像处理、声音处理等领域。
详细描述
信号与系统是信息传输和处理的基础，它们在通信、图 像处理、声音处理等领域中发挥着重要的作用。通过信 号的传输和处理，可以实现信息的传递、转换和存储， 为各种应用提供必要的信息支持。同时，信号与系统的 理论和方法也在其他领域中得到了广泛的应用，如生物 医学工程、地震勘探、雷达探测等。随着信息技术的发 展，信号与系统的应用范围还将不断扩大，为人们的生 活和工作带来更多的便利和效益。
信号的测量与监测
控制系统需要对各种物理量进行测量和监测，以实现自动化控制， 测量和监测技术能够将各种物理量转换为可处理的电信号。
信号的反馈与控制
反馈和控制技术能够根据系统输出和期望值的偏差，自动调整系统参 数，使系统输出达到期望值。
介绍了信号与系统分析的常用方法，如时域分析、频域分析、复频域 分析等。
信号与系统的应用
列举了一些信号与系统的实际应用案例，如通信系统、控制系统等， 以展示信号与系统在工程实践中的重要性。
未来发展方向与展望
信号处理的新技术
介绍了一些新兴的信号处理技 术，如深度学习在信号处理中 的应用、稀疏信号处理等，并 探讨了这些技术对未来信号处 理领域的影响。
详细描述
信号是信息传输的载体，它可以表示声音、图像、文字等不同形式的信息。信号具有时间、幅度、相 位等特征，这些特征在不同类型的信号中有所不同。根据不同的特征和用途，信号可以分为连续信号 和离散信号、确定信号和随机信号、模拟信号和数字信号等类型。
系统的定义与分类
总结词
系统是实现特定功能的整体，由相互关联的元素组成，可以分为线性系统和非线性系统、时不变系统和时变系统 等类型。
信号与系统是信息传输和处理的基础，广泛应用于通 信、图像处理、声音处理等领域。
详细描述
信号与系统是信息传输和处理的基础，它们在通信、图 像处理、声音处理等领域中发挥着重要的作用。通过信 号的传输和处理，可以实现信息的传递、转换和存储， 为各种应用提供必要的信息支持。同时，信号与系统的 理论和方法也在其他领域中得到了广泛的应用，如生物 医学工程、地震勘探、雷达探测等。随着信息技术的发 展，信号与系统的应用范围还将不断扩大，为人们的生 活和工作带来更多的便利和效益。
信号的测量与监测
控制系统需要对各种物理量进行测量和监测，以实现自动化控制， 测量和监测技术能够将各种物理量转换为可处理的电信号。
信号的反馈与控制
反馈和控制技术能够根据系统输出和期望值的偏差，自动调整系统参 数，使系统输出达到期望值。
英文版《信号与系统》第678章讲义
Frequency-Domain:
X j
H j
ht
yt Y j
Y j X j H j §6.1 The Magnitude-Phase Representation （ 幅度-相位） of the Fourier Transform
xt
Sampling
xt
x p t
pt
n
t nT
x0 xT x2T
-3T -2T
-T
0
T
2T
3T
4T
12
t
Chapter 7 Sampling Theorem:
Sampling
Let xt be a band-limited signal with X j 0 , M Then xt is uniquely determined by its samples xnT , n 0,1, 2 if where s s 2 M T
to obtain a signal g t with Fourier transform G j . Determine the maximum value of 0 for which it is guaranteed that
y t cos t / 3 1/ 3 cos t 1 cos
3t 3 y t cos t 1 / 3 cos t 1 cos 3 t 1
4
Chapter 6 2. Nonlinear Phase
§6.2 The Magnitude-Phase Representation of the Frequency Response of LTI Systems
MIT信号与系统网络课程练习题答案
1 x(−t) 2
1 t
−4 −2
-1
2
4
1
xe (t)
t
−4 −2
-1
2
4
8
xo (t)
1 t
−4 −2
-1
2
4
The value of the even part (and the odd part for that matter) at t = 0 is ambiguous as it depends on how the plot for x(t) is defined at t = 0. The plots in this solution assume that the value of x(t) at t = 0 is halfway between 0 and 2, i.e. 1. Using a different definition you may get an even part that is discontinuous at t = 0. This is also correct provided it is consistent with your assumption of what the value of x(t) is at the discontinuity. For instance, if you assume that x(0) = 2, then the plot of the even part will have a “spike” at t = 0 of height 2.
t x(1 − 3 )
2 1 9 t
−6 −3
3
6
−1
t Figure 2.a.3: x(1 − 3 )
《信号与系统》课件
1
2
0 , k其他
■
k 0
k 1
k 2
k其他
第1-18页
1.3 信号的基本运
算
二、信号的时间变换运算
1. 反转
演示
将 f (t) → f (–t) ， f (k) → f (–k) 称为对信号f (·
)
的反转或反折。从图形上看是将f (·
)以纵坐标为轴反
转180o。如
f (t)
反转 t → - t
■
第1-11页
1.2 信号的描述和分
类
例1 判断下列信号是否为周期信号，若是，确定其周期。
（1）f1(t) = sin2t + cos3t
（2）f2(t) = cos2t + sinπt
解：两个周期信号x(t)，y(t)的周期分别为T1和T2，若其
周期之比T1/T2为有理数，则其和信号x(t)+y(t)仍然是周
《信号与系统》
第一章 信号与系统
1.1 绪言
● 思考问题：什么是信号？什么是系统？为什么把这两个概念联系在一起？
●一、信号的概念
1. 消息(message):
● 人们常常把来自外界的各种报道统称为消息。消息：反映知识状态的改变。
2. 信息(information): 它是信息论中的一个术语。
● 通常把消息中有意义的内容称为信息。信息量=[ 收到消息前对某事件的无知程度
（2）信号的图形表示--波
形
第1-6页
“信号”与“函数”两词常相互通用。
■
二、信号的分类
1.2 信号的描述和分
类
1. 确定信号和随机信号
可以用确定时间函数表示的信号，称为确定信号
2
0 , k其他
■
k 0
k 1
k 2
k其他
第1-18页
1.3 信号的基本运
算
二、信号的时间变换运算
1. 反转
演示
将 f (t) → f (–t) ， f (k) → f (–k) 称为对信号f (·
)
的反转或反折。从图形上看是将f (·
)以纵坐标为轴反
转180o。如
f (t)
反转 t → - t
■
第1-11页
1.2 信号的描述和分
类
例1 判断下列信号是否为周期信号，若是，确定其周期。
（1）f1(t) = sin2t + cos3t
（2）f2(t) = cos2t + sinπt
解：两个周期信号x(t)，y(t)的周期分别为T1和T2，若其
周期之比T1/T2为有理数，则其和信号x(t)+y(t)仍然是周
《信号与系统》
第一章 信号与系统
1.1 绪言
● 思考问题：什么是信号？什么是系统？为什么把这两个概念联系在一起？
●一、信号的概念
1. 消息(message):
● 人们常常把来自外界的各种报道统称为消息。消息：反映知识状态的改变。
2. 信息(information): 它是信息论中的一个术语。
● 通常把消息中有意义的内容称为信息。信息量=[ 收到消息前对某事件的无知程度
（2）信号的图形表示--波
形
第1-6页
“信号”与“函数”两词常相互通用。
■
二、信号的分类
1.2 信号的描述和分
类
1. 确定信号和随机信号
可以用确定时间函数表示的信号，称为确定信号
《信号与系统讲义》课件
《信号与系统讲义》PPT 课件
信号与系统是理解和分析信号处理的基础。本课件将介绍信号与系统的基本 概念、时域信号与频域信号、连续信号与离散信号、线性时不变系统、卷积 运算、采样与重构，以及系统的频率响应和频率特性。
信号与系统的基本概念
了解信号与系统的基本概念是理解信号处理的关键。本节将介绍信号的定义、 分类以及常见的信号类型，以及系统的定义和特性。
卷积运算
卷积运算是信号处理中常用的操作。本节将介绍卷积运算的定义和性质，并 通过实例演示如何使用卷积运算来处理信号。
采样与重构
采样是将连续信号转换为离散信号的过程，而重构则是将离散信号还原为连续信号的过程。本节将介绍 采样和重构的原理和方法。
பைடு நூலகம்
系统的频率响应和频率特性
系统的频率响应和频率特性描述了系统对不同频率的信号的响应情况。本节 将介绍频率响应和频率特性的概念，以及它们在信号处理中的应用。
时域信号与频域信号
在信号处理中，时域信号和频域信号是两种常见的表示方式。本节将解释时 域和频域的概念，以及如何在两个域中相互转换。
连续信号与离散信号
信号可以是连续的，也可以是离散的。本节将讨论连续信号和离散信号的区别，以及在信号处理中如何 处理这两种类型的信号。
线性时不变系统
线性时不变系统是信号处理中常用的模型。本节将介绍线性时不变系统的基本概念和特性，以及如何利 用系统的响应来分析信号的处理过程。
信号与系统是理解和分析信号处理的基础。本课件将介绍信号与系统的基本 概念、时域信号与频域信号、连续信号与离散信号、线性时不变系统、卷积 运算、采样与重构，以及系统的频率响应和频率特性。
信号与系统的基本概念
了解信号与系统的基本概念是理解信号处理的关键。本节将介绍信号的定义、 分类以及常见的信号类型，以及系统的定义和特性。
卷积运算
卷积运算是信号处理中常用的操作。本节将介绍卷积运算的定义和性质，并 通过实例演示如何使用卷积运算来处理信号。
采样与重构
采样是将连续信号转换为离散信号的过程，而重构则是将离散信号还原为连续信号的过程。本节将介绍 采样和重构的原理和方法。
பைடு நூலகம்
系统的频率响应和频率特性
系统的频率响应和频率特性描述了系统对不同频率的信号的响应情况。本节 将介绍频率响应和频率特性的概念，以及它们在信号处理中的应用。
时域信号与频域信号
在信号处理中，时域信号和频域信号是两种常见的表示方式。本节将解释时 域和频域的概念，以及如何在两个域中相互转换。
连续信号与离散信号
信号可以是连续的，也可以是离散的。本节将讨论连续信号和离散信号的区别，以及在信号处理中如何 处理这两种类型的信号。
线性时不变系统
线性时不变系统是信号处理中常用的模型。本节将介绍线性时不变系统的基本概念和特性，以及如何利 用系统的响应来分析信号的处理过程。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Note: To really understand these examples, we need to understand frequency contents of aperiodic signals ⇒ the Fourier Transform
Note for DT:
Passband
Stopband
Highpass Filters
Remember: highest frequency in DT
high frequency
high frequency
Bandpass Filters
Demo: Filtering effects on audio signals
Example #1: Audio System
Adjustable Filter
Equalizer
Speaker
Bass, Mid-range, Treble controls
For audio signals, the amplitude is much more important than the phase.
Signals and Systems
Fall 2003 Lecture #7
25 September 2003
1.
Fourier Series and LTI Systems
2.
Frequency Response and Filtering
3.
Examples and Demos
The Eigenfunction Property of Complex Exponentials
Example #2: Frequency Selective Filters
— Filter out signals outside of the frequency range of interest
Lowpass Filters: Only show amplitude here.
Stopband
CT: CT
"System Function"
DT: DT
"System Function"
Fourier Series: Periodic Signals and LTI Systems
So
or powers of signals get modified through filter/system
Includes both amplitude & phase
Includes both amplitude & phase
The Frequency Response of an LTI System CT Frequency response: DT Frequency response:
Frequency Shaping and Filtering
Rolls off at lower ω as M+N+1 increases
Example #5: Simple DT “Edge” Detector — DT 2-point “differentiator”
Passes high-frequency components
Demo: DT filters, LP, HP, and BP applied to DJ Industrial average
Highpass
CT
DT
Bandpass
CT
lower cut-off upper cut-off
DT
Example #3: DT Averager/Smoother
FIR (Finite Impulse Response) filters
LPF
Example #4: Nonrecursive DT (FIR) filters
Hale Waihona Puke Example #7: A Filter Bank
HPF BPF #1 BPF #M
LPF
Demo: Apply different filters to two-dimensional image signals.
Face of a monkey. Image removed do to copyright considerations
• By choice of H(jω) (or H(ejω)) as a function of ω, we can shape the frequency composition of the output
- Preferential amplification - Selective filtering of some frequencies
Idealized Filters
CT
Stopband
DT
Passband
ωc — cutoff frequency
Stopband
Note: |H| = 1 and ∠H = 0 for the ideal filters in the passbands, no need for the phase plot.
Original sign Filtered sign
Year
Dollars
Example #6: Edge enhancement using DT differentiator
Courtesy of Jason Oppenheim. Used with permission.
Courtesy of Jason Oppenheim. Used with permission.
Note for DT:
Passband
Stopband
Highpass Filters
Remember: highest frequency in DT
high frequency
high frequency
Bandpass Filters
Demo: Filtering effects on audio signals
Example #1: Audio System
Adjustable Filter
Equalizer
Speaker
Bass, Mid-range, Treble controls
For audio signals, the amplitude is much more important than the phase.
Signals and Systems
Fall 2003 Lecture #7
25 September 2003
1.
Fourier Series and LTI Systems
2.
Frequency Response and Filtering
3.
Examples and Demos
The Eigenfunction Property of Complex Exponentials
Example #2: Frequency Selective Filters
— Filter out signals outside of the frequency range of interest
Lowpass Filters: Only show amplitude here.
Stopband
CT: CT
"System Function"
DT: DT
"System Function"
Fourier Series: Periodic Signals and LTI Systems
So
or powers of signals get modified through filter/system
Includes both amplitude & phase
Includes both amplitude & phase
The Frequency Response of an LTI System CT Frequency response: DT Frequency response:
Frequency Shaping and Filtering
Rolls off at lower ω as M+N+1 increases
Example #5: Simple DT “Edge” Detector — DT 2-point “differentiator”
Passes high-frequency components
Demo: DT filters, LP, HP, and BP applied to DJ Industrial average
Highpass
CT
DT
Bandpass
CT
lower cut-off upper cut-off
DT
Example #3: DT Averager/Smoother
FIR (Finite Impulse Response) filters
LPF
Example #4: Nonrecursive DT (FIR) filters
Hale Waihona Puke Example #7: A Filter Bank
HPF BPF #1 BPF #M
LPF
Demo: Apply different filters to two-dimensional image signals.
Face of a monkey. Image removed do to copyright considerations
• By choice of H(jω) (or H(ejω)) as a function of ω, we can shape the frequency composition of the output
- Preferential amplification - Selective filtering of some frequencies
Idealized Filters
CT
Stopband
DT
Passband
ωc — cutoff frequency
Stopband
Note: |H| = 1 and ∠H = 0 for the ideal filters in the passbands, no need for the phase plot.
Original sign Filtered sign
Year
Dollars
Example #6: Edge enhancement using DT differentiator
Courtesy of Jason Oppenheim. Used with permission.
Courtesy of Jason Oppenheim. Used with permission.