2018年MBA管理类联考数学真题及解析
MBA联考数学模拟题2018年(8)_真题(含答案与解析)-交互

MBA联考数学模拟题2018年(8) (总分100, 做题时间90分钟) 单项选择题1.已知数列-1,a1,a2,-4是等差数列,-1,b1,b2,b3,-4成等比数列,则=______.SSS_SINGLE_SELA 1/2B -1/2C 1/2或-1/2D 1/4E 1/3分值: 4答案:A[解析] 由-1,a1,a2,-4成等差数列,则-4(-1)+3·d,得公差d=-1.由-1,b1,b2,b3,-4成等比数列,得-4=(-1)q 4,即公比q 2 =2,b2=(-1)q 2 =-2.因此.选A.2.若等差数列{an }满足5a7-a3-12=0,则______.SSS_SINGLE_SELA 15B 24C 30D 45E 60分值: 4答案:D[解析] 解法1 ,又5a7 -a3-12=0即5(a8-d)-(a8-5d)-12=0,所以a8=3,原式S15=15×3=45.解法2 (特殊数列法)令an =C(常数列),5a7-a3-12=4C-12=0,得到C=3,所以3.已知数列{an }的前n项和Sn=3+2 n,则这个数列是______.SSS_SINGLE_SELA 等差数列B 等比数列C 既非等差数列,又非等比数列D 既是等差数列,又是等比数列E 无法判定分值: 4答案:C[解析] 由已知a1 =S1=3+2=5,当n≥2时,an=Sn-Sn-1=(3+2 n )-(3+2n-1 )=2 n-1,将n=1代入a1 =2 1-1 =1,与a1=S1=5不相等,从而通项公式为这个数列既非等差数列,也非等比数列,选C.4.若方程(a 2 +c 2 )x 2 -2c(a+b)x+b 2 +c 2 =0有两个实根,则______.SSS_SINGLE_SELA a,b,c成等比数列B a,c,b成等比数列C b,a,c成等差数列D a,b,c成等差数列E 以上答案均不正确分值: 4答案:B[解析] 方程有实根Δ≥0,4c 2 (a+b) 2 -4(a 2 +c 2 )(b 2 +c 2)≥0,化简得(ab-c 2 ) 2≤0,得到c 2 =ab,即a,c,b成等比数列.所以选B.此题为真题,但仅从c 2 =ab推不出a,c,b成等比,所以此题不严密.5.三个不相同的非零实数a,b,c成等差数列,又a,c,b恰成等比数列,则==______.SSS_SINGLE_SELA 2B 4C -4D -2E 3分值: 4答案:B[解析] a,b,c成等差数列,则.a,c,b成等比数列,则有ab=c 2由c=2b-a,得(2b-a) 2 =ab,整理可知a 2 -5ab+4b 2 =0或,解得.因a≠b,所以,选B.6.若α 2,1,β 2成等比数列,而成等差数列,则=______.SSS_SINGLE_SELA -1/2或1B -1/3或1C 1/2或1D 1/3或1分值: 4答案:B[解析] 由已知1=α 2β 2且,即αβ=±1.若αβ=1,则有α+β=2,α 2+2αβ+β 2 =4,因此α 2+β 2 =2,.若αβ=-1,则有α+β=-2,α 2+2αβ+β 2 =4.因此α 2+β 2 =6,.选B.7.若在等差数列中前5项和S5 =15,前15项和S15=120,则前10项和S10=______.SSS_SINGLE_SELA 40B 45C 50D 55E 60分值: 4答案:D[解析] 因为S5,S10-S5,S15-S10也成等差数列,即15,S10-15,120-S10成等差数列,所以2(S10-15)=15+(120-S10),解得S10=55.故本题应选D.8.设有两个数列则使前者成为等差数列,后者成为等比数列的实数a的值有______.SSS_SINGLE_SELA 0个B 1个C 2个D 3个分值: 4答案:B[解析] 依题意得,,所以,满足题干条件的实数a只有一个,.故本题应选B.9.若6,a,c成等差数列,且36,a 2,-c 2也成等差数列,则c=______.SSS_SINGLE_SELA -6B 2C 3或-2D -6或2E 以上答案均不正确分值: 4答案:D[解析] 根据已知条件有,即,解得c=-6或c=2.所以本题答案为D.10.7个数排成一排,奇数项成等差数列,偶数项成等比数列,且奇数项的和与偶数项的积的差为42,首项、末项、中间项之和为27,则中间项为______.SSS_SINGLE_SELA -2B -1C 0D 1E 2分值: 4答案:E[解析] 由已知,可设这7个数为a1,a2,a1+d,a2q,a1+2d,a2q2,a1+3d.满足整理得消去a1,d得(a2q) 3 +2(a2q)-12=0,解得a2q=2,选E.11.三个数顺序排成等比数列,其和为114,这三个数依前面的顺序又是某等差数列的第1,4,25项,则此三个数的各位上的数字之和为______.SSS_SINGLE_SELA 24B 33C 24或33D 22或33E 24或35分值: 4答案:C[解析] 设三个数为x,xq,xq 2,由已知x+xq+xq 2 =114.从xq=x+3d,xq 2 =x+24d消去d可得q 2 -8q+7=0,即q=7,q=1,分别代入x+xq+xq 2 =114得x=2,x=38,从而这三个数依次是2,14,98或38,38,38.即此三个是各位上的数字之和为2+1+4+9+8=24或3+8+3+8+3+8=33.选C.12.______.SSS_SINGLE_SELA 85/768B 85/512C 85/384D 255/256E 以上结论都不正确分值: 4答案:C[解析] 故选C.求和问题常转化为等差、等比数列求和.13.______.A.B.C.308D.E.SSS_SIMPLE_SINA B C D E分值: 4答案:E[解析]所以选E.14.设数列{xn }满足logaxn+1=1+logaxn(a>0,a≠1),且x1+x2+…+x100 =100,则x101+x102+…+x200的值等于______.•**•**•**•**E.以上结论都不正确SSS_SIMPLE_SINA B C D E分值: 4答案:D[解析] 由loga xn+1=1+logaxn(a>0,a≠1)得logaxn+1=logaaxn,因此,即数列{xn}是公比为a的等比数列.设x1 +x2+…+x100=b1,x101+x102+…+x200=b2,…,即在数列{xn}中每隔100项求和,按原顺序排列构成新数列{bn },则{bn}为等比数列,公比q=a 100,所以b2 =b1q=100a 100,即x101 +x102+…+x200=100a 100,故本题应选D.15.______.A.B.C.D.E.以上结论都不正确SSS_SIMPLE_SINA B C D E分值: 4答案:B[解析] 注意到从而所以选B.16.______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E分值: 4答案:B[解析]所以选B.17.}是等差数列,数列的前n项和为______.若{anA.B.C.D.E.以上结果均不正确SSS_SIMPLE_SINA B C D E分值: 4答案:D[解析] 设数列{a}的公差为d,则n故选D.此题是分式求和裂项法的基本原理.18.______.A.nB.n-1C.2nD.E.SSS_SIMPLE_SINA B C D E分值: 4答案:E[解析] 我们用“通项入手法”分析.故选E.19.设{an }是非负等比数列,若a3=1,______.A.255B.C.D.E.SSS_SIMPLE_SINA B C D E分值: 4答案:B[解析] 由a3=1,为首项为公比为2的等比数列,所以20.等比数列{an }中,a3,a8是方程3x 2 +2x-18=0的两个根,则a4·a7=______.SSS_SINGLE_SELA -9B -8C -6D 6E 8分值: 4答案:C[解析] a4·a7=a3·a8=-6,选C.21.若等比数列{an }满足a2a4+2a3a5+a2a8=25,且a1>0,则a3+a5=______.SSS_SINGLE_SELA 8B 5C 2D -2E -5分值: 4答案:B[解析] 解法1 ,即(a3 +a5) 2 =25,又a1>0,所以a3+a5=5.选B.解法2 (特殊数列法)令an =C>0,则a2a4+2a3a5+a2a8=4C 2 =25,所以C=5/2,所以a3 +a5=5.22.在等差数列{an }中,a2=4,a4=8.若则n=______.SSS_SINGLE_SELA 16B 17C 19D 20E 21分值: 4答案:D[解析] 由则an=2+(n-1)2=2n.所以23.设数列{an }满足:a1=1,则a100=______.A.1650 B.1651C.D.3300E.3301SSS_SIMPLE_SINA B C D E分值: 4答案:B[解析] 由题意得相加得:所以24.等差数列{an }的前n项和为Sn,已知S3=3,S6=24,则此等差数列的公差d等于______.A.3B.2C.1D.E.SSS_SIMPLE_SINA B C D E分值: 4答案:B[解析] 解法1 根据等差数列求和公式解得d=2.解法2 由解法3 根据经验公式Sn ,S2n-Sn,S3n-S2n也成等差数列,且公差为n 2d,即S3,S6-S3,S9-S6成等差数列,且公差为9d,所以9d=(S6-S3 )-S3=18,即d=2.25.已知数列{an }满足n=1,2,3,…,且a2>a1,那么a1的取值范围是______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E分值: 4答案:E[解析] 由于a2>a1,代入得,整理得,即-1<a1<.此题典型错误为由1。
2018管理类联考数学真题-张全军

2018届(2017年12月)管理类联考数学真题张全军整理一、问题求解:1.学科竞赛设一等奖、二等奖和三等奖. 比例为1:3:8,获奖率为30%,已知10人获一等奖,则参加竞赛的人数为( ).(A)300 (B)400 (C)500 (D)550 (E)6002.为了解某公司员工的年龄结构,按男女的比例进行随机检查,结果如下:)岁.(A)32, 30 (B)32, 29.5 (C)32, 27 (D)30, 27 (E)29.5, 273.某单位采取分段收费的方式收取网络流量(单位:GB)费用;每月流量20(含)以内免费;流量20-30(含)的每GB收费1元,流量30到40(含)的每GB收费3元,流量40以上的每GB 收费5元. 小王这个月用了45GB的流量,则他应该交费( )元.(A)45 (B)65 (C)75 (D)85 (E)1354.如图,圆O是三角形ABC的内切圆,若三角形ABC的面积与周长的大小之比为1:2,则圆O的面积为( ).(A)π(B)2π(C)3π(D)4π(E)5π5.设实数,a b 满足||2a b −=,33||26a b −=,则22a b +=( ).(A)30(B)22(C)15(D)13(E)106.有96位顾客至少购买了甲、乙、丙三种商品中的一种,经调查:同时购买甲、乙两种商品的有8位,同时购买甲、丙两种商品的有12位,同时购买乙、丙两种商品的有6位,三种同时购买有2位,则仅购买一种商品的顾客有( )位.(A)70(B)72(C)74(D)76(E)827.如图,四边形1A 1B 1C 1D 是平行四边形,2A ,2B ,2C ,2D 分别是1A 1B 1C 1D 四边的中点,3A ,3B ,3C ,3D 分别是2A 2B 2C 2D 四边的中点,依次下去,得到四边形序列m A m B m C mD (m =1,2,3…),设m A m B m C m D 的面积为m S 且1S =12,则1S +2S +3S +…= ( ).(A)16(B)20(C)24(D)28(E)308.将6张不同的卡片2张一组分别装入甲、乙、丙3个袋子中,若指定的两张卡片要在同一组,则不同的袋法有( )种.(A)12(B)18(C)24(D)30(E)369.甲、乙两人进行围棋比赛,约定先胜2盘者赢得比赛;已知每盘棋甲获胜的概率是0.6,乙获胜的概率是0.4,若乙在第一盘获胜,则甲赢得比赛的概率为( ).(A)0.144(B)0.288(C)0.36(D)0.4(E)0.610.已知圆C:2x +2()y a −=b ,若圆C 在点(1,2)处的切线与y 轴的交点为(0,3),则ab =( ).(A)-2(B)-1(C)0(D)1(E)211.羽毛球队有4名男运动和3名女运动员,从中选出两对参加混双比赛,则不同的选派方式有( )种.(A)9(B)18(C)24(D)36(E)7212.从标号为1到10的10张卡片中随机抽取2张,它们的标号之和能被5整除的概率为( ).(A)15(B)19(C)29(D)215(E)74513.某单位为检查3个部门的工作,由这3个都门的主任和外聘的3名人员组成检查组,2人一组检查工作,每组有1名外聘成员. 规定本部门主任不能检查本部门,则不同的安排方式有 ( )种.(A)6 (B)8(C)12(D)18(E)3614.如图,圆柱体的底面半径为2,高为3,垂直于底面的平面截圆柱体所得截面为矩形ABCD ,若弦AB 所对的圆心角是π3,则截掉部分(较小部分)的体积为( ).(A)3π−(B)26π−(C)2π−(D)2π− (E)π15.函数{}8,max )(22+−=x x x f 的最小值为( ).(A)8 (B)7(C)6(D)5(E)4二、条件充分性判断:16.设为x ,y 实数,则2x y +≤.(1)222x y +≤. (2)1xy ≤.17.设{}n a 为等差数列,则能确定129a a a +++的值.(1)已知1a 的值. (2)已知5a 的值.18.设m ,n 是正整数,则能确定m n +的值.(1)131m n +=. (2)121m n +=.19.甲、乙、丙三人的年收入成等比数列,则能确定乙的年收入的最大值.(1)已知甲、丙两人的年收入之和.(2)已知甲、丙两人的年收入之积.20.如图,在矩形ABCD 中,AE FC =,则三角形AED 与四边形BCFE 能拼接成一个直角三角形.(1)2EB FC =.(2)ED EF =.21.甲购买了若干件A 玩具,乙购买了若干件B 玩具送给幼儿园,甲比乙少花了100元,则能确定甲购买的玩具件数.(1)甲与乙共购买了50件玩具.(2)A 玩具的价格是B 玩具的2倍.22.已知点(,0)1,3(2,1)P m A B ,(),,点(,)x y 在三角形PAB 上,则x y -的最小值与最大值分别为-2和1.(1) 1.m ≤(2) 2.m ≥−23.如果甲公司的年终奖总额增加25%,乙公司的年终奖总额减少10%,两者相等,则能确定两公司的员工人数之比.(1)甲公司的人均年终奖与乙公司的相同.(2)两公司的员工人数之比与两公司的年终奖总额之比相等.24.,a b 为实数,则222x y y +=圆与直线x ay b +=不相交.(1)||a b −>(2)||a b +>25.设函数2()f x x ax =+,则()f x 的最小值与(())f f x 的最小值相等.(1)2a ≥.(2)0a ≤.。
MBA联考数学模拟题2018年(50)_真题(含答案与解析)-交互

MBA联考数学模拟题2018年(50)(总分100, 做题时间90分钟)单项选择题1.如图,小圆圈表示网络的节点,节点之间的连线表示它们有网线相连,连线标注的数字表示该段网线单位时间内可以通过的最大信息量。
现从节点B向节点A传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为______SSS_SINGLE_SELA 28B 23C 20D 19E 93分值: 4答案:D[解析] 本题的关键是要理解信息传递量在信号线上如何传递,很多同学容易错选E。
依题意可知,首先找出B到A的路线,共计4条,分别是:BFGA,信息最大通过量为6;BCDA,信息最大通过量为3;BEDA,信息最大通过量为4;BHGA,信息最大通过量为6。
故单位时间内传递的信息最大通过量为3+4+6+6=19。
2.如图,小黑点表示网络的节点,节点之间的连线表示它们有网络相连,连线上标注的数字表示该段网线单位时间内可以通过的最大信息量。
现在从节点A向节点B传递信息,信息可分开沿不同的路线同时传递,则单位时间内传递的最大信息量为______SSS_SINGLE_SELA 9B 21C 13D 8E 18分值: 2.5答案:D[解析] 按照题目要求,信号从A传递到B,可以分成这样几种情况,由A到D 再到B,或由A到C再到B:由A到D再到B最大信息量为5;由A到C再到B 最大信息量为3。
根据分类计数原理知共有3+5=8。
从4名男生和3名女生中选出3人,分别从事3项不同的工作。
若这3人中至少有1名女生,则选派方案共有______种SSS_SINGLE_SELA 31B 186C 124D 81E 168分值: 2.5答案:B[解析] 方法1:正面处理法,“至少有1名女生”,即选派的女生可以是1名、可以是2名、也可以是3名。
由分类计数原理得,选派方案共有(种)。
方法2:反面处理法,“至少有1名女生”,的反面是“一个女生也没有”,由此,选派方案共有(种)。
MBA联考数学模拟题2018年(44)_真题(含答案与解析)-交互

MBA联考数学模拟题2018年(44)(总分100, 做题时间90分钟)单项选择题1.已知|a|=5,|b|=7,ab<0,则|a-b|=______.SSS_SINGLE_SELA 2B -2C 12D -12该题您未回答:х该问题分值: 4答案:C[解析] 由题意a=±5,b=±7,又由于ab<0,故a=5,b=-7或a=-5,b=7.若a=5,b=-7,则|a-b|=|5+7|=12;若a=-5,b=7,则|a-b|=|-5-7|=12,所以选C.去绝对值要讨论.2.若则|1-2x|+|1-3x|+…+|1-10x|=______.SSS_SINGLE_SELA 2B 3C 4D 5E 6该题您未回答:х该问题分值: 4答案:B[解析] 若,可得8x>1,7x<1.则原式=1-2x+1-3x+1-4x+…+1-7x+8x-1+9x-1+10x-1=6-3=3,选B.零点分段去绝对值.3.已知t 2 -3t-18≤0,则|t+4|+|t-6|=______.SSS_SINGLE_SELA 2t-2B 10C 3D 2t+2该题您未回答:х该问题分值: 4答案:B[解析] t 2 -3t-18≤0,则有-3≤t≤6成立,因此|t+4|+|t-6|=t+4+6-t=10,选B.零点分段去绝对值.4.已知|2x+1|+|2x-5|=定值,则x的取值范围为______.A.B.-1≤x≤1C.D.E.以上均不正确SSS_SIMPLE_SINA B C D E该题您未回答:х该问题分值: 4答案:D[解析] |2x+1|+|2x-5|=定值,则需两个绝对值内异号,即(2x+1)(2x-5)≤0,从而.所以选D.已知条件对零点分段有要求.5.y=2x+|4-5x|+|1-3x|+4恒为常数,则x的取值范围为______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E该题您未回答:х该问题分值: 4答案:A[解析] 若y=2x+|4-5x|+|1-3x|+4恒为定值,则需成立,因此所以选A.已知条件对零点分段有要求.6.若0<a<1,-2<b<-1,则的值为______.SSS_SINGLE_SELA 0B -1C -2D -3E 2该题您未回答:х该问题分值: 4答案:D[解析] 因为0<a<1,-2<b<-1,所以a-1<0,b+2>0,a+b<0.从而故本题应选D.去绝对值要根据正负号讨论,要利用不等式性质得到a+b<0.7.实数a,b,c在数轴上的位置如图所示,图中O为原点,则代数式|a+b|-|b-a|+|a-c|+c=______.SSS_SINGLE_SELA a-2bB -a-2cC 3aD -3a+2cE 2b+2c该题您未回答:х该问题分值: 4答案:D[解析] 由图知c>0,b<a<0,因此a+b<0,b-a<0,a-c<0,由绝对值定义,|a+b|-|b-a|+|a-c|+c=-a-b+b-a+c-a+c=-3a+2c,答案是D.去掉绝对值,只要比较绝对值内式子的符号.8.已知|x-y+1|+(2x-y) 2 =0,则logx=______.ySSS_SINGLE_SELA 0B 1C -1D 2E -2该题您未回答:х该问题分值: 4答案:A[解析] 由绝对值性质|x-y+1|≥0,又由于(2x-y) 2≥0,从而由已知,这两式都必须等于零,即得x=1,y=2.因此logy x=log21=0.答案是A.利用绝对值和平方的非负性.9.若则a+b+c的值是______.SSS_SINGLE_SELA 0B 280C 100D -100E 无法确定该题您未回答:х该问题分值: 4答案:C[解析] 由题意可得所以答案为C.非负项之和为零,则每一项都为零.10.已知x∈[2,5],|a|=5-x,|b|=x-2,则|b-a|的取值范围是______.SSS_SINGLE_SELA [-3,5]B [0,6]C [1,3]D [3,5]E [0,3]该题您未回答:х该问题分值: 4答案:E[解析] 因为x∈[2,5],所以|b-a|≤|b|+|a|=5-x+x-2=3.当b=a时,即5-x=x-2,时,|b-a|=0.所以0≤|b-a|≤3.故本题应选E.下面解法有问题吗?|a|=5-x∈[0,3],-3≤a≤3,|b|=x-2∈[0,3],-3≤b≤3,所以|b-a|的取值范围是[0,6].11.设a,b,c为整数,且|a-b| 20 +|c-a| 41 =1,则|a-b|+|a-c|+|b-c|=______.SSS_SINGLE_SELA 2B 3C 4D -3E -2该题您未回答:х该问题分值: 4答案:A[解析] a,b,c为整数,|a-b|,|c-a|均非负,又|a-b| 20 +|c-a| 41 =1,则|a-b|和|c-a|一个为0,一个为1.不妨令|a-b|=0,|c-a|=1,则将a=b代入所求表达式得:|a-b|+|a-c|+|b-c|=2|a-c|=2,选A.本题可以直接用特值代入法,取a=c=1,b=0,则|a-b|+|a-c|+|b-c|=|1-0|+|1-1|+|0-1|=2.12.满足关系式的x是______.SSS_SINGLE_SELA 0B 2C 0或2D 0或-2E 2或-2该题您未回答:х该问题分值: 4答案:A[解析] 由题意,所以即解得x=0.答案是A.要注意增根.13.已知a是质数,x,y均为整数,则方程的解的个数是______个.SSS_SINGLE_SELA 1B 2C 3D 4E 5该题您未回答:х该问题分值: 4答案:E[解析] x+y与x-y同奇偶,因此a为偶数,又a为质数,所以a=2.由得共五组解,所以选E.此题有一定的难度,综合利用了奇偶性、质数等性质.14.若ab<|ab|,则一定有______.SSS_SINGLE_SELA a<0,b<0B a>0,b<0C a<0,b>cD ab<0E ab≥0该题您未回答:х该问题分值: 4答案:D[解析] 因为ab<|ab|,则a,b中任何一个都不等于零.因此,当ab>0时,ab=|ab|,因此只能一正一负,即ab<0.答案是D.用选项排除法也可.15.设y=|x-a|+|x-20|+|x-a-20|,其中0<a<20,则对于满足a≤x≤20的x值,y的最小值是______.SSS_SINGLE_SELA 10B 15C 20D 25E 30该题您未回答:х该问题分值: 4答案:C[解析] 由已知x-a≥0,x-20≤0,x-a-20≤0,因此y=x-a+20-x+a+20-x=40-x.当x=20时,y取最小值40-20=20,选C.根据已知条件去掉绝对值.16.不等式|x 2 -2x|<3x-6的解集是______.SSS_SINGLE_SELA (-∞,-3)∪(3,+∞)B (-3,2)C (-∞,2)∪(3,+∞)D (2,3)E (3,+∞)该题您未回答:х该问题分值: 4答案:D[解析] 由题意得所以2<x<3.故本题应选D.绝对值零点分段求不等式.17.已知f(x)=|x-1|-2|x|+|x+2|,且-2≤x≤1,则f(x)的最大值与最小值的和为______.SSS_SINGLE_SELA 0B 1C 2D 3E -2该题您未回答:х该问题分值: 4答案:C[解析] 解法1 f(x)=|x-1|-2|x|+|x+2|= f(x)如图所示.即f(x)在-2≤x≤1区间,最大值f(0)=3,最小值f(-2)=-1,即3+(-1)=2.所以选C.解法2 当-2≤x≤1时,|x-1|+|x+2|=3,所以f(x)=|x-1|+|x+2|-2|x|=3-2|x|,0≤|x|≤2,即f(x)在-2≤x≤1区间,最大值f(0)=3,最小值f(-2)=-1,所以3+(-1)=2.18.无论x,y取何值,x 2 +y 2 -2x+12y+40的值都是______.SSS_SINGLE_SELA 正数B 负数C .零D 非负数E 非正数该题您未回答:х该问题分值: 4答案:A[解析] 原式=x 2 -2x+1+y 2 +12y+36+3=(x-1) 2 +(y+6) 2 +3.从而无论x,y 取何值,都有(x-1) 2 +(y+6) 2 +3>0,答案是A.常用配方判断符号,即a 2 +b 2≥0,当且仅当a=0且b=0时等号成立.19.若x 2 +xy+y=14,y 2 +xy+x=28,则x+y的值等于______.SSS_SINGLE_SELA 6C 6或-7D -6或7E 以上结论均不正确该题您未回答:х该问题分值: 4答案:C[解析] 已知的两个等式相加得x 2 +2xy+y 2 +x+y=42,即(x+y) 2 +(x+y)-42=0.因而(x+y-6)(x+y+7)=0,所以x+y-6=0或x+y+7=0,即有x+y=6或-7.20.设y=x 4 -4x 3 +8x 2 -8x+5,式中x为任意实数,则y的取值范围是______.SSS_SINGLE_SELA 一切实数B y>0C y≥5D y≥2E 不能确定该题您未回答:х该问题分值: 4答案:D[解析] y=x 4 -4x 3 +8x 2 -8x+5=(x 2 -2x) 2 +4(x 2 -2x)+5=[(x 2 -2x)+2] 2 +1=[(x-1) 2 +1] 2+1≥2,故本题应选D.21.若(z-x) 2 -4(z-y)(y-x)=0,那么下列正确的是______.SSS_SINGLE_SELA x=y=zB z=x+yC y是x,z的几何平均D y是x,z的算术平均值E 以上结果均不正确该题您未回答:х该问题分值: 4答案:D[解析] (z-x) 2 -4(z-y)(y-x)=z 2 -2xz+x 2 -4yz+4y 2 +4xz-4xy=x 2 +(-2y) 2 +z 2 -4xy-4yz+2xz=(x-2y+z) 2,即x-2y+z=0,所以,即y是x,z的算术平均值.故本题正确选项为D.22.已知 a 2 +b 2 +c 2 -ab-bc-ac=______.SSS_SINGLE_SELA 4C 2D 1E 0该题您未回答:х该问题分值: 4答案:B[解析] 由可得a-b=1,b-c=-2,a-c=-1,23.设实数x,y适合等式则x+y的最大值为______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E该题您未回答:х该问题分值: 3答案:C[解析] 因为所以从而,选C.利用非负性求最值.24.若x 2 -3x+Bxy+y 2 -3y-40=(x+y+m)(x+y+n),则m,n的值分别为______.SSS_SINGLE_SELA m=8,n=5B m=8,n=-5C m=-8,n=5D m=-8,n=-5E 以上结论均不正确该题您未回答:х该问题分值: 3答案:E[解析] (x+y+m)(x+y+n)=x 2 +(m+n)x+2xy+y 2 +(m+n)y+mn,从而有成立,所以m=-8,n=5或m=5,n=-8.答案是E.25.a,b,c是不全相等的任意实数,若x=a 2 -bc,y=b 2 =ac,z=c 2 -ab,则x,y,z______.SSS_SINGLE_SELA 都大于0B 至少有一个大于0C 至少有一个小于0D 都不小于0该题您未回答:х该问题分值: 3答案:B[解析] 由于a,b,c不全相等,又2(x+y+z)=2a 2 +2b 2 +2c 2 -2ab-2bc-2ac=(a-b) 2 +(b-c) 2 +(c-a) 2>0 所以,x+y+z>0.即x,y,z中至少有一个大于零.选B.配方+非负性.26.若(1-2x+y)是4xy-4x 2 -y 2 -m的一个因式,则m的值等于______.SSS_SINGLE_SELA 4B 1C -1D 2E 0该题您未回答:х该问题分值: 3答案:C[解析] 设4xy-4x 2 -y 2 -m=(1-2x+y)M,M是4xy-4x 2 -y 2 -m的另外一个因式,取x=1,y=1,这时4-4-1-m=0,得m=-1,故本题应选C.1。
2018年管理类联考真题及答案解析

2018届管理类专业硕士研究生全国联考真题一、问题求解:第1—15小题,每小题3分,共45分. 下列每题给出的A、B、C、D、E五个选项中, 只有一项是符合试题要求的. 请在答题卡上将所选项的字母涂黑.1、学科竞赛设一等奖、二等奖和三等奖,比例为1:3:8,获奖率为30%、已知10人获得一等奖,则参加竞赛的人数为(A)300 (B)400(C)500 (D)550(E)600【答案】B2、为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是(单位:岁)(A)32,30 (B)32, 29.5(C)32, 27 (D)30, 27(E)29.5, 27【答案】A3、某单位采取分段收费的方式收取网络流量(单位:GB)费用:每月流量20(含)以内免费,流量20到30(含)的每GB收费1元,流量30到40(含)的每GB收费3元,流量40以上的每GB收费5元,小王这个月用了45GB的流量,则他应该交费(A)45元(B)65元(C)75元(D)85元(E)135元【答案】B4、如图,圆O是三角形ABC的内切圆,若三角形ABC的面积与周长的大小之比为1:2,则圆O的面积为【答案】A(A)π(B)2π(C)3π(D)4π(E)5π5、设实数,满足|-|=2,|-|=26, 则+=(A)30 (B)22(C)15 (D)13(E)10【答案】E6、甲、乙两人进行围棋比赛,约定先胜2盘者赢得比赛。
已知每盘棋甲获胜的概率是0.6,乙获胜的概率是0.4,若乙在第一盘获胜,则甲赢得比赛的概率为(A)0.144 (B)0.288(C)0.36 (D)0.4(E)0.6【答案】C7、如图,四边形平行四边形, , , ,分别是四边的中点,, , ,分别是四边的中点,依次下去。
得到四边形序列(m=1,2,3…),设的面积为且 =12,则 + + +…=(A)16 (B)20 (C)24 (D)28 (E)30【答案】C8、已知圆 + =b,若圆C在点(1.2)处的切线与y轴的交点为(0.3),则ab=(A)1-2 (B)-1 (C)0 (D)1 (E)2【答案】E9、有96位顾客至少购买了甲、乙、丙三种商品中的一种,经调查:同时购买甲、乙两种商品的有8位,同时购买甲、丙两种商品的有12位,同时购买乙、丙两种商品的有6位,三种同时购买有2位,则仅购买一种商品的顾客有(A)70位(B)72位(C)74位(D)76位(E)82位【答案】C10、将6张不同的卡片2张一组分别装入甲、乙、丙3个袋子中,若指定的两张卡片要在同一组,则不同的袋法有(A)12种(B)18种(C)24种(D)30种(E)36种【答案】B11、某单位为检查3个部门的工作。
MBA联考数学模拟题2018年(43)_真题(含答案与解析)-交互

MBA联考数学模拟题2018年(43)(总分100, 做题时间90分钟)单项选择题1.方程x 2 -3|x|-2=0的最小根的倒数是______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E分值: 4.5答案:C[解析] 原方程可化为|x| 2 -3|x|-2=0,解得;因此,,即较小的根为,其倒数为故本题正确选项为C.利用绝对值性质x 2 =|x| 2转化为关于|x|的一元二次方程,注意中间变量|x|≥0.2.已知方程x 2 -6x+8=0有两个相异的实根,下列方程中仅有一根在已知两根之间的方程是______.A.x 2 +6x+9=0B.C.x 2 -4x+2=0D.x 2 -5x+7=0E.x 2 -6x+5=0SSS_SIMPLE_SINA B C D E分值: 4.5答案:C[解析] 方程x 2 -6x+8=0的两根为x1 =2,x2=4,而方程A两根都为-3,方程B的两根都为,方程C的两根为,方程D无实根,方程E的两根为1,5.因此只有方程C仅有一根在2与4之间.选C.3.已知关于z的方程x 2 -6x+(a-2)|x-3|+9-2a=0有两个不同的实数根,则实数a 的取值范围是______.SSS_SINGLE_SELA a=2或a>0B a<0C a>0或a=-2D a=-2分值: 3答案:C[解析] 原方程可化为(x-3) 2 +(a-2)|x-3|-2a=0,即|x-3| 2 +(a-2)|x-3|-2a=0.因此(|x-3|-2)(|x-3|+a)=0,则|x-3|-a=0,即|x-3|=2,或|x-3|=-a,所以当a>0或a=-2时原方程有两个不同的实数根,选C.4.已知关于x的一元二次方程x 2 +2(m+1)x+(3m 2 +4mn+4n 2 +2)=0有实根,则m,n的值为______.A.B.C.D.E.以上答案均不正确SSS_SIMPLE_SINA B C D E分值: 4.5答案:D[解析] 方程有实根,则Δ≥0,即4(m+1) 2 -4(3m 2 +4mn+4n 2+2)≥0成立,整理可得(2n+m) 2 +(m-1) 2≤0,因此m=1,,答案是D.完全平方项之和小于等于零,则每一项都为零.5.若一元二次方程(a-2)x 2 -2ax+a+1=0有两个实根,则a的取值范围是______.SSS_SINGLE_SELA a<-2或a>2B -2<a<2C a>-2且a≠2D a≥-2且a≠2E a∈R且a≠2分值: 4.5答案:D[解析] 一元二次方程(a-2)x 2 -2ax+a+1=0有两个实根Δ≥0且a-2≠0,即(-2a) 2 -4(a-2)(a+1)≥0且a-2≠0,得a≥-2且a≠2,选D.6.关于x的两个方程x 2 +4mx+4m 2 +2m+3=0,x 2 +(2m+1)x+m 2 =0中至少有一个方程有实根,则m的取值范围是______.A.B.C.D.E.以上答案均不正确SSS_SIMPLE_SINA B C D E分值: 4.5答案:A[解析] 设两个方程的根判别式分别为Δ1和Δ2,如果两个方程均无实数根,则因此,当时,两个方程均无实根.故至少一个方程有实数根时,m的取值范围是m≤ .选A.至少一个方程有实根,可能其中一个方程有实根,也可能两个方程有实根,讨论起来比较麻烦.我们从至少一个方程有实根的反面去讨论,即每一个方程均无实根,找出m的范围,在这个范围之外的m就能保证至少一个方程有实根.7.解方程,则______.SSS_SINGLE_SELA 方程有两个正实根B 方程只有一个正实根C 方程只有一个负实根D 方程只有一正一负两个实根E 方程有两个负实根分值: 4.5答案:C[解析] 原方程可化为.令2 x =t,t>0,则原方程化为,即t 2 +2t-2=0,所以,即.因为,所以,选C.8.若x 2 +bx+1=0的两个根为x1和x2,且则b的值是______.SSS_SINGLE_SELA -10B -5C 3D 5E 10分值: 4.5答案:B[解析] 已知,由韦达定理:x1 x2=1,x1+x2=-b,得b=-5.选B.9.关于x的方程x 2 +mx+3m-9=0的两根之比为2:3,则实数m的值等于______.A.m=5B.C.D.E.m=-5SSS_SIMPLE_SINA B C D E分值: 4.5答案:B[解析] 设方程x 2 +mn+3m-9=0的两根为x1,,由韦达定理得于是2m 2 -25m+75=0,解之得m=5或故本题正确选项为B.10.关于x的一元二次方程x 2 -x+a(1-a)=0有两个不相等的正根,则实数a的取值范围是______.A.0<a<1B.C.D.E.SSS_SIMPLE_SINA B C D E分值: 4.5答案:E[解析] 设原方程的两实根为x1,x2,则x1≠x2,x1>0,x2>0的等价条件组为解之得0<a<1且选E.11.已知x1,x2是一元二次方程2x 2 -2x+m+1=0的两个实数根,如果x1,x2满足不等式,且m为整数,则m的取值为______.SSS_SINGLE_SELA 2B 2或1C -2D -1E -2或-1分值: 4.5答案:E[解析] 由于Δ=(-2) 2 -4×2×(m+1)≥0,即.由.又由于x1 +x2=1,,所以m>-3,因此.由于m为整数,从而m=-2或m=-1,选E.综合利用Δ与韦达定理.12.若方程x 2 +px+37=0恰好有两个正整数解,则的值是______.SSS_SINGLE_SELA -2B -1C 0D 1E 2分值: 4.5答案:A[解析] 根据韦达定理,又x1,x2为正整数解,且37是一个质数,则x1=1,x2=37,p=-38.正确的选择是A.13.设α,β为关于x的方程x 2 -2ax+a+6=0的两个实根,则(α-1) 2+(β-1) 2的最小值为______.A.B.18C.8D.9E.-10SSS_SIMPLE_SINA B C D E分值: 4.5答案:C[解析] 由韦达定理得α+β=2a,αβ=a+6方程x 2 -2ax+a+6=0有两个实根,即Δ=4a 2 -4(a+6)≥ a≤-2或a≥3.显然当a=3时,函数f(a)=4a 2 -6a-10取最小值f(3)=4×9-6×3-10=8,选C.本题综合考查了方程判别式、韦达定理、二次函数求最值(顶点取不到).14.若两个方程x 2 +ax+b=0和x 2 +bx+a=0只有一个公共根,则______.SSS_SINGLE_SELA a=bB a+b=-1且a≠bC a+b=1D a+b=0E a+b=-1分值: 4.5答案:B[解析] 设方程x 2 +ax+b=0和x 2 +bx+a=0的公共根为x,则两式相减消去平方项得(a-b)x+b-a=0,由于两个方程只有一个公共根,所以a≠b,且公共根,把x=1代入.得1+a+b=0,即a+b=-1,选B.15.设m是不为零的整数,关于x的二次方程mx 2 -(m-1)x+1=0有有理根,则m=______.SSS_SINGLE_SELA 6B 4C 2D 1E -1分值: 4.5答案:A[解析] 一个整系数的一元二次方程有有理根,那么它的判别式一定是完全平方数,令Δ=(m-1) 2 -4m=n 2,其中n是非负整数,于是m 2 -6m+1=n 2,所以(m-3) 2 -n 2 =8,即(m-3+n)(m-3-n)=8.由于m-3+n≥m-3-n,并且(m-3+n)+(m-3-n)=2(m-3)是偶数,所以m-3+n与m-3-n同奇偶,所以所以,因此m=6,故本题正确选项为A.本题也可用选项代入法,因为Δ=(m-1) 2 -4m,用m=6代入得到Δ=(6-1) 2 -4×6=1 2为完全平方式,其他都不成立.16.关于x的一元二次方程x 2 +(3a-1)x+a+8=0有两个不相等的实数根x1,x2,且x1<1,x2>1,则实数a的取值范围是______.SSS_SINGLE_SELA a>-2B a<-2C 0<a<1D a<-1<0E 以上结论均不正确分值: 4.5答案:B[解析] 设f(x)=x 2 +(3a-1)x+a+8,从而关于x的一元二次方程x 2 +(3a-1)x+a+8=0的两,个不相等的实数根在x=1两侧的等价条件为f(1)<0,即1 2 +(3a-1)×1+a+8<0,解得a<-2,选B.17.要使方程3x 2 +(m-5)x+(m 2 -m-2)=0的两根分别满足0<x1<1和1<x2<2,则实数m的取值范围是______.A.-2<m<-1B.-4<m<-1C.-4<m<-2D.E.-3<m<1SSS_SIMPLE_SINA B C D E分值: 4.5答案:A[解析] 设f(x)=3x 2 +(m-5)x+(m 2 -m-2),两根分别满足0<x1<1和1<x2<2,则应该满足所以-2<m<-1,选A.18.设方程3x 2 -8x+a=0的两个实根为x1,x2,若的算术平均值为2,则a的值等于______.A.-2B.-1C.1D.E.2SSS_SIMPLE_SINA B C D E分值: 4.5答案:E[解析] 由及韦达定理,得所以a=2,选E.19.已知方程x 3 +2x 2 -5x-6=0的根为x1 =-1,x2,x3,则______.A.B.C.D.SSS_SIMPLE_SINA B C D分值: 3.5答案:A[解析] 因为x 3 +2x 2 -5x-6=0,所以(x+1)(x 2 +x-6)=0,因为x1=-1,所以x2,x3是一元二次方程x 2 +x-6=0的两个根.由x2 +x3=-1,x2x3=-6,得故本题应选A.20.设方程3x 2 +mx+5=0的两个根x1,x2满足则m=______.SSS_SINGLE_SELA 5B -5C 3D -3分值: 3.5答案:B[解析] 因为x1,x2是方程3x 2 +mx+5=0的两个根,由韦达定理得因此即解之得m=-5,选B.21.若三次方程ax 3 +bx 2 +cx+d=0的三个不同实根x1,x2,x3满足:x1+x2 +x3=0,x1x2x3=0,则下列关系式中恒成立的是______.SSS_SINGLE_SELA ac=0B ac<0C ac>0D a+c<0E a+c>0分值: 4.5答案:B[解析] 解法1 特殊值法:设三次方程为x(x+1)(x-1)=0,即x 3 -x=0,取a=1,c=1,则ac<0.只有B正确.解法2 由三个不同实根x1,x2,x3满足x1x2x3=0,则不妨设x1=0,则d=0,即原方程为ax 3 +bx 2 +cx=x(ax 2 +bx+c)=0.进一步,x2,x3是方程ax 2 +bxd+c=0的两个根,由x2 +x3=0,说明x2,x3两根异号,所以.解法3 根据一元三次方程ax 3 +bx 2 +cx+d=0的韦达定理,即ax 3+cx=0,得x(ax 2 +c)=0,所以x=0.三个不同实根x1,x2,x3,所以ac<0.解法3有超纲嫌疑,你会自己推导出一元三次方程的韦达定理吗?(利用多项式对应相等).22.已知二次方程x 2 -2ax+10x+2a 2 -4a-2=0有实根,求其两根之积的最小值为______.SSS_SINGLE_SELA -4B -3C -2D -1E -6分值: 4.5答案:A[解析] 两根之积x1·x2=2a 2 -4a-2=2(a-1) 2 -4,当a=1时达到最小值,经验证a=1时方程有实根,满足题干,选A.若题目改为求两根之积的最大值,则由判别式Δ=(-2a+10) 2 -4(2a 2 -4a-2)≥0 -9≤a≤3,当a=-9时,离对称轴a=1比较远,所以有最大值x1·x2=2(-9-1) 2 -4=196.23.则x=______.SSS_SINGLE_SELA -2B -1C 0D 1E 2分值: 4.5答案:B[解析] 即x=-1.1。
2018年管理类联考真题与答案解析

26. 人民既是历史的创造者,也是历史的见证者;既是历史的“剧中人”
,也是历史的“剧
作者”。离开人民,文艺就会变成无根的浮萍、无病的呻吟、无魂的躯壳。观照人民的生活、
命运、情感,表达人民的心愿、心情、心声,我们的作品才会在人民中传之久远。
根据以上陈述,可以得出以下哪项?
(A)只有不离开人民,文艺才不会变成无根的浮萍、无病的呻吟、无魂的躯壳。
(A ) 0.144 (C) 0.36
( B) 0.288 ( D) 0.4
(E) 0.6
【答案】 C
0.6,
7、如图, 四边形 边的中点, , ,
平行四边形, , 分别是
, , , 分别是
四
四边的中点,依次下去。得到四边形
序列
( m=1,2, 3… ),设
的面积为
且 =12,则
+ + +…=
(A )16 【答案】 C
项符合试题要求得判断 , 在答题卡上将所选项得字母涂黑 .
16、甲乙丙三人的年收入成等比数列,则能确定乙的年收入的最大值
( 1)已知甲、丙两人的年收入之和; 【答案】 D
( 2)已知甲、丙两人的年收入之积。
17、设为 , 实数,则
,
( 1) 【答案】 A
;
( 2)
18、设
为等差数列,则能确定
( 1)已知 【答案】 B
29. 分心驾驶是指驾驶人为满足自己的身体舒适、 心情愉悦等需求而没有将注意力全部集中
于驾驶过程的驾驶行为,常见的分心行为有抽烟、饮水、进食、聊天、刮胡子、使用手机、
照顾小孩等。某专家指出,分心驾驶已成为我国道路交通事故的罪魁祸首。
以下哪项如果为真,最能支持上述专家的观点 ?
MBA联考数学模拟题2018年(2)_真题(含答案与解析)-交互

MBA联考数学模拟题2018年(2)(总分75, 做题时间90分钟)一、问题求解下列每题给出的A、B、C、D、E五个选项中。
只有一项是符合试题要求的.1.已知则______.SSS_SINGLE_SELA n<m<1B m<n<1C 1<m<nD 1<n<mE n<1<m该问题分值: 3答案:C[解析] 如下图,由的图象可知,若则m>1,n>1,且n>m.即1<m<n.故本题应选C2.a,b,c是不全相等的任意实数,若x=a 2 -bc,y=b 2 -ac,z=c 2 -ab,则x,y,z为______.SSS_SINGLE_SELA 都大于0B 至少有一个大于0C 至少有一个小于0D 都不小于0E 都小于0该问题分值: 3答案:B[解析] 对任意实数a,b,c,有a 2 +b 2≥2ab,b 2 +c 2≥2bc,a 2 +c 2≥2ac其中各不等式中的等号当且仅当不等式中两数相等时成立.由题设条件,a,b,c不全相等,所以上面三个不等式中至少有一个成立严格不等式.因此,将三个不等式两边相加,可得a 2 +b 2 +c 2>ab+bc+ac即(a 2 -bc)+(b 2 -ac)+(c 2 -ab)>0由此得到x+y+z>0.故x,y,z三个数中至少有一个大于零.故本题应选B.3.设则f(x)的定义域是______.SSS_SINGLE_SELA -4≤x≤4B -4<x<4C 0≤x≤4D -4≤x≤16E 0<x≤4该问题分值: 3答案:E[解析] 由已知条件,有16-x 2≥0,x>0,16-x>0解得0<x≤4.故本题应选E.4.车间共有40人,某次技术操作考核的平均成绩为80分,其中男工平均成绩为83分,女工平均成绩为78分.该车间有女工______.SSS_SINGLE_SELA 16人B 18人C 20人D 24人E 28人该问题分值: 3答案:D[解析] 设该车间有男工x(人),女工y(人),则解得y=24.故本题应选D.5.商店委托搬运队运送500只瓷花瓶,双方商定每只花瓶运费0.50元,若搬运中打破一只,则不但不计运费,还要从运费中扣除2.00元.已知搬运队共收到240元,则搬运中打破了花瓶______.SSS_SINGLE_SELA 3只B 4只C 5只D 6只E 7只该问题分值: 3答案:B[解析] 设搬运中打破了x只花瓶,由已知条件,得方程0.5(500-x)-2x=240解得x=4.故本题应选B.6.商店某种服装换季降价,原来可买8件的钱现在可买13件,这种服装价格下降的百分比是______.SSS_SINGLE_SELA 36.5%B 37.5%C 38.5%D 40%E 42Z该问题分值: 3答案:C[解析] 设该服装原价每件x元,现价为每件y元,由已知条件,有8x=13y,即.由分比定理,得故本题应选C.7.一项复印工作,如果由复印机A,B单独完成,分别需50分钟,40分钟.现两台机器同时工作了20分钟,B机器损坏需维修,余下的工作由A机器单独完成,则完成这项复印工作共需时间______.SSS_SINGLE_SELA 10分钟B 15分钟C 18分钟D 20分钟E 25分钟该问题分值: 3答案:E[解析] 复印机A,B单独工作时,一分钟可完成全部工作的.根据题意,完成这项工作共需时间故本题应选E.8.若对一切正实数x恒成立,则y的取值范围是______.SSS_SINGLE_SELA 1<y<3B 2<y<4C 1<y<4D 3<y<5E 2<y<5该问题分值: 3答案:A[解析] 因对一切x>0,有可得所以y>0.不等式可化为此不等式对任意x>0成立,于是此不等式对使取得最小值的x成立,由于min所以,当即x=1时,有最小值2.所以,原不等式化为即y 2 -4y+3<0,解得1<y<3.故本题应选A.9.已知a、b、c三数成等差数列,又成等比数列,设a、β是方程ax 2 +bx-c=0的两个根,且α>β,则α 3β-αβ 3 =______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E答案:D[解析] 由题设条件,且b 2 =ac.于是化简得(a-c) 2 =0.所以,a=c,因此,原方程化为x 2 +x-1=0.利用韦达定理,有α+β=-1,αβ=-1,所以故本题应选D.10.如下图,半圆ADB以C为圆心,半径为1,且CD⊥AB,分别延长BD和AD至E 和F,使得圆弧AE和BF分别以B和A为圆心,则图中阴影部分的面积为______.A.B.C.D.E.π-1SSS_SIMPLE_SINA B C D E该问题分值: 3答案:C[解析] 设图中阴影部分面积为S(见题附图),则故本题应选C.11.在数列{an }中,a1=1,a2=2,Sn为前n项的和,Sn-Sn-1+an-2(n≥3),则S7=______.SSS_SINGLE_SELA 8B 10C 12D 14E 16答案:B[解析] 因为Sn =Sn-1+an-2(n≥3).所以Sn -Sn-1=an=an-2.(n≥3)于是,a3 =a1=1,a4=a2=2,a5=a3=1,a6=a4=2,a7=a5=1.即此数列为1,2,1,2,….易得S7=10.故本题应选B.12.已知集合A={0,1,2,3,5}.以集合A中每两个元素的乘积作为集合B的元素,则集合B的子集个数是______.SSS_SINGLE_SELA 98B 102C 116D 120E 128该问题分值: 3答案:E[解析] 由题意,集合B={0,2,3,5,6,10,15},B含有7个元素,其子集合包括空集和全集B,故B的子集数为注意到有可得B的子集个数是1+7+21+35+35+21+7+1=128故本题应选E.13.将3人分配到4间房的每一间中,若每人被分配到这4间房的每一间房中的概率都相同,则第一、二、三号房中各有1人的概率是______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E该问题分值: 3答案:D[解析] 设事件A={第一、二、三号房中各有一人},A包含的基本事件数为,而基本事件总数,即3人随机分到4间房中的分法有4 3种.所以故本题应选D.14.10件产品中有3件是不合格品,今从中任取两件,则两件中至少有一件合格品的概率为______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E该问题分值: 3答案:C[解析] 设事件A={任取两件产品中至少有一件合格品}.则故本题应选C.15.若圆C:(x+1) 2 +(y-1) 2 =1与x轴切于A点、与y轴切于B点.则与此圆相切于劣弧中点M(注:小于半圆的弧称为劣弧)的切线方程是______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E该问题分值: 3答案:A[解析] 如下图,圆C与x轴相切于A点,与y轴相切于B点,则OM的方程必为y=-x.解方程组可得直线OM与圆的交点M过M的圆的切线与OM垂直.斜率k=1,所求切线为即故本题应选A.二、条件充分性判断要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论.A、B、C、D、E五个选项为判断结果,请选择一项符合试题要求的判断.• A.条件(1)充分,但条件(2)不充分.• B.条件(2)充分,但条件(1)不充分.• C.条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.• D.条件(1)充分,条件(2)也充分.• E.条件(1)和(2)单独都不充分,条件(1)和条件(2)联合起来也不充分.SSS_SIMPLE_SIN1.(1)x=4y (2)x+y=1A B C D E该问题分值: 3答案:A[解析] 将题干中原分式化简:不难看出,条件(1)充分,条件(2)不充分.故本题应选A.SSS_SIMPLE_SIN2.m能被6整除.(1)m=n(n+5)-(n-3)(n+2),n是自然数(2)m=n(n-1)(n-2),n是自然数A B C D E该问题分值: 3答案:D[解析] 由条件(1),有m=n 2 +5n-n 2 +n+6=6(n+1)所以m可被6整除.由条件(2),当n=0,1,2,3时,m显然可被6整除.当n>3时,组合数是整数.而可知m可被6整除.故本题应选D.SSS_SIMPLE_SIN3.不等式|x-2|+|4-x|<s无解.(1)s≤2 (2)s>2A B C D E该问题分值: 3答案:A[解析] 由条件(1),s≤2.当x<2时,原不等式化为2-x+4-x<s,得,与x<2矛盾,此时不等式无解;当2≤x≤4时,原不等式化为x-2+4-x<s,得s>2,与条件(1)矛盾,此时不等式无解;当x>4时,原不等式化为x-2+x-4<s,得,与x>4矛盾,此时不等式无解.由此可知条件(1)充分、条件(2)不充分.故本题应选A.SSS_SIMPLE_SIN4.方程4x 2 +(a-2)x+a-5=0有两个不等的负实根.(1)a<6 (2)a>5A B C D E该问题分值: 3答案:C[解析] 据韦达定理,方程4x 2 +(a-2)x+a-5=0有两个不等的实根的条件是:Δ=(a-2) 2 -16(a-5)>0即(a-14)(a-6)>0,即a>14或a<6方程4x 2 +(a-2)x+a-5=0有两个负实根的条件是:a-5>0,a-2>0,得a>5 故5<a<6时,方程4x 2 +(a-2)x+a-5=0有两个不同的负实根.即条件(1)和条件(2)联合成立才充分.故本题应选C.SSS_SIMPLE_SIN5.x=10.(1)(2)3x+2y+z=56A B C D E该问题分值: 3答案:E[解析] 条件(1)、(2)单独均不充允若两个条件合在一起,由条件(1),设则x=4k,y=5k,x=6k.代入条件(2),有12k+10k+6k=56解得k=2.于是x=8,y=10,z=12.可见两条件合在一起仍不充分.故本题应选E.SSS_SIMPLE_SIN6.{an }的前n项和Sn与{bn}的前n项和Tn满足S19:T19=3:2.(1){an }和{bn}是等差数列 (2)a10:b10=3:2A B C D E该问题分值: 3答案:C[解析] 条件(1)、(2)单独都不充分.两个条件合在一起,由条件(1),可得所以,若数列{an },{bn}的公差分别为d1,d2,则故本题应选C.SSS_SIMPLE_SIN7.从含有2件次品,n-2(n>2)件正品的咒件产品中随机抽查2件,其中恰有1件次品的概率为0.6.(1)n-5 (2)n-6A B C D E该问题分值: 3答案:A[解析] 由条件(1),所求概率条件(1)充分.由条件(2),所求概率条件(2)不充分.故本题应选A.SSS_SIMPLE_SIN8.2 x+y +2 a+b =17.(1)a,b,x,y满足(2)a,b,x,y满足A B C D E该问题分值: 3答案:C[解析] 条件(1)、(2)单独均不充分.若条件(1)、(2)合在一起时,有所以,故必有a=0,b=0,于是x-3=0,得x=3,将上述结果代入条件(1)或(2),得.y=1.因此2 x+y +2 a+b =2 4 +2 0 =17.故本题应选C.SSS_SIMPLE_SIN9.a=4.(1)直线ax+3y-5=0过连接A(-1,-2),B(2,4)两点的线段的中点(2)点M(3.6,a)在A(2,-4),B(5,11)两点的连线上A B C D E该问题分值: 3答案:D[解析] 由条件(1),线段AB的中点M的坐标为又M在直线ax+3y-5=0上,所以得a=4,故条件(1)充分.由条件(2),过A,B两点的直线方程为即5x-y-14=0.而M(3.6,a)在直线AB上,有5×3.6-a-14=0,得a=4,故条件(2)充分.故本题应选D.SSS_SIMPLE_SIN10.曲线ax 2 +by 2 =1通过4个定点.(1)a+b=1 (2)a+b=2A B C D E该问题分值: 3答案:D[解析] 由条件(1),a+b=1,所以ax 2 +by 2 =a+b=1,即a(x 2 -1)+b(y 2 -1)=0.对于满足x 2 =1,y 2 =1的点(x,y)都在此曲线上,解得x=±1,y=±1.即曲线通过定点(1,1),(1,-1),(-1,1),(-1,-1).所以条件(1)充分.由条件(2),a+b=2.所以ax 2 +by 2 =1可化为.即对满足的点都在此曲线上,解得即曲线过定点条件(2)也充分.故本题应选D.1。
MBA联考数学模拟题2018年(6)_真题(含答案与解析)-交互

MBA联考数学模拟题2018年(6)(总分100, 做题时间90分钟)单项选择题1.若实数a,b,c满足:a 2 +b 2 +c 2 =9,则代数式(a-b) 2 +(b-c) 2 +(c-a) 2的最大值是______.SSS_SINGLE_SELA 21B 27C 29D 32E 39分值: 3答案:B[解析] (a-b) 2 +(b-c) 2 +(c-a) 2 =2(a 2 +b 2 +c 2 )-2(ab+bc+ac)=3(a 2 +b 2 +c 2 )-(a 2 +b 2 +c 2 +2ab+2bc+2ac)=3(a 2 +b 2 +c 2 )-(a+b+c) 2=27-(a+b+c) 2≤27(当a+b+c=0时取最大值).选B.利用非负性求最值.2.如果x 3 +ax 2 +bx+8有两个因式x+1和x+2,则a+b的值等于______.SSS_SINGLE_SELA 7B 8C 15D 21E 30分值: 3答案:D[解析] 设f(x)=x 3 +ax 2 +bx+8,由于x+1和x+2是f(x)的因式,因此有f(-1)=0,f(-2)=0,即即a+b=7+14=21.3.若x 4 +ax 2 -bx+2能被x 2 +3x+2整除,则a,b的值等于______.SSS_SINGLE_SELA a=6,b=-3B a=-6,b=3C a=2,b=-5D a=-5,b=2E a=-3,b=6分值: 3答案:B[解析] 设f(x)=x 4 +ax 2 -bx+2.由于x 2 +3x+2=(x+2)(x+1),所以x+1和x+2必是f(x)的因式.因此有f(-1)=0,f(-2)=0,即4.已知多项式f(x)除以x+2所得余数为1,除以x+3所得余数为-1,则多项式f(x)除以(x+2)(x+3)所得余式为______.SSS_SINGLE_SELA 2x-5B 2x+5C x-1D x+1E 2x-1分值: 3答案:B[解析] 在多项式除法当中,余式次数必须低于除式次数,由于除式(x+2)(x+3)是二次式,可设r(x)=ax+b,故有f(x)=(x+2)(x+3)q(x)+ax+b,因为f(x)除以x+2所得余数为1,所以f(-2)=1;又因为f(x)除以x+3所得余数为-1,所以f(-3)=-1,即因此,f(x)除以(x+2)(x+3)所得余式为2x+5.故本题应选B.5.多项式x n +a n除以x+a的余式是______.•**•**•**为奇数时,余式为2an;n为偶数时,余式为0•**为奇数时,余式为0;n为偶数时,余式为2anE.以上结论均不正确SSS_SIMPLE_SINA B C D E分值: 4答案:D[解析] 设f(x)=x n +a n,从而f(-a)=(-a) n +a n,显然n为奇数时,f(-a)=(-a) n +a n =0;n为偶数时,f(-a)=(-a) n +a n =2a n.即当n为奇数时,余式为0;n为偶数时,余式为2a n.故本题应选D.6.的值等于______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E分值: 4答案:E[解析] 设2007=a,则原式故本题应选E.先约分再代入.7.若______.A.B.C.D.4E.2SSS_SIMPLE_SINA B C D E分值: 4答案:C[解析] 所以选C.8.已知______.SSS_SINGLE_SELA -3B -2C -1D 0E 1分值: 4答案:C[解析] 由对角相乘化为等式,从而(a+b) 2 =ab,即a 2 +b 2 =-ab,因此所以选C.分式条件等式,转化为等式条件等式,注意向目标(欲求)的式子靠拢.9.若______.SSS_SINGLE_SELA 2B 3C 4D -3E -2分值: 4答案:C[解析] 设所以选C.10.已知a,b,c,d为不等于零的实数,且a≠b,c≠d,ad+bc≠0,设m2= 则有______.A.m1 +m2+m3>m1m2m3B.m1 +m2+m3=m1m2m3C.m1 +m2+m3<m1m2m3D.E.m1 +m2+m3与m1m2m3大小关系不确定SSS_SIMPLE_SINA B C D E分值: 4答案:B[解析] 答案为B.此题若把选项E改为:m1 +m2+m3=2m1m2m3,就可以用特殊值法.取a=2,b=1,c=3,d=2,此时满足条件a≠b,c≠d,ad+bc≠0,很容易得出:,选B.11.已知的值等于______.SSS_SINGLE_SELA 3B 1/2C 1/3D 1/6E 1/4分值: 4答案:C[解析] 因为于是所以故本题正确选项为C.12.若______.A.B.C.D.E.SSS_SIMPLE_SINA B C D E分值: 4答案:E[解析] 因为x≠0,所以选E.13.在直角坐标系中,坐标都是整数的点称为整点,设k为整数,当直线y=x-3与y=kx+k的交点为整点时,k有几个取值?______.SSS_SINGLE_SELA 2个B 4个C 5个D 6个E 10个分值: 4答案:D[解析] 根据题意,联立y=x-3和y=kx+k解得,当x为整数时y必为整数,则k-1=±1,±2,±4,所以k可以为-3,-1,0,2,3,5,共6个,故选D.14.若等式对任意的x(x≠±3)恒成立,则mn=______.SSS_SINGLE_SELA -8B 8C -16D 16E 以上结论都不正确分值: 4答案:C[解析] 因为所以(m-n)x-3(m+n)=8x,于是解之得m=4,n=-4,因此mn=-16.故本题应选C.15.(a+3)},集合B={a,b},若A∩B={2},则A∪B非空真子设集合A={5,log2集有______个.SSS_SINGLE_SELA 4B 5C 6D 7E 8分值: 4答案:C(a+3)=2,所以a+3=2 2,所以a=1,b=2.[解析] 因为A∩B={2},所以log2所以A∪B={1,2,5},其非空真子集个数为2 3 -2=6个,选C.16.已知:B={x||x+1|=x+1},则为______.SSS_SINGLE_SELA (-2,1]B [-1,+∞)C (-1,1)D [-1,1]E 以上都不正确分值: 4答案:D[解析] A=(1,+∞)∪(-∞,-2],B=[-1,+∞),所以=(-2,1]∩[-1,+∞)=[-1,1],选D.17.已知集合A={x|x 2 -2x-8<0,x∈R},集合B={x|x 2 -3ax+2a 2 =0,x∈R},若A∩B= ,则a的范围是______.SSS_SINGLE_SELA a≤-2B a≥4C -2≤a≤4D a≤-2,a≥4E 以上都不正确分值: 4答案:D[解析] A=(-2,4),B={x|x=a或x=2a},若A∩B= a,2a都不属于(-2,4)所以选D.注意a,2a的大小不确定,要分类讨论.18.若-1<a<0,则有______.A.B.C.D.E.以上都不正确SSS_SIMPLE_SINA B C D E分值: 4答案:B[解析] 利用y=x a幂函数比较大小,当-1<a<0,所以当x>0时,y=x a单调减少,所以选B.指数相同底不同,用幂函数单调性比较大小.19.设实数x,y满足x+2y=3,则x 2 +y 2 +2y的最小值为______.A.4B.5C.6D.E.SSS_SIMPLE_SINA B C D E分值: 4答案:A[解析] 将x=3-2y代入,x 2 +y 2 +2y=5y 2 -10y+9=5(y-1) 2+4≥4.20.若lg2=0.3010,lg3=0.4771,3 200与2 300的大小关系是______.•**<2300•**≤2300•**>2300•**≥2300E.不能确定SSS_SIMPLE_SINA B C D E分值: 4答案:C[解析] 由于lgx是单调增加的函数,且lg3 200 =200lg3=95.42>lg2 300=300lg2=90.3,因此3 200>2 300.选C.利用对数性质比较大小.此外还可以得到2 100 =10 100lg2 =10 30.1,因此2 100是31位数.21.如abc≠1,且则______.SSS_SINGLE_SELA 1B 0.25C 0.5D 2E 1.5分值: 4答案:C[解析] 由对数运算可得所以因为abc≠1所以logx a+logxb+logxc=logxabc≠0.所以即[(logx a-logxb) 2 +(logxa-logxc) 2 +(logxb-logxc)2 ]=0.所以logx a=logxb=logxc,可得a=b=c,所以,选C.按各种等式化简思路,先把对数都化同底,然后一边为零,因式分解或配平方.利用a 3 +b 3 +c 3 -3abc=(a+b+c)(a 2 +b 2 +c 2 -ab-ac-bc).22.已知0<a<1,b>1,且ab>1,则下列正确的是______.A.B.C.D.E.以上都不正确SSS_SIMPLE_SINA B C D E分值: 4答案:B[解析] 由0<a<1,b>1,且ab>1,即可得.又,所以,选B.23.求函数的值域为______.SSS_SINGLE_SELA (0,4)B (-∞,4)C (-∞,4]D (-∞,4]E 以上都不对分值: 4答案:C[解析] 设则t≥0,所以x=1-t 2代入得y=f(t)=2×(1-t 2 )+4t=-2t 2 +4t+2=-2(t-1) 2 +4,因为t≥0,所以y≤4,所求值域为(-∞,4],选C.转化为二次函数求值域,要注意中间变量有范围.24.若不等式x 2+ax+1≥0对一切都成立,则a的取值范围是______.A.a≥0B.-1<a<0C.D.E.以上都不正确SSS_SIMPLE_SINA B C D E分值: 4答案:D[解析] 设,则对称轴为.若,即a≤-1时,则f(x)在上是减函数,应有,所以有.若,即a≥0时,则f(x)在上是增函数,有f(0)=1>0恒成立,所以有a≥0.若,即-1<a<0时,则应有成立,所以有-1<a<0.综上,当时,不等式x 2+ax+1≥0对一切都成立,选D.该题属于取值区间固定,对称轴变动导致最值需要讨论.25.设1≤x≤64,函数y=(log2 x) 4 +12(log2x) 2· 的最大值和最小值分别为______.SSS_SINGLE_SELA 54,2B 81,9C 81,0D 54,0E 以上都不正确分值: 4答案:C[解析] 设t=log2x,则0≤t≤6,且y=t 4 +12t 2 (3-t)=t 2 (t 2 -12t+36)=t 2 (t-6) 2 =(t 2 -6t) 2 =[(t-3) 2 -9] 2.由于(t-3) 2 -9在0≤t≤6时的最大值是0,最小值是-9,因此函数y=(log2 x) 2· 的最大值和最小值分别是81和0,选C.x) 4 +12(log226.已知a>0,b>0,c>0,且b>a+c,那么方程ax 2 +bx+c=0的根的情况______.SSS_SINGLE_SELA 有一个正根、一个负根B 有两个等根C 有两个正根D 有两个负根E 无实根分值: 4答案:D[解析] 因为a>0,所以抛物线y=f(x)=ax 2 +bx+c开口向上;又因为c>0,所以抛物线截距为正;又因为b>0,所以抛物线对称轴位于y轴左方;再由b>a+c,所以f(-1)=a-b+c<0.所以f(-1)<0<f(0)=c,f(x)=0有一根在(-1,0)内,另一根在(-∞,-1)内,因此,方程f(x)=0有两个负根,故选D.一元二次方程的实质是二次函数与x轴的交点,本题利用二次函数图像来研究根的问题.利用二次函数研究根的分布问题将在方程一章中进一步讨论.1。
2018考研:管理类综合联考(199)真题与解析

A. 9 种 B.18 种 C.24 种 D.36 种 E.72 种
【答案】D
12. 从标号位 1 到 10 的 10 张卡片中随机抽取 2 张,它们的标号之和能被 5 整除的概率为( )
A. 1
B. 1
C. 2
D. 2
E. 7
5
9
9
15
45
【答案】E
2
13. 某单位检查 3 个部门的工作,由 3 个部门的主任和外聘的 3 名人员组成检查组,分两人一组检查工作,
D、E 五个选项中,只有一项是符合试题要求的。请在答题卡上将所选项的字母涂黑。
26. 人民既是历史的创造者,也是历史的见证者;既是历史的“剧中人”,也是历史
的“剧作者”。离开人民,文艺就会变成无根的浮萍、无病的呻吟、无魂的躯壳。观照人
民的生活、命运、情感,表达人民的心愿、心情、心声,我们的作品才会在人民中传之久
类型
(B)由于所列城市并非我国的所有城市,所以上面所列的 9 类天气一定不是所有的天
气类型
(C)由于所列城市在同一天不一定展示所有的天气类型,所以上面所列的 9 类天气可
能不是所有的天气类型
(D)由于所列城市在同一天可能展示所有的天气类型,所以上面所列的 9 类天气一定
是所有的天气类型
5
(E)由于所列城市分处我国的东南西北中,所以上面所列的 9 类天气一定就是所有的 天气类型
27. 盛夏时节的某一天,某市早报刊载了由该市专业气象台提供的全国部分城市当天
天气预报,择其内容列表如下:
天津
阴
上海
雷阵雨
昆明
小雨
呼和浩特
阵雨
哈尔滨
少云
乌鲁木齐
晴
2018年管理类MBA综合考试数学真题及详细答案解析(word版)

2018年管理类MBA综合考试数学真题及详细答案解析一、问题求解:第1~15小题,每小题3分,共45分。
下列每题给出的A、B、C、D、E五个选项中,只有一项是符合试题要求的。
请在答题卡上将所选项的字母涂黑。
1. 学科竞赛设一等奖、二等奖和三等奖,比例为1:3:8,获奖率为30%,已知10人获得一等奖,则参加竞赛的人数为()A.300 B. 400 C. 500 D. 550 E. 600解析:(B)解法1:由一等奖:二等奖:三等奖=1:3:8,且一等奖10人,可推出二等奖、三等奖分别为30人和80人,所以获奖人数为10+30+80=120人,所以参加竞赛的人数为12030%=400÷人。
解法2:设参加竞赛的人数为x,根据题意有130%10400138x x=⇒=++。
2. 为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是(单位:岁) A. 32, 30 B. 32, 29.5 C. 32, 27 D. 30, 27 E. 29.5, 27解析:(A)23+26+28+30+32+34+36+38+41==329x男23+25+27+27+29+31==276x 女329+276==3015x⨯⨯总3. 某单位采取分段收费的方式收取网络流量(单位: GB)费用,每月流量20(含)以内免费,流量20到30(含)的每GB收费1元,流量30到40(含)的每GB收费3元,流量40以上的每GB收费5元,小王这个月用了45GB的流量,则他应该交费()A. 45元B. 65元C. 75元D. 85元E. 135元解析:(B)各个流量段所需缴费数额见下表:所以小王应该缴费0+10+30+25=65元。
4. 如图,圆O 是三角形ABC 的内切圆,若三角形ABC 的面积与周长的大小之比为1:2,则圆O 的面积为( ) A. π B.2π C. 3π D. 4π E. 5π解析:(A )解法1:设三角形边长分别为,,a b c ,内切圆O 的半径为r ,则三角形周长L a b c =++,三角形面积12S Lr =(最好记住该结论)。
2018管理类联考数学真题

2018年全国硕士研究生招生考试 管理类专业学位联考综合能力数学试题一、问题求解:第1~15小题,每小题3分,共45分。
下列每题给出的A 、B 、C 、D 、E五个选项中,只有一项是符合试题要求的。
1. 学科竞赛设一等奖、二等奖和三等奖,比例为1:3:8,获奖率为30%,已知10人获得一等奖,则参加竞赛的人数为 A. 300B. 400C.500D. 550E. 6002. 为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是 (单位:岁) A. 32 ,30B. 32,29.5C. 32,27D. 30,27E. 29.5,273. 某单位采取分段收费的方式收取网络流量(单位:GB)费用:每月流量20(含)以内免费,流量20到30(含)的每GB 收费1元,流量30到40(含)的每GB 收费3元,流量40以上的每GB 收费5元.小王这个月用了45GB 的流量,则他应该交费 A. 45元B. 65元C. 75元D. 85元E. 135元4. 如图,圆O 是三角形ABC 的内切圆,若三角形ABC 的面积与周长的大小之比为1:2,则圆O 的面积为B图1A. πB. 2πC. 3πD. 4πE. 5π5. 设实数,a b 满足2a b −=,3326a b −=,则22a b += A. 30B. 22C. 15D. 13E. 106. 6张不同的卡片,2张一组分别装入甲、乙、丙三个袋中,若指定的两张卡片要在同一组,则不同的装法有A. 12B. 18C. 24D. 30E. 367. 四边形1111A B C D 是平行四边形,2222A B C D 、、、分别为1111A B C D 四边的中点,3333A B C D 、、、分别是2222A B C D 四边的中点,依次下去,得到四边形序列n n n nA B C D ()1,2,3,n =⋅⋅⋅,设n n n n A B C D 的面积为n S ,且112S =,则123S S S +++⋅⋅⋅=A. 16B. 20C. 24D. 28E. 3011128. 甲、乙两人进行围棋比赛,约定先胜2局者赢得比赛,已知每盘围棋甲获胜的概率是0.6,乙获胜的概率是0.4,若乙在第一盘获胜,则甲赢得比赛的概率为 A. 0.144B. 0.288C. 0.36D. 0.4E. 0.69. 已知圆()22:C x y a b +−=.若圆C 在点()1,2处的切线与y 轴的交点为()0,3,则ab = A. -2 B. -1 C. 0 D. 1 E. 2 10. 有96位顾客至少购买了甲、乙、丙三种商品中的一种.经调查:同时购买了甲、乙两种商品的有8位,同时购买了甲、丙两种商品的有12位,同时购买了乙、丙两种商品的有6位,同时购买了三种商品的有2位,则仅购买一种商品的顾客有 A. 79位 B. 72位C. 74位D. 76位E. 82位11. 函数(){}22max ,8=−+f x x x 的最小值为A. 8B. 7C. 6D. 5E. 4 12. 某单位为检查3个部门的工作,由这3个部门主任和外聘的3名人员组成检查部,分2人一组检查工作,每组有1名外聘成员.规定本部门主任不能检查本部门,则不同的安排方式有A. 6种B. 8种C. 12种D. 18种E. 36种 13. 从标号为1到10的10张卡片中随机抽取2张,它们的标号之和能被5整除的概率为A.15B.19C.29D.215E.74514.如图,圆柱体的底面半径为2,高为3,垂直于底面的平面截圆柱体所得截面为矩形ABCD .若弦AB 所对的圆心角是3π,则截掉部分(较小部分)的体积为A. 3π−B.26π−C. 2π−D. 2π−E. πABCD图 315. 羽毛球队有4名男运动员和3名女运动员,从这选出两对参加混双比赛,则不同的选拔方式有 A. 9种 B. 18种 C. 24种 D. 36种 E. 72种二、条件充分性条件判断:第16~25小题小题,每小题3分,共30分。
2018年考研管理类联考数学试题解析
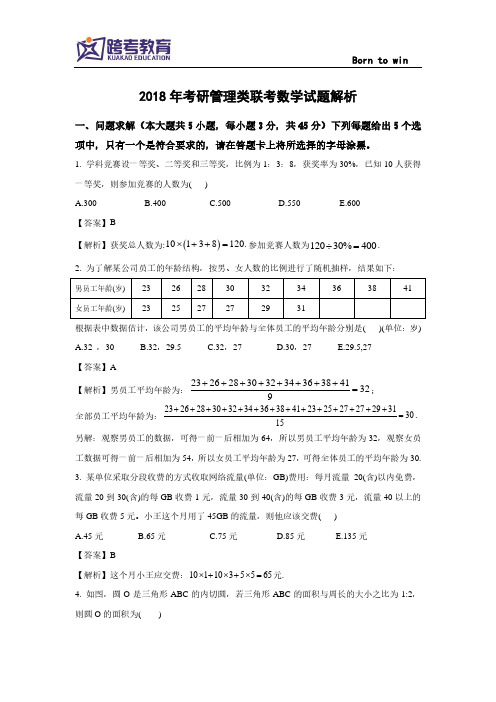
一等奖,则参加竞赛的人数为( )
A.300
B.400
C.500
D.550
E.600
【答案】B
【解析】获奖总人数为:10 1 3 8 120. 参加竞赛人数为120 30% 400 .
2. 为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:
男员工年龄(岁) 23
26 28
全部员工平均年龄为: 23 26 28 30 32 34 36 38 41 23 25 27 27 29 31 30 . 15
另解:观察男员工的数据,可得一前一后相加为 64,所以男员工平均年龄为 32,观察女员
工数据可得一前一后相加为 54,所以女员工平均年龄为 27,可得全体员工的平均年龄为 30.
B.65 元
C.75 元
D.85 元
E.135 元
【答案】B
【解析】这个月小王应交费:101103 55 65 元.
4. 如图,圆 O 是三角形 ABC 的内切圆,若三角形 ABC 的面积与周长的大小之比为 1:2,
则圆 O 的面积为( )
Born to win
A
O
B
C
图.1
A.
【答案】A 【解析】
B. 2
C. 3
D. 4
A
a1
b1
E. 5
a2
rO
b2
B
c1
c2
C
S
1 2
a1r
1 2
b1r
1 2
a2r
1 2
b2r
1 2
c1r
1 2
c2r
1 2
r
a1
b1
a2
b2
MBA数学真题附解析

MBA联考数学真题2018年一、问题求解下列每题给出的A、B、C、D、E五个选项中,只有1项是符合试题要求的。
提交纠错信息评价难易度提交知识点1. 学科竞赛设一、二、三等奖,比例1:3:8,获奖率30%,已知10人已获一等奖,则参赛人数为______•A.300•B.400•C.500•D.550•E.600B[解析] 由总量=分量÷分量百分比,可得参赛总人数为:10÷(30%÷12)=400。
[考点] 比例问题应用题。
2. 为了解某公司员工年龄结构,按男女人数比例进行随机抽样,结果如下:男员工年龄(岁)232628303234363841女员工年龄(岁)232527272931据表中数据统计,该公司男员工的平均年龄与全体员工平均年龄分别是______•A.32,30•B.32,29.5•C.32,27•D.30,27•E.29.5,27A[解析] 由表可知,男员工的平均年龄=32,女员工的平均年龄=27,男女员工人数之比为9:6=3:2,总平均年龄为。
[考点] 平均值问题。
3. 某单位分段收流量(单位:GB)费:每日20(含)GB以内免收,20到30(含)GB每GB收1元,30到40(含)GB每GB收3元,40GB以上每GB收5元,小王本月用45GB,应该交费______元•A.45•B.65•C.75•D.85•E.135B[解析] 应该交费:10+10×3+5×5=65(元)。
[考点] 分段计费。
4. 圆O是△ABC的内切圆,△ABC的面积与周长比1:2,则图O 的面积为______•A.π•B.2π•C.3π•D.4π•E.5πA[解析] 设内切圆的半径为r,△ABC的三边为a,b,c,则,化简可得r=1,圆的面积为π。
[考点] 平面几何求面积问题。
5. 实数a,b满足|a3-b3|=26,|a-b|=2,则a2+b2=______ •A.30•B.22•C.15•D.13•E.10E[解析] 由已知条件可知a=3,b=1,则|a2+b2|=10。
全国硕士研究生考试-管理类联考2018年数学真题

2018年全国硕士研究生招生考试管理类专业学位联考——数学一、问题求解:第1~15小题,每小题3分,共45分。
下列每题给出的A、B、C、D、E五个选项中,只有一项是符合试题要求的。
请在答题卡上将所选项的字母涂黑。
(2018-1)学科竞赛设一等奖、二等奖和三等奖,比例为1:3:8,获奖率为30%,已知10人获得一等奖,则参加竞赛的人数是()(A)300 (B)400 (C)500 (D)550 (E)600 (2018-2)为了解某公司员工的年龄结构,按男、女人数的比例进行了随机抽样,结果如下:根据表中数据估计,该公司男员工的平均年龄与全体员工的平均年龄分别是(单位:岁)(A)32,30 (B)32,29.5 (C)32,27 (D)30,27 (E)29.5,27 (2018-3)某单位采取分段收费的方式收取网络流量(单位:GB)费用:每月流量20(含)以内免费,流量20到30(含)的每GB收费1元,流量30到40(含)的每GB收费3元,流量40以上的每GB收费5元。
小王这个月用了45GB的流量,则他应缴费()(A)45元(B)65元(C)75元(D)85元(E)135元(2018-4)如图,圆O是三角形ABC的内切圆,若三角形ABC的面积与周长的大小之比为1:2,则圆O的面积为()(A)(B)(C)(D)(E)(2018-5)设实数a,b满足︱a-b︱=2,︱a3-b3︱=26,则a2+b2=()(A)30 (B)22 (C)15 (D)13 (E)10 (2018-6)有96位顾客至少购买了甲、乙、丙三种商品中的一种,经调查:同时购买了甲、乙两种商品的有8位,同时购买了甲、丙两种商品的有12位,同时购买了乙、丙两种商品的有6位,同时购买了三种商品的有2位,则仅购买了一种商品的顾客有()B C(A )70位 (B )72位 (C )74位 (D )76位 (E )82位 (2018-7)如图,四边形A 1B 1C 1D 1是平行四边形,A 2,B 2,C 2,D 2分别是A 1B 1C 1D 1四边的中点,A 3B 3C 3D 3分别是A 2B 2C 2D 2四边的中点,依次下去,得到四边形序列A n B n C n D n (n=1,2,3,…),设A n B n C n D n 的面积为S n ,且S 1=12,则S 1+S 2+S 3+…=()(A )16 (B )20(C )24 (D )28 (E )30 (2018-8)将6张不同的卡片2张一组分别装入甲、乙、丙3个袋中,若指定的两张卡片要放在同一组,则不同的装法有()(A )12种 (B )18种 (C )24种 (D )30种 (E )36种 (2018-9)甲、乙两人进行围棋比赛,约定先胜两盘者赢得比赛,已知每盘棋甲获胜的概率是0.6,乙获胜的概率是0.4.若乙在第一盘获胜,则甲赢得比赛的概率为()(A )0.14 (B )0.288 (C )0.36 (D )0.4 (E )0.6 (2018-10)已知圆C :x 2+(y-a )2=b ,若圆C 在点(1,2)处的切线与y 轴的交点为(0,3),则ab=()(A )-2 (B )-1 (C )0 (D )1 (E )2 (2018-11)羽毛球队有4名男运动员和3名女运动员,从中选出2对参加混双比赛,则不同的选派方式有()(A )9种 (B )18种 (C )24种 (D )36种 (E )72种 (2018-12)从标号为1到10的10张卡片中随机抽取2张,它们的标号之和能被5整除的概率为()(A )1/5 (B )1/9 (C )2/9 (D )1/15 (E )7/45 (2018-13)某单位为检查3个部门的工作,由这3个部门的主任和外聘的3名人员组成检查组,分2人一组检查工作,每组有1名外聘成员,规定本部门主任不能检查本部门,则不同的安排方式有()(A )6种 (B )8种 (C )12种 (D )18种 (E )36种1 2 1(2018-14)如图,圆柱体的底面半径为2,高为3,垂直于底面的平面截圆柱体所得截面为矩形ABCD,若弦AB所对的圆心角是,则截掉部分(较小部分)的体积为()(C)(D)(E)(2018-15)函数f(x)=max{x2,-x2+8}的最小值为()(A)8 (B)7 (C)6 (D)5 (E)4二、条件充分性判断:第16~25小题,每小题3分,共30分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年管理类专业联考综合能力数学试题及解析一、问题求解:第1~15小题,每小题3分,共45分。
下列每题给出的A .B .C .D .E 五个选项中,只有一项是符合试题要求的,请在答题卡上将所选项的字母涂黑。
1、某品牌的电冰箱连续两次降价10%后的售价是降价前的() A.80%B.81%C.82%D.83%E.85%2、甲、乙、丙三种货车的载重量成等差数列,2辆甲种车和1辆乙种车满载量为95吨,1辆甲种车和3辆丙种车满载量为150吨。
则用甲、乙、丙各1辆车一次最多运送货物()吨 A.125B.120C.115D.110E.1053、张老师到一所中学进行招生咨询,上午接受了45名同学的咨询,其中的9名同学下午又咨询了张老师,占张老师下午咨询学生的10%。
一天中向张老师咨询的学生人数为() A.81B.90C.115D.126E.1354、某种机器人可搜索到的区域是半径为1米的圆,若该机器人沿直线行走10米。
其搜索过的区域的面积(单位:平方米)为() A.102π+B.10π+C.202π+D.20π+E.10π5、不等式12x x -+≤的解集为() A.(],1-∞B.3,2⎛⎤-∞ ⎥⎝⎦C.31,2⎡⎤⎢⎥⎣⎦D.[)1,+∞E.3,2⎡⎫+∞⎪⎢⎣⎭6、在1与100之间,能被9整除的整数的平均值为() A.27B.36C.45D.54E.637、某试卷由15道选择题组成,每道题有4个选项,只有一项是符合试题要求的,甲有6道题能确定正确选项,有5道题能排除2个错误选项,有4道题能排除1个错误选项。
若从每题排除后剩余的选项中选1个作为答案,则甲能得满分的概率为()A.451123⋅B.541123⋅C.541123+D.541324⎛⎫⋅ ⎪⎝⎭E.541324⎛⎫+ ⎪⎝⎭8、某公司用1万元购买了价格分别是1750元和950元的甲、乙两种办公设备,则购买的甲、乙办公设备的件数分别为() A.3,5B.5,3C.4,4D.2,6E.6,29、如图1,在扇形AOB 中,,1,4AOB OA AC OB π∠==⊥,则阴影部分的面积为()图1A.184π- B.188π- C.142π-D.144π- E.148π-10、老师问班上50名同学周末复习的情况,结果有20人复习过数学,30人复习过语文,6人复习过英语,且同时复习了数学和语文的有10人,语文和英语的有2人,英语和数学的有3人。
若同时复习过这三门课的人数为0,则没有复习过这三门课程的学生的人数是() A.7B.8C.9D.10E.1111、甲从1,2,3中抽取一数,记为a ,乙从1,2,3,4中抽取一数,记为b 。
规定当a b >或1a b +<时甲获胜,则甲获胜的概率为() A.16B.14C.13D.512E.1212、已知ABC ∆和'''A B C ∆满足''''::2:3AB A B AC AC ==,'A A π∠+∠=,则ABC∆和'''A B C ∆的面积之比为()C.2:3D.2:5E.4:913、将6人分为3组,每组2人,则不同的分组方式有()种 A.12B.15C.30D.45E.9014、甲、乙、丙三人每轮各投篮10次,投了三轮。
投中数如下表:记123,,σσσ分别为甲、乙、丙投中数的方差,则() A.123σσσ>>B.132σσσ>>C.213σσσ>>D.231σσσ>>E.321σσσ>>15、将长、宽、高分别是12,9和6的长方体切割成正方体,且切割后无剩余,则能切割成相同正方体的最少个数为() A.3B.6C.24D.96E.648二.条件充分性判断:第16~25题,每小题3分,共30分。
要求判断每题给出的条件(1)和条件(2)能否充分支持题干所陈述的结论。
A .B .C .D .E 五个选项为判断结果,请选择一项符合试题要求的判断。
A :条件(1)充分,但条件(2)不充分B :条件(2)充分,但条件(1)不充分C :条件(1)和(2)单独都不充分,但条件(1)和(2)联合起来充分D :条件(1)充分,条件(2)也充分E :条件(1)和(2)单独都不充分,条件(1)和(2)联合起来也不充分 16、某人需要处理若干份文件,第一小时处理了全部文件的15,第二小时处理了剩余文件的14,则此人需要处理的文件共25份 (1)前两个小时处理了10份文件 (2)第二小时处理了5份文件17、某人从A 地出发,先乘时速为220千米的动车,后转乘时速为100千米的汽车达到B 地,则A ,B 两地的距离为960千米 (1)乘动车时间与乘汽车时间相等(2)乘动车时间与乘汽车的时间之和为6小时 18、直线y ax b =+与抛物线2y x =有两个交点 (1)24a b > (2)0b >19、能确定某企业产值的月平均增长率 (1)已知一月份的产值 (2)已知全年的总产值20、圆220x y ax by c +--+=与x 轴相切,则能确定c 的值 (1)已知a 的值 (2)已知b 的值21、如图2,一个铁球沉入水池中,则能确定铁球的体积 (1)已知铁球露出水面的高度 (2)已知水深及铁球与水面交线的周长22、某人参加资格考试,有A 类和B 类可选择,A 类的合格标准是抽3道题至少会做2道,B 类的合格标准是2道题需都会做,则此人参加A 类合格的机会大 (1)此人A 类题中有60%会做 (2)此人B 类题中有80%会做图223、设,a b 是两个不相等的实数,则函数()22f x x ax b =++的最小值小于零(1)1,a ,b 成等差数列 (2)1,a ,b 成等比数列24、已知,,a b c 为三个实数,则{}min ,,5a b b c a c ---≤ (1)5a ≤,5b ≤,5c ≤ (2)15a b c ++=25、某机构向12位教师征题,共征集到5种题型的试题52道,则能确定供题教师的人数 (1)每位供题教师提供的试题数相同 (2)每位供题教师提供的题型不超过2种解析1、【B 】考点:增长率问题解析:设原始售价为单位“1”,则两次连续降价后的售价为()2110.10.81⨯-= 故,连续降价两次后的价格是降价前的81% 2、【E 】考点:等差数列、简单方程应用解析:设甲、乙、丙的载重量分别为,,a b c 吨则()()()2..............1295...........23150..........3b a c a b a c =+⎧⎪+=⎨⎪+=⎩,解得303540a b c =⎧⎪=⎨⎪=⎩故105a b c ++= 3、【D 】考点:比例、集合应用 解析:根据“=部分量总量部分量的占比”,得到下午的咨询学员有99010%=名其中下午90名中有9名上午已经咨询过,所以下午新的咨询学员90-9=81名故,一天中总的咨询学员45+81=126名 4、【D 】 考点:平面几何解析:根据题干意思可知机器人搜索过的区域图形如下2102120S ππ=⨯+⨯=+5、【B 】考点:绝对值不等式 解析:(特值法)根据选项特征,取0x =时,不等式左边01012=-+=≤成立,排除C 、D 、E取32x =时,不等式左边3312222=-+=≤成立,排除A故,不等式的解集3,2⎛⎤-∞ ⎥⎝⎦6、【D 】考点:整除、平均数解析:1到100之间能被9整除的整数有:9,18,27…,99共11个数 故平均数91827995411X ++++==7、【B 】 考点:独立概型解析:根据题干意思可得,能排除2个错误选项的题,每题做正确的概率12,5个题都正确概率512⎛⎫ ⎪⎝⎭能排除1个错误选项的题,每题做正确的概率13,4个题都正确的概率413⎛⎫⎪⎝⎭故,甲能得满分的概率为545411112323⎛⎫⎛⎫⨯=⨯ ⎪ ⎪⎝⎭⎝⎭8、【A 】考点:实数、简单方程解析:设购买甲、乙办公设备的件数分别为,a b 则175095010000a b +=,化简有3519200a b += 带选项验证,可得3,5a b == 9、【A 】 考点:平面几何解析:由题干可知22OC AC ==2211211242284AOCAOB S S S ππ⎛⎫=-=⨯⨯-⨯=- ⎪ ⎪⎝⎭阴扇 10、【C 】 考点:集合应用解析:三个集合的关系表达如图,则三门课程都没有复 习的学生人数()502030610239-++---=人 11、【E 】 考点:古典概型 解析:具体事件分两类第一类:a b >,有2,1;3,1;3,2,共三种 第二类:1a b +<,有1,3;1,4;2,4,共三种 总事件数:3412⨯=种 故甲获胜的概率 331122+= 12、【E 】考点:三角形面积公式解析:有已知'A A π∠+∠='sin sin A A ⇒=()1sin (12)ABC S AB AC A ∆=⋅ ()''''''''1sin (22)A B C S A B AC A ∆=⋅ 图1数学语文英语0人从而()()'''''''12242339ABC A B CS AB AC S A B AC ∆∆⋅⨯⇒===⋅⨯ 13、【B 】考点:排列组合分组问题解析:根据分组原理列式222642153!C C C = 14、【B 】 考点:方差公式 解析:一列数的方差()()()2222121n S x x x x x x n ⎡⎤=-+-++-⎣⎦故132σσσ>> 15、【C 】考点:立体几何、公约数解析:被切割成的正方体的棱长一定是长方体三边长的公约数,则正方体棱长()12,9,63= 有312963n ⨯⨯=(n 表示切割成的正方体的个数),解得24n = 16、【D 】 考点:比例应用解析:条件(1)前两个小时共完成总量的比值111215545⎛⎫+-⨯= ⎪⎝⎭ 则总的文件数210255÷=。
充分 条件(2)第二个小时处理的文件占总量的比值1111545⎛⎫-⨯= ⎪⎝⎭则总的文件数15255÷=。
充分 17、【C 】 考点:行程应用解析:条件(1)、(2)单独不充分,考虑联合,则乘动车和乘汽车的时间都为3小时 AB 之间的距离长度()2201003960+⨯=千米。
充分 18、【B 】 考点:解析几何 解析:化简题干220y ax b x ax b y x=+⎧⇒--=⎨=⎩有两个不相等的实数根,则240a b +>条件(1)1,1a b ==-满足24a b >,但是不能推出240a b +>。
