高等数值分析(曲线拟合)ppt课件
合集下载
曲线拟合PPT演示文稿
第四讲 曲线拟合
1
第四讲主要知识点
1、曲线拟合的概念 2、曲线拟和的方法 3、解矛盾方程组
2
函数插值问题回忆
• 设已知某个函数关系y f (x) 在某些离散点上的函数值：
x x0 x1 y y0 y1
x n 1 x n y n 1 y n
• 插值问题：根据这些已知数据来构造函数 y f (x)
合函数形式为 pm (x)a0a1xam xm (mn1) ， 求系数 a0*,a1*, ,am * ，使得
n
n
m
( a 0 ,a 1 , ,a m )[ y i p m ( x i) ] 2 [ y ia k x ik ] 2
p m * (x ) i 1 a 0 * a 1 * x a m * x i m 0
15
拟合例题
例2 有一滑轮组，要举起W公斤的重物需要用 F公斤的力，实验所得的数据如下表。
求适合上述关系的近似公式。
16
拟合例题
解 首先，将这些数据画在直角坐标系中，从图形上 看，数据点的分布大致呈一条直线，所以设所求
的拟合直线为 yabx ，
得关于a和b的线性方程组
17
其他类拟合问题
最小二乘法并不只限于多项式，也可用于任 何具体给出的函数形式。特别重要的是有些非线 性最小二乘拟合问题通过适当的变换可以转化为 线性最小二乘问题求解。
确定a和b取何值时，二元函数
的值最小?
N
Q(a,b) [yi (abxi)]2 i1
11
直线拟合
由微积分的知识可知，这一问题的求解， 可归结为求二元函数
Q (a, b) 的极值问题，即 a 和 b
应满足：
12
直线拟合
1
第四讲主要知识点
1、曲线拟合的概念 2、曲线拟和的方法 3、解矛盾方程组
2
函数插值问题回忆
• 设已知某个函数关系y f (x) 在某些离散点上的函数值：
x x0 x1 y y0 y1
x n 1 x n y n 1 y n
• 插值问题：根据这些已知数据来构造函数 y f (x)
合函数形式为 pm (x)a0a1xam xm (mn1) ， 求系数 a0*,a1*, ,am * ，使得
n
n
m
( a 0 ,a 1 , ,a m )[ y i p m ( x i) ] 2 [ y ia k x ik ] 2
p m * (x ) i 1 a 0 * a 1 * x a m * x i m 0
15
拟合例题
例2 有一滑轮组，要举起W公斤的重物需要用 F公斤的力，实验所得的数据如下表。
求适合上述关系的近似公式。
16
拟合例题
解 首先，将这些数据画在直角坐标系中，从图形上 看，数据点的分布大致呈一条直线，所以设所求
的拟合直线为 yabx ，
得关于a和b的线性方程组
17
其他类拟合问题
最小二乘法并不只限于多项式，也可用于任 何具体给出的函数形式。特别重要的是有些非线 性最小二乘拟合问题通过适当的变换可以转化为 线性最小二乘问题求解。
确定a和b取何值时，二元函数
的值最小?
N
Q(a,b) [yi (abxi)]2 i1
11
直线拟合
由微积分的知识可知，这一问题的求解， 可归结为求二元函数
Q (a, b) 的极值问题，即 a 和 b
应满足：
12
直线拟合
曲线拟合-PPT精选文档
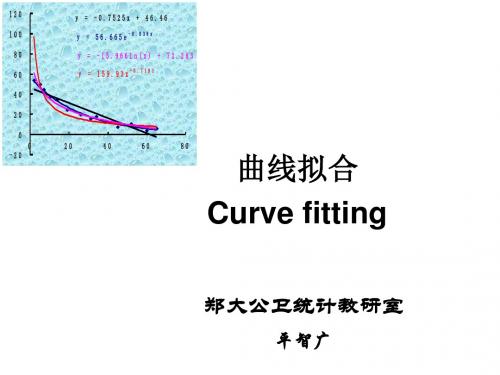
-11.2705
-8.0196 -4.0604 0.0000 3.9012 7.6049
12.62
15.77 18.01 19.75 21.16 22.36
0.1017
0.0053 0.0361 1.0921 0.0563 0.0566
1.6
23.8
0.4700
0.2209 566.44
4.1078 2671.63
54 50 45 37 35 25 20 16 18 13
4.双曲形式关系
6.多项式形式关系
(一) 指数关系曲线
ˆ ae y
两种形式：
y
bx
ˆ ab y
x
a >0,b>0
a >0,b<0
0
x
当a>0，b>0时，Y随x的↑而↑，曲线凹向上； 当a>0，b<0时，Y随x的↑而↓，曲线也是凹向上。
(二) 对数关系曲线
方程为:
y
ˆ y a b ln x
(五) S型曲线 • S型曲线由于其曲线形状与动、植物的生长过程的 基本特点类似，故又称生长曲线，曲线一开始时 增长较慢，而在以后的某一范围内迅速增长，达 到一定的限度后增长又缓慢下来，曲线呈拉长 的”S”，故称S曲线 • 最著名的曲线是Logistic生长曲线，它最早由比利 时数学家 P.F.Vehulst 于 1838 年导出，但直至 20 世 纪 20 年代才被生物学家及统计学家 R.Pearl 和 L.J. Reed 重新发现，并逐渐被人们所发现。目前它已 广泛应用于多领域的模拟研究。
解决办法
曲线直线化估计(Curve estimation) 非 线 性 / 曲 线 回 归 (Nonlinear/curvilinear regression)
数值分析课件-6曲线拟合
第六章 曲线拟合的最小二乘 /函数平方逼近初步实例：考察某种纤维的强度与其拉伸倍数的关系,下表是实际测定的24个纤维样品的强度与相应的拉伸倍数是记录:编 号拉伸倍数 强 度编 号拉伸倍数 强 度1 1.9 1.4135 5.522 1.314 5.253 2.1 1.8156 5.54 2.5 2.516 6.3 6.45 2.7 2.817 6.566 2.7 2.5187.1 5.37 3.53198 6.58 3.5 2.72087944218.98.5104 3.5229811 4.5 4.2239.58.112 4.63.524108.1i i y x ii y x 一.实例讲解6.2 数据拟合(最小二乘法)§2(())m nj j i i i j a x f ϕ===-∑∑2(())mi i i S x f ==-∑三、法方程组22δ∑==nj j j x a x S 0)()(ϕ由的函数为拟合系数),,1,0(n j a j =可知因此可假设01(,,,)n F a a a 2(())mnj j i i i j a x f ϕ===-∑∑因此求最小二乘解转化为二次函数四、加权最小二乘法(,)(0,1,,)i i x f i m = 对于一组给定的数据点(,)(0,1,,)i i x f i m = 在拟合的数据点中各点的重要性可能是不一样的()(,)0,1,,i i i i x x f i mρρ= 假设=表示数据点的权(或权重),权:即权重或者密度，统称为权系数.定义加权平方误差为222m i i i δρδ==∑2(())mi i i i S x f ρ==-∑-----(9)6.3 连续函数的最佳平方逼近§0102**222*[,],{,,,}[,].(),()();()[()()]()[()()]()().min n ni i i b a b a S f C a b span C a b S x S x a x f S x f x S x dx x f x S x dx S x f x ϕϕϕϕρρ=∈Φ∈Φ=⊂∀∈Φ=-=-=-∑⎰⎰ 设为的最佳平方逼近1. 最佳平方逼近问题-----(14)0(,)(,)(,)()()()(,)()()()0,1,,x n k i i k k i b k i k i a b k k k a a f d x x x dx d f x f x x dxk nG dϕϕϕϕϕρϕϕϕρϕ=⎧==⎪⎪⎪=⇒⎨⎪==⎪⎪=⎩⇒=∑⎰⎰ ⎪⎪⎪⎪⎭⎫ ⎝⎛),(),(),(01000n ϕϕϕϕϕϕ ),(),(),(11101n ϕϕϕϕϕϕ ),(),(),(10n n n n ϕϕϕϕϕϕ G =最小二乘法方法评注曲线拟和的最小二乘法是实验数据处理的常用方法。
数值分析3-4(最小二乘法)ppt课件
i0
j0
f (xi )]k (xi )
展开
n
m
m
a j ( xi ) j ( xi )k ( xi ) ( xi ) f ( xi )k ( xi )
j0 i0
i0
法方程
解方程组
有唯一解ak ak (k 0,1,..., n)
则S ( x) a00 ( x) a11( x) ... ann ( x)
本例经过计算可得
max i
|
(1) i
|
0.568
103
, max i
|
(2) i
|
0.277
103
而均方误差为
m
m
(
(1) i
)2
1.19 103 ,
(
( i
2)
)
2
0.34 103
i 1
i 1
由此可知第二个模型较好。
结论：
选择拟合曲线的数学模型，并不一定开始 就能选好，往往需要通过分析若干模型后， 经过实际计算才能选到较好的模型，如本 例的指数模型就比双曲线模型好得多。
三、求解步骤
确定拟合曲线的形式
最困难！
确定变量对应的数据
确定法方程
求解法方程
四、举例
例1. 已知一组实验数据如下，求它的拟合曲线.
xi
1
2
3
4
5
fi
4 4.5 6
8 8.5
ωi
21311
解 根据所给数据，在坐标纸上标出，从图 中看到各点在一条直线附近，故可选择 线性函数作拟合曲线，即令
S1( x) a0 a1 x
数据的曲线拟合.PPT
1930 1940 1950
y 75,995 91,972 105,711 123,203 131,669 150,697
t 1960 1970 1980
1990 2000
y 179,323 203,212 226,505 249,633 281,422
2、 X 取 1，2，…，20，y=x+3sin(x),分别用 6 阶、 10 阶曲线进行逼近。
%三次样条插值
wi=interp1(x,y,xi,'cubic');
%三次多项式插
plot(x,y,'o',xi,yi,'r+',xi,zi,'g*',xi,wi,'k.-')
legend('原始点','线性点','三次样条','三次多项式'
xi=[0.2500 0.3500 0.4500];
yi=interp1(x,y,xi,'spline')
-0.5971
3.6472 -9.7295
十阶多项式： p=
Columns 1 through 6 0.0000 -0.0000 0.0004 -0.0114 0.1814 -1.8065 Columns 7 through 11 11.2360 -42.0861 88.5907 -92.8155 40.2671
y=[2 24 32 21 10 6 3 1 1 1];
plot(x,y,'r-*')
求均值与方差：
赔款额（元）
0—400 400—800 800—1200 1200—1600 1600—2000
第三章(曲线拟合)
因为x0≠x1,所以a,b可唯一确定,且有
y1 y0 a x1 x0 y1 y0 b y0 x0 x1 x0
第4章 插值法
代入式(4―3)得
y1 y0 P ( x1 x0 ) 1 ( x ) y0 x1 x0
《 计 算 方 法 》
(4―4)
图 4.1
第4章 插值法
A(x0,y0),B(x1,y1),C(x2,y2)的抛物线来近似地代替f(x),见图
4.2。
第4章 插值法
《 计 算 方 法 》
图 4.2
第4章 插值法
§3 代数多项式插值的存在唯一性
《 计 算 方 法 》
线性插值和二次插值都属于代数多项式插值。对 于一般的代数插值问题,就是寻求一个不高于n次的代数 多项式 Pn(x)=a0+a1x+a2x2+…+anxn (4―9)
现要构造一个二次函数
φ(x)=P2(x)=ax2+bx+c 近似地代替f(x),并满足插值原则(4―2)
《 计 算 方 法 》
(4―6) (4―7)
P2(xi)=yi, i=0,1,2,… 由(4―7)式得
2 ax0 bx0 c y0 2 ax1 bx1 c y1 ax 2 bx c y 2 2 2
第4章 插值法
10 9
《 计 算 方 法 》
§ 曲 线 拟 合 法
§ 数 值 微 分
§
8
§ 7 牛 顿 前 差 和 后 差 插 值 多 项 式
§ 6 牛 顿 均 差 插 值 多 项 式
§
5
§ 4 代 数 多 项 式 的 余 项
§ 3 代 数 多 项 式 插 值 的 存 在 唯 一 性
y1 y0 a x1 x0 y1 y0 b y0 x0 x1 x0
第4章 插值法
代入式(4―3)得
y1 y0 P ( x1 x0 ) 1 ( x ) y0 x1 x0
《 计 算 方 法 》
(4―4)
图 4.1
第4章 插值法
A(x0,y0),B(x1,y1),C(x2,y2)的抛物线来近似地代替f(x),见图
4.2。
第4章 插值法
《 计 算 方 法 》
图 4.2
第4章 插值法
§3 代数多项式插值的存在唯一性
《 计 算 方 法 》
线性插值和二次插值都属于代数多项式插值。对 于一般的代数插值问题,就是寻求一个不高于n次的代数 多项式 Pn(x)=a0+a1x+a2x2+…+anxn (4―9)
现要构造一个二次函数
φ(x)=P2(x)=ax2+bx+c 近似地代替f(x),并满足插值原则(4―2)
《 计 算 方 法 》
(4―6) (4―7)
P2(xi)=yi, i=0,1,2,… 由(4―7)式得
2 ax0 bx0 c y0 2 ax1 bx1 c y1 ax 2 bx c y 2 2 2
第4章 插值法
10 9
《 计 算 方 法 》
§ 曲 线 拟 合 法
§ 数 值 微 分
§
8
§ 7 牛 顿 前 差 和 后 差 插 值 多 项 式
§ 6 牛 顿 均 差 插 值 多 项 式
§
5
§ 4 代 数 多 项 式 的 余 项
§ 3 代 数 多 项 式 插 值 的 存 在 唯 一 性
20_数值分析5_6曲线拟合
0x, 1x, , nx, n m,
{jx} ( C[a,b] ) 在点集 {x0,x1, , xm} 上线性无关 . 问题 在曲线族 y ( x )
n j0
c j j ( x ) 中寻找一条曲线
y*(x),
使其能按照某种原则去拟合数据(5.92), 用 y*(x) 代替数据 (5.92) 反映的函数关系.
求血药浓度随时间的变化规律c(t).
10
2
c (t ) c 0 e
10
1
kt
c , k 为待定系数
10
0
0
2
4
6
8
半对数坐标系(semilogy)下的图形
曲线拟合问题的提法
已知一组（二维）数据，即平面上 m+1个点（xi,yi) i=0,1,…m, 寻求一个函数（曲线）y=f(x), 使 f(x)在某种准 则下与所有数据点最为接近，即曲线拟合得最好。 y + + +
(5.97)
* c0 ( f , 0 ) * c1 ( f , 1 ) * cn ( f , n )
证 (必要性) 记
F (C ) ( A C Y , A C Y )
m
i0
A ( C C *) 0
A (C
C *), A ( C C *) 0 .
F ( C ) F ( C *)
方程 ATAC* ATY 叫做最小二乘的法方程 或正规方程.
由 ATA 的正定性, 知法方程的解存在且唯一.
五、最小二乘法的精度
拟合曲线对数据的拟合精度, 可用误差平方和 来刻画.
数值分析05曲线拟合
在次数确定之后， 在次数确定之后，只需确定多项式系数 令，
a0 , a1,L, an 即可
n n k
Q = ∑[ yk − P (xk )] = ∑ yk − (a0 + a1xk +La x ) n
2 k =0 k =0
m
m
[
]
2
我们的目的是求一组
使得Q最小 最小。 a0 , a1,L, an，使得 最小。
i =0 j =0
n m
m
n
m
j
j
i
k
i
i =0
m
i
k
i
∑[∑ϕ (x )ϕ (x )]a = ∑yϕ (x )
j =0 i =0 j i k i j i =0 i k i
k = 0,1,L, n
将上面的n+1个等式联立得到法方程组： 个等式联立得到法方程组： 将上面的 个等式联立得到法方程组
P⋅ a = b
xi
强 度 1.4 1.3 1.8 2.5 2.8 2.5 3 2.7 4 3.5 4.2 3.5
y i 编 号 拉伸倍数 x i
13 14 15 16 17 18 19 20 21 22 23 24 5 5.2 6 6.3 6.5 7.1 8 8 8.9 9 9.5 10
强度 5.5 5 5.5 6.4 6 5.3 6.5 7 8.5 8 8.1 8.1
Matlab程序：sample1.m 程序： 程序
二、一般线性最小二乘拟合
, , 是给定的一组数据， 设 (xi , yi ) ( i = 0,1 2,L m)是给定的一组数据，在给定的
函数类 Φ = span{ϕ0(x),ϕ1(x),L,ϕn(x)} 中，确定一个 函数
第五章曲线拟合PPT课件
第5章 曲线拟合
华南师范大学数学科学学院 谢骊玲
曲线拟合的概念
在科学和工程试验中，经常产生一组数据 (x1,y1),…,(xN,yN),如果所有的数值 {xk}, {yk} 有多位有效数字精度，则能用多项式插值； 若数据的精度不高，或者有试验误差，则 只能使用多项式拟合。
问题：如何找到一个经过数据点附近（不总是穿过） 的最佳逼近表达式？
线性最小二乘法（续2）
矩阵形式：构造矩阵F
f1(x1)
f1(x2 )
F
f1(x3 )
f1(xN )
f2 (x1) f2 (x2 ) f2 (x3 )
f2 (xN )
fM (x1)
f
M
(
x2
)
f
M
(
x3
)
fM (xN )
f1(x1)
则
F'
f2(x1)
f1(x2) f2(x2)
f1(x3) f2(x3)
华南师范大学数学科学学院 谢骊玲
多项式拟合
使用函数集合{fj(x)=xj-1}, j=1,…, M+1作线性最小 二乘，则得到的拟合函数f(x)为M阶多项式 f(x)=c1+c2x+c3x2+…+cM+1xM
使用最小二乘多项式拟合非线性数据的方法简单有 效，但如果数据不具有多项式特性，则求出的曲线可 能产生大的振荡。这种现象称为多项式摆动，它在高 阶多项式情况下更容易发生。由于这个原因，一般很 少使用超过6阶的多项式，除非已知被拟合的曲线是 真实的多项式。
几何意义是：数据点到曲线的垂直距离平方和最小
华南师范大学数学科学学院 谢骊玲
最小二乘拟合直线
定理5.1 设{(xk, yk)}kN1有N个点，其中横坐标{xk}是
华南师范大学数学科学学院 谢骊玲
曲线拟合的概念
在科学和工程试验中，经常产生一组数据 (x1,y1),…,(xN,yN),如果所有的数值 {xk}, {yk} 有多位有效数字精度，则能用多项式插值； 若数据的精度不高，或者有试验误差，则 只能使用多项式拟合。
问题：如何找到一个经过数据点附近（不总是穿过） 的最佳逼近表达式？
线性最小二乘法（续2）
矩阵形式：构造矩阵F
f1(x1)
f1(x2 )
F
f1(x3 )
f1(xN )
f2 (x1) f2 (x2 ) f2 (x3 )
f2 (xN )
fM (x1)
f
M
(
x2
)
f
M
(
x3
)
fM (xN )
f1(x1)
则
F'
f2(x1)
f1(x2) f2(x2)
f1(x3) f2(x3)
华南师范大学数学科学学院 谢骊玲
多项式拟合
使用函数集合{fj(x)=xj-1}, j=1,…, M+1作线性最小 二乘，则得到的拟合函数f(x)为M阶多项式 f(x)=c1+c2x+c3x2+…+cM+1xM
使用最小二乘多项式拟合非线性数据的方法简单有 效，但如果数据不具有多项式特性，则求出的曲线可 能产生大的振荡。这种现象称为多项式摆动，它在高 阶多项式情况下更容易发生。由于这个原因，一般很 少使用超过6阶的多项式，除非已知被拟合的曲线是 真实的多项式。
几何意义是：数据点到曲线的垂直距离平方和最小
华南师范大学数学科学学院 谢骊玲
最小二乘拟合直线
定理5.1 设{(xk, yk)}kN1有N个点，其中横坐标{xk}是
《曲线拟合》PPT课件
曲线拟合
Curve fitting
医学研究中X和Y的数量关系常常不是线性的，如毒 物剂量与动物死亡率，人的生长曲线，药物动力学等， 都不是线性的。如果用线性描述将丢失大量信息，甚至 得出错误结论。
此时可以用曲线直线化估计（Curve estimation） 或非线性回归(Nonlinear regression) 方法分析。
散点图辨析
预后指数Y
60 50 40 30 20 10
0 0
对数曲线 指数曲线
10 20 30 40 50 60 70 病人住院天数X
如果条件允许最好采用非线性回 归（Nonlinear Regression）拟合幂 函数曲线与指数函数曲线
注意绘制散点图，并结合专业知 识解释
采用SAS进行曲线拟合
①幂函数： Yˆ ea X b 或 ln(Yˆ) a bln(X )
②对数：
Yˆ a bln(X )
③指数函数： Yˆ eabX
或 ln(Yˆ) a bX
④多项式： Yˆ a b1X b2 X 2 bn X n
⑤logistic：
Yˆ
1/(1
eabX
)
或
ln[
Yˆ
/(1
Yˆ)]
-8.0196 -4.0604 0.0000 3.9012 7.6049 11.1860 -12.8898
Yˆ
7.23 12.62 15.77 18.01 19.75 21.16 22.36
23.40
残差平方
0.1380 0.1017 0.0053 0.0361 1.0921 0.0563 0.0566 0.1597
(lnX)2 Y2
2.5902 57.76 0.8396 151.29 0.2609 246.49 0.0498 331.24 0.0000 349.69 0.0332 457.96 0.1132 510.76 0.2209 566.44 4.1078 2671.63
Curve fitting
医学研究中X和Y的数量关系常常不是线性的，如毒 物剂量与动物死亡率，人的生长曲线，药物动力学等， 都不是线性的。如果用线性描述将丢失大量信息，甚至 得出错误结论。
此时可以用曲线直线化估计（Curve estimation） 或非线性回归(Nonlinear regression) 方法分析。
散点图辨析
预后指数Y
60 50 40 30 20 10
0 0
对数曲线 指数曲线
10 20 30 40 50 60 70 病人住院天数X
如果条件允许最好采用非线性回 归（Nonlinear Regression）拟合幂 函数曲线与指数函数曲线
注意绘制散点图，并结合专业知 识解释
采用SAS进行曲线拟合
①幂函数： Yˆ ea X b 或 ln(Yˆ) a bln(X )
②对数：
Yˆ a bln(X )
③指数函数： Yˆ eabX
或 ln(Yˆ) a bX
④多项式： Yˆ a b1X b2 X 2 bn X n
⑤logistic：
Yˆ
1/(1
eabX
)
或
ln[
Yˆ
/(1
Yˆ)]
-8.0196 -4.0604 0.0000 3.9012 7.6049 11.1860 -12.8898
Yˆ
7.23 12.62 15.77 18.01 19.75 21.16 22.36
23.40
残差平方
0.1380 0.1017 0.0053 0.0361 1.0921 0.0563 0.0566 0.1597
(lnX)2 Y2
2.5902 57.76 0.8396 151.29 0.2609 246.49 0.0498 331.24 0.0000 349.69 0.0332 457.96 0.1132 510.76 0.2209 566.44 4.1078 2671.63
数值分析课件Chapter7曲线拟合与线性最小二乘问题.ppt
法方程组可写成：GT F T FGx GT F T b
可以验证 x GT (GGT )1(F T F )1 F T b
是法方程组的一个解，故是原方程组的一个最小二乘解
推论7.1.2 若 rankA ，r则方n程组
有无穷多个最小二乘解。
Ax b
Def 2 方程组 Ax b 的所有最小二乘解中2-范数最小
8.9
8.5
10
4
3.5
22
9
8
11
4.5
4.2
23
9.5
8.1
12
4.6
3.5
24
10
8.1
可以看出,纤维强度随 拉伸倍数增加而增加
并且24个点大致分 布在一条直线附近
因此可认为强度与 拉伸倍数之间的主 要关系是线性关系
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
y ( x ) a bx
该直线称为这一问题的数学模型。
线性无关，下面讨论正交分解的具体实现方法。
记 A [a1, a2 , , an ]，Q [q1, q2 , , qr ] 其中 a1, a2 , , ar线性无关，q1, q2 , , qr两两正交。
Gram-Schmidt正交化方法： 由 A QU 得
a1 u11q1 a2 u12q1 u22q2
y a bx c 1 x
1( x) 1;
2(x)
x;
3(x)
1 x
三、最小二乘问题解的存在性、唯一性
Def 1 设 A R，m若n 存在 x 精R确n地满足
可以验证 x GT (GGT )1(F T F )1 F T b
是法方程组的一个解，故是原方程组的一个最小二乘解
推论7.1.2 若 rankA ，r则方n程组
有无穷多个最小二乘解。
Ax b
Def 2 方程组 Ax b 的所有最小二乘解中2-范数最小
8.9
8.5
10
4
3.5
22
9
8
11
4.5
4.2
23
9.5
8.1
12
4.6
3.5
24
10
8.1
可以看出,纤维强度随 拉伸倍数增加而增加
并且24个点大致分 布在一条直线附近
因此可认为强度与 拉伸倍数之间的主 要关系是线性关系
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
y ( x ) a bx
该直线称为这一问题的数学模型。
线性无关，下面讨论正交分解的具体实现方法。
记 A [a1, a2 , , an ]，Q [q1, q2 , , qr ] 其中 a1, a2 , , ar线性无关，q1, q2 , , qr两两正交。
Gram-Schmidt正交化方法： 由 A QU 得
a1 u11q1 a2 u12q1 u22q2
y a bx c 1 x
1( x) 1;
2(x)
x;
3(x)
1 x
三、最小二乘问题解的存在性、唯一性
Def 1 设 A R，m若n 存在 x 精R确n地满足
数值分析ppt第3章_函数逼近与曲线拟合
则称(u, v) 为X上u与v的内积，对应了内积的线性空间 称为内积空间. 定义中(1)当K为实数域R时为 (u, v)＝(v, u) .
上页 下页
如果(u, v)=0，则称u与v正交(记为u⊥v)，这是 向量相互垂直概念的推广. 关于内积空间有以下重 要定理. 定理2 设X为一个内积空间,对任意u, v∈X有如 下不等式成立
上页 下页
如果x, y∈ Cn，带权内积定义为
( x , y ) i xi yi
i 1பைடு நூலகம்
n
(14)
这里{ωi}仍为正实数序列. 在C[a, b]上也可以类是定义带权内积，为此先给 出权函数定义.
上页
下页
定义4 设[a, b]是有限或无限区间，在[a, b]上的 非负函数ρ(x)满足条件：
( u, v ) ( u, u)( v , v ).
它称为柯西－施瓦茨(Cauchy-Schwarz)不等式.
2
上页
下页
证明 当v=0时,显然成立. 设v≠0，则 (v, v)>0,
且对任何数t 有(这里设为实空间)
0 ( u tv, u tv) ( u, u) 2t ( u, v ) t (v , v ).
上页
下页
3.1.3 内积与内积空间
在线性代数中，Rn上的两个向量 x＝(x1,x2,…,xn)T
与y＝(y1,y2,…,yn)T的内积定义为
(x, y)= x1 y1 +x2 y2 +…+xn yn. 若将它推广到一般的线性空间X，则有下面的定义.
上页
下页
定义3 设X是数域K(R或C)上的线性空间，对任 意u,v∈X，有K中一个数与之对应，记为(u, v)，它满 足以下条件：
上页 下页
如果(u, v)=0，则称u与v正交(记为u⊥v)，这是 向量相互垂直概念的推广. 关于内积空间有以下重 要定理. 定理2 设X为一个内积空间,对任意u, v∈X有如 下不等式成立
上页 下页
如果x, y∈ Cn，带权内积定义为
( x , y ) i xi yi
i 1பைடு நூலகம்
n
(14)
这里{ωi}仍为正实数序列. 在C[a, b]上也可以类是定义带权内积，为此先给 出权函数定义.
上页
下页
定义4 设[a, b]是有限或无限区间，在[a, b]上的 非负函数ρ(x)满足条件：
( u, v ) ( u, u)( v , v ).
它称为柯西－施瓦茨(Cauchy-Schwarz)不等式.
2
上页
下页
证明 当v=0时,显然成立. 设v≠0，则 (v, v)>0,
且对任何数t 有(这里设为实空间)
0 ( u tv, u tv) ( u, u) 2t ( u, v ) t (v , v ).
上页
下页
3.1.3 内积与内积空间
在线性代数中，Rn上的两个向量 x＝(x1,x2,…,xn)T
与y＝(y1,y2,…,yn)T的内积定义为
(x, y)= x1 y1 +x2 y2 +…+xn yn. 若将它推广到一般的线性空间X，则有下面的定义.
上页
下页
定义3 设X是数域K(R或C)上的线性空间，对任 意u,v∈X，有K中一个数与之对应，记为(u, v)，它满 足以下条件：
3.4 离散数据的曲线拟合——数值分析课件PPT
i 1
i 1
பைடு நூலகம்
i 1
以上计算可用下表的形式表示（更简便）
i xi yi xi2
xi3
0 0.00 0.10 0.00
1 0.25 0.35 0.0625
2 0.50 0.81 0.25
3 0.75 1.09 0.5625
4 1.00 1.96 1.00
xi4
xi yi xi2 yi
2.5 4.31 1.875 1.5625 1.3828 3.27 2.7975
a
(a0*
,,
an*
)T，
d (( f ,0),,( f ,n))T ,
结论： （1）必要条件
误差与基函数正 交
n
由(3.4.3) (k , j )a*j ( f ,k ) j0
(k 0,1,, n),
n
(k , a*j j ) ( f ,k ) (k 0,1,, n), j0
得( f p*,k ) 0，(k 0,1, , n)
以上的平方误差与连续函数最佳平方逼近的平方误 差有相同形式的表达式。
(2)多项式的拟合
前面讨论了子空间 S 中的最小二乘拟合。 在离散数据 { xi , yi }mi0 的最小
二乘拟合中，最简单、最常用的数学模型是多项式
p(x) a0 a1x an xn.
即在多项式空间 span{1, x,, xn } 中作曲线拟合，称为多项式拟合。
5
(0,0 ) 11 5 i 1
5
(1,2 ) xi xi2 1.5625 i 1
5
5
(0,1) 1 xi 2.5 (1,1) xi2 1.875
i 1
i 1
5
Chapter6曲线拟合_数值分析
第六章 曲线拟合
6.1.2 曲线拟合问题
仍然是已知 x1 … xm ; y1 … ym, 求一个简单易 算的近似函数 f(x) 来拟合这些数据。
但是① m 很大；
②
yi 本身是测量值，不准确，即 yi f (xi)
这时没必要取 f(xi) = yi , 而要使 i=f(xi) yi 总体上
定理6.3.3 设A是n×k阶矩阵，x∈Rn, 那么下列三种情况是 等价的： ①x⊥R(A); ②AＴx=0; ③x∈N(AＴ). 这里，N(AＴ)={AＴx=0, x∈Rn}称为AＴ的核子空间. 证：由N(AＴ)的定义， ②与③显然等价. 下面证明①与②等价. 记A=(α1,α2,…，αk)， 那么，αi∈R(A) (i=1,2,…,k). 假设x⊥R(A), 即αiＴx=0 (i=1,2,…，k). 从而AＴx=0. 另一方面，如果AＴx=0, 那么有z∈Rk， 使Az=y∈R(A). 这时，yＴx=zＴAＴx=0,即x⊥y. 由z的任意性， 得Az是任意的， 因此x⊥R(A).
• 设U是Rn中的子空间， x∈Rn. 如果x与U中 任意向量正交， 称向量x与子空间U正交， 记为x⊥U. • 设U，V是Rn中两个子空间， 如果任意x∈U 和任意y∈V是正交的， 称子空间U与子空 间V正交， 记为U⊥V. • 设U，V是Rn中互补的子空间. 如果U⊥V， 那么称U，V互为正交补子空间， 记U=V⊥ 或V=U⊥. 可以证明， 一个子空间的正交补 子空间是惟一的.
法方程组(或正规方程组)
例1
数据 ti 0 20 40 60 80 100 fi 81.4 77.7 74.2 72.4 70.3 68.8
6.3 线性最小二乘问题
设A是m×n阶矩阵(m>n), 称线性方程组 Ax=b (1) 为超定方程组; 这里x∈Rn,b∈Rm. 如果A的秩r(A)=n, 称A为列满秩矩阵. 记残向量r=b-Ax，考虑确定一个向量x， 使‖r‖2 2＝‖b-Ax‖2 2, 达到最小的问题称 为线性最小二乘问题， 这样的x称为方程组(1) 的最小二乘解.
6.1.2 曲线拟合问题
仍然是已知 x1 … xm ; y1 … ym, 求一个简单易 算的近似函数 f(x) 来拟合这些数据。
但是① m 很大；
②
yi 本身是测量值，不准确，即 yi f (xi)
这时没必要取 f(xi) = yi , 而要使 i=f(xi) yi 总体上
定理6.3.3 设A是n×k阶矩阵，x∈Rn, 那么下列三种情况是 等价的： ①x⊥R(A); ②AＴx=0; ③x∈N(AＴ). 这里，N(AＴ)={AＴx=0, x∈Rn}称为AＴ的核子空间. 证：由N(AＴ)的定义， ②与③显然等价. 下面证明①与②等价. 记A=(α1,α2,…，αk)， 那么，αi∈R(A) (i=1,2,…,k). 假设x⊥R(A), 即αiＴx=0 (i=1,2,…，k). 从而AＴx=0. 另一方面，如果AＴx=0, 那么有z∈Rk， 使Az=y∈R(A). 这时，yＴx=zＴAＴx=0,即x⊥y. 由z的任意性， 得Az是任意的， 因此x⊥R(A).
• 设U是Rn中的子空间， x∈Rn. 如果x与U中 任意向量正交， 称向量x与子空间U正交， 记为x⊥U. • 设U，V是Rn中两个子空间， 如果任意x∈U 和任意y∈V是正交的， 称子空间U与子空 间V正交， 记为U⊥V. • 设U，V是Rn中互补的子空间. 如果U⊥V， 那么称U，V互为正交补子空间， 记U=V⊥ 或V=U⊥. 可以证明， 一个子空间的正交补 子空间是惟一的.
法方程组(或正规方程组)
例1
数据 ti 0 20 40 60 80 100 fi 81.4 77.7 74.2 72.4 70.3 68.8
6.3 线性最小二乘问题
设A是m×n阶矩阵(m>n), 称线性方程组 Ax=b (1) 为超定方程组; 这里x∈Rn,b∈Rm. 如果A的秩r(A)=n, 称A为列满秩矩阵. 记残向量r=b-Ax，考虑确定一个向量x， 使‖r‖2 2＝‖b-Ax‖2 2, 达到最小的问题称 为线性最小二乘问题， 这样的x称为方程组(1) 的最小二乘解.
数值分析曲线拟合最新PPT资料
（4.4）
由求多元函数极值的必要条件，有
I
ck
m
n
2 [ f (xi ) c j j (xi )]k (xi ) 0
i0
j0
(k 0,1,, n).
这里关于c0, c1,..., cn的线性方程组,可以改写为
当k
0时,
Q c0
m
0,有 [
i0
f
(xi )
n
cj
j0
j (xi )]0 (xi )
其中输入参数 为要拟合的数据0， 为0拟合多项式的次1 数1，
nn
关于多项式拟合，Matlab中有现成的程序
用最小二乘标准构造出误差的平方和 用最小二乘标准构造出误差的平方和
大致猜测离散数据,应符合的函数关系式 用最小二乘标准构造出误差的平方和
Q(c , c ,..., c ) [ f ( x ) ( x )] (正1)交根、据正离交散函数数据族描、点标画准散正点交图函,由数散族点图中点的分m布情况
0
0
10
i0 10
yi
10
( 1)c0
i0
10
10
(
i0
xi )c1
10
10
,内积( X ,Y ) xi yi
0
i0
xi yi
(
i0
xi )c0
(
i0
xi2 )c1
i0
(3)由最小二乘法得标准方程(正规方程)
10
i0 10
yi
10
( 1)c0
i0
10
10
(
i0
xi )c1
m
即 [ f (xi ) s(xi )]2最小 (最小二乘标准) i0