[VIP专享]错解剖析得真知数学必修五错题集

合集下载

(新)高中数学错解剖析得真知(四)

错解剖析得真知（三十一）第十章导数及其应用§10.1导数及其运算一、知识导学1.瞬时变化率：设函数在附近有定义，当自变量在附近改变量为时，函数值相应地改变，如果当趋近于0时，平均变化率趋近于一个常数c（也就是说平均变化率与某个常数c的差的绝对值越来越小，可以小于任意小的正数），那么常数c称为函数在点的瞬时变化率。

2.导数：当趋近于零时，趋近于常数c。

可用符号“”记作：当时，或记作，符号“”读作“趋近于”。

函数在的瞬时变化率，通常称作在处的导数，并记作。

3.导函数：如果在开区间内每一点都是可导的，则称在区间可导。

这样，对开区间内每个值，都对应一个确定的导数。

于是，在区间内，构成一个新的函数，我们把这个函数称为函数的导函数。

记为或（或）。

4.导数的四则运算法则：1）函数和（或差）的求导法则：设，是可导的，则即，两个函数的和（或差）的导数，等于这两个函数的导数的和（或差）。

2）函数积的求导法则：设，是可导的，则即，两个函数的积的导数，等于第一个函数的导数乘上第二个函数，加上第一个函数乘第二个函数的导数。

3）函数的商的求导法则：设，是可导的，，则5.复合函数的导数:设函数在点处有导数,函数在点的对应点处有导数,则复合函数在点处有导数,且.6.几种常见函数的导数：(1) (2)(3) (4)(5) (6)(7) (8)二、疑难知识导析1.导数的实质是函数值相对于自变量的变化率2.运用复合函数的求导法则,应注意以下几点（1）利用复合函数求导法则求导后,要把中间变量换成自变量的函数,层层求导.(2) 要分清每一步的求导是哪个变量对哪个变量求导，不能混淆，一直计算到最后，常出现如下错误，如实际上应是。

(3) 求复合函数的导数，关键在于分清楚函数的复合关系，选好中间变量，如选成，计算起来就复杂了。

3.导数的几何意义与物理意义导数的几何意义，通常指曲线的切线斜率.导数的物理意义，通常是指物体运动的瞬时速度。

数学运算错题集(三)(201-300题)剖析

数学运算错题集（三）201、某商场开展购物优惠活动：一次购买300元及以下的商品九折优惠；一次购买超过300元的商品，其中300元九折优惠，超过300元的部分八折优惠。

小王购物第一次付款144元，第二次又付款310元。

如果他―次购买并付款，可以节省多少元？（）A. 16B.22.4C.30.6D.48202、甲、乙两地相距10千米。

A以每小时5千米的速度从甲地步行前往乙地，每行走60分钟他要休息20分钟。

B以每小时3千米的速度从乙地步行前往甲地，每行走30分钟他要休息10分钟。

如果他们都是8点整出发，那么他们相遇的时间是（）A. 9点15B. 9点35C. 9点40D. 9点50答案：B方法一：代入法：对于走走停停的题目，斜月沉沉老师教过大家“代入法”。

我们代入C，C时刻，距离出发是100分钟，A走了80分钟，走了5＋5/3，B走了80分钟，走了4千米，这个时候AB一共走了超过10，所以直接秒杀B。

方法二：甲每行走60分钟他要休息20分钟。

乙每行走30分钟他要休息10分钟，1小时20分钟后，他们刚好走了5+3=8米，还是两米的距离，又同时开始走，那么2/(5+3)=1/4小时，刚好15分钟，于是1小时20分钟+15分钟，刚好是1小时35分钟，从8点整出发，1小时35分钟，是9:35. 203、（2006浙江）从平面a外一点P引与a相交的直线，使得点与交点的距离等于1，则满足条件的直线条数一定不可能是：（）A. 0条B. 1条C. 2条D. 无数条答案：C根据题意可知，存在三种情况：（1）当P点到该平面的距离为1时，这样的直线只有一条，（2）当P点到该平面的距离小于1时，这样的直线有无数条；（3）当P点到该平面的距离大于1时，这样的直线不存在。

因此，选C。

204、为迎接校运动会学生会决定将160把折扇平均分给甲乙两个社团，由于乙社团另有任务，所以甲社团开始工作3小时后，乙社团才开始工作，因此比甲社团推迟20分钟完成任务，已知，乙社团每小时制作折扇个数是甲三倍，则乙社团每个时制作（）个。

高中必修1-5错解分析--第1-3章修改稿

第一章集合与常用逻辑用语§1.1 集合的概念与运算一、知识导学1.集合：一般地，一定范围内某些确定的、不同的对象的全体构成一个集合.2.元素：集合中的每一个对象称为该集合的元素，简称元.3.子集：如果集合A 的任意一个元素都是集合B 的元素（若A a ∉则B a ∈），则称集合A 为集合B 的子集，记为A ⊆B 或B ⊇A ；如果A ⊆B ，并且A ≠B ，这时集合A 称为集合B 的真子集，记为A B 或B A.4.集合的相等：如果集合A 、B 同时满足A ⊆B 、B ⊇A ，则A=B.5.补集：设A ⊆S ，由S 中不属于A 的所有元素组成的集合称为S 的子集A 的补集，记为 A C s .6.全集：如果集合S 包含所要研究的各个集合，这时S 可以看做一个全集，全集通常记作U.7.交集：一般地，由所有属于集合A 且属于B 的元素构成的集合，称为A 与B 的交集，记作A ⋂B.8.并集：一般地，由所有属于集合A 或者属于B 的元素构成的集合，称为A 与B 的并集，记作A ⋃B.9.空集：不含任何元素的集合称为空集，记作Φ.10.有限集：含有有限个元素的集合称为有限集.11.无限集：含有无限个元素的集合称为无限集.12.集合的常用表示方法：列举法、描述法、图示法（Venn 图）.13.常用数集的记法：自然数集记作N ，正整数集记作N +或N *，整数集记作Z ，有理数集记作Q ，实数集记作R .二、疑难知识导析1.符号⊆，，⊇，，=，表示集合与集合之间的关系，其中“⊆”包括“”和“=”两种情况，同样“⊇”包括“”和“=”两种情况.符号∈，∉表示元素与集合之间的关系.要注意两类不同符号的区别.2.在判断给定对象能否构成集合时，特别要注意它的“确定性”，在表示一个集合时，要特别注意它的“互异性”、“无序性”.3.在集合运算中必须注意组成集合的元素应具备的性质.4.对由条件给出的集合要明白它所表示的意义，即元素指什么，是什么范围．用集合表示不等式（组）的解集时，要注意分辨是交集还是并集，结合数轴或文氏图的直观性帮助思维判断．空集是任何集合的子集，但因为不好用文氏图形表示，容易被忽视，如在关系式中，B =Φ易漏掉的情况.5.若集合中的元素是用坐标形式表示的，要注意满足条件的点构成的图形是什么，用数形结合法解之.6.若集合中含有参数，须对参数进行分类讨论，讨论时既不重复又不遗漏.7.在集合运算过程中要借助数轴、直角坐标平面、Venn 图等将有关集合直观地表示出来.8.要注意集合与方程、函数、不等式、三角、几何等知识的密切联系与综合使用.9.含有n 个元素的集合的所有子集个数为：n 2，所有真子集个数为：n 2-1三、经典例题导讲[例1] 已知集合M={y |y =x 2＋1,x∈R },N={y|y =x ＋1,x∈R }，则M∩N=（）A ．（0，1），（1，2）B ．{（0，1），（1，2）}C ．{y|y=1,或y=2}D ．{y|y≥1}错解：求M∩N 及解方程组⎩⎨⎧+=+=112x y x y 得⎩⎨⎧==10y x 或 ⎩⎨⎧==21y x ∴选B错因：在集合概念的理解上，仅注意了构成集合元素的共同属性，而忽视了集合的元素是什么．事实上M 、N 的元素是数而不是实数对(x,y )，因此M 、N 是数集而不是点集,M 、N 分别表示函数y =x 2＋1(x∈R )，y =x ＋1(x∈R )的值域，求M∩N 即求两函数值域的交集．正解：M={y |y =x 2＋1,x∈R }={y |y ≥1}， N={y|y=x ＋1,x∈R }={y|y∈R }．∴M∩N={y |y ≥1}∩{y|(y∈R)}={y |y ≥1}, ∴应选D ．注：集合是由元素构成的，认识集合要从认识元素开始，要注意区分{x |y =x 2＋1}、{y |y =x2＋1,x ∈R }、{(x ,y )|y =x 2＋1,x ∈R }，这三个集合是不同的．[例2] 已知A={x |x 2－3x ＋2=0},B={x |ax －2=0}且A∪B=A，求实数a 组成的集合C ．错解：由x 2－3x ＋2=0得x =1或2．当x =1时，a =2，当x =2时，a=1．错因：上述解答只注意了B 为非空集合，实际上，B=时，仍满足A∪B=A .当a =0时，B=，符合题设，应补上，故正确答案为C={0，1，2}．正解：∵A∪B=A ∴B A 又A={x |x 2－3x ＋2=0}={1，2}∴B=或{}{}21或 ∴C={0，1，2}[例3]已知m ∈A,n ∈B, 且集合A={}Z a a x x ∈=,2|，B={}Z a a x x ∈+=,12|，又C={}Z a a x x ∈+=,14|，则有：（）A ．m +n ∈A B. m +n ∈B C.m +n ∈C D. m +n 不属于A ，B ，C 中任意一个错解：∵m ∈A ，∴m =2a ,a Z ∈,同理n =2a +1,a ∈Z, ∴m +n =4a +1,故选C错因是上述解法缩小了m +n 的取值范围.正解：∵m ∈A, ∴设m =2a 1,a 1∈Z , 又∵n B ∈,∴n =2a 2+1,a 2∈ Z ,∴m +n =2(a 1+a 2)+1,而a 1+a 2∈ Z , ∴m +n ∈B, 故选B.[例4］已知集合A={x|x 2－3x －10≤0}，集合B={x|p ＋1≤x≤2p－1}．若BA ，求实数p 的取值范围．错解：由x 2－3x －10≤0得－2≤x≤5．欲使B A ，只须3351212≤≤-⇒⎩⎨⎧≤-+≤-p p p ∴ p 的取值范围是－3≤p≤3.错因：上述解答忽略了"空集是任何集合的子集"这一结论，即B=时，符合题设．正解：①当B≠时，即p ＋1≤2p－1p≥2.由B A 得：－2≤p＋1且2p －1≤5.由－3≤p≤3.∴ 2≤p≤3②当B=时，即p ＋1>2p －1p ＜2.由①、②得：p≤3.点评：从以上解答应看到：解决有关A∩B=、A∪B=，A B 等集合问题易忽视空集的情况而出现漏解，这需要在解题过程中要全方位、多角度审视问题．[例5] 已知集合A={a,a ＋b,a ＋2b}，B={a,ac,ac 2}．若A=B ，求c 的值．分析：要解决c 的求值问题，关键是要有方程的数学思想，此题应根据相等的两个集合元素完全相同及集合中元素的确定性、互异性，无序性建立关系式．解：分两种情况进行讨论．（1）若a ＋b=ac 且a ＋2b=ac 2，消去b 得：a ＋ac 2－2ac=0，a=0时，集合B 中的三元素均为零，和元素的互异性相矛盾，故a≠0．∴c 2－2c ＋1=0，即c=1，但c=1时，B 中的三元素又相同，此时无解．（2）若a ＋b=ac 2且a ＋2b=ac ，消去b 得：2ac 2－ac －a=0，∵a≠0，∴2c 2－c －1=0，即(c －1)(2c ＋1)=0，又c≠1，故c=－21．点评：解决集合相等的问题易产生与互异性相矛盾的增解，这需要解题后进行检验. [例6] 设A 是实数集，满足若a∈A，则a -11∈A ，1≠a 且1∉A. ⑴若2∈A，则A 中至少还有几个元素？求出这几个元素.⑵A 能否为单元素集合？请说明理由.⑶若a∈A，证明：1－a1∈A. ⑷求证：集合A 中至少含有三个不同的元素.解：⑴2∈A ⇒ －1∈A ⇒21∈A ⇒ 2∈A ∴ A 中至少还有两个元素：－1和21 ⑵如果A 为单元素集合，则a ＝a -11 即12+-a a ＝0该方程无实数解，故在实数范围内，A 不可能是单元素集⑶a∈A ⇒ a -11∈A ⇒ a --1111∈A ⇒111---a a ∈A ，即1－a 1∈A ⑷由⑶知a∈A 时，a-11∈A， 1－a 1∈A .现在证明a,1－a 1, a -11三数互不相等.①若a=a -11,即a2-a+1=0 ，方程无解，∴a ≠a-11 ②若a=1－a 1，即a 2-a+1=0，方程无解∴a ≠1－a1 ③若1－a 1 =a -11，即a2-a+1=0，方程无解∴1－a 1≠a -11. 综上所述，集合A 中至少有三个不同的元素.点评：⑷的证明中要说明三个数互不相等，否则证明欠严谨.[例7] 设集合A={a |a =12+n ,n ∈N +}，集合B={b |b =542+-k k ,k ∈N +}，试证：A B ．证明：任设a ∈A，则a =12+n =(n ＋2)2－4(n ＋2)＋5 (n ∈N +), ∵ n∈N*，∴ n ＋2∈N*∴ a∈B 故 ①显然，1{}*2,1|Nn n a a A ∈+==∈，而由 B={b |b =542+-k k ,k ∈N +}={b |b =1)2(2+-k ，k ∈N +}知1∈B，于是A≠B②由①、② 得A B ．点评：（1）判定集合间的关系，其基本方法是归结为判定元素与集合之间关系．（2）判定两集合相等，主要是根据集合相等的定义．四、典型习题导练1．集合A={x|x 2－3x －10≤0，x ∈Z}，B={x|2x 2－x －6＞0， x ∈ Z}，则A ∩B 的非空真子集的个数为（）A ．16B ．14C ．15D ．322．数集{1，2，x 2－3}中的x 不能取的数值的集合是（）A ．{2，-2 }B ．{－2，－5 }C ．{±2，±5 }D ．{5，－5}3. 若P={y|y=x 2,x∈R}，Q={y|y=x 2＋1,x∈R}，则P∩Q 等于（）A ．PB ．QC ．D ．不知道4. 若P={y|y=x 2,x∈R}，Q={(x ，y)|y=x 2,x∈R}，则必有（）A ．P∩Q=B ．P QC ．P=QD ．PQ5．若集合M ＝｛11|<xx ｝，N ＝{x |2x ≤x }，则M N ＝（） A ．}11|{<<-x x B ．}10|{<<x xC ．}01|{<<-x xD ．∅6.已知集合A={x|x 2＋(m ＋2)x ＋1=0,x∈R }，若A∩R ＋=，则实数m 的取值范围是_________．7.（06高考全国II 卷）设a R ∈，函数2()22.f x ax x a =--若()0f x >的解集为A ，{}|13,B x x A B φ=<<≠，求实数a 的取值范围。

高一数学必修5不等式易错题及错解分析

必修 5 不等式易错题及错解剖析一、选择题：1．设 f ( x) lg x , 若 0<a<b<c, 且 f(a)>f(b)>f(c),则以下结论中正确的选项是A (a-1)(c-1)>0B ac>1C ac=1D ac>1错解原由是没有数形联合意识 , 正解是作出函数f ( x)lg x 的图象 , 由图可得出选 D.2．不等式 ( x 1) x 20 的解集是A { x | x 1}B { x | x 1}C { x | x 2且x 1}D { x | x2或 x 1}错解：选 B ，不等式的等价转变出现错误，没考虑 x=-2 的情况。

正确答案为 D 。

3．某工厂第一年的产量为 A ，第二年的增加率为 a, 第三年的增加率为b ，这两年的均匀增长率为 x, 则Axa b xa b Cxab D xa bB2222错解：对观点理解不清，不可以灵巧运用均匀数的关系。

正确答案为B 。

4．已知1 a b 3且2a b 4 ，则 2a+3b 的取值范围是A(13,17) B ( 7,11) C ( 7,13) D( 9 ,13)2 2 2 22 22 2错解：对条件“ 1 a b 3且2 a b 4 ”不是等价转变，解出 a,b 的范围，再求 2a+3b的范围，扩大了范围。

正解：用待定系数法，解出2a+3b= 5(a+b)1 (a-b), 求出结果为22D 。

5．若不等式 ax 2 +x+a ＜ 0 的解集为 Φ，则实数 a 的取值范围（）A a ≤ - 1 或 a ≥1B a ＜1C -1≤ a ≤1D a≥12222 22正确答案： D错因：学生对一元二次不等式与二次函数的图象之间的关系还不可以掌握。

6．已知函数 y=㏒ 1 (3x2ax5)在 [-1 ，+∞）上是减函数，则实数a 的取值范围（）2A a ≤ -6B - 60 ＜ a ＜-6C -8＜ a ≤ -6 D － 8≤ a ≤-6正确答案： C错因：学生忘掉考虑定义域真数大于0 这一隐含条件。

【易错题】高中必修五数学上期末试题(含答案)(1)

【易错题】高中必修五数学上期末试题(含答案)(1)一、选择题1．若函数y ＝f (x )满足：集合A ＝{f (n )|n ∈N *}中至少有三个不同的数成等差数列，则称函数f (x )是“等差源函数”，则下列四个函数中，“等差源函数”的个数是( ) ①y ＝2x ＋1；②y ＝log 2x ；③y ＝2x＋1；④y ＝sin44x ππ+（）A ．1B ．2C ．3D ．42．已知在中，，，分别为角，，的对边，为最小角，且，，，则的面积等于（） A ．B ．C ．D ．3．已知点(),P x y 是平面区域()4{04y x y x m y ≤-≤≥-内的动点, 点()1,1,A O -为坐标原点, 设()OP OA R λλ-∈u u u r u u u r的最小值为M ,若2M ≤恒成立, 则实数m 的取值范围是（）A ．11,35⎡⎤-⎢⎥⎣⎦B ．11,,35⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭C ．1,3⎡⎫-+∞⎪⎢⎣⎭D ．1,2⎡⎫-+∞⎪⎢⎣⎭4．数列{}{},n n a b 为等差数列，前n 项和分别为,n n S T ，若3n 22n n S T n +=，则77a b =（） A ．4126B ．2314C ．117D ．1165．设x y ，满足约束条件70310,350x y x y x y +-⎧⎪-+⎨⎪--⎩，，„„…则2z x y =-的最大值为（）.A ．10B ．8C ．3D ．26．在等差数列{}n a 中，若1091a a <-，且它的前n 项和n S 有最大值，则使0n S >成立的正整数n 的最大值是（） A ．15B ．16C ．17D ．147．数列{}n a 中，对于任意,m n N *∈，恒有m n m n a a a +=+，若118a =，则7a 等于( ) A ．712B ．714C ．74D ．788．在ABC ∆中，内角,,A B C 所对的边分别为,,a b c ，且()cos 4cos a B c b A =-，则cos2A =（） A ．78B ．18C．78-D ．18-9．若a 、b 、c >0且a (a ＋b ＋c )＋bc ＝4－23，则2a ＋b ＋c 的最小值为( )A ． 3－1B ． 3＋1C ．23＋2D ．23－210．变量,x y 满足条件1011x y y x -+≤⎧⎪≤⎨⎪>-⎩，则22(2)x y -+的最小值为（） A ．322B ．5C ．5D ．9211．如图，为了测量山坡上灯塔CD 的高度，某人从高为=40h 的楼AB 的底部A 处和楼顶B 处分别测得仰角为=60βo，=30αo ，若山坡高为=35a ，则灯塔高度是（）A ．15B ．25C ．40D ．6012．在等差数列 {}n a 中， n S 表示 {}n a 的前 n 项和，若 363a a += ，则 8S 的值为（）A ．3B ．8C ．12D ．24二、填空题13．若,a b ∈R ，0ab >，则4441a b ab++的最小值为___________.14．设x ＞0，y ＞0，x ＋2y ＝4，则(4)(2)x y xy++的最小值为_________.15．数列{}n a 满足：1a a =（a R ∈且为常数），()()()*13343n n n n n a a a n N a a +⎧->⎪=∈⎨-≤⎪⎩，当100a =时，则数列{}n a 的前100项的和100S 为________.16．《九章算术》“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第5节的容积为升；17．若x ，y 满足约束条件1300x y x y x y -≥-⎧⎪+≤⎪⎨≥⎪⎪≥⎩，则2z x y =-的最大值是__________．18．设n S 是等差数列{}n a 的前n 项和，若510S =，105S =-，则公差d =（___）． 19．若ABC ∆的三个内角45A =︒，75B =︒，60C =︒，且面积6S =+形的外接圆半径是______20．已知a b c R ∈、、，c 为实常数，则不等式的性质“a b a c b c >⇐+>+”可以用一个函数在R 上的单调性来解析，这个函数的解析式是()f x =_________三、解答题21．在()f x 中，角,,A B C 的对边分别为,,a b c ，满足(2)cos cos b c A a C -=． (1)求角A 的大小(2)若3a =，求ABC △的周长最大值．22．ABC △的内角,,A B C 的对边分别为,,a b c，且cos )()cos a B C c b A -=-．（1）求A ；（2）若b =D 在BC 边上，2CD =，3ADC π∠=，求ABC △的面积．23．在ABC ∆sin cos C c A =．（Ⅰ）求角A 的大小；（Ⅱ）若ABC S ∆，2b c +=+a 的值． 24．已知{}n a 为等差数列，且36a =-，60a =．（1）求{}n a 的通项公式；（2）若等比数列{}n b 满足18b =-，2123b a a a =++，求数列{}n b 的前n 项和公式． 25．在△ABC 中，已知AC ＝4，BC ＝3，cosB ＝－14. (1)求sin A 的值； (2)求·BA BC u u u v u u u v的值.26．已知函数()2sin(2)(||)2f x x πϕϕ=+<部分图象如图所示.（1）求ϕ值及图中0x 的值；（2）在ABC ∆中，角,,A B C 的对边分别为,,a b c，已知()2,c f C ==-sin B =2sin A ，求a 的值．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】①y ＝2x ＋1，n ∈N *，是等差源函数；②因为log 21，log 22，log 24构成等差数列，所以y ＝log 2x 是等差源函数；③y ＝2x ＋1不是等差源函数，因为若是，则2(2p ＋1)＝(2m ＋1)＋(2n ＋1)，则2p ＋1＝2m ＋2n ，所以2p ＋1－n ＝2m －n ＋1，左边是偶数，右边是奇数，故y ＝2x ＋1不是等差源函数； ④y ＝sin 44x ππ⎛⎫+⎪⎝⎭是周期函数，显然是等差源函数.答案：C.2．C解析：C 【解析】【分析】根据同角三角函数求出；利用余弦定理构造关于的方程解出，再根据三角形面积公式求得结果. 【详解】由余弦定理得：，即解得：或为最小角本题正确选项：【点睛】本题考查余弦定理解三角形、三角形面积公式的应用、同角三角函数关系，关键是能够利用余弦定理构造关于边角关系的方程，从而求得边长.3．C解析：C 【解析】试题分析：直线()4x m y =-恒过定点(0,4)，当0m >时，约束条件()4{04y x y x m y ≤-≤≥-对应的可行域如图，则()OP OA R λλ-∈u u u r u u u r的最小值为0M=，满足2M ≤，当0m =时，直线()4x m y =-与y 轴重合，平面区域()4{04y x y x m y ≤-≤≥-为图中y 轴右侧的阴影区域，则()OP OA R λλ-∈u u u r u u u r的最小值为0M =，满足2M ≤，当0m <时，由约束条件()4{04y x y x m y ≤-≤≥-表示的可行域如图，点P 与点B 重合时，()OP OA R λλ-∈u u u r u u u r的最小值为M OB =u u u r ，联立{(4)y x x m y ==-，解得44(,)11m mB m m --，所以421m OB m =-u u u r ，由4221m m ≤-，解得1135m -≤≤，所以103m -≤≤，综上所述，实数m 的取值范围是1,3⎡⎫-+∞⎪⎢⎣⎭，故选C.考点：简单的线性规划.【方法点晴】本题主要考查了二元一次不等式组所表示的平面区域、简单的线性规划求最值问题，着重考查了数形结合思想方法及分类讨论的数学思想方法的应用，关键是正确的理解题意，作出二元一次不等式组所表示的平面区域，转化为利用线性规划求解目标函数的最值，试题有一定的难度，属于难题.4．A解析：A【解析】依题意，113713113713132412226132a aa Sb bb T+⋅===+⋅.5．B解析：B【解析】【分析】作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数即可求解.【详解】作出可行域如图：化目标函数为2y x z=-，联立70310x yx y+-=⎧⎨-+=⎩，解得5,2A（）.由图象可知，当直线过点A时，直线在y轴上截距最小，z有最大值25-28⨯=.【点睛】本题主要考查了简单的线性规划，数形结合的思想，属于中档题.6．C解析：C【解析】【分析】由题意可得90a>，10a<，且910a a+<，由等差数列的性质和求和公式可得结论．【详解】∵等差数列{}n a的前n项和有最大值，∴等差数列{}n a为递减数列，又1091aa<-，∴90a>，10a<，∴9100a a +<，又()118181802a a S +=<，()117179171702a a S a +==>，∴0n S >成立的正整数n 的最大值是17，故选C ．【点睛】本题考查等差数列的性质，涉及等差数列的求和公式，属中档题．7．D解析：D 【解析】因为11,8m n m n a a a a +=+=,所以2112,4a a == 42122a a ==,3123,8a a a =+= 73478a a a =+=.选D.8．C解析：C 【解析】【分析】根据题目条件结合三角形的正弦定理以及三角形内角和定理可得sin A ，进而利用二倍角余弦公式得到结果. 【详解】∵()cos 4cos a B c b A =-． ∴sin A cos B ＝4sin C cos A ﹣sin B cos A 即sin A cos B +sin B cos A ＝4cos A sin C ∴sin C ＝4cos A sin C ∵0＜C ＜π，sin C ≠0． ∴1＝4cos A ，即cos A 14=，那么27cos2218A cos A =-=-．故选C 【点睛】本题考查了正弦定理及二倍角余弦公式的灵活运用，考查计算能力，属于基础题．9．D解析：D 【解析】由a (a ＋b ＋c )＋bc ＝4－，得(a ＋c )·(a ＋b )＝4－23. ∵a 、b 、c >0.∴(a ＋c )·(a ＋b )≤22b c 2a ++⎛⎫ ⎪⎝⎭(当且仅当a ＋c ＝b ＋a ，即b ＝c 时取“＝”)，∴2a ＋b ＋c ≥2423－＝2(3－1)＝23－2. 故选：D点睛：在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误10．C解析：C 【解析】由约束条件画出可行域，如下图，可知当过A(0,1)点时，目标函数取最小值5，选C.11．B解析：B 【解析】【分析】过点B 作BE DC ⊥于点E ，过点A 作AF DC ⊥于点F ，在ABD ∆中由正弦定理求得AD ，在Rt ADF ∆中求得DF ，从而求得灯塔CD 的高度．【详解】过点B 作BE DC ⊥于点E ，过点A 作AF DC ⊥于点F ，如图所示，在ABD ∆中，由正弦定理得，sin sin AB ADADB ABD=∠∠，即sin[90(90)]sin(90)h ADαβα=︒--︒-︒+，cos sin()h AD αβα∴=-，在Rt ADF ∆中，cos sin sin sin()h DF AD αβββα==-，又山高为a ，则灯塔CD 的高度是3340cos sin 22356035251sin()2h CD DF EF a αββα⨯⨯=-=-=-=-=-．故选B ．【点睛】本题考查了解三角形的应用和正弦定理，考查了转化思想，属中档题．12．C解析：C 【解析】【分析】由题意可知，利用等差数列的性质，得18363a a a a +=+=，在利用等差数列的前n 项和公式，即可求解，得到答案。

高中数学必修一第五章三角函数易错题集锦(带答案)

高中数学必修一第五章三角函数易错题集锦单选题1、将函数f (x )=sin 12x 的图象向左平移φ(φ>0)个单位得到函数g (x )=cos 12x 的图象，则φ的最小值是（） A ．π4B ．π2C ．πD ．2π答案：C分析：依据平移然后判断可知12φ=π2+2k π(k ∈Z )，简单判断可知结果.由已知可得sin 12(x +φ)=cos 12x =sin (12x +π2)， ∴12φ=π2+2k π(k ∈Z )，∴φ=π+4k π(k ∈Z )． ∵φ>0，∴φ的最小值是π．故选：C2、设函数f(x)=cos (ωx +π6)在[−π,π]的图像大致如下图，则f (x )的最小正周期为（）A ．10π9B ．7π6C ．4π3D ．3π2 答案：C分析：由图可得：函数图象过点(−4π9,0)，即可得到cos (−4π9⋅ω+π6)=0，结合(−4π9,0)是函数f (x )图象与x轴负半轴的第一个交点即可得到−4π9⋅ω+π6=−π2，即可求得ω=32，再利用三角函数周期公式即可得解.由图可得：函数图象过点(−4π9,0)，将它代入函数f (x )可得：cos (−4π9⋅ω+π6)=0又(−4π9,0)是函数f (x )图象与x 轴负半轴的第一个交点，所以−4π9⋅ω+π6=−π2，解得：ω=32所以函数f(x)的最小正周期为T=2πω=2π32=4π3故选：C小提示：本题主要考查了三角函数的性质及转化能力，还考查了三角函数周期公式，属于中档题.3、智能主动降噪耳机工作的原理是通过耳机两端的噪声采集器采集周围的噪声，然后通过主动降噪芯片生成与噪声相位相反、振幅相同的声波来抵消噪声（如图）．已知噪声的声波曲线y=Asin(ωx+φ)（其中A>0，ω>0，0≤φ<2π）的振幅为1，周期为2π，初相为π2，则通过主动降噪芯片生成的声波曲线的解析式为（）A．y=sinx B．y=cosx C．y=−sinx D．y=−cosx答案：D分析：设噪声的声波曲线y=Asin(ωx+φ)，由题意求出A，ω，φ，即可得到降噪芯片生成的声波曲线的解析式.由噪声的声波曲线y=Asin(ωx+φ)（其中A>0，ω>0，0≤φ<2π）的振幅为1，周期为2π，初相为π2，可得ω=2πT =2π2π=1，A=1，φ=π2，所以噪声的声波曲线的解析式为y=sin(x+π2)=cosx，所以通过主动降噪芯片生成的声波曲线的解析式为y=−cosx.故选D．4、已知函数f(x)=sin(x+π3)．给出下列结论：①f(x)的最小正周期为2π；②f(π2)是f(x)的最大值；③把函数y=sinx的图象上所有点向左平移π3个单位长度，可得到函数y=f(x)的图象．其中所有正确结论的序号是（）A．①B．①③C．②③D．①②③答案：B分析：对所给选项结合正弦型函数的性质逐一判断即可.因为f(x)=sin(x+π3)，所以周期T=2πω=2π，故①正确；f(π2)=sin(π2+π3)=sin5π6=12≠1，故②不正确；将函数y=sinx的图象上所有点向左平移π3个单位长度，得到y=sin(x+π3)的图象，故③正确.故选：B.【点晴】本题主要考查正弦型函数的性质及图象的平移，考查学生的数学运算能力，逻辑分析那能力，是一道容易题.5、《掷铁饼者》是希腊雕刻家米隆于约公元前450年雕刻的青铜雕像，它取材于现实生活中的体育竞技活动，刻画的是一名强健的男子在掷铁饼过程中最具有表现力的瞬间．现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”，掷铁饼者的每只手臂长约π4m，肩宽约为π8m，“弓”所在圆的半径约为1.25m，则如图掷铁饼者双手之间的距离约为（）A．π2m B．5√24m C．5π8m D．2m答案：B分析：由题意知这段弓所在弧长，结合弧长公式求出其所对圆心角，双手之间的距离为其所对弦长．由题得：弓所在的弧长为：l=π4+π4+π8=5π8；所以其所对的圆心角α=5π854=π2；∴两手之间的距离d =2Rsin π4=√2×1.25AB =5√24m ．故选：B6、设函数f(x)=2sin(ωx +φ)−1(ω>0,0⩽φ⩽π2)的最小正周期为4π，且f(x)在[0,5π]内恰有3个零点，则φ的取值范围是（） A ．[0,π3]∪{5π12}B ．[0,π4]∪[π3,π2] C ．[0,π6]∪{5π12}D ．[0,π6]∪[π3,π2]答案：D分析：根据周期求出ω=12，结合φ的范围及x ∈[0,5π]，得到5π2⩽φ+5π2⩽3π，把φ+5π2看做一个整体，研究y =sinx −12在[0,3π]的零点，结合f(x)的零点个数，最终列出关于φ的不等式组，求得φ的取值范围因为T =2πω=4π，所以ω=12.由f(x)=0，得sin(12x +φ)=12.当x ∈[0,5π]时，12x +φ∈[φ,φ+5π2]，又0⩽φ⩽π2，则5π2⩽φ+5π2⩽3π.因为y =sinx −12在[0,3π]上的零点为π6，5π6，13π6，17π6，且f(x)在[0,5π]内恰有3个零点，所以{0⩽φ⩽π6,13π6⩽φ+5π2<17π6或{π6<φ⩽π2,17π6⩽φ+5π2,解得φ∈[0,π6]∪[π3,π2]. 故选：D.7、设0<α<π，sinα+cosα=713，则1−tanα1+tanα的值为（）A ．177B ．717C ．−177D ．−717 答案：C分析：依题意可知π2<α<π，得到cosα−sinα<0，再利用正余弦和差积三者的关系可求得cosα−sinα的值，将所求关系式切化弦，代入所求关系式计算即可．由sinα+cosα=713，平方得到1+sin2α=49169，∴sin2α=49169−1=−120169=2sinαcosα， 0<α<π， ∴ π2<α<π，∴cosα<0，而sinα>0， ∴cosα−sinα<0；令t =cosα−sinα(t <0)，则t 2=1−sin2α，∴t 2=1−sin2α=1+120169=289169，t <0∴t =−1713∴ 1−tanα1+tanα=cosα−sinαcosα+sinα=137(cosα−sinα)=137×(−1713)=−177，故选：C ．8、若函数f(x)=sin(ωx +π3)(0<ω<3)的图象向右平移2π3个长度单位后关于点(π2,0)对称，则f(x)在[−7π24,π2]上的最小值为（）A ．1B ．−√22C ．−√32D ．√6−√24答案：C分析：由图像平移过程写出平移后的解析式g(x)=sin(ωx +π3−2ωπ3)，利用正弦函数的对称性求参数ω，最后由正弦型函数的单调性求区间最小值即可.将f(x)向右平移2π3个长度单位后，得到g(x)=sin[ω(x −2π3)+π3]=sin(ωx +π3−2ωπ3)，∵g(x)关于(π2,0)对称，∴g(π2)=sin(ωπ2+π3−2ωπ3)=sin(π3−ωπ6)=0，∴π3−ωπ6=kπ,k ∈Z ，即ω=2−6k,k ∈Z ，又0<ω<3，则ω=2，即f(x)=sin(2x +π3)，由x ∈[−7π24,π2]知：2x +π3∈[−π4,4π3]，则sin(2x +π3)∈[−√32,1]， ∴f(x)在[−7π24,π2]上的最小值为−√32. 故选：C. 多选题9、在平面直角坐标系xOy 中，角α以Ox 为始边，终边经过点P(1,m)(m <0)，则下列各式一定为正的是（） A ．sinα+cosαB ．cosα−sinαC ．sinαcosαD ．sinαtanα 答案：BD分析：由三角函数定义确定正负，再由符号法则可选出正确答案.因为角α终边经过点P(1,m)(m <0)，所以α在第四象限，sinα<0,cosα>0,tanα<0， sinα+cosα正负无法判断；cosα−sinα>0；sinαcosα<0；sinαtanα>0，故BD 正确. 故选：BD10、对于①sinθ>0，②sinθ<0，③cosθ>0，④cosθ<0，⑤tanθ>0，⑥tanθ<0，则θ为第二象限角的充要条件为（）A ．①③B ．①④C ．④⑥D ．②⑤答案：BC解析：根据θ为第二象限角判断出sinθ、cosθ、tanθ的符号，从而可得出θ为第二象限角的充要条件. 若θ为第二象限角，则sinθ>0，cosθ<0，tanθ<0.所以，θ为第二象限角⇔{sinθ>0cosθ<0或{sinθ>0tanθ<0或{cosθ<0tanθ<0.故选：BC.小提示：本题考查三角函数值的符号与象限角之间的关系，考查分析问题和解决问题的能力，属于基础题.11、下列结论正确的是（）A．−7π6是第三象限角B．若圆心角为π3的扇形的弧长为π，则该扇形的面积为3π2C．若角α的终边上有一点P(−3,4)，则cosα=−35D．若角α为锐角，则角2α为钝角答案：BC分析：A中，由象限角的定义即可判断；B中，由弧长公式先求出半径，再由扇形面积公式即可；C中，根据三角函数的定义即可判断；D中，取α=30°即可判断.选项A中，−7π6=−2π+5π6，是第二象限角，故A错误；选项B中，设该扇形的半径为r，则π3⋅r=π，∴r=3，∴S扇形=12×π3×32=3π2，故B正确；选项C中，r=√(−3)2+42=5，cosα=xr =−35，故C正确；选项D中，取α=30°，则α是锐角，但2α=60°不是钝角，故D错误．故选：BC．填空题12、将函数f(x)的图象向右平移φ(φ>0)个单位长度，得到函数g(x)=sin(x+π6)的图象．若x=0是函数F(x)=f(x)−g(x)的一个零点，则φ的最小值是______.分析：直接利用函数的关系式变换和函数的图象的平移变换的应用求出函数f (x )=g (x +φ)=sin (x +φ+π6)，再利用函数的零点是方程的根和三角函数的性质求出φ的最小值.由题意，可知函数g (x )=sin (x +π6)的图象向左平移φ(φ>0)个单位长度，可得函数f (x )的图象，所以f (x )=g (x +φ)=sin (x +φ+π6).因为x =0是函数F (x )=f (x )−g (x )的一个零点，所以F(0)=f(0)−g(0)=0，即sin (φ+π6)−sin π6=0，所以sin (φ+π6)=12，因此有φ+π6=2k π+π6 (k ∈Z )或φ+π6=2k π+5π6(k ∈Z )，解得φ=2k π (k ∈Z )或φ=2k π+2π3(k ∈Z ).因为φ>0，所以当φ=2k π (k ∈Z )时，φ的最小值是2π；当φ=2k π+2π3(k ∈Z )时，φ的最小值是2π3.综上，φ的最小值是2π3. 所以答案是：2π3.13、若cos (α−β)=12，cos (α+β)=−35，则tanαtanβ=___________.答案：−11分析：由余弦的和差角公式得cosαcosβ=−120，sinαsinβ=1120，进而得tanαtanβ=−11解：因为cos (α−β)=12，所以cosαcosβ+sinαsinβ=12. 因为cos (α+β)=−35，所以cosαcosβ−sinαsinβ=−35，所以cosαcosβ=12(12−35)=−120，sinαsinβ=12(12+35)=1120，所以tanαtanβ=1120−120=−11.所以答案是：−1114、已知角θ的终边经过点M (3m,1−m )，且tanθ=2，则实数m =______．分析：根据三角函数的定义，已知角终边上的点(x,y )，则角的正切值为yx ，可得答案由三角函数的定义可知tanθ=1−m 3m=2，解得m =17．所以答案是：17 解答题15、已知函数f (x )=4cosxsin (x −π3)+√3．（Ⅰ）求函数f (x )在区间[π4,π2]上的值域．（Ⅱ）在△ABC 中，角A ，B ，C ，所对的边分别是a ，b ，c ，若角C 为锐角，f (C )=√3，且c =2，求△ABC 面积的最大值．答案：（Ⅰ）[1,2]；（Ⅱ）√3分析：（Ⅰ）利用差角的正弦公式、辅助角公式化简函数，结合正弦函数的性质，可得函数f(x)在区间[π4，π2]上的值域；（Ⅱ）先求出C ，再利用余弦定理，结合基本不等式，即可求得△ABC 面积的最大值．解：（Ⅰ）f(x)=4cosxsin(x −π3)+√3=4cosx (sinxcos π3−cosxsin π3)+√3=4cosx (12sinx −√32cosx)+√3=2sinxcosx −2√3cos 2x +√3=sin2x −√3cos2x =2sin(2x −π3)，由π4⩽x ⩽π2，有π6⩽2x −π3⩽2π3，所以12≤sin (2x −π3)≤1 ∴函数f(x)的值域为[1,2]．（Ⅱ）由f (C )=√3，有sin(2C −π3)=√32， ∵C 为锐角，∴2C −π3=π3，∴C =π3． ∵c =2，∴由余弦定理得：a 2+b 2−ab =4，∵a2+b2⩾2ab，∴4=a2+b2−ab⩾ab．∴S△ABC=12absinC=√34ab⩽√3，∴当a=b，即△ABC为正三角形时，△ABC的面积有最大值√3．。

(完整版)高中数学易错题

高中数学易错题数学概念的理解不透必修一（1）若不等式ax 2+x+a ＜0的解集为 Φ，则实数a 的取值范围（） A.a ≤-21或a ≥21 B.a ＜21 C.-21≤a ≤21 D.a ≥ 21【错解】选A.由题意，方程ax 2+x+a=0的根的判别式20140a ∆<⇔-<⇔ a ≤-21或a ≥21，所以选A.【正确解析】D .不等式ax 2+x+a ＜0的解集为 Φ，若a=0,则不等式为x<0解集不合已知条件，则a 0≠；要不等式ax 2+x+a ＜0的解集为 Φ，则需二次函数y=ax 2+x+a 的开口向上且与x 轴无交点，所以a>0且20140120a a a ⎧∆≤⇔-≤⇔≥⎨>⎩.必修一（2）判断函数f(x)=(x －1)xx-+11的奇偶性为____________________【错解】偶函数.f(x)=(x -===，所以()()f x f x -===，所以f （x ）为偶函数.【正解】非奇非偶函数.y=f(x)的定义域为：(1)(1)01011101x x xx x x +-≥⎧+≥⇔⇔-≤<⎨-≠-⎩，定义域不关于原点对称，所以此函数为非奇非偶函数.1) 必修二（4）1l ，2l ，3l 是空间三条不同的直线，则下列命题正确的是（） (A)12l l ⊥，23l l ⊥13//l l ⇒ （B ）12l l ⊥，3//l l ⇒13l l ⊥(C)123////l l l ⇒ 1l ，2l ，3l 共面（D ）1l ，2l ，3l 共点⇒1l ，2l ，3l 共面【错解】错解一：选A.根据垂直的传递性命题A 正确；错解二：选C.平行就共面；【正确解答】选B.命题A 中两直线还有异面或者相交的位置关系；命题C 中这三条直线可以是三棱柱的三条棱，因此它们不一定共面；命题D 中的三条线可以构成三个两两相交的平面，所以它们不一定共面.必修五（5）x=ab 是a 、x 、b 成等比数列的( )A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件【错解】C.当.x=ab 时，a 、x 、b 成等比数列成立；当a 、x 、b 成等比数列时，x=ab 成立 .【正确解析】选D.若x=a=0，x=ab 成立，但a 、x 、b 不成等比数列，所以充分性不成立；反之，若a 、x 、b成等比数列，则2x ab x =⇔=x=ab 不一定成立，必要性不成立.所以选D.排列组合（6）(1)把三枚硬币一起掷出，求出现两枚正面向上，一枚反面向上的概率. 分析:（1）【错解】三枚硬币掷出所有可能结果有2×2×2=8种，而出现两正一反是一种结果，故所求概率P=.81【正解】在所有的8种结果中，两正一反并不是一种结果，而是有三种结果：正、正、反，正、反、正，反、正、正，因此所求概率,83=P 上述错解在于对于等可能性事件的概念理解不清，所有8种结果的出现是等可能性的，如果把上述三种结果看作一种结果就不是等可能性事件了，应用求概率的基本公式n m P =自然就是错误的.公式理解与记忆不准（7）若1,0,0=+>>y x y x ，则yx41+的最小值为___________.【错解】 y x 41+8)2(14422=+≥≥y x xy ，错解原因是忽略等号成立条件. 【正解】yx 41+=945)(4≥++=+++yx xy yy x xy x（8）函数y=sin 4x+cos 4x －43的相位____________，初相为__________ .周期为_________，单调递增区间为____________.【错解】化简y=sin 4x+cos 4x －43=1cos 44x ，所以相位为4x ，初相为0，周期为2π，增区间为….【正确解析】y=sin 4x+cos 4x －43=11cos 4sin(4)442x x π=+.相位为42x π+，初相为2π，周期为2π，单调递增区间为21[,]()42k k k Z ππ-∈. 审题不严（1）读题不清必修五（9）已知()f x 是R 上的奇函数，且当0x >时，1()()12x f x =+，则()f x 的反函数的图像大致是【错解】选B.因为1()2x y =在0x >内递减，且1()()12x f x =+过点（0，2），所以选B. 【正确解答】A .根据函数与其反函数的性质，原函数的定义域与值域同其反函数的值域、定义域相同.当10,0()1,122x x y ><<⇒<<，所以选A.或者首先由原函数过点（0，2），则其反函数过点（2，0），排除B 、C ；又根据原函数在0x >时递减，所以选A. 排列组合（10）一箱磁带最多有一盒次品.每箱装25盒磁带，而生产过程产生次品磁带的概率是0.01.则一箱磁带最多有一盒次品的概率是 .【错解】一箱磁带有一盒次品的概率240.01(10.01)⨯-，一箱磁带中无次品的概率25(10.01)-，所以一箱磁带最多有一盒次品的概率是240.01(10.01)⨯-+25(10.01)-.【正确解析】一箱磁带有一盒次品的概率124250.01(10.01)C ⋅⨯-，一箱磁带中无次品的概率02525(10.01)C ⋅-，所以一箱磁带最多有一盒次品的概率是124250.01(10.01)C ⋅⨯-+02525(10.01)C ⋅-.（2）忽视隐含条件必修一（11）设βα、是方程0622=++-k kx x 的两个实根，则22)1()1(-+-βα的最小值是（）不存在)D (18)C (8)B (449)A (-【错解】利用一元二次方程根与系数的关系易得：,6,2+==+k k αββα2222(1)(1)2121αβααββ∴-+-=-++-+2()22()2αβαβαβ=+--++23494().44k =--选A.【正确解析】利用一元二次方程根与系数的关系易得：,6,2+==+k k αββα2222(1)(1)2121αβααββ∴-+-=-++-+2()22()2αβαβαβ=+--++23494().44k =--Θ 原方程有两个实根βα、，∴0)6k (4k 42≥+-=∆ ⇒.3k 2k ≥-≤或当3≥k 时，22)1()1(-+-βα的最小值是8；当2-≤k 时，22)1()1(-+-βα的最小值是18.选B. 必修一(12)已知(x+2)2+ y 24=1, 求x 2+y 2的取值范围.【错解】由已知得 y 2=－4x 2－16x －12，因此 x 2+y 2=－3x 2－16x －12=－3(x+38)2+328， ∴当x=－83 时，x 2+y 2有最大值283 ，即x 2+y 2的取值范围是(－∞, 283].【正确解析】由已知得 y 2=－4x 2－16x －12，因此 x 2+y 2=－3x 2－16x －12=－3(x+38)2+328 由于(x+2)2+ y 24 =1 ⇒ (x+2)2=1－ y 24≤1 ⇒ －3≤x ≤－1，从而当x=－1时x 2+y 2有最小值1.∴ x 2+y 2的取值范围是[1, 283 ].（此题也可以利用三角函数和的平方等于一进行求解）必修一（13）方程1122log (95)log (32)20x x ------=的解集为___________________- 【错解】111122222log (95)log (32)20log (95)log (32)log 40x x x x --------=⇔----=11111122log (95)log 4(32)954(32)(31)(33)0x x x x x x -------=-⇔-=-⇔--=1310x --=或1330x --=所以x=1或x=2.所以解集为{1，2}.【正解】111122222log (95)log (32)20log (95)log (32)log 40x x x x --------=⇔----=111111221954(32)log (95)log 4(32)3203302950x x x x x x x x -------⎧-=-⎪-=-⇔->⇔-=⇔=⎨⎪->⎩所以解集为{2}.字母意义含混不清（14）若双曲线22221x y a b -=-的离心率为54，则两条渐近线的方程为（）A.0916x y ±= B.0169x y ±= C.034x y ±= D.043x y±= 【错解】选D.22222222252593310416164443c c a b b b b x y e y x a a a a a a +==⇒===+⇒=⇒=±⇒=±⇒±=，选D. 【正确解析】2222222211x y y x a b b a-=-⇒-=，与标准方程中字母a,b 互换了.选C.4.运算错误（1）数字与代数式运算出错若)2,1(),7,5(-=-=b a ρρ，且（b a ρρλ+）b ρ⊥，则实数λ的值为____________.【错解】(5,72)a b λλλ+=--+r r ，则（b a ρρλ+）()052(72)03b a b b λλλλ⊥⇔+⋅=⇔-+-+=⇒=r r r r.【正确解析】(5,72)a b λλλ+=--+r r，（ba ρρλ+）19()052(72)05b a b b λλλλ⊥⇔+⋅=⇔-+-+=⇒=r r r r必修二18. 已知直线l 与点A （3，3）和B （5，2）的距离相等，且过二直线1l ：3x －y －1=0和2l：x+y－3=0的交点，则直线l的方程为_______________________【错解】先联立两直线求出它们交点为（1，2），设所求直线的点斜式，再利用A、B到12k=⇔=-，所以所求直线为x+2y-5=0.【正确解析】x-6y+11=0或x+2y-5=0.联立直线1l：3x－y－1=0和2l：x+y－3=0的方程得它们的交点坐标为（1，2），令过点（1，2）的直线l为：y-2=k(x-1)（由图形可看出直线l的斜率必然存在），11,62k k=⇔==-，所以直线l的方程为:x-6y+11=0或x+2y-5=0.（2）运算方法（如公式、运算程序或运算方向等）选择不当导致运算繁杂或不可能得解而出错必修二19. 已知圆(x－3)2+y2=4和直线y=mx的交点分别为P，Q两点，O为坐标原点，则OQOP⋅的值为.【运算繁杂的解法】联立直线方程y=mx与圆的方程(x－3)2+y2=4消y，得关于x的方程22(1)650m x x+-+=，令1122(,),(,)P x y Q x y，则12122265,11x x x xm m+=⋅=++，则221212251my y m x xm==+，由于向量OPuuu r与向量OQuuu r共线且方向相同，即它们的夹角为0，所以212122255511mOP OQ OP OQ x x y ym m⋅=⋅=+=+=++u u u r u u u r.【正确解析】根据圆的切割线定理，设过点O的圆的切线为OT（切点为T），由勾股定理，则222325OP OQ OT⋅==-=.（3）忽视数学运算的精确性，凭经验猜想得结果而出错曲线x2－122=y的右焦点作直线交双曲线于A、B两点，且4=AB，则这样的直线有___________条.【错解】4条.过右焦点的直线，与双曲线右支交于A、B时，满足条件的有上、下各一条（关于x轴对称）；与双曲线的左、右分别两交于A、B两点，满足条件的有上、下各一条（关于x 轴对称），所以共4条.【正解】过右焦点且与X 轴垂直的弦AB （即通径）为222241b a ⨯==，所以过右焦点的直线，与双曲线右支交于A 、B 时，满足条件的仅一条；与双曲线的左、右分别两交于A 、B 两点，满足条件的有上、下各一条（关于x 轴对称），所以共3条. 5.数学思维不严谨（1）数学公式或结论的条件不充分24.已知两正数x,y 满足x+y=1,则z=11()()x y x y++的最小值为 .【错解一】因为对a>0,恒有12a a +≥,从而z=11()()x y x y++≥4,所以z 的最小值是4.【错解二】22222()2x y xy z xy xy xy +-==+-≥21)-=，所以z 的最小值是1). 【正解】z=11()()x y x y ++=1y xxy xy x y+++=21()222x y xy xy xy xy xy xy +-++=+-，令t=xy, 则210()24x y t xy +<=≤=，由2()f t t t =+在10,4⎛⎤⎥⎝⎦上单调递减,故当t=14时 2()f t t t =+有最小值334,所以当12x y ==时z 有最小值334.（2）以偏概全，重视一般性而忽视特殊情况必修一(1)不等式|x+1|(2x －1)≥0的解集为____________解析：（1）【错解】1[,)2+∞.因为|x+1|≥0恒成立，所以原不等式转化为2x-1≥0，所以1[,)2x ∈+∞【正确解析】}1{),21[-⋃+∞.原不等式等价于|x+1|=0或2x-1≥0，所以解集为1[,){1}2x ∈+∞⋃-.必修一(2)函数y =的定义域为 .(2) 【错解】10(1)(1)011x x x x x+≥⇒+-≥⇒≥-或1x ≤-.【正解】(1)(1)0(1)(1)010111011x x x x x x x x x+-≥+-≤⎧⎧+≥⇒⇒⇒-≤<⎨⎨-≠≠-⎩⎩（3）解题时忽视等价性变形导致出错 27.已知数列{}n a 的前n 项和12+=n n S ，求.n a【错解】 .222)12()12(1111----=-=+-+=-=n n n n n n n n S S a 【正确解析】当1=n 时，113a S ==，n 2≥时，1111(21)(21)222nn n n n n n n a S S ----=-=+-+=-=.所以13(1)2(2)n n n a n -⎧=⎪=⎨≥⎪⎩.选修实数a 为何值时，圆012222=-+-+a ax y x 与抛物线x y 212=有两个公共点. 【错解】将圆012222=-+-+a ax y x 与抛物线 x y 212=联立，消去y ，得 ).0(01)212(22≥=-+--x a x a x ①因为有两个公共点，所以方程①有两个相等正根，得⎪⎪⎩⎪⎪⎨⎧>->-=∆.01021202a a ，解之得.817=a【正确解析】要使圆与抛物线有两个交点的充要条件是方程①有一正根、一负根；或有两个相等正根.当方程①有一正根、一负根时，得⎩⎨⎧<->∆.0102a 解之，得.11<<-a因此，当817=a 或11<<-a 时，圆012222=-+-+a ax y x 与抛物线x y 212=有两个公共点.(1)设等比数列{}n a 的全n 项和为n S .若9632S S S =+，求数列的公比q .【错解】 ,2963S S S =+Θq q a q q a q q a --⋅=--+--∴1)1(21)1(1)1(916131， .012(363）＝整理得--q q q1q 24q ,0)1q )(1q 2(.01q q 20q 33336=-=∴=-+∴=--≠或得方程由.【正确解析】若1=q ，则有.9,6,3191613a S a S a S ===但01≠a ，即得,2963S S S ≠+与题设矛盾，故1≠q .又依题意 963S 2S S =+ ⇒ q q a q q a q q a --⋅=--+--1)1(21)1(1)1(916131 ⇒ 01q q 2(q 363）＝--,即,0)1)(12(33=-+q q 因为1≠q ，所以,013≠-q 所以.0123=+q 解得 .243-=q空间识图不准必修二直二面角α－l －β的棱l 上有一点A ，在平面α、β内各有一条射线AB ，AC 与l 成450，AB βα⊂⊂AC ,，则∠BAC= .【错解】如右图.由最小角定理，12221cos cos cos 23BAC BAC πθθ∠=⋅=⨯=⇒∠=. 【正确解析】3π或23π.如下图.当6CAF π∠=时，由最小角定理，时，12221cos cos cos 2223BAC BAC πθθ∠=⋅=⨯=⇒∠=；当AC 在另一边DA 位置23BAC π∠=.。

人教版A版高中数学高二必修五 3.3线性规划问题错解分类辨析

精心校对线性规划问题错解分类辨析山东秦振线性规划问题应用广泛、综合性强、解题需要一定的技巧，学生在学习中经常遇到困难，下面就学生在解题中出现的错误分类辨析如下，供大家参考。

一、未弄清题意例1 某人有一面积为1802m 的房间，拟分隔成两类房间作为旅游客房，大房间每间面积182m ，可住游客5名，每名游客每天住宿费40元；小房间每间面积152m ，可住游客3名，每名游客每天住宿费50元；装修大房间每间需1000元，装修小房间每间需要600元；如果他只能筹款8000元用于装修，且游客能住满客房，在充分利用借款情况下，根据游客的不同需求他应隔出大房间和小房间各多少间，能获得最大的收益？错解设他应隔出大房间x 间，小房间y 间，并获得最大收益。

则线性约束条件为*0,0,1815180,10006008000,,.x y x y x y x y N ⎧≥⎪≥⎪⎪+≤⎨⎪+≤⎪⎪∈⎩目标函数：200150z x y =+。

化简线性约束条件：*6560,5340,0,0,,.x y x y x y x y N ⎧+≤⎪+≤⎪⎪≥⎨⎪≥⎪⎪∈⎩作出可行域：如图1所示。

作直线:2001500l x y +=，即430x y +=。

将l 平移至可行域的点A ，这时l 与原点的距离最大，此时：200150z x y =+取最大值。

解方程组6560,5340.x y x y +=⎧⎨+=⎩解得20,760.7x y ⎧=⎪⎪⎨⎪=⎪⎩∴2060,77A ⎛⎫ ⎪⎝⎭。

由于最优解(),x y 中x 、y 都是整数，∴可行域内点2060,77A ⎛⎫⎪⎝⎭不是最优解。

可验证：经过可行域的整点且使200150z x y =+取最大值的整点是()0,12和()3,8。

此时max 1800z =元。

答：应隔出小房间12间；或大房间3间，小房间8间，可获最大利润。

辨析错因是未理解题意，仅找出整点使目标函数的利润最大，却忽视了比较两种分隔精心校对方法在使用借款与满足游客的不同需求时的区别。

人教B版人教B版高中数学必修五不等式易错题练习

高中数学学习材料金戈铁骑整理制作不等式易错题练习1、不等式的性质：（1）同向不等式可以相加；异向不等式可以相减：若,a b c d >>，则a c b d +>+（若,a b c d ><，则a c b d ->-），但异向不等式不可以相加；同向不等式不可以相减；（2）左右同正不等式：同向的不等式可以相乘，但不能相除；异向不等式可以相除，但不能相乘：若0,0a b c d >>>>，则ac bd >（若0,0ab c d >><<，则a bc d>）；（3）左右同正不等式：两边可以同时乘方或开方：若0a b >>，则nn ab >或n n a b >；（4）若0,ab a b >>，则11a b<；若0,ab a b <>，则11a b>.如（1）（2）已知11,13x y x y -≤+≤≤-≤，则3x y -的取值范围是______（答：137x y ≤-≤）；（3）已知a b c >>，且0a b c ++=则c a 的取值范围是______（答：12,2⎛⎫-- ⎪⎝⎭）2. 不等式大小比较的常用方法：（1）作差：作差后通过分解因式、配方等手段判断差的符号得出结果；（2）作商（常用于分数指数幂的代数式）；（3）分析法；（4）平方法；（5）分子（或分母）有理化；（6）利用函数的单调性；（7）寻找中间量或放缩法；（8）图象法。

其中比较法（作差、作商）是最基本的方法。

如（1）设01,0aa t >≠>且，比较11log log 22a a t t +和的大小答：当1a >时，11log log 22a a t t +≤（1t =时取等号）；当01a <<时，11log log 22a a t t +≥（1t =时取等号））；（2）设24212,,22a a a p a q a -+->=+=-，2a >，试比较,p q 的大小（答：p q >）；（3）比较1log 3x +与()2log 201xx x >≠且的大小.答：当01x <<或43x >时，1log 32log 2x x +>；当413x <<时，1log 32log 2x x +<；当43x =时，1log 32log 2x x += 3. 利用重要不等式求函数最值时，你是否注意到：“一正二定三相等，和定积最大，积定和最小”这17字方针。

苏教版高中数学必修五数列错误剖析文字素材

解数列题常见错误剖析数列是高中数学的重要内容之一，也是历年来高考的热点，如果没有正确理解数列的有关概念，解题就容易出错．现选出一些典型错误进行剖析，供大家参考．一、审题不细例1 在等差数列{}n a 中，331n a n =-，记n n b a =，求数列{}n b 的前30项和．错解：∵{}n a 成等差数列， ∴{}n b 也成等差数列．又∵331n n b a n ==-，∴128b =，3059b =． ∴数列{}n b 的前30项和1303030()30(2859)130522b b S +⨯+===．剖析：这里错把{}n b 也当作等差数列，实际上解此题的关键是搞清绝对值符号内的a n 的正负，易知当10n ≤时，0n a <；当11n ≥时，0n a >．正解：30121011301210111230()()S a a a a a a a a a a a =+++++=-+++++++L L L L110113010()20()14561075522a a a a ++=-+=+=．二、搞错项数例2 在等差数列{}n a 中，350n a n =-，求此数列的第10项到第30项之和．错解：设第10项到第30项和为S ，因为数列{}n a 是等差数列，所以103020()20(2040)20022a a S +-+===．剖析：关键是没有搞清数列的项数，从第10项到第30项共有21项．正解：103021()21(2040)21022a a S +-+===．三、忽视特殊情形例3 已知数列{}n a 的前n 项和21n S n n =++，求此数列的通项n a ．错解：2211[(1)(1)1]2n n n a S S n n n n n -=-=++--+-+=．剖析：在利用数列前n 项和公式求数列通项时一定要考虑1n =的特殊情况，数列{}n a 通项应为1112n nn S n a S S n -=⎧⎪=⎨-⎪⎩，，，． ≥．正解：3122n n a n n =⎧=⎨⎩，，，　． ≥四、忽视特值项例4 在数列{}n a 中，5105n a n =-，则当n =____时，n S 取最小值．错解：由51050n a n =->，解得21n >．所以n S 取得最小值时，21n =．剖析：此解忽视了正负项中间的零值项210a =，所以2021S S =．正解：n S 取得最小值时，n 为20或21．五、忽视整体思想例5 （04高考福建文5）设n S 是等差数列{}n a 的前n 项和，若5359a a =，则95SS 等于（）（A ）1 （B ）1- （C ）2 （D ）12错解：∵5359a a =，即114529a d a d +=+， ∴ 145a d +=，129a d +=．∴2d =-，113a =． ∴9598913(2)2154513(2)2S S ⨯⨯+⨯-==⨯⨯+⨯-．剖析：本题的结果虽然是正确的，但过程错误．由114529a d a d +=+，我们可以令145a d t +=，129(0)a d t t +=≠，再进行下面的计算．不过这样做太繁琐，下面我们给出一种简便的方法．正解：∵1952a a a +=，1532a a a +=，∴ 199515539()995215()5592a a S a a a S a +⨯====+⨯．故选（A ）．。

(易错题)高中数学必修五第三章《不等式》测试(含答案解析)(2)

组织机构代码： 806790662
企业类型：
有限责任公司分公司(国有控股)
所属行业：
零售业
经营状态：
存续
注册资本：
/
注册时间：
2000-09-30
注册地址：
河北省青县新华东路３３号
营业期限：
2000-09-30 至/
经营范围：
零售预包装食品、卷烟、酒类、汽油、柴油（闭杯闪点≤60℃）、润滑油；日用百货便利店经营、汽车
三、对外投资信息
截止 2018 年 11 月 25 日，根据国内相关网站检索及天眼查数据库分析，未查询到相关信息。不排除因信息公开来源尚未公开、公开形式存在差异等情况导致的信息与客观事实不完全一致的情形。仅供客户参考。
四、企业发展
4.1 融资历史
截止 2018 年 11 月 25 日，根据国内相关网站检索及天眼查数据库分析，未查询到相关信息。不排除因信息公开来源尚未公开、公开形式存在差异等情况导致的信息与客观事实不完ቤተ መጻሕፍቲ ባይዱ一致的情形。仅供客户参考。
清洗服务、广告、房屋租赁、汽车用品（危险化学品经营许可证有效期至 2019 年 5 月 7 日）**（依法须经批准的项目，经
相关部门批准后方可开展经营活动）
登记机关：
青县工商行政管理局
核准日期：
2016-11-11
1.2 分支机构
3

截止 2018 年 11 月 25 日，根据国内相关网站检索及天眼查数据库分析，未查询到相关信息。不排除因信息公开来源尚未公开、公开形式存在差异等情况导致的信息与客观事实不完全一致的情形。仅供客户参考。
4.2 投资事件
截止 2018 年 11 月 25 日，根据国内相关网站检索及天眼查数据库分析，未查询到相关信息。不排除因信息公开来源尚未公开、公开形式存在差异等情况导致的信息与客观事实不完全一致的情形。仅供客户参考。

数学必修五完整笔记含习题和答案

目录必修5知识点总结 ............................... 错误!未定义书签。

含参不等式 ..................................... 错误!未定义书签。

一元二次不等式 ................................. 错误!未定义书签。

均值不等式 ..................................... 错误!未定义书签。

整式不等式（高次不等式） ....................... 错误!未定义书签。

分式不等式 ..................................... 错误!未定义书签。

绝对值不等式 ................................... 错误!未定义书签。

不等式关系 ..................................... 错误!未定义书签。

线性归纳....................................... 错误!未定义书签。

必修5知识点总结1、正弦定理：在C ∆AB 中，a 、b 、c 分别为角A 、B 、C 的对边，R 为C ∆AB 的外接圆的半径，则有2sin sin sin a b cR C===A B ． 2、正弦定理的变形公式：①2sin a R =A ，2sin b R =B ，2sin c R C =；②sin 2a R A =，sin 2b R B =，sin 2c C R =；③::sin :sin :sin a b c C =A B ； ④sin sin sin sin sin sin a b c a b cC C++===A +B +A B ．（正弦定理主要用来解决两类问题：1、已知两边和其中一边所对的角，求其余的量。

2、已知两角和一边，求其余的量。

）⑤对于已知两边和其中一边所对的角的题型要注意解的情况。

高中数学经典错题深度剖析及针对训练独立事件、独立重复试验的概率和条件概率

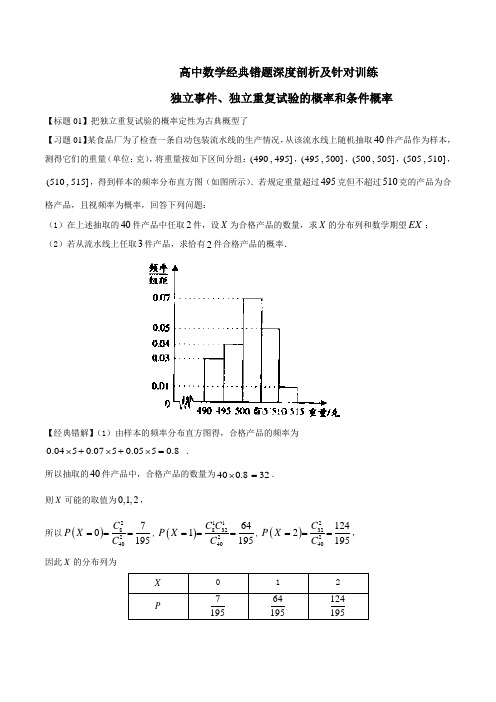
高中数学经典错题深度剖析及针对训练独立事件、独立重复试验的概率和条件概率【标题01】把独立重复试验的概率定性为古典概型了【习题01】某食品厂为了检查一条自动包装流水线的生产情况，从该流水线上随机抽取40件产品作为样本，测得它们的重量（单位：克），将重量按如下区间分组：(490,495]，(495,500]，(500,505]，(505,510]，(510,515]，得到样本的频率分布直方图（如图所示）．若规定重量超过495克但不超过510克的产品为合格产品，且视频率为概率，回答下列问题：（1）在上述抽取的40件产品中任取2件，设X 为合格产品的数量，求X 的分布列和数学期望EX ；（2）若从流水线上任取3件产品，求恰有2件合格产品的概率．【经典错解】（1）由样本的频率分布直方图得，合格产品的频率为0.0450.0750.0550.8⨯+⨯+⨯=．所以抽取的40件产品中，合格产品的数量为400.832⨯=．则X 可能的取值为0,1,2，所以()2824070195C P X C ===,()11832240641195C C P X C ===,()2322401242195C P X C ===，因此X 的分布列为故X 数学期望76412431280121951951951955EX =⨯+⨯+⨯==．（2）由题得从流水线上任取3件产品，求恰有2件合格产品的概率213283404961235C C P C == 【详细正解】(1)同上；（2）因为从流水线上任取1件产品合格的概率为40.85=，所以从流水线上任取3件产品，恰有2件合格产品的概率为223144855125P C ⎛⎫⎛⎫== ⎪⎪⎝⎭⎝⎭．【习题01针对训练】某工厂在试验阶段大量生产一种零件，这种零件有A 、B 两项技术指标需要检测，设各项技术指标达标与否互不影响.若仅有A ，A 、B 两项技术指标都不达标的（1）求一个零件经过检测为合格品的概率；（2）若任意抽取该种零件4个，设ξ表示其中合格品的个数，求ξ的分布列及数学期望E ξ．【标题02】把独立重复试验的概率定性为独立事件的概率了【习题02】某次数学考试中有三道选做题，分别为选做题1,2,3．规定每位考生必须且只须在其中选做一题.甲、乙、丙三名考生选做这一题中任意一题的可能性均为13，每位学生对每题的选择是相互独立的，各学生的选择相互之间没有影响．求这三个人选做的是同一道题的概率.【经典错解】由题得设这三个人选做的是同一道题为事件A ,则1111()33327P A =鬃=【详细正解】由题得设这三个人选做的是同一道题为事件A ,则131111()3339P A C =鬃?.【深度剖析】(1)经典错解错在把独立重复试验的概率定性为独立事件的概率了.（2）这三个人选做的是同一道题为事件A ，则A 实际上是三个互斥事件和和事件，因为甲乙丙可能同时选做第一题或第二题或第三题，而每一个互斥事件的概率又是三个独立事件同时发生的概率.错解把事件A 直接定性为独立事件同时发生的概率了，是错的.（3）解答概率题时，要先定性（六大概型：古典概型、几何概型、互斥事件的概率、独立事件同时发生的概率、独立重复试验的概率和条件概率），后定量.在定性时，要仔细分析，不要把事件定性错了.【习题02针对训练】某市公租房的房源位于A 、B 、C 三个片区，设每位申请人只申请其中一个片区的房源，且申请其中任一个片区的房源是等可能的，求该市的任4位申请人中：（1）恰有2人申请A 片区房源的概率；（2）申请的房源所在片区的个数的ξ分布列与期望．【标题03】对事件)4,3,2,1(0=≥i S i 且28=S 理解错误【习题03】某人抛掷一枚均匀骰子，构造数列}{n a ，使⎩⎨⎧-=)(,1)(,1次掷出奇数当第次掷出偶数当第n n a n ，记n n a a a S +++= 21 求)4,3,2,1(0=≥i S i 且28=S 的概率.【经典错解】记事件A ：28=S ，即前8项中，5项取值1，另3项取值－1，∴28=S 的概率858)21()(⋅=C A P记事件B ：)4,3,2,1(0=≥i S i ，将)4,3,2,1(0=≥i S i 分为两种情形：（1）若第1、2项取值为1，则3，4项的取值在1和-1中任意取值；（2）若第1项为1，第2项为－1，则第3项必为1，第四项在1和-1中任意取值. ∴()P B =83)21()21(32=+ ∴所求事件的概率为()()P P A P B =⋅ =858)21(83⋅⋅C 【详细正解】∵)4,3,2,1(0=≥i S i ∴前4项的取值分为两种情形①若1、3项为1；则余下6项中3项为1，另3项为-1即可.即8361)21(⋅=C P ；②若1、2项为正，为避免与第①类重复，则第3项必为-1，则后5项中只须3项为1，余下2项为-1，即8352)21(⋅=C P ，∴所求事件的概率为783536215)21()(=⋅+=C C P【习题03针对训练】一种电脑屏幕保护画面，只有符号""""X O 和随机地反复出现，每秒钟变化一次，每次变化只出现""""X O 和之一，其中出现""O 的概率为p ，出现""X 的概率为q ，若第k 次出现""O ，则记1=k a ；出现""X ，则记1-=k a ，令n n a a a S +⋅⋅⋅++=21． (1)时，求3S 的分布列及数学期望． (2)时，求），，，且4321(028=≥=i S S i 的概率．【标题04】对事件“A B 、两组中有一组恰有两支弱队”没有理解清楚【习题04】已知8支球队中有3支弱队，以抽签方式将这8支球队分为A B 、两组，每组4支，求A B 、两组中有一组恰有两支弱队的概率.【经典错解】将8支球队均分为A B 、两组，共有4448C C 种方法：A B 、两组中有一组恰有两支弱队的分法为：先从3支弱队取2支弱队，又从5支强队取2支强队，组成这一组共有2325C C 种方法，其它球队分在另一组，只有一种分法.∴所求事件的概率为：7344482225=C C C C . 【详细正解】将8支球队均分为A B 、两组，共有4448C C 种方法：A B 、两组中有一组恰有两支弱队的分法为：先从3支弱队取2支弱队，又从5支强队取2支强队，组成这一组共有2325C C 种方法.再把这这组队伍分给A 组或B 组，有12C种方法，所以所求事件的概率P=76244482225=C C C C .【习题04针对训练】某中学在高一开设了数学史等4门不同的选修课，每个学生必须选修，且只能从中选一门.该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同. （1）求恰有2门选修课这3个学生都没有选择的概率；（2）设随机变量ξ为甲、乙、丙这三个学生选修数学史这门课的人数，求ξ的分布列及期望、方差．【标题05】概型判断错误【习题05】某人有5把不同的钥匙，逐把地试开某房门锁，试问他恰在第3次打开房门的概率.【经典错解】由于此人第一次不能开房门的概率为45，若第一次未开，第2次不能打开房门的概率应为34；所以此人第3次打开房门的概率为31. 【详细正解】第1次未打开房门的概率为54；第2次未开房门的概率为43；第3次打开房门的概率为31，所求概率为：51314354=⨯⨯=P .【习题05针对训练】某种项目的射击比赛，开始时在距目标100米处射击，如果命中记3分，且停止射击，若第一次射击未命中，可以进行第二次射击，但目标已经在150米处，这时命中记2分，且停止射击；若第二次仍未命中，还可以进行第三次射击，此时目标已在200米处，若第三次命中则记1分，并停止射击；若三次都未命中，则记0分，已知射手甲在100m 处击中目标的概率为，他的命中率与目标的距离的平方成反比，且各次射击都是独立的．（1）求这名射手在三次射击中命中目标的概率；（2）求这名射手比赛中得分的均值．【标题06】没有注意事件的先后顺序导致遗漏了一些情况【习题06】某运动员射击一次所得环数x 的分布列如下：现进行两次射击，以该运动员两次射击中最高的环数作为他的成绩记为ξ，求ξ的分布列.【经典错解】ξ的取值为8，9，10.ξ=7，两次环数为7,7；ξ=8，两次成绩为7，8或8，8；ξ=9，两次成绩7，9或8，9或9，9；ξ=10，两次队数为7，10或8，10或9，10或10，10. ∴04.02.02.0)7(=⨯==ξP 15.03.03.02.0)8(2=+⨯==ξP23.03.03.03.03.02.0)9(2=+⨯+⨯==ξP 2.02.03.03.02.03.02.0)10(2=+⋅+⋅⨯==ξP （分布列略）【详细正解】8=ξ，即两次成绩应为7，8或8，7或8，8实际为三种情形，21.03.03.02.02)8(2=+⨯⨯==ξP 9=ξ两次环数分别为7,9（或9,7）；8,9（或9,8），9.9∴39.03.03.03.023.02.02)9(2=+⨯⨯+⨯⨯==ξP ，同理36.02.042.03.0212.0)10(22=+⨯⨯+⨯==ξP 【深度剖析】(1)经典错解错在没有注意事件的先后顺序导致遗漏了一些情况.（2）8=ξ，即两次成绩应为7，8或8，7或8，8实际为三种情形，21.03.03.02.02)8(2=+⨯⨯==ξP9=ξ两次环数分别为7,9（或9,7）；8,9（或9,8），9.9 ∴39.03.03.03.023.02.02)9(2=+⨯⨯+⨯⨯==ξP ，同理36.02.042.03.0212.0)10(22=+⨯⨯+⨯==ξP .【习题06针对训练】学校要用三辆校车从南校区把教职工接到校本部，已知从南校区到校本部有两条公路，校车走公路①堵车的概率为14，不堵车的概率为34；校车走公路②堵车的概率为p ，不堵车的概率为1p -．若甲、乙两辆校车走公路①，丙校车由于其他原因走公路②，且三辆车是否堵车相互之间没有影响．（Ⅰ）若三辆校车中恰有一辆校车被堵的概率为716，求走公路②堵车的概率；（Ⅱ）在（1）的条件下，求三辆校车中被堵车辆的辆数ξ的分布列和数学期望.【标题07】把独立事件的概率定性为互斥事件的概率了【习题07】甲投篮命中概率为0.8，乙投篮命中概率为0.7，每人投3次，两人恰好都命中2次的概率是多少？【经典错解】设“甲恰好投中2次”为事件A ，“乙恰好投中2次”为事件B ，则两人恰好投中2次为A B +.所以()()()P A B P A P B +=+ =825.03.07.02.08.0223223=⨯+⨯C C .【详细正解】设“甲恰好投中2次”为事件A ，“乙恰好投中2次”为事件B ，则两人恰好都投中2次为AB .所以()()()P AB P A P B =⋅ =2222330.80.20.70.3C C ⨯⨯⨯0.169=【习题07针对训练】地为绿化环境，移栽了银杏树2棵，梧桐树3棵.它们移栽后的成活率分别为23、12，每棵树是否存活互不影响，在移栽的5棵树中：（1）求银杏树都成活且梧桐树成活2棵的概率；（2）求成活的棵树ξ的分布列与期望.【标题08】把独立事件同时发生的概率定性为独立重复试验了【习题08】某射手射击一次，击中目标的概率是0.5，现该射手连射4次，（1）求恰好前3次击中的概率；（2）恰好第3次击中的概率.【经典错解】（1）由题得334111()()224P C ==；（2P =(10.5)(10.5)0.5(10.5)-⨯-⨯⨯-0.0625= 【详细正解】（1）由题得3111()2216P ==；（2）P =(10.5)(10.5)0.5(10.5)-⨯-⨯⨯-0.0625=【习题08针对训练】甲、乙两人进行乒乓球比赛，采用“五局三胜制”，即五局中先胜三局为赢，若每场比赛甲获胜的概率是23，乙获胜的概率是13，则比赛以甲三胜一负而结束的概率为________．【标题09】把古典概型定性为独立重复试验了【习题09】某产品100件，其中恰有5件次品，现从中任意抽取5件，求恰有一件次品的概率. 【经典错解】由题得145595(A)()()100100P C = 【详细正解】由题得145955100()0.2144C C P A C == 【深度剖析】(1)经典错解错在把古典概型定性为独立重复试验了.（2）所求事件的概型应该是一个古典概型，而错解把它当作是独立重复试验了.因为已知中的抽取，是一次性地从100件产品中抽取5件，所以没有抽多次，所以根本上不是独立重复试验.如果有的同学分5次来抽，每次抽取一件，也不是独立重复.因为第一次抽取时，抽到次品的概率是5100，第二次抽取时，只有99件产品，此时抽到次品的概率肯定不是5100，由于概率不同，所以也不是独立重复试验.【习题09针对训练】现有一批产品共有10件,其中8件为正品,2件为次品. (1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率； (2)如果从中一次取3件,求3件都是正品的概率. 【标题10】把条件概率定性为古典概型了【习题10】一盒中放有大小相同的10个小球，其中8个黑球、2个红球，现甲、乙二人先后各自从盒子中无放回地任意抽取2个小球，已知甲取到了2个黑球，则乙也取到2个黑球的概率是________．【经典错解】由题得228622108151()453C C P A C C ===【详细正解】记事件“甲取到2个黑球”为A ，“乙取到2个黑球”为B ，则有(|)P B A ＝()()P AB P A ＝22862288C C C C ⋅⋅＝1528，即事件“甲取到2个黑球，乙也取到2个黑球”的概率是1528．【习题10针对训练】某险种的基本保费为a （单位：元），继续购买该险种的投保人称为续保人，续保人的本年度的保费与其上年度的出险次数的关联如下：设该险种一续保人一年内出险次数与相应概率如下：（1）求一续保人本年度的保费高于基本保费的概率；（2）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率；（3）求续保人本年度的平均保费与基本保费的比值．【标题11】审题不清忽略了“有放回地取”这个关键词【习题11】一个袋中有4个大小相同的小球，其中红球1个，白球2个，黑球1个，现从袋中有放回地取球，每次随机取1个．求连续取两次都是白球的概率；【经典错解】由题得22241()6A P A A ==.【详细正解】记事件A 为“连续取两次都是白球”，所以()P A 14．【深度剖析】(1)经典错解错在审题不清，忽略了“有放回地取”这个关键词.（2）抽样常用的有“有放回抽样”和“不放回抽样”两种，所以在解题时一定要注意抽样的方法.【习题11针对训练】一个袋中装有形状大小完全相同的球9个，其中红球3个，白球6个，每次随机取1个，直到取出．．．．3．次红球即停止．．．．．．．．(1)从袋中不放回地取球，求恰好取4次停止的概率1P ； (2)从袋中有放回地取球;①求恰好取5次停止的概率2P ；②记5次之内(含5次)取到红球的个数为ξ，求随机变量ξ的分布列及数学期望．【标题12】对事件“某位顾客返券的金额为30元”没有理解透彻【习题12】某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置.若指针停在A 区域返券60元；停在B 区域返券30元；停在C 区域不返券.例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．求某位顾客返券的金额为30元的概率.【经典错解】设A =某位顾客返券的金额为30元,则111()236P A ==.【详细正解】设A =某位顾客返券的金额为30元,则11111()23323P A =+= .【习题12针对训练】某运动员射击一次所得环数x 的分布列如下：现进行两次射击，以该运动员两次射击中最高的环数作为他的成绩记为ξ，求(8)P x =.【标题13】把此种条件概率和“丢开法”条件概率混淆了【习题13】10名同学中，有7个人获得了全国数学联赛一等奖，3人没有获得.现在从中任选2名同学，已知其中1名同学获得全国一等奖，求另外一名同学也获得全国一等奖的概率. 【经典错解】由题得6293P ==. 【详细正解】设A =2名同学中有1人获得全国一等奖，B =2名同学中另外一个同学也获得全国一等奖，由题得27112737()211(|)(A)422C n AB P B A n C C C ====+,所以另外一名同学也获得全国一等奖的概率为12.【习题13针对训练】抛掷红、蓝两颗骰子，设事件A 为“蓝色骰子的点数为3或6”，事件B 为“两颗骰子的点数之和大于8”．当已知蓝色骰子的点数为3或6时，则两颗骰子的点数之和大于8的概率为________．【标题14】把古典概型定性为独立重复试验概率了【习题14】某产品100件，其中恰有5件次品，现从中任意抽取5件，求恰有一件次品的概率. 【经典错解】由题得145595(A)()()100100P C = 【详细正解】由题得145955100()0.2144C C P A C == 【深度剖析】（1）经典错解错在把古典概型定性为独立重复试验概率了.（2）所求事件的概型应该是一个古典概型，而错解把它当作是独立重复试验了.因为已知中的抽取，是一次性地从100件产品中抽取5件，所以没有抽多次，所以根本上不是独立重复试验.如果有的同学分5次来抽，每次抽取一件，也不是独立重复.因为第一次抽取时，抽到次品的概率是5100，第二次抽取时，只有99件产品，此时抽到次品的概率肯定不是5100，由于概率不同，所以也不是独立重复试验. 【习题14针对训练】现有一批产品共有10件,其中8件为正品,2件为次品. (1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率. (2)如果从中一次取3件,求3件都是正品的概率.【标题15】概率定性定错了【习题15】某射手射击一次，击中目标的概率是0.5，现该射手连射4次，（1）求恰好前3次击中的概率；（2）恰好第3次击中的概率.【经典错解】（1）由题得334111()()224P C ==;（2）P= (10.5)(10.5)0.5(10.5)-⨯-⨯⨯-0.0625=【详细正解】（1）由题得3111()2216P ==；（2）P=(10.5)(10.5)0.5(10.5)-⨯-⨯⨯-0.0625=【习题15针对训练】甲、乙两人进行乒乓球比赛，采用“五局三胜制”，即五局中先胜三局为赢，若每场比赛甲获胜的概率是23，乙获胜的概率是13，则比赛以甲三胜一负而结束的概率为________．高中数学经典错解深度剖析及针对训练第29讲：独立事件的概率、独立重复试验的概率和条件概率参考答案【习题01针对训练答案】（1（2满足条件的事件是恰有2人申请A 片区房源，共有2242C C ∴根据等可能事件的概率公式得到224248327C C P == （2）由题意知ξ的可能取值是1,2,3.431(1)327P ξ=== 231222341423414(2)327A C C C C C P ξ+=== 234344(3)39C A P ξ=== ∴ξ的分布列是：∴1144651232727927E ξ=⨯+⨯+⨯= 【习题03针对训练答案】(1)详见解析；(2)218780．【习题03针对训练解析】(1)3,1,1,33--=S()()0318183=⨯+⨯+⨯-+⨯-=EX(2)前4次有2次出现""O 的概率是前4次有3次出现""O 的概率是前4次有4次出现""O 的概率是P (ξ= 0 ) =P (ξ= 1) =P (ξ= 2 ) =P (ξ= 3 ) =∴ξ的分布列为：E np ξ=34416D npq ξ==⨯⨯=【习题05针对训练答案】（1）95144；（2）8548.【习题05针对训练解析】记第一、二、三次射击命中目标分别为事件,,A B C三次均未命中目标的事件为D．依题意1 ()2P A=．（Ⅱ）依题意，设射手甲得分为ξ，则1121(3)(2)2299P Pξξ====⨯=171749(1)(0)298144144P Pξξ==⨯⨯===∴ξ的分布列为∴32102914414448Eξ=⨯+⨯+⨯+⨯=．【习题06针对训练答案】(Ⅰ； (Ⅱ【习题06针对训练解析】（1）由已知条件得即31p=，则所以p的值为（2）解：ξ可能的取值为0，1，2，3所以ξ的分布列为：，【习题7针对训练答案】（1）6；（2）详见解析.ξ∴的分布列为6E ξ∴=. 【习题08针对训练答案】827【习题08针对训练解析】甲三胜一负即前3次中有2次胜1次负，而第4次胜，∴P＝C3223⎛⎫⎪⎝⎭2·13⎛⎫⎪⎝⎭·23＝827，∴甲三胜一负而结束的概率为827.【习题09针对训练答案】（1）0.512；（2）7 15.【习题10针对训练答案】(1)0.55 ； (2)311；（3）1.23.【习题10针对训练解析】（1）记A为事件：“一续保人本年度的保费不高于基本保费”．则()0.200.200.100.050.55P A=+++=（2）记B为事件：“一续保人本年度的保费比基本保费60%”．()0.100.050.15P B=+=所以()()0.153 (|A)()()0.5511P AB P BP BP A P A====，所以一续保人本年度的保费高于基本保费，求其保费比基本保费高出60%的概率为3 11.（3）续保人本年度的平均保费估计值为0.850.300.15 1.250.20 1.50.20 1.750.1020.05 1.23 EX a a a a a a a =⨯+⨯+⨯+⨯+⨯+⨯=所以续保人本年度的平均保费与基本保费的比值为1.23.【习题11针对训练答案】(1)128；(2) ①881②13181.【习题11针对训练解析】(1)113363149128C C APA==(2)①22224121833381 P C⎛⎫⎛⎫=⨯⨯⨯=⎪ ⎪⎝⎭⎝⎭②随机变量ξ的取值为0,1,2,3; 由n 次独立重复试验概率公式()()1n kk kn n P k C p p -=-，得()505132013243P C ξ⎛⎫==⨯-= ⎪⎝⎭ ()41511801133243P C ξ⎛⎫==⨯⨯-=⎪⎝⎭ ()231511802133243P C ξ⎛⎫⎛⎫==⨯⨯-= ⎪ ⎪⎝⎭⎝⎭()328080173124381P ξ++==-=随机变量ξ的分布列是ξ的数学期望是 3280801713101232432432438181E ξ=⨯+⨯+⨯+⨯=∴()P B =1036＝518．当蓝色骰子的点数为3或6时，两颗骰子的点数之和大于8的结果有5个，故()P AB ＝536．∴(|)P B A ＝()()P AB P A ＝53613＝512．【习题14针对训练答案】（1）0.512；（2）715. 【习题14针对训练解析】(1)有放回地抽取3次,按抽取顺序(,,)x y z 记录结果,则,,x y z 都有10种可能,所以基本事件总数为10×10×10=103(种)；设事件A 为“连续3次都取正品”,则包含的基本事件共有8×8×8=83种,因此338()0.51210P A ==.(2)可以看作不放回抽样3次,顺序不同,基本事件不同,按抽取顺序记录(,,)x y z ,。

(易错题)高中数学必修五第三章《不等式》测试(答案解析)

一、选择题1．设正数m ，n ，2m n u +=，222v m n mn =++，则2u v ⎛⎫ ⎪⎝⎭的最大值是（） A ．14B ．13C ．12D ．12．设实数x ，y 满足约束条件21,22,x y x y -≤⎧⎨-≥⎩则x y +的最小值是（）A ．2B ．-2C ．1D ．-13．设x ，y R +∈，1x y +=，求14x y+的最小值为（）．A ．2B ．4C ．8D ．94．已知变量,x y 满足约束条件5021010x y x y x +-≤⎧⎪-+≤⎨⎪-≥⎩，则目标函数=21z x y =+-的最大值为（） A ．6B ．7C ．8D ．95．设x ，y 满足约束条件4100,20,0,0,x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩则23z x y =-的最大值为（）A ．10B ．8C ．5D ．6-6．设0a >，0b >，则下列不等式中不．恒成立的是（）． A ．12a a+≥B ．222(1)a b a b +≥+- C≥D ．3322a b ab +≥7．已知实数x y 、满足不等式组21010x x y m x y ≤⎧⎪-+≥⎨⎪+-≥⎩,若目标函数2z x y =-+的最大值不超过4,则实数m 的取值范围是 A．(B．⎡⎣C．⎡⎤⎣⎦D ．[8．已知点（x ，y ）在直线x +2y =4上移动，则24x y +的最小值是（） A．B．C ．6D ．89．设x ，y 满足约束条件261322x y x y y -≤⎧⎪⎪+≥⎨⎪≤⎪⎩，则1z x y =-+的最小值是（）A ．1-B ．0C ．1D ．210．若a ，b 是任意实数，且a >b ，则下列不等式成立的是( ) A ．a 2>b 2B ．1b a< C ．lg(a －b )>0D ．11()()33ab<11．已知集合{}24120A x x x =--≤，{}440B x x =->，则AB =（）A ．{}12x x <≤B ．{}2x x ≥-C ．{}16x x <≤D ．{}6x x ≥-12．设,,a b c ∈R ，且a b >，则（）A ．ac bc >B ．11a b< C ．22a b >D ．33a b >二、填空题13．若正数,x y 满足113122x y xy++=，则xy 的最小值为_________. 14．已知对满足4x y xy +=的任意正实数x ，y ，都有22210x xy y ax ay ++--+≥，则实数a 的取值范围为___________.15．若实数m 和n 满足242329231m m n n m n ⨯-⋅+⨯=++，则23m n +的取值范围为______．16．设x ，y 满足约束条件2020260x y x y -≥⎧⎪+≥⎨⎪+-≤⎩，则z x y =+的最大值是________.17．实数,x y 满足约束条件20,10,0,x y x y y -≥⎧⎪--≤⎨⎪≥⎩若目标函数(0,0)z ax by a b =+>>的最大值为4，则ab 的最大值为______18．某厂拟生产甲、乙两种适销产品，每件销售收入分别为3000元、2000元．甲、乙产品都需要在A ，B 两种设备上加工，在每台A ，B 设备上加工1件甲产品所需工时分别为1h 、2h ，加工1件乙产品所需工时分别为2h 、1h ，A ，B 两种设备每月有效使用时数分别为400h 和500h ．若合理安排生产可使收入最大为______元．19．已知0a >，0b >，若a ，1，b 依次成等差数列，则41a b+的最小值为________．20．当x ，y 满足270101x y x y x +-≤⎧⎪--≤⎨⎪⎩时，|2|x y a -≤恒成立，则实数a 的取值范围是________．三、解答题21．用铁皮做一个体积为350cm ，高为2cm 的长方体无盖铁盒，这个铁盒底面的长与宽各为多少cm 时，用料最省？22．某地要建造一条防洪堤，其横断面为等腰梯形，腰与底边所成的角为60°，考虑到防洪堤的坚固性及石块用料等因素，设计其横断面面积为93平方米，且高度不低于3米，记防洪堤横断面的腰长为x （米），外周长（梯形的上底BC 与两腰长的和）为y （米）.（1）求y 关于x 的函数关系式，并指出其定义域；（2）当防洪堤的腰长x 为多少米时，断面的外周长y 最小？求此时外周长的值．23．已知函数2()()f x x ax a R =-∈. （1）若2a =，求不等式()3f x ≥的解集；（2）若[1,)x ∈+∞时，2()2f x x ≥--恒成立，求a 的取值范围.24．（1）若关于x 的不等式m 2x 2﹣2mx ＞﹣x 2﹣x ﹣1恒成立，求实数m 的取值范围．（2）解关于x 的不等式（x ﹣1）（ax ﹣1）＞0，其中a ＜1．25．某单位计划建造一间背面靠墙的小屋，其地面面积为12m 2，墙面的高度为3m ，经测算，屋顶的造价为5800元，房屋正面每平方米的造价为1200元，房屋侧面每平方米的造价为800元，设房屋正面地面长方形的边长为x m ，房屋背面和地面的费用不计. （1）用含x 的表达式表示出房屋的总造价；（2）当x 为多少时，总造价最低？最低造价是多少？ 26．已知关于x 的一元二次不等式()22600kx x k k -+<≠.（1）若不等式的解集是{|3x x <-或}2x >-，求k 的值；（2）若不等式的解集是R ，求k 的取值范围.【参考答案】***试卷处理标记，请不要删除一、选择题1．B 解析：B 【分析】化简22211()44u mn vm n mn=+⨯++，再结合基本不等式，即可求解. 【详解】由题意，正数m ，n ，2m nu +=，222v m n mn =++，则2222222222()12112()444m n u m n mn mn v m n mn m n mn m n mn+++===+⨯++++++2111111111444444213()11mnm m m n n n n m=+⨯=+⨯≤+⨯=+++++，当且仅当m n n m =时，即m n =时，等号成立,所以2u v ⎛⎫ ⎪⎝⎭的最大值是为13.故选：B . 【点睛】利用基本不等式求最值时，要注意其满足的三个条件：“一正、二定、三相等”：（1）“一正”：就是各项必须为正数；（2）“二定”：就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”：利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.2．C解析：C 【分析】先作出约束条件对应的可行域，然后分析目标函数的几何意义，结合图形即可求解. 【详解】作出约束条件2122x y x y -≤⎧⎨-≥⎩所表示的平面区域如图所示：移动直线x y z +=，可知当其过点A 时取得最小值，解方程组2122x y x y -≤⎧⎨-≥⎩，求得1x y =⎧⎨=⎩，即(1,0)A ，代入求得101=+=z ，所以x y +的最小值是1，故选：C. 【点睛】方法点睛：该题考查的是有关线性规划的问题，解题方法如下：（1）根据题中所给的约束条件画出可行域；（2）根据目标函数的意义找到最优解；（3）解方程组求得最优解的坐标；（4）代入求得最小值，得到结果.3．D解析：D 【分析】由“1”有代换利用基本不等式可得最小值．【详解】因为x ，y R +∈，1x y +=，所以141444()5529x y x yx y x y x y y x y x ⎛⎫+=++=++≥+⨯= ⎪⎝⎭，当且仅当4x y y x =，即12,33x y ==时，等号成立．故选：D ．【点睛】易错点睛：本题考查用基本不等式求最小值．解题关键是利用“1”的代换凑配出定值．用基本不等式求最值必须满足三个条件：一正二定三相等．特别是相等这个条件常常会不满足，因此就不能用基本不等式求得最值．4．C解析：C【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，把最优解的坐标代入目标函数得答案．【详解】由约束条件5021010x yx yx+-≤⎧⎪-+≤⎨⎪-≥⎩作出可行域如图，联立150xx y=⎧⎨+-=⎩，解得A（1，4），化目标函数z＝x+2y﹣1为y1 222x z=-++，由图可知，当直线y1222x z=-++过A时，z有最大值为8．故选C．【点睛】本题考查简单的线性规划，考查了目标函数的几何意义，考查数形结合的解题思想方法，是中档题．5．C解析：C【分析】作出不等式对应的平面区域，利用目标函数的几何意义，求目标函数的最大值即可．【详解】画出约束条件所表示的平面区域，如图所示，由23z x y=-得到233zy x=-，平移直线233zy x=-，当过A时直线截距最小，z最大，由4100yx y=⎧⎨--=⎩得到5(,0)2A，所以23z x y =-的最大值为max 523052z =⨯-⨯=，故选C ．【点睛】本题主要考查简单线性规划求解目标函数的最值问题．其中解答中正确画出不等式组表示的可行域，利用“一画、二移、三求”，确定目标函数的最优解是解答的关键，着重考查了数形结合思想，及推理与计算能力，属于基础题．6．D解析：D 【解析】分析：根据基本不等式、作差法、分析法论证A,B,C 正确，举反例得D 错误. 详解：332222()()a b ab a b a ab b +-=-+-， 51a b -<<有3322a b ab <+，故D 项错误，其余恒成立：11122,a a a a a a+≥⋅=⇒+≥ 2222222(1)(1)(1)02(1),a b a b a b a b a b +-+-=-+-≥⇒+≥+-当a b ≥时2220a b a b ab a b a b b a b a b ---+≥---+=⇒-当a b <0a b a b ->>D ．点睛：本题考查根据基本不等式、作差法、分析法论证等知识点，考查推理论证能力.7．D解析：D 【分析】将2z x y =-+化为2y x z =+,作出可行域和目标函数基准直线2y x =(如图所示),当直线2y x z =+将左上方平移时,直线2y x z =+在y 轴上的截距z 增大,由图象,得当直线2y x z =+过点A 时,z 取得最大值,联立2010x y m x y ⎧-+=⎨+-=⎩,得2211,22m m A ⎛⎫-+ ⎪⎝⎭,则22112422m m -+-⨯+≤,解得33m -≤≤;故选D.点睛：线性规划的实质是把代数问题几何化，即数形结合的思想.需要注意的是：一、准确无误地作出可行域；二、画标准函数所对应的直线时，要注意与约束条件中的直线的斜率进行比较，避免出错；三、一般情况下，目标函数的最大或最小会在可行域的端点或边界上取得.8．D解析：D 【分析】运用基本不等式2422422x y x y +≥=【详解】因为20,40xy>>，所以242422422228x y xy x y ++≥===，（当且仅当24x y =时取“=”）．故答案为D. 【点睛】利用两个数的基本不等式求函数的最值必须具备三个条件： ①各项都是正数； ②和（或积）为定值； ③等号取得的条件．9．C解析：C 【分析】作出约束条件所表示的平面区域，结合图象确定目标函数的最优解，代入求解，即可得到答案.【详解】作出x，y满足约束条件261322x yx yy-≤⎧⎪⎪+≥⎨⎪≤⎪⎩，所对应的可行域，如图所示，目标函数1z x y=-+可化为1y x z=+-，当直线1y x z=+-过点A时，此时直线在y轴上的截距最大值，此时目标函数取得最小值，又由2132yx y=⎧⎪⎨+=⎪⎩，解得(2,2)A，所以目标函数的最小值为min2211z=-+=.故选：C.【点睛】本题主要考查简单线性规划求解目标函数的最值问题．其中解答中正确画出不等式组表示的可行域，利用“一画、二移、三求”，确定目标函数的最优解是解答的关键，着重考查了数形结合思想，及推理与计算能力，属于基础题．10．D解析：D【详解】试题分析：A中1,2a b==-不成立，B中1,12a b=-=-不成立，C中0,1a b==-不成立，D中由指数函数单调性可知是成立的11．C解析：C【分析】根据不等式的解法，求得集合{}26A x x=-≤≤，{}1B x x=>，结合集合交集的运算，即可求解.【详解】由题意，集合{}{}2412026A x x x x x =--≤=-≤≤，{}{}4401B x x x x =->=>，根据集合交集的概念与运算，可得{}16A B x x ⋂=<≤. 故选：C. 【点睛】本题考查集合的交集的概念及运算，其中解答中正确求解集合,A B ，结合集合的交集的概念及运算求解是解答的关键，着重考查运算求解能力，属于基础题.12．D解析：D 【分析】结合不等式的性质、特殊值判断出错误选项，利用差比较法证明正确选项成立. 【详解】A 选项，当0c ≤ 时，由a b >不能得到ac bc >，故不正确；B 选项，当0a >，0b <（如1a =，2b =-）时，由a b >不能得到11a b<，故不正确； C 选项，由()()22a b a b a b -=+-及a b >可知当0a b +<时（如2a =-，3b =-或2a =，3b =-）均不能得到22a b >，故不正确；D 选项，()()()233222324b a b a b a ab b a b a b ⎡⎤⎛⎫-=-++=-⋅++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦，因为,a b 不同时为0，所以223024b a b ⎛⎫++> ⎪⎝⎭，所以可由a b >知330a b ->，即33a b >，故正确.故选：D 【点睛】本小题主要考查不等式的性质以及差比较法，属于中档题.二、填空题13．【分析】将化为后利用基本不等式得再解一元二次不等式可得结果【详解】由得因为所以当且仅当时等号成立所以所以所以或所以或（舍）所以即的最小值为故答案为：【点睛】易错点睛：利用基本不等式求最值时要注意其必解析：92【分析】将113122x y xy++=化为232y x xy ++=后，利用基本不等式得23xy -≥一元二次不等式可得结果. 【详解】由113122x y xy++=得232y x xy ++=，因为0,0x y >>，所以232xy y x -=+≥2y x =时，等号成立.所以2302≥，所以2)22≥2-≥2≤，2≥2≤-（舍），所以92xy ≥，即xy 的最小值为92. 故答案为：92. 【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方14．【分析】利用基本不等式求得的取值范围对不等式分离常数结合函数单调性求得的取值范围【详解】依题意则当且仅当时等号成立由为正实数得令在上递增所以时有最小值所以故答案为：【点睛】利用基本不等式求最值要注意解析：829a ≤【分析】利用基本不等式求得x y +的取值范围，对不等式22210x xy y ax ay ++--+≥分离常数a ，结合函数单调性求得a 的取值范围.【详解】依题意4x y xy +=，则141y x+=，()144559x y x y x y y x y x ⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当4,26x yx y y x===时等号成立.由22210x xy y ax ay ++--+≥，,x y 为正实数得()()210x y a x y +-++≥，1a x y x y≤+++，令9t x y =+≥，1t t +在[)9,+∞上递增，所以9t =时1t t +有最小值182999+=，所以829a ≤故答案为：829a ≤ 【点睛】利用基本不等式求最值，要注意掌握“1”的代换的方法.15．【分析】设方程化简为得到再结合基本不等式得到根据一元二次不等式不等式的解法即可求解【详解】设因为可得所以解得或又由当且仅当时即时等号成立整理得解得所以即则的取值范围为故答案为：【点睛】方法点睛：设利解析：(1,2]. 【分析】设23m n t =+，方程化简为221523m n t t --=⨯⨯，得到2210t t -->，再结合基本不等式，得到23440t t --≤，根据一元二次不等式不等式的解法，即可求解. 【详解】设23m n t =+，因为242329231m m n n m n ⨯-⋅+⨯=++，可得221523m n t t --=⨯⨯，所以2210t t -->，解得1t >或12t <-，又由222235215235()24m n mnt t t +--=⨯⨯≤⨯=，当且仅当23m n =时，即0m n ==时等号成立，整理得23440t t --≤，解得223t -≤≤，所以12t <≤，即则23m n +的取值范围为(1,2].故答案为：(1,2]. 【点睛】方法点睛：设23m n t =+，利用换元法把方程化简为221523m n t t --=⨯⨯，根据指数函数的性质和基本不等式，得出不等式2210t t -->和23440t t --≤是解答的关键.16．8【分析】根据xy 满足的约束条件画出可行域然后平移直线当直线在y 轴上截距最大时目标函数取得最大值【详解】依题意xy 满足约束条件可行域如图所示阴影部分：易得点平移直线（图中虚线）当直线经过C 点时在y 轴【分析】根据x ，y 满足的约束条件2020260x y x y -≥⎧⎪+≥⎨⎪+-≤⎩画出可行域，然后平移直线0x y +=，当直线在y 轴上截距最大时，目标函数取得最大值. 【详解】依题意x ，y 满足约束条件2020260x y x y -≥⎧⎪+≥⎨⎪+-≤⎩可行域如图所示阴影部分：易得点()2,2A -、()2,2B 、()10,2C -，平移直线0x y +=（图中虚线），当直线0x y +=经过C 点时，在y 轴上的截距最大，目标函数z x y =+有最大值，1028max z =-=，所以目标函数z x y =+的最大值是8. 故答案为：8. 【点睛】方法点睛：本题考查线性规划求最值，考查数形结合思想. 线性规划问题考查的方式是由二元一次不等式组给出线性约束条件确定可行域，求可行域的面积、或确定形状；或者是在线性约束条件下求目标函数的取值范围、最值或取得最值时的点的坐标的确定以及由此衍生出来的其他相关问题，比如直线的斜率、平面距离的最值等问题.17．2【分析】作出不等式对应的平面区域利用z 的几何意义确定取得最大值的条件然后利用基本不等式进行求可得的最大值【详解】作出不等式对应的平面区域由得则目标函数对应直线的斜率平移直线由图象可知当直线经过点A解析：2作出不等式对应的平面区域,利用z 的几何意义确定取得最大值的条件，然后利用基本不等式进行求，可得ab 的最大值. 【详解】作出不等式对应的平面区域,由(0,0)z ax bya b =+>>得a zy x b b=-+，则目标函数对应直线的斜率0a b -<，平移直线ay x b=-，由图象可知当直线经过点A 时，直线的截距最大，此时z 最大.由2010x y x y -=⎧⎨--=⎩解得(2,1)A此时z 的最大值为2422z a b ab =+=，当且仅当2,1b a ==时取等号.24ab ∴解2ab 故答案为: 2. 【点睛】本题主要考查线性规划的基本应用，以及基本不等式的应用，利用数形结合求出目标函数取得最大值的条件是解决本题的关键.18．800000【分析】设每月生产甲产品件生产乙产品件每月收入为元列出实际问题中xy 所需满足的条件作出可行域数形结合求出目标函数的最大值【详解】设每月生产甲产品件生产乙产品件每月收入为元目标函数为需要满解析：800000 【分析】设每月生产甲产品x 件，生产乙产品y 件，每月收入为z 元，列出实际问题中x 、y 所需满足的条件，作出可行域，数形结合求出目标函数30002000z x y =+的最大值. 【详解】设每月生产甲产品x 件，生产乙产品y 件，每月收入为z 元，目标函数为30002000z x y =+，需要满足的条件是2400250000x y x y x y +≤⎧⎪+≤⎪⎨≥⎪⎪≥⎩，作出可行域如图所示，目标函数30002000z x y =+可转化直线3122000y x z =-+，数形结合知当直线经过点A 时z 取得最大值．解方程组24002500x y x y +=⎧⎨+=⎩，可得点()200,100A ，则z 的最大值为30002002000100z =⨯+⨯=800000元．故答案为：800000 【点睛】本题考查线性规划解决实际问题，属于基础题.19．【分析】由a1b 依次成等差数列可得再利用乘1法及基本不等式计算即可求得答案【详解】且a1b 依次成等差数列当且仅当即取等号故的最小值为故答案为：【点睛】本题考查基本不等式的性质以及应用涉及等差中项的定解析：92【分析】由a ，1，b 依次成等差数列，可得2a b +=，再利用乘“1”法及基本不等式计算，即可求得答案．【详解】0a >，0b >，且a ，1，b 依次成等差数列， ∴2a b +=，∴()411411414941(52)2222b a b a a b a b a b a b a b ⎛⎫⎛⎫+=++=+++≥+⋅= ⎪ ⎪⎝⎭⎝⎭，当且仅当4b a a b =，即43a =，23b =，取等号，故14a b +的最小值为92．故答案为：92．【点睛】本题考查基本不等式的性质以及应用，涉及等差中项的定义，考查了分析能力和计算能力，属于中档题．20．【分析】先根据条件作出可行域然后求出的取值范围由恒成立即即可得出答案【详解】由满足作出可行域如图设则表示直线在轴上的截距的相反数则由得当直线过点时有最大值4当直线过点时有最小值所以所以故答案为：【点解析：)4，⎡+∞⎣ 【分析】先根据条件作出可行域，然后求出2z x y =-的取值范围，由|2|x y a -≤恒成立，即max |2|x y a -≤，即可得出答案.【详解】由x ，y 满足270101x y x y x +-≤⎧⎪--≤⎨⎪⎩，作出可行域，如图.设2z x y =-，则2y x z =-，z 表示直线2y x z =-在y 轴上的截距的相反数.则()()1,0,1,3A C ,由27010x y x y +-=⎧⎨--=⎩，得()3,2B .当直线2y x z =-过点()3,2B 时，z 有最大值4，当直线2y x z =-过点()1,3C 时，z 有最小值-1.所以|2|4x y -≤，所以4a ≤故答案为：[)4+∞，. 【点睛】本题考查简单的线性规划问题和恒成立求参数的问题，属于中档题.三、解答题21．铁盒底面的长与宽均为5cm 时，用料最省. 【分析】法一：因为体积为350cm 高为2cm ，所以底面积是定值25，设长为xcm ，则宽为25x，列出表面积结合基本不等式即可；法二：列出表面积后，利用求导函数的方法求最值. 【详解】解法1：设铁盒底面的长为xcm ，宽为25x，则.. 表面积251002544425S x x x x=++⨯=++..2565≥=.. 当且仅当25x x=，即5x =时，表面积有最小值65. 所以这个铁盒底面的长与宽均为5cm 时，用料最省.答：这个铁盒底面的长与宽均为5cm 时，用料最省. 解法2：设铁盒底面的长为xcm ，宽为25x，表面积为2ycm ，则. ()2510025444250y x x x x x=++⨯=++> 22210041004x y x x -'=-=.. 令2241000x y x-'==得，5x =. 当()0,5x ∈时，0y '<，函数224100x y x-'=为减函数；当()5,+∈∞x 时，0y '>，函数224100x y x-'=为增函数；所以当5x =时，y 有最小值65.答：这个铁盒底面的长与宽均为5cm 时，用料最省. 22．(1)1832,(26)2xy BC x x x =+=+≤<;(2)外周长的最小值为米，此时腰长为.【分析】()1由腰与底边所成的角为60︒，求出h x =，182x BC x =-，结合限制条件求出定义域26x ≤<，从而得到y 关于x 的函数关系式()2由()1得1832x y x=+，运用基本不等式求出结果【详解】（1）()12AD BC h =+,其中2,2x AD BC BC x h x =+⋅=+= ∴182x BC x =-由,261802h x x x BC x ⎧=≥⎪⎪≤<⎨⎪=->⎪⎩得 ∴1832,(26)2xy BC x x x =+=+≤<.(2)1832x y x =+≥=当且仅当[)1832,62x x x ==即时等号成立 ∴外周长的最小值为. 【点睛】本题是一道函数的应用题，解题时需要理清题目中各数量之间的关系，然后根据题意列出函数表达式，在求最值时一般运用基本不等式来求解，注意等号成立的条件 23．（1）{|1x x ≤-或3}x ≥；（2）(,4]-∞. 【解析】试题分析：（1）先对不等式移项并因式分解得()()310x x -+≥，再根据不等号方向得不等式解集，（2）先化简不等式，并分离12a x x ⎛⎫≤+ ⎪⎝⎭，转化为求对应函数最值：()min a h x ≤，其中()12h x x x⎛⎫=+ ⎪⎝⎭，再根据基本不等式求()h x 最值，即得a 的取值范围. 试题（1）若()2,3a f x =≥即()()2230,310x x x x --≥-+≥所以原不等式的解集为{|1x x ≤-或3}x ≥ （2）()22f x x ≥--即12a x x ⎛⎫≤+⎪⎝⎭在[)1,x ∈+∞时恒成立，令()12h x x x ⎛⎫=+ ⎪⎝⎭，等价于()min a h x ≤在[)1,x ∈+∞时恒成立，又()124h x x x ⎛⎫=+≥= ⎪⎝⎭，当且仅当1x x =即1x =等号成立，所以4a ≤. 故所求a 的取值范围是(],4-∞. 24．(1) m 34-＞；(2)见解析【分析】（1）利用△＜0列不等式求出实数m 的取值范围；（2）讨论0＜a ＜1、a ＝0和a ＜0，分别求出对应不等式的解集．【详解】（1）不等式m 2x 2﹣2mx ＞﹣x 2﹣x ﹣1化为（m 2+1）x 2﹣（2m ﹣1）x +1＞0，由m 2+1＞0知，△＝（2m ﹣1）2﹣4（m 2+1）＜0，化简得﹣4m ﹣3＜0，解得m 34-＞，所以实数m 的取值范围是m 34-＞；（2）0＜a ＜1时，不等式（x ﹣1）（ax ﹣1）＞0化为（x ﹣1）（x 1a -）＞0，且1a＞1，解得x ＜1或x 1a＞，所以不等式的解集为{x |x ＜1或x 1a＞}； a ＝0时，不等式（x ﹣1）（ax ﹣1）＞0化为﹣（x ﹣1）＞0，解得x ＜1，所以不等式的解集为{x |x ＜1}；a ＜0时，不等式（x ﹣1）（ax ﹣1）＞0化为（x ﹣1）（x 1a -）＜0，且1a＜1，解得1a＜x ＜1，所以不等式的解集为{x |1a＜x ＜1}．综上知，0＜a ＜1时，不等式的解集为{x |x ＜1或x 1a＞}； a ＝0时，不等式的解集为{x |x ＜1}； a ＜0时，不等式的解集为{x |1a＜x ＜1}．【点睛】本题考查了不等式恒成立问题和含有字母系数的不等式解法与应用问题，是基础题． 25．（1）16()36005800(0)f x x x x ⎛⎫=++> ⎪⎝⎭（2）当底面的长宽分别为4m ，3m 时，可使房屋总造价最低，34600元. 【分析】（1）设底面的长为x m ，表示出正面，侧面面积，可得总造价；（2）由基本不等式可得最小值．【详解】解：（1）设底面的长为x m ，宽y m ，则12y x=m. 设房屋总造价为()f x ，由题意可得1216()3120038002580036005800(0)f x x x x x x ⎛⎫=⋅+⨯⨯⨯+=++> ⎪⎝⎭（2）16()360058003600580034600f x x x ⎛⎫=++≥⨯= ⎪⎝⎭，当且仅当16x x=即4x =时取等号. 答：当底面的长宽分别为4m ，3m 时，可使房屋总造价最低，总造价是34600元. 【点睛】本题考查函数的应用，解题关键是根据已知条件引入变量（长度x ），列出总造价的函数式，从而再由基本不等式求得最小值．26．（1）25-；（2）6⎛⎫-∞ ⎪ ⎪⎝⎭，-. 【分析】（1）由不等式的解集为{}32x x x <->-或知0k <,且3-，2-是方程2260kx x k -+=的两根，代入可解.（2）不等式的解集为R ，知二次函数图像恒在x 轴下方，则利用0k <且24240k ∆=-<可解【详解】（1）∵不等式的解集为{}32x x x <->-或∴3-，2-是方程2260kx x k -+=的两根，且0k < ∴25k =- （2）∵不等式的解集为R∴0k <且24240k ∆=-<∴k <∴k 的取值范围是(-∞，【点睛】解含参数的一元二次不等式时分类讨论的依据(1)二次项中若含有参数应讨论是等于0，小于0，还是大于0，然后将不等式转化为一次不等式或二次项系数为正的形式．(2)当不等式对应方程的实根的个数不确定时，讨论判别式∆与0的关系．(3)确定无实根时可直接写出解集，确定方程有两个实根时，要讨论两实根的大小关系，从而确定解集形式．。

(易错题)高中数学必修五第三章《不等式》测试(包含答案解析)(3)

一、选择题1．设0,0a b >>，若4a b +=.则49a b+的最小值为（） A ．254B ．252 C ．85D ．1252．设x ，y 满足约束条件5010550x x y x y -≤⎧⎪-+≥⎨⎪+-≥⎩，且(0,0)z ax by a b =+>>的最大值为1，则56a b+的最小值为（） A ．64B ．81C ．100D ．1213．已知实数,x y 满足条件202035x y x y x y -≥⎧⎪+≥⎨⎪+≤⎩，则2z x y =+的最大值是（）A ．0B ．3C ．4D ．54．已知关于x 的不等式210x ax -+≥在区间[1,2]上有解，则实数a 的取值范围为（） A ．2a ≤B ．2a ≥C ．52a ≥D ．52a ≤5．若x ､y 满足约束条件36022x y x y y +-≤⎧⎪+≥⎨⎪≤⎩，则22x y +的最小值为（）A ．5B ．4C ．2D6．已知实数,x y 满足24240x y x y y -≥⎧⎪+≤⎨⎪≤⎩，则32z x y =-的最小值是（）A ．4B ．5C ．6D ．77．设x ，y 满足约束条件4100,20,0,0,x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩则23z x y =-的最大值为（）A ．10B ．8C ．5D ．6-8．已知α，β满足11123αβαβ-≤+≤⎧⎨≤+≤⎩，则3αβ+的取值范围是（）A ．[1,7]B ．[5,13]-C ．[5,7]-D ．[1,13]9．设变量,x y 、满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩，则目标函数2z x y =+的最大值为（）A ．2B ．3C ．4D ．910．已知函数()3x f x -=，对任意的1x ，2x ，且12x x <，则下列四个结论中，不一定正确的是（）A ．()()()1212f x x f x f x +=⋅B ．()()()1212f x x f x f x ⋅=+C ．()()()12120x x f x f x --<⎡⎤⎣⎦D ．()()121222f x f x x x f ++⎛⎫<⎪⎝⎭ 11．已知正数a ，b 满足2a b +=，则2238a b ⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭的最小值为( ) A ．36B ．42C ．49D ．6012．已知实数x ,y 满足210210x y x x y -+≥⎧⎪<⎨⎪+-≥⎩,则221z x y =--的取值范围是( )A ．5,53⎡⎤⎢⎥⎣⎦B ．5,53⎡⎤-⎢⎥⎣⎦C ．5,53⎡⎫⎪⎢⎣⎭D ．5,53⎡⎫-⎪⎢⎣⎭二、填空题13．已知正数a ，b 满足30a b ab +-+=，则ab 的最小值是________．14．西气东输工程把西部的资源优势变为了经济优势，实现了气能源需求与供给的东西部衔接，同时该项工程的建设也加快了西部及沿线地区的经济发展.在输气管道工程建设过程中，某段直线形管道铺设需要经过一处平行峡谷，勘探人员在峡内恰好发现一处四分之一圆柱状的圆弧拐角，用测量仪器得到此横截圆面的圆心为O ，半径OM ON =且为1米，而运输人员利用运输工具水平横向移动直线形输气管不可避免的要经过此圆弧拐角，需从宽为38米的峡谷拐入宽为16米的峡谷.如图所示，位于峡谷悬崖壁上的两点A ，B 的连线恰好与圆弧拐角相切于点T （点A ，T ，B 在同一水平面内），若要使得直线形输气管能够顺利地通过圆弧拐角，其长度不能超过______________米.15．已知对满足4x y xy +=的任意正实数x ，y ，都有22210x xy y ax ay ++--+≥，则实数a 的取值范围为___________. 16．在下列函数中， ①1y x x=+②1123212y x x x ⎛⎫=++< ⎪-⎝⎭③()2114141x y x x x x ⎛⎫=++> ⎪+⎝⎭ ④22221πsin cos 0,sin cos 2y x x x x x ⎛⎫⎛⎫=+∈ ⎪ ⎪⎝⎭⎝⎭其中最小值为2的函数是__________.17．已知点(3,A ，O 是坐标原点，点(),P x y的坐标满足0200y x y -≤+≥⎨⎪≥⎪⎩，设z 为OA 在OP 上的投影，则z 的取值范围是__________.18．已知0a >，0b >，若a ，1，b 依次成等差数列，则41a b+的最小值为________． 19．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且2c cosB ＝2a ＋b ，若△ABC 的面，则ab 的最小值为_______． 20．若实数x ，y 满足约束条件103030x y x y x -+≥⎧⎪+-≥⎨⎪-≤⎩，则3z x y =-的最小值为__________．三、解答题21．定义两个函数的关系：函数()m x ，()n x 的定义域为A ，B ，若对任意的1x A ∈，总存在2x B ∈，使得()()12m x n x =，我们就称函数()m x 为()n x 的“子函数”.设,0a b >，已知函数()f x=23(1)b a b+--，22||11()1822||x g x x a a x x =+-++. （1）当1a =时，求函数()f x 的单调区间；（2）若函数()f x 是()g x 的“子函数”，求22a b ab+的最大值.22．近年来，某市在旅游业方面抓品牌创建，推进养生休闲度假旅游产品升级，其景区成功创建国家5A 级旅游景区填补了该片区的空白，某投资人看到该市旅游发展的大好前景后，打算在该市投资甲、乙两个旅游项目，根据市场前期调查，甲、乙两个旅游项目五年后可能的最大盈利率分别为01000和0080，可能的最大亏损率分别为0040和0020，投资人计划投资金额不超过5000万，要求确保亏损不四超过1200万，问投资人对两个项目各投资多少万元，才能使五年后可能的盈利最大？23．已知关于x 的一元二次不等式2(1)0ax a x b -++<的解集为112x x x ⎧⎫-⎨⎬⎩⎭或．（Ⅰ）求,a b 的值；（Ⅱ）若不等式2(2)30bx m a x m +++-≥对任意实数[0,4]m ∈恒成立，求实数x 的取值范围．24．已知函数2221,()?23,x ax x af x x ax x a ⎧-+<⎪⎪=⎨⎪+-≥⎪⎩，其中 0a >．（1）若()()01ff =，求a 的值．（2）若函数()f x 的图象在x 轴的上方，求a 的取值范围． 25．如果x ，y R ∈，比较()222+x y 与()2xy x y +的大小．26．已知圆22:4210C x y x y +---=．（1）求y 轴被圆C 所截得的线段的长；（2）过圆C 圆心的直线与两坐标轴在第一象限内围成的三角形面积为S ，求S 的最小值．【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】用“1”的代换凑配出定值后用基本不等式可得最小值．【详解】0,0,4a b a b >>+=()(4914914912513134444b a a b a b a b a b ⎛⎫⎛⎫∴+=++=++≥⨯+= ⎪ ⎪⎝⎭⎝⎭ 当且仅当49b aa b =，即812,55a b ==时取等号. 故选：A ．【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方2．D解析：D 【分析】作出可行域，作出目标函数对应的直线，平移该直线得最优解，从而得,a b 的关系式561a b +=，然后用“1”的代换，配凑出积为定值，用基本不等式得最小值．【详解】作出约束条件表示的可行域，如图，ABC 内部（含边界），作直线直线0ax by += ，z ax by =+中，由于0,0a b >>，ab是直线的纵截距，直线向上平移时，纵截距增大，所以当直线z ax by =+经过点()5,6时，z 取得最大值，则561a b +=，所以()56565661306160121b a a b a b a b a b ⎛⎫⎛⎫+=++=++≥+= ⎪ ⎪⎝⎭⎝⎭，当且仅当111a b ==时，等号成立，故56a b+的最小值为121．故选：D ．【点睛】关键点点睛：本题考查简单的线性规划，考查用基本不等式求最值．解题思路是利用简单的线性规划求得变量,a b 满足的关系式，然后用“1”的代换凑配出定值，再用基本不等式求得最小值．求最值时注意基本不等式的条件：一正二定三相等，否则易出错．3．C解析：C 【分析】画出满足条件的目标区域，将目标函数化为斜截式2y x z =-+，由直线方程可知，要使z 最大，则直线2y x z =-+的截距要最大，结合可行域可知当直线2y x z =-+过点A 时截距最大，因此，解出A 点坐标，代入目标函数，即可得到最大值. 【详解】画出满足约束条件202035x y x y x y -≥⎧⎪+≥⎨⎪+≤⎩的目标区域，如图所示:由2z x y =+,得2y x z =-+，要使z 最大，则直线2y x z =-+的截距要最大，由图可知,当直线2y x z =-+过点A 时截距最大，联立20350x y x y -=⎧⎨+-=⎩,解得(1,2)A ，所以2z x y =+的最大值为：1224⨯+=，故选:：C. 【点睛】方法点睛：求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.4．D解析：D 【分析】由题意得分离参数将不等式等价于不等式1a x x ≤+在区间[1,2]上有解，设()1f x x x=+，由函数()1f x x x=+在[1,2]上单调递增，可求得实数a 的取值范围.【详解】由题意得：关于x 的不等式210x ax -+≥在区间[1,2]上有解，等价于不等式1a x x≤+在区间[1,2]上有解，设()1f x x x =+，则函数()1f x x x =+在[1,2]上单调递增，所以()()(152)2f f f x ≤=≤，所以实数a 的取值范围为52a ≤，故选：D. 【点睛】方法点睛：对于不等式有解的问题，常常有以下情况：()m f x >有解⇔()min m f x >，()m f x <有解⇔()max m f x <. 5．C解析：C 【分析】由不等式组作出可行域，如图,目标函数22xy +可视为可行域中的点与原点距离的平方，故其最小值应为原点到直线2x y +=的距离平方，根据点到直线的距离公式可得选项. 【详解】由不等式组做出可行域如图，目标函数22xy +可视为可行域内的点与原点距离的平方，故其最小值为原点到直线2x y +=的距离的平方，由点到直线的距离公式可知，原点到直线2x y +=的距离为22d ==，所以所求最小值为2. 故选:C.【点睛】本题主要考查线性规划问题，首先由不等式组作出相应的可行域，作图时，可将不等式0Ax By C ++≥转化为y kx b ≤+（或y kx b ≥+），明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线，其次确定目标函数的几何意义，是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等，最后结合图形确定目标函数最值取法、值域范围.6．C解析：C【分析】由约束条件画出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组得到最优解的坐标，代入目标函数得到答案.【详解】由实数x，y满足2424x yx yy-≥⎧⎪+≤⎨⎪≤⎩得到可行域如图：z＝3x﹣2y变形为y＝32x﹣2z，由24yx y=⎧⎨-=⎩，解得B（2，0）当此直线经过图中B时，在y轴的截距最大，z最小，所以z的最小值为3×2﹣2×0＝6；故选C．【点睛】本题主要考查线性规划中利用可行域求目标函数的最值，求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.7．C解析：C【分析】作出不等式对应的平面区域，利用目标函数的几何意义，求目标函数的最大值即可．【详解】画出约束条件所表示的平面区域，如图所示，由23z x y=-得到233zy x=-，平移直线233zy x =-，当过A 时直线截距最小，z 最大，由04100y x y =⎧⎨--=⎩ 得到5(,0)2A ，所以23z x y =-的最大值为max 523052z =⨯-⨯=，故选C ．【点睛】本题主要考查简单线性规划求解目标函数的最值问题．其中解答中正确画出不等式组表示的可行域，利用“一画、二移、三求”，确定目标函数的最优解是解答的关键，着重考查了数形结合思想，及推理与计算能力，属于基础题．8．A解析：A 【解析】分析：该问题是已知不等关系求范围的问题，可以用待定系数法来解决．详解：设α+3β=λ（α+β）+v （α+2β） =（λ+v ）α+（λ+2v ）β．比较α、β的系数，得123v v λλ+=⎧⎨+=⎩，从而解出λ=﹣1，v=2．分别由①、②得﹣1≤﹣α﹣β≤1，2≤2α+4β≤6，两式相加，得1≤α+3β≤7．故α+3β的取值范围是[1，7]．故选A点睛：本题考查待定系数法，考查不等式的基本性质，属于基础题．9．D解析：D 【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论. 【详解】画出满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩的可行域，如图，画出可行域ABC ∆，(2,0)A ，(1,1)B ，(3,3)C ，平移直线2z x y =+，由图可知，直线2z x y =+经过(3,3)C 时目标函数2z x y =+有最大值，2z x y =+的最大值为9.故选D. 【点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.10．B解析：B 【分析】将函数()3xf x -=代入选项，由指数幂的运算性质可判断A 、B ；由函数的单调性可判断C ；由基本不等式可判断D ；即可得解. 【详解】对于A ，1212)(1212()333()()x x x x f x x f x f x -+--=⋅=⋅+=，故A 一定正确；对于B ，()12123x x f x x -=⋅，1212()()33x x f x f x --++=，()()()1212f x x f x f x ⋅=+不一定成立，故B 不一定正确；对于C ，因为()3xf x -=为减函数，故满足1212()[()()]0x x f x f x --<，故C 一定正确；对于D ，因为12x x <，所以1212()()22332x x f x f x --++=>=1212232x x x x f +-+⎛⎫= ⎪⎝⎭=，故D 一定正确. 故选：B. 【点睛】本题考查了指数函数性质及基本不等式的应用，考查了运算求解能力与转化化归思想，属于中档题.11．C解析：C 【分析】由已知可得2294(3)(8)(4)(9)37b a b aa b a b a b++=++=++，然后结合基本不等式即可求解．【详解】解：因为正数a ，b 满足2a b +=，所以22949(3)(8)(4)(9)3737249b a b a a b a b a b a b++=++=+++=，当且仅当65a =，45b =时取等号．故选：C ．【点睛】本题主要考查了利用基本不等式求解最值，属于基础题．12．D解析：D 【分析】画出可行域，根据目标函数的截距，利用数形结合，即可求出z 的取值范围. 【详解】作出可行域如下：由221z x y =--得12zy x +=-，平移直线12zy x +=-，由平移可知当直线12zy x +=-，经过点C 时，直线12zy x +=-的截距最小，此时z 取得最大值，由210x x y =⎧⎨+-=⎩，解得21x y =⎧⎨=-⎩，即(2,1)C -，此时2214215z x y =--=+-=，可知当直线12zy x +=-，经过点A 时，直线12zy y x +==-的截距最大，此时z 取得最小值，由21010x y x y -+=⎧⎨+-=⎩，得1323x y ⎧=⎪⎪⎨⎪=⎪⎩，即1(3A ，2)3代入221z x y =--得125221333z =⨯-⨯-=-，故5[3z ∈-，5)故选：D ．【点睛】本题主要考查线性规划的应用，利用数形结合是解决线性规划问题中的基本方法，属于中档题．二、填空题13．9【分析】由已知结合基本不等式即可直接求解【详解】为正实数当且仅当时取等号即解得：或（舍去）当且仅当时取等号即的最小值是9故答案为：9【点睛】关键点点睛：本题主要考查了利用基本不等式求最值解题的关键解析：9 【分析】由已知结合基本不等式2a b ab +≥，即可直接求解．【详解】30a b ab +-+=，3a b ab ∴+=-,a b 为正实数，2a b ab ∴+≥，当且仅当a b =时取等号， 32ab ab ∴-≥，230ab ab ∴--≥，即()()310ab ab -+≥解得：3ab ≥或1ab ≤-（舍去），9ab ∴≥，当且仅当3a b ==时取等号，即ab 的最小值是9．故答案为：9 【点睛】关键点点睛：本题主要考查了利用基本不等式求最值，解题的关键是利用基本不等式将已知条件转换成关于ab 的一元二次不等式，进而解不等式得解，考查学生的转化思想与运算能力，属于基础题．14．75【分析】设则可得AB 长度的表达式利用凑1法结合基本不等式即可求得答案【详解】设其中延长OM 交AB 于D 过B 做SB 垂线交DO 于G 延长ON 交AB 于E 过A 做SA 垂线交NO 于F 如图所示：在中AF=39则即解析：75 【分析】设=MOT θ∠，则可得AB 长度的表达式，利用凑“1”法，结合基本不等式，即可求得答案. 【详解】设=MOT θ∠，其中(0)2πθ∈，，延长OM ，交AB 于D ，过B 做SB 垂线，交DO 于G ，延长ON ，交AB 于E ，过A 做SA 垂线，交NO 于F ，如图所示：在Rt AEF 中，AEF θ∠=，AF =39，则sin AF AE θ=，即39sin AE θ=，在Rt BDG 中，DBG θ∠=，17BG =，则cos BG BD θ=，即17cos BD θ=，在Rt DOE 中， OT DE ⊥，OT=1，所以11,cos sin DO EO θθ==，又1122DO EO DE OT ⨯⨯=⨯⨯，所以1sin cos DE θθ=，所以39171()sin cos sin cos AB f AE BD DE θθθθθ==+-=+-=39cos 17sin 1sin cos θθθθ+-，因为4sin 3cos 5sin()5θθθϕ+=+≤，其中3tan 4ϕ=，当且仅当2πθϕ+=时，等号成立，所以1(4sin 3cos )(39cos 17sin )139cos 17sin 15()sin cos sin cos f θθθθθθθθθθθ++-+-=≥22221(68sin 207sin cos 117cos )(sin cos )5sin cos θθθθθθθθ++-+==2263207112sin sin cos cos 716207555(9tan )sin cos 5tan 5θθθθθθθθ++=++72077555≥⨯=，当且仅当169tan tan θθ=，即4tan 3θ=时等号成立，所以若要使得直线形输气管能够顺利地通过圆弧拐角，其长度不能超过75米. 故答案为：75. 【点睛】解题的关键是根据题意，得到AB 长度的表达式，难点在于需利用凑“1”法，将表达式化简成齐次式，结合基本不等式求解，考查计算化简的能力，属中档题.15．【分析】利用基本不等式求得的取值范围对不等式分离常数结合函数单调性求得的取值范围【详解】依题意则当且仅当时等号成立由为正实数得令在上递增所以时有最小值所以故答案为：【点睛】利用基本不等式求最值要注意解析：829a ≤【分析】利用基本不等式求得x y +的取值范围，对不等式22210x xy y ax ay ++--+≥分离常数a ，结合函数单调性求得a 的取值范围.【详解】依题意4x y xy +=，则141y x+=，()144559x y x y x y y x y x ⎛⎫+=++=++≥+= ⎪⎝⎭，当且仅当4,26x y x y y x===时等号成立. 由22210x xy y ax ay ++--+≥，,x y 为正实数得()()210x y a x y +-++≥，1a x y x y≤+++，令9t x y =+≥，1t t +在[)9,+∞上递增，所以9t =时1t t +有最小值182999+=，所以829a ≤故答案为：829a ≤ 【点睛】利用基本不等式求最值，要注意掌握“1”的代换的方法.16．①③【分析】结合基本不等式对四个函数逐个分析可得出答案【详解】对于①函数是定义域为的偶函数当时当且仅当时等号成立根据对称性可知函数的最小值为2满足题意；对于②因为所以则当且仅当即时等号成立所以即函数解析：①③ 【分析】结合基本不等式，对四个函数逐个分析，可得出答案. 【详解】对于①，函数1y x x=+是定义域为()(),00,-∞+∞的偶函数，当()0,x ∈+∞时，12x x +≥=，当且仅当1x =时等号成立，根据对称性可知，函数1y x x=+的最小值为2，满足题意；对于②，11123214124212112y x x x x x x ⎛⎫=++=-++=--+- ⎪---⎝⎭，因为12x <，所以120x ->，则11244212x x -+-≥=--，当且仅当11212x x -=-，即0x =时等号成立，所以1124212y x x ⎛⎫=--+-≤ ⎪-⎝⎭，即函数1123212y x x x ⎛⎫=++< ⎪-⎝⎭的最大值为2，没有最小值，不满足题意；对于③，222114144141x x xy x x x x x +⎛⎫=++=+ ⎪++⎝⎭，因为1x >，所以2104x x+>，所以2214241x x y x x +=+≥=+，当且仅当221441x x x x +=+，即2x =所以()2114141xy x x x x ⎛⎫=++> ⎪+⎝⎭的最小值为2，符合题意；对于④，22221sin cos sin cos y x x x x=+，因为π0,2x ⎛⎫∈ ⎪⎝⎭，所以sin cos 0x x >，所以22221sin cos 2sin cos x x x x +≥=，当且仅当22221sin cos sin cos x x x x=，即sin cos 1x x =时等号成立，因为11sin cos sin 222x x x =≤，所以sin cos 1x x ≠，即函数22221sin cos sin cos y x x x x=+的最小值不是2，不符合题意；故答案为：①③. 【点睛】本题考查函数的最值，考查基本不等式的应用，考查学生的推理能力与计算能力，属于中档题.17．【分析】作出可行域根据投影的定义得数形结合求出的取值范围即求z 的取值范围【详解】作出可行域如图所示∴当时；当时的取值范围是故答案为：【点睛】本题考查简单的线性规划和向量的投影属于中档题解析：[]3,3-【分析】作出可行域.根据投影的定义得z AOP =∠，数形结合求出AOP ∠的取值范围，即求z 的取值范围. 【详解】作出可行域，如图所示cos 3OA OP z OA AOP AOP OP⋅==⋅∠=∠.5,66AOP ππ⎡⎤∠∈⎢⎥⎣⎦，∴当6AOP π∠=时，max 2336z π==；当56AOP π∠=时，min 52336z π==-，z ∴的取值范围是[]3,3-. 故答案为：[]3,3-. 【点睛】本题考查简单的线性规划和向量的投影，属于中档题.18．【分析】由a1b 依次成等差数列可得再利用乘1法及基本不等式计算即可求得答案【详解】且a1b 依次成等差数列当且仅当即取等号故的最小值为故答案为：【点睛】本题考查基本不等式的性质以及应用涉及等差中项的定解析：92【分析】由a ，1，b 依次成等差数列，可得2a b +=，再利用乘“1”法及基本不等式计算，即可求得答案．【详解】0a >，0b >，且a ，1，b 依次成等差数列， ∴2a b +=，∴()411411414941(52)2222b a b a a b a b a b a b a b ⎛⎫⎛⎫+=++=+++≥+⋅= ⎪ ⎪⎝⎭⎝⎭，当且仅当4b a a b =，即43a =，23b =，取等号，故14a b +的最小值为92．故答案为：92．【点睛】本题考查基本不等式的性质以及应用，涉及等差中项的定义，考查了分析能力和计算能力，属于中档题．19．【解析】分析：由正弦定理将2ccosB ＝2a ＋b 转化成由三角形内角和定理将利用两角和的正弦公式展开化简求得的值由余弦定理三角形的面积公式及基本不等式关系求得ab 的最小值详解：2ccosB ＝2a ＋b 由解析：13【解析】分析：由正弦定理将2c cosB ＝2a ＋b 转化成2sin cos 2sin sin C B A B =+，由三角形内角和定理，将()sin sin A B C =+，利用两角和的正弦公式展开，化简求得sin C 的值，由余弦定理、三角形的面积公式及基本不等式关系，求得ab 的最小值. 详解：2c cosB ＝2a ＋b ，由正弦定理转化成2sin cos 2sin sin C B A B =+∴()2sin cos 2sin sin C B B C B =++化简得：2sin cos sin 0B C B +=，又0,sin 0BB π<，得1cos 2C =-，0C π<<，得23C π=，则△ABC 的面积为1sin 2S ab C ==，即3c ab =，由余弦定理得2222cos c a b ab C =+-，化简得22229a b ab a b ++=，222a b ab +≥，当且仅当a b =时取等， ∴2229ab ab a b +≤，即13ab ≥，故ab 的最小值是13. 故答案为13. 点睛：本题考查正余弦定理、三角形内角和定理及基本不等式相结合.20．1【分析】由约束条件作出可行域化目标函数为直线方程的斜截式数形结合得到最优解联立方程组求出最优解的坐标代入目标函数得答案【详解】画出不等式组对应的可行域如图所示由可得数形结合可得当直线过A 时直线在y解析：1 【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案．【详解】画出不等式组对应的可行域，如图所示，由3z x y =-可得3y x z =-，数形结合可得当直线3y x z =-过A 时，直线在y 轴上的截距最大，z 有最小值，联立1030x y x y -+=⎧⎨+-=⎩，解得A （1，2），此时z 有最小值为3×1﹣2＝1．故答案为：1【点睛】本题主要考查简单线性规划求解目标函数的最值问题．其中解答中正确画出不等式组表示的可行域，利用“一画、二移、三求”，确定目标函数的最优解是解答的关键，着重考查了数形结合思想，及推理与计算能力，属于基础题．三、解答题21．（1）减区间为(],1-∞，增区间为[3,)+∞；（2）18. 【分析】（1）根据函数的解析式有意义，求得函数的定义域，再结合二次函数的性质和复合函数的单调性的判定方法，即可求解；（2）先求得函数()f x 的值域为233,b a b ⎡⎫+--+∞⎪⎢⎣⎭，利用基本不等式，求得函数()g x 的值域为116,)[a -+∞，根据题意，得到2331,[),[16)b a b a+--+∞⊆-+∞，结合基本不等式，即可求解. 【详解】（1）由题意，函数2233()431b f x x x b+=-+-有意义，则满足2430x x -+≥，解得1x ≤或3x ≥，即定义域为{|1x x ≤或3}x ≥，又由函数243y x x =-+在减区间为(],1-∞，增区间为[3,)+∞，根据复合函数的单调性的判定方法，可得()f x 的减区间为(],1-∞，增区间为[3,)+∞.（2）由函数233()1b f x b+=--，可得()f x 的值域为233,b a b ⎡⎫+--+∞⎪⎢⎣⎭， 211111()||||20422016||2||2g x x x x a x a a ⎛⎫⎛⎫=+++-≥+⨯-=- ⎪ ⎪⎝⎭⎝⎭，当且仅当1||||x x =时，即1x =±，等号成立，所以()g x 的值域为116,)[a-+∞，因为()f x 是()g x 的“子函数，所以2331,[),[16)b a b a+--+∞⊆-+∞，所以233116b a b a+--≥-，即13316a b a b +++≤，又13(3)()103()b aa b a b a b++=++，221331316(3)6422a b a b a b a b ⎛⎫+++ ⎪⎛⎫⎛⎫++≤≤= ⎪ ⎪ ⎪⎝⎭⎝⎭⎪⎝⎭，当且仅当1338a b a b+=+=时取“=”，即a =b =或a =，b = 所以103()64b a a b ++≤，即2218a b b aab a b+=+≤所以22a b ab +的最大值为18.【点睛】利用基本不等式求最值时，要注意其满足的三个条件：“一正、二定、三相等”：（1）“一正”：就是各项必须为正数；（2）“二定”：就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”：利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方. 22．甲乙两项目投资额分别为1000 万元和4000万元【解析】试题分析：设投资人对甲，乙两个项目分别投资,x y 万元.根据已知条件可列出可行域为5000{0.40.212000,0x y x y x y +≤+≤≥≥，目标函数为0.8z x y =+，画出可行域，根据图像可知目标函数在点()1000,4000处取得最大值. 试题设投资人对甲，乙两个项目分别投资,x y 万元5000{0.40.212000,0x y x y x y +≤+≤≥≥求0.8z x y =+最大值如图作出可行域当目标函数结果点()1000,4000A 时，0.8z x y =+取得最大值为4200 万元，此时对甲乙两项目投资额分别为1000 万元和4000 万元盈利最大. 23．（Ⅰ）2,1a b =-=；（Ⅱ）{}(,1]1[3,)-∞-⋃⋃+∞．【详解】试题分析：（1）一元二次不等式的解集的端点即相应的二次方程的根；（2）二次不等式恒成立问题结合相应的函数图象特征，抓端点值即可. 试题（Ⅰ）由根与系数的关系得11122,1112a aa b b a +⎧-+=⎪⎪⇒=-=⎨⎪-⨯=⎪⎩ （Ⅱ）由题意()2430x m x m +-+-≥对任意[]0,4m ∈恒成立，即()21430m x x x -+-+≥令()()2143g m x m x x =-+-+，即()()220430410g x x g x ⎧=-+≥⎪⎨=-≥⎪⎩，故(]{}[),113,x ∈-∞-⋃⋃+∞. 24．（1）1或3；（2）02a <<．【分析】（1）首先根据分段函数求得(0)1f =，然后根据2a与1的大小关系分类计算(1)f ，由(1)1f =求得a 值；（2）()0f x >恒成立，转化两个二次函数在某个区间上大于0恒成立，即当2x a<时，210x ax -+>恒成立和2x a≥时，230x ax +->恒成立，两者结合即得．【详解】解：（1）因为0a >，所以20a>，从而()01f =．当21>a即02a <<时，()()()01111f f f a ==-+=，解得1a =，符合；当21a≤即2a ≥时，()()()01131f f f a ==+-=，解得3a =，符合．所以a 的值为1或3．（2）因为()f x 的图象在x 轴的上方，所以对任意的x ∈R ，()0f x >恒成立． ①当2x a<时，210x ax -+>恒成立，其中0a >． 1︒ 当22a a <即02a <<时，则()2min 4024a af x f -⎛⎫==> ⎪⎝⎭，解得02a <<． 2︒ 当22a a ≥即2a ≥时，则224210f a a aa ⎛⎫=-⨯+≥ ⎪⎝⎭，解得02a <≤，所以2a =．所以02a <≤． ②当2x a≥时，230x ax +->恒成立，其中0a >．则()2min22230f x f a a a a ⎛⎫⎛⎫⎛⎫==+⨯-> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，解得02a <<．综上，02a <<．【点睛】本题考查分段函数，考查不等式恒成立问题，解题关键是转化为二次函数大于0在某个区间上恒成立，结合二次函数知识易得． 25．()()2222x y xy x y ≥++，当且仅当x y =时等号成立【分析】运用作差比较法，结合配方法进行比较大小即可.【详解】()()()2222442224433222x y xy x y x y x y xy x xy y x y x y xy +-++--++=+--=()()()()()()()2223333222324y x x y yy x x y xyx y xxy yx y x y ⎡⎤⎛⎫=-+-=--=-++=-++⎢⎥⎪⎝⎭⎢⎥⎣⎦()20x y -≥，223024y x y ⎛⎫++≥ ⎪⎝⎭，()2223024y x y x y ⎡⎤⎛⎫∴-++≥⎢⎥ ⎪⎝⎭⎢⎥⎣⎦． ()()2222x y xy x y ∴≥++，当且仅当x y =时等号成立.【点睛】本题考查了用作差比较法进行比较两个多项式的大小，考查了配方法的应用，属于中档题.26．（1）2）4 【分析】（1）将0x =代入22:4210C x y x y +---=可得2210y y --=，将线段长为12y y -=和韦达定理相结合即可得出结果；（2）设:1(,0)x yl a b a b +=>，由直线过圆心可得211a b=+，利用基本不等式可得8ab ≥，最后根据三角形面积公式即可得出结果. 【详解】（1）设圆22:4210C x y x y +---=与y 轴的交点为()10y ,，()20,y ，将0x =代入22:4210C x y x y +---=可得2210y y --=，即122y y +=，121y y ⋅=-，所以y 轴被圆C 所截得的线段的长为12y y -==（2）设:1(,0)x yl a b a b +=>，由于l 过(2,1)C ，∴211a b=+，利用基本不等式，得2118ab a b =+≥≥，∴142S ab =≥，即S 的最小值为4，此时4,2a b ==，:142x yl +=，即:240l x y +-= 【点睛】本题主要考查了直线截圆所得弦长问题，直线截距式的应用，利用基本不等式求最值，属于中档题.。

高中必修1-5错误解题分析系列-《5.5推理与证明》

5.5 推理与证明一、基础知识导学1. 推理一般包括合情推理和演绎推理.2. 合情推理：根据已有的事实和正确的结论（包括定义、公理、定理等）、实验和实践的结果，以及个人的经验和直觉等推测某些结果的推理过程.归纳、类比是合情推理常用的思维方法.3. 归纳推理：根据一类事物的部分对象具有某种性质，推出这类事物的所有对象都具有这种性质的推理.4. 归纳推理的一般步骤：⑴通过观察个别情况发现某些相同性质；⑵从已知的相同性质中推出一个明确表达的一般性命题（猜想）. 5. 类比推理：根据两类不同事物之间具有某些类似性，推出其中一类事物具有另一类事物类似的性质的推理.6. 类比推理的一般步骤：⑴找出两类事物之间的相似性或一致性；⑵从一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）.7. 演绎推理：根据一般性的真命题导出特殊性命题为真的推理.8. 直接证明的两种基本方法：分析法和综合法；间接证明的一种基本方法──反证法.9. 分析法：从原因推导到结果的思维方法. 10. 综合法：从结果追溯到产生这一结果的原因的思维方法. 11. 反证法：判定非q 为假，推出q 为真的方法.12. 应用反证法证明命题的一般步骤：⑴分清命题的条件和结论；⑵做出与命题结论相矛盾的假定；⑶由假定出发，应用正确的推理方法，推出矛盾的结果；⑷间接证明命题为真. 13. 数学归纳法：设｛p n ｝是一个与自然数相关的命题集合，如果⑴证明起始命题p 1成立；⑵在假设p k 成立的前提上，推出p k ＋1也成立，那么可以断定，｛p n ｝对一切正整数成立. 14. 数学归纳法的步骤：（1）证明当（如或2等）时，结论正确；（2）假设时结论正确，证明时结论也正确．二、疑难知识导析1.归纳推理是根据一类事物的部分对象具有某种性质，推出这类事物的所有对象都具有这种性质的推理.而类比推理是根据两类不同事物之间具有某些类似性，推出其中一类事物具有另一类事物类似的性质的推理.2. 应用反证法证明命题的逻辑依据：做出与命题结论相矛盾的假定，由假定出发，应用正确的推理方法，推出矛盾的结果3. 数学归纳法是一种证明方法，归纳推理是一种推理方法. 三、经典例题导讲[例1] {n a }是正数组成的数列,其前n 项和为n s ,并且对于所有的自然数n ,n a 与2的等差中项等于n s 与2的等比中项.(1)写出数列{n a }的前3项;(2)求数列{n a }的通项公式(写出推证过程); 错解：由(1)猜想数列{n a }有通项公式n a =4n -2. 下面用数学归纳法证明数列{n a }的通项公式是n a =4n -2. (n ∈N ).①当n =1时,因为4×1-2=2,又在(1)中已求出1a =2,所以上述结论成立.②假设n=k 时结论成立,即有k a =4k -2.由题意,有k k s a 222=+将k a =4k -2代入上式，得k s k 22=，解得22k s k =由题意,有1111,222+++++==+k k k k k a s s s a将22k s k =代入，化简得 016442121=-+-++ka a k k解得k a k 421±=+.∴2)1(4421-+=+=+k k a k 这就是说,当n=k+1时,上述结论成立.根据①、②,上述结论对所有的自然数n 成立. 错因在于解题过程中忽视了取值的取舍. 正解：由(1)猜想数列{an}有通项公式a n =4n-2. 猜想数列{n a }有通项公式n a =4n -2.下面用数学归纳法证明数列{n a }的通项公式是n a =4n -2. (n ∈N ).①当n =1时,因为4×1-2=2,又在(1)中已求出1a =2,所以上述结论成立.②假设n=k 时结论成立,即有k a =4k -2.由题意,有k k s a 222=+将k a =4k -2代入上式，得k s k 22=，解得22k s k =由题意,有1111,222+++++==+k k k k k a s s s a将22k s k =代入，化简得 016442121=-+-++ka a k k解得k a k 421±=+.由01>+k a ∴2)1(4421-+=+=+k k a k 这就是说,当n=k+1时,上述结论成立.根据①、②,上述结论对所有的自然数n 成立. [例2] 用数学归纳法证明对于任意自然数，错解：证明：假设当（∈k N ）时，等式成立，即，那么当时，这就是说，当时，等式成立．可知等式对任意∈k N 成立．错因在于推理不严密，没有证明当的情况．正解：证明：（1）当时，左式，右式，所以等式成立．（2）假设当（）时，等式成立，即，那么当时，这就是说，当时，等式成立．由（1）、（2），可知等式对任意∈k N成立．[例3]是否存在自然数m，使得对任意自然数，都能被整除，若存在，求出的最大值，并证明你的结论；若不存在，说明理由．分析本题是开放性题型，先求出)1(f，)2(f，)3(f…再归纳、猜想、证明．解：，，，……猜想，能被36整除，用数学归纳法证明如下：（1）当时，，能被36整除．（2）假设当kk N）时，能被36整除．n=，（∈那么，当时，由归纳假设，能被36整除，当为自然数时，为偶数，则能被36整除．∴能被36整除，这就是说当时命题成立．由（1）、（2）对任意，)(n f 都能被36整除．当取大于36的自然数时，36)1(=f 不能被整除，所以36为最大．[例4] 设点1A 是曲线C ：)0,0(1>>=y x xy 与直线x y =的交点，过1A 点作直线x y =的垂线交轴于1B ，过1B 点作直线x y =的平行线交曲线C 于2A ，再过2A 点作1B 2A 的垂线作交X 轴于2B ，如此继续下去可得到一系列的点，，…，，…如图，试求的横坐标的通项公式．分析本题并没有指明求通项公式的方法，可用归纳——猜想——证明的方法，也可以通过寻求与的递推关系式求的通项公式．解：解法一与（，）联立，解得直线的方程为，令，得，所以点直线的方程为与联立，消元得（），解得，所以点（，）．直线的方程为，令，得，所以点同样可求得点（，0）…… 由此推测（，0），即用数学归纳法证明（1）当时，由点的坐标为（，0），即，所以命题成立．（2）假设当时命题成立，即，0），则当时，由于直线的方程为，把它与（，）联立，消去可得（），∴于是即点的坐标为（，）．∴直线的方程为令得，即点的坐标为（，0）∴当时，命题成立．解法二设点，的坐标分别为（，0）、（，0），建立与的递推关系，即，由数列是等差数列，且，公差可求得（），．用数学归纳法证明与自然数n有关的几何命题，由k过渡到k＋1常利用几何图形来分析图形前后演变情况．[例5]有n个圆，其中每两个圆都相交于两点，并且每三个圆都不相交于同一点，求证：这n个圆把平面分成f(n)＝n2-n＋2个部分．证明①当n＝1时，即一个圆把平面分成二个部分f(1)=2又n＝1时，n2-n＋2＝2，∴命题成立②假设n＝k时，命题成立，即k个圆把平面分成f(k)＝k2-k＋2个部分，那么设第k＋1个圆记⊙O，由题意，它与k个圆中每个圆交于两点，又无三圆交于同一点，于是它与其它k个圆相交于2k个点．把⊙O分成2k条弧而每条弧把原区域分成2块，因此这平面的总区域增加2k块，即f(k＋1)＝k2-k＋2＋2k=(k＋1)2-(k＋1)＋2即n＝k＋1时命题成立．由①②可知对任何n∈N命题均成立．说明: 本题如何应用归纳假设及已知条件，其关键是分析k增加“1”时，研究第k＋1个圆与其它k个圆的交点个数问题．[例6] 已知n≥2，n∈N②假设n=k时，原不等式成立．由①②可知，对任何n ∈N(n ≥2)，原不等式均成立．四、典型习题导练1.用数学归纳法证明等式“1＋2＋3＋…＋（n ＋3）=2)4)(3(++n n (n N )”，当n =1时，左边应为____________.2.已知数列{n a }的前n 项和n n a n s -=2，则{n a }的前四项依次为_______,猜想n a =__________.3.已知数列:,}{且满足的各项都是正数n a .),4(,21,110N n a a a a n n n ∈-==+证明N n a a n n ∈<<+,21. 4.已知不等式n n n 其中],[log21131212>+++ 为大于2的整数，][log2n 表示不超过n2log的最大整数. 设数列}{n a 的各项为正，且满足,4,3,2,),0(111=+≤>=--n a n na a b b a n n n 证明 ,5,4,3,][log222=+<n n b ba n .5. 自然状态下的鱼类是一种可再生资源，为持续利用这一资源，需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用x n 表示某鱼群在第n 年年初的总量，n ∈N *，且x 1＞0.不考虑其它因素，设在第n 年内鱼群的繁殖量及捕捞量都与x n 成正比，死亡量与x n 2成正比，这些比例系数依次为正常数a ，b ，c. （1）求x n+1与x n 的关系式；（2）猜测：当且仅当x 1，a ，b ，c 满足什么条件时，每年年初鱼群的总量保持不变？（3）设a ＝2，c ＝1，为保证对任意x 1∈（0,2），都有x n ＞0，n ∈N *，则捕捞强度b 的最大允许值是多少？证明你的结论.。