第三章 信道及其容量
合集下载
第三章信道与信道容量
i 1
r
j 1
r
p ( a i b j ) log p ( b j / a i ) H ( Y / X )
H ( ) log( r 1)
信道容量
C max { H ( Y ) H ( ) log( r 1)}
p(X )
log r H ( ) log( r 1)
信源
信道
信宿
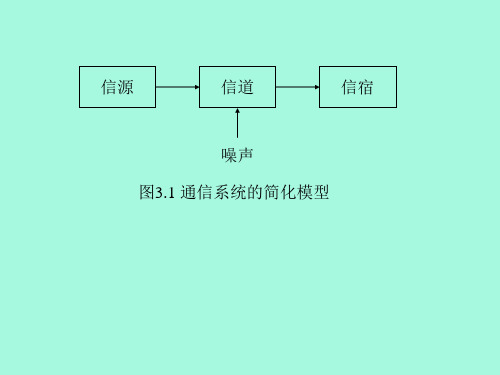
噪声 图3.1 通信系统的简化模型
第三章 信道与信道容量
• §3-1 引言 • 1〉什么是信道? • 信道是传送信息的载体——信号所通过的通道。 如:二人对话:二人间的空气就是信道; 打电话:电话线就是信道; 看电视、听收音机:收、发间的空间就是信道。
2〉信道的作用
• • • • • • • • 信道主要用于传输与存储信息。 3〉研究信道的目的 1)描述、度量、分析不同类型信道; 2)计算其容量,即极限传输能力,并分析其特性。 4>信道传输能力取决于: 1)本身特性 2)信号形式 3)信源特性
每列只有一个非零元素:
信道疑义度
H (X /Y ) 0
C max { I ( X ; Y )}
p(X )
max { H ( X )} log r
p(X )
信道输入符 号集符号数
3.确定信道(归并信道)
b1 a1 1 a2 1 a3 1 P a 4 0 a5 0 a6 0
特点:
(1) 当输入信源X达到最大熵值时,输出随机变量 Y同时达到最大熵值,即:
H(X)=log r
(2) 当输入X等概分布时:
p ( a i / b j ) p (b j / a i )
课件:第三章信道及其容量

第三章 信道及其容量
1
研究信道的目的是研究信道能传输的最大信息量, 即信道的最大传输能力。 1、如何描述在信道中传输的消息的信息量大小—— 平均互信息/信息传输率 2、信道的最大信息传输率是多少?——信道容量/ 传信能力
2
第三章 信道及其容量
3.1 信道的数学模型与分类 3.2 信道疑义度与平均互信息 3.3 离散无记忆的扩展信道 3.4 离散信道的信道容量 3.5 连续信道的信道容量 3.6 信源与信道的匹配 3.7 信道编码定理
效地折合成信道干扰,看成是由一个噪声源产生的,它将作用 于所传输的信号上。 a) 加性干扰:它是由外界原因产生的随机干扰,它与信道的
输入信号统计无关,因而信道的输出是输入和干扰的叠加。 【主要研究的干扰】 b) 乘性干扰:信道的输出信号可看成输入信号和某些随机参 量相乘的结果。
16
(6)根据信道有无记忆特性将信道分为: 无记忆信道 输出仅与当前输入有关,而与过去的输入和输 出无关。 有记忆信道 输出不仅与当前输入有关,而且与过去的输入 和输出有关。 本章的讨论基于无记忆、恒参、单用户离散信道,它是
|
x)
1 0
y f (x) y f (x)
其典型信道如下图所示:
22
(2)有干扰无记忆信道
该信道为实际常用信道,信道中存在干扰。 信道输入和输出符号之间不存在确定的对应关系,接收到Y后 不能完全消除对X的不确定性。信道输入和输出间的条件概率是一 般的概率分布。 信道任一时刻的输出符号只统计依赖于对应时刻的输入符号, 则这种信道称为无记忆信道,其条件概率满N 足
p(y | x) p(Y1, ,YN | X1, , XN )
条件概率p( y | x) 称为信道的传递概率或转移概率。 信道的数学模型可以用数学符号表示为:
1
研究信道的目的是研究信道能传输的最大信息量, 即信道的最大传输能力。 1、如何描述在信道中传输的消息的信息量大小—— 平均互信息/信息传输率 2、信道的最大信息传输率是多少?——信道容量/ 传信能力
2
第三章 信道及其容量
3.1 信道的数学模型与分类 3.2 信道疑义度与平均互信息 3.3 离散无记忆的扩展信道 3.4 离散信道的信道容量 3.5 连续信道的信道容量 3.6 信源与信道的匹配 3.7 信道编码定理
效地折合成信道干扰,看成是由一个噪声源产生的,它将作用 于所传输的信号上。 a) 加性干扰:它是由外界原因产生的随机干扰,它与信道的
输入信号统计无关,因而信道的输出是输入和干扰的叠加。 【主要研究的干扰】 b) 乘性干扰:信道的输出信号可看成输入信号和某些随机参 量相乘的结果。
16
(6)根据信道有无记忆特性将信道分为: 无记忆信道 输出仅与当前输入有关,而与过去的输入和输 出无关。 有记忆信道 输出不仅与当前输入有关,而且与过去的输入 和输出有关。 本章的讨论基于无记忆、恒参、单用户离散信道,它是
|
x)
1 0
y f (x) y f (x)
其典型信道如下图所示:
22
(2)有干扰无记忆信道
该信道为实际常用信道,信道中存在干扰。 信道输入和输出符号之间不存在确定的对应关系,接收到Y后 不能完全消除对X的不确定性。信道输入和输出间的条件概率是一 般的概率分布。 信道任一时刻的输出符号只统计依赖于对应时刻的输入符号, 则这种信道称为无记忆信道,其条件概率满N 足
p(y | x) p(Y1, ,YN | X1, , XN )
条件概率p( y | x) 称为信道的传递概率或转移概率。 信道的数学模型可以用数学符号表示为:
第3章信道与信道容量-PPT精品

• 信道种类
1无干扰信道
2有干扰无记忆信道
3有干扰有记忆信道
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
3
3.1信道分类和表示参数
二进制对称信道(BSC)
1-p 0
p
0 p
1p p
P
p
1p
1
1
1-p
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
X
+
Y
pY(y/ai)
1 e(yai)2/22
2
G
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
6
3.1信道分类和表示参数
波形信道
x(t)
y(t)
+
n(t)
pY(y/x)pY(y1,y2,yL/x1,x2,xL)
pY(y/x)pxp,yx((xx,)y)pxp,yx((xx,)n)pn(n)
p (bj/a i)
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
13
3.2离散单个符号信道及其容量
对称信道容量
C=maIx(X;Y)ma[H x(X)H(X|Y)]
p(ai)
p(ai)
ma[H x(Y)H(Y| X)]
p(ai)
maHx(Y)H(Y/X)
p(ai)
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
7
3.2离散单个符号信道及其容量
信息传输率
信道在单位时间内平均传输的信息量定义为信 息传输速率
R=I(X;Y)=H(X)-H(X/Y) 比特/符号
Rt=I(X;Y)/t
第3章信道及信道容量

X P(Y/X) Y
2019/11/27
信道及信道容量
x1
P(y1/x1)
y1
x2
P(y2/x2)
y2
…
…
…
P(ym/xn)
xn
ym
P(y1 / x1) P(y2 / x1) P(ym / x1)
P(Y / X) P(y1 / x2) P(y2 / x2) P(ym / x2 )
信道及信道容量
例5
信源P(XX)
0 p
1
1
p
信道P(Y
/
X)
1
q
q
1 q
q
平均互信息量及p-I(X;Y)和q-I(X;Y)曲线
P(y1 0) pq (1 p)(1 q) pq pq P(y2 1) p(1 q) (1 p)q pq pq H(Y) (pq pq) log( pq pq) (pq pq) log( pq pq) H(pq pq)
I(X;Y) H(Y) H(Y / X) H(pq pq) H(q) 信道固定时q为常数,作p-I(X;Y)曲线 当p 0时,I(X; Y) H(q) H(q) 0
p 0.5时,I(X; Y) H(0.5) H(q) 1 H(q)
2019/11/27
I(X; Y)
i1
m
P(x i y j ) log
j1
P(y j ) P(y j / xi )
n
i1
m
P(x i y j ) log
j1
P(xi ) P(xi / y j )
nm
2019/11/27
信道及信道容量
x1
P(y1/x1)
y1
x2
P(y2/x2)
y2
…
…
…
P(ym/xn)
xn
ym
P(y1 / x1) P(y2 / x1) P(ym / x1)
P(Y / X) P(y1 / x2) P(y2 / x2) P(ym / x2 )
信道及信道容量
例5
信源P(XX)
0 p
1
1
p
信道P(Y
/
X)
1
q
q
1 q
q
平均互信息量及p-I(X;Y)和q-I(X;Y)曲线
P(y1 0) pq (1 p)(1 q) pq pq P(y2 1) p(1 q) (1 p)q pq pq H(Y) (pq pq) log( pq pq) (pq pq) log( pq pq) H(pq pq)
I(X;Y) H(Y) H(Y / X) H(pq pq) H(q) 信道固定时q为常数,作p-I(X;Y)曲线 当p 0时,I(X; Y) H(q) H(q) 0
p 0.5时,I(X; Y) H(0.5) H(q) 1 H(q)
2019/11/27
I(X; Y)
i1
m
P(x i y j ) log
j1
P(y j ) P(y j / xi )
n
i1
m
P(x i y j ) log
j1
P(xi ) P(xi / y j )
nm
信息论基础第3章离散信道及其信道容量

也就是说,通过信息处理后,一般只会增加信息的 损失,最多保持原来获得的信息,不可能比原来获得的 信息有所增加。一旦失掉了信息,用任何处理手段也不 可能再恢复丢失的信息,因此也称为信息不增性原理。
《信息论基础》
3.6 多符号离散信道及其信道容量
【例】求图所示的二元无记忆离散对称信道的二次 扩展信道的信道容量。
【例】 已知两个独立的随机变量 X、Y 的分布律如下。
X P(x)
a1 0.5
a2 0.5
,
Y P( y)
b1 0.25
b2 b3 0.25 0.5
计算 H X , H Y , H XY , H X |Y , H Y | X , I X ;Y 。
《信息论基础》
3.4 信道容量的定义
I (ai ) 减去已知事件 bj 后对 ai 仍然存在的不确定性 I (ai | bj ) ,实际就是事件
bj 出现给出关于事件 ai 的信息量。
【例】 甲在一个16 16 的方格棋盘上随意放一枚棋
子,在乙看来棋子放入哪一个位置是不确定的。如果甲 告知乙棋子放入棋盘的行号,这时乙获得了多少信息 量?
《信息论基础》
第3章 离散信道及其信道容量
通信系统的基本功能是实现信息的传递,信道是信息 传递的通道,是信号传输的媒质。一般而言,信源发出的 消息,必须以适合于信道传输的信号形式经过信道的传输, 才能被信宿接收。
从信源的角度看,信源发出的每个符号承载的平均信 息量由信源熵来定量描述;而从信宿的角度看,信宿收到 的每个符号平均能提供多少信息量由平均互信息来定量描 述。在信息论中,信道问题主要研究在什么条件下,信道 能够可靠传输的信息量最大,即信道容量问题。
《信息论基础》
3.7 信源与信道的匹配
《信息论基础》
3.6 多符号离散信道及其信道容量
【例】求图所示的二元无记忆离散对称信道的二次 扩展信道的信道容量。
【例】 已知两个独立的随机变量 X、Y 的分布律如下。
X P(x)
a1 0.5
a2 0.5
,
Y P( y)
b1 0.25
b2 b3 0.25 0.5
计算 H X , H Y , H XY , H X |Y , H Y | X , I X ;Y 。
《信息论基础》
3.4 信道容量的定义
I (ai ) 减去已知事件 bj 后对 ai 仍然存在的不确定性 I (ai | bj ) ,实际就是事件
bj 出现给出关于事件 ai 的信息量。
【例】 甲在一个16 16 的方格棋盘上随意放一枚棋
子,在乙看来棋子放入哪一个位置是不确定的。如果甲 告知乙棋子放入棋盘的行号,这时乙获得了多少信息 量?
《信息论基础》
第3章 离散信道及其信道容量
通信系统的基本功能是实现信息的传递,信道是信息 传递的通道,是信号传输的媒质。一般而言,信源发出的 消息,必须以适合于信道传输的信号形式经过信道的传输, 才能被信宿接收。
从信源的角度看,信源发出的每个符号承载的平均信 息量由信源熵来定量描述;而从信宿的角度看,信宿收到 的每个符号平均能提供多少信息量由平均互信息来定量描 述。在信息论中,信道问题主要研究在什么条件下,信道 能够可靠传输的信息量最大,即信道容量问题。
《信息论基础》
3.7 信源与信道的匹配
第三章信道与信道容量

3.1信道的基本概念 信道的基本概念
• 2. 信道模型及信道参数
• • • • • •
信道的三要素:输入 输出 信道的三要素 输入,输出 输入 输出,p(y/x) 根据信道是否存在干扰及有无记忆,可分为 可分为: 根据信道是否存在干扰及有无记忆 可分为 1)无干扰 无干扰 2)有干扰无记忆 有干扰无记忆 3)有干扰有记忆 有干扰有记忆 对于有干扰无记忆信道进一步分为: 对于有干扰无记忆信道进一步分为
这里I ( xI ; Y ) = ∑ p( yj / xi ) log p( yj / xi )
j =0
Q −1
p( yj )
• 2 离散时间无记忆信道的容量
这类信道中最重要的一种是加性高斯白噪 信道,对它而言 声(AWGN)信道 对它而言,离散输入 ={ 信道 对它而言,离散输入X= x0,x1,…,xq-1}和模拟输出 ={ 和模拟输出Y={ , 和模拟输出 ={-∞,∞} } 之间的最大平均互信息即信道容量由下式 给出(单位是比特 符号): 单位是比特/符号 给出 单位是比特 −符号 : q 1
1 ∞ p ( y / A) 1 ∞ p ( y / − A) C = ∫ p ( y / A) log 2 dy + ∫ p ( y / − A) log 2 dy −∞ −∞ 2 2 p( y) p( y )
•
3.带限波形信道的容量 带限波形信道的容量
一个受加性高斯白噪声干扰的带限波形信道的容量
1 C = lim max I ( X ; Y ) T →∞ Px T
香农公式
C = W log(1 +
1.
Pav ) = W log(1 + SNR) WN 0
带宽一定时,信道容量随 的增加而单调增加, 带宽一定时,信道容量随SNR的增加而单调增加,因此增大 的增加而单调增加 信号功率、减小信道噪声可以增加信道容量。 信号功率、减小信道噪声可以增加信道容量。 2. 如果 如果SNR固定,信道容量随着带宽的增加而增加。 固定, 固定 信道容量随着带宽的增加而增加。
信息论与编码第三章

模
型
P<Y1=V1,Y2=V2…Yn=Vn/X=U1…X=Un>
n
Õ = p(YR = UR / X = uR )
决定DMC特点的条件概率P<yj/xi>可写成矩阵形 式
P = [ pij ]
3.2.1
转移概率矩阵
æ p( y0 / x0) p( y1 / x0)
数
ç
学 模
P
=
ç ç
p( y0 / x1)
数 即P<Y=0/X=1>=P<Y=1/X=0>=P
学
模 型
P<Y=1/X=1>=P<Y=0/X=0>=1-P
01
这种对称二进二出的
0 é P P ù 信道叫做二进制对称信
P=1
ê ëê
P
ú P ûú
道,简称BSC信道.
3.2.1
信道模型:
数 学 模
1-P
0
0
P
型
P
1
1
1-P
这种信道的输出符号仅与对应时刻输 入符号有关,与以前输入无关,故称此信道是 无记忆信道的.
3.1
信道分类:
信
道
1.有线信道和无线信道
分
类
有线信道:明线、对称电缆、同轴电
缆及
光缆等.
无线信道:地波传播、短波电离层反 射、
超短波或微波视距中继、
3.1
2.恒参信道和随参信道
信 道
恒参信道:信道的统计特性不随时间而变化.如明
分 线、对称电缆、同轴电缆、光缆、卫星中继信道
类
一般被视为恒参信道.
p0,Q - 1 ö ÷
第三章信道及信道容量PPT课件

第三章 信道及信道容量
第一节 信道分类及表示参数 第二节 单符号离散信道及其容量 第三节 离散序列信道及其容量 第四节 连续信道及其容量
05.12.2020
1
研究信道容量的意义?
信道是信息传输的通道。由于干扰而丢失的信息为 H(X|Y ); 在接收端获取的关于发送端信源X的信息量是:
I(X;Y)=H(X)-H(X|Y) 即:信道中平均每个符号传送的信息量。对于信道,所关心的问 题是平均每个符号传送的最大信息量。这就是信道容量C=max I(X;Y) bit/符号
每个数字对应一种颜色(反之未必),数字已知,则颜色确 定,H(X|Y)=0。H(X,Y)=H(Y)=…..
6、2.21(3)信号放大问题。课上已经强调过,仍出错。
7、向孔祥品学习
05.12.2020
9
复习:第四节 连续信源的熵和互信息
一、单符号连续信源的熵 相对熵(差熵)
H c(X ) p X (x)lop X g (x)dx Hc(XY )p(xy)lopg(xy)dxdy Hc(Y/X )p(xy)lopg(y/x)dxdy
(2) 离散无记忆信道(DMC-Discrete Memoryless Channel)
仍是单符号离散信道,符号集中的符号数目大于2 。
05.12.2020
7
转移概率矩阵(传递阵矩)P :
P11 P12 P1m
P [
P ij
]
P21
P22
P2m
Pn1
Pn2
Pnm
m
m
转移概率矩 元阵 素中 之 1。 各 和 P(b 行 j等 |ai)的 于 Pij1
2 Pm2,通常m0,2 P,此时有:
H0C5.1(2X.202)0
第一节 信道分类及表示参数 第二节 单符号离散信道及其容量 第三节 离散序列信道及其容量 第四节 连续信道及其容量
05.12.2020
1
研究信道容量的意义?
信道是信息传输的通道。由于干扰而丢失的信息为 H(X|Y ); 在接收端获取的关于发送端信源X的信息量是:
I(X;Y)=H(X)-H(X|Y) 即:信道中平均每个符号传送的信息量。对于信道,所关心的问 题是平均每个符号传送的最大信息量。这就是信道容量C=max I(X;Y) bit/符号
每个数字对应一种颜色(反之未必),数字已知,则颜色确 定,H(X|Y)=0。H(X,Y)=H(Y)=…..
6、2.21(3)信号放大问题。课上已经强调过,仍出错。
7、向孔祥品学习
05.12.2020
9
复习:第四节 连续信源的熵和互信息
一、单符号连续信源的熵 相对熵(差熵)
H c(X ) p X (x)lop X g (x)dx Hc(XY )p(xy)lopg(xy)dxdy Hc(Y/X )p(xy)lopg(y/x)dxdy
(2) 离散无记忆信道(DMC-Discrete Memoryless Channel)
仍是单符号离散信道,符号集中的符号数目大于2 。
05.12.2020
7
转移概率矩阵(传递阵矩)P :
P11 P12 P1m
P [
P ij
]
P21
P22
P2m
Pn1
Pn2
Pnm
m
m
转移概率矩 元阵 素中 之 1。 各 和 P(b 行 j等 |ai)的 于 Pij1
2 Pm2,通常m0,2 P,此时有:
H0C5.1(2X.202)0
[高等教育]第3章 信道与信道容量
![[高等教育]第3章 信道与信道容量](https://img.taocdn.com/s3/m/6a524bdfc8d376eeaeaa318c.png)
p11 p P 21 pn1
2018/11/24
各行概率 之和为1
p12 p22 pn 2 p1m p2 m pnm
9
转移概率矩阵
信道模型
3. 离散输入、连续输出信道
输入符号集:X={a1, a2,…, an} 输出未经量化,即Y={-∞,∞}
2018/11/24 21
对称DMC信道 ③ 当信道输入符号等概率分布时,对称 DMC信道达到其信道容量。
C max I ( X ; Y ) max H Y H Y / X
Px Px
max H Y H Y / ai
Px
max H Y H Y / ai
如果以e为底,即取自然对数时,信道容量的单位是 奈特/符号。
如果已知符号传送周期是T 秒,信道容量Ct=C /T, 单位为bit/s或nat/s。
C max I ( X ; Y ) max H X H X / Y
p ( ai ) p ( ai )
2018/11/24 14
Px
log m H Y / ai
2018/11/24 22
对称DMC信道
例:信道转移概率矩阵为 求:信道容量 解: C log n H Y / ai
log n H 1 , , n 1
,
1 n 1 1 P n 1 n 1 n 1
将记忆很强的L个符号当作矢量符号,各矢量符号之间 认为是无记忆的。 将转移概率看成马尔可夫链的形式。
2018/11/24 7
信道模型
1. 二进制离散信道:BSC信道
2018/11/24
各行概率 之和为1
p12 p22 pn 2 p1m p2 m pnm
9
转移概率矩阵
信道模型
3. 离散输入、连续输出信道
输入符号集:X={a1, a2,…, an} 输出未经量化,即Y={-∞,∞}
2018/11/24 21
对称DMC信道 ③ 当信道输入符号等概率分布时,对称 DMC信道达到其信道容量。
C max I ( X ; Y ) max H Y H Y / X
Px Px
max H Y H Y / ai
Px
max H Y H Y / ai
如果以e为底,即取自然对数时,信道容量的单位是 奈特/符号。
如果已知符号传送周期是T 秒,信道容量Ct=C /T, 单位为bit/s或nat/s。
C max I ( X ; Y ) max H X H X / Y
p ( ai ) p ( ai )
2018/11/24 14
Px
log m H Y / ai
2018/11/24 22
对称DMC信道
例:信道转移概率矩阵为 求:信道容量 解: C log n H Y / ai
log n H 1 , , n 1
,
1 n 1 1 P n 1 n 1 n 1
将记忆很强的L个符号当作矢量符号,各矢量符号之间 认为是无记忆的。 将转移概率看成马尔可夫链的形式。
2018/11/24 7
信道模型
1. 二进制离散信道:BSC信道
信息论与编码(第三版) 第3章 信道与信道容量

2信道输入的先验分布不是最佳分布,那么信息传输率不 能够达到信息容量
3信息量R必须小于信道容量C,否则传输过程中会造成信 息损失,出现错误;
如果R<C成立端
噪声问题
无 映射(输 噪 入到输出)
条件转移 矩阵
H(Y|X)=0
Y X n
一对一
X:信道输入 Y:信道输出 n:信道噪声
p(bj|ai):后向概率
表示当接收符号为bj时, 信道输入为ai的概率,所 以也称为后验概率
贝叶斯公式
p(ai
| bj)
p(aibj ) p(bj )
p(ai ) p(bj | ai )
r
p(ai ) p(bj | ai )
i1
后验概率都是十分 重要的,可以通过
p(b1 )
p(a1 )
第3章 信道与信道容量
目录
3.1信道分类 3.2 单符号离散信道及其容量
➢ 3.2.1 数学模型 ➢ 3.2.2信道容量 ➢ 3.2.3 离散信道容量的迭代算法
3.3 离散序列信道及其容量 3.4 信源与信道的匹配 3.5 连续信道及其容量
➢ 3.5.1 连续单符号加性信道 ➢ 3.5.2 多维无记忆加性连续信道 ➢ 3.5.3 加性高斯白噪声波形信道
只能进行单方向的通信
也称多端信道,输入端或者 输出端至少有一端具有两个 或者两个以上用户,并且可
以实现双向通信
输入、输出的取值特性
离散信道
也称为数字信道,该类信道中输入空间、输出 空间均为离散事件集合,集合中事件数量是有 限的,或者有限可数的,随机变量取值都是离 散的
连续信道
也称为模拟信道,输入空间、输出空间均为连续事 件集合,集合中事件的数量是无限的、不可数的
3信息量R必须小于信道容量C,否则传输过程中会造成信 息损失,出现错误;
如果R<C成立端
噪声问题
无 映射(输 噪 入到输出)
条件转移 矩阵
H(Y|X)=0
Y X n
一对一
X:信道输入 Y:信道输出 n:信道噪声
p(bj|ai):后向概率
表示当接收符号为bj时, 信道输入为ai的概率,所 以也称为后验概率
贝叶斯公式
p(ai
| bj)
p(aibj ) p(bj )
p(ai ) p(bj | ai )
r
p(ai ) p(bj | ai )
i1
后验概率都是十分 重要的,可以通过
p(b1 )
p(a1 )
第3章 信道与信道容量
目录
3.1信道分类 3.2 单符号离散信道及其容量
➢ 3.2.1 数学模型 ➢ 3.2.2信道容量 ➢ 3.2.3 离散信道容量的迭代算法
3.3 离散序列信道及其容量 3.4 信源与信道的匹配 3.5 连续信道及其容量
➢ 3.5.1 连续单符号加性信道 ➢ 3.5.2 多维无记忆加性连续信道 ➢ 3.5.3 加性高斯白噪声波形信道
只能进行单方向的通信
也称多端信道,输入端或者 输出端至少有一端具有两个 或者两个以上用户,并且可
以实现双向通信
输入、输出的取值特性
离散信道
也称为数字信道,该类信道中输入空间、输出 空间均为离散事件集合,集合中事件数量是有 限的,或者有限可数的,随机变量取值都是离 散的
连续信道
也称为模拟信道,输入空间、输出空间均为连续事 件集合,集合中事件的数量是无限的、不可数的
第3章 信道与信道容量

max p(x)
H C (Y )
1 log
2
2e
2
pn(n)=N(0, 2) 连续单符号信道
噪声是均值为零、方差为 2的加性高斯噪声
34
3.4 连续信道及其容量
连续单符号加性信道
pY (y) =N(0,P),pn(n)=N(0, 2),y=x+n,所以 pX (x)=N(0, S)
3
3.1 信道分类和表示参数
二进制对称信道(BSC)
P
1 p
p
p 1 p
4
3.1 信道分类和表示参数
离散无记忆信道
a1 a2
b1
p11 p12 p1m
b2 b3
P
p21
p22
p2m
an
bm
pn1
pn2
pnm
5
3.1 信道分类和表示参数
离散输入、连续输出信道
pY ( y / ai )
31
3.3 离散序列信道及其容量
扩展信道
(1 p)2 p(1 p) p(1 p) p2
1
P
p(1 p(1
p) p)
(1 p)2 p2
p2 (1 p)2
p(1
p)
p(1 p)
p2 p(1 p) p(1 p) (1 p)2
C2 log2 4 H[(1 p)2 , p(1 p), p(1 p), p 2 ]
1 1 1 1
13
3 1
6 1
6 1
6 6 3 3
1 1 1
2 1
3 1
6 1
6 2 3
1 1 1
3 6 2
12
3.2 离散单个符号信道及其容量
第三章 信道和信道容量

求信息传输率R及信道容量。
第三章 信道和信道容量
四、一般离散信道的信道容量
对于非特殊性质的固定信道,根据定义,其信
道容量是对所有可能的输入概率分布P(X)求平
均互信息的极大值。由于I(X;Y)是P(X)的上凸函数,
其极大值一定存在。 注意:达到信道容量的最佳分布不一定是唯一的, 只要输入概率分布满足定理中的条件,并使I最大, 即成为信道的最佳输入分布。
通信系统一般模型:
信源 调制 信道 解调 信宿
广义信道
各种物理信道中存在的干扰限制了通信的距离与速 率,为反映信道干扰对传输性能的影响,可用刻划 各种干扰的模型来表示信道。
如:发送为xi(信道输入), 接收为yj(信道输出),则信道特性为: Pji=P(yj/xi),用(条件)转移概率描述
第三章 信道和信道容量
若平均传输一个符号需要t秒,则信道每秒钟平 均传输的信息量为:
Rt=(1/t)I(X;Y) bit/秒 定义:最大的信息传输率为信道容量C,即: C=max{I(X;Y)} bit/符号
P(x)
第三章 信道和信道容量
达到信道容量时,相应的输入概率分布称为最佳 输入分布,若平均传输一个符号需要t秒,则:
Ct≈Ps/N0
第三章 信道和信道容量
结论:
当频带很宽时,或信噪比很低时,信道容 量等于信号功率与噪声功率密度比,此比
值是加性高斯噪声信道信息传输率的极限
值。在上述宽频带条件下,信号淹没在噪
声中仍可传送信息。
由香农公式得到的值是非高斯信道(实际 信道)的信道容量的下限值。
第三章 信道和信道容量
三、多维无记忆高斯加性连续信道
P(X)
结论:信道的转移矩阵中,每列有一个也仅有一个
第三章 信道与信道容量 习题解答

但与理论不矛盾因为信息速率不光与信源熵有关还与每秒发送的符号数有关该信源的两个消息是非同价代码每个码元消息的时间长度不同等概率时信源熵提高了但每秒发送的符号数下降了因此才有此结果
第三章 信道与信道容量 习题解答
1.设信源
通过一干扰信道,接收符号为
信道传递矩阵为
(1) 信源 中符号 和 分别含有的自信息量。
(4)说明如果信噪比降低,则为保持信道容量不变,必须加大信道带宽。反之加大信道带宽,则可降低对信 噪比的要求。如果信道带宽降低,则为保持信道容量不变,必须加大信号功率信噪比。反之加大信号功率信 噪比,则可降低对信道带宽的要求。
12.在一个理想通信系统中,已知信道中功率信噪比为 10分贝,为了使功率节省一半又不损失信息量,有 几种办法?请计算并讨论各自的优缺点。
,
将各数据代入: 解得:
如果
则
将各数据代入: 解得:
14.在理想系统中,若信道带宽与消息带宽的比为 10,当接收机输入端功率信噪比分别为 0.1和 10时,试
比较输出端功率信噪比的改善程度,并说明
与
之间是否存在阀值效应。
解:已知
根据公式:
前者改善不明显,后者改善明显,故存在阀值效应。 15.设加性高斯白噪声信道中,信道带宽 3kHz,又设
解:设将电阻按阻值分类看成概率空间 X:
,
按功耗分类看成概率空间 Y:
已知:
,
通过计算
, ,
,
得
通过测量阻值获得的关于瓦数的平均信息量:
6.有一以“点”和“划”构成的老式电报系统,“点”的长度为 30毫秒,“划”的长度为 150毫秒,“点”和“划”出现的
4
概率分别为 0.8和 0.2,试求信息速率为多少?“点”、“划”出现的概率相等时,信息速率为多少?是否“点”、“划” 出现的概率相等时信息速率一定最高?是否和理论相矛盾?为什么? 解:
第三章 信道与信道容量 习题解答
1.设信源
通过一干扰信道,接收符号为
信道传递矩阵为
(1) 信源 中符号 和 分别含有的自信息量。
(4)说明如果信噪比降低,则为保持信道容量不变,必须加大信道带宽。反之加大信道带宽,则可降低对信 噪比的要求。如果信道带宽降低,则为保持信道容量不变,必须加大信号功率信噪比。反之加大信号功率信 噪比,则可降低对信道带宽的要求。
12.在一个理想通信系统中,已知信道中功率信噪比为 10分贝,为了使功率节省一半又不损失信息量,有 几种办法?请计算并讨论各自的优缺点。
,
将各数据代入: 解得:
如果
则
将各数据代入: 解得:
14.在理想系统中,若信道带宽与消息带宽的比为 10,当接收机输入端功率信噪比分别为 0.1和 10时,试
比较输出端功率信噪比的改善程度,并说明
与
之间是否存在阀值效应。
解:已知
根据公式:
前者改善不明显,后者改善明显,故存在阀值效应。 15.设加性高斯白噪声信道中,信道带宽 3kHz,又设
解:设将电阻按阻值分类看成概率空间 X:
,
按功耗分类看成概率空间 Y:
已知:
,
通过计算
, ,
,
得
通过测量阻值获得的关于瓦数的平均信息量:
6.有一以“点”和“划”构成的老式电报系统,“点”的长度为 30毫秒,“划”的长度为 150毫秒,“点”和“划”出现的
4
概率分别为 0.8和 0.2,试求信息速率为多少?“点”、“划”出现的概率相等时,信息速率为多少?是否“点”、“划” 出现的概率相等时信息速率一定最高?是否和理论相矛盾?为什么? 解:
第3章.信道与信道容量

p(Y | X) p( y1 | x1) p( y2 | x2 ) p( yL | xL )
即每个输出信号只与当前的输入信号之间有转移概率关 系,而与其他非该时刻的输入信号、输出信号都无关, 也就是无记忆性。
14
3.1.2 信道参数
有干扰无记忆信道 按照输入输出信号的符号数目,有干扰信道可以进一步 划分为: (1)二进制离散信道 (2)离散无记忆信道 (3)离散输入、连续输出信道 (4)波形信道
22
3.2 离散单个符号信道及其容量
信息传输率
有时需要了解的是信道在单位时间内平均传输的信息量,
若已知平均传输一个符号所需的时间为t秒,则将信道
在单位时间内平均传输的信息量定义为信息传输速率,
即:
I ( X ;Y ) Rt t bit / s
注意:
R:单位为bit / 符号
信息传输率
Rt:单位为bit / s
maxH (Y ) H (Y | X ) p(ai )
max
p(ai )
H
(Y
)
H
(Y
|ai)393.2.2 对称DMC信道
对称DMC信道的容量 如果信道输入符号等概率分布,即p(ai)=1/n,则由于转 移概率矩阵的列对称,所以:
p(bj )
i
p(ai
)
p(bj
|
ai
)
1 n
i
p(bj | ai )
信息论不研究信号在信道中传输的物理过程,并假定信 道的传输特性已知,这样信息论就可以抽象地将信道用 下图所示的模型来描述。
3
3.1.1 信道的分类
信道
输入量X (随机过程)
P(Y | X ) 信道
输出量Y (随机过程)
即每个输出信号只与当前的输入信号之间有转移概率关 系,而与其他非该时刻的输入信号、输出信号都无关, 也就是无记忆性。
14
3.1.2 信道参数
有干扰无记忆信道 按照输入输出信号的符号数目,有干扰信道可以进一步 划分为: (1)二进制离散信道 (2)离散无记忆信道 (3)离散输入、连续输出信道 (4)波形信道
22
3.2 离散单个符号信道及其容量
信息传输率
有时需要了解的是信道在单位时间内平均传输的信息量,
若已知平均传输一个符号所需的时间为t秒,则将信道
在单位时间内平均传输的信息量定义为信息传输速率,
即:
I ( X ;Y ) Rt t bit / s
注意:
R:单位为bit / 符号
信息传输率
Rt:单位为bit / s
maxH (Y ) H (Y | X ) p(ai )
max
p(ai )
H
(Y
)
H
(Y
|ai)393.2.2 对称DMC信道
对称DMC信道的容量 如果信道输入符号等概率分布,即p(ai)=1/n,则由于转 移概率矩阵的列对称,所以:
p(bj )
i
p(ai
)
p(bj
|
ai
)
1 n
i
p(bj | ai )
信息论不研究信号在信道中传输的物理过程,并假定信 道的传输特性已知,这样信息论就可以抽象地将信道用 下图所示的模型来描述。
3
3.1.1 信道的分类
信道
输入量X (随机过程)
P(Y | X ) 信道
输出量Y (随机过程)
第3章 信道及信道容量

– 缓冲电路,非门 – 移位加密法
X ;Y P ( X ;Y ) = 0 1
a b X → Y ≡ c ... z
01 0 1 1 0
X
Y
a b c ... z
c a d X ;Y b e , =c P X Y ; ( ) ... ... b z
n i =1
P( xi ) = 1 )=1
3
H
P( y
j =1
m
j
一、单符号离散信道及信道容量-续
如果信道无噪,当信源发出
消息xi,信宿接收的也是 xi,信道的输出yj等于输入 xi。
如果信道有噪,通过信道的
消息产生失真,信道的输出 yj一般不等于输入xi ,但它 们之间存在某种关系,由于 噪声的随机性,这种关系可 以用条件概率P(yj/xi)来描 述。
I ( x1 = 0; y1 = 0 ) = − lbP ( y1 ) + lbP ( y1 / x1 ) = − lb0.55 + lb1 ≈ 0.862(bit) I ( x 2 = 1; y1 = 0 ) = − lbP ( y1 ) + lbP ( y1 / x 2 ) = − lb0.55 + lb0.25 ≈ −1.138(bit)
= P ( x i y j ) lb = I (Y ; X )
– ②非负性 I ( X ;Y ) ≥ 0
i =1 j =1 n n P ( x j / yi ) P( x j )
– ①对称性 I ( X ;Y ) = I ( Y ; X )
– ③极值性
I ( X ;Y ) ≤ H ( X ) I ( X ;Y ) ≤ H (Y )
X ;Y P ( X ;Y ) = 0 1
a b X → Y ≡ c ... z
01 0 1 1 0
X
Y
a b c ... z
c a d X ;Y b e , =c P X Y ; ( ) ... ... b z
n i =1
P( xi ) = 1 )=1
3
H
P( y
j =1
m
j
一、单符号离散信道及信道容量-续
如果信道无噪,当信源发出
消息xi,信宿接收的也是 xi,信道的输出yj等于输入 xi。
如果信道有噪,通过信道的
消息产生失真,信道的输出 yj一般不等于输入xi ,但它 们之间存在某种关系,由于 噪声的随机性,这种关系可 以用条件概率P(yj/xi)来描 述。
I ( x1 = 0; y1 = 0 ) = − lbP ( y1 ) + lbP ( y1 / x1 ) = − lb0.55 + lb1 ≈ 0.862(bit) I ( x 2 = 1; y1 = 0 ) = − lbP ( y1 ) + lbP ( y1 / x 2 ) = − lb0.55 + lb0.25 ≈ −1.138(bit)
= P ( x i y j ) lb = I (Y ; X )
– ②非负性 I ( X ;Y ) ≥ 0
i =1 j =1 n n P ( x j / yi ) P( x j )
– ①对称性 I ( X ;Y ) = I ( Y ; X )
– ③极值性
I ( X ;Y ) ≤ H ( X ) I ( X ;Y ) ≤ H (Y )
第3章信道与信道容量(参考)

max[ H (Y ) H (Y | X )]
p ( ai ) p ( ai )
max H (Y ) H (Y / X )
C log m H (Y | ai ) log m pij log pij
j 1
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著 14
m
3.2离散单个符号信道及其容量
Eg. 求信道容量
1 3 P 1 6 1 3 1 6 1 6 1 3 1 6 1 3
1 1 1 1 C log2 4 H ( , , , ) 0.082bit / 符号 3 3 6 6
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著 15
3.2离散单个符号信道及其容量
方法三
0.5 0.3 0.2 P 0.3 0.5 0.2
0.5 0.3, 0.2 0.3 0.5 0.2
C log2 2 H (0.5,0.3,0.2) 0.8 log2 0.8 0.2 log2 0.4 0.036bit / 符号
• 信道种类 • 无干扰信道 • 有干扰无记忆信道 • 有干扰有记忆信道
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
3
信道参数
无干扰(无噪声)信道
1, y f (x) p ( Y / X) 0, y f (x)
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
C max I ( X ; Y )
p ( ai )
普通高等教育“十五”国家级规划教材《信息论与编码》 曹雪虹等编著
9
3.2离散单个符号信道及其容量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H(X)是在接收到输出Y以前,关于输入变量X的先验不 确定性,称为先验熵。
接受到bj后,关于X的不确定性为
H ( X | b j ) P ( x | b j ) l og
X
1 P( x | b j )
这是接收到输出符号bj后关于X的后验熵。 后验熵是当信道接收端接收到输出符号 bj 后,关于输入 符号的信息测度。 后验熵在输出符号集Y范围内是个随机量,对后验熵在符 号集Y中求数学期望,得条件熵----信道疑义度:
s
ar P(b1|ar) P(b2|ar) … P(bs|ar)
p11 p P 21 : p r1
p12 p 22 : pr 2
p1s ... p 2 s : : ... p rs ...
pij 0
p
j 1
ij
1
矩阵P完全描述了信道的特性,可用它作为离散单符号 信道的另一种数学模型的形式。
解:X:{0,1} Y:{0,1,2} 此时,r =2,s =3, 传递矩阵为:
0 0 1 2 1
1- p
q
1
p 1 p 0 0 1 q q
符号“2”表示接收到了“0”、“1”以外的特殊符 号
• 一般离散单符号信道的传递概率可用矩阵形式表示,即 b1 b2 … bs
a1 P(b1|a1) P(b2|a1) … P(bs|a1) a2 P(b1|a2) P(b2|a2) … P(bs|a2) … …. … …
二、平均互信息
互信息量 I(xi ; yj):收到消息yj 后获得关于xi的信息量
p( xi | y j ) 1 1 I ( xi ; y j ) I ( x) I ( x / y) log log log p( xi ) p( xi | y j ) p( xi )
即:互信息量表示先验的不确定性减去尚存的不确定性, 这就是收信者获得的信息量 对于无干扰信道,I(xi ; yj) = I(xi); 对于全损信道,I(xi ; yj) = 0;
平均互信息I(X;Y)是信道传递的概率P(y/x)的∪ 型凸函数。 • 当信源固定后,选择不同的信道来传输同一信源符 号,在信道输出端获得关于信源的信息量是不同的。
信道输入端X与输出端Y完全统计独立
p ( y | x) P( y ) x X y Y p ( x | y ) P( x) x X y Y
H(X|Y) = H(X) , H(Y|X) = H(Y) 所以 I(X;Y) = 0 [I(X;Y) = H(X) - H(X|Y)]
其中:P( y ) P( x)P( y | x)
X
所以,平均互信息I(X;Y)只是信源X的概率分布P(x)
和信道的传递概率P(y/x)的函数,即:
I(X;Y) = f [P(x), P(y|x)]
平均互信息I(X;Y)是输入信源的概率分布P(x) 的∩型凸函数。
• (1)对固定信道,选择不同的信源(其概率分布不同)与信 道连接,在信道输出端接收到每个符号后获得的信息量是不 同的。 • (2)对于每一个固定信道,一定存在有一种信源(某一种概 率分布P(x)),使输出端获得的平均信息量为最大。
X
.
. ar
P(bj/ai)
.
. bs
Y
[例1] 二元对称信道,[BSC,Binary Symmetrical Channel] 解:此时,X:{0,1} ; Y:{0,1} ; r=s=2,a1=b1=0;a2=b2=1。 传递概率: 1-p
P (b1 | a1 ) P (0 | 0) 1 p p P (b2 | a2 ) P (1 | 1) 1 p p P (b1 | a2 ) P (0 | 1) p P (b2 | a1 ) P (1 | 0) p
信道的输入和输出没有依赖关系,信息无法传输, 称为全损信道。 接收到Y后不可能消除有关输入端X的任何不确定 性,所以获得的信息量等于零。同样,也不能从X中获得 任何关于Y的信息量。 平均互信息I(X;Y)等于零,表明了信道两端随机变 量的统计约束程度等于零。
二种极限信道各类熵与平均互信息之间的关系 无损信道: H(X|Y)=H(Y|X)=0
平均互信息与各类熵之间关系的集合图(维拉图)表示:
H(X|Y) = H(X) - I(X;Y) H(Y|X) = H(Y) - I(X;Y) H(XY) = H(X)+H(Y)- I(X;Y) H(XY)
图中,左边的圆代表随机 变量X的熵,右边的圆代 表随机变量Y的熵,两个 圆重叠部分是平均互信息
H ( X | Y ) E[ H ( X / b j )] P(b j )H ( X / b j )
s
1 P(b j ) P(ai | b j ) log P( a i | b j ) j 1 i 1 1 P( xy) log P( x | y ) X ,Y
s
r
j 1
a2=1 a1=0
0=b1
p
p
1- p
1=b2
• p是单个符号传输发生错误的概率。 •(1-p)表示是无错误传输的概率。 • 转移矩阵:
0 1
0 1 - p
1 p
p 1 p
[例2]二元删除信道。[BEC,Binary Eliminated Channel]
0
p 0 2 1- q 1
j i j i
关于平均互信息I(X;Y)
互信息 I(x ; y) 代表收到某消息y后获得关于某事件x的 信息量。它可取正值,也可取负值。 若互信息I(x ; y)<0,说明在未收到信息量y以前对消息
x是否出现的不确定性较小,但由于噪声的存在,接收到消 息y后,反而对x是否出现的不确定程度增加了。
I(X;Y)是I (x ; y)的统计平均,所以I(X;Y) >= 0。
y = f (x)
1 y f ( x ) P( y | x ) 0 y f ( x )
(2)有干扰无记忆信道 • 信道输入和输出之间的条件概率是一般的概率分布。 • 如果任一时刻输出符号只统计依赖于对应时刻的输入符号, 则这种信道称为无记忆信道。
P( y | x ) P( y1y 2...y N | x1x2...xN ) P( y i | xi )
(3)交互性(对称性) 即 I(X;Y) = I(Y;X) 当 X、Y统计独立时 I(X;Y) = I(Y;X)=0 当信道无干扰时(一一对应)
I(X;Y) = I(Y;X)=H(X)=H(Y)
(4)凸状性
I ( X ; Y ) I (Y ; X ) P( xy ) log
X ,Y
P( y | x) P( y | x) P( x)P( y | x) log P( y ) P( y ) X ,Y
H(X/Y)
H(Y/X)
I(X;Y)。每个圆减去
I(X;Y)后剩余的部分代表 两个疑义度。
H(X)
I(X;Y)
H(Y)
• 两种特殊信道
(1)、离散无干扰信道 ( 无损信道 )
1 i j p ( y j | xi ) 0 i j y f ( x) y f ( x)
1 i j p ( xi | y j ) 0 i j
I(X;Y)=H(X)=H(Y)
无损信道:完全重迭 全损信道: H(X|Y) = H(X) H(Y|X) = H(Y) I(X;Y) = 0 全损信道:完全独立
3.2
平均互信息的性质
平均互信息 I(X;Y) 具有以下特性:
(1)非负性
即 I(X;Y) >= 0
当X、Y统计独立时等式成立。
(2)极值性 即 I(X;Y) <= H(X) 当 H(X/Y)=0 时,即信道中传输信息无损时,等式 成立。
二、离散信道的数学模型
条件概率 P(y/x) 描述了输入信号和输出信号之间统计 依赖关系。反映了信道的统计特性。
• 根据信道的统计特性即条件概率 P(y/x)的不同, 离散信道又可分成三种情况:
• 无干扰信道 • 有干扰无记忆信道
• 有干扰有记忆信道
(1)无干扰(噪声)信道 信道中没有随机性的干扰或者干扰很小,输出信号 y与输入信号 x 之间有确定的、一 一对应的关系。即:
第三章 信道及其容量
信道的任务是以信号方式传输信息和存储信息。 研究信道中能够传送或存储的最大信息量,即 信道容量。
3.1
信源
信道的数学模型和分类
干扰源 编码器 调制器 物理信道 实际信道 解调器 译码器 信宿
编码信道
等效信道
图3.1.1 数字通信系统的一般模型
3.1
信道的数学模型和分类
y f ( x) y f ( x)
信道的输入和输出一一对应,信息无损失地传输, 称为无损信道。 H(X|Y) = H(Y|X) = 0 [损失熵和噪声熵都为“0” ]
由于噪声熵等于零,因此,输出端接收的信息就等 于平均互信息: I(X;Y) = H(X) = H(Y)
(2)、输入输出独立信道 ( 全损信道 )
邮递信道
一、信道的分类
根据载荷消息的媒体不同
电信道
光信道 声信道 输入和输出信号的形式 根据信息传输的方式
信道的统计特性
信道的用户多少
根据信息传输的方式分类中 根据信道的用户多少:两端(单用户)信道 多端(多用户)信道 根据信道输入端和输出端的关联: 无反馈信道 反馈信道 根据信道的参数与时间的关系: 固定参数信道 时变参数信道 根据输入和输出信号的特点: 离散信道 连续信道 半离散或半连续信道 波形信道
X
1 ; p ( x)
H (Y )= p( y) log
