第3章 机器人运动学(2)汇总
第三章机器人运动学

第三章机器人运动学机器人运动学是研究机器人如何在二维或三维空间中进行运动的学科。
它涉及到机器人的轨迹规划、运动控制和路径规划等重要内容。
本章将介绍机器人运动学的基本概念和常用模型,帮助读者全面了解机器人的运动规律和控制原理。
1. 机器人运动学的基本概念机器人运动学是研究机器人位置和姿态变化的学科,包括正运动学和逆运动学两个方面。
正运动学研究机器人的末端执行器的位置和姿态如何由关节变量确定;逆运动学则研究机器人如何通过末端执行器的位置和姿态来确定关节变量的值。
机器人的运动学建模一般采用DH(Denavit-Hartenberg)参数表示方法。
DH 参数是由Denavit和Hartenberg提出的一种机器人坐标系的选择和旋转轴的确定方法。
通过定义一系列关节坐标系,建立起机器人的坐标系链,并确定各个关节的旋转轴和约定的方向,可以方便地描述机器人的运动学特性。
2. 机器人正运动学机器人正运动学是研究机器人末端执行器位置和姿态如何由关节变量确定的问题。
在机器人的正运动学中,常用的方法有几何法和代数法。
2.1 几何法几何法是一种较为直观的方法,通过对机器人各个关节坐标系的位置和旋转进行推导,得到机器人末端执行器的位置和姿态。
几何法适用于无约束和无外力干扰的情况,可以简单快速地推导出机器人的正运动学方程。
2.2 代数法代数法是一种基于运动学链的代数运算的方法,通过DH参数建立起机器人的坐标系链,并通过矩阵运算推导出机器人的正运动学方程。
代数法在机器人正运动学的推导和计算过程中更具有普适性和灵活性。
3. 机器人逆运动学机器人逆运动学是研究机器人如何通过末端执行器的位置和姿态来确定关节变量的值的问题。
机器人逆运动学在机器人运动规划和路径控制中起到重要的作用。
机器人逆运动学的求解一般采用迭代方法,通过迭代计算来逼近解析解,实现对机器人关节变量的求解。
逆运动学的求解过程中可能会出现奇异点和多解的情况,需要通过约束条件和优化方法来处理。
第3章 机器人运动

3 齐次坐标变换 3.1齐次坐标变换 3.1齐次坐标变换 假设机器人手部拿一个钻头在 工件上实施钻孔作业,已知钻 头中心P点相对于手腕中心的 位置,求P点相对于基座的位 置。
x i o
zb kb yb jb o, ib xb P
z
k
j
y
分别在基座和手部设置为固定坐标系和动坐标系, 如图所示。
P点 相对于固定坐标系
1 4 0 −3 0 7 0 1
T中第一列的三个元素(0,1,0)T表示活动坐标系的u轴与 固定坐标系三个坐标轴之间的投影,故u轴平行于y轴;T中第 二列的三个元素(0,0,1)T表示活动坐标系的v轴与固定坐 标系三个坐标轴之间的投影,故v轴平行于z轴;T中第三列的 三个元素(1,0,0)T表示活动坐标系的w轴与固定坐标系三 个坐标轴之间的投影,故轴w平行于x轴;T中第四列的三个元 素(4,-3,7)T表示活动坐标系的原点与固定坐标系原点之 间的距离。
b
3.3.2 举例 ⋅ i i
z kb k o, xb i o xi y j y j
1 0 0 R = 0 1 0 0 0 1
所以
x0 X 0 = y0 z0
0 0 1 0 0 1 0 0
1 0 A = Trans( x0 , y0 , z0 ) = 0 0
上面所述的坐标变换每步都是相对于固定坐标系进行的,也可以 相对于动坐标系进行变换: 坐标系 {o , : u , v, w} 初始与固定坐标系 {o:x, y, z} 相重合,首先相对于固定坐标系平移
4i − 3 j + 7 k ;然后绕活动系的v轴旋转900;最后绕w轴旋转900。
变换的几何表示如图所示。这是合成变换矩阵为
机器人技术基础课件第三章-机器人运动学精选全文完整版

如此类推,对于六连杆机器人,有下列矩阵:
06T 01T 12T 23T 34T 45T 56T
3.2 3.2 机械手运动学方程
26
0 6
T
3.1.4 连杆变换矩阵及其乘积
06T 01T12T 23T 34T 45T 56T
机器人运动学方程
此式右边表示了从固定参考系到手部坐标系的各连杆
一个六连杆机械手可具有六个自由度,每个连杆含 有一个自由度,并能在其运动范围内任意定位与定向。 其中三个自由度用于规定位置,而另外三个自由度用 来规定姿态。
8
3.1.1 连杆坐标系
机械手的运动方向
机器人手部的位置和姿态也可以
用固连于手部的坐标系{B}的位姿
来表示
关节轴为ZB, ZB轴的单位方向 矢量α称为接近矢量,指向朝外。
(1) 坐标系{i-1}绕xi-1轴转角αi-1,使Zi-1与Zi平行,算子为Rot(x, αi-1) ; (2) 沿Xi-1轴平移ai-1,使Zi-1和Zi共线, 算子为Trans(ai-1,0,0); (3)绕Zi轴转角θi; 使得使Xi-1与Xi平行, 算子为Rot(z,θi);
(4) 沿Zi轴平移di。使得i-1系和i系重合, 算子为Trans(0,0,di)。
3.2.1 机器人正运动学方程
连杆 i 1
2
3
连杆长 度ai-1
0
a0
a1
连杆偏距 di 0
0
d2
连杆扭角 αi-1 00
00
-900
关节角 θi
θ1(00) θ2(00) θ3(00)
3.2.1 机器人正运动学方程
该3自由度机器人的运动学方程为:
第三章机器人运动学

αi
3.2.3连杆附加坐标系的规定
(4)建立连杆坐标系的步骤
确定关节轴,并画出轴的延长线。 找出关节轴i和i+1的公垂线或交点,作为坐标系i的原点。 规定Zi的指向是沿着第i个关节轴。 规定Xi轴得指向是沿着轴i和i+1的公垂线的方向,如果关节轴 i和i+1相交,则Xi轴垂直于关节轴i和i+1所在的平面。 Yi 轴的方向由右手定则确定。 当第一个关节变量为0时,规定坐标系{0}和{1} 重合,对于坐 标系{N},尽量选择坐标系使得连杆参数为0.
3.2.3连杆附加坐标系的规定
为了描述每个连杆和相邻连杆之间的相对位置关系,需要在每个连杆 上定义一个固连坐标系. (1)连杆中的中间连杆 规定: 坐标系{i}的Z轴称为Zi,与 关节轴i重合; 坐标系{i}的原点位于公垂 线ai与关节轴i的交点处. Xi轴沿ai方向由关节i指向 关节i+1 (若: ai =0,则Xi垂直于Zi和Zi+1所 在的平面;按照右手定则绕Xi轴的 转角定义为αi ,由于Xi轴的符号 有两种,则转角的符号也有两种.) Yi轴由右手定则确定
3.2.5 PUMA560运动学方程
(2)连续连杆变换 定义了连杆坐标系和相应得连杆参数,就能建立运动学 方程,坐标系{N}相对于坐标系{0}的变换矩阵为:
0 N
0
T T T T
0 1 1 2 2 3
N 1 N
T
变换矩阵 NT 是关于n个关节变量的函数,这些变量可以通 过放置在关节上的传感器测得,则机器人末端连杆再基坐标系 (笛卡尔坐标系)中的位置和姿态就能描述出来。
2) joint angle 关节角 描述两个相邻连杆绕公共轴线旋 转的夹角θi. 当i为转动关节时,关节角为一变量.
电机拖动技术基础第三章机器人的运动学PPT课件

►3.1 刚体的位姿描述 ►3.2 坐标变换 ►3.3 齐次坐标和齐次变换 ►3.4 变换方程和欧拉角 ►3.5 机器人运动学的正问题和逆问题
3.1 刚体的位姿描述
一、位姿的定义
刚体参考点的位置(坐标系的位置)和刚体的姿态统称为刚体的位姿。
(为描述机器人本身的各个连杆之间.机器人和环境之间的运动关系,将
n
n o a
手爪的方位由旋转矩阵R规定。
R n
o
a
手爪的位置由位置矢量 p
规定。
代表手p 爪坐标系的原点。
则手爪的位姿可由四个矢量
来 来描述。
noa p
记为:
T n o a p
3.2 坐标变换
定义:由于空间中任意点P在不同坐标系中的描述不同,所以需要 研究从一个坐标系的描述到另一个坐标系的描述之间的变换关,通 常称为坐标变换。
{S}代表工作站(操作台)坐标系(工作站框)
{G}代表目标坐标系(目标框) 它们之间的位姿关系用相应的齐次变换来描述。图3-6 机器人与环境坐标系
B S
T描述工作站框{S}相对于基座{B}的位姿,
S G
T描述目标框{G}相对于工作站{S}的位姿。
对物体进行操作时(搬运或装配机器人),工具框{T}相对目标框{G} 的位姿 直接GT T 影响操作效果。 是机GT T器人控制和轨迹规划的对象。
=
相对于固定坐标系运动 相对于活动坐标系运动
2.变换过程的可逆性
齐次坐标变换过程是可逆的. 若有 ,则逆变换
。
所以有 I44BATABT A B0R BP 1AO BA0R AP 1BO
A BR0BAR
A BRAPB1OBPAO
机器人基础与数字孪生系统 第3章 机器人运动学

第3章 机器人运动学
【3.1齐次变换】
【3.1.1】位置描述——位置矢量
● 刚体位姿描述:齐次变换(矩阵)、矢量法、四元数
● 齐次变换法:
▲ 将运动、变换和映射与矩阵运算联系起来,具有明显的几何特征。
▲ 在操作臂运动/动力学、机器人控制算法、计算机图学、视觉信息处理、手-眼建模标
BT
0
● 齐次变换:
A
p = BA R B p A pBo
A
pBo
1
齐次坐标
A p BA R
1 0
旋转矩阵
齐次坐标
A
pBo B p
1 1
平移矢量
【3.2 DH约定和MDH约定】
【3.2.1】关节与连杆
Z
R3
● 自由度:物体能够相对于坐标系进行独立运动的数目称为自由度
最后根据右手定则确定Yi 轴。
i -1
i+1
i
P
Zi -1
Yi -1 d
i
ai - 1
{
θi
ai
X i -1
Oi -1
Yi
i
Zi
Oi
Xi
【3.2 DH约定和MDH约定】
【3.2.2】连杆坐标系
Ji
Ji-1
Ji+1
Ci-1
Ci+1
Ci
● 方法二:对于相邻两个连杆Ci 和Ci+1,有3个关节,
r31
r12
r22
r32
r13
r23
r33
A
B
R 是正交矩阵,满足如下关系:
第三章机器人运动学

XX,a click to unlimited possibilities
汇报人:XX
目录
01 机 器 人 运 动 学 基 础 03 机 器 人 运 动 学 求 解
方法
05 机 器 人 运 动 学 的 发
展趋势和挑战
02 机 器 人 关 节 类 型 和 运动学模型
04 机 器 人 运 动 学 在 实 践中的应用
迭代求解算法
迭代求解算法的基本思想是通过不断迭代逼近解的过程 常见的迭代求解算法包括雅可比迭代法、高斯-赛德尔迭代法等 迭代求解算法的收敛性和收敛速度是评价算法优劣的重要指标 迭代求解算法在机器人运动学中具有广泛的应用,可以提高机器人的运动精度和稳定性
Part Four
机器人运动学在实 践中的应用
添加标题
添加标题
添加标题
添加标题
变换矩阵:描述机器人末端执行器 相对于参考坐标系的位姿变化,由 平移和旋转矩阵组合而成。
齐次坐标和变换矩阵的应用场景: 机器人轨迹规划、姿态控制、碰撞 检测等。
运动学方程
定义:描述机器 人关节运动的数 学模型
建立方法:根据 机器人结构和运 动需求进行建模
求解过程:通过 数值计算得到机 器人末端执行器 的位置和姿态
添加标题
添加标题
添加标题
添加标题
变换矩阵:描述机器人末端执行器 在各个坐标系之间位置和姿态关系 的数学工具
逆运动学:已知目标位置和姿态, 求解机器人关节角度的过程
齐次坐标和变换矩阵
齐次坐标:描述机器人末端执行器 的位置和姿态,通过将实际坐标系 与参考坐标系进行转换得到。
齐次坐标和变换矩阵在机器人运动 学中的重要性:实现机器人末端执 行器的精确控制和定位。
机器人学基础_第3章机器人运动学

移动连杆坐标系的建立
移动连杆坐标系的规定:
• 坐标轴Zi:与i+1关节的轴线重合; • 坐标轴Xi:沿移动关节i轴线与关节i+1轴线的公垂线,指向i+1关节; • 坐标轴Yi:按右手直角坐标系法则确定; • 坐标原点Oi: (1)当关节i轴线和关节i+1轴线相交时,取交点; (2)当关节i轴线和关节i+1轴线异面时,取两轴线的公垂线与关节i轴
动到使其原点与连杆i坐标系原点重合的地方。 • (4) 绕Xi旋转αi角,使Zi–1转到与Zi同一直线上。 • 连杆i–1的坐标系经过上述变换与连杆i的坐标系
重合。如果把表示相邻连杆相对空间关系的矩阵 称为A矩阵,那么根据上述变换步骤,从连杆i到 连杆i–1的坐标变换矩阵Ai为
•
(3.13)
• 同理,对联轴器的齐次坐标变换矩阵有 •
• 手部的位置矢量为固定参考系原点指向手 部坐标系{B}原点的矢量P,手部的方向矢 量为n、o、a。于是手部的位姿可用4 4 矩阵表示为
•
•
nX oX a X PX
T
nY
oY
aY
PY
nZ 0
oz 0
aZ 0
PZ 1
• 思考:
• ①说明位姿矩阵的左上角3×3矩阵的几何 意义。
• ②分别说明n, o, a, P的几何意义。
a1 = l 1 =100
a2 = l 2 =100
旧课复习与总结
转动连杆坐标系的建立
• 坐标轴Zi:与i+1关节的轴线重合; • 坐标轴Xi:沿连杆i两关节轴线的公垂线,指向i+1关节; • 坐标轴Yi:按右手直角坐标系法则确定; • 坐标原点Oi: (1)当关节i轴线和关节i+1轴线相交时,取交点; (2)当关节i轴线和关节i+1轴线异面时,取两轴线的公垂
《机器人运动学》PPT课件 (2)

i
ai
杆件参数的意义-di和 i
确定杆件相对位置关系,由另外2个参数决定,一个是杆
件的距离:di,一个是杆件的回转角:i
Ai+1
di 是从第i-1坐标
系的原点到Zi-1轴 和Xi轴的交点沿Z
Ai-
i-1轴测量的距离
1
i 绕 Zi-1轴由Xi-1
轴转向Xi轴的关节
角
Ai
1.广义连杆(D-H坐标)
全为转动关节: Zi坐标轴; Xi坐标轴; Yi坐标轴;
连杆长度ai; 连杆扭角αi; 两连杆距离di; 两杆夹角θi
全为转动关节: Zi坐标轴:沿着i+1关节的运动轴; Xi坐标轴:沿着Zi和Zi-1的公法线,指向离开Zi-1轴
的方向; Yi坐标轴:按右手直角坐标系法那么制定; 连杆长度ai; Zi和Zi-1两轴心线的公法线长度; 连杆扭角αi: Zi和Zi-1两轴心线的夹角; 两连杆距离di:相邻两杆三轴心线的两条公法线间
特殊情况坐标系的建立原那么
z i zi-1
两个关节轴相交
xi
oi
yi
Oi— Ai与Ai+1关节轴线的交
点
Zi— Ai+1轴线
Xi— Zi和Zi-1构成的面的法
Ai+1
线
Yi— 右手定那么
Ai
两个关节轴线平行
先建立
Ai-1
∑0i-1
然后建立 ∑0i+1
最后建立 ∑0i
Ai
Ai+1
Ai+2
yi-1 zi-1
ai杆长—沿 xi 轴, zi-1 轴与 xi 轴交点到 0i 的距离
yi1
课件:第三章机器人运动学

• 3.1 机器人运动方程的表示
• 3.1.2 运动位置和坐标
• 一旦机械手的运动姿态由某个姿态变换规定之后,它在基坐标系中的 位置就能够由左乘一个对应于矢量p的平移变换来确定。
1 0 0 px
T6
0 0
1 0
0 1
p
y
某姿态变换
pz
0 0
0
1
Robotics运动学
3.1 机器人运动方程的表示
3.1.3 连杆变换矩阵 1.广义连杆(D-H坐标)
所有关节全为转动关节时: Zi坐标轴; Xi坐标轴; Yi坐标轴;
连杆长度ai;连杆两端关节公共法线距离 连杆扭角αi;垂直于ai所在平面内两轴的夹角 两连杆距离di;两连杆的相对位置di 两杆夹角θ 两连杆法线的夹角
Robotics运动学
3.1 机器人运动方程的表示
s c 0 0ny
oy
ay
p
y
s
c
0 0
0
0
0 0
1 0
0 1
nz 1
oz 1
az 1
pz 1
sc
0
ss
0
c 0
0 1
(3-39)
Robotics运动学
3.2 机械手运动方程的求解
3.2.1欧拉变换解
重写为
f11(n) f11(o) f11(a) f11( p) cc cs s 0
保持姿态,执行器要绕其自身Y和Z轴反向旋转.
Sph( , , r) Rot(z, )Rot( y, )Trans(0,0, r)Rot( yA, )Rot(zA, )
1 0 0 rcs
0
1
0
rss
第三章 机器人运动学
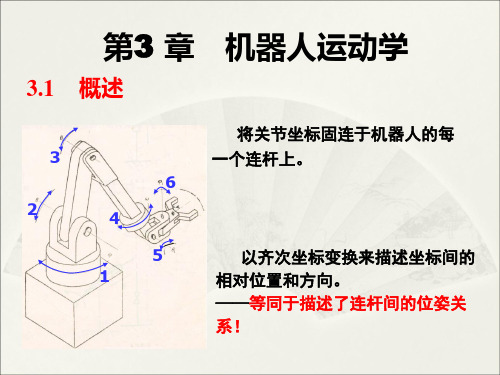
cos 3 sin 3 A3 0 0
sin 3 0 0 cos 3 0 0 0 1 0 0 0 1
0 l2 cos 2 0 l2 sin 2 1 0 0 1
SCARA机器人
( Selective Compliance Assembly Robot Arm )
第3 章 机器人运动学
3.1
3
概述
将关节坐标固连于机器人的每 一个连杆上。
6
2 4 5 1 以齐次坐标变换来描述坐标间的 相对位置和方向。 ——等同于描述了连杆间的位姿关 系!
3 6 2 4 5 1
齐次变换矩阵 A1 描述第1连杆 相对于参考坐标系{O}的位姿
0
p A1 1 p
A
0 1
0 l2 cos 2 0 l2 sin 2 1 0 0 1
1 0 A3 0 0
0 1 0 0
0 0 0 0 1 d3 0 1
cos 4 sin 4 A4 0 0
sin 4 cos 4 0 0
坐标系{i}固连于连杆i 坐标系{i}固连于关节i+1 z 轴与关节轴重合,方向 自由确定。
x 轴是连杆长度的延长线,
方向由关节i指向关节i+1。
坐标系{i}由坐标系{i-1}通过4次齐次变换而得到的。
4次齐次变换都 是相对于当前 坐标系进行的!
Ai1 Rot zi 1,i Ai3 Trans ai ,0,0
齐次变换矩阵 A2 描述第1连杆 相对于第2连杆的位姿
1
p A2 2 p
0
p A1 A2 2 p
T2 A1 A2
第三章机器人运动学PPT课件
由这些矢量描述的空间称为关节空间。
• 正向运动学:关节空间末端笛卡儿空间,单射 • 逆向运动学:末端笛卡儿空间关节空间,复射
不同的关节空间,相同的 末端笛卡儿空间
关节空间与末端笛卡儿空 间映射关系
第三章 机器人的运动学
3.1 工业机器人运动学
,它的齐
次坐标就是
,即满足Px=ωPx/ω,Py=ωPy/ω,
Pz=ωPz/ω(ω是非零整数)。可以看出,在三维直角坐标系中,
由于ω取值的不同,一个点的齐次坐标的表达不唯一。
齐次坐标不仅可以规定点的位置(ω为非零整数),还可以
用来规定矢量的方向(第四个元素为零时)。列向量
(
)表示空间的无穷远点,a,b和c称为它的方向
单位主矢量相对于坐标系{A}的方向余弦组成:
xB
yB
zB
xA
yA
zA
其中:co scoxB s ,xA ()
既表示了刚体F在{A}系中的方位,也描述了{B}系在{A}系中的 姿态。
3.1.2.2 坐标变换
一、坐标平移
如图3-5,坐标系{B}与{A} 方向相同,但原点不重合。
图3-5 坐标平移
此式称为平移方程。其中 是B系中的原点在A系中的表示。
0
0
0
1
1
1
给定坐标系{A},{B}和{C},已知{B}相对{A}的描述为 ,
{C}相对{B}的描述为
AP A BTBP BPC BTCP APC ATCP
,则有
APA BTC BTCP
CATABTCBT
从而定义复合变换
。
同理得出:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一旦方向被确定之后,用一个相应的p向量的位移变换 可得到机器人末端执行器在基坐标中的位置:
1 0 0 px
旋转
0 1 0 py
变换
T6 = 0 0 1 pz 0001
矩阵
(3.16)
机器人运动学—刚体位姿描述和齐次变换
一、齐次坐标
在选定的直角坐标系{A}中,空间 任一点P的位置可用3×1的位置矢量 Ap表示,其左上标代表选定的参考坐 标系:
连续变换的若干A矩阵的积称为T矩阵,对于一个六连杆(六自由
度)机械手有
T6 = A1 A2 A3 A4 A5 A6
(3.1)
六连杆的机械手有六个自由度,其中三个自由度用来确定位置,
三个自由度用来确定方向。T6表示机械手在基坐标中的位置与方向。 则变换矩阵T6有下列元素
T6 =
nx ox ax px
ny oy ay py nz oz az pz 0 001
0001 00
01
RPY(,θ,ψ) =
cos –sin 0 0 sin cos 0 0 0 0 10
0 0 01
cosθ sinθsinψ sinθcosψ 0
0
cosψ –sinψ 0
-sinθ cosθsinψ cosθcosψ 0 (3.14)
0
0
01
RPY( ,θ,ψ) =
ห้องสมุดไป่ตู้
cosøcosθ sinøcosθ
图3.2是一致的。
z z’
ψ
z’’
θ z’’’ ø
0
ø
y’’’
ø y’’
θ ψ
y’
y
θ
ψ
x’
x
θ x’’ ø x’’’
图3.3 基于基坐标的欧拉角
3.4 摇摆、俯仰和偏转 ( Roll, Pitch and Yaw )
摇摆、俯仰和偏转为另一种旋转,如图3.4所示。
就像水中航行的一条小船一样,绕着它前进的方向(z轴)旋转 称为
3.1 引言 ( Introduction )
采用齐次变换来描述在各种坐标系中机械手的位置与方向。通过
各种正交坐标系的齐次变换和非正交关节坐标系中机械手末端的齐次
变换,最后建立运动方程。
注意,对任何数目关节的各种机械手均可以这样进行。
描述一个连杆与下一个连杆之间关系的齐次变换称A矩阵。A矩阵
是描述连杆坐标系之间的相对平移和旋转的齐次变换。
摇摆,绕着它的横向中轴(y轴)旋转θ 称为俯仰,绕着它甲板的垂直向上 的方向(x轴)旋转ψ 称为偏转。借助于这种旋转来描述机械手的末端执行 器如图3.5所示。
图3.4 摇摆、俯仰和偏 转角
图3.5 机械手的末端执行器的摇 摆、俯仰和偏 转
3.4 摇摆、俯仰和偏转 ( Roll, Pitch and Yaw )
第3章 机器人运动学 —运动学方程
3.1 引言 3.2 姿态描述 3.3 欧拉角 3.4 摇摆、俯仰和偏转 3.5 位置的确定 3.6 圆柱坐标 3.7 球坐标
3.8 T6的说明 3.9 各种A矩阵的说明 3.10 根据A矩阵来确定T6 3.11 斯坦福机械手的运动方程 3.12 肘机械手的运动方程 3.13 小结
规定旋转的次序为
RPY(ø,θ,ψ)=Rot(z, )Rot(y,θ)Rot(x,ψ) (3.12)
即绕x轴旋转ψ,接着绕y轴旋转θ,最后绕z轴旋转 ,这
个变换如下:
cosθ 0 sinθ 0 1 0
00
0 1 0 0 0 cosψ –sinψ 0
RPY(,θ,ψ) = Rot(z, ) –sinθ0 cosθ 0 0 sinψ cosψ 0 (3.13)
图3.1 末端执行器的描述
(3.2)
3.2 姿态描述 ( Specification of Orientation )
对式(3-2)中16个元素一一赋值就可确定T6。假定机 械手可以到达要求的位置,而单位旋转矢量o和a正交,即
o·o = 1
(3.3)
a·a = 1
(3.4)
a形成单位向量
a a
|a|
o·a = 0
(3.5)
(3.6)
构成与o和a正交的n
n o×a
(3.7)
在o和a形成的平面上旋转o,使得o与n和a正交
单位向量o是
o a×n
o o
|o|
(3.8) (3.9)
根据第三章(1)给出的一般性的旋转矩阵Rot (k ,θ),它把机械手末端的姿态 规定为绕k轴旋转θ角。
z z’
3.3欧拉角 ( Euler Angles )
式中PX,PY,PZ是点P在坐标系{A}中的 三个位置坐标分量,如图2-1所示。如用 四个数组成的(4×1)列阵表示三维空间直 角坐标系{A}中点p,则列阵[Px Py Pz 1]T 称为三维空间点P的齐次坐标
必须注意,齐次坐标的表示不是唯一的。我们将其各元素同乘 一非零因子w后,仍然代表同一点P,即
-sinθ 0
cosøsinθsinψ – sinøcosψ cosøsinθcosψ + sinøsinψ
sinøsinθsinψ + cosøcosψ sinøsinθcosψ–cosøsinψ
cosθsinψ
cosθcosψ
0
0
0
0 (3.15)
0 1
3.5 位置的确定 ( Specification of Position )
(3.2)
如图3.1所示,机器人 的末端执行器(手爪)的 姿态(方向)由 n、o、a 三个旋转矢量描述,其坐 标位置由平移矢量 p 描述, 这就构成了式(3.2)中的 变换矩阵 T。
由于 n、o、a 三个旋 转矢量是正交矢量,所以 有
n = o×a
T6 =
nx ox ax px
ny oy ay py nz oz az pz 0 001
ø
姿态变更常用绕x,y或z 轴的一系列旋转来确定。欧 拉角描述方法是:先绕z轴旋
转,然后绕新的y(即y/)轴旋
转θ,最后绕更新的z(z//)轴 旋转ψ(见图3.2)。欧拉变
换Euler(,θ,ψ)可以通过连
乘三个旋转矩阵来求得:
z’’ z’’’ ψ θ
0
y’’’
ψ
y’y’’
øθ
y
ø
x
θψ
x’
x’’’
式中:a=w px; b=w py; c=w pz
二、齐次变换 刚体的运动是由转动和平移组成的。为了能用同一矩阵表
x’’
图3.2 欧拉角
Euler(,θ,ψ)=Rot(z,).Rot(y,θ).Rot(z,ψ) (3.10)
在一系列旋转中,旋转的 次序是重要的。应注意,旋转 序列如果按相反的顺序进行, 则是绕基坐标中的轴旋转:
绕z轴旋转ψ ,接着绕y轴 旋转θ,最后再一次绕z轴旋转
,结果如图3.3所示,它与
