圆锥曲线极点极线问题
圆锥曲线的极线与极点
圆锥曲线的极线与极点
圆锥曲线的极线与极点是极坐标系下描述曲线的一种方法。
在极坐标系下，圆锥曲线上的每一个点都可以用极坐标（r，θ）来表示，其中r表示点到极点的距离，θ表示点与极轴的夹角。
圆锥曲线的极线是通过极点的直线，它与曲线的交点即为极点对应的点。
对于不同类型的圆锥曲线，极线的性质也不同。
例如，对于椭圆和双曲线，极点在曲线的中心处，极线通过中心点且垂直于极轴。
而对于抛物线，极点在焦点处，极线为与焦轴垂直的直线。
极点极线当极点在圆锥曲线内的写法
极点极线当极点在圆锥曲线内的写法圆锥曲线是高中数学学习中比较重要且难以学习的部分。
其中，极点极线是较为复杂的概念。
本文将介绍极点极线当极点在圆锥曲线内的写法。
一、极点极线的定义
极点极线是指在平面直角坐标系中，从一点向圆锥曲线上的所有点引一条直线，那么这条直线叫做极线，这个点就是极点。
二、圆锥曲线的分类
圆锥曲线一共有四种类型：圆、椭圆、双曲线和抛物线。
不同类型的圆锥曲线的性质不同。
本文主要介绍当极点在圆锥曲线内时的情况。
三、椭圆的情况
当极点在椭圆内部时，极线的两个端点分别交于椭圆的两个焦点上，且与椭圆的切线垂直。
四、双曲线的情况
当极点在双曲线内部时，极线的两个端点分别交于双曲线的两个焦点上，且与双曲线的渐近线垂直。
五、抛物线的情况
当极点在抛物线内部时，极线的两个端点分别交于抛物线的顶点和抛物线的对称轴上，且与抛物线的准线垂直。
六、圆的情况
当极点在圆内部时，极线是过圆心并垂直于圆的直径的直线。
总结：极点极线是圆锥曲线的一个重要概念，不同类型的圆锥曲线在极点极线方面会有不同的表现。
当极点在圆锥曲线内部时，可以根据不同的类型进行判断。
圆锥曲线的极点与极线问题
圆锥曲线的极点与极线问题圆锥曲线的极点与极线问题导言圆锥曲线是数学中的一个重要分支，其所涵盖的概念和性质有着深远的研究价值。
其中，圆锥曲线的极点与极线问题是一个具有特殊意义的主题。
在本文中，我将以深度和广度的方式来探讨圆锥曲线的极点与极线，希望能够使读者对这一问题有全面、深刻和灵活的理解。
一、圆锥曲线的基本定义与性质1.1 什么是圆锥曲线圆锥曲线是由一个平面与一个平行于它的不相交的直线切割圆锥所得到的曲线。
根据切割的方式和角度不同，圆锥曲线可以分为椭圆、双曲线和抛物线三类。
1.2 圆锥曲线的焦点与离心率圆锥曲线的焦点是指在其上的特殊点，其具有特殊的几何性质。
离心率是一个衡量圆锥曲线形状的参数，也是圆锥曲线性质的重要指标。
二、极点与极线的基本概念2.1 极点的定义与性质在平面上给定一个圆锥曲线，其直角坐标系中的原点O被称为该圆锥曲线的极点。
极点在圆锥曲线的研究中具有重要的地位，它与曲线的各种性质密切相关。
2.2 极线的定义与性质对于圆锥曲线上的任意一点P，以极点为中心，作直线OP，称为圆锥曲线的极线。
极线是一个与极点相关的直线，它与曲线的位置和特性有着密切的联系。
三、不同类型曲线的极点与极线问题3.1 椭圆的极点与极线对于椭圆，其极点为原点O，极线为过原点O的直线。
椭圆的极点处于其主轴的中点位置，其极线是关于两个焦点的对称直线。
3.2 双曲线的极点与极线对于双曲线，其极点为原点O，极线为过原点O的渐近线。
双曲线的极点处于离心率之间的位置，其极线是关于两个焦点的渐近线。
3.3 抛物线的极点与极线对于抛物线，其极点为其焦点，极线为过焦点的直线。
抛物线的极点位于抛物线的顶点位置，其极线是关于焦点的直线。
四、个人观点与理解圆锥曲线的极点与极线问题是一个十分有趣且具有挑战性的数学问题。
通过研究圆锥曲线的极点与极线，我们能够更深入地理解曲线的性质和特性。
极点是曲线的重要几何特征，它能够从不同的角度揭示出曲线的各种性质。
圆锥曲线极点极线应用篇5
圆锥曲线极点极线应用篇5一、引言圆锥曲线是高中数学的重要内容，极点极线是解决圆锥曲线问题的一种重要方法。
本篇文档将详细介绍如何应用极点极线解决圆锥曲线问题。
二、极点极线基本概念在解析几何中，一个点对于一个曲线而言，具有特殊的意义。
这个点被称为曲线的极点，而连接这个点和曲线上任何一点的直线被称为这条曲线的极线。
在圆锥曲线中，这个概念同样适用。
三、应用方法1.点与曲线的关系：通过寻找曲线的极点，可以找到曲线上某个点的位置。
通过已知点和曲线的极线，可以求出未知点的坐标。
2.曲线间的关系：不同曲线的极线可能交于一点，或者两曲线具有相同的极线。
这种情况下，可以通过研究这个共有的极线来研究两个曲线之间的关系。
3.最值问题：在解决最值问题时，可以考虑用极点极线的方法。
通过建立极线方程，可以将问题转化为求函数最值的问题。
四、实例解析1.已知抛物线方程为y^2=4x，求点(2,2)在抛物线上的位置。
解：根据抛物线的定义，可得到抛物线的极点为原点。
因为点(2,2)在抛物线上，所以它的极线与抛物线的交点就是所求。
通过解方程y^2-4y=0，可得到点(2,2)在抛物线上的位置为(1,0)。
2.求椭圆x^2/4+y^2/3=1上的点到直线x+y=0的距离最小时的椭圆方程。
解：这个问题的关键在于找到椭圆的极线和所求直线之间的关系。
椭圆的极线是两条射线，它们和坐标轴构成的两个三角形的面积越大，距离最小。
通过计算，可以得到当椭圆的长轴在$x$轴上时，距离最小。
此时，椭圆的方程为x^2/7+y^2/3=1。
五、总结通过极点极线的方法，我们可以更深入地理解圆锥曲线，找到解决问题的方法。
在解决具体问题时，要灵活运用基本概念和方法，通过建立方程、函数等方法，解决实际问题。
六、扩展阅读1.进一步了解极点和极线的性质和应用，可以阅读相关的数学文献和教材。
2.练习解一些更复杂的问题，以提高自己的解题能力。
3.参考一些优秀的数学解题视频和博客，获取更多的解题思路和方法。
圆锥曲线的极点与极线问题
圆锥曲线的极点与极线问题
摘要：
一、圆锥曲线的极点与极线的概念与定义
二、圆锥曲线极点与极线的重要结论
三、如何证明圆锥曲线中极点极线的性质
四、极点极线在圆锥曲线解题中的应用
正文：
一、圆锥曲线的极点与极线的概念与定义
圆锥曲线是数学中的一个重要概念，它可以用来描述各种物理现象。
极点与极线是圆锥曲线中的两个重要概念。
极点是指圆锥曲线上某一点的切线与过该点的直径的交点，而极线则是指过圆锥曲线上一点的切线与该点关于直径的对称点的连线。
二、圆锥曲线极点与极线的重要结论
在研究圆锥曲线的极点与极线时，我们可以发现一些重要的结论。
例如，对于椭圆和双曲线，它们的极点与极线总是相互垂直的。
而对于抛物线，其极点与极线则共线。
这些结论对于理解和解决圆锥曲线的相关问题非常有帮助。
三、如何证明圆锥曲线中极点极线的性质
要证明圆锥曲线中极点极线的性质，我们需要运用一些几何和数学知识。
首先，我们可以通过画图和观察来发现一些初步的结论。
然后，我们可以运用数学的证明方法，如代数证明、几何证明等，来证明这些结论的正确性。
四、极点极线在圆锥曲线解题中的应用
在解决圆锥曲线的相关问题时，极点极线的概念和性质可以给我们提供很多帮助。
例如，在求解圆锥曲线的切线问题时，我们可以通过找到极点和极线来简化问题。
在解决圆锥曲线与直线的交点问题时，我们也可以通过极点极线来找到答案。
圆锥曲线的极点与极线问题(一)
圆锥曲线的极点与极线问题(一)圆锥曲线的极点与极线问题相关问题：•什么是圆锥曲线的极点和极线？•如何求解圆锥曲线的极点和极线的定义？•圆锥曲线的极点和极线有什么应用？•如何通过已知条件求解圆锥曲线上的极点和极线？•圆锥曲线的极点和极线与其他几何图形之间有何联系？解释说明：什么是圆锥曲线的极点和极线？圆锥曲线的极点是指在平面内选择一条直线（称为极线），通过该直线作圆锥曲线上任意一点的平行线，该平行线与直线的交点即为极点。
如何求解圆锥曲线的极点和极线的定义？•对于椭圆和双曲线，极点是无穷远处（在平行于直线与该曲线的交点），极线是直线。
•对于抛物线，极点是抛物线的焦点，极线是渐近线。
圆锥曲线的极点和极线有什么应用？•在几何图形的研究和推导中，通过极点和极线的概念可以简化问题，并有助于解决相关的几何性质与推论。
•在工程和设计领域中，圆锥曲线的极点和极线可以用于确定曲线上特定位置的要素，如焦点位置、切线方向等。
如何通过已知条件求解圆锥曲线上的极点和极线？•对于椭圆和双曲线，可以通过已知的焦点和直线方程，使用平行线性质找到对应的极线和极点。
•对于抛物线，可以通过已知的焦点和直线方程，使用渐近线的性质找到对应的极线和极点。
圆锥曲线的极点和极线与其他几何图形之间有何联系？•极点和极线可以看作是圆锥曲线上的一种特殊构造，与其他几何图形的焦点、渐近线等有类似的性质。
•极点和极线的概念也可以推广到其他几何图形中，例如超越曲线等。
不同类型的曲线可能有不同的极点和极线定义。
以上是关于圆锥曲线的极点与极线问题的相关问题和解释说明。
通过了解这些问题，可以更好地理解和应用圆锥曲线的极点和极线的概念。
高中数学极点极线及高中圆锥曲线必备公式
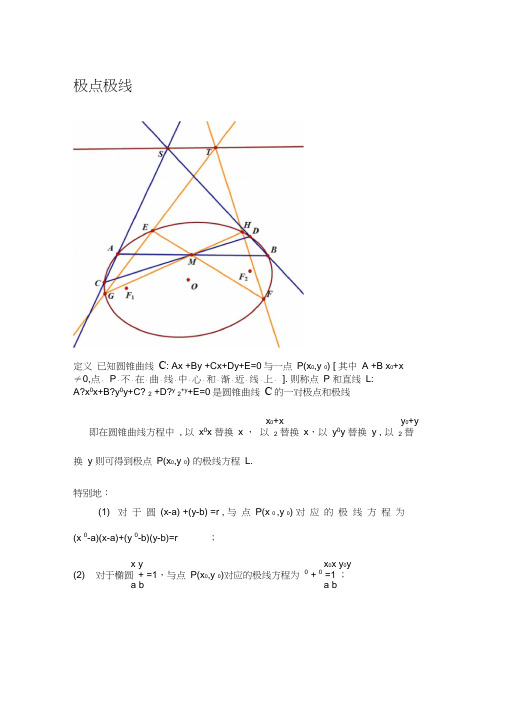
极点极线定义已知圆锥曲线С: Ax +By +Cx+Dy+E=0与一点P(x0,y 0) [ 其中 A +B x0+x≠0,点．P．不．在．曲．线．中．心．和．渐．近．线．上．]. 则称点P 和直线L:A?x0x+B?y0y+C? 2 +D?y2+y+E=0是圆锥曲线С的一对极点和极线x0+x y0+y 即在圆锥曲线方程中, 以x0x 替换x ，以2替换x，以y0y 替换y , 以2替换y 则可得到极点P(x0,y 0) 的极线方程L.特别地：(1) 对于圆(x-a) +(y-b) =r , 与点P(x 0 ,y 0) 对应的极线方程为(x 0-a)(x-a)+(y 0-b)(y-b)=r ；x y x0x y0y(2) 对于椭圆+ =1，与点P(x0,y 0)对应的极线方程为0 + 0 =1 ；a b a bx y x 0x y 0y(3) 对于双曲线 a -b =1，与点 P(x 0,y 0)对应的极线方程为 a 0 -b 0 =1 ；(4) 对于抛物线 y =2px ，与点 P(x 0,y 0) 对应的极线方程为 y 0y=p(x 0+x) ； 性质 一般地,有如下性质 [焦．点．所．在．区．域．为．曲．线．内．部． ]: ① 若极点 P 在曲线С上,则极线 L 是曲线С在P 点的切线；② 若极点 P 在曲线С外,则极线 L 是过极点 P 作曲线С的两条切线的切点连线；③ 若极点 P 在曲线С内,则极线 L 在曲线С外且与以极点 P 为中点的弦平行 [仅是 斜率相 等 ]( 若是 圆 , 则此时中 点 弦的 方程 为(x 0-a)(x-a)+(y 0-b)(y-b)=x 0x y 0y x 0 y 0；若是椭圆,则此时中点弦的方程为 a x x +b y y =x a +y bx 0x y 0y x 0 y 0双曲线,则此时中点弦的方程为 a x0x -b y0y =x a 0 -y b 0 ；若是抛物线 ,则此时中点弦的 方程为 y 0y-p(x 0+x)=y 0 -2px 0) ；(x 0-a) +(y 0-b) 若是④当P(x0,y 0)为圆锥曲线的焦点F(c,0) 时，极线恰为该圆锥曲线的准线．．；⑤极点极线的对偶性:Ⅰ.已知点P和直线L是关于曲线С的一对极点和极线,则L上任一点Pn对应的极线Ln必过点P,反之亦然,任意过点P的直线Ln对应的极点Pn必在直线L上[图．Ⅱ.过点P作曲线C的两条割线L1、L2，L1交曲线C于AB，L2交曲线C于MN，则直线AM、BN的交点T，直线AN、BM的交点S必都落在点P 关于曲线C的极线L 上[ 图．中．点．P．与．直．线．S．．T是．一．对．极．点．极．线．；．点．T．与．直．线．S．．P是．一．对．极．点．极．线．] ；即OP = OR OROQⅢ. 点 P 是曲线 C 的极点，它对应的极线为 L ，则有 :1）若C 为椭圆或双曲线，O 是C 的中心，直线 OP 交C 与R ，交L 于Q ，则OP?OQ=OR如图中学数学中极点与极线知识的现状与应用虽然中学数学中没有提到极点极线,但事实上,它的身影随处可见,只是没有点破而已.教材内改名换姓,“视”而不“见” .由④可知椭圆x a +y b =1的焦点的极a线方程为: x= . 焦点与准线是圆锥曲线一章中的核心内容, 它揭示了圆锥曲线c的统一定义, 更是高考的必考知识点. 正是因为它太常见了, 反而往往使我们“视”而不“见” .圆锥曲线基础必备1、长轴短轴与焦距，形似勾股弦定理长轴=2“，短轴= 2b,焦距= 2c.则：a2 =b2 -^c2 1、准线方程准焦距.〃方、"方涂以r..& 0・ 刁2sm —cos — sm 0_ 2 2 1 +cos0 2 cos 2—2 & 所以：椭圆的焦点三角形的面积为S 胚恶=b tail-.4.焦三角形计面积"半角正切進乘焦三角形：以椭圆的两个焦点巧・耳为顶点，另一个顶点」 在椭圆上的三角形称为焦三角形•半角是指—Z 与P 巧的一半. 则焦三角形的面积为： 证明：设阿| =小|昭| = S 由余弦定理:m 2 +n 2 - 2mn cos^= 4c 2=4a即：-2mn - = 2mn - 4b 2,故: Sgf =-m n sin0 =-』+ cos& l + cos0又:0 =tan —三、椭圆的相关公式 切线平分焦周角, 切点连线求方程, 弦与中线斜率积, 细看中点弦方程,称为弦切角定理① 极线屯理须牢记② 准线去除准焦距③ 恰似弦中点轨迹④艮卩：2D = (1+ cos0)mn .1、 切线平分焦周角，称为弦切角定理弦切角定理：切线平分椭圆焦周角的外角，平分双 曲线的焦周角.焦周角是焦点三角形中，焦距所对应的角.弦切角是指椭圆的弦与其切线相交于椭圆上时它 们的夹角，当弦为焦点弦时（过焦点的弦），那么切 线是两个焦点弦的角平 分线.第6页2. 切点连线求方程，圾线定理须牢记若旳（X05）在椭圆卡+$ = 1外，则过昨作椭圆的两 条切线，切点、为P 』,巧，则点耳和切点弦马•勺分别称 为椭圆的极点和极线.切点弦耳乃的直线方程即极线方程是笫？页3、弦与中线斜■率积.准线去涂准焦距|弦指椭圆内的一弦•中线指弦AB 的中点M 与 原点O 的连线，即2AB 得中线•这两条直线的斜率的VY - Q 2於乘积，等于准线距离去除准焦^p= — .其k k_ p 结杲是：0M = T =~V第8页（称为极线定理）4、细看中点弦方程，恰似弦中点、轨迹|中点、弦AB 的方程:在椭圆中，若弦的中点、为弦仙称为中点弦，则中点弦的方程就是弦中点M 的轨迹方程：在椭圆中，过椭圆内点 p 皿、m 的弦AB , 其中点、M 的方程就是 S . y o y … /( y 2. 一7*+矿二正+歹，仍为椭圆.这两个方程有些相似，要擦亮眼睛，千万不要搞 混了.第9页是直线方程.圆锥曲线必背口诀（红字为口诀）-双曲线一、双曲线定义双曲线有四定义.差比交线反比何1、定义1:（差）平面内，到两个定点唇码的距离之差的绝对值为定值2“（小于这两个定点间的距离冈砂）的点的轨迹称为双曲线。
极点与极线法解高中圆锥曲线
极点与极线背景下的高考试题极点与极线是高等几何中的重要概念，当然不是《高中数学课程标准》规定的学习内容，也不属于高考考查的范围，但由于极点与极线是圆锥曲线的一种基本特征，因此在高考试题中必然会有所反映，自然也会成为高考试题的命题背景.1.从几何角度看极点与极线定义1 如图1，设P 是不在圆锥曲线上的一点，过P 点引两条割线依次交圆锥曲线于四点,,,E F G H ，连接,EH FG交于N ，连接,EG FH 交于M ，则直线MN 为点P 对应的极线. 若P 为圆锥曲线上的点，则过P 点的切线即为极线.由图1同理可知， PM 为点N 对应的极线，PN 为点M 所对应的极线.因而将MNP 称为自极三点形.设直线MN 交圆锥曲线 于点,A B 两点，则,PA PB 恰为圆锥曲线的两条切线.定理1 (1)当P 在圆锥曲线Γ上时，则点P 的极线是曲线Γ在P 点处的切线；(2)当P 在Γ外时，过点P 作Γ的两条切线，设其切点分别为,A B ，则点P 的极线是直线AB (即切点弦所在的直线)；(3) 当P 在Γ内时，过点P 任作一割线交Γ于,A B ，设Γ在,A B 处的切线交于点Q ，则点P 的极线是动点Q 的轨迹.定理2 如图2，设点P 关于圆锥曲线Γ的极线为l ，过点P 任作一割线交Γ于,A B ，交l 于Q ，则PA PBAQ BQ= ①；反之，若有①成立，则称点,P Q 调和分割线段AB ，或称点P 与Q 关于Γ调和共轭，或称点P (或点Q )关于圆锥曲线 Γ的调和共轭点为点Q (或点P ).点P 关于圆锥曲线Γ的调和共轭点是一条直线，这条直线就是点P 的极线.推论1 如图2，设点P 关于圆锥曲线Γ的调和共轭 点为点Q ，则有211PQ PA PB =+ ②；反之，若有②成立， 则点P 与Q 关于Γ调和共轭. 可以证明①与②是等价的.事实上，由①有11AQ BQ PQ PA PB PQ PQ PQ PA PB PA PB PA PB --=⇒=⇒-=-11()2PQ PA PB ⇒⋅+= 211PQ PA PB⇒=+.特别地，我们还有推论2 如图3，设点P 关于有心圆锥曲线Γ(设其中心为O )的调和共轭点为点Q ，PQ 连线经过圆锥曲线的中心，则有2OR OP OQ =⋅ ，反之若有此式成立，则点P 与Q 关于Γ调和共轭.证明：设直线PQ 与Γ的另一交点为R '，则PR PR OP OR OP ORRQ R Q OR OQ OR OQ '-+=⇒='-+，化简图1图2即可得2OR OP OQ =⋅.反之由此式可推出PR PR RQ R Q'='，即点P 与Q 关于Γ调和共轭. 推论3 如图4，,A B 圆锥曲线Γ的一条 对称轴l 上的两点(不在Γ上)，若,A B 关于Γ调 和共轭，过B 任作Γ的一条割线，交Γ于,P Q 两点，则PAB QAB ∠=∠.证明：因Γ关于直线l 对称，故在Γ上存在,P Q 的对称点,P Q ''.若P '与Q 重合，则Q '与P也重合，此时,P Q 关于l 对称，有PAB QAB ∠=∠；若P '与Q 不重合，则Q '与P 也不重合，由于,A B关于Γ调和共轭，故,A B 为Γ上完全四点形PQ QP ''的对边交点，即Q '在PA 上，故,AP AQ 关于直线l 对称，也有PAB QAB ∠=∠.定理3 (配极原则)点P 关于圆锥曲线Γ的极线p 经过点Q ⇔点Q 关于Γ的极线q 经过点P ；直线p 关于Γ的极点P 在直线q 上⇔直线q 关于Γ的极点Q 在直线p 上.由此可知，共线点的极线必共点；共点线的极点必共线. 以上未加证明的定理，可参阅有关高等几何教材，如【1】，其中定理1的初等证法可参阅文【2】.2.从代数角度看极点与极线定义2 已知圆锥曲线22:220Ax Cy Dx Ey F Γ++++=，则称点00(,)P x y 和直线0000:()()0l Ax x Cy y D x x E y y F ++++++=是圆锥曲线Γ的一对极点和极线.事实上，在圆锥曲线方程中，以0x x 替换2x ，以02x x +替换x ，以0y y 替换2y ，以02y y+替换y 即可得到点00(,)P x y 的极线方程. 特别地：(1)对于椭圆22221x y a b +=，与点00(,)P x y 对应的极线方程为00221x x y y a b+=；(2)对于双曲线22221x y a b -=，与点00(,)P x y 对应的极线方程为00221x x y y a b -=；(3)对于抛物线22y px =，与点00(,)P x y 对应的极线方程为00()y y p x x =+. (4)如果圆锥曲线是椭圆22221x y a b+=，当00(,)P x y 为其焦点(,0)F c 时，极线恰为椭圆的准线；如果圆锥曲线是双曲线22221x y a b-=，当00(,)P x y 为其焦点(,0)F c 时，极线恰为双曲线的准线；如果圆锥曲线是抛物线22y px =，当00(,)P x y 为其焦点(,0)2p F 时，极线恰为抛物线的准线.3.从极点与极线角度看圆锥曲线试题图4 R【例1】(2010江苏卷文理18)在平面直角坐标系xOy 中，如图，已知椭圆15922=+y x 的左右顶点为,A B ，右焦点为F ．设过点(,)T t m 的直线,TA TB 与此椭圆分别交于点1122(,),(,)M x y N x y ，其中0m >，1200y y ><，．(1)设动点P 满足422=-PB PF ，求点P 的轨迹；(2)设12123x x ==，，求点T 的坐标；(3)设9=t ，求证：直线MN 必过x 轴上的一定点（其坐标与m 无关）．分析与解：前面两问比较简单，这里从略. 对于(3)，当9=t 时，T 点坐标为(9,)m ，连MN ，设直线AB 与MN 的交点为K ，根据 极点与极线的定义可知，点T 对应的极线经过K ， 又点T 对应的极线方程为9195x m y⋅⋅+=，即 15m yx ⋅+=，此直线恒过x 轴上的定点K (1,0)， 从而直线MN 也恒过定点K (1,0). 【例2】 (2008安徽卷理22)设椭圆2222:1(0)x y C a b a b+=>>过点M ，且左焦点为1(F .(1)求椭圆C 的方程；(2)当过点(4,1)P 的动直线l 与椭圆C 交于两个不同的点,A B 时，在线段AB 上取点Q ，满足AP QB AQ PB ⋅=⋅，证明点Q分析与解：(1)易求得答案22142x y +=. (2)由条件可有PA PBAQ BQ=，说明点,P Q 关于 圆锥曲线C 调和共轭.根据定理2，点Q 的轨迹就是点P 对应的极线，即41142x y ⋅⋅+=，化简得220x y +-=. 故点Q 总在定直线220x y +-=上.【例3】( 1995全国卷理26)已知椭圆22:12416x y C +=，直线:1128x y l +=，P 是l 上一点，射线OP 交椭圆于点R ，又点Q 在OP 上且满足2OQ OP OR ⋅=，当点P 在l 上移动时，求点Q 的轨迹方程.,并说明轨迹是什么曲线.分析与解：由条件知2OR OP OQ =⋅可知点,P Q 关于圆锥曲线C 调和共轭，而点Q 可看作是点P 的极线与直线OP 的交点.设(12,88)P t t -，则与P 对应的极线方程为12(88)12416t x t y⋅-⋅+=，化简得 (1)2tx t y +-= ③图5,)m图6x又直线OP 的方程为8812ty x t-=，化简得 223ty x t-=④ 解由③④联立方程组得22654244542t x t t tx t t ⎧=⎪⎪-+⎨-⎪=⎪-+⎩，消去t 得222346x y x y +=+，可化为22(1)(1)15523x y --+=(,x y 不同时为0)，故点Q 的轨迹是以(1,1)为中心，，且长轴平行于x 轴的椭圆，但需去掉坐标原点.【例4】(2006年全国卷II 理21)已知抛物线24x y = 的焦点为F ，,A B 是抛物线上的两动点，且AF FB λ=(0)λ>，过,A B 两点分别作抛物线的切线，并设其交点为P . (1)证明FP AB ⋅为定值；(2)设ABP ∆的面积为S ，写出()S f λ=的表达式， 并求S 的最小值.分析与解：(1)显然，点P 的极线为AB ，故可设点0(,1)P x -，再设1122(,),(,)A x y B x y ，,,F A B 三点对应的极线方程分别为1y =-，112()x x y y =+，222()x x y y =+，由于,,A B F 三点共线，故相应的三极线共点于0(,1)P x -，将1y =-代入后面两个极线方程得1012022(1)2(1)x x y x x y =-⎧⎨=-⎩，两式相减得12012()2()x x x y y -=-.又02121(,2),(,)FP x AB x x y y =-=--，故02121()2()0FP AB x x x y y ⋅=---=. (2)设AB 的方程为1y kx =+，与抛物线的极线方程002()x x y y =+对比可知直线AB对应的极点为(2,1)P k -，把1y kx =+代入24x y =并由弦长公式得24(1)AB k =+，所以212(12ABP S AB FP k ∆==+. 显然，当0k =时，S 取最小值4. 【例5】(2005江西卷理22)设抛物线2:C y x = 的焦点为F ，动点P 在直线:20l x y --=上运动，过P 作抛物线的两条切线,PA PB ，且与抛物线分别相切于,A B 两点. (1)求APB ∆的重心G 的轨迹方程； (2)证明PFA PFB ∠=∠.分析与解：(1)设点001122(,),(,),(,)P x y A x y B x y ， 与002y y x x +=对比可知直线:20l x y --=对应的极点为1(,2)2，P 为直线l 上的动点，则点P 对应的极线AB 必恒过点1(,2)2.图8图9设1:2()2AB y k x -=-，可化为2222k y k x +-=，故直线AB 对应的极点为(,2)22k k P -，将直线AB 的方程代入抛物线方程得2202kx kx -+-=，由此得2121212,(1)44x x k y y k x x k k +=+=+-+=-+，APB ∆的重心G 的轨迹方程为122212223322422222333k k x x k k x k k k y y k k k y ⎧+++⎪===⎪⎪⎨⎪++--++--+⎪===⎪⎩，消去k 即得 21(42)3y x x =-+.(2)设221122(,),(,)A x x B x x ，由(1)知1212,22k x x k x x +==-，又1(0,)4F ，由(1)知(,2)22k k P -，即1212(,)2x x P x x +，所以2111(,)4FA x x =-，12121(,)24x x FP x x +=-，2221(,)4FB x x =-.221211************111111()()()()244444cos 11()()4x x x x x x x x x x x FP FA PFA FP FA FP FP x FP x x ++--+++⋅∠====⋅++-.同理1214cos x x FP FB PFB FP FB FP+⋅∠==⋅. 所以有PFA PFB ∠=∠.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆锥曲线的极点与极线在高考中的应用定勇（省宁国中学 ，242300）圆锥曲线的极点与极线理论在高考中应用较多，原因有二：其一，有高等数学背景，结论非常完美；其二，运用高中知识解决问题，能够考查学生思维、计算多方面能力.文[1]给出了两个较为简洁的结论：命题1 椭圆12222=+b y a x ，点()00,y x P 对应的极线12020=+b y y a x x .双曲线12222=-b y a x ，点()00,y x P 对应的极线12020=-by y a x x .抛物线px y 22=，点()00,y x P 对应的极线000=+-px y y px .命题 2圆锥曲线中极线共点于P ，则这些极线相应的极点共线于点P 相应的极线.反之亦然.称为极点与相应极线对偶性.以上结论在文[2]中有证明.如图给出椭圆的极点与对应极线的简图：题1、（2010文15）.已知椭圆12:22=+y x C 的两焦点为12,F F ,点()00,y x P 满足2200012x y <+<,则|1PF |+2PF |的取值围为_______，直线1200=+y y x x 与椭圆C 的公共点个数_____.P 在椭圆内 P 在椭圆外解析：第一个问题，依题意知，点P 在椭圆部.画出图形，由数形结合可得围为[)22,2.第二个问题，其实是非常容易做错的题目.因为()00,y x P 在椭圆12:22=+y x C 的部，所以很多学生误以为直线与椭圆一定有两个交点，但直线1200=+y y xx 并不经过()00,y x P .还有学生看到1200=+y y xx 这样的结构，认为是切线，所以判断有一个公共点.事实上，1200=+y y x x 是()00,y x P 对应的极线，()00,y x P 在椭圆12:22=+y x C 的部，由命题2画出相应极线，此直线与椭圆不可能有交点，故交点数为0个.如果能够用极点与极线理论，本题能够快速解决.而常规方法只能联立方程用判别式判断了.题2、（2010文21）已知以原点O 为中心，(5,0)F 为右焦点的双曲线C 的离心率52e =. （Ⅰ）求双曲线C 的标准方程及其渐近线方程；（Ⅱ）如题图，已知过点11(,)M x y 的直线1l ：1144x x y y +=与过点22(,)N x y （其中21x x ≠）的直线2l ：2244x x y y +=的交点E 在双曲线C 上，直线MN 与双曲线的两条渐近线分别交于G 、H 两点，求OH OG ⋅的值.解析：（I ）C 的标准方程为.1422=-y x C 的渐近线方程为.21x y ±= （II ）如图，直线44:11`=+y y x x l 和44:122=+y y x x l 上显然是椭圆4422=+y x 的两条切线，由题意点),(E E y x E 在直线44:11`=+y y x x l 和44:122=+y y x x l 上，MN 即是由E 点生成的椭圆的极线.因此直线MN 的方程为.44=+y y x x E EMN 的方程求出后剩下工作属常规计算.设G 、H 分别是直线MN 与渐近线02=-y x 及02=+y x 的交点，由方程组⎩⎨⎧=+=+⎩⎨⎧=-=+,02,4402,44y x y y x x y x y y x x E E E E 及 解得.2224,22,24⎪⎪⎩⎪⎪⎨⎧--=-=⎪⎪⎩⎪⎪⎨⎧+=+=E E N E E N E E C EE C y x y y x x y x y y x x 故44222222E E E E E E E E OG OG x y x y x y x y ⋅=⋅-⋅+-+-.41222EE y x -= 因为点E 在双曲线.44,142222=-=-E E y x y x 有上所以2212 3.4E E OG OH x y ⋅==- 分析：如果是常规方法求直线MN 的方程，只能是观察：由题意点),(E E y x E 在直线44:11`=+y y x x l 和44:122=+y y x x l 上，因此有E E E x x y y x x 211,44=+442=+E y y 故点M 、N 均在直线44=+y y x x E E 上，因此直线MN 的方程为.44=+y y x x E E 应该说很难观察，所以很多学生只能不了了之.题3、（201018）、在平面直角坐标系xoy 中，如图，已知椭圆15922=+y x 的左、右顶点为A 、B ，右焦点为F.设过点T （m t ,）的直线TA 、TB 与椭圆分别交于点M ),(11y x 、),(22y x N ，其中m>0,0,021<>y y .（Ⅰ）设动点P 满足422=-PB PF ,求点P 的轨迹； （Ⅱ）设31,221==x x ，求点T 的坐标； （Ⅲ）设9=t ,求证：直线MN 必过x 轴上的一定点（其坐标与m 无关）.解析：（Ⅰ）（Ⅱ）很简单，略.（Ⅲ）我们先看看常规做法：点T 的坐标为(9,)m直线)3(12:+=x my TA ，与椭圆联立得)8040,80)80(3(222++--m m m M直线)3(6:-=x my TB ，与椭圆联立得)2020,20)20(3(222+-+-m m m N 当12x x ≠时，直线MN 方程为：22222222220)20(380)80(320)20(3202080402020m m m m m m x m m m m m m y +--+-+--=+++++ 令0y =，解得：1x =.此时必过点D （1，0）；当12x x =时，直线MN 方程为：1x =，与x 轴交点为D （1，0）. 所以直线MN 必过x 轴上的一定点D （1，0）.分析：怎么样？目瞪口呆吧.应该说，一点也不难，但是很难算对.如果知道点T 的坐标为()m ,9，事实上T 的轨迹是9=x ，可以看成是一条极线：15091=+y x ，所以它一定过定点D （1，0）.题4、已知椭圆C的离心率e =，长轴的左右端点分别为()1A 2,0-，()2A 2,0。
（Ⅰ）求椭圆C 的方程；（Ⅱ）设直线x my 1=+与椭圆C 交于P 、Q 两点，直线1A P 与2A Q 交于点S 。
试问：当m 变化时，点S 是否恒在一条定直线上？若是，请写出这条直线方程，并证明你的结论；若不是，请说明理由。
解法一：（Ⅰ）设椭圆C 的方程为()2222x y 1a b 0a b +=>>。
…………………1分∵a 2=，c e a ==c =222b a c 1=-=。
……………… 4分∴椭圆C 的方程为222x y 14+=。
……………………………………… 5分（Ⅱ）取m 0,=得P ,Q 1,⎛⎛ ⎝⎭⎝⎭，直线1A P的方程是y =+ 直线2A Q的方程是y =交点为(1S . …………7分,若P 1,,Q ⎛⎛ ⎝⎭⎝⎭，由对称性可知交点为(2S 4,. 若点S 在同一条直线上，则直线只能为:x 4=。
…………………8分以下证明对于任意的m,直线1A P 与直线2A Q 的交点S 均在直线:x 4=上。
事实上，由22x y 14x my 1⎧+=⎪⎨⎪=+⎩得()22my 14y 4,++=即()22m 4y 2my 30++-=， 记()()1122P x ,y ,Q x ,y ，则1212222m 3y y ,y y m 4m 4--+==++。
………… 9分设1A P 与交于点00S (4,y ),由011y y ,42x 2=++得1016y y .x 2=+设2A Q 与交于点00S (4,y ),''由022y y ,42x 2'=--得2022y y .x 2'=- (10)1200126y 2y y y x 2x 2'-=-+-()()()()1221126y my 12y my 3x 2x 2--+=+-()()()1212124my y 6y y x 2x 2-+=+- ()()221212m 12m m 4m 40x 2x 2---++==+-，……12分 ∴00y y '=，即0S 与0S '重合，这说明，当m 变化时，点S 恒在定直线:x 4=上。
13分 解法二：（Ⅱ）取m 0,=得P ,Q 1,⎛⎛ ⎝⎭⎝⎭，直线1A P的方程是y =+直线2A Q的方程是y =交点为(1S . ………………………………………… 7分 取m 1,=得()83P ,,Q 0,155⎛⎫- ⎪⎝⎭，直线1A P 的方程是11y x ,63=+直线2A Q 的方程是1y x 1,2=-交点为()2S 4,1.∴若交点S 在同一条直线上，则直线只能为:x 4=。
……………8分以下证明对于任意的m,直线1A P 与直线2A Q 的交点S 均在直线:x 4=上。
事实上，由22x y 14x my 1⎧+=⎪⎨⎪=+⎩得()22my 14y 4,++=即()22m 4y 2my 30++-=，记()()1122P x ,y ,Q x ,y ，则1212222m 3y y ,y y m 4m 4--+==++。
………………9分 1A P 的方程是()11y y x 2,x 2=++2A Q 的方程是()22yy x 2,x 2=--消去y,得()()1212y yx 2x 2x 2x 2+=-+-… ①以下用分析法证明x 4=时，①式恒成立。
要证明①式恒成立，只需证明12126y 2y ,x 2x 2=+-即证()()12213y my 1y my 3,-=+即证()12122my y 3y y .=+……………… ②∵()1212226m 6m2my y 3y y 0,m 4m 4---+=-=++∴②式恒成立。
这说明，当m 变化时，点S 恒在定直线:x 4=上。
解法三：（Ⅱ）由22x y 14x my 1⎧+=⎪⎨⎪=+⎩得()22my 14y 4,++=即()22m 4y 2my 30++-=。
记()()1122P x ,y ,Q x ,y ，则1212222m 3y y ,y y m 4m 4--+==++。
…………… 6分 1A P 的方程是()11y y x 2,x 2=++2A Q 的方程是()22yy x 2,x 2=-- ……7分由()()1122y y x 2,x 2y y x 2,x 2⎧=+⎪+⎪⎨⎪=-⎪-⎩得()()1212y y x 2x 2,x 2x 2+=-+- …………………9分即()()()()21122112y x 2y x 2x 2y x 2y x 2++-=+--()()()()21122112y my 3y my 12y my 3y my 1++-=+--1221212my y 3y y 23y y +-=+ 112211232m 2m 3y y m 4m 424.2m 3y y m 4--⎛⎫+-- ⎪++⎝⎭==-⎛⎫-+ ⎪+⎝⎭………………………………12分这说明，当m 变化时，点S 恒在定直线:x 4=上。