1定积分的概念
高数定积分定义

高数定积分定义
定积分是微积分中的一个重要概念,它是对函数在一定区间上的
积分结果的确定。
在数学中,积分是微积分中的一种基本概念,定义
了一种反向操作,即由导数得到原函数。
定积分的定义是指在函数y=f(x)的x轴某一区间[a,b]上,将其分割成许多小的矩形,并将这些矩形的面积分别求出。
当分割的小矩形
数趋向于无穷大时,这些小矩形组成的面积总和即为该函数在区间[a, b]上的定积分,用符号∫abf(x)dx表示。
其中dx代表自变量的微元,f(x)代表被积函数,而a和b是积分
的上下限。
上述式子也可以看作是在曲线y=f(x)与x轴之间的面积之
积分。
为了方便计算,往往将上述区间分割成等分的若干小区间,其中
小区间的个数记作n,区间长为Δx。
于是有Δx=(b-a)/n,而小矩形
面积为f(xi)Δx,其中xi为小区间的中点。
将这些面积相加,即可得到该函数在区间[a, b]上的近似定积分。
在极限n趋向于无穷大的情况下,上述近似定积分将趋近于函数
在区间[a, b]上的定积分,即∫abf(x)dx。
因此,定积分又可以描述为曲线y=f(x)在区间[a, b]上与x轴之
间面积大小的确定。
而由于定积分的值只与积分区间及被积函数有关,因此在定积分的计算中,被积函数函数的表达式及积分区间的范围就
成为了最为重要的关键。
定积分在实际问题中的应用非常广泛,例如可以用于求曲线与坐标轴的面积,求函数在某个区间上的平均值,以及求物体在某一时间间隔内的位移等问题。
同时,定积分也是微积分中重要的积分概念之一,有较高的理论和实际应用价值。
1 定积分概念

.1 定积分概念定义设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点,把区间[a,b]分成n个小区间,设有常数I,如果对于任意给定的正数ε,总存在一个正数δ,使得对于区间[a,b]的任何分法,不论在中怎样取法,只要,总有成立,则称I是f(x)在区间[a,b]上的定积分,记作。
接下来的问题是:函数f(x)在[a,b]上满足怎样的条件,f(x)在[a,b]上一定可积?以下给出两个充分条件。
定理1设f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。
定理2设f(x)在区间[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
如果我们对面积赋以正负号,在x轴上方的图形面积赋以正号,在x轴下方的图形面积赋以负号,则在一般情形下,定积分的几何意义为:它是介于x 轴、函数f(x)的图形及两条直线x = a、x = b之间的各部分面积的代数和。
.2 牛顿-莱步尼兹公式及实例定理如果函数F(x)是连续函数f(x)在区间[a,b]上的一个原函数,则。
(1)证已知函数F(x)是连续函数f(x)的一个原函数,又根据前面的定理知道,积分上限的函数也是f(x)的一个原函数。
于是这两个原函数之差为某个常数(第四章第一节),即。
(2)在上式中令x = a,得。
又由Φ (x)的定义式及上节定积分的补充规定知Φ (a) = 0,因此,C = F(a)。
以F(a)代入(2)式中的C,以代入(2)式中的Φ (x),可得,在上式中令x = b,就得到所要证明的公式(1) 。
由积分性质知,(1)式对a>b的情形同样成立。
为方便起见,以后把F(b) – F(a)记成。
公式(1)叫做牛顿(Newton)-莱步尼兹(Leibniz)公式,它给定积分提供了一种有效而简便的计算方法,也称为微积分基本公式。
例1 计算定积分。
解。
例2计算。
解。
例3计算。
解。
例4计算正弦曲线y = sinx在[0, ]上与x轴所围成的平面图形的面积。
1 定积分的概念
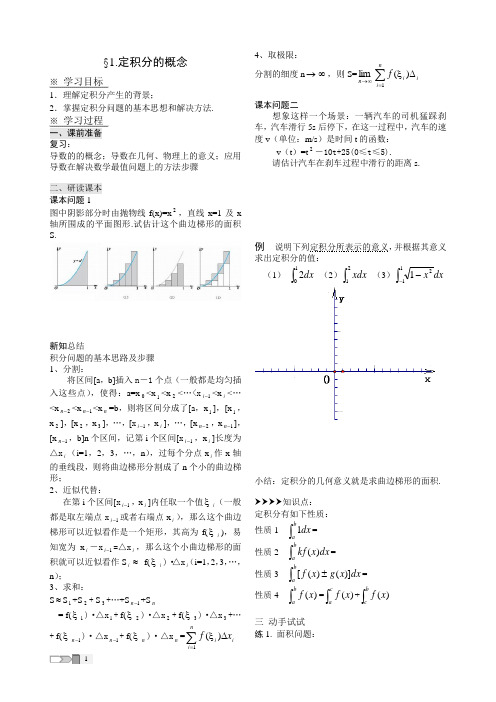
§1.定积分的概念※ 学习目标1.理解定积分产生的背景;2.掌握定积分问题的基本思想和解决方法. ※ 学习过程 一、课前准备 复习:导数的的概念;导数在几何、物理上的意义;应用导数在解决数学最值问题上的方法步骤二、研读课本 课本问题1图中阴影部分时由抛物线f(x)=x 2,直线x=1及x 轴所围成的平面图形.试估计这个曲边梯形的面积S.新知总结积分问题的基本思路及步骤 1、分割:将区间[a ,b]插入n -1个点(一般都是均匀插入这些点),使得:a=x 0<x 1<x 2<…<x 1-i <x i <…<x 2-n <x 1-n <x n =b ,则将区间分成了[a ,x 1],[x 1,x 2],[x 2,x 3],…,[x 1-i ,x i ],…,[x 2-n ,x 1-n ],[x 1-n ,b]n 个区间,记第i 个区间[x 1-i ,x i ]长度为△x i (i=1,2,3,…,n ),过每个分点x i 作x 轴的垂线段,则将曲边梯形分割成了n 个小的曲边梯形;2、近似代替:在第i 个区间[x 1-i ,x i ]内任取一个值ξi (一般都是取左端点x 1-i 或者右端点x i ),那么这个曲边梯形可以近似看作是一个矩形,其高为f(ξi ),易知宽为x i -x 1-i =△x i ,那么这个小曲边梯形的面积就可以近似看作S i ≈ f(ξi )·△x i (i=1,2,3,…,n );3、求和:S ≈S 1+S 2+ S 3+…+S 1-n +S n = f(ξ1)·△x 1+ f(ξ2)·△x 2+ f(ξ3)·△x 3+…+ f(ξ1-n )·△x 1-n + f(ξn )·△x n =∑=∆ξni i i x f 1)(4、取极限:分割的细度n →∞,则S=∞→n lim∑=∆ξni iif 1)(课本问题二想象这样一个场景:一辆汽车的司机猛踩刹车,汽车滑行5s 后停下,在这一过程中,汽车的速度v (单位:m/s )是时间t 的函数:v (t )=t 2-10t+25(0≤t ≤5).请估计汽车在刹车过程中滑行的距离s.例 说明下列定积分所表示的意义,并根据其意义求出定积分的值: (1)⎰12dx (2)⎰21xdx (3)⎰--1121dx x小结:定积分的几何意义就是求曲边梯形的面积.知识点: 定积分有如下性质:性质1⎰ba dx 1=性质2 ⎰b a dx x kf )(=性质3 ⎰±b a dx x g x f )]()([=性质4 ⎰b ax f )(=⎰cax f )(+⎰bcx f )(三 动手试试 练1. 面积问题:设S 表示由曲线y=x ,直线x=1以及x 轴所围成平面图形的面积.(1)画出该平面图形;(2)试估计该平面图形的面积,并写出估计值的误差.练2. 做功问题一根弹性系数为0.4N/cm 的弹簧,其拉力F 随着弹簧拉伸的长度x 的变化而不断变化,根据胡克定律可知:F=F(x)=0.4x.如图所示,弹簧的一端固定在墙上,另一端固定在物体上,在不考虑摩擦力的情况下物体在力F 作用下匀速移动,从原来位置 移动10cm.估计这一过程中拉力所做的功W.练3.用图形表示下列定积分: (1)⎰102dx x (2)⎰21ln xdx (3)⎰-11dx e x※ 总结提升 学习小结1. 积分问题的基本思路及步骤:1、分割;2、近似代替;3、求和;4取极限. 2. 积分的几何意义就是求曲边梯形的面积. ※ 课后练习:(1-4选择题)1.利用定积分的几何意义求下列定积分(1)⎰212xdx (2)⎰-224dx x(3)⎰-11dx x2.已知⎰10dx e x=e ,⎰102dx x ,求下列定积分:(1)⎰+12)(dx x e x(2)⎰-12)2(dx x e x3.如果汽车在某一段时间内的速度函数为v (t )=20t ,0≤t ≤5,试估计汽车在这段时间内走过的距离,并写出估计值的误差.4.设力F (单位:N )的方向与抛物线运动的方向一致,力的大小随着物体走过的路程x (单位:m )而变化,可以表示为F=F(x)=x11,估计力F 在0—10m 这段路程内所做的功,要求误差不超过1N ·m.。
1.5.3《定积分的概念》课件-(1)

5 S v(t )dt (t 2)dt 0 0 3
1 1 2
O
1 1 2 3 j n - 1
t
n n n n
n
注:
1 .当
f ( )x 的极限存在时,其极限值仅与被积函数 f(x) 及积分区间 [a,b] 有关,而与区间 a, b 的分法及
i 1 i
n
i
y y=f ( x)
b
c
b
f (x)dx。
f )( dx x)dx f (x f )( dx x) dx f (x )f dx (x f )( dx x dx f (。 x)dx a fa(x a)。 a a a c c c
b
b
c
c
b
b
b
c
b
f (x)dx。
0
y
f(x)=x2
y
f(x)=(x-1)2-1
f(x)=x2
y
f(x)=1
y
0
a
x
-1 0
2
x
a
0
b x
-1 0
2 x
①
②
③
2
④
(2)在图②中,被积函数 f ( x) x 在[1 , 2] 解: 上连续,且f ( x) 0, 根据定积分的几何意 义,可得阴影部分的面 积为 A 2 x 2 dx
f ( x )dx f ( x )dx f ( x )dx
a c
c
b
y
y f ( x)
O
a
c1 a
C
b x
b c2
b
a
f ( x )dx f ( x )dx f ( x )dx f ( x )dx
1 定积分的概念

高等数学(上)
定理3 设函数 f ( x ) 在区间 [a , b] 上有界,
且只有有限个间断点,则 f ( x ) 在
区间[a , b]上可积.
定理4 设函数
则
f ( x ) 在区间 [a , b] 上有界且单调,
2
n
2
1 n 2 3 i n i 1
1 n( n 1)(2n 1) 3 n 6
1 1 1 1 2 6 n n
1 因为 max{x1 , x2 , xn } n
高等数学(上)
所以 0 n ,
故有
[a , b ]
上可积。
f ( x)
在区间
例1 设 R, 则
b
a
dx (b a ).
高等数学(上)
例2 利用定义计算定积分
0 x
1
2
dx .
解 由于 f (x) = x2 在 [ 0 , 1 ] 上连续 , 因此可积 .
所以取如下划分:
将
[0,1] 分成 n 等分,分点为
0
1
xdx
n n n (2) lim 2 2 2 2 2 n n 1 n 2 n n n 1 dx 1 1 lim 2 n 0 1 x2 n i i 1 1 n
高等数学(上)
用和式极限表示定积分: ba ba 2(b a ) n(b a ) lim ) f (a ) f (a ) f (a n n n n n
i b a lim f a (b a ) n n n i 1 b 1 n i f a (b a ) f ( x )dx n i 1 n a
定积分的概念和基本思想

定积分的概念和基本思想一、定积分的概念和基本思想1、定积分的概念一般地,如果函数$f(x)$在区间$[a,b]$上连续,用分点$a=x_0<x_l<$$\cdots<$$x_{i-l}<x_i<$S\cdots<$$x_n=b$将区间$ la, b] S等分成$n$ 个小区间,在每个小区间$[x_{iT},x_i]$上任取一点$ C _i (i=l, 2, \cdots, n)$,作和式$\underset{i=l}{\overset{n}{\sum}}f(4 _i)Ax=$$\underset{i=l}{\overset {n} {\sum ))\frac(b-a} {n}f(C_i)$,当Sn-8$时,上述和式无限接近某个常数,这个常数叫做函数$f (x) $在区间$[a,b]$上的定积分,记作$\int_{a} * (b}f (x) (\rm d}x$,即$\int_{a}*{b}f(x){\rmd}x=$$\underset(n~* °°}{\lim}\underset{i=l}{\overset{n}{\sum}}\frac{b_ a}{n}f(g_i)$,这里,$a$与$b$分别叫做积分下限与积分上限,区间$[a,b]$叫做积分区间,函数$f(x)$叫做被积函数,$x$叫做积分变量,$f(x) {\rm d}x$叫做被积式。
(1)定积分$\int_{a}*{b}f(x) {\rm d}x$不是一个函数式,而是一个数值(极限值),它只与被积函数以及积分区间有关,而与积分变量无关,即$\int_{a}*{b}f(x){\rm d}x=$S\int_{a}*{b}f(t)(\rm d}t=$$\int_{a}*{b}f(u){\rm d}u$o(2)定义中区间的分法和$ g _i$的取法是任意的。
2、定积分的基本思想定积分的基本思想就是以直代曲,即求曲边梯形的而积时,将曲边梯形分割成一系列的小曲边梯形,用小矩形近似代替,利用矩形面积和逼近的思想方法求出曲边梯形的面积。
定积分的定义

定积分的定义
定积分是积分的一种,是函数f()在区间[a,b]上的积分和的极限。
这里应注意定积分与不定积分之间的关系:若定积分存在,则它是一个具体的数值(曲边梯形的面积),而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系,一个函数,可以存在不定积分,而不存在定积分,也可以存在定积分,而不存在不定积分。
定积分的分类
不定积分
即已知导数求原函数。
若F’()=f(),那么[F()+C]'=f(),(C∈R,c属于常数)也就是说,把f()积分,不一定能得到F(),因为F()+C的导数也是f()(C是任意常数)。
所以f()积分的结果有无数个,是不确定的。
所以一律用F()+C代替,这就称为不定积分。
即如果一个导数有原函数,那么它就有无限多个原函数。
定积分
定积分就是求函数f()在区间[a,b]中的图像包围的面积。
即由
y=0,=a,=b,y=f()所围成图形的面积。
这个图形称为曲边梯形,特例是曲边三角形。
定积分的常用积分法
换元积分法
如果f()∈c([a,b]);=ψ(t)在[a,β]上单值可导;当
a≤t≤β时,a≤ψ(t)≤b,且ψ(a)=a,ψ(β)=b,则∫ba f()d=∫βa f(ψ(t))ψ’(t)dt
定积分的分点问题
定积分是把函数在一些区间上的图象[a,b]分成n份,用平行于y轴
的直线把其分割成无数个矩形,再求当n→+∞时所有这些矩形面积的和。
习惯上,人们用等差级数分点,即相邻两端点的间距Δ是相等的。
但是
必须指出,即使Δ不相等,积分值仍然相同。
定积分的基本概念

定积分的基本概念
一、定积分的基本概念
1.定积分的定义
定积分是指在区间[a,b]中,用函数f(x)的值在x处取的积分,其中x取值于a到b之间的某个点,f(x)的积分称为定积分。
也可以表示为
∫a, bf(x)dx=∫f(x)dx
即:将函数f(x)从x=a到x=b的定积分。
2.定积分的性质
(1)定积分是一种积分的形式,它是在定的一段区间内对某个函数f(x)求积分的形式。
(2)定积分可以表示为:∫f(x)dx=F(b)-F(a),其中F(x)是f(x)的积分函数。
(3)定积分可以表示为:∫a, bf(x)dx=∑[f(x1)+f(x2)+…
+f(xn)],其中x1,x2,…,xn为积分区间[a, b]的各个各点。
(4)定积分是一种表示曲线与坐标轴围成的面积的一种数学工具。
二、定积分的计算
1.定积分的数值计算
数值计算定积分,即把范围[a,b]离散成一定的小段,在每个小段上求f(x)的值,再用这些值进行总和,来求出定积分的近似值。
2.定积分的解析计算
解析计算此类定积分,即首先求出f(x)的积分方程,在范围[a,b]内,求得它的解后,再把范围[a,b]的定积分解析成积分函数F(x)的量对应的差值F(b)-F(a)。
三、定积分的应用
定积分的应用主要是用于求出曲线与坐标轴围成的面积,也可以用于求求解线性微分方程,求解有关动力学问题的时候,还有一些物理的和化学的问题,这些问题用的都是定积分的知识。
1定积分的定义

§積分的意義1.我們把區間[],a b 分割成等長度的n 等分且限制函數值()0f x ≥,黎曼和是圖形下區域面積的近似值﹐而n 趨近於∞的極限值是這區域的面積。
(1) 分割出來的區間可以不等寬﹐定∆j x =1j j x x --(j =1,2,,n ),黎曼和nj 1=Σ*()j f x x ∆﹐取極限=0lim →∆x nj 1=Σ*()j f x j x ∆,x ∆是12,,,n x x x ∆∆∆中的最大值。
但這個方法有時並不方便﹐我們不採用這種不等寬度的分割而回到原來的等寬度分割。
(2) 函數()f x 的值有正有負。
對於上面(2)的放寬是有必要的,至少可運用到多項式或一些我們熟知的函數。
不管是等寬分割或不等寬分割,對任意區間[],a b 上的連續函數﹐極限值0lim →∆x nj 1=Σ*()j f x j x ∆存在且唯一,這時黎曼和的極限值就是這函數的定積分。
2.定積分的定義:若函數()f x 是定義在[],a b 的連續函數﹐設01n a x x x b =<<<=是區間[],a b 的一等寬分割,x ∆=na b -﹐在區間1,j j x x -⎡⎤⎣⎦任取一點*j x ﹐稱為參考點,則()f x 從a 到b 的定積分是∞→n lim nj 1=Σ*()jf x x ∆,而以符號⎰b ax f )(dx 表示。
※(1) 符號⎰是萊布尼茲首先引用的稱為積分符號。
(2) 函數()f x 稱為被積分函數。
(3) a 是積分的下限,b 是積分的上限,當a =b 時﹐積分值規定為0,即⎰b ax f )(dx =0。
規定:⎰b ax f )(dx =-⎰b ax f )(dx 。
(4) 符號dx 本身沒有獨特的意義,⎰b ax f )(dx 代表一極限值,⎰b at f )(dt ﹐⎰b ay f )(dy ﹐⎰b az f )(dz 表示同一定積分。
1的定积分

1的定积分1的定积分是一个重要的数学概念,也是微积分中的一个重要内容。
它是由著名的微积分学家、微分几何学家、力学学家狄拉克首先提出来的。
他发现,积分可以用来表达一个函数的空间变化。
对于同一个函数,不同的被积分区域是不同的,因此,对于不同的被积分区域,可以求出不同的积分值。
1的定积分就是这样一个积分,它可以用来研究函数的变化率,从而确定函数的行为。
1的定积分定义如下:给定一个函数f(x),它的1的定积分为:∫f(x)dx,其中a∈[a,b],这里的定积分被称为狄拉克积分。
1的定积分有一个重要的性质,即它可以有效地表示一个函数在某一个区域内的变化率。
通常情况下,当函数的积分值大于0时,函数在该区域内是增加的,而当函数的积分值小于0时,函数在该区域内是减少的。
1的定积分的计算方法有多种。
其中,最简单的是采用梯形法,即将被积分区域分成若干小矩形,然后分别求其下面的矩形的面积,最后把这些面积相加求和,得出1的定积分的值。
另外,也可以采用更复杂的数值积分方法,如Simpson积分法,Gauss-Kronrod求积法,Trapezoidal积分法等,以计算出更精确的定积分结果。
1的定积分在数学,物理,化学和工程学等多个领域有着广泛的应用。
在物理学中,它可以用来求解微分方程,即求解物理系统中的动态变化;在数学中,它可以用来求解定积分和无穷级数的值;在化学和工程学中,它可以用来求解复杂的物理和化学过程的传递系数等等。
总之,1的定积分在数学、物理、化学和工程等各个领域均有着重要的作用,它可以有效地帮助我们了解函数的变化规律,研究物理和化学等复杂过程的传递系数,甚至可以应用在定积分和无穷级数的求解中。
因此,1的定积分是一个非常重要的概念,并且可以应用到很多不同领域中。
高等数学第五章第一节定积分的概念及性质课件.ppt

二、定积分定义
a x0 x1 x2 xn b ,
任一种分法 任取
总趋于确定的极限 I ,则称此极限 I 为函数
上的定积分,
记作
b
a
f
( x) dx
即
b a
f
(
x)
dx
lim
0
n
i1
f
(
i
)
xi
o
a x1
此时称 f ( x ) 在 [ a , b ] 上可积 .
在区间
i
x xi1xi b
证: f (i ) xi 0
i1
b
n
a
f
( x) d
x
lim
0 i1
f
(i ) xi
0
推论1. 若在 [a , b] 上
则
推论2.
(a b)
证: f (x) f (x) f (x)
b
b
b
a f (x) dx a f (x) dx a f (x) dx
即
b
b
a f (x) dx a f (x) dx
使
因此定理成立.
说明:
• 积分中值定理对
• 可把
b
a f (x) dx f ( )
ba
因
y f (x) y
oa bx
故它是有限个数的平均值概念的推广.
例4. 计算从 0 秒到 T 秒这段时间内自由落体的平均 速度.
解: 已知自由落体速度为
v gt
故所求平均速度
1 1 g T 2 gT
第一节
第五章
定积分的概念及性质
一、定积分问题举例 二、 定积分的定义 三、 定积分的性质
定积分的概念与性质(1)

a = x0 < x1 < x 2 < ⋯ < xi −1 < xi < ⋯ < x n −1 < x n = b
把曲边梯形的底[a,b]分成 个小区间 : [ xi −1 , xi ] 分成n个小区间 把曲边梯形的底 分成 小区间长度记为: ∆x i = x i − x i −1 (i = 1,2,3, ⋯ , n ) 过各分点作垂直于x轴的直线段, 过各分点作垂直于 轴的直线段,把整个曲边梯形分 轴的直线段 个小曲边梯形, 成n个小曲边梯形,其中第 个小曲边梯形的面积记为 ∆ A i 个小曲边梯形 其中第i个小曲边梯形的面积记为 y y=f(x)
确定的极限 I , 我们称这个极限 I 为函数 f ( x ) 上的定积分 定积分, 在区间[a , b ]上的定积分, 记为
积分上限
积分和
∫a f ( x )dx = I = lim ∑ f (ξ i )∆xi λ → 0 i =1
积分 限
b
n
被 积 函 数
被 积 表 达 式
积 分 变 量
[a , b] 积分
∫a f ( x )dx = A
b
曲边梯形的面积
∫a
b
f ( x )dx = − A 曲边梯形的面积
的负值
17
一般情形, 一般情形
∫
b
a
的几何意义为: f ( x)dx 的几何意义为:
它是介于 x 轴、函数 f ( x )及两条直线 x = a , x = b 之间的各部分面积的代 数和. 数和. 轴上方的面积取正号; 在 x 轴上方的面积取正号; 在 x 轴下方的面 积取负号. 积取负号.
1≤i≤n
对上述和式取极限就得物体以变速v(t)从时刻 到时刻 这段 对上述和式取极限就得物体以变速 从时刻a到时刻 从时刻 到时刻b这段 时间内运动的距离s, 时间内运动的距离 即
定积分概念、性质(1)

◆定积分的基本性质
1
b
a
f
x
g
x
dx
b
a
f
x dx
b
a
g
xdx
可推广至有限个函数的代数和的情形。
2
b
a
k
f
x dx
k
b
a
f
x dx
3
b
a
f
x
dx
c
a
f
x dx
b
c
f
x dx
·a ·c ·b ·b ·a ·c
c
b
f
xdx
a
b
f
xdx
c
a
f
xdx
无论 a, b, c 的相对位置如何,(3)式均成立。
dx
2 0
sin
x
cos
x
dx
cos x sin x2 0 1 1 0 2 0
x 1, x 1
8 设
f
x
1 2
x2,
x
1
,求 2 f x dx 0
a
a
因 f (x) f (x) f (x)
性质6(介值定理):设f(x)在[a,b]上可取得最大值M和
最小值m, 于是, 由性质5有
b
m(b a) a f (x)dx M (b a)
几何意义也很明显
性质7 (积分中值定理):若函数f (x)在[a,b]上连续,
则至少存在一点 [a,b]使得
0
(1 3
x3 )
1 0
1 3
变:(2 x 1)dx 1
计算定积分 b f(x)dx a
a 0,b 2, f (x) x3
2013考研第一讲:积分及其等式、不等式问题(数学三)

∫ g(t ) f (t )dt
a
x
∫ g(t )dt
a
x
在 (a , b]上单调增加 ]
解 对于 x ∈(a,b]
F'( x) = g( x) f ( x)∫ g(t )dt − g( x)∫ g(t ) f (t )dt
a a x x x
(∫ g(t )dt )2
a
=
g( x) (∫ g(t )dt )2
b a
∫ f ( x) g( x)dx = f (ξ)∫ g( x)dx
a
b
(7)定积分值与变量的名称无关 定积分值与变量的名称无关: 定积分值与变量的名称无关 若 y= f (x)在 [a, b] 上连续 , 则 在 ]
b a
∫ f ( x)dx = ∫ f (t )dt
a
b
(8)微积分第一基本定理 若 f (x) 在 [a, b]上连续 , 则变 微积分第一基本定理: 微积分第一基本定理 ] 上限积分函数 F( x) = ∫ f (t )dt 在[a, b]上可微 且有 ]上可微,
定积分及其等式、 第一讲 定积分及其等式、不等式问题
1°定积分的概念 °
b
(1) 定积分的定义 定积分的定义:
∫ f ( x)dx = lim ∑ f (ξi )∆xi
n λ→0 i =0
其中极限值与区间 [a , b] 的划分 , ξi ∈[ xi −1, xi ] 的 ] 选取无关 . (2) 定积分的几何意义 定积分的几何意义: 曲边梯形的面积: 曲边梯形的面积
0
1
试证: 试证 在 (0 , 1) 内至少存在一点 ξ , 使
f (ξ) + ∫ f ( x)dx = 0
第四章 §1 定积分的概念

b a b a
2.定积分的几何意义
x=a 与_____ x=b , y=0 (1)当 f(x)≥0 时, f(x)dx 表示的是_______ ______ y=f(x) 所围成曲边梯形的面积. 和________
[一点通] 解决这类问题, 是通过分割自变量的区间求得过剩 估计值和不足估计值,分割得越细,估计值就越接近精确值;当 分割成的小区间的长度趋于 0 时,过剩估计值和不足估计值都趋 于要求的值.
1.把区间[0,1]n 等分,所得 n 个小区间,每个小区间的长度为 ( 1 A.n 3 C.n 2 B.n 1 D. 2n )
f(x)dx± g(x)dx (3) [f(x)± g(x)]dx=________________;
f(x)dx+ f(x)dx (4) f ( x )d x = ________________. b b a
b a b a
b a b a
f(x)dx+ g(x)dx=3, f(x)dx- g(x)dx=-5,
1 0 1 0
1 0
两式相加,得2 f(x)dx=-2, 故 f(x)dx=-1.
1 0
(2)∵ 2f(x)dx=2 f(x)dx=5, 5 ∴ f(x)dx= . 2
b 1 1 b b ∫ ∫ 于是 [2-f(x)]dx= a2dx- afxdx 3a 3
1 1 1 ×12+ ×1.22+ × 2 2 2 1 1 2 2 1.4 + ×1.6 + ×1.8 ×0.2= 2 2
2
1定积分的概念与性质

x x
t
f
(t)dt
2 lim
sin 3
f
( )
2 lim 3 f ( ) 6.
五、小结
1.定积分的实质:特殊和式的极限. 2.定积分的思想和方法:
分割 求和 取极限
化整为零
求近似以直(不变)代曲(变)
积零为整
取极限
精确值——定积分
1.定积分的性质
bx
用矩形面积近似取代曲边梯形面积
y
y
oa
b xo a
bx
(四个小矩形)
(九个小矩形)
显然,小矩形越多,矩形总面积越接近 曲边梯形面积.
观察下列演示过程,注意当分割加细时, 矩形面积和与曲边梯形面积的关系.
播放
曲边梯形如图所示, 在区间[a,b]内插入若干
个分点,a x0 x1 x2 xn1 xn b,
c
b
a f ( x)dx c f ( x)dx.
(定积分对于积分区间具有可加性)
性质4
b
a
1
dx
b
a
dx
b
a.
性质5 如果在区间[a,b]上 f ( x) 0,
则
b
a
f
(
x
)dx
0.
(a b)
证 f ( x) 0, f (i ) 0, (i 1,2,,n)
4
2
M f () 2 2, m f () 2 ,
4
2
ba , 24 4
2 4
2 4
sin xdx x
1.定积分的概念及性质

1 i 1 i i n1
n个小的曲边梯形 .这些小的曲边梯形的面 积为 A1 , A2 ,, An 21
第二步:近似 .在每个小区间[ xi 1 , xi ] 上任取一点 i , 以 [ xi 1 , xi ]为底, f ( i ) 为高的小矩形面积为
矩形面积和与曲边梯形面积的关系.
播放
5
曲边梯形如图 , 第一步:分割 .在区间[a , b]内插入若干个分点 , a x0 x1 x2 xn1 xn b,
y
把区间 [a , b] 分成 n 个小区间 [ x i 1 , x i ], 长 度为 Δx i x i x i 1 ;
b
b
因为 f ( x ) f ( x ) f ( x ) ,
b a
所以 f ( x )dx
n n
b
b
a kf ( x )dx
lim kf ( i )Δxi lim k f ( i )Δx i
0
i 1
0
i 1
k lim f ( i )Δx i k f ( x )dx .
b
n
0
i 1
a
39
2.对积分区间的可加性
性质3 设a c b, 则
v ( i )Δt i . i 1
25
i 1
路程的精确值 s lim 0
n
上述两个问题的具体含 义并不相同,一 个是几何问题,另一个 是物理问题.但是所求 的量表现了相同的数学 形式.在数学上抛开这 些问题的实际意义,抓住它们在数学关系上 共同的性质与特性加以概括,抽象出定积分 的概念.
1 定积分的概念
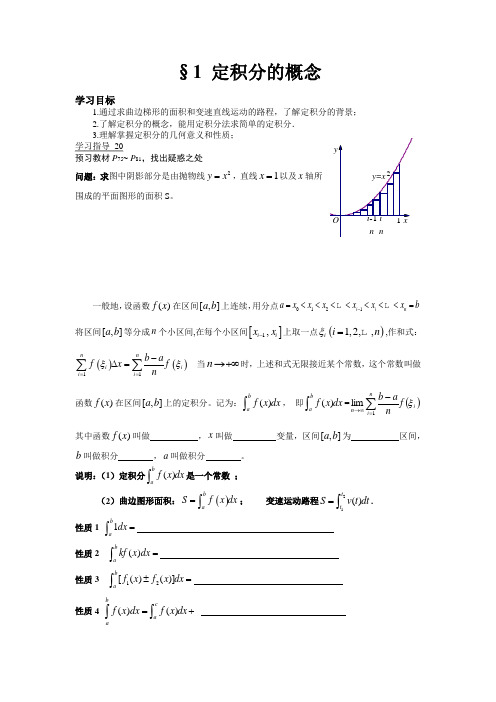
§1 定积分的概念学习目标1.通过求曲边梯形的面积和变速直线运动的路程,了解定积分的背景;2.了解定积分的概念,能用定积分法求简单的定积分.3.理解掌握定积分的几何意义和性质; 学习指导 20 预习教材P 75~ P 81,找出疑惑之处问题:求图中阴影部分是由抛物线2y x =,直线1=x 以及x 轴所围成的平面图形的面积S 。
一般地,设函数()f x 在区间[,]a b 上连续,用分点0121i i n a x x x x x x b -=<<<<<<<= 将区间[,]a b 等分成n 个小区间,在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ= ,作和式:()()11nni i i i b af x f nξξ==-∆=∑∑当n →+∞时,上述和式无限接近某个常数,这个常数叫做函数()f x 在区间[,]a b 上的定积分。
记为:()baf x dx ⎰, 即()baf x dx ⎰=()i ni n f nab ξ∑=∞→-1lim 其中函数()f x 叫做 ,x 叫做 变量,区间[,]a b 为 区间,b 叫做积分 ,a 叫做积分 。
说明:(1)定积分()baf x dx ⎰是一个常数 ;(2)曲边图形面积:()baS f x dx =⎰; 变速运动路程21()t t S v t dt =⎰.性质11badx =⎰性质2 ()ba kf x dx =⎰性质312[()()]baf x f x dx ±=⎰性质4()()bc aaf x dx f x dx =+⎰⎰当堂练习:+20 1、定积分⎰bacdx (常数0c >)的几何意义是2、由sin y x =,0x =,2x π=,0y =所围成图形的面积写成定积分的形式是3、连续函数0)(>x f ,则当b a <时,定积分⎰badx x f )(的符号( )A.一定是正的B.一定是负的C.当b a <<0时是正的D.以上都不对 4、与定积分dx x ⎰π230sin 相等的是( )A.⎰π230sin xdx B.⎰π230sin xdxC.⎰πsin xdx -⎰ππ23sin xdx D.⎰⎰+23220sin sin πππxdx xdx5、定积分⎰badx x f )(的大小( )A 、与)(x f 和积分区间[]b a ,有关,与i ξ的取法无关B 、与)(x f 有关,与区间[]b a ,及i ξ的取法无关C 、与)(x f 和i ξ的取法有关,与积分区间[]b a ,无关D 、与)(x f 、区间[]b a ,和i ξ的取法都有关 6、下列等式或不等式成立的个数是( ) ①⎰⎰=101)()(dx x f dt t f ②dx x dx x xdx ⎰⎰⎰=+ππππ220sin sin sin③dx x dx x a aa⎰⎰=-02④11dx <⎰⎰A 、1B 、2C 、3D 、4 7、计算下列定积分 (1)21(1)x dx +⎰; (2)22x dx -⎰; (3)a-⎰(0a >);(4)()4f x dx ⎰其中(),011,134,34x x f x x x x ≤<⎧⎪=≤≤⎨⎪-<≤⎩.。
高中数学同步教学 第4章 §1 定积分的概念

因此1x3dx=14. 0
• 『规律总结』 用定义法求积分的步骤 • (1)分割:将积分区间[a,b]n等分. • (2()3近)求似和:代i=n替1 b:-n a取f(ξi点).ξi∈[xi-1,xi],可取ξi=xi-1或者ξi=xi.
n
(4)求极限:bf(x)dx=lim
a
n→∞i=1
b-n af(ξi).,
• 〔跟踪练习1〕
• 用定积分的定义求由y=3x,x=0,x=1,y=0围成的图形的面
积.
[解析]
①分割:把区间[0,1]等分成 n 个小区间[i-n 1,ni ](i=1,2,…,n),其
长度为 Δx=1n,把曲边梯形分成 n 个小曲边梯形,其面积记为 ΔSi=(i=1,2,3,…,
n).
②近似代替:用小矩形的面积近似代替小曲边梯形的面积,ΔSi f(i-n 1)Δx=
积时,把区间[1,2]等分成 n 个小区间,则第 i 个小区间为( B )
A.[i-n 1,ni ]
B.[n+ni-1,n+n i]
C.[i-1,i]
D.[ni ,i+n 1]
[解析] 把区间[1,2]等分成 n 个小区间后,每个小区间的长度为1n,且第 i 个
小区间的左端点不小于 1.故选 B.
3.下列值等于 1 的是( C )
0
0
互动探究学案
命题方向1 ⇨定积分的定义
典例 1 求1x3dx. 0
[思路分析] 这里的被积函数 f(x)=x3 显然是连续函数.现按定义中包含的几 个步骤来求1x3dx.
0
[解析] (1)分割[0,1]: 0<1n<2n<…<n-n 1<nn=1.
(2)近似代替:作和 1n3·1n+2n3·1n+…+nn3·1n.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:积分区间为[0,2]
0
A
2 x
A f ( x)dx
0
2
2
0
xdx
面积A f ( x)dx
a
b
( f ( x) 0)
变速运动的路程 S:
S(t)
记为
vt dt
T2 T1
训练2:一辆汽车以速度v(t)=3t+5(m/s)作直线运 动,试用定积分表示汽车在t1=1s到t2=3s期间所经 过的路程 . 解:
v(t )dt
a
b
两种不同的算法得出的结果应该相同,故有
v(t )dt S (b) S (a)
a
b
或写作
v(t )dt S (t )
a
b
b a
2、微积分学基本公式
设函数F(x)是连续函数f (x)在区间[α ,b]上的 任意一个原函数,则
b
a
f ( x)dx F ( x ) a F (b) F (a)
f x 的最大值。几何演示
sin xdx cos x 0 ( cos ) ( cos0) 2
0
训练:求 | x | dx
1
2
解:
2
1
| x | dx ( x)dx xdx
1
0
2
x 2
2 0
x 2 1
0 2 2
0
1 4 ( 0 ) ( 0) 2 2 1 5 2 2 2
定积分的概念
The Concept of Definite Integral
4.1 积分的概念与性质
Deviation Analysis
知识目标
1、理解定积分的概念和几何意义; 2、掌握定积分的性质; 3、掌握积分基本公式及其应用
能力目标
1、会利用定积分的概念与性质求简单的定积分 2、会用定积分解决生活和专业中的实际问题.
0
y
2
0 -3
x
3
◆定积分的基本性质 性质1(数乘) 被积式中的常数因子可以提到积分 号前面,即
kf ( x)dx k
a
b
b
a
f ( x)dx
y=kf(x)
(k为常数).
y kf(a) y=f(x) f(a) o b
kf ( x)dx
a
b
b a
f ( x)dx
x
a
性质2(加减法) 两个函数代数和的积分等于这两个函数积分的代数 和,即
A?
o
分割
a
b
求
x
取极限
近似
和
定积分(The Definite Integral)的定义
若 I= lim f ( i )x i 存在,则称此极限为
0 i 1
n
函数 f(x)在区间[a,b]上的定积分,记为
b
a
f ( x)dx ,即
积分上限
f ( i )x i a f ( x )dx I lim 0 i 1
积分下限
b
n
被 积 函 数
被 积 表 达 式
积 分 变 量
[a , b] 积分区间
详细定义见课本略
注:
1 .当
f ( )x 的极限存在时,其极限值仅与被积函数 f(x) 及积分区间 [a,b] 有关,而与区间 a, b 的分法及
i 1 i
n
i
点的取法无关。 2.定积分的值与积分变量用什么字母表示无关,即有
x 轴、直线 x a 、
x b 所围成.
A?
o
a
b x
求曲边梯形的面积 A 的思路如下:
用矩形面积近似取代曲边梯形面积:
y
y
o
a
(四个小矩形)
b
x o
a
(九个小矩形)
b
x
显然,小矩形越多,矩形总面积越接近 曲边梯形面积.
y
练习 1. 求
2
0
| sin x |dx
x 1, f x 2.设 1 2 x , 2
x 1 x 1
,求
2
0
f x dx
小结:定积分的定义是一种构造性定义,
通过四步骤归结为一个和式的极限. 1.定积分的实质:特殊和式的极限. 2.定积分的思想和方法:
S v(t )dt (3t 5)dt
1 1
3
3
S vt dt
T2 T1
四、几何意义(Geometry significance)
◆定积分的几何意义
1、
f ( x ) 0, f ( x ) 0,
y
a f ( x )dx A a f ( x )dx A
a c
c
b
y
c a
f ( x)dx
y=f(x)
b c
f ( x)dx
o
a
c
b
x
性质4
f ( x) 1, 则 如果在区间[a,b]上,
b
a
f ( x)dx b a
y f(x)=1 1
b
b a
1dx
o
a
x
性质5
若在区间[a, b]上,有 f ( x) g ( x),则 f ( x)dx g ( x)dx
a 1
b
2
A3
表示曲线与 x 轴围成的图形面积的代数和。
y f x
a
A1
A2
A3
b
◆定积分的几何意义
若f
( x) 是偶函数,则
a
a
f x dx 2 f x dx
0
a
-a
a
a
若f
( x)是奇函数,则
a
f x dx 0
a
-a
◆定积分几何意义的应用
b
b
曲边梯形的面积 曲边梯形的面积 的负值
y a b x
y=f(x)>0 A
0 a
b x
0
A y=f(x)<0
◆定积分的几何意义
2.如果f(x)在[a,b]上时正,时负,如下图
y
y=f(x)
A1
a 0
A3
A2
b
x
b
a
f ( x)dx A1 A2 A3
◆定积分的几何意义
f x dx A A
b
a
f ( x)dx f (t )dt f (u)du
a a
b
b
b a 3.规定: f ( x)dx f ( x)dx a b
a
a
f ( x)dx 0
曲边梯形面积A:
A lim f (i )xi
0
i 1
n
记为
b
a
f x dx
4.1 积分的概念与性质 训练1 某工件的形状如图所示,用定积分表示此工 件平面的面积。 y
牛顿-莱布尼兹(Newton-Leibniz)公式
b
例4:计算定积分
(1) x 2 dx
1
4
1 解: ( x 3) ' x2 3
0
4
1
1 3 43 13 2 x dx x 21 3 1 3 3
4
(2) sin xdx
解: ( cos x) ' sin x
(ln x) dx (ln x)dx
训练:比较大小
(1) ( 2)
1
0
xdx, x 2 dx
0
1
4 0
cos xdx, 4 sin xdx
0
引例3:求作变速直线运动的物体从时刻a到时刻b所经过 的路程。
(1)若已知路程函数S(t),那么要求的路程是:S(b)-S(a)
(2)若已知速度函数v(t),则按引例1可知,所求路程为:
一、问题的提出
实例1 (求曲边梯形(Curved edge echelon)的面 积) 何谓曲边梯形? 请看下列两图形。
平面封闭图形均可 理解成数个曲边梯 形的集合。
如图,有一曲边梯形置于直角坐标系xoy中。
曲边梯形由连续曲线
y f ( x ) ( f ( x ) 0) 、
y
y f ( x)
分割
求近似
化整为零
以直(不变)代曲(变)
求和
积零为整
取极限
精确值——定积分
引例曲边梯形的面积
exit
估值定理
exit
积分中值定理
exit
牛顿-莱布尼兹公式
返回
再见!
性质6
6
m b a f x dx M b a
a
b
其中 m 是 f x 的最小值,M 是
(1) 3dx 3 (7 1) 18 1
1 (2) 2 xdx (2 8) 3 15 1 2
4
7
8
3 2 1
7 1 4
◆定积分几何意义的应用
(3)
3
3
2
1 9 2 9 x dx 3 2 2
2
(4) sin xdx 0
a a
b
b
y y=f(x) f(a) y=g(x) g(a) o b
