中考复习题六
【通用版】2019年春中考数学总复习 第二轮 中考题型专题 专题复习(六)几何综合题试题

专题复习(六) 几何综合题1.(2016·德州)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.(1)如图1、四边形ABCD 中、点E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 的中点.求证:中点四边形EFGH 是平行四边形;(2)如图2、点P 是四边形ABCD 内一点、且满足PA =PB 、PC =PD 、∠APB =∠CPD.点E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 的中点.猜想中点四边形EFGH 的形状、并证明你的猜想;(3)若改变(2)中的条件、使∠APB=∠CPD=90°、其他条件不变、直接写出中点四边形EFGH 的形状.(不必证明)图1 图2解:(1)证明:连接BD.∵E 、H 分别是AB 、AD 的中点、 ∴EH =12BD 、EH ∥BD.∵F 、G 分别是BC 、CD 的中点、 ∴FG =12BD 、FG ∥BD.∴EH =FG 、EH ∥FG.∴中点四边形EFGH 是平行四边形. (2)中点四边形EFGH 是菱形. 证明:连接AC 、BD.∵∠APB =∠CPD、∴∠APB +∠AP D =∠CPD+∠APD、即∠BPD=∠APC. 又∵PA=PB 、PC =PD 、∴△APC ≌△BPD(SAS ).∴AC=BD.∵点E 、F 、G 分别为边AB 、BC 、CD 的中点、 ∴EF =12AC 、FG =12BD.∴EF=FG.又∵四边形EFGH 是平行四边形、∴中点四边形EFGH 是菱形.图3(3)当∠APB=∠CPD=90°时、如图3、AC 与BD 交于点O 、BD 与EF 、AP 分别交于点M 、Q 、中点四边形EFGH 是正方形.理由如下:由(2)知:△APC≌△BPD、∴∠PAC =∠PBD. 又∵∠AQO=∠BQP、∴∠AOQ =∠APB =90°. 又∵EF∥AC、∴∠OMF =∠AOQ=90°. 又∵EH∥BD、∴∠HEF =∠OMF=90°. 又∵四边形EFGH 是菱形、∴中点四边形EFGH 是正方形.2.(2016·菏泽)如图、△ACB 和△DCE 均为等腰三角形、点A 、D 、E 在同一直线上、连接BE. (1)如图1、若∠CAB=∠CBA=∠CDE=∠CED=50°. ①求证:AD =BE ; ②求∠AEB 的度数;(2)如图2、若∠ACB=∠DCE=120°、CM 为△DCE 中DE 边上的高、BN 为△ABE 中AE 边上的高、试证明:AE =23CM +233BN.图1 图2解:(1)①证明:∵∠CAB=∠CBA=∠CDE=∠CED、∴AC =BC 、CD =CE. ∵∠CAB =∠CBA=∠CDE=∠CED、 ∴∠ACB =∠DCE.∴∠ACD=∠BCE. ∴△ACD ≌△BCE(SAS ).∴AD=BE. ②由①得△ACD≌△BCE、∴∠ADC =∠BEC=180°-∠CDE=130°.∴∠AEB =∠BEC-∠CED=130°-50°=80°.(2)证明:在等腰△DCE 中、∵CD =CE 、∠DCE =120°、CM ⊥DE 、 ∴∠DCM =12∠DCE=60°、DM =EM.在Rt △CDM 中、DM =CM·tan ∠DCM =CM·tan 60°=3CM 、∴DE =23CM. 由(1)、得∠ADC =∠BEC=150°、AD =BE 、 ∴∠AEB =∠BEC-∠CED=120°. ∴∠BEN =60°. 在Rt △BEN 中、BE =BN sin 60°=233BN.∴AD =BE =233BN.又∵AE=DE +AD 、∴AE =23CM +233BN.3.(2016·东营)如图1、△ABC 是等腰直角三角形、∠BAC =90°、AB =AC 、四边形ADEF 是正方形、点B 、C 分别在边AD 、AF 上、此时BD =CF 、BD ⊥CF 成立.(1)当△ABC 绕点A 逆时针旋转θ(0°<θ<90°)时、如图2、BD =CF 成立吗?若成立、请证明;若不成立、请说明理由.(2)当△ABC 绕点A 逆时针旋转45°时、如图3、延长DB 交CF 于点H 、交AF 于点N. ①求证:BD⊥CF;②当AB =2、AD =32时、求线段DH 的长.图1 图2 图3解:(1)BD =CF 成立.证明:∵AB=AC 、∠BAD =∠CAF=θ、AD =AF 、 ∴△ABD ≌△ACF(SAS ).∴BD =CF.(2)①证明:由(1)得、△ABD ≌△ACF 、 ∴∠HFN =∠ADN. 又∵∠HNF=∠AND、 ∴∠NHF =∠NAD=90°. ∴HD ⊥HF 、即BD⊥CF.②连接DF 、延长AB 交DF 于点M.在△MAD 中、∵∠MAD =∠MDA=45°、 ∴∠BMD =90°.∵AD =32、四边形ADEF 是正方形、 ∴MA =MD =322=3、FD =6.∴MB =3-2=1、DB =12+32=10. 在Rt △BMD 和Rt △FHD 中、 ∵∠MDB =∠HDF、 ∴△BMD ∽△FHD. ∴MD HD =BD FD 、即3HD =106.∴DH=9105.4.(2016·宁夏)在矩形ABCD 中、AB =3、AD =4、动点Q 从点A 出发、以每秒1个单位的速度、沿AB 向点B 移动;同时点P 从点B 出发、仍以每秒1个单位的速度、沿BC 向点C 移动、连接QP 、QD 、PD.若两个点同时运动的时间为x 秒(0<x≤3)、解答下列问题:(1)设△QPD 的面积为S 、用含x 的函数关系式表示S ;当x 为何值时、S 有最大值?并求出最小值; (2)是否存在x 的值、使得QP⊥DP?试说明理由.解:(1)∵四边形ABCD 为矩形、∴BC =AD =4、CD =AB =3. 当运动x 秒时、则AQ =x 、BP =x 、∴BQ =AB -AQ =3-x 、CP =BC -BP =4-x. ∴S △ADQ =12AD ·AQ=12×4x=2x 、S △BPQ =12BQ·BP=12(3-x)x =32x -12x 2、S △PCD =12PC·CD=12·(4-x)×3=6-32x.又S 矩形ABCD =AB·BC=3×4=12、∴S =S 矩形ABCD -S △ADQ -S △BPQ -S △PCD =12-2x -(32x -12x 2)-(6-32x)=12x 2-2x +6=12(x -2)2+4、即S =12(x -2)2+4.∴S 为开口向上的二次函数、且对称轴为直线x =2.∴当0<x≤2时、S 随x 的增大而减小; 当2<x≤3时、S 随x 的增大而增大、 又当x =0时、S =6、当S =3时、S =92.但x 的范围内取不到x =0、∴S 不存在最大值. 当x =2时、S 有最小值、最小值为4.(2)存在、理由:由(1)可知BQ =3-x 、BP =x 、CP =4-x. 当QP⊥DP 时、则∠BPQ+∠DPC=∠DPC+∠PDC、 ∴∠BPQ =∠PDC.又∵∠B=∠C、 ∴△BPQ ∽△CDP. ∴BQ PC =BP CD 、即3-x 4-x =x 3、解得x =7+132(舍去)或x =7-132. ∴当x =7-132时、QP ⊥DP.5.(2016·泰安)(1)已知:△ABC 是等腰三角形、其底边是BC 、点D 在线段AB 上、E 是直线BC 上一点、且∠DEC =∠DCE、若∠A=60°(如图1)、求证:EB =AD ;(2)若将(1)中的“点D 在线段AB 上”改为“点D 在线段AB 的延长线上”、其他条件不变(如图2)、(1)的结论是否成立、并说明理由;(3)若将(1)中的“若∠A=60°”改为“∠A=90°”、其他条件不变、则EBAD 的值是多少?(直接写出结论、不要求写解答过程)图1 图2解:(1)证明:过D 点作BC 的平行线交AC 于点F. ∵△ABC 是等腰三角形、∠A =60°、 ∴△ABC 是等边三角形.∴∠ABC=60°. ∵DF ∥BC 、∴∠ADF =∠ABC=60°. ∴△ADF 是等边三角形. ∴AD =DF 、∠AFD =60°.∴∠DFC =180°-60°=120°.∵∠DBE =180°-60°=120°、∴∠DFC =∠DBE. 又∵∠FDC=∠DCE、∠DCE =∠DEC、 ∴∠FDC =∠DEC、ED =CD. ∴△DBE ≌△CFD(AAS ). ∴EB =DF.∴EB=AD.(2)EB =AD 成立.理由如下:过D 点作BC 的平行线交AC 的延长线于点F. 同(1)可证△ADF 是等边三角形、 ∴AD =DF 、∠AFD =60°.∵∠DBE =∠ABC=60°、∴∠DBE =∠AFD. ∵∠FDC =∠D CE 、∠DCE =∠DEC、 ∴∠FDC =∠DEC、ED =CD. ∴△DBE ≌△CFD(AAS ). ∴EB =DF.∴EB=AD. (3)EBAD= 2.理由如下: 如图3、过D 点作BC 的平行线交AC 于点G.图3∵△ABC 是等腰三角形、∠A =90°、 ∴∠ABC =∠ACB=45°、∴∠DBE =180°-45°=135°. ∵DG ∥BC 、∴∠GDC =∠DCE、∠DGC =180°-45°=135°. ∴∠DBE =∠DGC. ∵∠DCE =∠DEC、∴ED =CD 、∠DEC =∠GDC.∴△DBE ≌△CGD(AAS ).∴BE=GD. ∵∠ADG =∠ABC=45°、∠A =90°、 ∴△ADG 是等腰直角三角形. ∴DG =2AD.∴BE=2AD.∴EBAD = 2.6.(2016·烟台)【探究证明】(1)在矩形ABCD 中、EF ⊥GH 、EF 分别交AB 、CD 于点E 、F 、GH 分别交AD 、BC 于点G 、H.求证:EF GH =ADAB ;【结论应用】(2)如图2、在满足(1)的条件下、又AM⊥BN、点M 、N 分别在边BC 、CD 上.若EF GH =1115、则BNAM 的值为________;【联系拓展】(3)如图3、四边形ABCD 中、∠ABC =90°、AB =AD =10、BC =CD =5、AM ⊥DN 、点M 、N 分别在边BC 、AB 上、求DNAM 的值.图1 图2 图3解:(1)证明:过点A 作AP∥EF、交CD 于点P 、过点B 作BQ∥GH、交AD 于点Q. ∵四边形ABCD 是矩形、∴AB ∥DC 、AD ∥BC.∴四边形AEFP 、四边形BHGQ 都是平行四边形.∴AP=EF 、GH =BQ. 又∵GH⊥EF、∴AP ⊥BQ.∴∠QAP +∠AQB=90°.∵四边形ABCD 是矩形、∴∠DAB =∠D=90°. ∴∠DAP +∠DPA=90°.∴∠AQB =∠DPA. ∴△PDA ∽△QAB.∴AP BQ =AD AB .∴EF GH =ADAB .(2)∵EF⊥GH、AM ⊥BN 、∴由(1)中的结论可得EF GH =AD AB 、BN AM =ADAB、∴BN AM =EF GH =1115.故答案为1115. (3)连接AC 、过点D 作AB 的平行线交BC 的延长线于点E 、作AF⊥AB 交直线DE 于点F. ∵∠BAF =∠B=∠E=90°、 ∴四边形ABEF 是矩形.易证△ADC≌△ABC、∴∠ADC =∠ABC=90°. ∴∠FDA +∠EDC=90°.又∵∠EDC+∠ECD=90°、∴∠FDA =∠ECD. 又∵∠E=∠F、 ∴△ADF ∽△DCE. ∴DE AF =DC AD =510=12. 设DE =x 、则AF =2x 、DF =10-x.在Rt △ADF 中、AF 2+DF 2=AD 2、即(2x)2+(10-x)2=100、解得x 1=4、x 2=0(舍去). ∴AF =2x =8.∴DN AM =AF AB =810=45.7.(2016·武汉)在△ABC 中、P 为边AB 上一点.(1)如图1、若∠ACP=∠B、求证:AC 2=AP·AB; (2)若M 为CP 的中点、AC =2.①如图2、若∠PBM=∠ACP、AB =3、求BP 的长;②如图3、若∠ABC=45°、∠A =∠BMP=60°、直接写出BP 的长.图1 图2 图3解:(1)证明:∵∠ACP=∠B、∠CAP =∠BAC、 ∴△ACP ∽△ABC. ∴AC AB =AP AC、即AC 2=AP·AB. (2)①作CQ∥BM 交AB 的延长线于点Q 、则∠PBM=∠Q. ∵∠PBM =∠ACP、∴∠ACP =∠Q. 又∠PAC=∠CAQ、∴△APC ∽△ACQ. ∴AC AQ =AP AC、即AC 2=AP·AQ. 又∵M 为PC 的中点、BM ∥CQ 、∴设BP =x 、则BQ =x.∴AP=3-x 、AQ =3+x. ∴22=(3-x)(3+x)、解得x 1=5、x 2=-5(不合题意、舍去). ∴BP = 5. ②BP =7-1.作CQ⊥AB 于点Q 、作CP 0=CP 交AB 于点P 0. ∵AC =2、∴AQ =1、CQ =BQ = 3.设AP 0=x 、则P 0Q =PQ =1-x 、BP =3-1+x 、 ∵∠BPM =∠CP 0A 、∠BMP =∠CAP 0、 ∴△AP 0C ∽△MPB 、∴AP 0MP =P 0CBP.解得x =7-3或x =-7-3(舍去).∴BP =3-1+7-3=7-1.8.(2016·岳阳)数学活动——旋转变换(1)如图1、在△ABC 中、∠ABC =130°、将△ABC 绕点C 逆时针旋转50°得到△A′B′C、连接B B′.求∠A′B′B 的大小; (2)如图2、在△ABC 中、∠ABC =150°、AB =3、BC =5、将△ABC 绕点C 逆时针旋转60°得到△A ′B ′C 、连接BB′.以A′为圆心、A ′B ′长为半径作圆.①猜想:直线BB′与⊙A′的位置关系、并证明你的结论; ②连接A′B、求线段A′B 的长度;(3)如图3、在△ABC 中、∠ABC =α(90°<α<180°)、AB =m 、BC =n 、将△ABC 绕点C 逆时针旋转2β角度(0°<2β<180°)得到△A′B′C、连接A′B 和BB′.以A′为圆心、A ′B ′长为半径作圆.问:角α与角β满足什么条件时、直线BB′与⊙A′相切、请说明理由.并求此条件下线段A′B 的长度.(结果用角α或角β的三角函数及字母m 、n 所组成的式子表示)图1 图2 图3解:(1)由旋转得:∠A′B′C=∠ABC=130°、CB =CB′、∠BCB ′=50°、 ∴∠BB ′C =12(180°-∠BCB′)=65°.∴∠A ′B ′B =∠A′B′C-∠BB′C=130°-65°=65°. (2)①猜想:直线BB′与⊙A′相切.证明:由旋转得:∠A′B′C=∠ABC=150°、CB =CB′、∠BCB ′=60°、 ∴∠BB ′C =12(180°-∠BCB′)=60°.∴∠A ′B ′B =∠A′B′C-∠BB′C=150°-60°=90°、即B′B⊥A′B′. 又A′B′为半径、∴直线BB′与⊙A′相切.②由旋转得:A′B′=AB =3、B ′C =BC =5、∠BCB ′=60°、 ∴△BCB ′为等边三角形.∴BB′=BC =5.在Rt △A ′B ′B 中、A ′B =(A′B′)2+(BB′)2=32+52=34. (3)满足的条件:α+β=180°.理由:在△BB′C 中、∠BB ′C =180°-2β2=90°-β、∴∠A ′B ′B =α-∠BB′C=α-(90°-β)=α+β-90°.∵α+β=180°、∴∠A ′B ′B =α+β-90°=180°-90°=90°、即B′B⊥A′B′. ∴直线BB′与⊙A′相切. 过点C 作CD⊥BB′于点D. ∴∠B ′CD =12∠BCB′=β.在Rt △B ′CD 中、B ′D =B′C·s in β=BC·sin β=n sin β、∴BB ′=2B′D=2n sin β. 由α+β=180°得到△A′B′B 为直角三角形、9.(2016·宜昌)在△ABC 中、AB =6、AC =8、BC =10.D 是△ABC 内部或BC 边上的一个动点(与B 、C 不重合).以D 为顶点作△DEF、使△DEF∽△ABC(相似比k>1)、EF ∥BC. (1)求∠D 的度数;(2)若两三角形重叠部分的形状始终是四边形AGDH.①连接GH 、AD 、当GH⊥AD 时、请判断四边形AGDH 的形状、并证明;②当四边形AGDH 的面积最大时、过A 作AP⊥EF 于P 、且AP =AD 、求k 的值.解:(1)∵AB 2+AC 2=62+82=102=BC 2、 ∴∠BAC =90°.又∵△DEF∽△ABC、∴∠D =∠BAC =90°. (2)①四边形AGDH 是正方形.证明:延长ED 、FD 分别交BC 于点M 、N. ∵△DEF ∽△ABC 、∴∠E =∠B. 又∵EF∥BC、∴∠E =∠EMC.∴∠B=∠EMC.∴ED∥BA. 同理FD∥AC.∴四边形AGDH 是平行四边形.又∵∠FDE=90°、∴四边形AGDH 是矩形. 又∵AD⊥GH、∴四边形AGDH 是正方形.②当D 点在△ABC 内部时、四边形AGDH 的面积不可能最大.其理由是:如图1、点D 在内部时、延长GD 到D′、过D′作MD′⊥AC 于点M 、则四边形GD′MA 的面积大于矩形AGDH 的面积、∴当点D 在△ABC 内部时、四边形AGDH 的面积不可能最大. 按上述理由、只有当D 点在BC 边上时、面积才有可能最大.图1 图2如图2、D 在BC 上时、易证明DG∥AC、 ∴△GDB ∽△ACB. ∴BG BA =GD AC 、即BA -AG BA =AH AC . ∴6-AG 6=AH 8、即AH =8-43AG. ∴S 矩形AGDH =AG·AH=AG×(8-43AG)=-43AG 2+8AG =-43(AG -3)2+12.当AG =3时、S 矩形AGDH 最大、此时DG =AH =4.即当AG =3、AH =4、S 矩形AG DH 最大.在Rt △BGD 中、BD =BG 2+DG 2=5、则DC =BC -BD =5. 即D 为B C 上的中点时、S 矩形AGDH 最大.∴在Rt △ABC 中、AD =BC2=5、∴PA =AD =5.延长PA 交BC 于点Q 、∵EF ∥BC 、QP ⊥EF 、 ∴QP ⊥BC.∴QP 是EF 、BC 之间的距离. ∴D 到EF 的距离为PQ 的长. 在Rt △ABC 中、12AB·AC=12BC·AQ、∴AQ =4.8.又∵△DEF∽△ABC、∴k =PQ AQ =PA +AQ AQ =5+4.84.8=4924.10.(2016·河南)(1)发现如图1、点A 为线段BC 外一动点、且BC =a 、AB =b.填空:当点A 位于CB 延长线上时、线段AC 的长取得最大值、且最大值为a +b .(用含a 、b 的式子表示)图1(2)应用点A 为线段BC 外一动点、且BC =3、AB =1.如图2所示、分别以AB 、AC 为边、作等边三角形ABD 和等边三角形ACE 、连接CD 、BE.①请找出图中与BE 相等的线段、并说明理由; ②直接写出线段BE 长的最大值. (3)拓展如图3、在平面直角坐标系中、点A 的坐标为(2、0)、点B 的坐标为(5、0)、点P 为线段AB 外一动点、且PA =2、PM =PB 、∠BPM =90°.请直接写出线段AM 长的最大值及此时点P 的坐标.图2 图3 备用图解:(2)①DC=BE.理由如下: ∵△ABD 和△ACE 为等边三角形、∴AD =AB 、AC =AE 、∠BAD =∠CA E =60°.∴∠BAD +∠BAC=∠CAE+∠BAC、即∠CAD=∠EAB. ∴△CAD ≌△EAB.∴DC =BE. ②BE 长的最大值是4.(3)AM 的最大值为3+22、点P 的坐标为(2-2、2).提示:如图3、构造△BNP≌△MAP、则NB =AM 、易得△APN 是等腰直角三角形、AP =2、∴AN =2 2.由(1)知、当点N 在BA 的延长线上时、NB 有最大值(如备用图).∴AM=NB =AB +AN =3+2 2. 过点P 作PE⊥x 轴于点E 、PE =AE = 2. 又∵A(2、0)、∴P(2-2、2).。
九年级化学中考专题复习六:物质的微观构成新课标人教版

中考专题复习六:物质的微观构成【知识导图】(1)(2)[解读考点]1、认清一些易混淆的概念的联系和区别,如元素与原子,原子与分子、离子等。
下表为构成物质的三种微粒分子、原子、离子的对比:2、分子、原子、离子都是构成物质的粒子。
如水、酒精、二氧化碳等物质是由分子构成的,金刚石、红磷等是由原子构成的。
金属也是由原子构成的物质。
多数碱类、盐类,如氢氧化钠、氯化钠等都是由离子构成的。
3、用微粒的观点解释某些常见的现象,如酒精的挥发、物质的热胀冷缩、电解水实验等。
4、掌握原子的结构,明确原子(或离子)结构示意图中各部分的含义。
[洞察考向]1、“认识物质的微观性,知道分子、原子、离子等都是构成物质的粒子,并用粒子的观点解释某些常见的现象”是《化学课程标准》强调掌握的内容,也是中考命题的热点。
中考命题往往以生产、生活及科学、技术、社会中的一些现象为背景材料,运用分子、原子、离子的观点解决实际问题,去探求物质的构成、去探究粒子的性质、去揭示化学反应的实质等。
2、粒子结构中核内质子数、核电荷数、中子数、核外电子数以及相对原子质量之间的等量关系是中考考试的热点,就这一热点问题,中考命题有以下几种考查方式:由粒子的结构,判断粒子中质子数、核电荷数、中子数、电子数及相对原子质量等;通过信息给定粒子的构成,推测粒子具有的化学性质,或与相对应的粒子结构比较,指出化学性质的异同;由给定粒子中质子数、电子数,判断粒子的种类;或给出一组构成原子的各种粒子的数据,从中去发现规律。
3、给定部分原子的结构示意图或元素周期表,让学生总结相关信息的开放性试题将会增加。
[真题剖析] 1.(2008·某某)生活中的下列现象可以用分子的知识加以解释,其中错误的是()A.气体热胀冷缩主要是因为气体分子间的距离随温度的变化而改变B.蔗糖溶解是因为蔗糖分子变小了C.打开浓盐酸的试剂瓶,能闻到刺激性气味,是因为分子在不断地运动D.液氧和氧气都能使带火星的木条复燃,是因为同种物质的分子化学性质相同解析:在掌握分子的性质时要注意联系生活实例,便于理解记忆。
中考历史总复习 主题六 中华民族的抗日战争(备用题库)模拟试题

亲爱的同学:这份试卷将再次记录你的自信、沉着、智慧和收获,我们一直投给你信任的目光……学习资料专题主题六中华民族的抗日战争题组一局部抗战和西安事变1.(2018重庆A,9,1分)1936年12月,经过中国共产党和各方面的共同努力,西安事变得以和平解决。
由此带来的影响是( )A.标志着新民主主义革命的开始B.推动了国民革命运动的发展C.基本结束了国共十年内战D.揭开了中华全民族抗战的序幕答案 C 依据所学可知,西安事变的和平解决标志着国共十年内战基本结束,故C符合题意。
五四运动标志着新民主主义革命的开始;国共两党第一次合作,推动了国民革命运动的发展;七七事变揭开了中国全民族抗战的序幕。
故A、B、D均不符合题意,应排除。
2.(2018内蒙古呼和浩特,8,1分)1936年12月12日,张学良和杨虎城扣押蒋介石,要求停止内战,联共抗日,史称“西安事变”。
下列因西安事变促成的“变化”是( )A.中日民族矛盾上升为中国社会的主要矛盾B.中国共产党的政策由抗日反蒋变为一致抗日C.张学良、杨虎城停止进攻红军,逼蒋抗日D.内战基本结束,抗日民族统一战线初步形成答案 D 解答本题需要注意题干的落脚点“因西安事变促成的‘变化’”。
西安事变的和平解决,标志着十年内战基本结束,抗日民族统一战线初步形成。
因此D项正确。
A、B两项属于西安事变的背景;C项属于西安事变的经过。
3.(2018湖南长沙,17,3分)关于第二次世界大战的开始时间,史学界有三种说法:1931年说、1937年说、1939年说。
提出“1931年说”的主要依据是( )A.1931年九一八事变揭开了世界反法西斯战争的序幕B.1931年七七事变后中华民族开始全民族抗战C.1931年国共两党开始第二次合作D.1931年日军占领南京答案 A 1931年9月18日,日本发动了震惊中外的九一八事变,这成为中国人民抗日战争的起点,揭开了世界反法西斯战争的序幕。
故选A项。
1937年七七事变后中华民族开始全民族抗战;1937年9月,国共两党开始第二次合作;1937年12月,日军占领南京。
中考数学复习专题6数的开方和二次根式试题(A卷,含解析)

专题6 数的开方和二次根式一、选择题1. (浙江杭州,1,3分)9=( )A .2B .3C .4D .5 【答案】B .【逐步提示】本题考查了二次根式的性质,解题的关键是能利用a a =2(a >0)进行解答,首先应将被开方数9写成32,再利用“a a =2(a >0)”即可锁定答案.【解析】因为9=23=3,故选择B .【解后反思】本题亦可以理解为求9的算术平方根,根据算术平方根的定义进行切入思考与计算:看什么正数的平方等于9,这个正数就是9的算术平方根.另外,二次根式实质上就是非负数的算术平方根,熟练地掌握二次根式的性质:(1)2)(a =a (a ≥0);(2)2a =a =⎩⎨⎧<-≥)0()0(a a a a ,是进行二次根式化简求值的基础.【关键词】二次根式;二次根式的求值;算术平方根2.(浙江杭州,5,3分)下列各式的变形中,正确的是( ) A .x 2·x 3=x 6B .x x =2C .(x 2-x 1)÷x =x -1 D .x 2-x +1=(x -21)2+41 【答案】B .【逐步提示】本题考查了代数式的恒等变形,解题的关键是掌握整式的乘除法法则、二次根式的性质、及完全平方公式的特点.解题时,先按同底数幂乘法法则、整式乘除法法则计算A .C 选项的式子,判断这两个选项的变形的正确性;再根据完全平方式的特点,对D 选项的式子进行变形,从而判断选项D 的正确性;最后根据二次根式性质判断B 选项的正确性,从而轻松解题. 【解析】∵x 2·x 3=x 2+3=x 5,x x =2,(x 2-x 1)÷x =(x 2-x 1)·x 1=x -21x,x 2-x +1=x 2-x +41+43=(x -21)2+43,∴只有选项B 正确,故选择B . 【解后反思】本题是代数式的有关运算,涉及到整式的运算、二次根式的性质,分式的运算.只要熟练地掌握相关的运算法则与性质,对各个选项的变形逐一判断,即可得到正确答案.四个选项的变形,分别考查了代数式的四个领域:同底数幂相乘,底数不变,指数相加,即:a m ×a n =a m +n(m 、n 都是正整数);整式除法,转化为乘法,然后利用分式乘法法则进行计算;配方法得掌握完全平方公式的结构特征:前平方、后平方、积的2倍在中间,就不难进行代数式的配方变形.【关键词】代数式的恒等变形;同底数的乘除法;二次根式的性质;配方法;整式的除法3.(浙江宁波,4,4分)使二次根式1x -有意义的x 的取值范围是( )A. x ≠1B. x > 1C. x ≤1D. x ≥1 【答案】D【逐步提示】本题考查了二次根式的概念,解题的关键是正确理解二次根式有意义的条件. 先根据二次根式有意义的条件建立关于x 的不等式,再解这个不等式确定x 的取值范围. 【解析】根据题意,得10x -≥,解得x ≥1,故选择D .【解后反思】形式)0(≥a a 的式子是二次根式,因此二次根式的被开方数a 应满足条件a ≥0. 解答与二次根式概念有关的问题通常是根据这个条件建立不等式来求解. 【关键词】二次根式 4.(重庆B ,7,4分)若二次根式2a -有意义,则a 的取值范围是( ) A .a ≥2 B .a ≤2 C .a >2 D .a ≠2 【答案】A【逐步提示】a 所在的代数式为二次根式,必须使被开方数为非负数.【解析】由题意可知a -2≥0,解得a ≥2. 故选A .【解后反思】求代数式中字母的取值范围,要看给出的代数式是整式、分式、二次根式,还是有关代数式的组合,然后结合整式、分式及二次根式成立的条件判断即可. 【关键词】二次根式 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35.36.37.38.39.二、填空题1.(山东聊城,13,3分)计算:278132⋅÷ =【答案】12【逐步提示】第一步直接利用二次根式乘除法法则把二次根式乘除法转化为被开方数的乘除法, 第二步计算二次根式乘除法, 第三步化简二次根式.278132⋅81827=272=916=34=12323⨯÷⨯⨯⨯⨯.故填12 .【解后反思】考查了二次根式的乘法,解题的关键是正确运用二次根式的乘法法则及二次根式的化简.二次根式相乘,把被开方数相乘,根指数不变;二次根式相乘,把被开方数相乘,根指数不变.【关键词】二次根式;二次根式乘法;二次根式除法;;2.(山东青岛,9,33282= .【答案】2【逐步提示】先计算分子中的减法,再进行除法运算.【详细解答】解:原式42222222,故答案为2.【解后反思】1.二次根式混合运算顺序:先乘方,再乘除,最后加减;2.二次根式运算的结果一般要化为最简二次根式;3.每个根式都可看成“单项式”,多项式的乘法法则及乘法公式仍然适用.【关键词】二次根式的混合运算3. (山东威海,14,3)188_____________.2【逐步提示】首先化简二次根式使其成为最简二次根式,然后合并同类二次根式.18832222=2 .【解后反思】一个二次根式,满足以下几个条件就被称为最简二次根式:(1) 被开放数不含有开得尽的因数或因式;(2)被开方数中不含分母;(3)分母中不含根号.同类二次根式:化简成最简二次根式之后,被开方数相同的二次根式称为同类二次根式.二次根式的加减步骤是先化简二次根式,然后再合并同类二次根式,法则类似于合并同类项.【关键词】二次根式;最简二次根式;同类二次根式,二次根式的加减4. (天津,14,3分)计算5353+)(-)的结果等于 .【答案】2【逐步提示】本题考查了二次根式的运算.利用乘法公式中的平方差公式(a+b)(a-b)=a2-b2,进行运算,合并化简即可.【解析】(53)(53)+-=22(5)(3)-=5-3=2,故答案为2.【解后反思】本题考查了二次根式的混合运算以及平方差公式,能根据算式的特点利用平方差公式简化运算是解题的关键.【关键词】二次根式的运算;平方差公式5. ( 四川省巴中市,9,3分)下列二次根式中,与3是同类二次根式的是( )A. 18B.13C.24D.0.3 【答案】B.【逐步提示】本题考查了二次根式的化简,以及同类二次根式的概念,解题的关键是应用二次根式的性质,将二次根式进行化简.先将各二次根式化简成最简二次根式,再根据同类二次根式的定义进行选择. 【详细解答】解:18=32,13=133,24=26,0.3=13010,其中只有133 与3是同类二次根式,故选择B.【解后反思】一个二次根式是否为最简二次根式,必须满足两个条件(1)根号内不含有开方开得尽的因数或因式,(2)二次根式的根号内不含有分母;而同类二次根式是指把二次根式化为最简二次根式后,被开方数相同的就是同类二次根式,被开方数不同的就不是同类二次根式, 【关键词】最简二次根式;同类二次根式;6. ( 四川南充,2,3分)下列计算正确的是( )A .1223=B .3322= C .3x x x -=- D .2x x = 【答案】A【逐步提示】本题考查了二次根式的化简、商的算术平方根,解题的关键是熟练掌握上述运算法则.根据对应的运算法则逐个计算再作出判断. 【详细解答】解:124323=⨯=,选项A 正确;336222==,选项B 错误; 因为3x -≥0,则x ≤032x x x x x -=-=--,选项C 2x x =,选项D 错误;故选择A .【解后反思】此题主要考查了二次根式的化简,正确掌握二次根式的性质是解题关键.【关键词】二次根式的化简;二次根式的乘法;二次根式的除法7(四川省自贡市,3,4分)下列根式中,不是最简二次根式的是 A .10 B .8 C .6 D .2【答案】B【逐步提示】看被开方数是否含有能开方的因式,若含有,则不是最简二次根式,若不含有则是最简二次根式. 【详细解答】解:B 选项中被开方数8可以分解为4×2,4可以开平方,所以B 不是最简二次根式,故选择B. 【解后反思】二次根式的化简主要运用二次根式的乘除法法则及二次根式的性质进行运算:1. 乘法法则:(a 0,b 0)a b ab •=≥≥.2.除法法则:(a 0,b 0)aa b b÷=≥>. 3.a a =2.【关键词】二次根式的化简8.(浙江金华,12,4分)能够说明“2x x =不成立...”的x 的值是 (写出一个即可). 【答案】如-1等(只要填一个负数即可)【逐步提示】认真审题,根据2x x =成立的条件,确定不成立的x 的值.【解析】因为2x x =成立的条件为x ≥0,所以“2x x =不成立...”的x 的值是所有负数,答案不唯一,故答案可以为如-1等(只要填一个负数即可) .【解后反思】根据公式成立的条件确定出公式不成立的条件. 【关键词】二次根式9.(浙江宁波,13,4分)实数-27 的立方根是 . 【答案】-3【逐步提示】本题考查了立方根的概念,解题的关键是掌握利用逆运算求立方根的方法.利用立方和开立方运算是互逆运算进行求解.【解析】由于(-3)3=-27,所以-27 的立方根是-3,故答案为-3 .【解后反思】任何实数的立方根只有一个;正数的立方根是正数,负数的立方根是负数,零的立方根是零.求一些特殊实数的立方根也是利用数的立方的逆运算来求的. 【关键词】 立方根的概念及求法10.(浙江衢州,12,4分)二次根式3x -中字母x 的取值范围是___.【答案】x ≥3.【逐步提示】由二次根式的被开方式是非负数,列出不等式求解. 【解析】依题意,得x -3≥0,解得x ≥3,故答案为x ≥3.【解后反思】正确理解二次根式的被开方式是非负数,是顺利求解此类问题的关键. 【关键词】二次根式的意义,不等式.11.(浙江舟山,12,4分)二次根式x -1中,字母x 的取值范围是 . 【答案】x ≥1【逐步提示】本题考查了二次根式的概念,解题的关键是根据二次根式有意义的条件建立关于x 的不等式求解. 二次根式有意义,必须满足被开方数是非负数.【解析】由题意,得x -1≥0,∴x ≥1,故答案为 x ≥1 .【解后反思】在一般的函数关系中自变量的取值范围主要考虑以下四种情况:⑴函数关系式为整式形式:自变量取值范围为任意实数;⑵函数关系式为分式形式:分母≠0;⑶函数关系式含算术平方根:被开方数≥0;⑷函数关系式含指数为0的幂的形式:底数≠0.【关键词】函数定义及其取值范围;解一元一次不等式12.. ( 四川乐山,14,3分)在数轴上表示实数a 的点如图7所示,化简2(5)2a a -+-的结果为___ _.图7a 52【答案】3.【逐步提示】观察数轴易得2<a <5,再将2(5)2a a -+-化简获解.【详细解答】解:由数轴得2<a <5,∴ 2(5)2a a -+-=5-a+a-2=5-2=3,故答案为3.【解后反思】(1)绝对值:正数的绝对值是它本身,负数的绝对值等于它的相反数,0的绝对值是0.(2) 二次根式有意义的条件是:被开方数必须是非负数.否则二次根式无意义. 【关键词】数轴;绝对值;二次根式 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39.三、解答题1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.。
中考地理复习 专题六 地理时事热点

1.俄罗斯和乌克兰的自然环境与经济。 2.卡塔尔的自然环境对人们生活的影响。 3.俄罗斯、乌克兰、卡塔尔的资源现状。
读乌克兰的地理位置图,完成(1)~(2)题。
(1)关于乌克兰地理位置的描述,正确的是 ①位于东半球 ②位于北温带 ③位于高纬度 ④位于北美洲 A.①② B.①③ C.②④ D.③④
(A)
(2)关于乌克兰危机对世界各国的影响,下列说法正确的是
①阻碍全球经济复苏
②引发大规模难民潮
③促进美俄南北对话
④国际能源价格波动
A.①②③ B.①③④
C.②③④ D.①②④
(1)山脉既能使暖湿气流顺着山坡爬升,形成丰富的降水;也能防风固沙, 图中四条山脉对宁夏平原防风固沙作用最明显的是②②(填序号);还能阻 挡寒冷气流,冬季南北两侧温差最大的山脉是④④(填序号)。 (2)习总书记主持召开黄河流域生态保护和高质量发展座谈会,黄河流域 9 省区的书记都前来参会,其中⑤省的简称是豫豫。
专题六 地理时事热点
类型一 中国特色建设与发展
1.同江中俄跨江铁路大桥通车 资料 当地时间 2022 年 4 月 27 日,俄罗斯横跨中国黑龙江(俄罗斯
称阿穆尔河)通往中国的首座跨境铁路桥——下列宁斯科耶-同江铁路 大桥当天在俄犹太自治州开通。中俄同江-下列宁斯阔耶界河铁路桥位 于中国黑龙江省同江市与俄罗斯下列宁斯阔耶市之间,主桥长约 2.2 公 里,其中中方境内段长 1 886 米,俄方段长 329 米,设计运营时速 100 公里,年过货能力 2 100 万吨。
(3)习总书记一直都非常关心黄河的生态保护,黄河上游要做好水源地的
【一轮通关】备战2024年中考地理一轮复习真题通关练专题06 居民与聚落(解析版)

2024年地理中考专题复习——居民与聚落一、选择题1.在平原地区规模较大聚落的分布形态多为()A.点状B.团块状C.环状D.条带状【答案】B【解析】平原地区地形平坦,在平原地区规模较大聚落的分布形状多为团块状,故B正确。
沙漠及干旱地区一般呈点状,岛屿一般呈环状,河流或山谷一般呈条带状,故答案为:B。
读下列四幅传统民居景观图,完成下面小题。
2.承载着北京传统文化的民居是()A.①B.②C.③D.④3.便于拆卸、搬运和安装的民居是()A.①B.②C.③D.④【答案】2.D 3.B【解析】2.解:①皖南民居是安徽的传统民居,②蒙古包是游牧民族的传统民居,③窑洞是黄土高原的传统民居,④四合院,是中国的一种传统合院式建筑,其格局为一个院子四面建有房屋,从四面将庭院合围在中间,故名四合院,至少有3000多年的历史,在中国各地有多种类型,其中以北京四合院为典型,故答案为:D。
3.蒙古包是蒙古族牧民居住的一种房子,建造和搬迁都很方便,适于牧业生产和游牧生活,故答案为:B。
大岭村位于广州市番禺区珠江口附近,距市中心约20千米。
该村有900余年历史,被评为“中国文化历史名村”。
如图示意大岭村的聚落空间格局,它体现了人与自然的和谐。
据此完成各小题。
4.该聚落格局与自然的和谐表现为()A.背靠菩山有利于冬季防寒B.南临玉带河利于冬季通风C.村落巷道的布局不便于联系D.自然生态区有利于灌溉5.实现“绿”持续发展理念,当地采取的措施中最合理的是()A.拆除古代民居,建设现代楼房B.大力发展经济,提高农民收入C.停止农业活动,封山育林净水D.保护传统建筑,发展文化旅游【答案】4.A 5.D【解析】4.A.该聚落背靠山脉,可以挡住寒冷的冬季风,A正确;B.冬季需要保暖,对通风的需求不大,B错误;C.巷道的布局利于联系,C错误;D.自然生态区不应该被用于灌溉,D错误;故答案为:A。
5.A.对古代民居应该加以保护,A错误;B.应该兼顾发展经济和环境保护,B错误;C.不能完全停止农业活动,C错误;D.在保护传统建筑的基础上发展文化旅游,既保护传统又可以提升收入,D正确;故答案为:D。
广东省深圳市数学中考专题复习专题6 方程不等式的实际应用(中考20题或21题)

(1)求甲、乙两工程队单独完成此项工程各需要多少天?
解:设乙单独完成此项工程需要x天,则甲单独完成需要2x 天,
答:学校购进甲种口罩400盒,购进乙种口罩600盒.
(2)现已知甲,乙两种口罩的数量分别是20个/盒,25个/盒, 按照教育局要求,学校必须储备足够使用十天的口罩,该校师生 共计800人,每人每天2个口罩,问购买的口罩数量是否能满足教 育局的要求?
解:购买的口罩总数为: 400×20+600×25=23 000(个), 全校师生两周需要的用量为: 800×2×10=16 000(个). ∵23 000>16 000, ∴购买的口罩数量能满足教育局的要求.
根据题意可得:2x0+220x=1,解得:x=30, 经检验x=30是原方程的解. 故x+30=60,
答:甲、乙两工程队单独完成此项工程各需要60天,30天;
(2)若此项工程由甲工程队单独施工,再由甲、乙两工程队合 作施工完成剩下的工程,已知甲工程队每天需付施工费1万元, 乙工程队施工每天需付施工费2.5万元,要使施工费用不超过64 万元,则甲工程队至少要单独施工多少天?
训练 1.(2020秋·福田区校级期中)疫情期间,为保护学生和教师 的健康,某学校用33 000元购进甲、乙两种医用口罩共计1 000 盒,甲,乙两种口罩的售价分别是30元/盒,35元/盒. (1)求甲、乙两种口罩各购进了多少盒?
解:设学校购进甲种口罩x盒,购进乙种口罩y盒, 依题意,得:3x0+x+y=315y0=0033 000,解得:xy==640000.
仁爱版英语中考真题复习专题6 书面表达(答案与解析版)

专题06 书面表达2019七、书面表达61.假如你有机会和任何一个名人共进午餐。
请根据以下要点和要求用英语写一篇短文。
1.要点:1)这个名人是谁;2)你为什么想和他或她共进午餐;3)你想和他或她谈论什么。
2.要求:1)文中不得出现真实姓名和学校名称;2)词数80左右。
【答案】例文I’d like to have lunch with Ren Zhengfei, the founder of the well-known Chinese tech company Huawei.Mr. Ren is considered as a great man who always has everything mapped out ahead. And under his leadership, Huawei has become a high-tech giant worldwide. Over the lunch, I will listen to his success story. Then I will ask him what is important to make it h appen. If time permits, I’ll ask for his advice for us teenagers today.I’m expecting this lunch already.【解析】【详解】这是一篇材料作文,根据材料中的相关信息介绍一下你想和哪位名人共进午餐。
主要从1)这个名人是谁;2)你为什么想和他或她共进午餐;3)你想和他或她谈论什么。
这三个方面去介绍。
注意时态应为一般现在时或一般将来时。
人称为第一人称。
注意作文中必须包含材料上的所有信息,并适当发挥。
写作时,避免使用汉语式的英语,尽量使用我们熟悉的句子或短语。
语法要正确,表达要符合英语习惯,注意时态、时间状语的搭配及主谓一致问题。
写作中适当使用连词,注意上下文联系紧密,符合逻辑关系,表达具有条理性。
2023届中考物理一轮复习专题练习06 力学-重力、弹力、摩擦力、压力、浮力作图题

2023届中考物理一轮复习专题练习6-力学-重力、弹力、摩擦力、压力、浮力作图题1.如图所示,小球浸没在水中,处于静止状态,以球心为作用点,作出小球受力的示意图。
2.如图,请画出静止的小球的受力示意图。
3.请在图中画出小球的受力示意图(细线处于竖直方向)。
4.如图所示,“冰墩墩”单脚站在水平地面上向右滑行,请在O点作出它所受摩擦力f的示意图;5.如图一木块静止在水面上,请作出木块所受重力和浮力的示意图。
6.如图所示,在斜面上的杯中悬浮着一个重力为3N的小球,请作出小球所受的浮力的示意图。
7.一小朋友沿滑梯下滑,请作出滑梯所受压力F的示意图。
8.图甲是一名攀岩运动员拉着绳子停在峭壁上的情景,图乙是这一时刻的简化图。
请以重心“O”为作用点,在图乙中画出。
(1)运动员所受的重力G;(2)峭壁对运动员的支持力F。
9.按要求作图:2022年北京冬奥会吉祥物“冰墩墩”随平板车一起向左做匀速直线运动,请画出“冰墩墩”所受力的示意图(O为重心)。
10.质地均匀的小球从弹簧正上方竖直下落,压缩弹簧减速下降,请作出此时小球所受重力G和弹力F的示意图。
11.如图所示物块正在光滑的水平面上向右滑动,并拉伸弹簧,画出物块受力的示意图(不计空气阻力)。
12.如图所示用绳拴着一物体在水平面内,沿箭头方向做圆周运动,画出物体所受力的示意图(不考虑空气阻力)。
13.如图所示,重100N的货物A随小车B在拉力F的作用下一起向右做匀速直线运动,请在图中画出货物A所受力的示意图。
14.如图(a)所示,空缆车随缆绳做匀速直线运动,在图(b)中画出缆车的轿厢(以方框表示)受力示意图(不计空气阻力)。
15.如图所示,物体A放在水平平板车上,随车一起向右做直线运动,请画出车突然加速时物体A所受力的示意图(不计空气阻力)。
16.如图所示,物体A与弹簧连接,静止在光滑的斜面上,请画出A的受力示意图。
17.图为在粗糙的水平面上滚动的小球,在图中画出小球所受力的示意图。
人教版九年级数学中考总复习 专题六 方案设计题 含解析及答案
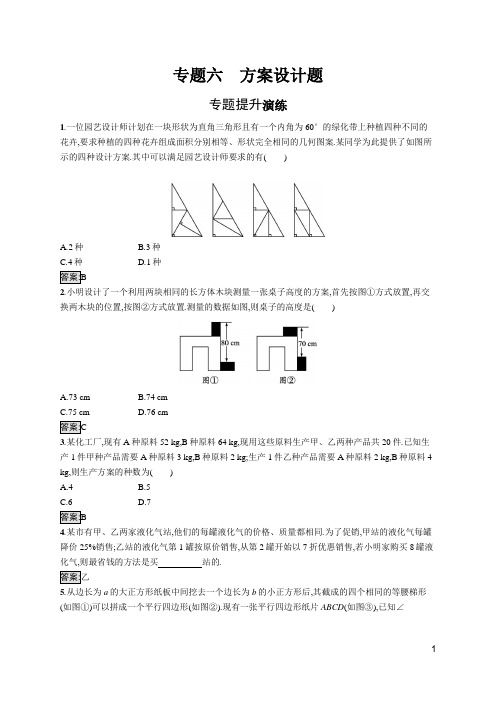
专题六方案设计题专题提升演练1.一位园艺设计师计划在一块形状为直角三角形且有一个内角为60°的绿化带上种植四种不同的花卉,要求种植的四种花卉组成面积分别相等、形状完全相同的几何图案.某同学为此提供了如图所示的四种设计方案.其中可以满足园艺设计师要求的有()A.2种B.3种C.4种D.1种2.小明设计了一个利用两块相同的长方体木块测量一张桌子高度的方案,首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是()A.73 cmB.74 cmC.75 cmD.76 cm3.某化工厂,现有A种原料52 kg,B种原料64 kg,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3 kg,B种原料2 kg;生产1件乙种产品需要A种原料2 kg,B种原料4 kg,则生产方案的种数为()A.4B.5C.6D.74.某市有甲、乙两家液化气站,他们的每罐液化气的价格、质量都相同.为了促销,甲站的液化气每罐降价25%销售;乙站的液化气第1罐按原价销售,从第2罐开始以7折优惠销售,若小明家购买8罐液化气,则最省钱的方法是买站的.5.从边长为a的大正方形纸板中间挖去一个边长为b的小正方形后,其截成的四个相同的等腰梯形(如图①)可以拼成一个平行四边形(如图②).现有一张平行四边形纸片ABCD(如图③),已知∠A=45°,AB=6,AD=4.若将该纸片按图②的方式截成四个相同的等腰梯形,然后按图①的方式拼图,则得到的大正方形的面积为 .+6√26.某市准备争创全国卫生城市,某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍. (1)求温馨提示牌和垃圾箱的单价各是多少元;(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10 000元,请你列举出所有购买方案,并指出哪种方案所需资金最少,最少是多少元.设温馨提示牌的单价是x 元, 则垃圾箱的单价是3x 元,由题意得2x+3×3x=550,解得x=50.故温馨提示牌的单价是50元,垃圾箱的单价是150元. (2)设购买温馨提示牌m 个, 则购买垃圾箱(100-m )个,由题意得50m+150(100-m )≤10000, 解得m ≥50.又100-m ≥48,∴m ≤52.∵m 为整数,∴m 的取值为50,51,52. 方案一:当m=50时,100-m=50,即购买50个温馨提示牌和50个垃圾箱,其费用为50×50+50×150=10000(元); 方案二:当m=51时,100-m=49,即购买51个温馨提示牌和49个垃圾箱,其费用为51×50+49×150=9900(元);方案三:当m=52时,100-m=48,即购买52个温馨提示牌和48个垃圾箱,其费用为52×50+48×150=9800(元).∵10000>9900>9800,∴方案三所需资金最少,最少是9800元.7.某旅行团32人在景区A 游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人. (1)求该旅行团中成人与少年分别是多少人?(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B 游玩.景区B 的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童. ①若由成人8人和少年5人带队,则所需门票的总费用是多少元?②若剩余经费只有1 200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.设该旅行团中成人x 人,少年y 人,根据题意,得{x +y +10=32,x =y +12,解得{x =17,y =5,故该旅行团中成人17人,少年5人.(2)①由题意得,所需门票的总费用是:100×8+100×0.8×5+100×0.6×(10-8)=1320(元). ②设可以安排成人a 人,少年b 人带队, 则1≤a ≤17,1≤b ≤5. 当10≤a ≤17时,若a=10,则费用为100×10+100×0.8×b ≤1200,解得b ≤52, ∴b 的最大值是2,此时a+b=12,费用为1160元. 若a=11,则费用为100×11+100×0.8×b ≤1200,解得b ≤54, ∴b 的最大值是1,此时a+b=12,费用为1180元.若a ≥12,则100a ≥1200,即成人门票至少需要1200元,不合题意,舍去.当1≤a<10时,若a=9,则费用为100×9+100×0.8×b+100×0.6×1≤1200,解得b ≤3, ∴b 的最大值是3,a+b=12,费用为1200元.若a=8,则费用为100×8+100×0.8×b+100×0.6×2≤1200,解得b ≤72,∴b 的最大值是3,a+b=11<12,不合题意,舍去.同理,当a<8时,a+b<12,不合题意,舍去.综上所述,最多可以安排成人和少年共12人带队,有三个方案:成人10人,少年2人;成人11人,少年1人;成人9人,少年3人.其中成人10人,少年2人时购票费用最少.。
2020中考复习 物理经典考题训练——专题六:光和眼睛

2020中考复习物理经典考题训练——专题六:光和眼睛考点一:光的直线传播1.大约两千四百年前,我国的学者墨翟和它的学生做了世界上第一个小孔成像的实验,解释了小孔成像的原理。
小光同学将两个长度均为50cm,直径为5cm的直筒套在一起,做成如图的仪器(M筒的直径稍大,可以套在N筒上并能前后移动)(1)小孔成的像是倒立的________像。
可以用光的________-解释。
所成的像与小孔的形状________。
(2)若直筒M,N位置不动,让物体远离N筒,像距________,像的大小________(以上两空选填“变大”“不变”或“变小”)。
(3)十五的夜晚,将小孔对准明月,测得月亮最大像的直径是9.1mm,已知月球到地球的距离为380000km。
月球的直径约为________km。
考点二:光的反射平面镜成像1.关于镜面反射和漫反射,下列说法正确的是()A. 镜面反射遵守光的反射定律,漫反射不遵守光的反射定律B. 平静的水面能映出岸上景物的倒影,是因为光在水面发生了漫反射C. 我们能从不同的地区看见天上的月亮,是因为月球对太阳光发生了镜面反射D. 人们能从不同方向看见本身不发光的物体,是因为光在这些物体表面发生了漫反射2.如图所示四种现象中,由于光的反射而形成的()A. 在岸上看到水中的腿变“短”了B. 在平静湖面上群山的倒影C. 透过玻璃砖看到钢笔“错位”了D. 手影3.下列图片中的物理现象与所对应的物理知识相符的是()A. 手影游戏﹣﹣光的色散B. 小孔成像﹣﹣光的折射C. 照镜子﹣﹣光的反射D. 鱼在哪里﹣﹣光沿直线传播4.某人的身高为1.70m,站在竖直的平面镜前1.5m处,他在镜中的像到平面镜的距离为________m,他以0.5m/s的速度靠近平面镜时,他在镜中的像会________(选填“变大”、“变小”或“不变”).5.如图所示,在探究平面镜成像特点的实验中,为使实验的效果更好,实验室内光线应________一些(选填“强”或“弱”);实验中某同学将玻璃板及点燃的蜡烛放置好后,在玻璃板另一侧移动未点燃的蜡烛,观察到未点燃的蜡烛与点燃蜡烛的像重合时,记录下了物、像、镜的位置,接下来的操作应是________(选填“整理实验器材”或“改变蜡烛位置多次实验”),实验结束后同学们发现像与物对应点的连线与镜面________.6.身高1.75m的小明站在竖直放置的平面镜前1.5m处,他在镜中的像距他 ________ m.如果平面镜向他移动0.5m,他的像高 ________1.75m(选填“大于”“小于”或“等于”);现在的像相对于原来的像移动了 ________ m.7.学习了光学知识后,小明对有关实验进行了思考和创新:(1)用如图甲所示的装置研究光的反射规律,其中有一个可沿虚线折转的光屏.①光屏在实验中的作用是:________ ;.________②实验时,光屏应如何放置?________(2)如图乙所示,在探究平面镜成像规律实验中,①小明采用透明玻璃板代替平面镜来完成探究活动,虽然不如平面镜清晰,但却能在观察到A蜡烛像的同时,也能观察到B蜡烛,这是为了能确定像的________ .②当点燃的蜡烛放在玻璃板前20cm的A处时,玻璃板后B处的蜡烛好像也被点燃了;移去B处的蜡烛,取一光屏放在B处,发现光屏上并没有出现蜡烛的像,这说明平面镜所成的像是________ 像.③小明将玻璃板移去,在玻璃板位置放一凸透镜,B处放一光屏,发现光屏上恰好成清晰的倒立、等大的烛焰像,则该凸透镜的焦距是________ cm.8.小明同学自备器材,主动探究“平面镜成像的规律”,其情形如图所示,他先把一块平板玻璃垂直立在水平桌面上,再准备A、B两支大小、外形完全一样的蜡烛,然后把点燃的蜡烛A立在玻璃板前,又把蜡烛B放在玻璃板后面,并移动蜡烛B的位置,使它与蜡烛A的像完全重合.(1)用平面镜代替玻璃板,上述实验________ (填“能”或“不能”)进行,因为________ (2)实验时,取两根相同的蜡烛,是为了验证物与像________ 关系;某同学发现看到蜡烛A的像不清晰,于是他将蜡烛B也点燃,用来增加像的亮度.他这样做________ (填“能”或“不能”)使看到的像更清晰.(3)如果把蜡烛A向镜面移动一段距离,又移动蜡烛B去与蜡烛A的像比较,会发现蜡烛A像的大小________ (选项“变大”、“变小”或“不变”).(4)如果在蜡烛A像的位置放一个光屏,光屏上________ 承接到像(选项“会”或“不会”),这说明平面镜所成的像是________ 像.(选填“虚”或“实”)考点三:光的折射1.若岸边的人能看到水中的鱼,它看到的鱼其实是()A. 鱼下方的虚像B. 鱼上方的的虚像C. 鱼下方的的实像D. 鱼上方的的实像2.如图所示的四种情景,属于光的折射现象的是()3.如图所示,是光在空气和玻璃之间发生折射的光路图,从图中可以看出,空气在界面的________侧(选填“左”或“右”),此过程中还有部分光发生了反射,反射角的大小是________ .4.如图所示,MN是两种均匀介质的分界面,已知两种介质其中一种是空气.一束光从一种介质进入另一种介质,则入射角大小等于 ________ 度,折射角大小等于 ________ 度,其中界面MN的 ________(填“左”或“右”)侧是空气.5.如图,OA、OB和OC是射到空气和玻璃界面上的入射线、反射线和折射线三条光线,则________是法线,反射角为________度,折射角为________度.6.如图所示,一束光射向一块玻璃砖.画出这束光进入玻璃和离开玻璃后的径迹。
春中考数学总复习 第二轮 中考题型专题 专题复习(六)几何综合题试题-人教版初中九年级全册数学试题

专题复习(六) 几何综合题1.(2016·某某)我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形. (1)如图1,四边形ABCD 中,点E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 的中点.求证:中点四边形EFGH 是平行四边形;(2)如图2,点P 是四边形ABCD 内一点,且满足PA =PB ,PC =PD ,∠APB =∠CPD.点E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 的中点.猜想中点四边形EFGH 的形状,并证明你的猜想;(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH 的形状.(不必证明)图1 图2解:(1)证明:连接BD. ∵E 、H 分别是AB 、AD 的中点, ∴EH =12BD ,EH ∥BD.∵F 、G 分别是BC 、CD 的中点, ∴FG =12BD ,FG ∥BD.∴EH =FG ,EH ∥FG.∴中点四边形EFGH 是平行四边形. (2)中点四边形EFGH 是菱形. 证明:连接AC 、BD.∵∠APB =∠CPD,∴∠APB +∠APD=∠CPD+∠APD,即∠BPD=∠APC. 又∵PA=PB ,PC =PD ,∴△APC ≌△BPD(SAS ).∴AC=BD.∵点E 、F 、G 分别为边AB 、BC 、CD 的中点, ∴EF =12AC ,FG =12BD.∴EF=FG.又∵四边形EFGH 是平行四边形, ∴中点四边形EFGH 是菱形.图3(3)当∠APB=∠CPD=90°时,如图3,AC与BD交于点O,BD与EF,AP分别交于点M,Q,中点四边形EFGH是正方形.理由如下:由(2)知:△APC≌△BPD,∴∠PAC=∠PBD.又∵∠AQO=∠BQP,∴∠AOQ=∠APB=90°.又∵EF∥AC,∴∠OMF=∠AOQ=90°.又∵EH∥BD,∴∠HEF=∠OMF=90°.又∵四边形EFGH是菱形,∴中点四边形EFGH是正方形.2.(2016·某某)如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°.①求证:AD=BE;②求∠AEB的度数;(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=23CM+233BN.图1 图2解:(1)①证明:∵∠CAB=∠CBA=∠CDE=∠CED,∴AC=BC,CD=CE. ∵∠CAB=∠CBA=∠C DE=∠CED,∴∠ACB=∠DCE.∴∠ACD=∠BCE.∴△ACD≌△BCE(SAS).∴AD=BE.②由①得△ACD≌△BCE,∴∠ADC=∠BEC=180°-∠CDE=130°.∴∠AEB =∠BEC-∠CED=130°-50°=80°.(2)证明:在等腰△DCE 中,∵CD =CE ,∠DCE =120°,CM ⊥DE , ∴∠DCM =12∠DCE=60°,DM =EM.在Rt △CDM 中,DM =CM·tan ∠DCM =CM·tan 60°=3CM ,∴DE =23CM. 由(1),得∠ADC =∠BEC=150°,AD =BE , ∴∠AEB =∠BEC-∠CED=120°. ∴∠BEN =60°. 在Rt △BEN 中,BE =BN sin 60°=233BN.∴AD =BE =233BN.又∵AE=DE +AD ,∴AE =23CM +233BN.3.(2016·东营)如图1,△ABC 是等腰直角三角形,∠BAC =90°,AB =AC ,四边形ADEF 是正方形,点B 、C 分别在边AD 、AF 上,此时BD =CF ,BD ⊥CF 成立.(1)当△ABC 绕点A 逆时针旋转θ(0°<θ<90°)时,如图2,BD =CF 成立吗?若成立,请证明;若不成立,请说明理由.(2)当△ABC 绕点A 逆时针旋转45°时,如图3,延长DB 交CF 于点H ,交AF 于点N. ①求证:BD⊥CF;②当AB =2,AD =32时,求线段DH 的长.图1 图2 图3解:(1)BD =CF 成立.证明:∵AB=AC ,∠BAD =∠CAF=θ,AD =AF , ∴△ABD ≌△ACF(SAS ).∴BD =CF. (2)①证明:由(1)得,△ABD ≌△ACF , ∴∠HFN =∠ADN. 又∵∠HNF=∠AND, ∴∠NHF =∠NAD=90°. ∴HD ⊥HF ,即BD⊥CF.②连接DF ,延长AB 交DF 于点M. 在△MAD 中,∵∠MAD =∠MDA=45°, ∴∠BMD =90°.∵AD =32,四边形ADEF 是正方形, ∴MA =MD =322=3,FD =6.∴MB =3-2=1,DB =12+32=10. 在Rt △BMD 和Rt △FHD 中, ∵∠MDB =∠HDF, ∴△BMD ∽△FHD. ∴MD HD =BD FD ,即3HD =106.∴DH=9105.4.(2016·某某)在矩形ABCD 中,AB =3,AD =4,动点Q 从点A 出发,以每秒1个单位的速度,沿AB 向点B 移动;同时点P 从点B 出发,仍以每秒1个单位的速度,沿BC 向点C 移动,连接QP ,QD ,PD.若两个点同时运动的时间为x 秒(0<x≤3),解答下列问题:(1)设△QPD 的面积为S ,用含x 的函数关系式表示S ;当x 为何值时,S 有最大值?并求出最小值; (2)是否存在x 的值,使得QP⊥DP?试说明理由.解:(1)∵四边形ABCD 为矩形,∴BC =AD =4,CD =AB =3. 当运动x 秒时,则AQ =x ,BP =x , ∴BQ =AB -AQ =3-x ,CP =BC -BP =4-x. ∴S △ADQ =12AD ·AQ=12×4x=2x ,S △BPQ =12BQ·BP=12(3-x)x =32x -12x 2,S △PCD =12PC·CD=12·(4-x)×3=6-32x.又S 矩形ABCD =AB·BC=3×4=12,∴S =S 矩形ABCD -S △ADQ -S △BPQ -S △PCD =12-2x -(32x -12x 2)-(6-32x)=12x 2-2x +6=12(x -2)2+4,即S =12(x -2)2+4.∴S 为开口向上的二次函数,且对称轴为直线x =2.∴当0<x≤2时,S 随x 的增大而减小; 当2<x≤3时,S 随x 的增大而增大, 又当x =0时,S =6,当S =3时,S =92.但x 的X 围内取不到x =0,∴S 不存在最大值. 当x =2时,S 有最小值,最小值为4.(2)存在,理由:由(1)可知BQ =3-x ,BP =x ,CP =4-x. 当QP⊥DP 时,则∠BPQ+∠DPC=∠DPC+∠PDC, ∴∠BPQ =∠PDC.又∵∠B=∠C, ∴△BPQ ∽△CDP. ∴BQ PC =BP CD ,即3-x 4-x =x 3,解得x =7+132(舍去)或x =7-132. ∴当x =7-132时,QP ⊥DP.5.(2016·某某)(1)已知:△ABC 是等腰三角形,其底边是BC ,点D 在线段AB 上,E 是直线BC 上一点,且∠DEC =∠DCE,若∠A=60°(如图1),求证:EB =AD ;(2)若将(1)中的“点D 在线段AB 上”改为“点D 在线段AB 的延长线上”,其他条件不变(如图2),(1)的结论是否成立,并说明理由;(3)若将(1)中的“若∠A=60°”改为“∠A=90°”,其他条件不变,则EB AD 的值是多少?(直接写出结论,不要求写解答过程)图1 图2解:(1)证明:过D 点作BC 的平行线交AC 于点F. ∵△ABC 是等腰三角形,∠A =60°, ∴△ABC 是等边三角形.∴∠ABC=60°. ∵DF ∥BC ,∴∠ADF =∠ABC=60°. ∴△ADF 是等边三角形. ∴AD =DF ,∠AFD =60°.∴∠DFC =180°-60°=120°.∵∠DBE =180°-60°=120°,∴∠DFC =∠DBE. 又∵∠FDC=∠DCE,∠DCE =∠DEC, ∴∠FDC =∠DEC,ED =CD. ∴△DBE ≌△CFD(AAS ). ∴EB =DF.∴EB=AD. (2)EB =AD 成立.理由如下:过D 点作BC 的平行线交AC 的延长线于点F. 同(1)可证△ADF 是等边三角形, ∴AD =DF ,∠AFD =60°.∵∠DBE =∠ABC=60°,∴∠DBE =∠AFD. ∵∠FDC =∠DCE,∠DCE =∠DEC, ∴∠FDC =∠DEC,ED =CD. ∴△DBE ≌△CFD(AAS ). ∴EB =DF.∴EB=AD. (3)EBAD= 2.理由如下: 如图3,过D 点作BC 的平行线交AC 于点G.图3∵△ABC 是等腰三角形,∠A =90°, ∴∠ABC =∠ACB=45°, ∴∠DBE =180°-45°=135°. ∵DG ∥BC ,∴∠GDC =∠DCE,∠DGC =180°-45°=135°. ∴∠DBE =∠DGC. ∵∠DCE =∠DEC, ∴ED =CD ,∠DEC =∠GDC.∴△DBE ≌△CGD(AAS ).∴BE=GD. ∵∠ADG =∠ABC=45°,∠A =90°, ∴△ADG 是等腰直角三角形. ∴DG =2AD.∴BE=2AD.∴EBAD = 2.6.(2016·某某)【探究证明】(1)在矩形ABCD 中,EF ⊥GH ,EF 分别交AB ,CD 于点E ,F ,GH 分别交AD ,BC 于点G ,H.求证:EF GH =ADAB ;【结论应用】(2)如图2,在满足(1)的条件下,又AM⊥BN,点M ,N 分别在边BC ,CD 上.若EF GH =1115,则BNAM 的值为________;【联系拓展】(3)如图3,四边形ABCD 中,∠ABC =90°,AB =AD =10,BC =CD =5,AM ⊥DN ,点M ,N 分别在边BC ,AB 上,求DNAM 的值.图1 图2 图3解:(1)证明:过点A 作AP∥EF,交CD 于点P ,过点B 作BQ∥GH,交AD 于点Q. ∵四边形ABCD 是矩形,∴AB ∥DC ,AD ∥BC.∴四边形AEFP 、四边形BHGQ 都是平行四边形.∴AP=EF ,GH =BQ. 又∵GH⊥EF,∴AP ⊥BQ.∴∠QAP +∠AQB=90°.∵四边形ABCD 是矩形,∴∠DAB =∠D=90°. ∴∠DAP +∠DPA=90°.∴∠AQB =∠DPA. ∴△PDA ∽△QAB.∴AP BQ =AD AB .∴EF GH =ADAB .(2)∵EF⊥GH,AM ⊥BN ,∴由(1)中的结论可得EF GH =AD AB ,BN AM =ADAB ,∴BN AM =EF GH =1115.故答案为1115. (3)连接AC ,过点D 作AB 的平行线交BC 的延长线于点E ,作AF⊥AB 交直线DE 于点F. ∵∠BAF =∠B=∠E=90°,∴四边形ABEF 是矩形.易证△ADC≌△ABC,∴∠ADC =∠ABC=90°. ∴∠FDA +∠EDC=90°.又∵∠EDC+∠EC D =90°,∴∠FDA =∠ECD. 又∵∠E=∠F, ∴△ADF ∽△DCE. ∴DE AF =DC AD =510=12. 设DE =x ,则AF =2x ,DF =10-x.在Rt △ADF 中,AF 2+DF 2=AD 2,即(2x)2+(10-x)2=100,解得x 1=4,x 2=0(舍去). ∴AF =2x =8.∴DN AM =AF AB =810=45.7.(2016·某某)在△ABC 中,P 为边AB 上一点. (1)如图1,若∠ACP=∠B,求证:AC 2=AP·AB; (2)若M 为CP 的中点,AC =2.①如图2,若∠PBM=∠ACP,AB =3,求BP 的长;②如图3,若∠ABC=45°,∠A =∠BMP=60°,直接写出BP 的长.图1 图2 图3解:(1)证明:∵∠ACP=∠B,∠CAP =∠BAC, ∴△ACP ∽△ABC. ∴AC AB =AP AC,即AC 2=AP·AB. (2)①作CQ∥BM 交AB 的延长线于点Q ,则∠PBM=∠Q. ∵∠PBM =∠ACP,∴∠ACP =∠Q. 又∠PAC=∠CAQ,∴△APC ∽△ACQ. ∴AC AQ =AP AC,即AC 2=AP·AQ. 又∵M 为PC 的中点,BM ∥CQ ,∴设BP =x ,则BQ =x.∴AP=3-x ,AQ =3+x. ∴22=(3-x)(3+x),解得x 1=5,x 2=-5(不合题意,舍去).∴BP = 5. ②BP =7-1.作CQ⊥AB 于点Q ,作CP 0=CP 交AB 于点P 0. ∵AC =2,∴AQ =1,CQ =BQ = 3.设AP 0=x ,则P 0Q =PQ =1-x ,BP =3-1+x , ∵∠BPM =∠CP 0A ,∠BMP =∠CAP 0, ∴△AP 0C ∽△MPB ,∴AP 0MP =P 0CBP.∴MP ·P 0C =12P 0C 2=(3)2+(1-x )22=AP 0·BP =x(3-1+x).解得x =7-3或x =-7-3(舍去). ∴BP =3-1+7-3=7-1.8.(2016·某某)数学活动——旋转变换(1)如图1,在△ABC 中,∠ABC =130°,将△ABC 绕点C 逆时针旋转50°得到△A′B′C,连接B B′.求∠A′B′B 的大小;(2)如图2,在△ABC 中,∠ABC =150°,AB =3,BC =5,将△ABC 绕点C 逆时针旋转60°得到△A ′B ′C ,连接BB′.以A′为圆心,A ′B ′长为半径作圆.①猜想:直线BB′与⊙A′的位置关系,并证明你的结论; ②连接A′B,求线段A′B 的长度;(3)如图3,在△ABC 中,∠ABC =α(90°<α<180°),AB =m ,BC =n ,将△ABC 绕点C 逆时针旋转2β角度(0°<2β<180°)得到△A′B′C,连接A′B 和BB′.以A′为圆心,A ′B ′长为半径作圆.问:角α与角β满足什么条件时,直线BB′与⊙A′相切,请说明理由.并求此条件下线段A′B 的长度.(结果用角α或角β的三角函数及字母m 、n 所组成的式子表示)图1 图2 图3解:(1)由旋转得:∠A′B′C=∠ABC=130°,CB =CB′,∠BCB ′=50°, ∴∠BB ′C =12(180°-∠BCB′)=65°.∴∠A ′B ′B =∠A′B′C-∠BB′C=130°-65°=65°. (2)①猜想:直线BB′与⊙A′相切.证明:由旋转得:∠A′B′C=∠ABC=150°,CB =CB′,∠BCB ′=60°, ∴∠BB ′C =12(180°-∠BCB′)=60°.∴∠A ′B ′B =∠A′B′C-∠BB′C=150°-60°=90°,即B′B⊥A′B′. 又A′B′为半径, ∴直线BB′与⊙A′相切.②由旋转得:A′B′=AB =3,B ′C =BC =5,∠BCB ′=60°, ∴△BCB ′为等边三角形.∴BB′=BC =5.在Rt △A ′B ′B 中,A ′B =(A′B′)2+(BB′)2=32+52=34. (3)满足的条件:α+β=180°.理由:在△BB′C 中,∠BB ′C =180°-2β2=90°-β,∴∠A ′B ′B =α-∠BB′C=α-(90°-β)=α+β-90°.∵α+β=180°,∴∠A ′B ′B =α+β-90°=180°-90°=90°,即B′B⊥A′B′. ∴直线BB′与⊙A′相切. 过点C 作CD⊥BB′于点D. ∴∠B ′CD =12∠BCB′=β.在Rt △B ′CD 中,B ′D =B′C·s in β=B C·sin β=n sin β,∴BB ′=2B′D=2n sin β. 由α+β=180°得到△A′B′B 为直角三角形,∴A ′B =(A′B′)2+(BB′)2=m 2+(2n sin β)2=m 2+4n 2sin 2β.9.(2016·某某)在△ABC 中,AB =6,AC =8,BC =10.D 是△ABC 内部或BC 边上的一个动点(与B ,C 不重合).以D 为顶点作△DEF,使△DEF∽△ABC(相似比k>1),EF ∥BC. (1)求∠D 的度数;(2)若两三角形重叠部分的形状始终是四边形AGDH.①连接GH ,AD ,当GH⊥AD 时,请判断四边形AGDH 的形状,并证明; ②当四边形AGDH 的面积最大时,过A 作AP⊥EF 于P ,且AP =AD ,求k 的值.解:(1)∵AB 2+AC 2=62+82=102=BC 2,∴∠BAC =90°.又∵△DEF∽△ABC,∴∠D =∠BAC =90°.(2)①四边形AGDH 是正方形.证明:延长ED 、FD 分别交BC 于点M 、N.∵△DEF ∽△ABC ,∴∠E =∠B.又∵EF∥BC,∴∠E =∠EMC.∴∠B=∠EMC.∴ED∥BA.同理FD∥AC.∴四边形AGDH 是平行四边形.又∵∠FDE=90°,∴四边形AGDH 是矩形.又∵AD⊥GH,∴四边形AGDH 是正方形.②当D 点在△ABC 内部时,四边形AGDH 的面积不可能最大.其理由是:如图1,点D 在内部时,延长GD 到D′,过D′作MD′⊥AC 于点M ,则四边形GD′MA 的面积大于矩形AGDH 的面积,∴当点D 在△ABC 内部时,四边形AGDH 的面积不可能最大.按上述理由,只有当D 点在BC 边上时,面积才有可能最大.图1 图2如图2,D 在BC 上时,易证明DG∥AC,∴△GDB ∽△ACB.∴BG BA =GD AC ,即BA -AG BA =AH AC . ∴6-AG 6=AH 8,即AH =8-43AG. ∴S 矩形AGDH =AG·AH=AG×(8-43AG)=-43AG 2+8AG =-43(AG -3)2+12. 当AG =3时,S 矩形AGDH 最大,此时DG =AH =4.即当AG =3,AH =4,S 矩形AG DH 最大.在Rt △BGD 中,BD =BG 2+DG 2=5,则DC =BC -BD =5.即D 为B C 上的中点时,S 矩形AGDH 最大.∴在Rt △ABC 中,AD =BC 2=5,∴PA =AD =5. 延长PA 交BC 于点Q ,∵EF ∥BC ,QP ⊥EF ,∴QP ⊥BC.∴QP 是EF 、BC 之间的距离.∴D 到EF 的距离为PQ 的长.在Rt △ABC 中,12AB·AC=12BC·AQ, ∴AQ =4.8.又∵△DEF∽△ABC,∴k =PQ AQ =PA +AQ AQ =5+4.84.8=4924.10.(2016·某某)(1)发现如图1,点A 为线段BC 外一动点,且BC =a ,AB =b.填空:当点A 位于CB 延长线上时,线段AC 的长取得最大值,且最大值为a +b .(用含a ,b 的式子表示)图1(2)应用点A 为线段BC 外一动点,且BC =3,AB ,分别以AB ,AC 为边,作等边三角形ABD 和等边三角形ACE ,连接CD ,BE. ①请找出图中与BE 相等的线段,并说明理由;②直接写出线段BE 长的最大值.(3)拓展如图3,在平面直角坐标系中,点A 的坐标为(2,0),点B 的坐标为(5,0),点P 为线段AB 外一动点,且PA =2,PM =PB ,∠BPM =90°.请直接写出线段AM 长的最大值及此时点P 的坐标.图2 图3 备用图解:(2)①DC=BE.理由如下:∵△ABD和△ACE为等边三角形,∴AD=AB,AC=AE,∠BAD=∠CA E=60°.∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.∴△CAD≌△EAB.∴DC=BE.②BE长的最大值是4.(3)AM的最大值为3+22,点P的坐标为(2-2,2).提示:如图3,构造△BNP≌△MAP,则NB=AM,易得△APN是等腰直角三角形,AP=2,∴AN=2 2.由(1)知,当点N在BA的延长线上时,NB有最大值(如备用图).∴AM=NB=AB+AN=3+2 2.过点P作PE⊥x轴于点E,PE=AE= 2.又∵A(2,0),∴P(2-2,2).。
2022年中考英语综合复习题(六)

知识运用(两节,共20小题,满分20分)A )单项选择从A 、B 、C 三个选项中选择最佳答案填空。
(共10小题,每小题1分)()1.Can you suggest some places where I can make _______one -day trip from Shanghai?A.a B.an C.the ()2.They argued among _______and finally drew a conclusion.A.them B.their C.themselves ()3.Ants will form a bridge if there is a river in the path,_______the other ants can travel across.A.so B.for C.but ()4.It took the ancient Chinese people several _______years to finish building the Great Wall.A.hundred B.hundreds C.hundreds of ()5.This is _______painting I have ever seen in the exhibition.A.precious B.more precious C.the most precious ()6.The detective promised to try his best to solve the case,_______?A.didn ’t he B.doesn ’t he C.hasn ’t he ()7.The rubbish _______from the grass,and then the campsite was clean again.A.removed B.is removed C.was removed ()8.—_______you rush me now?I ’m working on another report.—I ’m sorry,but Miss Grace has to check this report this afternoon.A.Need B.Should C.Must ()9.—I heard the coach didn ’t think much of her.—But she makes up for _______she didn ’t have in physical skills with her clever brain and hard work.A.whoever B.whatever C.whenever ()10.—Excuse me.Could you please tell me _______?I want to buy some fresh food.—Sure.It ’s between the bookstore and the post office.A.why is the supermarket crowded B.where the supermarket is C.how can I get to the supermarket 综合复习题(六)(满分:100分)2022年中考英语B)完形填空阅读短文,掌握其大意,从A、B、C三个选项中选择最佳答案填空。
人教九年级中考数学复习题(六)--圆(含答.案)

九年级中考数学复习题(六)圆一、选择题(每题3分,共30分)1、如图,⊙O 的半径13,弦AB 的长度是24,AB ON ⊥,垂足为N ,则ON=( )A 、5B 、7C 、9D 、112、如图,AB 是⊙O 的直径,BC 是⊙O 的弦,若 60=∠OBC ,则BAC ∠的度数是( )A 、 75B 、 60C 、 45D 、303、在Rt ABC ∆中,,4,3,90cm BC cm AC C ===∠ 则它的外心与顶点C 的距离为( )A 、cm 2B 、cm 5.2C 、cm 3D 、cm 44、已知⊙O 的半径为5,点O 到同一平面内直线l 的距离为4,则直线l 与⊙O 的位置关系是( )A 、相离B 、相切C 、相交D 、无法判断5、正六边形的边心距为3,则该正六边形的边长是( ) A 、3 B 、2 C 、3 D 、326、如图,PA ,PB 是⊙O 的切线,切点分别为A ,B ,若OA=2, 60=∠P ,则AB 的长为( ) A 、π32 B 、π C 、π34 D 、π35 7、如图,在半径为cm 13的圆形铁片上切下一块高为cm 8的弓形铁片,则弓形弦AB 的长为( )A 、cm 10B 、16cmC 、24cmD 、26cm8、如图,四边形ABCD 内接于⊙O ,若四边形ABCO 是平行四边形,则ADC ∠的大小为( )A 、 45B 、 30C 、 60D 、759、如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB 与小圆有公共点,则弦AB 的取值范围是( )A 、108≤≤AB B 、108≤<ABC 、54≤≤ABD 、54≤<AB10、如图,PA ,PB 切⊙O 于A 、B 两点,CD 切⊙O 于点E ,交PA 、PB 于C 、D ,若⊙O 的半径为r ,PCD ∆的周长等于r 3,则APB ∠tan 的值是( )A 、13125B 、512C 、1353D 、1332二、填空题(每题4分,共24分)11、如图,⊙O 是ABC ∆的外接圆, 68=∠A ,则OBC ∠的大小是 .12、如图,在平面直角坐标系中,点O 为坐标原点,点P 在第一象限,⊙P 与x 轴交于OA 两点,点A 的坐标为(6,0),⊙P 的半径为13,则点P 的坐标为 .13、如图,AB 和⊙O 切于点B ,AB=5,OB=3,则A tan = .14、如图,正六边形ABCDEF 内接于⊙O ,正六边形的周长是12,则⊙O 的半径是 .15、如图,正方形ABCD 内接于半径为2的⊙O ,则图中阴影部分的面积为 .16、如图,已知等边ABC ∆的边长为6,以AB 为直径的⊙O 与边AC ,BC 分别交于D ,E 两点,则劣弧DE 的长为 .三、解答题一(每题6分,共18分)17、如图,AT 切⊙O 于点A ,AB 是⊙O 的直径,若 40=∠ABT ,求ATB ∠的度数.18、如图,⊙O 的直径AB 过弦CD 的中点E ,若 25=∠C ,求D ∠的大小.19、已知一个圆锥的底面半径为2,母线长为5,求这个圆锥的侧面积.(结果保留π)四、解答题二(每题7分,共21分)20、如图,CD 为⊙O 的直径,弦AB 交CD 于点E ,连接BD 、OB.(1)求证:AEC ∆ DEB ∆;(2)若,2,8,==⊥DE AB AB CD 求⊙O 的半径.21、如图,在Rt ABC ∆中,90=∠B ,点O 在边AB 上,以点O 为圆心,OA 为半径的圆经过点C ,过点C 作直线MN ,使.2A BCM ∠=∠(1)判断直线MN 与⊙O 的位置关系,并说明理由;(2)若OA=4, 60=∠BCM ,求图中阴影部分的面积.22、如图,点O 为Rt ABC ∆斜边AB 上的一点,以OA 为半径的⊙O 与BC 切于点D ,与AC 交于点E ,连接AD.(1)求证:AD 平分BAC ∠;(2)若 60=∠BAC ,OA=2,求阴影部分的面积(结果保留π)五、解答题三(每题9分,共27分)23、如图,ABC ∆中,AB=AC ,以AB 为直径作⊙O ,交BC 于点D ,交CA 的延长线于点E ,连结AD ,DE.(1)求证:D 是BC 的中点;(2)若DE=3,BD-AD=2,求⊙O 的半径;(3)在(2)的条件下,求弦AE 的长.24、如图,AB 是⊙O 的直径,点C 在AB 的延长线上,AB=4,BC=2,P 是⊙O 上半部分的一个动点,连接OP ,CP.(1)求OPC ∆的最大面积;(2)求OCP ∠的最大度数;(3)如图2,延长PO 交⊙O 于点D ,连接DB.当CP=DP 时,求证:CP 是⊙O 的切线.25、如图,点A 、B 、C 、D 是直径为AB 的⊙O 上的四个点,C 是劣弧BD 的中点,AC 与BD 交于点E.(1)求证:AC CE DC ⋅=2(2)若AE=2,EC=1,求证:AOD ∆是正三角形.(3)在(2)的条件下,过点C 作⊙O 的切线,交AB 的延长线于点H ,求ACH ∆的面积.九年级中考数学复习题(六)圆参考答案一、ADBCB CCCAB二、11、 22 12、(3,2) 13、53 14、2 15、2-π 16、π 三、 切解AT 、 :17⊙O 于点A ,AB 是⊙O 的直径,90=∠∴BAT90=∠+∠∴ATB ABT又40=∠ABT 504090=-=∠∴ATB18、解:,25,25=∠=∠∴=∠C A C ⊙O 的直径AB 过弦CD 的中点E ,∴,90, =∠∴⊥AED CD AB 652590=-=∠∴D19、解:ππ1025=⨯⨯=侧S ,答:这个圆锥的侧面积为.10π四、20、解:(1)证明:,,BED CEA DBE C ∠=∠∠=∠AEC ∆∴ .DEB ∆(2)设 ⊙O 的半径为r ,8,=⊥,AB CD AB CD 是直径 ,,4==∴BE AE在Rt ,OB BE ,OEOBE 222=+∆中 即,4)2(222r r =+-.5=∴r21、解:(1)MN 是⊙O 的切线,理由如下:连接OCOCA OAC OC OA ∠=∠∴=,,2,2A BCM A OCA A BOC ∠=∠∠=∠+∠=∠,BOC BCM ∠=∠∴,,90,90,90MN OC BCO BCM BCO BOC B ⊥∴=∠+∠∴=∠+∠∴=∠∴MN 是⊙O 的切线. .343163242136041203222130412060)1()2(2-=⨯⨯-⨯=-=∴===∴=∠==∆=∠∴=∠=∠∆ππOAC OAC S S S ,,BC OC BO ,BCO ,OA ,OC BCO Rt ,AOC ,BCM BOC 扇形阴影中在知由 .:)1(22OD 、连接证明BC 是⊙O 的切线,D 为切点,∴.BC OD ⊥.//BAC AD OAD ,CAD OADADO OA ,OD CAD ,ADO ACOD BC ,AC ∠∠=∠∠=∠∴=∠=∠∴∴⊥平分即又又(2)解:连接OE ,ED , ,,60OA OE BAC ==∠OAE ∆∴为等边三角形,.32360260602//3021,30,602ππ=⨯⨯==∴=∠=∠=∴∴∠=∠∴=∠=∠=∠=∠∴=∠∴∆∆ODEOEDAED S S ,EAD DOE S S AO ,ED OAD ,ADE ,BAC EAD OAD ADE AOE 扇形阴影又又五、为证明解AB 、 :)1(:23⊙O 的直径,.BC AD ⊥∴又,AC AB =.的中点是BC D ∴ ,AD BD AB ,,AD ,BD ABD Rt ,AD ,AD BD ,DE BD DE ,DC E ,C E ,B C B AC AB 101313123,,)2(2222=+=+=∴==∆=∴=-==∴=∴∠=∠∴∠=∠∠=∠∴=中在又又 则⊙O 的半径为.210 (3)连接BE ,AB 是⊙O 的直径,C ,C ,BEC ADC ,BEC ADC BEC ∠=∠=∠=∠∆∆=∠∴ 90,90中和在∴ADC ∆ ,BEC ∆.5104,51091063,=-=∴=⨯=⋅=∴=∴AC CE AE CA CB CD CE CBCA CE CD .44224)1(:24的最大面积为的面积最大此时边上的高为最大值时当是定值的边长解OPC ,BC OB ,OC OB OP ,,BC AB ,OPC ,,OC OC OP ,OC OPC 、∆∴=+===∴==∆⊥∴∆ (2)当PC 与⊙O 相切,.30,30,21sin 2490 的最大度数为中在的度数最大时即OCP OCP OC OP OCP ,,OP ,OC OPC ,OPC Rt ,OCP ,PC OP ∠∴=∠∴==∠∴===∠∆∠⊥(3)如图,连接AP 、BP , .4,,,,,.,PBD OPC PBDOPC BD ,,PC PD OC D C D A C A PC AP DB CP DB AP DOB AOP ∠=∠∴∆≅∆∴===∠=∠∴∠=∠∠=∠∴=∴==∴∠=∠ 又PD 是⊙O 的直径,,90,90PC OP OPC PBD ⊥∴=∠∴=∠∴又OP 是⊙O 的半径,∴CP 是⊙O 的切线.DCE ,ACD CDB ,DAC ,BD C 、∠=∠∠=∠∴ 又的中点是劣弧证明:)1(25ACD ∆∴ DCE ∆,AC CE DC CECD DC AD ⋅=∴=2, 312,1,2)2(=+=+=∴==EC AE AC EC AE3,32==∴DC DC 即,如图,连接OC ,OD ,,BD C 的中点是劣弧 3==∴DC BC ,AB 是⊙O 的直径, 90=∠∴ACB ,AB=32)3(32222=+=+BC AC , 3===∴OD OC OBDOC BOC ∆∆∴和均是正三角形,.,60180,120是正三角形又AOD OD ,OA BOD DOA BOD ∆∴==∠-=∠∴=∠∴,AGC G ,AH CG C 90:)3(=∠⊥则于点作过点解 是CH ⊙O 的切线,,90, =∠∴⊥∴HCO CH OC .4392333212133223323233212130,.30,30609090,60=⨯⨯=⋅=∴==∴===⨯==∴=∠∆=∴∆∴∠=∠∴=∠=-=∠-=∠∴=∠∆CG AH S ,AG AH ,AC ,AG AC CG ,CAG ,ACG Rt GH ,AG ,ACH H CAH CAB COH H COH AHC 中在是等腰三角形。
初中数学中考一轮复习专题6 三角形 重点、考点知识、方法总结及真题练习
A.
B.
【答案】A.
C.
D.
【解析】解:三角形具有稳定性.
故选:A.
知识点 2 等腰三角形
等腰三角形的概念不性质
1、等腰三角形:有两条边相等的三角形叫做等腰三角形.相等的两边叫做三角形的腰,第三
边叫做三角形的底.
2、等腰三角形的性质
①等腰三角形的腰相等
②等腰三角形的两个底角相等(简记为”等边对等角“)
2.如图,在△ABC 中,AB=AC.以点 C 为圆心,以 CB 长为半径作圆弧,交 AC 的延长线于
点 D,连结 BD.若∠A=32°,则∠CDB 的大小为 度.
【答案】37 【解析】解:∵AB=AC,∠A=32°,∴∠ABC=∠ACB=74°, 又∵BC=DC,∴∠CDB=∠CBD= ∠ACB=37°.
.
【答案】40° 【解析】解:∵BO、CO 分别平分∠ABC、∠ACB, ∴∠OBC= ∠ABC,∠OCB= ∠ACB,
而∠BOC+∠OBC+∠OCB=180°, ∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣ (∠ABC+∠ACB),
∵∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A, ∴∠BOC=180°﹣ (180°﹣∠A)=90°+ ∠A,
3.如图,在△ABC 中,∠A=36°,AB=AC,BD 平分∠ABC,则图中等腰三角形的个数
是
.
【答案】3
【解析】解:∵AB=AC,∠A=36°∴△ABC 是等腰三角形,
∠ABC=∠ACB=
=72°,
BD 平分∠ABC,∴∠EBD=∠DBC=36°,
∴在△ABD 中,∠A=∠ABD=36°,AD=BD,△ABD 是等腰三角形,
中考数学复习课件练习:专题复习六 几何综合题有答案

中考数学复习课件+练习:专题复习(六) 几何综合题(有答案)专题复习(六)几何综合题类型1类比探究的几何综合题1.(2019·岳阳)问题背景:已知∠EDF的顶点D 在△ABC的边AB所在直线上(不与A,B重合).DE交AC所在直线于点M,DF交BC所在直线于点N.记△ADM的面积为S1,△BND 的面积为S2.(1)初步尝试:如图1,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD =2时,则S1·S2=12;(2)类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图2所示位置,求S1·S2的值;(3)延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.(Ⅰ)如图3,当点D在线段AB上运动时,设AD=a,BD=b,求S1·S2的表达式(结果用a,b和α的三角函数表示);(Ⅱ)如图4,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1·S2的表达式,不必写出解答过程.解:(1)在图1中,∵△ABC是等边三角形,∴AB=CB=AC=6,∠A=∠B=60°. ∵DE∥BC,∠EDF=∠A=60°,∴∠BND=∠EDF=60°.∴∠BDN=∠ADM=60°.∴△ADM,△BDN都是等边三角形.∴S1=34×22=3,S2=34×42=4 3.∴S1S2=12.(2)在图2中,设AM=x,BN=y.∵∠MDB=∠MDN+∠NDB=∠A+∠AMD,∠MDN=∠A,∴∠AMD=∠NDB.∵∠A=∠B,∴△AMD∽△BDN.∴AMBD=ADBN.∴x2=4y.∴xy=8.∵S1=12AD·AM sin60°=3x,S2=12DB·BN sin60°=32y,∴S 1S 2=3x·32y =32xy =12. (3)(Ⅰ)在图3中,设AM =x ,BN =y , 同法可证△AMD ∽△BDN ,可得xy =ab.∵S 1=12AD·AM sin α=12ax sin α, S 2=12DB·BN sin α=12by sin α, ∴S 1S 2=14(ab)2sin 2α. (Ⅱ)在图4中,设AM =x ,BN =y ,同法可证△AMD ∽△BDN ,可得xy =ab ,∵S 1=12AD·AM sin α=12ax sin α, S 2=12DB·BN sin α=12by sin α, ∴S 1S 2=14(ab)2sin 2α. 2.(2019·自贡)如图,已知∠AOB =60°,在∠AOB 的平分线OM 上有一点C ,将一个120°角的顶点与点C 重合,它的两条边分别与直线OA ,OB 相交于点D ,E.(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给予证明;若不成立,线段OD,OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.图1图2图3解:(1)∵OM是∠AOB的平分线,∴∠AOC=∠BOC=12∠AOB=30°.∵CD⊥OA,∴∠ODC=90°.∴∠OCD=60°.∴∠OCE=∠DCE-∠OCD=60°.在Rt△OCD中,OD=OC·cos30°=32OC,同理,OE=32OC.∴OD+OE=3OC.(2)(1)中的结论仍然成立.理由:过点C作CF⊥OA于点F,CG⊥OB于点G,∴∠OFC=∠OGC=90°.∵∠AOB=60°,∴∠FCG=120°.同(1)的方法得OF=32OC,OG=32OC.∴OF+OG=3OC.∵CF⊥OA,CG⊥OB,且点C是∠AOB 的平分线OM上一点,∴CF=CG.∵∠DCE=∠FCG=120°,∴∠DCF=∠ECG.∴△CFD≌△CGE.∴DF=EG.∴OF=OD+DF=OD+EG,OG=OE-EG.∴OF+OG=OD+EG+OE-EG=OD+OE.∴OD+OE=3OC.(3)(1)中的结论不成立,结论为OE-OD=3OC.3.(2019·东营)(1)某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC 上,∠BAO=30°,∠OAC=75°,AO=33,BO∶CO=1∶3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).请回答:∠ADB=75°,AB=43;(2)请参考以上解决思路,解决问题:如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=33,∠ABC =∠ACB=75°,BO∶OD=1∶3,求DC的长.图1图2 图3解:过点B作BE∥AD交AC于点E.∵AC⊥AD,∴∠DAO =∠BEO=90°.∵∠AOD =∠EOB,∴△AOD∽△EOB.∴BODO=EOAO=BEDA.∵BO∶OD=1∶3,∴EOAO=BEDA=13.∵AO=33,∴EO= 3.∴AE=4 3. ∵∠ABC=∠ACB=75°,∴∠BAC=30°,AB=AC.∴AB=AC=AEcos30°=8.∴BE=12AB=4,AD=3BE=12.在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,得CD=413. 4.(2019·江西)在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.图1图2图3图4(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是BP=CE,CE与AD的位置关系是AD⊥CE;(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);(3)如图4,当点P在线段BD的延长线上时,连接BE.若AB=23,BE=219,求四边形ADPE的面积.解:(1)提示:连接AC,延长CE交AD于点H,证明△ABP≌△ACE.(2)结论仍然成立.理由:选图2,连接AC交BD于点O,设CE交AD于点H.∵四边形ABCD是菱形,∠ABC=60°,∴△ABC,△ACD都是等边三角形,∠ABD =∠CBD=30°.∴AB=AC.∵△APE是等边三角形,∴AP=AE,∠BAC=∠PAE=60°.∴∠BAP=∠CAE.∴△BAP≌△CAE.∴BP=CE,∠ACE=∠ABP=30°.∵∠CAH=60°,∴∠CAH+∠ACH=90°.∴∠AHC=90°,即CE⊥AD.(3)连接AC交BD于点O,连接CE交AD 于点H.由(2)可知,EC⊥AD,CE=BP.在菱形ABCD中,AD∥BC,∴EC⊥BC.∵BC=AB=23,BE=219,在Rt△BCE中,EC=(219)2-(23)2=8.∴BP=CE=8.∵AC与BD是菱形的对角线,∴∠ABD=12∠ABC=30°,AC⊥BD. ∴BD=2BO=2AB·cos30°=6.∴OA=12AB=3,DP=BP-BD=8-6=2.∴OP=OD+DP=5.在Rt△AOP中,AP=AO2+OP2=27,∴S四边形ADPE =S△ADP+S△AEP=12×2×3+34×(27)2=8 3.5.(2019·烟台)【问题解决】一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?小明通过观察、分析、思考,形成了如下思路:思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;思路二:将△APB绕点B顺时针旋转90°,得到△CP′B,连接PP′,求出∠APB的度数.请参考小明的思路,任选一种写出完整的解答过程.【类比探究】如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=11,求∠APB的度数.图1图2解:【问题解决】思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,∴△ABP′≌△CBP.∴∠PBP′=90°,BP′=BP=2,AP′=CP=3.在Rt△PBP′中,BP=BP′=2,∴∠BPP′=45°,根据勾股定理,得PP′=2 BP=2 2.∵AP=1,∴AP2+PP′2=1+8=9.∵AP′2=32=9,∴AP2+PP′2=AP′2.∴△APP′是直角三角形,且∠APP′=90°.∴∠APB=∠APP′+∠BPP′=90°+45°=135°.【类比探究】将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,∴△ABP′≌△CBP.∴∠PBP′=90°,BP′=BP=1,AP′=CP=11.在Rt△PBP′中,BP=BP′=1,∴∠BPP′=45°,根据勾股定理,得PP′=2 BP= 2.∵AP=3,∴AP2+PP′2=9+2=11.∵AP′2=(11)2=11,∴AP2+PP′2=AP′2.∴△APP′是直角三角形,且∠APP′=90°.∴∠APB=∠APP′-∠BPP′=90°-45°=45°.6.(2019·黄石)在△ABC中,E,F分别为线段AB,AC上的点(不与A,B,C重合).(1)如图1,若EF∥BC,求证:S△AEFS△ABC=AE·AFAB·AC;(2)如图2,若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由;(3)如图3,若EF上一点G恰为△ABC的重心,AEAB=34,求S△AEFS△ABC的值.图1图2图3 解:(1)∵EF∥BC,∴△AEF∽△ABC.∴AEAB=AFAC.∴S△AEFS△ABC=(AEAB)2=AEAB·AFAC=AE·AFAB·AC.(2)若EF不与BC平行,(1)中的结论仍然成立.分别过点F,C作AB的垂线,垂足分别为N,H.∵FN⊥AB,CH⊥AB,∴FN∥CH.∴△AFN∽△ACH.∴FNCH=AFAC.∴S△AEFS△ABC=12AE·FN12AB·CH=AE·AFAB·AC.(3)连接AG并延长,交BC于点M,连接BG并延长,交AC于点N,连接M,N,则M,N分别是BC,AC的中点,∴MN∥AB,且MN=12AB.∴GM GA =GN GB =12,且S △ABM =S △ACM . ∴AG AM =23. 设AF AC=a , 由(2)知,S △AEG S △ABM=AE·AG AB·AM =34×23=12, S △AFG S △ACM =AG·AF AM·AC =23a , 则S △AEF S △ABC =S △AEG +S △AFG 2S △ACM =S △AEG 2S △ABM +S △AFG 2S △ACM=14+13a. 而S △AEF S △ABC =AE·AF AB·AC =34a , ∴14+13a =34a ,解得a =35. ∴S △AEF S △ABC =34×35=920. 7.(2019·河南)(1)问题发现如图1,在△OAB 和△OCD 中,OA =OB ,OC =OD ,∠AOB =∠COD =40°,连接AC ,BD 相交于点M.填空:①AC BD的值为1; ②∠AMB 的度数为40°;(2)类比探究如图2,在△OAB 和△OCD 中,∠AOB =∠COD =90°,∠OAB =∠OCD =30°,连接AC交BD 的延长线于点M.请判断AC BD的值及∠AMB 的度数,并说明理由;(3)拓展延伸在(2)的条件下,将△OCD 绕点O 在平面内旋转,AC ,BD 所在直线交于点M.若OD =1,OB =7,请直接写出当点C 与点M 重合时AC 的长.图1图2 图3解:(2)AC BD=3,∠AMB =90°. 理由如下:∵∠AOB =∠COD =90°,∠OAB =∠OCD=30°,∴CODO=AOBO=3,∠COD+∠AOD=∠AOB+∠AOD,即∠AOC=∠BOD.∴△AOC∽△BOD.∴ACBD=CODO=3,∠CAO=∠DBO.∵∠AOB=90°,∴∠DBO+∠ABD+∠BAO=90°.∴∠CAO+∠ABD+∠BAO=90°.∴∠AMB=90°.(3)AC的长为23或3 3.提示:在△OCD旋转的过程中,(2)中的结论仍然成立,即ACBD=3,∠AMB=90°.如图所示,点C与点M重合,AC1,AC2的长即为所求.8.(2019·淄博)(1)操作发现:如图1,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC 为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是MG=NG;位置关系是MG⊥NG;(2)类比思考:如图2,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其他条件不变,小明发现的上述结论还成立吗?请说明理由;(3)深入研究:如图3,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其他条件不变,试判断△GMN 的形状,并给予证明.图1图2图3解:(1)连接BE,CD相交于点H,∵△ABD和△ACE都是等腰直角三角形,∴AB=AD,AC=AE,∠BAD=∠CAE=90°.∴∠CAD=∠BAE.∴△ACD≌△AEB(SAS).∴CD=BE,∠ADC=∠ABE.∴∠BDC+∠DBH=∠BDC+∠ABD+∠ABE=∠BDC+∠ABD+∠ADC=∠ADB+∠ABD=90°.∴∠BHD=90°.∴CD⊥BE.∵点M,G分别是BD,BC的中点,∴MG//12CD.同理NG//12BE.∴MG=NG,MG⊥NG.故答案为MG=NG,MG⊥NG.(2)连接CD,BE,相交于点H,同(1)的方法得,MG=NG,MG⊥NG.(3)连接EB,DC,延长线相交于点H,同(1)的方法得,△ABE≌△ADC,MG=NG.∴∠AEB=∠ACD.∴∠CEH+∠ECH=∠AEH-∠AEC+180°-∠ACD-∠ACE=∠ACD-45°+180°-∠ACD-45°=90°.∴∠DHE=90°.同(1)的方法得,MG⊥NG.类型2与图形变换有关的几何综合题1.(2019·襄阳)如图1,已知点G在正方形ABCD 的对角线AC上,GE⊥BC,垂足为E,GF⊥CD, 垂足为F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:AGBE的值为2;(2)探究与证明:将四边形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:四边形CEGF在旋转过程中,当B,E,F 三点在一条直线上时,如图3所示,延长CG交AD于点H.若AG=6,GH=22,则BC=35.图1图2图3解:(1)①证明:∵四边形ABCD是正方形,∴∠BCD=90°,∠BCA=45°.∵GE⊥BC,GF⊥CD,∴∠CEG=∠CFG=∠ECF=90°.∴四边形CEGF是矩形,∠CGE=∠ECG =45°.∴EG=EC.∴四边形CEGF是正方形.(2)连接CG,由旋转性质可知,∠BCE=∠ACG=α.在Rt△CEG和Rt△CBA中,CECG=cos45°=22,CBCA=cos45°=22.∴CGCE=CACB= 2.又∵∠ECG=∠ECA=∠ACB-∠ECA,即∠ACG=∠BCE,∴△ACG∽△BCE.∴AGBE=CACB= 2.∴线段AG与BE之间的数量关系为AG=2BE.2.(2019·仙桃)问题:如图1,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为BC=DC+EC;探索:如图2,在Rt△ABC与Rt△ADE中,AB =AC ,AD =AE ,将△ADE 绕点A 旋转,使点D 落在BC 边上,试探索线段AD ,BD ,CD 之间满足的等量关系,并证明你的结论;应用:如图3,在四边形ABCD 中,∠ABC =∠ACB =∠ADC =45°.若BD =9,CD =3,求AD 的长.图1图2 图3解:探索:BD 2+CD 2=2AD 2.连接CE.∵∠BAD +∠DAC =90°=∠DAC +∠CAE ,∴∠BAD =∠CAE.在△ABD 和△ACE 中,⎩⎪⎨⎪⎧AB =AC ,∠BAD =∠CAE ,AD =AE ,∴△ABD ≌△ACE(SAS ).∴BD =CE ,∠B =∠ACE.∵Rt △ABC 与Rt △ADE 是等腰直角三角形,∴DE 2=2AD 2.∴∠B =45°.∴∠ACB +∠ACE =45°+45°=90°.∴∠DCE=90°.∴DC2+CE2=DE2,即BD2+CD2=2AD2.应用:以AD为腰作等腰Rt△ADE,连接CE,由“探索”可知,△ABD≌△ACE(SAS).∴CE=BD=9.∵∠ADC=∠ADE=45°,∴∠EDC=90°.在Rt△CDE中,由勾股定理,得DE=92-32=6 2.在等腰Rt△ADE中,AD=22DE=6.3.(2019·宜昌)在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E,且在AD上,BE交PC于点F.(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;(2)如图2,①求证:BP=BF;②当AD=25,且AE<DE时,求cos∠PCB 的值;③当BP=9时,求BE·EF的值.图1 图2 图2备用图解:(1)证明:在矩形ABCD 中,∠A =∠D =90°,AB =DC ,∵点E 是AD 中点,∴AE =DE.在△AEB 和△DEC 中,⎩⎪⎨⎪⎧AB =DC ,∠A =∠D =90°,AE =DE ,∴△AEB ≌△DEC(SAS ).(2)①证明:在矩形ABCD 中,∠ABC =90°. ∵△BPC 沿PC 折叠得到△GPC ,∴∠PGC =∠PBC =90°,∠BPC =∠GPC. ∵BE ⊥CG ,∴BE ∥PG.∴∠GPF =∠PFB.∴∠BPF =∠PFB.∴BP =BF.②当AD =25时,∵∠BEC =90°,∴∠AEB +∠PEC =90°. ∵∠AEB +∠ABE =90°,∴∠DEC =∠ABE.∵∠A =∠D =90°,∴△ABE ∽△DEC.∴AB AE =DE DC.设AE=x,则DE=25-x,∴12x=25-x12.∴x=9或x=16.∵AE<DE,∴AE=9,DE=16.∴由勾股定理,得CE=20,BE=15.由折叠得,BP=PG,BC=GC,∴BP=BF =PG.∵BE∥PG,∴△ECF∽△GCP.∴EFGP=CECG.设BP=BF=PG=y,∴15-yy=2025.∴y=253,即BP=253.在Rt△PBC中,由勾股定理,得PC=25103,cos∠PCB=BCPC=31010.③连接FG,∵∠GEF=∠G=90°,∴BE∥PG. ∵BF∥PG,BF=PG=BP,∴四边形BPGF是菱形.∴BP∥GF,且BP=GF.∴∠GFE=∠EBA. ∴△GEF∽△EAB.∴EFGF=ABEB.∴BE·EF=AB·GF=AB·BP=12×9=108. 4.(2019·永州)如图1,在△ABC中,矩形EFGH 的一边EF在AB上,顶点G,H分别在BC,AC上,CD是边AB上的高,CD交GH于点I.若CI=4,HI=3,AD=92,矩形DFGI恰好为正方形.图1图2图3(1)求正方形DFGI的边长;(2)如图2,延长AB至P,使得AC=CP.将矩形EFGH沿BP的方向平移,当点G刚好落在CP上时,试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形,为什么?(3)如图3,连接DG,将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′,正方形DF′G′I′分别与线段DG,DB相交于点M,N,求△MN G′的周长.解:(1)∵HI∥AD,∴HIAD=CICD.∴392=4CD.∴CD=6.∴ID=CD-CI=2.∴正方形的边长为2.(2)如图2,设点G落在PC上时对应的点为点G′,点F的对应点为点F′.∵CA=CP,CD⊥PA,∴∠ACD=∠PCD,∠A=∠P.∵HG′∥PA,∴∠CHG′=∠A,∠CG′H=∠P.∴∠CHG′=∠CG′H.∴CH=CG′.∴IH=IG′=DF′=3.∵IG∥DB,∴IGDB=CICD.∴2DB=46.∴DB=3.∴DB=DF′=3.∴点B与点F′重合.∴移动后的矩形与△CBP重叠部分是三角形,即△BGG′.(3)将△DMI′绕点D顺时针旋转90°得到△DRF′,此时N,F′,R共线.∴∠MDR=90°.∵∠NDM=45°,∠NDM+∠NDR=90°,∴∠NDM=∠NDR=45°.∵DN=DN,DM=DR,∴△NDM≌△NDR.∴MN=NR=NF′+RF′=NF′+MI′.∴△MNG′的周长=MN+MG′+NG′=NF′+NG′+MI′=F′G′+I′G′=2I′G′=4. 5.(2019·岳阳)已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD 所在的直线对折,使点B落在点B′处,连接AB′,BB′,延长CD交BB′于点E,设∠ABC=2α.(0°<α<45°)(1)如图1,若AB=AC,求证:CD=2BE;(2)如图2,若AB≠AC,试求CD与BE的数量关系;(用含α的式子表示)(3)如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连接EF交BC 于点O,设△COE的面积为S1,△COF的面积为S2,求S1S2.(用含α的式子表示)图1图2图3解:(1)证明:∵点B,B′关于EC对称,∴BB′⊥EC,BE=EB′.∴∠DEB=∠DAC=90°.∵∠EDB=∠ADC,∴∠DBE=∠ACD.∵AB=AC,∠BAB′=∠CAD=90°,∴△BAB′≌△CAD.∴CD=BB′=2BE.(2)如图2,结论:CD=2BE·tan2α.理由:由(1)可知,∠ABB′=∠ACD,∠BAB′=∠CAD=90°,∴△BAB′∽△CAD.∴BB′CD=ABAC=1tan2α.∴2BECD=1tan2α.∴CD=2BE·tan2α.(3)如图3,在Rt△ABC中,∠ACB=90°-2α.∵EC平分∠ACB,∴∠ECB=12(90°-2α)=45°-α.∵∠BCF=45°+α,∴∠ECF=45°-α+45°+α=90°. ∴∠BEC+∠ECF=180°.∴BB′∥CF.∴△BEO∽△CFO.∴EOFO=BECF=BEBC=sin(45°-α).∵S1S2=EOFO,∴S1S2=sin(45°-α).6.(2019·潍坊)如图1,在▱ABCD中,DH⊥AB 于点H,CD的垂直平分线交CD于点E,交AB 于点F,AB=6,DH=4,BF∶FA=1∶5.(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.①求四边形BHMM′的面积;②直线EF上有一动点N,求△DNM周长的最小值;(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.图1图2图3解:(1)①在▱ABCD中,AB=6,直线EF 垂直平分CD,∴DE=FH=3.又BF∶FA=1∶5,∴BF=1,FA=5.∴AH=2.∵Rt△AHD∽Rt△MHF,∴HMFH=HAHD.∴HM3=24.∴HM=3 2.根据平移的性质,得MM′=CD=6,∴S四边形BHMM′=S△BMM′+S△BHM=12×6×32+12×4×32=15 2.②连接CM交直线EF于点N,连接DN. ∴CN=DN.∵MH=32,∴DM=52.在Rt△CDM中,MC2=DC2+DM2.∴MC2=62+(52)2,即MC=132.∵MN+DN的最小值=MN+CN=MC,∴△DNM周长的最小值为9.(2)∵BF∥CE,∴△DNM周长的最小值为9.(2)∵BF∥CE,∴QFQF+4=BFCE=13.∴QF=2.∴PK=PK′=6.过点K′作E′F′∥EF,分别交CD于点E′,交QK于点F′.当点P在线段CE上时,在Rt△PK′E′中,PE′2=PK′2-E′K′2,∴PE′=2 5.∵Rt△PE′K′∽Rt△K′F′Q,∴PE′K′F′=E′K′F′Q.∴252=4F′Q.∴F′Q=45 5.∴PE=PE′-EE′=25-455=655.∴CP=CE-PE=15-655.同理可得,当点P在线段ED上时,CP=15+655.综上可得,CP的长为15-655或15+655.类型3与动点有关的几何综合题1.(2019·黄冈)如图,在平面直角坐标系xOy中,菱形OABC的边OA在x轴正半轴上,点B,C 在第一象限,∠C=120°,边长OA=8.点M从原点O出发沿x轴正半轴以每秒1个单位长度的速度作匀速运动,点N从A出发沿边AB-BC-CO以每秒2个单位长度的速度作匀速运动,过点M作直线MP垂直于x轴并交折线OCB 于点P,交对角线OB于点Q,点M和点N同时出发,分别沿各自路线运动,点N运动到原点O时,M和N两点同时停止运动.(1)当t=2时,求线段PQ的长;(2)求t为何值时,点P与N重合;(3)设△APN的面积为S,求S与t的函数关系式及t的取值范围.解:(1)当t=2时,OM=2,在Rt△OPM中,∠POM=60°,∴PM=OM·tan60°=2 3.在Rt△OMQ中,∠QOM=30°,∴QM=OM·tan30°=23 3.∴PQ =PM -QM =23-233=433. (2)由题意,得8+(t -4)+2t =24,解得t =203. (3)①当0<t <4时,S =12·2t·43=43t ; ②当4≤t <203时,S =12×[8-(t -4)-(2t -8)]×43=403-63t ;③当203≤t <8时,S =12×[(t -4)+(2t -8)-8]×43=63t -403;④当8≤t ≤12时,S =S 菱形ABCO -S △AON -S △ABP -S △PCN=323-12(24-2t)×43-12×[8-(t -4)]×43-12(t -4)×32[8-(24-2t)] =-32t 2+123t -56 3. 综上,S =⎩⎪⎪⎪⎨⎪⎪⎪⎧43t ;(0<t <4)403-63t ;(4≤t <203)63t -403;(203≤t <8)-32t 2+123t -56 3.(8≤t ≤12) 2.(2019·青岛)已知:如图,四边形ABCD ,AB ∥DC ,CB ⊥AB ,AB =16 cm ,BC =6 cm ,CD =8 cm .动点P 从点D 开始沿DA 边匀速运动,动点Q 从点A 开始沿AB 边匀速运动,它们的运动速度均为2 cm /s .点P 和点Q 同时出发,以QA ,QP 为边作平行四边形AQPE ,设运动的时间为t(s ),0<t <5.根据题意解答下列问题:(1)用含t 的代数式表示AP ;(2)设四边形CPQB 的面积为S(cm 2),求S 与t 的函数关系式;(3)当QP ⊥BD 时,求t 的值;(4)在运动过程中,是否存在某一时刻t ,使点E 在∠ABD 的平分线上?若存在,求出t 的值;若不存在,请说明理由.解:(1)过点D 作DH ⊥AB 于点H ,则四边形DHBC 是矩形,∴CD =BH =8,DH =BC =6.∴AH =AB -BH =8,AD =DH 2+AH 2=10,BD =CD 2+BC 2=10.∴AP =AD -DP =10-2t.(2)过点P 作PN ⊥AB 于点N ,连接PB. 在Rt △APN 中,PA =10-2t ,∴PN =PA·sin ∠DAH =35(10-2t),AN =PA·cos ∠DAH =45(10-2t). ∴BN =16-AN =16-45(10-2t), S =S △PQB +S △BCP =12·(16-2t)·35(10-2t)+12×6×[16-45(10-2t)]=65t 2-545t +72(0<t <5). (3)当PQ ⊥BD 时,∠PQN +∠DBA =90°, ∵∠QPN +∠PQN =90°,∴∠QPN =∠DBA.∴tan ∠QPN =QN PN =34.∴45(10-2t)-2t35(10-2t)=34.解得t=3527.经检验,t=3527是分式方程的解,∴当t=3527s时,PQ⊥BD.(4)存在.理由:连接BE交DH于点K,过点K作KM⊥BD于点M.当BE平分∠ABD时,△KBH≌△KBM,∴KH=KM,BH=BM=8.设KH=KM=x,在Rt△DKM中,(6-x)2=22+x2,解得x=8 3.过点E作EF⊥AB于点F,则△AEF≌△QPN,∴EF=PN=35(10-2t),AF=QN=45(10-2t)-2t,∴BF =16-[45(10-2t)-2t]. ∵KH ∥EF ,∴KH EF =BH BF. ∴8335(10-2t )=816-[45(10-2t )-2t].解得t =2518. 经检验,t =2518是分式方程的解. ∴当t =2518s 时,点E 在∠ABD 的平分线上.3.(2019·绵阳)如图,已知△ABC 的顶点坐标分别为A(3,0),B(0,4),C(-3,0).动点M ,N 同时从A 点出发,M 沿A →C ,N 沿折线A →B →C ,均以每秒1个单位长度的速度移动,当一个动点到达终点C 时,另一个动点也随之停止移动,移动的时间记为t 秒,连接MN.(1)求直线BC 的解析式;(2)移动过程中,将△AMN 沿直线MN 翻折,点A 恰好落在BC 边上点D 处,求此时t 值及点D 的坐标;(3)当点M ,N 移动时,记△ABC 在直线MN 右侧部分的面积为S ,求S 关于时间t 的函数关系式.备用图解:(1)设直线BC 的解析式为y =kx +b ,则有⎩⎨⎧b =4,-3k +b =0,解得⎩⎨⎧k =43,b =4.∴直线BC 的解析式为y =43x +4. 图1(2)如图1,连接AD 交MN 于点O′.由题意可知,四边形AMDN 是菱形,M(3-t ,0),N(3-35t ,45t), ∴O′(3-45t ,25t),D(3-38t ,45t). ∵点D 在BC 上,∴45t =43×(3-85t)+4,解得t =3011. ∴t =3011s 时,点A 恰好落在BC 边上点D 处,此时D(-1511,2411). 图2(3)如图2,当0<t ≤5时,△ABC 在直线MN 右侧部分是△AMN ,S =12×t ×45t =25t 2; 如图3,当5<t ≤6时,△ABC 在直线MN 右侧部分是四边形ABNM.图3S =S △ABC -S △CMN =12×6×4-12×(6-t)×[4-45(t -5)]=-25t 2+325t -12. 4.(2019·广东)已知Rt △OAB ,∠OAB =90°,∠ABO =30°,斜边OB =4,将Rt △OAB 绕点O 顺时针旋转60°,如图1,连接BC.(1)填空:∠OBC =60°;(2)如图1,连接AC ,作OP ⊥AC ,垂足为P,求OP的长度;(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止.已知点M的运动速度为单位长度/秒,点N的运动速度为1单位长度/秒.设运动时间为x秒,△OMN的面积为y,求当x为何值时,y取得最大值?最大值为多少?(结果可保留根号)图1图2备用图解:(2)∵OB=4,∠ABO=30°,∴OA=12OB=2,AB=3OA=2 3.∴S△AOC =12OA·AB=12×2×23=2 3.∵△BOC是等边三角形,∴BC=BO=4.∴∠OBC=60°,∠ABC=∠ABO+∠OBC =90°.∴AC=AB2+BC2=27.∴OP=2S△AOCAC=4327=2217.(3)①当0<x ≤83时,点M 在OC 上运动,点N 在OB 上运动,此时过点N 作NE ⊥OC 且交OC 于点E.则NE =ON·sin 60°=32x , ∴y =12OM·NE =12××32x ,即y =338x 2. ∴当x =83时,y 有最大值,最大值为833. ②当83<x ≤4时,点M 在BC 上运动,点N 在OB 上运动.图3过点M 作MH ⊥OB 于点H.则BM =8-,MH =BM·sin 60°=32(8-1.5x), ∴y =12ON·MH =-338x 2+23x. ∵当x =83时,y 取最大值,∴y <833. ③当4<x ≤时,点M ,N 都在BC 上运动,过点O作OG⊥BC于点G.则MN=12-,OG=AB=23,图4∴y=12MN·OG=123-532x.∵当x=4时,y有最大值,∴y<2 3.综上所述,y有最大值,最大值为83 3.类型4与实践操作有关的几何综合题1.(2019·齐齐哈尔)折纸是一项有趣的活动,同学们小时候都玩过折纸,可能折过小动物、小花、飞机、小船等,折纸活动也伴随着我们初中数学的学习.在折纸过程中,我们可以通过研究图形的性质和运动,确定图形位置等,进一步发展空间观念,在经历借助图形思考问题的过程中,我们会初步建立几何直观.折纸往往从矩形纸片开始,今天,就让我们带着数学的眼光来玩一玩折纸,看看折叠矩形的对角线之后能得到哪些数学结论.实践操作如图1,将矩形纸片ABCD沿对角线AC翻折,使点B′落在矩形ABCD所在平面内,B′C 和AD相交于点E,连接B′D.图1图2解决问题(1)在图1中.①B′D和AC的位置关系为B′D∥AC(互相平行);②将△AEC剪下后展开,得到的图形是菱形;(2)若图1中的矩形变为平行四边形(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中一个结论加以证明,若不成立,请说明理由;(3)小红沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形,沿对称轴再次折叠后,得到的仍是轴对称图形,则小红折叠的矩形纸片的长和宽之比为1∶1或3∶1.拓展应用(4)在图2中,若∠B=30°,AB=43,当△AB′D恰好为直角三角形时,BC的长度为4或6或8或12.解:结果仍成立.①选择结论①证明.∵四边形ABCD是平行四边形,∴AD//BC.∴∠DAC=∠BCA.由折叠性质,得BC=B′C,∠BCA=∠ACB′,∴∠DAC=∠ACB′,B′C=AD.∴AE=CE,∴B′E=DE.∴∠CB′D=ADB′.∵∠AEC=∠B′ED,∠ACB′=∠CAD,∴∠ADB′=∠DAC.∴B′D∥AC.②选择结论②证明.设点E的对应为点F,连接AF.由折叠性质,得AE=AF,CE=CF.由①知AE=CE,∴AE=CE=AF=CF.∴四边形AECF是菱形.2.(2019·山西)综合性实践问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM,试判断线段AM与DE的位置关系.探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:证明:∵BE=AB,∴AE=2AB.∵AD=2AB,∴AD=AE.∵四边形ABCD是矩形,∴AD∥BC.∴EMDM=EBAB.(依据1)∵BE=AB,∴EMDM=1.∴EM=DM,即AM是△ADE的DE边上的中线.又∵AD=AE,∴AM⊥DE.(依据2)∴AM垂直平分DE.反思交流:(1)①上述证明过程中的“依据1”“依据2”分别是指什么?②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE 的左下方作正方形CEFG,发现点G在线段BC 的垂直平分线上,请你给出证明;探索发现:(3)如图3,连接CE,以CE为一边在CE 的右上方作正方形CEFG,可以发现点C,点B 都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.图1图2 图3解:(1)①依据1:两条直线被一组平行线所截,所得到的对应线段成比例(或平行线分线段成比例).依据2:等腰三角形顶角的平分线,底边上的中线及底边上的高互相重合(或等腰三角形的“三线合一”).②点A在线段GF的垂直平分线上.(2)证明:过点G作GH⊥BC于点H.∵四边形ABCD为矩形,点E在AB的延长线上,∴∠CBE=∠ABC=∠GHC=90°.∴∠BCE+∠BEC=90°.∵四边形CEFG为正方形,∴CG=CE,∠GCE=90°.∴∠BCE+∠BCG=90°.∴∠BEC=∠BCG.∴△GHC≌△CBE(AAS).∴HC=BE.∵四边形ABCD是矩形,∴AD=BC.∵AD=2AB,BE=AB,∴BC=2BE=2HC.∴HC=BH.∴GH垂直平分BC.∴点G在BC的垂直平分线上.(3)点F在BC边的垂直平分线上(或点F在AD边的垂直平分线上).过点F作FM⊥BC于点M,过点E作EN⊥FM于点N.∴∠BMN=∠ENM=∠ENF=90°.∵四边形ABCD是矩形,点E在AB的延长线上,∴∠CBE=∠ABC=90°.∴四边形BENM 为矩形.∴BM=EN,∠CEB+∠CEN=90°.∵四边形CEFG为正方形,∴EF=EC,∠CEF=90°.∴∠CEN+∠FEN=90°.∴∠CEB=∠FEN.∴△ENF≌△EBC(AAS).∴NE=BE.∴BM=BE.。
2023初中信息科技中考理论复习题6

2023初中信息科技中考理论复习题61.下列关于PowerPoint2013中设置动画说法正确的是()A、不同对象可以使用不同的动画效果B、一张幻灯片中同一类对象只能使用相同动画效果C、同一类对象只能设置相同的动画效果D、对象动画出现的顺序设置好以后是不能改变的2.在PowerPoint 2013中,要实现幻灯片从第3张到第6张跳转,可执行“插入”中的()A、自定义动画B、预设动画C、超链接或动作D、幻灯片切换3.演讲时要想让演示文稿更有说服力,下列做法不可取的是()A、用艺术字设置鲜明主题B、用尽量多的文字来解释C、选用适合内容的图片D、插入适合的背景音乐4.演示文稿中,合适的版面能让人在接受信息的同时,受到感染和启迪。
下列设计技巧不可取的是()A、利用黄金分割原理使画面更有美感B、页面中留有一定的空白,产生视觉冲击C、插入图片、文本框等可视化信息D、所有内容利用项目符号来编辑5.PowerPoint2013中,下列演示文稿的对象,不能设置超链接的是()A、文本框B、图片C、背景D、图形6.PowerPoint2013中幻灯片的切换方式是指()A、插入新幻灯片时的切换方式B、不同视图的切换方式C、切换不同的设计模版方式D、幻灯片放映时幻灯片间的过渡形式7.刘洋同学用PPT设计了一个演示文稿,首页如左图所示,背景主色调是蓝色,标题颜色使用了黄色,这两种颜色在色相环中互为()。
A、互补色B、同类色C、邻近色D、不确定8.PowerPoint2013中,为了保持多个对象间的位置关系相对固定,可以采用()A、用模板来编辑B、将对象进行组合C、设置图片格式D、设置自定义动画9.演示文稿的配色非常重要,如果颜色搭配不好会严重影响演示文稿的表达效果,以下关于配色的说法中,不恰当的是()。
A、主色调的选择应该根据内容来决定B、辅助色或修饰色宜选用跟主色调一致的同类色或邻近色C、文字的颜色宜选用跟背景色对比强烈的互补色D、尽量多的选取颜色进行搭配增强视觉冲击力10.张伟同学用演示文稿为同学们做关于人工智能的主题报告,在展示的过程中,下列做法无法实现的是()。
2022年中考物理总复习题型训练06:作图题(广东省深圳市)

2022年中考物理总复习题型训练06:作图题(广东省深圳市)作图题根据图甲所示的实物电路图,在图乙的虚线框内画出与它对应的电路图.【答案】解:由实物图知,两灯泡并联,开关控制整个电路,按要求画出电路图即可.如图所示:【解析】先分析电路的连接方式,然后根据实物图画出对应的电路图.作图题如图,使用笔画线代替导线完成电路.要求:两灯并联,开关控制干路,电流表测量干路电流,导线不能交叉.【答案】解:如图所示:【解析】解:由题意可知,两灯泡应并联,电流表应位于干路,然后与开关和电源组成电路,补充实物连接如图所示:.由题意可知,两灯泡并联,开关控制整个电路、电流表测通过两灯的总电流说明开关和电流表位于干路.作图题请用笔画线代替导线,将背面接线示意图中连有开关的电灯和三孔插座接入家庭电路中.【答案】如图所示:?【解析】灯泡接法:火线进入开关,再进入灯泡顶端的金属点,零线直接接入灯泡的螺旋套,这样在断开开关能切断火线,接触灯泡不会发生触电事故.既能控制灯泡,又能更安全.三孔插座的接法:上孔接地线;左孔接零线;右孔接火线.如下图所示:【考点精析】掌握家庭电路的接线方法是解答本题的根本,需要知道在安装电路时,要把电能表接在干路上,保险丝应接在火线上(一根已足够);控制开关也要装在火线上,在安装螺丝口电灯泡时,火线应通过开关再接到灯头中,且接在灯头锡块上.作图题小丽家中有一盏用声控开关和光控开关控制的电灯,电灯在光线昏暗并且有人经过时才发光,可以达到方便节电的目的,同时由于有不固定的家用电器,需接入一只三孔插座,请将如图所示的原理图连接完整.【答案】解:如图所示:【解析】解:晚上,天黑光控开关闭合,有人走动发出声音,声控开关闭合,灯亮,说明两个开关不能独立工作,即两个开关串联,再和灯泡串联,要注意开关应先接在火线上;插座的接法是:左零右火中接地;电路图如图所示:根据并联电路和串联电路的特点确定开关的连接方式,即开关并联时,任何一个开关闭合灯泡都可以工作,而串联电路只有当两个开关同时闭合时,灯泡才可以工作,所以声控开关和光控开关串联后控制灯泡.三孔插座的接法是:左零右火中间地;据此连接电路;作图题如图所示,把螺线管沿着东西方向水平悬挂起来,然后给导线通电,要使螺线管转动后,静止时A端指南,请标出导线中的电流方向.【答案】解:如图所示:【解析】解:要想使螺线管的N极(A端)指向南,螺线管的S 极(B)指向北,即螺线管的A端为S极,B端为N极.利用安培定则可以确定螺线管中电流的方向是左后方流入,右前方流出,如下图所示:【考点精析】关于本题考查的通电螺线管的磁场,需要了解通电螺线管的性质:①通过电流越大,磁性越强;②线圈匝数越多,磁性越强;③插入软铁芯,磁性大大增强;④通电螺线管的极性可用电流方向来改变才能得出正确答案.作图题如图所示,开关闭合时,电磁铁上端为N极,下端为S极,在图中括号内标出控制电路电源的正负极,并将工作电路图连接完整.要求:开关闭合时,电动机转,小灯泡不亮;开关断开时,小灯泡亮,电动机不转.【答案】解:如图所示:【解析】解:电磁铁上端为N极,下端为S极,根据安培定则可知,电源的左端为负极,右端为正极;开关闭合时,电磁铁具有磁性,会吸引衔铁,使电动机的电路接通;开关断开时,衔铁在弹簧拉力的作用下与电磁铁分离,使小灯泡的电路接通,如图所示:【考点精析】根据题目的已知条件,利用电磁继电器的组成、原理和特点的相关知识可以得到问题的答案,需要掌握电磁继电器:实质上是一个利用电磁铁来控制的开关.它的作用可实现远距离操作,利用低电压、弱电流来控制高电压、强电流.还可实现自动控制.作图题根据如图所示的实物连线图,在虚线方框中画出对应的电路图.【答案】解:电流从正极开始分支,一支经灯泡L1 ,另一支经开关S2、灯泡L2 ,然后两支汇合共同经过S1回到电源负极.如图所示:【解析】根据实物图可知,两灯泡并联,开关S1控制整个电路,S2控制L2 ,根据实物图完成电路图即可.作图题图中给出了几种元件,在图上用笔画线表示导线把电路元件连接起来,要求L1、L2并联,用滑动变阻器改变通过L2的电流大小,滑片P向右移动时灯L2变亮.【答案】解:滑动变阻器按一上一下的原则与灯泡L2串联,且必须把右下方接线柱接入电路;然后它们再与灯泡L1并联,开关在干路上,如下图所示:【解析】两灯泡并联,用滑动变阻器改变通过L2的电流大小说明滑动变阻器只与L2串联,滑片P向右移动时灯L2变亮说明电路中的电流变大,电路的总电阻变小,滑动变阻器接入电路的电阻变小,故必须把右下方接线柱接入电路.作图题如图所示,用笔画线代替导线将插座、电灯和开关正确接到电路中.【答案】解:如图所示:【解析】解:(1)三孔插座的上面的孔接地线,左孔接入零线,右孔接火线.如图.(2)电灯的接法:火线先过开关再入灯泡,然后接入顶端的金属点,零线直接接入螺旋套.如图.【考点精析】利用家庭电路的接线方法对题目进行判断即可得到答案,需要熟知在安装电路时,要把电能表接在干路上,保险丝应接在火线上(一根已足够);控制开关也要装在火线上,在安装螺丝口电灯泡时,火线应通过开关再接到灯头中,且接在灯头锡块上.作图题如图是家庭常用的一个插线板的示意图.在使用中会发现:插线板上的指示灯在开关断开时不发光,插孔不能提供工作电压;而在开关闭合时指示灯发光,插孔可以提供工作电压;如果指示灯损坏,开关闭合时插孔也能提供工作电压.根据上述现象,请在图中画出开关、指示灯和插孔的连接方式,并把接线板与电源线接通.【答案】解:如图所示:【解析】解:插线板上的指示灯在开关闭合时会发光,插孔正常通电,说明开关同时控制灯泡和插座,灯泡和插座之间可能是串联,也可能是并联,如果两者并联,开关应该在干路上;如果指示灯损坏,开关闭合时插孔也能正常通电,说明灯泡和插座之间是并联的,开关接在灯泡、插座和火线之间控制火线使用更安全.如图所示:【考点精析】本题主要考查了家庭电路的接线方法的相关知识点,需要掌握在安装电路时,要把电能表接在干路上,保险丝应接在火线上(一根已足够);控制开关也要装在火线上,在安装螺丝口电灯泡时,火线应通过开关再接到灯头中,且接在灯头锡块上才能正确解答此题.作图题根据图示通电螺线管周围的磁感线方向,在图中标出通电螺线管的N极和电源的正极.【答案】解:如下图所示.【解析】解:在磁体的周围,磁感线是从磁体的N极出发,回到S极,所以图示的螺线管的右端为N极.根据螺线管的N极和线圈的绕向,利用右手螺旋定则可以确定电流是从螺线管的左端流入,右端流出.从而可以确定电源的左端为正极.如下图所示.【考点精析】利用磁感线的概念和特点和安培定则对题目进行判断即可得到答案,需要熟知磁感线:描述磁场的强弱和方向而假想的曲线.磁体周围的磁感线是从它北极出来,回到南极.(磁感线是不存在的,用虚线表示,且不相交)磁场中某点的磁场方向、磁感线方向、小磁针静止时北极指的方向相同;安培定则:用右手握螺线管,让四指弯向螺线管中电流方向,则大拇指所指的那端就是螺线管的北极(N极).安培定则简记:入线见,手正握;入线不见,手反握.大拇指指的一端是北极(N极).(注意:入的电流方向应由下至上放置).作图题如图所示,当给电磁铁M通电,发现弹簧开始被压缩,过一会儿,条形磁铁和弹簧重新处于静止.此时把滑动变阻器的滑片P向B 端滑动,弹簧的长度逐渐变短.请用笔画线代替导线,把电路连接完整(导线不能交叉,弹簧在其弹性范围内).【答案】解:如图所示:.【解析】解:弹簧的长度逐渐变短,说明磁铁受到的斥力变大,故螺旋管的上端为S极,根据安培定则可知,电磁铁的上端应接电源的正极;把滑动变阻器的滑片P向B端滑动,弹簧的长度逐渐变短,说明此时的电流变大,故应接滑动变阻器的B接线柱,作图题如图是一个模拟交通路口红绿灯工作的实验电路,请你用笔画线代替导线,只添加两根导线,实物电路图补充完整.要求:红灯亮时,黄灯和绿灯都不亮;当红灯灭时,黄灯和绿灯可以分别亮一盏.【答案】解:如图所示:【解析】解:由题知,红灯亮时,黄灯和绿灯都不亮;当红灯灭时,黄灯和绿灯可以分别亮一盏;说明三个灯泡互不影响,即三灯是并联的;结合所给实物图可知,S1控制红灯和黄灯,S2控制绿灯和黄灯.如图所示:,当S1掷到左端时,红灯亮,黄灯和绿灯都不亮;当S1掷到右端且S2掷到左端时,红灯灭,黄灯亮,绿灯不亮;当S1掷到右端且S2掷到右端时,红灯灭,绿灯亮,黄灯不亮.根据各灯发光情况分析判断灯泡的连接方式和开关的作用,再连接实物.作图题科技改变生活,如图是一款街道路灯采用电磁继电器实现自动化智能控制的电路,其中R0为保护电阻.请你用铅笔画线将电路原理图连接完整,使工作电路能正常工作(与触点的接线只能接在静触点上,图中已给出静触点E、F、G、H的四根引线;连线不能交叉),达到白天因光敏电阻变小而灯熄,夜晚因光敏电阻变大而灯亮的效果.【答案】解:符合题意的电路图如下所示:【解析】本题考查学生使用电磁继电器的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级下册复习检测题(Units6-10)选择题(共70分)一、听力测试(25分)第一节听下面的8段对话,选择最佳答案。
每段对话仅读一遍。
( ) 1. What’s the man’s family name?A. Jim.B. Allan.C. Green.( ) 2. What are they talking about?A. Sports.B. Food.C. Weather.( ) 3. What time will they meet?A. 1:30.B. 1:15.C. 1:45.( ) 4. What does the man want?A. Water.B. Milk.C. Tea.( ) 5. What happened over there?A. A car hit a bike.B. A man fell off the bike.C. A truck hit a man. ( ) 6. What’s Sara going to do this evening?A. To watch TV.B. To see a film.C. To go the concert.( ) 7. What is Mary going to do?A. To show someone around the factory.B. To visit the factory.C. To talk about the factory.( ) 8. What does Jenny mean?A. Mr. Smith is very good.B. Mr. Smith is very clever.C. Mr. Smith can repair TV sets.第二节听下面的5段对话或独白,选出一个与对话或独白内容相符的问题的答案。
对话或独白读两遍。
听第一段材料,回答第9至11小题。
( ) 9. Why was the boy late?A. Something is wrong with his watch.B. He missed the bus.C. He lost his watch.( ) 10. What is the boy going to do?A. Play in the garden.B. Leave the garden.C. Sweep the garden. ( ) 11. Which part of the garden is left for the boy?A. The front part.B. The back part.C. The whole part.听第二段材料,回答第12至14小题。
( ) 12. What homework has Li Ming left at home?A. English homework.B. Chinese homework.C. Math homework. ( ) 13. How will the teacher be if Li Ming doesn’t hand in his homework on time?A. Happy.B. Angry.C. Embarrassed.( ) 14. How will Li Ming go home to fetch his homework?A. By bike.B. By bus.C. On foot.听第三段材料,回答第15至17小题。
( ) 15. Who is Rose’s favorite singer?A. Zhou Jielun.B. Liu Dehua.C. Wang Lihong.( ) 16. Why does she like him?A. Because she thinks he is the most creative singer. She loves his voice.B. Because she thinks he’s energetic.C. Because she thinks he’s clever.( ) 17. What does she think of Wang Fei?A. She is the smartest.B. She is the quietest.C. She is the coolest.听第四段材料,回答第18至20小题。
( ) 18. What’s wrong with Li Ming?A. He didn’t pass the English exam.B. He has no chance to practice English.C. He will have an English exam soon.( ) 19. Why does Li Ming say it’s hard to meet English people?A. Because he goes out less.B. Because there are no English people there.C. Because he’s not allowed to meet them.( ) 20. Why do English people never speak to Li Ming?A. Because they don’t know him.B. Because his English is too bad.C. Because he doesn’t speak first.听第五段材料,回答第21至25小题。
( ) 21. Whose son was Ali?A. An old man’s son.B. A teacher’s son.C. A farmer’s son. ( ) 22. When did he see the old man by the side of the road?A. One afternoon.B. One evening.C. One morning.( ) 23. Where did Ali take the old man?A. To a hospital.B. To his home.C. To the nearest farm.( ) 24. What did Ali tell the old man?A. He said he was a teacher.B. He said he was a farmer.C. He said his father was a famous teacher.( ) 25. Why couldn’t Ali get the money the old man left?A. Because he couldn’t tell the old man his real name.B. Because his father had lots of money.C. Because the old man didn’t believe him.二、单项选择(15分)从各小题A、B、C、D四个选项中,选出一个可以填入空白处的最佳选项。
( ) 26. beautiful girl she is!A. WhatB. HowC. What aD. How a( ) 27. –Who’s the better person for the job, Tom or Dave?–I’m afraid can do it well, for they’re both too careless.A. neitherB. eitherC. noneD. both( ) 28.Erin the rules of etiquette. Let’s go and give her some suggestions.A. obeyedB. madeC. followedD. broke( ) 29. –Would you like beer?–I don’t like beer. Give me coke .A. tooB. insteadC. eitherD. yet( ) 30. –Is Jack good at swimming?–Yes. swimming, he’s also good at skating.A. ExceptB. BesidesC. ButD. Beside( ) 31. –Would you like to see the film Confucius with me this evening?–I’d love to, but I it.A. had seenB. have seenC. watchD. am watching( ) 32.You can the web pages to find more information about this topic.A. look forB. look afterC. look outD. look through( ) 33. –Excuse me, could you please your cigarette?–No, problem.A. put upB. put outC. put onD. put off( ) 34. –Would you like to provide me with some travel information about London?–Sorry. Ask Jack. He there twice.A. has beenB. has goneC. wentD. goes( ) 35. –How long have you the new dictionary?–I have it for a long time.A. bought, boughtB. kept, boughtC. bought, keptD. kept, had ( ) 36. –Your school is so beautiful!–Yes. Everyone loves our school. Whenever we see litter on the ground,we’ll .A. pick it upB. set it upC. throw it aboutD. fix it up( ) 37. –They haven’t paid for their tickets, have they?–. They didn’t pay any money.A. Yes, they haveB. No, they haven’tC. Yes, they haven’tD. No, they have( ) 38. –Would you mind my turning on the TV?–. I’m writing my paper.A. Go aheadB. You’d better notC. Certainly notD. Not at all ( ) 39. –Did Mrs. King leave a message?–Yes. She wanted to know this Sunday.A. who you would go shoppingB. if you would go shopping with herC. that you will go shoppingD. when will you go shopping with her ( ) 40. –Could you come back at five o’clock?–. I’ll be at a birthday party at that time.A. I hope soB. Yes, I think soC. I’m afraid notD. I’m afraid so三、完型填空(10分)阅读下面短文,从短文后各题所给的A、B、C、D四个选项中,选出一个可以填入空白处的最佳选项。
