(完整版)使用simulinkbode图的绘制
BODE图画图过程
电机定位系统校正(BODE图)MATLAB软件具有强大的计算能力和绘图功能,能够快速、准确地做出频域特性曲线。
利用MATLAB^制系统的Bode图,为控制系统设计和分析提供了极大的方便。
1.创建M-file文挡,并输入如下程序,运行后生成LTI对象my_sys:J=3.2284e-6;b=3.5077e-6;K=0.0274;R=4;L=2.75e-6;num=[0 0 0 K];den=[(J*K) (J*R+(L*b)) ((b*R)+O2) 0]; my_sys=tf( nu m,de n);打开Matlab7.0软件,并新建一个空文档,将程序复制到文档内,如图1所示:图12.运行程序并保存运行结果。
如图2所示:图2图43. 打开 Start-Toolboxes — ControlSystem — SISO Design Tool启动SISO Design,如图3所示4. 将my_sys 程序导入到SISO Design Tool 中, 如图4所示啪号TW Hi^vicn ToniP il ■ ErLE ・ Vi, mr r za-ipMi-i k t Dqri £x> al>1* E □'l'l. •冷日■丁 11*』]1卜l>] X o 4 T 11; »M s K 1 mi4||'=4Dp山 watLa ft — 15-S-IQ Jt 午肌"■存-i-s — 15-5-in 上午恥ny_2F2c !x|F L 1« Edu I 上LIM tmp viiK«l&rl 姿kl 尸L C. TadulllaJpIIH n y. L R ann曲闻出田画田田刚Dur r ■n.l 卫a r nryCtiaiTijinfl Hi ®f-15-5-JQ 上牛奔■■■jip.sygG ii — 15-5-10 上午和 iSB (TT = EJS >尺jgtrt.Hci nr ||T ^ nkm 1rn mfi B * njrtlini£>■ |si90 ・ui.fi 1 v f Ja S D .EM 1 色■'i -Fi'Mii ^mpp+if-slnrCi|r TBH.*: n i. B-Bf I arv^(Bft-olKl fir tiv? for “偷史 俺±&n )埔1口曲riw^uefCf rijSr.14 fftcrt图65.在View 菜单中,关闭根轨迹显示,只显示开环的 Bode 图。
MATLAB中bode图绘制技巧(精)

MATLAB中bode图绘制技巧(精)Matlab中Bode图的绘制技巧学术收藏2010-06-04 21:21:48 阅读54 评论0 字号:大中小订阅我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图: 1.576e010 s^2 H(s= ------------------------------------------------------------------------------------------ s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014 (这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
我们可以用下面的语句:num=[1.576e010 0 0]; den=[1 1.775e005 1.579e010 2.804e012 2.494e014]; H=tf(num,den; bode(H 这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions 我们可以看到以下内容:ans = Title: [1x1 struct] XLabel: [1x1 struct] YLabel: [1x1 struct]TickLabel: [1x1 struct]Grid: 'off' XLim: {[1 10]}XLimMode: {'auto'}YLim: {[1 10]} YLimMode: {'auto'}IOGrouping: 'none'InputLabels: [1x1 struct]OutputLabels: [1x1 struct]InputVisible: {'on'} OutputVisible: {'on'}FreqUnits: 'rad/sec'FreqScale: 'log' MagUnits: 'dB'MagScale: 'linear'MagVisible: 'on' MagLowerLimMode: 'auto'MagLowerLim: 0PhaseUnits: 'deg'PhaseVisible: 'on'PhaseWrapping: 'off' PhaseMatching: 'off'PhaseMatchingFreq: 0 PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;P.Grid='on'; P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den; bode(H,P 这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
绘制伯德图
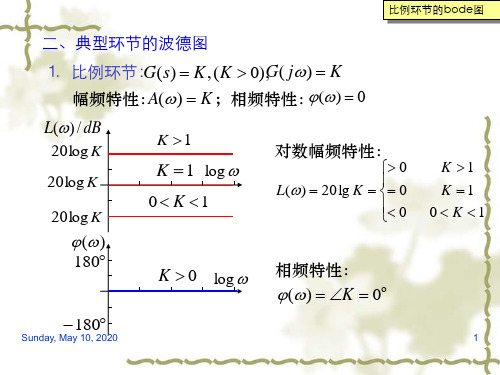
幅频和相频特性为:
A( ) (1 T 2 2 )2 (2 T )2, ( ) tg 1
1 T 1 ,o ,称为转折频率或交换频率。 T
Monday, March 09, 2015
可以用这两段渐近线近似的表示惯性环节的对数幅频特性。
3
惯性环节的Bode图
10 渐近线 0 -10 -20 0° -45° -90° 1 20T
20dB / Dec
图中,红、绿线分别是低频、高频渐近线,蓝线是实际曲线。
T
( )
2.0
-63.4
3.0
-71.5
4.0
-76
5.0
-78.7
7.0
-81.9
10
-84.3
20
-87.1
50
-88.9
100
-89.4
1 1 当 0时, (0) 0;当 时, ( ) ;当 时, () 。 T T 4 2 由图不难看出相频特性曲线在半对数坐标系中对于(0, -45°) 点是斜对称的,这是对数相频特性的一个特点。
当时间常数T 变化时,对数幅频特性和对数相频特性的形状 都不变,仅仅是根据转折频率1/T 的大小整条曲线向左或向 右平移即可。而当增益改变时,相频特性不变,幅频特性上 下平移。
Monday, March 09, 2015 6
振荡环节的频率特性
K Kn 2 ⒋ 振荡环节的频率特性: G( s) 2 2 T s 2Ts 1 s 2 n s n 2
0 L( ) 20 lg K 0 0
K 1 K 1 0 K 1
( )
180
K 0
log
如何绘制伯德图

1
s2
K n 2 2ns n2
讨论 0 1时旳情况。当K=1时,频率特征为:
G(
j )
(1 T
1
2 2 )
j2T
幅频特征为:
A( )
1
(1 T 2 2 )2 (2T )2
相频特征为:
(
)
tg
1
1
2T T 2
2
对数幅频特征为:L() 20 log A() 20 log (1 T 2 2 )2 (2T )2
2
当 1 时,有谐振峰值。
2
M p A( p ) 2
1
1 2
由幅频特征
A( )
1
(1 T 2 2 )2 (2T )2
当
0
,A(0 )
1
2
,L(0) 20lg 2 。
所以在转折频率附近旳渐近线依不同阻尼系数与实际曲线可能
有很大旳误差。
11/29/2023
10
幅值 A()与 T 旳关系:
T 2.0 3.0 4.0 5.0 7.0 10 20 50 100
( ) -63.4 -71.5 -76 -78.7 -81.9 -84.3 -87.1 -88.9 -89.4
当 0时,(0) 0;当 1 时,( 1 ) ;当 时,() 。
T
T4
2
由图不难看出相频特征曲线在半对数坐标系中对于(0, -45°)
2
L( ) 20lg (1 T 2 2 )2 (2T )2
低频渐近线: T 1时,L() 0
高频渐近线: T 1时,L( ) 20lg (1 T 2 2 )2 (2T )2 40logT
转折频率为:o
1 T
如何绘制伯德图PPT课件

是一条斜率为-n×20dB/dec,且在 00
ω =1(弧度/秒)处过零分贝线(ω
0.01 0.1
1
轴)的直线。相频特性是一条与ω 900
无关,值为-n×900且与ω 轴平行的 1800 直线。两个积分环节串联的Bode图
如图5-13所示。
图5-13 两个积分环节串联的Bode图
8
(三) 惯性环节
1
L() dB
40
20
0
0.01 0.1
1
-20
-40
( )
90o
45o
0
0.01 0.1
1
-45o
-90o
10
100
10
100
2
用伯德图分析系统有如下优点: (1) 将幅频特性和相频特性分别作图,使系统(或环
节) 的幅值和相角与频率之间的关系更加清晰;
(2) 幅值用分贝数表示,可将串联环节的幅值相乘变为相 加运算,可简化计算;
一阶微分环节的对数幅频特性如图5-16所示,渐近线的转折频
率 为1,转折频率处渐近特性与精确特性的误差为
,
其误20差lg 均2为正3d分B 贝数,误差范围与惯性环节类似。
相频特性是
当 时, G( j ); arctg
(5-78)
0 G( j0) 00
12
当 1 时,G( j 1) 450 ;
成的折线称为对数幅频特性的渐近线。如图5-14所示。
9
惯性环节的相频特性为
G( j ) arctgT (5-75)
当 0时,G( j0) 00;
当 1 时,G( j 1 ) 450;
BODE图的讲解

L() 20 lg () *90
共二十三页
( )
§5.3.1 典型环节的Bode图
§5.3.1 典型(diǎnxíng)环节的Bode图
⑶ 积分(jīfēn) G( j ) 1
环节
j
L() 20lg () 90
当 G( j) ( 1 ) j
L() 20 lg () 90*
⑷ 惯性环节
§5.3.1 典型(diǎnxíng)环节的Bode图
⑹ 节
振荡(zhèndàng)G环(s)
n2 s2 2ns n2
G(
j )
1
2
2 n
1
j2
n
L( ) 20lg
[1
2 n2
]2
[2
n
]2
( )
arctan 2
n
1 -
2
2 n
1
n
1
n
L() 0 () 0
L( ) 40lg n
第一转折频率之左 的特性及其延长线
共二十三页
内容(nèiróng)总结
1)由开环频率特性 求出幅频特性 和相频特性 ,或实频 特性 和虚频特性。不含零点时,模值和相位一般会单调收缩 ,当有零点时,曲线可能会扭曲。(4) (非直线)特性曲线可以绘制 渐近对数(duìshù)幅频特性,进一步简化绘制过程。是一条斜率为+ 20db/dec,过(1,0)点的直线,记作〔+20〕。谐振频率wr 和谐振 峰值Mr。① 两惯性环节转折频率很接近时
30dB
20( lgc
lg
2)
20 lg
c
2
lg c 30 1.5
2 20
c 2 101.5 63.2 rad s
控制系统仿真 计算机辅助设计 matlab simulink 2010版PPT 100510基传递函数模型的控制系统设计-Bode图法

Bode图法基本要求为了获得比较高的开环增益及满意的相对稳定性,必须改变开环频率特性响应曲线的形状,这主要体现为:1)在低频区和中频区增益应该足够大,2)且中频区的对数幅频特性的斜率应为-20dB/dec,并有足够的带宽,以保证适当的相角裕度;3)而在高频区,要使增益尽可能地衰减下来,以便使高频噪声的影响达到最小。
Bode图设计方法的频域指标为。
K c ,,ωγ基本思路在Bode图中的对数频率特性的低频区表征了闭环系统的稳态特性,中频区表征了系统的相对稳定性和响应性,而高频区表征了系统的抗干扰特性。
在大多数实际情况中,校正问题实质上是在稳态精度和相对稳定性之间取折衷的问题。
05101520M a g n i t u d e (d B )10-11010110210310403060P h a s e (d e g )Bode DiagramFrequency (rad/sec)串联超前校正描述:超前校正装置的主要作用是改变系统开环Bode 图中曲线的形状来产生足够大的超前相角,以补偿原系统中过大的相角滞后,从而提高系统的相对稳定性,致使闭环系统的频带扩宽。
设超前校正装置的传递函数为TsaTss G c ++=11)(1>a mm a φφsin 1sin 1−+=alg 10mφ串联超前校正Bode图的几何设计方法1.根据稳态指标要求确定未校正系统的型别和开环增益,并绘制Bode图;2.根据动态指标要求确定超前校正装置的参数;第一种情形:给出了的要求值(1)确定超前校正所应提供的最大超前相角(2)求解的值)20~5( ,)](180[0°°°=+′∠+−=εεωγφc m j G amm a φφsin 1sin 1−+=a j G m lg 10)(lg 200−=′ω(确定)m ωc ω)(0s G ′如果,说明值选择合理,能够满足相角裕度要求,否则按如下方法重新选择的值:c m ωω≈a a 2)(1c j G a ω′=a j G c lg 10)(lg 200−=′ω11sin 1+−=′−a a mφm mφφ≥′若,则正确,否则重新调整值。
自动控制原理之伯德图
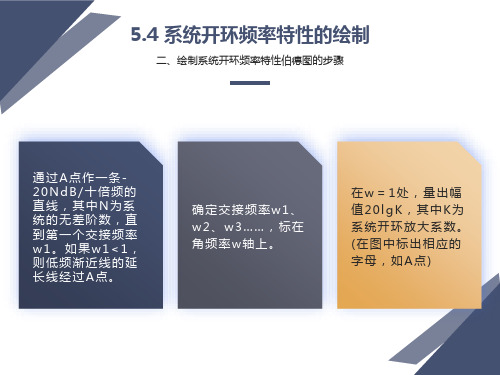
画出各串联典型环节相频特性,将它们相加后得到系统开环相频特开环系统对数幅频特性图
01
L
02
5.4 系统开环频率特性的绘制
以后每遇到一个交接频率,就改变一次渐近线斜率。 每当遇到 环节的交接频率时,渐近线斜率
增加-20dB/十倍频; 每当遇到 环节的交接频率时,斜率增加
+20dB/十倍频; 每当遇到 环节的交接频率时,
通过A点作一条-20NdB/十倍频的直线,其中N为系统的无差阶数,直到第一个交接频率w1。如果w1<1,则低频渐近线的延长线经过A点。
确定交接频率w1、w2、w3……,标在角频率w轴上。
在w=1处,量出幅值20lgK,其中K为系统开环放大系数。(在图中标出相应的字母,如A点)
二、绘制系统开环频率特性伯德图的步骤
斜率增加-40dB/十倍频。
系统开环频率特性的绘制
5
⑤ 绘出用渐近线表示的对数幅频特性以后,如果需要,可以进行修正。通常只需修正交接频率处以及交接频率的二倍频和1/2倍频处的幅值就可以了。 对于一阶项,在交接频率处的修正值为±3dB; 在交接频率的二倍频和1/2倍频处的修正值为±1dB。 对于二阶项,在交接频率处的修正值可由公式 求出。
5.4 系统开环频率特性的绘制
系统开环对数幅频特性L(ω)通过0分贝线,即 时的频率 称为穿越频率。穿越频率 是开环对数相频特性的一个很重要的参量。
01
02
03
绘制开环系统对数相频特性时,可分环节绘出各分量的对数相频特性,然后将各分量的纵坐标相加,就可以得到系统的开环对数相频特性。
matlab绘制bode图技巧(可编辑修改word版)
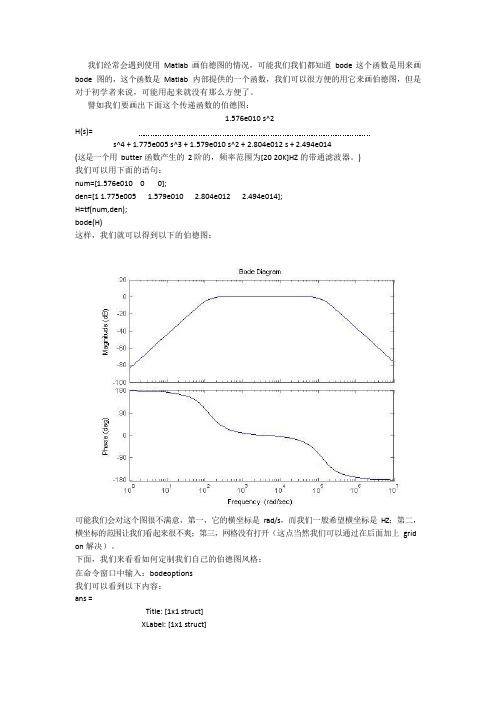
我们经常会遇到使用Matlab 画伯德图的情况,可能我们我们都知道bode 这个函数是用来画bode 图的,这个函数是Matlab 内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:1.576e010 s^2H(s)=s^4 + 1.775e005 s^3 + 1.579e010 s^2 + 2.804e012 s + 2.494e014(这是一个用butter 函数产生的2 阶的,频率范围为[20 20K]HZ 的带通滤波器。
)我们可以用下面的语句:num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H)这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on 解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions我们可以看到以下内容:ans =Title: [1x1 struct]XLabel: [1x1 struct]YLabel: [1x1 struct]TickLabel: [1x1 struct]Grid: 'off'XLim: {[1 10]}XLimMode: {'auto'}YLim: {[1 10]}YLimMode: {'auto'}IOGrouping: 'none'InputLabels: [1x1 struct]OutputLabels: [1x1 struct]InputVisible: {'on'}OutputVisible: {'on'}FreqUnits: 'rad/sec'FreqScale: 'log'MagUnits: 'dB'MagScale: 'linear'MagVisible: 'on'MagLowerLimMode: 'auto'MagLowerLim: 0PhaseUnits: 'deg'PhaseVisible: 'on'PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;P.Grid='on';P.XLim={[10 40000]};P.XLimMode={'manual'};P.FreqUnits='HZ';num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf(num,den);bode(H,P)这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB 处的频率值。
bode图 nyquist图

系统开环Bode图的绘制
单回路开环系统Bode图的绘制步骤
确定各环节的转折频率并由小到大标示在对数频率轴上; 计算20lgK,在ω=1 rad/s处找到纵坐标等于20lgK 的点, 过该点作斜率等于 -20v dB/dec的直线,向左延长此线至所 有环节的转折频率之左,得到最低频段的渐近线。 向右延长最低频段渐近线,每遇到一个转折频率改变一次 渐近线斜率; 对惯性环节,- 20dB/dec 振荡环节, - 40dB/dec 一阶微分环节,+20dB/dec 二阶微分环节,+40dB/dec 对渐近线进行修正以获得准确的幅频特性; 相频特性曲线由各环节的相频特性相加获得。
延迟环节 是不是 最小相位环节 ?
系统开环Bode图的绘制
Bode图的绘制举例
系统开环Bode图的绘制
单回路开环系统Bode图的绘制
系统开环Nyquist图的绘制
概述
K ( n s 1) ( k s 2 k k s 1)
2 2
G( s) s
v
n 1
k 1
2 2 i 1 j 1
系统开环Nyquist图的绘制
概述
G( s ) G1 ( s )G2 ( s )...Gn ( s )
G( j ) A1 ( )e
j1 ( )
A2 ( )e
j 2 ( )
.. An ( )e
j n ( )
A( ) A1 ( ) A2 ( )... An ( )
系统开环Bode图的绘制
最小相位环节的频率特性
(1)定义
凡在右半S 平面上有开环零点或极点的系 统,称为非最小相位系统。 “最小相位” 是指,具有相同幅频特性的 一些环节,其中相角位移有最小可能值的,称 为最小相位环节;反之,其中相角位移大于最 小可能值的环节称为非最小相位环节;后者常 在传递函数中包含右半S平面的零点或极点。
MATLAB中bode图绘制技巧
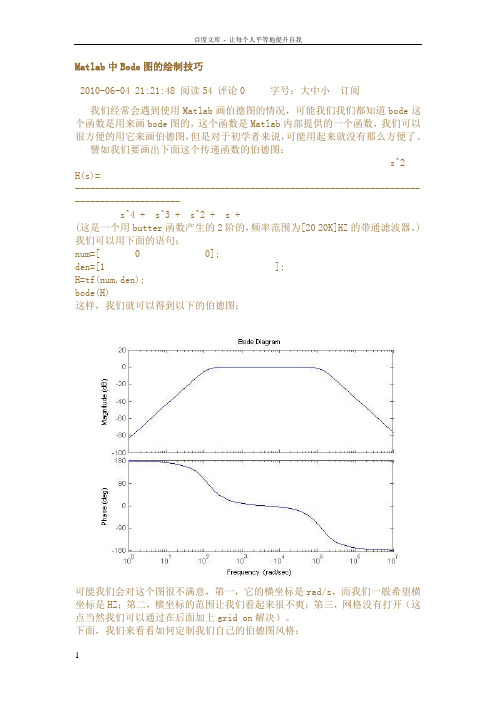
Matlab中Bode图的绘制技巧2010-06-04 21:21:48 阅读54 评论0 字号:大中小订阅我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:s^2H(s)=------------------------------------------------------------------------------------------s^4 + s^3 + s^2 + s +(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
) 我们可以用下面的语句:num=[ 0 0];den=[1 ];H=tf(num,den);bode(H)这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions我们可以看到以下内容:ans =Title: [1x1 struct]XLabel: [1x1 struct]YLabel: [1x1 struct]TickLabel: [1x1 struct]Grid: 'off'XLim: {[1 10]}XLimMode: {'auto'}YLim: {[1 10]}YLimMode: {'auto'}IOGrouping: 'none'InputLabels: [1x1 struct]OutputLabels: [1x1 struct]InputVisible: {'on'}OutputVisible: {'on'}FreqUnits: 'rad/sec'FreqScale: 'log'MagUnits: 'dB'MagScale: 'linear'MagVisible: 'on'MagLowerLimMode: 'auto'MagLowerLim: 0PhaseUnits: 'deg'PhaseVisible: 'on'PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;='on';={[10 40000]};={'manual'};='HZ';num=[ 0 0];den=[1 ];H=tf(num,den);bode(H,P)这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
7.2.4控制系统的博德图(1)

1.实验目的(1)利用计算机做出开环系统的博德图;(2)观察记录控制系统的开环频域性能;(3)控制系统的开环频率特性分析。
2.实验步骤(1)运行MATLAB(2)练习相关m函数3.实验内容(1),T=0.1,做ζ=2,1,0.5,0.1,0.01时的图并保持:键入如下程序:num=[1];den=[0.01 0.4 1];bode(num,den);hold on;num=[1];den=[0.01 0.2 1];bode(num,den);hold on;num=[1];den=[0.01 0.1 1];bode(num,den);hold on;num=[1];den=[0.01 0.02 1];bode(num,den);hold on;num=[1];den=[0.01 0.002 1];bode(num,den);hold on;查看MATLAB绘制的博德图:(2)要求:1)作出博德图,在曲线上标出:幅频特性——初始段斜率、高频段斜率、开环截止频率、中段穿越频率。
相频特性——低频段渐进相位角、高频段渐进相位角、-180°线的穿越频率。
键入如下程序,绘制出博德图:num=[31.6];den=[0.001 0.11 1 1]; bode(num,den);在图上取如下点:由图上点可知:低频段的斜率=高频段的斜率=开环截止频率为16.2中频穿越斜率=低频段渐进相位角为-91.1°(-90°)高频段渐进相位角为-269°(-270°)-180°线的穿越频率为31.82)由稳定裕度命令计算系统的稳定裕度L g和相位裕度γc并确定系统的稳定性。
键入如下程序:z=[];p=[0,-10,-100];k=31600;sys=zpk(z,p,k);bode(sys)margin(sys)[Gm,Pm,wg,wp]=margin(sys)[Gm,Pm,wg,wp]=margin(m,p,w)由博德图上可以读到,系统的稳定裕度L g=11dB,γc=22°稳定裕度L g > 6dB相位裕度γ c > 0°,但是<30°所以系统稳定,但是相位裕度低于30°,所以接近于临界稳定点,系统会趋于等幅震荡,稳定性相对较差。
MATLAB中bode图绘制技巧

Matlab中Bode图的绘制技巧2010-06-04 21:21:48 阅读54 评论0 字号:大中小订阅我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:s^2H(s)=------------------------------------------------------------------------------------------s^4 + s^3 + s^2 + s +(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
) 我们可以用下面的语句:num=[ 0 0];den=[1 ];H=tf(num,den);bode(H)这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions我们可以看到以下内容:ans =Title: [1x1 struct]XLabel: [1x1 struct]YLabel: [1x1 struct]TickLabel: [1x1 struct]Grid: 'off'XLim: {[1 10]}XLimMode: {'auto'}YLim: {[1 10]}YLimMode: {'auto'}IOGrouping: 'none'InputLabels: [1x1 struct]OutputLabels: [1x1 struct]InputVisible: {'on'}OutputVisible: {'on'}FreqUnits: 'rad/sec'FreqScale: 'log'MagUnits: 'dB'MagScale: 'linear'MagVisible: 'on'MagLowerLimMode: 'auto'MagLowerLim: 0PhaseUnits: 'deg'PhaseVisible: 'on'PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;='on';={[10 40000]};={'manual'};='HZ';num=[ 0 0];den=[1 ];H=tf(num,den);bode(H,P)这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
实验三 系统Bode图及Nyquist曲线的绘制实验报告.docx
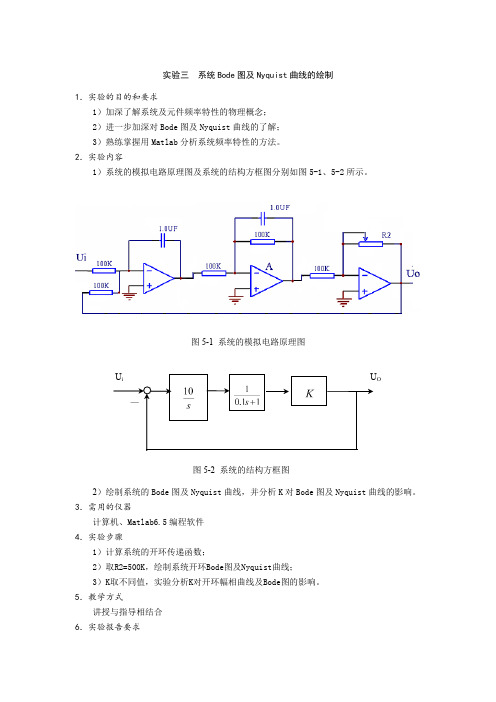
实验三系统Bode图及Nyquist曲线的绘制1.实验的目的和要求1)加深了解系统及元件频率特性的物理概念;2)进一步加深对Bode图及Nyquist曲线的了解;3)熟练掌握用Matlab分析系统频率特性的方法。
2.实验内容1)系统的模拟电路原理图及系统的结构方框图分别如图5-1、5-2所示。
图5-1 系统的模拟电路原理图图5-2 系统的结构方框图2)绘制系统的Bode图及Nyquist曲线,并分析K对Bode图及Nyquist曲线的影响。
3.需用的仪器计算机、Matlab6.5编程软件4.实验步骤1)计算系统的开环传递函数;2)取R2=500K,绘制系统开环Bode图及Nyquist曲线;3)K取不同值,实验分析K对开环幅相曲线及Bode图的影响。
5.教学方式讲授与指导相结合6.实验报告要求1)、计算开环传函G k(s)=10s ×10.1s+1×K =10K0.1s2+s2)、取R2=500K,绘制Bode图和Nyquist图⑴、Simulink指令块Bode图:Nyquist图:3)、K取不同值,对开环幅相曲线及Bode图的影响⑴、K取不同值,对开环幅相曲线的影响程序:》y1=tf([50],[0.1,1,0]);y2=tf([100],[0.1,1,0]);y3=tf([200],[0.1,1,0]);nyquist(y1);set(findobj('Color','b'),'LineWidth',3)hold on;nyquist(y2);nyquist(y3);set(findobj('Color','r'),'LineWidth',6);grid;legend('k=5响应曲线','K=10响应曲线','K=20响应曲线'); title('李山 1206074118');图形:分析,φ(jw)=arctan(10w)得出,K的改变不会影响角度的由公式A(w)=|G(jw)|=10k0.01w4+w2变化,只会影响幅值。
5.3.2开环系统bode图的绘制

5.3.2 开环系统Bode 图的绘制将开环传递函数()G s 表示成式(5-48)形式的典型环节组合形式,有12121212()20lg ()20lg[()()()]20lg ()20lg ()20lg ()()()()()()()()l l l l L A A A A A A A L L L ω=ω=ωωω⎧⎪=ω+ω++ω⎪⎨=ω+ω++ω⎪⎪ϕω=ϕω+ϕω+ϕω⎩ (5-58) 式中,)(ωi L 和)(ωϕi 分别表示各典型环节的对数幅频特性和对数相频特性。
式(5-58)表明,只要能作出)(ωj G 所包含的各典型环节的对数幅频和对数相频曲线,将它们进行代数相加,就可以求得开环系统的Bode 图。
实际上,在熟悉了对数幅频特性的性质后,可以采用更为简捷的办法直接画出开环系统的Bode 图,具体步骤如下。
(1) 将开环传递函数写成尾1标准形式:()211()2211(1)[()21]()(1)[()21]m p pzh i h i zh zh n q v qv pk j k j pk pks s s K z G s s s s s p -==--==+++=+++∏∏∏∏ξωωξωω 确定系统开环增益K 和型别v ,把各典型环节的转折频率由小到大依次标在频率轴上。
(2) 绘制开环对数幅频特性低频段的渐近线。
由于低频段渐近线的频率特性为()v K j ω,所以它就是过点(K lg 20,1)、斜率为20dB/dec v -的直线。
(3) 在低频段渐近线的基础上,沿频率增大的方向每遇到一个转折频率就改变一次斜率,其规律是遇到惯性环节的转折频率,斜率变化20dB/dec -;遇到一阶复合微分环节的转折频率,斜率变化20dB/dec ;遇到二阶复合微分环节的转折频率,斜率变化40dB/dec ;遇到振荡环节的转折频率,斜率变化40dB/dec -;直到所有转折全部进行完毕。
最右端转折频率之后的渐近线斜率应该是20()dB/dec n m --,其中,m n ,分别为)(s G 分母、分子的阶数。
(完整版)Matlab中Bode图的绘制技巧(精)
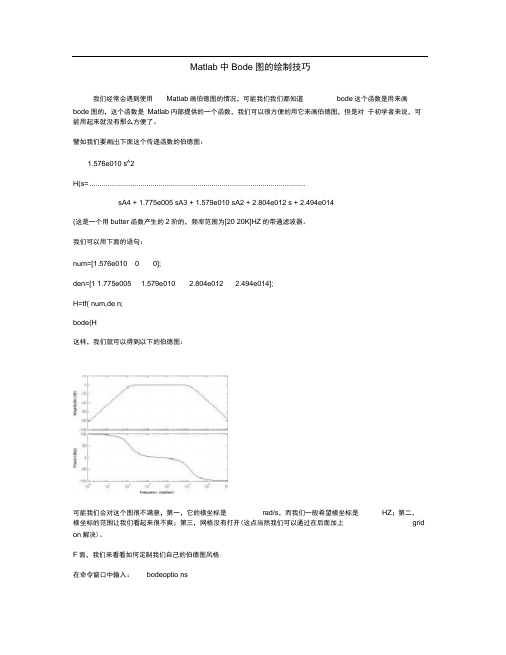
Matlab中Bode图的绘制技巧我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画岀下面这个传递函数的伯德图:1.576e010 s A2H(s= ..........................................................................................................sA4 + 1.775e005 sA3 + 1.579e010 sA2 + 2.804e012 s + 2.494e014(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
我们可以用下面的语句:num=[1.576e010 0 0];den=[1 1.775e005 1.579e010 2.804e012 2.494e014];H=tf( num,de n;bode(H这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
F面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptio ns我们可以看到以下内容:ans =Title: [1x1 struct] XLabel: [1x1 struct] YLabel: [1x1 struct] TickLabel: [1x1 struct] Grid: 'off' XLim: {[1 10]} XLimMode: {'auto'} YLim: {[1 10]} YLimMode: {'auto'} IOGrouping: 'none' InputLabels: [1x1 struct] OutputLabels: [1x1 struct] InputVisible: {'on'} OutputVisible: {'on'} FreqUnits: 'rad/sec' FreqScale: 'log' MagUnits: 'dB' MagScale: 'linear' MagVisible: 'on' MagLowerLimMode: 'auto' MagLowerLim: 0 PhaseUnits: 'deg' PhaseVisible: 'on' PhaseWrapping: 'off'是这样的,运行命令 ctrlpref ,出现控制系统工具箱的设置页面, Units 改为Hz 就好了PhaseMatchi ng: 'off'PhaseMatchi ngFreq: 0PhaseMatchi ngValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图: P=bodeopti ons;P.Grid='o n';P.XLim={[10 40000]};P.XLimMode={'ma nual'};P.Freq Un its='HZ';num=[1.576e010 00]; den=[1 1.775e0051.579e0102.804e012 2.494e014];H=tf( num,de n;bode(H,P这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ ,范围是[10 40K]HZ ,而且打开了网格,便于我们观察-3DB 处的频率值。
自动控制原理simulink实验指导

自动控制原理上机实验指导书王芳、杨志超编写南京工程学院电力工程学院二〇〇七年二月目录Simulink仿真集成环境简介 (2)实验一典型环节的性能分析 (11)实验二二阶系统的性能分析 (14)实验三自动控制系统的稳定性和稳态误差分析 (17)实验四自动控制系统根轨迹的分析 (22)实验五自动控制系统的频域分析 (27)实验六控制系统的校正及设计 (32)实验七非线性系统的稳定性分析 (39)Simulink仿真集成环境简介Simulink是可视化动态系统仿真环境。
1990年正式由Mathworks公司引入到MATLAB中,它是Slmutation 和Link的结合。
这里主要介绍它的使用方法和它在控制系统仿真分析和设计操作的有关内容。
1、进入Simulink操作环境双击桌面上的MATLAB图标,启动MATLAB,进入开发环境,如图0-1所示:图0-1 MATLAB开发环境从MATLAB的桌面操作环境画面进入Simulink操作环境有多种方法,介绍如下:①点击工具栏的Simulink图标,弹出如图0-2的图形库浏览器画面。
②在命令窗口键入“simulink”命令,可自动弹出图形库浏览器。
上述两种方法需从该画面“File”下拉式菜单中选择“New/Model”,或点击图标,得到图0-3的图形仿真操作画面。
③从“File”下拉式菜单中选择“New/Model”,弹出图0-3所示的未命名的图形仿真操作画面。
从工具栏中点击图形库浏览器图标,调出图0-2的图形库浏览器画面。
图0-3用于仿真操作,图0-2的图形库用于提取仿真所需的功能模块。
图0-2 Simulink图形库浏览器画面图0-3 simulink仿真操作环境画面2、提取所需的仿真模块在提取所需仿真模块前,应绘制仿真系统框图,并确定仿真所用的参数。
图0-2中的仿真用图形库,提供了所需的基本功能模块,能满足系统仿真的需要。
该图形库有多种图形子库,用于配合有关的工具箱。
MATLAB中调用simulink并绘制bode图技巧

Matlab中Bode图的绘制技巧
用simulink提供的linmod()或者linmod2()两个函数,从连续系统中提取线性模型,两个函数命令执行后都可以得到一个[a,b,c,d]表达的状态空间模型。
利用bode(sys)或者bode(a,b,c,d)函数绘制系统的对数幅频和相频特性曲线。
1) 修正原来的simulink模型,使其输入用inport表示,输出用outport表示。
这些端口在6.1版中分别位于sources和sinks组。
2)编写m文件内容为:
[A,B,C,D]=linmod(‘untitled1’) % untitled1’为系统的动态模型或simulink文件名。
[num,den]=ss2tf(A,B,C,D); %转换成传递函数模型
printsys(num,den,’s’); %显示系统的传递函数模型
sys=ss(A,B,C,D);
bode(sys); %即可绘制系统的开环系统bode图
bode(A,B,C,D); %也可以采用此语句代替上面紫色语句
3)、直接在命令窗执行m文件。
实验五MATLAB绘制Bode图(精)

实验五MATLAB绘制Bode图、Nyquist图实验学科:自动控制理论姓名:XXX学号:XXX班级:XXX实验五 MATLAB绘制Bode图、Nyquist图实验一、实验目的1. 掌握计算机绘制系统的Bode图、Nyquist图、根轨迹曲线方法;2. 观察系统对单位阶跃信号的时域响应曲线;3. 通过仿真结果和理论计算的对照,加深对系统特性的理解。
二、实验设备PC、MATLAB三、实验结果1. 各传递函数的Bode图(1 K (K = 1, K = 0.5GH(s = 1GH(s = 0.5(2 (T = 0.2, T = 0.4(3 (K = 0.5, T = 0.4; K = 1.0; T = 0.2(4 (K = 1.0, T = 0.4; K = 1.0; T = 0.22. 各传递函数的Nyquist图(1 K (K = 1, K = 0.5GH(s = 1GH(s = 0.5(2 (T = 0.2, T = 0.4(3 (K = 0.5, T = 0.4; K = 1.0; T = 0.2(4 (K = 1.0, T = 0.4; K = 1.0; T = 0.23. 各传递函数的根轨迹曲线(1 K (K = 1, K = 0.5GH(s = 1, GH(s = 0.5(2 (T = 0.2, T = 0.4(5 (K = 0.5, T = 0.4; K = 1.0; T = 0.2(6 (K = 1.0, T = 0.4; K = 1.0; T = 0.24. 各传递函数对单位阶跃信号的时域响应曲线(1 K (K = 1, K = 0.5GH(s = 1GH(s = 0.5(2 (T = 0.2, T = 0.4(7 (K = 0.5, T = 0.4; K = 1.0; T = 0.2(8 (K = 1.0, T = 0.4; K = 1.0; T = 0.25. 各传递函数的特征量如下表所示传递函数GH(S剪切频率(rad/s 相角余量(°特征方程的根GH(s = 1GH(s = 0.55 90 -52.5 90 -2.52.89 135 -∞135 -2.52.5 135 -5 5 135 -10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在Matlab中,大多时候,我们都是用M语言,输入系统的传递函数后,用bode函数绘制bode图对系统进行频率分析,这样做,本人觉得效率远不如Simulink建模高。
如何在Matlab/Simulink中画bode图,以前也在网上查过些资料,没看到太多有用的参考。
今天做
助教课的仿真,又要画电机控制中电流环的bode图,模型已经建好,step response也很容易看出来,可这bode图怎么也出不来,又不愿意用m语言写出传递函数再画。
baidu和google 了好一阵,几乎没有一个帖子说的清清楚楚的,经过一番摸索,终于掌握了Simulink里画bode图的方法。
.其实,Simulink里画bode图,非常的easy,也很方便。
写此文的目的是希
望对那些常用Simulink进行仿真希望画bode图又不愿用M语言的新手有所帮助。
以下均是以Matlab R2008a为例。
首先,在simulink里建好model。
如图1,这里需要注意的是,输入和输出要用input port 和output port,这样以后画bode图的时候,系统就会知道是这两个变量之间的关系。
图1 建好model
其次,选择线性分析。
Tools->Control Design ->Linear Analysis。
如图2。
图2 选择Linear Ansysis
将出现如图3所示的Control and Estimation Tools Manager窗口。
图3 Control and Estimation Tools Manager窗口
第三步,激动人心的时刻到了,哈哈。
如果你是按照前面的步骤来的,那么这时候,你就应
前面的方框打上该可以直接画出bode图,在窗口的下方,将“Plot linear analysis result in a ”
,即画output port和勾,已打的就不用管了,再在后面的下拉框里选择“bode response plot”
按钮,就OK了。
其实除了bode图,还input port之间的bode图,再点击“Linearize Model”
可以画其他很多响应曲线,比如step response、impulse response和Nyquist图等等,只需选择相应的step response plot,inpulse response plot或者Nyquist plot等等。
方法都是相同的。
如图4所示。
选择选择“bode response plot”,
图4 画出bode图
稍等片刻,便出现了图1中output port和input port的bode图了。
是不是很简单?!
图5 model的bode图
至此,bode已经画完。
如果此时还想看看step response或者Nyquist图,也是可以的。
只需在bode图上右击,选择Plot Types->Step或者Nyquist等等,as you need!我们选择step,便会出现阶跃响应图。
如图6、7所示。
图6 画阶跃响应图7 显示阶跃响应
上面的bode图和step response都没有网格,看着不精确,没关系。
在图上右击,选择Grid,就能出现网格了。
想要知道曲线上某点的坐标时,只需在该点上单击,就会显示出该点的坐标值。
如图8a,8b。
图8a
图8b 显示网格和曲线上的坐标
关于图画里的操作,就介绍这么多,其他的功能自己去摸索。
回到图3中的Control and Estimation Tools Manager窗口。
在该窗口中,除了可以画bode
图之外,还可以看到系统的状态方程、传递函数或者零极点方程。
运行完“Linearize Model”
下的“Model”,在下方的下拉列表里选择“Zero Pole Gain”后,单击左侧“Linearization Task”
),就能看到系统输入输出的零极点增益
或者“Transefer Funciton”
(也可以选择“State Space”
方程。
如下图9。
图9 查看系统输入输出之间的关系描述(状态议程、零极点增益、传递函数)
通过Linear Analysis工具,我们可以得到很多关于系统的直观的或者非直观的信息,如
bode图、Nyquist图、状态方程、传递函数等等。
以上简单介绍了Matlab/Simulink中利用Control Design的Linear Analysis绘制系统的bode 图,及查看系统输入输出关系的描述。
Matlab的功能十分强大,还有许多功能需要探索,
以便其更好的帮助我们完成系统建模仿真和控制等。
