圆组合图形练习题
六年级奥数题_圆和组合图形(B)

陆老师奥数培训讲义圆和组合图形(六年级)报名:例1】.如图,阴影部分的面积是多少?例 2】.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大多少平方厘米.?例】 3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是多少平方厘米? (π取3.14,结果精确到1平方厘米)例4】.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).例5】.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.π图中阴影部分的周长是厘米.)(=14.3练习题1.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是多少平方厘米?.2.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是多少平方厘米.?3.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是多少平方厘米?.4.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是多少度./?5.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是多少平方厘米? (π取3.14)2———————————————答 案——————————————————————例1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.例2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).例3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).例4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).例5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米). 练习题1. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米). 又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).2. 19.1416.⌒花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).3. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).4. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ,解得x=60.5. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米).11. 如图,小正方形的边长为2r,则①的面积为: 72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯,②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1)又9232=-x S ,于是有23184+-=S x ,解得S=6.14. 圆板的正面滚过的部分如右图阴影部分所求, 它的面积为:)420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).二、解答题11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率22)取12.已知右图正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.D13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?。
六年级奥数题圆及组合图形(含分析答案解析)

ED C B A 六年级奥(Ao)数题圆及组合图形(含分析答案解析)一、填空(Kong)题1.算(Suan)出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影(Ying)部分面积是 平(Ping)方厘米.3.一个(Ge)扇形圆心角,以扇形的半(Ban)径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所(Suo)示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米..积为2平方厘米,等腰直角三角形的面积为 .6厘米27.扇形的面积是31.4平方厘(Li)米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度(Du).8.图中扇(Shan)形的半径OA =OB =6厘(Li)米., AC 垂(Chui)直OB 于(Yu)C ,那么(Me)图中阴影部分的面积是 平方厘米.9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率)6 CB AO 4512 15 2012.如图,半(Ban)圆S 1的面积(Ji)是14.13平方厘米,圆S 2的面积是19.625平方厘米.那(Na)么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知(Zhi)圆心是O ,半(Ban)径r =9厘(Li)米,,那么(Me)阴影部分的面积是多少平方厘米?14.右图中4个圆的圆心是正方(Fang)形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?S 2S 1 CB A0 1 2———————————————答(Da) 案——————————————————————1. 18平(Ping)方厘米.由图示可知,正方形两条对角线的长都是6厘米(Mi),正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为(平(Ping)方厘米).2. 1.14平方厘(Li)米.由图示可知,图中(Zhong)阴影部分面积为两个圆心角为的扇形面积(Ji)减去直角三角形的面积.即(平方厘(Li)米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是.BE=CE=(厘米).于是阴影部分周长为(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米. 半圆面积为(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为(厘米).⌒⌒A10DCB OE 6.平方(Fang)厘米.将(Jiang)等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆(Yuan)的半径为厘(Li)米.图中阴影部分面积是正方形与圆的面积之差的,于(Yu)是有,解(Jie)得.故等腰直(Zhi)角三角形的面积为(平方厘(Li)米).7..扇形面积是圆面积的,故扇形圆心角为的即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为(厘米),故三角形ACO 的面积为(平方厘米).而扇形面积为(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为(厘米).图形总面积为两个圆面积加上正方形的面积,即(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即(平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的.三角(Jiao)形AED 的面(Mian)积是;正方(Fang)形面积是,圆面(Mian)积的41是(Shi),故阴影部分面积(Ji)为:(平方厘(Li)米).12. 由已知半(Ban)圆S 1的面积是14.13平方厘米得半径的平方为(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 , 同理,于是.扇形面积为:(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为(平方厘米).正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即 (平方厘米),所有空白部分面积为平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 (平方厘米).。
圆的组合图形面积及答案

圆的组合图形面积姓名:【知识与方法】要解决与圆有关的题目,需要注意以下几点:1、熟练掌握有关圆的概念和面试公式:圆的面积= 圆的周长=扇形的面积= 扇形的弧长=〔n是圆心角的度数〕2、掌握解题技巧和解题方法:加减法、分割重组法、旋转平移法、对折法、抵消法、等积变形法、等量代换法、添辅助线法。
例1.求阴影局部的面积。
(单位:厘米)解:这是最根本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14〔平方厘米〕例2.正方形面积是7平方厘米,求阴影局部的面积。
(单位:厘米)解:这也是一种最根本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影局部的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影局部的面积。
(单位:厘米)解:最根本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影局部的面积:2×2-π=0.86平方厘米。
解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影局部的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影局部的每一个小局部称为“叶形〞,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影局部的8倍。
例6.如图:小圆半径为2厘米,大圆半径是小圆的3倍,问:空白局部甲比乙的面积多多少厘米?解:两个空白局部面积之差就是两圆面积之差〔全加上阴影局部〕π-π()=100.48平方厘米〔注:这和两个圆是否相交、交的情况如何无关〕例7.求阴影局部的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影局部的面积。
小学数学六年级奥数《圆和组合图形(2)》练习题(含答案)
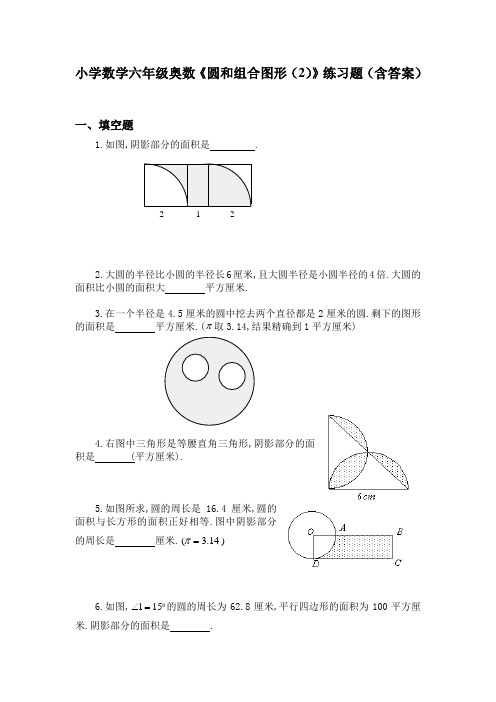
小学数学六年级奥数《圆和组合图形(2)》练习题(含答案)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 . 2 1 27.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解答题E D C B A GF O D C A B 2 甲 乙11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率22) 取12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++= 5.204.1645=⨯=(厘米). 6. 6548(平方厘米). 如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为 ⌒61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. 19.1416.花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米). 8. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ, 解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米11. 如图,小正方形的边长为2r ,则①的面积为: 72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯, ②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1) 又9232=-x S ,于是有23184+-=S x ,解得S=6.14. 圆板的正面滚过的部分如右图阴影部分所求,它的面积为: )420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ 07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).D。
六年级组合图形、圆形、阴影部分面积
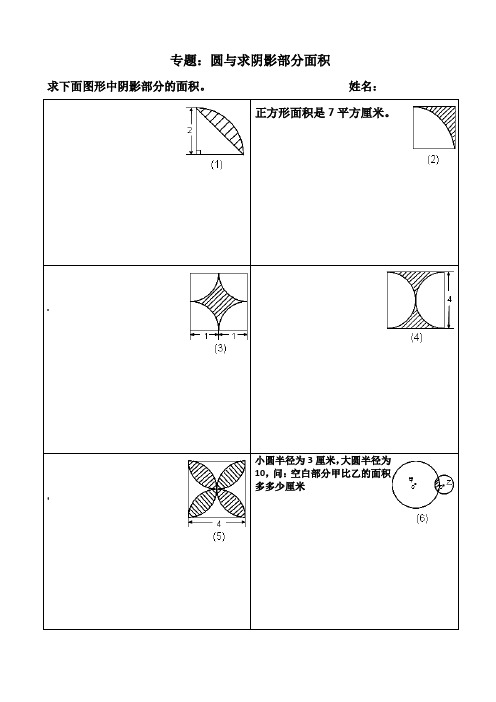
专题:圆与求阴影部分面积求下面图形中阴影部分的面积。
姓名:正方形面积是7平方厘米。
:: 小圆半径为3厘米,大圆半径为10,问:空白部分甲比乙的面积多多少厘米>已知直角三角形面积是12平方厘米,求阴影部分的面积。
图中圆的半径为5厘米,求阴影部分的面积。
\已知AC=2cm ,求阴影部分面积。
正方形ABCD的面积是36cm²/例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积。
$ 大正方形的边长为6厘米,小正方形的边长为4厘米。
求阴影的面积。
完整答案例1解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=(平方厘米)例2解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=平方厘米例3解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=平方厘米。
例4解:同上,正方形面积减去圆面积,16-π()=16-4π=平方厘米例5解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7解:正方形面积可用(对角线长×对角线长÷2,求) 正方形面积为:5×5÷2=所以阴影面积为:π÷=平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=平方厘米例9解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米(注: 8、9、10三题是简单割、补或平移)例11解:这种图形称为环形,可以用两个同心圆的面积差或例12.解:三个部分拼成一个半圆面积.差的一部分来求。
圆的组合图形面积及答案

圆的拉拢图形里积之阳早格格创做姓名:【知识取要领】要办理取圆有闭的题目,需要注意以下几面:1、流利掌握有闭圆的观念战里试公式:圆的里积= 圆的周少=扇形的里积= 扇形的弧少=(n是圆心角的度数)2、掌握解题本领妥协题要领:加减法、分隔沉组法、转动仄移法、对于合法、对消法、等积变形法、等量代换法、加辅帮线法.例1.供阳影部分的里积.(单位:厘米)解:那是最基原的要领:圆里积减去等腰曲角三角形的里积,×-2×1=1.14(仄圆厘米)例2.正圆形里积是7仄圆厘米,供阳影部分的里积.(单位:厘米)解:那也是一种最基原的要领用正圆形的里积减去圆的里积.设圆的半径为r,果为正圆形的里积为7仄圆厘米,所以=7,所以阳影部分的里积为:7-=7-×7=1.505仄圆厘米例3.供图中阳影部分的里积.(单位:厘米)解:最基原的要领之一.用四个圆组成一个圆,用正圆形的里积减去圆的里积,所以阳影部分的里积:2×2-π=0.86仄圆厘米.例4.供阳影部分的里积.(单位:厘米)解:共上,正圆形里积减去圆里积,16-π()=16-4π=3.44仄圆厘米例5.供阳影部分的里积.(单位:厘米)解:那是一个用最时常使用的要领解最罕睹的题,为便当起睹,咱们把阳影部分的每一个小部分称为“叶形”,是用二个圆减去一个正圆形,π()×2-16=8π-16=9.12仄圆厘米其余:此题还不妨瞅成是1题中阳影部分的8倍.例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空黑部分甲比乙的里积多几厘米?解:二个空黑部分里积之好便是二圆里积之好(齐加上阳影部分)π-π()=100.48仄圆厘米(注:那战二个圆是可相接、接的情况怎么样无闭)例7.供阳影部分的里积.(单位:厘米)解:正圆形里积可用(对于角线少×对于角线少÷2,供) 正圆形里积为:5×5÷2=12.5所以阳影里积为:π÷4-12.5=7.125仄圆厘米(注:以上几个题皆不妨间接用图形的好去供,无需割、补、删、减变形) 例8.供阳影部分的里积.(单位:厘米)解:左里正圆形上部阳影部分的里积,等于左里正圆形下部空黑部分里积,割补以去为圆,所以阳影部分里积为:π()=3.14仄圆厘米例9.供阳影部分的里积.(单位:厘米)解:把左里的正圆形仄移至左边的正圆形部分,则阳影部分合成一个少圆形,所以阳影部分里积为:2×3=6仄圆厘米例10.供阳影部分的里积.(单位:厘米)解:共上,仄移安排二部分至中间部分,则合成一个少圆形,所以阳影部分里积为2×1=2仄圆厘米(注: 8、9、10三题是简朴割、补或者仄移)11、例13.供阳影部分的里积.(单位:厘米)解: 连对于角线后将"叶形"剪启移到左上头的空黑部分,凑成正圆形的一半.所以阳影部分里积为:8×8÷2=32仄圆厘米12、例14.供阳影部分的里积.(单位:厘米)解:梯形里积减去圆里积,(4+10)×4-π=28-4π=15.44仄圆厘米 . 13、例16.供阳影部分的里积.(单位:厘米)解:[π+π-π]=π(116-36)=40π=125.6仄圆厘米14、例17.图中圆的半径为5厘米,供阳影部分的里积.(单位:厘米)解:上头的阳影部分以AB为轴翻转后,所有阳影部分成为梯形减去曲角三角形,或者二个小曲角三角形AED、BCD里积战.所以阳影部分里积为:5×5÷2+5×10÷2=37.5仄圆厘米16、例19.正圆形边少为2厘米,供阳影部分的里积.解:左半部分上头部分顺时针,底下部分顺时针转动到左半部分,组成一个矩形.所以里积为:1×2=2仄圆厘米17、例25.如图,四个扇形的半径相等,供阳影部分的里积.(单位:厘米)分解:四个空黑部分不妨拼成一个以2为半径的圆.所以阳影部分的里积为梯形里积减去圆的里积,4×(4+7)÷2-π=22-4π=9.44仄圆厘米18、例27.如图,正圆形ABCD的对于角线AC=2厘米,扇形ACB是以AC为曲径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,供阳影部分的里积.解: 果为2==4,所以=2以AC为曲径的圆里积减去三角形ABC里积加上弓形AC里积,π-2×2÷4+[π÷4-2]=π-1+(π-1)=π-2=1.14仄圆厘米19、例28.供阳影部分的里积.(单位:厘米)解法一:设AC中面为B,阳影里积为三角形ABD里积加弓形BD的里积,三角形ABD的里积为:5×5÷2=12.5弓形里积为:[π÷2-5×5]÷2=7.125所以阳影里积为:12.5+7.125=19.625仄圆厘米20、例30.如图,三角形ABC是曲角三角形,阳影部分甲比阳影部分乙里积大28仄圆厘米,AB=40厘米.供BC的少度. 解:二部分共补上空黑部分后为曲角三角形ABC,一个为半圆,设BC少为X,则40X÷2-π÷2=28所以40X-400π=56 则X=32.8厘米21、例33.供阳影部分的里积.(单位:厘米)解:用大圆的里积减去少圆形里积再加上一个以2为半径的圆ABE里积,为(π+π)-6=×13π-6=4.205仄圆厘米22、例34.供阳影部分的里积.(单位:厘米)解:二个弓形里积为:π-3×4÷2=π-6 阳影部分为二个半圆里积减去二个弓形里积,截止为π+π-(π-6)=π(4+-)+6=6仄圆厘米。
第十八讲 圆的组合图形的相关练习

第十三 讲 圆的组合图形训练知识要点1、 三角形的面积 =2⨯底高. 2、 等腰直角三角形的面积 =24=直角边的平方斜边的平方. 3、 长方形的面积 =⨯长宽. 4、 正方形的面积 = 边长的平方 = 2对角线的平方.5、 菱形的面积 =2对角线之积.6、 梯形的面积 =()2⨯上底+下底高.7、 圆的面积 =π⨯半径的平方. 8、 扇形的面积 =360π⨯⨯︒圆心角半径的平方. 例题讲解例1 如图,以半圆的半径8厘米为直径在半圆内作一个圆,求图中阴影部分的面积.(π取3.14)例2如图,正方形的边长是6厘米,则阴影部分的周长是______厘米,面积是______平方厘米.(π取3.14)例3如图,正方形的边长为6分米,求阴影部分的面积.(π取3.14)例4如图,求阴影部分的面积.(π取3.14)2例5如图,长方形的宽是8厘米,求阴影部分的面积.(π取3.14)例6图中,三个同心圆的半径分别为2、6、10,则图中阴影部分占大圆面积的______%.AB例7如图,圆O 的直径为8厘米,则阴影部分的面积是多少平方厘米?(π取3.14)例8如图,正方形的边长为2厘米,以圆弧为分界线的A 、B 两部分的面积的差是______平方厘米.(π取3.14)例9如图,其中四个圆的直径均为4厘米,那么阴影部分的面积为______平方厘米.(π取3.14)A例10如图,扇形AFB 恰为一个圆的14,BCDE 是正方形,边长为3,AFBG 也是正方形,边长为4,求图中阴影部分的面积.(π取3.14)例11如图,ABC ∆是等腰直角三角形,D 是半圆周的中点,BC 是半圆的直径.已知:AB = BC = 10,求阴影部分的面积.(π取3.14)例12如图,ABC ∆是等腰直角三角形,腰AB 长为4厘米,求阴影部分的面积.(π取3.14)ABABC DO 例13如图,一个大正方形各边都被四等分,分成十六个小正方形,图A 是一个圆,图B 是由三个半圆围成的图形,那么图A 与图B 的周长的大小关系是______,图A 与图B 的面积的大小关系是______.例14如图,有半径为5厘米、4厘米、3厘米的三个圆,A 部分(即两小圆的重叠部分)的面积与阴影部分的面积相比,哪个大?大多少?例15如图,梯形ABCD 的面积是25平方厘米,求圆环的面积.( 取3.14)例16如图是由正方形和半圆形组成的图形,其中P 点为半圆周的中点,Q 点为正方形一边的中点,那么阴影部分的面积是多少平方厘米?(π取3.14)例17如图,直角梯形的面积是54平方厘米,求阴影部分的面积.(π取3.14)例18如图,直径AB 为3厘米的半圆以点A 为圆心逆时针旋转60°,使AB 到达AC 的位置,求图中阴影部分的面积.(π取3.14)B10O例19如图,90AOB ∠=︒,C 为AB 的中点,已知阴影甲的面积为16厘米,求阴影乙的面积.(π取3.14)例19如图,ABC ∆是直角三角形,AB = 20米,阴影(1)的面积比阴影(2)的面积小23平方米,求BC 的长度是多少米?(π取3.14)课后作业1如图,正方形的边长为4厘米,阴影部分的面积是______平方厘米.2如图,阴影部分的面积是100平方厘米,求圆环的面积.3边长为1的正方形中,分别以边长为直径作3个半圆.求围成的阴影部分的面积.4如图,长方形的长为5厘米,宽为4厘米,则阴影部分的周长为______厘米,面积是______平方厘米.5已知等腰直角三角形ABC,D为斜边中点,AC = BC = 2分米,弧DF、弧DH分别是以B、C为圆心画的弧,求阴影部分的面积.6如图,圆的半径都是3厘米,则阴影部分的面积为______平方厘米.7如图,小正方形的边长4厘米,大正方形边长6厘米,DBE的面积为3.2平方厘米,求阴影部分的面积.E。
小学五年级数学下册圆计算组合图形面积期末复习练习题

五年级计算组合图形面积期末复习练习题
1、求下列各图阴影部分的面积(单位:厘米)
2、计算下面图形的面积。
(单位:厘米)
3、计算下面图形中涂色部分的面积。
(单位:厘米)
①②
3 1
5 3
4、求下面图形中涂色部分的面积。
(单位:厘米)
①②
5 5
8
5、如下图示,AB=4厘米,求涂色部分的面积。
A O B
6、计算下图中涂色部分的面积。
(6分)
←15厘米→7、如下图,正方形的面积是2平方分米,求圆的面积。
8、下面两个圆中直角等腰三角形的面积都是5平方厘米,求圆的面积。
①②
O
O
9. 计算下图中阴影部分的面积.
10. 求阴影部分的面积.
11.求出阴影部分的周长和面积。
(单位:厘米)
12、图中圆与长方形面积相等,长方形长6.28米。
阴影部分面积多少平方米?。
圆的组合图形练习

• 圆的组合图形概述 • 圆的组合图形基本元素 • 圆的组合图形练习方法 • 圆的组合图形练习示例 • 圆的组合图形练习总结与建议
01
圆的组合图形概述
定义与特点
定义
圆的组合图形是由一个或多个圆 形元素按照一定的规则和结构组 合而成的图案。
特点
具有简洁、优雅、和谐、对称等 美学特点,常常用于装饰、设计 、艺术等领域。
重要性
圆的组合图形练习是数学学习中的重 要内容,通过练习可以提高学生的空 间想象能力、几何思维能力和问题解 决能力。
方法
在圆的组合图形练习中,可以采用多 种方法,如通过观察、想象、推理和 计算来探究圆的性质和特点,利用圆 的性质解决实际问题,探究圆的组合 图形的构造和性质等。
建议:提供进一步练习和提高的建议和方向
• 实际应用:建议学生将圆的组合图形练习与实际生活联系起来,通过解决实际 问题来提高自己的应用能力和问题解决能力。例如,可以探究圆在机械设计、 建筑设计、物理学等领域的应用,以及利用圆的性质解决实际问题的方法。
THANKS
感谢观看
VS
详细描述
首先,使用圆规绘制一个大圆形作为时钟 的主体部分。然后,在圆形内部绘制一个 稍小的圆形作为时钟的刻度盘。接下来, 在刻度盘上标出12个数字和时针、分针 、秒针的位置。最后,使用黑色笔勾勒出 整个时钟的轮廓,并添加数字和指针的细 节。
示例四:绘制一个圆形徽章
总结词
通过绘制圆形徽章,掌握如何将圆与其他图 形结合,创造出具有象征意义的图案。
总结词
通过绘制圆形花环,掌握如何将多个圆形组合成一个完整的图案。
详细描述
首先,使用圆规绘制多个不同大小的圆形,并将它们排列成一个花环的形状。然后,在每个圆形之间添加弧线或 波浪线,以增加花环的装饰效果。最后,使用黑色笔勾勒出整个花环的轮廓,使图案更加清晰。
六年级奥数题:圆和组合图形 (3)
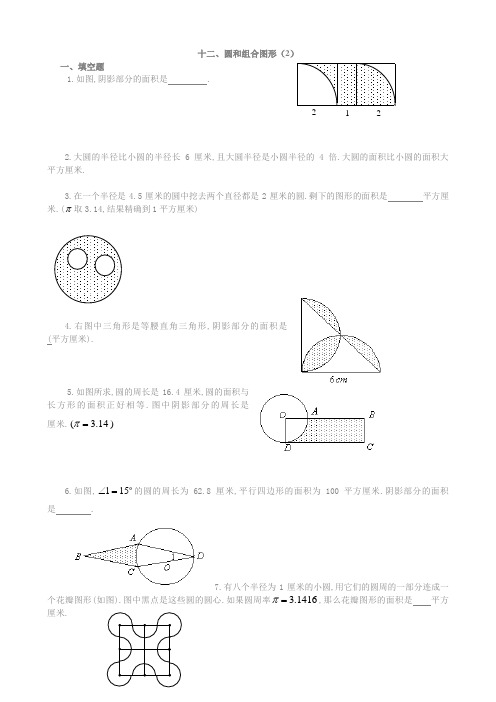
十二、圆和组合图形(2)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .7.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.2 1 28.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,311倍,那么,CAB∠是 度.10.厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解答题 11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值. 214.如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?练习11、 如图18-2所示,AE =ED ,BC=3BD ,S △ABC =30平方厘米。
求阴影部分的面积。
2、 如图18-3所示,AE=ED ,DC =13 BD ,S △ABC =21平方厘米。
六年级奥数题圆和组合图形(A)
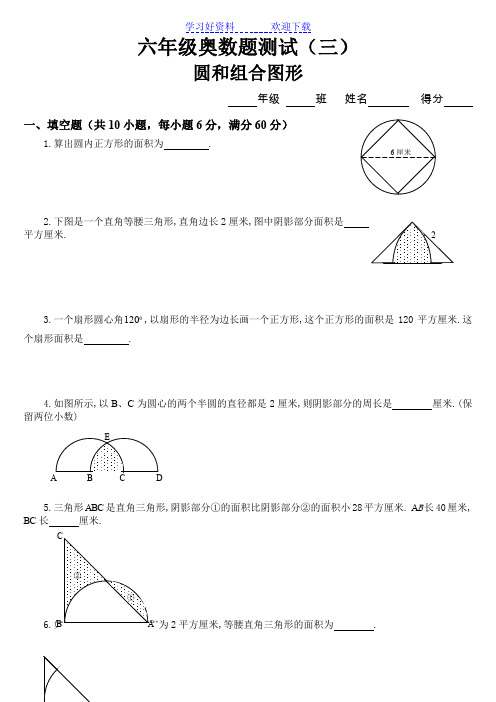
六年级奥数题测试(三)圆和组合图形年级 班 姓名 得分一、填空题(共10小题,每小题6分,满分60分) 1.算出圆内正方形的面积为 .2.下图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. A B 长40厘米,2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.两个阴影部分面积的和是 平方厘米.D 是半圆周的中点, BC 是半圆的直径,已知:AB =?(圆周率14.3=π)4512.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米六年级奥数题测试(三)答案:圆和组合图形1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米. 半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米. 将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫ ⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米).7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43⌒ ⌒圆面积加上正方形的面积,即 75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷ (平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的41. 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;正方形面积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为: 22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+ 125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米.阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA ,同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米). 正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即 2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米.故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
(完整)六年级奥数题:圆和组合图形(含分析答案)
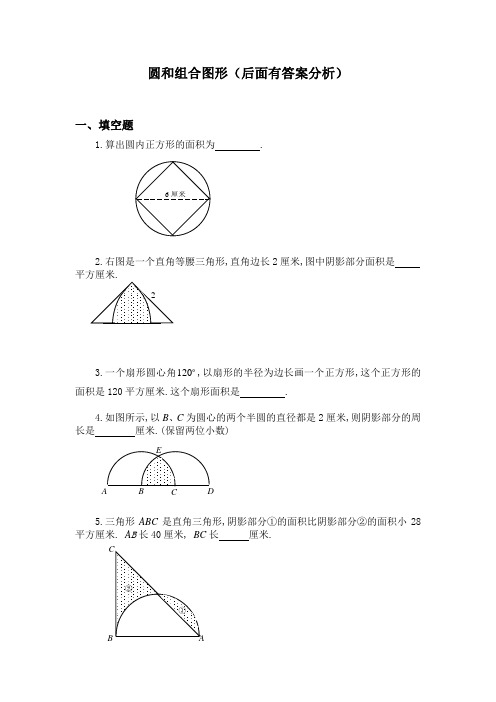
圆和组合图形(后面有答案分析)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B、C为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米.(保留两位小数)5.三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平⌒ ⌒方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米. 将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫ ⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米).7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即 75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷ (平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的41. 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;正方形面积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为: 22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+ 125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA ,同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为 221221=⨯⨯⨯(平方厘米). 正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即 2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
圆与组合图形

圆与组合图形一.选择题(共4小题)1.如图,4个圆的直径都是2cm,圆心分别在四边形ABCD的四个顶点上,阴影部分的面积的和是()cm2.A.37.68B.25.12C.9.42D.6.28C.18.75兀平方厘米D.15兀平方厘米3.如图,正方形的边长为5厘米,以AD为半径,以D为圆心做弧线与BD交于E点,以AB为直径做半圆交BD于F.则图中阴影部分的面积是()平方厘米.(兀取3)4.如图,将A ABC绕点A逆时针旋转30。
后得到A ADE,点B经过的路径为弧BD,已知AC=3,BC=4,A.6.25B.7.25C.8.25D.10.254B=5,则图中阴影部分的面积为()A. 2512B. 4冗3C.3兀4D. 5冗12二.填空题(共8小题)115.如图,两个圆重叠部分的面积相当于小圆的1,相当于大圆的—.点O是小圆的圆心,A、B两点分812别是两圆的交点,直角三角形AOB的面积是40cm2,大圆的面积是cm2.6•下面涂色部分的周长是cm,面积是cm2・7•如图,阴影部分的面积是9cm2,则圆环的面积是cm2・8.如图,将直径AB=10的半圆绕着点A逆时针旋转30。
,点B落在点C,则图中阴影部分的面积是—(结果保留冗)10.如图,四个圆的半径都为3cm,圆心分别在四边形的四个顶点上,则阴影部分的面积为cm2.(兀取13.如图,半圆S的面积是14.13cm2,圆S的面积是19.625cm2,求长方形(阴影部分)的面积.1214.如图,正方形边长为8厘米,大阴影三角形面积比小阴影三角形面积大16.8平方厘米,线段AE长多少厘米?DCAB E15.求阴影部分的面积.(单位:cm)18.三角形ABC是直角三角形,阴影I的面积比阴影II的面积小25cm2,AB=8cm,求BC的长度.(兀取3.14)19.如图所示,阴影部分的面积是85平方厘米,圆环的面积是多少平方厘米?(兀取3.14)20.如图,在直角三角形中,一个直角边长为6厘米,另一个直角边长为8厘米.求阴影部分的面积.21.如图,将两个半径分别是2厘米和3厘米的半圆如图放置,求阴影部分的周长.22.如图是一个漂亮而巧妙的图形,图中大圆的直径是10厘米,求阴影部分的面积.23.A ACB是等腰直角三角形,求阴影面积.四.应用题(共1小题)26.萌萌爸爸到商店买了4瓶啤酒,售货员将4瓶啤酒用胶带缠在一起(如图).瓶身直径为7cm,缠4圈28.如图是由两个完全一样的直角三角形叠在一起而成的,求阴影部分的面积.(单位:厘米)B S g C27.一块草地的形状如图的阴影部分,它的周长和面积各是多少?29•求图中阴影部分的面积(结果精确到0.01,冗取3.14)30.如图,BCEF是平行四边形,三角形ABC是直角三角形,BC长8厘米,AC长7厘米,阴影部分面积比三角形ADH的面积大12平方厘米.求HC的长度.31.如图所示,在半径为4cm的图中有两条互相垂直的线段,阴影部分面积A与其它部分面积B之差(大面积等于6平方公分,求五边形ABGEF的面积.33.如图所示,在一个边长为1的大正方形中有两个小正方形,他们的面积分别为m、n.猜猜看,是m大还是n大?并求-的值?34.如图所示,正方形ABCD的面积为2平方厘米,它的对角线长AC=2厘米,扇形ACD是以D为圆心,以AD为半径的圆面积的一部分,那么,阴影部分的面积是多少平方厘米?(冗取3.14)35.如图:直角三角形ABC中AB=15厘米,BC=20厘米,AC=25厘米,OD=5.84厘米.阴影部分是小正方形,求这个正方形的边长是多少厘米?36.如图,是大小两个正方形组成的图形,大正方形边长是8厘米,小正方形边长为6厘米,求阴影部分的面积.38.在长方形ABCD中,AD=15厘米,AB=8厘米,四边形EFGO的面积是9平方厘米,阴影部分的面C D37.如图,正方形ABCD的边AB、BC分别在三角形BEF的BE、BF边上,顶点D在EF边上,点D把EF积是多少平方厘米?39.如图,直角梯形ABCD的上底和高相等,正方形DEFH的边长是6厘米,阴影部分的面积是多少平方厘米?从图看出:S=S所以S=S于是S=S=ABHDABEBOHDEO阴影DHEA BEJ40.图中长方形的面积是180平方厘米,S与S的面积都是60平方厘米,阴影部分的面积是多少平方厘米?1241•如图,三角形ABC是等腰直角三角形,AB二AC二8cm,Z C二45。
小学五年数学下册第十单元《圆》计算组合图形面积期末复习练习题

五年级计算组合图形面积期末复习练习题
1、求下列各图阴影部分的面积(单位:厘米)
2、计算下面图形的面积。
(单位:厘米)
3、计算下面图形中涂色部分的面积。
(单位:厘米)
①
②
3 1
5 3
4、求下面图形中涂色部分的面积。
(单位:厘米)
① ②
5 5
8
5、如下图示,AB =4厘米,求涂色部分的面积。
A
O B
6、计算下图中涂色部分的面积。
(6分)
←15
→
7、如下图,正方形的面积是2平方分米,求圆的面积。
8、下面两个圆中直角等腰三角形的面积都是5平方厘米,求圆的面积。
①②
O
O
9. 计算下图中阴影部分的面积.
10. 求阴影部分的面积.
11.求出阴影部分的周长和面积。
(单位:厘米)
12、图中圆与长方形面积相等,长方形长6.28米。
阴影部分面积多少
平方米?
后使用,感谢您的下载!。
苏教版五年级数学下56.圆的组合图形练习

正方形的面积: 1.8×1.8=3.24(米2) 半圆形的面积: 3.14×0.9×0.9÷2=1.2717(米2) 这扇窗户的面积: 3.24+1.2717=4.5117(米2)
求图形中涂色部分的面积。 (单位:cm)
9.量出需要的数据(取整毫米数), 计算涂色部分的面积。
厘米,你能算出黄色部分的面积吗?
.0
求下图中涂色部分的面积。(单位:米)
80
100
10
10
小结:这节课你有什么收获?
教学反思:
求组合图形的面积这部分内容最能体现学生思维 的灵活性。本节课我组织学生通过自主探究与汇报交 流探索出这个组合图形的面积计算方法,在学生探索 之后安排了学生展示学习成果的机会,让有想法的同 学充分展示自己的想法,让不会的同学在其他同学的 汇报和讲解下再次学习,再次思考,达到掌握的目的。 在课堂教学中充分发挥小组合作学习的优势,力求使 每个学生都能够有成功的体验。
复习:一、填空 1.圆的面积公式:( s=π r² )
2.看图列式求面积
r=3cm
d=8cm
S=3.14×3 2
r=8÷2=4(cm) S=3.14×42
复习:
1.圆环的面积公式:
( S环=π R²— π r² ) 2. 一个环形铁片,外圆直径9厘米,内
圆直径5厘米,求思考方法:
1、观察。不规则图形是由哪些基本图形形成的。 2、分析。是基本图形面积的和、面积的差。 3、列式计算。
一个半径8米的圆形水池,周围 有一条2米宽的小路,求这条小路的 占地面积。
.2 88
开放性练习
只许测量一次,求出阴影的面积 (尽量想出不同的方法)。
思考题:图中正方形的面积是8平方
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西师版六年级上册圆的组合图形面积练习题
1、求下列各图阴影部分的面积(单位:厘米)
2、计算下面图形的面积。
(单位:厘米)
3、计算下面图形中涂色部分的面积。
(单位:厘米) ①
②
3 1
5
3
4、求下面图形中涂色部分的面积.(单位:厘米) ① ②
5 5 8
5、如下图示,AB=4厘米,求涂色部分的面积。
A O B
6、计算下图中涂色部分的面积。
←
15厘米
→
7、如下图,正方形的面积是2平方分米,求圆的面积。
O
8、下面两个圆中直角等腰三角形的面积都是5平方厘米,求圆的面积.
①②
O
O
9。
计算下图中阴影部分的面积. 10. 求阴影部分的面积.
11.求出阴影部分的周长和面积。
(单位:厘米)
ﻫ12、图中圆与长方形面积相等,长方形长6。
28米.阴影部分面积多少平方米?。
