《用待定系数法确定一次函数表达式》习题
八上数学每日一练:待定系数法求一次函数解析式练习题及答案_2020年解答题版

八上数学每日一练:待定系数法求一次函数解析式练习题及答案_2020年解答题版答案解析答案解析答案解析答案解析2020年八上数学:函数_一次函数_待定系数法求一次函数解析式练习题1.(2020金山.八上期末) 已知:y 与2x-3成正比例,且当x=4时,y=10,求y 与x 的函数解析式考点: 待定系数法求一次函数解析式;2.(2020武汉.八上期末) 一次函数y =kx +b 中(k 、b 为常数,k≠0),若-3≤x≤2,则-1≤y≤9,求一次函数的解析式.考点: 一次函数的性质;待定系数法求一次函数解析式;3.(2019杭州.八上期末) 已知一次函数y =kx +4(k≠0).(1) 当 x =-1 时,y =2,求此函数的表达式;(2) 函数图象与 x 轴、y 轴的交点分别为 A 、B , 求出△AOB 的面积;(3) 利用图象求出当y≤3时,x 的取值范围.考点: 一次函数图象与坐标轴交点问题;待定系数法求一次函数解析式;一次函数与不等式(组)的综合应用;4.(2019句容.八上期末) 学完《平面直角坐标系》和《一次函数》这两章后,老师布置了这样一道思考题:已知:如图,在长方形中, ,,点为 的中点,和 相交于点.求 的面积.小明同学应用所学知识,顺利地解决了此题,他的思路是这样的:以所在的直线为轴,以所在的直线为轴建立适当的平面直角坐标系,写出图中一些点坐标.根据一次函数的知识求出点的坐标,从而求得 的面积.请你按照小明的思路解决这道思考题.考点: 坐标与图形性质;待定系数法求一次函数解析式;一次函数与二元一次方程(组)的综合应用;5.(2018徐州.八上期末) 已知一次函数y=kx+2的图象经过点(﹣1,4).答案解析(1) 求k 的值;(2) 画出该函数的图象;(3) 当x≤2时,y 的取值范围是考点: 一次函数的图象;待定系数法求一次函数解析式;2020年八上数学:函数_一次函数_待定系数法求一次函数解析式练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
待定系数法求一次函数表达式

∴ 函数的解析式为 y= 0.2x +8 (-20≤x≤100)
变式2 :求下图中直线的函数表达式
解:设这个一次函数的解析式为y=kx+b. ∵y=kx+b的图象过点(0,3)与(1,0).
y
∴ b=3 k+b=0
解得 k=-3 b=3
Page 4
练习1:已知一次函数的图象经过点(1,5)与 (-1,-1).求这个函数的表达式。 解 : 设这个一次函数的表达式为y=kx+b (k≠0). ∵根据题意,得: k+b=5 -k+b=-1 解得 k=3 b=2
∴这个一次函数的解析式为y=3x+2
Page 5
变式1:已知一次函数y=kx+b,当x=1时, y=1,当x=2时,y=3.求这个一次函数的解 析式。
• • • •
例3、已知温度计中水银(或酒精)柱的高度y(厘
米)是温度x(℃)的一次函数。某型号的实验用水银 温度计能测量-20℃至100℃的温度,当温度为10℃时水 银柱高10厘米;温度为50℃水银柱高18厘米。求这个函 数的表达式。
y=kx+b(k≠0) , 解: 设这个函数的表达式为_______________
k
b
步骤概括: 设、 代、 求、写 注意:对于是实际问题时所求的结果还得考虑自
变量的取値范围。
Page 10
思考1:已知一次函数y=kx+b 的图象 与y=2x平行且过点(2,-1).求这个函数 x=5时的函数值.
∵ y=kx+b 的图象与y=2x平行. 解:
∴ k=2 ∴
∴ y=2x-b
b=-5
用待定系数法确定一次函数表达式

用待定系数法确定一次函数表达式一.客观性试题研究:✧选择题部分1.如图,在矩形ABCD中,已知A(﹣3,2),C(2,0),则直线BD的解析式为()A.B. y=C.D.2.已知y=kx+b,且当x=1时,y=﹣2;当x=2时,y=﹣1,则k,b的值是()A. k=1,b=﹣3B. k=1,b=﹣1C. k=﹣3,b=﹣5D. k=3,b=13.若函数y=kx的图象经过(1,﹣2)点,那么它一定经过()A.(2,﹣1)B.C.(﹣2,1)D.4.已知正比例函数的图象过点(﹣2,3),则此函数的解析式是()A.y=B.C.y=D ..5.如图,若点P(﹣2,4)关于y轴的对称点在一次函数y=x+b的图象上,则b的值()A.﹣2B. 2C.﹣6D. 66.在y=kx+b(k≠0)中,若x=1时y=2;若x=2时y=1,则当x=3时y=()A.﹣2B. 1C. 3D. 07.若一次函数y=(3+k)x+18﹣2k2的图象过原点,则k为()A.±3B.﹣2C. 3D.任何实数8.已知一次函数的图象经过点(﹣2,0)和点(0,﹣5),则这个函数的解析式为()A.﹣5B. y=2x﹣5C. y=﹣2x﹣5D.﹣59.如图,四边形OABC是矩形,点O是平面直角坐标系的原点,点A、C分别在x、y轴上,点B的坐标是(3,4),则直线AC的函数表达式是()A.y=B. y=.y=.y=10.已知正比例函数y=kx,当x=﹣3时,y=6.那么该正比例函数应为()AB. y=﹣2x C.D. y=2x11.已知函数y=﹣x+m与y=mx﹣4的图象的交点在x轴的负半轴上,那么m的值为()A.﹣2B. 2C.±4D.±212.已知直线y=mx﹣1上有一点B(1,n)为()A.B.C.D.13.如图,一次函数图象经过点A,且与正比例函数y=﹣x的图象交于点B,则该一次函数的表达式为()A. y=﹣x+2B. y=x+2C. y=x﹣2D. y=﹣x﹣214.一次函数y=mx+|m﹣1|的图象过点(0,2),且y随x的增大而增大,则m=()A.﹣1 B. 3 C. 1 D.﹣1或3✧填空题部分15.若y与x﹣1成正比例,且x=2时y=6,则x=﹣2时y=________.16.已知y与x成正比例,且当x=3时,y=12,则当x=1时,y=________.17.一次函数图象经过点(3,0)和(1,4),这个一次函数的解析式是________.18.一个函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,﹣3a)与点(a,﹣6),则这条直线的解析式是________.19.一次函数y=kx+b(k≠0)的图象过点(1,﹣1),且与直线y=﹣2x+5平行,则此一次函数的解析式为________.20.如图,该直线是某个一次函数的图象,则此函数的解析式为________.21.已知正比例函数y=kx的图象经过点(﹣1,2),则k=________,此函数图象经过第________象限.22.请写出一个同时具备:①y随着x的增大而减小;②函数图象为经过点(1,﹣3)的一次函数表达式________(写一个即可)二.主观性试题研究✧解答题部分23.直线y=kx+b交坐标轴于A(-2,0),B(0,3)两点,求不等式kx+b>0的解集.24.已知一次函数y=kx+5经过点(2,1).(1)求这个函数的解析式;(2)在平面直角坐标系中画出这个函数的图象.25.已知直线l过(1,3)和(3,1)两点,且与x轴,y轴分别交于点A,B,(1)求直线l的函数关系式y AB;(2)在图中,画出直线l;(3)求△AOB的面积;(4)当x_____时,y AB>0.26.已知一次函数y=kx+b的图象过点(3,5)与(﹣4,﹣9),(1)求这个一次函数解析式.(2)利用函数图象求当x为何值时,y>0.27.若方程组x+3y=13x-2y=-8⎧⎨⎩的解所对应的点在一次函数y=kx﹣3的图象上,求k的值.28.已知一次函数的图象经过点(2,5)与(4,11)(1)求这个函数的解析式;(2)若点P(m,14)在此函数图象上,求m的值.29.已知y﹣1与x成正比例,且x=﹣2时,y=4(1)求出y与x之间的函数关系式;(2)设点(a,﹣2)在这个函数的图象上,求a的值;(3)如果自变量x的取值范围是0≤x≤5,求y的取值范围.30.已知一次函数的图象经过点(0,4),并且与直线y=﹣2x相交于点(2,m),求这个一次函数的解析式.31.已知y﹣2与x+1成正比例函数关系,且x=﹣2时,y=6.(1)写出y与x之间的函数关系式;(2)求当x=﹣3时,y的值;(3)求当y=4时,x的值.32.已知一次函数y=kx+b(k、b是常数,且k≠0)的图象经过点A(﹣3,0)、B(0,﹣2).求这个一次函数的解析式?。
待定系数法求函数解析式10题

待定系数法求函数解析式10题1. 题目:已知一次函数y = kx + b的图象经过点(1,3)和( - 1, - 1),求这个一次函数的解析式。
- 解答:- 因为一次函数y = kx + b的图象经过点(1,3)和( - 1, - 1),所以把这两个点分别代入函数解析式中。
- 当x = 1,y = 3时,得到3=k×1 + b,也就是k + b=3;当x=-1,y = - 1时,得到-1=k×(-1)+b,也就是-k + b=-1。
- 现在有了一个方程组k + b = 3 -k + b=-1。
- 把这两个方程相加,(k + b)+(-k + b)=3+(-1),得到2b = 2,解得b = 1。
- 把b = 1代入k + b = 3,得到k+1 = 3,解得k = 2。
- 所以这个一次函数的解析式是y = 2x+1。
2. 题目:二次函数y = ax^2+bx + c的图象经过点(0,1),(1,2),( - 1,4),求这个二次函数的解析式。
- 解答:- 因为二次函数y = ax^2+bx + c的图象经过点(0,1),(1,2),( - 1,4)。
- 当x = 0,y = 1时,代入解析式得1=a×0^2+b×0 + c,也就是c = 1。
- 当x = 1,y = 2时,得到2=a×1^2+b×1 + c,也就是a + b + c=2;当x=-1,y = 4时,得到4=a×(-1)^2+b×(-1)+c,也就是a - b + c = 4。
- 因为c = 1,所以把c = 1代入a + b + c = 2和a - b + c = 4中,得到a + b+1 = 2 a - b+1 = 4。
- 化简这两个方程得a + b = 1 a - b = 3。
- 把这两个方程相加,(a + b)+(a - b)=1 + 3,得到2a = 4,解得a = 2。
8 用待定系数法求一次函数解析式--经典

∴
1 k = 10
{ 2000k + b = 700
1000k + b = 800
解这个方程组得{ :
1 = 10
b =900 x + 900
因此,购买量y与单价x的函数解析式为 y
当y=
400时得
1 10
x + 900 =400
例3.已知一次函数的图象如下图,写 出它的关系式.
解 :设y=kx+b(k≠0). 由直线经过点(2,0),(0,-3)得
3 函数关系式是 y x 3 2
2k b 0 b 3
3 k , 2 解得 b 3.
变式6:已知一次函数y=kx+b 的图象 过点A(3,0).与y轴交于点B,若△AOB 的面积为6,求这个一次函数的解析 y 式.
判断三点A(3,1),B(0,-2),C(4,2) 是否在 同一条直线上. [分析] 由于两点确定一条直线,故选取其中两点, 求经过这两点的函数表达式,再把第三个点的坐标 代入表达式中,若成立,说明在此直线上;若不成 立,说明不在此直线上.
k 1, ∴ 1 3k b, b 2. 2 0 b , ∴过A,B两点的直线的表达式为y=x-2. ∵当x=4时,y=4-2=2. ∴点C(4,2)在直线y=x-2上. ∴三点A(3,1), B(0,-2),C(4,2) 在同一条直线上.
反思总结
求一次函数关系式常见题型: 1.利用点的坐标求函数关系式 2. 利用图像求函数关系式 3.利用表格信息确定函数关系式 4.根据实际情况收集信息求函数关系式
5.其它
八年级.数学 第二 一次函数 21.3 用待定系数法确定一次函数表达式

12/12/2021
21.3 用待定系数法确定一次函数表达式
【归纳总结】确定一次函数表达式的方法:
(1)待定系数法:已知x,y的两组值或两点坐标,利用方程 组确定k,b的值. (2)位置确定法:两直线平行,k的值相等;两直线交于y轴 上同一点,b的值相等.
(3)列方程确定法:实际问题中的列二元一次方程法.
反思
已知函数 y=kx+b 中,自变量 x 的取值范围是-1≤x≤7,相应的 函数值的范围是-12≤y≤8,求函数的表达式.
解:由-1≤x≤7,得-k+b≤kx+b≤7k+b, 即-k+b≤y≤7k+b. 又∵-12≤y≤8,∴- 7kk++bb==8-. 12,解得kb= =2-.95.,5. ∴函数的表达式为 y=2.5x-9.5.
解:(1)将 A(-3,-2),B(1,6)代入 y=kx+b, 得方程组- k+3bk+ =b6= ,-2,解得kb= =24, ,则此一次函数的表达式为 y=2x+4. (2)在 y=2x+4 中,令 x=0,得 y=4;令 y=0,得 x=-2,则此函数图像与 x 轴的交点坐标是(-2,0),与 y 轴的交点坐标是(0,4),所以此函数图像与坐标
12/12/2021
21.3 用待定系数法确定一次函数表达式 例2 教材补充例题 已知一次函数的图像经过点P(3,5),且 平行于直线y=2x.求该一次函数的表达式.
用待定系数法求一次函数解析式

y=3x-30
60 元上网费用; (2)若小李 4 月份上网 20 小时,他应付________
(3)若小李 5 月份上网费用为 75 元,则他在该月份的上网时间 是__________.
35
点拨:(1)当 x≥30 时,设函数解析式为 y=kx+b,
30k b 60 k 3 则 ,解得 .所以 y=3x-30. b 30 40k b 90
k=2 ∴ y=2 x +2 ∴ x=-1 时 y=度y(厘米)在一定限度内 所挂重物质量x(千克)的一次函数,现已测得 不挂重物时弹簧的长度是6厘米,挂4千克质量 的重物时,弹簧的长度是7.2厘米,求这个一次 函数的解析式。
解:设这个一次函数的解析式为:y=kx+b 根据题意,把x=0,y=6和x=4,y=7.2代入,得: b=6 k=0.3 4k+b=7.2 解得 b=6
Page 2
变式3:已知一次函数y=2x+b 的 图象过点(2,-1).求这个一次函数 的解析式.
解: ∵ y=2x+b 的图象过点(2,-1).
∴ -1=2×2 + b
解得
b=-5
∴这个一次函数的解析式为y=2x-5
Page
3
变式4:已知一次函数y=kx+b 的图象 与y=2x平行且过点(2,-1).求这个一 次函数的解析式. ∵ y=kx+b 的图象与y=2x平行. 解:
当B点的坐标为(0,4)时,则 y=kx+4
4 ∴ 0=3k+4, ∴k= - ∴ 3 4 ∴ 0=3k+4, ∴k= 3
y= -
4 x+4 3
当B点的坐标为(0,-4)时,则 y=kx-4
待定系数法求一次函数表达式

例4:在弹性限度内,弹簧长度y(cm)是所挂物体质量x(g)的一次函 数.已知一根弹簧挂10g物体时的长度为10cm,挂30g物体时的长度 为15cm,试求y与x的函数表达式
Hale Waihona Puke 拓展探究1.已知: y与x成正比例,且当 x=3时 y=7,求y与x的函数解析式.
变式1 : y与x-1成正比例,且当 x=3时 y=7,求y与x的函数解析式. 变式2 : y+3与x-1成正比例,且当 x=3时 y=7,求y与x的函数解析式.
(1)求这个函数的解析式 (2)求当x=3时,y的值。
例3:(1)已知y是 x的一次函数,当 x=-1时 y=3,当 x =2 时 y=-3, 求y关于 x 的函数解析式.
(2)已知y是 x的正比例函数,当x=2时,y=-4, 求这个函数的解析式.
练:已知y是x的一次函数,又表给出了部分对应值,则m的值是_______.
练:已知:y-1与x成正比例,当x=1时,y=3. 写出y与x之间的函数关系式
拓展探究:
2.已知y=y1+y2 ,y1与x成正比例,y2与x-1成正比例,且 x=3时 y=4; x=1时 y=2. 求y与x的函数解析式.
练:已知y=y1+y2 ,y1与x成正比例,y2与x-2成正比例,且 x=-1时 y=2; x=3时 y=-2. 求y与x的函数解析式.
例1:已知一次函数y=kx+b。当x=3时,y= 0;当x=0时,y=-4。 (1)求k,b的值 (2)求当x=2时,y的值
例2:已知正比例函数y=kx,当x=3时,y=4. 求当x=2时,y的值
练1:在一次函数y=kx-3中,当x=3时,y=6。则k= 练2:已知一次函数y=kx+b中,当x=1时,y=3,当x=-1时,y=7。
21.3用待定系数法确定一次函数的表达式课后练习
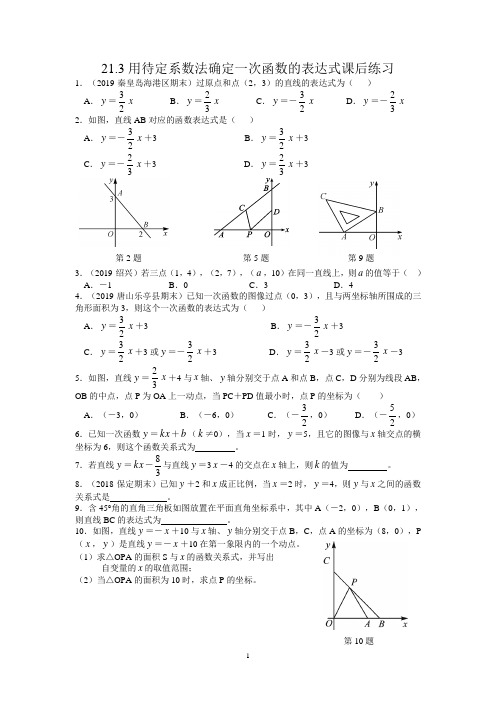
第10题 21.3用待定系数法确定一次函数的表达式课后练习 1.(2019·秦皇岛海港区期末)过原点和点(2,3)的直线的表达式为( ) A .y =23x B .y =32x C .y =-23x D .y =-32x 2.如图,直线AB 对应的函数表达式是( )A .y =-23x +3 B .y =23x +3 C .y =-32x +3 D .y =32x +3 3.(2019·绍兴)若三点(1,4),(2,7),(a ,10)在同一直线上,则a 的值等于( )A .-1B .0C .3D .44.(2019·唐山乐亭县期末)已知一次函数的图像过点(0,3),且与两坐标轴所围成的三角形面积为3,则这个一次函数的表达式为( ) A .y =23x +3 B .y =-23x +3 C .y =23x +3或y =-23x +3 D .y =23x -3或y =-23x -3 5.如图,直线y =32x +4与x 轴、y 轴分别交于点A 和点B ,点C ,D 分别为线段AB ,OB 的中点,点P 为OA 上一动点,当PC +PD 值最小时,点P 的坐标为( )A .(-3,0)B .(-6,0)C .(-23,0)D .(-25,0) 6.已知一次函数y =kx +b (k ≠0),当x =1时,y =5,且它的图像与x 轴交点的横坐标为6,则这个函数关系式为 。
7.若直线y =kx -38与直线y =3x -4的交点在x 轴上,则k 的值为 。
8.(2018·保定期末)已知y +2和x 成正比例,当x =2时,y =4,则y 与x 之间的函数关系式是 。
9.含45°角的直角三角板如图放置在平面直角坐标系中,其中A (-2,0),B (0,1),则直线BC 的表达式为 。
10.如图,直线y =-x +10与x 轴、y 轴分别交于点B ,C ,点A 的坐标为(8,0),P (x ,y )是直线y =-x +10在第一象限内的一个动点。
《用待定系数法求一次函数解析式》练习题

=-200x+11 000,当 y=0 时,x=55,∴返回到家的时间为 8:55.
易错点:对图表中的一次函数关系不能作出明确判断
10 .目前,我国大约有 1.3 亿高血压病患者,预防高血压不容忽
视.“千帕(kpa)”和“毫米汞柱(mmHg)”都是表示血压的单位.请
你根据表格提供的信息,判断下列各组换算正确的是( C )
14.(导学号69654150)(2017·苏州)某长途汽车客运公司规定旅客可免费 携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是 行李质量x(kg)的一次函数.已知行李质量为20 kg时需付行李费2元,行 李质量为50 kg时需付行李费8元.
(1)当行李的质量x超过规定时,求y与x之间的函数解析式;
1
1 (2)当 y=0 时, x-2=0,得 x=10. 5 答:旅客最多可免费携带行李 10 kg.
15.(导学号69654151)(2016·河北)某商店能通过调低价格的方式促销n
4.已知一次函数 y=kx+b 的图象经过点 A(0,-2),B(1,0),则 b=
2 . -2 ,k=____ ____
5.已知一次函数图象经过A(-2,-3),B(1,3)两点. (1)求这个一次函数的解析式; (2)试判断P(-1,1)是否在这个函数图象上?
解:(1)设一次函数的解析式为 y=kx+b,∵A(-2,-3),B(1,3)
端点同时出发,甲从点A出发,向终点B运动,乙从点B出发,向终点
A运动.已知线段AB长为90 cm,甲的速度为2.5 cm/s.设运动时间为
x(s),甲、乙两点之间的距离为y(cm),y与x的函数图象如图所示,则
图中线段DE所表示的函数解析式为_________________________ .(并 y=4.5k-90(20≤x≤36) 写出自变量的取值范围)
待定系数法(练习专用)

,此直线的关系式为
学习目标
• 1、能根据题中提供信息,确定一次函数 的表达式。 • 2、运用一次函数解决问题。
求图中直线的解析式:
y
2
o
1
x
如图所示,已知直线 AB和x轴交于点B,和y 轴交于点A。
y 5 4 3 2 1
①写出A、B两点 的坐标。 ②求直线AB的 表达式。
-3 -2 -1
该直线解析式为 y 2x 5或y 2x 5
4、某一次函数当-3≤x≤1时,对应的 y值为1≤y≤9,求该函数的解析式。
求函数解关系的一般步骤是怎样的呢? 可归纳为:“一设、二列、三解、四定” 一设:设出函数关系式的一般形式y=kx+b; 二列:根据已知两点的坐标列出关于k、b的二 元一次方程组; 三解:解这个方程组,求出k、b的值; 四定:把求得的k、b的值代入y=kx+b,得出函数 关系式。
回归目标
• 1、能根据题中提供信息,确定一次函数 的表达式。 • 2、运用一次函数解决问题。
例:如图,直线 y 3x 2 3 与x轴、y轴分别交于点A,点B, 与直线 y 33 x 交于点C。动点E从原点O出发, 以每秒1个单位长度的速度沿OA 方向向终点A运动,动点F同时 从点A出发,以每秒1个单位长 度的速度沿折线AC—CO方向向 终点O运动,设点F运动的时间 为t(秒). (1)设△OEF的面积为S,求S与t 之间的函数关系式,并写出自 变量t的取值范围. (2)当1≤t≤2时,是否存在某 一时刻,使得△OEF是等腰三角 形?若存在,求出t的值;若不 存在,说明理由.
课时小结:
1.用待定系数法求一次函 数解析式
2.用待定系数法求一次函 数解析式的步骤
一次函数待定系数法专练

一次函数待定系数法专练一.选择题(共12小题)1.(2014•宜宾)如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是()x的一次函数,下表中列出了部分对应值,则m等于().3.(2012•黔南州)如图,直线AB对应的函数表达式是()x+3 x+36.(2011•咸宁)如图,在平面直角坐标系中,▱OABC的顶点A在x轴上,顶点B的坐标为(6,4).若直线l经过点(1,0),且将▱OABC分割成面积相等的两部分,则直线l的函数解析式是()C.C D.9.(2011•济南模拟)如图,四边形OABC是矩形,点O是平面直角坐标系的原点,点A、C分别在x、y轴上,点B的坐标是(3,4),则直线AC的函数表达式是().C D.12.(2009•辽宁)如图,直线m是一次函数y=kx+b的图象,则k的值是()二.填空题(共12小题)13.(2014•常州)在平面直角坐标系xOy中,已知一次函数y=kx+b(k≠0)的图象过点P(1,1),与x轴交于点A,与y轴交于点B,且tan∠ABO=3,那么点A的坐标是_________.14.(2014•牡丹江)已知函数y=kx+b(k≠0)的图象与y轴交点的纵坐标为﹣2,且当x=2时,y=1.那么此函数的解析式为_________.p的值为_________.16.(2014•永州一模)已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则此一次函数的解析式为_________.17.(2014•普陀区二模)一次函数的图象过点(0,3)且与直线y=﹣x平行,那么函数解析式是_________.18.(2014•河西区模拟)已知一次函数的图象经过(﹣1,2)和(﹣3,4),则这个一次函数的解析式为_________.19.(2014•曲靖模拟)直线y=kx+b经过A(﹣1,1)和B(﹣3,0)两点,则k=_________.20.(2013•上海)李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是_________升.21.(2013•常州)已知一次函数y=kx+b(k、b为常数且k≠0)的图象经过点A(0,﹣2)和点B(1,0),则k=_________,b=_________.22.(2013•梧州)若一条直线经过点(﹣1,1)和点(1,5),则这条直线与x轴的交点坐标为_________.23.(2013•湖州模拟)如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0).设直线AB的解析式为y=kx+m,若是整数时,k也是整数,满足条件的k值共有_________个.y是x的一次函数,下表列出了部分对应值,则m=_________.三.解答题(共6小题)25.(2014•钦州)某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:(1)该地出租车的起步价是_________元;(2)当x>2时,求y与x之间的函数关系式;(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?26.(2014•怀化)设一次函数y=kx+b(k≠0)的图象经过A(1,3)、B(0,﹣2)两点,试求k,b的值.27.(2014•定州市一模)如图,在平面直角坐标系中,直线l1:y=kx+b经过第一象限的点A(1,2)和点B(m,n)(m>1),且mn=2,过点B作BC⊥y轴,垂足为C,△ABC的面积为2.(1)求B点的坐标;(2)求直线l1的函数表达式;(3)直线l2:y=ax经过线段AB上一点P(P不与A、B重合),求a的取值范围.28.(2014•白云区一模)如图,点N(0,6),点M在x轴负半轴上,ON=3OM.A为线段MN上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C.矩形ABOC的面积为2.(1)点M的坐标为_________;(2)求直线MN的解析式;(3)求点A的坐标(结果用根号表示).29.(2014•门头沟区二模)如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标、点B的横坐标如图所示.(1)求直线AB的解析式;(2)点P在直线AB上,是否存在点P使得△AOP的面积为1,如果有请直接写出所有满足条件的点P的坐标.30.(2014•大兴区二模)已知:如图,在平面直角坐标系xOy中,一次函数y=﹣4x+8的图象分别与x、y轴交于点A、B,点P在x轴的负半轴上,△ABP的面积为12.若一次函数y=kx+b的图象经过点P和点B,求这个一次函数y=kx+b表达式.一次函数待定系数法专练参考答案与试题解析一.选择题(共12小题)1.(2014•宜宾)如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是(),,x的一次函数,下表中列出了部分对应值,则m等于().代入得:3.(2012•黔南州)如图,直线AB对应的函数表达式是()x+3 x+3x+3∴6.(2011•咸宁)如图,在平面直角坐标系中,▱OABC的顶点A在x轴上,顶点B的坐标为(6,4).若直线l经过点(1,0),且将▱OABC分割成面积相等的两部分,则直线l的函数解析式是()C∴,.C D.±±.9.(2011•济南模拟)如图,四边形OABC是矩形,点O是平面直角坐标系的原点,点A、C分别在x、y轴上,点B的坐标是(3,4),则直线AC的函数表达式是().C D.,,,,,12.(2009•辽宁)如图,直线m是一次函数y=kx+b的图象,则k的值是(),,则二.填空题(共12小题)13.(2014•常州)在平面直角坐标系xOy中,已知一次函数y=kx+b(k≠0)的图象过点P(1,1),与x轴交于点A,与y轴交于点B,且tan∠ABO=3,那么点A的坐标是(﹣2,0)或(4,0).就是已知一次函数的一次项系数是或﹣±.时,求可得;时,求可得.x+或x+14.(2014•牡丹江)已知函数y=kx+b(k≠0)的图象与y轴交点的纵坐标为﹣2,且当x=2时,y=1.那么此函数的解析式为y=x﹣2.得:k=y=xp的值为1.∴,16.(2014•永州一模)已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则此一次函数的解析式为y=x+2或y=﹣x+2.17.(2014•普陀区二模)一次函数的图象过点(0,3)且与直线y=﹣x平行,那么函数解析式是y=﹣x+3.18.(2014•河西区模拟)已知一次函数的图象经过(﹣1,2)和(﹣3,4),则这个一次函数的解析式为y=﹣x+1.)代入得:,19.(2014•曲靖模拟)直线y=kx+b经过A(﹣1,1)和B(﹣3,0)两点,则k=.得:k=b=故答案为:20.(2013•上海)李老师开车从甲地到相距240千米的乙地,如果油箱剩余油量y(升)与行驶里程x(千米)之间是一次函数关系,其图象如图所示,那么到达乙地时油箱剩余油量是20升.x+35×21.(2013•常州)已知一次函数y=kx+b(k、b为常数且k≠0)的图象经过点A(0,﹣2)和点B(1,0),则k=2,b=﹣2.∴.22.(2013•梧州)若一条直线经过点(﹣1,1)和点(1,5),则这条直线与x轴的交点坐标为(﹣,0).,,轴的交点坐标为(﹣,,23.(2013•湖州模拟)如图,点A,B分别在一次函数y=x,y=8x的图象上,其横坐标分别为a,b (a>0,b>0).设直线AB的解析式为y=kx+m,若是整数时,k也是整数,满足条件的k值共有2个.是整数、的值,然后求出∴=+1=+1∵=或、y是x的一次函数,下表列出了部分对应值,则m=3.,,三.解答题(共6小题)25.(2014•钦州)某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:(1)该地出租车的起步价是7元;(2)当x>2时,求y与x之间的函数关系式;(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?x+4x+426.(2014•怀化)设一次函数y=kx+b(k≠0)的图象经过A(1,3)、B(0,﹣2)两点,试求k,b的值.,,27.(2014•定州市一模)如图,在平面直角坐标系中,直线l1:y=kx+b经过第一象限的点A(1,2)和点B(m,n)(m>1),且mn=2,过点B作BC⊥y轴,垂足为C,△ABC的面积为2.(1)求B点的坐标;(2)求直线l1的函数表达式;(3)直线l2:y=ax经过线段AB上一点P(P不与A、B重合),求a的取值范围.)分别代入m=﹣n=,,∴x+;)代入a=的取值范围是<28.(2014•白云区一模)如图,点N(0,6),点M在x轴负半轴上,ON=3OM.A为线段MN上一点,AB⊥x轴,垂足为B,AC⊥y轴,垂足为C.矩形ABOC的面积为2.(1)点M的坐标为(﹣2,0);(2)求直线MN的解析式;(3)求点A的坐标(结果用根号表示).,±1+y=3+;﹣.,)29.(2014•门头沟区二模)如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标、点B的横坐标如图所示.(1)求直线AB的解析式;(2)点P在直线AB上,是否存在点P使得△AOP的面积为1,如果有请直接写出所有满足条件的点P的坐标.∴x+2OP30.(2014•大兴区二模)已知:如图,在平面直角坐标系xOy中,一次函数y=﹣4x+8的图象分别与x、y轴交于点A、B,点P在x轴的负半轴上,△ABP的面积为12.若一次函数y=kx+b的图象经过点P和点B,求这个一次函数y=kx+b表达式.∴坐标代入得:,。
待定系数法求一次函数的解析式练习题精选全文

可编辑修改精选全文完整版
待定系数法求一次函数的解析式练习题
一、旧知识回顾
1,填空题:
(1)若点A(-1,1)在函数y=kx的图象上则k= .
(2)在一次函数y=kx-3中,当x=3时y=6则k= .
(3)一次函数y=3x-b过A(-2,1)则b= ,。
(4)一次函数y=3x-b过A(-2,1)则b= ,该图象经过点B(,-1)和点C(0,). 2.练习:
(1)已知一次函数的图象经过点(1,-1)和点(-1,2)。
求这个函数的解析式。
(2)已知一次函数y=kx+b中,当x=1时,y=3,当x=-1时,y=7。
求这个函数的解析式。
且求当x=3时,y的值。
(3)师:已知直线上两点坐标,能求出这条直线的解析式,若不直
接告诉两点的坐标,已知这条直线的图象,能否求出它的解析式?
如右图求函数的解析式。
:
二.练习:
1.尝试练习:
(1)已知一次函数 y=kx+2,当x=5时,y的值为4,求k的值。
(3)一次函数y=kx+5与直线y=2x-1交于点P(2,m),求k、m的值.
3已知一个正比例函数和一个一次函数,它们的图象都经过点P(-2,1),且一次函数图象与y轴交于点Q(0,3)。
求出这两个函数的解析式。
4:正比例函数y=kx与一次函数y=kx+b的图象如图所示,它们的交点
A的坐标为(3,4),且OB=10.
(1)求这两个函数的解析式;
(2)求△OAB的面积.
5.一次函数的图象是经过原点的直线,并且这条直线过第四象限及点(2,-3a)与点
(a,6),求这个函数的解析式
x
y
A
O
B。
21.3用待定系数法确定一次函数的表达式

课时作业(二十一)[21.3 用待定系数法确定一次函数表达]一、选择题1. 若正比例函数y =kx 的图像经过点(1,-2),则正比例函数的表达式为链接听课例2归纳总结( )A. y =2xB. y =-2xC. y =12xD. y =-12x2.如图K -21-1,直线AB 所对应的函数表达式是( )图K -21-1A .y =-32x +3B .y =32x +3C .y =-23x +3D .y =23x +33.在平面直角坐标系中,点M ,N 在同一个正比例函数图像上的是( ) A .M(2,-3),N(-4,6) B .M(-2,3),N(4,6)C .M(-2,-3),N(4,-6)D .M(2,3),N(-4,6)4.将函数y =-3x 的图像沿y 轴向上平移2个单位长度后,所得图像对应的函数表达式为( )A .y =-3x +2B .y =-3x -2C .y =-3(x +2)D .y =-3(x -2)5.若一次函数y =kx +b 的图像经过点(2,-1)和(-3,4),则它的图像不经过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 6. 2017·石家庄二中月考如果一次函数的图像与直线y =-x +1平行,且过点(8,2),那么此一次函数的表达式为链接听课例2归纳总结( )A. y =-x -2B. y =-x -6C. y =-x +10D. y =-x -1 二、填空题7. 若一次函数y=kx+b的图像经过点A(1,-1),B(-1,3),则k________0(填“>”或“<”).8.如果函数y=kx+b(k≠0)的图像与y轴交点的纵坐标为-2,且当x=2时,y=1,那么此函数的表达式为____________.9. 已知y与2x+1成正比例,且当x=1时,y=2,则当x=0时,y=__________.10.如图K-21-2,过点A的一次函数的图像与正比例函数y=2x的图像相交于点B,则这个一次函数的表达式是____________.图K-21-211. 一辆汽车在行驶过程中,路程y(千米)与时间x(时)之间的函数关系如图K-21-3所示.当0≤x≤1时,y关于x的函数表达式为y=60x,那么当1≤x≤2时,y关于x的函数表达式为______________.图K-21-312. 若一次函数y=kx+b的图像经过(0,1)和(2,9)两点,且与x轴交于点A,则点A 的坐标是________.13. 若直线y=kx-4与两坐标轴所围成的三角形的面积等于4,则该直线所对应的函数表达式为________________.链接听课例3归纳总结三、解答题14.已知一次函数y=kx+3的图像经过点A(1,4).(1)求这个一次函数的表达式;(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图像上.15.已知一次函数y=kx+b的图像经过点A(-1,-1)和点B(1,-3).求:(1)一次函数的表达式;(2)直线AB与坐标轴围成的三角形的面积.链接听课例3归纳总结16.2017·保定模拟已知y 是x 的一次函数,且当x =-4时,y =9;当x =6时,y =-1.(1)求这个一次函数的表达式; (2)当x =-12时,求函数y 的值;(3)求当-3<y ≤1时,自变量x 的取值范围.17.直线AB 与y 轴交于点A ,与x 轴交于点B ,点A 的纵坐标、点B 的横坐标如图K -21-4所示.(1)求直线AB 所对应的函数表达式;(2)点P 在直线AB 上,是否存在点P 使得△AOP 的面积为1?如果存在,请直接写出所有满足条件的点P 的坐标.图K -21-418.莲城超市以10元/件的价格购进一批商品,根据前期销售情况,可知每天销售量y(件)与该商品定价x(元/件)是一次函数关系,其图像如图K -21-5所示.(1)求销售量y 与定价x 之间的函数表达式(不需要写出自变量的取值范围); (2)如果超市将该商品的销售价定为13元/件,不考虑其他因素,求超市每天销售这种商品所能获得的利润.链接听课例4归纳总结图K -21-5分类讨论已知一个一次函数的自变量的取值范围是2≤x≤6,函数值的取值范围是5≤y ≤9,求该一次函数的表达式.详解详析[课堂达标] 1.B 2.A3.A [解析] 设正比例函数的表达式为y =kx.A . -3=2k ,解得k =-32,-4×⎝⎛⎭⎫-32=6,6=6,∴点N 在正比例函数y =-32x 的图像上;B . 3=-2k ,解得k =-32,4×⎝⎛⎭⎫-32=-6,-6≠6,∴点N 不在正比例函数y =-32x 的图像上;C . -3=-2k ,解得k =32,4×32=6,6≠-6,∴点N 不在正比例函数y =32x 的图像上;D . 3=2k ,解得k =32,-4×32=-6,-6≠6,∴点N 不在正比例函数y =32x 的图像上.故选A .4.A 5.C 6.C 7.< 8.y =32x -2 9.2310.y =-x +3 [解析] ∵点B 在正比例函数y =2x 的图像上,横坐标为1,∴y =2×1=2,∴点B(1,2).设一次函数表达式为y =kx +b.∵一次函数的图像过点A(0,3),与正比例函数y =2x 的图像相交于点B(1,2),可得方程组⎩⎨⎧b =3,k +b =2,解得⎩⎨⎧b =3,k =-1,则这个一次函数的表达式为y =-x +3.11.y =100x -40 [解析] 根据题意,把x =1代入y =60x ,得y =60.当1≤x ≤2时,函数图像过点(1,60)与(2,160),可得所求的函数表达式为y =100x -40.12.⎝⎛⎭⎫-14,0 13.y =2x -4或y =-2x -4 [解析] 易求得直线与x 轴的交点坐标为⎝⎛⎭⎫4k ,0,由三角形面积公式,得4=4|k|×4×12,所以|k|=2,即k =±2,故所求直线所对应的函数表达式为y=2x -4或y =-2x -4.14.解:(1)由题意,得k +3=4,解得k =1,所以该一次函数的表达式是y =x +3. (2)由(1)知,一次函数的表达式是y =x +3. 当x =-1时,y =2,即点B(-1,5)不在该一次函数的图像上; 当x =0时,y =3,即点C(0,3)在该一次函数的图像上; 当x =2时,y =5,即点D(2,1)不在该一次函数的图像上.15.解:(1)∵一次函数y =kx +b 的图像经过点A(-1,-1)和点B(1,-3),∴⎩⎨⎧-k +b =-1,k +b =-3,解得⎩⎨⎧k =-1,b =-2,∴一次函数的表达式为y =-x -2.(2)在y =-x -2中,分别令x =0,y =0,可求得一次函数图像与两坐标轴的交点坐标分别为(0,-2),(-2,0), ∴直线AB 与两坐标轴围成的三角形的面积为 12×2×2=2. 16.解:(1)设这个一次函数的表达式为y =kx +b ,∴⎩⎨⎧-4k +b =9,6k +b =-1, 解得⎩⎨⎧k =-1,b =5,∴这个一次函数的表达式为y =-x +5. (2)当x =-12时,y =-(-12)+5=112.(3)∵k =-1,∴y 随x 的增大而减小.当y =-3时,-3=-x +5,解得x =8; 当y =1时,1=-x +5,解得x =4.故当-3<y ≤1时,自变量x 的取值范围是4≤x<8. 17.解:(1)根据题意,得点A(0,2),B(4,0),设直线AB 所对应的函数表达式为y =kx +b(k ≠0),则⎩⎨⎧b =2,4k +b =0,∴⎩⎪⎨⎪⎧k =-12,b =2,∴直线AB 所对应的函数表达式为y =-12x +2.(2)假设存在点P ,设点P 的横坐标为a. 根据题意,得S △AOP =12OA·|a|=|a|=1,解得a =1或a =-1.当a =1时,y =32;当a =-1时,y =52.所以存在点P 使得△AOP 的面积为1,点P 的坐标为⎝⎛⎭⎫1,32或⎝⎛⎭⎫-1,52. 18.解:(1)设y 与x 之间的函数表达式是y =kx +b ,则⎩⎨⎧11k +b =10,15k +b =2,解得⎩⎨⎧k =-2,b =32,∴销售量y 与定价x 之间的函数表达式为y =-2x +32.(2)当x =13时,(13-10)y =(13-10)×(-2×13+32)=18. 答:超市每天销售这种商品所能获得的利润为18元. [素养提升]解:设该一次函数的表达式是y =kx +b(k ≠0). 一次函数y =kx +b 的自变量的取值范围是2≤x ≤6,相应函数值的取值范围是5≤y ≤9,则 ①若k>0,则当x =2时,y =5;当x =6时,y =9.根据题意,列出方程组⎩⎨⎧2k +b =5,6k +b =9,解得⎩⎨⎧k =1,b =3,所以该一次函数的表达式是y =x +3;②若k<0,则当x =2时,y =9;当x =6时,y =5.根据题意,列出方程组⎩⎨⎧2k +b =9,6k +b =5,解得⎩⎨⎧k =-1,b =11,所以该一次函数的表达式是y =-x +11.综上所述,该一次函数的表达式是y =x +3或y =-x +11.。
5.3.2 待定系数法求一次函数表达式 浙教版数学八年级上册素养提升卷(含解析)

第5章 一次函数5.3 一次函数第2课时 待定系数法求一次函数表达式基础过关全练知识点 待定系数法求一次函数表达式1.已知y 是x 的正比例函数,当x=3时,y=-6,则y 关于x 的函数关系式为( )A.y=2xB.y=-2xC.y=12x D.y=-12x2.【一题多变】一次函数y=kx+b(k≠0),当x=1时,y=1;当x=2时,y=-4,则k 与b 的值为( )A.3,-2B.-3,4C.-5,6D.6,-5[变式] 根据下表中一次函数的自变量x 与因变量y 的对应值,可得p 的值为( )x -201y3pA.1B.-1C.3D.-33.(2021安徽中考)某品牌鞋子的长度y cm 与鞋子的码数x 之间满足一次函数关系.若22码鞋子的长度为16 cm,44码鞋子的长度为 27 cm,则38码鞋子的长度为( )A.23 cmB.24 cmC.25 cmD.26 cm 4.【教材变式·P153作业题T1】(2022浙江杭州拱墅期末)已知函数y=-3x+b,当x=-1时,y=-13,则b= .5.(2022浙江衢州期末)已知y+2与x-3成正比,且当x=0时,y=1,则当y=4时,x的值为 .6.【新课标例92变式】如图,两摞相同规格的纸杯整齐地叠放在桌面上,根据图中给出的数据,写出纸杯的高度y(cm)与纸杯的数量x(个)满足的一次函数表达式: ;若桌面上有12个纸杯整齐地叠放成一摞,则它的高度为 cm.图1 图2能力提升全练7.【跨学科·物理】小明在做“练习使用弹簧测力计”的实验时,用x(单位:N)表示弹簧受到的拉力,用y(单位:cm)表示挂上重物后弹簧的总长(在弹性限度范围内,y是x的一次函数),记录实验数据如下:x/N1 2.53…y/cm589…小明得出下列结论:①在弹性限度范围内,y关于x的关系式是y=2x+3;②不挂重物时弹簧的长度为3c m;③若弹簧总长不能超过13 cm,则弹簧所受到的拉力不能超过5 N.其中正确结论的个数是( )A.3B.2C.1D.08.【新独家原创】国庆期间,小丽一家自驾从嘉兴到杭州游玩,上午9:00出发时,地图上显示距离杭州84 km,9:48进入杭甬高速公路,地图上显示距离杭州28 km,假设汽车距离杭州的路程s(km)是行驶时间t(min)的一次函数.(1)求汽车距离杭州的路程s(km)与行驶时间t(min)之间的函数关系式;(2)当汽车进入常台高速公路时,地图上显示距离杭州77 km,此时是上午几点?9.【新课标例70变式】全世界大部分国家都采用摄氏温标预报天气,但美国、英国等国家仍然采用华氏温标,两种温标有如下的对应关系:摄氏温度x/℃10203040华氏温度y/°F506886104(1)小明观察发现,华氏温度y和摄氏温度x之间成一次函数关系,请你求出y与x之间的函数关系式;(2)当华氏温度在131 °F~167 °F之间时,求对应的摄氏温度的范围;(3)华氏温度的值可能和摄氏温度的值相等吗?请说明理由.10.【数学文化】漏刻是中国古代的一种计时工具.据史书记载,西周时期就已经出现了漏刻,这是中国古代人们对函数思想的创造性应用.小明同学依据漏刻的原理制作了一个简单的漏刻计时工具模型,研究发现水位h(cm)是时间t(min)的一次函数.下表是小明记录的部分数据,其中有一个h的值记录错误,请排除错误数据,并利用正确的数据解决问题.t(min)…1235…h(cm)… 2.4 2.8 3.44…(1)记录错误的h的值应为 ;(2)求水位h(cm)与时间t(min)的一次函数表达式;(3)求水位为10 cm时对应的时间t.素养探究全练11.【模型观念】小明对学校添置的一批课桌、凳子进行观察后,发现它们可以根据人的身高来调节高度.于是,他测量了一套课桌、凳子相对应的四档高度,得到如下数据:第一档第二档第三档第四档凳高x(cm)37.040.042.045.0桌高y(cm)70.074.878.082.8(1)小明经过对数据的探究发现:桌高y(cm)是凳高x(cm)的一次函数,请你求出这个一次函数的解析式(不要求写出x的取值范围);(2)小明回家后,测量了家里的写字台和凳子的高度,写字台的高度为77 cm,凳子的高度为43.5 cm,请你判断它们是否配套,并说明理由.答案全解全析基础过关全练1.B 设y 关于x 的函数关系式为y=kx(k≠0),把x=3,y=-6代入,得3k=-6,解得k=-2,∴y 关于x 的函数关系式为y=-2x.故选B.2.C 把x=1,y=1;x=2,y=-4代入y=kx+b,得k +b =1,2k +b =-4,解得k =-5,b =6.故选C.[变式] A 设一次函数的表达式为y=kx+b(k≠0),把x=-2,y=3;x=1,y=0代入y=kx+b,得-2k +b =3,k +b =0,解得k =-1,b =1,∴y 与x 之间的函数关系式为y=-x+1,当x=0时,y=1,即p=1.故选A.3.B ∵鞋子的长度y(cm)与鞋子的码数x 之间满足一次函数关系,∴设函数解析式为y=kx+b(k≠0),由题意得22k +b =16,44k +b =27,解得k =12,b =5,∴函数解析式为y=12x+5,当x=38时,y=12×38+5=24.故选B.4.答案 -103解析 把x=-1,y=-13代入y=-3x+b,得-13=-3×(-1)+b,解得b=-103.5.答案 -3解析 设y+2=k(x-3)(k≠0),把x=0,y=1代入得,-3k=3,解得k=-1,∴y+2=-(x-3),即y=-x+1,当y=4时,-x+1=4,解得x=-3,∴x 的值为-3.6.答案 y=1.5x+4.5;22.5解析 由题意可设y=kx+b(k≠0),由题图可得15=7k+b,10.5=4k+b,解得k=1.5,b=4.5,所以该一次函数的关系式为y=1.5x+4.5,当x=12时,y=1.5×12+4.5=22.5.能力提升全练7.A 设在弹性限度范围内,y关于x的关系式是y=kx+b(k≠0),根据题意得k+b=5,3k+b=9,解得k=2,b=3,∴在弹性限度范围内,y关于x的关系式是y=2x+3,故①正确;当x=0时,y=3,即不挂重物时弹簧的长度为3 cm,故②正确;当y≤13时,2x+3≤13,解得x≤5,即若弹簧总长不能超过13 cm,则弹簧所受到的拉力不能超过5 N,故③正确.故①②③都正确,故选A.8.解析 (1)根据题意可得,当t=0时,s=84;当t=48时,s=28,设s与t之间的函数关系式为s=kt+b(k≠0),把t=0,s=84;t=48,s=28代入,得b=84,48k+b=28,解得b=84,k=-76,∴s与t之间的函数关系式为s=-76t+84.(2)当s=77时,-76t+84=77,解得t=6,∴当汽车进入常台高速公路时,地图上显示距离杭州77 km,此时是上午9:06.9.解析 (1)设摄氏温度x(℃)与华氏温度y(°F)之间的函数关系式为y=kx+b(k≠0),由题表得10k+b=50,20k+b=68,解得k=1.8,b=32,即y=1.8x+32.(2)当y=131时,131=1.8x+32,解得x=55,当y=167时,167=1.8x+32,解得x=75,∴当华氏温度在131 °F~167 °F之间时,对应的摄氏温度在55 ℃~75 ℃之间.(3)能相等.理由:根据题意可得x=1.8x+32,解得x=-40,∴当摄氏温度为-40 ℃时,华氏温度与摄氏温度的值相等.10.解析 (1)由题表数据知,每增加1 min,水位上升0.4 cm,∵2.8+0.4=3.2,∴当t=3时,h的值记录错误,应为3.2,∴记录错误的h的值应为3.2.(2)设这个一次函数的表达式为h=kt+b(k≠0),将t=2,h=2.8;t=3,h=3.2代入得2.8=2k+b,3.2=3k+b,∴k=0.4,b=2,∴h=0.4t+2.(3)当h=10时,10=0.4t+2,∴t=20.∴当h=10时,对应的时间t=20.素养探究全练11.解析 (1)设所求一次函数的解析式为y=kx+b(k≠0),将(37.0,70.0)和(42.0,78.0)分别代入,得70=37k+b ,78=42k+b,解得k=1.6,b=10.8,∴所求一次函数的解析式为y=1.6x+10.8.(2)不配套.理由如下:当x=43.5时,y=1.6×43.5+10.8=80.4.∵77≠80.4,∴不配套.。
北师大版八年级数学上册_典中点《待定系数法求一次函数的表达式》目标练

《5.7 待定系数法求一次函数的表达式》目标练练点1 待定系数法(方程组)求一次函数的表达式1.【教材P127做一做变式】已知一次函数y=kx+b的图象经过点(2,7),(-3,2),则该一次函数的表达式为()A.y=x+5B.y=-x+3C.y=x-5D.y=2x+52.【2021·南京金陵汇文学校月考】已知3,2xy=⎧⎨=-⎩和2,1xy=⎧⎨=⎩是二元一次方程ax+by+3=0的两个解,则一次函数y=ax+b(a≠0)的表达式为()A.y=-2x-3B.9377 y x=--C.y=-9x+3D.23977 y x=+3.已知y是x的一次函数,下表中列出了部分对应值,则m等于()A.-1B.0C.1 2D.2练点2 求一次函数表达式的应用4.若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则满足kx+b>1的x的取值范围为()A.x<0B.x>0C.x<1D.x>15.如图,在平面直角坐标系中,已知点A (2,1),B (0,0),C (2,0),直线AE 将△ABC 的面积分成相等的两部分,则直线AE 对应的函数表达式为( )A .y =x -1B .y =-x +1C .y =12x -1 D .y =-12x +1 纠易错 对函数性质理解不透彻而漏解6.已知一次函数y =kx +b ,当-3≤x ≤1时,-1≤y ≤8,则b 的值是( )A .54B .234C .52344或 D .414发散点1 利用求一次函数的表达式确定图形的面积7.【2019·乐山】如图,已知过点B (1,0)的直线1l 与直线2l :y =2x +4相交于点P (-1,a ).(1)求直线1l 的表达式;(2)求四边形PAOC 的面积.发散点2 利用求一次函数的表达式确定点的坐标8.【2020·南通】如图,直线1l :y =x +3与过点A (3,0)的直线2l 交于点C (1,m ),与x 轴交于点B .(1)求直线2l 的表达式;(2)点M 在直线1l 上,MN ∥y 轴,交直线2l 于点N ,若MN =AB ,求点M 的坐标.参考答案1.答案:A2.答案:B3.答案:B4.答案:D5.答案:A6.答案:C解析:解此题应考虑一次函数的增减性,分两种情况求解: 将x =1,y =8代入,得8=k +b ;将x =-3,y =-1代入,得-1=3k +b , 解得k =94,b =234. 所以函数表达式为92344y x =+,经检验符合题意. 将x =1,y =-1代入,得-1=k +b ;将x =-3,y =8代入,得8=-3k +b ,解得k =49-,b =54. 所以函数表达式为9544y x =-+,经检验符合题意. 综上可得b=52344或. 7.答案:见解析解析:(1)因为点P (-1,a )在直线2l :y =2x +4上, 所以2×(-1)+4=a ,即a =2.则P 点的坐标为(-1,2).设直线1l 的表达式为y =kx +b (k ≠0),将B (1,0),P (-1,2)的坐标分别代入,得0,2,k b k b +=⎧⎨-+=⎩ 解得1,1.k b =-⎧⎨=⎩所以直线1l 的表达式为y =-x +1.(2)因为直线1l 与y 轴相交于点C ,所以C 点的坐标为(0,1),则OC =1.又因为直线2l 与x 轴相交于点A , 所以A 点的坐标为(-2,0),则AB =3.又易知OB =1,而PAB BOC PAOC S SS =-四边形, 所以1153211222PAOC S =⨯⨯-⨯⨯=四边形. 8.答案:见解析解析:(1)在y =x +3中,令y =0,得x =-3, 所以B (-3,0).把x =1代入y =x +3,得y =4,所以C (1,4).设直线2l 的表达式为y =kx +b , 由题意得4,30,k b k b +=⎧⎨+=⎩解得2,6.k b =-⎧⎨=⎩ 所以直线2l 的表达式为y =-2x +6.(2)AB =3-(-3)=6.设M (a ,a +3),由MN ∥y 轴, 得N (a ,-2a +6),|3(26)|6,MN a a AB =+--+==解得a =3或a =-1.所以M (3,6)或(-1,2).。
待定系数法求一次函数的解析式常见题型

待定系数法求一次函数的解析式
例1、已知一次函数的图象经过点(2,1)和(-1,-3)求此一次函数的关系式.
步骤:
1、已知一次函数y=ax+b的图象经过点A(2,0)与B(0,4).(1)求一次函数的解析式,并在直角坐标系内画出这个函数的图象;(2)如果(1)中所求的函数y的值在-4≤y≤4范围内,求相应的y的值在什么范围内.
2、已知一次函数y=kx+b的图像与y=2x+1的交点的横坐标为2,与直线y =-x-8的交点的纵坐标为-7,求直线的表达式。
例2、求图象经过点(2,-1),且与直线y=2x+1平行的一次函数的表达式
例3、已知y=p+z,这里p是一个常数,z与x成正比例,且x=2时,y=1;x=3时,y=-1.(1)写出y与x之间的函数关系式;(2)如果x的取值范围是1≤x≤4,求y 的取值范围.
例4、已知一次函数的图象,交x轴于A(-6,0),交正比例函数的图象于点B,且点B•在第三象限,它的横坐标为-2,△AOB的面积为6平方单位,•求正比例函数和一次函数的解析式.
例5、在直角坐标系x0y中,一次函数
3
的图象与x轴,y轴,分别交于A、B两点,•点C坐标为(1,0),点D在x轴上,且∠BCD=∠ABD,求图象经过B、D•两点的一次函数的解析式.
例6、已知直线y=kx+b经过),
0,
2
5
(且与坐标轴所围成的三角形的面积为
4
25
,求该直线的表达式。
14.如图,这是某工厂2002年蜡烛库存量
y(吨)与时间t(月)关系的图像,其中年
初库存量为5吨.
①根据图像写出y与x的函数关系式;
②根据函数关系式求6月份的库存量.。
湘教版八下数学用待定系数法确定一次函数表达式习题课件

【总结提升】点的坐标在求函数表达式中的作用 1.函数表达式与函数图象可以相互转化,实现这种转化的工具就 是点的坐标. 2.若已知图象上某点的坐标,就可以把该点的横、纵坐标作为表 达式中的一对x,y的值,代入函数表达式,从而得到一个关于待定 系数的方程.
知识点 2 一次函数在实际中的应用 【例2】“五一”节期间,申老师一家自驾游去了离家170km的 某地,如图是他们离家的距离y(km)与汽车行驶时间x(h)之间的 函数图象.
4.写出一个过点(0,3),且函数值y随自变量x的增大而减小的一
次函数表达式:
.(填上一个答案即可)
【解析】∵一次函数y随x增大而减小,
∴k<0,可令k=-1.
设所求函数表达式为y=-x+b,把(0,3)代入得b=3.
∴满足条件的一个函数表达式为y=-x+3.
答案:y=-x+3(答案不唯一,保证k值为负数,b=3即可)
令y=0,由y=-2x+1,得x 1,
2
∴直线AB与坐标轴的交点坐标分别是(0,1)和 (1 ,0),
2
所以所围成的三角形面积为:1 1 1 1 .
22 4
题组二:一次函数在实际中的应用 1.小敏从A地出发向B地行走,同时小聪从B地出发向A地行走.如 图所示,相交于点P的两条线段l1,l2分别表示小敏、小聪离B地 的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的 速度分别是 ( ) A.3km/h和4km/h B.3 km/h和3km/h C.4km/h和4km/h D.4km/h和3km/h
∴Rt△COD≌Rt△BOD,BO=CO,∴C点坐标为(-1,0),易证知
△AOB≌△DOC,∴D点坐标为(0,-2),设直线CD的函数表达式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《用待定系数法确定一次函数表达式》习题
1、若点A(-1,1)在函数y=kx的图象上则k=_________.
2、在一次函数y=kx-3中,当x=3时y=6则k=_________.
3、一次函数y=3x-b过A(-2,1)则b=_________.
4、已知一次函数的图象经过点(1,-1)和点(-1,2).求这个函数的解析式.
5、已知一次函数y=kx+b中,当x=1时,y=3,当x=-1时,y=7
(1)求这个函数的解析式.
(2)求当x=3时,y的值.
6、师:已知直线上两点坐标,能求出这条直线的解析式,若不直接告诉两点的坐标,已知这条直线的图象,能否求出它的解析式?若可以请求出函数的解析式.
如:
7、一次函数的图象经过点(2,1)和(1,5),则这个一次函数()
A.y=4x+9B.y=4x-9C.y=-4x+9D.y=-4x-9
8、已知点P的横坐标与纵坐标之和为1,且这点在直线y=x+3上,则该点是()
A.(-7,8)B.(-5,6)C.(-4,5)D.(-1,2)
9、若点A(-4,0)、B(0,5)、C(m,-5)在同一条直线上,则m的值是()
A.8 B.4 C.-6 D.-8
10、练一练:
(1)已知一次函数y=kx+2,当x=5时,y的值为4,求k的值.
(2)已知直线y=kx+b经过(9,0)和点(24,20),求这个函数的解析式.
(3)一次函数y=kx+5与直线y=2x-1交于点P(2,m),求k、m的值.
(4)一次函数y=3x-b过A(-2,1)则b=________,该图象经过点B(_____,-1)和点C(0,____).
(5)已知函数y=kx+b的图象与另一个一次函数y=-2x-1的图象相交于y轴上的点A,且x轴下方的一点B(3,n)在一次函数y=kx+b的图象上,n满足关系n2=9.求这个函数的解析式.
(提示:先利用题中条件确定A和B的坐标,再用待定系数法求函数解析式)。
