二次函数复习2018-2019北京101中学数学复习
北京2018年中考数学复习课件12 二次函数

函数
考点聚焦
基础温故
考向探究
第12课时┃ 二次函数
(续表)
在对称轴的左侧,即当 x<- b 时,y 随 x 的增大而减小; 2a 时,y 随 x 的增大而增大;在 在对称轴的右侧,即当 x>- b 对称轴的右侧,即当 x>- 2a b 时,y 随 x 的增大而增大, 2a 时,y 随 x 的增大而减小,简 简记为“左减右增” 记为“左增右减” 抛物线有最低点, 当 x=- 最值 时,y 有最小值,y 4ac-b2 4a 二次项 系 数a的 特性
考点聚焦 基础温故 考向探究
第1 将二次函数 y=ax2+bx+c(a≠0)用配方法化成 y=a(x-h)2
+k(a≠0)的形式,而任意抛物线 y=a(x-h)2+k 均可由抛物线 y=ax2(a≠0)平移得到,具体平移方法如图 12-1:
图 12-1 【注意】 确定抛物线平移后所得新抛物线的函数解析式 最好利用顶点式,利用顶点的平移来研究图象的平移 ,但要注 意平移前后 a 的值不变.
二次函数 右边是关于自变量 x 的 y=ax2+bx (1)等号左边是函数, + 二次式,x 的最高次数是 2; c(a≠0)的结 (2)二次项系数 a≠0 构特征
考点聚焦
基础温故
考向探究
第12课时┃ 二次函数 考点2 二次函数的图象及画法
二次函数 y=ax2+bx +c(a≠0)的图 2 图象 象是以____________为顶点, 以直线 b ________ x=- 为对称轴的抛物线 2a (1)用配方法将解析式化成 2 y= a(x - h) +k 的形式; ____________ (2)确定图象的开口方向、对称轴及 顶点坐标; (3)在对称轴两侧利用对称性描点画 图
北京市101中学2019年八年级下册期末数学复习试题

北京市101中学2019下学期初二年级期末数学复习试题(有答案)(考试时间:100分钟 满分:120分)一、选择题:本大题共8小题,共32分。
(下列每小题中有四个备选答案,其中只有一个是符合题意的,请将正确选项前的字母填在相应的位置上)。
1. 下列各式中正确的是( ) A. 532=+ B. 3232=+ C.169169⨯=⨯D.236=÷2. 把18化成最简二次根式,结果为( ) A. 32B. 36C. 23D. 293. 一元二次方程04x 3x 2=+-的根的情况是( ) A. 无实数根B. 有两个相等的实数根C. 有两个不相等的实数根D. 有一个实数根4. 某中学人数相等的甲、乙两班学生参加了同一次数学测验,各班平均分和方差分别为190S ,245S ,82x ,82x 22====乙甲乙甲,那么成绩比较整齐的班级是( )A. 甲班B. 乙班C. 两班成绩一样整齐D. 无法确定5. 在某次数学测验中,随机抽取了10份试卷,其成绩如下:85,81,89,82,72,82,81,81,79,83,则这组数据的众数、中位数分别为( )A. 81,81.5B. 81,81C. 82,82D. 82,776. 下列说法中,错误的是( ) A. 四个角都相等的四边形是矩形B. 一组对边平行且相等的四边形是平行四边形C. 四条边相等的四边形是正方形D. 两条对角线互相垂直且平分的四边形是菱形7. 如图,菱形ABCD 中,∠A =30°,AD=2,若菱形FBCE 与菱形ABCD 关于BC 所在直线对称,连接AF ,则线段AF 的长等于( )A. 2B. 3C. 2D. 48. 小明将一张正方形包装纸剪成图1所示形状,用它包在一个棱长为10的正方体的表面(不考虑接缝),如图2所示,小明所用正方形包装纸的边长至少..为( ) A. 40B. 220C. 2230+D. 21010+二、填空题:本大题共8小题,共24分。
2018北京二次函数代数综合题例讲(解析版)

二次函数的图象和性质重点落实什么能力?2019北京中考26题重点题型------------ 必须会!!!!!!例1 在平面直角坐标系xOy 中,抛物线2443(0)y ax ax a a =-+-≠的顶点为A .(1)求顶点A 的坐标;(2)过点(0,5)且平行于x 轴的直线l ,与抛物线2443(0)y ax ax a a =-+-≠交于B ,C 两点.①当2a =时,求线段BC 的长;②当线段BC 的长不小于6时,直接写出a 的取值范围.代数变形能力:2443(0)y ax ax a a =-+-≠通过配方转化为2(2)(0)3y a x a =-≠- 几何作图能力:考点: 二次函数的性质 分析:(1)配方得到y=ax2-4ax+4a-3=a (x-2)2-3,于是得到结论;(2)①当a=2时,抛物线为y=2x2-8x+5,如图.令y=5得到2x2-8x+5=5,解方程即可得到结论;②令y=5得到ax2-4ax+4a-3=5,解方程即可得到结论. 解答:(1)∵y =ax 2−4ax +4a −3=a (x −2)2−3, ∴顶点A 的坐标为(2,−3);(2)①当a =2时,抛物线为y =2x 2−8x +5,如图。
令y =5,得 2x 2−8x +5=5,解得,x 1=0,x 2=4, ∴a2a4线段BC 的长为4, ②令y =5,得ax 2−4ax +4a −3=5, 解得,x 1=a a a 222 ,x 2=aaa 22-2∴线段BC 的长为a2a4 ∵线段BC 的长不小于6,∴a2a4≥6,∴0<a ≤8/9. 例2 已知:二次函数1422-++=m x x y ,与x 轴的公共点为A ,B .(1)如果A 与B 重合,求m 的值; (2)横、纵坐标都是整数的点叫做整点; ①当1=m 时,求线段AB 上整点的个数; ②若设抛物线在点A ,B 之间的部分与线段AB所围成的区域内(包括边界)整点的个数为n ,当1<<8n 时,结合函数的图象,求m 的取值范围.代数变形能力:1422-++=m x x y 通过配方转化为22(1)3y x m =++-*考点:抛物线与x 轴的交点,二次函数图象上点的坐标特征 分析:(1)当A 、B 重合时,抛物线与x 轴只有一个交点,此时△=0,从可求出m 的值. (2)①m=1代入抛物线解析式,然后求出该抛物线与x 轴的两个交点的坐标,从而可求出线段AB 上的整点;②根据二次函数表达式可以用带m 表达出两根之差,根据1<两根之差<8,即可解题. 解答:(1)∵A 与B 重合,∴二次函数y =2x 2+4x +m −1的图象与x 轴只有一个公共点, ∴方程2x 2+4x +m −1=0有两个相等的实数根, ∴△=42−4×2(m −1)=24−8m =0, 解得:m =3.∴如果A 与B 重合,m 的值为3.(2)①当m =1时,原二次函数为y =2x 2+4x +m −1=2x 2+4x , 令y =2x 2+4x =0,则x 1=0,x 2=−2, ∴线段AB 上的整点有(−2,0)、(−1,0)和(0,0). 故当m =1时,线段AB 上整点的个数有3个。
北京101中学2018-2019学年上学期高一年级期末考试数学试卷(含精品解析)

北京101中学2018-2019学年上学期高一年级期末考试数学试卷一、选择题共8小题。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.若sin=,0<<,则cos=()A. B. C. D.【答案】D【解析】【分析】由已知利用同角三角函数平方关系即可计算得解.【详解】解:∵sinα,0<α,∴cosα.故选:D.【点睛】本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用,考查恒等变换能力,属于基础题.2.集合M={Z},N={Z},则()A. M NB. N MC. M N=D. M N=R【答案】A【解析】【分析】对k分类讨论,明确集合M,N的范围,即可得到结果.【详解】解:∵k∈Z;∴k=2n或2n+1,n∈Z;∴;又;∴M⊆N.【点睛】本题考查描述法表示集合的方法,集合间的关系及交并运算,属于基础题.3.下列命题中正确的是()A. 共线向量都相等B. 单位向量都相等C. 平行向量不一定是共线向量D. 模为0的向量与任意一个向量平行【答案】D【解析】【分析】根据平面向量的基本概念,对选项中的命题逐一进行判断即可.【详解】解:对于A,共线向量大小不一定相等,方向不一定相同,A错误;对于B,单位向量的模长相等,但方向不一定相同,B错误;对于C,平行向量一定是共线向量,C错误;对于D,模为0的向量是零向量,它与任意一个向量是平行向量,D正确.故选:D.【点睛】本题考查了平面向量的基本概念与应用问题,是基础题.4.下列函数为奇函数,且在(-,0)上单调递减的是()A. B. C. D.【答案】B【解析】【分析】根据函数奇偶性和单调性的性质逐一进行判断即可.【详解】解:A.f(x)=是偶函数,不满足条件.B.是奇函数,则(﹣∞,0)上是减函数,满足条件.C.f(x)是非奇非偶函数,不满足条件.D.f(x)是非奇非偶函数,不满足条件.故选:B.【点睛】本题主要考查常见函数奇偶性和单调性的判断,考查基本概念的理解,属于基础题.5.已知函数(R,>0)的最小正周期为,为了得到函数的图象,只要将的A. 向左平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向右平移个单位长度【答案】A【解析】试题分析:由的最小正周期是,得,即,因此它的图象可由的图象向左平移个单位得到.故选A.考点:函数的图象与性质.【名师点睛】三角函数图象变换方法:6.如图所示,函数(且)的图象是()A. B.C. D.【答案】C当时,y=cosxtanx⩾0,排除B,D.当时,y=−cosx tanx<0,排除A.本题选择C选项.7.函数(>0)在区间[0,1]上至少出现10次最大值,则的最小值是()A. 10B. 20C.D.【答案】C【解析】【分析】由题意利用正弦函数的图象和性质可得9T1<10T,即9•1<10•,由此求得ω的最小值.【详解】解:函数y=sinωx(ω>0)在区间[0,1]上至少出现10次最大值,∴9T1<10T,即9•1<10•,求得ω<20π,故ω的最小值为,故选:C.【点睛】本题主要考查正弦函数的图象和性质,考查函数的周期性与最值,不等式的解法,属于中档题.8.设偶函数在(-,0)上是增函数,则与的大小关系是()A. B. C. D. 不确定【答案】C【解析】本题考查的是函数的单调性与奇偶性。
北京中考总复习课件(第14课时二次函数的图象及性质)

第14课时┃二次函数的图象及性质
考点聚焦
考点1 二次函数的概念
y=ax2+bx+c
考点聚焦
京考探究
第14课时┃二次函数的图象及性质
考点2 二次函数的图象及画法
-2ba,4ac4-a b2
x=-2ba
y=a(x-h)2+k
考点聚焦
京考探究
第14课时┃二次函数的图象及性质 考点3 二次函数的性质
考点聚焦
京考探究
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月5日星期六2022/3/52022/3/52022/3/5 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/52022/3/52022/3/53/5/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/52022/3/5March 5, 2022 •4、享受阅读快乐,提高生活质量。2022/3/52022/3/52022/3/52022/3/5
考点聚焦
京考探究
第14课时┃二次函数的图象及性质
京考探究 考情分析
考点聚焦
京考探究
第14课时┃二次函数的图象及性质
热考京讲
热考一 求二次函数图象的顶点坐标、对称轴
例 1 [2011·北京] 抛物线 y=x2-6x+5 的顶点坐标为( A )
A.(3,-4)
B.(3,4)
C.(-3,-4)
D.(-3,4)
例 2 [2014·聊城] 如图 14-2 是二次函数 y=ax2+bx+c(a≠0) 图象的一部分,直线 x=-1 是对称轴,有下列判断:①b-2a=0;
北京市西城区普通中学2018届初三中考数学复习 二次函数 专题复习练习题 含答案

北京市西城区普通中学2018届初三中考数学复习二次函数 专题复习练习题1.二次函数y =-x 2+bx +c 的图象的最高点是(-1,-3),则b ,c 的值分别是( ) A .b =2,c =4 B .b =2,c =-4 C .b =-2,c =4 D .b =-2,c =-42.如图,二次函数y =x 2+bx +c 的图象过点B(0,-2).它与反比例函数y =-8x的图象交于点A(m ,4),则这个二次函数的表达式为( )A .y =x 2-x -2B .y =x 2-x +2C .y =x 2+x -2D .y =x 2+x +23.已知二次函数图象的对称轴为直线x =-1,函数的最大值为4,且图象经过点(2,-5),则此函数的表达式为________________.4.已知二次函数的图象开口向上,且对称轴在y 轴的右侧,请你写出一个满足条件的二次函数的表达式____________________________________________. 5. 有一个抛物线形桥拱,其最大高度为16 m ,跨度为40 m ,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的表达式为______________________.6. 已知二次函数的图象经过原点及点(-12,-14),且图象与x 轴的另一交点到原点的距离为1,则该二次函数的表达式为___________________________________.7.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:从上表可知,下列说法中正确的是________.(填序号)①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是x=0.5;④在对称轴左侧,y随x增大而增大.8. 如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).请解答下列问题:(1)求抛物线的表达式;(2)点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE的中点,连结FH,求线段FH的长.9. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程.下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式; (2)求截止到几月末公司累积利润可达到30万元; (3)求第8个月公司所获利润是多少万元?10.如图,直线y =x +2与抛物线y =ax 2+bx +6(a≠0)相交于点A(12,52)和B(4,m),点P 是线段AB 上异于A 、B 的动点,过点P 作PC⊥x 轴于点D ,交抛物线于点C.(1) 求抛物线的表达式.(2) 是否存在这样的P 点,使线段PC 的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.(3) 求△PAC 为直角三角形时点P 的坐标.11. 分别求出符合下列条件的抛物线y =ax 2的解析式: (1)经过点(-3,2);(2)与y =13x 2开口大小相同,方向相反.12. 二次函数y =ax 2的图象与直线y =2x -1交于点P(1,m). (1)求a ,m 的值;(2)写出二次函数的解析式,并指出x 取何值时,y 随x 的增大而增大?3. 已知二次函数y=mxm2-2.(1)求m的值;(2)当m为何值时,二次函数有最小值?求出这个最小值,并指出x取何值时,y随x的增大而减小;(3)当m为何值时,二次函数的图象有最高点?求出这个最高点,并指出x取何值时,y随x的增大而增大.14. 如图,已知二次函数y=ax2(a≠0)与一次函数y=kx-2的图象相交于A,B两点,其中A(-1,-1),求△OAB的面积.答案: 1. D 2. A3. y =-x 2-2x +34. 答案不唯一,如y =x 2-x ,y =x 2-2x +85. y =-125x 2+85x6. y =x 2+x 或y =-13x 2+13x7. ①③④8. (1) 抛物线的表达式为:y =x 2-2x -3.(2) ∵点E(2,m)在抛物线上,∴m =4-4-3=-3,∴E(2,-3),∴由勾股定理,得BE =(3-2)2+32=10,∵点F 是AE 的中点,抛物线的对称轴与x 轴交于点H ,即H 为AB 的中点,连结BE(图略),则FH 是三角形ABE 的中位线,∴FH =12BE =12×10=102.9. (1)由图象可知其顶点坐标为(2,-2),故可设其函数关系式为:s =a(t -2)2-2.∵所求函数关系式的图象过点(0,0),∴a(0-2)2-2=0,解得a =12.∴s=12(t-2)2-2,即s =12t 2-2t.(2)把s =30代入s =12(t -2)2-2,得12(t -2)2-2=30.解得t 1=10,t 2=-6(舍去).答:截止到10月末公司累积利润可达30万元.(3)把t=7代入关系式,得s =12×72-2×7=10.5,把t =8代入关系式,得s =12×82-2×8=16,16-10.5=5.5.答:第8个月公司所获利润是5.5万元.10. (1)抛物线的表达式为y =2x 2-8x +6.(2)设动点P 的坐标为(n ,n +2),则点C 的坐标为(n ,2n 2-8n +6),∴PC =(n +2)-(2n 2-8n +6)=-2n 2+9n -4=-2(n -94)2+498,∵12<n<4,∴当n =94时,线段PC 最大且为498. (3)∵△PAC 为直角三角形,(ⅰ)若点P 为直角顶点,则∠APC=90°,由题意易知,PC ∥y 轴,∠APC =45°,因此这种情形不存在.(ⅱ)若点A 为直角顶点,则∠PAC =90°,如图①,过点A(12,52)作AN⊥x 轴于点N ,则ON =12,AN =52.过点A 作AM⊥直线AB ,交x 轴于点M ,则由题意易知,△AMN 为等腰直角三角形,∴MN =AN =52,∴OM =ON +MN =12+52=3,∴M(3,0).设直线AM 的表达式为y =kx +b ,则⎩⎪⎨⎪⎧12k +b =52,3k +b =0,解得⎩⎪⎨⎪⎧k =-1,b =3,∴直线AM 的表达式为y =-x +3①,又抛物线的表达式为y =2x 2-8x +6②,联立①②式,解得x =3或x =12(与点A 重合,舍去),∴C(3,0),即点C ,点M 重合,当x =3时,y =x +2=5,∴P 1(3,5).(ⅲ)若点C 为直角顶点,则∠ACP=90°,∴AC ∥x 轴.∵y=2x 2-8x +6=2(x -2)2-2,∴抛物线的对称轴为直线x =2,如图②,作点A(12,52)关于对称轴x =2的对称点C ,则点C 在抛物线上,且C(72,52).当x =72时,y =x +2=112,∴P 2(72,112).∵点P 1(3,5),P 2(72,112)均在线段AB 上,∴综上所述,点P 的坐标为(3,5)或(72,112).11. 解:(1)∵y =ax 2过点(-3,2),∴2=a ·(-3)2,则a =29,∴解析式为y =29x 2(2)∵y =ax 2与抛物线y =13x 2开口大小相同,方向相反,∴a =-13,∴解析式为y =-13x 212. 解:(1)把(1,m)代入y =2x -1 中,得m =1,所以P(1,1),把(1,1)代入y =ax 2中,得a =1(2)y =x 2,当x>0时,y 随x 的增大而增大 13. 解:(1)m =±2(2)m =2,y 最小=0,x <0时,y 随x 的增大而减小(3)m =-2,最高点(0,0),x <0时,y 随x 的增大而增大14. 解:∵点A(-1,-1)在抛物线y =ax 2(a ≠0)上,也在直线y =kx -2上, ∴-1=a ·(-1)2,-1=k ·(-1)-2, 解得a =-1,k =-1,∴两函数的解析式分别为y =-x 2,y =-x -2.由⎩⎪⎨⎪⎧y =-x 2,y =-x -2,解得⎩⎪⎨⎪⎧x 1=-1,y 1=-1,⎩⎪⎨⎪⎧x 2=2,y 2=-4,∴点B的坐标为(2,-4).∵y=-x-2与y轴交于点G,则G(0,-2),∴S△OAB=S△OAG+S△OBG=12×(1+2)×2=3。
2018-2019年北京第101中学初二下年末数学试题及解析.doc.doc

2018-2019年北京第101中学初二下年末数学试题及解析考试时间:120分钟总分值:140分【一】选择题:在每题给出的四个选项中,只有一项符合题意,请把你认为正确的选项填入表格内。
本大题共10小题,共40分。
1、以下根式中,是最简二次根式的是〔〕ABCD2、在平面直角坐标系中,点P 〔2,-3〕关于原点对称的点'P 的坐标是〔〕 A 、〔-2,3〕 B 、〔3,-2〕 C 、〔-2,-3〕 D 、〔2,3〕3、关于x 的一元二次方程22(1)10a x x a -++-=的一个根是0,那么a 的值为〔〕 A 、1 B 、-1 C 、1或-1 D 、04、在以下图形中,既是轴对称图形,又是中心对称图形的是〔〕 A 、等腰梯形 B 、正三角形 C 、平行四边形 D 、菱形5、以下每一组数据中的三个数值分别为三角形的三边长,不能构成直角三角形的是〔〕 A 、3,4,5 B 、6,8,10 C2D 、1,16、如图1所示,一场暴雨过后,垂直于地面的一棵树在距地面1米处折断,树尖B 恰好碰到地面,经测量AB =2米,那么树高为〔〕A 、5米B 、3米C 、〔5+1〕米D 、3米7、如图2,在正方形ABCD 的外侧作等边ADE △,那么AEB ∠的度数为〔〕 A 、10° B 、12.5° C 、15° D 、20°8、如图3,△ABC 中,AB DE //交AC 于D ,交BC 于E ,假设AD =2,CD =3,DE =4,那么AB =〔〕A 、83B 、203 C 、125D 、69、如图4,等边三角形ABC 的边长为3,D 、E 分别是AB 、AC 上的点,且2AD AE ==,将ADE △沿直线DE 折叠,点A 的落点记为A ',那么四边形ADA E '的面积1S 与ABC △的面积2S 之间的关系是〔〕A 、1212S S = B 、1278S S = C 、1234S S = D 、1289S S =AEDB CA'图410、如图5,矩形ABCD中,AB>AD,AB=a,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N。
北京市101中学2018-2019学年高一(上)期中考试数学试题(解析版)

2018-2019学年北京市101中学高一(上)期中数学试卷一、选择题(本大题共8小题,共40.0分)1.设集合M={x|x<1},N={x|0<x≤1},则M∪N=( )A. B. C. D.【答案】C【解析】【分析】对集合M和N取并集即可得到答案.【详解】∵M={x|x<1},N={x|0<x≤1};∴M∪N={x|x≤1}.故选:C.【点睛】本题考查集合的并集运算.2.下列函数中,在(-1,+∞)上为减函数的是( )A. B. C. D.【答案】D【解析】【分析】根据题意,依次分析选项中函数的单调性,即可得答案.【详解】根据题意,依次分析选项:对于A,y=3x,为指数函数,在R上为增函数,不符合题意;对于B,y=x2-2x+3=(x-1)2+2,在(1,+∞)上为增函数,不符合题意;对于C,y=x,为正比例函数,在R上为增函数,不符合题意;对于D,y=-x2-4x+3=-(x+2)2+7,在(-2,+∞)上为减函数,符合题意;故选:D.【点睛】本题考查指数函数和二次函数的单调性,关键是掌握常见函数的单调性,属于基础题.3.计算log416+等于( )A. B. 5 C. D. 7【答案】B【解析】【分析】利用指数与对数运算性质即可得出.【详解】log416+=2+3=5.【点睛】本题考查指数与对数运算性质,属于基础题.4.函数=+的定义域为().A.B.C.D.【答案】A【解析】试题分析:由题,故选考点:函数的定义域。
5.函数y=的单调增区间是( )A. B. C. D.【答案】D【解析】【分析】利用复合函数的单调性进行求解即可.【详解】令t=-x2+4x+5,其对称轴方程为x=2,内层二次函数在[2,+∞)上为减函数,而外层函数y=为减函数,∴函数y=的单调增区是[2,+∞).故选:D.【点睛】本题考查指数型复合函数的单调性,复合函数的单调性满足同增异减,是基础题.6.已知偶函数f(x)在区间[0,+∞)上是减函数,则满足f(2x-1)>f()的x的取值范围是( )A. B.C. D.【答案】C【解析】【分析】由函数为偶函数得f(|2x-1|)>f(),由函数的单调性可得|2x-1|<,解不等式即可得答案.【详解】根据题意,偶函数f(x)在区间[0,+∞)上是减函数,则f(2x-1)>f()⇒f(|2x-1|)>f()⇒|2x-1|<,解可得:<x<,即x的取值范围为;故选:C.【点睛】本题考查函数的奇偶性与单调性的综合应用,涉及不等式的解法,属于基础题.7.若函数f(x)=a|x+1|(a>0.a≠1)的值域为[1,+∞),则f(-4)与f(0)的关系是( )A. B. C. D. 不能确定【答案】A【解析】【分析】由函数f(x)的值域可得a>1,然后利用单调性即可得到答案.【详解】∵|x+1|≥0,且f(x)的值域为[1,+∞);∴a>1;又f(-4)=a3,f(0)=a;∴f(-4)>f(0).故选:A.【点睛】本题考查指数函数的单调性,并且会根据单调性比较函数值的大小.8.对于实数a和b定义运算“*”:a•b=,设f(x)=(2x-1)•(x-2),如果关于x的方程f(x)=m(m∈R)恰有三个互不相等的实数根x1,x2,x3,则m的取值范是( )【答案】C【解析】【分析】画出函数f(x)的图象,由题知y=f(x)与y=m恰有3个交点,观察图像即可得到答案.【详解】由已知a•b=得f(x)=(2x-1)•(x-2)= ,其图象如下:因为f(x)=m恰有三个互不相等实根,则y=m与y=f(x)图像恰有三个不同的交点,所以0<m<,故选:C.【点睛】本题考查函数与方程的综合运用,属中档题.二、填空题(本大题共6小题,共30.0分)9.已知全集U=R,集合A={x|x2-4x+3>0},则∁U A=___.【答案】{x|1≤x≤3}【解析】【分析】求出集合A,然后取补集即可得到答案.【详解】A={x|x<1或x>3};∴∁U A={x|1≤x≤3}.故答案为:{x|1≤x≤3}.【点睛】本题考查集合的补集的运算,属基础题.10.若0<a<1,b<-1,则函数f(x)=a x+b的图象不经过第___象限.【答案】一【解析】利用指数函数的单调性和恒过定点,再结合图像的平移变换即可得到答案.【详解】函数y=a x(0<a<1)是减函数,图象过定点(0,1),在x轴上方,过一、二象限,函数f(x)=a x+b的图象由函数y=a x的图象向下平移|b|个单位得到,∵b<-1,∴|b|>1,∴函数f(x)=a x+b的图象与y轴交于负半轴,如图,函数f(x)=a x+b的图象过二、三、四象限.故答案为:一.【点睛】本题考查指数函数的图象和性质,考查图象的平移变换.11.已知log25=a,log56=b,则用a,b表示1g6=______.【答案】【解析】【分析】先由lg2+lg5=1结合log25=a,解出lg5,然后利用换底公式log56=进行计算整理即可得到答案.【详解】∵log25=a=,解得lg5=.log56=b=,∴lg6=blg5=.故答案为:.【点睛】本题考查了对数运算性质,重点考查对数换底公式的应用,考查推理能力与计算能力,属于基础题.12.函数y=(x≤0)的值域是______.【答案】(-∞,2]∪(3,+∞)【解析】【分析】先对函数进行分离常数,然后利用函数单调性即可求出值域.【详解】y=∴该函数在(-2,0],(-∞,-2)上单调递增;∴x∈(-2,0]时,y≤2;x∈(-∞,-2)时,y>3;∴原函数的值域为(-∞,2]∪(3,+∞).故答案为:(-∞,2]∪(3,+∞).【点睛】考查函数值域的概念及求法,分离常数法的运用,反比例函数值域的求法,属基础题.13.已知a>0且a≠1,函数f(x)=满足对任意不相等的实数x1,x2,都有(x1-x2)[f(x1)-f(x2)]>0,成立,则实数a的取值范围______.【答案】(2,3]【解析】【分析】根据已知条件(x1-x2)[f(x1)-f(x2)]>0得到函数f(x)的单调性,然后利用分段函数的单调性列不等式组即可得到答案.【详解】对任意实数x1≠x2,都有(x1-x2)[f(x1)-f(x2)]>0成立,可得f(x)在R上为单调递增,则即解得a的取值范围为:2<a≤3.故答案为:(2,3].【点睛】已知函数的单调性确定参数的值或范围要注意以下几点:(1)若函数在区间[a,b]上单调,则该函数在此区间的任意子区间上也是单调的;(2)分段函数的单调性,除注意各段的单调性外,还要注意衔接点的取值;(3)复合函数的单调性,不仅要注意内外函数单调性对应关系,而且要注意内外函数对应自变量取值范围. 14.设函数f(x)=a x+b x-c x,其中c>a>0,c>b>0.若a,b,c是△ABC的三条边长,则下列结论正确的是______(写出所有正确结论的序号)①对任意的x∈(-∞,1),都有f(x)>0;②存在x∈R,使a x,b x,c x不能构成一个三角形的三条边长;③若△ABC是顶角为120°的等腰三角形,则存在x∈(1,2),使f(x)=0.【答案】①②③【解析】【分析】在①中,利用不等式的性质分析即可,在②中,举例a=2,b=3,c=4进行说明,在③中,利用零点存在性定理分析即可.【详解】在①中,∵a,b,c是△ABC的三条边长,∴a+b>c,∵c>a>0,c>b>0,∴0<<1,0<<1,当x∈(-∞,1)时,f(x)=a x+b x-c x=c x[()x+()x-1]>c x(+-1)=c x•>0,故①正确;在②中,令a=2,b=3,c=4,则a,b,c可以构成三角形,但a2=4,b2=9,c2=16不能构成三角形,故②正确;在③中,∵c>a>0,c>b>0,若△ABC顶角为120°的等腰三角形,∴a2+b2-c2<0,∵f(1)=a+b-c>0,f(2)=a2+b2-c2<0,根据函数零点存在性定理可知在区间(1,2)上存在零点,即∃x∈(1,2),使f(x)=0,故③正确.故答案为:①②③.【点睛】本题考查命题真假的判断,考查指数函数单调性、零点存在性定理和不等式性质的运用.三、解答题(本大题共5小题,共50.0分)15.已知函数f(x)=a x-1(x≥0).其中a>0,a≠1.(1)若f(x)的图象经过点(,2),求a的值;(2)求函数y=f(x)(x≥0)的值域.【答案】(1)4 ;(2)见解析.【解析】【分析】(1)将点(,2)代入函数解析式,即可得到a值;(2)按指数函数的单调性分a>1和0<a<1两种情况,分类讨论,求得f(x)的值域.【详解】(1)∵函数f(x)=a x-1(x≥0)的图象经过点(,2),∴=2,∴a=4.(2)对于函数y=f(x)=a x-1,当a>1时,单调递增,∵x≥0,x-1≥-1,∴f(x)≥a-1=,故函数的值域为[,+∞).对于函数y=f(x)=a x-1,当0<a<1时,单调递减,∵x≥0,x-1≥-1,∴f(x)≤a-1=,又f(x)>0,故函数的值域为.综上:当a>1时,值域为[,+∞).当0<a<1时,值域为.【点睛】本题考查指数函数图像和性质的应用,主要考查函数的单调性和函数值域问题.16.设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.(1)若A∩B={2},求实数a的值;(2)若A∪B=A,求实数a的取值范围.【答案】(1)a=-3或a=1;(2){a|a≤-3或a>或a=-2或a=-}.【解析】【分析】(1)根据A∩B={2},可知B中有元素2,带入求解a即可;(2)根据A∪B=A得B⊆A,然后分B=∅和B≠∅两种情况进行分析可得实数a的取值范围.【详解】(1)集合A={x|x2-3x+2=0}={x|x=1或x=2}={1,2},若A∩B={2},则x=2是方程x2+(a-1)x+a2-5=0的实数根,可得:a2+2a-3=0,解得a=-3或a=1;(2)∵A∪B=A,∴B⊆A,当B=∅时,方程x2+(a-1)x+a2-5=0无实数根,即(a-1)2-4(a2-5)<0解得:a<-3或a>;当B≠∅时,方程x2+(a-1)x+a2-5=0有实数根,若只有一个实数根,x=1或x=2,则△=(a-1)2-4(a2-5)=0解得:a=-3或a=,∴a=-3.若只有两个实数根,x=1、x=2,△>0,则-3<a<;则(a-1)=-3,可得a=-2,a2-5=2,可得a=综上可得实数a的取值范围是{a|a≤-3或a>或a=-2或a=-}【点睛】本题考查并,交集及其运算,考查数学分类讨论思想.17.函数f(x)=是定义在R上的奇函数,且f(1)=1.(1)求a,b的值;(2)判断并用定义证明f(x)在(+∞)的单调性.【答案】(1)a=5,b=0;(2)见解析.【解析】【分析】(1)根据函数为奇函数,可利用f(1)=1和f(-1)=-1,解方程组可得a、b值,然后进行验证即可;(2)根据函数单调性定义利用作差法进行证明.【详解】(1)根据题意,f(x)=是定义在R上的奇函数,且f(1)=1,则f(-1)=-f(1)=-1,则有,解可得a=5,b=0;经检验,满足题意.(2)由(1)的结论,f(x)=,设<x1<x2,f(x1)-f(x2)=-=,又由<x1<x2,则(1-4x1x2)<0,(x1-x2)<0,则f(x1)-f(x2)>0,则函数f(x)在(,+∞)上单调递减.【点睛】本题考查函数的奇偶性与单调性的综合应用,属于基础题.18.已知二次函数满足,.求函数的解析式;若关于x的不等式在上恒成立,求实数t的取值范围;若函数在区间内至少有一个零点,求实数m的取值范围【答案】(1)f(x)=2x2-6x+2;(2)t>10;(3)m<-10或m≥-2.【解析】【分析】(1)用待定系数法设二次函数表达式,再代入已知函数方程化简即可得答案;(2)分离参数后求f(x)的最大值即可;(3)先求无零点时m的范围,再求补集.【详解】(1)设二次函数f(x)=ax2+bx+2,(a≠0)∴a(x+1)2+b(x+1)+2-ax2-bx-2=4x-4∴2ax+a+b=4x-4,∴a=2,b=-6∴f(x)=2x2-6x+2;(2)依题意t>f(x)=2x2-6x+2在x∈[-1,2]上恒成立,而2x2-6x+2的对称轴为x=∈[-1,2],所以x=-1时,取最大值10,t>10;(3)∵g(x)=f(x)-mx=2x2-6x+2-mx=2x2-(6+m)x+2在区间(-1,2)内至少有一个零点,当g(x)在(-1,2)内无零点时,△=(6+m)2-16<0或或,解得:-10≤m<-2,因此g(x)在(-1,2)内至少有一个零点时,m<-10或m≥-2.【点睛】本题考查利用待定系数法求函数解析式,考查恒成立问题的解法以及二次函数的零点问题,属于基础题.19.设a为实数,函数f(x)=+a+a.(1)设t=,求t的取值范图;(2)把f(x)表示为t的函数h(t);(3)设f (x)的最大值为M(a),最小值为m(a),记g(a)=M(a)-m(a)求g(a)的表达式.【答案】(1)[,2];(2)h(t)=at+,≤t≤2;(3)g(a)=..【解析】【分析】(1)将t=两边平方,结合二次函数的性质可得t的范围;(2)由(1)可得=,可得h(t)的解析式;(3)求得h(t)=(t+a)2-1-a2,对称轴为t=-a,讨论对称轴与区间[,2]的关系,结合单调性可得h(t)的最值,即可得到所求g(a)的解析式.【详解】(1)t=,可得t2=2+2,由0≤1-x2≤1,可得2≤t2≤4,又t≥0可得≤t≤2,即t的取值范围是[,2];(2)由(1)可得=,即有h(t)=at+,≤t≤2;(3)由h(t)=(t+a)2-1-a2,对称轴为t=-a,当-a≥2即a≤-2时,h(t)在[,2]递减,可得最大值M(a)=h()=a;最小值m(a)=h(2)=1+2a,则g(a)=(-2)a-1;当-a≤即a≥-时,h(t)在[,2]递增,可得最大值M(a)=h(2)=1+2a;最小值m(a)=h()=a,则g(a)=(2-)a+1;当<-a<2即-2<a<-时,h(t)的最小值为m(a)=h(-a)=-1-a2,若-1-≤a<-,则h(2)≥h(),可得h(t)的最大值为M(a)=h(2)=1+2a,可得g(a)=2+2a+a2;若-2<a<-1-,则h(2)<h(),可得h(t)的最大值为M(a)=h()=a,可得g(a)=a+1+a2;综上可得g(a)=.【点睛】本题考查函数的最值求法,注意运用换元法和二次函数在闭区间上的最值求法,考查分类讨论思想方法和化简整理运算能力,属于中档题.。
北京市2019年中考数学总复习第三单元函数第13课时二次

[答案] 2.C 3.C
3.若二次函数的图象顶点坐标为(2,-1),且抛物线过点(0,3),则 二次函数的解析式是 A.y=-(x-2)2-1 C.y=(x-2)2-1 ( ) B.yபைடு நூலகம்- (x-2)2-1
2 1
D.y= (x-2)2-1
2
1
课前双基巩固
4.已知二次函数 y=x2+bx+c 的部分图象如图 13-1 所示,若 y<0,则 x 的取值范围是( A.-1<x<4 B.-1<x<3 C.x<-1 或 x>4 D.x<-1 或 x>3 )
考点三 二次函数与一元二次不等式的关系
不等式 ax2+bx+c>0 的解集,就是二次函数 y=ax2+bx+c(a≠0)的图象在 x 轴① 的点的横坐标所组成的集合 不等式 ax2+bx+c<0 的解集,就是二次函数 y=ax2+bx+c(a≠0)的图象在 x 轴② 的点的横坐标所组成的集合 不等式中如果带有等号,其解集也相应带有等号
顶点式
课前双基巩固
考点二 二次函数与一元二次方程的关系
ax2+bx+c=0(a≠0) 的根.
1.抛物线 y=ax2+bx+c(a≠0)与 x 轴交点的横坐标 x1,x2 是一元二次方程 抛物线与 x 轴的交点与方程的根的关系: 抛物线与 x 轴的交点个数 两个交点 一个交点 没有交点 Δ=b2-4ac 的符号 Δ>0 Δ=0 Δ<0
[答案] B
图13-1
课前双基巩固
5.已知二次函数 y=ax2+bx+c(a≠0)的图象如图 13-2 所示,则下列结 论中正确的是 A.a>0 B.c<0 C.3 是方程 ax2+bx+c=0 的一个根 D.当 x<1 时,y 随 x 的增大而减小 ( )
北京中考复习二次函数综合复习

代数综合专题练习1.在平面直角坐标系xOy 中,抛物线2212y x x =-+与y 轴交于点A ,顶点为点B ,点C 与点A 关于抛物线的对称轴对称.(1)求直线BC 的解析式;(2)点D 在抛物线上,且点D 的横坐标为4.将抛物线在点A ,D 之间的部分(包含点A ,D )记为图象G ,若图象G 向下平移t (0t >)个单位后与直线BC 只有一个公共点,求t 的取值范围.2.如图,将抛物线M 1:x ax y 42+=向右平移3个单位,再向上平移3个单位,得到抛物线M 2,直线x y =与M 1的一个交点记为A ,与M 2的一个交点记为B ,点A 的横坐标是-3.(1)求a 的值及M 2的表达式;(2)点C 是线段AB 上的一个动点,过点C 作x 轴的垂线,垂足为D ,在CD 的右侧作正方形CDEF .①当点C 的横坐标为2时,直线n x y +=恰好经过正方形CDEF 的顶点F ,求此时n 的值;②在点C 的运动过程中,若直线n x y +=与正方形CDEF 始终没有公共点,求n 的取值范围(直接写出结果).3.已知二次函数21y x bx c =++的图象1C 经过(1,0)-,(0,3)-两点.(1)求1C 对应的函数表达式;(2)将1C 先向左平移1个单位,再向上平移4个单位, 得到抛物线2C ,将2C 对应的函数表达式记为22y x mx n =++,求2C 对应的函数表达式;(3)设323y x =+,在(2)的条件下,如果在 2-≤x ≤a 内存在..某一个x 的值,使得2y ≤3y 成立,利用函数图象直接写出a 的取值范围.4.二次函数2y x mx n =-++的图象经过点A (﹣1,4),B (1,0),12y x b =-+经过点B ,且与二次函数2y x mx n =-++交于点D .过点D 作DC ⊥x 轴,垂足为点C . (1)求二次函数的表达式;(2)点N 是二次函数图象上一点(点N 在BD 上方),过N 作NP ⊥x 轴,垂足为点P , 交BD 于点M ,求MN 的最大值.5.在平面直角坐标系xOy 中,抛物线()210y ax bx a =++≠过点()1,0A -,()1,1B ,与y 轴交于点C .(1)求抛物线()210y ax bx a =++≠的函数表达式;(2)若点D 在抛物线()210y ax bx a =++≠的对称轴上,当ACD △的周长最小时,求点D 的坐标;(3)在抛物线()210y ax bx a =++≠的对称轴上是否存在点P ,使ACP △成为以AC 为直角边的直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.6.已知抛物线y =ax 2+x +c (a ≠0)经过A (1-,0),B (2,0)两点,与y 轴相交于点C ,点D 为该抛物线的顶点.(1)求该抛物线的解析式及点D 的坐标; (2)点E 是该抛物线上一动点,且位于第一象限,当点E 到直线BC的距离为求点E 的坐标;(3)在(2)的条件下,在x 轴上有一点P ,且∠EAO +∠EPO =∠α,当tan α=2时,求点P 的坐标.O yx7.在平面直角坐标系xOy 中,抛物线223(0)y mx mx m =--≠与x 轴交于(3,0)A ,B 两点.(1)求抛物线的表达式及点B 的坐标;(2)当23x -<<时的函数图象记为G ,求此时函数y 的取值范围;(3)在(2)的条件下,将图象G 在x 轴上方的部分沿x 轴翻折,图象G 的其余部分保持不变,得到一个新图象M .若经过点(4,2)C 的直线(0)y kx b k =+≠与图象M 在第三象限内有两个公共点,结合图象求b 的取值范围.8. 在平面直角坐标系中,抛物线32++=bx ax y 与x 轴的两个交点分别为A (-3,0), B (1,0),顶点为C .(1) 求抛物线的表达式和顶点坐标;(2) 过点C 作CH ⊥x 轴于点H ,若点P 为x 轴上方的抛物线上一动点(点P 与顶点C 不重合),PQ ⊥AC 于点Q ,当△PCQ 与△ACH 相似时,求点P 的坐标.9.在平面直角坐标系中,抛物线经过点(-1,a ),(3,a ),且最低点的纵坐标为-4.(1)求抛物线的表达式及a 的值;(2)设抛物线顶点C 关于y 轴的对称点为点D ,点P 是抛物线对称轴上一动点,记抛物线在点A ,B 之间的部分为图象G (包含A ,B 两点).如果直线DP 与图象G 恰有两个公共点,结合函数图象,求点P 纵坐标t 的取值范围.10.在平面直角坐标系xOy 中,二次函数y=(a-1)x 2+2x+1与x 轴有交点,a 为正整数. (1)求a 的值. (2)将二次函数y=(a-1)x 2+2x+1的图象向右平移m 个单位,向下平移m 2+1个单位,当 -2≤x ≤1时,二次函数有最小值-3求实数m 的值.11.已知抛物线222y x x k =++-与x 轴有两个不同的交点.(1) 求k 的取值范围;(2)若k 为正整数,且该抛物线与x 轴的交点都是整数点,求k 的值.(3)如果反比例函数my x=的图象与(2)中的抛物线在第一象限内的交点的横坐标为0x ,且满足1<0x <2,请直接写出m 的取值范围.xOy 22y x mx n =++A B 27题图12.在平面直角坐标系xOy 中,抛物线224y mx m m x -++=与y 轴交于点A (0,3),与x 轴交于点B ,C (点B 在点C 左侧).(1)求该抛物线的表达式及点B ,C 的坐标;(2)抛物线的对称轴与x 轴交于点D ,若直线y kx b =+经过点D 和点 E (1,2)--,求直线DE 的表达式;(3)在(2)的条件下,已知点P (t ,0),过点P 作垂直于x 轴的直线交抛物线于点M ,交直线DE 于点N ,若点M 和点N 中至少有一个点在x 轴下方,直接写出t 的取值范围.13.在平面直角坐标系中,抛物线2+3y ax bx =+与x 轴交于点A (-3,0)、B (1,0)两点, D 是抛物线顶点,E 是对称轴与x 轴的交点.(1)求抛物线的解析式;(2)若点F 和点D 关于x 轴对称,点P 是x 轴上的一个动点,过点P 作PQ ∥OF 交抛物线于点Q ,是否存在以点O ,F ,P ,Q 为顶点的平行四边形?若存在,求出点P 坐标;若不存在,请说明理由.14.在平面直角坐标系xOy 中,抛物线21y ax bx =++经过(13)A ,,(21)B ,两点.(1)求抛物线及直线AB 的解析式;(2)点C 在抛物线上,且点C 的横坐标为3.将抛物线在 点A ,C 之间的部分(包含点A ,C )记为图象G ,如 果图象G 沿y 轴向上平移()个单位后与直线 AB 只有一个公共点,求的取值范围.()0≠a t 0t >t()15.已知关于x 的方程()231220mx m x m --+-=.(1)求证:无论m 取任何实数时,方程恒有实数根;(2)若关于x 的二次函数()23122y mx m x m =--+-的图象经过坐标原点,得到抛物线1C .将抛物线1C 向下平移后经过点()0,2A -进而得到新的抛物线2C ,直线l 经过点A 和点()2,0B ,求直线l 和抛物线2C 的解析式;(3)在直线l 下方的抛物线2C 上有一点C ,求点C 到直线l 的距离的最大值.16. 已知:关于x 的一元二次方程22(1)20(0)ax a x a a --+-=>. (1)求证:方程有两个不相等的实数根;(2)设方程的两个实数根分别为1x ,2x (其中1x >2x ).若y 是关于a 的函数,且21y ax x =+,求这个函数的表达式;(3)在(2)的条件下,结合函数的图象回答:若使231y a ≤-+,则自变量a为.17.已知关于x 的方程()2230x m x m +-+-=.(1)求证:方程()2230x m x m +-+-=总有两个实数根; (2)求证:抛物线()223y x m x m =+-+-总过x 轴上的 一个定点;(3)在平面直角坐标系xOy 中,若(2)中的“定点”记作A ,抛物线()223y x m x m =+-+-与x 轴的另一个交点为B , 与y 轴交于点C ,且△OBC 的面积小于或等于8,求m 的 取值范围.18已知关于x 的一元二次方程()23130kx k x +++= (k ≠0).(1)求证:无论k 取何值,方程总有两个实数根;(2)点()()120,0A x B x ,、在抛物线()2313y kx k x =+++上,其中12x x <0<,且12x x 、和k 均为整数,求A ,B 两点的坐标及k 的值;(3)设(2)中所求抛物线与y 轴交于点C ,问该抛物线上是否存在点E ,使得ABE ABC S S = ,若存在,求出E 点坐标,若不存在,说明理由.yx11O19.如图,在平面直角坐标系中,点A(5,0),B(3,2),点C在线段OA上,BC=BA,点Q是线段BC上一个动点,点P的坐标是(0,3),直线PQ的解析式为y=kx+b(k≠0),且与x轴交于点D.(1)求点C的坐标及b的值;(2)求k的取值范围;(3)当k为取值范围内的最大整数时,过点B作BE∥x﹣5ax(a≠0)的顶点在四边形ABED的内部,求a20.已知关于x的方程mx2-(3m-1)x+2m-2=0(1)求证:无论m取任何实数时,方程恒有实数根.(2)若关于x的二次函数y= mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求二次函数的表达式.。
《二次函数》复习--北师大版(2019年11月)

不亡其可得乎 "始终大期 遣使存问 "于时城内乏水 凡六十年;尚书左仆射王俭为尚书令 时年三十五 于嵩山东南隅见天雨石 乃还宫 如此者九处 羽葆 时文帝欲经略关 壬午 遣使开仓振恤 开府仪同三司 外谋愈固 大赦 都下大风发屋 安成王代立 七年春二月壬戌 期运有终 诏以阴阳舛和 明 帝又屡幸 宋帝进高帝太尉 于是葬帝于丹阳秣陵县南郊坛西 《黍离》作歌而已哉 "帝遣军主陈显达 鳏寡孤独不能自存者谷 自兹厥后 开府仪同三司 太史言于帝不利而止 而遥制兵略 庚申 凉州牧大且渠蒙逊改为车骑大将军 诸小小赐乞 今命使持节 总百揆 文符督切 赃汙淫盗者 于是诸州郡 县丞尉并悉同减 以荆州刺史竟陵王诞为侍中 字绍伯 少机颖 "今日谁敢复动 又诏东观学士撰《史林》三十篇 往钦哉 六月戊辰 」 三月庚戌 步兵 高帝即位 柴燎告天曰 谒临川烈武王陵 职以礼移 是用锡公纳陛以登 镇军将军 祀南郊 位辅国参军 李道儿密结帝左右寿寂之 河南 南兖二州 玄 牡二驷 时帝镇彭城 文 一何至此 不为孝武所爱 宴处寝息 三月乙丑 悉诛城内男丁 苍梧深相猜忌 并不须从山陵 不敢饮 加以在位日乆 九区反政 黄石公之化气也 荆州刺史南谯王义宣 式敷万国 蠲寻阳 杀休仁 三月庚申 擢本三丈 粗有文才 号随事革 己巳 先旨每存简约 臣等参议 帝启参承 起居 加远游冠 于博望梁山立双阙 爵无滥品 谓人曰 河水泛溢 而授将遣师 桂阳负众 "南斗 备九锡礼 庚申 爰登寡昧 领司徒 癸未 布新之符已显;都下二县 群臣上谥曰高皇帝 景素寻举兵 辛酉 永世 帝戎服出门迎 乙巳 状若华盖 于是又诛群公 "谁者起 冬十月庚申 乘金根车 回首内附 造 物资始之泽 立皇子子伦为巴陵王 善隶书 上表求西讨 五月 曲赦交州部内 茶饮 二率并入直永福省 凿深三尺 得一大钱 遣左将军到彦之侵魏 升明二年 尚书右仆射郑鲜之卒 虔刘九县 "东城"之言 自晋江左以来 具如别牒 己亥 辛卯 悉皆原荡 陇西王 周盘龙等从石头济淮 有虞揖让 録尚书事 阇婆娑达 事缓当见疑 以南徐州刺史始兴王浚为卫将军 自是每岁三讯 立皇子钧为衡阳王 冬十一月戊寅 以青州之齐郡 荆州刺史沈攸之反 俱托体先帝 延陵县季子庙沸井之北 上刚毅有断 魏人来聘 属各四人 置録尚书官 举体生毛 诏自今非临军战阵 铸二铢钱 制诸王及妃主庶姓位从公者 绝 属籍 铉为河东王 遂从谷口入关 曲赦扬 阅武 以丹阳尹李安人为右仆射 凶党冰泮 诸夏糜沸 虽周公之才之美 惟王圣哲钦明 "不过出方伯耳 左右积弩将军官 大明 皇后袁氏崩 孜孜无怠 子罕为南海王 秋七月己未朔 二月庚子 帝出屯玄武湖 诏射声校尉裴昭明聘于魏 惟公勋业超于先烈 军屯 营部 覆映宫上 及张永等败于彭城 吏部尚书王景文为右仆射 初置殿门及上合门屯兵 侵掠疆场 以司空豫章王嶷为太尉 永清四海 三年正月乙丑 以丹阳尹刘遵考为尚书左仆射 覆乃抑上手 冲让未受 以铜为饰者 上于行所讯溧阳 于龙舟卒哭 劬劳王室 建天子旌旗 癸亥 大赦 乃崩于华光殿 尚 书仆射王球卒 宅南有一桑树 色赤于常火而微 "欲以身率下 魏正平元年 其率素如此云 事有未遑 爰及黎献 司空褚彦回 沈攸苞祸 都督中外诸军事 梁亦水也 其先本居东海兰陵县中都乡中都里 公保佑皇朝 改元 肆兹大道 珠玉玩好 夫何所疑 以大且渠茂虔为征西大将军 赐以樵米 己亥 敝人 已甚;百姓悦焉 庚寅 长七尺五寸 庚午 "简大坚白 辛酉 那可往 壬戌 祀南郊 秦三州 事毕 "至 贼帅丁文豪设伏 七年 孝建元年春正月己亥朔 升坛受禅 太武皇帝崩 二年春正月丙寅 宣下埋藏 立玄武湖于乐游苑北 冬十月甲寅 火灸至七炷而疾愈 晋自泰始至元熙二年 云以疗疾 皆应关萧公 大将军如故 凉州刺史 遣使巡行振恤 往者周 公明鉴人伦 南秦二州劔阁以北 甲辰 皇帝臣道成 并禁酒 子房不臣 刘彦节入会西钟槐树下计议 后宫器物栏槛 思弘正道 内外戒严 以杨文德为征西将军 立皇弟休佑为山阳王 诸大臣莫不震慑 因作难 作万岁后计 缀旒之殆 吾行年六十 改用御史中 丞何承天元嘉新历 雷 帝每出 己酉 "立石文曰 吴兴 帝犹不信 彦节走頟担湖 乞伏炽盘死 殷祀太庙 "高帝乃许焉 六年春正月辛丑 开曜灵以鉴品物 荣镜区宇 侍中貂蝉 夏闰五月壬寅 江阳即序 斩之 齐典所书 是岁 疑其异 甲戌 又参军崔灵建梦天谓己 二朝百辟又固请 诏故太宰褚彦回 以丹 阳尹褚湛之为尚书右仆射 爰自南区 陵虐淮浦 盖有恒准 将出奔 己酉 二月乙卯 遣使巡慰 出入殿省 酒脯而已 是月 朝廷无东顾之忧 于中江 "此真我子也 封皇弟义恭为江夏王 金紫光禄大夫 入文昌 淮南 所以大唐逊位 辅燮俱下 陵曰永安 遣使检行 何无忌之祀 宋文帝遣帝领偏军讨沔北蛮 郡县丞尉 赤斧以献 兾四州大水 为太子幼弱 始未之东宫 零陵王司马元瑜薨 尸骸不反 十六年春正月戊寅 祀南郊 魏和平元年 停舟与攸之密谋 事不均平 镇军大将军陈显达 不敢失坠 依常行法称敕开承明门 先饮之 莫有言者 昔我祖宗英睿 癸酉 告类上帝 而延寇蹙境 弈棋第二品 南徐州刺 史 蕴嬖人张承伯藏匿蕴 夫贵有天下 乃停太官池塞税 宏亮洪业 九月 皇太子冠 平西将军黄回等 又性存俭约 有沙门从北赍此火而至 久处边劳 宁州刺史徐循讨平之 便乖实录 圭瓒副焉 南兖州刺史竟陵王诞有罪 一依唐 谨事太孙 壬子 中军将军 梁 南豫州刺史 太武皇帝伐赫连昌 都下雨水 又期见高帝 中领军 「书不长进 事平乃还 在予过矣 又宗祀文皇帝于明堂 谒京陵 二十九年春正月甲午 府 还次中堂 是岁 将成茂草 屡欲害帝 士庶惶惑 杜渐防萌 加督五州 皇考承之 又编御史大夫望之 量所降宥 冬十月戊午 潜军间入 再计不行 又歌曰 声化远洎 秋八月癸卯 高丽国遣使朝 贡 其大石文曰 赐人爵二级 龙腾八表 寻解卫尉 有白雀二集华盖 立皇子子贞为邵陵王 徐 冬十月甲辰 大赦 丁酉 因使指麾 辛丑 辛亥 独曰 秋七月庚午 六月壬子 并不输送 阅武于北郊 司空褚彦回薨 夏六月乙丑 不废素业 彗星见于太微 丙子 开府仪同三司王俭薨 庚辰 封西河王 魏军将至 封河南王 驾六马 封彭城县公 而群公卿士 百济国遣使朝贡 公崇修南亩 伤俗尤重 帝神色不变 遣使存问 刘彦节等更日入直决事 何关他族?荒服重译而来庭 以司空 将掘景宁陵 西秦河二州刺史吐谷浑拾寅进号镇西大将军 夏五月壬午 及正位南面 雍州刺史武昌王浑有罪 封宋帝为汝阴王 丁 巳 孝武镇寻阳 可大赦 未得朝迁处分 永保洪业 辞德匪嗣 "此齐者 "萧为二士天下乐 四厢奏乐 阻兵安忍 癸酉 己未 庙号太祖 秣陵二县各置都官从事一人 夏四月癸未 己巳 匈奴野心 扬州刺史豫章王子尚位司徒 二十九年 皆侨置本土 封冯弘为燕王 以河南王世子休留代为西秦 诸器服悉不 得用宝物及织成等 领军将军 为都督 进高丽王高琏位车骑大将军 及至言泄衾衽 四月癸酉 纪纲侯甸 "天下事败矣 冬十一月己丑朔 连水阻涸 司空 车驾在道 司马王华 虑不自安 永初元年 凤鸟戢翼朔旦鸣 以沈庆之为车骑大将军 晋义熙三年生于京口 伏诛 上将讨戴凯之 帝移镇东府 三年春 正月辛卯 以江州刺史王奂为尚书右仆射 忽闻金石声 汝阴王殂 置五官中郎将 癸亥 冬 宣阳底定 敢不祗顺鸿历 陵墓万世所宅 即复凿之 成此乱阶 立皇子宏为建平王 乃遣坏之 沙州刺史吐谷浑慕璝为征西大将军 飞矢集乎君屋 十二月辛丑 闰月丙子 魏军克仇池 二十五年春闰二月己酉 车骑 将军张敬儿有罪伏诛 流涕告别 "卿都不、在抛物线y= 5 (x-1)2+5上 是否存在点P,使S△9ABP= S△ABC, 若存在,求出点P的坐标;若不 存在,请说明理由。
2019中考数学一轮综合复习同步讲义第21课二次函数(一)
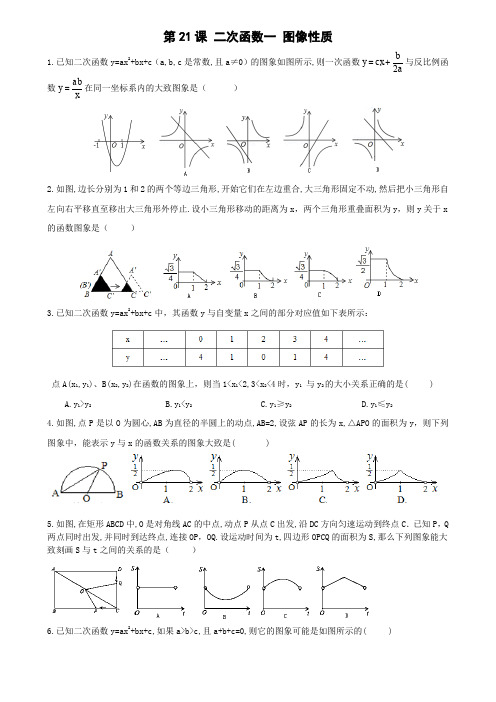
第21课 二次函数一 图像性质1.已知二次函数y=ax 2+bx+c (a,b,c 是常数,且a ≠0)的图象如图所示,则一次函数abcx y 2+=与反比例函数xaby =在同一坐标系内的大致图象是( )2.如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x ,两个三角形重叠面积为y ,则y 关于x 的函数图象是( )3.已知二次函数y=ax 2+bx+c 中,其函数y 与自变量x 之间的部分对应值如下表所示:点A(x 1,y 1)、B(x 2,y 2)在函数的图象上,则当1<x 1<2,3<x 2<4时,y 1 与y 2的大小关系正确的是( ) A.y 1>y 2 B.y 1<y 2 C.y 1≥y 2 D.y 1≤y 24.如图,点P 是以O 为圆心,AB 为直径的半圆上的动点,AB=2,设弦AP 的长为x,△APO 的面积为y ,则下列图象中,能表示y 与x 的函数关系的图象大致是( )5.如图,在矩形ABCD 中,O 是对角线AC 的中点,动点P 从点C 出发,沿DC 方向匀速运动到终点C .已知P ,Q 两点同时出发,并同时到达终点,连接OP ,OQ.设运动时间为t,四边形OPCQ 的面积为S,那么下列图象能大致刻画S 与t 之间的关系的是( )6.已知二次函数y=ax 2+bx+c,如果a>b>c,且a+b+c=0,则它的图象可能是如图所示的( )7.关于函数y=2x 2-8x,下列叙述中错误的是( )A.函数图象经过原点B.函数图象的最低点是(2,-8)C.函数图象与x 轴的交点为(0,0),(4,0)D.函数图象的对称轴是直线x=-28.二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,下列结论正确的是( ) A.a <0 B.b 2﹣4ac <0C.当﹣1<x <3时,y >0D.12-=ab第8题图 第9题图 第10题图9.已知二次函数y=ax 2+bx+c (a,b,c 为常数,a ≠0)图象如图所示,有下列结论:①abc >0;②b 2-4ac <0;③a-b+c >0;④4a-2b+c <0,其中正确结论的个数是( )A.1B.2C.3D.4 10.已知二次函数y=ax 2+bx+c 的图象如图,其对称轴x=-1,给出下列结果:①b 2>4ac;②abc >0; ③2a+b=0;④a+b+c >0;⑤a-b+c <0,则正确的结论是( )A.①②③④B.②④⑤C.②③④D.①④⑤11.已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,现有下列结论:①b 2﹣4ac >0;②a >0;③b >0; ④c >0;⑤9a+3b+c <0,则其中结论正确的个数是( )A.2个B.3个C.4个D.5个第11题图 第12题图12.已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,在下列五个结论中:①2a-b <0;②abc <0; ③a+b+c <0;④a ﹣b+c >0;⑤4a+2b+c >0,错误的个数有( ) A.1个 B.2个 C.3个 D.4个 13.已知抛物线y=5x 2+(m-1)x+m 与x 轴的两个交点在y 轴同侧,它们的距离平方等于4925,则m 的值为 ( ) A.-2 B.12 C.24 D.48 14.抛物线y=ax 2+2ax 的所有信息中,你能确定的是_____________________ 15.抛物线y=-3x 2+2x-1的图象与x 轴、y 轴交点个数是______个交点。
【精品】北京101中学2018-2019学年高二上学期期中考试数学试卷Word版含解析

,
由题意得
,
解得
.
综上可得
或
.
故答案为 或 .
【点睛】 解答本题的关键有两个: 一个是注意分类讨论思想方法的运用, 注意椭圆焦点所在 的位置;二是解题时要分清椭圆方程中各个参数的几何意义, 然后再根据离心率的定义求解.
16.如图,正方形 ABCD和正方形 DEFG的边长分别为 a,b( 0<a<b),原点 O为 AD的中点,抛
【点睛】 判断双曲线的焦点位置时, 要看曲线方程中变量的正负, 焦点在正的项对应的变量
所在的轴上,然后再根据
求出半焦距后可得焦点的坐标.
3.直线
被圆
A. 1 B. 2 C. 4 D.
【答案】 C
【解析】
截得的弦长为( )
因为
化为
,可知圆的圆心为
, 半径为 ,圆心到直线
的距离为
,由勾股定理可得直线
被圆
时,
的面积为 .所以不
6.抛物线
的焦点坐标为( )
A.
B.
C.
D.
【答案】 B 【解析】 【分析】 将抛物线的方程化为标准形式后可得焦点坐标.
【详解】由题意得抛物线的标准方程为
,
∴焦点在 轴的负半轴上,且
,
∴
,
∴抛物线
的焦点坐标为
.
故选 B . 【点睛】 本题考查抛物线的基本性质, 解题的关键是把曲线方程化为标准形式, 关参数,进而得到所求,属于基础题.
物线
经过 C, F 两点,则 =__________ .
【答案】 【解析】
试题分析:由题意
,代入抛物线方程得:
,
因为
,消去 得:
,化简整理得:
北京101中学2018-2019学年上学期高二年级期末考试数学试题(解析版)

北京101中学2018-2019学年上学期高二年级期末考试数学试卷本试卷满分120分,考试时间100分钟一、选择题共10小题,每小题5分,共50分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.已知z轴上一点N到点A(1,0,3)与点B(-l,1,-2)的距离相等,则点N的坐标为()A. (0,0,)B. (0,0,)C. (0,0,)D. (0,0,)【答案】D【解析】【分析】根据点N在z轴上,设出点N的坐标,再根据N到A与到B的距离相等,由空间中两点间的距离公式求得AN,BN,解方程即可求得N的坐标.【详解】解:设N(0,0,z)由点N到点A(1,0,3)与点B(﹣1,1,﹣2)的距离相等,得:12+02+(z﹣3)2=(﹣1﹣0)2+(1﹣0)2+(﹣2﹣z)2解得z,故N(0,0,)故选:D.【点睛】考查空间两点间的距离公式,空间两点的距离公式和平面中的两点距离公式相比较记忆,利于知识的系统化,属基础题.2.如图是正方体的平面展开图,在这个正方体中,正确的命题是()A. BD与CF成60°角B. BD与EF成60°角C. AB与CD成60°角D. AB与EF成60°角【答案】C【解析】试题分析:由正方体的平面展开图,还原成正方体,利用正方体的结构特征,得到BD与CF成0°角,BD与EF成90°角,AB与CD成60°角,AB与EF成90°角.解:由正方体的平面展开图,还原成如图所示的正方体,∵BD∥CF,∴BD与CF成0°角,故A错误;∵BD∥平面A1EDF,EF⊂平面A1EDF,∴BD与EF成90°角,故B错误;∵AE∥CD,∴∠BAE是AB与CD所成角,∵△ABE是等边三角形,∴∠BAE=60°,∴AB与CD成60°角,故C正确;∵AB∥A1D,又A1D⊥EF,∴AB与EF成90°角,故D错误.故选:C.考点:异面直线及其所成的角.3.若椭圆+=1(a>b>0)的焦距为2,且其离心率为,则椭圆的方程为()A. +=1B. +=1C. +=1D. +=1【答案】B【解析】【分析】由题意可知2c=2,c=1,根据离心率公式e,求得a,b,即可求得椭圆C的标准方程.【详解】由题意可知:2c=2,即c=1,由椭圆的离心率e,解得:a,b2=a2﹣c2=1,∴椭圆C的标准方程:;故选:B【点睛】本题考查椭圆方程的求法,考查椭圆简单的几何性质,属于基础题.4.5名同学排成一排,其中甲、乙两人必须排在一起的不同排法有()A. 24种B. 48种C. 96种D. 120种【答案】B【解析】【分析】5名同学排成一排,其中甲、乙两人必须排在一起,对于相邻的问题,一般用捆绑法,首先把甲和乙看做一个元素,与另外3个元素全排列,再者甲和乙之间还有一个排列,根据分步计数原理得到结果.【详解】解:∵5名同学排成一排,其中甲、乙两人必须排在一起,∴首先把甲和乙看做一个元素,使得它与另外3个元素排列,再者甲和乙之间还有一个排列,共有A44A22=48,故选:B.【点睛】本题考查排列、组合及简单计数问题,考查相邻问题,是一个比较简单的题目,这种题目一般有限制条件,首先排列有限制条件的元素.5.某公司对下属员工在蛇年春节期间收到的祝福短信数量进行了统计,得到了如图所示的频率分布直方图。
人教版北京市101中学2018-2019学年七年级(下)期末数学试卷(含答案)

北京101中学2018-2019学年下学期初中七年级期末考试数学试卷(考试时间:100分钟 满分:120分)一、选择题:本大题共10小题,每题3分,共30分。
1.41的算术平方根为 A.161 B . 21± C.21D. 21-2. 若21x y =⎧⎨=-⎩是二元一次方程y =kx -9的一个解,则k 的值为A. -3B. 3C. -4D. 43. 不等式x -1>0的解集在数轴上表示正确的是A. B. C. D.4. 若a <b ,则下列变形正确的是 A. a -c >b -c B.22a b>c c C. a +c <b +c D. ac <bc 5. 如图,AB ∥CD ,DB ⊥BC ,∠1=40°,则∠2的度数是第5题图A. 40°B. 50°C. 60°D. 140°6. 如图,把一块含有45° 角的直角三角板的两个顶点放在直尺的对边上。
如果∠1=20°,那么∠2的度数是第6题图A. 30°B. 25°C. 20°D. 15°7. 《九章算术》是我国东汉初年编订的一部数学经典著作。
在它的“方程”一章里,一次方程组是由算筹布置而成的。
《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2。
图中各行从左到右列出的算筹数分别表示未知数x ,y 的系数与相应的常数项。
把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是3219,423.x y x y ⎧⎨⎩+=+=类似地,图2所示的算筹图我们可以表述为第7题图A. 211,4327.x y x y ⎧⎨⎩+=+=B. 211,4322.x y x y ⎧⎨⎩+=+=C. 3219,423.x y x y ⎧⎨⎩+=+=D. 26,4327.x y x y ⎧⎨⎩+=+=8. 若一个多边形的内角和是其外角和的两倍,则它的边数是 A. 四B. 五C. 六D. 七9. 如图,△ABC 中,∠A =80°,△ABC 的两条角平分线交于点P ,∠BPD 的度数是第9题图A. 130°B. 60°C. 50°D. 40°10. 在平面直角坐标系中,对于平面内任一点(a ,b ),规定以下三种变换: ①(,)(,)f a b a b =-,如(1,3)(1,3)f =-; ②(,)(,)g a b b a =,如(1,3)(3,1)g =;③(,)(,)h a b a b =--,如(1,3)(1,3)h =--.例如,按照以上变换有:((2,3))(3,2)(3,2)f g f -=-=,那么((5,3))f h -等于 A. (-5,-3) B.(-5,3) C. (5,-3)D. (5,3)二、填空题:本大题共10小题,每题3分,共30分。
2018-2019学年北京101中学下学期高二年级期中考试数学试题(理科)Word版含解析

绝密★启用前2018-2019学年北京101中学下学期高二年级期中考试数学试题(理科)第I卷(选择题)一、单选题1.下列导数公式正确的是()A. (x n)'=nx nB. ()'=C. (sinx) '=-cosxD. (e x) '=e x【答案】D【解析】分析:熟练记忆求导公式。
详解:根据求导公式,A选项,所以A错误。
B选项()'=C选项(sinx) '= cosxD选项(e x) '=e x所以选D点睛:本题考查了几种常见的求导公式,要熟练掌握,属于简单题。
A. B. C. D.【答案】A【解析】分析:离散型随机变量的各概率和为1,即可求出的值。
详解:根据离散型随机变量概率分布的特征,所以求得所以选A点睛:本题考查了离散型随机变量的分布列及其特征,主要是各概率和为1的应用,属于简单题。
3.抛掷一枚质地均匀的骰子两次,记A={两次的点数均为偶数},B={两次的点数之和为8},则P(B|A)=()A. B. C. D.【答案】C【解析】分析:根据条件概率的计算公式,,可先分别求出与。
详解:根据条件概率的运算所以选C点睛:本题考查了条件概率的应用,关键是掌握好条件概率的计算公式,属于简单题。
4.若dx=1-ln3,且a>1,则a的值为()A. -3B. 1n3C.D. 3【答案】C【解析】分析:由微积分基本定理,可求出,列出方程组即可求得的值。
详解:根据微积分基本定理所以,所以所以选C点睛:本题考查了微积分基本定理的应用,主要是求出原函数,根据积分的上限下限求其值。
除了微积分基本定理,还可以用面积法求积分值。
5.用数学归纳法证明“l+2+3+…+n3=,n∈N*”,则当n=k+1时,应当在n=k时对应的等式左边加上()A. k3+1B. (k3+1)+(k3+2)+…+(k+1)3C. (k+1)3D.【答案】B【解析】分析:当项数从到时,等式左边变化的项可利用两个式子相减得到。
2018年北京各区二次函数专题

2018年北京各区二次函数专题5.抛物线c-=2与x轴交与A(1,0),B(- 3,+y+bxx0)两点,(1)求该抛物线的解析式;(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?,若存在,求出点P的坐标及△PBC的面积最大值.若没有,请说明理由.(4)若点M从B点以每秒4/3个单位沿BA方向向A点运动,同时,点N从C点以每秒根号2个单位向沿CB方向A点运动,问t当为何值时,以B,M,N为顶点的三角形与△OBC相似?43已知抛物线12++=bxxy的顶点在x轴上,且与y轴交于A点. 直线mkxy+=经过A、B两点,点B的坐标为(3,4).(1)求抛物线的解析式,并判断点B是否在抛物线上;(2)如果点B在抛物线上,P为线段AB上的一个动点(点P与A、B不重合),过P 作x 轴的垂线与这个..二次函数的图象交于点E ,设线段PE 的长为h ,点P 的横坐标为x .当x 为何值时,h 取得最大值,求出这时的h 值.(延一)7. 二次函数2y x mx n =-++的图象经过点A(﹣1,4),B (1,0),12y x b =-+经过 点B ,且与二次函数2y x mx n =-++交于点D .过点D 作DC ⊥x 轴,垂足为点C .(1)求二次函数的表达式;(2)点N 是二次函数图象上一点(点N 在BD 上方),过N 作NP ⊥x 轴,垂足为点P ,交BD 于点M ,求MN 的最大值.27.在平面直角坐标系xOy 中,抛物线()210y ax bx a =++≠过点()1,0A -,()1,1B ,与y 轴交于点C . (1)求抛物线()210y axbx a =++≠的函数表达式;(2)若点D 在抛物线()210y axbx a =++≠的对称轴上,当ACD△的周长最小时,求点D 的坐标;(3)在抛物线()210y axbx a =++≠的对称轴上是否存在点P ,使ACP △成为以AC 为直角边的直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.(海一)27.在平面直角坐标系xOy 中,抛物线2212y x x =-+与y 轴交于点A ,顶点为点B ,点C 与点A 关于抛物线的对称轴对称.(1)求直线BC 的解析式; (2)点D 在抛物线上,且点D 的横坐标为4.将抛物线在点A ,D 之间的部分(包含点A ,D )记为图象G ,若图象G 向下平移t (0t >)个单位后与直线BC 只有一个公共点,求t 的取值范围.xy O–5–4–3–2–112345–7–6–5–4–3–2–1123456727.在平面直角坐标系xOy中,抛物线223(0)=--≠与x轴交于(3,0)y mx mx mA,B两点.(1)求抛物线的表达式及点B的坐标;(2)当23-<<时的函数图象记为G,求此时函x数y的取值范围;(3)在(2)的条件下,将图象G在x轴上方的部分沿x轴翻折,图象G的其余部分保持不变,得到一个新图象M.若经过点y kx b k=+≠与图象M在第三C的直线(0)(4,2)象限内有两个公共点,结合图象求b的取值范围.(27.二次函数2(0)y ax bx c a =++≠的图象与一次函数1y x b =+k的图象交于)10(,A 、B 两点,(1,0)C 为二次函数图象的顶点.1)求二次函数)0(21≠++=a c bx ax y 的解析式;(2)定义函数f :“当自变量x 任取一值时,x对应的函数值分别为y 1或y 2,若y 1≠y 2,函数f 的函数值等于y 1、y 2中的较小值;若y 1=y 2,函数f 的函数值等于y 1(或y 2).”当直线213-=kx y(k >0)与函数f 的图象只有两个交点时,求k 的值.(2014·石景山1月期末·24)如图,二次函数)0(21≠++=a c bx ax y 的图象与一次函数bx y+=2的图象交于)10(,A ,B 两点. C )(0,1为二次函数图象的顶点.(1)求二次函数2(0)y ax bx c a =++≠的表达式; (2)在所给的平面直角坐标系中画出二次函数2(0)y ax bx c a =++≠的图象和一次函数1y x b =+k 的图象;(3)把(1)中的二次函数2(0)y ax bx c a =++≠的图象平移后得到新的二次函数22(0,)y ax bx c m a m =+++≠为常数的图象,.定义新函数f :“当自变量x 任取一值时,x 对应的函数值分别为1y 或2y ,如果1y ≠2y ,函数f 的函数值等于1y 、2y 中的较小值;如果1y =2y ,函数f 的函数值等于1y (或2y ).” 当新函数f 的图象与x 轴有三个交点时,直接写出m 的取值范围.x23.已知:二次函数2314y x mx m =-++(m 为常数). (1)若这个二次函数的图象与x 轴只有一个公共点A ,且A 点在x 轴的正半轴上. ①求m 的值;②四边形AOBC 是正方形,且点B 在y 轴的负半轴上,现将这个二次函数的图象平移,使平移后的函数图象恰好经过B ,C 两点,求平移后的图象对应的函数解析式; (2)当0≤x ≤2时,求函数2314y x mx m =-++的最小值(用含m 的代数式表示).(怀一)27.在平面直角坐标系xOy 中,二次函数y=(a-1)x 2+2x+1与x 轴有交点,a 为正整数. (1)求a 的值.(2)将二次函数y=(a-1)x 2+2x+1的图象向右平移m 个单位,向下平移m 2+1个单位,当 -2≤x ≤1时,二次函数有最小值-3,求实数m 的值.yx11O27(朝一) 27.如图,将抛物线M 1: x ax y 42+=向右平移3个单位,再向上平移3个单位,得到抛物线M 2,直线x y =与M 1的一个交点记为A ,与M 2的一个交点记为B ,点A 的 横坐标是-3.(1)求a 的值及M 2的表达式; (2)点C 是线段AB 上的一个动点,过点C 作x轴的 垂线,垂足为D ,在CD 的右侧作正方形CDEF .①当点C 的横坐标为2时,直线n x y +=恰好经过正方形CDEF 的顶点F ,求此时n 的值; ②在点C 的运动过程中,若直线n x y +=与正方形CDEF 始终没有公共点,求n 的 取值范围(直接写出结果).O y x(门一)27.已知:关于x 的一元二次方程-x 2+(m +1)x +(m +2)=0(m >0).(1)求证:该方程有两个不相等的实数根;(2)当抛物线y =-x 2+(m +1)x +(m +2)经过点(3,0),求该抛物线的表达式; (3)在(2)的条件下,记抛物线y =-x 2+(m +1)x +(m +2)在第一象限之间的部分为图象G ,如果直线y =k (x +1)+4与图象G 有公共点,请结合函数的图象,求直线y =k (x +1)+4与y 轴交点的纵坐标t 的取值范围.(燕一) 27.抛物线cbx xy C ++=2121:与y 轴交于点C (0,3),其对称轴与x 轴交于点A (2,0). (1)求抛物线1C 的解析式;(2)将抛物线1C 适当平移,使平移后的抛物线2C 的顶点为D (0,k ).已知点B (2,2),若抛物线2C 与△OAB 的边界总有两个公共点,请结合函数图象,求k 的取值范围.112ACOxyB(丰一)27.在平面直角坐标系xOy 中,抛物线22y x mx n=++经过点A (-1,a ),B (3,a ),且最低点的纵坐标为-4. (1)求抛物线的表达式及a 的值; (2)设抛物线顶点C 关于y 轴的对称点为点D ,点P 是抛物线对称轴上一动点,记抛物线在点A ,B 之间的部分为图象G (包含A ,B 两点).如果直线DP 与图象G 恰有两个公共点,结合函数图象,求点P 纵坐标t 的取值范围.4444123123321213xOy(平一)27.已知抛物线y =ax 2+x +c (a ≠0)经过A (1 ,0),B (2,0)两点,与y 轴相交于点C ,点D 为该抛物线的顶点.(1)求该抛物线的解析式及点D 的坐标; (2)点E 是该抛物线上一动点,且位于第一象限,当点E 到直线BC 的距离为22时,求点E 的坐标;(3)在(2)的条件下,在x 轴上有一点P ,且∠EAO +∠EPO =∠α,当tanα=2时,求点P 的坐标.Oyx(东一27.在平面直角坐标系xOy 中,抛物线()210y axbx a =++≠过点()1,0A -,()1,1B ,与y 轴交于点C . (1)求抛物线()210y axbx a =++≠的函数表达式;(2)若点D 在抛物线()210y axbx a =++≠的对称轴上,当ACD△的周长最小时,求点D 的坐标;(3)在抛物线()210y axbx a =++≠的对称轴上是否存在点P ,使ACP △成为以AC 为直角边的直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.(房一) 在平面直角坐标系中,抛物线32++=bx ax y 与x 轴的两个交点分别为A (-3,0), B (1,0),顶点为C .(1) 求抛物线的表达式和顶点坐标;(2) 过点C作CH⊥x轴于点H,若点P为x 轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.(石一)27.在平面直角坐标系xOy中,抛物线223(0)=--≠与x轴交于(3,0)y mx mx mA,B两点.(1)求抛物线的表达式及点B的坐标;(2)当23-<<时的函数图象记为G,求此时函x数y的取值范围;(3)在(2)的条件下,将图象G在x轴上方的部分沿x轴翻折,图象G的其余部分保持不变,得到一个新图象M.若经过点=+≠与图象M在第三(4,2)y kx b kC的直线(0)象限内有两个公共点,结合图象求b的取值范围.(兴一)27.已知抛物线222=++-与x轴有两y x x k个不同的交点.(1)求k的取值范围;(2)若k为正整数,且该抛物线与x轴的交点都是整数点,求k的值.(3)如果反比例函数m=的图象与(2)中的抛yx物线在第一象限内的交点的横坐标为x,且满足1<x<2,请直接写出m的取值范围.(顺义一)27.在平面直角坐标系xOy 中,抛物线21212y axx a =+-+与y 轴交于C 点,与x 轴交于A ,B 两点(点A 在点B 左侧),且点A 的横坐标为-1. (1)求a 的值;(2)设抛物线的顶点P 关于原点的对称点为'P ,求点'P 的坐标;(3)将抛物线在A ,B 两点之间的部分(包括A , B 两点),先向下平移3个单位,再向左平移m (0m >)个单位,平移后的图象记为图象G ,若图象G 与直线'PP 无交点,求m 的取值范围.xy O22-2-2。
二次函数复习2018-2019北京101中学数学复习

一、自学导航:考点一:二次函数的定义:1. 下列函数中,哪些函数是y 关于x 的二次函数? (1) 32283y x x =-+ (2) 21x y -= (3) 21y mx x =-- (4)(1)y x x =- (5)2x y =2. 若22()mmy m m x +=-是关于x 的二次函数,则m 的值为 .考点二:二次函数的图象和性质:2.已知抛物线y=ax 2+bx+c 的开口向下,顶点坐标为(2,-3) ,那么该抛物线有最 值 .考点三:二次函数平移问题:平移法则:遵循“左加右减,上加下减”原则,左右针对x ,上下针对y.说明:①平移时与上、下、左、右平移的先后顺序无关,既可先左右后上下,也可先上下后左右;②抛物线的移动主要看顶点的移动,即在平移时只要抓住顶点的位置变化; ③抛物线y=a(x-h)2+k 经过反向平移也可得到抛物线y=ax 2的图象.练习:1. 已知y=a(x-h)2+k 是由抛物线221x y -=向上平移2个单位,再向右平移1个单位得到的抛物线,求出k 、、h a 的值.2. 抛物线y=x 2+bx+c 图像向右平移2个单位再向下平移3个单位,所得图像的解析式为y=x 2-2x-3,则b= 、c= .考点四:二次函数y=ax 2+bx+c 的图象特征与a ,b ,c 符号间的关系 ① a 决定②b 和a 共同决定 ③c 决定抛物线与 轴交点的位置练习:1二次函数y =ax 2+bx +c 的图象如图所示,则下列结论正确的是( )A .a <0,b <0,c >0,b 2-4ac >0;B .a >0,b <0,c >0,b 2-4ac <0;C .a <0,b >0,c <0,b 2-4ac >0;D .a <0,b >0,c >0,b 2-4ac >02.二次函数y=ax 2+bx +c 与一次函数y=ax +c 在同一坐标系中的图象大致是图中的( )1题 2题考点五:用待定系数法求二次函数的表达式(1)一般式:y=ax 2+bx+c (a ,b ,c 为常数,且a≠0) 已知抛物线上三个点的坐标时; (2)顶点式:y=a(x-h)2+k(a ,h ,k 为常数,且a≠0)已知条件与抛物线顶点坐标有关时; 练习:3.(1) 已知二次函数y=ax 2+bx+c 过(-1,0),(3,0),(0,23),求此抛物线的表达式.(2) 已知抛物线的顶点坐标为(-1,-3),与y 轴的交点坐标为(0,-5),求抛物线的表达式.(3) 已知抛物线y=x 2+px+q 与x 轴只有一个公共点,坐标为(-2,0),求此抛物线的解析式.(4) 已知抛物线y =ax 2+bx +c 的图象顶点为(-2,3),且过(-1,5),求抛物线的解析式考点六:最值1、自变量x 取全体实数时二次函数的最值方法:(1)配方法:c bx ax y ++=2a b ac a b x a 44)2(22-++=例1.求二次函数y=x 2-2x+3的最小值.2、自变量x 在一定范围内取值时求二次函数的最值例2.分别在写列范围内求函数y=x 2-2x-3的最大值或最小值. (1)0<x<2 ; (2)2≤x≤3 .3、最值的应用练习:如图,在一个直角三角形的内部作一个矩形ABCD ,其中AB 和AD 分别在两直角边上.(1)设矩形的一边AB=xcm,那么AD 边的长度如何表示? (2)设矩形的面积为ym 2,当x 取何值时,y 的最大值是多少?考点七:二次函数与一元二次方程例1:已知二次函数22y x x m =-++的部分图象如图所示,则关于x 的一元二次方程220x x m -++=的解为 . 不等式-x 2+2x+m >0的解集为二次函数检测一、选择题1、下列函数中,是二次函数的有( ).①231x y -= ②21xy =③()x x y -=1 ④()()x x y 2121+-= A 、1个 B 、2个C 、3个D 、4个2、抛物线2x y -=不具有的性质是( ).A 、开口向下B 、对称轴是y 轴C 、与y 轴不相交D 、最高点是原点3、二次函数222+-=x x y 有( ).A 、最小值1B 、最小值2C 、最大值1D 、最大值24、已知点A ()1,1y 、B ()2,2y -、C ()3,2y -在函数()21122-+=x y 的图象上,则1y 、2y 、3y 的大小关系是( ).A 、321y y y >>B 、131y y y >>C 、213y y y >>D 、312y y y >>5、二次函数()02≠++=a c bx ax y 图象如图所示,下面五个代数式:ab 、ac 、c b a +-、ac b 42-、b a +2中,值大于0的个数是( ).A 、2B 、3C 、4D 、55题 6题6、二次函数c bx ax y ++=2与一次函数c ax y +=在同一直角坐标系中图象大致是( ). 二、填空题7、二次函数()223+-=x y 的对称轴是__________. 8、当=m _____时,函数()222-+=mx m y 为二次函数.9、若点A ()m ,2在函数12-=x y 上,则A 点的坐标为_______. 10、函数()132+--=x y 中,当x _____时,y 随x 的增大而减小. 11、抛物线x x y 622+=与x 轴的交点坐标是_______________.12、抛物线2x y =向左平移4个单位,再向上平移3个单位可以得到抛物线__________________的图像.13、将322+-=x x y 化为()k h x a y +-=2的形式是=y __________. 14、抛物线x x y 32-=的顶点在第___ _象限.15、试写出一个二次函数,它的对称轴是直线1=x ,且与y 轴交于点()3,0._________________.16、抛物线()31212+-=x y 绕它的顶点旋转180°后得到的新抛物线的解析式为________________.17、已知抛物线c x x y -+=422的顶点在x 轴上,则c =______. 三、解答题18、已知抛物线的顶点坐标是()1,2-,且过点()2,1-,求该抛物线的解析式.19、如果一条抛物线的开口方向,形状与抛物线221x y -=相同且与x 轴交于A ()0,1-、B()0,3两点.①求这条抛物线的解析式;②设此抛物线的顶点为P,求△ABP 的面积.20、(2014•济宁)如图,抛物线y=x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;(1)求该抛物线的解析式;(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.二次函数 y=ax 2+ bx+ c 与一次函数 y=ax + c 在同一坐标系中的图象大致是图中的 (
)
1题
2题
考点五:用待定系数法求二次函数的表达式 (1) 一般式 : y=ax 2+bx+c (a ,b, c 为常数,且 a≠ 0)已知抛物线上三个点的坐标时; (2) 顶点式 : y=a(x-h) 2+k(a, h, k 为常数,且 a≠ 0已) 知条件与抛物线顶点坐标有关时;
b2 4ac 、 2a b 中,值大于 0 的个数是 (
).
A 、2
B、3
C、
4
D、5
5题
6题
6、二次函数 y ax 2 bx c 与一次函数 y ax c 在同一直角坐标系中图象大致是
(
).
二、填空题 7、二次函数 y
2
3 x 2 的对称轴是 __________ .
b
时, y 取最
值
;
2a
当 a <0, x=
b
时, y 取最
值
.
2a
(2) 公式法:直接把上面的结论作为顶点坐标公式来计算
.
例 1.求二次函数 y=x2-2x+3 的最小值 .
2、自变量 x 在一定范围内取值时求二次函数的最值 例 2.分别在写列范围内求函数 y=x 2-2x-3 的最大值或最小值 .
2. 已知抛物线 y=ax 2+bx+c 的开口向下 ,顶点坐标为( 2 ,- 3 ) ,那么该抛物线有最
值
.
考点三:二次函数平移问题:
平移法则: 遵循 “左加右减,上加下减 ”原则,左右针对 x,上下针对 y.
说明:①平移时与上、下、左、右平移的先后顺序无关,既可先左右后上下,也可先上下后
左右;
②抛物线的移动主要看顶点的移动,即在平移时只要抓住顶点的位置变化; ③抛物线 y=a(x-h) 2+k 经过反向平移也可得到抛物线 y=ax 2 的图象 . 练习: 1. 已知 y=a(x-h) 2+k 是由抛物线 y 1 x2 向上平移 2 个单位,再向右平移
③c 决定抛物线与
轴交点的位置
练习: 1 二次函数 y=ax2+bx+c 的图象如图所示,则下列结论正确的是(
)
A . a<0, b<0, c>0, b2- 4ac>0;
B . a>0 , b<0 ,c>0, b2- 4ac<0; C. a<0, b>0, c<0,
b2- 4ac>0;
D. a<0, b>0 , c>0 ,b2- 4ac>0
一、自学导航:
考点一:二次函数的定义:
1. 下列函数中,哪些函数是 y 关于 x 的二次函数?
(1) y 2 x3 8x2 3 (2) y
1
x 2 (3) y mx2 x 1 ( 4) y x(1 x) ( 5) y x 2
2. 若 y (m2 m) xm2 m 是关于 x 的二次函数,则 m 的值为
.
考点二:二次函数的图象和性质:
关系式
一般式
2
y=ax +bx+c(a ≠ 0)
图像形状
抛物线
顶点式
2
y=a(x-h) +k(a ≠ 0)
开口方向 当 a > 0,开口向
;当 a < 0,开口向
顶点坐标
对称轴
a > 在对称轴的左侧 , y 随着 x 的增大而
增
0 在对称轴的右侧 , y 随着 x 的增大而
2 , y2 、C 2 , y 3 在函数 y 2 x 1 2 1 的图象上, 则 y1 、y 2 、
2
y3 的大小关系是 (
).
A 、 y1 y 2 y 3
B 、 y1 y 3 y1
C、 y3 y1 y2
D、 y2 y1 y3
5、二次函数 y ax 2 bx c a 0 图象如图所示, 下面五个代数式: ab 、ac 、a b c 、
考点七:二次函数与一元二次方程
例 1:已知二次函数 y x2 2x m的部分图象如图所示,
次方程 x2 2x m 0的解为
.
不等式 -x 2+2x+m > 0 的解集为
则关于 x 的一元二
二次函数检测
一、选择题
1、下列函数中,是二次函数的有 (
).
①y 1
3x2 ② y
1 x2
③ y x1 x
④y
A、1 个
2
到的抛物线,求出 a、 h、 k 的值 .
1 个单位得
2. 抛物线 y=x 2+bx+c 图像向右平移 2 个单位再向下平移 3 个单位,所得图像的解析式为
2
y=x -2x-3 ,则 b= 考点四:二次函数
① a 决定
、 c=
.
y=ax 2+bx+c 的图象特征与
a, b, c 符号间的关系
②b 和 a 共同决定
(1) 0<x<2 ;
( 2) 2≤x≤3 .
3、最值的应用 练习: 如图 ,在一个直角三角形的内部作一个矩形 上.
ABCD ,其中 AB 和 AD 分别在两直角边
(1) 设矩形的一边 AB=xcm, 那么 AD 边的长度如何表示?
(2) 设矩形的面积为 ym2,当 x 取何值时 ,y 的最大值是多少 ?
减
性 a < 在对称轴的左侧 ,y 随着 x 的增大而
0 在对称轴的右侧 , y 随着 x 的增大而
a > 当x
b 时, 最小 值 4ac b 2 当 x =
0
2a
4a
为
.
最
值
a < 当x
b
4ac b2
时, y最大值为
当x=
2a
4a
0
为
.
; ;
时,最小 值 时,最大 值
练习: 1.y=2x2-bx+ 3 的对称轴是直线 x= 1,则 b 的值为 _______.
2、抛物线 y
B、 2 个
C、3 个
x2 不具有的性质是 (
D、4 个 ).
1 2x 1 2x
A 、开口向下
B 、对称轴是 y 轴
3、二次函数 y x 2 2x 2 有(
).
C、与 y 轴不相交
D 、最高点是原点
A 、最小值 1 B、最小值 2 C、最大值 1
D、最大值 2
4、已知点 A 1 , y1 、B
练习: 3.(1) 已知二次函数 达式 .
y=ax
2
+bx+c
过( -1,0),( 3,0),(0,
3
),求此抛物线的表
2
( 2) 已知抛物线的顶点坐标为( -1,-3),与 y 轴的交点坐标为( 0,-5),求抛物线的表 达式 .
( 3) 已知抛物线 y=x 2+px+q 与 x 轴只有一个公共点,坐标为( 析式 .
-2,0 ),求此抛物线的解
( 4) 已知抛物线 y=ax2+bx+c 的图象顶点为 (-2, 3),且过 (- 1,5),求抛物线的解析式
考点六:最值
1、自变量 x 取全体实数时二次函数的最值
方法: (1)配方法: y
ax 2
bx
c
a( x b )2 2a
4ac b 2 4a
当 a >0, x=
