2020河北省中考数学考试试卷
河北省2020年中考数学试题(解析版)

6.如图 1,已知 ABC ,用尺规作它的角平分线.
如图 2,步骤如下,
第一步:以 B 为圆心,以 a 为半径画弧,分别交射线 BA , BC 于点 D , E ; 第二步:分别以 D , E 为圆心,以 b 为半径画弧,两弧在 ABC 内部交于点 P ;
第三步:画射线 BP .射线 BP 即为所求.
81012 变形得:
k
92 1112 1
k 8 10 12
9 19 1111111
8 10 12 8101012
8 10 12 10 .
故选:B.
【点睛】本题考查了平方差公式的应用,灵活运用平方差公式是解题的关键.
10.如图,将 ABC 绕边 AC 的中点 O 顺时针旋转 180°.嘉淇发现,旋转后的 CDA 与 ABC 构成平行四
7.若 a ¹ b ,则下列分式化简正确的是( )
A.
a2 a b2 b
B.
a2 a b2 b
【答案】D
C. a2 a b2 b
D.
1 2
a
a
1b b
2
【解析】
【分析】
根据 a≠b,可以判断各个选项中的式子是否正确,从而可以解答本题.
【详解】∵a≠b,
∴
a b
2 2
a b
,选项
A
错误;
a b
∴a 0;
第二步:分别以
D
,
E
为圆心,大于
1 2
DE
的长为半径画弧,两弧在
ABC
内部交于点
P
;
∴ b 1 DE 的长; 2
第三步:画射线 BP .射线 BP 即为所求.
综上,答案为: a 0 ; b 1 DE 的长, 2
2020年河北省中考数学试题(图片版含答案)

2020年河北省初中毕业生升学文化课考试数学试卷注意事项:1・本试卷共X页,总分120分,考试时间120分钟.2・答题前,考生务必将姓名、准考证号填写在试卷和答题卡相应位≡±.3・答选择题时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;答非选择题时,将答案写在答Sg卡上.写在本试卷上无效.4・考试结束后,将本试卷和答SS卡一井交回.一、选择题(本大題有16个小题,共42分.1〜10小題各3分・11〜16小題各2分.在每小題给出的四个选项中,只有一项是符合題目要求的)1・如图1.在平面内作己知亘线加的垂线,可作垂线的条数有A∙ 0 条B∙ 1 条~ fn图1 C・2条 D.无数条2.墨迹椅盖了尊式“ Z3∙x = χ2 (XH0)”中的运算符号,则覆盖的是A- +- B- "uC- ×D・÷3.对于①x —3Xy = X(I・3刃,②(X + 3)(x — 1) = X a÷2x-3 »从左到右的变形・表述正确的是A・都是因式分解,B・都是乘法运算C・Φ½B式分解,②圧乘法运算D・①是乘法运算,②是因式分解4.图2的两个几何体分别由7个和6个相同的小正方体搭成.比较两个几何体的三视图,正确的是A・仅主视图不同B・仅俯视图不同'OQ C・仅左视图不同D・主视图、左视图和俯视图都相同5.图3是小颖曲三次购买苹果单价的统计图,第四次又买的苹果单价是。
元/千克・发现这四个单价的中位数恰好也足众数,则α =A. 9 B- 8C *7 D∙ 66∙如图4' C知∕MC,用尺规作它的和平分线如图4∙2∙步骤如下,姑步・・灯为圆心,以诅半径嘶■分别交射线呗眈于点D & 第二炽分别以D, E为圆心.以必半径吹两弧业初C内部交于点P;第三步:画射线&P.射线EP即为所求A. a.方均无限制C. α有最小限制,b无限制7.若a≠b・则下列分式化简正确的是B・α AO, b>∣DE 的长D∙ α No, b <-DE的长2B・应,b-2 b8∙在图5所示的网格中・以点O为位似中心,四边形ABCD 的位似图形是A・四边形NPMQ B.四边形NPMRC.四边形N〃M0D.四边形MMR9.若(!iz>x∏2-1)=8xl0xl2,则“k下列正确的是1 -α2A图5作补充•下列正确的足H.若斤为正幣教•则(&+«+•••+&「S------- V ------- Zit*IO •如图b 將“"C 堆边,4「的屮z ∙ OWRliIteH IKO a •筋汎发现・旋转厉的厶Cw U^ABC 构 MMpI 叫讪仪 HHlJnII 卜,点儿C 分別Hi>J 7 Λ G X 处, 而,m 了点D 处.:CB AD 9J 口边彫ABCD 是半行四边形•小明为保IlL 站m 的Jff PP 更严悴• ffl ⅛ΛH*<l 1 U^Cn-AD. f∏ w Λ四边形 ... WZ 何Λ. KiHffl 理严ib 不必补允 B ∙应补允:∖IAB≈CD.C.应补充:fl AR//CD.D ∙应补充:H0Λ≈()C.12. taffl7∙从笔ri 的公路I 旁一点P 岀发•向西走6km 到达人从P 出发向北走6km 也到达/・卜列说法错误的是• •A ・从点P 向北偏西45°走3km 到达/ B. 公Wn 的走向堆南偏两45∙ C. 公埒/的走向是北偏东45°13.己知光連为300 000千米/杪,光经过f 秒(IWfWlO )传播的览肉用科学记故注&示为4? XIO A千米.IM n nl(½为A. 5 C. 5 PlCB ・6 D ・ 5 Λ 6N. ff -ItSth -已如:点O 力△・(〃('的'卜心・C8(XUU ∙・*Z.4.- SJSJ 的解呑为: 以及它的外忆翹 α iitt OB.OC.切图 8.由ZMXu-IMF .65* .而miKi%∣的不卅全•"还⅛fιM -个不屈的備.・F 列刿妙止的的足A. IMiMift 的対,且Z4的列个VLlt ∏5' B ・MuK 说的不对∙rt<y 65C. SZti 求的rΛMid ∙对・厶4应紂Mr D ・两人林不対・Z.4应"3个不同(ft数学试卷D ∙ k 2A.北尽IS.如图9 •现婴在抛物线yκ(4-n上找点PS b).针対6的不同収值,所找点P的个数,三人的说法如下,甲:若b = 5,则点P的个数为0;乙:若b=4.则点P的个数为1;丙:若b=3,则点P的个数为∣∙下列判断正确的是A.乙错,丙对B.甲和乙都错C.乙对,丙错D・I卩情,內对∣6.图IO是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是 1.2, 3. 4. 5.选取其中三块(可重复选取)按图10 的方式组成图案,使所围成的三用形是面积最大的直角• •三角形,则选取的三块纸片的面积分别是图IO A- 1, 4, 5 B. 2, 3, 5C. 3∙49 5D. 2. 2, 4二.填空题(本大题有3个小题•共12分• 17〜18小題各3分;19小题有3个空•每空2分)17._______________________________________ 己知:√ΓS->∕2≡α√2-√2=5√2 r IlM ab^ _______________________________________18.________________________________________________ 正六边形的一个内角是正丹边形一个外角的4倍,则F l= ___________________________________19.图11是8个台阶的示意图•每个台阶的高和宽分别足1和2.每个台阶凸出的角的顶点记作几S为1~8的整数)•曲数八'(x<0)的图象为曲线厶(1)若2过点环则" ____________ ;(2)若Z过点门,则它必定还过另一点&・则m≡_____________ I(3)若曲线丄使得TLT*这些点分布在它的两侧・毎.侧各4个点,则&的整数值冇________ 个・三、解答题(本大题冇7个小越•共66分•解拧应坷出文孑说明、证明过稈或演題步骤)20.(本小题満分R分)己知两个有理数:-9和5・(1)计算;匕聖艺;2(2)若再添一个负整数刃.且-9・5与刊这三个数的平均数仍小T求"的值•21.(本小题满分8分)有一电脑稈序:每按一次按键,屏幕的A区就会自动加上/・同时B区就会口动诚去3α,且均显示化简后的结果・己知A, B 两区初始显示的分别是25和-16・如图12・如,第一次按⅛t⅛, A I B两区分别显示:2;胃訂E器鸟^<1)从初始状态按2次后,分别求A, B两区显示的结果;(2)从初始状态按4次后,计算A, B两区代数式的和,请判断这个和能为负数吗?说明理由22・(本小题满分9分)如图13•点O为X〃中点,分别延长0/1到点C, OB到点D・使OC = OD.以点0 为圆心,分别以6, OQ为半径在CD上方作两个半圆•点P为小半圆上任一点(不与点A,〃車合),连接OP 并延长交大半圆于点E,连接*£・CP.(1)① 求证:∆A0E^∆P0C;②写出Zl, Z2和ZC1三者间的数蛍关系,井说明理由.(2)若OC≈2OA=2l当ZC最大时,皐悸指出CP与小半圆的位置关系,并求此时S吨OD(答集保窗兀>・Ill23・(本小题满分9分)用承垂捋数〃衡凰水平放置的长方休木板的最大承3i.fi.实验室冇些同材质冋长同 宽而厚度不-的木板,实验发规:木板承航拾数“与木板耳度X (厘米〉的平方成正比. 当x=3时,"=3・(1>求卩与X 的函数关系式・(2〉如图】4・选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为X (厘米〉, ① 求0与X 的函数关系式: ② Jr 为何值时,。
2020年河北省中考数学试题和答案

2020年河北省中考数学试卷一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条2.(3分)墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+B.﹣C.×D.÷3.(3分)对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x ﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解4.(3分)如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同5.(3分)如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A.9B.8C.7D.66.(3分)如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求.下列正确的是()A.a,b均无限制B.a>0,b>DE的长C.a有最小限制,b无限制D.a≥0,b<DE的长7.(3分)若a≠b,则下列分式化简正确的是()A.=B.=C.=D.=8.(3分)在如图所示的网格中,以点O为位似中心,四边形ABCD 的位似图形是()A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR9.(3分)若=8×10×12,则k=()A.12B.10C.8D.610.(3分)如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形…”之间作补充,下列正确的是()A.嘉淇推理严谨,不必补充B.应补充:且AB=CDC.应补充:且AB∥CDD.应补充:且OA=OC11.(2分)若k为正整数,则=()A.k2k B.k2k+1C.2k k D.k2+k 12.(2分)如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是()A.从点P向北偏西45°走3km到达lB.公路l的走向是南偏西45°C.公路l的走向是北偏东45°D.从点P向北走3km后,再向西走3km到达l13.(2分)已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n千米,则n可能为()A.5B.6C.5或6D.5或6或7 14.(2分)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A应有3个不同值15.(2分)如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对16.(2分)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A.1,4,5B.2,3,5C.3,4,5D.2,2,4二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.(3分)已知:﹣=a﹣=b,则ab=.18.(3分)正六边形的一个内角是正n边形一个外角的4倍,则n =.19.(6分)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作T m(m为1~8的整数).函数y=(x<0)的图象为曲线L.(1)若L过点T1,则k=;(2)若L过点T4,则它必定还过另一点T m,则m=;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有个.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(8分)已知两个有理数:﹣9和5.(1)计算:;(2)若再添一个负整数m,且﹣9,5与m这三个数的平均数仍小于m,求m的值.21.(8分)有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16,如图.如,第一次按键后,A,B两区分别显示:(1)从初始状态按2次后,分别求A,B两区显示的结果;(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能为负数吗?说明理由.22.(9分)如图,点O为AB中点,分别延长OA到点C,OB到点D,使OC=OD.以点O为圆心,分别以OA,OC为半径在CD 上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.(1)①求证:△AOE≌△POC;②写出∠1,∠2和∠C三者间的数量关系,并说明理由.(2)若OC=2OA=2,当∠C最大时,直接指出CP与小半圆的位置关系,并求此时S扇形EOD(答案保留π).23.(9分)用承重指数w衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.(1)求W与x的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄.①求Q与x的函数关系式;②x为何值时,Q是W薄的3倍?[注:(1)及(2)中的①不必写x的取值范围]24.(10分)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l'.x﹣10y﹣21(1)求直线l的解析式;(2)请在图上画出直线l'(不要求列表计算),并求直线l'被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.25.(10分)如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O 最近时n的值;(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.26.(12分)如图1和图2,在△ABC中,AB=AC,BC=8,tanC =.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N 时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P 到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=,请直接写出点K被扫描到的总时长.答案一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.参考答案:解:在同一平面内,与已知直线垂直的直线有无数条,所以作已知直线m的垂线,可作无数条.故选:D.2.参考答案:解:∵x3x=x2(x≠0),∴覆盖的是:÷.故选:D.3.参考答案:解:①x﹣3xy=x(1﹣3y),从左到右的变形是因式分解;②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形是整式的乘法,不是因式分解;所以①是因式分解,②是乘法运算.故选:C.4.参考答案:解:解法一:从正面看,两个几何体均为第一层和第二层都是两个小正方形,故主视图相同;从左面看,两个几何体均为第一层和第二层都是两个小正方形,故左视图相同;从上面看,两个几何体均为第一层和第二层都是两个小正方形,故俯视图相同.解法二:第一个几何体的三视图如图所示第二个几何体的三视图如图所示:观察可知这两个几何体的主视图、左视图和俯视图都相同,故选:D.5.参考答案:解:由统计图可知,前三次的中位数是8,∵第四次又买的苹果单价是a元/千克,这四个单价的中位数恰好也是众数,∴a=8,故选:B.6.参考答案:解:以B为圆心画弧时,半径a必须大于0,分别以D,E为圆心,以b为半径画弧时,b必须大于DE,否则没有交点,故选:B.7.参考答案:解:∵a≠b,∴,故选项A错误;,故选项B错误;,故选项C错误;,故选项D正确;故选:D.8.参考答案:解:∵以点O为位似中心,∴点C对应点M,设网格中每个小方格的边长为1,则OC==,OM==2,OD=,OB==,OA==,OR==,OQ=2,OP==2,OH==3,ON==2,∵==2,∴点D对应点Q,点B对应点P,点A对应点N,∴以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故选:A.9.参考答案:解:方程两边都乘以k,得(92﹣1)(112﹣1)=8×10×12k,∴(9+1)(9﹣1)(11+1)(11﹣1)=8×10×12k,∴80×120=8×10×12k,∴k=10.经检验k=10是原方程的解.故选:B.10.参考答案:解:∵CB=AD,AB=CD,∴四边形ABCD是平行四边形,故应补充“AB=CD”,故选:B.11.参考答案:解:=((k•k)k=(k2)k=k2k,故选:A.12.参考答案:解:如图,由题意可得△PAB是腰长6km的等腰直角三角形,则AB=6km,如图所示,过P点作AB的垂线PC,则PC=3km,则从点P向北偏西45°走3km到达l,选项A错误;则公路l的走向是南偏西45°或北偏东45°,选项B,C正确;则从点P向北走3km后到达BP中点D,此时CD为△PAB的中位线,故CD=AP=3,故再向西走3km到达l,选项D正确.13.参考答案:解:当t=1时,光传播的距离为1×300000=300000=3×105(千米),则n=5;当t=10时,光传播的距离为10×300000=3000000=3×106(千米),则n=6.因为1≤t≤10,所以n可能为5或6,故选:C.14.参考答案:解:如图所示:∠A还应有另一个不同的值∠A′与∠A 互补.故∠A′=180°﹣65°=115°.故选:A.15.参考答案:解:y=x(4﹣x)=﹣x2+4x=﹣(x﹣2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为4,∴甲、乙的说法正确;若b=3,则抛物线上纵坐标为3的点有2个,∴丙的说法不正确;16.参考答案:解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是=,当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是=;当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是=,∵,∴所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5,故选:B.二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.参考答案:解:原式=3﹣=a﹣=b,故a=3,b=2,则ab=6.故答案为:6.18.参考答案:解:正六边形的一个内角为:,∵正六边形的一个内角是正n边形一个外角的4倍,∴正n边形一个外角为:120°÷4=30°,∴n=360°÷30°=12.故答案为:12.19.参考答案:解:(1)∵每个台阶的高和宽分别是1和2,∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),∵L过点T1,∴k=﹣16×1=﹣16,故答案为:﹣16;(2)∵L过点T4,∴k=﹣10×4=﹣40,∴反比例函数解析式为:y=﹣,当x=﹣8时,y=5,∴T5在反比例函数图象上,∴m=5,故答案为:5;(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,若曲线L过点T3(﹣12,3),T5(﹣8,5)时,k=﹣12×3=﹣36,若曲线L过点T4(﹣10,4),T5(﹣8,5)时,k=﹣40,∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,∴﹣36<k<﹣28,∴整数k=﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个,∴答案为:7.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.参考答案:解:(1)==﹣2;(2)根据题意得,<m,∴﹣4+m<3m,∴m﹣3m<4,∴﹣2m<4,∴m>﹣2,∵m是负整数,∴m=﹣1.21.参考答案:解:(1)A区显示的结果为:25+2a2,B区显示的结果为:﹣16﹣6a;(2)这个和不能为负数,理由:根据题意得,25+4a2+(﹣16﹣12a)=25+4a2﹣16﹣12a=4a2﹣12a+9;∵(2a﹣3)2≥0,∴这个和不能为负数.22.参考答案:解:(1)①在△AOE和△POC中,,∴△AOE≌△POC(SAS);②∠1+∠C=∠2,理由是:∵△AOE≌△POC,∴∠E=∠C,∵∠1+∠E=∠2,∴∠1+∠C=∠2;(2)当∠C最大时,CP与小半圆相切,如图,∵OC=2OA=2,∴OC=2OP,∵CP与小半圆相切,∴∠OPC=90°,∴∠OCP=30°,∴∠DOE=∠OPC+∠OCP=120°,∴.23.参考答案:解:(1)设W=kx2(k≠0).∵当x=3时,W=3,∴3=9k,解得k=,∴W与x的函数关系式为W=x2;(2)①设薄板的厚度为x厘米,则厚板的厚度为(6﹣x)厘米,∴Q=W厚﹣W薄=(6﹣x)2﹣x2=﹣4x+12,即Q与x的函数关系式为Q=﹣4x+12;②∵Q是W薄的3倍,∴﹣4x+12=3×x2,整理得,x2+4x﹣12=0,解得,x1=2,x2=﹣6(不合题意舍去),故x为2时,Q是W薄的3倍.24.参考答案:解:(1)∵直线l:y=kx+b中,当x=﹣1时,y=﹣2;当x=0时,y=1,∴,解得,∴直线l的解析式为y=3x+1;(2)依题意可得直线l′的解析式为y=x+3如图,解得,∴两直线的交点为A(1,4),∵直线l′:y=x+3与y轴的交点为B(0,3),∴直线l'被直线l和y轴所截线段的长为:AB==;(3)把y=a代入y=3x+1得,a=3x+1,解得x=;把y=a代入y=x+3得,a=x+3,解得x=a﹣3;分三种情况:①当第三点在y轴上时,a﹣3+=0,解得a=;②当第三点在直l上时,2×=a﹣3,解得a=7;③当第三点在直线l'上时,2×(a﹣3)=,解得a=;∴直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,则a的值为或7或.25.参考答案:解:(1)∵经过第一次移动游戏,甲的位置停留在正半轴上,∴必须甲对乙错,因为一共有四种情形,都对或都错,甲对乙错,甲错乙对,∴P甲对乙错=.(2)根据题意可得,n次答对,向西移动4n,(10﹣n)次答错,向东移了2(10﹣n),∴m=5﹣4n+2(10﹣n)=25﹣6n.n=4时,离原点最近.(3)起初,甲乙的距离是8,易知,当甲乙一对一错时,二者之间距离缩小2,当甲乙同时答对打错时,二者之间的距离缩小2,∴当进行了k次移动游戏后,甲与乙的位置相距2个单位时,共缩小了6个单位或10个单位,∴6÷2=3或10÷2=5,∴k=3或k=5.26.参考答案:解:(1)如图1中,过点A作AH⊥BC于H.∵AB=AC,AH⊥BC,∴BH=CH=4,∠B=∠C,∴tan∠B=tan∠C==,∴AH=3,AB=AC===5.∴当点P在BC上时,PA⊥BC时,点P到A的最短距离为3.(2)如图1中,∵∠APQ=∠B,∴PQ∥BC,∴△APQ∽△ABC,∵PQ将△ABC的面积分成上下4:5,∴=()2=,∴=,∴AP=,∴PM=AP﹣AM=﹣2=.(3)当0≤x≤3时,如图1﹣1中,过点P作PJ⊥CA交CA的延长线于J.∵PQ∥BC,∴=,∠AQP=∠C,∴=,∴PQ=(x+2),∵sin∠AQP=sin∠C=,∴PJ=PQ•sin∠AQP=(x+2).当3≤x≤9时,如图2中,过点P作PJ⊥AC于J.同法可得PJ=PC•sin∠C=(11﹣x).综上,PJ=;(4)由题意点P的运动速度==单位长度/秒.当3<x≤9时,设点P移动的路程为x,CQ=y.∵∠APC=∠B+∠BAP=∠APQ+∠CPQ,∠APQ=∠B,∴∠BAP=∠CPQ,∵∠B=∠C,∴△ABP∽△PCQ,∴=,∴=,∴y=﹣(x﹣7)2+,∵﹣<0,∴x=7时,y有最大值,最大值=,∵AK=,∴CK=5﹣=<当y=时,=﹣(x﹣7)2+,解得x=7±,∴点K被扫描到的总时长=(+6﹣3)÷=23秒.。
河北省2020年中考数学试题(解析版)

2020年河北省初中毕业生升学文化课考试数学试卷一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,在平面内作已知直线m 的垂线,可作垂线的条数有( )A. 0条B. 1条C. 2条D. 无数条 【答案】D【解析】【分析】在同一平面内,过已知直线上的一点有且只有一条直线垂直于已知直线;但画已知直线的垂线,可以画无数条.【详解】在同一平面内,画已知直线的垂线,可以画无数条;故选:D .【点睛】此题主要考查在同一平面内,垂直于平行的特征,解题的关键是熟知垂直的定义.2.墨迹覆盖了等式“3x 2x x =(0x ≠)”中的运算符号,则覆盖的是( ) A. +B. -C. ×D. ÷【答案】D【解析】【分析】直接利用同底数幂的除法运算法则计算得出答案.【详解】∵3x 2x x =(0x ≠), 32x x x ÷=,∴覆盖的是:÷.故选:D .【点睛】本题主要考查了同底数幂的除法运算,正确掌握相关运算法则是解题关键.3.对于①3(13)x xy x y -=-,②2(3)(1)23x x x x +-=+-,从左到右的变形,表述正确的是( )A. 都是因式分解B. 都是乘法运算C. ①是因式分解,②是乘法运算D. ①是乘法运算,②是因式分解【答案】C【解析】【分析】根据因式分解的定义进行判断即可;【详解】①左边多项式,右边整式乘积形式,属于因式分解;②左边整式乘积,右边多项式,属于整式乘法;故答案选C.【点睛】本题主要考查了因式分解的定义理解,准确理解因式分解的定义是解题的关键.4.如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A. 仅主视图不同B. 仅俯视图不同C. 仅左视图不同D. 主视图、左视图和俯视图都相同【答案】D【解析】【分析】分别画出所给两个几何体的三视图,然后比较即可得答案.【详解】第一个几何体的三视图如图所示:第二个几何体的三视图如图所示:观察可知这两个几何体的主视图、左视图和俯视图都相同,故选D.【点睛】本题考查了几何体的三视图,正确得出各几何体的三视图是解题的关键.5.如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A. 9B. 8C. 7D. 6【答案】B【解析】【分析】根据统计图中的数据结合中位数和众数的定义,确定a的值即可.【详解】解:由条形统计图可知,前三次的中位数是8∵第四次又买的苹果单价是a元/千克,这四个单价的中位数恰好也是众数∴a=8.故答案为B.【点睛】本题考查条形统计图、中位数和众数的定义,掌握中位数和众数的定义是解答本题的关键.∠,用尺规作它的角平分线.6.如图1,已知ABC如图2,步骤如下,第一步:以B 为圆心,以a 为半径画弧,分别交射线BA ,BC 于点D ,E ;第二步:分别以D ,E 为圆心,以b 为半径画弧,两弧在ABC ∠内部交于点P ;第三步:画射线BP .射线BP 即为所求.下列正确的是( )A. a ,b 均无限制B. 0a >,12b DE >的长 C. a 有最小限制,b 无限制D. 0a ≥,12b DE <的长 【答案】B【解析】【分析】根据作角平分线的方法进行判断,即可得出结论. 【详解】第一步:以B 为圆心,适当长为半径画弧,分别交射线BA ,BC 于点D ,E ;∴0a >;第二步:分别以D ,E 为圆心,大于12DE 的长为半径画弧,两弧在ABC ∠内部交于点P ; ∴12b DE >的长; 第三步:画射线BP .射线BP 即为所求. 综上,答案为:0a >;12b DE >的长, 故选:B .【点睛】本题主要考查了基本作图,解决问题的关键是掌握作角平分线的方法.7.若a b ,则下列分式化简正确的是( ) A. 22a a b b +=+ B. 22a a b b -=- C. 22a a b b = D. 1212a a bb = 【答案】D【解析】【分析】根据a≠b,可以判断各个选项中的式子是否正确,从而可以解答本题.【详解】∵a≠b,∴22a ab b +≠+,选项A错误;22a ab b-≠-,选项B错误;22a ab b≠,选项C错误;1212a abb=,选项D正确;故选:D.【点睛】本题考查分式的混合运算,解答本题的关键是明确分式混合运算的计算方法.8.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是()A. 四边形NPMQB. 四边形NPMRC. 四边形NHMQD. 四边形NHMR【答案】A【解析】【分析】以O为位似中心,作四边形ABCD的位似图形,根据图像可判断出答案.【详解】解:如图所示,四边形ABCD的位似图形是四边形NPMQ.故选:A【点睛】此题考查了位似图形的作法,画位似图形的一般步骤为:①确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,确定位似图形.9.若()()229111181012k --=⨯⨯,则k =( ) A. 12 B. 10 C. 8 D. 6【答案】B【解析】【分析】利用平方差公式变形即可求解.【详解】原等式()()229111181012k --=⨯⨯变形得: ()()229111181012k --=⨯⨯()()()()919111111181012-+-+=⨯⨯ 810101281012⨯⨯⨯=⨯⨯ 10=.故选:B .【点睛】本题考查了平方差公式的应用,灵活运用平方差公式是解题的关键.10.如图,将ABC ∆绕边AC 的中点O 顺时针旋转180°.嘉淇发现,旋转后的CDA ∆与ABC ∆构成平行四边形,并推理如下: 点A ,C 分别转到了点C ,A 处,而点B 转到了点D 处.∵CB AD =,∴四边形ABCD 是平行四边形.小明为保证嘉淇的推理更严谨,想在方框中“∵CB AD =,”和“∴四边形……”之间作补充.下列正确的是( )A. 嘉淇推理严谨,不必补充B. 应补充:且AB CD =, C . 应补充:且//AB CDD. 应补充:且OA OC =,【答案】B【解析】【分析】 根据平行四边形的判定方法“两组对边分别相等的四边形是平行四边形”即可作答.【详解】根据旋转的性质得: CB=AD ,AB=CD ,∴四边形ABDC 是平行四边形;故应补充“AB=CD ”,故选:B .【点睛】本题主要考查了平行四边形的判定和旋转的性质,牢记旋转前、后的图形全等,熟练掌握平行四边形的判定方法是解题的关键.11.若k 为正整数,则()k k k k k k ++⋅⋅⋅+=个( ) A. 2k k B. 21k k + C. 2k k D. 2k k +【答案】A【解析】【分析】根据乘方的定义及幂的运算法则即可求解.【详解】()k k kk k k ++⋅⋅⋅+=个()()2k k k k k ⋅==2k k , 故选A .【点睛】此题主要考查幂的运算,解题的关键是熟知其运算法则.12.如图,从笔直的公路l 旁一点P 出发,向西走6km 到达l ;从P 出发向北走6km 也到达l .下列说法错.误.的是( )A. 从点P 向北偏西45°走3km 到达lB. 公路l的走向是南偏西45° C. 公路l 走向是北偏东45°D. 从点P 向北走3km 后,再向西走3km 到达l【答案】A【解析】【分析】根据方位角的定义及勾股定理逐个分析即可.【详解】解:如图所示,过P 点作AB 的垂线PH ,选项A :∵BP=AP=6km ,且∠BPA=90°,∴△PAB 为等腰直角三角形,∠PAB=∠PBA=45°,又PH ⊥AB ,∴△PAH 为等腰直角三角形,∴PH=2=PA ,故选项A 错误; 选项B :站在公路上向西南方向看,公路l 的走向是南偏西45°,故选项B 正确;选项C :站在公路上向东北方向看,公路l 的走向是北偏东45°,故选项C 正确;选项D :从点P 向北走3km 后到达BP 中点E ,此时EH 为△PEH 的中位线,故EH=12AP=3,故再向西走3km 到达l ,故选项D 正确.故选:A .【点睛】本题考查了方位角问题及等腰直角三角形、中位线等相关知识点,方向角一般以观测者的位置为中心,所以观测者不同,方向就正好相反,但角度不变.13.已知光速为300000千米秒,光经过t 秒(110t ≤≤)传播的距离用科学记数法表示为10n a ⨯千米,则n 可能为( )A. 5B. 6C. 5或6D. 5或6或7【答案】C【解析】【分析】科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.【详解】解:当t=1时,传播的距离为300000千米,写成科学记数法为:5310⨯千米,当t=10时,传播的距离为3000000千米,写成科学记数法为:6310⨯千米,∴n 的值为5或6,故选:C .【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.14.有一题目:“已知;点O 为ABC ∆的外心,130BOC ∠=︒,求A ∠.”嘉嘉的解答为:画ABC ∆以及它的外接圆O ,连接OB ,OC ,如图.由2130BOC A ∠=∠=︒,得65A ∠=︒.而淇淇说:“嘉嘉考虑的不周全,A ∠还应有另一个不同的值.”,下列判断正确的是( )A. 淇淇说的对,且A ∠的另一个值是115°B. 淇淇说的不对,A ∠就得65°C. 嘉嘉求的结果不对,A ∠应得50°D. 两人都不对,A ∠应有3个不同值【答案】A【解析】【分析】直接利用圆内接四边形的性质结合圆周角定理得出答案.【详解】解:如图所示:∵∠BOC=130°,∴∠A=65°,∠A 还应有另一个不同的值∠A′与∠A 互补.故∠A′=180°−65°=115°.故选:A .【点睛】此题主要考查了三角形的外接圆,正确分类讨论是解题关键. 15.如图,现要在抛物线(4)y x x =-上找点(,)P a b ,针对b 的不同取值,所找点P 的个数,三人的说法如下,甲:若5b =,则点P 的个数为0;乙:若4b =,则点P 的个数为1;丙:若3b =,则点P 的个数为1.下列判断正确的是( )A. 乙错,丙对B. 甲和乙都错C. 乙对,丙错D. 甲错,丙对【答案】C【解析】【分析】分别令x(4-x)的值为5,4,3,得到一元二次方程后,利用根的判别式确定方程的根有几个,即可得到点P的个数.【详解】当b=5时,令x(4-x)=5,整理得:x2-4x+5=0,△=(-4)2-4×5=-6<0,因此点P的个数为0,甲的说法正确;当b=4时,令x(4-x)=4,整理得:x2-4x+4=0,△=(-4)2-4×4=0,因此点P有1个,乙的说法正确;当b=3时,令x(4-x)=3,整理得:x2-4x+3=0,△=(-4)2-4×3=4>0,因此点P有2个,丙的说法不正确;故选:C.【点睛】本题考查二次函数与一元二次方程,解题的关键是将二次函数与直线交点个数,转化成一元二次方程根的判别式.16.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大..的直角三角形,则选取的三块纸片的面积分别是()A. 1,4,5B. 2,3,5C. 3,4,5D. 2,2,4【答案】B【解析】【分析】根据勾股定理,222+=a b c ,则小的两个正方形的面积等于大三角形的面积,再分别进行判断,即可得到面积最大的三角形.【详解】解:根据题意,设三个正方形的边长分别为a 、b 、c ,由勾股定理,得222+=a b c ,A 、∵1+4=5,则两直角边分别为:1和2,则面积为:112=12⨯⨯;B 、∵2+3=512C 、∵3+4≠5,则不符合题意;D 、∵2+2=4112=;1>, 故选:B .【点睛】本题考查了正方形的性质,勾股定理的应用,以及三角形的面积公式,解题的关键是熟练掌握勾股定理,以及正方形的性质进行解题.二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.==,则ab =_________.【答案】6【解析】【分析】根据二次根式的运算法则即可求解.-==∴a=3,b=2∴ab =6故答案为:6.【点睛】此题主要考查二次根式的运算,解题的关键是熟知其运算法则.18.正六边形的一个内角是正n 边形一个外角的4倍,则n =_________.【答案】12【解析】【分析】先根据外角和定理求出正六边形的外角为60°,进而得到其内角为120°,再求出正n 边形的外角为30°,再根据外角和定理即可求解.【详解】解:由多边形的外角和定理可知,正六边形的外角为:360°÷6=60°,故正六边形的内角为180°-60°=120°,又正六边形的一个内角是正n 边形一个外角的4倍,∴正n 边形的外角为30°,∴正n 边形的边数为:360°÷30°=12.故答案为:12.【点睛】本题考查了正多边形的外角与内角的知识,熟练掌握正多边形的内角和和外角和定理是解决此类题目的关键.19.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作m T (m 为1~8的整数).函数k y x=(0x <)的图象为曲线L .(1)若L 过点1T ,则k =_________;(2)若L 过点4T ,则它必定还过另一点m T ,则m =_________;(3)若曲线L 使得18~T T 这些点分布在它的两侧,每侧各4个点,则k 的整数值有_________个.【答案】 (1). -16 (2). 5 (3). 7【解析】【分析】(1)先确定T 1的坐标,然后根据反比例函数k y x=(0x <)即可确定k 的值; (2)观察发现,在反比例函数图像上的点,横纵坐标只积相等,即可确定另一点;(3)先分别求出T 1~T 8的横纵坐标积,再从小到大排列,然后让k 位于第4个和第5个点的横纵坐标积之间,即可确定k 的取值范围和k 的整数值的个数.【详解】解:(1)由图像可知T 1(-16,1)又∵.函数k y x =(0x <)的图象经过T 1 ∴116k =-,即k=-16; (2)由图像可知T 1(-16,1)、T 2(-14,2)、T 3(-12,3)、T 4(-10,4)、T 5(-8,5)、T 6(-6,6)、T 7(-4,7)、T 8(-2,8)∵L 过点4T∴k=-10×4=40 观察T 1~T 8,发现T 5符合题意,即m=5;(3)∵T 1~T 8的横纵坐标积分别为:-16,-28,-36,-40,-40,-36,-28,-16∴要使这8个点为于L 的两侧,k 必须满足-36<k <-28∴k 可取-29、-30、-31、-32、-33、-34、-35共7个整数值.故答案为:(1)-16;(2)5;(3)7.【点睛】本题考查了反比例函数图像的特点,掌握反比例函数图像上的点的横纵坐标积等于k 是解答本题的关键.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤) 20.已知两个有理数:-9和5.(1)计算:(9)52-+; (2)若再添一个负整数m ,且-9,5与m 这三个数的平均数仍小于m ,求m 的值. 【答案】(1)-2;(2)1m =-.【解析】【分析】(1)根据有理数的混合运算法则即可求解;(2)根据平均数的定义列出不等式即可求出m 的取值,故可求解.【详解】(1)(9)52-+=422-=-; (2)依题意得(9)53m -++<m 解得m >-2∴负整数m =-1.【点睛】此题主要考查有理数、不等式及平均数,解题的关键是熟知有理数、不等式的运算法则. 21.有一电脑程序:每按一次按键,屏幕的A 区就会自动加上2a ,同时B 区就会自动减去3a ,且均显示化简后的结果.已知A ,B 两区初始显示的分别是25和-16,如图.如,第一次按键后,A ,B 两区分别显示:(1)从初始状态按2次后,分别求A ,B 两区显示的结果;(2)从初始状态按4次后,计算A ,B 两区代数式的和,请判断这个和能为负数吗?说明理由.【答案】(1)2252a +;166a --;(2)24a 12a+9-;和不能为负数,理由见解析.【解析】【分析】(1)根据题意,每按一次按键,屏幕的A 区就会自动加上2a ,B 区就会自动减去3a ,可直接求出初始状态按2次后A ,B 两区显示的结果.(2)依据题意,分别求出初始状态下按4次后A ,B 两区显示的代数式,再求A ,B 两区显示的代数式的和,判断能否为负数即可.【详解】解:(1)A 区显示结果为:22225+a +a =25+2a ,B 区显示结果为:163a 3a=166a ﹣--﹣-;(2)初始状态按4次后A 显示为:2222225+a +a +a a 254a +=+B 显示为:163a 3a 3a 3a=1612a ﹣----﹣-∴A+B=225+4a +(-1612a)-=24a 12a+9-=2(2a 3)-∵2(2a 3)0≥-恒成立,∴和不能为负数.【点睛】本题考查了代数式运算,合并同类项,完全平方公式问题,解题关键在于理解题意,列出代数式进行正确运算,并根据完全平方公式判断正负.22.如图,点O 为AB 中点,分别延长OA 到点C ,OB 到点D ,使OC OD =.以点O 为圆心,分别以OA ,OC 为半径在CD 上方作两个半圆.点P 为小半圆上任一点(不与点A ,B 重合),连接OP 并延长交大半圆于点E ,连接AE ,CP .(1)①求证:AOE POC ∆∆≌;②写出∠1,∠2和C ∠三者间的数量关系,并说明理由.(2)若22OC OA ==,当C ∠最大时,直接..指出CP 与小半圆的位置关系,并求此时EOD S 扇形(答案保留π).【答案】(1)①见详解;②∠2=∠C+∠1;(2)CP 与小半圆相切,43π. 【解析】【分析】(1)①直接由已知即可得出AO=PO ,∠AOE=∠POC ,OE=OC ,即可证明;②由(1)得△AOE ≌△POC ,可得∠1=∠OPC ,根据三角形外角的性质可得∠2=∠C+∠OPC ,即可得出答案;(2)当C ∠最大时,可知此时CP 与小半圆相切,可得CP⊥OP,然后根据222OC OA OP ===,可得在Rt △POC 中,∠C=30°,∠POC=60°,可得出∠EOD ,即可求出S 扇EOD .【详解】(1)①在△AOE 和△POC 中=AO PO AOE POC OE OC =⎧⎪⎨⎪=⎩∠∠,∴△AOE ≌△POC ;②∠2=∠C+∠1,理由如下:由(1)得△AOE ≌△POC ,∴∠1=∠OPC ,根据三角形外角的性质可得∠2=∠C+∠OPC ,∴∠2=∠C+∠1;(2)在P 点的运动过程中,只有CP 与小圆相切时∠C 有最大值,∴当C ∠最大时,可知此时CP 与小半圆相切,由此可得CP ⊥OP ,又∵222OC OA OP ===,∴可得在Rt △POC 中,∠C=30°,∠POC=60°,∴∠EOD=180°-∠POC=120°,∴S 扇EOD =2120360R π⨯⨯=43π. 【点睛】本题考查了全等三角形的性质和判定,三角形的外角,切线的性质,扇形面积的计算,掌握知识点灵活运用是解题关键.23.用承重指数W 衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W 与木板厚度x (厘米)的平方成正比,当3x =时,3W =.(1)求W 与x 的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x (厘米),Q W W =-厚薄.①求Q 与x 的函数关系式;②x 为何值时,Q 是W 薄的3倍?【注:(1)及(2)中的①不必写x 的取值范围】【答案】(1)213W x =;(2)①124Q x =-;②2cm x =. 【解析】【分析】(1)设W=kx 2,利用待定系数法即可求解;(2)①根据题意列出函数,化简即可;②根据题意列出方程故可求解.【详解】(1)设W=kx 2,∵3x =时,3W =∴3=9k∴k=13∴W 与x 的函数关系式为213W x =; (2)①∵薄板的厚度为xcm ,木板的厚度为6cm∴厚板的厚度为(6-x )cm ,∴Q=2211(6)41233x x x ⨯=-+-- ∴Q 与x 的函数关系式为124Q x =-;②∵Q 是W 薄的3倍∴-4x+12=3×213x解得x1=2,x2=-6(不符题意,舍去)经检验,x=2是原方程的解,∴x=2时,Q 是W 薄的3倍.【点睛】此题主要考查函数与方程的应用,解题的关键是根据题意找到等量关系列出函数或方程求解.24.表格中的两组对应值满足一次函数y kx b =+,现画出了它的图象为直线l ,如图.而某同学为观察k ,b 对图象的影响,将上面函数中的k 与b 交换位置后得另一个一次函数,设其图象为直线l '.(1)求直线l 的解析式;(2)请在图上画出..直线l '(不要求列表计算),并求直线l '被直线l 和y 轴所截线段的长; (3)设直线y a =与直线l ,l '及y 轴有三个不同的交点,且其中两点关于第三点对称,直接..写出a 的值. 【答案】(1)l :31y x ;(22;(3)a 的值为52或175或7 【解析】【分析】(1)根据待定系数法即可求解;(2)根据题意得到直线l ',联立两直线求出交点坐标,再根据两点间的距离公式即可求解;(3)分对称点在直线l ,直线l '和y 轴分别列式求解即可.【详解】(1)依题意把(-1,-2)和(0,1)代入y kx b =+, 得21k b b -=-+⎧⎨=⎩, 解得31k b =⎧⎨=⎩, ∴直线l 的解析式为31y x , (2)依题意可得直线l '的解析式为3y x ,作函数图像如下:令x=0,得y=3,故B (0,3), 令313y x y x =+⎧⎨=+⎩,解得14x y =⎧⎨=⎩, ∴A (1,4),∴直线l '被直线l 和y 轴所截线段的长AB=22(10)(43)2-+-=;(3)①当对称点在直线l 上时,令31a x ,解得x=13a -, 令3a x =+,解得x=3a -,∴2×13a -=a-3, 解得a=7;②当对称点在直线l '上时,则2×(a-3)=13a -, 解得a=175; ③当对称点在y 轴上时,则13a -+(3a -)=0, 解得a=52; 综上:a 的值为52或175或7. 【点睛】此题主要考查一次函数与几何综合,解题的关键是熟知待定系数法、一次函数的图像与性质及坐标的对称性.25.如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终..停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;(3)从图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接..写出k的值.【答案】(1)14P=;(2)256m n=-;当4n=时,距离原点最近;(3)3k=或5【解析】【分析】(1)对题干中三种情况计算对应概率,分析出正确的概率即可;硬币朝上为正面、反面的概率均为12,甲和乙猜正反的情况也分为三种情况:①甲和乙都猜正面或反面,概率为12,②甲猜正,乙猜反,概率为14,③甲猜反,乙猜正,概率为14,(2)根据题意可知乙答了10次,答对了n次,则打错了(10-n)次,再根据平移的规则推算出结果即可;(3)刚开始的距离是8,根据三种情况算出缩小的距离,即可算出缩小的总距离,分别除以2即可得到结果;【详解】(1)题干中对应的三种情况的概率为:①11111+= 22222⨯⨯;②11111+= 24244⨯⨯;③11111+= 24244⨯⨯;甲的位置停留在正半轴上的位置对应情况②,故P =14. (2)根据题意可知乙答了10次,答对了n 次,则打错了(10-n )次,根据题意可得,n 次答对,向西移动4n ,10-n 次答错,向东移了2(10-n ),∴m=5-4n+2(10-n )=25-6n ,∴当n=4时,距离原点最近.(3)起初,甲乙的距离是8,易知,当甲乙一对一错时,二者之间距离缩小2,当甲乙同时答对打错时,二者之间的距离缩小2,∴当加一位置相距2个单位时,共缩小了6个单位或10个单位,∴62=3÷或102=5÷,∴3k =或5k =.【点睛】本题主要考查了概率的求解,通过数轴的理解进行准确分析是解题的关键. 26.如图1和图2,ABC ∆中,AB AC =,8BC =,3tan 4C =.点K 在AC 边上,点M ,N 分别在AB ,BC 上,且2AM CN ==.点P 从点M 出发沿折线MB BN -匀速移动,到达点N 时停止;而点Q 在AC 边上随P 移动,且始终保持APQ B ∠=∠.(1)当点P 在BC 上时,求点P 与点A 的最短距离;(2)若点P 在MB 上,且PQ 将ABC ∆的面积分成上下4:5两部分时,求MP 的长;(3)设点P 移动的路程为x ,当03x ≤≤及39x ≤≤时,分别求点P 到直线AC 的距离(用含x 的式子表示);(4)在点P 处设计并安装一扫描器,按定角APQ ∠扫描APQ ∆区域(含边界),扫描器随点P 从M 到B 再到N 共用时36秒.若94AK =,请直接..写出点K 被扫描到的总时长. 【答案】(1)3;(2)43MP =;(3)当03x ≤≤时,24482525d x =+;当39x ≤≤时,33355d x =-+;(4)23t s =【解析】【分析】(1)根据当点P 在BC 上时,PA ⊥BC 时PA 最小,即可求出答案;(2)过A 点向BC 边作垂线,交BC 于点E ,证明△APQ ∽△ABC ,可得2APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,根据S S 上下=45可得 24=9APQABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,可得23AP AB =,求出AB=5,即可解出MP ; (3)先讨论当0≤x≤3时,P 在BM 上运动,P 到AC 的距离:d=PQ ·sinC ,求解即可,再讨论当3≤x≤9时,P 在BN 上运动,BP=x-3,CP=8-(x-3)=11-x ,根据d=CP·sinC 即可得出答案;(4)先求出移动的速度=936=14,然后先求出从Q 平移到K 耗时,再求出不能被扫描的时间段即可求出时间.【详解】(1)当点P 在BC 上时,PA ⊥BC 时PA 最小,∵AB=AC ,△ABC 为等腰三角形,∴PA min =tanC·2BC =34×4=3; (2)过A 点向BC 边作垂线,交BC 于点E ,S 上=S △APQ ,S 下=S 四边形BPQC ,∵APQ B ∠=∠,∴PQ ∥BC ,∴△APQ ∽△ABC ,∴AP AD PQ AB AC BC==, ∴2APQABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭,当S S 上下=45时,24=9APQ ABC S AP S AB ∆∆⎛⎫= ⎪⎝⎭, ∴23AP AB =, AE=2BC ·tan 3C =, 根据勾股定理可得AB=5, ∴2253AP MP AB +==, 解得MP=43; (3)当0≤x≤3时,P BM 上运动,P 到AC 的距离:d=PQ·sinC ,由(2)可知sinC=35, ∴d=35PQ , ∵AP=x+2, ∴25AP x PQ AB BC+==, ∴PQ=285x +⨯, ∴d=23855x +⨯⨯=24482525x +, 当3≤x≤9时,P 在BN 上运动,BP=x-3,CP=8-(x-3)=11-x ,d=CP·sinC=35(11-x )=-35x+335, 综上()()24480325253333955x x d x x ⎧+≤≤⎪⎪=⎨⎪-+≤≤⎪⎩; (4)AM=2<AQ=94, 移动的速度=936=14, ①从Q 平移到K ,耗时:92414-=1秒, ②P 在BC 上时,K 与Q 重合时CQ=CK=5-94=114, ∵∠APQ+∠QPC=∠B+∠BAP ,APQ B ∠=∠∴∠QPC=∠BAP ,又∵∠B=∠C ,∴△ABP ∽△PCQ ,设BP=y ,CP=8-y ,AB BP PC CQ =,即51184y y =-, 整理得y 2-8y=554-, (y-4)2=94, 解得y 1=52,y 2=112, 52÷14=10秒, 112÷14=22秒, ∴点K 被扫描到的总时长36-(22-10)-1=23秒.【点睛】本题考查了相似三角形的判定和性质,锐角三角函数,一次函数的应用,结合知识点灵活运用是解题关键。
2020年河北省中考数学试卷和答案解析

2020年河北省中考数学试卷和答案解析一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条解析:根据垂直、垂线的定义,可直接得结论.参考答案:解:在同一平面内,与已知直线垂直的直线有无数条,所以作已知直线m的垂线,可作无数条.故选:D.点拨:本题考查了垂直和垂线的定义.掌握垂线的定义是解决本题的关键.2.(3分)墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+B.﹣C.×D.÷解析:直接利用同底数幂的除法运算法则计算得出答案.参考答案:解:∵x3x=x2(x≠0),∴覆盖的是:÷.故选:D.点拨:此题主要考查了同底数幂的除法运算,正确掌握相关运算法则是解题关键.3.(3分)对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x ﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解解析:根据因式分解的定义(把一个多项式化成几个整式积的形式,叫因式分解,也叫分解因式)判断即可.参考答案:解:①x﹣3xy=x(1﹣3y),从左到右的变形是因式分解;②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形是整式的乘法,不是因式分解;所以①是因式分解,②是乘法运算.故选:C.点拨:此题考查了因式分解.解题的关键是掌握因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解.4.(3分)如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同解析:根据主视图是从物体的正面看得到的视图,俯视图是从上面看得到的图形,左视图是左边看得到的图形,可得答案.参考答案:解:解法一:从正面看,两个几何体均为第一层和第二层都是两个小正方形,故主视图相同;从左面看,两个几何体均为第一层和第二层都是两个小正方形,故左视图相同;从上面看,两个几何体均为第一层和第二层都是两个小正方形,故俯视图相同.解法二:第一个几何体的三视图如图所示第二个几何体的三视图如图所示:观察可知这两个几何体的主视图、左视图和俯视图都相同,故选:D.点拨:本题考查了简单组合体的三视图,利用三视图的意义是解题关键.5.(3分)如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A.9B.8C.7D.6解析:根据统计图中的数据和题意,可以得到a的值,本题得以解决.参考答案:解:由统计图可知,前三次的中位数是8,∵第四次又买的苹果单价是a元/千克,这四个单价的中位数恰好也是众数,∴a=8,故选:B.点拨:本题考查条形统计图、中位数、众数,解答本题的关键是明确题意,利用数形结合的思想解答.6.(3分)如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求.下列正确的是()A.a,b均无限制B.a>0,b>DE的长C.a有最小限制,b无限制D.a≥0,b<DE的长解析:根据角平分线的画法判断即可.参考答案:解:以B为圆心画弧时,半径a必须大于0,分别以D,E为圆心,以b为半径画弧时,b必须大于DE,否则没有交点,故选:B.点拨:本题考查作图﹣基本作图,解题的关键是熟练掌握作角平分线的方法,属于中考常考题型.7.(3分)若a≠b,则下列分式化简正确的是()A.=B.=C.=D.=解析:根据a≠b,可以判断各个选项中的式子是否正确,从而可以解答本题.参考答案:解:∵a≠b,∴,故选项A错误;,故选项B错误;,故选项C错误;,故选项D正确;故选:D.点拨:本题考查分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.熟练掌握分式的基本性质是解题的关键.8.(3分)在如图所示的网格中,以点O为位似中心,四边形ABCD 的位似图形是()A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR解析:由以点O为位似中心,确定出点C对应点M,设网格中每个小方格的边长为1,则OC=,OM=2,OD=,OB=,OA=,OR=,OQ=2,OP=2,OH=3,ON=2,由=2,得点D对应点Q,点B对应点P,点A对应点N,即可得出结果.参考答案:解:∵以点O为位似中心,∴点C对应点M,设网格中每个小方格的边长为1,则OC==,OM==2,OD=,OB==,OA==,OR==,OQ=2,OP==2,OH==3,ON==2,∵==2,∴点D对应点Q,点B对应点P,点A对应点N,∴以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故选:A.点拨:本题考查了位似变换、勾股定理等知识;熟练掌握位似中心,找出点C对应点M是解题的关键.9.(3分)若=8×10×12,则k=()A.12B.10C.8D.6解析:根据平方差公式和分式方程的解法,即可得到k的值.参考答案:解:方程两边都乘以k,得(92﹣1)(112﹣1)=8×10×12k,∴(9+1)(9﹣1)(11+1)(11﹣1)=8×10×12k,∴80×120=8×10×12k,∴k=10.经检验k=10是原方程的解.故选:B.点拨:此题考查了平方差公式和解分式方程,熟练掌握平方差公式和解分式方程的方法是解本题的关键.10.(3分)如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形…”之间作补充,下列正确的是()A.嘉淇推理严谨,不必补充B.应补充:且AB=CDC.应补充:且AB∥CDD.应补充:且OA=OC解析:根据两组对边分别相等的四边形是平行四边形判定即可.参考答案:解:∵CB=AD,AB=CD,∴四边形ABCD是平行四边形,故应补充“AB=CD”,故选:B.点拨:本题考查平行四边形的判定,旋转变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.11.(2分)若k为正整数,则=()A.k2k B.k2k+1C.2k k D.k2+k解析:根据乘方的定义及幂的运算法则即可求解.参考答案:解:=((k•k)k=(k2)k=k2k,故选:A.点拨:本题考查了幂的乘方.解题的关键掌握幂的乘方的运算法则:底数不变,指数相乘.12.(2分)如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是()A.从点P向北偏西45°走3km到达lB.公路l的走向是南偏西45°C.公路l的走向是北偏东45°D.从点P向北走3km后,再向西走3km到达l解析:先作出图形,根据勾股定理和等腰直角三角形的性质即可求解.参考答案:解:如图,由题意可得△PAB是腰长6km的等腰直角三角形,则AB=6km,如图所示,过P点作AB的垂线PC,则PC=3km,则从点P向北偏西45°走3km到达l,选项A错误;则公路l的走向是南偏西45°或北偏东45°,选项B,C正确;则从点P向北走3km后到达BP中点D,此时CD为△PAB的中位线,故CD=AP=3,故再向西走3km到达l,选项D正确.故选:A.点拨:本题考查的是勾股定理的应用,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.13.(2分)已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n千米,则n可能为()A.5B.6C.5或6D.5或6或7解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n 为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.参考答案:解:当t=1时,光传播的距离为1×300000=300000=3×105(千米),则n=5;当t=10时,光传播的距离为10×300000=3000000=3×106(千米),则n=6.因为1≤t≤10,所以n可能为5或6,故选:C.点拨:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.14.(2分)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A应有3个不同值解析:直接利用圆内接四边形的性质结合圆周角定理得出答案.参考答案:解:如图所示:∠A还应有另一个不同的值∠A′与∠A互补.故∠A′=180°﹣65°=115°.故选:A.点拨:此题主要考查了三角形的外接圆,正确分类讨论是解题关键.15.(2分)如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对解析:求出抛物线的顶点坐标为(2,4),由二次函数的性质对甲、乙、丙三人的说法分别进行判断,即可得出结论.参考答案:解:y=x(4﹣x)=﹣x2+4x=﹣(x﹣2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为4,∴甲、乙的说法正确;若b=3,则抛物线上纵坐标为3的点有2个,∴丙的说法不正确;故选:C.点拨:本题考查了二次函数图象上点的坐标特征、抛物线的顶点坐标等知识;熟练掌握二次函数图象上点的坐标特征是解题的关键.16.(2分)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A.1,4,5B.2,3,5C.3,4,5D.2,2,4解析:根据题意可知,三块正方形的面积中,两个较小的面积之和等于最大的面积,再根据三角形的面积,分别计算出各个选项中围成的直角三角形的面积,比较大小,即可解答本题.参考答案:解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是=,当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是=;当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是=,∵,∴所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5,故选:B.点拨:本题考查勾股定理的逆定理,解答本题的关键是明确题意,利用勾股定理的逆定理解答.二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.(3分)已知:﹣=a﹣=b,则ab=6.解析:直接化简二次根式进而得出a,b的值求出答案.参考答案:解:原式=3﹣=a﹣=b,故a=3,b=2,则ab=6.故答案为:6.点拨:此题主要考查了二次根式的加减,正确化简二次根式是解题关键.18.(3分)正六边形的一个内角是正n边形一个外角的4倍,则n =12.解析:根据多边形的内角和公式求出正六边形的一个内角等于120°,再根据多边形的外角和是360°即可解答.参考答案:解:正六边形的一个内角为:,∵正六边形的一个内角是正n边形一个外角的4倍,∴正n边形一个外角为:120°÷4=30°,∴n=360°÷30°=12.故答案为:12.点拨:本题主要考查了多边形的外角和定理,理解多边形外角和中外角的个数,以及正多边形的边数之间的关系,是解题关键.19.(6分)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作T m(m为1~8的整数).函数y=(x<0)的图象为曲线L.(1)若L过点T1,则k=﹣16;(2)若L过点T4,则它必定还过另一点T m,则m=5;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有7个.解析:(1)由题意可求T1~T8这些点的坐标,将点T1的坐标代入解析式可求解;(2)将点T4的坐标代入解析式可求k的值,将点T5代入,可求解;(3)由曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,可得T1,T2,T7,T8与T3,T4,T5,T6在曲线L的两侧,即可求解.参考答案:解:(1)∵每个台阶的高和宽分别是1和2,∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),∵L过点T1,∴k=﹣16×1=﹣16,故答案为:﹣16;(2)∵L过点T4,∴k=﹣10×4=﹣40,∴反比例函数解析式为:y=﹣,当x=﹣8时,y=5,∴T5在反比例函数图象上,∴m=5,故答案为:5;(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,若曲线L过点T3(﹣12,3),T5(﹣8,5)时,k=﹣12×3=﹣36,若曲线L过点T4(﹣10,4),T5(﹣8,5)时,k=﹣40,∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,∴﹣36<k<﹣28,∴整数k=﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个,∴答案为:7.点拨:本题考查了反比例函数的应用,求出各点的坐标是本题的关键.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(8分)已知两个有理数:﹣9和5.(1)计算:;(2)若再添一个负整数m,且﹣9,5与m这三个数的平均数仍小于m,求m的值.解析:(1)根据有理数的加法、除法法则计算即可;(2)根据平均数的定义列不等式,解不等式,由m是负整数即可求出m的值.参考答案:解:(1)==﹣2;(2)根据题意得,<m,∴﹣4+m<3m,∴m﹣3m<4,∴﹣2m<4,∴m>﹣2,∵m是负整数,∴m=﹣1.点拨:此题考查了有理数的运算,解不等式和平均数.熟练掌握有理数的运算法则,解不等式的方法是解本题的关键.21.(8分)有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16,如图.如,第一次按键后,A,B两区分别显示:(1)从初始状态按2次后,分别求A,B两区显示的结果;(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能为负数吗?说明理由.解析:(1)根据题意列出代数式即可;(2)根据题意得到25+4a2+(﹣16﹣12a),根据整式加减的法则计算,然后配方,根据非负数的性质即可得到结论.参考答案:解:(1)A区显示的结果为:25+2a2,B区显示的结果为:﹣16﹣6a;(2)这个和不能为负数,理由:根据题意得,25+4a2+(﹣16﹣12a)=25+4a2﹣16﹣12a=4a2﹣12a+9;∵(2a﹣3)2≥0,∴这个和不能为负数.点拨:本题考查了配方法的应用,非负数的性质,整式的加减,正确的理解题意是解题的关键.22.(9分)如图,点O为AB中点,分别延长OA到点C,OB到点D,使OC=OD.以点O为圆心,分别以OA,OC为半径在CD 上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.(1)①求证:△AOE≌△POC;②写出∠1,∠2和∠C三者间的数量关系,并说明理由.(2)若OC=2OA=2,当∠C最大时,直接指出CP与小半圆的位置关系,并求此时S扇形EOD(答案保留π).解析:(1)①利用公共角相等,根据SAS证明三角形全等便可;②由全等三角形得∠C=∠E,再利用三角形外角性质得结论;(2)当CP与小半圆O相切时,∠C最大,求出∠DOE便可根据扇形的面积公式求得结果.参考答案:解:(1)①在△AOE和△POC中,,∴△AOE≌△POC(SAS);②∠1+∠C=∠2,理由是:∵△AOE≌△POC,∴∠E=∠C,∵∠1+∠E=∠2,∴∠1+∠C=∠2;(2)当∠C最大时,CP与小半圆相切,如图,∵OC=2OA=2,∴OC=2OP,∵CP与小半圆相切,∴∠OPC=90°,∴∠OCP=30°,∴∠DOE=∠OPC+∠OCP=120°,∴.点拨:本题主要考查了圆的切线的性质,全等三角形的判定与性质,三角形的外角性质,直角三角形的性质,扇形的面积计算,关键在于掌握各个定理,灵活运用这些性质解题.23.(9分)用承重指数w衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W =3.(1)求W与x的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄.①求Q与x的函数关系式;②x为何值时,Q是W薄的3倍?[注:(1)及(2)中的①不必写x的取值范围]解析:(1)由木板承重指数W与木板厚度x(厘米)的平方成正比,可设W=kx2(k≠0).将x=3时,W=3代入,求出k=,即可得出W与x的函数关系式;(2)①设薄板的厚度为x厘米,则厚板的厚度为(6﹣x)厘米,将(1)中所求的解析式代入Q=W厚﹣W薄,化简即可得到Q与x的函数关系式;②根据Q是W薄的3倍,列出方程﹣4x+12=3×x2,求解即可.参考答案:解:(1)设W=kx2(k≠0).∵当x=3时,W=3,∴3=9k,解得k=,∴W与x的函数关系式为W=x2;(2)①设薄板的厚度为x厘米,则厚板的厚度为(6﹣x)厘米,∴Q=W厚﹣W薄=(6﹣x)2﹣x2=﹣4x+12,即Q与x的函数关系式为Q=﹣4x+12;②∵Q是W薄的3倍,∴﹣4x+12=3×x2,整理得,x2+4x﹣12=0,解得,x1=2,x2=﹣6(不合题意舍去),故x为2时,Q是W薄的3倍.点拨:本题考查了二次函数的应用,待定系数法求二次函数的解析式,求出W与x的函数关系式是解题的关键.24.(10分)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l'.x﹣10y﹣21(1)求直线l的解析式;(2)请在图上画出直线l'(不要求列表计算),并求直线l'被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.解析:(1)根据待定系数法求得即可;(2)画出直线l,求得两直线的交点,根据勾股定理即可求得直线l'被直线l和y轴所截线段的长;(3)求得两条直线与直线y=a的交点横坐标,分三种情况讨论求得即可.参考答案:解:(1)∵直线l:y=kx+b中,当x=﹣1时,y=﹣2;当x=0时,y=1,∴,解得,∴直线l的解析式为y=3x+1;(2)依题意可得直线l′的解析式为y=x+3如图,解得,∴两直线的交点为A(1,4),∵直线l′:y=x+3与y轴的交点为B(0,3),∴直线l'被直线l和y轴所截线段的长为:AB==;(3)把y=a代入y=3x+1得,a=3x+1,解得x=;把y=a代入y=x+3得,a=x+3,解得x=a﹣3;分三种情况:①当第三点在y轴上时,a﹣3+=0,解得a=;②当第三点在直l上时,2×=a﹣3,解得a=7;③当第三点在直线l'上时,2×(a﹣3)=,解得a=;∴直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,则a的值为或7或.点拨:本题考查了一次函数图象与几何变换,两直线相交问题,待定系数法求一次函数的解析式,分类讨论是解题的关键.25.(10分)如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O 最近时n的值;(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.解析:(1)利用概率公式计算即可.(2)根据题意可知乙答了10次,答对了n次,则打错了(10﹣n)次,再根据平移的规则推算出结果即可;(3)刚开始的距离是8,根据三种情况算出缩小的距离,即可算出缩小的总距离,分别除以2即可得到结果.参考答案:解:(1)∵经过第一次移动游戏,甲的位置停留在正半轴上,∴必须甲对乙错,因为一共有四种情形,都对或都错,甲对乙错,甲错乙对,∴P甲对乙错=.(2)根据题意可得,n次答对,向西移动4n,(10﹣n)次答错,向东移了2(10﹣n),∴m=5﹣4n+2(10﹣n)=25﹣6n.n=4时,离原点最近.(3)起初,甲乙的距离是8,易知,当甲乙一对一错时,二者之间距离缩小2,当甲乙同时答对打错时,二者之间的距离缩小2,∴当进行了k次移动游戏后,甲与乙的位置相距2个单位时,共缩小了6个单位或10个单位,∴6÷2=3或10÷2=5,∴k=3或k=5.点拨:本题考查概率公式,数轴,代数式等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.26.(12分)如图1和图2,在△ABC中,AB=AC,BC=8,tanC =.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N 时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P 到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=,请直接写出点K被扫描到的总时长.解析:(1)在图1中,过点A作AH⊥BC于H.解直角三角形求出AH即可.(2)如图1,证明△APQ∽△ABC,可得,根据=可得,可得,根据(1)中AB=5,即可解出MP;(3)分两种情形:当0≤x≤3时,当3≤x≤9时,分别画出图形求解即可.(4)求出CK的长度,以及CQ的最大值,利用路程与速度的关系求解即可.参考答案:解:(1)如图1中,过点A作AH⊥BC于H.∵AB=AC,AH⊥BC,∴BH=CH=4,∠B=∠C,∴tan∠B=tan∠C==,∴AH=3,AB=AC===5.∴当点P在BC上时,PA⊥BC时,点P到A的最短距离为3.(2)如图1中,∵∠APQ=∠B,∴PQ∥BC,∴△APQ∽△ABC,∵PQ将△ABC的面积分成上下4:5,∴=()2=,∴=,∴AP=,∴PM=AP﹣AM=﹣2=.(3)当0≤x≤3时,如图1﹣1中,过点P作PJ⊥CA交CA的延长线于J.∵PQ∥BC,∴=,∠AQP=∠C,∴=,∴PQ=(x+2),∵sin∠AQP=sin∠C=,∴PJ=PQ•sin∠AQP=(x+2).当3≤x≤9时,如图2中,过点P作PJ⊥AC于J.同法可得PJ=PC•sin∠C=(11﹣x).综上,PJ=;(4)由题意点P的运动速度==单位长度/秒.当3<x≤9时,设点P移动的路程为x,CQ=y.∵∠APC=∠B+∠BAP=∠APQ+∠CPQ,∠APQ=∠B,∴∠BAP=∠CPQ,∵∠B=∠C,∴△ABP∽△PCQ,∴=,∴=,∴y =﹣(x﹣7)2+,∵﹣<0,∴x=7时,y 有最大值,最大值=,∵AK =,∴CK=5﹣=<当y =时,=﹣(x﹣7)2+,解得x=7±,∴点K 被扫描到的总时长=(+6﹣3)÷=23秒.点拨:本题属于三角形综合题,考查了等腰三角形的性质,解直角三角形,相似三角形的判定和性质,二次函数的性质等知识,解题的关键是理解题意,学会构建二次函数解决CQ的最值问题,属于中考压轴题.第31页(共31页)。
【解析版】2020年河北省中考数学试卷

【解析版】2020年河北省中考数学试卷一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条【分析】根据垂直、垂线的定义,可直接得结论.【解答】解:在平面内,与已知直线垂直的直线有无数条,所以作已知直线的垂线,可作无数条.故选:D.【点评】本题考查了垂直和垂线的定义.掌握垂线的定义是解决本题的关键.2.(3分)墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+B.﹣C.×D.÷【分析】直接利用同底数幂的除法运算法则计算得出答案.【解答】解:∵x3x=x2(x≠0),∴覆盖的是:÷.故选:D.【点评】此题主要考查了同底数幂的除法运算,正确掌握相关运算法则是解题关键.3.(3分)对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解【分析】根据因式分解的定义(把一个多项式化成几个整式积的形式,叫因式分解,也叫分解因式)判断即可.【解答】解:①x﹣3xy=x(1﹣3y),从左到右的变形是因式分解;②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形是整式的乘法,不是因式分解;所以①是因式分解,②是乘法运算.故选:C.【点评】此题考查了因式分解.解题的关键是掌握因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解.4.(3分)如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同【分析】根据主视图是从物体的正面看得到的视图,俯视图是从上面看得到的图形,左视图是左边看得到的图形,可得答案.【解答】解:从正面看,两个几何体均为第一层和第二层都是两个小正方形,故主视图相同;从左面看,两个几何体均为第一层和第二层都是两个小正方形,故左视图相同;从上面看,两个几何体均为第一层和第二层都是两个小正方形,故俯视图相同.故选:D.【点评】本题考查了简单组合体的三视图,利用三视图的意义是解题关键.5.(3分)如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A.9B.8C.7D.6【分析】根据统计图中的数据和题意,可以得到a的值,本题得以解决.【解答】解:由统计图可知,前三次的中位数是8,∵第四次又买的苹果单价是a元/千克,这四个单价的中位数恰好也是众数,∴a=8,故选:B.【点评】本题考查条形统计图、中位数、众数,解答本题的关键是明确题意,利用数形结合的思想解答.6.(3分)如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求.下列正确的是()A.a,b均无限制B.a>0,b>DE的长C.a有最小限制,b无限制D.a≥0,b<DE的长【分析】根据角平分线的画法判断即可.【解答】解:以B为圆心画弧时,半径a必须大于0,分别以D,E为圆心,以b为半径画弧时,b必须大于DE,否则没有交点,故选:B.【点评】本题考查作图﹣基本作图,解题的关键是熟练掌握五种基本作图,属于中考常考题型.7.(3分)若a≠b,则下列分式化简正确的是()A.=B.=C.=D.=【分析】根据a≠b,可以判断各个选项中的式子是否正确,从而可以解答本题.【解答】解:∵a≠b,∴,故选项A错误;,故选项B错误;,故选项C错误;,故选项D正确;故选:D.【点评】本题考查分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.熟练掌握分式的基本性质是解题的关键.8.(3分)在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是()A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR 【分析】由以点O为位似中心,确定出点C对应点M,设网格中每个小方格的边长为1,则OC=,OM=2,OD=,OB=,OA=,OR=,OQ=2,OP=2,OH=3,ON=2,由=2,得点D对应点Q,点B对应点P,点A对应点N,即可得出结果.【解答】解:∵以点O为位似中心,∴点C对应点M,设网格中每个小方格的边长为1,则OC==,OM==2,OD=,OB==,OA==,OR==,OQ=2,OP==2,OH==3,ON==2,∵==2,∴点D对应点Q,点B对应点P,点A对应点N,∴以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故选:A.【点评】本题考查了位似变换、等腰直角三角形的性质、勾股定理等知识;熟练掌握位似中心,找出点C对应点M是解题的关键.9.(3分)若=8×10×12,则k=()A.12B.10C.8D.6【分析】根据平方差公式和分式方程的解法,即可得到k的值.【解答】解:方程两边都乘以k,得(92﹣1)(112﹣1)=8×10×12k,∴(9+1)(9﹣1)(11+1)(11﹣1)=8×10×12k,∴80×120=8×10×12k,∴k=10.经检验k=10是原方程的解.故选:B.【点评】此题考查了平方差公式和解分式方程,熟练掌握平方差公式和解分式方程的方法是解本题的关键.10.(3分)如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形…”之间作补充,下列正确的是()A.嘉淇推理严谨,不必补充B.应补充:且AB=CDC.应补充:且AB∥CDD.应补充:且OA=OC【分析】根据两组对边分别相等的四边形是平行四边形判定即可.【解答】解:∵CB=AD,AB=CD,∴四边形ABCD是平行四边形,故选:B.【点评】本题考查平行四边形的判定,旋转变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.11.(2分)若k为正整数,则=()A.k2k B.k2k+1C.2k k D.k2+k【分析】根据幂的乘方的运算法则:底数不变,指数相乘解答即可.【解答】解:=((k•k)k=(k2)k=k2k,故选:A.【点评】本题考查了幂的乘方.解题的关键掌握幂的乘方的运算法则:底数不变,指数相乘.12.(2分)如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km 也到达l.下列说法错误的是()A.从点P向北偏西45°走3km到达lB.公路l的走向是南偏西45°C.公路l的走向是北偏东45°D.从点P向北走3km后,再向西走3km到达l【分析】先作出图形,根据勾股定理和等腰直角三角形的性质即可求解.【解答】解:如图,由题意可得△PAB是腰长6km的等腰直角三角形,则AB=6km,则PC=3km,则从点P向北偏西45°走3km到达l,选项A错误;则公路l的走向是南偏西45°或北偏东45°,选项B,C正确;则从点P向北走3km后,再向西走3km到达l,选项D正确.故选:A.【点评】本题考查的是勾股定理的应用,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.13.(2分)已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n千米,则n可能为()A.5B.6C.5或6D.5或6或7【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.【解答】解:当t=1时,光传播的距离为1×300000=300000=3×105(千米),则n=5;当t=10时,光传播的距离为10×300000=3000000=3×106(千米),则n=6.因为1≤t≤10,所以n可能为5或6,故选:C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.14.(2分)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A应有3个不同值【分析】直接利用圆内接四边形的性质结合圆周角定理得出答案.【解答】解:如图所示:∠A还应有另一个不同的值∠A′与∠A互补.故∠A′=180°﹣65°=115°.故选:A.【点评】此题主要考查了三角形的外接圆,正确分类讨论是解题关键.15.(2分)如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对【分析】求出抛物线的顶点坐标为(2,4),由二次函数的性质对甲、乙、丙三人的说法分别进行判断,即可得出结论.【解答】解:y=x(4﹣x)=﹣x2+4x=﹣(x﹣2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为4,∴甲、乙的说法正确;若b=3,则抛物线上纵坐标为3的点有2个,∴丙的说法不正确;故选:C.【点评】本题考查了二次函数图象上点的坐标特征、抛物线的顶点坐标等知识;熟练掌握二次函数图象上点的坐标特征是解题的关键.16.(2分)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A.1,4,5B.2,3,5C.3,4,5D.2,2,4【分析】根据题意可知,三块三角形的面积中,两个较小的面积之和等于最大的面积,再根据三角形的面积,分别计算出各个选项中围成的直角三角形的面积,比较大小,即可解答本题.【解答】解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是=,当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是=;当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是=,∵,∴所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5,故选:B.【点评】本题考查勾股定理的逆定理,解答本题的关键是明确题意,利用勾股定理的逆定理解答.二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.(3分)已知:﹣=a﹣=b,则ab=6.【分析】直接化简二次根式进而得出a,b的值求出答案.【解答】解:原式=3﹣=a﹣=b,故a=3,b=2,则ab=6.故答案为:6.【点评】此题主要考查了二次根式的加减,正确化简二次根式是解题关键.18.(3分)正六边形的一个内角是正n边形一个外角的4倍,则n=12.【分析】根据多边形的内角和公式求出正六边形的一个内角等于120°,再根据多边形的外角和是360°即可解答.【解答】解:正六边形的一个内角为:,∵正六边形的一个内角是正n边形一个外角的4倍,∴正n边形一个外角为:120°÷4=30°,∴n=360°÷30°=12.故答案为:12.【点评】本题主要考查了多边形的外角和定理,理解多边形外角和中外角的个数,以及正多边形的边数之间的关系,是解题关键.19.(6分)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作T m(m为1~8的整数).函数y=(x<0)的图象为曲线L.(1)若L过点T1,则k=﹣16;(2)若L过点T4,则它必定还过另一点T m,则m=5;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有7个.【分析】(1)由题意可求T1~T8这些点的坐标,将点T1的坐标代入解析式可求解;(2)将点T4的坐标代入解析式可求k的值,将点T5代入,可求解;(3)由曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,可得T1,T2,T7,T8与T3,T4,T5,T6在曲线L的两侧,即可求解.【解答】解:(1)∵每个台阶的高和宽分别是1和2,∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),∵L过点T1,∴k=﹣16×1=﹣16,故答案为:﹣16;(2)∵L过点T4,∴k=﹣10×4=﹣40,∴反比例函数解析式为:y=﹣,当x=﹣8时,y=5,∴T5在反比例函数图象上,∴m=5,故答案为:5;(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,若曲线L过点T3(﹣12,3),T5(﹣8,5)时,k=﹣12×3=﹣36,若曲线L过点T4(﹣10,4),T5(﹣8,5)时,k=﹣40,∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,∴﹣36<k<﹣28,∴整数k=﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个,∴答案为:7.【点评】本题考查了反比例函数的应用,求出各点的坐标是本题的关键.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(8分)已知两个有理数:﹣9和5.(1)计算:;(2)若再添一个负整数m,且﹣9,5与m这三个数的平均数仍小于m,求m的值.【分析】(1)根据有理数的加法、除法法则计算即可;(2)根据题意列不等式,解不等式,由m是负整数即可求出m的值.【解答】解:(1)==﹣2;(2)根据题意得,<m,∴﹣4+m<3m,∴m﹣3m<4,∴﹣2m<4,∴m>﹣2,∵m是负整数,∴m=﹣1.【点评】此题考查了有理数的运算,解不等式.熟练掌握有理数的运算法则,解不等式的方法是解本题的关键.21.(8分)有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16,如图.如,第一次按键后,A,B两区分别显示:(1)从初始状态按2次后,分别求A,B两区显示的结果;(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能为负数吗?说明理由.【分析】(1)根据题意列出代数式即可;(2)根据题意得到25+4a2+(﹣16﹣12a),根据整式加减的法则计算,然后配方,根据非负数的性质即可得到结论.【解答】解:(1)A区显示的结果为:25+2a2,B区显示的结果为:﹣16﹣6a;(2)这个和不能为负数,理由:根据题意得,25+4a2+(﹣16﹣12a)=25+4a2﹣16﹣12a=4a2﹣12a+9;∵(2a﹣3)2≥0,∴这个和不能为负数.【点评】本题考查了配方法的应用,非负数的性质,整式的加减,正确的理解题意是解题的关键.22.(9分)如图,点O为AB中点,分别延长OA到点C,OB到点D,使OC=OD.以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.(1)①求证:△AOE≌△POC;②写出∠l,∠2和∠C三者间的数量关系,并说明理由.(2)若OC=2OA=2,当∠C最大时,直接指出CP与小半圆的位置关系,并求此时S (答案保留π).扇形EOD【分析】(1)①利用公共角相等,根据SAS证明三角形全等便可;②由全等三角形得∠C=∠E,再利用三角形外角性质得结论;(2)当CP与小半圆O相切时,∠C最大,求出∠DOE便可根据扇形的面积公式求得结果.【解答】解:(1)①在△AOE和△POC中,,∴△AOE≌△POC(SAS);②∵△AOE≌△POC,∴∠E=∠C,∵∠1+∠E=∠2,∴∠1+∠C=∠2;(2)当∠C最大时,CP与小半圆相切,如图,∵OC=2OA=2,∴OC=2OP,∵CP与小半圆相切,∴∠OPC=90°,∴∠OCP=30°,∴∠DOE=∠OPC+∠OCP=120°,∴.【点评】本题主要考查了圆的切线的性质,全等三角形的判定与性质,三角形的外角性质,直角三角形的性质,扇形的面积计算,关键在于掌握各个定理,灵活运用这些性质解题.23.(9分)用承重指数w衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.(1)求W与x的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x (厘米),Q =W 厚﹣W 薄.①求Q 与x 的函数关系式;②x 为何值时,Q 是W 薄的3倍?[注:(1)及(2)中的①不必写x 的取值范围]【分析】(1)由木板承重指数W 与木板厚度x (厘米)的平方成正比,可设W =kx 2(k≠0).将x =3时,W =3代入,求出k =,即可得出W 与x 的函数关系式;(2)①设薄板的厚度为x 厘米,则厚板的厚度为(6﹣x )厘米,将(1)中所求的解析式代入Q =W 厚﹣W 薄,化简即可得到Q 与x 的函数关系式;②根据Q 是W 薄的3倍,列出方程﹣4x+12=3×x 2,求解即可.【解答】解:(1)设W =kx 2(k≠0).∵当x =3时,W =3,∴3=9k ,解得k =,∴W 与x 的函数关系式为W =x 2;(2)①设薄板的厚度为x 厘米,则厚板的厚度为(6﹣x )厘米,∴Q =W 厚﹣W 薄=(6﹣x )2﹣x 2=﹣4x+12,即Q 与x 的函数关系式为Q =﹣4x+12;②∵Q 是W 薄的3倍,∴﹣4x+12=3×x 2,整理得,x 2+4x ﹣12=0,解得,x 1=2,x 2=﹣6(不合题意舍去),故x为2时,Q是W的3倍.薄【点评】本题考查了二次函数的应用,待定系数法求二次函数的解析式,求出W与x的函数关系式是解题的关键.24.(10分)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l'.x﹣10y﹣21(1)求直线l的解析式;(2)请在图上画出直线l'(不要求列表计算),并求直线l'被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.【分析】(1)根据待定系数法求得即可;(2)画出直线l,求得两直线的交点,根据勾股定理即可求得直线l'被直线l和y轴所截线段的长;(3)求得两条直线与直线y=a的交点横坐标,分三种情况讨论求得即可.【解答】解:(1)∵直线l:y=kx+b中,当x=﹣1时,y=﹣2;当x=0时,y=1,∴,解得,∴直线l的解析式为y=3x+1;∴直线l′的解析式为y=x+3;(2)如图,解得,∴两直线的交点为(1,4),∵直线l′:y=x+3与y轴的交点为(0,3),∴直线l'被直线l和y轴所截线段的长为:=;(3)把y=a代入y=3x+1得,a=3x+1,解得x=;把y=a代入y=x+3得,a=x+3,解得x=a﹣3;当a﹣3+=0时,a=,当(a﹣3+0)=时,a=7,当(+0)=a﹣3时,a=,∴直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,则a的值为或7或.【点评】本题考查了一次函数图象与几何变换,两直线相交问题,待定系数法求一次函数的解析式,分类讨论是解题的关键.25.(10分)如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.【分析】(1)利用概率公式计算即可.(2)利用两点之间的距离公式计算即可.(3)不妨设甲连续k次正确移动后两人相距2个单位,则有|8+2k﹣4k|=2,解得k=3或5.如果k次中,有1次两人都对都错,则有|6+2(k﹣1)﹣4(k﹣1)|=2,解得k=3或5,如果k次中,有2次两人都对都错,则有|4+2(k﹣2)﹣4(k﹣2)|=2,解得k =3或5,探究规律,可得结论.【解答】解:(1)∵经过第一次移动游戏,甲的位置停留在正半轴上,∴必须甲对乙错,因为一共有四种情形,都对或都错,甲对乙错,甲错乙对,=.∴P甲对乙错(2)由题意m=5﹣4n+2(10﹣n)=25﹣6n.n=4时,离原点最近.(3)不妨设甲连续k次正确移动后两人相距2个单位,则有|8+2k﹣4k|=2,解得k=3或5.如果k次中,有1次两人都对都错,则有|6+2(k﹣1)﹣4(k﹣1)|=2,解得k=3或5,如果k次中,有2次两人都对都错,则有|4+2(k﹣2)﹣4(k﹣2)|=2,解得k=3或5,…,综上所述,满足条件的k的值为3或5.【点评】本题考查概率公式,数轴,代数式等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.26.(12分)如图1和图2,在△ABC中,AB=AC,BC=8,tanC=.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=,请直接写出点K被扫描到的总时长.【分析】(1)如图1中,过点A作AH⊥BC于H.解直角三角形求出AH即可.(2)利用相似三角形的性质求解即可.(3)分两种情形:当0≤x≤3时,当3<x≤9时,分别画出图形求解即可.(4)求出CK的长度,以及CQ的最大值,利用路程与速度的关系求解即可.【解答】解:(1)如图1中,过点A作AH⊥BC于H.∵AB=AC,AH⊥BC,∴BH=CH=4,∠B=∠C,∴tan∠B=tan∠C==,∴AH=3,AB=AC===5.∴当点P在BC上时,点P到A的最短距离为3.(2)如图1中,∵∠APQ=∠B,∴PQ∥BC,∴△APQ∽△ABC,∵PQ将△ABC的面积分成上下4:5,∴=()2=,∴=,∴AP=,∴PM=AP=AM=﹣2=.(3)当0≤x≤3时,如图1﹣1中,过点P作PJ⊥CA交CA的延长线于J.∵PQ∥BC,∴=,∠AQP=∠C,∴=,∴PQ=(x+2),∵sin∠AQP=sin∠C=,∴PJ=PQ•sin∠AQP=(x+2).当3≤x≤9时,如图2中,过点P作PJ⊥AC于J.同法可得PJ=PC•sin∠C=(11﹣x).(4)由题意点P的运动速度==单位长度/秒.当3<x≤9时,设CQ=y.∵∠APC=∠B+∠BAP=∠APQ+∠CPQ,∠APQ=∠B,∴∠BAP=∠CPQ,∵∠B=∠C,∴△ABP∽△PCQ,∴=,∴=,∴y=﹣(x﹣7)2+,∵﹣<0,∴x=7时,y有最大值,最大值=,∵AK=,∴CK=5﹣=<当y=时,=﹣(x﹣7)2+,解得x=7±,∴点K被扫描到的总时长=(+6﹣3)÷=23秒.方法二:①点P在AB上的时候,有11/4个单位长度都能扫描到点K;②在BN阶段,当x在3~5.5(即7﹣1.5)的过程,是能扫到K点的,在5.5~8.5(即7+1.5)的过程是扫不到点K的,但在8.5~9(即点M到N全部的路程)能扫到点K.所以扫到的时间是[(9﹣8.5)+(5.5﹣3)+]÷=23(秒).【点评】本题属于三角形综合题,考查了等腰三角形的性质,解直角三角形,相似三角形的判定和性质,二次函数的性质等知识,解题的关键是理解题意,学会构建二次函数解决CQ的最值问题,属于中考压轴题.。
2020年河北省中考数学试卷

2020年河北省中考数学试卷2020年河北省中考数学试卷一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)(2020?河北)如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条2.(3分)(2020?河北)墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+B.﹣C.×D.÷3.(3分)(2020?河北)对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解4.(3分)(2020?河北)如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同5.(3分)(2020?河北)如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A.9B.8C.7D.66.(3分)(2020?河北)如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a 为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求.下列正确的是()A.a,b均无限制B.a>0,bDE的长C.a有最小限制,b无限制D.a≥0,bDE的长7.(3分)(2020?河北)若a≠b,则下列分式化简正确的是()A.B.C.D.8.(3分)(2020?河北)在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是()A.四边形NPMQB.四边形NPMRC.四边形NHMQD.四边形NHMR9.(3分)(2020?河北)若8×10×12,则k=()A.12B.10C.8D.610.(3分)(2020?河北)如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形…”之间作补充,下列正确的是()A.嘉淇推理严谨,不必补充B.应补充:且AB=CDC.应补充:且AB∥CDD.应补充:且OA=OC11.(2分)(2020?河北)若k为正整数,则()A.k2kB.k2k+1C.2kkD.k2+k12.(2分)(2020?河北)如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是()A.从点P向北偏西45°走3km到达lB.公路l的走向是南偏西45°C.公路l的走向是北偏东45°D.从点P向北走3km后,再向西走3km到达l13.(2分)(2020?河北)已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n千米,则n可能为()A.5B.6C.5或6D.5或6或714.(2分)(2020?河北)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A 应有3个不同值15.(2分)(2020?河北)如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P 的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对16.(2分)(2020?河北)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A.1,4,5B.2,3,5C.3,4,5D.2,2,4二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.(3分)(2020?河北)已知:ab,则ab=.18.(3分)(2020?河北)正六边形的一个内角是正n边形一个外角的4倍,则n=.19.(6分)(2020?河北)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y(x<0)的图象为曲线L.(1)若L过点T1,则k=;(2)若L过点T4,则它必定还过另一点Tm,则m=;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有个.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(8分)(2020?河北)已知两个有理数:﹣9和5.(1)计算:;(2)若再添一个负整数m,且﹣9,5与m这三个数的平均数仍小于m,求m的值.21.(8分)(2020?河北)有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16,如图.如,第一次按键后,A,B两区分别显示:(1)从初始状态按2次后,分别求A,B两区显示的结果;(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能为负数吗?说明理由.22.(9分)(2020?河北)如图,点O为AB中点,分别延长OA到点C,OB到点D,使OC=OD.以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.(1)①求证:△AOE≌△POC;②写出∠l,∠2和∠C三者间的数量关系,并说明理由.(2)若OC=2OA=2,当∠C最大时,直接指出CP与小半圆的位置关系,并求此时S扇形EOD(答案保留π).23.(9分)(2020?河北)用承重指数w衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.(1)求W与x的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄.①求Q与x的函数关系式;②x为何值时,Q是W薄的3倍?[注:(1)及(2)中的①不必写x的取值范围]24.(10分)(2020?河北)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l''.x﹣10y﹣21(1)求直线l的解析式;(2)请在图上画出直线l''(不要求列表计算),并求直线l''被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.25.(10分)(2020?河北)如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.26.(12分)(2020?河北)如图1和图2,在△ABC中,AB=AC,BC=8,tanC.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK,请直接写出点K被扫描到的总时长.2020年河北省中考数学试卷参考答案与试题解析一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)(2020?河北)如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条【解答】解:在平面内,与已知直线垂直的直线有无数条,所以作已知直线的垂线,可作无数条.故选:D.2.(3分)(2020?河北)墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+B.﹣C.×D.÷【解答】解:∵x3x =x2(x≠0),∴覆盖的是:÷.故选:D.3.(3分)(2020?河北)对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解【解答】解:①x﹣3xy=x(1﹣3y),从左到右的变形是因式分解;②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形是整式的乘法,不是因式分解;所以①是因式分解,②是乘法运算.故选:C.4.(3分)(2020?河北)如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同【解答】解:从正面看,两个几何体均为第一层和第二层都是两个小正方形,故主视图相同;从左面看,两个几何体均为第一层和第二层都是两个小正方形,故左视图相同;从上面看,两个几何体均为第一层和第二层都是两个小正方形,故俯视图相同.故选:D.5.(3分)(2020?河北)如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A.9B.8C.7D.6【解答】解:由统计图可知,前三次的中位数是8,∵第四次又买的苹果单价是a元/千克,这四个单价的中位数恰好也是众数,∴a=8,故选:B.6.(3分)(2020?河北)如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求.下列正确的是()A.a,b均无限制B.a>0,bDE的长C.a有最小限制,b无限制D.a≥0,bDE的长【解答】解:以B为圆心画弧时,半径a必须大于0,分别以D,E为圆心,以b为半径画弧时,b必须大于DE,否则没有交点,故选:B.7.(3分)(2020?河北)若a≠b,则下列分式化简正确的是()A.B.C.D.【解答】解:∵a≠b,∴,故选项A错误;,故选项B错误;,故选项C错误;,故选项D正确;故选:D.8.(3分)(2020?河北)在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是()A.四边形NPMQB.四边形NPMRC.四边形NHMQD.四边形NHMR【解答】解:∵以点O为位似中心,∴点C对应点M,设网格中每个小方格的边长为1,则OC,OM2,OD,OB,OA,OR,OQ =2,OP2,OH3,ON2,∵2,∴点D对应点Q,点B对应点P,点A对应点N,∴以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故选:A.9.(3分)(2020?河北)若8×10×12,则k=()A.12B.10C.8D.6【解答】解:方程两边都乘以k,得(92﹣1)(112﹣1)=8×10×12k,∴(9+1)(9﹣1)(11+1)(11﹣1)=8×10×12k,∴80×120=8×10×12k,∴k=10.经检验k=10是原方程的解.故选:B.10.(3分)(2020?河北)如图,将△ABC绕边AC 的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形…”之间作补充,下列正确的是()A.嘉淇推理严谨,不必补充B.应补充:且AB=CDC.应补充:且AB∥CDD.应补充:且OA=OC【解答】解:∵CB=AD,AB=CD,∴四边形ABCD是平行四边形,故选:B.11.(2分)(2020?河北)若k为正整数,则()A.k2kB.k2k+1C.2kkD.k2+k【解答】解:((k?k)k=(k2)k=k2k,故选:A.12.(2分)(2020?河北)如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是()A.从点P向北偏西45°走3km到达lB.公路l的走向是南偏西45°C.公路l的走向是北偏东45°D.从点P向北走3km后,再向西走3km到达l【解答】解:如图,由题意可得△PAB是腰长6km的等腰直角三角形,则AB=6km,则PC=3km,则从点P向北偏西45°走3km到达l,选项A错误;则公路l的走向是南偏西45°或北偏东45°,选项B,C正确;则从点P向北走3km后,再向西走3km到达l,选项D正确.故选:A.13.(2分)(2020?河北)已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n千米,则n可能为()A.5B.6C.5或6D.5或6或7【解答】解:当t=1时,光传播的距离为1×300000=300000=3×105(千米),则n=5;当t=10时,光传播的距离为10×300000=3000000=3×106(千米),则n=6.因为1≤t≤10,所以n可能为5或6,故选:C.14.(2分)(2020?河北)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A 应有3个不同值【解答】解:如图所示:∠A还应有另一个不同的值∠A′与∠A互补.故∠A′=180°﹣65°=115°.故选:A.15.(2分)(2020?河北)如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对【解答】解:y=x(4﹣x)=﹣x2+4x=﹣(x﹣2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为4,∴甲、乙的说法正确;若b=3,则抛物线上纵坐标为3的点有2个,∴丙的说法不正确;故选:C.16.(2分)(2020?河北)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A.1,4,5B.2,3,5C.3,4,5D.2,2,4【解答】解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是,当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是;当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是,∵,∴所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5,故选:B.二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.(3分)(2020?河北)已知:ab,则ab=6.【解答】解:原式=3ab,故a=3,b=2,则ab=6.故答案为:6.18.(3分)(2020?河北)正六边形的一个内角是正n边形一个外角的4倍,则n=12.【解答】解:正六边形的一个内角为:,∵正六边形的一个内角是正n边形一个外角的4倍,∴正n边形一个外角为:120°÷4=30°,∴n=360°÷30°=12.故答案为:12.19.(6分)(2020?河北)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作Tm(m为1~8的整数).函数y(x<0)的图象为曲线L.(1)若L过点T1,则k=﹣16;(2)若L过点T4,则它必定还过另一点Tm,则m=5;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有7个.【解答】解:(1)∵每个台阶的高和宽分别是1和2,∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),∵L过点T1,∴k=﹣16×1=﹣16,故答案为:﹣16;(2)∵L过点T4,∴k=﹣10×4=﹣40,∴反比例函数解析式为:y,当x=﹣8时,y=5,∴T5在反比例函数图象上,∴m=5,故答案为:5;(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k =﹣14×2=﹣28,若曲线L过点T3(﹣12,3),T5(﹣8,5)时,k=﹣12×3=﹣36,若曲线L过点T4(﹣10,4),T5(﹣8,5)时,k=﹣40,∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,∴﹣36<k<﹣28,∴整数k=﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个,∴答案为:7.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(8分)(2020?河北)已知两个有理数:﹣9和5.(1)计算:;(2)若再添一个负整数m,且﹣9,5与m这三个数的平均数仍小于m,求m的值.【解答】解:(1)2;(2)根据题意得,m,∴﹣4+m<3m,∴m﹣3m<4,∴﹣2m<4,∴m>﹣2,∵m是负整数,∴m=﹣1.21.(8分)(2020?河北)有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16,如图.如,第一次按键后,A,B两区分别显示:(1)从初始状态按2次后,分别求A,B两区显示的结果;(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能为负数吗?说明理由.【解答】解:(1)A区显示的结果为:25+2a2,B区显示的结果为:﹣16﹣6a;(2)这个和不能为负数,理由:根据题意得,25+4a2+(﹣16﹣12a)=25+4a2﹣16﹣12a=4a2﹣12a+9;∵(2a﹣3)2≥0,∴这个和不能为负数.22.(9分)(2020?河北)如图,点O为AB中点,分别延长OA到点C,OB到点D,使OC=OD.以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.(1)①求证:△AOE≌△POC;②写出∠l,∠2和∠C三者间的数量关系,并说明理由.(2)若OC=2OA=2,当∠C最大时,直接指出CP 与小半圆的位置关系,并求此时S扇形EOD(答案保留π).【解答】解:(1)①在△AOE和△POC中,,∴△AOE≌△POC(SAS);②∵△AOE≌△POC,∴∠E=∠C,∵∠1+∠E=∠2,∴∠1+∠C=∠2;(2)当∠C最大时,CP与小半圆相切,如图,∵OC=2OA=2,∴OC=2OP,∵CP与小半圆相切,∴∠OPC=90°,∴∠OCP=30°,∴∠DOE=∠OPC+∠OCP=120°,∴.23.(9分)(2020?河北)用承重指数w衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.(1)求W与x的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄.①求Q与x的函数关系式;②x为何值时,Q是W薄的3倍?[注:(1)及(2)中的①不必写x的取值范围]【解答】解:(1)设W=kx2(k≠0).∵当x=3时,W=3,∴3=9k,解得k,∴W与x的函数关系式为Wx2;(2)①设薄板的厚度为x厘米,则厚板的厚度为(6﹣x)厘米,∴Q=W厚﹣W薄(6﹣x)2x2=﹣4x+12,即Q与x的函数关系式为Q=﹣4x+12;②∵Q是W薄的3倍,∴﹣4x+12=3x2,整理得,x2+4x﹣12=0,解得,x1=2,x2=﹣6(不合题意舍去),故x为2时,Q是W薄的3倍.24.(10分)(2020?河北)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l''.x﹣10y﹣21(1)求直线l的解析式;(2)请在图上画出直线l''(不要求列表计算),并求直线l''被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.【解答】解:(1)∵直线l:y=kx+b中,当x=﹣1时,y=﹣2;当x=0时,y=1,∴,解得,∴直线l的解析式为y=3x+1;∴直线l′的解析式为y=x+3;(2)如图,解得,∴两直线的交点为(1,4),∵直线l′:y=x+3与y轴的交点为(0,3),∴直线l''被直线l和y轴所截线段的长为:;(3)把y=a代入y=3x+1得,a=3x+1,解得x;把y=a代入y=x+3得,a=x+3,解得x=a﹣3;当a﹣30时,a,当(a﹣3+0)时,a=7,当(0)=a﹣3时,a,∴直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,则a的值为或7或.25.(10分)(2020?河北)如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.【解答】解:(1)∵经过第一次移动游戏,甲的位置停留在正半轴上,∴必须甲对乙错,因为一共有四种情形,都对或都错,甲对乙错,甲错乙对,∴P甲对乙错.(2)由题意m=5﹣4n+2(10﹣n)=25﹣6n.n=4时,离原点最近.(3)不妨设甲连续k次正确后两人相距2个单位,则有|8+2k﹣4k|=2,解得k=3或5.如果k次中,有1次两人都对都错,则有|6+2(k﹣1)﹣4(k﹣1)|=2,解得k=3或5,如果k次中,有2次两人都对都错,则有|4+2(k﹣2)﹣4(k﹣2)|=2,解得k=3或5,…,综上所述,满足条件的k的值为3或5.26.(12分)(2020?河北)如图1和图2,在△ABC中,AB=AC,BC=8,tanC.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK,请直接写出点K被扫描到的总时长.【解答】解:(1)如图1中,过点A作AH⊥BC于H.∵AB=AC,AH⊥BC,∴BH=CH=4,∠B=∠C,∴tan∠B=tan∠C,∴AH=3,AB=AC5.∴当点P在BC上时,点P到A的最短距离为3.(2)如图1中,∵∠APQ=∠B,∴PQ∥BC,∴△APQ∽△ABC,∵PQ将△ABC的面积分成上下4:5,∴()2,∴,∴AP,∴PM=AP=AM2.(3)当0≤x≤3时,如图1﹣1中,过点P作PJ⊥CA交CA的延长线于J.∵PQ∥BC,∴,∠AQP=∠C,∴,∴PQ(x+2),∵sin∠AQP=sin∠C,∴PJ=PQ?sin∠AQP(x+2).当3≤x≤9时,如图2中,过点P作PJ⊥AC于J.同法可得PJ=PC?sin∠C(11﹣x).(4)由题意点P的运动速度单位长度/秒.当3<x≤9时,设CQ=y.∵∠APC =∠B+∠BAP=∠APQ+∠CPQ,∠APQ=∠B,∴∠BAP=∠CPQ,∵∠B=∠C,∴△ABP∽△PCQ,∴,∴,∴y(x﹣7)2,∵0,∴x=7时,y有最大值,最大值,∵AK,∴CK =5当y时,(x﹣7)2,解得x=7±,∴点K被扫描到的总时长=(6﹣3)23秒.方法二:①点P 在AB上的时候,有11/4个单位长度都能扫描到点K;②在BN阶段,当x在3~5.5(即7﹣1.5)的过程,是能扫到K点的,在5.5~8.5(即7+1.5)的过程是扫不到点K的,但在8.5~9(即点M到N 全部的路程)能扫到点K.所以扫到的时间是[(9﹣8.5)+(5.5﹣3)]23(秒).第26页(共26页)。
2020河北省中考数学试题(解析版)

【点睛】本题考查了方位角问题及等腰直角三角形、中位线等相关知识点,方向角一般以观测者的位置为中心,所以观测者不同,方向就正好相反,但角度不变.
13.已知光速为300000千米秒,光经过 秒( )传播的距离用科学记数法表示为 千米,则 可能为()
A.5B.6C.5或6D.5或6或7
【答案】C
8.在如图所示的网格中,以点 为位似中心,四边形 的位似图形是()
A.四边形 B.四边形
C.四边形 D.四边形
【答案】A
【解析】
【分析】
以O为位似中心,作四边形ABCD的位似图形,根据图像可判断出答案.
【详解】解:如图所示,四边形 的位似图形是四边形 .
故选:A
【点睛】此题考查了位似图形的作法,画位似图形的一般步骤为:①确定位似中心;②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,确定位似图形.
2020年河北省初中毕业生升学文化课考试
数学试卷
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,在平面内作已知直线 的垂线,可作垂线的条数有()
A.0条B.1条C.2条D.无数条
【答案】D
【解析】
【分析】
∴正n边形的外角为30°,
∴正n边形的边数为:360°÷30°=12.
故答案为:12.
【点睛】本题考查了正多边形的外角与内角的知识,熟练掌握正多边形的内角和和外角和定理是解决此类题目的关键.
(2020年河北)19.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作 ( 为1~8的整数).函数 ( )的图象为曲线 .
2020年河北省中考数学试题(含答案)

2020年河北省初中毕业生升学文化课考试数 学 试 卷说明:1本卷共四大题,27小题,全卷满分120分,考试时间为150分钟。
2,本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分。
本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题. 本试卷满分为120分,考试时间为120分钟.卷Ⅰ(选择题,共30分)注意事项:1.答卷Ⅰ前,考生务必将自己的姓名、准考证号、科目填涂在答题卡上.考试结束,监考人员将试卷和答题卡一并收回.2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.答在试卷上无效.一、选择题(本大题共12个小题,1~6小题,每小题2分;7~12小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列各数中,为负数的是( )A .0 B.2- C.1 D.122.计算3()ab 的结果是( )A .3ab B.3a b C.33a b D.3ab 3.图1中几何体的主视图是( )4.下列各数中,为不等式组23040x x ->⎧⎨-<⎩解的是( )A .1- B.0 C.2 D.45.如图2,CD 是O ⊙的直径,AB 是弦(不是直径),AB CD ⊥于点E ,则下列结论正确的是( )A .AE BE > B.AD BC = C.12D AEC =∠∠ D.ADE CBE △∽△ 6.掷一枚质地均匀的硬币10次,下列说法正确的是( ) A.每2次必有1次正面向上 B .可能有5次正面向上 C .必有5次正面向上 D .不可能有10次正面向上7.如图3,点C 在AOB ∠的OB 边上,用尺规作出了CN OA ∥,作图痕迹中,FG 是( )A .以点C 为圆心,OD 为半径的弧 B.以点C 为圆心,DM 为半径弧C.以点E 为圆心,OD 为半径的弧 D.以点E 为圆心,DM 为半径的 8.用配方法解方程2410x x ++=,配方后的方程是( )A .2(2)3x += B.2(2)3x -= C.2(2)5x -= D.2(2)5x += 9.如图4,在ABCD 中,70A ∠=︒,将ABCD 折叠,使点D C 、分别落在点F 、E处(点,F E 都在AB 所在的直线上),折痕为MN ,则AMF ∠等于( )A .70 B.40 C.30 D.20 10.化简22111x x ÷--的结果是( ) A .21x - B.321x - C.21x + D.2(1)x +11.如图5,两个正方形的面积分别为16,9,两阴影部分的面积分别为a ,b ()a b >,则()a b -等于( )A .7 B.6 C.5 D.412.如图6,抛物线21(2)3y a x =+-与221(3)12y x =-+交于点(13)A ,,过点A 作x 轴的平行线,分别交两条抛物线于点B C ,.则以下结论: ①无论x 取何值,2y 的值总是正数. ②1a =.③当0x =时,214y y -=.④23AB AC =.其中正确结论是( )A .①② B.②③ C.③④ D.①④2020年河北省初中毕业生升学文化课考试数 学 试 卷 卷Ⅱ(非选择题,共9 0分)注意事项:1.答卷Ⅱ前,将密封线左侧的项目填写清楚.2.答卷Ⅱ时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.二、填空题(本大题共6个小题,每小题3分,共18分.把答案写在题中横线上) 13.5-的相反数是 .14.如图7,AB CD ,相交于点O ,AC CD ⊥于点C ,若BOD ∠=38,则A ∠等于 . 15.已知1y x =-,则2()()1x y y x -+-+的值为 .16.在12⨯的正方形网格格点上放三枚棋子,按图8所示的位置已放置了两枚棋子,若第三枚棋子随机放在其他格点上,则以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为 .17.某数学活动小组的20位同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己顺序数的倒数加1,第1位同学报111⎛⎫+ ⎪⎝⎭,第2位同学报112⎛⎫+⎪⎝⎭,第3位同学报113⎛⎫+⎪⎝⎭……这样得到的20个数的积为 .18.用4个全等的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图91-,用n 个全等的正六边形按这种方式拼接,如图92-,若围成一圈后中间也形成一个正多边形,则n 的值为 .三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤) 19.(本小题满分8分)计算:021153)6(1)32⎛⎫--+⨯-+-⎪⎝⎭. 20.(本小题满分8分)如图10,某市A B ,两地之间有两条公路,一条是市区公路AB ,另一条是外环公路AD DC CB --.这两条公路转成等腰梯形ABCD ,其中DC AB AB AD DC ∥,::=10:5:2.(1) 求外环公路总长和市区公路长的比;(2) 某人驾车从A 地出发,沿市区公路去B 地,平均速度是40km/h ,返回时沿外环公路行驶,平均速度是80km/h ,结果比去时少用了110h ,求市区公路的长.21.(本小题满分8分)某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了如下尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).=__________;(1)a ___________,x乙(2)请完成图11中表示乙成绩变化情况的折线;(3)①观察图11,可看出______的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.②请你从平均数和方差的角度分析,谁将被选中.22.(本小题满分8分)如图12,四边形ABCD 是平行四边形,点(10)(31)(33)A B C ,,,,,.反比例函数(0)my x x=>的图象经过点D ,点P 是一次函数33(0)y kx k k =+-≠的图象与该反比例函数图象的一个公共点.(1)求反比例函数的解析式;(2)通过计算,说明一次函数33(0)y kx k k =+-≠的图象一定过点C ;(3)对于一次函数33(0)y kx k k =+-≠,当y x 随的增大而增大时,确定点P 横坐标的取值范围(不必写出过程). 23.(本小题满分9分)如图131-,点E 是线段BC 的中点,分别以B C ,为直角顶点的EAB EDC △和△均是等腰直角三角形,且在BC 的同侧.(1)AE ED 和的数量关系为___________,AE ED 和的位置关系为___________;(2)在图131-中,以点E 为位似中心,作EGF △与EAB △位似,点H 是BC 所在直线上的一点,连接GH HD ,,分别得到了图132-和图133-;①在图132-中,点F 在BE 上,EGF EAB △与△的相似比是1:2,H 是EC 的中点.求证:.GH HD GH HD =⊥,②在图133-中,点F 在BE 的延长线上,EGF EAB △与△的相似比是k :1,若2BC =,请直接写出CH 的长为多少时,恰好使得GH HD GH HD =⊥且(用含k 的代数式表示). 24.(本小题满分9分)某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长(单位:cm )在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:2cm )成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长成正比例,在营销过程中得到了表格中的数据.(1) 求一张薄板的出厂价与边长之间满足的函数关系式; (2) 已知出厂一张边长为40cm 的薄板,获得的利润是26元(利润=出厂价-成本价).① 求一张薄板的利润与边长之间满足的函数关系式;② 当边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?参考公式:抛物线2(0)y ax bx c a =++≠的顶点坐标是2424b ac b a a ⎛⎫-- ⎪⎝⎭,.25.(本小题满分10分)如图14,(50)(30).A B --,,,点C 在y 轴的正半轴上,CBO ∠=45,CD AB ∥,90CDA =∠.点P 从点(40)Q ,出发,沿x 轴向左以每秒1个单位长的速度运动,运动时间为t 秒.(1) 求点C 的坐标;(2) 当15BCP =∠时,求t 的值;(3) 以点P 为圆心,PC 为半径的P ⊙随点P 的运动而变化,当P ⊙与四边形ABCD 的边(或边所在的直线)相切时,求t 的值.26.(本小题满分12分)如图151-和图152-,在ABC △中,51314cos .13AB BC ABC ===,,∠ 探究在如图151-,AH BC ⊥于点H ,则AH =_______,AC =_______, ABC △的面积ABC S △=___________.拓展如图152-,点D 在AC 上(可与点A C ,重合),分别过点A C ,作直线BD 的垂线,垂足为E F ,.设.BD x AE m CF n ===,,(当点D 与点A 重合时,我们认为ABC S △=0. (1)用含x m ,或n 的代数式表示ABD S △及CBD S △;(2)求()m n +与x 的函数关系式,并求()m n +的最大值和最小值.(3)对给定的一个x 值,有时只能确定唯一的点D ,指出这样的x 的取值范围. 发现请你确定一条直线,使得A B C ,,三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.2020年河北省初中毕业生升学文化课考试数学试题参考答案二、填空题(每小题3分,满分18分) 13.5 14.52 15.1 16.3417.21 18.6 三、解答题(本大题共8小题,共72分)19.解:021153)6(1)32⎛⎫--+⨯-+-⎪⎝⎭=51(23)1-+-+ ··········································································· 5分 =4. ····························································································· 8分 20.解:(1)设10AB x =km ,则5AD x =km ,2CD x =km . 四边形ABCD 是等腰梯形,DC AB ∥,5.BC AD x ∴==12.AD DC CB x ∴++=∴外环公路总长和市区公路长的比为12x x :10=6:5. ··········································· 3分(2)由(1)可知,市区公路物长为10x km ,外环公路的总长为12x km .由题意,得10121408010x x =+. ············································································· 6分 解这个方程,得1x =.1010x ∴=.答:市区公路的长为10km. ··············································································· 8分 21.解:(1)4,6 ··························································································· 2分 (2)如图1 ··································································································· 3分(3)①乙 ····································································································· 4分2222221[(76)(56)(76)(46)(76)]5S =-+-+-+-+-乙=1.6. ································ 5分 由于22S S <乙甲,所以上述判断正确. ····································································· 6分②因为两人成绩的平均水平(平均数)相同,乙的成绩比甲稳定,所以乙将被选中. ···· 8分 22.解:(1)由题意,2AD BC ==,故点D 的坐标为(1,2). ··························· 2分 反比例函数mx的图象经过点(12)D ,, 2. 2.1mm ∴=∴= ∴反比例函数的解析式为2.y x= ······································································· 4分(2)当3x =时,333 3.y k k =+-=∴一次函数33(0)y kx k k =+-≠的图象一定过点C . ········································· 6分(3)设点P 的横坐标为23.3a a <<, ································································ 8分 (注:对(3)中的取值范围,其他正确写法,均相应给分)23.解:(1)AE ED AE ED =⊥,. ······························································ 2分 (2)①证明:由题意,90.B C AB BE EC DC =====∠∠,EGF EAB △与△位似且相似比是1:2,1190.22GFE B GF AB EF EB ∴====∠∠,, GFE C ∴=∠∠.12EH HC EC ==,111.222GF HC FH FE EH EB EC BC EC CD ∴==+=+===, HGF DHC ∴△≌△. ···················································································· 5分 .GH HD GHF HDC ∴==,∠∠又9090HDC DHC GHF DHC +=∴+=∠∠,∠∠..GHD ∴∠=90GH HD ∴⊥. ······························································································· 7分 ②CH 的长为k . ···························································································· 9分24.解:(1)设一张薄板的边长为x cm ,它的出厂价为y 元,基础价为n 元,浮动价为kx 元,则y kx n =+. ·························································································· 2分由表格中的数据,得50207030.k n k n =+⎧⎨=+⎩, 解得210.k n =⎧⎨=⎩,所以210.y x =+ ··························································································· 4分 (2)①设一张薄板的利润为P 元,它的成本价为2mx 元,由题意,得22210.P y mx x mx =-=+- ·········································································· 5分将4026x P ==,代入2210P x mx =+-中,得2262401040m =⨯+-⨯.解得1.25m = 所以21210.25P x x =-++ ············································································· 7分 ②因为1025a =-<,所以,当22512225b x a =-=-=⎛⎫⨯- ⎪⎝⎭(在5~50之间)时,221410242535.14425ac b P a ⎛⎫⨯-⨯- ⎪-⎝⎭===⎛⎫⨯- ⎪⎝⎭最大值即出厂一张边长为25cm 的薄板,获得的利润最大,最大利润是35元. ······················ 9分 (注:边长的取值范围不作为扣分点) 25.解:(1)45BCO CBO ==∠∠,3.OC OB ∴==又点C 在y 轴的正半轴上,∴点C 的坐标为(0,3) ················································································ 2分(2)当点P 在点B 右侧时,如图2. 若15BCP =∠,得30PCO =∠.故tan 303OP OC ==4t =······················································ 4分 当点P 在点B 左侧时,如图3,由15BCP =∠, 得60PCO =∠,故tan 6033PO OC ==此时4t =+t ∴的值为4+4+·········································································· 6分(3)由题意知,若P ⊙与四边形ABCD 的边相切,有以下三种情况:①当P ⊙与BC 相切于点C 时,有90BCP =∠,从而45OCP =∠得到3OP =. 此时1t =. ···································································································· 7分 ②当P ⊙与CD 相切于点C 时,有PC CD ⊥,即点P 与点O 重合,此时4t =. ···································································································· 8分 ③当P ⊙与AD 相切时,由题意,90DAO =∠,∴点A 为切点,如图4.22222(9)(4)PC PA t PO t ==-=-,.于是222(9)(4)3t t -=-+.解处 5.6t =.t ∴的值为1或4或5.6. ················································································ 10分26.解:探究:12,15,84 ············································································· 3分 拓展:(1)由三角形面积公式,得ABD CBD S mx S nx △△11=,=22. ···························· 4分 (2)由(1)得22ABD CBD S Sm n x x==△△,, 22168ABD CBD S S m n x x x∴+=+=△△. ································································· 5分 由于AC 边上的高为22845615155ABC S ⨯==△, x ∴的取值范围是56145x ≤≤.()m n +随x 的增大而减小, ∴当565x =时,()m n +的最大值为15. ····························································· 7分 当14x =时,()m n +的最小值为12. ································································· 8分 (3)x 的取值范围是565x =或13x <≤14. ····················································· 10分 发现:AC 所在的直线, ·············································································· 11分 最小值为565. ······························································································ 12分 友情提示:一、认真对待每一次考试。
2020年河北省中考数学考试试题及解析

一、选择题(每小题3分,共30分)1. 已知集合A={x|x>2}, B={x|x≤3},则A∩B=()A. {x|x>3}B. {x|2<x≤3}C. {x|x≤2}D. {x|x>2}答案:B. {x|2<x≤3}解析:A∩B表示A和B的交集,即A和B 中共同满足的元素,即2<x≤3,故选B. {x|2<x≤3}。
2. 已知函数f(x)=2sin2x,则f(π/6)的值为()A. 2B. -2C. 1D. -1答案:D. -1解析:f(x)=2sin2x,当x=π/6时,f(π/6)=2sin2π/6=2sinπ/3=2(-1/2)=-1,故选D. -1。
3. 已知椭圆x2/25+y2/9=1的离心率为5/4,则该椭圆的长轴长为()A. 5B. 4C. 9D. 25答案:A. 5解析:椭圆的离心率e=c/a,其中c为短轴长,a为长轴长,已知椭圆x2/25+y2/9=1的离心率为5/4,则c/a=5/4,即a=4c,由题意知c=9,故a=4c=4×9=36,即长轴长为36,故选A. 5。
4. 已知等比数列{an}的公比为q,且a1=2,则a2a3=()A. 2qB. 2q2C. 4qD. 4q2答案:B. 2q2解析:等比数列{an}的公比为q,且a1=2,则a2=2q,a3=2q2,故a2a3=2q×2q2=2q2,故选B. 2q2。
5. 已知抛物线y2=4x的焦点为F,点P(2,2)在抛物线上,则点P到焦点F的距离为()A. 2B. 4C. 8D. 16答案:A. 2解析:抛物线y2=4x的焦点为F,点P(2,2)在抛物线上,则PF的距离为|PF|=√(x2-x1)2+(y2-y1)2=√(2-0)2+(2-0)2=2,故选A. 2。
二、填空题(每小题3分,共15分)6. 已知等差数列{an}中,a1=6,a4=18,则a7=___答案:30解析:等差数列{an}中,a1=6,a4=18,由等差数列的性质可知,公差d=a4-a1=18-6=12,故a7=a1+(7-1)d=6+6×12=30,即a7=30。
2020年河北省中考数学试题及参考答案(word解析版)
2020年河北省初中学业毕业生升学文化课考试数学试卷(总分120分,考试时间120分钟)一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条2.墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+ B.﹣C.×D.÷3.对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解4.如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同5.如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A.9 B.8C.7 D.66.如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求.下列正确的是()A.a,b均无限制B.a>0,b>DE的长C.a有最小限制,b无限制D.a≥0,b<DE的长7.若a≠b,则下列分式化简正确的是()A.=B.=C.=D.=8.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是()A.四边形NPMQ B.四边形NPMRC.四边形NHMQ D.四边形NHMR9.若=8×10×12,则k=()A.12 B.10 C.8 D.610.如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC 构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形…”之间作补充,下列正确的是()A.嘉淇推理严谨,不必补充B.应补充:且AB=CDC.应补充:且AB∥CD D.应补充:且OA=OC11.若k为正整数,则=()A.k2k B.k2k+1C.2k k D.k2+k12.如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是()A.从点P向北偏西45°走3km到达lB.公路l的走向是南偏西45°C.公路l的走向是北偏东45°D.从点P向北走3km后,再向西走3km到达l13.已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n 千米,则n可能为()A.5 B.6 C.5或6 D.5或6或714.有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC 以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A应有3个不同值15.如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对16.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A.1,4,5 B.2,3,5C.3,4,5 D.2,2,4二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.已知:﹣=a﹣=b,则ab=.18.正六边形的一个内角是正n边形一个外角的4倍,则n=.19.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作T m(m为1~8的整数).函数y=(x<0)的图象为曲线L.(1)若L过点T1,则k=;(2)若L过点T4,则它必定还过另一点T m,则m=;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有个.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(本小题满分8分)已知两个有理数:﹣9和5.(1)计算:;(2)若再添一个负整数m,且﹣9,5与m这三个数的平均数仍小于m,求m的值.21.(本小题满分8分)有一电脑程序:每按一次按键,屏幕的A 区就会自动加上a 2,同时B 区就会自动减去3a ,且均显示化简后的结果.已知A ,B 两区初始显示的分别是25和﹣16,如图.如,第一次按键后,A ,B 两区分别显示:(1)从初始状态按2次后,分别求A ,B 两区显示的结果;(2)从初始状态按4次后,计算A ,B 两区代数式的和,请判断这个和能为负数吗?说明理由. 22.(本小题满分9分)如图,点O 为AB 中点,分别延长OA 到点C ,OB 到点D ,使OC =OD .以点O 为圆心,分别以OA ,OC 为半径在CD 上方作两个半圆.点P 为小半圆上任一点(不与点A ,B 重合),连接OP 并延长交大半圆于点E ,连接AE ,CP . (1)①求证:△AOE ≌△POC ;②写出∠l ,∠2和∠C 三者间的数量关系,并说明理由.(2)若OC =2OA =2,当∠C 最大时,直接指出CP 与小半圆的位置关系,并求此时S 扇形EOD (答案保留π).23.(本小题满分9分)用承重指数w 衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W 与木板厚度x (厘米)的平方成正比,当x =3时,W =3.(1)求W 与x 的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x (厘米),Q =W 厚﹣W 薄. ①求Q 与x 的函数关系式;②x 为何值时,Q 是W 薄的3倍?[注:(1)及(2)中的①不必写x 的取值范围] 24.(本小题满分10分)表格中的两组对应值满足一次函数y =kx+b ,现画出了它的图象为直线l ,如图.而某同学为观察k ,b 对图象的影响,将上面函数中的k 与b 交换位置后得另一个一次函数,设其图象为直线l'.x ﹣1 0 y﹣21(1)求直线l的解析式;(2)请在图上画出直线l'(不要求列表计算),并求直线l'被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.25.(本小题满分10分)如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k 的值.26.(本小题满分12分)如图1和图2,在△ABC中,AB=AC,BC=8,tanC=.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P到直线AC的距离(用含x 的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P 从M到B再到N共用时36秒.若AK=,请直接写出点K被扫描到的总时长.答案与解析一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条【知识考点】垂线.【专题】线段、角、相交线与平行线;推理能力.【思路分析】根据垂直、垂线的定义,可直接得结论.【解答过程】解:在平面内,与已知直线垂直的直线有无数条,所以作已知直线的垂线,可作无数条.故选:D.【总结归纳】本题考查了垂直和垂线的定义.掌握垂线的定义是解决本题的关键.2.墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+ B.﹣C.×D.÷【知识考点】同底数幂的除法.【专题】整式;符号意识.【思路分析】直接利用同底数幂的除法运算法则计算得出答案.【解答过程】解:∵x3x=x2(x≠0),∴覆盖的是:÷.故选:D.【总结归纳】此题主要考查了同底数幂的除法运算,正确掌握相关运算法则是解题关键.3.对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解【知识考点】多项式乘多项式;因式分解的意义;因式分解﹣提公因式法.【专题】整式;运算能力.【思路分析】根据因式分解的定义(把一个多项式化成几个整式积的形式,叫因式分解,也叫分解因式)判断即可.【解答过程】解:①x﹣3xy=x(1﹣3y),从左到右的变形是因式分解;②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形是整式的乘法,不是因式分解;所以①是因式分解,②是乘法运算.故选:C.【总结归纳】此题考查了因式分解.解题的关键是掌握因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解.4.如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同【知识考点】简单组合体的三视图.【专题】投影与视图;几何直观.【思路分析】根据主视图是从物体的正面看得到的视图,俯视图是从上面看得到的图形,左视图是左边看得到的图形,可得答案.【解答过程】解:从正面看,两个几何体均为第一层和第二层都是两个小正方形,故主视图相同;从左面看,两个几何体均为第一层和第二层都是两个小正方形,故左视图相同;从上面看,两个几何体均为第一层和第二层都是两个小正方形,故俯视图相同.故选:D.【总结归纳】本题考查了简单组合体的三视图,利用三视图的意义是解题关键.5.如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A.9 B.8C.7 D.6【知识考点】条形统计图;中位数;众数.【专题】统计与概率;数据分析观念.【思路分析】根据统计图中的数据和题意,可以得到a的值,本题得以解决.【解答过程】解:由统计图可知,前三次的中位数是8,∵第四次又买的苹果单价是a元/千克,这四个单价的中位数恰好也是众数,∴a=8,故选:B.【总结归纳】本题考查条形统计图、中位数、众数,解答本题的关键是明确题意,利用数形结合的思想解答.6.如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求.下列正确的是()A.a,b均无限制B.a>0,b>DE的长C.a有最小限制,b无限制D.a≥0,b<DE的长【知识考点】作图—基本作图.【专题】作图题;应用意识.【思路分析】根据角平分线的画法判断即可.【解答过程】解:以B为圆心画弧时,半径a必须大于0,分别以D,E为圆心,以b为半径画弧时,b必须大于DE,否则没有交点,故选:B.【总结归纳】本题考查作图﹣基本作图,解题的关键是熟练掌握五种基本作图,属于中考常考题型.7.若a≠b,则下列分式化简正确的是()A.=B.=C.=D.=【知识考点】分式的基本性质.【专题】分式;运算能力.【思路分析】根据a≠b,可以判断各个选项中的式子是否正确,从而可以解答本题.【解答过程】解:∵a≠b,∴,故选项A错误;,故选项B错误;,故选项C错误;,故选项D正确;故选:D.【总结归纳】本题考查分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变.熟练掌握分式的基本性质是解题的关键.8.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是()A.四边形NPMQ B.四边形NPMRC.四边形NHMQ D.四边形NHMR【知识考点】位似变换.【专题】平移、旋转与对称;推理能力.【思路分析】由以点O为位似中心,确定出点C对应点M,设网格中每个小方格的边长为1,则OC=,OM=2,OD=,OB=,OA=,OR=,OQ=2,OP=2,OH=3,ON=2,由=2,得点D对应点Q,点B对应点P,点A对应点N,即可得出结果.【解答过程】解:∵以点O为位似中心,∴点C对应点M,设网格中每个小方格的边长为1,则OC==,OM==2,OD=,OB==,OA==,OR==,OQ=2,OP==2,OH==3,ON==2,∵==2,∴点D对应点Q,点B对应点P,点A对应点N,∴以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故选:A.【总结归纳】本题考查了位似变换、等腰直角三角形的性质、勾股定理等知识;熟练掌握位似中心,找出点C对应点M是解题的关键.9.若=8×10×12,则k=()A.12 B.10 C.8 D.6【知识考点】平方差公式;因式分解﹣运用公式法.【专题】整式;分式方程及应用;运算能力.【思路分析】根据平方差公式和分式方程的解法,即可得到k的值.【解答过程】解:方程两边都乘以k,得(92﹣1)(112﹣1)=8×10×12k,∴(9+1)(9﹣1)(11+1)(11﹣1)=8×10×12k,∴80×120=8×10×12k,∴k=10.经检验k=10是原方程的解.故选:B.【总结归纳】此题考查了平方差公式和解分式方程,熟练掌握平方差公式和解分式方程的方法是解本题的关键.10.如图,将△ABC绕边AC的中点O顺时针旋转180°.嘉淇发现,旋转后的△CDA与△ABC 构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB=AD,”和“∴四边形…”之间作补充,下列正确的是()A.嘉淇推理严谨,不必补充B.应补充:且AB=CDC.应补充:且AB∥CD D.应补充:且OA=OC【知识考点】平行四边形的判定;旋转的性质.【专题】多边形与平行四边形;平移、旋转与对称;应用意识.【思路分析】根据两组对边分别相等的四边形是平行四边形判定即可.【解答过程】解:∵CB=AD,AB=CD,∴四边形ABCD是平行四边形,故选:B.【总结归纳】本题考查平行四边形的判定,旋转变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.11.若k为正整数,则=()A.k2k B.k2k+1C.2k k D.k2+k【知识考点】幂的乘方与积的乘方.【专题】整式;运算能力.【思路分析】根据幂的乘方的运算法则:底数不变,指数相乘解答即可.【解答过程】解:=((k•k)k=(k2)k=k2k,故选:A.【总结归纳】本题考查了幂的乘方.解题的关键掌握幂的乘方的运算法则:底数不变,指数相乘.12.如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是()A.从点P向北偏西45°走3km到达lB.公路l的走向是南偏西45°C.公路l的走向是北偏东45°D.从点P向北走3km后,再向西走3km到达l【知识考点】方向角;勾股定理的应用.【专题】等腰三角形与直角三角形;几何直观;应用意识.【思路分析】先作出图形,根据勾股定理和等腰直角三角形的性质即可求解.【解答过程】解:如图,由题意可得△PAB是腰长6km的等腰直角三角形,则AB=6km,则PC=3km,则从点P向北偏西45°走3km到达l,选项A错误;则公路l的走向是南偏西45°或北偏东45°,选项B,C正确;则从点P向北走3km后,再向西走3km到达l,选项D正确.故选:A.【总结归纳】本题考查的是勾股定理的应用,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.13.已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n 千米,则n可能为()A.5 B.6 C.5或6 D.5或6或7【知识考点】科学记数法—表示较大的数.【专题】实数;数感.【思路分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.【解答过程】解:当t=1时,光传播的距离为1×300000=300000=3×105(千米),则n=5;当t=10时,光传播的距离为10×300000=3000000=3×106(千米),则n=6.因为1≤t≤10,所以n可能为5或6,故选:C.【总结归纳】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.14.有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC 以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A应有3个不同值【知识考点】三角形的外接圆与外心.【专题】圆的有关概念及性质;几何直观.【思路分析】直接利用圆内接四边形的性质结合圆周角定理得出答案.【解答过程】解:如图所示:∠A还应有另一个不同的值∠A′与∠A互补.故∠A′=180°﹣65°=115°.故选:A.【总结归纳】此题主要考查了三角形的外接圆,正确分类讨论是解题关键.15.如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对【知识考点】二次函数图象上点的坐标特征.【专题】二次函数图象及其性质;推理能力.【思路分析】求出抛物线的顶点坐标为(2,4),由二次函数的性质对甲、乙、丙三人的说法分别进行判断,即可得出结论.【解答过程】解:y=x(4﹣x)=﹣x2+4x=﹣(x﹣2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为4,∴甲、乙的说法正确;若b=3,则抛物线上纵坐标为3的点有2个,∴丙的说法不正确;故选:C.【总结归纳】本题考查了二次函数图象上点的坐标特征、抛物线的顶点坐标等知识;熟练掌握二次函数图象上点的坐标特征是解题的关键.16.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A.1,4,5 B.2,3,5C.3,4,5 D.2,2,4【知识考点】勾股定理的逆定理.【专题】等腰三角形与直角三角形;应用意识.【思路分析】根据题意可知,三块三角形的面积中,两个较小的面积之和等于最大的面积,再根据三角形的面积,分别计算出各个选项中围成的直角三角形的面积,比较大小,即可解答本题.【解答过程】解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是=,当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是=;当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是=,∵,∴所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5,故选:B.【总结归纳】本题考查勾股定理的逆定理,解答本题的关键是明确题意,利用勾股定理的逆定理解答.二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.已知:﹣=a﹣=b,则ab=.【知识考点】二次根式的加减法.【专题】二次根式;运算能力.【思路分析】直接化简二次根式进而得出a,b的值求出答案.【解答过程】解:原式=3﹣=a﹣=b,故a=3,b=2,则ab=6.故答案为:6.【总结归纳】此题主要考查了二次根式的加减,正确化简二次根式是解题关键.18.正六边形的一个内角是正n边形一个外角的4倍,则n=.【知识考点】多边形内角与外角.【专题】多边形与平行四边形;正多边形与圆;运算能力.【思路分析】根据多边形的内角和公式求出正六边形的一个内角等于120°,再根据多边形的外角和是360°即可解答.【解答过程】解:正六边形的一个内角为:,∵正六边形的一个内角是正n边形一个外角的4倍,∴正n边形一个外角为:120°÷4=30°,∴n=360°÷30°=12.故答案为:12.【总结归纳】本题主要考查了多边形的外角和定理,理解多边形外角和中外角的个数,以及正多边形的边数之间的关系,是解题关键.19.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作T m(m为1~8的整数).函数y=(x<0)的图象为曲线L.(1)若L过点T1,则k=;(2)若L过点T4,则它必定还过另一点T m,则m=;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有个.【知识考点】反比例函数的应用.【专题】反比例函数及其应用;应用意识.【思路分析】(1)由题意可求T1~T8这些点的坐标,将点T1的坐标代入解析式可求解;(2)将点T4的坐标代入解析式可求k的值,将点T5代入,可求解;(3)由曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,可得T1,T2,T7,T8与T3,T4,T5,T6在曲线L的两侧,即可求解.【解答过程】解:(1)∵每个台阶的高和宽分别是1和2,∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),∵L过点T1,∴k=﹣16×1=﹣16,故答案为:﹣16;(2)∵L过点T4,∴k=﹣10×4=﹣40,∴反比例函数解析式为:y=﹣,当x=﹣8时,y=5,∴T5在反比例函数图象上,∴m=5,故答案为:5;(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,若曲线L过点T3(﹣12,3),T5(﹣8,5)时,k=﹣12×3=﹣36,若曲线L过点T4(﹣10,4),T5(﹣8,5)时,k=﹣40,∵曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,∴﹣36<k<﹣28,∴整数k=﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个,∴答案为:7.【总结归纳】本题考查了反比例函数的应用,求出各点的坐标是本题的关键.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(本小题满分8分)已知两个有理数:﹣9和5.(1)计算:;(2)若再添一个负整数m,且﹣9,5与m这三个数的平均数仍小于m,求m的值.【知识考点】解一元一次不等式.【专题】实数;一元一次不等式(组)及应用;运算能力.【思路分析】(1)根据有理数的加法、除法法则计算即可;(2)根据题意列不等式,解不等式,由m是负整数即可求出m的值.【解答过程】解:(1)==﹣2;(2)根据题意得,<m,∴﹣4+m<3m,∴m﹣3m<4,∴﹣2m<4,∴m>﹣2,∵m是负整数,∴m=﹣1.【总结归纳】此题考查了有理数的运算,解不等式.熟练掌握有理数的运算法则,解不等式的方法是解本题的关键.21.(本小题满分8分)有一电脑程序:每按一次按键,屏幕的A区就会自动加上a2,同时B区就会自动减去3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16,如图.如,第一次按键后,A,B两区分别显示:(1)从初始状态按2次后,分别求A,B两区显示的结果;(2)从初始状态按4次后,计算A,B两区代数式的和,请判断这个和能为负数吗?说明理由.【知识考点】非负数的性质:偶次方;整式的加减;配方法的应用.【专题】整式;运算能力.【思路分析】(1)根据题意列出代数式即可;(2)根据题意得到25+4a2+(﹣16﹣12a),根据整式加减的法则计算,然后配方,根据非负数的性质即可得到结论.【解答过程】解:(1)A区显示的结果为:25+2a2,B区显示的结果为:﹣16﹣6a;(2)这个和不能为负数,理由:根据题意得,25+4a2+(﹣16﹣12a)=25+4a2﹣16﹣12a=4a2﹣12a+9;∵(2a﹣3)2≥0,∴这个和不能为负数.【总结归纳】本题考查了配方法的应用,非负数的性质,整式的加减,正确的理解题意是解题的关键.22.(本小题满分9分)如图,点O为AB中点,分别延长OA到点C,OB到点D,使OC=OD.以点O为圆心,分别以OA,OC为半径在CD上方作两个半圆.点P为小半圆上任一点(不与点A,B重合),连接OP并延长交大半圆于点E,连接AE,CP.(1)①求证:△AOE≌△POC;②写出∠l,∠2和∠C三者间的数量关系,并说明理由.(2)若OC=2OA=2,当∠C最大时,直接指出CP与小半圆的位置关系,并求此时S扇形EOD(答案保留π).【知识考点】全等三角形的判定与性质;直线与圆的位置关系;扇形面积的计算.【专题】图形的全等;圆的有关概念及性质;与圆有关的位置关系;与圆有关的计算.【思路分析】(1)①利用公共角相等,根据SAS证明三角形全等便可;②由全等三角形得∠C=∠E,再利用三角形外角性质得结论;(2)当CP与小半圆O相切时,∠C最大,求出∠DOE便可根据扇形的面积公式求得结果.【解答过程】解:(1)①在△AOE和△POC中,,∴△AOE≌△POC(SAS);②∵△AOE≌△POC,∴∠E=∠C,∵∠1+∠E=∠2,∴∠1+∠C=∠2;(2)当∠C最大时,CP与小半圆相切,如图,∵OC=2OA=2,∴OC=2OP,∵CP与小半圆相切,∴∠OPC=90°,∴∠OCP=30°,∴∠DOE=∠OPC+∠OCP=120°,∴.【总结归纳】本题主要考查了圆的切线的性质,全等三角形的判定与性质,三角形的外角性质,直角三角形的性质,扇形的面积计算,关键在于掌握各个定理,灵活运用这些性质解题.23.(本小题满分9分)用承重指数w衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.(1)求W与x的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄.①求Q与x的函数关系式;②x为何值时,Q是W薄的3倍?[注:(1)及(2)中的①不必写x的取值范围]【知识考点】二次函数的应用.【专题】二次函数的应用;应用意识.【思路分析】(1)由木板承重指数W与木板厚度x(厘米)的平方成正比,可设W=kx2(k≠0).将x=3时,W=3代入,求出k=,即可得出W与x的函数关系式;(2)①设薄板的厚度为x厘米,则厚板的厚度为(6﹣x)厘米,将(1)中所求的解析式代入Q =W厚﹣W薄,化简即可得到Q与x的函数关系式;②根据Q是W薄的3倍,列出方程﹣4x+12=3×x2,求解即可.【解答过程】解:(1)设W=kx2(k≠0).∵当x=3时,W=3,∴3=9k,解得k=,∴W与x的函数关系式为W=x2;(2)①设薄板的厚度为x厘米,则厚板的厚度为(6﹣x)厘米,∴Q=W厚﹣W薄=(6﹣x)2﹣x2=﹣4x+12,即Q与x的函数关系式为Q=﹣4x+12;②∵Q是W薄的3倍,∴﹣4x+12=3×x2,。
2020年河北省中考数学试卷及答案

2020 年河北省中考数学试卷一、选择题(本大题共16 小题,共42 分。
1 ~10 小题各 3 分,11 ~16 小题各 2 分,小题给出的四个选项中,只有一项是符合题目要求的)1 .( 3 分)下列运算结果为正数的是()A .(﹣ 3 ) 2B .﹣ 3 ÷ 2C .0 × (﹣2020 )D . 2 ﹣ 32 .(3 分)把0.0813 写成 a × 10 n ( 1 ≤ a <10 ,n 为整数)的形式,则 a 为()A . 1B .﹣ 2C .0.813D .8.133 .( 3 分)用量角器测得∠ MON 的度数,下列操作正确的是()A .B .C .D .4 .( 3 分)= ()A .B .C .D .5 .( 3 分)图 1 和图 2 中所有的小正方形都全等,将图 1 的正方形放在图 2 中①②③④ 的某一位置,使它与原来7 个小正方形组成的图形是中心对称图形,这个位置是()A .①B .②C .③D .④6 .( 3 分)如图为张小亮的答卷,他的得分应是()A .100 分B .80 分C .60 分D .40 分7 .( 3 分)若△ ABC 的每条边长增加各自的10% 得△ A′B′C′ ,则∠ B′ 的度数与其对应角∠ B 的度数相比()A .增加了10%B .减少了10%C .增加了( 1 + 10% )D .没有改变8 .( 3 分)如图是由相同的小正方体木块粘在一起的几何体,它的主视图是()A .B .C .D .9 .( 3 分)求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD 是菱形,对角线AC ,BD 交于点O .求证:AC ⊥ BD .以下是排乱的证明过程:① 又BO=DO ;②∴ AO ⊥ BD ,即AC ⊥ BD ;③∵四边形ABCD 是菱形;④∴ AB=AD .证明步骤正确的顺序是()A .③ → ② → ① → ④B .③ → ④ → ① → ②C .① → ② → ④ →③ D .① → ④ → ③ → ②10 .( 3 分)如图,码头 A 在码头 B 的正西方向,甲、乙两船分别从A ,B 同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是()A .北偏东55°B .北偏西55°C .北偏东35°D .北偏西35°11 .( 2 分)如图是边长为10cm 的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm )不正确的是()A .B .C .D .12 .( 2 分)如图是国际数学日当天淇淇和嘉嘉的微信对话,根据对话内容,下列选项错误的是()A . 4 + 4 ﹣=6B . 4 + 4 0 + 4 0 =6C . 4 + =6D . 4 ﹣ 1 ÷ + 4=613 .( 2 分)若= + ,则中的数是()A .﹣ 1B .﹣ 2C .﹣ 3D .任意实数14 .( 2 分)甲、乙两组各有12 名学生,组长绘制了本组 5 月份家庭用水量的统计图表,如图,甲组12 户家庭用水量统计表4 5 6 9用水量(吨)户数 4 5 2 1比较 5 月份两组家庭用水量的中位数,下列说法正确的是()A .甲组比乙组大B .甲、乙两组相同C .乙组比甲组大D .无法判断15 .( 2 分)如图,若抛物线y= ﹣x 2 + 3 与x 轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k ,则反比例函数y= (x >0 )的图象是()A .B .C .D .16 .( 2 分)已知正方形MNOK 和正六边形ABCDEF 边长均为 1 ,把正方形放在正六边形中,使OK 边与AB 边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点 B 顺时针旋转,使KM 边与BC 边重合,完成第一次旋转;再绕点 C 顺时针旋转,使MN 边与CD 边重合,完成第二次旋转;… 在这样连续 6 次旋转的过程中,点 B ,M 间的距离可能是()A . 1.4B . 1.1C .0.8D .0.5二、填空题(本大题共 3 小题,共10 分。
2020年河北省中考数学试卷含答案解析

2020年河北省中考数学试卷一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条2.(3分)墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+B.﹣C.×D.÷3.(3分)对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解4.(3分)如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同5.(3分)如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A .9B .8C .7D .66.(3分)如图1,已知∠ABC ,用尺规作它的角平分线. 如图2,步骤如下,第一步:以B 为圆心,以a 为半径画弧,分别交射线BA ,BC 于点D ,E ; 第二步:分别以D ,E 为圆心,以b 为半径画弧,两弧在∠ABC 内部交于点P ; 第三步:画射线BP .射线BP 即为所求. 下列正确的是( )A .a ,b 均无限制B .a >0,b >12DE 的长 C .a 有最小限制,b 无限制D .a ≥0,b <12DE 的长7.(3分)若a ≠b ,则下列分式化简正确的是( ) A .a+2b+2=abB .a−2b−2=abC .a 2b =abD .12a 12b =ab8.(3分)在如图所示的网格中,以点O 为位似中心,四边形ABCD 的位似图形是( )A .四边形NPMQB .四边形NPMRC .四边形NHMQD .四边形NHMR9.(3分)若(92−1)(112−1)k=8×10×12,则k =( )A .12B .10C .8D .610.(3分)如图,将△ABC 绕边AC 的中点O 顺时针旋转180°.嘉淇发现,旋转后的△CDA 与△ABC 构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB =AD ,”和“∴四边形…”之间作补充,下列正确的是 ( )A .嘉淇推理严谨,不必补充B .应补充:且AB =CDC .应补充:且AB ∥CD D .应补充:且OA =OC11.(2分)若k 为正整数,则(k +k +⋯+k)k ︸k 个k=( )A .k 2kB .k 2k +1C .2k kD .k 2+k12.(2分)如图,从笔直的公路l 旁一点P 出发,向西走6km 到达l ;从P 出发向北走6km 也到达l .下列说法错误的是( )A .从点P 向北偏西45°走3km 到达lB .公路l 的走向是南偏西45°C .公路l 的走向是北偏东45°D.从点P向北走3km后,再向西走3km到达l13.(2分)已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n千米,则n可能为()A.5B.6C.5或6D.5或6或7 14.(2分)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A应有3个不同值15.(2分)如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对16.(2分)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A.1,4,5B.2,3,5C.3,4,5D.2,2,4二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.(3分)已知:√18−√2=a√2−√2=b√2,则ab=.18.(3分)正六边形的一个内角是正n边形一个外角的4倍,则n=.19.(6分)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作T m(m为1~8的整数).函数y=kx(x<0)的图象为曲线L.(1)若L过点T1,则k=;(2)若L过点T4,则它必定还过另一点T m,则m=;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有个.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(8分)已知两个有理数:﹣9和5.(1)计算:(−9)+52;(2)若再添一个负整数m ,且﹣9,5与m 这三个数的平均数仍小于m ,求m 的值. 21.(8分)有一电脑程序:每按一次按键,屏幕的A 区就会自动加上a 2,同时B 区就会自动减去3a ,且均显示化简后的结果.已知A ,B 两区初始显示的分别是25和﹣16,如图. 如,第一次按键后,A ,B 两区分别显示:(1)从初始状态按2次后,分别求A ,B 两区显示的结果;(2)从初始状态按4次后,计算A ,B 两区代数式的和,请判断这个和能为负数吗?说明理由.22.(9分)如图,点O 为AB 中点,分别延长OA 到点C ,OB 到点D ,使OC =OD .以点O 为圆心,分别以OA ,OC 为半径在CD 上方作两个半圆.点P 为小半圆上任一点(不与点A ,B 重合),连接OP 并延长交大半圆于点E ,连接AE ,CP . (1)①求证:△AOE ≌△POC ;②写出∠l ,∠2和∠C 三者间的数量关系,并说明理由.(2)若OC =2OA =2,当∠C 最大时,直接指出CP 与小半圆的位置关系,并求此时S扇形EOD(答案保留π).23.(9分)用承重指数w 衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W 与木板厚度x (厘米)的平方成正比,当x =3时,W =3. (1)求W 与x 的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄.①求Q与x的函数关系式;②x为何值时,Q是W薄的3倍?[注:(1)及(2)中的①不必写x的取值范围]24.(10分)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l'.x﹣10y﹣21(1)求直线l的解析式;(2)请在图上画出直线l'(不要求列表计算),并求直线l'被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.25.(10分)如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.26.(12分)如图1和图2,在△ABC中,AB=AC,BC=8,tan C=34.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=94,请直接写出点K被扫描到的总时长.2020年河北省中考数学试卷参考答案与试题解析一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条【解答】解:在平面内,与已知直线垂直的直线有无数条,所以作已知直线的垂线,可作无数条.故选:D.2.(3分)墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+B.﹣C.×D.÷【解答】解:∵x3x=x2(x≠0),∴覆盖的是:÷.故选:D.3.(3分)对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解【解答】解:①x﹣3xy=x(1﹣3y),从左到右的变形是因式分解;②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形是整式的乘法,不是因式分解;所以①是因式分解,②是乘法运算.故选:C.4.(3分)如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同【解答】解:从正面看,两个几何体均为第一层和第二层都是两个小正方形,故主视图相同;从左面看,两个几何体均为第一层和第二层都是两个小正方形,故左视图相同;从上面看,两个几何体均为第一层和第二层都是两个小正方形,故俯视图相同.故选:D.5.(3分)如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A.9B.8C.7D.6【解答】解:由统计图可知,前三次的中位数是8,∵第四次又买的苹果单价是a元/千克,这四个单价的中位数恰好也是众数,∴a=8,故选:B.6.(3分)如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求.下列正确的是()A .a ,b 均无限制B .a >0,b >12DE 的长 C .a 有最小限制,b 无限制D .a ≥0,b <12DE 的长【解答】解:以B 为圆心画弧时,半径a 必须大于0,分别以D ,E 为圆心,以b 为半径画弧时,b 必须大于12DE ,否则没有交点,故选:B .7.(3分)若a ≠b ,则下列分式化简正确的是( ) A .a+2b+2=abB .a−2b−2=abC .a 2b =abD .12a 12b =ab【解答】解:∵a ≠b , ∴a+2b+2≠ab ,故选项A 错误;a−2b−2≠a b,故选项B 错误;a 2b 2≠a b,故选项C 错误; 12a 12b =ab ,故选项D 正确;故选:D .8.(3分)在如图所示的网格中,以点O 为位似中心,四边形ABCD 的位似图形是( )A .四边形NPMQB .四边形NPMRC .四边形NHMQD .四边形NHMR【解答】解:∵以点O 为位似中心,∴点C 对应点M ,设网格中每个小方格的边长为1,则OC =√22+12=√5,OM =√42+22=2√5,OD =√2,OB =√32+12=√10,OA =√32+22=√13,OR =√22+12=√5,OQ =2√2,OP =√62+22=2√10,OH =√62+32=3√5,ON =√62+42=2√13, ∵OM OC=√5√5=2, ∴点D 对应点Q ,点B 对应点P ,点A 对应点N ,∴以点O 为位似中心,四边形ABCD 的位似图形是四边形NPMQ , 故选:A . 9.(3分)若(92−1)(112−1)k=8×10×12,则k =( )A .12B .10C .8D .6【解答】解:方程两边都乘以k ,得 (92﹣1)(112﹣1)=8×10×12k ,∴(9+1)(9﹣1)(11+1)(11﹣1)=8×10×12k , ∴80×120=8×10×12k , ∴k =10.经检验k =10是原方程的解. 故选:B .10.(3分)如图,将△ABC 绕边AC 的中点O 顺时针旋转180°.嘉淇发现,旋转后的△CDA 与△ABC 构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB =AD ,”和“∴四边形…”之间作补充,下列正确的是 ( )A.嘉淇推理严谨,不必补充B.应补充:且AB=CDC.应补充:且AB∥CDD.应补充:且OA=OC【解答】解:∵CB=AD,AB=CD,∴四边形ABCD是平行四边形,故选:B.=()11.(2分)若k为正整数,则(k+k+⋯+k)k︸k个kA.k2k B.k2k+1C.2k k D.k2+k=((k•k)k=(k2)k=k2k,【解答】解:(k+k+⋯+k)k︸k个k故选:A.12.(2分)如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km 也到达l.下列说法错误的是()A.从点P向北偏西45°走3km到达lB.公路l的走向是南偏西45°C.公路l的走向是北偏东45°D.从点P向北走3km后,再向西走3km到达l【解答】解:如图,由题意可得△P AB是腰长6km的等腰直角三角形,则AB=6√2km,则PC=3√2km,则从点P向北偏西45°走3√2km到达l,选项A错误;则公路l的走向是南偏西45°或北偏东45°,选项B,C正确;则从点P向北走3km后,再向西走3km到达l,选项D正确.故选:A.13.(2分)已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n千米,则n可能为()A.5B.6C.5或6D.5或6或7【解答】解:当t=1时,光传播的距离为1×300000=300000=3×105(千米),则n=5;当t=10时,光传播的距离为10×300000=3000000=3×106(千米),则n=6.因为1≤t≤10,所以n可能为5或6,故选:C.14.(2分)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A应有3个不同值【解答】解:如图所示:∠A还应有另一个不同的值∠A′与∠A互补.故∠A′=180°﹣65°=115°.故选:A.15.(2分)如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对【解答】解:y=x(4﹣x)=﹣x2+4x=﹣(x﹣2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为4,∴甲、乙的说法正确;若b=3,则抛物线上纵坐标为3的点有2个,∴丙的说法不正确;故选:C.16.(2分)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A .1,4,5B .2,3,5C .3,4,5D .2,2,4【解答】解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是√1×√42=√42, 当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是√2×√32=√62; 当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形; 当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是√2×√22=√42, ∵√62>√42, ∴所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5, 故选:B .二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.(3分)已知:√18−√2=a √2−√2=b √2,则ab = 6 . 【解答】解:原式=3√2−√2=a √2−√2=b √2, 故a =3,b =2, 则ab =6. 故答案为:6.18.(3分)正六边形的一个内角是正n 边形一个外角的4倍,则n = 12 . 【解答】解:正六边形的一个内角为:(6−2)×180°6=120°,∵正六边形的一个内角是正n 边形一个外角的4倍, ∴正n 边形一个外角为:120°÷4=30°, ∴n =360°÷30°=12. 故答案为:12.19.(6分)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作T m(m为1~8的整数).函数y=kx(x<0)的图象为曲线L.(1)若L过点T1,则k=﹣16;(2)若L过点T4,则它必定还过另一点T m,则m=5;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有7个.【解答】解:(1)∵每个台阶的高和宽分别是1和2,∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),∵L过点T1,∴k=﹣16×1=﹣16,故答案为:﹣16;(2)∵L过点T4,∴k=﹣10×4=﹣40,∴反比例函数解析式为:y=−40 x,当x=﹣8时,y=5,∴T5在反比例函数图象上,∴m=5,故答案为:5;(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,若曲线L过点T3(﹣12,3),T5(﹣8,5)时,k=﹣12×3=﹣36,若曲线L 过点T 4(﹣10,4),T 5(﹣8,5)时,k =﹣40, ∵曲线L 使得T 1~T 8这些点分布在它的两侧,每侧各4个点, ∴﹣36<k <﹣28,∴整数k =﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个, ∴答案为:7.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤) 20.(8分)已知两个有理数:﹣9和5. (1)计算:(−9)+52;(2)若再添一个负整数m ,且﹣9,5与m 这三个数的平均数仍小于m ,求m 的值. 【解答】解:(1)(−9)+52=−42=−2;(2)根据题意得,−9+5+m3<m ,∴﹣4+m <3m , ∴m ﹣3m <4, ∴﹣2m <4, ∴m >﹣2, ∵m 是负整数, ∴m =﹣1.21.(8分)有一电脑程序:每按一次按键,屏幕的A 区就会自动加上a 2,同时B 区就会自动减去3a ,且均显示化简后的结果.已知A ,B 两区初始显示的分别是25和﹣16,如图. 如,第一次按键后,A ,B 两区分别显示:(1)从初始状态按2次后,分别求A ,B 两区显示的结果;(2)从初始状态按4次后,计算A ,B 两区代数式的和,请判断这个和能为负数吗?说明理由.【解答】解:(1)A 区显示的结果为:25+2a 2,B 区显示的结果为:﹣16﹣6a ; (2)这个和不能为负数,理由:根据题意得,25+4a 2+(﹣16﹣12a )=25+4a 2﹣16﹣12a =4a 2﹣12a +9; ∵(2a ﹣3)2≥0, ∴这个和不能为负数.22.(9分)如图,点O 为AB 中点,分别延长OA 到点C ,OB 到点D ,使OC =OD .以点O 为圆心,分别以OA ,OC 为半径在CD 上方作两个半圆.点P 为小半圆上任一点(不与点A ,B 重合),连接OP 并延长交大半圆于点E ,连接AE ,CP . (1)①求证:△AOE ≌△POC ;②写出∠l ,∠2和∠C 三者间的数量关系,并说明理由.(2)若OC =2OA =2,当∠C 最大时,直接指出CP 与小半圆的位置关系,并求此时S扇形EOD(答案保留π).【解答】解:(1)①在△AOE 和△POC 中, {OA =OP∠AOE =∠POC OE =OC, ∴△AOE ≌△POC (SAS ); ②∵△AOE ≌△POC , ∴∠E =∠C , ∵∠1+∠E =∠2, ∴∠1+∠C =∠2;(2)当∠C 最大时,CP 与小半圆相切, 如图,∵OC=2OA=2,∴OC=2OP,∵CP与小半圆相切,∴∠OPC=90°,∴∠OCP=30°,∴∠DOE=∠OPC+∠OCP=120°,∴S扇形ODE =120π×22360=43π.23.(9分)用承重指数w衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.(1)求W与x的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄.①求Q与x的函数关系式;②x为何值时,Q是W薄的3倍?[注:(1)及(2)中的①不必写x的取值范围]【解答】解:(1)设W=kx2(k≠0).∵当x=3时,W=3,∴3=9k,解得k=1 3,∴W与x的函数关系式为W=13x 2;(2)①设薄板的厚度为x厘米,则厚板的厚度为(6﹣x)厘米,∴Q=W厚﹣W薄=13(6﹣x)2−13x2=﹣4x+12,即Q与x的函数关系式为Q=﹣4x+12;②∵Q是W薄的3倍,∴﹣4x+12=3×13x 2,整理得,x2+4x﹣12=0,解得,x1=2,x2=﹣6(不合题意舍去),故x为2时,Q是W薄的3倍.24.(10分)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l'.x﹣10y﹣21(1)求直线l的解析式;(2)请在图上画出直线l'(不要求列表计算),并求直线l'被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.【解答】解:(1)∵直线l :y =kx +b 中,当x =﹣1时,y =﹣2;当x =0时,y =1,∴{−k +b =−2b =1,解得{k =3b =1, ∴直线l 的解析式为y =3x +1;∴直线l ′的解析式为y =x +3;(2)如图,解{y =x +3y =3x +1得{x =1y =4, ∴两直线的交点为(1,4),∵直线l ′:y =x +3与y 轴的交点为(0,3),∴直线l '被直线l 和y 轴所截线段的长为:√12+(4−3)2=√2;(3)把y =a 代入y =3x +1得,a =3x +1,解得x =a−13; 把y =a 代入y =x +3得,a =x +3,解得x =a ﹣3;当a ﹣3+a−13=0时,a =52,当12(a ﹣3+0)=a−13时,a =7, 当12(a−13+0)=a ﹣3时,a =175, ∴直线y =a 与直线l ,l ′及y 轴有三个不同的交点,且其中两点关于第三点对称,则a 的值为52或7或175.25.(10分)如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.【解答】解:(1)∵经过第一次移动游戏,甲的位置停留在正半轴上,∴必须甲对乙错,因为一共有四种情形,都对或都错,甲对乙错,甲错乙对,∴P甲对乙错=1 4.(2)由题意m=5﹣4n+2(10﹣n)=25﹣6n.n=4时,离原点最近.(3)不妨设甲连续k次正确后两人相距2个单位,则有|8+2k﹣4k|=2,解得k=3或5.如果k次中,有1次两人都对都错,则有|6+2(k﹣1)﹣4(k﹣1)|=2,解得k=3或5,如果k次中,有2次两人都对都错,则有|4+2(k﹣2)﹣4(k﹣2)|=2,解得k=3或5,…,综上所述,满足条件的k的值为3或5.26.(12分)如图1和图2,在△ABC中,AB=AC,BC=8,tan C=34.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P 移动的路程为x ,当0≤x ≤3及3≤x ≤9时,分别求点P 到直线AC 的距离(用含x 的式子表示);(4)在点P 处设计并安装一扫描器,按定角∠APQ 扫描△APQ 区域(含边界),扫描器随点P 从M 到B 再到N 共用时36秒.若AK =94,请直接写出点K 被扫描到的总时长.【解答】解:(1)如图1中,过点A 作AH ⊥BC 于H .∵AB =AC ,AH ⊥BC ,∴BH =CH =4,∠B =∠C ,∴tan ∠B =tan ∠C =AH BH =34,∴AH =3,AB =AC =√AH 2+BH 2=√32+42=5.∴当点P 在BC 上时,点P 到A 的最短距离为3.(2)如图1中,∵∠APQ =∠B ,∴PQ ∥BC ,∴△APQ ∽△ABC ,∵PQ 将△ABC 的面积分成上下4:5,∴S △APQ S △ABC =(AP AB )2=49, ∴AP AB =23, ∴AP =103,∴PM =AP =AM =103−2=43. (3)当0≤x ≤3时,如图1﹣1中,过点P 作PJ ⊥CA 交CA 的延长线于J .∵PQ ∥BC ,∴AP AB =PQ BC ,∠AQP =∠C , ∴x+25=PQ 8, ∴PQ =85(x +2),∵sin ∠AQP =sin ∠C =35,∴PJ =PQ •sin ∠AQP =2425(x +2). 当3≤x ≤9时,如图2中,过点P 作PJ ⊥AC 于J .同法可得PJ =PC •sin ∠C =35(11﹣x ).(4)由题意点P 的运动速度=936=14单位长度/秒.当3<x ≤9时,设CQ =y .∵∠APC =∠B +∠BAP =∠APQ +∠CPQ ,∠APQ =∠B ,∴∠BAP =∠CPQ ,∵∠B =∠C ,∴△ABP ∽△PCQ ,∴AB CP =BP CQ , ∴511−x =x−3y ,∴y =−15(x ﹣7)2+165,∵−15<0,∴x =7时,y 有最大值,最大值=165,∵AK =94,∴CK =5−94=114<165 当y =114时,114=−15(x ﹣7)2+165, 解得x =7±32, ∴点K 被扫描到的总时长=(114+6﹣3)÷14=23秒. 方法二:①点P 在AB 上的时候,有11/4个单位长度都能扫描到点K ;②在BN 阶段,当x 在3~5.5(即7﹣1.5)的过程,是能扫到K 点的,在5.5~8.5(即7+1.5)的过程是扫不到点K 的,但在8.5~9(即点M 到N 全部的路程)能扫到点K .所以扫到的时间是[(9﹣8.5)+(5.5﹣3)+114]÷14=23(秒).。
2020年河北省中考数学试题及答案
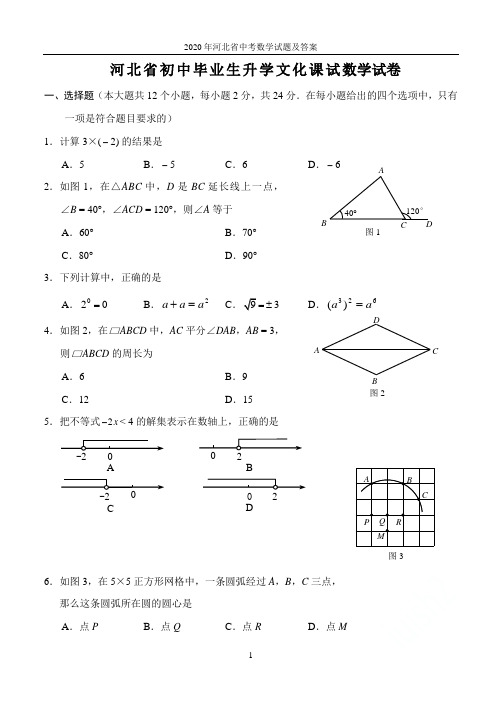
河北省初中毕业生升学文化课试数学试卷一、选择题(本大题共12个小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.计算3×(-2) 的结果是A .5B .-5C .6D .-62.如图1,在△ABC 中,D 是BC 延长线上一点,∠B = 40°,∠ACD = 120°,则∠A 等于 A .60° B .70°C .80°D .90°3.下列计算中,正确的是A .020=B .2a a a =+C3±D .623)(a a =4.如图2,在□ABCD 中,AC 平分∠DAB ,AB = 3,则□ABCD 的周长为 A .6 B .9 C .12D .155.把不等式2x -< 4的解集表示在数轴上,正确的是6.如图3,在5×5正方形网格中,一条圆弧经过A ,B ,C 三点, 那么这条圆弧所在圆的圆心是 A .点PB .点QC .点RD .点MABCD图2ABCD 40°120°图1图3A BD2C -27.化简ba b b a a ---22的结果是 A .22b a -B .b a +C .b a -D .18.小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的1元纸币为x 张,根据题意,下面所列方程正确的是 A .48)12(5=-+x x B .48)12(5=-+x x C .48)5(12=-+x xD .48)12(5=-+x x9.一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km /h ,水流速度为5 km /h .轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t (h ),航行的路程为s (km ),则s 与t 的函数图象大致是10.如图4,两个正六边形的边长均为1,其中一个正六边形的一边恰在另一个正六边形的对角线上,则这个图形(阴影部分)外轮廓线的周长是 A .7B .8C .9D .1011.如图5,已知抛物线c bx x y ++=2的对称轴为2=x ,点A ,B 均在抛物线上,且AB 与x 轴平行,其中点A 的坐标为图4AB C D(0,3),则点B 的坐标为 A .(2,3) B .(3,2) C .(3,3)D .(4,3)12.将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图6-1.在图6-2中,将骰子 向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成 一次变换.若骰子的初始位置为图6-1所示的状态,那么按 上述规则连续完成10次变换后,骰子朝上一面的点数是A .6B .5C .3D .2二、填空题(本大题共6个小题,每小题3分,共18分.把答案写在题中横线上)13.-的相反数是 .14.如图7,矩形ABCD 的顶点A ,B 在数轴上, CD = 6,点A对应的数为1-,则点B 所对应的数为 . 15.在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从图8的四张卡片中任意拿走一张,使剩下的卡片从左到右连成一个三位数,该数就是他猜的价格.若商品的价格是360元,那么他一次就能猜中的概率是 .16.已知x = 1是一元二次方程02=++n mx x 的一个根,则222n mn m ++的值为 .图7图8图6-1图6-217.某盏路灯照射的空间可以看成如图9所示的圆锥,它的高AO = 8米,母线AB 与底面半径OB 的夹角为α,34tan =α, 则圆锥的底面积是 平方米(结果保留π). 18.把三张大小相同的正方形卡片A ,B ,C 叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示.若按图10-1摆放时,阴影部分的面积为S 1;若按图10-2摆放时,阴影部分的面积为S 2,则S 1 S 2(填“>”、“<”或“=”).三、解答题(本大题共8个小题,共78分.解答应写出文字说明、证明过程或演算步骤) 19.(本小题满分8分)解方程:1211+=-x x .20.(本小题满分8分)如图11-1,正方形ABCD 是一个6 × 6网格电子屏的示意图,其中每个小正方形的边长为1.位于AD 中点处的光点P 按图11-2(1)请在图11-1中画出光点P 经过的路径; (2)求光点P 经过的路径总长(结果保留π).图11-2图10-1图10-2D图11-121.(本小题满分9分)甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.(1)在图12-1中,“7分”所在扇形的圆心角等于 °.(2)请你将图12-2的统计图补充完整. (3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?甲校成绩统计表 乙校成绩扇形统计图图12-1乙校成绩条形统计图图12-222.(本小题满分9分)如图13,在直角坐标系中,矩形OABC 的顶点O 与坐标原点重合,顶点A ,C 分别在坐标轴上,顶点B 的坐标为(4,2).过点D (0,3)和E (6,0)的直线分别与AB ,BC 交于点M ,N .(1)求直线DE 的解析式和点M 的坐标; (2)若反比例函数xmy =(x >0)的图象经过点M ,求该反比例函数的解析式,并通过计算判断点N 是否在该函数的图象上; (3)若反比例函数xmy =(x >0)的图象与△MNB 有公共点,请直接..写出m 的取值范围.23.(本小题满分10分)观察思考某种在同一平面进行传动的机械装置如图14-1,图14-2是它的示意图.其工作原理是:滑块Q在平直滑道l上可以左右滑动,在Q滑动的过程中,连杆PQ也随之运动,并且PQ带动连杆OP绕固定点O摆动.在摆动过程中,两连杆的接点P在以OP为半径的⊙O上运动.数学兴趣小组为进一步研究其中所蕴含的数学知识,过点O作OH ⊥l于点H,并测得OH =4分米,PQ = 3分米,OP = 2分米.解决问题(1)点Q与点O间的最小距离是分米;点Q与点O间的最大距离是分米;点Q在l上滑到最左端的位置与滑到最右端位置间的距离是分米.(2)如图14-3,小明同学说:“当点Q滑动到点H的位置时,PQ与⊙O是相切的.”你认为他的判断对吗?为什么?(3)①小丽同学发现:“当点P运动到OH上时,点P到l 的距离最小.”事实上,还存在着点P到l距离最大的位置,此时,点P到l的距离是分米;②当OP绕点O左右摆动时,所扫过的区域为扇形,求这个扇形面积最大时圆心角的度数.llQ图14-2图14-1图15-2AD O BC 21MN 图15-1AD B MN12图15-3AD OBC 21MNO 24.(本小题满分10分)在图15-1至图15-3中,直线MN 与线段AB 相交 于点O ,∠1 = ∠2 = 45°.(1)如图15-1,若AO = OB ,请写出AO 与BD 的数量关系和位置关系;(2)将图15-1中的MN 绕点O 顺时针旋转得到图15-2,其中AO = OB . 求证:AC = BD ,AC ⊥ BD ;(3)将图15-2中的OB 拉长为AO 的k 倍得到图15-3,求ACBD的值.25.(本小题满分12分)如图16,在直角梯形ABCD 中,AD ∥BC ,90B ∠=︒,AD = 6,BC = 8,33=AB ,点M 是BC 的中点.点P 从点M 出发沿MB 以每秒1个单位长的速度向点B 匀速运动,到达点B 后立刻以原速度沿BM 返回;点Q 从点M 出发以每秒1个单位长的速度在射线MC 上匀速运动.在点P ,Q 的运动过程中,以PQ 为边作等边三角形EPQ ,使它与梯形ABCD 在射线BC 的同侧.点P ,Q 同时出发,当点P 返回到点M 时停止运动,点Q 也随之停止. 设点P ,Q 运动的时间是t 秒(t >0).(1)设PQ 的长为y ,在点P 从点M 向点B 运动的过程中,写出y 与t 之间的函数关系式(不必写t 的取值范围).(2)当BP = 1时,求△EPQ 与梯形ABCD 重叠部分的面积.(3)随着时间t 的变化,线段AD 会有一部分被△EPQ 覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接..写出t 的取值范围;若不能,请说明理由.PQ 图16(备用图)26.(本小题满分12分)某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售. 若只在国内销售,销售价格y (元/件)与月销量x (件)的函数关系式为y =1001-x +150, 成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w 内(元)(利润 = 销售额-成本-广告费).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a 元/件(a 为 常数,10≤a ≤40),当月销量为x (件)时,每月还需缴纳1001x 2元的附加费,设月利润为w 外(元)(利润 = 销售额-成本-附加费).(1)当x = 1000时,y = 元/件,w 内 = 元; (2)分别求出w 内,w 外与x 间的函数关系式(不必写x 的取值范围);(3)当x 为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a 的值;(4)如果某月要将5000件产品全部销售完,请你通过分析帮公司决策,选择在国内还是在国外销售才能使所获月利润较大?参考公式:抛物线2(0)y ax bx c a =++≠的顶点坐标是24(,)24b ac b a a--.河北省初中毕业生升学文化课考试数学试题参考答案一、选择题二、填空题13.5 14.5 15.4116.1 17.36 π 18. = 三、解答题19.解:)1(21-=+x x , 3=x . 经检验知,3=x 是原方程的解.20.解: (1)如图1;【注:若学生作图没用圆规,所画路线光滑且基本准确即给4分】(2)∵90π346π180⨯⨯=,∴点P 经过的路径总长为6 π.21.解:(1)144;(2)如图2;)甲校的平均分为8.3分,中位数为7分;由于两校平均分相等,乙校成绩的中位数大于甲 校的中位数,所以从平均分和中位数角度上判断, 乙校的成绩较好.(4)因为选8名学生参加市级口语团体赛,甲校得10分的有8人,而乙校得10分的只有5人,所以D图1乙校成绩条形统计图分数 图2应选甲校.22.解:(1)设直线DE 的解析式为b kx y +=,∵点D ,E 的坐标为(0,3)、(6,0),∴ ⎩⎨⎧+==.60,3b k b解得 ⎪⎩⎪⎨⎧=-=.3,21b k ∴ 321+-=x y .∵ 点M 在AB 边上,B (4,2),而四边形OABC 是矩形, ∴ 点M 的纵坐标为2.又 ∵ 点M 在直线321+-=x y 上,∴ 2 = 321+-x .∴ x = 2.∴ M (2,2). (2)∵xm y =(x >0)经过点M (2,2),∴ 4=m .∴x y 4=.又 ∵ 点N 在BC 边上,B (4,2),∴点N 的横坐标为4. ∵ 点N 在直线321+-=x y 上, ∴ 1=y .∴ N (4,1).∵ 当4=x 时,y =4x = 1,∴点N 在函数 xy 4= 的图象上. (3)4≤ m ≤8.23.解:(1)4 5 6;(2)不对.∵OP = 2,PQ = 3,OQ = 4,且42≠32 + 22,即OQ 2≠PQ 2 + OP 2, ∴OP 与PQ 不垂直.∴PQ 与⊙O 不相切. (3)① 3;②由①知,在⊙O 上存在点P ,P '到l 的距离为3,此时,OP 将不能再向下转动,如图3.OP 在绕点O 左右摆动过程中所扫过的最大扇形就是P 'OP .连结P 'P ,交OH 于点D .∵PQ ,P 'Q '均与l 垂直,且PQ =P '3Q '=,l∴四边形PQ Q 'P '是矩形.∴OH ⊥P P ',PD =P 'D . 由OP = 2,OD = OH -HD = 1,得∠DOP = 60°. ∴∠PO P ' = 120°.∴ 所求最大圆心角的度数为120°.24.解:(1)AO = BD ,AO ⊥BD ;(2)证明:如图4,过点B 作BE ∥CA 交DO 于E ,∴∠ACO = ∠BEO .又∵AO = OB ,∠AOC = ∠BOE ,∴△AOC ≌ △BOE .∴AC = BE . 又∵∠1 = 45°, ∴∠ACO = ∠BEO = 135°. ∴∠DEB = 45°.∵∠2 = 45°,∴BE = BD ,∠EBD = 90°.∴AC = BD . 延长AC 交DB 的延长线于F ,如图4.∵BE ∥AC ,∴∠AFD = 90°.∴AC ⊥BD .(3)如图5,过点B 作BE ∥CA 交DO 于E ,∴∠BEO = ∠ACO .又∵∠BOE = ∠AOC , ∴△BOE ∽ △AOC .∴AOBOAC BE =. 又∵OB = kAO ,由(2)的方法易得 BE = BD .∴k ACBD=.25.解:(1)y = 2t ;(2)当BP = 1时,有两种情形:①如图6,若点P 从点M 向点B 运动,有 MB = BC 21= 4,MP = MQ = 3,∴PQ = 6.连接EM ,∵△EPQ 是等边三角形,∴EM ⊥∵AB = 33,∴点E 在AD 上.图4A D OB C21 MNE FA O BC1D 2图5M NE∴△EPQ 与梯形ABCD 重叠部分就是△EPQ ,其面积为39.②若点P 从点B 向点M 运动,由题意得 5=t .PQ = BM + M Q -BP = 8,PC = 7.设PE 与AD 交于点F ,Q E 与AD 或AD 的延长线交于点G ,过点P 作PH ⊥AD 于点H ,则 HP = 33,AH = 1.在Rt △HPF 中,∠HPF = 30°, ∴HF = 3,PF = 6.∴FG = FE = 2.又∵FD = 2, ∴点G 与点D 重合,如图7.此时△EPQ 与梯形ABCD的重叠部分就是梯形FPCG ,其面积为3227.(3)能.4≤t ≤5.26.解:(1)140 57500;(2)w 内 = x (y -20)- 62500 = 1001-x 2+130 x 62500-, w 外 = 1001-x 2+(150a -)x . (3)当x = )1001(2130-⨯-= 6500时,w 内最大;分由题意得 2214()(62500)1300(150)100114()4()100100a ⨯-⨯----=⨯-⨯-, 解得a 1 = 30,a 2 = 270(不合题意,舍去).所以 a = 30. (4)当x = 5000时,w 内 = 337500, w 外 =5000500000a -+.若w 内 < w 外,则a <32.5; 若w 内 = w 外,则a = 32.5; 若w 内 > w 外,则a >32.5.所以,当10≤ a <32.5时,选择在国外销售; 当a = 32.5时,在国外和国内销售都一样;图7当32.5<a ≤40时,选择在国内销售.。
2020年河北省中考数学试题(含答案)

2020年河北省中考数学试卷一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)(2020•河北)如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条2.(3分)(2020•河北)墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+B.﹣C.×D.÷3.(3分)(2020•河北)对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解4.(3分)(2020•河北)如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同5.(3分)(2020•河北)如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A .9B .8C .7D .66.(3分)(2020•河北)如图1,已知∠ABC ,用尺规作它的角平分线. 如图2,步骤如下,第一步:以B 为圆心,以a 为半径画弧,分别交射线BA ,BC 于点D ,E ; 第二步:分别以D ,E 为圆心,以b 为半径画弧,两弧在∠ABC 内部交于点P ; 第三步:画射线BP .射线BP 即为所求. 下列正确的是( )A .a ,b 均无限制B .a >0,b >12DE 的长 C .a 有最小限制,b 无限制D .a ≥0,b <12DE 的长7.(3分)(2020•河北)若a ≠b ,则下列分式化简正确的是( ) A .a+2b+2=abB .a−2b−2=abC .a 2b =abD .12a 12b =ab8.(3分)(2020•河北)在如图所示的网格中,以点O 为位似中心,四边形ABCD 的位似图形是( )A .四边形NPMQB .四边形NPMRC .四边形NHMQD .四边形NHMR9.(3分)(2020•河北)若(92−1)(112−1)k=8×10×12,则k =( )A .12B .10C .8D .610.(3分)(2020•河北)如图,将△ABC 绕边AC 的中点O 顺时针旋转180°.嘉淇发现,旋转后的△CDA 与△ABC 构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB =AD ,”和“∴四边形…”之间作补充,下列正确的是 ( )A .嘉淇推理严谨,不必补充B .应补充:且AB =CDC .应补充:且AB ∥CD D .应补充:且OA =OC11.(2分)(2020•河北)若k 为正整数,则(k +k +⋯+k)k ︸k 个k=( )A .k 2kB .k 2k +1C .2k kD .k 2+k12.(2分)(2020•河北)如图,从笔直的公路l 旁一点P 出发,向西走6km 到达l ;从P 出发向北走6km 也到达l .下列说法错误的是( )A .从点P 向北偏西45°走3km 到达lB .公路l 的走向是南偏西45°C.公路l的走向是北偏东45°D.从点P向北走3km后,再向西走3km到达l13.(2分)(2020•河北)已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n千米,则n可能为()A.5B.6C.5或6D.5或6或7 14.(2分)(2020•河北)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A应有3个不同值15.(2分)(2020•河北)如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对16.(2分)(2020•河北)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A.1,4,5B.2,3,5C.3,4,5D.2,2,4二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.(3分)(2020•河北)已知:√18−√2=a√2−√2=b√2,则ab=.18.(3分)(2020•河北)正六边形的一个内角是正n边形一个外角的4倍,则n=.19.(6分)(2020•河北)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作T m(m为1~8的整数).函数y=kx(x<0)的图象为曲线L.(1)若L过点T1,则k=;(2)若L过点T4,则它必定还过另一点T m,则m=;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有个.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(8分)(2020•河北)已知两个有理数:﹣9和5.(1)计算:(−9)+52;(2)若再添一个负整数m ,且﹣9,5与m 这三个数的平均数仍小于m ,求m 的值. 21.(8分)(2020•河北)有一电脑程序:每按一次按键,屏幕的A 区就会自动加上a 2,同时B 区就会自动减去3a ,且均显示化简后的结果.已知A ,B 两区初始显示的分别是25和﹣16,如图.如,第一次按键后,A ,B 两区分别显示:(1)从初始状态按2次后,分别求A ,B 两区显示的结果;(2)从初始状态按4次后,计算A ,B 两区代数式的和,请判断这个和能为负数吗?说明理由.22.(9分)(2020•河北)如图,点O 为AB 中点,分别延长OA 到点C ,OB 到点D ,使OC =OD .以点O 为圆心,分别以OA ,OC 为半径在CD 上方作两个半圆.点P 为小半圆上任一点(不与点A ,B 重合),连接OP 并延长交大半圆于点E ,连接AE ,CP . (1)①求证:△AOE ≌△POC ;②写出∠l ,∠2和∠C 三者间的数量关系,并说明理由.(2)若OC =2OA =2,当∠C 最大时,直接指出CP 与小半圆的位置关系,并求此时S扇形EOD(答案保留π).23.(9分)(2020•河北)用承重指数w 衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W 与木板厚度x (厘米)的平方成正比,当x =3时,W =3.(1)求W与x的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄.①求Q与x的函数关系式;②x为何值时,Q是W薄的3倍?[注:(1)及(2)中的①不必写x的取值范围]24.(10分)(2020•河北)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l'.x﹣10y﹣21(1)求直线l的解析式;(2)请在图上画出直线l'(不要求列表计算),并求直线l'被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.25.(10分)(2020•河北)如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.26.(12分)(2020•河北)如图1和图2,在△ABC中,AB=AC,BC=8,tan C=3 4.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB ﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=94,请直接写出点K被扫描到的总时长.2020年河北省中考数学试卷参考答案与试题解析一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(3分)(2020•河北)如图,在平面内作已知直线m的垂线,可作垂线的条数有()A.0条B.1条C.2条D.无数条【解答】解:在平面内,与已知直线垂直的直线有无数条,所以作已知直线的垂线,可作无数条.故选:D.2.(3分)(2020•河北)墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是()A.+B.﹣C.×D.÷【解答】解:∵x3x=x2(x≠0),∴覆盖的是:÷.故选:D.3.(3分)(2020•河北)对于①x﹣3xy=x(1﹣3y),②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形,表述正确的是()A.都是因式分解B.都是乘法运算C.①是因式分解,②是乘法运算D.①是乘法运算,②是因式分解【解答】解:①x﹣3xy=x(1﹣3y),从左到右的变形是因式分解;②(x+3)(x﹣1)=x2+2x﹣3,从左到右的变形是整式的乘法,不是因式分解;所以①是因式分解,②是乘法运算.故选:C.4.(3分)(2020•河北)如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是()A.仅主视图不同B.仅俯视图不同C.仅左视图不同D.主视图、左视图和俯视图都相同【解答】解:从正面看,两个几何体均为第一层和第二层都是两个小正方形,故主视图相同;从左面看,两个几何体均为第一层和第二层都是两个小正方形,故左视图相同;从上面看,两个几何体均为第一层和第二层都是两个小正方形,故俯视图相同.故选:D.5.(3分)(2020•河北)如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是a元/千克,发现这四个单价的中位数恰好也是众数,则a=()A.9B.8C.7D.6【解答】解:由统计图可知,前三次的中位数是8,∵第四次又买的苹果单价是a元/千克,这四个单价的中位数恰好也是众数,∴a=8,故选:B.6.(3分)(2020•河北)如图1,已知∠ABC,用尺规作它的角平分线.如图2,步骤如下,第一步:以B为圆心,以a为半径画弧,分别交射线BA,BC于点D,E;第二步:分别以D,E为圆心,以b为半径画弧,两弧在∠ABC内部交于点P;第三步:画射线BP.射线BP即为所求.下列正确的是()A .a ,b 均无限制B .a >0,b >12DE 的长 C .a 有最小限制,b 无限制D .a ≥0,b <12DE 的长【解答】解:以B 为圆心画弧时,半径a 必须大于0,分别以D ,E 为圆心,以b 为半径画弧时,b 必须大于12DE ,否则没有交点,故选:B .7.(3分)(2020•河北)若a ≠b ,则下列分式化简正确的是( ) A .a+2b+2=abB .a−2b−2=abC .a 2b =abD .12a 12b =ab【解答】解:∵a ≠b , ∴a+2b+2≠ab ,故选项A 错误;a−2b−2≠a b,故选项B 错误;a 2b 2≠a b,故选项C 错误; 12a 12b =ab ,故选项D 正确;故选:D .8.(3分)(2020•河北)在如图所示的网格中,以点O 为位似中心,四边形ABCD 的位似图形是( )A .四边形NPMQB .四边形NPMRC .四边形NHMQD .四边形NHMR【解答】解:∵以点O 为位似中心, ∴点C 对应点M ,设网格中每个小方格的边长为1,则OC =√22+12=√5,OM =√42+22=2√5,OD =√2,OB =√32+12=√10,OA =√32+22=√13,OR =√22+12=√5,OQ =2√2,OP =√62+22=2√10,OH =√62+32=3√5,ON =√62+42=2√13, ∵OM OC=√5√5=2, ∴点D 对应点Q ,点B 对应点P ,点A 对应点N ,∴以点O 为位似中心,四边形ABCD 的位似图形是四边形NPMQ , 故选:A .9.(3分)(2020•河北)若(92−1)(112−1)k=8×10×12,则k =( )A .12B .10C .8D .6【解答】解:方程两边都乘以k ,得 (92﹣1)(112﹣1)=8×10×12k ,∴(9+1)(9﹣1)(11+1)(11﹣1)=8×10×12k , ∴80×120=8×10×12k , ∴k =10.经检验k =10是原方程的解. 故选:B .10.(3分)(2020•河北)如图,将△ABC 绕边AC 的中点O 顺时针旋转180°.嘉淇发现,旋转后的△CDA 与△ABC 构成平行四边形,并推理如下:小明为保证嘉淇的推理更严谨,想在方框中“∵CB =AD ,”和“∴四边形…”之间作补充,下列正确的是 ( )A .嘉淇推理严谨,不必补充B .应补充:且AB =CDC .应补充:且AB ∥CD D .应补充:且OA =OC【解答】解:∵CB =AD ,AB =CD , ∴四边形ABCD 是平行四边形, 故选:B .11.(2分)(2020•河北)若k 为正整数,则(k +k +⋯+k)k ︸k 个k=( )A .k 2kB .k 2k +1C .2k kD .k 2+k【解答】解:(k +k +⋯+k)k ︸k 个k=((k •k )k =(k 2)k =k 2k ,故选:A .12.(2分)(2020•河北)如图,从笔直的公路l 旁一点P 出发,向西走6km 到达l ;从P 出发向北走6km 也到达l .下列说法错误的是( )A .从点P 向北偏西45°走3km 到达lB .公路l 的走向是南偏西45°C .公路l 的走向是北偏东45°D .从点P 向北走3km 后,再向西走3km 到达l 【解答】解:如图,由题意可得△P AB 是腰长6km 的等腰直角三角形, 则AB =6√2km ,则PC=3√2km,则从点P向北偏西45°走3√2km到达l,选项A错误;则公路l的走向是南偏西45°或北偏东45°,选项B,C正确;则从点P向北走3km后,再向西走3km到达l,选项D正确.故选:A.13.(2分)(2020•河北)已知光速为300000千米/秒,光经过t秒(1≤t≤10)传播的距离用科学记数法表示为a×10n千米,则n可能为()A.5B.6C.5或6D.5或6或7【解答】解:当t=1时,光传播的距离为1×300000=300000=3×105(千米),则n=5;当t=10时,光传播的距离为10×300000=3000000=3×106(千米),则n=6.因为1≤t≤10,所以n可能为5或6,故选:C.14.(2分)(2020•河北)有一题目:“已知:点O为△ABC的外心,∠BOC=130°,求∠A.”嘉嘉的解答为:画△ABC以及它的外接圆O,连接OB,OC.如图,由∠BOC=2∠A=130°,得∠A=65°.而淇淇说:“嘉嘉考虑的不周全,∠A还应有另一个不同的值.”下列判断正确的是()A.淇淇说的对,且∠A的另一个值是115°B.淇淇说的不对,∠A就得65°C.嘉嘉求的结果不对,∠A应得50°D.两人都不对,∠A应有3个不同值【解答】解:如图所示:∠A还应有另一个不同的值∠A′与∠A互补.故∠A′=180°﹣65°=115°.故选:A.15.(2分)(2020•河北)如图,现要在抛物线y=x(4﹣x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下,甲:若b=5,则点P的个数为0;乙:若b=4,则点P的个数为1;丙:若b=3,则点P的个数为1.下列判断正确的是()A.乙错,丙对B.甲和乙都错C.乙对,丙错D.甲错,丙对【解答】解:y=x(4﹣x)=﹣x2+4x=﹣(x﹣2)2+4,∴抛物线的顶点坐标为(2,4),∴在抛物线上的点P的纵坐标最大为4,∴甲、乙的说法正确;若b=3,则抛物线上纵坐标为3的点有2个,∴丙的说法不正确;故选:C.16.(2分)(2020•河北)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A .1,4,5B .2,3,5C .3,4,5D .2,2,4【解答】解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是√1×√42=√42, 当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是√2×√32=√62; 当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形; 当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是√2×√22=√42, ∵√62>√42, ∴所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5, 故选:B .二、填空题(本大题有3个小题,共12分.17~18小题各3分;19小题有3个空,每空2分)17.(3分)(2020•河北)已知:√18−√2=a √2−√2=b √2,则ab = 6 . 【解答】解:原式=3√2−√2=a √2−√2=b √2, 故a =3,b =2, 则ab =6. 故答案为:6.18.(3分)(2020•河北)正六边形的一个内角是正n 边形一个外角的4倍,则n = 12 . 【解答】解:正六边形的一个内角为:(6−2)×180°6=120°,∵正六边形的一个内角是正n 边形一个外角的4倍, ∴正n 边形一个外角为:120°÷4=30°, ∴n =360°÷30°=12. 故答案为:12.19.(6分)(2020•河北)如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作T m(m为1~8的整数).函数y=kx(x<0)的图象为曲线L.(1)若L过点T1,则k=﹣16;(2)若L过点T4,则它必定还过另一点T m,则m=5;(3)若曲线L使得T1~T8这些点分布在它的两侧,每侧各4个点,则k的整数值有7个.【解答】解:(1)∵每个台阶的高和宽分别是1和2,∴T1(﹣16,1),T2(﹣14,2),T3(﹣12,3),T4(﹣10,4),T5(﹣8,5),T6(﹣6,6),T7(﹣4,7),T8(﹣2,8),∵L过点T1,∴k=﹣16×1=﹣16,故答案为:﹣16;(2)∵L过点T4,∴k=﹣10×4=﹣40,∴反比例函数解析式为:y=−40 x,当x=﹣8时,y=5,∴T5在反比例函数图象上,∴m=5,故答案为:5;(3)若曲线L过点T1(﹣16,1),T8(﹣2,8)时,k=﹣16,若曲线L过点T2(﹣14,2),T7(﹣4,7)时,k=﹣14×2=﹣28,若曲线L过点T3(﹣12,3),T5(﹣8,5)时,k=﹣12×3=﹣36,若曲线L 过点T 4(﹣10,4),T 5(﹣8,5)时,k =﹣40, ∵曲线L 使得T 1~T 8这些点分布在它的两侧,每侧各4个点, ∴﹣36<k <﹣28,∴整数k =﹣35,﹣34,﹣33,﹣32,﹣31,﹣30,﹣29共7个, ∴答案为:7.三、解答题(本大题有7个小题,共66分.解答应写出文字说明、证明过程或演算步骤) 20.(8分)(2020•河北)已知两个有理数:﹣9和5. (1)计算:(−9)+52;(2)若再添一个负整数m ,且﹣9,5与m 这三个数的平均数仍小于m ,求m 的值. 【解答】解:(1)(−9)+52=−42=−2;(2)根据题意得,−9+5+m3<m ,∴﹣4+m <3m , ∴m ﹣3m <4, ∴﹣2m <4, ∴m >﹣2, ∵m 是负整数, ∴m =﹣1.21.(8分)(2020•河北)有一电脑程序:每按一次按键,屏幕的A 区就会自动加上a 2,同时B 区就会自动减去3a ,且均显示化简后的结果.已知A ,B 两区初始显示的分别是25和﹣16,如图.如,第一次按键后,A ,B 两区分别显示:(1)从初始状态按2次后,分别求A ,B 两区显示的结果;(2)从初始状态按4次后,计算A ,B 两区代数式的和,请判断这个和能为负数吗?说明理由.【解答】解:(1)A 区显示的结果为:25+2a 2,B 区显示的结果为:﹣16﹣6a ; (2)这个和不能为负数,理由:根据题意得,25+4a 2+(﹣16﹣12a )=25+4a 2﹣16﹣12a =4a 2﹣12a +9; ∵(2a ﹣3)2≥0, ∴这个和不能为负数.22.(9分)(2020•河北)如图,点O 为AB 中点,分别延长OA 到点C ,OB 到点D ,使OC =OD .以点O 为圆心,分别以OA ,OC 为半径在CD 上方作两个半圆.点P 为小半圆上任一点(不与点A ,B 重合),连接OP 并延长交大半圆于点E ,连接AE ,CP . (1)①求证:△AOE ≌△POC ;②写出∠l ,∠2和∠C 三者间的数量关系,并说明理由.(2)若OC =2OA =2,当∠C 最大时,直接指出CP 与小半圆的位置关系,并求此时S扇形EOD(答案保留π).【解答】解:(1)①在△AOE 和△POC 中, {OA =OP∠AOE =∠POC OE =OC, ∴△AOE ≌△POC (SAS ); ②∵△AOE ≌△POC , ∴∠E =∠C , ∵∠1+∠E =∠2, ∴∠1+∠C =∠2;(2)当∠C 最大时,CP 与小半圆相切, 如图,∵OC=2OA=2,∴OC=2OP,∵CP与小半圆相切,∴∠OPC=90°,∴∠OCP=30°,∴∠DOE=∠OPC+∠OCP=120°,∴S扇形ODE =120π×22360=43π.23.(9分)(2020•河北)用承重指数w衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.(1)求W与x的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄.①求Q与x的函数关系式;②x为何值时,Q是W薄的3倍?[注:(1)及(2)中的①不必写x的取值范围]【解答】解:(1)设W=kx2(k≠0).∵当x=3时,W=3,∴3=9k,解得k=1 3,∴W与x的函数关系式为W=13x 2;(2)①设薄板的厚度为x厘米,则厚板的厚度为(6﹣x)厘米,∴Q=W厚﹣W薄=13(6﹣x)2−13x2=﹣4x+12,即Q与x的函数关系式为Q=﹣4x+12;②∵Q是W薄的3倍,∴﹣4x+12=3×13x 2,整理得,x2+4x﹣12=0,解得,x1=2,x2=﹣6(不合题意舍去),故x为2时,Q是W薄的3倍.24.(10分)(2020•河北)表格中的两组对应值满足一次函数y=kx+b,现画出了它的图象为直线l,如图.而某同学为观察k,b对图象的影响,将上面函数中的k与b交换位置后得另一个一次函数,设其图象为直线l'.x﹣10y﹣21(1)求直线l的解析式;(2)请在图上画出直线l'(不要求列表计算),并求直线l'被直线l和y轴所截线段的长;(3)设直线y=a与直线l,l′及y轴有三个不同的交点,且其中两点关于第三点对称,直接写出a的值.【解答】解:(1)∵直线l:y=kx+b中,当x=﹣1时,y=﹣2;当x=0时,y=1,∴{−k +b =−2b =1,解得{k =3b =1, ∴直线l 的解析式为y =3x +1;∴直线l ′的解析式为y =x +3;(2)如图,解{y =x +3y =3x +1得{x =1y =4, ∴两直线的交点为(1,4),∵直线l ′:y =x +3与y 轴的交点为(0,3),∴直线l '被直线l 和y 轴所截线段的长为:√12+(4−3)2=√2;(3)把y =a 代入y =3x +1得,a =3x +1,解得x =a−13;把y =a 代入y =x +3得,a =x +3,解得x =a ﹣3;当a ﹣3+a−13=0时,a =52,当12(a ﹣3+0)=a−13时,a =7, 当12(a−13+0)=a ﹣3时,a =175, ∴直线y =a 与直线l ,l ′及y 轴有三个不同的交点,且其中两点关于第三点对称,则a 的值为52或7或175.25.(10分)(2020•河北)如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率P;(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,且他最终停留的位置对应的数为m,试用含n的代数式表示m,并求该位置距离原点O最近时n的值;(3)从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.【解答】解:(1)∵经过第一次移动游戏,甲的位置停留在正半轴上,∴必须甲对乙错,因为一共有四种情形,都对或都错,甲对乙错,甲错乙对,∴P甲对乙错=1 4.(2)由题意m=5﹣4n+2(10﹣n)=25﹣6n.n=4时,离原点最近.(3)不妨设甲连续k次正确后两人相距2个单位,则有|8+2k﹣4k|=2,解得k=3或5.如果k次中,有1次两人都对都错,则有|6+2(k﹣1)﹣4(k﹣1)|=2,解得k=3或5,如果k次中,有2次两人都对都错,则有|4+2(k﹣2)﹣4(k﹣2)|=2,解得k=3或5,…,综上所述,满足条件的k的值为3或5.26.(12分)(2020•河北)如图1和图2,在△ABC中,AB=AC,BC=8,tan C=3 4.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB ﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P 处设计并安装一扫描器,按定角∠APQ 扫描△APQ 区域(含边界),扫描器随点P 从M 到B 再到N 共用时36秒.若AK =94,请直接写出点K 被扫描到的总时长.【解答】解:(1)如图1中,过点A 作AH ⊥BC 于H .∵AB =AC ,AH ⊥BC ,∴BH =CH =4,∠B =∠C ,∴tan ∠B =tan ∠C =AH BH =34,∴AH =3,AB =AC =2+BH 2=√32+42=5.∴当点P 在BC 上时,点P 到A 的最短距离为3.(2)如图1中,∵∠APQ =∠B ,∴PQ ∥BC ,∴△APQ ∽△ABC ,∵PQ 将△ABC 的面积分成上下4:5,∴S △APQ S △ABC =(AP AB )2=49,∴AP AB =23,∴AP =103,∴PM =AP =AM =103−2=43.(3)当0≤x ≤3时,如图1﹣1中,过点P 作PJ ⊥CA 交CA 的延长线于J .∵PQ ∥BC ,∴AP AB =PQ BC ,∠AQP =∠C , ∴x+25=PQ 8, ∴PQ =85(x +2),∵sin ∠AQP =sin ∠C =35,∴PJ =PQ •sin ∠AQP =2425(x +2).当3≤x ≤9时,如图2中,过点P 作PJ ⊥AC 于J .同法可得PJ =PC •sin ∠C =35(11﹣x ).(4)由题意点P 的运动速度=936=14单位长度/秒.当3<x ≤9时,设CQ =y .∵∠APC =∠B +∠BAP =∠APQ +∠CPQ ,∠APQ =∠B ,∴∠BAP =∠CPQ ,∵∠B =∠C ,∴△ABP ∽△PCQ ,∴AB CP =BP CQ , ∴511−x =x−3y,∴y =−15(x ﹣7)2+165, ∵−15<0, ∴x =7时,y 有最大值,最大值=165,∵AK =94,∴CK =5−94=114<165当y =114时,114=−15(x ﹣7)2+165, 解得x =7±32,∴点K 被扫描到的总时长=(114+6﹣3)÷14=23秒. 方法二:①点P 在AB 上的时候,有11/4个单位长度都能扫描到点K ;②在BN 阶段,当x 在3~5.5(即7﹣1.5)的过程,是能扫到K 点的,在5.5~8.5(即7+1.5)的过程是扫不到点K 的,但在8.5~9(即点M 到N 全部的路程)能扫到点K .所以扫到的时间是[(9﹣8.5)+(5.5﹣3)+114]÷14=23(秒).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方形纸片,面积分别是 1,2,3,4,5,选取其中三块(可重复选取)按图 10 的方式组成
图案,使所围成的三角形是面积最大的直角三角形,则选取
的三块纸片的面积分别是
A. 1,4,5
B . 2,3,5
C. 3,4,5
D . 2,2,4
二、填空题
17 已知: 18 - 2 a 2 - 2 b 2 ,则 ab=_______.
2020 年河北省中考数学考试试卷
2020 年河北省中考数学试题
一、选择题
1. 如图 1,在平面内作已知直线 m 的垂线,可作垂线的条数有( )
m
图1
A. 0 条
B. 1 条
C .2 条D. 无数条来自2. 墨迹覆盖了等式“x3 x=x2(x≠0)”中的运算符号,则覆盖的是( )
A. + B. - C. × D. ÷
A 12 B10 C 8 D 6
10. 如图 6,将△ABC 绕边 AC 的中点 O 顺时针旋转 180°,嘉淇发现,旋转后的△CDA 与
△ABC 构成平行四边形,并推理如下:
点 A,C 分别转到了点 C,A 处, 而点 B 转到了 D 处, ∵CB=AD, ∴四边形 ABCD 是平行四边形.
A
D
O
三人的说法如下,
y
甲:若 b=5,则点 P 的个数为 0;
乙:若 b=4,则点 P 的个数为 1;
y=x(4-x)
丙:若 b=3,则点 P 的个数为 1。
x
下列判断正确的是
O
A. 乙对,丙错
B. 甲和乙都错
图9
C. 乙对,丙错
D. 甲错,丙对
16. 图 10 是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案,现有五种正
淇淇说:“嘉嘉考虑的不周全,∠A 还应有另一个不同的值。”
下列判断正确的是( )
A
A. 淇淇说的对,且∠A 的另一个值是 115° D
B. 淇淇说的不对,∠A 就得 65°
C. 嘉嘉求的结果不对,∠A 应得 50°
B
C
D. 两人都不对,∠A 应有 3 个不同值
图8
15. 如图 9,现要在抛物线 y=x(4-x)上找点(a,b),针对 b 的不同取值,所找点 P 的个数,
3. 对于①x-3xy = x(1-3y),②(x + 3)(x-1)= x2 + 2x-3,从左到右的变形,表述正
确的是( )
A. 都是因式分解
B. 都是乘法运算 C. ①是因式分解,②是乘法运算 D. ①是乘法运算,②是因式分解
4. 图 2 的两个几何体分别由 7 个和 6 个相同的小正方体搭成,比较两个几何体的三视图,
已知两个有理数:-9 和 5.
图 10
18 正六边形的一个内角是正 n 边形一个外角的 4 倍,则 n=________. 19 图 11 是 8 个台阶的示意图,每个台阶的高和宽分别是 1 和 2,每个台阶凸出的角的顶点
第3页共6页
2020 年河北省中考数学考试试卷
记作 Tm(m 为 1~8 的整数),函数 y k(x<0)的图像为曲线 L。 x
正确的是( )
A. 仅主视图不同
B. 仅俯视图不同
C. 仅左视图不同
D. 主视图、左视图和俯视图都相同
5. 图 3 是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是 a 元/千克,发现
这四个单价的中位数恰好也是众数,则 a =( )
单价(千克) 9
8
6
第1次 第2次 第3次
次数
A. 9 B. 8 C. 7 D. 6
(1)若 L 过点 T1,则 k=______;
T8
(2)若 L 过点 T4,则它必定还过另一点 Tm,则
到
m=_______;
(3)若曲线 L 使得 T1~T5 这些点分布在它的两侧,每
T1
L
侧各 4 个点,则 k 的整数值有______个。
1x
三、解答题
图 11 -2
20. (本小题满分 8 分)
C
a2 a b2 b
D
1 2
a
a
1b b
2
8. 在图 5 所示的网格中,以点 O 为位似中心,四边形 ABCD 的位似图形是( )
A. 四边形 NPMQ
B. 四边形 NPMR
B. 四边形 NHMQ
D. 四边形 NHMR
9. 若 92 -1 112 -1 810 12 ,则 k = ( ) k
A
D
A
DA
DA
B
B
B
PB
P
C
C
E
C
E
C
图 4-1
第一步
第二步
第三步
下列正确的是( )
A. a,b 均无限制
B . a>0,b>½DE 的长
B. a 有最小限制,b 无限制
D . a≥0,b<½DE 的长
7. 若 a≠b,则下列分式化简正确的是( )
A.
a2 a b2 b
B a-2 a b-2 b
L
北
东
P
13. 已知光速为 300 000 千米/秒,光经过 t 秒(1≤t≤10)传播的距离用科学计数法表示
为 a×10n 千米,则 n 可能为( )
A.5
B. 6
C. 5 或 6
D.5或6或7
14. 有一题目:“已知:点 O 为△ABC 的外心,∠BOC=130°,求∠A。”嘉嘉的解答为:画
△ABC 以及它的外接圆 O,连接 OB,OC,如图 8,由∠BOC=2∠A=130°,得∠A=65°。而
6. 如图 4-1,已知∠ABC,用尺规作它的角平分线。
如图 4-2,步骤如下,
第一步:以 B 为圆心,以 a 为半径画弧,分别交射线 BA,BC 于点 D,E;
第二步: 分别以 D,E 为圆心,以 b 为半径画弧,两弧在∠ABC 内部交于点 P;
第1页共6页
2020 年河北省中考数学考试试卷
第三步:画射线 BP,射线 BP 即为所求。
B 图6
小明为保证嘉淇的推理更严谨,想在方框中“∵CB = AD,”和“四边形……”之间作补
充,下列正确的是( )
A. 嘉淇推理严谨,不必补充
B. 应补充:且 AB = CD
C. 应补充:且 AB∥CD
D. 应补充:且 OA = OC
(k Kk)k
11. 若 k 为正整数,则
k个k
=( )
A k2k
B k2k+1 C 2kk D k2+k
12. 如图 7,从笔直的公路 l 旁一点 P 出发,向西走 6km 到达 l;从 P 出发向北走 6km 也
到达 l,下列说法错.误.的是( )
第2页共6页
2020 年河北省中考数学考试试卷
A. 从点 P 向北偏西 45°走 3km 到达 l B. 公路 l 的走向是南偏西 45° C. 公路 l 的走向是北偏东 45° D. 从点 P 想北走 3km 后,再向西走 3km 到达 l
