ch 聚类分析数据

合集下载

CH11 聚类分析

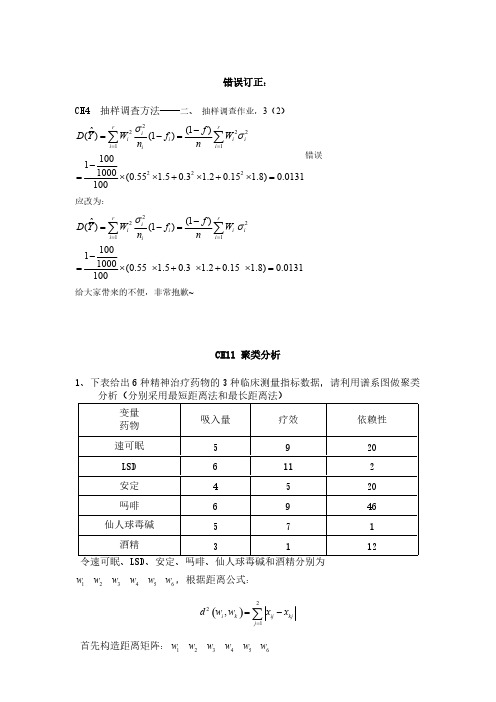
27

0

4 D(w4 , h9 ) min{d (w4 , w6 ), d (w4 , h7 )} min{45, 27} 27 D(h8, h9 ) min{d (h8, w6 ), d (h8, h7 )} min{19, 21} 19
得新距离矩阵为：
w4 h8
h9

w4 h8 h9
0
h10 h8 h9 ， D(h8 , h9 ) 19 ，平台高度： f (h10 ) 19 5 D(w4 , h10 ) min{d (w4 , h8 ), d (w4 , h9 )} min{46, 27} 27
得新距离矩阵为：
得新距离矩阵为： w4 w6 h7 h8
w4 0 45 27 46
w6
h7 h8

0
h9 w6 h7 ， D(w6 , h7 ) d (w6 , h7 ) 13，平台高度： f (h9 ) 13
6
48
0 19 0
45
0 19 21
13
0 21 0
2、 D(w2 , h7 ) max{d (w2 , w1), d (w2 , w3)} max{21, 26} 26 D(w4 , h7 ) max{d (w4 , w1), d (w4 , w3)} max{27,32} 32
D(w5, h7 ) max{d (w5, w1), d (w5, w3)} max{21, 22} 22
clusternumber研究发展国际金融经济研究财政研究控制决策中国技经自动化科技论坛改革科学技管情报学报中外管理国际金研系统工程系统科数统计管理预测会计研究宏观经济科研管理科学学研经济科学金融研究中国工经管理现代经济理管运筹学报企业管理管理工程中国管科数量经济中国软科系工学报系统理实管理世界regrfactorscore11221122undefinederror60619cannotopentextfilespsserr

DM-Ch-08 数据挖掘算法——聚类分析

Hierarchy algorithms(层次算法): Create a hierarchical
(de)composition of the set of data using some criterion Density-based(基于密度方法): based on connectivity and density functions Grid-based(基于网格方法): based on a multiple-level granularity structure Model-based (基于模型方法) : A model is hypothesized for each of the clusters(簇) to find the best fit of data
10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 6 7 8 9 10
第 24 页
k-平均值法聚类算法说明
平方误差准则
E i 1 pC i | p m i |
k 2
其中p: 对象; mi : 簇Ci的均值方法局限性:
只有当簇均值有定义时才能使用，不适合分类数据必须事先指定簇的数目 k 对噪声和离群点数据敏感，不易处理不适合于发现非球状簇
第 25 页
k-中心点法聚类方法
找到代表性对象, 称为簇的中心点
PAM 算法, 1987
从初始中心点集合开始，在能改进聚类结果的总距离的条件下，用一个非中心点替换一个中心点反复迭代 (最小化每个对象与对应参考节点相异度的总值 )
m f 1 ( x1 f x 2 f n
...
x nf
if
)
f {1, 2 ,..., p }

聚类分析数据

聚类分析数据聚类分析是一种数据分析方法，它将相似的数据点分组为具有共同特征的簇。

通过聚类分析，我们可以发现数据中的潜在模式、结构和关联性，从而帮助我们理解数据集的特征和性质。

本文将详细介绍聚类分析的基本概念、常用方法和应用场景。

一、概念介绍聚类分析是一种无监督学习方法，它不需要事先标记好的训练样本。

聚类分析的目标是将数据点划分为不同的簇，使得同一簇内的数据点相似度较高，而不同簇之间的相似度较低。

聚类分析的结果通常以可视化的方式展示，例如散点图或热力图。

二、常用方法1. K-means聚类K-means聚类是最常用的聚类算法之一。

它将数据点分为K个簇，其中K是用户事先指定的。

算法的核心思想是通过迭代优化来找到使得簇内差异最小化的簇中心。

K-means聚类的步骤包括初始化簇中心、分配数据点到最近的簇、更新簇中心，重复执行这些步骤直到满足停止准则。

2. 层次聚类层次聚类是一种基于距离的聚类方法，它将数据点逐步合并成越来越大的簇。

层次聚类可以分为凝聚式和分裂式两种。

凝聚式层次聚类从每个数据点作为一个簇开始，然后逐渐合并最相似的簇，直到达到指定的簇数目。

分裂式层次聚类从所有数据点作为一个簇开始，然后逐渐分裂成更小的簇，直到达到指定的簇数目。

3. 密度聚类密度聚类是一种基于密度的聚类方法，它将数据点分为高密度区域和低密度区域。

密度聚类的核心思想是通过计算每个数据点的密度来确定簇的边界。

常用的密度聚类算法包括DBSCAN和OPTICS。

三、应用场景聚类分析在各个领域都有广泛的应用，下面介绍几个常见的应用场景。

1. 市场细分聚类分析可以帮助企业将市场细分为不同的消费者群体。

通过对消费者的购买行为、偏好和特征进行聚类分析，企业可以更好地了解不同群体的需求，从而制定个性化的营销策略。

2. 社交网络分析聚类分析可以帮助研究人员发现社交网络中的社区结构。

通过对社交网络中的节点（用户）进行聚类分析，可以揭示出节点之间的紧密关系和群体特征，从而更好地理解社交网络的组织结构和信息传播模式。

聚类分析_精品文档

1聚类分析内涵1.1聚类分析定义聚类分析（Cluste.Analysis）是一组将研究对象分为相对同质的群组(clusters)的统计分析技术.也叫分类分析(classificatio.analysis)或数值分类(numerica.taxonomy), 它是研究（样品或指标）分类问题的一种多元统计方法, 所谓类, 通俗地说, 就是指相似元素的集合。

聚类分析有关变量类型:定类变量,定量(离散和连续)变量聚类分析的原则是同一类中的个体有较大的相似性, 不同类中的个体差异很大。

1.2聚类分析分类聚类分析的功能是建立一种分类方法, 它将一批样品或变量, 按照它们在性质上的亲疏、相似程度进行分类.聚类分析的内容十分丰富, 按其聚类的方法可分为以下几种:(1)系统聚类法: 开始每个对象自成一类, 然后每次将最相似的两类合并, 合并后重新计算新类与其他类的距离或相近性测度. 这一过程一直继续直到所有对象归为一类为止. 并类的过程可用一张谱系聚类图描述.(2)调优法(动态聚类法): 首先对n个对象初步分类, 然后根据分类的损失函数尽可能小的原则对其进行调整, 直到分类合理为止.(3)最优分割法(有序样品聚类法): 开始将所有样品看成一类, 然后根据某种最优准则将它们分割为二类、三类, 一直分割到所需的K类为止. 这种方法适用于有序样品的分类问题, 也称为有序样品的聚类法.(4)模糊聚类法: 利用模糊集理论来处理分类问题, 它对经济领域中具有模糊特征的两态数据或多态数据具有明显的分类效果.(5)图论聚类法: 利用图论中最小支撑树的概念来处理分类问题, 创造了独具风格的方法.(6)聚类预报法：利用聚类方法处理预报问题, 在多元统计分析中, 可用来作预报的方法很多, 如回归分析和判别分析. 但对一些异常数据, 如气象中的灾害性天气的预报, 使用回归分析或判别分析处理的效果都不好, 而聚类预报弥补了这一不足, 这是一个值得重视的方法。

CH11 聚类分析

错误订正：CH4 抽样调查方法——二、抽样调查作业，3（2）222211222(1)ˆ()(1)10011000(0.55 1.50.3 1.20.15 1.8)0.0131100rri i i i ii i if D Y W f W n n σσ==-=-=-=⨯⨯+⨯+⨯=∑∑错误应改为：22211(1)ˆ()(1)10011000(0.55 1.50.3 1.20.15 1.8)0.0131100rri i i i ii i if D Y W f W n n σσ==-=-=-=⨯⨯+⨯+⨯=∑∑ 给大家带来的不便，非常抱歉~CH11 聚类分析1、下表给出6种精神治疗药物的3种临床测量指标数据，请利用谱系图做聚类令速可眠、LSD 、安定、吗啡、仙人球毒碱和酒精分别为123456 w w w w w w ，根据距离公式：()221,i k ij kjj dw w x x ==-∑首先构造距离矩阵：123456 w w w w w w123664560215272118026466230322213()048450190ij w w w d w w w ⨯⎛⎫⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭一）最短距离法：（聚合指数）1126,,,w w w 各自成为一类：126,,,h h h71313h w w h h ==，1313(,)(,)5D h h d w w ==，平台高度：7()5f h =2272123(,)min{(,),(,)}min{21,26}21D w h d w w d w w === 474143(,)min{(,),(,)}min{27,32}27D w h d w w d w w ===575153(,)min{(,),(,)}min{21,22}21D w h d w w d w w === 676163(,)min{(,),(,)}min{18,13}13D w h d w w d w w ===得新距离矩阵为：24567 w w w w h24567046623210484527019210130w w w w h ⎛⎫⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭82525h w w h h ==，2525(,)(,)6D h h d w w ==，平台高度：8()6f h =3484245686265787275(,)min{(,),(,)}min{46,48}46(,)min{(,),(,)}min{23,19}19(,)min{(,),(,)}min{21,21}21D w h d w w d w w D w h d w w d w w D h h d h w d h w ========= 得新距离矩阵为： 4678 w w h h46780452746013190210w w h h ⎛⎫⎪ ⎪⎪ ⎪ ⎪⎝⎭967h w h =，6767(,)(,)13D w h d w h ==，平台高度：9()13f h =4494647898687(,)min{(,),(,)}min{45,27}27(,)min{(,),(,)}min{19,21}19D w h d w w d w h D h h d h w d h h ======得新距离矩阵为： 489 w h h489046270190w h h ⎛⎫⎪⎪ ⎪⎝⎭1089h h h =，89(,)19D h h =，平台高度：10()19f h =54104849(,)min{(,),(,)}min{46,27}27D w h d w h d w h ===得新距离矩阵为： 410w h4100270w h ⎛⎫⎪⎝⎭11610h w h =，410(,)27D w h =，平台高度：11()27f h =所有点已聚为一类，停止计算。

聚类分析数据

聚类分析数据聚类分析是一种常用的数据分析方法，用于将一组数据划分为不同的类别或群组，使得同一类别内的数据相似度较高，不同类别之间的数据相似度较低。

聚类分析可以帮助我们发现数据中的潜在模式和结构，并为进一步的数据分析和决策提供重要参考。

在进行聚类分析之前，首先需要明确分析的目标和数据集。

假设我们要分析一批顾客的购买行为数据，以了解他们的购买偏好和行为模式，从而为市场营销策略提供支持。

我们收集了一份包含顾客ID、购买金额、购买频次等信息的数据集。

接下来，我们需要选择适当的聚类算法。

常用的聚类算法包括K均值聚类、层次聚类和密度聚类等。

在这里，我们选择使用K均值聚类算法进行分析。

K均值聚类是一种基于距离的聚类算法，通过计算数据点之间的距离，并将其划分为K 个类别。

在进行K均值聚类之前，我们需要对数据进行预处理。

常见的预处理方法包括数据标准化、缺失值处理和异常值处理等。

在这里，我们对购买金额和购买频次进行了数据标准化，以消除不同变量尺度之间的差异。

接下来，我们使用K均值聚类算法对数据进行聚类。

首先，我们需要选择合适的聚类数K。

一种常用的方法是通过观察不同K值下的聚类结果，选择合适的K 值。

在这里，我们选择K=3进行聚类。

然后，我们使用K均值聚类算法对数据进行迭代计算，直到达到收敛条件。

在每一次迭代中，算法会根据数据点与聚类中心的距离，将数据点分配到最近的聚类中心所代表的类别。

然后，更新聚类中心的位置，以使得同一类别内的数据点到聚类中心的距离最小化。

在完成聚类计算后，我们可以对聚类结果进行分析和解释。

一种常见的方法是绘制聚类结果的散点图，以便观察不同类别之间的分布情况。

此外，我们还可以计算每个类别的中心点，以了解不同类别的特征。

最后，我们可以根据聚类结果进行进一步的数据分析和决策。

例如，我们可以将顾客划分为不同的目标群体，针对不同群体制定个性化的营销策略，以提高市场竞争力和销售业绩。

综上所述，聚类分析是一种有效的数据分析方法，可以帮助我们发现数据中的潜在模式和结构。

caliniski-harabaz指数

caliniski-harabaz指数什么是caliniskiharabaz指数？Calinski-Harabasz指数，又被称为CH指数，是一种用来评估聚类算法效果的指标。

它基于聚类结果的离散程度和簇之间的分离程度来计算一个聚类的质量。

在聚类分析中，我们希望将相似的数据点分配到同一个簇中，同时不同簇之间的数据点应该有较大的差异。

CH指数正是为了这个目标而设计的。

CH指数计算公式如下：CH = (BSS / (k-1)) / (WSS / (n-k))其中，BSS是簇之间的方差，WSS是簇内的方差，k是簇的数量，n是样本总数。

下面，我们将一步一步讲解如何计算CH指数。

1. 计算数据的距离矩阵在计算CH指数之前，首先需要计算数据点之间的距离。

常见的距离度量方法有欧氏距离、曼哈顿距离等。

根据具体问题选择合适的距离度量方法，并计算样本之间的距离。

2. 进行聚类分析使用一个聚类算法，比如k-means算法，对数据进行聚类分析。

k-means 算法是一种常见的无监督学习算法，它将数据点分配到不同的簇中，使得每个簇内的数据点相似度最大化，而不同簇之间的数据点相似度最小化。

3. 计算簇内的方差对于每个簇，计算簇内所有数据点的方差。

方差可以衡量数据点与簇中心之间的差异程度，方差越小表示簇内的数据点越相似。

4. 计算簇之间的方差计算不同簇之间的方差。

簇之间的方差可以衡量不同簇之间的分离程度，方差越大表示不同簇之间的数据点差异程度越大。

5. 计算CH指数利用簇内方差和簇间方差计算CH指数。

CH指数越大，表示聚类效果越好。

现在，让我们通过一个简单的示例来理解如何计算CH指数。

假设我们有一组样本数据如下：[1,1], [1,2], [2,2], [3,3], [4,4], [4,3]1. 首先，我们计算数据点之间的距离矩阵。

距离矩阵如下：0 1 2 3 4 50 0 1 √2 √8 √18 √131 1 0 1 √4 √9 √82 √2 1 0 1 √5 √23 √8 √4 1 0 1 √24 √18 √9 √5 1 0 15 √13 √8 √2 √2 1 02. 然后，我们使用k-means算法进行聚类分析。

ch 聚类数据挖掘技术

可以作为一个独立的工具来获得数据的分布情况：聚类分析是获得数据分布情况的有效方法通过观察聚类得到的每个簇的特点;可以集中对特定的某些簇作进一步分析这在诸如市场细分目标顾客定位业绩估评生物种群划分等方面具有广阔的应用前景
聚类分析可以完成孤立点挖掘：许多数据挖掘算法试图使孤立点影响最小化;或者排除它们然而孤立点本身可能是非常有用的如在欺诈探测中;孤立点可能预示着欺诈行为的存在
广泛的应用领域
商务：帮助市场分析人员从客户信息库中发现不同的客户群;用购买模式来刻画不同的客户群的特征
土地使用：在地球观测数据库中识别土地使用情况相似的地区
保险业：汽车保险单持有者的分组城市规划：根据房子的类型;价值和地理分布对房子分
组生物学：推导植物和动物的分类;对基因进行分类
PAM作为最早提出的k中心点算法之一;它选用簇中位置最中心的对象作为代表对象;试图对n个对象给出k个划分
代表对象也被称为是中心点;其他对象则被称为非代表对象
最初随机选择k个对象作为中心点;该算法反复地用非代表对象来代替代表对象;试图找出更好的中心点;以改进聚类的质量
在每次迭代中;所有可能的对象对被分析;每个对中的一个对象是中心点;而另一个是非代表对象
五数据相似性的度量距离
距离越大;相似性越小点间距离与类间距离
类间距离基于点间距离计算距离函数应同时满足
1 di;j≥0 2 di;i= 0 3 di;j= dj;i 4 di;j≤di;k+ dk;j
▪常用点间距离—相异度
数据矢量x=x1;x2;…xn; y=y1;y2;…yn
欧式距离城区距离切比雪夫距离明科夫斯基距离 ……………
k中心点算法kmedoids

轮廓系数 ch值

轮廓系数 ch值轮廓系数（Silhouette Coefficient）是一种聚类算法评价指标，用于衡量在聚类结果中每个数据对象与所属的簇之间的紧密度和分类效果。

其值介于-1到1之间，取值越大，说明聚类效果越好。

轮廓系数计算方法如下：$ SCi = \frac {b_i - a_i}{max(a_i, b_i)} $其中，a表示当前数据对象i到同簇其他点的平均距离，b表示i到其他簇的所有点的平均距离中的最小值。

轮廓系数的取值范围是从-1到1的，轮廓系数值越接近于1，表明聚类的效果越好，轮廓系数越接近于-1则表示聚类效果越差。

如果轮廓系数的值接近于0，则表明数据对象i在它所处的簇内、簇外的距离相近，聚类划分不显著。

轮廓系数的特点：1. 轮廓系数具有无需先验知识、对聚类方法不受限、全局性的评价优点。

2. 轮廓系数的计算比较直观，易于实现，不需要迭代等运算操作。

3. 轮廓系数能够反映聚类的紧密性和分离度，既能反映簇内物品的相似度，又能反映簇间物品的差异性。

4. 提供了一种定量的评价聚类质量的方法，不仅适用于聚类分析领域，也可以适用于分类、推荐算法等领域的评价。

5. 不受聚类算法影响，所以比其他评价指标更加稳定。

然而，轮廓系数也有其缺点：1. 当簇数量很大时，轮廓系数会失效。

2. 当数据集规模很大时，轮廓系数计算复杂度比较高，难以实现。

3. 轮廓系数只能用于凸型簇的评价，不能处理非凸簇。

CH系数是Cluster Separation（簇分离）和Cluster Cohesion（簇内部连贯性）两个指标的组合。

其中簇分离指标表示簇与簇之间的距离，簇内连贯性指标表示簇内部点到簇中心的平均距离。

CH系数越大，表示聚类结果的质量越好。

1.用簇中心之间的距离表示簇之间的距离，计算各个簇之间的距离。

2.计算每个簇i内部点与簇中心的距离平方，求出每个簇的簇内连贯性。

3.将簇分离指标和簇内连贯性指标相加，得到CH系数。

除了CH系数和轮廓系数之外，还有其他的聚类算法评价指标，例如DB指数（Davies-Bouldin Index）、ARI（Adjusted Rand Index）和NMI（Normalized Mutual Information）等，可以根据具体情况选择适合的评价指标。

【聚类评价】Calinski-Harabaz（CH）

【聚类评价】Calinski-Harabaz（CH）Calinski-Harabaz（CH）CH指标通过计算类中各点与类中⼼的距离平⽅和来度量类内的紧密度，通过计算各类中⼼点与数据集中⼼点距离平⽅和来度量数据集的分离度，CH指标由分离度与紧密度的⽐值得到。

从⽽，CH越⼤代表着类⾃⾝越紧密，类与类之间越分散，即更优的聚类结果。

在scikit-learn中， Calinski-Harabasz Index对应的⽅法是metrics.calinski_harabaz_score.CH和轮廓系数适⽤于实际类别信息未知的情况，以下以K-means为例，给定聚类数⽬K，则：类内散度为：W(K)=∑k=1K∑C(j)=k||xj−x¯¯¯k||2 W(K)=∑k=1K∑C(j)=k||xj−x¯k||2 类间散度：B(K)=∑k=1Kak||x¯¯¯k−x¯¯¯||2 B(K)=∑k=1Kak||x¯k−x¯||2 则CH为：CH(K)=B(K)(N−K)W(K)(K−1) CH(K)=B(K)(N−K)W(K)(K−1)CH相对来说速度可能会更快。

在这⾥我⾃⼰码了⼀个kmeans的代码，计算并输出其中的ch和轮廓系数from sklearn.cluster import KMeansimport numpy as npimport pandas as pdimport matplotlib.pyplot as plt%matplotlib inlinefrom sklearn.datasets.samples_generator import make_blobsfrom sklearn.metrics import calinski_harabaz_scorefrom sklearn import metricsfrom sklearn import preprocessing# X为样本特征，Y为样本簇类别，共1000个样本，每个样本2个特征，共4个簇，簇中⼼在[-1,-1], [0,0],[1,1], [2,2]，簇⽅差分别为[0.4, 0.2, 0.2]X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1], [0,0], [1,1], [2,2]], cluster_std=[0.4, 0.2, 0.2, 0.2],random_state =9)plt.scatter(X[:, 0], X[:, 1], marker='o')plt.show()#X=np.array([[2,3,6],[8,7,9],[2,8,3],[3,6,1]])k=5y_pred = KMeans(n_clusters=k, random_state=9).fit_predict(X)plt.scatter(X[:, 0], X[:, 1], c=y_pred)plt.show()c=KMeans(n_clusters=k, random_state=7)y_pred = c.fit_predict(X)kmeans_model = c.fit(X)labels = kmeans_bels_print('这个是k={}次时的CH值：'.format(k),metrics.calinski_harabaz_score(X,y_pred))print('这个是k={}次时的轮廓系数：'.format(k),metrics.silhouette_score(X, labels, metric='euclidean'))。

python数据分析之聚类分析（clusteranalysis）

python数据分析之聚类分析（clusteranalysis）何为聚类分析聚类分析或聚类是对⼀组对象进⾏分组的任务，使得同⼀组（称为聚类）中的对象（在某种意义上）与其他组（聚类）中的对象更相似（在某种意义上）。

它是探索性数据挖掘的主要任务，也是统计数据分析的常⽤技术，⽤于许多领域，包括机器学习，模式识别，图像分析，信息检索，⽣物信息学，数据压缩和计算机图形学。

聚类分析本⾝不是⼀个特定的算法，⽽是要解决的⼀般任务。

它可以通过各种算法来实现，这些算法在理解群集的构成以及如何有效地找到它们⽅⾯存在显着差异。

流⾏的群集概念包括群集成员之间距离较⼩的群体，数据空间的密集区域，间隔或特定的统计分布。

因此，聚类可以表述为多⽬标优化问题。

适当的聚类算法和参数设置（包括距离函数等参数）使⽤，密度阈值或预期聚类的数量）取决于个体数据集和结果的预期⽤途。

这样的聚类分析不是⾃动任务，⽽是涉及试验和失败的知识发现或交互式多⽬标优化的迭代过程。

通常需要修改数据预处理和模型参数，直到结果达到所需的属性。

常见聚类⽅法常⽤的聚类算法分为基于划分、层次、密度、⽹格、统计学、模型等类型的算法，典型算法包括K均值（经典的聚类算法）、DBSCAN、两步聚类、BIRCH、谱聚类等。

K-means聚类算法中k-means是最常使⽤的⽅法之⼀，但是k-means要注意数据异常：数据异常值。

数据中的异常值能明显改变不同点之间的距离相识度，并且这种影响是⾮常显著的。

因此基于距离相似度的判别模式下，异常值的处理必不可少。

数据的异常量纲。

不同的维度和变量之间，如果存在数值规模或量纲的差异，那么在做距离之前需要先将变量归⼀化或标准化。

例如跳出率的数值分布区间是[0,1]，订单⾦额可能是[0,10000 000]，⽽订单数量则是[0,1000]，如果没有归⼀化或标准化操作，那么相似度将主要受到订单⾦额的影响。

DBSCAN有异常的数据可以使⽤DBSCAN聚类⽅法进⾏处理，DBSCAN的全称是Density-Based Spatial Clustering of Applications with Noise，中⽂含义是“基于密度的带有噪声的空间聚类”。

CH.7 聚类分析

32
至此，我们已经可以根据所选择的距离构成样本点间的距离表,样本点之间被连接起来。
G Gp
G1
G… 2
Gn
q
G1
0
d12
…
d1n
G2
┇
d21 ┇
0 ┇
d2n ┇
Gn
dn1
dn2
7
思考：样本点之间按什么刻画相似程度思考：样本点和小类之间按什么刻画相似程度思考：小类与小类之间按什么来刻画相似程度
8
§2 相似系数和距离
一、变量测量尺度的类型为了将样本进行分类，就需要研究样品之间的关系；而为了将变量进行分类，就需要研究变量之间的关系。但无论是样品之间的关系，还是变量之间的关系，都是用变量来描述的，变量的类型不同，描述方法也就不同。通常，变量按照测量它们的尺度不同，可以分为三类。 (1)间隔尺度。指标度量时用数量来表示，其数值由测量或计数、统计得到，如长度、重量、收入、支出等。一般来说，计数得到的数量是离散数量，测量得到的数量是连续数量。在间隔尺度中如果存在绝对零点，又称比例尺度。
12
2、极差规格化变换规格化变换是从数据矩阵的每一个变量中找出其最大值
和最小值，这两者之差称为极差，然后从每个变量的每个原始数据中减去该变量中的最小值，再除以极差，就得到规格化数据。即有：
xij min( xij )
x* ij
i1,2, ,n
Rj
(i 1,2,3, ,n; j 1,2,3, , p)
由此，我们的问题是如何来选择样品间相似的测度指标，如何将有相似性的类连接起来？
6
聚类分析根据一批样品的许多观测指标，按照一定的数学公式具体地计算一些样品或一些参数(指标)的相似程度，把相似的样品或指标归为一类，把不相似的归为一类。

聚类分析数据

聚类分析数据聚类分析是一种数据挖掘技术，用于将一组数据划分为不同的类别或者群组。

它可以匡助我们发现数据中的模式、关系和趋势，从而更好地理解数据和做出决策。

在本文中，我们将介绍聚类分析的基本概念、流程和常用的聚类算法，并通过一个实际案例来演示如何应用聚类分析来解决问题。

一、聚类分析的基本概念聚类分析是一种无监督学习方法，它不需要预先标记的训练数据，而是根据数据之间的相似性将其划分为不同的类别。

在聚类分析中，我们通常使用距离或者相似度作为衡量数据之间关系的指标。

常用的聚类算法包括K均值聚类、层次聚类和密度聚类等。

其中，K均值聚类是最常用的一种方法，它将数据划分为K个不重叠的类别，使得同一类别内的数据之间的距离最小化。

二、聚类分析的流程聚类分析的流程包括数据准备、特征选择、相似度计算、聚类算法选择和结果评估等步骤。

1. 数据准备：首先，我们需要采集和整理待分析的数据。

数据可以来自各种来源，如数据库、文本文件或者实验观测。

确保数据的完整性和准确性非常重要。

2. 特征选择：根据分析目的和数据特点，选择合适的特征进行聚类分析。

特征应具有区分度和代表性，能够区分不同类别的数据。

3. 相似度计算：计算数据之间的相似度或者距离。

常用的相似度计算方法包括欧氏距离、曼哈顿距离和余弦相似度等。

相似度计算的选择取决于数据的类型和特征的性质。

4. 聚类算法选择：根据数据的特点和分析目的，选择合适的聚类算法。

常用的聚类算法有K均值聚类、层次聚类和密度聚类等。

不同的算法适合于不同的数据类型和聚类目标。

5. 结果评估：评估聚类结果的质量和稳定性。

常用的评估指标包括轮廓系数、Davies-Bouldin指数和Calinski-Harabasz指数等。

评估结果可以匡助我们判断聚类的效果和调整参数。

三、聚类分析的应用案例为了更好地理解聚类分析的应用，我们以一个电商公司为例，通过对用户购买行为进行聚类分析，匡助公司制定个性化的营销策略。

matlab 聚类 ch指标

matlab 聚类 ch指标
本文将介绍在matlab中使用ch指标进行聚类分析的方法。

聚类分析是一种常见的数据挖掘方法，用于将数据样本划分为不同的组或类别。

ch 指标是一种用于评估聚类结果质量的指标，具有较高的准确性和可靠性。

本文将详细介绍 ch 指标的计算原理和在 matlab 中的实现方法，帮助读者更好地理解聚类分析和数据挖掘的基本原理。

同时，本文还将介绍如何通过调整聚类参数来优化聚类结果，并提供实例演示和代码示例，帮助读者快速掌握聚类分析技术和 ch 指标的应用。

- 1 -。