分式混合运算专项练习158题(有答案)
初二下分式混合计算练习1(附答案)

初二下分式混合计算练习1一.解答题(共40小题)1.计算:(1)(﹣1)2016+x0﹣+(2)÷.2.化简:(a2﹣4)÷.3.(1)计算()﹣1+|1﹣|﹣(π﹣3)0﹣;(2)化简•÷.4.计算:÷•.5.计算:.6.化简分式:.7.化简:.8.计算:•.9.计算:.10.计算:÷(x+5)•.11.计算:÷(x+y).12.计算:(1)(2)(+)÷.13.计算:(1)÷;(2)(﹣)•(x﹣y)2.14.计算:(1)(xy﹣x2)÷(2).15.计算:•.16..17.化简:(xy﹣x2)÷÷.18.化简:+.19.计算﹣.20.化简:.21.化简:a﹣b﹣.22.化简:(a+1﹣)•.23.计算:(﹣).24.计算:(1)(x﹣y)2﹣(x﹣2y)(x+y)(2)÷(2x﹣)25.化简:(x﹣5+)÷.26.先化简,再求值:÷(1+),其中x=﹣1.27.先化简,再求值:(1﹣)÷,从﹣1,2,3中选择一个适当的数作为x值代入.28.先化简再求值:,其中x满足x2+x﹣2=0.29.先化简:÷+,再求当x+1与x+6互为相反数时代数式的值.30.先化简,再求值:(+)÷,其中x=6.31.先化简,再求值:(1﹣)÷﹣,其中x2+2x﹣15=0.32.先化简,再求值:(﹣1)÷,其中x=2+.33.先化简,再求值:÷•,其中a=2016.34.先化简,再求值:(﹣)÷,其中x满足2x+4=0.35.先化简,再求值:(),其中x=2.36.先化简,再求值:(﹣)÷,其中x=﹣.37.先化简,再求值:(﹣x﹣1)÷,其中x=,y=.38.化简+,并代入原式有意义的数进行计算.39.化简:.40.化简下列各式(1)(a﹣b)2+(2a﹣b)(a﹣2b)(2).初二下分式混合计算练习1参考答案与试题解析一.解答题(共40小题)1.(2016•徐州)计算:(1)(﹣1)2016+x0﹣+(2)÷.【分析】(1)先计算负整数指数幂、零指数幂、化简二次根式然后计算加减法;(2)利用完全平方公式、平方差公式、化除法为乘法进行约分化简.【解答】解:(1)原式=1+1﹣3+2=1;(2)原式=×=x.【点评】本题考查了分式的乘除法、实数的运算以及负整数指数幂等知识点,属于基础题.2.(2016•市南区一模)化简:(a2﹣4)÷.【分析】原式利用除法法则变形,约分即可得到结果.【解答】解:原式=(a+2)(a﹣2)•=a(a﹣2)=a2﹣2a.【点评】此题考查了分式的乘除法,熟练掌握运算法则是解本题的关键.3.(2016•如皋市校级二模)(1)计算()﹣1+|1﹣|﹣(π﹣3)0﹣;(2)化简•÷.【分析】(1)原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及立方根定义计算即可得到结果;(2)原式利用除法法则变形,约分即可得到结果.【解答】解:(1)原式=2+﹣1﹣1﹣2=﹣2;(2)原式=﹣••(a+1)(a﹣1)=﹣(a﹣2)(a+1)=﹣a2+a+2.【点评】此题考查了分式的乘除法,以及实数的运算,熟练掌握运算法则是解本题的关键.4.(2016秋•金平区期末)计算:÷•.【分析】原式利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果.【解答】解:原式=÷•=••=.【点评】此题考查了分式的乘除法,分式乘除法的关键是约分,约分的关键是找公因式.5.(2015•眉山)计算:.【分析】将每个分式的分子、分母分解因式后将除法变为乘法后约分即可.【解答】解:=•=.【点评】本题考查了分式的乘除法,解题的关键是能够对分式的分子、分母进行因式分解,难度不大.6.(2015•深圳模拟)化简分式:.【分析】原式利用除法法则变形,约分即可得到结果.【解答】解:原式=•=.【点评】此题考查了分式的乘除法,熟练掌握运算法则是解本题的关键.7.(2015秋•怀集县期末)化简:.【分析】两个分式相除,先根据除法法则转化为乘法运算.然后再进行约分、化简即可.【解答】解:==.【点评】解答分式的除法运算,关键把除法运算转化成乘法运算,然后进行约分.8.(2015春•绿园区期末)计算:•.【分析】先进行因式分解,再约分即可求解.【解答】解:•=•=.【点评】本题主要考查了分式的乘除法,解题的关键是正确因式分解.9.(2015秋•台山市期末)计算:.【分析】原式利用除法法则变形,约分即可得到结果.【解答】解:原式=•=.【点评】此题考查了分式的乘除法,熟练掌握运算法则是解本题的关键.10.(2015秋•仙游县期末)计算:÷(x+5)•.【分析】原式利用除法法则变形,约分即可得到结果.【解答】解:原式=••=2.【点评】此题考查了分式的乘除法,熟练掌握运算法则是解本题的关键.11.(2015秋•祁阳县校级期中)计算:÷(x+y).【分析】原式利用除法法则变形,约分即可得到结果.【解答】解:原式=••=.【点评】此题考查了分式的乘除法,熟练掌握运算法则是解本题的关键.12.(2015秋•北京校级期中)计算:(1)(2)(+)÷.【分析】(1)先对分子分母因式分解,再约分,把除法化为乘法,再约分即可;(2)先算括号里面的,再把除法化为乘法,再约分即可.【解答】解:(1)原式=••,=﹣2;(2)原式=•=.【点评】本题考查了分式的乘除法,分式的乘除混合运算一般是统一为乘法运算,如果有乘方,还应根据分式乘方法则先乘方,即把分子、分母分别乘方,然后再进行乘除运算.13.(2015春•陕西校级月考)计算:(1)÷;(2)(﹣)•(x﹣y)2.【分析】(1)先运用分式的除法法则将分式的除法转化为乘法,同时将分子、分母分解因式,然后约分化简;(2)首先把括号里的进行通分,然后进行乘法运算.【解答】解:(1)原式=•(2分)=;(4分)(2)原式=•(x﹣y)2(6分)=•(x﹣y)2(7分)=x﹣y.(8分)【点评】(1)是分式的除法运算,分式的除法和实数的除法一样,均是转化为乘法来完成的;(2)是分式的混合运算,本题中分式的减法运算作为因式,一定要先运算减法,再做乘法,同时将分子、分母中能够分解因式的部分进行因式分解.14.(2015秋•夏津县校级月考)计算:(1)(xy﹣x2)÷(2).【分析】(1)原式利用除法法则变形,约分即可得到结果;(2)原式利用除法法则变形,约分即可得到结果.【解答】解:(1)原式=﹣x(x﹣y)•=﹣x2y;(2)原式=•=.【点评】此题考查了分式的乘除法,熟练掌握运算法则是解本题的关键.15.(2014•滨州)计算:•.【分析】把式子中的代数式进行因式分解,再约分求解.【解答】解:•=•=x【点评】本题主要考查分式的乘除法,解题的关键是进行因式分解再约分.16.(2014春•常宁市校级月考).【分析】把式子中的代数式进行因式分解,再约分求解.【解答】解:÷=×=.【点评】本题主要考查分式的乘除法,解题的关键是进行因式分解再约分.17.(2013•广东模拟)化简:(xy﹣x2)÷÷.【分析】先运用分式的除法法则将分式的除法转化为乘法,同时将分子、分母中的多项式分解因式,然后约分化简.【解答】解:原式=﹣x(x﹣y)•=﹣y.【点评】本题主要考查了分式的除法运算,做题时把除法运算转化为乘法运算,然后进行解答.18.(2016•甘孜州)化简:+.【分析】先通分变为同分母分式,然后再相加即可解答本题.【解答】解法一:+=+==.解法二:+=+=+=.【点评】本题考查分式的加减法,解题的关键是明确分式的加减法的计算方法.19.(2016•南京)计算﹣.【分析】首先进行通分运算,进而合并分子,进而化简求出答案.【解答】解:﹣=﹣==.【点评】此题主要考查了分式的加减运算,正确进行通分运算是解题关键.20.(2016•十堰)化简:.【分析】首先把第一个分式的分子、分母分解因式后约分,再通分,然后根据分式的加减法法则分母不变,分子相加即可.【解答】解:=++2=++2=++==【点评】本题考查了分式的加减法法则、分式的通分、约分以及因式分解;熟练掌握分式的通分是解决问题的关键.21.(2016•福州)化简:a﹣b﹣.【分析】先约分,再去括号,最后合并同类项即可.【解答】解:原式=a﹣b﹣(a+b)=a﹣b﹣a﹣b=﹣2b.【点评】此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.22.(2016•泸州)化简:(a+1﹣)•.【分析】先对括号内的式子进行化简,再根据分式的乘法进行化简即可解答本题.【解答】解:(a+1﹣)•====2a﹣4.【点评】本题考查分式的混合运算,解题的关键是明确分式的混合运算的计算方法.23.(2016•聊城)计算:(﹣).【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.【解答】解:原式=•=•=﹣.【点评】此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.24.(2016•重庆)计算:(1)(x﹣y)2﹣(x﹣2y)(x+y)(2)÷(2x﹣)【分析】(1)根据平方差公式、多项式乘多项式法则进行计算;(2)根据分式混合运算法则进行计算.【解答】解:(1)(x﹣y)2﹣(x﹣2y)(x+y)=x2﹣2xy+y2﹣x2+xy+2y2=﹣xy+3y2;(2)÷(2x﹣)=×=.【点评】本题考查的是整式的混合运算、分式的混合运算,掌握平方差公式、多项式乘多项式法则、分式的混合运算法则是解题的关键.25.(2016•陕西)化简:(x﹣5+)÷.【分析】根据分式的除法,可得答案.【解答】解:原式=•=(x﹣1)(x﹣3)=x2﹣4x+3.【点评】本题考查了分式混合运算,利用分式的除法转化成分式的乘法是解题关键.26.(2016•抚顺)先化简,再求值:÷(1+),其中x=﹣1.【分析】分式的化简,要熟悉混合运算的顺序,分子、分母能因式分解的先因式分解;除法要统一为乘法运算,注意化简后,将,代入化简后的式子求出即可.【解答】解:=÷(+)=÷=×=,把,代入原式====.【点评】此题主要考查了分式混合运算,要注意分子、分母能因式分解的先因式分解;除法要统一为乘法运算是解题关键.27.(2016•安顺)先化简,再求值:(1﹣)÷,从﹣1,2,3中选择一个适当的数作为x值代入.【分析】先根据分式混合运算的法则把原式进行化简,再选取合适的x的值代入进行计算即可.【解答】解:原式=•=,当x=3时,原式==3.【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.28.(2016•乐山)先化简再求值:,其中x满足x2+x﹣2=0.【分析】原式通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把已知等式变形后代入计算即可求出值.【解答】解:原式=•=•=x(x+1)=x2+x,∵x2+x﹣2=0,∴x2+x=2,则原式=2.【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.29.(2016•曲靖)先化简:÷+,再求当x+1与x+6互为相反数时代数式的值.【分析】先把分子分母因式分解和除法运算化为乘法运算,再约分得到原式=,然后利用x+1与x+6互为相反数可得到原式的值.【解答】解:原式=•+=+=,∵x+1与x+6互为相反数,∴原式=﹣1.【点评】本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.30.(2016•江西)先化简,再求值:(+)÷,其中x=6.【分析】先算括号里面的,再算除法,最后把x=6代入进行计算即可.【解答】解:原式=÷=÷=•=,当x=6时,原式==﹣.【点评】本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.31.(2016•齐齐哈尔)先化简,再求值:(1﹣)÷﹣,其中x2+2x﹣15=0.【分析】先算括号里面的,再算除法,最后算减法,根据x2+2x﹣15=0得出x2+2x=15,代入代数式进行计算即可.【解答】解:原式=•﹣=﹣=,∵x2+2x﹣15=0,∴x2+2x=15,∴原式=.【点评】本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.32.(2016•营口)先化简,再求值:(﹣1)÷,其中x=2+.【分析】首先通分计算小括号里的算式,然后把除法转化成乘法进行约分计算,最后再把x=2+代入计算即可.【解答】解:(﹣1)÷=(﹣)÷=×==x﹣2当x=2+时,原式=2+﹣2=.【点评】此题主要考查了分式的化简求值问题,要熟练掌握,解答此题的关键是要明确:在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.33.(2016•黄石)先化简,再求值:÷•,其中a=2016.【分析】先算除法,再算乘法,把分式化为最简形式,最后把a=2016代入进行计算即可.【解答】解:原式=••=(a﹣1)•=a+1,当a=2016时,原式=2017.【点评】本题考查的是分式的化简求值,在解答此类问题时要注意把分式化为最简形式,再代入求值.34.(2016•广安)先化简,再求值:(﹣)÷,其中x满足2x+4=0.【分析】原式括号中利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出已知方程的解得到x的值,代入计算即可求出值.【解答】解:原式=•=,由2x+4=0,得到x=﹣2,则原式=5.【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.35.(2016•常德)先化简,再求值:(),其中x=2.【分析】先算括号里面的,再算除法,最后把x的值代入进行计算即可.【解答】解:原式=[+]÷[﹣]=÷=÷=•=,当x=2时,原式==.【点评】本题考查的是分式的化简求值,在解答此类问题时要注意把分式化为最简形式,再代入求值.36.(2016•益阳)先化简,再求值:(﹣)÷,其中x=﹣.【分析】先括号内通分,然后计算除法,最后代入化简即可.【解答】解:原式==.当时,原式=4.【点评】本题考查分式的化简求值,解题的关键熟练掌握分式的混合运算法则,注意运算顺序,属于基础题,中考常考题型.37.(2016•烟台)先化简,再求值:(﹣x﹣1)÷,其中x=,y=.【分析】首先将括号里面进行通分,进而将能分解因式的分解因式,再化简求出答案.【解答】解:(﹣x﹣1)÷,=(﹣﹣)×=×=﹣,把x=,y=代入得:原式=﹣=﹣1+.【点评】此题主要考查了分式的化简求值,正确因式分解是解题关键.38.(2016•南昌校级自主招生)化简+,并代入原式有意义的数进行计算.【分析】先分解因式化简分式,再利用分式有意义的条件求原式即可.【解答】解:简+=+=+=1,当取x≠1或﹣1时,原式=1.【点评】本题主要考查了分式的化简求值,解题的关键是熟记分式有意义的条件.39.(2015•长乐市一模)化简:.【分析】原式第二项约分后,去括号合并即可得到结果.【解答】解:原式=a+b﹣=a+b﹣(a+b)=a+b﹣a﹣b=0.【点评】此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.40.(2016•重庆校级模拟)化简下列各式(1)(a﹣b)2+(2a﹣b)(a﹣2b)(2).【分析】(1)利用乘法公式展开,然后合并同类项即可;(2)先把括号内通分后进行同分母的减法运算,再把分子分母因式分解和除法运算化为乘法运算,然后约分即可.【解答】解:(1)原式=a2﹣2ab+b2+2a2﹣ab﹣4ab+2b2=3a2﹣7ab+3b2;(2)原式=、====.【点评】本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了整式的混合运算.第21页(共21页)。
分式的混合运算专项训练—2023-2024学年七年级数学下册(沪科版)(解析版)

分式的混合运算专项训练考卷信息:本套训练卷共40题,题型针对性较高,覆盖面广,选题有深度,可加强学生对分式的混合运算各种方法的理解!1.(2023上·山东菏泽·七年级统考期中)计算:(1)3x −61−x−x+5x2−x(2)x−yx+3y ÷x2−y2x2+6xy+9y2−2yx+y【答案】(1)8x(2)1【分析】(1)先对各个分式分子分母因式分解,再通分,利用分式加减运算法则运算后约分即可得到答案;(2)先对各个分式分子分母因式分解,根据分式混合运算顺序,先计算乘除,再利用分式加减运算法则运算后约分即可得到答案.【详解】(1)解:3x −61−x−x+5x2−x=3(x−1)x(x−1)+6xx(x−1)−x+5x(x−1)=8x−8 x(x−1)=8(x−1) x(x−1)=8x;(2)解:x−yx+3y ÷x2−y2x2+6xy+9y2−2yx+y=x−yx+3y ⋅(x+3y)2(x+y)(x−y)−2yx+y=x+3yx+y −2yx+y=x+y x+y=1.【点睛】本题考查分式混合运算,涉及通分、约分、因式分解等知识.掌握分式混合运算法则及运算顺序,熟记因式分解的方法,准确找到最简公分母通分是解决分式混合运算的关键.2.(2023上·天津东丽·七年级统考期末)计算(1)4a 3b⋅b 2a 4÷(1a )2 (2)a a−1÷a 2−a a 2−1−1a−1【答案】(1)23a ;(2)a a−1【分析】(1)先将除法写成乘法,再计算乘法,分子、分母约分化为最简分式;(2)先将除法写成乘法,计算乘法得到最简分式,再与后一项相减即可得到答案.【详解】(1)原式=4a 3b ⋅b 2a 4⋅a 2=23a ;(2)原式=a a−1⋅(a+1)(a−1)a(a−1)−1a−1=a+1a−1−1a−1=a a−1. 【点睛】此题考查分式的混合运算,先将除法化为乘法,再约分结果,再计算加减法.3.(2023上·山东菏泽·七年级统考期末)计算(1)12m 2−9−2m−3(2)(2a −12a a+2)÷a−4a 2+4a+4【答案】(1)−2m+3(2)2a 2+4a【分析】(1)通分计算即可;(2)先通分算减法,再算除法.【详解】(1)解:原式=12−2(m+3)(m+3)(m−3)=−2(m −3)(m +3)(m −3)=−2m+3;(2)解:原式=[2a(a+2)a+2−12a a+2]⋅(a+2)2a−4=2a 2+4a −12a a +2⋅(a +2)2a −4=2a 2−8a a +2⋅(a +2)2a −4=2a(a−4)a+2⋅(a+2)2a−4=2a(a+2)=2a2+4a,【点睛】此题考查分式的混合运算,通分、因式分解和约分是解答的关键.4.(2023下·江苏常州·七年级校考期中)计算:(1)2x+y −1x−y.(2)(1−1m+1)÷m2m+1.【答案】(1)x−3yx2−y2(2)1m【分析】(1)根据异分母分式减法运算法则,先通分,再根据同分母分数减法运算求解即可得到答案;(2)根据分式混合运算法则及运算顺序,先算括号里的异分母分式减法运算,再利用乘除互化将除法转化为乘法运算求解即可得到答案.【详解】(1)解:2x+y −1x−y=2(x−y)(x+y)(x−y)−x+y(x+y)(x−y)=2x−2y−x−y (x+y)(x−y)=x−3y (x+y)(x−y)=x−3yx2−y2;(2)解:(1−1m+1)÷m2m+1=(m+1m+1−1m+1)÷m2m+1=m+1−1m+1×m+1m2=mm+1×m+1m2=1m.【点睛】本题考查分式混合运算,涉及分式加减乘除运算、通分、约分等知识,熟练掌握分式混合运算法则及运算顺序是解决问题的关键.5.(2023下·江苏常州·七年级统考期中)计算:(1)4ac3b ⋅(−6b22ac2)(2)a+2a−3÷a2−42a−6(3)x23x−9−3x−3(4)(4a+2+a−2)÷aa+2【答案】(1)−4bc(2)2a−2(3)x+33(4)a【分析】(1)根据分式的乘法运算法则进行计算即可得到答案;(2)先将分式除法变为乘法,再根据分式的乘法运算法则和平方差公式进行计算即可得到答案;(3)先进行通分,再计算分式减法,最后利用平方差进行约分即可得到答案;(4【详解】(1)解:4ac3b ⋅(−6b22ac2)=−4bc;(2)解:a+2a−3÷a2−42a−6=a+2a−3×2(a−3)(a+2)(a−2)=2a−2;(3)解:x23x−9−3x−3=x23(x−3)−3×33(x−3)=x2−93(x−3)=(x+3)(x−3)3(x−3)=x+33;(4)解:(4a+2+a−2)÷aa+2=(4a+2+(a−2)(a+2)a+2)×a+2a=4+a2−4a+2×a+2a=a.【点睛】本题考查了分式的混合运算,平方差公式,熟练掌握相关运算法则是解题关键.6.(2023下·河南南阳·七年级统考期中)计算:(1)2x−6x2−6x+9÷3−xx2−9(2)(8a+3+a−3)÷a2+2a+1a+3【答案】(1)−2x+6x−3(2)a−1a+1【分析】(1)根据完全平方式、平方差公式化简,再把除法转化成乘法计算即可;(2)括号内先通分,再根据完全平方公式、平方差公式化简,再把除法转化成乘法计算即可.【详解】(1)解:原式=2(x−3)(x−3)2×(x+3)(x−3)3−x=−2x+6x−3(2)解:原式=(8+a2−9a+3)×a+3(a+1)2=(a+1)(a−1)×1(a+1)2=a−1a+1【点睛】本题考查分式计算,掌握完全平方式、平方差公式是关键.7.(2023下·江苏淮安·七年级校考期中)计算:(1)a2a−1−a−1(2)(a+2−42−a )÷(aa−2)【答案】(1)1a−1(2)a【分析】(1)先对原式通分变为同分母的分式,再相减即可解答本题;(2)先将括号内的进行计算,再将除法转换为乘法后,再约分即可得到答案.【详解】(1)a2a−1−a−1=a2 a−1−(a+1)(a−1)a−1=a2−(a+1)(a−1)a−1=a 2−(a 2−1)a−1 =a 2−a 2+1a−1=1a−1(2)(a +2−42−a )÷(a a−2)=(a +2+4a−2)÷(a a−2) =a 2−4+4a−2÷(a a−2) =a 2a−2×a−2a=a 【点睛】本题主要考查了分式的混合运算,解题的关键是明确分式混合运算的计算方法.8.(2023上·山东泰安·七年级统考期中)计算(1)x x−1−x 2+2x x 2−2x+1÷x+2x ; (2)(a+2a−2−a a+2)÷3a+2a 2+2a .【答案】(1)−x (x−1)2(2)2a a−2【分析】该题主要考查了分式的混合运算问题;(1)先算除法再算减法即可;(2)先算括号再算除法即可.【详解】(1)原式=x x−1−(x+2)x (x−1)2⋅x x+2=x x −1−x 2(x −1)2=x (x −1)−x 2(x −1)2=−x (x−1)2;=−x x 2−2x +1(2)原式=[(a+2)2(a−2)(a+2)−a(a−2)(a−2)(a+2)]÷3a+2a(a+2)=2(3a+2)(a−2)(a+2)⋅a(a+2)3a+2=2aa−2.9.(2023上·山东烟台·七年级统考期中)计算:(1)b2ca ×acb÷(−ca)2(2)a2−4a ÷(a+1−5a−4a)【答案】(1)a2b(2)a+2a−2【分析】(1)根据分式的乘除运算法则进行化简即可求出答案.(2)根据分式的加减运算以及乘除运算法则即可求出答案.【详解】(1)解:原式=bc2⋅a2c2=a2b.(2)解:原式=(a+2)(a−2)a ÷a2−4a+4a=(a+2)(a−2)a⋅a(a−2)2=a+2a−2.【点睛】本题考查分式的混合运算,解题的关键是熟练运用分式的加减运算法则以及乘除运算法则,本题属于基础题型.10.(2023上·山东东营·七年级校考期中)计算下列各式.(1)(−a2bc )3⋅(−c2a)2÷(bca)4;(2)a2a−1−a−1.【答案】(1)−a8bc3(2)1a−1【分析】(1)先根据积的乘方等于乘方的积,幂的乘方计算各分式,然后利用同底数幂相乘,底数不变指数相加;同底数幂相除,底数不变指数相减;进行分式的乘除运算即可;(2)先加括号,进行通分,根据平方差公式求解多项式乘多项式,然后进行加减运算即可.【详解】(1)解:(−a2bc )3⋅(−c2a)2÷(bca)4=−a6b3c3⋅c4a2÷b4c4a4=−a4b3c⋅a4 b4c4=−a8bc3;(2)解:a2a−1−a−1=a2a−1−(a+1)=a2−(a+1)(a−1)a−1=a2−a2+1a−1=1a−1.【点睛】本题考查了积的乘方,幂的乘方,分式的乘除混合运算,同底数幂的乘除运算,异分母分式的减法运算,平方差公式等知识.解题的关键在于熟练掌握各知识的运算法则并正确的运算.11.(2023上·河南许昌·七年级统考期末)计算:(3xx−1−xx+1)⋅x2−1x+1【答案】2x2+4xx+1【分析】利用分式的混合运算顺序:先括号内的分式减法运算,再括号外的分式2乘法运算即可化简原式.【详解】解:(3xx−1−xx+1)⋅x2−1x+1=3x(x+1)−x(x−1)(x−1)(x+1)⋅(x−1)(x+1)x+1=3x2+3x−x2+xx+1=2x2+4xx+1.【点睛】本题考查分式的混合运算,熟练掌握分式的混合运算法则并正确求解是解答的关键.12.(2023上·重庆沙坪坝·七年级重庆一中校考阶段练习)计算:(1)(x−y)2−x(x−3y)(2)m2−25m+3÷(1−8m+3)【答案】(1)xy+y2(2)m+5【分析】(1)先用完全平方公式与单贡式乘以多项式法则展开,再合并同类项即可.(2)先计算括号内的,再计算除法,用除法法则转化成乘法计算即可.【详解】(1)解:原式=x2−2xy+y2−x2+3xy=xy+y2;(2)解:原式=(m+5)(m−5)m+3÷m−5m+3=(m+5)(m−5)m+3⋅m+3m−5=m+5.【点睛】本题考查多项式混合运算,分式混合运算,熟练掌握多项式与分式混合运算法则是解题的关键.13.(2023上·山东菏泽·七年级统考期中)计算(1)4x22x−3+93−2x(2)3b24a2⋅(a−6b)(3)xx−1−x+3x2−1⋅x2+2x+1x+3(4)(1x−4+1x+4)÷2x2−16【答案】(1)2x+3(2)−b8a(3)−1x−1(4)x【分析】(1)利用分式的加法计算即可.(2)利用分式的乘法计算即可.(3)利用分式的混合运算法则计算即可.(4)利用分式的混合运算法则计算即可.【详解】(1)4x22x−3+93−2x=4x22x−3−92x−3=4x2−92x−3=(2x−3)(2x+3)2x−3=2x+3.(2)3b24a2⋅(a−6b)=−b8a.(3)xx−1−x+3x2−1⋅x2+2x+1x+3=xx−1−x+3(x−1)(x+1)⋅(x+1)2x+3=xx−1−x+1x−1=x−x−1x−1=−1x−1.(4)(1x−4+1x+4)÷2x2−16=(1x−4+1x+4)×(x+4)(x−4)2=1x−4×(x+4)(x−4)2+1x+4×(x+4)(x−4)2=x+42+x−42=x.【点睛】本题考查了分式的混合运算,熟练掌握运算法则是解题的关键.14.(2023下·重庆南岸·七年级统考期末)计算:(1)a−ba+b ÷a2−aba3−ab2;(2)(2x−3−1x)⋅x2−3xx2+6x+9【答案】(1)a−b(2)1x+3【分析】(1)直接根据分式的除法法则进行计算即可;(2)先将括号里面通分运算,再利用分式的混合运算法则计算得出答案.【详解】(1)解:原式=a−ba+b ⋅a3−ab2 a2−ab=a−ba+b⋅a(a2−b2)a(a−b)=(a+b)(a−b)a+b=a−b;(2)解:原式=[2x−(x−3)x(x−3)]⋅x(x−3)(x+3)2=x+3x(x−3)⋅x(x−3)(x+3)2=1x+3.【点睛】本题考查的是分式的混合运算,熟知分式的混合运算法则是解答此题的关键.15.(2023下·重庆北碚·七年级统考期末)计算:(1)2a2b÷(−a2b )2⋅a4b2;(2)(a2+3aa−3−3)÷a2+9a2−9.【答案】(1)2ab(2)a+3【分析】(1)先算乘方,再算乘除,即可解答;(2)先利用异分母分式加减法法则计算括号里,再算括号外,即可解答.【详解】(1)原式=2a2b⋅4b2a2⋅a 4b2=2ab(2)原式=(a2+3aa−3−3a−9a−3)⋅a2−9a2+9=a2+9a−3⋅(a+3)(a−3)a2+9=a+3【点睛】本题考查了分式的混合运算,准确熟练地进行计算是解题的关键.16.(2023下·广东清远·七年级统考期中)分式计算:(1)3x−3−xx−3(2)yxy+x +1xy−x(3)x2x+1−x+1(4)(3xx−2−xx+2)÷xx2−4.【答案】(1)−1(2)y2+1xy2−x(3)1x+1(4)2x+8【分析】(1)根据同分母的分式的加减法进行计算即可求解;(2)根据异分母的分式的加法进行计算即可求解;(3)根据分式与整式的运算进行计算即可求解;(4)先计算括号的分式的减法,再将除法转化为乘法进行计算即可求解.【详解】(1)3x−3−xx−3=3−xx−3 =−1;(2)yxy+x +1xy−x=y(y−1)+y+1x(y+1)(y−1)=y2+1xy2−x;(3)x2x+1−x+1=x2−(x−1)(x+1)x+1=x2−x2+1x+1=1x+1;(4)(3xx−2−xx+2)÷xx2−4=3x(x+2)−x(x−2)(x−2)(x+2)⋅(x+2)(x−2)x=3(x+2)−(x−2)=3x+6−x+2=2x+8.【点睛】本题考查了分式的混合运算,熟练掌握分式的运算法则是解题的关键.17.(2023上·山东济宁·七年级统考期末)计算:(xx+2−2x+2)÷x2−4x+4x+2.【答案】1x−2【分析】首先运用同分母分式减法法则计算括号内的,再利用分式除法运算法则求解即可.【详解】解:(xx+2−2x+2)÷x2−4x+4x+2=x−2x+2÷x2−4x+4x+2=x−2x+2⋅x+2x2−4x+4=x−2x+2⋅x+2(x−2)2=1x−2.【点睛】本题主要考查了分式的混合运算,解题的关键是熟练运用分式的减法运算法则和乘除运算法则18.(2023上·山东泰安·七年级统考期中)计算:(1)2x2x−y +yy−2x;(2)1−x−yx+2y ÷x2−y2x2+4xy+4y2.【答案】(1)1(2)−yx+y【分析】(1)本题考查了分式的加减,利用同分母分式加减法法则进行计算,即可解答;(2)本题考查了分式的混合运算,先算分式的除法,再算加减,即可解答;【详解】(1)解:原式=2x−y2x−y=2x−y 2x−y=1;(2)解:原式=1−x−yx+2y ×(x+2y)2(x+y)(x−y)=1−x+2y x+y=−yx+y.19.(2023下·江苏常州·七年级常州市第二十四中学校考期中)计算:(1)6x+3+2xx+3;(2)a2−b2a ÷(a+b2−2aba).【答案】(1)2(2)a+ba−b【分析】(1)根据同分母分式加法计算法则求解即可;(2)根据分式的混合计算法则求解即可.【详解】(1)解:6x+3+2xx+3=6+2x x+3=2(x+3) x+3=2;(2)解:a2−b2a ÷(a+b2−2aba)=a2−b2a÷a2+b2−2aba=(a+b)(a−b)a÷(a−b)2a=(a+b)(a−b)a⋅a(a−b)2=a+ba−b.【点睛】本题主要考查了分式的混合计算,同分母分式加法,熟知相关计算法则是解题的关键.20.(2023上·山东菏泽·七年级统考期末)计算:(1)4x2−1−2x2+x;(2)(2x2x−2−x−2)÷2x2+8x2−4.【答案】(1)2x2−x(2)x+22【分析】(1)利用提公因式和平方差公式进行计算即可; (2)利用提公因式和平方差公式进行计算即可. 【详解】(1)4x 2−1−2x 2+x=4(x +1)(x −1)−2x (x +1)=4x −2(x −1)x (x +1)(x −1)=2x +2x (x +1)(x −1)=2x 2−x ; (2)(2x 2x−2−x −2)÷2x 2+8x 2−4=[2x 2x −2−(x +2)(x −2)x −2]÷2x 2+8x 2−4=(2x 2−x 2+4x −2)⋅(x +2)(x −2)2(x 2+4)=x 2+4x −2⋅(x +2)(x −2)2(x 2+4) =x+22.【点睛】本题考查了分式的混合运算,熟练运用分式运算法则和平方差公式是解题的关键. 21.(2023下·江西鹰潭·七年级统考期末)先化简x 2−4x+4x 2−1÷x−2x+1+2x−1,再从−2,−1,1,2中选一个合适的整数作为x 的值代入求值. 【答案】x x−1,x =−2时,原式=23【分析】先把除法转化为乘法,再约分,然后计算加法,由分式有意义的条件确定x 的值,最后代入化简后的式子即可求出答案. 【详解】解:x 2−4x+4x 2−1÷x−2x+1+2x−1=(x −2)2(x +1)(x −1)⋅x +1x −2+2x −1 =x −2x −1+2x −1=xx−1,由分式有意义的条件可知:x ≠−1,x ≠1,x ≠2, ∴x =−2, 当x =−2时, 原式=−2−2−1=23.【点睛】本题考查分式的化简求值,熟练掌握运算法则是解题的关键. 22.(2023下·福建宁德·七年级统考期末)先化简,再求值:(1−a a+1)÷a+3a 2+2a+1,其中a =−5.【答案】a+1a+3,2【分析】先根据分式的减法法则算括号内的减法,再根据分式的除法法则把除法变成乘法,再根据分式的乘法法则进行计算,最后代入求出答案即可. 【详解】解:(1−aa+1)÷a+3a 2+2a+1 =1a +1⋅(a +1)2a +3 =a +1a +3当a =−5时,原式=a+1a+3=−5+1−5+3=2.【点睛】本题考查了分式的化简求值,能正确根据分式的运算法则进行化简是解此题的关键,注意运算顺序. 23.(2023下·江西景德镇·七年级统考期末)先化简,再求值:(x 2+2x+1x 2−1−3x−1)÷x 2−2x x−1其中x =17【答案】1x ,代数式的值为7【分析】根据乘法公式,分式的性质,分式的加减乘除混合运算化简,再代入求出即可. 【详解】解:(x 2+2x+1x 2−1−3x−1)÷x 2−2x x−1=[(x +1)2(x +1)(x −1)−3x −1]÷x(x −2)x −1=(x +1x −1−3x −1)×x −1x(x −2)=x −2x −1×x −1x(x −2)=1x ,当x =17时,原式=1x=117=7.【点睛】本题主要考查分式的化简求值,掌握乘法公式,分式的性质,分式的混合运算法则是解题的关键.24.(2023下·江苏淮安·七年级统考期末)先化简,再求值:当a =2时,求代数式(a −aa+1)÷a 2−2a a 2−4×1a+2的值.【答案】aa+1;23【分析】运用乘法公式,分式的性质,分式的混合运算进行化简,再代入求值即可. 【详解】解:(a −a a+1)÷a 2−2a a 2−4×1a+2=(a 2+a a +1−a a +1)÷a(a −2)(a +2)(a −2)×1a +2=a 2a +1×a +2a ×1a +2 =a a+1,当a =2时,原式=aa+1=22+1=23.【点睛】本题主要考查分式的化简求值,掌握乘法公式,分式的性质,分式的混合运算法则,代入求值等知识是解题的关键.25.(2023上·四川绵阳·七年级校联考阶段练习)先化简,再求值:(2x+2x 2−1+1)÷x+1x 2−2x+1,其中x =4 【答案】x −1,3【分析】根据分式混合运算法则先化简,再代值求解即可得到答案. 【详解】解:(2x+2x 2−1+1)÷x+1x 2−2x+1 =(2x +2x 2−1+x 2−1x 2−1)×x 2−2x +1x +1=x 2+2x+1x 2−1×x 2−2x+1x+1, =(x+1)2(x+1)(x−1)×(x−1)2x+1,=x −1;当x =4时,原式=4−1=3.【点睛】本题考查了分式的混合运算和求值,能正确运用分式的运算法则进行化简是解此题的关键. 26.(2023上·湖北武汉·七年级武汉外国语学校(武汉实验外国语学校)校考期末)(1)计算:[3a 3⋅a 3+(−3a 3)2]÷(−2a −2)3;(2)先化简,再求值:(a 2a−1−a −1)÷a−a 2a 2−2a+1,其中a =2.【答案】(1)−32a 12;(2)−1a ,−12【分析】(1)根据幂的混合运算法则求解即可;(2)首先根据分式的混合运算法则求解,然后将a =2代入求解即可. 【详解】解:(1)[3a 3⋅a 3+(−3a 3)2]÷(−2a −2)3 =(3a 6+9a 6)÷(−8a −6) =12a 6÷(−8a −6) =−32a 12; (2)(a 2a−1−a −1)÷a−a 2a 2−2a+1=(a 2a −1−a 2−1a −1)÷−a (a −1)(a −1)2=1a −1⋅a −1−a=−1a ,当a =2时,原式=−12.【点睛】此题考查了幂的混合运算,分式的混合运算,解题的关键是熟练掌握以上运算法则. 27.(2023上·吉林白山·七年级统考期末)先化简,再求值:1﹣x−2y x+y ÷x 2−4xy+4y 2x 2−y 2,其中x =﹣2,y =12.【答案】﹣yx−2y ,16.【分析】原式利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,之后将x 、y 代入计算即可求得答案. 【详解】解:原式=1﹣x−2yx+y ⋅(x+y )(x−y )(x−2y )2=1−x−y x−2y =﹣yx−2y ,当x =﹣2,y =12时,原式=16.【点睛】本题考查了分式的化简求值,熟练的掌握分式的运算法则是解本题的关键,在解题的时候,要注意式子的整理和约分.28.(2023上·广东惠州·七年级统考期末)已知A =xy−y 2y 2−x 2÷(1x−y −1x+y ). (1)化简A ;(2)当x 2+y 2=13,xy =−6时,求A 的值;(3)若|x −y |+√y +2=0,A 的值是否存在,若存在,求出A 的值,若不存在,说明理由.【答案】(1)−x−y2;(2)A=−52或52;(3)不存在,理由见详解.【分析】(1)先把括号里面的通分,再计算整式除法即可;(2)利用完全平方公式,求出x-y的值,代入化简后的A中,求值即可;(3)利用非负数的和为0,确定x、y的关系,把x、y代入A的分母,判断A的值是否存在.【详解】解:(1)A=xy−y2y2−x2÷(1x−y−1x+y)=y(x−y) (y−x)(y+x)×(x+y)(x−y)x+y−x+y=−y(x−y)(x−y)(x+y)×(x+y)(x−y)2y=−x−y2;(2)∵x2+y2=13,xy=-6∴(x-y)2=x2-2xy+y2=13+12=25∴x-y=±5,当x-y=5时,A=−52;当x-y=-5时,A=52.(3)∵|x−y|+√y+2=0,∴x-y=0,y+2=0当x-y=0时,A的分母为0,分式没有意义.∴当|x−y|+√y+2=0时,A的值不存在.【点睛】本题考查了分式的加减乘除运算、完全平方公式、非负数的和及分式有无意义的条件.题目综合性较强.初中阶段学过的非负数有:a的偶次幂,a(a≥0)的偶次方根,a|的绝对值.29.(2023上·山东泰安·七年级统考期中)(1)计算:3x(x−3)2−x3−x(2)计算:(x+1x2−1+xx−1)÷x+1x2−2x+1(3)先化简,再求值:已知ab =3,求a2+4ab+4b2a−b÷(3b2a−b−a−b)的值.【答案】(1)x2(x−3)2;(2)x﹣1;(3)a+2b2b−a,﹣5.【分析】(1)直接通分运算进而利用分式的混合运算法则计算得出答案; (2)直接将括号里面通分进而利用分式的混合运算法则计算得出答案; (3)直接将括号里面通分进而利用分式的混合运算法则计算得出答案. 【详解】解:(1)原式=3x+x(x−3)(x−3)2=x 2(x−3)2;(2)原式=x+1+x(x+1)(x−1)(x+1)⋅(x−1)2x+1=(x+1)2(x−1)(x+1)⋅(x−1)2x+1=x −1;(3)原式=(a+2b)2a−b÷3b 2−a(a−b)−b(a−b)a−b=(a+2b)2a−b⋅a−b(2b+a)(2b−a)=a+2b2b−a∵ab =3,∴a =3b ,所以原式=3b+2b 2b−3b=−5.【点睛】本题考查的知识点是分式的化简求值,掌握分式化简的一般步骤以及分式的混合运算法则是解此题的关键,注意化简过程中各项的符号变化. 30.(2023上·山东潍坊·七年级统考期中)计算: (1)aa+1+a−1a 2−1;(2)2aa+1−2a−4a 2−1÷a−2a 2−2a+1;(3)先化简再求值:(1−3x+2)÷x−1x 2+x−2,其中x 是﹣2,1,2中的一个数值. 【答案】(1)1;(2)2a+1;(3)x ﹣1,x =2时,原式=1. 【分析】(1)先约分,再相加即可求解;(2)先因式分解,将除法变为乘法约分,再通分,相减即可求解;(3)先计算括号里面的减法,再因式分解,将除法变为乘法约分化简,再把x =2代入计算即可求解. 【详解】(1)a a+1+a−1a 2−1,=aa+1+1a+1, =a+1a+1, =1;(2)2aa+1−2a−4a 2−1÷a−2a 2−2a+1, =2aa+1−2(a−2)(a+1)(a−1)⋅(a−1)2a−2,=2a a+1−2(a−1)a+1,=2a−2(a−1)a+1,=2a+1; (3)(1−3x+2)÷x−1x 2+x−2,=x+2−3x+2⋅(x−1)(x+2)x−1,=x ﹣1,∵x +2≠0,x ﹣1≠0, ∴x ≠﹣2,x ≠1,当x =2时,原式=2﹣1=1.【点睛】此题考查分式的混合运算及化简求值,正确将分式的分子与分母因式分解是解题的关键. 31.(2023上·吉林白城·七年级统考期末)先化简,再求值:x 2−1x 2−2x+1÷x+1x−1·1−x1+x,其中x =12.【答案】1−x1+x ,13.【分析】先将分式的分子和分母分解因式,将分式约分化简得到最简结果,再将未知数的值代入计算即可. 【详解】x 2−1x 2−2x+1÷x+1x−1·1−x1+x , =(x +1)(x −1)(x −1)2⋅x −1x +1⋅1−x1+x=1−x1+x ,当x =12时,原式=1−121+12=13.【点睛】此题考查分式的化简求值,化简时需先分解因式约去公因式得到最简分式,再将未知数的值代入求值即可.32.(2023上·山东烟台·七年级统考期中)先化简(a 2−4a+4a 2−4﹣aa+2)÷a−1a+2,再从a ≤2的非负整数解中选一个适合的整数代入求值. 【答案】−2a−1,2【分析】先将分式的分子和分母分解因式,再根据分式的化简求值的过程计算即可求解. 【详解】解:原式=[(a−2)2(a−2)(a+2)−aa+2]⋅a+2a−1,=(a−2a+2−aa+2)⋅a+2a−1,=−2a+2⋅a+2 a−1,=−2a−1.∵a≤2的非负整数解有0,1,2,又∵a≠1,2,∴当a=0时,原式=2.【点睛】此题考查分式的化简求值,化简时需先分解因式约去公因式得到最简分式,求值时选的数需满足分母不为0的数才可代入求值.33.(2023下·江苏盐城·七年级东台市三仓镇中学校考期中)先化简,再求值:x2−1(x−1)2÷x2+xx−1+2x,其中x为你喜欢的一个使原式有意义的整数.【答案】3x,1【详解】分析:根据据分式的混合运算的法则和步骤,先算乘除,再算加减,然后约分化简,最后代入求值即可,注意选择使分母不为零的数代入.详解:x2−1(x−1)2÷x2+xx−1+2x=(x+1)(x−1)(x−1)2÷x(x+1)x−1+2x=(x+1)(x−1)(x−1)2·x−1x(x+1)+2x=1 x +2x=3x当x=3时,原式=1.点睛:本考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.34.(2023上·四川泸州·七年级统考期中)先化简,再求值:(3a+1−a+1)÷a2−4a+4a+1,其中a=4.【答案】−a+2a−2,-3.【详解】试题分析:先根据分式的混合运算的法则,先算括号里面的(通分后计算),再把除法化为乘法约分化简,最后代入求值即可.试题解析:(3a+1−a+1)÷a2−4a+4a+1=3−a2+1a+1×a+1(a−2)2,=−(a+2)(a−2)a+1×a+1(a−2)2=−a+2a−2,当a=4时,原式=-3.35.(2023上·北京昌平·七年级校考期中)先化简,再求值:xx2−1⋅(x−1x−2),其中x(x+1)=2(x+1).【答案】−1x−1,-1【详解】试题分析:先根据分式的混合运算的法则,先把分式的化简,然后再根据方程求出符合条件的x代入求值,注意分式有意义的条件,即分母不能为零.试题解析:原式==.由解得或.因为x不能等于-1,所以当=2时,原式=.36.(2023下·湖南郴州·七年级校考期中)先化简,再求值:(x2x−1+91−x)÷x+3x−1,x在1,2,-3中选取适当的值代入求值.【答案】x-3,当x=2时,原式=-1【详解】解:(x2x−1+91−x)÷x+3x−1=(x+3)(x−3)x−1⋅x−1 x+3=x−3要是原式有意义,则x≠1,−3,则x=2原式=-137.(2023上·浙江杭州·七年级统考期中)先化简,再求值:(4x+6x2−1−2x−1)÷x+2x2−2x+1,其中x是不等式组{x+4>01−2x>3的整数解.【答案】2x−2x+1,4.【分析】原式中先计算分子,约分得到最简结果,求出不等式组的解集,找出解集中的整数解确定出x的值,代入计算即可求出值.【详解】原式= 4x+6−2(x+1)(x+1)(x−1)×(x−1)2x+2= 2(x+2)(x+1)(x−1)×(x−1)2x+2= 2(x−1)x+1=2x−2x+1解不等式组{x+4>01−2x>3得:-4<x<-1所以不等式组的整数解为-3,-2,即x=-3,-2.∵x≠-2∴x=-3,∴原式= 2(−3−1)−3+1=4.【点睛】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.38.(2023上·重庆·七年级西南大学附中校考期中)先化简,再求值:(2a−2−6a2−2a)÷a2−6a+9a−2,其中a满足2a2−6a+3=0.【答案】2a2−3a ,−43【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把已知等式变形后代入计算即可求出值.【详解】(2a−2−6a2−2a)÷a2−6a+9a−2=[2aa(a−2)−6a(a−2)]÷(a−3)2a−2=2(a−3)a(a−2)×a−2(a−3)2=2a(a−3)=2a2−3a∵2a2−6a+3=0∴2a2−6a=−3∴a2−3a=−32∴原式=2a2−3a =2−32=−43.【点睛】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.39.(2023上·山东聊城·七年级校考期末)(1)计算:(x2−4x+4x2−4−xx+2)÷x−1x+2(2)先化简a2−2aa2−1÷(2a−1a−1−a−1),然后从−2≤a≤2的范围内选取一个合适的整数作为a的值代入求值.【答案】(1)21−x ;(2)−1a+1,1【分析】(1)先计算括号内的分式减法,再计算分式的除法即可得;(2)先计算括号内的分式减法,再计算分式的除法,然后根据分式有意义的条件选取合适的a的值,代入计算即可得.【详解】解:(1)原式=[(x−2)2(x+2)(x−2)−xx+2]⋅x+2x−1=(x−2x+2−xx+2)⋅x+2x−1=−2x+2⋅x+2x−1=21−x;(2)原式=a(a−2)(a+1)(a−1)÷[2a−1a−1−(a+1)(a−1)a−1]=a(a−2)(a+1)(a−1)÷(2a−1a−1−a2−1a−1)=a(a−2)(a+1)(a−1)÷2a−1−a2+1a−1=a(a−2)(a+1)(a−1)÷2a−a2a−1=a(a−2)(a+1)(a−1)⋅a−12a−a2=a(a−2)(a+1)(a−1)⋅a−1a(2−a)=−1a+1,∵a+1≠0,a−1≠0,a≠0,2−a≠0,∴a≠−1,a≠1,a≠0,a≠2,∵a是−2≤a≤2的范围内的一个整数,∴a=−2,则原式=−1−2+1=1.【点睛】本题考查了分式的化简求值,熟练掌握分式的运算法则是解题关键. 40.(2023上·山东滨州·七年级统考期末)(1)计算:3(x−1)(x+2)−xx−1+1;(2)先化简,再求值:a−1a 2−4a+4÷(1+1a−2),请从1,2,3中选一个合适的数作为a 的值,代入求值. 【答案】(1)−1x+2;(2)1a−2,1.【分析】(1)根据分式的四则运算求解即可;(2)根据分式的四则运算进行化简,然后代数求解即可. 【详解】解:(1)3(x−1)(x+2)−xx−1+1 =3(x −1)(x +2)−x (x +2)(x −1)(x +2)+(x −1)(x +2)(x −1)(x +2)=3−x 2−2x +x 2+x −2(x −1)(x +2)=1−x(x −1)(x +2)=−1x +2(2)a−1a 2−4a+4÷(1+1a−2) =a −1(a −2)2÷(a −1a −2) =a −1(a −2)2×(a −2a −1) =1a−2,由题意可得:a −2≠0,a −1≠0 ∴a ≠1,a ≠2将a =3代入得,原式=13−2=1.【点睛】此题考查了分式的四则运算,化简求值,解题的关键是熟练掌握分式的四则运算以及分式的有关知识.。
分式的混合运算练习题

分式的混合运算练习题分式是数学中的一种常见表示形式,它由分子和分母构成,表示了两个数之间的比例关系。
混合运算则是指同时进行多种运算,如加减乘除等。
本文将提供一些分式的混合运算练习题,以帮助读者巩固和练习相关的数学知识。
1. 请计算以下分式的值:(a) $\frac{3}{4} + \frac{1}{2}$(b) $\frac{5}{6} - \frac{1}{3}$(c) $\frac{2}{3} \times \frac{4}{5}$(d) $\frac{2}{5} \div \frac{1}{4}$解答:(a) $\frac{3}{4} + \frac{1}{2} = \frac{3 \times 2 + 4 \times 1}{4 \times 2} = \frac{6+4}{8} = \frac{10}{8} = \frac{5}{4}$(b) $\frac{5}{6} - \frac{1}{3} = \frac{5 \times 3 - 6 \times 1}{6 \times 3} = \frac{15-6}{18} = \frac{9}{18} = \frac{1}{2}$(c) $\frac{2}{3} \times \frac{4}{5} = \frac{2 \times 4}{3 \times 5} =\frac{8}{15}$(d) $\frac{2}{5} \div \frac{1}{4} = \frac{2}{5} \times \frac{4}{1} =\frac{2 \times 4}{5 \times 1} = \frac{8}{5}$2. 请化简以下分式:(a) $\frac{9}{12}$(b) $\frac{15}{20}$(c) $\frac{24}{36}$(d) $\frac{16}{24}$解答:(a) $\frac{9}{12} = \frac{3 \times 3}{4 \times 3} = \frac{3}{4}$(b) $\frac{15}{20} = \frac{5 \times 3}{4 \times 5} = \frac{3}{4}$(c) $\frac{24}{36} = \frac{6 \times 4}{6 \times 6} = \frac{4}{6} = \frac{2}{3}$(d) $\frac{16}{24} = \frac{8 \times 2}{8 \times 3} = \frac{2}{3}$3. 请计算以下分式的和及差:(a) $\frac{1}{2} + \frac{3}{4} - \frac{1}{8}$(b) $\frac{3}{5} - \frac{3}{10} + \frac{1}{2}$(c) $\frac{5}{6} + \frac{2}{3} - \frac{1}{4}$(d) $\frac{7}{8} - \frac{1}{2} + \frac{3}{16}$解答:(a) $\frac{1}{2} + \frac{3}{4} - \frac{1}{8} = \frac{4 \times 4 + 3 \times 2 - 1}{8} = \frac{16+6-1}{8} = \frac{21}{8}$(b) $\frac{3}{5} - \frac{3}{10} + \frac{1}{2} = \frac{6 \times 2 - 3 \times 1 + 5}{10} = \frac{12-3+5}{10} = \frac{14}{10} = \frac{7}{5}$(c) $\frac{5}{6} + \frac{2}{3} - \frac{1}{4} = \frac{5 \times 2 + 2\times 4 - 3}{6 \times 4} = \frac{10+8-3}{24} = \frac{15}{24} =\frac{5}{8}$(d) $\frac{7}{8} - \frac{1}{2} + \frac{3}{16} = \frac{14 \times 2 - 8\times 1 + 3}{16} = \frac{28-8+3}{16} = \frac{23}{16}$4. 请计算以下分式的乘积及商:(a) $\frac{2}{3} \times \frac{3}{4} \times \frac{4}{5}$(b) $\frac{5}{6} \div \frac{1}{2} \div \frac{2}{3}$(c) $\frac{3}{4} \times \frac{1}{2} \div \frac{2}{5}$(d) $\frac{4}{3} \div \frac{3}{2} \times \frac{2}{5}$解答:(a) $\frac{2}{3} \times \frac{3}{4} \times \frac{4}{5} = \frac{2 \times 3 \times 4}{3 \times 4 \times 5} = \frac{24}{60} = \frac{2}{5}$(b) $\frac{5}{6} \div \frac{1}{2} \div \frac{2}{3} = \frac{5}{6} \times \frac{2}{1} \times \frac{3}{2} = \frac{5 \times 2 \times 3}{6 \times 1 \times 2} = \frac{30}{12} = \frac{5}{2}$(c) $\frac{3}{4} \times \frac{1}{2} \div \frac{2}{5} = \frac{3 \times 1 \times 5}{4 \times 2 \times 2} = \frac{15}{16}$(d) $\frac{4}{3} \div \frac{3}{2} \times \frac{2}{5} = \frac{4}{3}\times \frac{2}{3} \times \frac{2}{5} = \frac{4 \times 2 \times 2}{3 \times 3 \times 5} = \frac{16}{45}$通过以上练习题,我们可以巩固和练习分式的混合运算。
中考数学专项练习分式的混合运算(含解析)

中考数学专项练习分式的混合运算(含解析)【一】单项选择题1.计算的结果是〔〕A.B.C.x2+1D.x2﹣12.化简分式〔x-y+〕〔x+y-〕的结果为〔〕A.y2-x2B.x2-y2C.x2-4y2D.4x2-y23.x﹣=﹣y,且x+y≠0,那么xy的值为〔〕A.-1B.0C.1D.24.化简÷〔1+ 〕的结果是〔〕A.B.C.D.5.化简:〔1+ 〕÷结果为〔〕A.4xB.3xC.2xD.x6.化简〔1﹣〕÷的结果是〔〕A.〔x+1〕2B.〔x﹣1〕2C.D.7.以下运算结果为x﹣1的是〔〕A.1﹣B.•C.÷D.8.化简的结果是〔〕A.B.C.x+1D.x﹣19.假设分式□运算结果为x,那么在〝□〞中添加的运算符号为〔〕A.+B.﹣C.+或×D.﹣或÷10.化简的结果是()A.1B.C.D.-111.计算〔﹣〕÷的结果为〔〕A.B.C.D.12.以下等式成立的是〔〕A.+ =B.=C.=D.=﹣【二】填空题13.化简:〔1+ 〕÷的结果为________.14.÷·=________÷·________.15.化简:=________.16.有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下:那么第n次运算的结果yn=________〔用含字母x和n的代数式表示〕.17.计算:=________.【三】计算题18.计算:〔1〕;〔2〕.19.计算:〔1〕〔2〕.20.计算:①;②﹣a﹣1;③.21.计算:.22.计算或化简:①计算〔﹣〕÷.②a≠0,且满足a2﹣3a+1=0,求a2+ 的值.23.计算或化简:〔1〕.〔2〕.24.计算:.25.计算:〔1〕÷;〔2〕〔1+ 〕÷.【四】解答题26.:y= ,试说明不论x为任何有意义的值,y值均不变.27.化简:÷.【一】单项选择题1.计算的结果是〔〕A.B.C.x2+1D.x2﹣1【考点】分式的混合运算【解析】【解答】解:原式=[+ ]•〔x+1〕〔x﹣1〕=2x+〔x﹣1〕2=x2+1,应选C【分析】原式括号中两项通分并利用同分母分式的加法法那么计算,同时利用除法法那么变形,约分即可得到最简结果.2.化简分式〔x-y+〕〔x+y-〕的结果为〔〕A.y2-x2B.x2-y2C.x2-4yD.4x2-y2【考点】分式的混合运算【解析】【分析】先算小括号里的,再算乘法,把分子因式分解,化简即可.【解答】〔x-y+)〔x+y-)===x2-y2 .应选B、【点评】当整式与分式相加减时,一般可以把整式看作分母为1的分式,与其它分式进行通分运算.需注意:〔x+y)2-4xy=〔x-y)2 ,〔x-y)2+4xy =〔x+y)2的应用.3.x﹣=﹣y,且x+y≠0,那么xy的值为〔〕A.-1B.0C.1D.2【考点】分式的混合运算【解析】【解答】解:∵x﹣=﹣y,∴x+y=+= ,∵x+y≠0,∴xy=1,应选C【分析】等式移项变形,整理后根据x+y不为0求出xy的值即可.4.化简÷〔1+ 〕的结果是〔〕A.B.D.【考点】分式的混合运算【解析】【解答】解:原式=÷= •=,应选C【分析】原式括号中两项通分并利用同分母分式的加法法那么计算,同时利用除法法那么变形,约分即可得到结果.5.化简:〔1+ 〕÷结果为〔〕A.4xB.3xC.2xD.x【考点】分式的混合运算6.化简〔1﹣〕÷的结果是〔〕A.〔x+1〕2B.〔x﹣1〕2C.D.【考点】分式的混合运算【解析】【解答】解:〔1﹣〕÷===〔x﹣1〕2 ,应选B、【分析】先对括号内的式子通分,然后再将除法转化为乘法即可解答此题.7.以下运算结果为x﹣1的是〔〕A.1﹣B.•C.÷D.【考点】分式的混合运算【解析】【解答】解:A、1﹣= ,故此选项错误;B、原式= •=x﹣1,故此选项正确;C、原式= •〔x﹣1〕= ,故此选项错误;D、原式= =x+1,故此选项错误;应选:B、【分析】根据分式的基本性质和运算法那么分别计算即可判断.8.化简的结果是〔〕A.B.C.x+1D.x﹣1【考点】分式的混合运算9.假设分式□运算结果为x,那么在〝□〞中添加的运算符号为〔〕A.+B.﹣C.+或×D.﹣或÷【考点】分式的混合运算【解析】【解答】解:A、根据题意得:+ = ,不符合题意;B、根据题意得:﹣= =x,不符合题意;C、根据题意得:×= ,不符合题意;D、根据题意得:﹣= =x;÷= •=x,符合题意;应选D【分析】将运算符号放入原式,计算即可得到结果.10.化简的结果是()A.1B.C.D.-1【考点】分式的混合运算11.计算〔﹣〕÷的结果为〔〕A.B.C.D.【考点】分式的混合运算【解析】【解答】解:原式=÷= •=.应选A、【分析】首先把括号内的式子通分、相减,然后把除法转化为乘法,进行通分即可.12.以下等式成立的是〔〕A.+ =B.=C.=D.=﹣【考点】分式的混合运算【解析】【解答】解:A、原式= ,错误;B、原式不能约分,错误;C、原式= = ,正确;D、原式= =﹣,错误,应选C【分析】原式各项计算得到结果,即可做出判断.【二】填空题13.化简:〔1+ 〕÷的结果为________.【考点】分式的混合运算14.÷·=________÷·________.【考点】分式的混合运算15.化简:=________.【考点】分式的混合运算【解析】【解答】解:=1﹣=1﹣= = .【分析】把第二个分式的分子分母先因式分解,再把除法统一成乘法化简,最后算减法.16.有一个计算程序,每次运算都是把一个数先乘以2,再除以它与1的和,多次重复进行这种运算的过程如下:那么第n次运算的结果yn=________〔用含字母x和n的代数式表示〕.【考点】分式的混合运算17.计算:=________.【考点】分式的混合运算【三】计算题18.计算:〔1〕;〔2〕.【考点】分式的混合运算【解析】【分析】〔1〕原式利用除法法那么变形,约分即可得到结果;〔2〕原式先计算乘方运算,再计算除法运算,最后算加减运算即可得到结果.19.计算:〔1〕〔2〕.【考点】分式的混合运算【解析】【分析】〔1〕原式通分并利用同分母分式的加法法那么计算,即可得到结果;〔2〕原式括号中通分并利用同分母分式的减法法那么计算,同时利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算,约分即可得到结果.20.计算:①;②﹣a﹣1;③.【考点】分式的混合运算【解析】【分析】①原式利用除法法那么变形,约分即可得到结果;②原式两项通分并利用同分母分式的减法法那么计算即可得到结果;③原式括号中两项通分并利用同分母分式的加减法那么计算,约分即可得到结果.21.计算:.【考点】分式的混合运算【解析】【分析】原式括号中三项通分并利用同分母分式的减法法那么计算,约分即可得到结果.22.计算或化简:①计算〔﹣〕÷.②a≠0,且满足a2﹣3a+1=0,求a2+ 的值.【考点】分式的混合运算【解析】【分析】①原式括号中两项通分并利用同分母分式的减法法那么计算,同时利用除法法那么变形,约分即可得到结果;②等式整理求出a + 的值,再利用完全平方公式即可求出所求式子的值.23.计算或化简:〔1〕.〔2〕.【考点】分式的混合运算【解析】【分析】〔1〕、〔2〕根据分式混合运算的法那么进行计算即可.24.计算:.【考点】分式的混合运算【解析】【分析】先把括号内通分,再把分子分母因式分解和除法运算化为乘法运算,然后约分即可.25.计算:〔1〕÷;〔2〕〔1+ 〕÷.【考点】分式的混合运算【解析】【分析】〔1〕原式利用除法法那么变形,约分即可得到结果;〔2〕原式括号中两项通分并利用同分母分式的加法法那么计算,同时利用除法法那么变形,约分即可得到结果.【四】解答题26.:y= ,试说明不论x为任何有意义的值,y值均不变.【考点】分式的混合运算【解析】【分析】先算乘除,约分化为最简分式,后算加减,得到不论x为任何有意义的值,y值均不变.27.化简:÷.【考点】分式的混合运算【解析】【分析】利用分式的混合运算顺序求解即可.。
分式混合运算练习题(30题)

分式运算测试题1.若把分式xx y+中的x 、y 都扩大3倍,那么分式的值( ) A.扩大3倍 B.不变 C.缩小3倍 D. 缩小6倍2. 下列公式中是最简分式的是( )A .21227b a B .22()a b b a -- C .22x y x y ++ D .22x y x y --3. 计算22()ab ab 的结果为( ) A.b B .aC.1 D.1b 4. 分式223,2y xy x 的最简公分母是( ). A.36x B.25x C.x 6 D.26x 5.计算224338.42x x y x y y ⎛⎫⎛⎫-÷- ⎪ ⎪⎝⎭⎝⎭的结果是( ) A.x 3- B.x 3 C.x 12- D.x 126. 化简121112+-÷⎪⎭⎫ ⎝⎛-+a a a a 的结果是( )A .1+a B .11-a C .a a 1- D .1-a 7. 已知0a b -≠,且230a b -=,那么2a ba b+-的值是( ) A.-12 B.0 C.8 D.8或-128. 计算ab ba b a b a b a b a 22222-⨯⎪⎪⎭⎫ ⎝⎛+---+的结果是( ) (A) b a -1 B) ba +1(C) a -b (D) a +b . 9. 若b a b a +=+111,则b a a b +的值是( ) A.2 B.-1 C.1 D.0 10. 若===+nm m n ba b a b a 22)(,3)(,2)(则( ). A.36 B.-36 C.30 D.-30. 13 在式子5011111++=R R R 中,用含1R 的代数式表示为______________ 16 已知113x y -=,则代数式2522x xy y x xy y----的值为 17 计算:①22416842aa a a a ++⋅+-; ②2122442--++-x x x18先化简,再求值:(212x x --2144x x -+)÷222x x -,其中x =3.19知实数a 满足a 2+4a-8=0,求11+a -132-+a a ×961222+++-a a a a 的值。
八年级数学分式的混合运算练习题(附答案)

时间:案序:
知识目标:巩固分式的运算法则和顺序,并能正确熟练的进行计算,提高计算的准确率。
1、填空:(1) 。(2)若 。
(3)已知, ,那么 。
2、计算:(1) (2) (3)
(4) (5) (6)
; ;
3、化简求பைடு நூலகம்。
4、已知,
课题:16.2分式的混合运算练习2时间:案序:
知识目标:巩固分式的运算法则和顺序,并能正确熟练的进行计算,提高计算的准确率。
一、填空
1、已知 ,则 =_____________.
2、.在等号成立时,右边填上适当的符号: =_____ .
3、化简 的结果为__________
二、选择(4×7)
4、分式 , , 的最简公分母是()A.5cx3B.15abcx C. 15abcx2D.15abcx3
A. 、 B. 、 C. 、 D. 、
三、计算题9、 10、 11、
12、 13、 14、 -x-1
15先化简,再求值: - + ,其中a= .
四、16、有这样一道题:“计算 ÷ -x的值,其中x=2004”甲同学把“x=2004”错抄成“x=2040”,但他的计算结果也正确,你说这是怎么回事?
5、如果 ,那么A等于( )A. m-8 B.2-m C.18-3mD.3m-12
6、分式 约分之后正确的是()A. B. C. D.
7、下列分式中,计算正确的是
A. = B. C. =-1D.
8.甲、乙两人加工某种机器零件,已知甲每天比乙多做a个,甲做m个所用的天数与乙做n个所用的天数相等(其中m≠n),设甲每天做x个零件,则甲、乙两人每天所做零件的ਪ数分别是( )
分式混合运算(习题及答案)

分式混合运算(习题及答案)混合运算(题)例1:混合运算:解:原式可以化简为:frac{4-x}{x-2} \div \frac{12}{x+2-x^2}$$frac{4-x}{x-2} \times \frac{x+2-x^2}{12}$$frac{-(x-4)}{(x-2)(x+4)}$$例2:先化简,然后在$-2\leq x\leq 2$的范围内选取一个合适的整数$x$代入求值.解:先化简原式:frac{x(x+1)}{(x-1)(1-x)} \div \frac{2x}{x+1}$$frac{x(x+1)}{(x-1)(x-1)} \times \frac{x+1}{2x}$$frac{1}{2}$$由于$-2\leq x\leq 2$,且$x$为整数,因此使原式有意义的$x$的值为$-2$,$-1$或$2$。
代入计算可得:当$x=2$时,原式为$-2$。
巩固练1.计算:1)$$\frac{x-y}{x+2y} \div \frac{1}{2x+4y}$$化简原式:frac{x-y}{x+2y} \times \frac{2x+4y}{1}$$frac{2(x-y)}{x+2y}$$2)$$\frac{\frac{a}{a-1}-1}{a^2-2a+1} \div \frac{1}{a+1}$$ 化简原式:frac{\frac{a}{a-1}-1}{(a-1)^2} \times (a+1)$$frac{a-2}{(a-1)^2}$$3)$$\frac{2a-2ab}{a^2-b^2} \div \frac{a+b}{a+b}$$化简原式:frac{2a-2ab}{a^2-b^2} \times \frac{a+b}{a+b}$$frac{2a-2ab}{(a-b)(a+b)} \times \frac{a+b}{1}$$frac{2(1-b)}{a-b}$$4)$$\frac{y-1-\frac{8}{y-1}}{y^2+y} \div\frac{1}{y(y+1)}$$化简原式:frac{y-1-\frac{8}{y-1}}{y(y+1)} \times \frac{y(y+1)}{1}$$ frac{(y-1)^2-8}{y(y+1)^2}$$5)$$\frac{a^2-2ab+b^2}{b}\div \frac{1}{a-b}-1$$化简原式:frac{(a-b)^2}{b} \times \frac{a-b}{1}-1$$frac{(a-b)^3}{b}-1$$6)$$\frac{x^2-4x+4}{x(x-1)} \div \frac{x+2}{x-1}$$化简原式:frac{(x-2)^2}{x(x-1)} \times \frac{x-1}{x+2}$$frac{(x-2)^2}{x(x+2)}$$7)$$\frac{2}{(x-1)^2} - \frac{1}{(x-1)^2(x+1)}$$化简原式:frac{2(x+1)-1}{(x-1)^2(x+1)}$$frac{2x+1}{(x-1)^2(x+1)}$$8)$$\frac{3-x}{2(x-2)} \div \frac{5}{x-2}-\frac{5}{x-3}$$ 化简原式:frac{3-x}{2(x-2)} \times \frac{x-2}{5} - \frac{5}{x-3}$$ frac{(x-3)(x-1)}{2(x-2)5} - \frac{5}{x-3}$$frac{x^2-4x+7}{10(x-2)(x-3)}$$9)$$\frac{x-1}{x+1} \div \frac{x-3}{x-2} - \frac{5}{x^2-3x}$$化简原式:frac{(x-1)(x-2)}{(x+1)(x-3)} - \frac{5}{x(x-3)}$$frac{x^2-3x-2}{x(x-3)(x+1)(x-3)} - \frac{5(x+1)}{x(x-3)(x+1)(x-3)}$$frac{x^2-3x-2-5x-5}{x(x-3)(x+1)(x-3)}$$frac{x^2-8x-7}{x(x-3)(x+1)^2}$$10)$$\frac{1}{(x-1)(x+1)}-\frac{1}{x(x-1)}$$化简原式:frac{x-(x-1)}{x(x-1)(x+1)}$$frac{1}{x(x+1)}$$11)$$\frac{2}{x+y} - \frac{1}{y-x} \times \frac{y^2-x^2}{11}$$化简原式:frac{2(y-x)}{(y-x)(x+y)} - \frac{y+x}{11(x+y)}$$frac{y-x-2}{11(x+y)}$$2.化简求值:1)先化简,再求值:$\frac{x^2+2x+1}{x+2x+2} \div \frac{1}{x+2}$,其中$x=3-1$。
分式混合运算专题练习(经典集合)

分式的乘除乘方运算一、基础知识点: 1.约分把一个分式的分子与分母的公因式约去,叫做约分.约分的依据是分式的基本性质. 若分式的分子、分母是多项式,必须先把分子、分母分解因式,然后才能约去公因式.分子与分母没有公因式的分式,叫做最简分式,又叫做既约分式.分式的运算结果一定要化为最简分式. 2.分式的乘法 乘法法测:b a ·dc =bdac . 3.分式的除法 除法法则:b a ÷d c =b a ·c d =bcad 4.分式的乘方求n 个相同分式的积的运算就是分式的乘方,用式子表示就是(ba )n. 分式的乘方,是把分子、分母各自乘方.用式子表示为:(b a )n =n nba (n 为正整数) 二、典型例题例1、下列分式a bc 1215,a b b a --2)(3,)(222b a b a ++,b a b a +-22中最简分式的个数是( ).A.1B.2C.3D.4例2.计算:3234)1(xy y x ∙ a a a a 2122)2(2+⋅-+ x y xy 2263)3(÷41441)4(222--÷+--a a a a a 例3、 若432z y x ==,求222zy x zxyz xy ++++的值.例4、计算(1)3322)(c b a - (2)43222)()()(xy x y y x -÷-⋅-(3)2332)3()2(c b a bc a -÷- (4)232222)()()(xy xy xy x y y x -⋅+÷-例5计算:1814121111842+-+-+-+--x x x x x练习:1.计算:8874432284211xa x x a x x a x x a x a --+-+-+--例6.计算:2018119171531421311⨯+⨯++⨯+⨯+⨯ 练习1、()()()()()()()()1011001431321211++++++++++++x x x x x x x x例7、已知21)2)(1(12++-=+-+x Bx A x x x ,求A. B 的值。
分式混合运算专题练习

分式的乘除乘方运算例1、下列分式a bc 1215,a b b a --2)(3,)(222b a b a ++,b a b a +-22中最简分式的个数是( ).A.1B.2C.3D.4 例2.计算:3234)1(xy y x • a a a a 2122)2(2+⋅-+ x y xy 2263)3(÷41441)4(222--÷+--a a a a a 例3、 若432z y x ==,求222z y x zx yz xy ++++的值.例4、计算(1)3322)(c b a - (2)43222)()()(x y x y y x -÷-⋅-(3)2332)3()2(c b a bc a -÷- (4)232222)()()(xy xy xy x y y x -⋅+÷-例5计算:1814121111842+-+-+-+--x x x x x练习:1.计算:8874432284211x a x x a x x a x x a x a --+-+-+--例6.计算:2018119171531421311⨯+⨯++⨯+⨯+⨯练习1、()()()()()()()()1011001431321211++++++++++++x x x x x x x x例7、已知21)2)(1(12++-=+-+x B x A x x x ,求A. B 的值。
计算下列各题:(1)2222223223x y y x y x y x y x y x ----+--+ (2)1111322+-+--+a a a a .(3)29631a a --+ (4) 21x x --x -1 (5)3a a --263a a a +-+3a ,(6)xy y y x x y x xy --++-222 ⑺b a b b a ++-22 ⑻293261623x x x -+--+⑼xy y x y x y x 2211-⋅⎪⎪⎭⎫ ⎝⎛+-- ⑽ 222x x x +--2144x x x --+(11)a a a a a a 4)22(2-⋅+--.2.已知x 为整数,且918232322-++-++x x x x 为整数,求所有的符合条件的x 的值的和.3、混合运算:⑴2239(1)x x x x ---÷ ⑵232224x x x x x x ⎛⎫-÷ ⎪+--⎝⎭ ⑶ a a a a a a 112112÷+---+⑷ 444)1225(222++-÷+++-a a a a a a ⑸ )1x 3x 1(1x 1x 2x 22+-+÷-+-⑹ )252(23--+÷--x x x x ⑺ 221111121x x x x x +-÷+--+⑻2224421142x x x x x x x -+-÷-+-+ ⑼2211xyx y x y x y ⎛⎫÷- ⎪--+⎝⎭⑽ (abb a 22++2)÷ba b a --22 ⑾22321113x x x x x x x +++-⨯--+⑿ x x x x x x x x x 416)44122(2222+-÷+----+ (13)、22234()()()x y y y x x-⋅-÷-(14)、)252(423--+÷--m m m m (15)、x x x x x x x --+⋅+÷+--36)3(446222(16)、 ()3212221221------⎪⎭⎫ ⎝⎛ba cb b a (17)、⎪⎭⎫ ⎝⎛---÷⎪⎪⎭⎫ ⎝⎛+--x x x x x 23441823224.计算:x x x x x x x x -÷+----+4)44122(22,并求当3-=x 时原式的值.5、先化简,x x x x x x 11132-⋅⎪⎭⎫ ⎝⎛+--再取一个你喜欢的数代入求值:6、有这样一道题:“计算22211x x x -+-÷21x x x-+-x 的值,其中x=2 004”甲同学把“x=2 004”错抄成“x=2 040”,但他的计算结果也正确,你说这是怎么回事?7、计算、)1(1+a a +)2)(1(1++a a +)3)(2(1++a a +…+)2006)(2005(1++a a 。
分式混合运算专题练习(经典集合)
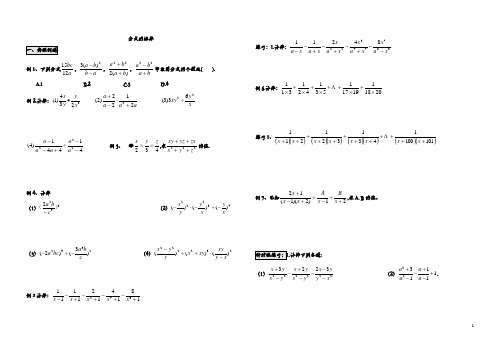
分式的运算一、典型例题例1、下列分式a bc 1215,a b b a --2)(3,)(222b a b a ++,b a b a +-22中最简分式的个数是( ).A.1B.2C.3D.4例2.计算:3234)1(x y y x ∙ a a a a 2122)2(2+⋅-+ x y xy 2263)3(÷41441)4(222--÷+--a a a a a 例3、 若432z y x ==,求222zy x zxyz xy ++++的值.例4、计算(1)3322)(c b a - (2)43222)()()(xy x y y x -÷-⋅-(3)2332)3()2(c b a bc a -÷- (4)232222)()()(xy xy xy x y y x -⋅+÷-例5计算:1814121111842+-+-+-+--x x x x x练习:1.计算:8874432284211x a x x a x x a x x a x a --+-+-+--例6.计算:2018119171531421311⨯+⨯++⨯+⨯+⨯练习1、()()()()()()()()1011001431321211++++++++++++x x x x x x x x例7、已知21)2)(1(12++-=+-+x Bx A x x x ,求A. B 的值。
针对性练习:1.计算下列各题:(1)2222223223xy yx y x y x y x y x ----+--+ (2)1111322+-+--+a a a a .(3)29631a a --+ (4) 21x x --x -1 (5)3a a --263a a a +-+3a ,(6)xy yy x x y x xy --++-222 ⑺b a b b a ++-22 ⑻293261623x x x -+--+⑼xy y x y x y x 2211-⋅⎪⎪⎭⎫ ⎝⎛+-- ⑽ 222x x x +--2144x x x --+(11)a a a a a a 4)22(2-⋅+--.2.已知x 为整数,且918232322-++-++x x x x 为整数,求所有的符合条件的x 的值的和.3、混合运算:⑴2239(1)x x x x ---÷ ⑵232224xx x x x x ⎛⎫-÷ ⎪+--⎝⎭⑶ a a a a a a 112112÷+---+⑷ 444)1225(222++-÷+++-a a a a a a ⑸ )1x 3x 1(1x 1x 2x 22+-+÷-+-⑹ )252(23--+÷--x x x x ⑺ 221111121x x x x x +-÷+--+⑻2224421142x x x x x x x -+-÷-+-+ ⑼2211xy x y x y x y ⎛⎫÷- ⎪--+⎝⎭⑽ (ab b a 22++2)÷ba b a --22 ⑾22321113x x x x x x x +++-⨯--+⑿ x x x x x x x x x 416)44122(2222+-÷+----+ (13)、22234()()()x y y y x x-⋅-÷-(14)、)252(423--+÷--m m m m (15)、x x x x xx x --+⋅+÷+--36)3(446222(16)、 ()3212221221------⎪⎭⎫ ⎝⎛ba cb b a (17)、⎪⎭⎫ ⎝⎛---÷⎪⎪⎭⎫ ⎝⎛+--x x x x x 23441823224.计算:x xx x x x x x -÷+----+4)44122(22,并求当3-=x 时原式的值.5、先化简,x x x x x x11132-⋅⎪⎭⎫ ⎝⎛+--再取一个你喜欢的数代入求值:6、有这样一道题:“计算22211x x x -+-÷21x x x -+-x 的值,其中x=2 004”甲同学把“x=2 004”错抄成“x=2 040”,但他的计算结果也正确,你说这是怎么回事?7、计算、)1(1+a a +)2)(1(1++a a +)3)(2(1++a a +…+)2006)(2005(1++a a 。
分式混合运算练习题答案

分式混合运算练习题答案分式混合运算练习题答案分式混合运算是数学中的一种重要概念,它涉及到分数的四则运算以及整数与分数的运算。
在解决分式混合运算的问题时,我们需要掌握一些基本的技巧和方法。
本文将通过一些例题来讲解分式混合运算的解题思路,并给出详细的答案。
例题一:计算下列分式混合运算的结果:$\frac{1}{2} + \frac{2}{3} \times\frac{3}{4} - \frac{4}{5}$解析:首先,我们需要按照运算法则来进行计算。
根据乘法和除法的优先级高于加法和减法,我们先计算$\frac{2}{3} \times \frac{3}{4}$,然后再进行加法和减法的运算。
$\frac{2}{3} \times \frac{3}{4} = \frac{2 \times 3}{3 \times 4} = \frac{6}{12} =\frac{1}{2}$接下来,我们将$\frac{1}{2} + \frac{1}{2}$,并减去$\frac{4}{5}$。
$\frac{1}{2} + \frac{1}{2} - \frac{4}{5} = \frac{2}{2} - \frac{4}{5} = 1 - \frac{4}{5} = \frac{1 \times 5 - 4}{5} = \frac{5 - 4}{5} = \frac{1}{5}$所以,$\frac{1}{2} + \frac{2}{3} \times \frac{3}{4} - \frac{4}{5} = \frac{1}{5}$。
例题二:计算下列分式混合运算的结果:$3 \div \frac{5}{6} \times \frac{2}{3} -\frac{1}{2}$解析:同样地,我们需要按照运算法则来进行计算。
首先,我们计算$\frac{5}{6} \times \frac{2}{3}$,然后再进行除法和减法的运算。
(完整版)分式混合运算练习题(30题)(最新整理)

D. 2 1 , 去分母得,2 (x 1) x 3 ; x 3 x 1
6. .赵强同学借了一本书,共 280 页,要在两周借期内读完.当他读了一半书时,发现平均每天要多
读 21 页才能在借期内读完.他读前一半时,平均每天读多少页?如果设读前一半时,平均每天读 x
页,则下面所列方程中,正确的是( )
3
用去 18.40 元钱,买的瓶数比第一次买的瓶数多 倍,问她第一次在供销大厦买了几瓶酸奶?
5
2
B. m 5 时,方程的解是正数
C. m 5 时,方程的解为负数
D.无法确定
3.方程
1
5
3
的根是(
)
1 x2 x 1 1 x
A. x =1 B. x =-1
C. x = 3 8
D. x =2
4.1 4 4 0, 那么 2 的值是(
x x2
x
) A.2
B.1 C.-2 D.-1
5.下列分式方程去分母后所得结果正确的是( )
① 1 x 2 2 x 4 0 ②. x 4
23
a
③. a 4; ④. x 2 9 1; ⑤ 1 6;
x
x3
x2
⑥ x 1 x 1 2 . A.2 个 aa
B.3 个
C.4 个
D.5 个
2. 关于 x 的分式方程 m 1,下列说法正确的是( ) x5
A.方程的解是 x m 5
的值. 18.计算:
﹣
19.计算: 21.计算:
20.化简
22.化简: 23.计算:(1)
24.化简:
; (2)
.
25.化简: 27.计算: 29.化简
. 26 化简:
分式混合运算专项练习158题(有答案)26页

分式混合运算专项练习158题(有答案)(1)(2)+﹣(3)(4)(5)(﹣)•÷(+)(6).(7)(8)(9)(10).(11)(12).(13)•÷(14)(﹣)÷.(15)(16)(17)(1+)÷(18)(19)(20)()2•+÷(21)(22)(23)(24)(25)(26)(27)(28).(29)(30).(31)(32)÷•.(33)()÷.(34)(35)(36)(37)(38)(39)(40).(41)(42)(43)(44)(﹣)÷(45)(46)(47)+(48)(49)(50).(51)(52).(53)(54).(55)÷•(56)1﹣÷.(57)(58)(59)÷(60)(61).(62)(63).(64)(+1)÷(1﹣)(65)(66)•﹣÷(67)(68).(69)(70)[﹣(﹣x﹣y)]÷(71)﹣÷x.(72)(73)(74)÷(x+3)•(75)(a ﹣)÷•(76)()÷•(2﹣x)2(77)•(﹣)2(78)(79)(80)(81)(82)(83)(84)(85)(86)(87)(88).(89)(90).(91)(92).(93)[+÷(+)2]•(94)(95)(96)(97)(98)(99)x﹣(100)(101)(102).(103).(104)(105).(106)(x2﹣y2)•÷(107)+﹣(108).(109)÷﹣.(110)(111).(112).(113)(114).(115).(116)(117)(118)(119)(120)(x2y﹣1)﹣3•(﹣x﹣2)﹣3÷(xy)﹣1.(121)(122)(﹣)•.(123)(124).(125).(126).(127).(128).(129)﹣(130)(131)1﹣÷.(132)(﹣)3÷•(﹣)2(133).(134)(135).(136).(137)(138).(139)(140).(141).(142)(143).(144).(145).(146).(147)(148)(149).(150)(151)(152)(153).(154)(155)(156).(157)(158).分式混合运算158题参考答案:(1)=﹣=(2)+﹣=++==(3)=﹣=2x+6﹣x+3=x+9 (4)=÷(﹣)=•(﹣)=﹣.(5)原式===.(6)原式===(7)原式==x+y(8)原式==a﹣1(9)原式==y﹣3(10)==3(x+2)﹣(x﹣2)=3x+6﹣x+2=2x+8.(11)原式==(12)原式==(﹣1)==(13)解:原式==(14)解:原式==(15)原式=÷•=••=.(16)原式=•=﹣=﹣=.(17)原式===.(18)===﹣y.(19)原式==1﹣==(20)原式===.(21)原式=××=.(22)原式==(23)原式==﹣1(24)原式===(25)=+﹣=,===(26)=﹣••=﹣(27)=﹣•,=﹣==﹣(28),=(﹣)•,=﹣,=,=,=﹣.(29)原式==(a+1)﹣(a﹣1)=2(30)原式=(31)原式==(32)原式==.(33)()÷=•=(34)原式===.(35)原式=•(a﹣1)2=a﹣1.(36)原式=×=(37)原式=×=(38)原式=×==(39)原式==a4b(40)原式==(41)=×=2(m﹣3)﹣(m+3)=m﹣9.(42)原式==﹣.(43)原式=﹣+=1﹣x+x2=x2﹣x+1.(44)原式=(﹣)×=×=.(45)原式===3(1+x)(46)原式==.(47)原式=×+=+=.(48)原式=﹣==(49)原式=••=.(50)原式=====.(51)原式=====(52)原式===.(53)原式==(54)原式=×=(55)原式=•=(56)原式=1﹣=1﹣==.(57)原式=﹣÷(58)原式=×=.(59)原式=÷(﹣)=÷=×=.(60)原式=﹣===﹣(61)原式=﹣•=﹣==.(62)原式=(63)原式=××(m+n)(m﹣n)=(m+n)2.(64)原式=÷=×=.(65)原式=﹣×=﹣=.(66)原式=×﹣×=﹣==.(67)原式==0(68)原式=+=(69)原式=(×=.(70)=.(71)===.(72)原式===(73)原式=﹣+====(74)原式=××=(75)原式=××=(76)原式=[﹣]ו(2﹣x)2=ו(2﹣x)2=(77)原式=××=(78)原式===.(79)=﹣+,==(80),=÷=•=﹣(81)原式==(82)原式==(83)原式=×= (84)原式=+﹣==. (85)原式=(x+1)(x ﹣1)(﹣﹣), =x+1﹣x+1﹣(x+1)(x ﹣1)=﹣x 2+3.(86)原式=﹣×=﹣=0.(87)原式=÷(﹣)=.(88)原式=(﹣)÷=×=.(89)原式=﹣×(m ﹣1)=﹣=﹣2m . (90)===(91)原式= (92)原式=.(93)原式=[+×]×=[+]×=(94) 原式==.(95)原式=(x+y )•﹣==x+y(96)原式==(97)原式=••=(98)原式=•+•=+==(99)原式==(100)原式===.(101)原式=﹣===(102)原式=•=•=.(103)原式=1﹣×=1﹣=﹣.(104)=×=(105)=××=x.(106)原式=(x+y)(x﹣y)××=y(107)原式=﹣﹣=﹣﹣==(108)=••==.(109)原式=•﹣=﹣==(110)=+=+﹣==(111)=﹣+=﹣+1=1.(112)原式=+•=+==1.(113)原式=﹣==(114)原式=•=•=•=y+9 (115)原式=1﹣•=1﹣===﹣(116)原式==x﹣y.(117)原式==(118)原式===(119)原式====﹣(120)原式=x﹣6y3•(﹣x6)÷x﹣1y﹣1=﹣y3÷x﹣1y﹣1=﹣xy4(121)原式=++==﹣(122)原式=(﹣)•=3(x+2)﹣(x﹣2)=3x+6﹣x+2=2x+8(123)原式=•=•=x﹣2(124)原式=1﹣÷[﹣]=1﹣÷=1﹣•=1﹣==﹣.(125)原式=﹣×=﹣==.(126)原式=[﹣]÷=[﹣]×x=×x=﹣.(127)原式=[]÷=[﹣]÷=×=(128)原式=[]•=•=y+9.(129)原式==(130)原式==0(131)原式=1﹣=.(132)原式=﹣••=﹣(133)原式=•﹣=﹣=原式=••=(134)(135)原式=[﹣]•=[﹣]•=•=(136)原式==﹣=(137)=(138)=,==.(139)=•=(x+y)(x﹣y)=x2﹣y2(140)=++===(141)原式=====(142)原式====2(143)原式=÷=•=.(144)原式=÷=•=.(145)原式=4a﹣1﹣+=﹣==(146)原式=×+=+==1.(147)==﹣(148)原式=+•=+=﹣=﹣(149)原式===0(150)原式=•=(151)原式=•=(152)原式=﹣===﹣(153)原式=[﹣]•=•=•=(154)原式===(155)原式=•=(156)原式=﹣a2b6••=﹣b5(157)原式===﹣(x+y)=﹣x﹣y(158)原式=÷=•=。
八上数学每日一练:分式的混合运算练习题及答案_2020年综合题版

2020年 八 上 数 学 : 数 与 式 _分 式 _分 式 的 混 合 运 算 练 习 题
1.
(2020襄城.八上期末) “丰收1号”小麦的试验田是边长为 米(a>1)的正方形减去一个边长为1米的正方形蓄水池后余
下的部分,“丰收2号”小麦的试验田是边长为( )米的正方形,两块试验田里的小麦都收获了500千克.
(3) ( 式的混合运算;分式的混合运算;0指数幂的运算性质;负整数指数幂的运算性质;
答案解析
4.
(2017沂水.八上期末) 化简:
(1) a﹣b﹣
;
(2) ( + )÷ . 考点: 分式的混合运算;
答案解析
5. (2017莘.八上期末) 计算 (1) •
(2) (3)
(1) 哪种小麦的单位面积产量高?
(2) 高的单位面积产量是低的单位面积产量的多少倍?
考点: 整式的混合运算;分式的混合运算;
答案解析
2.
(2018东城.八上期末) 定义:任意两个数 ,按规则
(1) 若
直接写出 的“如意数” ;
扩充得到一个新数 ,称所得的新数 为“如意数”.
(2) 如果 (3) 已知
,求 的“如意数” ,并证明“如意数” ;
,且 的“如意数”
,则 (用含 的式子表示)
考点: 分式的混合运算;
答案解析
3. (2017乌拉特前旗.八上期末) 计算: (1) (﹣2)3﹣( )﹣1+( ﹣1)0+(﹣
)2017×(1.5)2016
(2) (2a+1)(2a﹣1)﹣(a+2)2﹣3a(a+1)
分式混合运算专项理解练习158题(有答案解析)

.
(127)
.
(123) (124) (125)
(128)
.
.
(129)
﹣
.
(130)
分式混合运算---- 13
(131)1﹣
÷
.
(136)
.
(132)(﹣ )3÷ •(﹣ )2;
(137)
(133)
.
(138)
.
(134) (135)
(139)
.
(140)
.
分式混合运算---- 14
(141)
•
﹣
=
﹣
=
(134)原式= •
•=
(135)原式=[
﹣
=
•
=
]•
=[
﹣
]•
(136) 原式=
(137)
=
=
﹣
=
;
(138)
=
,
分式混合运算---- 26
= (139) (140) = (141)原式=
= (142)原式=
=
.
=
•
=(x+y)(x﹣y)=x2﹣y2;
= =
+
+
=
=
=
=
= =
=2;
(143)原式=
.
(104)
;
(109)
÷﹣
.
(105)
.
(110)
分式混合运算---- 11
(111)
.
(116)
(112)
.
(117)
(113)
(118)
(114)
.
(119)
(115)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分式混合运算专项练习158题(有答案)(1)(2) +﹣(3)(4)(5) (﹣)•÷(+)(6) .(7)(8)(9)(10) .(11) ;(12) .(13) •÷;(14) (﹣)÷.(15)(16)(17)(1+)÷(18)(19)(20) ()2•+÷(21) ;(22)(23)(24)(25)(26)(27) ;(28) .(29) ;(30) .(31) ;(32) ÷•.(33) ()÷.(34)(35)(36) ;(37) ;(38) ;(39)(40) .(41)(42)(43)(44) (﹣)÷(45)(46)(47) +(48) ;(49) .(50) .(51)(52).(53);(54).(55)÷•;(56)1﹣÷.(57)(58)(59)÷(60);(61).(62);(63).(64)(+1)÷(1﹣)(65)(66)•﹣÷(67);(68).(69)(70)[﹣(﹣x﹣y)]÷(71)﹣÷x.(72);(73);(74)÷(x+3)•;(75)(a ﹣)÷•(76)()÷•(2﹣x)2;(77)•(﹣)2(78)(79);(80)(81);(82);(83);(84)(85)(86)(87)(88).(89)(90).(91);(92).(93)[+÷(+)2]•(94)(95);(96)(97);(98)(99)x ﹣(100)(101)(102).(103).(104);(105).(106)(x2﹣y2)•÷;(107)+﹣(108).(109)÷﹣.(110)(111).(112).(113)(114).(115).(116)(117)(118)(119)(120)(x2y﹣1)﹣3•(﹣x﹣2)﹣3÷(xy)﹣1.(121);(122)(﹣)•.(123)(124).(125).(126).(127).(128).(129)﹣(130)(131)1﹣÷.(132)(﹣)3÷•(﹣)2;(133).(134)(135).(136).(137)(138).(139)(140).(141).(142);(143).(144).(145).(146).(147)(148);(149).(150)(151)(152)(153).(154)(155)(156).(157);(158).参考答案:(1)=﹣=;(2)+﹣=++==;(3)=﹣=2x+6﹣x+3=x+9;(4)=÷(﹣)=•(﹣)=﹣.(5)原式===.(6)原式===(7)原式==x+y(8)原式==a﹣1(9)原式==y﹣3(10)==3(x+2)﹣(x﹣2)=3x+6﹣x+2=2x+8.(11)原式==;(12)原式==(﹣1)==(13)解:原式==;(14)解:原式==(15)原式=÷•=••=.(16)原式=•=﹣=﹣=.(17)原式= = =.(18)===﹣y.(19)原式==1﹣==(20)原式===.(21)原式=××=.(22)原式==(23)原式==﹣1(24)原式===(25)=+﹣=, ===;(26)=﹣••=﹣;(27)=﹣•,=﹣==﹣;(28),=(﹣)•,=﹣,=,=,=﹣.(29)原式==(a+1)﹣(a﹣1)=2;(30)原式=(31)原式==;(32)原式==.(33)()÷=•=(34)原式===.(35)原式=•(a﹣1)2=a﹣1.(36)原式=×=;(37)原式=×=;(38)原式=×==;(39)原式==a4b;(40)原式==(41)=×=2(m﹣3)﹣(m+3)=m﹣9.(42)原式==﹣.(43)原式=﹣+=1﹣x+x2=x2﹣x+1.(44)原式=(﹣)×=×=.(45)原式===3(1+x);(46)原式==.(47)原式=×+=+=.(48)原式=﹣==;(49)原式=••=.(50)原式=====.(51)原式=====;(52)原式===.(53)原式==;(54)原式=×=(55)原式=•=;(56)原式=1﹣=1﹣==.(57)原式=﹣÷(58)原式=×=.(59)原式=÷(﹣)=÷=×=.(60)原式=﹣===﹣;(61)原式=﹣•=﹣==.(62)原式=;(63)原式=××(m+n)(m﹣n)=(m+n)2.(64)原式=÷=×=.(65)原式=﹣×=﹣=.(66)原式=×﹣×=﹣==.(67)原式==0;(68)原式=+=(69)原式=(×=.(70)=.(71)===.(72)原式===;(73)原式=﹣+====;(74)原式=××=;(75)原式=××=;(76)原式=[﹣]ו(2﹣x)2=ו(2﹣x)2=;(77)原式=××=(78)原式===.(79)=﹣+,==;(80),=÷=•=﹣(81)原式==;(82)原式==;(83)原式=×=(84)原式=+﹣==.(85)原式=(x+1)(x ﹣1)(﹣﹣),=x+1﹣x+1﹣(x+1)(x ﹣1)=﹣x 2+3.(86)原式=﹣×=﹣=0.(87)原式=÷(﹣)=.(88)原式=(﹣)÷=×=.(89)原式=﹣×(m ﹣1)=﹣=﹣2m . (90)===(91)原式=; (92)原式=.(93)原式=[+×]×=[+]×=(94) 原式==.(95)原式=(x+y )•﹣==x+y ;(96)原式==;(97)原式=••=;(98)原式=•+•=+==;(99)原式==(100)原式===.(101)原式=﹣===;(102)原式=•=•=.(103)原式=1﹣×=1﹣=﹣.(104)=×=;(105)=××=x.(106)原式=(x+y)(x﹣y)××=y;(107)原式=﹣﹣=﹣﹣==(108)=••==.(109)原式=•﹣=﹣==(110)=+=+﹣==;(111)=﹣+=﹣+1=1.(112)原式=+•=+==1.(113)原式=﹣==;(114)原式=•=•=•=y+9(115)原式=1﹣•=1﹣===﹣(116)原式==x﹣y.(117)原式==;(118)原式===;(119)原式====﹣;(120)原式=x﹣6y3•(﹣x6)÷x﹣1y﹣1=﹣y3÷x﹣1y﹣1=﹣xy4(121)原式=++==﹣;(122)原式=(﹣)•=3(x+2)﹣(x﹣2)=3x+6﹣x+2=2x+8(123)原式=•=•=x﹣2;(124)原式=1﹣÷[﹣]=1﹣÷=1﹣•=1﹣==﹣.(125)原式=﹣×=﹣==.(126)原式=[﹣]÷=[﹣]×x=×x=﹣.(127)原式=[]÷=[﹣]÷=×=(128)原式=[]•=•=y+9.(129)原式==;(130)原式==0;(131)原式=1﹣=.(132)原式=﹣••=﹣;(133)原式=•﹣=﹣=(134)原式=••=(135)原式=[﹣]•=[﹣]•=•=(136)原式==﹣=(137)=;(138)=,==.(139)=•=(x+y)(x﹣y)=x2﹣y2;(140)=++===(141)原式=====(142)原式====2;(143)原式=÷=•=.(144)原式=÷=•=.(145)原式=4a﹣1﹣+=﹣==(146)原式=×+=+==1.(147)==﹣(148)原式=+•=+=﹣=﹣;(149)原式===0(150)原式=•=;(151)原式=•=;(152)原式=﹣===﹣;(153)原式=[﹣]•=•=•=(154)原式===;(155)原式=•=;(156)原式=﹣a2b6••=﹣b5(157)原式===﹣(x+y)=﹣x﹣y;(158)原式=÷=•=.。
