差分方程讲解--老师

合集下载

数学建模差分方程PPT课件

或 G(x , yi , yi1 , , yin ) 0 或 H (x , yi , yi , , n yi ) 0
的方程都是差分方程。方程中所含未知函数角标的最大值与最小值的差数称为差分
方程的阶。若一个函数代入差分方程后，方程两端恒等，则称此函数为
差分方程的解。如果解中所含相互独立的任意常数的个数等于方程的阶数，则称该解为差分方程的通解。满足初始条件的解称为特解。
• 第一阶段: w(k)每周减1千克, c(k)减至下限10000千卡
w (k)w (k1)1 w ( k 1 ) w ( k ) c ( k 1 ) w ( k )
c(k1) 1[w(k)1] w (k)w (0)k
c(k1) w (0) 1(1k)
1 8000
0.025
120 200 k 00Cm 10000 k 10
2 x k 2 x k 1 x k 2 ( 1 ) x 0 , k 1 , 2 ,
二阶线性常系数差分方程
x0为平衡点研究平衡点稳定，即k, xkx0的条件
模型的推广 2 x k 2 x k 1 x k 2 ( 1 ) x 0
方程通解
xk
c1
k 1
c2
k 2
(c1, c2由初始条件确定)
相当于70千克的人每天消耗2000千卡 ~ 3200千卡；
3）运动引起的体重减少正比于体重，且与运动形式有关；
4）为了安全与健康，每周体重减少不宜超过1.5 千克，每周吸收热量不要小于10000千卡。
减肥计划
某甲体重100千克，目前每周吸收20000千卡热量，体重维持不变。现欲减肥至75千克。
1 2 k 是（3）的 k 重根，则只要将 Y1 (i),Y2 (i),,Yk (i) 换为

差分方程(1)-基础知识省名师优质课赛课获奖课件市赛课一等奖课件

形如
yx+2 + ayx+1 + byx = f (x).
(10)
(其中 a , b 0, 且均为常数)旳方程, 称为二阶常系数线性差分方程. 当 f (x) = 0 时, 即
yx+2 + ayx+1 + byx = 0
(11)
称为齐次差分方程; 当 f (x) 0时, 称为非齐次差分方程.
类似于二阶线性常微分方程, 二阶线性差分方程与其有相同旳解旳构造. 故先求齐次方程(11)旳通解.
故所求通解为
yx
C1
C2 (2)x
10 3
x
2x2.
(2) f (x) = Cqx 设特解旳待定式为
y x Bq x (q不是特征根); y x Bxq x (q是特征方程单根); y x Bx2q x (q是二重特征根). 其中 B 为待定系数.
例11 求差分方程 yx+2 3yx+1 + 2yx = 2x旳一种特解.
x B0 B1x Bm xm (a 1) (6)
或
y x (B0 B1x Bm xm ) x (a 1) (7)
其中B0 , B1 , , Bm为待定系数.
例5 求差分方程 yx+1 2yx = 3x2 旳一种特解.
解这里 a = 2, 设 y x B0 B1x B2 x2 , 代入差分方程, 得
解相应旳齐次方程旳特征方程为
2 3 + 2 = 0.
方程旳根为
1 = 1, 2 = 2,
因为 q = 2 =2, 设特解为 y x Bx2x ,
代入原方程, 得
B(x+2)2x+23B(x+1)2x+1+2Bx2x = 2x,

差分方程知识点总结

差分方程知识点总结一、差分方程的概念差分方程是指用差分运算符号（Δ）表示的方程。

差分运算符Δ表示的是某一变量在两个连续时间点的变化量。

差分方程通常用于描述离散时间下的变化规律，比如时间序列、离散动力系统等。

二、常见的差分方程1. 一阶线性差分方程一阶线性差分方程的一般形式为：y(t+1) - y(t) = a*y(t) + b，其中a和b为常数。

一阶线性差分方程常常用于描述某一变量在不同时间点之间的线性变化规律。

2. 二阶线性差分方程二阶线性差分方程的一般形式为：y(t+2) - 2*y(t+1) + y(t) = a*y(t) + b，其中a和b为常数。

二阶线性差分方程通常用于描述某一变量在不同时间点之间的二阶线性变化规律。

3. 线性非齐次差分方程线性非齐次差分方程的一般形式为：y(t+1) - a*y(t) = b，其中a和b为常数。

线性非齐次差分方程通常用于描述某一变量在不同时间点之间的线性变化规律，并且受到外部条件的影响。

4. 滞后差分方程滞后差分方程的一般形式为：y(t+1) = f(y(t))，其中f为某一函数。

滞后差分方程通常用于描述某一变量在不同时间点之间的非线性变化规律。

5. 差分方程组差分方程组是指由多个差分方程组成的方程组。

差分方程组通常用于描述多个变量之间的变化规律，比如混合动力系统、多变量时间序列等。

三、差分方程的解法1. 特征根法特征根法是解一阶或二阶线性差分方程的一种常用方法。

通过求解特征方程，可以求得差分方程的通解。

2. 递推法递推法是解一阶或二阶非齐次差分方程的一种常用方法。

通过递推关系，可以求得差分方程的特解。

3. Z变换法Z变换法是解一阶或二阶差分方程的一种常用方法。

通过对差分方程进行Z变换，可以将其转换为等价的代数方程，然后求解其解。

4. 数值解法对于复杂的差分方程，通常采用数值解法求解。

数值解法包括Euler法、Runge-Kutta法、递推法等，通过迭代计算逼近差分方程的解。

(完整版)差分方程的常见解法

(完整版)差分方程的常见解法差分方程的常见解法差分方程是数学中的一种重要方程类型，常用于描述离散事件系统的发展规律。

在求解差分方程时，我们可以采用以下几种常见的解法。

1. 直接求解法直接求解法是最简单且常用的差分方程求解方法之一。

它的基本思想是通过观察差分方程的规律，找到解的形式，并通过代入验证得到确切的解。

举例来说，对于一阶线性差分方程$y_{n+1} = ay_n + b$，我们可以猜测解的形式为$y_n = c\lambda^n$，其中$c$和$\lambda$为待定常数。

将此解代入方程，再通过已知条件解得$c$和$\lambda$的值，从而得到原差分方程的解。

2. 特征方程法特征方程法是一种常用于求解线性齐次差分方程的方法。

对于形如$y_{n+2} = ay_{n+1} + by_n$的差分方程，我们可以通过构造特征方程来求解。

具体步骤是，我们将差分方程中的项移动到一边，得到$y_{n+2} - ay_{n+1} - by_n = 0$。

然后，假设解的形式为$y_n =\lambda^n$，将其代入方程，得到特征方程$\lambda^2 - a\lambda - b = 0$。

解这个特征方程，得到特征根$\lambda_1$和$\lambda_2$，然后通解的形式为$y_n = c_1\lambda_1^n + c_2\lambda_2^n$，其中$c_1$和$c_2$为待定常数。

3. Z 变换法Z 变换法是一种广泛应用于差分方程求解的方法，特别适用于线性时不变差分方程。

该方法的基本思想是将差分方程转化为代数方程，并利用 Z 变换的性质求解。

对于差分方程$y_{n+1} = ay_n + b$，通过取 Z 变换，我们可以得到转化后的方程$Y(z) = azY(z) + b \frac{1}{1 - z^{-1}}$，其中$Y(z)$代表$y_n$的Z 变换。

然后，将方程整理，求解得到$Y(z)$，再通过反 Z 变换将其转换为差分方程的解$y_n$。

《高数3差分方程》课件

《高数3差分方程》PPT课件
# 高数3差分方程 PPT课件 ## 简介 - 差分方程的定义 - 差分方程的应用领域
什么是差分方程？
定义
差分方程是描述离散变量之间关系的数学方程。
应用领域
差分方程广泛应用于物理学、经济学、生物学和工程学等各个领域。
离散与连续
差分方程与微分方程的联系与区别。
常见的差分方程类型
参考资料
1 差分方程相关教材
《差分方程导论》、《差分方程与重积分》等。
2 差分方程的相关论文
搜寻关于差分方程研究的最新论文。
3 差分方程的相关网站
浏览在线差分方程教程和实例应用。
通过求解两个线性齐次差分方程的通解并取其乘积得到非齐次差分方程的通解。
齐次线性差分方程通解的求法
根据初始条件求解齐次线性差分方程的通解。
非齐次线性差分方程通解的求法
根据初始条件和非齐次项求解非齐次线性差分方程的通解。
差分方程在实际应用中的重要性
经济学中的应用
差分方程可用于描述经济模型中的离散变化。
生物学中的应用
差分方程可用于模拟生物体内离散变量的变化规律。
物理学中的应用
差分方程可用于研究离散物理系统的演化。
工程学中的应用
差分方程可用于分析工程系统中的离散变化与其他参数之间的关系。
总结
差分方程是研究离散变量之间关系的重要工具，广泛应用于各个学科中。了解差分方程的基础知识和求解方法对深入理解实际问题具有重要意义。
1
一阶线性常微分方程
描述离散变量一阶导数与其他变量之间的关系。
2
二阶线性常微分方程
描述离散变量二阶导数与其他变量之间的关系。

差分方程课件

例3 求 yt t 2 3t 的差分.
解由差分的运算性质，有
yt (t 3 ) 3 t (t 1) (3 )
2 t t 2 2 t
3 (2t 1) (t 1) 2 3 3 (2t 6t 3)
t 2 t t 2
.
1 差分方程的概念
差分满足以下性质：（1）（2）（3）
(Cyt ) Cyt (C为常数)
（yt zt ) yt zt
（yt zt ) zt yt yt 1zt
yt zt yt yt zt ( zt 0) （4）（ ) zt zt 1 zt
引例1： Fibonacci （斐波那契）数列
问题 13世纪意大利著名数学家Fibonacci在他的著作《算盘书》中记载着这样一个有趣的问题：一对刚出生的幼兔经过一个月可长成成兔，成兔再经过一个月后可以繁殖出一对幼兔. 若不计兔子的死亡数，问一年之后共有多少对兔子？
月份
幼兔成兔
0
1 0
1
引例2：日常的经济问题中的差分方程模型
1）. 银行存款与利率假如你在银行开设了一个1000元的存款账户，银行的年利率为7%. 用an表示n年后你账户上的存款额，那么下面的数列就是你每年的存款额： a0, a1, a2, a3, …, an,… 设r为年利率，由于an+1=an+r an, 因此存款问题的数学模型是： a0=1000, an+1=(1+r)an, n=1,2,3,…
yt t
( n)
t (t 1)(t 2) (t n 1) ，则
yt (t 1)( n) t ( n) (t 1)t (t 1) (t 1 n 1)

高等数学中的差分方程相关知识点详解

高等数学中的差分方程相关知识点详解在高等数学中，差分方程是一个非常重要的数学工具，它被广泛应用于各种科学领域，如物理、化学、工程学等。

差分方程与微分方程不同，在处理离散数据时更加方便，因此在实际应用中得到了广泛的应用。

接下来，我们将详细介绍差分方程的相关知识点。

1.差分方程的定义差分方程是一种用递推关系式描述离散变量间数值关系的数学工具，通常表示为：$a_n=F(a_{n-1},a_{n-2},...,a_{n-k})$其中，$a_n$表示一个数列的第$n$项，$k$为正整数，$F$为给定的函数。

差分方程起始值$a_0,a_1,...,a_{k-1}$也是给定的。

2.差分方程的求解方法求解差分方程的过程与求解微分方程的过程类似，需要先求出差分方程的通解，然后根据初始条件得到特解。

（1）求通解对于一个$k$阶差分方程，我们可以猜测一个$k$次线性递推数列$\{b_n\}$，即$b_n=c_1\lambda_1^n+c_2\lambda_2^n+...+c_k\lambda_k^n$，其中$c_1,c_2,...,c_k$是任意常数，$\lambda_1,\lambda_2,...,\lambda_k$是$k$个根。

将猜测的线性递推数列带入差分方程中得到：$c_1\lambda_1^n+c_2\lambda_2^n+...+c_k\lambda_k^n=F(c_1\la mbda_1^{n-1}+c_2\lambda_2^{n-1}+...+c_k\lambda_k^{n-1},c_1\lambda_1^{n-2}+c_2\lambda_2^{n-2}+...+c_k\lambda_k^{n-2},...,c_1\lambda_1^{n-k}+c_2\lambda_2^{n-k}+...+c_k\lambda_k^{n-k})$整理得到：$c_1(\lambda_1^n-F(\lambda_1^{n-1},\lambda_1^{n-2},...,\lambda_1^{n-k}))+c_2(\lambda_2^n-F(\lambda_2^{n-1},\lambda_2^{n-2},...,\lambda_2^{n-k}))+...+c_k(\lambda_k^n-F(\lambda_k^{n-1},\lambda_k^{n-2},...,\lambda_k^{n-k}))=0$由于$c_1,c_2,...,c_k$是任意常数，因此需要使方程的每个系数都等于$0$，也就是：$\lambda_1^n-F(\lambda_1^{n-1},\lambda_1^{n-2},...,\lambda_1^{n-k})=0$$\lambda_2^n-F(\lambda_2^{n-1},\lambda_2^{n-2},...,\lambda_2^{n-k})=0$...$\lambda_k^n-F(\lambda_k^{n-1},\lambda_k^{n-2},...,\lambda_k^{n-k})=0$将上述$k$个方程写成矩阵的形式，即可解得$\lambda_1,\lambda_2,...,\lambda_k$。

《高数3差分方程》PPT课件

( yt2 yt1 ) ( yt1 yt ) yt1 yt 2 yt ,
则原方程还可化为 2 yt 3t.
10
又如：可化为
yt2 2 yt1 yt 3t , yt 2 yt1 yt2 3t2 ,
2 yt 2 yt 3t.
定义5.1.3 如果一个函数代入差分方程后，方程两边恒等，则称此函数为差分方程的解.
yt (t 2 ) (t 1)2 t 2 2t 1,
2( yt ) 2(t 2 ) (yt ) (2t 1)
2(t 1) 1 (2t 1) 2,
3( yt ) (2 yt ) (2) 2 2 0. 例2 设 yt at (0 a 1), 求 ( yt ). 解 ( yt ) at1 at at (a 1).
kbt1 akbt cbt 即 k(b a) c ,
于是
yt*
b
c
a
bt
.
28
(2) 当 b a 时，令yt* ktbt 代入方程(6) , 得：
k(t 1)bt1 aktbt cbt
即 k(t 1)b akt c ,
解得 k c . a
于是
yt*
c a
tbt
ctbt1 .
当b a 和 b a 时，方程(6) 的通解分别为：
yt
c ba
bt
Aa t
和
yt ctbt1 Aat .
29
例6 求差分方程
yt 1
1 2
yt
5 t
的2 通解。
解对应齐次差分方程的通解为 Y A 1 t .
2
由于 a 1 , b 5 , a b,
22
故可设其特解为： yt* kbt .

第七节差分方程

第七节差分方程对连续型变量而言，我们常常回导致到微分方程的问题. 对离散型变量将导致一类的问题.一、差分的定义定义设)(x y y =是一个函数, 自变量从x 变化到x +1, 这时函数的增量记为)()1(x y x y y x -+=∆, 我们趁这个量为)(x y 在点x 步长为1的一阶差分,简称为)(x y 的一阶差分. 为了方便我们也记)(),1(1x y y x y y x x =+=+,即x x x y y y -=∆+1.称x x x x x x x x y y y y y y y y +-=---=∆∆+++++121122)()()(为)(x y 二阶差分,简记为x y 2∆.同样记)(2x y ∆∆为x y 3∆,并称为三阶差分.一般记)(1x n x n y y -∆∆=∆,称为n 阶差分.且有i n x i ni i n x ny C y -+=-=∆∑)1(0. 性质: 当a,b,C 是常数, y x 和z x 是函数时,(1) Δ(C )=0;(2) Δ(Cy x )= C Δ(y x );(3) Δ(ay x + b z x )= a Δy x + b Δ z x ;(4) Δ(y x z x )= z x+1Δy x +y x Δ z x = y x+1Δz x +z x Δy x ;(5) 1111++++∆-∆=∆-∆=⎪⎪⎭⎫ ⎝⎛∆x x x x x x x x x x x x x xz z z y y z z z z y y z z y . 例已知),0(≠=x x y x α求Δ(y x ).解 Δ(y x )= ααx x -+)1(.特别, 当n 为正整数时, Δ(y x )= i n n i i n x C-=∑1, 阶数降了一阶.推论若m, ,n 为正整数时, m,> n P(x)为n 次多项式,则0)(=∆x P m .例已知),10(≠<=a a y x x 求Δ(y x ).解 Δ(y x )= )1(1-=-+a a a a x x x .二、差分方程定义设是含有未知函数差分的等式，称为差分方程。

差分方程详解

差分方程百科内容来自于:差分方程是含有未知函数及其导数的方程，满足该方程的函数称为差分方程的解。

基本概念一、差分的概念设函数yt=f(t)在t=…，-2，-1，0，1，2，…处有定义,对应的函数值为…，y-2，y-1，y0，y1，y2，…，则函数yt=f(t)在时间t的一阶差分定义为Dyt=yt+1-yt=f(t+1)-f(t)。

依此定义类推，有Dyt+1=yt+2-yt+1=f(t+2)-f(t+1)，Dyt+2=yt+3-yt+2=f(t+3)-f(t+2)，………………一阶差分的性质(1) 若yt=C(C为常数)，则Dyt=0；(2) 对于任意常数k，D(kyt)=kDyt；(3) D(yt+zt)=Dyt+Dzt。

函数yt=f(t)在时刻t的二阶差分定义为一阶差分的差分，即D2yt= D (D yt)= D yt+1- D yt=(yt+2-yt+1)-(yt+1-yt)=yt+2-2yt+1+yt．依此定义类推，有D2yt+1= Dyt+2- Dyt+1=yt+3-2yt+2+yt+1，D2yt+2= Dyt+3-Dyt+2=yt+4-2yt+3+yt+2，………………类推，计算两个相继的二阶差分之差，便得到三阶差分D3yt= D2yt+1- D2yt=yt+3-3yt+2+3yt+1-yt，D3yt+1= D2yt+2- D2yt+1=yt+4-3yt+3+3yt+2-yt+1，………………一般地,k阶差分(k为正整数)定义为这里二、差分方程含有未知函数yt=f(t)以及yt的差分Dyt，D2yt，…的函数方程，称为常差分方程(简称差分方程)；出现在差分方程中的差分的最高阶数，称为差分方程的阶。

n阶差分方程的一般形式为F(t，yt，Dyt，…，Dnyt)=0，其中F是t，yt, Dyt，…，Dnyt的已知函数，且Dnyt一定要在方程中出现。

含有两个或两个以上函数值yt，yt+1，…的函数方程，称为(常)差分方程，出现在差分方程中未知函数下标的最大差，称为差分方程的阶。

《数学建模》课件：第7章差分方程模型(投影版)

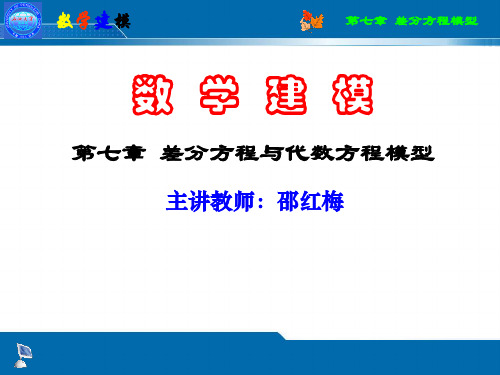
ai
i0
下面仅对 1阶情形给予证明，其余情形证明思想类似。
不妨设一阶线性常系数差分方程为： xk1 axk b
其对应的特征方程为 a 0，故特征根为 = a. 那么由定理1得：
它的平衡点 x = b 稳定的充要条件是 a 1. 下面证明这个结论.
1 a
差分方程稳定性理论简介
数学建模
求得的方程的解
x=x =
b
n
称为该差分方程的平衡点（奇解）。
ai
i0
若记该差分方程的一般解（通解）为 xk，它若满足：lkim xk x，
则称 x 是稳定的，否则，称 x 是不稳定的。
6. 特征方程
称代数方程： an n an1 n1 a1 a0 0
为差分方程 an xkn a1xk1 a0xk b 对应的特征方程。
x= b 1 a
稳定的充要条件是
a 1.
差分方程稳定性理论简介
数学建模
第七章差分方程模型
三、一阶非线性差分方程的平衡点和稳定性
考虑方程 xk1 f (xk )
（II）
其平衡点 x 由代数方程 x f (x) 解出。为了分析 x 的稳定性，
将f ( x )在 x 点作Taylor展开，只取一次项，方程（II）近似为
差分方程稳定性理论简介
数学建模
第七章差分方程模型
微分方程的差分方法
一、微分的差分方法
设函数 f (x)在 a, b 一阶连续可微，任给一个分割：a=x0 x1 xn b
已知 f (x) 在节点 xk 的函数值 f (xk ) (k 0,1, , n)，试求函数 f (x) 在节点
xk 处的导数值 f '(xk ) 的近似值。

差分方程含有三角函数的解法

差分方程含有三角函数的解法差分方程是数学中的一种重要的方程形式，它描述了变量之间的变化关系。

而含有三角函数的差分方程则更加复杂，但是同样具有重要的应用价值。

本文将介绍含有三角函数的差分方程的解法。

首先我们来了解一下什么是差分方程。

差分方程是一种离散形式的微分方程，它使用差分运算符（通常表示为△）来描述变量之间的变化。

差分方程的形式可以表示为：△y(n) = f(n, y(n))其中，y(n)表示第n个离散点的变量值，f(n, y(n))表示变量在该点的变化关系。

这个方程可以用来描述离散点之间的变化规律，例如时间序列、信号处理等。

接下来我们来介绍含有三角函数的差分方程的解法。

含有三角函数的差分方程通常可以通过迭代的方式求解。

假设我们要求解的差分方程为：△y(n) = A*sin(B*n) + C*cos(D*n)其中A、B、C、D为常数。

我们可以通过迭代的方式来逐步逼近解。

我们可以选取一个初始值y(0)，然后通过差分方程来逐步计算出后续的值。

具体的计算过程如下：y(1) = y(0) + △y(0)y(2) = y(1) + △y(1)...y(n) = y(n-1) + △y(n-1)其中，△y(n) = A*sin(B*n) + C*cos(D*n)。

通过不断迭代计算，我们可以得到y(n)的近似解。

当然，为了提高计算的精度，我们可以选择更小的△n（即离散点之间的间隔），并增加迭代的次数。

这样可以使得近似解更加接近真实解。

需要注意的是，含有三角函数的差分方程的解通常是周期性的。

根据三角函数的性质，我们可以知道sin(x)和cos(x)的周期都是2π。

因此，差分方程的解也会呈现出周期性的特点。

在实际应用中，含有三角函数的差分方程可以用来描述许多周期性现象。

例如，天文学中的行星运动、物理学中的波动现象等都可以通过差分方程来进行建模和分析。

因此，研究含有三角函数的差分方程的解法具有重要的理论和实际意义。

差分方程讲解--老师

§2 一阶线性差分方程
数值解与解析解的比较: 在求银行模型的数值解时只需要一个差分方程和一个初值. 这是数值解的一个强有力的性质—求数值解时无须要求差分方程具有特殊的性质. 只要从一个或多个初值开始进行迭代计算就行了. 另一方面, 因为没有第k项的一个一般的公式, 每一项必须从前一项或几项算得. 从一个数值解来预测解的长期性态可能是困难的.
差分方程从数列谈起
§1 数列的差分
§2 一阶线性差分方程 §3 一阶线性差分方程组
§1 数列的差分
一. 数列的概念
二. 数列差分的概念三. 差分表的性质
§1 数列的差分一. 数列的概念
一个数列就是实数的任何(有限或无限的) 有序集. 这些数称为数列的项或元素.
用an来表示数列的第n项, 称之为数列的通项. 定义1.1 一个数列是一个函数, 其定义域为全体正整数(有时, 为方便计, 是全体非负整数集合), 其值域包含在全体实数集中.
{2Sn} {2n3} {5, 7, 9, 11, }
以及
{3Sn} {2, 2, 2, 2, }
令
Sn An3 Bn2 Cn D.
§1 数列的差分
由S1 1, S2 5, S3 14, S4 30得 A B C D 1, 8A 4B 2C D 5(23 A 22 B 2C D 5), 27A 9B 3C D 14(33A 32B 3C D 14), 64A 16B 4C D 30(43A 42 B 4C D 30), 解关于A, B, C和D的方程组可得 A 1/3, B 1/2, C 1/6, D 0, 则
1 1 C 0 A B 2 2 1 2 1 1 an n n n(n 1) 2 2 2

差分方程_精品文档

程）法。本节主要讲述前3种方法，后2种方法将在后续章节中讲
解。
一、差分方程的初值问题（边界条件）
二、差分方程的解法（前3种方法）
三、传输算子的概念
返回
一、差分方程的初值问题（边界条件）
相应于连续时间系统中的起始条件和初始条件, 在离散时间系统中存在着起始样值与初始样值。
起始样值即在激励信号加入之前系统已具有的一组样值, 以符号y-(n)表示。
返回
例7-4-6 已知 y(n)+2y(n-1) =5u(n), 且y(-1) =1,
求完全解。
特征方程 a +2=0 a = -2
齐次解
yhn C1 2n
特解
因为x(n)=5u(n), n³0时为5（常数）
所以 yp(n) =D
代入原方程求特解 D+2D =5 (n 0)
完全解
所以 D 5
“E”表示将序列超前一个单位时间的运算。 E也称为移
序算子，利用移序算子可y(n写-1)出= 1: y(n)
对y于(n差+分1方)=程Eyy((nn)+1)
-
ay(n)
E
=x(n)
可改写为: （E - a）y(n) =x(n)
对于二例，可以引入
传输算子 HE 1
于是有：
Ea
而对于方程式 y(n) - ay(n-1) =x(n -1)
N
akCa nk 0
k 0
消去常数C，逐项除以a n-N 并化简得:
a0a N+a1a N-1+……+ aN-1a + aN=0
该式称为差分方程的特征方程，特征方程的根a1. a2 、……、 aN称为差分方程的特征根。

差分方程讲解--老师

数学建模差分方程PPT课件

差分方程(1)-基础知识省名师优质课赛课获奖课件市赛课一等奖课件

差分方程知识点总结

(完整版)差分方程的常见解法

《高数3差分方程》课件

差分方程课件

高等数学中的差分方程相关知识点详解

《高数3差分方程》PPT课件

第七节差分方程

差分方程详解

《数学建模》课件：第7章 差分方程模型(投影版)

差分方程含有三角函数的解法

差分方程讲解--老师

差分方程_精品文档

《数学建模》课件：第7章差分方程模型(投影版)