数字信号处理 MATLAB 上机实验 教学讲义
第一次实验 MATLAB的数字信号处理基础

第一次实验MAT1AB的数字信号处理基础一、实验目的1.掌握在MAT1AB中创建和编写脚本程序的步骤,熟悉在MAT1AB中进行基本的矩阵运算2.了解数字信号在计算机系统中的表示和数字信号处理的基本过程3.掌握用MAT1AB产生数字信号的方法二、实验内容1.熟悉在MAT1AB下创建脚本文件编制程序的方法在MAT1AB中,脚本文件时由一系列的命令构成并储存为.m格式的文件。
通常使用m文件来编写一个完整的仿真程序。
脚本文件的创建,可采用以下两种方式:(1)在菜单栏中选择Fi1e下拉框中New选项,可以新建多种MAT1AB文件,我们编辑仿真程序,通常选择第一项BIankM-Fi1e,即新建一个空的MAT1AB文件。
具体参见下图。
图1(2)采用菜单栏中新建按钮即可新建一个空的MAT1AB文件。
Jk MAT1AB7.9.0(R2009b)Fi1eEditDebugParaJ一一J2.MAT1AB中的数据表示MAT1AB中的基本数据单元为数组矩阵,MAT1AB中的数学运算都是基于矩阵的。
掌握了矩阵运算,就掌握了MAT1AB编程的关键。
MAT1AB中使用到的变量无需事先声明其数据类型,大小等,MAT1AB会自动根据赋值情况进行解析。
比如,可用通过以下命令产生一个矩阵:3.常用序列的MAT1AB实现(1)单位抽样序列。
在MAT1AB中可以用以下函数来实现单位抽样序列function[x,n]=impseq(nθ,n1z n2)%产生x(n)=de1ta(n-n0);n1<=n0<=n2if((nθ<n1)∣(nθ>∩2)∣(n1>n2))error('参数必须满足n1<=nθ<=n2,)endn=[n1:n2];x=[zeros(1,(nO-n1))4∕Zθros(1z(n2-nO))];stem(x);图3(2)单位阶跃序列。
在MAT1AB中可用〃>=0来实现〃(〃一%)。
《数字信号处理》上机实验指导书

《数字信号处理》上机实验指导书实验1 离散时间信号的产生1.实验目的数字信号处理系统中的信号都是以离散时间形态存在,所以对离散时间信号的研究是数字信号处理的基本所在。
而要研究离散时间信号,首先需要产生出各种离散时间信号。
MATLAB 是一套功能强大的工程计算及数据处理软件,广泛应用于工业,电子,医疗和建筑等众多领域。
使用MATLAB软件可以很方便地产生各种常见的离散时间信号,而且它还具有强大的绘图功能,便于用户直观地输出处理结果。
通过本实验,学生将学习如何用MATLAB产生一些常见的离散时间信号,并通过MATLAB中的绘图工具对产生的信号进行观察,加深对常用离散信号的理解。
2.实验要求本实验要求学生运用MATLAB编程产生一些基本的离散时间信号,并通过MATLAB的几种绘图指令画出这些图形,以加深对相关教学内容的理解,同时也通过这些简单的函数练习了MATLAB的使用。
3.实验原理(1)常见的离散时间信号1)单位抽样序列,或称为离散时间冲激,单位冲激:?(n)???1?0n?0 n?0如果?(n)在时间轴上延迟了k个单位,得到?(n?k)即:?1n?k ?(n?k)??0n?0?2)单位阶跃序列n?0?1 u(n)?n?0?0在MATLAB中可以利用ones( )函数实现。
x?ones(1,N);3)正弦序列x(n)?Acos(?0n??)这里,A,?0,和?都是实数,它们分别称为本正弦信号x(n)的振幅,角频率和初始相位。
f0??02?为频率。
x(n)?ej?n4)复正弦序列5)实指数序列x(n)?A?n(2)MATLAB编程介绍MATLAB是一套功能强大,但使用方便的工程计算及数据处理软件。
其编程风格很简洁,没有太多的语法限制,所以使用起来非常方便,尤其对初学者来说,可以避免去阅读大量的指令系统,以便很快上手编程。
值得注意得就是,MATLAB中把所有参与处理的数据都视为矩阵,并且其函数众多,希望同学注意查看帮助,经过一段时间的训练就会慢慢熟练使用本软件了。
数字信号处理相关MATLAB实验内容--第1章

实验1 离散时间信号的时域分析一、实验目的(1)了解MATLAB 语言的主要特点及作用;(2)熟悉MATLAB 主界面,初步掌握MATLAB 命令窗和编辑窗的操作方法;(3)学习简单的数组赋值、数组运算、绘图的程序编写;(4)了解常用时域离散信号及其特点;(5)掌握MATLAB 产生常用时域离散信号的方法。
二、知识点提示本章节的主要知识点是利用MATLAB 产生数字信号处理的几种常用典型序列、数字序列的基本运算;重点是单位脉冲、单位阶跃、正(余)弦信号的产生;难点是MATLAB 关系运算符“==、>=”的使用。
三、实验内容1. 在MATLAB 中利用逻辑关系式0==n 来实现()0n n -δ序列,显示范围21n n n ≤≤。
(函数命名为impseq(n0,n1,n2))并利用该函数实现序列:()()()632-+-=n n n y δδ;103≤≤-nn 0212. 在MATLAB 中利用逻辑关系式0>=n 来实现()0n n u -序列,显示范围21n n n ≤≤。
(函数命名为stepseq(n0,n1,n2))并利用该函数实现序列:()()()20522≤≤--++=n n u n u n y3. 在MATLAB 中利用数组运算符“.^”来实现一个实指数序列。
如: ()()5003.0≤≤=n n x n4. 在MATLAB 中用函数sin 或cos 产生正余弦序列,如:()()2003.0cos 553.0sin 11≤≤+⎪⎭⎫ ⎝⎛+=n n n n x πππ5. 已知()n n x 102cos 3π=,试显示()()()3,3,+-n x n x n x 在200≤≤n 区间的波形。
6. 参加运算的两个序列维数不同,已知()()6421≤≤-+=n n u n x ,()()8542≤≤--=n n u n x ,求()()()n x n x n x 21+=。
数字信号处理第三版用MATLAB上机实验

实验二:时域采样与频域采样一、时域采样1.用MATLAB编程如下:%1时域采样序列分析fs=1000A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=1000;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs); Xk=fft(xn);subplot(3,2,1);stem(n,xn);xlabel('n,fs=1000Hz');ylabel('xn');title('xn');subplot(3,2,2);plot(n,abs(Xk));xlabel('k,fs=1000Hz'); title('|X(k)|');%1时域采样序列分析fs=200A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=200;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs);Xk=fft(xn);subplot(3,2,3);stem(n,xn);xlabel('n,fs=200Hz'); ylabel('xn');title('xn');subplot(3,2,4);plot(n,abs(Xk));xlabel('k,fs=200Hz'); title('|X(k)|');%1时域采样序列分析fs=500A=444.128; a=222.144; w=222.144; ts=64*10^(-3); fs=500;T=1/fs;n=0:ts/T-1; xn=A*exp((-a)*n/fs).*sin(w*n/fs); Xk=fft(xn);subplot(3,2,5);stem(n,xn);xlabel('n,fs=500Hz');ylabel('xn');title('xn');subplot(3,2,6);plot(n,abs(Xk));xlabel('k,fs=500Hz'); title('|X(k)|');2.经调试结果如下图:20406080-200200n,fs=1000Hzxnxn2040608005001000k,fs=1000Hz|X (k)|51015-2000200n,fs=200Hzx nxn510150100200k,fs=200Hz |X(k)|10203040-2000200n,fs=500Hzx nxn102030400500k,fs=500Hz|X (k)|实验结果说明:对时域信号采样频率必须大于等于模拟信号频率的两倍以上,才 能使采样信号的频谱不产生混叠.fs=200Hz 时,采样信号的频谱产生了混叠,fs=500Hz 和fs=1000Hz 时,大于模拟信号频率的两倍以上,采样信号的频谱不产生混叠。
数字信号处理实验指导书--Matlab版

下:
由于 e jω 是频率的周期函数,所以系统的频率特性也是频率的周期函数,且周期为 2π ,因 此研究系统频率特性只要在[ −π ,π ]范围内就可以了。
三、实验内容及步骤
1、在实验上机前,认真复习离散卷积和差分方程的有关内容,仔细阅读本实验原理和 步骤。准备实验所需数据。
2、离散卷积计算。 1)在主界面下进入“实验五” 的“离散卷积”子系统,选定几组不同的 x(n)、h(n) 代入离散卷积程序计算 y(n),记录实验结果。 3、差分方程迭代解法 1)¨在主界面下进入“实验五” 的“差分方程”子系统,本实验要求首先确定系统方 程系数个数和需要输出 y(n)的样点个数,然后依次输入 a[0]~a[N]、b[0]~b[N]这些系数的 数值和 y(n)的初始值 y(0)~y(N-1),h(n)的初始值 h(0)~h(N-1),运行后即得冲激响应 h(n) 和阶跃信号激励下的响应 y(n)的结果和图形显示。 2)自己选择一个离散时间系统,写出其差分方程,设好初始条件进行实验并记录实验 结果。 4、在主界面下进入“实验六”即“离散系统 Z 域分析”,本实验中给出了计算系统
明了系统结构、参数、特性三者之间的关系,即同一结构,参数不同其特性也不同。 例如,下图所示离散系统:
数学模型由下列差分方程描述: y(n)=ay(n-1)+x(n)
系统函数 系统频率特性
H (z) = z , | z |> a z−a
幅度特性为
H (e jω )
=
e jω e jω − a
数字信号处理实验讲义

数字信号处理实验讲义实验一序列、频谱、卷积一、实验目的1.掌握序列的输入方法;2.熟悉不同序列的特征;3.了解确定性信号谱分析的方法;4.验证卷积的计算过程;二、实验要求1.利用matlab程序,生成几种常用的序列,如矩形序列,单位脉冲序列;2.绘制图形,观察序列特征;3.研究其频率特性,绘制图形,观察频率响应特征;4.利用matlab程序,验证卷积的过程;三、实验步骤1.矩形序列(1)生成长度为N的矩形序列,观察并记录生成的图形;n=1:50x=sign(sign(10-n)+1);close all;subplot(3,1,1);stem(x);title('单位矩形信号序列');(2)研究其频率特性,()∑∞-∞=-=n nj Nj en R e H ωω)(,分别研究其幅频特性和相频特性,观察并记录生成的图形;k=-25:25;X=x*(exp(-j*pi/25)).^(n'*k); magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title('单位矩形信号的幅度谱'); angX=angle(X); %绘制x(n)的相位谱subplot(3,1,3);stem(angX) ; title ('单位矩形信号的相位谱')2.单位脉冲序列(1)生成单位脉冲序列,观察并记录生成的图形;n=1:50; %定义序列的长度是50x=zeros(1,50); %注意:MATLAB中数组下标从1开始x(1)=1;close all;subplot(3,1,1);stem(x);title('单位冲击信号序列');(2) 研究其频率特性,()∑∞-∞=-=n nj j en x e H ωω)(,分别研究其幅频特性和相频特性,观察并记录生成的图形;k=-25:25;X=x*(exp(-j*pi/12.5)).^(n'*k); magX=abs(X); %绘制x(n)的幅度谱subplot(3,1,2);stem(magX);title('单位冲击信号的幅度谱'); angX=angle(X); %绘制x(n)的相位谱subplot(3,1,3);stem(angX) ; title ('单位冲击信号的相位谱')3.卷积过程∑∞-∞=-= =mmnhmxnhnxny)()()(*)()(,n=1:50; %定义序列的长度是50hb=zeros(1,50); %注意:MATLAB中数组下标从1开始hb(1)=1;hb(2)=2.5;hb(3)=2.5;hb(4)=1;close all;subplot(3,1,1);stem(hb);title('系统hb[n]');m=1:50; %定义序列的长度是50A=444.128; %设置信号有关的参数a=50*sqrt(2.0)*pi;T=0.001; %采样率w0=50*sqrt(2.0)*pi;x=A*exp(-a*m*T).*sin(w0*m*T);subplot(3,1,2);stem(x);title('输入信号x[n]');y=conv(x,hb);subplot(3,1,3);stem(y);title('输出信号y[n]');四、实验报告要求1.写出生成对应序列的matlab程序,并分析;2.记录生成的图形;3.描述对应的序列和频率特性的特征;4.验证卷积计算结果;五、思考:1.如何生成实指数序列?写出对应的matlab程序a1=2n=1:50x1=(a1.^n)subplot(1,1,1)stem(x1);title('实指数序列')2.编写程序验证卷积定律。
MATLAB数字信号处理课件

freqz的命令形式
• h = freqz(b,a,w) – 采用上面的形式时,需先对频率样本点向量w作出 定义。通常的做法是使用linspace函数。
• [h,w] = freqz(b,a) – w和p没有定义 ,默认w由(0~π)上均分的512点构 成,频率单位为rad/sample。
• [h,w] = freqz(b,a,p,’whole’) – 使用带参数’whole’选项的命令形式
• 还提供了从模拟低通滤波器原型转换为高通、 带通和带阻的转换函数,模拟滤波器转换为数 字滤波器的双线性变换法和冲激响应不变法, 模拟IIR滤波器的阶数选择函数以及数字滤波 器直接设计函数等等,使用起来非常方便。
• 本节以巴特沃思滤波器为例 介绍 MATLAB工 具箱提供的滤波器设计函数 使用方法。
20
实现2
• 实现1中第二条命令的形式 可改写为 freqz(b,a,256) 或freqz(b,a,256,2000)
• 可自动绘出频率在(0~π) 范围内的幅频特性和相频 特性图。
• 注意无返回输出参数调用 freqz函数绘出的相频特性 不能正确给定在ω=π处的 值,因为ω=π 属于下半个 单位圆。
带波纹δp ;阻带衰减δs。其中通带波纹和阻带衰减 也可以用分贝数给出
28
滤波器以容差方式给出的幅度指标
|H( jw)|
1
1-d p
过渡带
ds
通带
阻带
0
w p ws
w
29
5.4.2 IIR 滤波器设计
• MATLAB工具箱提供了几种模拟滤波器原型的 产生函数,如巴特沃思(Butterworth),切比雪夫 (Chebyshev)滤波器等。
30
数字信号处理实验

数字信号处理实验数字信号处理实验讲义前⾔ (2)实验⼀MATLAB简介 (3)实验⼆⽤FFT实现信号的谱分析 (5)实验三IIR数字巴特沃思滤波器的设计 (8)实验四FIR数字滤波器的设计 (9)前⾔信号处理与计算机的应⽤紧密结合。
⽬前⼴泛应⽤的MA TLAB⼯具软件包,以其强⼤的分析、开发及扩展功能为信号处理提供了强有⼒的⽀持。
在数字信号处理实验中,我们主要应⽤MA TLAB的信号处理⼯具箱及其灵活、便捷的编程⼯具,通过上机实验,帮助学⽣学习、掌握和应⽤MA TLAB软件对信号处理所学的内容加以分析、计算,加深对信号处理基本算法的理解。
实验⼀ MATLAB 简介实验⽬的1.熟悉MATLAB 软件的使⽤⽅法; 2.MA TLAB 的绘图功能;3.⽤MA TLAB 语句实现信号的描述及变换。
实验原理1.在MA TLAB 下编辑和运⾏程序在MA TLAB 中,对于简单问题可以在命令窗(command windows )直接输⼊命令,得到结果;对于⽐较复杂的问题则可以将多个命令放在⼀个脚本⽂件中,这个脚本⽂件是以m 为扩展名的,所以称之为M ⽂件。
⽤M ⽂件进⾏程序的编辑和运⾏步骤如下:(1)打开MA TLAB ,进⼊其基本界⾯;(2)在菜单栏的File 项中选择新建⼀个M ⽂件;(3)在M ⽂件编辑窗⼝编写程序;(4)完成之后,可以在编辑窗⼝利⽤Debug ⼯具调试运⾏程序,在命令窗⼝查看输出结果;也可以将此⽂件保存在某个⽬录中,在MATLAB 的基本窗⼝中的File 项中选择Run The Script ,然后选择你所要运⾏的脚本⽂件及其路径,即可得出结果;也可以将此⽂件保存在当前⽬录中,在MA TLAB 命令窗⼝,“>>”提⽰符后直接输⼊⽂件名。
2.MA TLAB 的绘图功能plot(x,y) 基本绘图函数,绘制 x 和y 之间的坐标图。
figure(n ) 开设⼀个图形窗⼝nsubplot(m,n,N) 分割图形窗⼝的MATLAB 函数,⽤于在⼀个窗⼝中显⽰多个图形,将图形窗⼝分为m ⾏n 列,在第N 个窗⼝内绘制图形。
数字信号处理实验MATLAB上机DOC
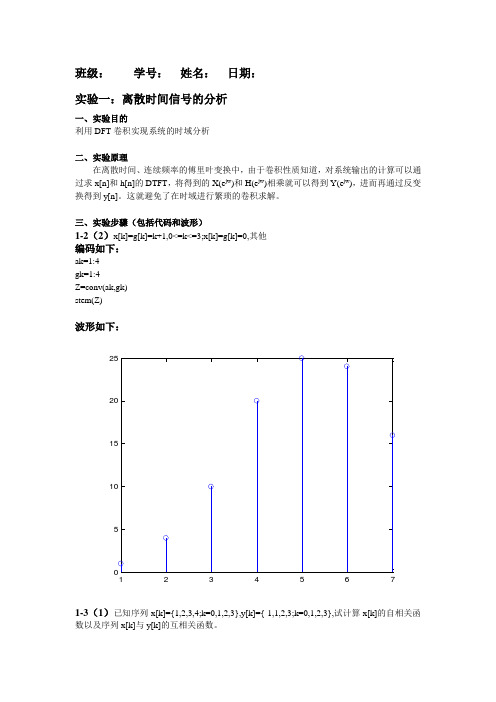
班级: 学号: 姓名: 日期: 实验一:离散时间信号的分析一、实验目的利用DFT 卷积实现系统的时域分析二、实验原理在离散时间、连续频率的傅里叶变换中,由于卷积性质知道,对系统输出的计算可以通过求x[n]和h[n]的DTFT ,将得到的X(e jw )和H(e jw )相乘就可以得到Y(e jw ),进而再通过反变换得到y[n]。
这就避免了在时域进行繁琐的卷积求解。
三、实验步骤(包括代码和波形)1-2(2)x[k]=g[k]=k+1,0<=k<=3;x[k]=g[k]=0,其他 编码如下:ak=1:4 gk=1:4Z=conv(ak,gk) stem(Z)波形如下:12345675101520251-3(1)已知序列x[k]={1,2,3,4;k=0,1,2,3},y[k]={-1,1,2,3;k=0,1,2,3},试计算x[k]的自相关函数以及序列x[k]与y[k]的互相关函数。
编码如下:x=[1,2,3,4];kx=0:3; y=[-1,1,-2,3];ky=0:3; xf=fliplr(x); s1=conv(x,xf); s2=conv(xf,y); yf=fliplr(y); s3=conv(yf,x);k1=kx(1)+ky(1):kx(end)+ky(end); kxf=-fliplr(kx);k2=kxf(1)+ky(1):kxf(end)+ky(end); kyf=-fliplr(ky);k3=kyf(1)+kx(1):kyf(end)+kx(end); subplot(2,2,1); stem(k1,s1);xlabel('k1');ylabel('s1'); subplot(2,2,2); stem(k2,s2);xlabel('k2');ylabel('s2'); subplot(2,2,3) stem(k3,s3);xlabel('k3');ylabel('s3');波形如下:0246102030k1s 1-4-2024-10-50510k2s 2-4-2024-10-50510k3s 3M-1已知g1[t]=cos(6*pi*t),g2=cos(14*pi*t),g3=cos(26*pi*t),以抽样频率f(max)=10HZ对上述三个信号进行抽样。
数字信号处理(MATLAB版)上机实验操作

实验一离散时间信号与系统一、实验目的:1、熟悉常见离散时间信号的产生方法;2、熟悉离散时间系统的单位脉冲响应和单位阶跃响应的求解方法;3、熟悉离散时间信号经过离散时间系统的响应的求解方法。
二、实验内容:已知离散时间系统差分方程为y(n)-0.5y(n-1)+0.06y(n-2)=x(n)+x(n-1),求1、该系统的单位脉冲响应并绘图;2、该系统的单位阶跃响应并绘图;3、已知x(n)=可自己指定用filter函数经过系统的响应并绘图;4、用conv_m函数求系统响应并绘图。
三、实验平台:MA TLAB集成系统四、设计流程:此处写个人自己的设计流程五、程序清单:此处写程序内容六、调试和测试结果:此处写程序的执行结果和实验过程中的调试经过、出现的错误和对应的解决方法七、教师评语与成绩评定此处由老师填写上机操作:实验一离散时间信号与系统实验内容:1.脉冲响应>> b =[1,1]; a = [1,-0.5,0.06];n = [-10:25];>> impz(b,a,n);>> title('Impulse Response'); xlabel('n'); ylabel('h(n)')2.单位阶跃响应>> x = stepseq(0,-10,25); s = filter(b,a,x);Warning: Function call stepseq invokes inexact match d:\MATLAB7\work\STEPSEQ.M.>> stem(n,s)>> title('Step Response'); xlabel('n');ylabel('s(n)')3.>> a=[1,-0.5,0.06];b=[1,1];>> n=-20:120;>> x1=exp(-0.05*n).*sin(0.1*pi*n+pi/3);>> s1=filter(b,a,x1);>> stem(n,s1);;xlabel('n');ylabel('s1(n)');4.>> a=[1,-0.5,0.06];b=[1,1];>> n=-20:120;>> h=impz(b,a,n);>> x1=exp(-0.05*n).*sin(0.1*pi*n+pi/3);>> [y,m]=conv_m(x1,n,h,n);Warning: Function call conv_m invokes inexact match d:\MATLAB7\work\CONV_M.M. >> stem(m,y);title('系统响应');xlabel('m');ylabel('y(m)');实验二离散信号与系统的连续频域分析一、实验目的:1、掌握离散时间信号的DTFT的MATLAB实现;2、掌握离散时间系统的DTFT分析;3、掌握系统函数和频率相应之间的关系。
《数字信号处理实验》课件第1章

⑥初步了解MATLAB的基本流程控制语句及其使用方 法。
⑦通过例题,初步了解用MATLAB进行二维图形绘制 的方法和常用图形函数。
(2)阅读例1-1、例1-2程序,预先编写“实验内容与方 法”3、4中练习题的程序。
六、实验报告
(1)列写“实验内容与方法”1、2项中各条命令的意义。 (2)列写“实验内容与方法”3、4项中各练习题的程序, 并打印运行结果。
(2)在MATLAB命令窗口输入: B=[1+2i,3+4i;5+6i,7+8i] C=[1,3;5,7]+[2,4;6,8]*i 观察输出结果。试一试,如果C式中i前的*号省略, 结果如何? 输入: D=sqrt(2+3i)
D*D E=C F=conj(C) G=conj(C) 观察以上各输出结果,并在每式的后面标注其含义。
二、实验涉及的MATLAB子函数
1.abs 功能:求绝对值(幅值)。 调用格式:
y=abs(x);用于计算x的绝对值。 当x为复数时,得到的是复数模(幅值),即
abs(x) (Re(x))2 (Im(x))2
当x为字符串时,abs(x)得到字符串的各个字符的
ASCII码,例如x=123
abs(x)=49 50 51;输入
6.title 功能:在图形的上方标注图名。 调用格式:
title(string);在图形的上方标注由字符串表示的图名, 其中string的内容可以是中文或英文。
7.xlabel 功能:在横坐标的下方标注说明。 调用格式:
xlabel(string);在横坐标的下方标注说明,其中string 的内容可以是中文或英文。
abs(abc),则ans=97 98 99。
2.plot 功能:按线性比例关系,在x和y两个方向上绘制二
基于Matlab的数字信号处理实验指导-精品
基于Matlab的数字信号处理实验指导第一章MATLAB基本知识MA TLAB是一种面向科学和工程计算的高级语言,包含的几十个工具箱,覆盖了通信、自动控制、信号处理、图像处理、生命科学等科技领域,现已成为国际公认的最优秀的科技界应用软件。
该软件的特点是:强大的计算功能、计算结果和编程可视化及极高的转换效率。
本章目的是帮助新用户在领略MA TLAB非凡能力的同时能轻松跨越MA TLAB的门槛。
§1.1 MATLAB语言的基本使用环境一.MATLAB的安装MA TLAB5.3 版本仅有一张光盘,运行其上的安装文件setup.exe,则可以按提示安装整个MA TLAB系统。
MA TLAB6.1 版本有两张光盘,将其中的程序盘插入驱动器,运行其上的安装文件setup.exe,则可以按提示安装整个MA TLAB系统。
MA TLAB6.x与以前的版本相比,在界面上的变化是很大的,以前的版本只给出一个又一个命令窗口,MA TLAB6.1的程序界面,除了其右侧的Command Window (命令窗口)之外,还有Launch Pad (程序调用板) 和Command History (命令的历史记录)两个子窗口,以及Workspace (工作空间管理程序) 和Current Directory (当前目录管理程序)等,使MA TLAB的操作更容易、方便了。
二.MATLAB5.3的操作步骤由于实验室安装的是MA TLAB5.3,下面我们介绍MA TLAB5.3的操作步骤。
双击桌面的MA TLAB5.3的图标,如图1-1,将进入MA TLAB5.3的Command Window (命令窗口),如图1-2。
图1-1 MA TLAB5.3的图标图1-2 MA TLAB5.3的命令窗口1.帮助[Help]选项Help Windows 打开分类帮助窗Help Tips 打开函数文件命令帮助窗Help Desk 打开以超文本形式存储的帮助文件主页Examples and Demos 打开演示窗主页About MA TLAB 注册图标、版本、制造商和用户信息选择[Help]中不同的类别,用户可以从相关的帮助信息得到帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
freqz:
因果LTI系统的的幅频响应和相频响应曲线,在matlab 中可以用以下函数作出: [H,w] =freqz(num,den,N),频率响应在单位圆的上半周取N 个等分点; [H,w]=freqz(num,den, N,'whole'),频率响应在单位圆取N 个等分点; H=freqz(num,den, w) ,频率响应在w设定的频率上。 该函数可以同时作出幅频和相频响应图 其中: num-----系统传递函数分子系数组成的行向量; den------系统传递函数分母系数组成的行向量; N ---------是频率响应的点数,最好为2的幂缺省值512; w --------是返回频率轴坐标向量。
stem(t,h2,'fill');
grid on; title('单位冲激响应2');
ylabel('h2(n)');
xlabel('n')
87
figure(2) zplane(num,den); %作出极-零图
figure(3) freqz(num,den,N,Fs); grid on; title('频率响应'); %做出幅频和相频响应曲线
68
69
• 随机信号:
【例】 rand产生均匀分布的白嘈声,randn产生高斯分
布的白噪声 t=0:0.01:1; y=randn(1,length(t)); plot(t,y);grid on;
70
4.2离散信号
•
周期序列 弦信号
【例】产生一个幅度为2,频率为4Hz,相位为 A=2; phi=pi/6; omega=2*pi/12; n=-10:10; x=A*sin(omega*n+phi); stem(n,x,'fill'); grid on;
1
1.5 2 frequency in rad
2.5
3
95
【例】比较高密度谱和高分辨率谱之间的差异,考虑
x(n)=cos(0.48*pi*n)+cos(0.52*pi*n)
(1)取x(n)(0 n 10 )时,求x(n)的DFT。 (2)将(1)中的x(n)以补零方式使x(n) 加 长到 0 n 100 ,求x(n)的DFT 。 (3)取x(n)( 0 n 100 )时,求x(n)的 DFT画出幅频特性。
79
conv of x and h 8
7
6
5
4
y
3
2
1
0
4
6
8
10
12 14 Time index n
16
18
20
22
80
4.4 LTI系统
filter:
因果LTI系统的的零状态响应,在matlab中可以用函数
y=filter(num,den,x) 实现。 其中: num------系统传递函数分子系数组成的行向量 den-------- 系统传递函数分母系数组成的行向量 x-------输入的离散序列 y-------输出的离散序列,y的长度与x的长度一样
/6的正71• 单位脉冲序列 (n) 和单位阶跃序列u(n) 可以用ones(1,n)和zeros(1,n)来生成单位脉冲 序列和单位阶跃序列 ones(1,n)命令产生1行n列的1值 zeros(1,n)命令产生1行n列的0值
72
【例】 产生单位脉冲序列 (n 3) 和单位阶跃序列u(n-3)
86
figure(1) subplot(2,1,1); stem(n,h1,'fill'); grid on; title('单位冲激响应1'); ylabel('h1(n)'); xlabel('n')
subplot(2,1,2); [h2,t]=impz(num,den, n,Fs); %计算单位冲激响应2
83
zplane:
离散系统的极-零图,在matlab中可以用以下函数作出: zplane(z,p),已知极点、零点; zplane(num,den); [hz,hp,ht]= zplane(z,p),返回极点、零点、坐标轴 等的句柄。
84
【例】 已知一个系统的传递函数为
H (e
jw
0.008 0.033 e jw 0.05e j 2 w 0.033 e j 3 w 0.008e j 4 w ) 1 2.37e jw 2.7e j 2 w 1.6e j 3 w 0.41e j 4 w
96
% spectrum_com1.m &part 1 % Spectrum based on the first 10 samples of x(n)
figure(1)
n1=[0:1:9];x=cos(0.48*pi*n1)+cos(0.52*pi*n1);y1=x(1:1:10); subplot(2,1,1);stem(n1,y1);title('signal x(n), 0 <= n <= 9');xlabel('n') axis([0,10,-2.5,2.5]) Y1=fft(y1);magY1=abs(Y1(1:1:6)); k1=0:1:5;w1=2*pi/10*k1; subplot(2,1,2);stem(w1/pi,magY1);title('Samples of DTFT Magnitude'); xlabel('frequency in pi units') axis([0,1,0,10])
88
89
90
91
【例】有一调幅信号
xa (t ) [1 cos(2 100t )]cos(2 600t )
•用做频谱分析,要求能分辨xa(t)的所有频率分量, •若用fs=3kHz频率抽样,抽样数据为512点, •做频谱分析,求X(k)=DFT[x(n)],512点, •画出X(k)的幅频特性|X(k)|。
•%图中横坐标值即为信号的实际频率(赫兹)。 •k=0:1:N-1;w=2*pi/N*k; •subplot(3,1,3);plot(w,magX);ylabel('DFT Magnitude');xlabel('frequency in rad') •axis([0,pi,0,250]) •%图中横坐标值为信号的数字频率(弧度),乘以fs除 94 以2*pi即为信号的实际频率(赫兹)。
b=ones(1,8); n3=2;n4=9; %完整b(n)序列的非平凡值和区间端点 c=conv(a,b); nc1=n1+n3;nc2=n2+n4;%计算卷积和确定卷积非平凡区间端点 kc=nc1:nc2; %构成非平凡区间的序号自变量 stem(kc,c,'b') title('conv of x and h'); ylabel('y');xlabel('Time index n');
76
77
【例】有序列
1 A(n) 0
1 B(n) 0
n 3,4,,12 else
n 2,3,,9 else
和
求这两个完整序列的卷积,并图示。
78
%完整序列卷积%conv1.m a=ones(1,10); n1=3;n2=12; %完整a(n)序列的非平凡值和区间端点
【例】产生一个高度为1,宽度为3,延时为2秒的矩形
脉冲 信号
t=-2:0.02:6; plot(t,rectpuls(t-2,3)); axis([-2,6,0,1.5]);
67
【例】 取样函数:用sinc(x)命令
N=1000; t=-10:20/N:10; x=sinc(t/pi); plot(t,x);grid on
Matlab基础介绍
一 二 三 四 、Matlab 简介 、Matlab 的安装与启动 、Matlab 编程基础 、Matlab 在数字信号处理课 程中的应用
1
四、 Matlab 在数字信号处理课程中的应用 举例 • • • • 常见连续信号 离散信号 离散卷积 LTI系统
65
4.1 常见连续信号
81
impz:
在 A(z)、B(z)已知情况下,用以下函数求系统的单 位抽样响应 h(n), t是所记录的0到n-1的取样点数矢量: [h,t]=impz(num,den),取样点数自动选取; [h,t]=impz(num,den, n) ,取样点数选取为0到n-1或由 矢量n 指定,取样间隔为1 ; [h,t]=impz(num,den, n,Fs) ,取样间隔为1/Fs; impz(num,den),只在当前窗口用stem(t,h)绘出单 位抽样响应 h(n)。
74
4.3 离散卷积
• matlab 中卷积运算的指令是c=conv(a,b),其中a和b是有 限长的序列。
【例】计算下面两个序列的卷积
a=[-2 0 1 –1 3]; b=[1 2 0 -1]; 两个序列的都从0开始的
75
%conva.m x=[-2 0 1 -1 3]; h=[1 2 0 -1 0]; y=conv(x,h); N=length(y)-1; n=0:1:N; stem(n,y,'fill'); grid on; title('conv of x and h'); ylabel('y'); xlabel('Time index n');
97
% part 2
% High density spectrum (100 samples) based on the first 10 samples of x(n) figure(2)
