基于matlab的衍射系统仿真 -
lmda=500e-9; %波长
r=1.2e-3; %
f = 1; %焦距
N = 19;
K =linspace(-0.1,0.1,N) ;
lmda1 =lmda*( 1+ K) ;
xm= 2000*lmda* f;
xs=linspace(-xm,xm,2000) ;
ys=xs;
z0 =zeros(2000) ;
B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;
B1=B/max(B);
end
NC=255; %绘制衍射仿真图样及强度曲线
Br=(B/max(B))*NC;
subplot(1,2,1)
image(y0,x0,Br);
colormap(gray(NC) );
Br=B1'*NC;
subplot(1,2,1)
image(y0,x0,Br);
colormap(gray(NC) );
subplot(1,2,2)
plot(B1,x0);
（3）初始仿真图样
初始的光源对L1透镜的张角为 rad。
（4）改变参数，即上下移动光源
光源向上移动少许距离后的衍射图样。
光源向下移动少许距离后的衍射图样。
d=7*a
③缝数量N
N=3
N=4
N=6
5)变化规律
根据仿真图样可以得出以下结论：
①改变缝宽a
增加缝宽a，亮纹间距减小；反之，亮纹间距增加。
②改变缝距d
增加缝距d，亮纹数量增加，亮纹间距减小；反之，亮纹数量减少，亮纹间距增加。
③缝数量N
增加缝数量N，亮纹变的越细亮；反之，亮纹宽度增加。
4.多缝的夫琅和费衍射，使用平行光照明，观察衍射图样随点光源位置（光源上下移动）的变化
subplot(1,2,2)
plot(B1,x0);
3)初始仿真图样
4)改变参数后的仿真图样（即增加入射角r）
5)变化规律
根据仿真图样可以得出以下结论：移动点光源位置，衍射条纹发生平行移动。具体规律为，点光源向上移动，则条纹向下平行移动，及条纹移动方向与点光源移动方向恰好相反。
5.多缝的夫琅和费衍射，使用扩展光源照明，前后、上下移动光源，观察衍射图样的变化
alpha=pi*a*sinphi/lam;
beta=pi*d*sinphi/lam; %相位差2*bata
B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;
B1=B/max(B);
end
NC=255; %绘制衍射仿真图样及强度曲线
C(j,i)=A(j,i)*exp(-imag*k*(x*p+y*q));
end
end
E(n,m)=sum(C(:));
end
end
E=abs(E);
I=E.^2;I=I.^(1/3);
I=I.*255/max(max(I));
L=I;I=I+256;
CM=[pink(255).^(2/3);gray(255)];
（5）变化规律
由图样可知，当光源向上移动时，图样向下移动，光源向下移动时，图样向上移动。同时，可以知道，扩展光源的光强分布与点光源的有所不同，主要体现在清晰度的变化。
三、感想
这次大作业要求对课本上的衍射部分有更深层次的理解，通过仿真实验，对菲涅尔衍射和夫琅禾费衍射的特点的理解加深了，对不同衍射孔的夫琅禾费衍射图样特点有了更感性的认识，对光源与衍射图样的关系也有了更深刻的掌握，并进一步熟悉了Matlab在工程光学方面的强大的仿真功能，我们相信对我们以后的学习会有很大的助益。
夫琅禾费衍射条件下：中央有一条特别明亮的亮条纹，其宽度是其他亮条纹的两倍；其他亮条纹的宽度相等，亮度逐渐下降。
2.改变孔径形状、尺寸，观察图样变化
1）原理图
矩孔衍射：
透镜焦距：1000mm;
照射光波长：500nm;
孔高：a（mm）；孔宽：b（mm）；
圆孔衍射：
圆孔直径：r（mm）；
照射光波长：500nm;
[x,y]=meshgrid(xs) ;
fori = 1: 19
s = 2*pi*r*sqrt(x.^2 + y.^2)./(lmda1( i) ) ;
z = 4*(besselj( 1,s)./( s + eps) ).^2; %光强公式
z0 = z0 + z;
end
z1 = z0 /19;
subplot(1,2,1)
y0=xm;
n=1001;
x0=linspace(-xm,xm,n); %构建接受屏矩阵
for i= 1: n %依次计算接受屏上的第i个点光强
for j=1:n %依次计算第j个入射点
r=pi*(j-501)/5000000; %各个入射点的角度不同
sinphi=x0(i)/f;
alpha=pi*a*(sinphi-sin(r))/lam;
surf(x,y,L);
axis([-edge,edge,-edge,edge,0,255]);
caxis([0,511]);
subplot(1,2,2);
image(x,y,I);
axis([-edge,edge,-edge,edge,0,511]);
view(2);
axissquare;
圆孔衍射：
照射光波长：500nm;
2）matlab代码
矩孔衍射：
focallength=1000;
lambda=500;
a=2.0;b=2.0;
resolution=64;
center=(resolution)/2;
A=zeros(resolution,resolution);
fori=1:1:resolution
可知：矩孔在一个维度上展宽一定倍数将导致衍射图样在相同维度上缩短相同倍数，同时能量会更向中心亮斑集中。
圆孔衍射：
r=1.5
r=1.2
圆孔半径增大，衍射图样中的同心圆环半径相应变小，更集中，而能量则更向中心亮斑集中。
进一步分析各种形状的衍射孔可得如下结论：
1.衍射孔在哪些方向上有几条对称轴，则衍射图样亦在哪些方向上有几条对称轴；
（1）原理图
与4类似。
（扩展光源即点光源无数个点光源移动后同时作用，产生的衍射图样的合成）
（2）matlab代码
clear
lam=500e-9; %定义波长lam=500nm
N=2; %单缝个数N
a=2e-4; %缝宽a
f=5; %后面的透镜焦距
d=5*a; %光栅常d=5；
xm=1*lam*f/a; %设定接受屏边界
Br=(B/max(B))*NC;
subplot(1,2,1)
image(y0,x0,Br);
colormap(gray(NC) );
subplot(1,2,2)
plot(B1,x0);
3)初始仿真图样
4)改变参数后的仿真图样
①改变缝宽a
a=0.0001
a=0.0003
②改变缝距d
d=4*a
d=6*a
lam=500e-6;%lam=input('波长(nm)');
x=-1:0.001:1;%接收屏边界
y=x./sqrt(x.^2+l^2);
z=a.*y/lam;
I=1000*(sinc(z)).^2;%计算接受屏某点光强
subplot(2,1,1)%绘制仿真图样及强度曲线
image(2,x,I)
colormap(gray(3))
title('单缝衍射条纹')
subplot(2,1,2)
plot(x,I)
title(光强分布)
3)初始仿真图样（d=10）
4)改变d之后的图样(d=1000)
5)变化规律
根据衍射屏以及接受屏的相对位置不同，由此产生菲涅尔衍射和夫琅禾费衍射的区别，根据我们模拟的情况得到菲涅尔衍射和夫琅禾费衍射的明显不同是
成绩：
《工程光学》综合性练习二
题目：基于matlab的衍射系统仿真
学院精密仪器与光电子工程学院
专业测控技术与仪器
年级20**级
班级**班
姓名
20**年**月
综合练习大作业二
一、要求
3-4人组成小组，对下面给出的各题目利用Matlab等工具进行仿真。练习结束时每组提交一份报告及仿真程序。在报告中应注明各仿真结果所对应的参数，如屏与衍射屏间距、孔径形状尺寸等。
四、参考文献
[1]光学衍射实验的MATLAB仿真[A].1004-7077(2010)梁兰菊田贵才张裕仕
[2]基于MATLAB的夫琅和费衍射实验的计算机仿真.张志峰 苏玉玲 蒋逢春
[3]基于Matlab的光学衍射实验仿真.陈芳芳钱淑珍吴平辉
Colormap(CM);
edge=(resolution-1)/20;
[X,Y]=meshgrid([-edge:0.1:edge]);
x=linspace(-edge,edge,resolution);
y=linspace(-edge,edge,resolution);
subplot(1,2,1);
r=0; %入射角r
y0=xm;
n=1001;
x0=linspace(-xm,xm,n);%构建接受屏矩阵
for i= 1: n %计算接受屏上第i个点的光强
sinphi=x0(i)/f;
alpha=pi*a*(sinphi-sin(r))/lam;
基于MATLAB的夫琅和费衍射实验的计算机仿真
式 中 Ｊ ｘ是 一 阶 贝塞 尔 函 数 ， 拟 时 令 ｆ ｌ ｈ ６ ０ｍ， ，） （ 模 ＝ ｍ，＝ ０ ｎ
ａ ０Ｏ １ 利用 ＭＡＴ Ａ ＝ ．０ ｍ， Ｌ Ｂ编程 ， 程序运行完毕后 ， 依次得到 以 下图形 ７ 。圆孔衍射和矩孔衍射的三维 图形基本相 同， 二维 图
平 面 上 会 聚 点 Ｑ（，） ｘｙ 的和 振 动 的 相 对 强 度 为 ： Ｉ Ｉ ｕ） Ｓｌ ） （ Ｑ） ｄｓ （ｌＰ ｍ ｒ
ｕ
ｖ
（） １
于学生的理解 。同时通过 多种元 件的夫琅和费衍射 计算机仿
真， 能够动态直观地呈现光学衍射 中各种物 理量之间 的关 系，
有利于大学物理实验中光学部分教学的开展 。因此 ， 我们应 当 充分利用计算机软件功 能为教学增添活力 ，为 学生理解复杂
Ｚ ａｇＺ ｉ ｎ Ｓ ｕｉｇ Ｊ ｎ ｅ ｇｈ ｎ ＹａｇＫ ｎ Ｌ ｎｅ ｇ Ｙａｇ ｎｊｎ ｈ ｎ ｈｆ ｇ ｕＹ ｌ ｉ ｇ ｎ ｃｕ ｎ ｕ ｉｕ ｆ ｎ ｇｕ ｅ ｎ ａ Ｆ Ｊ ｎ Ｈｏ
（】潘 柏 根 ， 施群 ， 志 建 ． 于 Ｖ ＋的 夫 琅 和 费 衍 射 仿 真 ［］ ５ 金 刘 基 ｃ＋ Ｊ．
仪 器 仪表 用 户 ，０ Ｏ４： ６６ ． ２ ｌ（）６ —９
［］夏 静 ， ６ 陆训 毅 ， 德 君 ． 杨 圆孔 、 方 孔 和 双 矩 孔 夫琅 和 赞 衍 射 的
Ｉ ｔｒ￣ｉｎＮ ｎｆｒ ｎ ｅ ｎ ｎｅｎ ｏ Ｃｏ ｅｅ ｃ ｏ Ｍ ｅ ｓ ｒｎ Ｔｅ ｈ ｌｇ ａ ｄ Ｍ ｅ ｈ ｔｏ ｉｓ ａ ｕｉ ｇ ｃ ｎｏｏ ｙ ｎ ｃ ａｒ ｎｃ
Ａｕ ｏ ａ ｉ ｎ Ｃｏ ｆ ｒ ｎ ｅ ｏ Ｉ ＥＥ： ０ — ０ ． ｔ ｍ ｔｏ ， ｎ ｅ ｅ ｃ ｆ Ｅ ９ ２ ９ ５
光学衍射图样的MATLAB仿真
1、建立几何模型：在Matlab中建立一个单缝衍射模型，包括一个光源、一 个单缝和一个观察点。
2、设置光源和观察条件：设置光源的波长为600纳米，强度为1瓦，方向为 垂直于缝的方向；观察点位于缝的右侧1米处，观察角度为45度。
3、进行仿真计算：利用Matlab中的相关函数进行仿真计算，得到观察点处 光的强度分布。
光学衍射图样的MATLAB仿真
目录
01 摘要
03 二、衍射的基本原理
02 一、引言 04 三、MATLAB在光学仿
真中的应用
目录
05 四、光学衍射图样的 MATLAB仿真
07 六、结论与展望
06 五、具体例子 08 参考内容
摘要
本次演示介绍了使用MATLAB进行光学衍射图样仿真的方法。首先介绍了衍射 的基本原理和MATLAB在光学仿真中的应用，然后详细阐述了如何使用MATLAB进行 衍射图样的仿真。通过具体的例子，展示了如何使用MATLAB模拟不同条件下的衍 射现象，并解释了仿真结果。最后，总结了本次演示的主要内容和贡献，并指出 了未来可能的研究方向。
参考内容
引言
光学衍射在许多领域中都具有重要应用，例如光学仪器设计、光谱分析、光 信息处理等。对光学衍射进行仿真可以帮助人们更好地理解光学系统的性能，预 测光的传播行为，优化光学设计。本次演示将介绍如何使用Matlab进行光学衍射 仿真。
准备工作
在进行光学衍射仿真之前，需要做好以下准备工作： 1、安装Matlab：首先需要安装Matlab软件，版本要求至少为R2018a或更高。
其中E(x,y)是电场强度，λ是光的波长，c是光速。通过求解这个方程，可 以得到衍射图样的电场分布。
三、MATLAB在光学仿真中的应 用
基于matlab的衍射系统仿真 -
成绩：《工程光学》综合性练习二题目：基于matlab的衍射系统仿真学院精密仪器与光电子工程学院专业测控技术与仪器年级20**级班级**班姓名20**年**月综合练习大作业二一、要求3-4人组成小组，对下面给出的各题目利用Matlab等工具进行仿真。
练习结束时每组提交一份报告及仿真程序。
在报告中应注明各仿真结果所对应的参数，如屏与衍射屏间距、孔径形状尺寸等。
二、仿真题目1.改变观察屏与衍射屏间距，观察观察屏上发生的衍射逐渐由菲涅耳衍射转为夫琅和费衍射1)原理图：S点光源发出的波长lam=500纳米S点发出光线经过单缝，缝宽a；单缝到衍射屏的距离L'2)Matlab代码clear;clcl=10;%l=input('单缝到衍射屏的距离L=');a=0.2;%a=input('单缝的宽度(mm)a=');lam=500e-6;%lam=input('波长(nm)');x=-1:0.001:1;%接收屏边界y=x./sqrt(x.^2+l^2);z=a.*y/lam;I=1000*(sinc(z)).^2;%计算接受屏某点光强subplot(2,1,1)%绘制仿真图样及强度曲线image(2,x,I)colormap(gray(3))title('单缝衍射条纹')subplot(2,1,2)plot(x,I)title(光强分布)3)初始仿真图样（d=10）4)改变d之后的图样(d=1000)5)变化规律根据衍射屏以及接受屏的相对位置不同，由此产生菲涅尔衍射和夫琅禾费衍射的区别，根据我们模拟的情况得到菲涅尔衍射和夫琅禾费衍射的明显不同是夫琅禾费衍射条件下：中央有一条特别明亮的亮条纹，其宽度是其他亮条纹的两倍；其他亮条纹的宽度相等，亮度逐渐下降。
2.改变孔径形状、尺寸，观察图样变化1）原理图矩孔衍射：透镜焦距：1000mm;照射光波长：500nm;孔高：a（mm）；孔宽：b（mm）；圆孔衍射：圆孔直径：r（mm）；照射光波长：500nm;照射光波长：500nm;2）matlab代码矩孔衍射：focallength=1000;lambda=500;a=2.0;b=2.0;resolution=64;center=(resolution)/2;A=zeros(resolution,resolution);for i=1:1:resolutionfor j=1:1:resolutionif abs(i-center)<a*10/2&abs(j-center)<b*10/2 A(j,i)=255;endendendE=ones(resolution,resolution);k=2*pi*10000/focallength/lambda;imag=sqrt(-1);for m=1:1:resolutionx=m-center;for n=1:1:resolutiony=n-center;C=ones(resolution,resolution);for i=1:1:resolutionp=i-center;for j=1:1:resolutionq=j-center;C(j,i)=A(j,i)*exp(-imag*k*(x*p+y*q)); endendE(n,m)=sum(C(:));endendE=abs(E);I=E.^2;I=I.^(1/3);I=I.*255/max(max(I));L=I;I=I+256;CM=[pink(255).^(2/3);gray(255)];Colormap(CM);edge=(resolution-1)/20;[X,Y]=meshgrid([-edge:0.1:edge]);x=linspace(-edge,edge,resolution);y=linspace(-edge,edge,resolution);subplot(1,2,1);surf(x,y,L);axis([-edge,edge,-edge,edge,0,255]);caxis([0,511]);subplot(1,2,2);image(x,y,I);axis([-edge,edge,-edge,edge,0,511]);view(2);axis square;圆孔衍射：clearlmda=500e-9;%波长r=1.2e-3;%f=1;%焦距N=19;K=linspace(-0.1,0.1,N);lmda1=lmda*(1+K);xm=2000*lmda*f;xs=linspace(-xm,xm,2000);ys=xs;z0=zeros(2000);[x,y]=meshgrid(xs);for i=1:19s=2*pi*r*sqrt(x.^2+y.^2)./(lmda1(i));z=4*(besselj(1,s)./(s+eps)).^2;%光强公式z0=z0+z;endz1=z0/19;subplot(1,2,1)imshow(z1*255);%平面图xlabel('x')ylabel('y')subplot(1,2,2)mesh(x,y,z1)%三维图colormap(gray)xlabel('x')ylabel('y')zlabel('光强')3）仿真图样：矩孔衍射：a=1，b=2a=2，b=2可知：矩孔在一个维度上展宽一定倍数将导致衍射图样在相同维度上缩短相同倍数，同时能量会更向中心亮斑集中。
实验7 衍射的Matlab模拟
实验7衍射的Matlab模拟一、实验目的：掌握衍射的matlab模拟。
二、实验内容：1）单个圆孔夫朗和费衍射的matlab模拟2）双圆孔夫朗和费衍射的matlab模拟3）同一波长，狭缝数量分别为1、2、3、6、9、10时候的夫朗和费衍射的matlab模拟4）对4个不同波长的光照射时，狭缝数量分别为1、3时候的夫朗和费衍射的matlab 模拟5）单个圆孔菲涅尔衍射的matlab模拟6）模拟圆孔（或者单缝）衍射时，衍射屏到接收屏距离不同的时候衍射的图样1)clearclclam=632.8e-9;a=0.0005;f=1;m=300;ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:mr=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lam;hh=(2*BESSELJ(1,x)).^2./x.^2;b(:,i)=(hh)'.*5000;B=b/max(b);endimage(xs,ys,b);colormap(gray(n));figure;plot(xs,B);colormap(green);-2.5-2-1.5-1-0.500.51 1.52 2.5x 10-3-2.5-2-1.5-1-0.50.511.522.5x 10-3-3-2-10123x 10-300.10.20.30.40.50.60.70.80.912)%双圆孔夫琅禾费衍射clear all close all clc %lam=632.8e-9;a=0.0005;f=1;m=300;ym=4000*lam*f;ys=linspace(-ym,ym,m);xs=ys;n=200;for i=1:m r=xs(i)^2+ys.^2;sinth=sqrt(r./(r+f^2));x=2*pi*a*sinth./lam;h=(2*BESSELJ(1,x)).^2./x.^2;d=10*a;deltaphi=2*pi*d*xs(i)/lam;hh=4*h*(cos(deltaphi/2))^2;b(:,i)=(hh)'.*5000;end image(xs,ys,b);colormap(gray(n));-2.5-2-1.5-1-0.500.51 1.52 2.5x 10-3-2.5-2-1.5-1-0.50.511.522.5x 10-33)lamda=500e-9;%波长N=[1236910];for j=1:6a=2e-4;D=5;d=5*a;ym=2*lamda*D/a;xs=ym;%屏幕上y 的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for i=1:n sinphi=ys(i)/D;alpha=pi*a*sinphi/lamda;beta=pi*d*sinphi/lamda;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N(j)*beta)./sin(beta)).^2;B1=B/max(B);end NC=256;%确定灰度的等级Br=(B/max(B))*NC;figure(j);subplot(1,2,1);image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2);plot(B1,ys,'k');end-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为1-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为2-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为3-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025狭缝数为9狭缝数为6-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.0254）lamda=400e-9:100e-9:700e-9;%波长N=[13];a=2e-4;D=5;d=5*a;for j=1:4ym=2*lamda(j)*D/a;xs=ym;%屏幕上y 的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for k=1:2for i=1:n sinphi=ys(i)/D;alpha=pi*a*sinphi/lamda(j);beta=pi*d*sinphi/lamda(j);B(i,:)=(sin(alpha)./alpha).^2.*(sin(N(k)*beta)./sin(beta)).^2;B1=B/max(B);end NC=256;%确定灰度的等级Br=(B/max(B))*NC;figure();subplot(1,2,1);image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2);狭缝数为10plot(B1,ys,'k');end end-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02Lamda=400nm,N=1-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025Lamda=400nm,N=3Lamda=500nm,N=1-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03Lamda=500nm,N=3Lamda=600nm,N=1-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.04Lamda=600nm,N=3Lamda=700nm,N=1-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.045）clearclcN=300;r=15;a=1;b=1;I=zeros(N,N);[m,n]=meshgrid(linspace(-N/2,N/2-1,N));D=((m-a).^2+(n-b).^2).^(1/2);i=find(D<=r);I(i)=1;subplot(2,2,1);imagesc(I)colormap([000;111])axis imagetitle('衍射前的图样')L=300;M=300;[x,y]=meshgrid(linspace(-L/2,L/2,M));lamda=632.8e-6;k=2*pi/lamda;z=1000000;Lamda=700nm,N=3h=exp(j*k*z)*exp((j*k*(x.^2+y.^2))/(2*z))/(j*lamda*z); H=fftshift(fft2(h));%传递函数B=fftshift(fft2(I));%圆孔频谱G=H.*B;U=fftshift(ifft2(G));Br=(U/max(U));subplot(2,2,2);imshow(abs(U));axis image;colormap(hot)%figure,imshow(C);title('衍射后的图样');subplot(2,2,3);mesh(x,y,abs(U));subplot(2,2,4);plot(abs(Br))6)lamda=500e-9;%波长N=1;%缝数，可以随意更改变换a=2e-4;D=3:7;d=5*a;for j=1:5ym=2*lamda*D(j)/a;xs=ym;%屏幕上y的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for i=1:nsinphi=ys(i)/D(j);alpha=pi*a*sinphi/lamda;beta=pi*d*sinphi/lamda;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;B1=B/max(B);endNC=256;%确定灰度的等级Br=(B/max(B))*NC;figure();subplot(1,2,1)image(xs,ys,Br);colormap(hot(NC));%色调处理subplot(1,2,2)plot(B1,ys,'k');end-0.4-0.200.20.4-0.015-0.01-0.00500.0050.010.01500.51-0.015-0.01-0.0050.0050.010.015D=3m-0.4-0.200.20.4-0.02-0.015-0.01-0.00500.0050.010.0150.0200.51-0.02-0.015-0.01-0.0050.0050.010.0150.02-0.4-0.200.20.4-0.025-0.02-0.015-0.01-0.00500.0050.010.0150.020.02500.51-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025D=5m D=4m-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.03-0.02-0.010.010.020.03-0.4-0.200.20.4-0.03-0.02-0.0100.010.020.0300.51-0.04-0.03-0.02-0.010.010.020.030.04D=7m D=6m。
matlab作业(衍射实验)
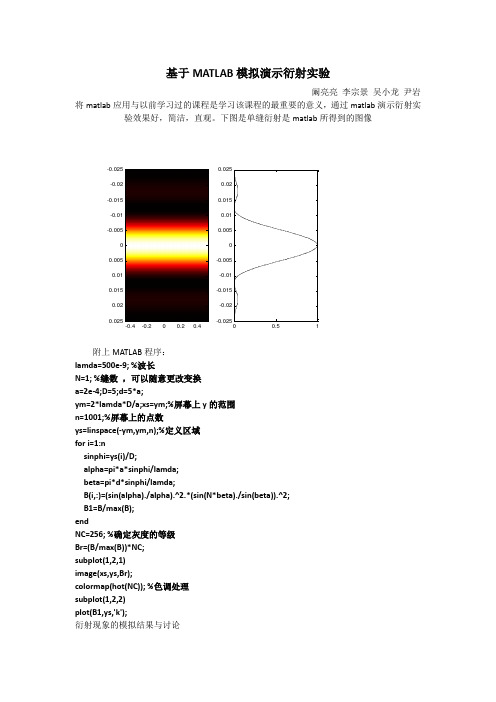
基于MATLAB 模拟演示衍射实验阚亮亮 李宗景 吴小龙 尹岩 将matlab 应用与以前学习过的课程是学习该课程的最重要的意义，通过matlab 演示衍射实验效果好，简洁，直观。
下图是单缝衍射是matlab 所得到的图像-0.025-0.02-0.015-0.01-0.0050.0050.010.0150.020.025附上MATLAB 程序：lamda=500e-9; %波长N=1; %缝数 ，可以随意更改变换a=2e-4;D=5;d=5*a;ym=2*lamda*D/a;xs=ym;%屏幕上y 的范围n=1001;%屏幕上的点数ys=linspace(-ym,ym,n);%定义区域for i=1:nsinphi=ys(i)/D;alpha=pi*a*sinphi/lamda;beta=pi*d*sinphi/lamda;B(i,:)=(sin(alpha)./alpha).^2.*(sin(N*beta)./sin(beta)).^2;B1=B/max(B);endNC=256; %确定灰度的等级Br=(B/max(B))*NC;subplot(1,2,1)image(xs,ys,Br);colormap(hot(NC)); %色调处理subplot(1,2,2)plot(B1,ys,'k');衍射现象的模拟结果与讨论在实验时改变N的值可以得到单缝以及多缝衍射的输出结果，并可以得到这样的结论:(1)当入射光波长一定时,单缝宽度a越小,衍射条纹越宽,衍射现象越显著;(2)单缝越宽,衍射越不明显,单缝宽度逐渐增大,衍射条纹越来越窄;(3)当缝宽a>>λ时,各级衍射条纹向中央明纹靠拢,而无法分辨,这时衍射现象消失。
结束语利用MATLAB对抽象物理现象进行计算机仿真时,首先必须对物理过程进行数学抽象,建立适合程序实现的数学模型,其次利用MATLAB软件包中的有关工具编制m文件,最后对物理过程和物理现象进行模拟,从而可以把抽象的物理问题进行简明、直观的动态展现。
基于MATLAB的光栅衍射仿真
基于MATLAB的光学光栅衍射仿真在“光栅衍射计算器”（钆计算器®）是一个基于MATLAB，电磁仿真程序，计算光栅结构，包括biperiodic光栅衍射效率。
该方案的功能包括一样的设施和灵活的光栅造型，结构参数（与任意数量的参数），超过衍射顺序不受选择限制的操纵。
另外，它在泛型编程及应用Matlab开发框架的实施提供了软件的灵活性和互操作性不与独立衍射分析程序可费用本条第1部份提供了钆Calc的概念性概述，归纳描述如何指定光栅结构，和如何进行了电磁计算。
这次报告会要紧以概念为导向，但有几个简单的代码例子提供给读者一个如何用GD- Calc软件接口来工作的感觉。
第2部份提供了一个更深切地介绍了软件界面，利用钨作为一个例子来讲明光子晶体结构光栅结构是如何规定的.本文的要紧核心是光栅结构标准。
电磁计算中的应用实例，载于所附文件，钆。
（在这篇文章，并在GD- 的代码例如都能够运行的免费演示/从Calc的网站教程中的代码。
光子晶体的例子是在演示脚本为基础。
）电磁理论与算法基础详见钆。
第1部份：概念概述MATLAB的开发环境一个在MATLAB环境下工作的优势是了解GD- Calc图的功能联系，而无需依托繁琐的数据转换和导入/导出进程中创建的。
例如，在半导体光刻技术的应用，光刻胶光栅的厚度和折射率的阻碍都可能暴露有关抗击致密，因此很自然地就会指定的厚度和折射率既是暴露用户概念函数。
这是专门有效的结构参数化，例如，曝光能够被概念为一个矢量的数量，在这种情形下，所有曝光依托数量，包括阻碍厚度，折射率，并计算出衍射效率，也一样向量化。
通常情形下，光栅的光学特性不是要紧关切它本身最为一个完整的系统，应该包括作为一个组件光栅光学响应。
MATLAB的通用编程能力，能够轻松地链接到用户的功能概念的光学系统模型的Gd - Calc中，它本身能够成通用的优化程序性能的优化设计中。
钆Calc是简单的MATLAB函数（），可纳入其他MATLAB 函数或脚本，而且需要实例化的参数，能够对用户概念的函数..尽管独立程序缺乏通用性和Matlab开发环境的灵活性，他们能够有简单和易于利用的优势。
基于matlab的光学衍射仿真
西安工业大学毕业设计(论文)开题报告题目：基于Matlab的光学衍射实验仿真系别光电信息系专业光电信息工程班级XXX姓名王XX学号X070104XX导师XX2010 年11 月27 日课题背景及研究意义衍射是光波的一种重要特征,对光波衍射现象的讨论是以惠更斯- 菲涅尔原理为基础的。
事实证明，在大多数光学问题中，可以采用光场的标量衍射理论来描述和计算。
光场的频率非常高，只能测量在一个比光的周期大得多的时间间隔内的平均值，在计算衍射光波场的光振动和光强分布时则利用菲涅尔- 基尔霍夫衍射积分公式[1,2,3]。
在物理光学的光的衍射教学过程中，光学实验内容比较抽象, 如不借助实验, 学生很难理解理论、实验原理和过程。
通常，学校的教学中，将光学理论教学与实验教学相分离，理论教学中需要实验现象来验证，而光学实验的进行一般要稳定的环境、高精密的仪器, 复杂的实验仪器以及光路的调试, 花费了技术人员相当多的时间，往往很难调试到理想的状态，搭建好的仪器和光路也会受到环境和温度的影响,有时实验结果将偏离理论预测。
为了在物理光学课程教学过程形象生动，需要现代化的教学手段，千方百计地为学生提供观察物理现象的机会，提高学生学习光学课程的兴趣，培养他们的思维水平和创新能力，应该充分利用计算机软件功能为教学增添活力，为学生理解复杂理论和实验做好铺垫，可以用MATLAB软件为平台,对光学实验进行计算机仿真，具有两个方面意义：一方面，利用仿真结果指导实际实验。
前期投资少，且可以减少贵重仪器的损伤等；另一方面，在教学上，将抽象难懂的概念、规律通过实验仿真生动、形象地表现出来，使学生更易于接受，具有明显的教学效果。
还可以鼓励学生自主探索，研究一些更深入的光学问题，这样可以拓宽知识面，提高能力[4,5,6]。
国内外研究情况在用计算机模拟[7]光学实验软件方面，国外的光学衍射模拟试验是在模拟设计和优化光学系统的过程中发展起来的。
在这方面，美国走在最前面，他们最具代表性的是劳伦斯利弗莫尔实验室光传输模拟计算软件Prop92[8,9]及大型总体优化设计软件CHAINOP 和PROPSUITE[10]。
光的干涉和衍射的matlab模拟
光的干涉和衍射的matlab模拟单缝夫琅和费衍射是光的衍射现象之一，如图2所示。
当单色光波通过一个狭缝时，光波会向周围扩散，形成一系列同心圆环。
这些圆环的亮度分布是由夫琅和费衍射公式描述的，即。
其中为入射光波长，为狭缝宽度，为衍射角。
夫琅和费衍射公式表明，随着衍射角的增大，圆环的半径会减小，而亮度则会逐渐减弱。
在MATLAB中，可以通过输入实验参数，如光波长和狭缝宽度，来观察圆环的亮度分布和半径随衍射角的变化情况。
同时，还可以探讨不同波长和狭缝宽度对圆环亮度和半径的影响。
4双缝衍射双缝衍射是光的干涉和衍射现象的结合，如图3所示。
当一束单色光波通过两个狭缝时，光波会在屏幕上形成一系列干涉条纹和衍射环。
干涉条纹的亮度分布与___双缝干涉相同，而衍射环的亮度分布则由夫琅和费衍射公式描述。
在MATLAB中，可以通过输入实验参数，如光波长、双缝间距和双缝宽度，来观察干涉条纹和衍射环的亮度分布和条纹间距、环半径随实验参数的变化情况。
同时，还可以探讨不同实验参数对干涉条纹和衍射环的影响。
5衍射光栅衍射光栅是一种利用衍射现象制成的光学元件，如图4所示。
当一束单色光波通过光栅时，光波会被分为多个衍射光束，形成一系列亮度不同的衍射条纹。
衍射条纹的亮度分布与夫琅和费衍射公式描述的圆环类似，但是条纹间距和亮度分布会受到光栅常数的影响。
在MATLAB中，可以通过输入实验参数，如光波长和光栅常数，来观察衍射条纹的亮度分布和条纹间距随实验参数的变化情况。
同时，还可以探讨不同实验参数对衍射条纹的影响。
总之，通过MATLAB模拟光的干涉和衍射现象，可以更加直观地理解和掌握这些重要的光学现象，同时也可以为实验设计和数据分析提供有力的工具和支持。
本文介绍了___双缝干涉、单缝夫琅禾费衍射和衍射光栅光谱的计算机模拟。
当一束单色平行光通过宽度可调的狭缝，射到其后的光屏上时，形成一系列亮暗相间的条纹。
单缝夫琅禾费衍射的光强分布可以通过惠更斯-费涅耳原理计算。
基于Matlab可视化界面的单缝衍射仿真分析
［ ６］Ｇ ｌ ａ ｅ Ｓ， ｉ ａ ． ｌｏ ｌ ｒ ｅ ｃｎ ｅ ｕ ￣ ｒ ｉ ［ ］／ ｏ ｗ ｓ ｒ Ｋｌ Ａｍ ｓ ａ ｉ ｓ ａ ｉ ｙｃ ｔ ｅ Ｃ ／ ｄ ｓ ｌＪ ｉ ｔ ｌｐ ｍ ｂ ｑ ｃ ｅｉ ｄ ｆ
．
件 的点 ， Ｋ算法失效 ， Ｇ 由此得 知本算 法有一 定的实际 应用 的价
值 ， 以上定理相吻合 。 与
ｒ ｌ ）ｌ Ｐ十１＋２ ≤ （ ＋１ ≤ 帖 （ ≤ ）
≤ （／ ＋１ ＝（ ＋１ ￣ ） ）
与假设矛盾 ， 即证 。
４ 结
＋曰
语
定理 ３ 设 ｎ为大于 ３的整数 ， Ａ， ａ ｂａ 均 为模 ｎ的 有 Ｂ， ， ， 整数 ， ｂ 为整数 ， 得 （ ，）， 使 ａ ｂ 为椭 圆曲线 Ｅ：。； Ｙ ＋ （ ｏ ） ｏ ｒ ｄｎ 上阶为 ｒ 的点 ， （ ｂ） 点 ａ， 为椭圆曲线 Ｅ： Ｙ ＋４ 』 ＋
Ｈ ｓｅ 理 有 ： ａｓ 定
来判 断阶的时候 ， 现很容 易找 到满足 条件 的点 （ ４ ７ ） 发 ９ ，３ 阶为
３ （ １阶的点有很 多个 ） 又存 在 阶为 ４的 点（ ６ ８ １４） 即可 １３ ， （２ ，２ ，
以 判定 ９ １ 拟 素 数 ， ７ 为 而用 ｒ＞ （ 彳 ｎ１＋１ ｚ一４ ３， 有 满 足条 ） ３ 没
那么如果 ｒ 为素数 ， ｎ为拟素数。 则
证明
（ ）椭 圆 曲线 的素 性检 验都 需 要构 造 ｚ ２ ／ ｚ上 的椭 圆曲
１
假 设 ｎ至 少 可 分 解 为 三 个 互 不 相 同 的素 因 子 之 积 ，
线， 满足 ＞（ 亍 ＋１ ， １ 常大时 ， 也需要非 常大 ， ｎ ） 当 ７ ， 非 ｒ 要寻
圆孔衍射与像分辨本领的matlab仿真分析
圆孔衍射与像分辨本领的matlab仿
真分析
衍射技术以其得天独厚的特性在一系列领域中发挥着重要作用，而圆孔衍射技
术更是其中最重要的应用。
以圆孔衍射理论研究和仿真分析来加深对其原理以及原理背后的分歧准确的说明属于数学处置，而matlab仿真分析可以理解圆孔衍射事
例的表述，使其能够详实地反映分析结果，并推进应用技术的实际研发。
圆孔衍射的matlab仿真分析是指利用matlab软件来处置圆孔衍射的分析问题，其特点是其计算速度快，精确度高，可以同时处置多种孔径形态的圆孔衍射。
MATLAB仿真分析运用Rayleigh衍射方程与Fresnel误差函数；它可以模拟任何扫
描尺度、光斑有效直径及衍射模式差异，测定衍射效果的衰变和聚焦程度，精确的表征像分辨率的改变指标。
此外，应用matlab仿真分析，可以准确可靠的量化把握不同孔径尺寸，材质
及照度等参数对像分辨率性能的影响，从而更好地开发和调校圆孔衍射系统以及其他光学模组；同时，matlab仿真可以高效地分析仿真原理分歧对性能参数影响的
复杂关系，以此作为参考来改进技术參数，使圆孔衍射系统能够达到最好的设计效果。
综上，matlab仿真分析是指利用matlab软件处置圆孔衍射的分析问题，可以
准确把握不同孔径尺寸，材质及照度等参数对像分辨率性能的影响，从而更好地开发和调校圆孔衍射系统，提升其像分辨本领，使其在一系列字段中有较高的应用价值。