蒸发器温度控制系统(1)
蒸发温度和冷凝温度怎么确定？怎么调试？
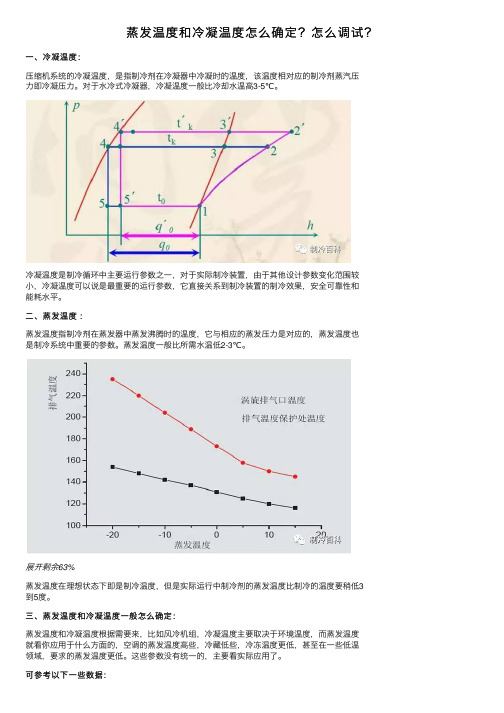
蒸发温度和冷凝温度怎么确定？怎么调试？⼀、冷凝温度：压缩机系统的冷凝温度，是指制冷剂在冷凝器中冷凝时的温度，该温度相对应的制冷剂蒸汽压⼒即冷凝压⼒。
对于⽔冷式冷凝器，冷凝温度⼀般⽐冷却⽔温⾼3-5℃。
冷凝温度是制冷循环中主要运⾏参数之⼀，对于实际制冷装置，由于其他设计参数变化范围较⼩，冷凝温度可以说是最重要的运⾏参数，它直接关系到制冷装置的制冷效果，安全可靠性和能耗⽔平。
⼆、蒸发温度：蒸发温度指制冷剂在蒸发器中蒸发沸腾时的温度，它与相应的蒸发压⼒是对应的，蒸发温度也是制冷系统中重要的参数。
蒸发温度⼀般⽐所需⽔温低2-3℃。
展开剩余63%蒸发温度在理想状态下即是制冷温度，但是实际运⾏中制冷剂的蒸发温度⽐制冷的温度要稍低3到5度。
三、蒸发温度和冷凝温度⼀般怎么确定：蒸发温度和冷凝温度根据需要来，⽐如风冷机组，冷凝温度主要取决于环境温度，⽽蒸发温度就看你应⽤于什么⽅⾯的，空调的蒸发温度⾼些，冷藏低些，冷冻温度更低，甚⾄在⼀些低温领域，要求的蒸发温度更低。
这些参数没有统⼀的，主要看实际应⽤了。
可参考以下⼀些数据：在⼀般情况下，⽔冷：蒸发温度＝冷⽔出⽔温度-5℃（⼲式蒸发器），若是满液式蒸发器，则-2℃。
冷凝温度＝冷却⽔出⽔温度 5℃风冷：蒸发温度＝冷⽔出⽔温度-5～10℃，冷凝温度＝环境温度 10～15℃，⼀般取15。
冷库：蒸发温度＝冷库设计温度-5～10℃。
四、蒸发器温度对制冷的影响与调节：蒸发温度等于外界实际温度减去传热温差。
蒸发温度过⾼，蒸发器出来的冷风温度⾼，降温慢，甚⾄根本达不到预期的温度。
对制冷循环的影响：过热度⾼，回⽓压⼒低，排⽓压⼒也随着降低，供液管道的压⼒降低，单位流量减少。
这⼀循环使库房降温慢，机器不停的⼯作，磨损⼤，效率低。
蒸发温度过低，要有尺度，如果还不⾄于使机头有潮车现象，库房降温没问题。
排⽓压⼒影响不⼤，排⽓温度降低。
能耗加⼤。
如果蒸发温度过低，超出了底线，回⽓管道带有液体，造成潮车，后果很严重。
空调蒸发器工作原理
空调蒸发器工作原理空调蒸发器是空调系统中的重要组成部分，它通过蒸发制冷的原理，将热空气转化为凉爽的空气，为人们创造舒适的室内环境。
了解空调蒸发器的工作原理，有助于我们更好地使用和维护空调设备，下面就让我们来深入了解空调蒸发器的工作原理。
首先，空调蒸发器是通过蒸发制冷的原理来降低空气温度的。
当空调系统启动时，制冷剂被压缩成高压气体，然后通过蒸发器内的蒸发管道，制冷剂释放热量并蒸发成低温气体。
在这个过程中，蒸发器内的风扇会将室内空气吹过蒸发管道，使得热空气与低温制冷剂接触，从而吸收热量并降低空气温度。
其次，空调蒸发器的工作原理还涉及到湿度调节。
在蒸发器内，当热空气与低温制冷剂接触时，空气中的水分也会凝结成水滴，从而降低空气的湿度。
这个过程类似于我们在炎热夏天出汗后感到凉爽的原理，通过蒸发器的作用，空调系统不仅可以降低空气温度，还可以调节空气湿度，为人们创造更加舒适的室内环境。
此外，空调蒸发器还可以过滤空气。
在空调系统中，蒸发器内的过滤器可以有效地过滤空气中的灰尘、细菌和异味等有害物质，从而提高室内空气的质量。
这不仅有助于保护空调设备的正常运行，还能够保障人们的健康。
因此，空调蒸发器在降温的同时，也起到了净化空气的作用。
总的来说，空调蒸发器通过蒸发制冷的原理，降低空气温度，调节空气湿度，并过滤空气，为人们创造舒适、清新的室内环境。
在实际使用中，我们需要定期清洁和维护空调蒸发器，以确保其正常工作。
同时，在购买空调设备时，也要注意选择质量可靠的蒸发器，以保证空调系统的高效运行和长期稳定使用。
通过对空调蒸发器工作原理的深入了解，我们可以更好地理解空调系统的运行机制，为我们的生活和工作提供更加舒适的室内环境。
希望本文能够帮助大家更好地使用和维护空调设备，享受到清凉舒适的空气。
基于SMPT—1000实验平台的蒸发器控制实验设计
基于SMPT—1000实验平台的蒸发器控制实验设计摘要：由于过程工业流程相对复杂，生产过程往往伴有高温、高压、强非线性等特性，把生产装置移到实验室进行控制是非常困难的。
SMPT-1000实验平台是运用高精度动态仿真技术将实际工业装置的各种对象特性用数字化手段完整地在小型化半实物实验装置上得到再现的一个实验平台，能够很好地模拟实际工业现场的状况，方便在实验室进行有针对性地控制实验和研究。
关键词：SMPT-1000；蒸发器；温度控制；工业控制方案一、控制要求及工艺流程本文主要对蒸发器进行控制。
根据“西门子杯全国大学生工业自动化挑战赛设计开发型竞赛组”的参赛题目，在浓缩液产量稳定4.63的前提下，保证浓缩液中组分（糖分）维持在7.4%～7.6%的波动范围之内。
所有操作要保证有序进行，工况要保持全程稳定，并要充分考虑生产过程中可能出现的异常情况。
从生产单元冷态起，按照开车步骤实施全自动顺序控制，保证开车稳步进行，保证系统无扰投运。
蒸发器的工艺流程为：浓缩的稀液由蒸发器上部进入，吸收过热蒸汽提供的热量，稀液中的水分变成二次蒸汽从蒸发器顶部排出，浓缩液从蒸发器底部排出。
二、特性分析1.对象特性分析通过综合分析，蒸发器装置是一个复杂的被控对象，主要输入变量包括稀液输入量、稀液浓度、过热蒸汽输入量等；主要输出变量是蒸发器的液位、蒸发器的温度、蒸发器的压力、浓缩液输出量、浓缩液浓度、二次蒸汽输出量等。
上述输入变量与输出变量之间相互关联。
本文主要对蒸发器的温度进行控制，蒸发器的温度主要由过热蒸汽的输入量决定，过热蒸汽输入量增加，蒸发器温度升高，同时蒸发器的温度受稀液的输入量的影响，当稀液输入量增加，会降低蒸发器的温度。
2.被控参数特性分析本文主要对蒸发器的温度进行控制。
温度动态特性的特点：其一，惯性大，容量滞后大，有些过程的时间常数达到十几分钟；其二，温度对象通常是多容的。
由于温度滞后大，控制起来不灵敏，但传统的PID控制方法也能达到很好的控制效果。
蒸发温度与冷凝温度,最全干货知识
蒸发温度与冷凝温度，最全干货知识一、蒸发温度：1什么是蒸发温度蒸发温度就是制冷剂从液体变为气体的临界温度，在制冷系统中，指的是制冷剂液体在蒸发器中从液体变为气体的饱和温度，一般制冷系统中的蒸发温度是测不出来的，只能用对应的蒸发压力来推导。
2蒸发温度与蒸发压力的关系蒸发压力（低压）越低，蒸发温度也就越低；蒸发压力（低压）越高，蒸发温度也就越高。
可以说，蒸发温度与蒸发压力是成正比变化的，蒸发压力与蒸发温度两者是对应的，知道蒸发温度，我们就能查表得出蒸发温度的数值。
3蒸发温度的估算在制冷设备调试的时候，我们经常要知道蒸发温度，进一步推算出蒸发压力，然后根据实际的压力，就能判断制冷系统是否有问题；下面是一个经验估值，提供给小伙伴们参考，如下：蒸发温度=环境温度/水温 -（10~20℃）；举例如下：例1夏天的空调室内温度设定26℃，我们就可以估算此时的蒸发温度=26-（10~20℃）=6℃，根据温度压力对照表，很容易就查出此时的蒸发压力为0.55Mpa（R22制冷剂）左右；例2-18的冷库，库房温度为-18℃，那么此时制冷系统的蒸发温度大概为多少呢？蒸发温度= -18-（10~20）=-28℃，根据温度压力对照表，很容易就查出此时的蒸发压力为0.21Mpa（R404A制冷剂）左右；注：这里有小伙伴要问了，到底是减10℃，还是减20℃呢；这里简单归结为；环境温度高时，减去高值（20℃）；环境温度低时，减去低值（10℃）；4蒸发温度与功率的关系我们先来看一个动画：从T-S图上很明显的看出，如果制冷系统的蒸发温度降低了，消耗的功率增加了；原因很简单的，蒸发温度降低了，在冷凝温度不变的情况下，压缩机的压比增大了，而压缩机的功率是和压比成正比关系的，即压比增大，压缩机的功率也增大。
可以如下简单理解：压缩机把5公斤的冷媒压缩到15公斤所用的功率；肯定比压缩机把1公斤的冷媒压缩到15公斤所用的功率大。
5蒸发温度与制冷量的关系从动画中很容易看出，蒸发温度降低，系统的制冷量也会降低；原因很简单：当蒸发温度降低的时候，吸气口的比体积降低，导致制冷系统中的制冷剂流量也降低了；简单来说就是，制冷剂循环量降低了，制冷系统的制冷量也就降低。
冬季冰机冷凝温度和蒸发温度的正常值解析
冬季冰机冷凝温度和蒸发温度的正常值解析一、冬季冰机冷凝温度的正常值冷凝温度是指冰箱冷冻系统中冷凝器排气的温度。
在冬季，冷凝温度通常应在30℃至50℃之间。
当冷凝温度过高时，可能会导致冷冻系统中的压力升高，同时也会增加冷凝器的工作量，降低冰箱的制冷效率。
而冷凝温度过低，则可能是由于冷凝器不工作或者冷凝器表面灰尘过多，影响热交换效果。
在正常情况下，冬季冰机冷凝温度的控制应该是在一个稳定的范围内，确保冰箱的正常工作。
二、冬季冰机蒸发温度的正常值蒸发温度是指在冷冻系统蒸发器中蒸发的制冷剂的温度。
在冬季，冰箱冷冻室内的温度通常应该在-18℃至-23℃之间。
蒸发温度过高可能会导致冷冻室内的温度不低，影响冷冻效果；而蒸发温度过低可能会导致冷凝器的传热不足，制冷效果不好。
确保冬季冰机蒸发温度的正常值是保证冷冻室内温度适宜的关键。
三、影响冬季冰机冷凝温度和蒸发温度的因素1. 外界温度外界温度的变化会直接影响冰箱系统的工作压力和传热效率，进而影响冷凝温度和蒸发温度的正常值。
在寒冷的冬季，外界温度较低，冰箱系统的制冷效果通常会有所增加。
2. 制冷剂冰箱冷冻系统中使用的制冷剂种类不同，对冷凝温度和蒸发温度的影响也不同。
不同的制冷剂对于不同的工作条件有着不同的适应性。
3. 冷冻室内的负荷冷冻室内的负荷大小也会影响蒸发温度的正常值。
如果负荷过大，制冷系统的工作量会增加，蒸发温度也会相应升高，反之亦然。
四、调节冬季冰机冷凝温度和蒸发温度的方法1. 清洁冷凝器和蒸发器定期清洁冷凝器和蒸发器表面的灰尘和污垢，确保其良好的传热效果，维持正常的制冷效率。
2. 调节系统压力根据外界温度的变化，调节制冷系统中的工作压力，使冷凝温度和蒸发温度保持在正常范围内。
3. 保持冷冻室内通风畅通保持冷冻室内通风畅通，避免冷冻室内温度过高，影响蒸发温度的正常值。
冬季冰机冷凝温度和蒸发温度的正常值是决定冰箱制冷效果的重要因素。
在日常使用中，用户需要定期清洁和保养冰箱制冷系统，以保证冷凝温度和蒸发温度处于正常范围内，确保冰箱的正常工作效果。
温室地源热泵温度控制系统设计
１ 地源 热泵 系统 介绍
温室 内采 暖 空调系 统 ，是均 匀 分布 于温 室各 个
区域 的通 风管 道系 统 。 控 制 系统 是 我 们设 计 的核 心 ，包 括 温 度 测量 、 数 据处 理和执 行 输 出，用 于完 成温 度 测量和 数 据 处 理 ，进 而控制 整个 空调 系统 的运 行 。
ｆ 或冷 源） 为循 环水 或 空气 ，地 热 热 泵 空调 系 统 的热
源 （ 冷 源） 般 使 用地 下 水 。地 下 水 在 ３ 左 右 或 一 ０ｍ 深度 基 本为恒 温 ，水温 不受太 阳辐 射 影响 ，这 一深
度 区域 称为恒 温 带 。不 同纬度 地 区 的恒温 带深 度不
温 室 地 源 热 泵 温 度 控 制 系 统 设 计
摘 要 ：本 文介绍 了温 室地 源 热泵 空调 系统 ．该 系统 以 可编程 逻辑控 制 器 （Ｌ 蒸 发 的 热 力 循 环 过 程 ，从 而 实 现 采 暖或 制
冷 。 压 缩机 （ｏ ｒｓｏ） Ｃ ｍｐｅｓｒ：起 着 压缩 和 输送 循 环 工
的 温度 、压 力调 节水流 流 量 ，根 据 负荷侧 空调使 用
情 况调 节运行 状 态 ，以此 实现 整 个 系统 的 节能和 高
效运 行 。
蒸 发器 中吸 收 的热量 连 同压缩 机 消耗 功所 转化 的热
量 在冷 凝器 中被 冷却 介质 带走 ，达 到制 热 的 目的 ； 膨 胀 阀 （ｘ ａ ｓ ｎＶａ ｅ或 节 流 阀（ ｈｏｔ ） Ｅ ｐｎｉ ｌ ） ｏ ｖ Ｔ ｒｔｅ：对 循 ｌ 环 工质 起到 节流 降压 作用 ，并调 节进 入蒸 发器 的循
动 动 作 ，无 需人 为操 作 ；手 动模 式 下 ， 以上所 有 均 可 独立 手 动操 作 ， 以便 检修 。 为确保 系 统 运行 持续 性 ，每 个部 位 水泵 机 组 设
汽车电气系统检修试题三及答案
汽车电气系统检修试题三及答案一、填空题。
（每题3分，共30分）1、增强防盗功能从两个方面入手增强( )功能和增强汽车锁止功能2、整个汽车导航系统至少有两大功能：一个是汽车跟踪监控功能，主要将已编码的GPS接收装置安装在汽车上，该汽车无论行驶到任何地方都可以通过计算机控制中心的电子地图上指示出它的所在方位；另一个是( )功能，车主可以将各个地区的交通路线电子图存储在软盘上，只要在车上接收装置中插入软盘，显示屏上就会立即显示出该车所在地区的位置及目前的交通状态，既可输入要去的目的地，预先编制出最佳行驶路线，又可接收计算机控制中心的指令，选择汽车行驶的路线和方向。
3、( )系统，利用发动机的冷却液热量采暖，多用于轿车。
4、制冷循环是由( )、放热、节流和吸热四个过程组成。
5、( )是利用汽车在行驶时各个部位所产生的不同压力进行通风。
6、电磁离合器安装在( )上，其作用是控制发动机与压缩机的动力传递。
7、蒸发器的温度控制的目的是( )。
8、蒸发压力调节器（EPR）安装在( )至压缩机入口的管路中。
9、近年来进口轿车上的空调系统大多采用( )，以保证怠速时能带空调稳定运转。
10、( )的作用是储存制冷剂，除去制冷剂中的水分，过滤制冷剂中的杂质。
二、选择题（每题2分，共10分）1、蒸发器出口处的制冷剂应（ ）A 全部汽化B 部分汽化C 全部液化2、膨胀管式制冷系统中的集液器应安装在（ ）A 冷凝器与膨胀阀之间B 蒸发器与膨胀阀之间C 蒸发器与压缩机之间3、在加注制冷剂时，如果以液体的方式加入（ ）A 只能从低压侧加入B 只能从高压侧加入C 从低压侧加入与从高压侧加入都可以4、如果制冷循环系统的制冷剂不足，接上压力表后会显示（ ） A 高低压表均显示压力过高B 高低压表均显示压力过低C 高压表显示压力过低，低压表显示压力过高5、如果制冷循环系统中有水分，接上压力表后会显示（ ）A 压力表在空调起动时正常，过一段时间低压表指示真空，高压表的也降低了很多，过几分钟又恢复正常，如此反复。
空调的工作原理
空调的工作原理空调是一种常见的家用电器，它能够调节室内温度，提供舒适的环境。
了解空调的工作原理对于正确使用和维护空调非常重要。
本文将详细介绍空调的工作原理。
一、制冷循环系统空调的工作原理基于制冷循环系统，该系统由压缩机、冷凝器、膨胀阀和蒸发器组成。
制冷循环系统通过改变制冷剂的压力和温度来实现制冷效果。
1. 压缩机：压缩机是制冷循环系统的核心部件，它负责将低压低温的制冷剂吸入，然后通过压缩使其成为高压高温的气体。
2. 冷凝器：冷凝器是将高温高压的制冷剂释放热量的地方。
通常，冷凝器位于室外，通过散热器将热量散发到空气中，使制冷剂变成高压液体。
3. 膨胀阀：膨胀阀是控制制冷剂流量的装置。
当高压液体通过膨胀阀流入蒸发器时，压力迅速下降，使制冷剂变成低压低温的气体。
4. 蒸发器：蒸发器是制冷循环系统中的另一个重要部件，它负责吸收室内热量并将其传递给制冷剂。
当低压低温的制冷剂通过蒸发器时，它吸收室内的热量，使室内温度降低。
二、制热循环系统除了制冷循环系统，空调还可以通过制热循环系统提供供暖功能。
制热循环系统与制冷循环系统类似，但是在蒸发器和冷凝器之间进行了反转。
1. 蒸发器：在制热循环系统中，蒸发器变成了室内的热源，吸收室内热量。
2. 膨胀阀：膨胀阀仍然起到控制制冷剂流量的作用。
3. 冷凝器：冷凝器变成了室内的热源，释放热量。
4. 压缩机：压缩机仍然负责将制冷剂压缩成高压高温的气体。
三、温度控制系统空调的温度控制系统是通过感应室内温度变化并调节制冷循环系统的运行来实现的。
1. 温度传感器：空调内部安装有温度传感器，用于感应室内温度的变化。
2. 控制面板：空调的控制面板允许用户设置所需的温度。
当室内温度高于设定温度时，控制面板将发送信号给制冷循环系统，启动制冷过程。
当室内温度达到设定温度时，控制面板将停止制冷过程。
3. 风扇：空调内部装有风扇，用于循环空气和调节室内温度。
当制冷循环系统工作时，风扇将吹送冷空气到室内。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 设计任务
液氨蒸发器采用出口产品温度为主被控变量，加热蒸汽流量为副被控变量。
主、副对象的传递函数分别为：
011()(201)(301)G s s s =++， 0.1021()0.21s
G s e s -=+
主、副扰动通道的传递函数分别为：
11
()0.21f G s s =+， 2()1f G s =
试分别采用单回路控制和串级控制设计温度控制系统。
设计要求如下：
（1）分别进行控制方案设计，给出相应的闭环系统原理图；
（2）对设计的控制系统进行仿真，整定控制器参数；
（3）给出系统的跟踪性能和抗干扰性能仿真，包括一次扰动和二次扰动；
（4）对不同控制方案对系统的影响做对比分析。
2 整体方案设计
2.1 单回路控制变量的选择
对于被控量和操作量选择的原则，其中，被控量选择的原则是能直接反映生产过程中产品产量和质量，选择的结果直接影响生产，因此此设计的被控量是温度。
操纵量是克服扰动影响、使系统重新恢复平稳运行的积极因素，应该遵循快速有效的克服干扰的原则去选择操纵量，因此此设计的操纵量是加热蒸汽流量。
2.2 串级控制系统的选择
串级控制系统选择主变量时要遵循以下原则：在条件许可的情况下，首先应尽量选择能直接反应控制目的的参数为主变量；其次要选择与控制目的有某种单值对应关系的间接单数作为主变量；所选的主变量必须有足够的变化灵敏度。
故在本系统中选择出口产品温度作为主变量。
副回路的设计质量是保证发挥串级系统优点的关键。
副变量的选择应遵循以下原则：应使主要干扰和更多的干扰落入副回路；应使主、副对象的时间常数匹配；应考虑工艺上的合理性、可能性和经
济型。
故选择本系统中的加热蒸汽流量为副变量。
又因为外环是主回路，内环是副回路，所以温度调控是主回路。
2.3 控制器的选择
PID控制器的参数整定是根据被控过程的特性确定PID控制器的比例系数、积分时间和微分时间的大小。
在串级控制系统中，由于对副回路没有太大的要求，所以只需要有比例环节即可（即P为常数，I=0）。
而对于要求较高的主回路，由于主变量一般不得有偏差，所以主回路一般由比例微分控制（P,I均为常数）。
3 系统仿真与参数整定
3.1 单回路系统的仿真与参数整定
针对设计要求，单回路前向通道中含有主、副控制器及扰动，而调节器一般位于扰动的前面，所以PID调节器在最前面。
设计中副被控变量为加热蒸汽流量，所以其作为反馈作用于输入端
图3-1-1单回路控制系统方框图
由方框图对应得到系统仿真图
图3-1-2 单回路控制系统simulink仿真图
仿真整定过程：
首先将PID的参数设置为仅存在比例调节，变换不同的P值以达到期望的效果。
图3-1-3
P=1,I=0，无扰动信号
图3-1-4
P=3,I=0，无扰动信号
图3-1-5
P=5,I=0，无扰动信号
图3-1-6 P=7，I=0，无扰动信号
上面四幅图片可得当P越大时，超调量越大，稳定性下降。
但是震荡频率加快，响应时间变短。
为了保持系统原来的衰减率，PI调节器比例带必须适当加
大。
又因为要使PI调节在稍微牺牲控制系统的动态品质以换取较好的稳态性能，所以P值不应过大，因此选择P=7。
图3-1-7
P=7，I=0.1，无扰动信号
图3-1-8
P=7，I=0.3，无扰动信号
积分环节的作用除消除系统的余差外，也加大了系统的振荡频率，使响应速度变快。
但是随着I的增大，超调量过大，也调节时间过长，系统动态性能降低，因此选择I=0.1最佳
图3-1-9
P=7，I=0.1，一次扰动信号
图3-1-10
P=7，I=0.1，二次扰动信号
通过反复试验过程，此时系统的阶跃响应效果比较理想，控制器参数整定比较合理。
加入扰动以后超调量有所增大，但后面能够达到期望值，具有一定的调节作用。
3.2 串级控制系统的仿真与参数整定
针对设计要求，产品温度作为主变量必然处于主回路，蒸汽流量作为副变量位于副回路中，扰动要加在调节器之后，因此得如下图所示框图：
图3-2-1串级控制系统方框图
由方框图对应得到系统仿真图
图3-2-2 串级控制系统simulink仿真图
仿真整定过程：
首先将主、副PID调节器设计为比例控制，增益分别为K1,K2，假设扰动均为零，在给定阶跃输入下得到输出响应y1(t),y2(t)。
串级系统的整定比单回路复杂，因为两个调节器串在一起工作，各回路之间相互联系，相互影响。
改变主、副调节器中的任何一个整定参数，对主、副回路的过渡过程都有影响，这种影响
程度取决于主、副对象的动态特性、而且待整定的参数比单回路多，因此，串级系统的整定必然比较困难和繁琐。
常用的工程整定方法有：试凑法，两步整定法和一步整定法。
其中一步整定法步骤为：选择一个合适的负调节器放大倍数K2，按纯比例控制规律设置负调节器。
本设计中经过多次调试，确定K2=12。
主调节器也先置于纯比例作用，使串级控制系统投入运行，用整定单回路的方法整定主调节器参数。
实验步骤如下图：
图3-2-3
K1=1，I=0，K2=12，无扰动
图3-2-4
K1=5,I=0,K2=12，无扰动
图3-2-5
K1=7,I=0,K2=12，无扰动
由上图可知P越大，系统的响应过程越好，超调量变大，震荡频率加大，响应时间变短。
由单回路控制得知P不应过大，因此选择K1=7。
因为副回路是随动系统，允许有误差，因为副调节器可以不引入积分作用，因此只需讨论主调节器的I值即可。
图3-2-6
K1=5,I=0.1,K2=12，无扰动
图3-2-7
K1=7,I=0.1,K2=12，无扰动
图3-2-8
K1=7,I=0.2,K2=12，无扰动
由上图很明显得知，K1增大震荡剧烈，超调量增大，调节时间变短，震荡频率加快。
而引入积分环节后，超调变小，调节时间变短。
I=0.2时较I=0.1时震荡剧烈，调节时间过长，所以I=0.1。
图3-2-9
K1=7,I=0.1,K2=12,一次扰动（主扰动）
图3-2-10
K1=7,I=0.1,K2=12,二次扰动（副扰动）
图3-2-11
K1=7，I=0.1，K2=12,一、二次扰动均作用系统
加入时间滞后环节后系统的仿真图
图3-2-12
此时系统的参数整定数值为
图3-2-13
K1=0.2，I=0.1，K2=0.3，一、二次扰动均作用
以下为整定过程中各参数变化后的效果
图3-2-14
K1=0.2，I=0.2，K2=0.3，一、二次扰动均作用（含时滞）
图3-2-15
K1=0.2，I=0.1，K2=1，一、二次扰动均作用（含时滞）
图3-2-16
K1=7，I=0.1，K2=0.3，一、二次扰动均作用（含时滞）
主、副调节器共同作用，使得系统响应加快，两种干扰同时作用时，使超调量进一步加大，调节时间变长。
串级控制系统由于副回路的存在，提高了系统的工作频率，减小了震荡周期，在衰减系数相同的情况下，缩短了调节时间，提高了系统的快速性。
4 小结
通过以上分析可知：串级控制的副控制器具有“粗调”的作用，而主控制器具有“细调”的作用。
由串级控制器和单回路控制器的仿真图比较可知，采用单回路控制，系统的阶跃响应达到要求时，系统对一次，二次扰动的抑制效果不是很好。
若主、副控制器两者相互配合，控制质量必然高于单回路控制系统。