高二数学暑假作业5无答案
【推荐下载】新课标最新年高二数学暑假作业5(必修5-选修2-3)

[键入文字]
新课标最新年高二数学暑假作业5(必修5-选修2-3)
在这个独属于学生的夏天的假期,准备了2015年高二数学暑假作业,希望你喜欢。
一选择题(本大题共小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.复数,则在复平面内的点位于第( )象限。
A.一B.二C.三D .四
2.右表提供了某厂节能降耗技术改造后生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.根据右表提供的数据,求出y关于x的线性回归方程为,那么表中t的值为( )
A.3 B.3.15 C.3.5 D.4.5
3.在1万平方公里的海域中有40平方公里的大陆架贮藏着石油,假若在海域中任意一点钻探,那么钻到油层面的概率是( )
A、B、C、D、
4.西大附中数学组有实习老师共5名,现将他们分配到高二年级的1、2、3三个班实习,每班至少1名,最多2名,则不同的分配方案有()
A.30种B.90种C.180种D.270种
1。
高二数学第二学期 暑假作业(无答案) 苏教版

假期作业1 集合与简单的逻辑联结词班级______ __ 姓名____ ____ 家长签名 一、填空题:(本大题共14小题,每小题5分,共70分)1. 若全集U R =,集合{|1}A x x =≥,则U C A = 。
2. (2011上海)已知{}{}{}1,2,3,4,5,6,7,8,1,3,5,7,2,4,5,U A B ===则()U AB ⋃=ð 。
3.设集合A={x||x-a|<1,x ∈R},B={x|1<x<5,x ∈R}.若A ∩B=,则实数a 的取值范围是 。
4. (2011重庆)设,,则 。
5.已知M={x|x=a 2+2a+4,a ∈Z},N={y|y=b 2-4b+6,b ∈Z},则M 、N 之间的关系是 6.设全集为U,若命题p:2010∈A ∩B,⌝ p 是 。
7.定义集合M 与N 的新运算如下:M*N={x|x ∈M 或x ∈N,但xM ∩N}.若M={0,2,4,6,8,10,12},N={0,3, 6,9,12,15},则(M*N)*M 等于 。
8.设U={0,1,2,3},A={x ∈U|x 2+mx=0},ðU A={1,2},则实数m=________. 9. 若,a b 为实数,则 “0<ab<1”是“b<a1”的 条件。
10. 已知集合{}|12,A x R x Z =∈-<为整数集,则集合A Z ⋂中所有元素的和等于________。
11. (2011全国) 已知集合M={0,1,2,3,4},N={1,3,5},P=M N ,则P 的子集共有 个。
12.(2011天津)设集合{}{}|20,|0A x R x B x R x =∈->=∈<,{}|(2)0C x R x x =∈->,则“x A B ∈⋃”是“x C ∈”的 条件。
13. (2011山东) 已知a ,b ,c ∈R ,命题“若a b c ++=3,则222a b c ++≥3”,的否命题是。
【推荐下载】苏教版高中高二数学暑假作业练习及答案

[键入文字]
苏教版高中高二数学暑假作业练习及答案
苏教版高中高二数学暑假作业练习及答案
【摘要】高中学生在学习中或多或少有一些困惑,的编辑为大家总结了苏教版高中高二数学暑假作业练习及答案,各位考生可以参考。
一、填空题(本大题共14小题,每小题5分,共70分)
1.命题:若a2+b2=0(a,b∈R),则a=b=0的逆否命题是____________.
解析 且的否定为或,因此逆否命题为若a≠0或b≠0,则a2+b2≠0.
答案 若a≠0或b≠0(a,b∈R),则a2+b2≠0
2.命题ax2-2ax-30不成立是真命题,则实数a的取值范围是____________.
解析 ax2-2ax-3≤0恒成立,
当a=0时,-3≤0成立;
当a≠0时,a小于0Δ=4a2+12a≤0,
解得-3≤a小于0.
1。
2021年高二数学暑期作业(套卷)(5)含答案
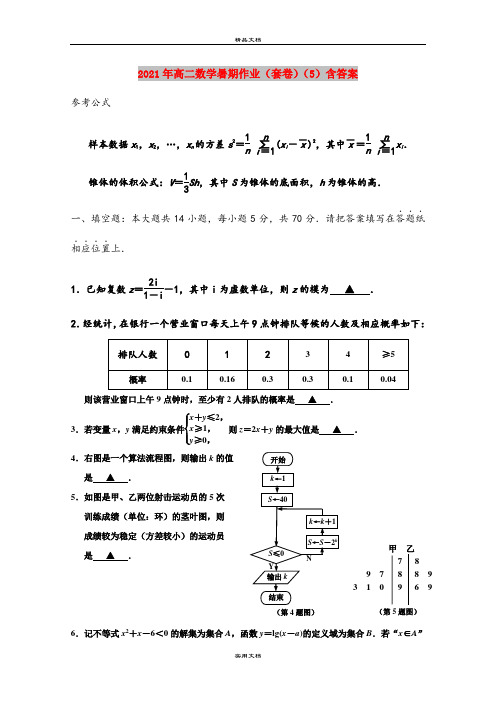
2021年高二数学暑期作业(套卷)(5)含答案参考公式样本数据x 1,x 2,…,x n 的方差s 2=1n i =1∑n (x i --x )2,其中-x =1n i =1∑nx i .锥体的体积公式:V =13Sh ,其中S 为锥体的底面积,h 为锥体的高.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题纸...相应位置....上.1.已知复数z =2i1-i-1,其中i 为虚数单位,则z 的模为 ▲ . 2.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:则该营业窗口上午9点钟时,至少有2人排队的概率是 ▲ .3.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤2,x ≥1,y ≥0,则z =2x +y 的最大值是 ▲ .4.右图是一个算法流程图,则输出k 的值 是 ▲ .5.如图是甲、乙两位射击运动员的5次 训练成绩(单位:环)的茎叶图,则 成绩较为稳定(方差较小)的运动员 是 ▲ .6.记不等式x 2+x -6<0的解集为集合A ,函数y =lg(x -a )的定义域为集合B .若“x ∈A ”甲 乙8 9 7 8 93 1 0 6 97 8 9 (第5题图)(第4题图)是“x ∈B ”的充分条件,则实数a 的取值范围为 ▲ . 7.在平面直角坐标系xOy 中,过双曲线C :x 2-y 23=1的右焦点F 作x 轴的垂线l ,则l 与双曲线C 的两条渐近线所围成的三角形的面积是 ▲ .8.已知正六棱锥P -ABCDEF 的底面边长为2,侧棱长为4,则此六棱锥的体积为 ▲ . 9.在△ABC 中, ∠ABC =120︒,BA =2,BC =3,D ,E 是线段AC 的三等分点,则→BD ·→BE 的值为 ▲ .10.记等差数列{a n }的前n 项和为S n .若S k -1=8,S k =0,S k +1=-10,则正整数k = ▲ . 11.若将函数f (x )=∣sin(ωx -π6)∣(ω>0)的图象向左平移π9个单位后,所得图象对应的函数为偶函数 ,则实数ω的最小值是 ▲ .12.已知x ,y 为正实数,则4x 4x +y +yx +y的最大值为 ▲ .13.在平面直角坐标系xOy 中,圆C 的方程为(x -1)2+(y -1)2=9,直线l :y =kx +3与圆C相交于A ,B 两点,M 为弦AB 上一动点,以M 为圆心,2为半径的圆与圆C 总有公共点,则实数k 的取值范围为 ▲ .14.已知a ,t 为正实数,函数f (x )=x 2-2x +a ,且对任意的x ∈[0,t ],都有f (x )∈[-a ,a ].若对每一个正实数a ,记t 的最大值为g (a ),则函数g (a )的值域为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题纸指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a cos C +c cos A =2b cos A . (1)求角A 的值;(2)求sin B +sin C 的取值范围.16.(本小题满分14分)在四棱锥P -ABCD 中,BC ∥AD ,PA ⊥PD ,AD =2BC ,AB =PB , E 为PA 的中点. (1)求证:BE ∥平面PCD ; (2)求证:平面PAB ⊥平面PCD .17.(本小题满分14分)如图,摩天轮的半径OA 为50m ,它的最低点A 距地面的高度忽略不计.地面上有一长度为240m 的景观带MN ,它与摩天轮在同一竖直平面内,且AM =60m .点P 从最低点A 处按逆时针方向转动到最高点B 处,记∠AOP =θ,θ ∈(0,π).(1)当θ =2π3 时,求点P 距地面的高度PQ ;(2)试确定θ 的值,使得∠MPN 取得最大值.18.(本小题满分16分)在平面直角坐标系xOy 中,设中心在坐标原点的椭圆C 的左、右焦点分别为F 1、F 2,右准线l :x =m +1与x 轴的交点为B ,BF 2=m .(第16题图)PABCDE(第17题图)AMNBO PQθ(1)已知点(62,1)在椭圆C 上,求实数m 的值; (2)已知定点A (-2,0).①若椭圆C 上存在点T ,使得TATF 1=2,求椭圆C 的离心率的取值范围;②当m =1时,记M 为椭圆C 上的动点,直线AM ,BM 分别与椭圆C 交于另一点P ,Q ,若AM → =λAP →,BM →=μBQ →,求证:λ+μ19.(本小题满分16分)已知函数f (x )=x 2-x +t ,t ≥0,g (x )=ln x . (1)令h (x )=f (x )+g (x ),求证:h (x )是增函数;(2)直线l 与函数f (x ),g (x )的图象都相切.对于确定的正实数t ,讨论直线l 的条数,并说明理由.20.(本小题满分16分)已知数列{a n }的各项均为正数,其前n 项的和为S n ,且对任意的m ,n ∈N *, 都有(S m +n +S 1)2=4a 2m a 2n . (1)求a 2a 1的值;(2)求证:{a n }为等比数列;(第18题图)(3)已知数列{c n },{d n }满足|c n |=|d n |=a n ,p (p ≥3)是给定的正整数,数列{c n },{d n }的前p 项的和分别为T p ,R p ,且T p =R p ,求证:对任意正整数k (1≤k ≤p ),c k =d k .高二数学暑假作业(五)参考答案一、填空题:本大题共14小题,每小题5分,共70分.1. 5 2.0.74 3.4 4.6 5.甲 6.(-∞,-3] 7.4 3 8.12 9.119 10.911.32 12. 43 13.[-34,+∞) 14.(0,1)∪{2}错误!未指定书签。
北京宏志中学高二文科数学暑假作业答案

北京宏志中学高二文科数学暑假作业 参考答案暑假作业(一)A1.B 2.B 3.C 4.{-1,0} 5.C 6.D 7.D 8.D 9.010.{(0,1),(-1,2)} 11.-1<a <212.实数m 的值为8 13.(1)C (2)4m1+m 2暑假作业(一)B1.B 2.C 3.D 4.2 5.A 6.C 7.C 8.A 9.{2,4,6} 10.[0,1)∪(3,+∞) 11.23 12.A ∪B ={-7,-4,-8,4,9} 13.(1)B ={x |4<x <5} (2)a =-1暑假作业(二)1.C 2.A 3.C 4.充分不必要 5.B 6.A 7.B 8.B 9.充分不必要10.⎣⎡⎦⎤-12,43 11.m >9 12.m ≤4 13.(1)(∁U B )∩A ={x |3≤x <4}(2)⎣⎡⎭⎫-12,13∪⎝ ⎛⎦⎥⎤13,3-52 暑假作业(三)1.C 2.D 3.D 4.“所有的三角形都不是直角三角形” 5.D 6.D 7.C 8.C9.(-∞,0)∪⎝⎛⎭⎫34,+∞ 10.①②④ 11.[1,+∞) 12.-2<a ≤2 13.{a |a >2或a <-2}暑假作业(四)A1.C 2.B 3.B 4.(1,3] 5.A 6.B 7.B 8.C9.[2,+∞) 10.[-14,0)∪(34,1] 11.1201512.(1)f [g (2)]=0 g [f (2)]=2 (2)f [g (x )]=⎩⎪⎨⎪⎧x 2-2x ,x ≥0,x 2-4x +3,x <0g [f (x )]=⎩⎪⎨⎪⎧x 2-2,x ≤-1或x ≥1,3-x 2,-1<x <1 13.(1)f (x )=x 2+2x g (x )=-x 2+2x (2)(-∞,0]暑假作业(四)B1.B 2.A 3.C 4.435.C6.B7.D8.B9.[-14,+∞) 10.x3+1 11.(-∞,1]12.(1)(-3,0)∪(2,3) (2)①[-1,1] ②[1,4] (3)(-∞,0]13.(1)B (2)A暑假作业(五) 1.B 2.C 3.B 4.(-12,23) 5.A 6.A 7.D 8.D9.C 10.[3,+∞) 11.(-∞,2] 12.[2,+∞) 13.(-1,1)14.(1)b =4 (2)函数f (x )=x +cx取得最小值2 c 当c ∈[1,2)时,f (x )的最大值为2+c2当c ∈(2,4]时,f (x )的最大值为1+c 当c =2时,f (x )的最大值为315.(1)略 (2)(-∞,3]16.(1)f (1)=0 (2)略 (3)[1+10,+∞)暑假作业(六)A1.B 2.D 3.B 4.-2 5.D 6.A 7.A 8.A 9.1 10.-2 11.120712.(1)m =1 (2)f (x )是奇函数 (3)f (x )在区间(0,+∞)上单调递增13.(1)f (x )=⎩⎪⎨⎪⎧4x 3-2ax ,-1≤x <0,-4x 3+2ax ,0≤x ≤1. (2)存在a =8使得f (x )的图像的最高点在直线y =12上暑假作业(六)B1.C 2.C 3.B 4.-3 5.C 6.B 7.B 8.D 9.3210.2 11.(-2,0)∪(3,+∞) 12.(1)m =0 (2)-1<a <0 13.(1)略 (2)f (x )=x 2-6x +8(3)f (0)+f (1)+f (2)+…+f (2013)=1暑假作业(七)1.A 2.D 3.D 4.(-∞,-3] 5.B 6.C 7.C 8.A 9.C 10.-2 -4 11.y =-x 2+2x +8 12.-1或313.-3或15 14.f (x )=x 2+x15.(1)[-214,15] (2)a =-13或-116.(1)f (x )=12x 2+x (2)m =12,t =8暑假作业(八)A1.B 2.D 3.C 4.2 5.B 6.C 7.A 8.D 9.-1 10.log 23 11.3 212.(1)1 (2)-43 13.(1)略 (2)a =6,b =8,c =10暑假作业(八)B 1.C 2.B 3.D 4.a 2b 45.B6.D7.C8.A9.3 10.ab +3ab +111.①③④12.(1)略 (2)3x <4y <6z13.(1)y =at 2-3t +3 (2)a =16 x =64暑假作业(九)1.B 2.B 3.B 4.[-1,2)∪(2,3]5.B 6.D 7.C 8.B 9.B 10.3 11.0和112.(11-a,0) 13.-1和0 [-14,3]14.(-∞,0]∪[1,2]15.(1)f (12013) +f (-12013) =0 (2)(-∞,-2]∪[4,+∞)16.(1)a =1 (2)λ=43暑假作业(十)1.C 2.D 3.D 4.③ 5.C 6.A 7.D 8.C9.B 10.(-2,1) 11.-2 12.(-1,-1) 13.10<abc <1214.f (x )=⎩⎪⎨⎪⎧x +1,-1≤x ≤0,14(x -2)2-1,x >0. 15.(0,13]∪[3,+∞) 16.(1)m ≥2e (2)(-e 2+2e +1,+∞)暑假作业(十一)1.D 2.C 3.A 4.3x -y +2=0 5.D 6.C 7.A 8.B 9.B 10.1 1 11.0 12.3x +y =0 13.-cos x14.(1)13x -y -32=0 (2)切点坐标为(1,-14)或(-1,-18),切线方程为y =4x -18或y =4x -1415.(1)f (x )=x -3x(2)证明略 定值为616.(1)x 0=1 (2)a ≥ e暑假作业(十二)1.B 2.A 3.C 4.(-∞,-3)∪(6,+∞) 5.A 6.B 7.D 8.C9.C 10.9 11.(0,12) 12.-4 13.(-1,0)∪(1,+∞)14.(1)a =4,b =4 (2)极大值为4(1-e -2)15.(1)a =2 (2)①当a ≤0时,函数f (x )的单调递减区间为(0,1),单调递增区间为(1,+∞);②当0<a <2时,则函数f (x )的单调递增区间为(0,a2),(1,+∞),单调递减区间为(a2,1);③a =2时,函数f (x )的单调递增区间为(0,+∞);④a >2时,函数f (x )的单调递增区间为(0,1),(a2,+∞)单调递减区间为(1,a2)16.(1)f (x )的单调递增区间为(0,+∞),单调递减区间为(-∞,0),f (x )有极小值1(2)g (x )=sin x +1 (3)[1,+∞)暑假作业(十三)1.D 2.B 3.D 4.(0,1) 5.D 6.C 7.A 8.B9.A 10.6 cm 3 cm 4 cm 11.3-1 12.[-42,9] 13.114.(1)f (x )=x 3+2x 2-4x +5(2)f (x )在[-3,1]上的最大值为1315.(1)f (x )的单调递增区间为(-π2,0),单调递减区间为(0,π2) (2)k ≤-1216.(1)S 1的最大值为4 (2)l 的范围是[8,4 5]专题一 突破高考解答题——函数与导数1.(1)f (x )=x +1x(2)(-∞,2]2.(1)(0,1) (2)[2ln 3-5,2ln 2-4)3.(1)①当a ≤0时,函数f (x )的单调递增区间为(0,+∞)②当a >0时,函数f (x )的单调递减区间为(2a2a,+∞),单调递增区间为(0,2a2a)(2)略4.(1)(-1,13) (2)(-1,-411) (3)[-38,0]5.(1) y =x -1 (2)略 (3)f (b )-f (a )b -a>f⎝⎛⎭⎫a +b 2暑假作业(十四) 1.A 2.D 3.C 4.(-3π2,0) 5.D 6.B 7.D 8.D9.⎩⎪⎨⎪⎧2x +3y ≤60,4x +2y ≤80,y -x ≤10,x ≥0,x ∈N *,y ≥0,y ∈N*10.b a -c <ab -d11.①④12.a n +b n <c n 13.5张暑假作业(十五)1.A 2.B 3.B 4.(0,8) 5.B 6.A 7.B 8.C9.-1 10.(-7,3) 11.-21412.(1)M ={x |0<x <2} (2)[-2,2]13.(1)a1+a 2 (2)1-k 2-2k +k 2暑假作业(十六)1.C 2.D 3.C 4.6 5.A 6.B 7.A 8.B 9.B 10.2 11.22 12.2 13.20 14.略15.(1)k =50 (2)建8层时,每平方米的平均综合费用为1225元16.a 为6,b 为3时,经沉淀后流出的水中该杂质的质量分数最小暑假作业(十七)1.C 2.B 3.B 4.D 5.D 6.C 7.D 8.A 9.C10.a >c >b 11.log a (1+a )>log a ⎝⎛⎭⎫1+1a 12.a ≥0,b ≥0且a ≠b 13.3 3214.略 15.略16.(1)a n =2n -1+2,S n =n (n +2) (2)略暑假作业(十八)1.A 2.A 3.A 4.2 5.D 6.C 7.A 8.B9.A 10.3 11.-12+2i 12.2 13.3+4i14.(1)a =b =3 (2)z =1-i 时,|z |min = 2 15.(1)m =5或m =-3 (2)m ≠5且m ≠-3 (3)m =-2 (4)m <-3或m >5(5)m =-3-414或m =-3+41416.(1)|z |=1 ⎝⎛⎭⎫-12,1 (2)略 (3)1暑假作业(十九)1.已知函数f (x )=sin ⎝⎛⎭⎪⎫ωx +π3(ω>0)的最小正周期为π,则该函数的图像( )A .关于点⎝ ⎛⎭⎪⎫π3,0对称 B .关于直线x =π4对称C .关于点⎝ ⎛⎭⎪⎫π4,0对称 D .关于直线x =π3对称解析 由已知,ω=2,所以f (x )=sin ⎝⎛⎭⎪⎫2x +π3,因为f ⎝ ⎛⎭⎪⎫π3=0,所以函数图像关于点⎝ ⎛⎭⎪⎫π3,0中心对称,故选A. 答案 A2.要得到函数的图像,只要将函数的图像( )A. 向左平移1个单位B. 向右平移1个单位C. 向左平移个单位 D.向右平移 个单位 解析 因为,所以将c o s (21)y x =+c o s 2y x =12121c o s (21)c o s (2()2y xx =+=+向左平移个单位,故选C. 答案 C3. 函数f (x )=A sin(ωx +φ)A >0,ω>0,|φ|<π2的部分图象如图所示,则将y =f (x )的图象向右平移π6个单位后,得到的图象对应的函数解析式为( ). A .y =sin 2xB .y =cos 2xC .y =sin ⎝ ⎛⎭⎪⎫2x +2π3D .y =sin ⎝ ⎛⎭⎪⎫2x -π6解析 由所给图象知A =1,34T =11π12-π6=3π4,T =π,所以ω=2πT =2,由sin ⎝ ⎛⎭⎪⎫2×π6+φ=1,|φ|<π2得π3+φ=π2,解得φ=π6,所以f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6,则f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6的图象向右平移π6个单位后得到的图象对应的函数解析式为y =sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π6+π6=sin ⎝ ⎛⎭⎪⎫2x -π6,故选D. 答案 D4.将函数y =sin 2x 的图象向左平移φ(φ>0)个单位,所得图象对应的函数为偶函数,则φ的最小值为( ).A.π6B.π3C.π4D.π12解析 将函数y =sin 2x 的图象向左平移φ个单位,得到函数y =sin 2(x +φ)=sin(2x +2φ)的图象,由题意得2φ=π2+k π(k ∈Z ),故φ的最小值为π4. 答案 C5. 如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置P (x ,y ).若初始位置为P 0⎝ ⎛⎭⎪⎫32,12,当秒针从P 0(注:此时t =0)正常开始走时,那么点P 的纵坐标y 与时间t 的函数关系为( ).A .y =sin ⎝ ⎛⎭⎪⎫π30t +π6B .y =sin ⎝ ⎛⎭⎪⎫-π60t -π6C .y =sin ⎝ ⎛⎭⎪⎫-π30t +π6D .y =sin ⎝ ⎛⎭⎪⎫-π30t -π3解析 由题意可得,函数的初相位是π6,排除B ,D.又函数周期是60(秒)且秒针按顺时针旋转,即T =⎪⎪⎪⎪⎪⎪2πω=60,所以|ω|=π30,即ω=-π30,故选C.答案 C6.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图像如图所示,则当t =1100秒时,电流强度是( ) A .-5安 B .5安 C .53安 D .10安解析 由函数图像知A =10,T 2=4300-1300=1100. ∴T =150=2πω,∴ω=100π. ∴I =10sin(100πt +φ). 又∵点⎝ ⎛⎭⎪⎫1300,10在图像上, ∴10=10sin ⎝ ⎛⎭⎪⎫100π×1300+φ ∴π3+φ=π2,∴φ=π6, ∴I =10sin ⎝ ⎛⎭⎪⎫100πt +π6.当t =1100时,I =10sin ⎝⎛⎭⎪⎫100π×1100+π6=-5. 答案 A 二、填空题 7.已知函数f (x )=sin(ωx+cos2y x =12φ)⎝ ⎛⎭⎪⎫ω>0,-π2≤φ≤π2的图像上的两个相邻的最高点和最低点的距离为22,则ω=________. 解析 由已知两相邻最高点和最低点的距离为22,而f (x )max -f (x )min =2,由勾股定理可得T2=22-22=2,∴T =4,∴ω=2πT =π2.答案 π28.已知函数f (x )=3sin ⎝ ⎛⎭⎪⎫ωx -π6(ω>0)和g (x )=2cos(2x+φ)+1的图象的对称轴完全相同,若x ∈⎣⎢⎡⎦⎥⎤0,π2,则f (x )的取值范围是________.解析 ∵f (x )与g (x )的图象的对称轴完全相同,∴f (x )与g (x )的最小正周期相等,∵ω>0,∴ω=2,∴f (x )=3sin ⎝ ⎛⎭⎪⎫2x -π6,∵0≤x ≤π2,∴-π6≤2x -π6≤5π6,∴-12≤sin ⎝ ⎛⎭⎪⎫2x -π6≤1,∴-32≤3sin ⎝ ⎛⎭⎪⎫2x -π6≤3,即f (x )的取值范围是⎣⎢⎡⎦⎥⎤-32,3.答案 ⎣⎢⎡⎦⎥⎤-32,39.已知函数f (x )=-2sin(2x +φ)(|φ|<π),若⎝ ⎛⎭⎪⎫π8,5π8是f (x )的一个单调递增区间,则φ的值为________.解析 令π2+2k π≤2x +φ≤3π2+2k π,k ∈Z ,k =0时,有π4-φ2≤x ≤3π4-φ2,此时函数单调递增,若⎝ ⎛⎭⎪⎫π8,5π8是f (x )的一个单调递增区间,则必有⎩⎪⎨⎪⎧π4-φ2≤π8,3π4-φ2≥5π8,解得⎩⎪⎨⎪⎧φ≥π4,φ≤π4,故φ=π4.答案 π410.在函数f (x )=A sin(ωx +φ)(A >0,ω>0)的一个周期内,当x =π9时有最大值12,当x =4π9时有最小值-12,若φ∈⎝⎛⎭⎪⎫0,π2,则函数解析式f (x )=________.解析 首先易知A =12,由于x =π9时f (x )有最大值12,当x =4π9时f (x )有最小值-12,所以T =⎝ ⎛⎭⎪⎫4π9-π9×2=2π3,ω=3.又12sin ⎝⎛⎭⎪⎫3×π9+φ=12,φ∈⎝ ⎛⎭⎪⎫0,π2,解得φ=π6,故f (x )=12sin ⎝⎛⎭⎪⎫3x +π6.答案12sin ⎝⎛⎭⎪⎫3x +π6三、解答题11.已知函数f (x )=3sin2x +2cos 2x .(1)将f (x )的图像向右平移π12个单位长度,再将周期扩大一倍,得到函数g (x )的图像,求g (x )的解析式;(2)求函数f (x )的最小正周期和单调递增区间. 解 (1)依题意f (x )=3sin2x +2·cos2x +12=3sin2x +cos2x +1 =2sin ⎝ ⎛⎭⎪⎫2x +π6+1,将f (x )的图像向右平移π12个单位长度,得到函数f 1(x )=2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π12+π6+1=2sin2x +1的图像,该函数的周期为π,若将其周期变为2π,则得g (x )=2sin x +1.(2)函数f (x )的最小正周期为T =π,当2k π-π2≤2x +π6≤2k π+π2(k ∈Z)时,函数单调递增, 解得k π-π3≤x ≤k π+π6(k ∈Z),∴函数的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π3,k π+π6(k ∈Z).12.已知向量m =(sin x,1),n =(3A cos x ,A2cos 2x )(A >0),函数f (x )=m ·n 的最大值为6. (1)求A ;(2)将函数y =f (x )的图象向左平移π12个单位,再将所得图象上各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )在⎣⎢⎡⎦⎥⎤0,5π24上的值域.解 (1)f (x )=m ·n =3A sin x cos x +A2cos 2x =A ⎝ ⎛⎭⎪⎫32sin 2x +12cos 2x =A sin ⎝ ⎛⎭⎪⎫2x +π6.因为A >0,由题意知A =6. (2)由(1)知f (x )=6sin ⎝ ⎛⎭⎪⎫2x +π6.将函数y =f (x )的图象向左平移π12个单位后得到 y =6sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π12+π6=6sin ⎝ ⎛⎭⎪⎫2x +π3的图象; 再将得到图象上各点横坐标缩短为原来的12倍,纵坐标不变,得到y =6sin ⎝ ⎛⎭⎪⎫4x +π3的图象.因此g (x )=6sin ⎝ ⎛⎭⎪⎫4x +π3. 因为x ∈⎣⎢⎡⎦⎥⎤0,5π24,所以4x +π3∈⎣⎢⎡⎦⎥⎤π3,7π6,故g (x )在⎣⎢⎡⎦⎥⎤0,5π24上的值域为[-3,6].13.已知函数f (x )=23sin x 2+π4cos ⎝ ⎛⎭⎪⎫x 2+π4-sin(x +π).(1)求f (x )的最小正周期;(2)若将f (x )的图象向右平移π6个单位,得到函数g (x )的图象,求函数g (x )在区间[0,π]上的最大值和最小值.解 (1)因为f (x )=3sin ⎝ ⎛⎭⎪⎫x +π2+sin x=3cos x +sin x =2⎝ ⎛⎭⎪⎫32cos x +12sin x=2sin ⎝ ⎛⎭⎪⎫x +π3,所以f (x )的最小正周期为2π.(2)∵将f (x )的图象向右平移π6个单位,得到函数g (x )的图象,∴g (x )=f ⎝ ⎛⎭⎪⎫x -π6=2sin[⎝ ⎛⎭⎪⎫x -π6+π3]=2sin ⎝ ⎛⎭⎪⎫x +π6.∵x ∈[0,π],∴x +π6∈⎣⎢⎡⎦⎥⎤π6,7π6,∴当x +π6=π2,即x =π3时,sin ⎝ ⎛⎭⎪⎫x +π6=1,g (x )取得最大值2.当x +π6=7π6,即x =π时,sin ⎝ ⎛⎭⎪⎫x +π6=-12,g (x )取得最小值-1.14.设函数f (x )=22cos ⎝ ⎛⎭⎪⎫2x +π4+sin 2x .(1)求f (x )的最小正周期;(2)设函数g (x )对任意x ∈R ,有g ⎝ ⎛⎭⎪⎫x +π2=g (x ),且当x ∈⎣⎢⎡⎦⎥⎤0,π2时,g (x )=12-f (x ).求g (x )在区间[-π,0]上的解析式.解 (1)f (x )=22cos ⎝ ⎛⎭⎪⎫2x +π4+sin 2x=22⎝ ⎛⎭⎪⎫cos 2x cos π4-sin 2x sin π4+1-cos 2x 2=12-12sin 2x ,故f (x )的最小正周期为π.(2)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,g (x )=12-f (x )=12sin 2x ,故 ①当x ∈⎣⎢⎡⎦⎥⎤-π2,0时,x +π2∈⎣⎢⎡⎦⎥⎤0,π2.由于对任意x ∈R ,g ⎝ ⎛⎭⎪⎫x +π2=g (x ),从而g (x )=g ⎝ ⎛⎭⎪⎫x +π2=12sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π2=12sin(π+2x )=-12sin 2x .②当x ∈⎣⎢⎡⎭⎪⎫-π,-π2时,x +π∈⎣⎢⎡⎭⎪⎫0,π2.从而g (x )=g (x +π)=12sin[2(x +π)]=12sin 2x .综合①、②得g (x )在[-π,0]上的解析式为 g (x )=⎩⎪⎨⎪⎧12sin 2x ,x ∈⎣⎢⎡⎭⎪⎫-π,-π2,-12sin 2x ,x ∈⎣⎢⎡⎦⎥⎤-π2,0.15.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A =23,sin B =5cos C . (1)求tan C 的值;(2)若a = 2,求△ABC 的面积. 解 (1)因为0<A <π,cos A =23, 得sin A =1-cos 2A =53.又5cos C =sin B =sin(A +C )=sin A cos C +cos A sin C=53cos C +23sin C . 所以tan C = 5.(2)由tan C =5,得sin C =56,cos C =16.于是sin B =5cos C =56.由a = 2及正弦定理a sin A =csin C ,得c = 3. 设△ABC 的面积为S ,则S =12ac sin B =52. 16. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,点(a ,b )在直线x (sin A -sin B )+y sin B =c sin C 上. (1)求角C 的值;(2)若a 2+b 2=6(a +b )-18,求△ABC 的面积. 解 (1)由题意得a (sin A -sin B )+b sin B =c sin C , 由正弦定理,得a (a -b )+b 2=c 2, 即a 2+b 2-c 2=ab , 由余弦定理,得cos C =a 2+b 2-c 22ab =12,结合0<C <π,得C =π3.(2)由a 2+b 2=6(a +b )-18,得(a -3)2+(b -3)2=0, 从而得a =b =3,所以△ABC 的面积S =12×32×sin π3=934. 17. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知A =π4,b sin ⎝ ⎛⎭⎪⎫π4+C -c sin ⎝ ⎛⎭⎪⎫π4+B =a .(1)求证:B -C =π2;(2)若a = 2,求△ABC 的面积.(1)证明 由b sin ⎝ ⎛⎭⎪⎫π4+C -c sin ⎝ ⎛⎭⎪⎫π4+B =a 应用正弦定理,得sin B sin ⎝ ⎛⎭⎪⎫π4+C -sin C sin ⎝ ⎛⎭⎪⎫π4+B =sin A ,sin B ⎝ ⎛⎭⎪⎫22sin C +22cos C -sin C ⎝ ⎛⎭⎪⎫22sin B +22cos B =22,整理得sin B cos C -cos B sin C =1,即sin(B -C )=1. 由于0<B ,C <34π,从而B -C =π2.(2)解 B +C =π-A =3π4,因此B =5π8,C =π8. 由a = 2,A =π4,得b =a sin B sin A =2sin 5π8,c =a sin C sin A =2sin π8, 所以△ABC 的面积S =12bc sin A = 2sin 5π8sin π8 = 2cos π8sin π8=12北京宏志中学文科暑假作业答案。
高二数学 暑假作业(5)(无答案)(新版)新人教版

—————————— 新学期 新成绩 新目标 新方向 ——————————2019年高二数学 暑假作业(5)一、选择题:1、 下列函数中,在区间()0,+∞不是增函数的是 ( )A. x y 2=B. x y lg =C. 3x y =D. 1y x= 2、函数y =(a 2-1)x 在(-∞,+∞)上是减函数,则a 的取值范围是 ( )A.|a |>1B.|a |>2C.a>2D.1<|a |<2 3、图中曲线分别表示l g a y o x =,l g b y o x =,l g c y o x =,l g d y o x =的图象,,,,a b c d 的关系是 () A 、0<a<b<1<d<cB 、0<b<a<1<c<dC 、0<d<c<1<a<bD 、0<c<d<1<a<b 二、填空题: 4、若f(x)是偶函数,其定义域为R,且在[0,+)∞上是减函数,则f(2a 2+a+1)<f(3a 2-2a+1)的a 的取值集合为________________.5、(),()x g x ϕ都是奇函数,f(x)=()()a x bg x ϕ++2在(0,+∞)上有最大值5,则f(x)在(-∞,0)上有最_______值________.三、解答题:6.设x ,y ,z ∈R +,且3x =4y =6z . (1)求证:yx z 2111=-; (2)比较3x ,4y ,6z的大小.x7、设1221)(+-=x x f (1)求f (x )的值域;(2)证明f (x )为R 上的增函数;一、选择题:1、已知b a ba 、,则2log 2log 0<<的关系是 ( )111010>>>><<<<<<b a D a b C a b B b a A 、、、、 2、函数f(x)=log 31(5-4x-x 2)的单调减区间为 ( )A.(-∞,-2)B.[-2,+∞]C.(-5,-2)D.[-2,1]3、已知)2(log ax y a-=在[0,1]上是x 的减函数,则a 的取值范围是 ( )A.(0,1)B.(1,2)C.(0,2)D.[2,+∞]二、填空题:4.函数()f x 对于任意实数x 满足条件()()12f x f x +=,若()15,f =-则()()5f f =_______.5.函数y=)124(log 221-+x x 的单调递增区间是 .三、解答题:6已知()32log ([1,9])f x x x =+∈,求函数22[()]()y f x f x =+的最大值与最小值。
高二数学下册暑假作业及答案

高二数学下册暑假作业及答案【导语】着眼于眼前,不要沉迷于玩乐,不要沉迷于学习进步没有别*的痛苦中,进步是一个由量变到质变的过程,只有足够的量变才会有质变,沉迷于痛苦不会改变什么。
无忧考网高二频道为你整理了《高二数学下册暑假作业及答案》,希望对你有所帮助!【一】1.(09年重庆高考)直线与圆的位置关系为()A.相切B.相交但直线不过圆心C.直线过圆心D.相离2.方程x2+y2+2ax-by+c=0表示圆心为C(2,2),半径为2的圆,则a、b、c的值依次为()A.2、4、4;B.-2、4、4;C.2、-4、4;D.2、-4、-43(2011年重庆高考)圆心在轴上,半径为1,且过点(1,2)的圆的方程为()A.B.C.D.4.直线3x-4y-4=0被圆(x-3)2+y2=9截得的弦长为()A.B.4C.D.25.M(x0,y0)为圆x2+y2=a2(a>0)内异于圆心的一点,则直线x0x+y0y=a2与该圆的位置关系是()A.相切B.相交C.相离D.相切或相交6、圆关于直线对称的圆的方程是().A.B.C.D.7、两圆x2+y2-4x+6y=0和x2+y2-6x=0的连心线方程为().A.x+y+3=0B.2x-y-5=0C.3x-y-9=0D.4x-3y+7=08.过点的直线中,被截得最长弦所在的直线方程为()A.B.C.D.9.(2011年四川高考)圆的圆心坐标是10.圆和的公共弦所在直线方程为____.11.(2011年天津高考)已知圆的圆心是直线与轴的交点,且圆与直线相切,则圆的方程为.12(2010山东高考)已知圆过点,且圆心在轴的正半轴上,直线被该圆所截得的弦长为,则圆的标准方程为____________ 13.求过点P(6,-4)且被圆截得长为的弦所在的直线方程.14、已知圆C的方程为x2+y2=4.(1)直线l过点P(1,2),且与圆C交于A、B两点,若|AB|=23,求直线l的方程;(2)圆C上一动点M(x0,y0),ON→=(0,y0),若向量OQ→=OM→+ON→,求动点Q的轨迹方程"人"的结构就是相互支撑,"众"人的事业需要每个人的参与。
(新课标)2020年高二数学暑假作业5

新课标2020年高二数学暑假作业5必修5--必修2-3一选择题(本大题共8小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.复数,则在复平面内的点位于第()象限。
A.一 B.二 C.三 D .四2.右表提供了某厂节能降耗技术改造后生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.根据右表提供的数据,求出y关于x的线性回归方程为,那么表中t的值为()A.3 B.3.15 C.3.5 D.4.53.在1万平方公里的海域中有40平方公里的大陆架贮藏着石油,假若在海域中任意一点钻探,那么钻到油层面的概率是()A、 B、 C、D、4.西大附中数学组有实习老师共5名,现将他们分配到高二年级的1、2、3三个班实习,每班至少1名,最多2名,则不同的分配方案有()A.30种 B.90种 C.180种 D.270种5.函数的导函数是()A. B. C. D .6.若函数是R上的单调函数,则实数m的取值范围是( )A、B、C、D、7.曲线(为参数)上的点到原点的最大距离为()A. 1 B. C.2 D.8.过椭圆+=1(0<b<a)中心的直线与椭圆交于A、B两点,右焦点为F2(c,0),则△ABF2的最大面积是()A.ab B.ac C.bc D.b2二.填空题(本大题共4小题,每小题5分,共20分。
把答案填在题中横线上)9.(几何证明选讲选做题)如如图,△是⊙的内接三角形,是⊙的切线,交于点,交⊙于点.若,,,,则_____.10.(不等式选讲选做题)不等式|x2-3x-4|>x+1的解集为________11.函数f(x)=x3+ax(x∈)在x=l处有极值,则曲线y=f(x)在原点处的切线方程是_____12.设抛物线的焦点为F,其准线与x轴的交点为Q,过点F作直线交抛物线C于A、B两点,若,则|AF|—|BF|=三.解答题(本大题共4小题,每小题10分,解答应写出文字说明,证明过程或演算步骤)13.已知关于的方程组有实数,求的值。
高二数学暑假作业5附答案

高二数学暑假作业五一、单选题1.变量x , y 满足约束条件⎪⎩⎪⎨⎧≥≤--≥-+10202y y x y x ,则目标函数3z x y =+的最小值为( )A. 2B. 4C. 5D. 62.已知实数0a >,0b >,11111a b +=++,则2a b +的最小值是()A.B. C. 3 D. 23.已知实数x ,y 满足,,则的最大值与最小值之差为()A.B.C. D. 与的取值有关4.若x ,y 满足⎪⎩⎪⎨⎧≥≤-+≥+-00402y y x y x ,则2z y x =-的最大值为().A. 8-B. 4-C. 1D. 25.如果0a b >>且0a b +>,那么以下不等式正确的个数是 ( )①23a b b <;②110a b>>;③32a ab <;④33a b > A. 1 B. 2 C. 3 D. 4 6.已知满足约束条件,若的最小值为6,则的值为( )A. 2B. 4C. 2和4D. 中的任意值7.已知各项都是正数的等比数列{}n a 中,存在两项()*,,m n a a m n N ∈使得14a =且7652a a a =+,则14m n+的最小值是() A. 32 B. 43 C. 23 D. 348.设0,0a b >>,若2是4a 和2b的等比中项,则21a b+的最小值为()A. B. 4 C. 92D. 59.若关于的不等式的解集是,则关于的不等式的解集是()A.B.C.D.10.设关于,x y 的不等式组⎪⎩⎪⎨⎧>-<+>+-00012m y m x y x 表示的平面区域内存在点()00,P x y ,满足0022x y -=,求得m 的取值范围是()A. 4,3⎛⎫-∞ ⎪⎝⎭ B.1,3⎛⎫-∞ ⎪⎝⎭ C.2,3⎛⎫-∞- ⎪⎝⎭ D.5,3⎛⎫-∞- ⎪⎝⎭11.设a ,b ,c 是互不相等的正数,则下列不等式中不恒成立的是( )A.2a b +≥ B. a 2+21a ≥a +1a C. a -b +1a b -≥2 D .6111>+++++cc b b a a 12.记不等式组⎪⎩⎪⎨⎧≤≤≥-+21022y x y x 的解集为D ,若(),,1x y D y a x ∀∈≤+,则实数a 的最小值是( )A. 0B. 1C. 2D. 4 13.设满足约束条件,则的取值范围为()A.B.C.D.14.若x ,y 满足约束条件⎪⎩⎪⎨⎧≥-+≤-≤-0220102y x y x ,则z x y =-的最大值为()A. 1-B. 2C. 1D. 015.若实数,x y 满足条件⎪⎩⎪⎨⎧≥-≤-≤+1236x y x y x ,则23x y +的最大值为()A. 21B. 17C. 14D. 516.不等式⎪⎪⎩⎪⎪⎨⎧≤+≥-≤ky x x y xy 0212表示的区域面积大于等于32,则实数k 的取值范围为()A. 1k ≥B. 2k ≥C. 3k ≥D. 4k ≥17.不等式102xx-≥+的解集为() A. []2,1- B. (]2,1- C. ()(),21,-∞-⋃+∞ D. (](),21,-∞-⋃+∞18.若满足约束条件,则的最小值是A.B.C.D.19.若,x y 满足约束条件⎪⎩⎪⎨⎧≤-+≥-+≤03044y x y x xy ,则1x y +的取值范围是()A. 5,113⎡⎤⎢⎥⎣⎦B. 13,115⎡⎤⎢⎥⎣⎦C. 3,115⎡⎤⎢⎥⎣⎦D. 15,113⎡⎤⎢⎥⎣⎦20.若实数,满足,且,则的最大值为()A.B. C. 9D.二、填空题21.不等式的解集为__________.22.已知为坐标原点,点的坐标为,点的坐标满足,则的最小值为__________.23.(2015高考新课标I ,理15)若满足约束条件,则的最小值为____________.24.已知正实数满足,则的最小值为____.25.设正项等比数列的前项和为,若,则的最小值为_______.26.在公比为的正项等比数列中,,则当取得最小值时,__________.27.已知函数()24f x x kx =-+对任意的[]1,3x ∈,不等式()0f x ≥恒成立,则实数k 的最大值为________.28.已知a >b >0,给出下列四个不等式:①a 2>b 2;②2a >2b -1④a 3+b 3>2a 2b .其中一定成立的不等式序号为________.三、解答题29.电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连已知电视台每周安排的甲、乙连续剧的总播放时间不多于600分钟,广告的总播放时间不少于30分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍.分别用,表示每周计划播出的甲、乙两套连续剧的次数.(I )用,列出满足题目条件的数学关系式,并画出相应的平面区域;(II )问电视台每周播出甲、乙两套连续剧各多少次,才能使收视人次最多?30.已知函数()194f x x x=++(0x >). (1)求()f x 的最小值,并指出此时x 的值;(2)求不等式()2151f x x x x≥++-的解集.31.已知在中,,,分别为角,,所对的边长,且.(1)求角的值; (2)若,求的取值范围. 32.(本小题满分12分)已知直线过点(1,2)且在x ,y 轴上的截距相等 (1)求直线的一般方程; (2)若直线在x ,y 轴上的截距不为0,点(),P a b 在直线上,求33a b+的最小值.高二数学暑假作业五参考答案1.B【解析】作出可行域如图:由得:,作直线:,当直线平移到过A点时,有最小值,由解得,所以,故选B.2.B【解析】∵,,∴当且仅当,即,时取等号.故选B点睛:本题主要考查了不等式,不等式求最值问题,属于中档题。
全新暑假作业:高中高二数学暑假作业答案.doc

全新暑假作业:高中高二数学暑假作业答案为大家整理的2014年全新暑假作业:高中高二数学暑假作业答案文章,供大家学习参考!更多最新信息请点击高二考试网、选择题:(本大题共10小题,每小题4分,共40分)题号1 2 3 4 5 6 7 8 9 10答案B D A A D B D B C D二、填空题(本大题共5小题,每小题4分,共20分,把答案填在相应横线上.)11. 12. 180 13. 14. 为参数) 15. 480三、解答题(本大题共5小题,共44分.解答应写出文字说明、证明过程或演算步骤.)16.(本小题满分6分)解:(Ⅰ)直线的方程可化为,即化为直角坐标方程为,将点代人上式满足,故点在直线上. …………………2分(Ⅱ)直线的参数方程为为参数),…………………3分曲线的直角坐标方程为,将直线的参数方程代人曲线的方程并整理得,所以…………………………6分17. (本小题满分8分)解:(Ⅰ)当时,当时,可化为,解得;当时,可化为,解得.综上可得,原不等式的解集为…………………………4分(Ⅱ) ………………6分函数有最小值的充要条件为即………………8分18. (本大题满分8分)解:(1)设选手甲答对一个问题的正确率为,则故选手甲回答一个问题的正确率……………2分(2)选手甲答了4道题进入决赛的概率为; ………………3分选手甲答了5道题进入决赛的概率为; ……………5分选手甲答了6道题进入决赛的概率为; …… …7分故选手甲可进入决赛的概率………… …8分19.(本小题满分8分)解(Ⅰ)男生女生合计收看10 6 16不收看6 8 14合计16 14 30由已知数据得:所以,没有充足的理由认为“通过电视收看世界杯”与性别有关. …………4分(Ⅱ) 的可能取值为,……6分所以的分布列为:0 1 2的均值为: …………………………8分20. ,因为.所以切线方程是……………3分(Ⅱ)函数的定义域是当时,令得…………………………5分①当,所以在上的最小值是,满足条件,于是;②当,即时,在上的最小值是,不合题意;③当,即时,在上单调递减,所以在上的最小值是,不合题意.综上所述有,. …………………………………10分。
2020年高二数学 Happy暑假,我的作业君(无答案)文 苏教版

第1天 集合与逻辑用语1.集合中元素与集合的关系: ;集合中元素的三个特性: 、 、常见集合的表示符号: 集合的表示方法: 、 、 2. 是任意集合的子集、φ是任意 的真子集 3.“p∨q”、“p∧q”、 “┓p”真值表4.命题“,()x M p x ∀∈”的否定是命题“,()x M p x ∃∈”的否定是命题“p∨q”的否定是 命题“p∧q”的否定是 5.如果p ⇒q ,p 是q 的 条件,q 是p 的如果p ⇒q ,q ⇒p ,p 是q 的 条件,记作 p ⇒q 与其逆否命题 等价。
1.已知集合}1,0,1,2{--=A ,集合{}R x x x B ∈≤-=,012,则=B A I _______.2.若集合M 满足M ≠⊂}2,1{,则这样的集合M 有____________个.3.集合{}{}0,||,1,0,1A x B ==-,若A B ⊆,则A B =I ;A B =U ;B C A = .4.已知全集R U =,集合{11}A x x =-≤≤,2{20}B x x x =-≥,则A B =I ;U A C B =U .5.已知集合{}P x x a =≤,{}sin ,Q y y R θθ==∈.若P Q ⊇,则实数a 的取值范围是 .6.设集合*{1,2,3,,}()M n n N =∈L ,对M 的任意非空子集A ,定义()f A A 为中的最大元素,当A 取遍M 的所有非空子集时,对应的()f A 的和为n S ,则①3S = ;②n S = 。
7.设S 为复数集C 的非空子集.若对任意x,y S ∈,都有x y,x y,xy S +-∈,则称S 为封闭集。
下列命题:①集合{},S a bi a b i =+为整数为虚数单位,为封闭集; ②封闭集一定是无限集;③若S 为封闭集,则一定有0S ∈;④若S 为封闭集,则满足S T C ⊆⊆的任意集合T 也是封闭集. 其中真命题是 (写出所有真命题的序号) 8.命题],,0[:π∈∃x p 使a x x <+cos 23sin 23;命题:(0,)q x ∀∈+∞,21ax x <+.若命题q p ∧为真,则实数a 的取值范围为_____.9.命题“0R x ∃∈,032020=-+x x ”的否定形式为 ;10.“0<c ”是“实系数一元二次方程02=++c x x 有两异号实根”的 条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
省深圳市2018年高二数学 暑假作业(5)
一、选择题:
1、 下列函数中,在区间()
0,+∞不是增函数的是
( )
A. x y 2=
B. x y lg =
C. 3x y =
D.
1y x
=
2、函数y =(a 21)x
在(∞,∞)上是减函数,则a 的取值范围是 ( )
A.|a |>1
B.|a |>2
C.a>
2
D.1<|a |<2
3、图中曲线分别表示l g a y o x =,l g b
y o x =,
l g c y o x =,
l g d y o x =的图象,,,,a b c d 的关系是 (
)
A 、0<a<b<1<d<c
B 、0<b<a<1<c<d
C 、0<d<c<1<a<b
D 、0<c<d<1<a<b
二、填空题:
4、若f(x)是偶函数,其定义域为R,且在[0,+)∞上是减函数,则f(2a 2a1)<f(3a 2
-2a1)的a 的取值集合为________________.
5、(),()x g x ϕ都是奇函数,f(x)=()()a x bg x ϕ+2在(0,∞)上有最大值5,则f(x)在(∞,0)上有最_______值________. 三、解答题:
6.设x ,y ,z ∈R ,且3x =4y =6z . (1)求证:y
x z 2111
=- (2)比较3x ,4y ,6z 的大小.
x
7、设
1
221)(+-=x
x f (1)求f (x )的值域;(2)证明f (x )为R 上的增函数;
一、选择题: 1
、
已
知
b
a b a 、,则2log 2log 0<<的关系是
( )
11
101
0>>>><<<<<<b a D a b C a b B b a A 、、、、
2、函数f(x)=log 3
1(54xx 2
)的单调减区间为 ( )
A.(∞,2)
B.[2,∞]
C.(5,2)
D.[2,1]
3、已知)2(log ax y a
-=在[0,1]上是x 的减函数,则a 的取值范围是 ( )
A.(0,1)
B.(1,2)
C.(0,2)
D.[2,∞] 二、填空题: 4.函数
()
f x 对于任意实数x 满足条件
()()
1
2f x f x +=
,若
()15,
f =-则
()()5f f =
_______.
5.函数y=
)
124(log 2
2
1-+x x 的单调递增区间是 .
三、解答题: 6已知()32log ([1,9])
f x x x =+∈,求函数22[()]()y f x f x =+的最大值与最小值。
7.设函数
)
1lg()(2++=x x x f .(1)判断函数f (x )的奇偶性;(2)证明函数f (x )在其
定义域上是单调增函数。
