20距离保护的整定计算实例
保护整定计算需注意的问题及案例分析

一、整定计算工作的基本概念及案例分析1、在进行继电保护定值计算中为什么要进行逐级配合,怎么样才算达到了逐级配合。
在进行继电保护定值计算要进行逐级配合主要就是满足保护的选择性要求,也就是说,计算的定值一定要满足在系统发生故障时有选择地切除故障,确保保护范围内故障可靠动作,保护范围外故障可靠不动作。
这就要求在计算保护定值时,一定要做到保护动作值(保护范围)与保护动作时间同时满足逐级配合才能保证选择性要求。
这一点对发电厂搞整定计算的人来说,一定要注意发变组和发电厂变压器的后备保护与电网保护定值的配合。
2006年韩城一厂#3变发生接地故障,韩城二厂#1、2号主变高压侧零序过流保护误动作就是一个典型事例。
系统上这样的事例也有。
110KV线路Ⅱ(未装设快速保护)末端发生接地故障,线路Ⅰ开关A的零序保护Ⅱ段动作跳闸。
2、在进行继电保护定值计算中为什么要进行灵敏度计算。
在进行继电保护定值计算中计算灵敏度,实际上就是计算保护范围,就是说在规定的保护范围发生故障后该保护要可靠启动,也就是通常所说的保护“四性”中的灵敏性。
要做到满足保护灵敏性,在整定计算中首先要搞清要计算的元件定值的保护功能是什么,例如在计算启动元件时一定要搞清是快速保护的启动元件,还是后备保护的启动元件,还是整个装置的启动元件,它们的保护范围在哪里,什么地方发生故障它们才能启动。
在计算保护动作值时,一定要搞清保护的对象,该保护保护范围是保护一个设备的一部分还是全部,对于后备保护来说还要搞清该保护保护范围是近后备还是远后备等等。
在搞清每一个要计算的保护元件的范围之后,认真按保护整定计算规程要求的各种灵敏度的具体数值进行计算。
在整定计算中,一定要注意按规程的要求校核保护灵敏度,也就是校核保护范围,当计算出的定值满足规程要求的灵敏度时,在保护范围内发生故障该时保护一定能够启动;当计算出的定值不满足规程要求的灵敏度时,在保护范围内发生故障时该保护有可能不能启动,保护装置就会拒动,造成的后果轻则扩大停电范围,严重的会造成设备烧毁甚至电网瓦解。
距离保护整定计算例题
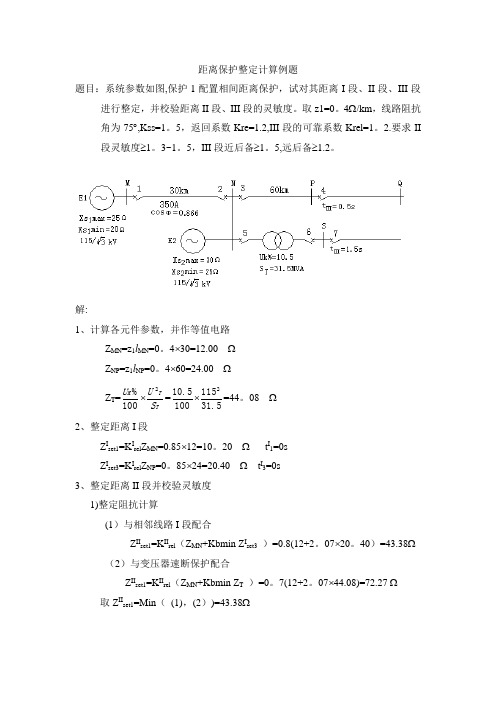
距离保护整定计算例题题目:系统参数如图,保护1配置相间距离保护,试对其距离I 段、II 段、III 段进行整定,并校验距离II 段、III 段的灵敏度。
取z1=0。
4Ω/km ,线路阻抗角为75︒,Kss=1。
5,返回系数Kre=1.2,III 段的可靠系数Krel=1。
2.要求II 段灵敏度≥1。
3~1。
5,III 段近后备≥1。
5,远后备≥1.2。
解:1、计算各元件参数,并作等值电路Z MN =z 1l MN =0。
4⨯30=12.00 Ω Z NP =z 1l NP =0。
4⨯60=24.00 ΩZ T =100%K U ⨯T T S U 2=1005.10⨯5.311152=44。
08 Ω2、整定距离I 段Z I set1=K I rel Z MN =0.85⨯12=10。
20 Ω t I 1=0s Z I set3=K I rel Z NP =0。
85⨯24=20.40 Ω t I 3=0s 3、整定距离II 段并校验灵敏度 1)整定阻抗计算(1)与相邻线路I 段配合Z II set1=K II rel (Z MN +Kbmin Z I set3 )=0.8(12+2。
07⨯20。
40)=43.38Ω (2)与变压器速断保护配合Z II set1=K II rel (Z MN +Kbmin Z T )=0。
7(12+2。
07⨯44.08)=72.27 Ω 取Z II set1=Min ( (1),(2))=43.38Ω2)灵敏度校验K II sen =MNset II Z Z 1=43。
38/12=3。
62 (>1。
5),满足规程要求 3)时限 t II 1=0。
5s 4、整定距离III 段并校验灵敏度 1)最小负荷阻抗 Z Lmin Z Lmin =Lman L I U min =LmanN I U 9.0=35.03/1109.0⨯=163。
31 ΩCos ϕL =0。
866, ϕL=30︒ 2)负荷阻抗角方向的动作阻抗Z act (30︒) Z act (30︒)=re ss rel L K K K Z min =2.15.12.131.163⨯⨯=75。
07-第七部分 输电线路相间的距离保护整定计算

I I Z op K .1 res Z AB
式中
I Z op .1
I K rel
0.8 ~ 0.85 ;
Z AB
图7-1 距离保护整定计算系统图 若被保护对象为线路变压器组,则送电侧线路距离保护第Ⅰ段可 按保护范围伸入变压器内部整定,即 (7-2) Z I K I Z K Z
2.与相邻距离保护第Ⅱ段配合 为了缩短保护切除故障时间,可与相邻线路相间距离保护第Ⅱ段 配合,则 III III II (7-10)
Kb. min Z op.2 Z op.1 K rel Z AB K rel
12
式中 K IIi ——距离保护第Ⅲ段可靠系数,取 0.8 ~ 0.85 ; rel
相间距离保护第Ⅱ段的灵敏度按下式校验
K
II sen
Z
II op .1
Z AB
≥
1 . 3 ~ 1 .5
当灵敏度不满足要求时,可与相邻线路相间距离第Ⅱ段配合,其 动作阻抗为 (7-5) II II II op.1 rel AB rel b. min op.2
Z
K Z
K K
Z
8
式中
——可靠系数,取 K rel
II Z op .2
≤ K rel
0 .8 ;
——相邻线路相间距离保护第Ⅱ段的整定值。
13
当距离保护第Ⅲ段的动作范围未伸出相邻变压器的另一侧时, 应与相邻线路不经振荡闭锁的距离保护第Ⅱ段的动作时间配 合,即
III t op.1 II t op.2
5
式中
II K rel
——距离保护第Ⅰ段可靠系数,取 0.8 ~ 0.85 ;
距离保护整定计算

对于方向阻抗继电器
Z’’’set
Z’’’op.r
Z .min
L
FL fk
当采用方向阻抗继电器作为测量元件时, 整定阻抗为:
Z
III set 1
K
III rel
1 Z L . min . K st .Kre cos(f k -f L)
因此,采用方向阻抗继电器时,保护的
灵敏度比采用全阻抗继电器时可提高:
+
III K b. min Z op.2
)
若相邻元件为变压器,应与变压器相间 短路后备保护配合,其动作阻抗为:
III Z op.1
III K rel (ZAB
+
III K b. min Z op. T
)
Z
III op . T
—— 变压器相间短路后备保护最小保护 范围所对应的阻抗值。
1、网络参数如图示,已知:系统等值阻抗
路阻抗角相同
I rel ——距离保护第1段的可靠系数,取0.8一0.85 rel ——伸入变压器部分第1段的可靠系数,取0.75;
距离保护第I段的动作时间仍为:
t’=0s
2、相间距离保护第Ⅱ段的整定
相间距离Ⅱ段应与相邻线路相间距离第Ⅰ段 或与 相邻元件速动保护配合,以保护本线路全长。
(1)、与相邻线路第Ⅰ段 配合。
保护区为被保护线路全长的80%~85%。
(2)若被保护线路末端仅有一台变压器,可看成线 路变压器组,按躲变压器各侧母线短路来整定。
动作阻抗为: Z I
op.1
ZT K Z L + K rel
I rel
K K ZL ——被保护线路的正序阻抗; ——线路末端变压器的阻抗,且假定阻抗角与线 ZT
湖北电网220kV线路距离保护整定计算优化

S t n l u ai n Op i z t n o sa c r c e t nf r2 0 k e t gCac l t t i o miai f o Dit n eP o t c i 2 V o o L n so b i o rGrd i e f Hu e we i P
鉴 于零 序 电流保 护存 在受 运行 方 式 影响 大 、 整 定复 杂等不适 应复杂 电 网的缺点 .从 2 0 0 5年开 始 , 湖北 电 网将零 序保 护作 了较 大 的简化 :停 用零序 电 流保 护 I、 Ⅱ段 , 零 序 电流保 护 Ⅲ、 将 Ⅳ段 固定 整 定 为 5 0 /. s3 0 /.s 其功 能仅 限 于反 应概 率 极 0 A4 .0 A45 . 0 低 的轻 微故障 和切除系统 高电阻接地 故障 。 至此 . 接 地故 障后备 保护 的功能基 本交给 接地距 离保护来 完 成 。作 为分 别独立 反应接地 故 障和相 间故障 的接 地 距 离保护 和相间距 离保 护 , 在主保 护拒 动时 , 其必 须 能快速 可靠 切除故 障 .这 又对距 离保护 配合定值 的 可靠性 、 速动性 和选 择性提 出了更高 的要求 。 1 . 距离 保护 整定 现状 3 长期 以来 . 湖北 电网相间距离和接地距离保 护的 整定计算严格按照逐级 配合 的原则 考虑。 随着湖北 电
收 稿 日期 :0 6 0 —1 20 — 3 4 作者简介 : 余
2 优 化 原 则
综合 考 虑前 述情况 . 离 保护 整定 计算 一 方 面 距
要做 到合 理发 挥 其各段 保 护效 力 . 而实现 距 离保 从 护 的最优 保护 效果 . 一方 面 可对 其计 算作 适 当 的 另 简化 . 高计 算效 率 。 提
继电保护技术培训(距离保护)

距离保护整定计算
二、相间距离保护的整定计算公式
2.3 距离Ⅲ段:
III Z set .1
Z ld . min Ⅲ K rel K re K ss
Z ld . min
0.9U e. x I fh. max
可靠系数Krel取1.2~1.3;返回系数Kre取1.15~1.25;自启动系数Kss取1.1~1.7。
A、助增分支(保护安装处至故障点sN Kb Z sN
四川能投集团继保培训
距离保护整定计算
二、相间距离保护的整定计算公式 分支系数的计算:
B、汲出分支(保护安装处至故障点有负荷引出,保护测量阻抗将减小)
汲出系数是小于1的数值
Kb
1 Z dz Z fhmin K h K zq cos( d fh ) Kk U fhmin I fhmax 0.9 110 3 I fhmax 0.9 110 3 0.35 163.5
带方向闭锁的距离保护
Z fh. min
系数取值: 1.2, K h Kk
II II I Z op .1 K rel Z AB K rel Kb. min Z op.2
Z A 1 I f .m n 2 M 3 k0 m 1 / E1 1 3k 5 V N
6 k0 m
6 k0 m
0.5s t8
6
7 10
8
9
t1 0.5s V A0
总分支系数
Kb.min Kb助Kb汲 2.52 0.575 1.35
四川能投集团继保培训
距离保护整定计算
二、相间距离保护的整定计算公式
2.2 距离Ⅱ段:
② 与相邻元件的速动保护配合:
距离保护第7讲:距离保护的整定及基本构成

3.5.1 距离保护的延时特性
➢距离保护一般采用阶段式配合的思想,配合关系类似于 三段式电流保护
3.5.2 距离保护的整定计算
➢ 距离保护需要配置相间距离 和接地距离
➢ 距离Ⅰ段、距离Ⅱ段一般采 用具有方向性的动作特性
➢ 距离Ⅲ段通常采用带有偏移 特性的动作特性
与本保护相配合的下游相邻元件保护段 (x 为Ⅰ 段或Ⅱ 段)的 最大动作延时
3.5.2 距离保护的整定计算 距离Ⅲ段整定
作用 本线路的近后备或下级线路的远后备
整定原则 CASE1:相邻线路配合段为距离Ⅱ段或距离Ⅲ段时
CASE2:相邻元件配置电流、电压保护时的配合
为相邻线电流、电压保护的最小保护范围对应的阻抗 值
如何保证Ⅱ段在任何运行方 式下选择性?
3.5.2 距离保护的整定计算
距离Ⅱ段整定
整定处理思想 距离Ⅱ段整定时应考虑灵敏系数最大的情况,即保护范围最 大时其动作范围不超过相邻线配合段保护范围。该种运行方 式对应于分支系数最小的情况。
3.5.2 距离保护的整定计算
距离Ⅱ段整定
整定方法 •CASE1:相邻元件为输电线路
在发电机和变压器保护中作为后备保护
3.12 距离保护的基本构成与工作流程
3.12.1 距离保护的构成
(一)微机保护的硬件构成
距离保护模拟量输入:三相电流加零序电流、 三相电压加零序电压、 断路 器另一侧单相电压共9路电量
3.12.1 距离保护的构成
(二)软件构成
1. 故障启动元件 2. 距离测量元件 3. 故障选相元件 4. 振荡闭锁元件 5. 故障处理逻辑 6. PT断线闭锁元件 7. 整组复归逻辑
•CASE2:相邻元件为变压器
继电保护定值整定计算公式大全

继电保护定值整定计算公式大全一、过电流保护的定值整定计算公式:1.零序过电流保护定值计算公式:IHON=IMS×(KA-1)÷{(RSTRE)÷3×Z3{(X´t)·{X´´{X´´´其中,IHON为零序过电流保护的运行电流定值;IMS为测量系统的基本电流选定定制;KA为零序过电流保护动作系数;RSTRE为设备额定短路阻抗;Z1为设备正序电抗;X1为设备正序电抗;X2为设备负序电抗;X3为设备零序电抗。
2.短路过电流保护的整定公式:I熔=IHc+(XlC×R)÷ZI_C×IΝ÷IP素分式其中,I熔为短路过电流保护的整定电流;IΙ2c为设备二次侧短路故障电流;XlC为电流互感器的互感系数;R为电流互感器的内阻;ZlC为电流互感器的线路阻抗;IN为变压器的额定电流;IP为变压器的额定功率。
二、跳闸保护的定值整定计算公式:1.距离保护的整定公式:SETR#1=CTK×SET×けtcoef÷Z其中,SETR#1为距离保护的整定系数;CTK为电流互感器的互感系数;SET为线路的距离设置;け为绕组当前日期;Z为线路的阻抗。
2.差动保护的整定公式:SETD#1=K1×SET其中,SETD#1为差动保护的整定系数;K1为变压器的变比。
三、频率保护的定值整定计算公式:1.频率保护的整定公式:Set(f)=a-b×f其中,Set为频率保护的整定值;a为整定值的常数;b为整定值的斜率;f为频率。
四、电压保护的定值整定计算公式:1.过电压保护的整定公式:U总=U设定×(KA-1)×(R2IMS)÷3其中,U总为过电压保护的整定电压;U设定为过电压保护的动作电压设定值;KA为过电压保护的动作系数;RIMS为测量系统的基本电流选定定制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例3-1 在图3—48所示网络中,各线路均装有距离保护,试对其中保护1的相间短路保护Ⅰ、Ⅱ、Ⅲ段进行整定计算。
已知线路AB的最大负荷电流350
max
L
=
⋅
I A,功率因数9.0
cos=
ϕ,各线路每公里阻抗Ω
=4.0
1
Z/km,阻抗角
70
k
=
ϕ,电动机
的自起动系数1
ss
=
K,正常时母线最低工作电压
min
MA⋅
U取等于110
(
9.0N
N
=
U
U kV)。
图3—48 网络接线图
解: 1.有关各元件阻抗值的计算
AB 线路的正序阻抗Ω
=
⨯
=
=12
30
4.0
L
1AB
AB
Z
Z
BC 线路的正序阻抗Ω
=
⨯
=
=24
60
4.0
L
1BC
BC
Z
Z
变压器的等值阻抗Ω
=
⨯
=
⋅
=1.
44
5.
31
115
100
5.
10
100
%2
T
2
T
k
T S
U
U
Z
2.距离Ⅰ段的整定
(1)动作阻抗:Ω
=
⨯
=
=2.
10
12
85
.0
rel
1.AB
op
Z
K
ZⅠ
Ⅰ
(2)动作时间:0
1
=
Ⅰ
t s
3.距离Ⅱ段
(1)动作阻抗:按下列两个条件选择。
1)与相邻线路BC的保护3(或保护5)的Ⅰ段配合
)
(
min
b
rel
rel
1.
op BC
AB
Z
K
K
Z
K
Z
⋅
+
=Ⅰ
Ⅱ
Ⅱ
式中,取8.0,85.0rel rel ==ⅡⅠK K , min b ⋅K 为保护3的Ⅰ段末端发生短路时对保护
1而言的
图3-49 整定距离Ⅱ段时求min .jz K 的等值电路
最小分支系数,如图3-49所示,当保护3的Ⅰ段末端1d 点短路时, 分支系数计算式为
215.112)15.01(B A B B A 12b ⨯⎪⎪⎭
⎫ ⎝⎛++=+⨯++==X Z X Z Z X X Z X I I K AB BC BC AB 为了得出最小的分支系数min b ⋅K ,上式中A X 应取可能最小值,即A X 最小,而B X 应取最大可能值,而相邻双回线路应投入,因而
19.12
15.11301220min .b =⋅⎪⎭⎫ ⎝⎛++=K 于是
Ω=⨯⨯+=''02.29)2485.019.112(8.01.dz
Z 2)按躲开相邻变压器低压侧出口2d 点短路整定(在此认为变压器装有可保护变压器全部的差动保护,此原则为与该快速差动保护相配合),
)(T min .b rel 1.op Z K Z K Z AB ⋅+=ⅡⅡ
此处分支系数min b ⋅K 为在相邻变压器出口2k 点短路时对保护1的最小分支系数,由图3-53可见
Ω
=⨯+==++=++==⋅3.72)1.4407.212(7.007.2130122011.op max .B min .A 13min b Ⅱ
Z X Z X I I K AB
此处取7.0rel =ⅡK 。
取以上两个计算值中较小者为Ⅱ段动作值,即取Ω=02.29op ⅡZ
(2)动作时间,与相邻保护3的Ⅰ段配合则
它能同时满足与相邻保护以及与相邻变压器保护配合的要求。
(3)灵敏性校验: 5.142.212
02.291.op sen >===
AB Z Z K Ⅱ ,满足要求. 4.距离Ⅲ段 (1) 动作阻抗:按躲开最小负荷阻抗整定。
因为继电器取为 0接线的方向阻抗继电器,所以有
Ω=⨯⨯=⋅⨯==-=⋅⋅⋅⋅5.16335.031109.031109.0)
cos(max L max A min A min .L L k ss re rel min
L 1.op I I U Z K K K Z Z ϕϕⅢⅢ
取 8.259.0cos ,70,1,15.1,2.11L sen k ss re rel =======-ϕϕϕK K K Ⅲ。
于是
Ω=-⨯⨯⨯=3.165)
8.2570cos(115.12.15.1631.op ⅢZ (2)动作时间 :t t t t t t ∆+=∆+=2310181
ⅢⅢⅢⅢ或 取其中较长者 0.25.035.01=⨯+=Ⅲt s
(3)灵敏性校验
1)本线路末端短路时的灵敏系数
s
t t t 5.031=∆+=Ⅰ
Ⅱ
5.178.1312
3.1651.op sen >===⋅AB Z Z K Ⅲ近,满足要求。
2)相邻元件末端短路时的灵敏系数
①相邻线路末端短路时的灵敏系数为
BC
AB Z K Z Z K max b op.1sen ⋅⋅+=Ⅱ远 式中,max b ⋅K 为相邻线路BC 末端3d 点短路时对保护1而言的最大分支系数,其计算等值电路如图3-50所示。
A X 取可能的最大值max A ⋅X ,B X 取可能的最小值min B ⋅X ,而
相邻平行线取单回线运行,则
48.225
251225min B min B max A 12max b =++=++==⋅⋅⋅⋅X X Z X I I K AB 于是 2.131.22448.2123.165sen >=⨯+=
⋅远K ,满足要求。
②相邻变压器低压侧出口的的d 2短路时的灵敏系数中,最大分支系数为 48.225
251225min B min B max A 13max b =++=++==⋅⋅⋅⋅Z Z Z Z I I K AB
于是 2.136.11
.4448.2123.165max b 1.set sen >=⨯+=+=⋅⋅B AB Z K Z Z K Ⅲ远 ,满足要求。
1如图电网,已知保护1采用限时电流速断保护,保护2采用电流速断保护,且Z DZ2=0.8Z BC ;试计算保护1整定计算所用的最小分支系数K fzmin 和最大分支系数K fzmax 。
答:K fzmin =1.2*14/(14+14)=0.6 K fzmax =1
2. 如图电网,已知保护1采用限时电流速断保护和定时限过电流保护,保护2采用电流速断保护,且Z DZ2=0.8Z BC ;试计算保护1整定计算所用的最小分支系数K fzmin 和最大分支系数K fzmax 。
答:Kfzmin =(1.2x18)/(18+18)=0.6 Kfzmax=1。
