工字型梁支座反力计算

合集下载

DJ40150安全系数及支座反力计算

DJ40150支座反力及安全系数计算1、悬臂工况：）P1—0#柱重；P1=2.1tP2 —1#柱及曲梁重量P2=13tP3—吊梁行车重量P3=7.4P4—2#柱及吊梁行车重量P4=15tP5—3#柱重量P5=2.5t2）倾覆力矩：M倾M倾= =689tm平衡力矩：当R B=0时M平==945tm稳定系数：n=M平/M倾=945/689=1.37＞1.3支座反力：R A1= 94.5tR B1= 11.5t2、架梁工况移动荷载P、固定荷载、均布荷载q作用机臂《机械设计手册》（化工版）P1362.1固定荷载作用：支座反力：R B= =44.6tR A= =46.6t各部弯矩：M B= -71.8tmM AB=130.2tm2.2移动荷载：[工况1] 1号吊梁行车于尾段起吊梁体1）移动荷载Q=8+(75+1)*1.05=88.2t 2）支座弯距M B/= -336.4tm3）支座反力：R B/=139t[工况2] 1号吊梁行车行至跨中时1）移动荷载Q=88.2t2）跨中弯距M AB/= 1067.4tm3）支座反力：R B//=88.7tR A//= 90.7 t3.机臂截面：选安全系数1.6 [σ]=210机臂抗弯模量W=1067.4*104/210=50828.6cm3机臂截面高h=1700mm端面惯性距I=W*85=4320428cm4端面实际惯性距I=4581215cm44.刚度计算4.1简支工况集中荷载：挠度f=PL3/48EI=16.75cm均布荷载：挠度f=5qL4/384EI=5.2cm4.2悬臂工况集中荷载：挠度f=PL3/3EI=7.3cm均布荷载：挠度f=q2L4/8EI-（q2-q1）*15*（12*35.52*43-4*35.53+7.5*152）/24EI=35.6cm。

梁的支座反力

梁的支座反力当外力作用于梁的构件时，支座起着重要的作用。

支座反力指的是支座对梁施加的力和力矩，可以在静力学的基础上进行计算。

本文将介绍梁的支座反力的计算方法及其在工程中的应用。

支座反力的计算方法通常基于平衡条件，即总力和总力矩为零。

考虑一个简单的梁系统，包括两个支座和一个外力作用点。

根据平衡条件，可以得到以下方程：ΣFx = 0 (1)ΣFy = 0 (2)ΣM = 0 (3)其中，ΣFx和ΣFy分别表示力在x和y方向上的合力，ΣM表示力矩的总和。

首先，我们可以利用方程(1)计算支座的水平反力。

如果梁系统处于静力平衡状态，那么支座的水平反力大小应该等于外力在x方向上的合力。

如果外力作用点与支座垂直线对称，那么水平反力应该为零。

接下来，我们可以利用方程(2)计算支座的垂直反力。

根据静力学的原理，垂直反力应该等于外力在y方向上的合力。

如果外力作用点在梁的中央，那么垂直反力应该等于外力的大小。

然而，在实际工程中，外力作用点往往不在梁的中央，这就需要利用方程(3)计算支座的力矩。

力矩是力在一个点产生的旋转效果，通过乘以距离，可以得到力矩的大小。

根据方程(3)，支座的力矩应该等于外力的力矩之和。

假设外力在支点A的力矩为MA，在支点B的力矩为MB，支座的力矩应该满足以下条件：ΣMA = ΣMB (4)通过方程(4)，我们可以计算出支座的力矩大小。

根据静力学的原理，力矩的大小等于力的大小乘以力臂的长度。

在这种情况下，力臂的长度等于外力作用点到支点的距离。

除了计算支座反力的基本原理之外，还存在一些特殊情况需要注意。

例如，在悬臂梁系统中，外力只作用于梁的一侧，而另一侧没有支座。

在这种情况下，支座反力的计算方法与之前所述的方法略有不同。

针对不同的情况，可以使用不同的计算方法来解决。

在实际工程中，支座反力的计算是非常重要的。

它可以帮助工程师确定支座的尺寸和强度，从而确保梁系统的稳定性和安全性。

此外，支座反力也可以用于计算梁系统的应力和变形，在结构设计和分析中起着关键作用。

————计算简单梁在集中荷载作用下的支座反力

————计算简单梁在集中荷载作用下的支座反力
计算简单梁在集中荷载作用下的支座反力涉及到静力学的基本原理和
公式。

在进行计算之前，需要知道梁的长度、受力情况、梁的材料性质等
信息。

以下是计算简单梁在集中荷载作用下的支座反力的详细步骤：
1.确定梁的受力情况：
-集中荷载作用在梁上的位置及大小。

假设集中荷载作用在梁上的位
置为离左端距离为a处，大小为F。

集中荷载的作用点可以位于梁上任意
位置。

-梁上的两个支座。

假设支座分别位于梁的左端和右端。

左端支座的
反力为R1，右端支座的反力为R2
2.建立平衡方程：
<-F->
-------------------------------------
AxB
-------------------------------------
R1R2
-沿横向施加平衡方程：ΣFx=0，根据静力学的基本原理，F=R1+R2
-沿纵向施加平衡方程：ΣFy=0，在x处，梁受到横向力F和竖向力
R1，所以ΣFy=0可以得到R1=F。

即左端支座的反力等于集中荷载的大小。

3.计算右端支座反力R2：
-将R1=F带入到横向平衡方程F=R1+R2，可得R2=0。

即右端支座反力为零。

4.最终结果：
-左端支座反力R1=F。

即集中荷载的大小。

总结：
简单梁在集中荷载作用下的支座反力的计算可以通过平衡方程和静力学的基本原理进行求解。

通过确定梁的受力情况，建立平衡方程并代入已知条件，可以计算出支座反力的大小。

计算简单梁在集中荷载作用下的支座反力

计算简单梁在集中荷载作用下的支座反力简单梁是钢筋混凝土或木材等材料制成的梁，由于其结构简单，计算支座反力相对较容易。

下面将从支座反力计算的原理、步骤和示例三个方面进行详细介绍。

一、原理：支座反力是指梁在集中荷载或均布荷载作用下，支座所产生的反力。

根据平衡原理，支座反力需要满足力的平衡条件。

在计算支座反力时，一般根据受力分析和力矩平衡来进行计算。

二、步骤：1.绘制受力图：首先，根据荷载的作用位置，绘制受力图。

在计算支座反力时，需要将受力图中的荷载分解为水平力和竖直力。

2.分析受力：根据受力图进行受力分析。

根据力的平衡条件，竖直方向的合力应该等于零，即ΣFy=0；水平方向的合力也应该等于零，即ΣFx=0。

通过受力分析，可以得到支座反力的表达式。

3.力矩平衡：根据力矩平衡条件，ΣM=0，可以得到受力杆件端点的支座反力。

力矩平衡需要选择合适的参考点，计算出每个力臂的力矩。

4.计算支座反力：根据受力分析和力矩平衡，可以计算出支座反力。

支座反力分为竖直方向的支座反力和水平方向的支座反力，根据力的平衡条件进行计算。

三、示例：假设有一个长度为4m的简单梁，两端由两个支座支撑。

在该梁上，有一个集中荷载作用，大小为10kN，作用位置距离距离梁左端1m。

1.受力图：绘制受力图，将荷载分解为水平力和竖直力。

竖直方向的力为10kN，水平方向的力为零。

2.分析受力：根据力的平衡条件，竖直方向的力的合力应该等于零，即ΣFy=0。

因此，左端支座的竖直反力为10kN，右端支座的竖直反力也为10kN。

3.力矩平衡：选择支点A为参考点，在该参考点处计算力矩。

由于水平方向的力为零，因此，对于竖直反力来说，力臂为0，力矩也为0。

4.计算支座反力：根据受力分析和力矩平衡，可知左端支座的竖直反力为10kN，右端支座的竖直反力也为10kN。

水平方向的支座反力为零。

综上所述，该简单梁在集中荷载作用下的支座反力为：左端支座的竖直反力为10kN，右端支座的竖直反力也为10kN，水平方向的支座反力为零。

梁的支座反力计算公式

梁的支座反力计算公式梁在建筑结构和工程力学中可是个重要的角色，而要搞清楚梁的受力情况，支座反力的计算那是必不可少的。

咱们先来说说啥是梁的支座反力。

简单来讲，梁放在一些支撑点上，这些支撑点对梁施加的力就叫支座反力。

想象一下，一根长长的木板放在几个石头上，石头给木板的力就是支座反力啦。

那支座反力咋算呢？这就得用到一些公式和方法。

常见的有静定梁的计算方法，像简支梁、悬臂梁、外伸梁等等。

就拿简支梁来说吧，假如有一个均布荷载作用在梁上。

有一次我在工地上看到一根钢梁，就像这样的简支梁，上面放着一堆均匀分布的建筑材料。

当时我就好奇这梁的支座反力到底是多少。

经过一番计算，发现如果均布荷载的大小是 q ，梁的长度是 L ，那么支座反力就分别是 RA = RB = qL / 2 。

这里的 RA 和 RB 分别是两个支座的反力。

再比如说悬臂梁，一端固定，另一端自由。

如果在自由端有一个集中力 P 作用，那固定端的支座反力就比较简单啦，竖向反力就是 P ，弯矩就是 P 乘以悬臂的长度。

外伸梁稍微复杂点，但基本原理还是一样的，就是要根据具体的荷载情况和梁的支撑条件来分析计算。

在实际工程中，计算梁的支座反力可重要了。

要是算错了，那梁可能就承受不住压力，说不定哪天就出问题了。

记得有一次，一个新手工程师在计算的时候粗心大意，把支座反力算错了，结果施工的时候梁出现了裂缝，这可把大家吓得不轻，赶紧重新核算和加固，才避免了更严重的后果。

总之，梁的支座反力计算公式虽然看起来有点复杂，但只要咱们掌握了基本原理，多做几道题，多在实际中观察和思考，就一定能算得又准又快。

可别像那个新手工程师一样，犯了不该犯的错误哟！这样咱们才能保证建筑和结构的安全可靠，让每一根梁都能稳稳地发挥作用。

工字钢受力计算

4、荷载：标准值Pk=Pg+ql
设计值Pd=Pg×γG+Pq×γQ
γG=1.2、γQ=1.4
二、选择受荷截面
1、截面类型： 4根工字钢：I40a
2、截面特性：
Ix
21720 cm4
Wx
1090 cm3
ly660 cm3翼缘 Nhomakorabea度tf16 mm
腹板厚度tw
10.5 mm
三、相关参数
1、材质：Q235
2、x轴塑性发展系数 γx
I40a工字钢梁受力计算
一、梁的静力计算概况
1、单跨梁形式：
简支梁
2、荷载受力形式：简支梁中间受集中载荷
取跨中最不利集中荷载（Pg），单边为1/2
I50c及桥面系自重:
4 根I40a型钢重
270.39 kg/m
12 根横向连接￠28钢筋
46.37 kg/m
合计（Pq）
3、计算模型基本参数：净跨 L
计算：
复核：
日期：
τA =τB
4、最大挠度fmax =8Pk×l3(384 E×I )
5、相对挠度 v = fmax / L
弯曲正应力σmax=188.04 N/mm2 <抗弯设计值
支座最大剪应力τmax=12.46 N/mm2 <抗剪设计值
跨中挠度相对值 v=1/466 <挠度控制值
计算结果 50 t重车 250 KN 15 m长
2.70 KN/m 0.46 KN/m 3.17 KN/m
10 m 281.68 KN 344.35 KN
备注宽0.8m
1.05
43.04 KN 215.22 KN.m
188.04 N/mm2 12.46 N/mm2

支座反力计算公式详解

支座反力计算公式详解以支座反力计算公式详解为标题的文章如下：支座反力是工程力学中一个重要的概念，用于描述支座对物体的支撑力。

在工程设计和结构分析中，准确计算支座反力是确保结构安全和稳定的关键步骤。

本文将详细解释支座反力的计算公式及其应用。

支座反力的计算公式主要包括平衡方程和力矩方程。

平衡方程是基本的力学原理，它表明一个物体处于静力平衡状态时，所有作用在物体上的力的合力和合力矩都为零。

在支座反力计算中，我们通常将物体的平衡方程分为水平方向和垂直方向两个方程。

对于水平方向的平衡方程，我们可以使用以下公式进行计算：∑Fx = 0这个公式表示水平方向上所有作用在物体上的力的合力为零。

我们需要将物体上的所有水平力相加，包括外力和支座反力。

一般来说，水平方向上的外力主要包括水平方向的施加力和摩擦力。

通过平衡方程，我们可以计算出支座反力在水平方向上的分量。

对于垂直方向的平衡方程，我们可以使用以下公式进行计算：∑Fy = 0这个公式表示垂直方向上所有作用在物体上的力的合力为零。

和水平方向类似，我们需要将物体上的所有垂直力相加，包括外力和支座反力。

垂直方向上的外力主要包括物体的重力和其他施加力。

通过平衡方程，我们可以计算出支座反力在垂直方向上的分量。

除了平衡方程，力矩方程也是计算支座反力的重要工具。

力矩是一个力绕某一点旋转的趋势，可以用来描述物体受力情况。

在支座反力计算中，我们通常选择一个合适的点作为参考点，计算物体受力的力矩。

根据力矩方程，我们可以计算出支座反力在参考点处的力矩和力的大小。

支座反力计算公式主要包括平衡方程和力矩方程。

通过这些公式，我们可以根据物体受力情况，准确计算出支座反力的大小和方向。

这对于工程设计和结构分析非常重要，可以确保结构的安全和稳定。

在实际应用中，支座反力的计算需要考虑多种因素，例如物体的形状、力的大小和方向、支座的类型等。

在进行计算时，我们需要仔细分析和理解物体的受力情况，并根据具体情况选择合适的计算方法和公式。

支座反力估算

支座反力估算支座反力估算是结构力学中常见的计算问题，用于确定支座在结构受力时所产生的反力大小和方向。

在工程设计和建筑施工中，准确估算支座反力对于保证结构的稳定性和安全性至关重要。

本文将介绍支座反力估算的基本原理和常见方法。

首先，我们需要了解支座反力的概念。

在结构受力时，支座承受结构的荷载，并通过产生反力来保持结构的平衡。

支座反力一般包括水平方向的水平力和竖直方向的垂直力。

水平力是由结构的水平受力引起的，而垂直力是由结构的重力和其他垂直受力引起的。

支座反力估算的基本原理是利用结构的平衡条件和受力平衡方程。

根据牛顿第一定律，结构处于静止或匀速运动时，受力平衡条件必须满足。

因此，我们可以通过编写受力平衡方程组来求解支座反力。

在实际计算中，支座反力估算方法有很多种，下面介绍几种常见的方法：1. 图解法：利用结构荷载和几何形状的图示进行推导和计算。

这种方法适用于简单的结构和荷载情况，可以直观地理解和计算支座反力。

2. 切割法：将结构切割成若干部分，分别计算每个部分的受力情况，然后将各部分受力合成得到支座反力。

这种方法适用于复杂结构和荷载情况，可以通过逐步切割和计算来简化问题。

3. 变位法：通过变换结构的位移或变形情况，利用结构刚度和变形关系求解支座反力。

这种方法适用于需要考虑结构变形和位移影响的情况，可以更准确地估算支座反力。

4. 力矩法：利用结构的受力平衡条件和力矩平衡条件求解支座反力。

这种方法适用于需要考虑结构力矩平衡的情况，可以通过编写受力平衡方程组和力矩平衡方程组来求解支座反力。

在实际应用中，根据具体情况选择合适的支座反力估算方法非常重要。

不同的方法适用于不同的结构和荷载情况，需要综合考虑结构形式、荷载类型、计算精度等因素。

此外，支座反力估算还需要考虑结构的约束条件和边界条件。

在实际工程中，支座通常有不同类型的约束，如铰接支座、固定支座等。

这些约束条件会对支座反力产生影响，需要在计算中进行合理处理。

支座反力计算案例

支座反力计算案例
就想象有这么一个跷跷板，这跷跷板就是咱们的梁，两边的支撑点就是支座。

假设这个跷跷板长5米，中间有个重100千克（为了好计算，咱就先不换算成力的单位牛啦，就假装1千克对应1个单位的力）的小胖子坐在离一端2米的地方。

那咱们来求两端支座的反力。

首先呢，咱得知道整个系统是平衡的，也就是所有的力和力矩得加起来等于零。

对于这个跷跷板，小胖子的重量就是一个向下的力，咱们叫它F。

那F = 100（单位）。

从左边支座到小胖子的距离是2米，从右边支座到小胖子的距离就是5 2 = 3米。

咱们设左边支座的反力为R1，右边支座的反力为R2。

根据力矩平衡，以左边支座为中心的话，小胖子产生的力矩就是F乘以2米，这个力矩得和右边支座R2产生的力矩平衡。

那就是F×2 = R2×5。

把F = 100代进去，100×2 = R2×5，那R2 = 100×2÷5 = 40（单位）。

然后根据垂直方向力的平衡，所有向上的力得等于所有向下的力。

那就是R1+R2 = F。

把F = 100，R2 = 40代进去，R1 = 100 40 = 60（单位）。

所以呢，左边支座的反力是60单位，右边支座的反力是40单位，就像跷跷板两边得使多大劲才能把小胖子稳稳地撑住一样。

咋样，是不是还挺好玩的？。

工字钢的所有计算公式

工字钢的所有计算公式截面几何参数如下:截面高度H =100mm截面宽度 B =100mm腹板厚度Tw =6mm翼缘厚度Tf =8mm交接圆弧半径Rw =13mmRA=RB=P/2Mc=Mmax=Pl/4fc=fmax=Pl^3/48EIθA=θB=Pl^2/16EI符号意义及单位P ——集中载荷，N；q ——均布载荷，N；R ——支座反力，作用方向向上者为正，N；M ——弯矩，使截面上部受压，下部受拉者为正，Nm；Q ——剪力，对邻近截面所产生的力矩沿顺时针方向者为正，N；f ——挠度，向下变位者为正，mm；θ ——转角，顺时针方向旋转者为正，°；E ——弹性模量，Gpa；I ——截面的轴惯性矩，m^4；ξ＝x/l，δ=x'/l，α＝a/l，β=b/l，γ=c/l从两方面考虑：第一，从梁的剪切应力考虑第二，从弯曲正应力考虑。

从型钢表中可以查到它的最大可用剪切强度TTmax=Q/Ib[BH^2/8-<(B-b)h^2>/8]式中: Tmax为最大剪切强度。

把可用剪切强度T代进去，可算出梁的最大承受载荷。

Q为均布载荷I为工字钢的截面惯矩可在型钢表中查得(cm^4).B为工字钢截面的最大宽度。

b为工字钢截面的最小宽度h为工字钢最小宽度截面的高度。

H为工字钢最大宽度截面的高度正应力的计算：Ysigma=M/WM=最大弯矩=载荷乘距离W=抗弯模量。

设Ysigma=允许的最大应力，可得出载荷的最大值。

工字钢单位重量表热轧普通工字钢每米重量表型号尺寸（毫米）截面面积（厘米2）理论重量（公斤/米）h b d t r110 100 68 4.5 7.6 3.3 14.3 11.212.6 126 74 5 8.4 3.5 18.1 14.214 140 80 5.5 9.1 3.8 21.5 16.916 160 88 6 9.9 4 26.1 20.518 180 94 6.5 10.7 4.3 30.6 24.120a 200 100 7 11.4 4.5 35.5 27.920b 200 102 9 11.4 4.5 39.5 31.122a 220 110 7.5 12.3 4.8 42 3322b 220 112 9.5 12.3 4.8 46.4 36.4 25a 250 116 8 13 5 48.5 38.125b 250 118 10 13 5 53.5 4228a 280 122 8.5 13.7 5.3 55.45 43.4 28b 280 124 10.5 13.7 5.3 61.05 47.9 32a 320 130 9.5 15 5.8 67.05 52.732b 320 132 11.5 15 5.8 73.45 57.7 32c 320 134 13.5 15 5.8 79.95 62.8 36a 360 136 10 15.8 6 76.3 59.936b 360 138 12 15.8 6 83.5 65.636c 360 140 14 15.8 6 90.7 71.240a 400 142 10.5 16.5 6.3 86.1 67.6 40b 400 144 12.5 16.5 6.3 94.1 73.8 40c 400 146 14.5 16.5 6.3 102 80.1 45a 450 150 11.5 18 6.8 102 80.445b 450 152 13.5 18 6.8 111 87.445c 450 154 15.5 18 6.8 120 94.550a 500 158 12 20 7 119 93.650b 500 160 14 20 7 129 10150c 500 162 16 20 7 139 10956a 560 166 12.5 21 7.3 135.25 106.2 56b 560 168 14.5 21 7.3 146.45 115 56c 560 170 16.5 21 7.3 157.85 123.9 63a 630 176 13 22 7.5 154.9 121.6 63b 630 178 15 22 7.5 167.5 131.5 63c 630 180 17 22 7.5 180.1 141。

工字梁计算

2 63 3 原点(0,0) 140 15.8
抗弯模量Wt 上下左 820721.101 820721.101
右
mm3
刚度为1/2000时的理论挠度矩形对自身形心的惯性矩序号对x轴对y轴 1 46016.9733 3612933.33 2 28453833.3 66313.3333 3 46016.9733 3612933.33 x 360 14 290 形心惯性矩 I 160.8 131971953 y 70 mm 7292180 mm4
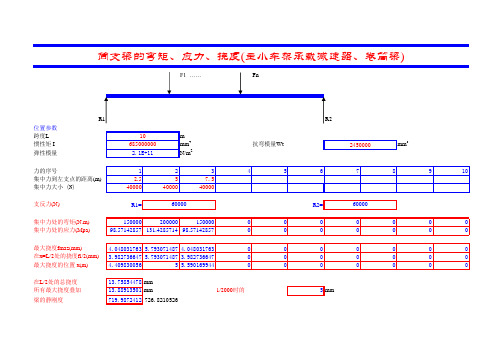
简支梁的弯矩、应力、挠度(主小车架承载减速器、卷筒梁)
F1 …… Fn
R1 位置参数跨度L 惯性矩 I 弹性模量力的序号集中力到左支点的距离(m) 集中力大小 (N) 支反力(N) 集中力处的弯矩(N.m) 集中力处的应力(Mpa) 最大挠度fmaz(mm) 在x=L/2处的挠度fl/2(mm) 最大挠度的位置 x(m) 在L/2处的总挠度所有最大挠度叠加梁的静刚度 10 685000000 2.1E+11 1 2.5 40000 R1= 2 5 40000 60000 0 0 0 0 0 0 0 0 0 0 m 4 mm 2 N/m 3 7.5 40000 4
fnr1r2位置参数跨度lm惯性矩imm4mm3弹性模量nm2力的序号12345678910集中力到左支点的距离m25575集中力大小n400004000040000支反力nr1r2集中力处的弯矩nm1500002000001500000000000集中力处的应力mpa9857142857131428571498571428570000000最大挠度fmazmm4048031763579307148740480317630000000在xl2处的挠度fl2mm3982736647579307148739827366470000000最大挠度的位置xm4409830056555901699440000000在l2处的总挠度1375854478mm所有最大挠度叠加1388913501mm刚度为12000时的理论挠度5mm梁的静刚度7199872412726821052660000抗弯模量wt2450000简支梁的弯矩应力挠度主小车架承载减速器卷筒梁21e116850000001060000单个矩形对自身形心的惯性矩1158序号对x轴对y轴146016973336129333322845383336631333333460169733361293333xy14形心160870mm惯性矩i1319719537292180mm42抗弯模量wt上下左右mm38207211018207211013158原点003602906363140140

简述计算支座反力的步骤

简述计算支座反力的步骤
小伙伴们！今天咱们来讲讲计算支座反力的步骤呀。

首先呢，你得把整个结构的受力图给画出来。

这可是基础中的基础哦！千万不能马虎，我有时候就因为粗心大意，画错了一点点，结果后面算出来的全错啦。

这个受力图啊，要把所有作用在结构上的力都标清楚，像重力啊、外力啥的。

这一步看起来简单，但建议不要跳过，要是跳过了，后续的计算就像在黑暗里摸瞎一样，很容易出错的呢！
然后呢，根据结构的类型来确定采用哪种平衡方程。

是平面汇交力系呢，还是平面一般力系？这可大有讲究哦。

如果是平面汇交力系，那就用两个力的投影方程就行啦；要是平面一般力系呢，就得用三个平衡方程。

这一步我通常会多花点时间，仔细琢磨琢磨结构到底属于哪一类，确认无误是关键！你可别小瞧这一步很多人就在这儿栽跟头呢，你是不是也觉得这里有点绕呢？
接下来开始列平衡方程咯。

把那些力按照坐标轴方向分解，然后代入平衡方程里面去求解。

这时候要特别小心符号哦！正方向和负方向可不能搞混啦。

有时候一个小符号搞错了，答案就差之千里呢。

这一点真的很重要，我都会再检查一次，真的！
最后呢，解出方程得到支座反力的值啦。

解完之后，我建议你再把求得的值代回到原方程里面去验证一下。

这就像做完数学题检查答案一样嘛。

万一算错了，还能及时发现改正呢。

支座反力计算

支座反力计算下载温馨提示：该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help yousolve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts,other materials and so on, want to know different data formats and writing methods, please pay attention!支座反力计算在工程结构设计中起着至关重要的作用。

均布荷载支座反力计算公式

均布荷载支座反力计算公式在工程结构设计中，均布荷载是一种常见的力，通常用来描述等距离范围内的力分布。

在计算均布荷载的支座反力时，可以使用以下公式：1.荷载的大小：均布荷载的大小通常用单位长度的力（如N/m）来表示。

如果均布荷载的总大小为P（N），而支座所在的距离为L（m），则单位长度的均布荷载为p=P/L。

2.支座的反力计算：支座的反力可分为水平方向和垂直方向的反力。

而支座反力的计算取决于结构的类型和约束条件。

-2.1.单向梁/板：如果是单向梁或板，只考虑垂直方向的支座反力，可以使用以下公式计算：R=p*L其中R是支座的反力（N），p是单位长度的均布荷载（N/m），L是支座所在的距离（m）。

-2.2.双向梁/板：如果是双向梁或板，需要考虑水平方向和垂直方向两个方向的支座反力。

在这种情况下，可以使用以下公式计算：Rx=p*LxRy=p*Ly其中Rx和Ry分别是水平方向和垂直方向的支座反力（N），p是单位长度的均布荷载（N/m），Lx和Ly分别是支座在水平方向和垂直方向上的距离（m）。

3.例子：为了更好地理解均布荷载的支座反力计算公式，以下将通过一个例子进行说明。

假设有一根长度为10m的双向梁，均布荷载的大小为1000N/m。

支座位于距离左端2m、底端1m的位置上。

我们需要计算出这个双向梁在支座处的水平方向和垂直方向的反力。

首先计算水平方向的反力：Rx=p*Lx=1000*2=2000N然后计算垂直方向的反力：Ry=p*Ly=1000*1=1000N因此，在这个例子中，双向梁在支座处的水平方向的反力为2000N，垂直方向的反力为1000N。

总结：均布荷载的支座反力计算公式可以根据结构的类型和约束条件来确定。

对于单向梁/板，只需考虑垂直方向的反力；而对于双向梁/板，需要同时计算水平方向和垂直方向的反力。

通过这些公式，我们可以计算出支座处的反力，进而进行结构的受力分析和设计。

支座反力估算

支座反力估算
支座反力的估算需要考虑多种因素，包括结构的自重、风荷载、雪荷载、地震荷载等，以及结构的形状、尺寸、支座类型等。

具体估算步骤如下：
1. 确定所有作用在结构上的荷载，包括自重和外部作用力。

2. 确定这些荷载在结构上产生的效应，如应力、应变和位移等。

3. 使用结构分析或经验公式来计算支座反力。

这通常需要应用结构力学或材料力学知识。

需要注意的是，支座反力的估算可能需要专业的结构工程师或工程师来进行，以确保结果的准确性和安全性。

在实际应用中，支座反力的计算还需要考虑多种因素，例如物体的形状、力的大小和方向、支座的类型等。

在进行计算时，需要仔细分析和理解物体的受力情况，并根据具体情况选择合适的计算方法和公式。

三号楼支模工字钢支撑梁设计计算书_20151119_135027311

三号楼工字钢支撑梁设计计算书计算依据：1、《钢结构设计规范》GB50017-2003计算说明：按照最不利情况考虑，两根工字钢之间上方有一次梁，按截面300*500计算，板厚按照140mm计算，工字钢按照间距1000mm设置。

一、基本参数承载能力极限状态：P=γG×Pgk+ γQ×Pqk=1.2×18.68+1.4×2.5=25.916KN正常使用极限状态：P'= Pgk+ Pqk=18.68+2.5=21.18KN1、抗弯验算Mmax=P×L/4=25.916×3/4=19.437KN·mσ= Mmax /(γxW)=19.437×106/(1.05×141×1000)=131.287N/mm2≤[f]=215 N/mm2 满足要求！2、抗剪验算Vmax=P/2=25.916/2=12.958kNτmax=Vmax[bh02-(b-δ)h2]/(8Izδ)=12.958×1000×[88×1602-(88-6)×140.22]/(8×1130×100 00×6)=15.314N/mm2≤[τ]=125N/mm2满足要求！3、挠度验算νmax=1/48*(P'×L3)/(E×Ix)=1/48×(21180×(3×1000)3)/(206000×1130×10000)=5.118mm≤[ν]＝L/250=3×1000/250=12mm满足要求！4、支座反力RA=P/2=25.916/2=12.958kNRB=P/2=25.916/2=12.958kN三号楼槽钢支撑梁设计计算书计算依据：1、《钢结构设计规范》GB50017-2003计算说明：按照板厚按照140mm计算，工字钢按照间距1000mm，立杆间距1000设置。

支座反力总结

支座反力总结引言在工程力学中，支座反力是指一个结构或构件在支撑点上受到的力的总和。

支座反力是结构分析的重要结果之一，对于工程设计、施工以及安全评估具有重要意义。

本文将总结支座反力的概念、计算方法以及常见应用。

支座反力的定义与分类支座反力是指一个结构在支撑点上受到的力的总和。

根据支撑点的类型和结构的约束条件，支座反力可以分为以下几类：1.钉子支座：在一个固定支座中，结构可以绕任意一个轴旋转，但在该轴向上不能发生横移动。

钉子支座在水平方向上提供反力，但不提供弯矩。

2.滑动支座：滑动支座在水平和垂直方向上都可以提供反力，但不提供弯矩。

滑动支座可以滑动，但不可以转动。

3.旋转支座：旋转支座可以提供反力和弯矩。

它可以绕一个轴旋转，但在该轴向上不能发生横移动。

4.固定支座：固定支座可以提供反力、弯矩和剪力。

它既不能滑动，也不能转动。

支座反力的计算方法支座反力的计算方法根据结构的类型和支座的约束条件而有所不同。

下面将介绍一些常见的计算方法。

钉子支座的反力计算钉子支座只能提供水平方向上的反力，不提供弯矩。

计算方法如下：1.在水平方向上的总受力为零。

即水平方向上的反力之和等于零。

2.根据结构的平衡条件，可以计算出每个支座上的反力。

滑动支座的反力计算滑动支座在水平和垂直方向上都可以提供反力，但不提供弯矩。

计算方法如下：1.在水平和垂直方向上的总受力为零。

即水平和垂直方向上的反力之和等于零。

2.根据结构的平衡条件，可以计算出每个支座上的反力。

旋转支座的反力计算旋转支座可以提供反力和弯矩。

计算方法如下：1.在垂直方向上的总受力为零。

即垂直方向上的反力之和等于零。

2.在水平方向上的总弯矩为零。

即所有支座上的弯矩之和等于零。

3.根据结构的平衡条件和弹性力学原理，可以计算出每个支座上的反力和弯矩。

固定支座的反力计算固定支座可以提供反力、弯矩和剪力。

计算方法如下：1.在垂直方向上的总受力为零。

即垂直方向上的反力之和等于零。

2.在水平方向上的总弯矩为零。

支座反力的计算

支座反力计算简单的静定结构可以通过力的平衡和力矩的平衡来建立两个方程式，每个方程是可以求一个未知量，就是说，简单的静定结构只能求两个未知力；对于超静定结构计算就复杂了，不过还是要用到平衡和力矩的平衡来建立方程，此外根据具体的情况增加其他方程联合求解，就是说，有多少个未知力就需要多少个方程式；例如：一条简支梁长为L，两头AB简支，从左到右在1/3L处有个P向下的集中力，求两端支座反力。

这就是简单的静定结构，解题如下：设两端的支座反力分别为：Ra和Rb根据垂直方向力的平衡条件得：Ra + Rb = P根据垂直方向力矩的平衡条件，以A为原点，得：Rb*L=P*1/3L（顺时针力矩等于逆时针力矩，A的支座反力过原点，力矩为零）联立两个方程组解得：Ra =2/3PRb =1/3P图解在这里是用不上，所有结构力学的书都有计算的方法的，最好就是找来看看，比我们在这里费尽心思的讲解要好得多。

例题：简支梁的支座反力计算杆件长5米，离A端头1.5米有集中荷载为100N，问A,B两支座的反力为多少最佳答案RA=70KN RB=30KN1.1.5支座反力计算在静定结构的受力分析中，通常须预先求出支座反力，再进行内力计算。

求支座反力时，首先应根据支座的性质定出支座反力（包括个数和方位），然后假定支座反力的方向，再由整体或局部的平衡条件确定其数值和实际指向。

以图1-6a所示多跨刚架为例，讨论支座反力计算。

图1-6此刚架有五个支座反力：、、、和。

由整体的三个平衡方程，加上铰D和铰C处弯矩分别为零的平衡条件，即可求出这五个支座反力。

从几何组成的角度看，D以右部分为三铰刚架，是基本部分；D以左部分是支承在地基和三铰刚架上的附属部分。

首先，取附属部分为隔离体(图1-6b)，由平衡方程求、和。

(a)然后，将D铰处的约束反力反向加在基本部分上，取D以右三铰刚架为隔离体(图1-6c)，利用平衡方程求和。

（b）（c）再取C以右半刚架为隔离体(图1-6d)，由铰C处弯矩为零的平衡方程求。

工字型梁支座反力计算

南楼增加工字型梁支座反力计算一、玻璃幕墙板块的自重荷载计算1、玻璃面板自重荷载标准值计算本处采用的是香槟色彩釉10mm单层玻璃幕墙G AK: 玻璃板块自重(不包括框):玻璃的重力密度为: 25.6kN/m3t:玻璃厚度为：10mmG AK=10×10-3×25.6=0.256 KN/m2G GK：考虑龙骨和各种零部件后的幕墙面板自重面荷载标准值G GK=0.4 KN/m22、玻璃面板自重荷载设计值计算r G：自重作用效应分项系数，取r G=1.2G G：考虑龙骨和各种零部件后的幕墙面板自重面荷载设计值G G=r G·G GK=1.2×0.4=0.48 KN/m23、玻璃幕墙板块自重荷载标准值计算G K：玻璃幕墙板块的重量标准值G K=G GK·B·H=0.4×9×3.3=11.88 KN4、玻璃幕墙板块自重荷载设计值计算G：玻璃幕墙板块的重量设计值G=r G·G K=1.2×11.88=14.256 KN二、玻璃幕墙板块承受的水平风荷载计算计算高度：z=37.8m地面粗糙类型：C 外表面负压区：墙面基本风压W0=0.3N/㎡计算分格尺寸 B L=9000mm H L=3300mm=1.861阵风系数：βg z风压高度变化系数μ=0.974z分格从属面积A f=9×3.3=29.7㎡考虑内压μ=1.0s1、水平风压标准值W=βg zμsμz W0=0.544 kP ak0W k取W k0与1kN/㎡的较大值，故W k=1 kN/㎡2、水平风压设计值W w=1.4W k=1.4 kN/㎡三、玻璃幕墙板块承受的水平地震荷载计算1、玻璃面板承受的水平地震荷载标准值计算αmax：水平地震影响系数最大值，取αmax=0.08βE：动力放大系数，取βE=5.0q EK：作用在幕墙上的地震荷载标准值计算q EK=αmax·βE·G GK=0.08×5.0×0.4=0.16 KN/m22、幕墙玻璃面板承受的水平地震荷载设计值计算r E：地震荷载作用效应分项系数，取r E=1.3q E：作用在幕墙上的地震荷载设计值q E=r E·q EK=1.3×0.16=0.208 KN/m2四、荷载组合1、风荷载和水平地震作用组合标准值计算ψW：风荷载作用效应分项系数，取ψW=1.0ψE：地震荷载作用效应分项系数，取ψE=0.5q K=ψW·W K+ψE·q EK=1.0×1.0+0.5×0.16=1.08 KN/m22、风荷载和水平地震作用组合设计值计算q=ψW·W W+ψE·q E=1.0×1.4+0.5×0.208=1.504 KN/m2五、荷载计算将工字型钢梁简化为两端交接的简支梁横梁上部荷载高度为 H t1=1650mm横梁下部荷载高度为 H t2=3300mm横梁跨度：B t=9000mm1、工字型钢梁承受水平荷载（上部与下部均简化为矩形均布荷载）标准值：q tk1= q K·H t1=1.08×1.65=1.782 KN/mq tk2= q K·H t2=1.08×3.325=3.591 KN/m设计值：q t1= q·H t1=1.504×1.65=2.482 KN/mq t2= q·H t2=1.504×3.300=5.001 KN/m（4.9632）2、工字型钢梁承受自重荷载横梁密度为78.5 KN/m³面积：0.25×0.02×2+0.02×（0.7-0.02×2）=0.0232㎡自重标准值：0.0232㎡×78.5KN/m³=1.8212KN/m自重设计值：1.2×1.8212=2.185KN/m3、水平荷载产生的最大弯矩M t-y=（2.482+5.001）×92/8=75.765KN·m4、竖直荷载产生的最大弯矩M t-x=（2.185+14.256/9）×92/8=38.161 KN·m5、水平荷载产生的剪力（水平风荷载+水平地震荷载）V1=（2.482+（4.9632）5.001）×9/2=33.67KN（33.503）6、竖直荷载产生的剪力（工字梁自重+玻璃幕墙块自重）V2=（2.185×9+14.256）/2=16.96KN。